引言
关于试样尺度、缺口和加载方式对材料疲劳性能的影响已有大量的研究工作$^{[13- 16]}$.如Neuber[17]和Peterson[18]采用临界距离方法研究了缺口试样的疲劳强度,并给出疲劳缺口系数$K_{\rm f}$、应力集中系数$K_{\rm t}$和缺口根部半径$r$之间的关系.Kuguel[19]提出高应力体积方法来预测缺口试样的疲劳强度,即$K_{\rm f}/K_{\rm t}=(V_{\rm n}/V_{\rm s})^{a}$, 其中$V_{\rm n}$和$V_{\rm s}$分别是缺口试样和光滑试样的高应力体积(即控制体积),$a$是材料常数.Murakami等[20]通过控制体积中最大夹杂物尺寸来解释高强钢在轴向加载下的疲劳强度低于旋转弯曲加载下的疲劳强度.Lanning等[21]采用最弱链模型对含缺口Ti-6Al-4V试样的高周疲劳强度进行预测.Naik等[22]借助临界平面损伤参数和缺口处的应力梯度发展了一种临界平面梯度方法预测Ti-6Al-4V高周疲劳寿命.Berto等[23]采用应变能密度方法研究了Ti-6Al-4V合金缺口试样在多轴加载下的疲劳强度.Härkegård 和Halleraker[24]基于26种不同几何形状光滑试样和缺口试样的疲劳极限数据对Neuber和Peterson方法、峰值应力法、临界距离法、应力梯度法、高应力体积法和弱链方法进行了对比.结果表明, 应力梯度法、弱链方法和高应力体积法给出最好的预测结果.最近, Sun等[25]将控制体积概念与概率统计理论结合起来,发展了一种概率控制体积方法来预测试样几何形状和加载方式对疲劳强度的影响,并较好地用于高强钢、钛合金以及全尺寸车轴的疲劳强度预测.该方法可看作是高应力体积或控制体积方法的发展.
本文以EA4T车轴钢为材料,研究了概率控制体积方法在关联试样尺度、缺口和加载方式对疲劳强度影响中的应用.首先采用旋转弯曲加载和轴向加载方式对不同几何形状EA4T车轴钢试样进行了疲劳实验.然后,采用概率控制体积方法对试样尺度、缺口和加载方式对疲劳强度的影响进行关联,并与临界距离和应变能密度方法进行了比较. 最后,提出一种基于控制体积的结构件疲劳强度预测方法,并用于具有不连续高应力区域试样的疲劳强度预测.
1 实验材料与方法
1.1 实验材料
图1
图1
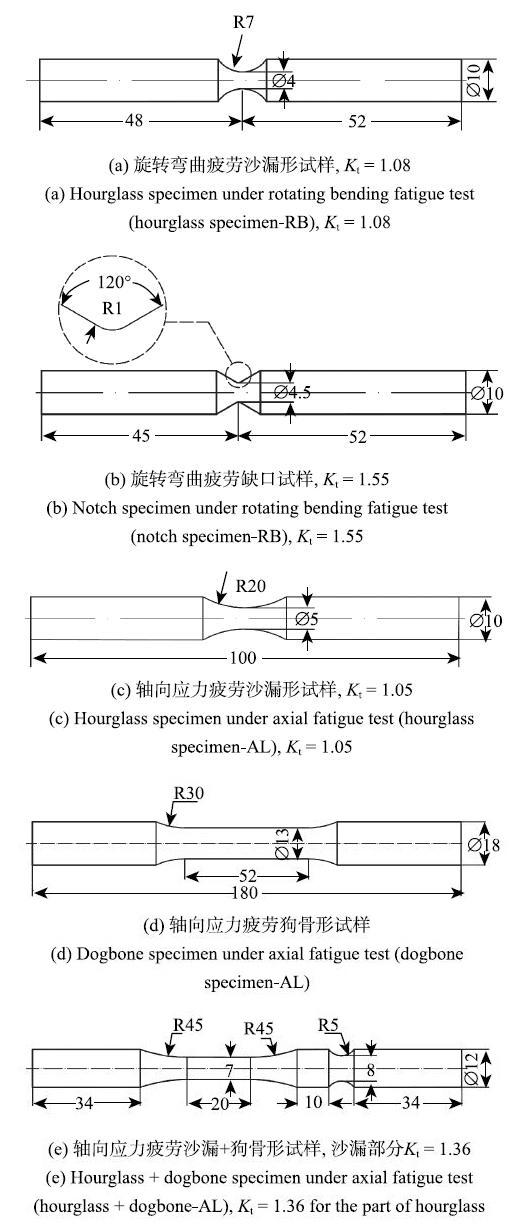
疲劳试样几何形状和尺寸(单位: mm)
Fig. 1
Shape and dimensions (in mm) of specimens for fatigue test
1.2 实验方法
拉伸实验采用液压伺服试验机进行, 应变速率为5$\times $10$^{ - 4}$s$^{ - 1}$. 疲劳实验采用旋转弯曲疲劳试验机(频率$f$= $50\sim $,80 Hz)和液压伺服试验机(频率$f= 5\sim35$Hz) 2种方式进行,应力比$R$均为$-1$. 实验前, 所有试样的实验段均进行抛光处理.疲劳试样断口采用扫描电子显微镜进行观察.
2 实验结果
2.1 S-N数据
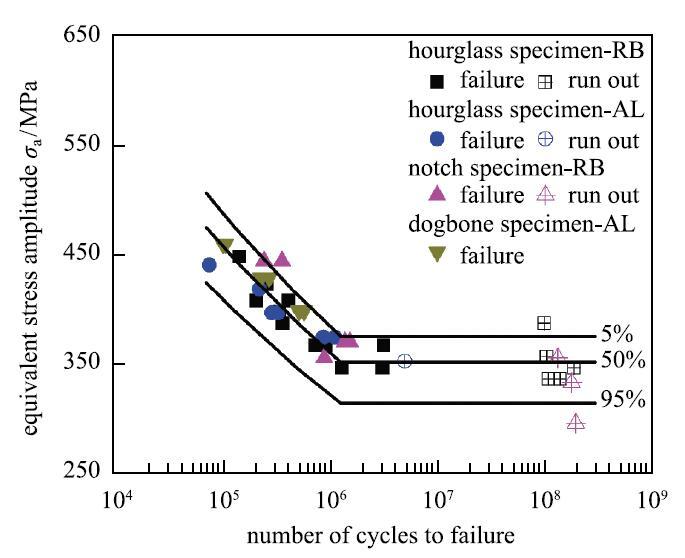
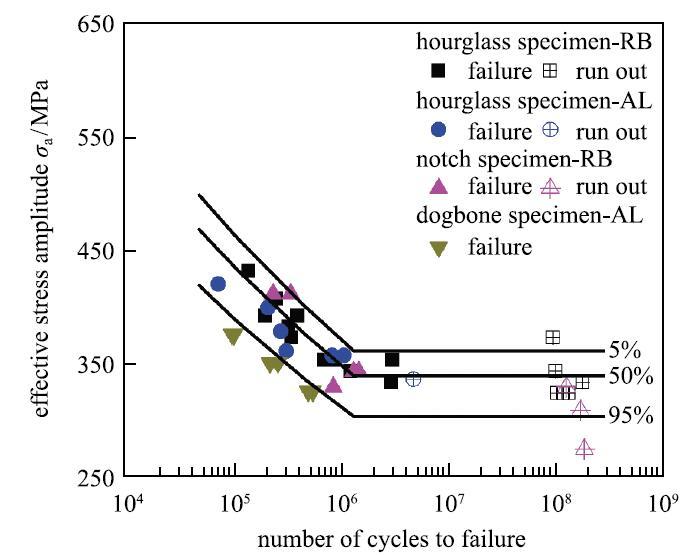
图2
2.2 疲劳断口
图3
图3
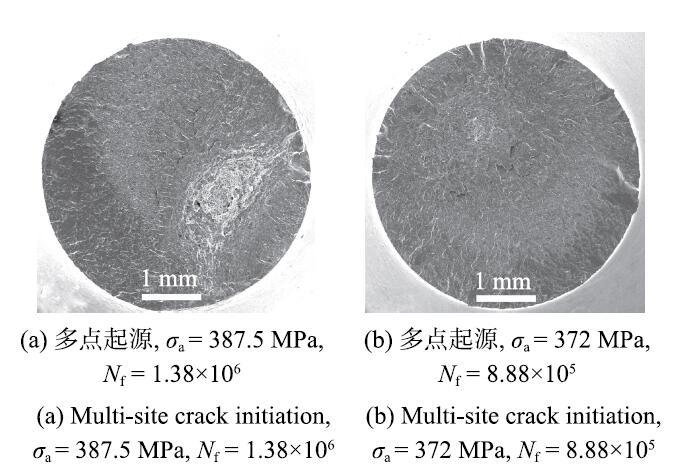
轴向应力疲劳沙漏形试样疲劳断口扫描电镜照片,箭头指向为裂纹萌生区域
Fig. 3
Scanning electron microscope pictures of hourglass specimens under axial fatigue test, in which the arrows point to denote the crack initiation regions
图4
图4
轴向应力疲劳狗骨形试样疲劳断口扫描电镜照片,箭头指向为裂纹萌生区域
Fig. 4
Scanning electron microscope pictures of dogbone specimens under axial fatigue test, in which the arrows point to denote the crack initiation regions
图5
图5
旋转弯曲疲劳缺口试样疲劳断口扫描电镜照片
Fig. 5
Scanning electron microscope pictures of notch specimen under rotating bending fatigue test
3 概率控制体积方法
该方法假定试样A和B通过高应力区域(即控制体积)可以看作相同加工工艺和热处理下多个具有相对小控制体积参考试样疲劳强度的最小值,并且参考试样的疲劳强度服从 韦布尔分布, 那么相同存活率下,试样A的疲劳强度$\sigma $$_{\rm A}$与试样B的疲劳强度$\sigma $$_{\rm B}$满足如下关系[25]
其中, $V_{\rm A}$和$V_{\rm B}$分别是试样A和B的控制体积,基于材料的疲劳破坏机理确定,通常可取为大于等于90%最大主应力区域; $k>0$和$\gamma \ge 0$分别是疲劳强度 韦布尔分布的形状参数和位置参数.
对于表面起源的疲劳破坏, 式(1)可写为
其中, $S_{\rm A}$和$S_{\rm B}$分别表示试样A和B的高应力区域表面积(即控制表面积).
特别地, 如果疲劳强度服从双参数 韦布尔分布,试样A和B的疲劳强度满足如下关系
或
通过式(1)$\sim$式(4),可以采用某一种试样的疲劳强度数据对其他几何形状和加载方式下试样的疲劳强度进行预测,也可以将具有不同控制体积试样的疲劳强度转换成某一给定控制体积对应的疲劳强度,这里称为等效疲劳强度.
4 预测结果与实验结果比较
4.1 P-S-N曲线预测结果与实验结果比较
表2 某些给定疲劳寿命下,疲劳强度韦布尔分布参数以及在5%, 50%和95%存活率下预测的疲劳强度
Table 2
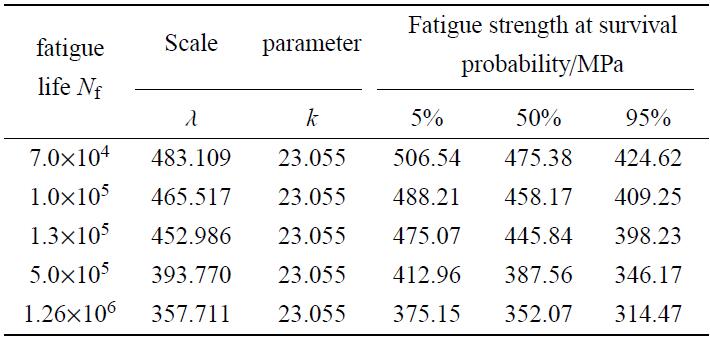 |
图6
图6
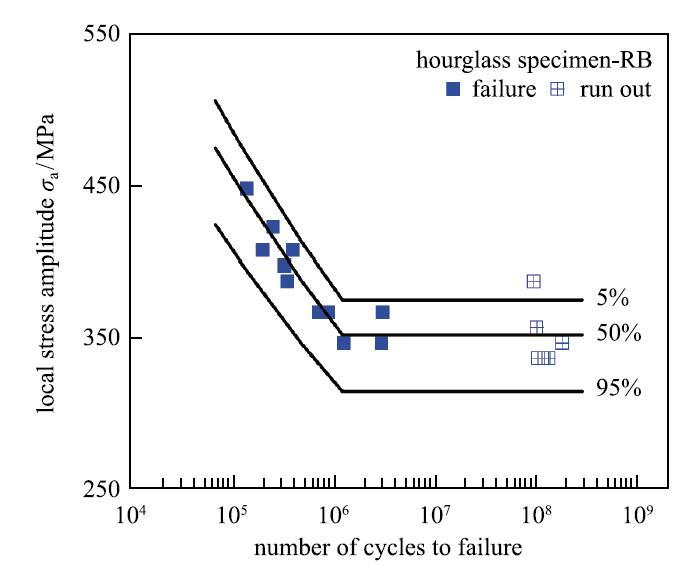
旋转弯曲疲劳沙漏形试样实验数据预测的P-S-N曲线与实验结果的比较
Fig. 6
Comparison of predicted P-S-N curves with experimental data for hourglass specimen-RB
4.2 疲劳强度预测结果与实验结果比较
4.2.1 概率控制体积方法
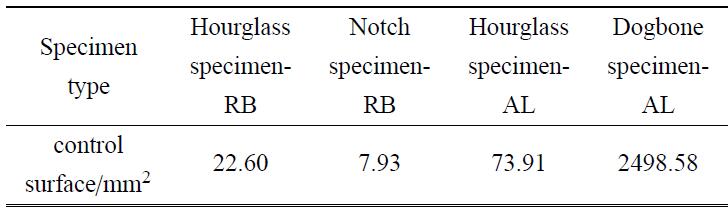
考虑到所有试样均起源于试样表面,采用控制表面积(大于等于90%最大主应力区域)来关联试样尺度、缺口和加载方式对EA4T车轴材料疲劳强度的影响.不同加载方式下试样的控制表面积均通过有限元计算得到, 具体如表3所示.
图7
图7
等效疲劳强度与疲劳寿命关系,线条为采用旋转弯曲疲劳沙漏形试样实验数据预测的P-S-N曲线
Fig. 7
Relation of equivalent stress amplitude and fatigue life, the lines denote the predicted P-S-N curves by the experimental data of hourglass specimen-RB
4.2.2 临界距离方法
其中, $\Delta \sigma _{{\rm eff}} $是等效应力范围, $\Delta \sigma_{1} $是最大主应力范围, $\Delta $$\sigma $$_{0}$是光滑试样疲劳极限范围, $r$是距离缺口根部的长度,$L$是材料的特征长度, 由下式计算
其中, $\Delta K_{\rm th}$是裂纹传播门槛值.
图8为采用临界距离方法给出的等效疲劳强度与疲劳寿命之间的关系,线条为运用文献[25]中的方法采用旋转弯曲疲劳沙漏形试样的等效疲劳强度与疲劳寿命数据预测的P-S-N曲线.本文中, 裂纹传播门槛值取[28] $\Delta K_{\rm th}=13$MPa$\cdot$m$^{1 / 2}$,疲劳极限取旋转弯曲疲劳沙漏形试样预测的50%存活率下的疲劳极限,即$\Delta $$\sigma $$_{0}=2$$\sigma$$_{a}$=2$\times $352 = 704 MPa. 图8表明,采用临界距离方法给出的不同几何形状试样在旋转弯曲加载或轴向加载下的等效疲劳强度与疲劳寿命数据点并没有很好地分布在同一个分散带内.若以旋转弯曲疲劳沙漏形试样的等效疲劳强度与疲劳寿命数据作为参考,临界距离方法给出的轴向应力疲劳狗骨形试样的等效疲劳强度偏低.
图8
图8
等效疲劳强度与疲劳寿命关系,线条为采用旋转弯曲疲劳沙漏形试样的等效疲劳强度与疲劳寿命数据预测的P-S-N曲线
Fig. 8
RRelation of equivalent stress amplitude and fatigue life, the lines denote the predicted P-S-N curves by the data of equivalent stress amplitude and fatigue life of hourglass specimen-RB
4.2.3应变能密度方法
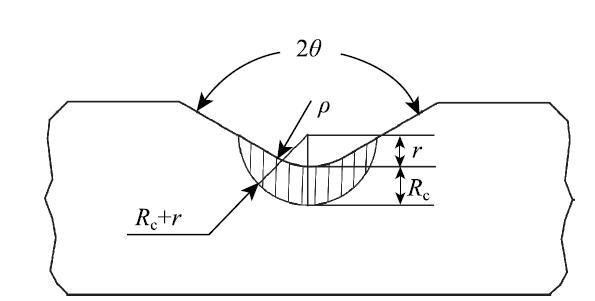
图9
对于(高周)疲劳载荷, 临界半径$R_{\rm c}$可通过下式进行估计[30]
其中, $\nu $是泊松比, $\Delta K_{\rm th}$是裂纹传播门槛值, $\Delta $$\sigma$$_{0}$是光滑试样疲劳极限范围.
图10为采用应变能密度方法给出的平均应变能密度与疲劳寿命之间的关系,线条为运用文献[25]中方法采用旋转弯曲疲劳沙漏形试样的平均应变能密度与疲劳寿命数据预测的P-S-N曲线.这里,旋转弯曲加载下试样的临界体积取图9所示阴影区域(最大主应力与加载力所在平面内)沿圆周方向顺时针和反时针各旋转一个很小的角度(3$^{\circ}$)形成的区域;轴向加载下试样的临界体积取图9所示阴影区域沿圆周方向旋转形成的环形区域,其中狗骨形试样的阴影区域取在实验段的中间位置. 可以看出,应变能密度方法与临界距离方法给出的结果类似.若以旋转弯曲疲劳沙漏形试样的平均应变能密度与疲劳寿命数据作为参考,应变能密度方法给出的轴向应力疲劳狗骨形试样的平均应变能密度偏低.
图10
图10
平均应变能密度与疲劳寿命关系,线条为采用旋转弯曲疲劳沙漏形试样的平均应变能密度与疲劳寿命数据预测的P-S-N曲线
Fig. 10
Relation of averaged strain energy density and fatigue life, the lines denote the predicted P-S-N curves by the data of averaged strain energy density and fatigue life of hourglass specimen-RB
图7、图8和图10表明,概率控制体积方法较临界距离方法和应变能密度方法更好地关联试样尺度、缺口和加载方式对EA4T车轴材料疲劳强度的影响.需要指出的是, 试样尺度往往对疲劳性能具有重要影响. 比如,相同寿命下大尺度狗骨形试样的疲劳强度低于小尺度狗骨形试样[6].这种情况下, 如采用临界距离方法或应变能密度方法, 在相同寿命下,不同尺度试样应具有相同的疲劳强度或应变能密度,即疲劳强度或应变能密度不依赖于试样尺度. 因此,临界距离方法和应变能密度方法通常不能有效地用于试样的尺度效应[11,31],这与图8中临界距离方法和图10中应变能密度方法给出的尺度相对较大的轴向应力疲劳狗骨形试样的等效疲劳强度和平均应变能密度偏低是一致的.
5 基于控制体积的结构件疲劳强度预测方法
概率控制体积方法表明, 试样的疲劳强度与其控制体积成反比,控制体积较大的试样具有较低的疲劳强度. 实际结构件形状和受载复杂,可能存在多个高应力区域. 因此,需要对可能发生疲劳破坏的高应力区域的疲劳强度分别进行计算,然后选取这些高应力区域中疲劳强度的最小值作为结构件的疲劳强度. 这里在概率控制体积方法基础上,提出一种基于控制体积的结构件疲劳强度预测方法. 具体步骤如下:
(1)获得某一小试样疲劳实验数据, 确定其疲劳破坏机理以及疲劳强度韦布尔分布参数.
(2)基于概率控制体积方法,对可能发生疲劳破坏的高应力区域进行疲劳强度计算.如存在多个高应力区域, 分别对其进行疲劳强度计算.
(3)对于只有一个高应力区域的结构件,该区域的疲劳强度即为结构件的疲劳强度. 如存在多个高应力区域,选取这些高应力区域中疲劳强度的最小值作为结构件的疲劳强度.
该方法不但可以对给定疲劳寿命下结构件的疲劳强度进行预测,也可以对结构件发生疲劳破坏的区域进行预测.下面以图1(e)中的沙漏+狗骨形试样为例,采用上述方法预测其发生疲劳破坏的区域. 在轴向应力疲劳载荷下, 图1(e)中所示试样有沙漏部分和狗骨部分两个不连续的高应力区域.沙漏部分最大局部应力$\sigma $$_{\rm H}$比狗骨部分最大局部应力$\sigma $$_{\rm D}$稍大,二者比值是1.01. 沙漏部分控制表面积$S_{\rm H}=$$64.77$mm$^{2}$, 狗骨部分控制表面积$S_{\rm D}\!=\!629.83$mm$^{2}$. 这里取第4.1节中采用旋转弯曲疲劳沙漏形试样实验数据得到的疲劳强度韦布尔分布形状参数$k\!=\!23.055$. 采用概率控制体积方法,即将沙漏部分和狗骨部分的控制表面积代入式(4), 得
图11
图11
轴向应力疲劳沙漏+狗骨形试样疲劳破坏照片
Fig. 11
Pictures of failed hourglass + dogbone specimens under axial fatigue test
6 结 论
关联试样尺度、缺口和加载方式对疲劳寿命或疲劳强度影响的方法是材料疲劳性能到结构件疲劳性能之间的"桥梁".本文在不同几何形状EA4T车轴钢试样的旋转弯曲疲劳或轴向应力疲劳实验基础上,研究了概率控制体积方法在关联试样尺度、缺口和加载方式对疲劳强度影响方面的效果.结果表明,基于概率统计理论和控制体积概念建立起来的概率控制体积方法能够有效地反映试样尺度、缺口和加载方式对EA4T车轴钢疲劳强度的影响.与临界距离方法和应变能密度方法相比,概率控制体积方法更好地符合实验数据. 在概率控制体积方法基础上,提出一种基于控制体积的结构件疲劳强度预测方法,并用于具有不连续高应力区域EA4T车轴钢试样的疲劳强度预测,预测结果与实验结果吻合. 可见,概率控制体积方法有望在合理解释材料疲劳实验数据差异,以及在结构件的疲劳性能预测方面发挥重要作用. 但需指出,实际结构件受载复杂,概率控制体积方法能否有效应用于复杂载荷状态下试样尺度和缺口对疲劳强度的影响,以及复杂载荷状态下结构件的疲劳强度预测,需要更多的实验结果进行检验.
参考文献
三剪应力统一强度理论研究
Study of three-shear stress unified strength theory
一种横观各向同性强度准则及变换应力空间
One kind of transverse isotropic strength criterion and the transformation stress space
Failure criterion of titanium alloy irregular sheet specimens for vibration-based bending fatigue testing
动载下裂纹应力强度因子计算的改进型扩展有限元法
Accurate computation on dynamic SIFs using improved XFEM
Specimen size effects on gigacycle fatigue properties of high-strength steel under ultrasonic fatigue testing
Fatigue life distribution and size effect in ductile cast iron for wind turbine components
Probabilistic fatigue assessment for railway axles and derivation of a simple format for damage calculations
Fatigue strengths of the 54SiCr6 steel under different cyclic loading conditions
Effect of loading condition on very high cycle fatigue behavior in a high strength steel
Effects of loading frequency and loading type on high-cycle and very-high-cycle fatigue of a high-strength steel
On the use of critical distance theories for the prediction of the high cycle fatigue limit stress in notched Ti--6Al--4V
Notch effect on fatigue strength reduction of bearing steel in the very high cycle regime
Effects of specimen size on fatigue life of metallic materials in high-cycle and very-high-cycle fatigue regimes
A combined critical distance and highly-stressed-volume model to evaluate the statistical size effect of the stress concentrator on low cycle fatigue of TA19 plate
Statistical size effect on multiaxial fatigue strength of notched steel components
A method for evaluating the effects of specimen geometry and loading condition on fatigue life of metallic materials
Theory of Notch Stresses: Principles for Exact Calculation of Strength with Reference to Structural Form and Material. 2nd Ed
Notch sensitivity Sines G, Waisman JL,eds. Metal Fatigue
A relation between theoretical stress concentration factor and fatigue notch factor deduced from the concept of highly stressed volume
Mechanism of fatigue failure in ultralong life regime
HCF notch predictions based on weakest-link failure models
A critical plane gradient approach for the prediction of notched HCF life
Fatigue strength of severely notched specimens made of Ti-6Al-4V under multiaxial loading
Assessment of methods for prediction of notch and size effects at the fatigue limit based on test data by Böhm and Magin
A method for predicting the effects of specimen geometry and loading condition on fatigue strength
Geometrical effects in fatigue: a unifying theoretical model
The theory of critical distances: A review of its applications in fatigue
Effect of specimen geometry on fatigue crack growth rates for the railway axle material EA4T
A review of the volume-based strain energy density approach applied to V-notches and welded structures
High temperature fatigue tests of notched specimens made of titanium Grade 2
HCF strength estimation of notched Ti--6Al--4V specimens considering the critical distance size effect