引言
柱体截面形式的改变会影响边界层分离点的位置以及分离方式,从而影响结构的受力,进而导致结构流致振动响应及尾流脱涡特性发生变化. 因此除了圆柱体外,方柱、三角形柱等其他不同截面类型的结构也逐渐受到了国内外学者的广泛关注.徐枫等[4]采用计算流体动力学方法对$Re=200$工况下不同截面柱体的流致振动进行了数值模拟.研究发现, 不同截面柱体对应不同的振动形式,且它们的动力响应受频率比(柱体固定频率与固定绕流的涡脱频率之比)的影响差异较大.何涛[5]采用分区强耦合算法对$Re=1500$工况下H型桥梁断面进行了数值模拟,发现结构运动主要由扭转振动控制, 且出现了明显的扭转颤振现象.丁林等[6]通过对$Re=3.0\times 10^{4}\sim 1.1\times$10$^{5}$范围内不同截面柱体振动振幅、频率和尾迹旋涡形态进行分析,发现随雷诺数的增加,不同形状的柱体结构流致振动响应均出现了4个不同的分支,并且尾迹旋涡形态会随着振动分支的转变而发生相应变化.Zhao等[7]研究了来流攻角参数对方柱动力响应的影响,并总结出在攻角为零的工况下, 锁定区间的范围达到最小值,结构振动响应相当微弱. 另外,他们还对$Re=200$工况下长宽比和质量比对矩形方柱振动响应的影响进行了研究[8].最近,Sen和Mittal[9-10]就质量比和固有频率对双自由度刚性方柱涡激振动的影响进行了数值研究, 他们观察到质量比越高结构驰振响应越剧烈.一些学者通过实验对不同攻角下方柱的涡激振动进行了研究,通过分析结构的动力响应特性揭示了驰振与涡激振动之间的转变关系[11-12].另外, Jiang 等[13]对$Re \le 400$范围内静止单方柱工况三维响应进行了研究, 发现当$Re=165.7$时,斯特劳哈尔数会急剧下降, 出现A和B两种不同的旋涡脱落 模式.
与单柱系统由于柱体本身的涡脱落而产生振动的情况不同,双柱系统中下游柱体的尾激振动主要受到上游柱体尾流的影响,因此双柱系统下游柱体的动力响应与单柱体结构存在显著的差异.与涡激振动相比, 在自身涡脱落与上游柱体尾流的影响下, 以尾激振动为主导振动机制的系统往往会产生更为剧烈的振动,且影响范围较广, 对结构的破坏更大,吸引了众多学者的广泛关注.一些学者通过对上游静止圆柱--等尺寸下游圆柱的尾激振动问题进行研究,总结了来流攻角[14-15]、雷诺数[16- 17]以及折减速度$U_{\rm r}$[18]等重要因素对下游圆柱动力响应及尾流模态的影响,并揭示了双柱系统在尾激振动的影响下诱发大幅振动的内在机理[18].Assi等[16]对$Re=2000\sim25~000$范围内交错排列双柱系统的尾激振动机理进行了实验研究,他们指出随雷诺数的增加,系统的互扰效应从初始的涡激效应逐渐转变为尾激效应.Nguyen等[17]通过研究发现,下游圆柱的尾激振动响应振幅会随着雷诺数的增加而增大.另外,已有的研究发现上游柱体对下游柱体的振动干扰受间距比$L$/$D$(其中, $L$为两柱体结构中心的距离)的影响较大$^{[19 - 23]}$,且柱体运动与间隙流之间的耦合机制会随着间距比的增加发生较大的改变.不同间距比工况下, 下游柱体在上游结构尾流及其自身涡脱落的影响下,均会出现大振幅区间. 但随着间距比的增加,结构振动响应的作用机理会发生转变. 陈威霖等[23]对$Re=100$时, 小间距比工况下($L/D=1.1\sim$1.5)串列双圆柱涡激振动进行了数值模拟,发现圆柱的涡激振动响应随间距比的变化具有较大的差异. 当$L/D=1.2\sim1.3$时, 大折减速度工况下, 出现了类似于高雷诺数时的尾流驰振现象.Tamimi 等[24]通过实验研究发现:随着间距比($L/D=4,8, 11)$的增大, 双圆柱系统会诱发3种不同的振动机制.然而上游静止圆柱与下游振动方柱系统中下游方柱的振动则主要与其自身的涡脱落有关,主导振动机制为涡激振动. 此外,一些学者已经对上游方柱后部柱体的尾激振动特性进行了研究.Bhatt和Alam[25]对$Re=100,200; L/D=2,6$工况下,静止上游方柱--横向振动下游方柱体的振动响应以及受力特性等进行了分析,并与单方柱工况进行了对比. 发现随折减速度的增加,下游方柱的振动响应会经历初始分支(initial branch)、上端分支(upperbranch)、下端分支(lower branch)、非同步分支(desynchronizationbranch)以及驰振(galloping branch)5个阶段,并且不同工况下每个阶段所对应的范围有所差异.Nitun和Tiwari[26]总结发现:在沿横流向振动的串列双方柱系统中,随间距比($L/D=2\sim 5$)的增大,下游方柱的尾流模态经历了从2S到2P再到2S的转变过程. 当频率比$f_{\rm r}=1$(激振频率与固定绕流的涡脱频率之比), $L/D=2\sim 3$时,下游方柱锁定区间内出现了准周期性振动响应(quasi-periodic response).Tu等[27]对上游静止方柱尺寸的变化对下游圆柱体双自由度尾激振动响应的影响进行了研究,得出随着上游方柱尺寸减小, 下游圆柱振动锁定区间范围扩大,运动轨迹和尾流模态变得更加复杂.
综上所述,本文对上游静止方柱与双自由度下游方柱的尾激振动问题进行了研究,主要分析雷诺数和折减速度这两个关键参数对下游方柱的动力响应特性的影响,并揭示了尾激振动的内在机理.这不仅具有重要的科学意义,还对实际工程应用具有显著的参考价值.
1 控制方程和数值方法
1.1 控制方程
在任意拉格朗日--欧拉方法描述下,不可压缩黏性流体的N-S方程和连续性方程的无量纲表达形式如下
式中, ${{u}}_{i}$为流体速度;${{w}}_{j}$为第$j$个方向上的网格移动速度; ${{p}}$为流体压力;$x_{i}$(二维问题中$i=1, 2$; 三维问题中$i=1, 2, 3$)为笛卡尔坐标;$t$为时间. $Re={{U}}_{\infty }D/v$为雷诺数, 其中$D$为特征长度,$U_{\infty }$为特征速度, $v$为动力黏性系数.
弹性支撑方柱结构运动体系可假设为质量--弹簧--阻尼系统,考虑下游方柱双向运动的结构运动控制方程如下
式中, ${{X}}$和${{Y}}$为$x_{1}$与$x_{2}$方向上的位移; $M_{\rm r}=m/m^{\ast }$为结构折合质量, 其中$m$为单位长度结构质量, $m^{\ast}$为流体质量; $\xi $为结构阻尼比, 本文忽略阻尼的影响,取$\xi =0$; $U_{\rm r}={{U}}_{\infty }/(f_{\rm n}D)$为折减速度,其中$f_{\rm n}$为结构固有频率; ${{C}}_{\rm L}=2{{F}}_{\rm L}/(\rho{U}_{\infty }^{2}D)$、${{C}}_{\rm D}=2{{F}}_{\rm D}/(\rho{U}_{\infty }^{2}D)$分别为为升力和阻力系数, ${{F}}_{\rm L}$和${{F}}_{\rm D}$分别是作用在$x_{1}$和$x_{2}$方向上流体力的分量.
1.2 网格更新技术
在求解流固耦合问题的过程中,经常会遇到由于网格质量恶化导致计算中断的问题.为了避免网格失效的问题,本文采用基于拉普拉斯算法的网格更新技术[28], 表达式如下
式中, ${{S}}_{i}$为第$j$个方向上的网格位移, $\gamma$为网格变形控制参数.
1.3 流固耦合计算步骤
本文所采用弱耦合分区算法的具体过程详见文献[29], 其计算框架如下:(1)运用特征线分裂算子有限元方法求解流体控制方程式(1)与式(2)可以获得$t^{(n+ 1)}$时刻流场的速度与压力变量,从而得到流体作用于结构上的流体力${{C}}_{\rm D}$与${{C}}_{\rm L}$;(2)然后把流体力代入式(3)与式(4)运用Newmark-$\beta$求解结构运动控制方程得到$t^{(n +1)}$时刻钝体结构动力响应($\ddot{X}$, $\dot{X})$与($\ddot{Y}$,$\dot{Y})$; (3)已知$t^{(n + 1)}$时刻钝体结构的速度与其他边界条件,基于拉普拉斯算法更新网格位置; (4)返回至第(1)步实施$t^{(n +2)}$时刻计算, 如此循环直至该系统达到稳定状态.
1.4 算例验证
图1
图1
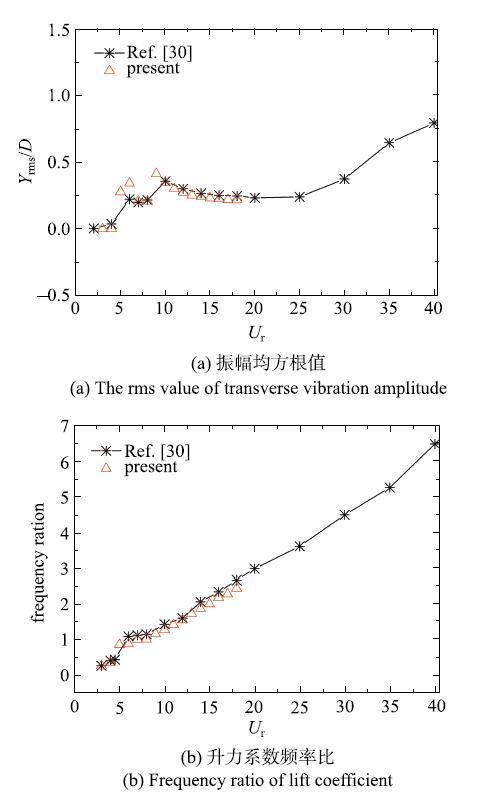
下游方柱的横流方向振幅均方根值和升力系数频率比随折减速度的变化对比图
Fig. 1
The comparisons of the rms value of transverse vibration amplitude and frequency ratio of the rear square cylinder behind a front stationary square cylinder as a function of $U_{\rm r}$
2 计算模型及网格独立性验证
2.1 计算模型和边界条件
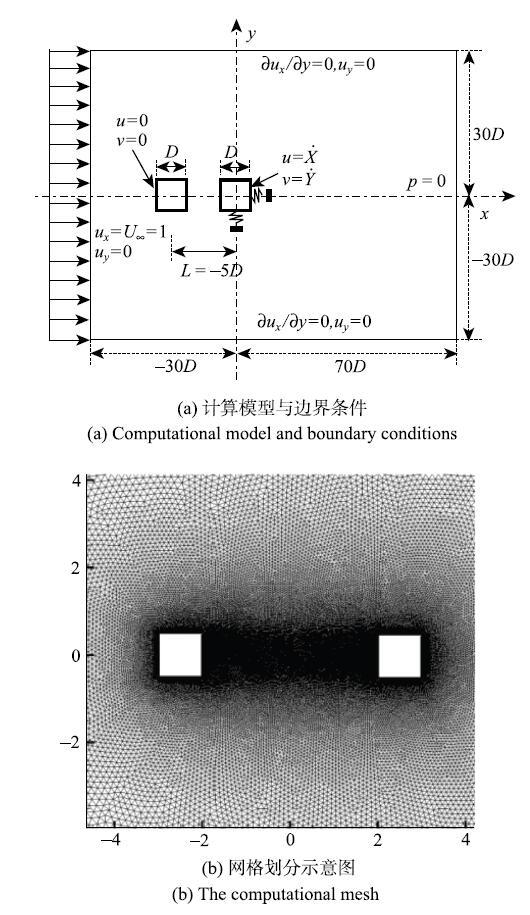
基于上述方法, 本文对均匀来流作用下,上游静止方柱与下游双自由度方柱的尾激振动问题进行了数值模拟研究.为了分析折减速度和雷诺数这两个关键参数对尾激振动系统的影响,选取折减速度$U_{\rm r}=3\sim 18$, 雷诺数$Re=40, 80, 120, 160,200$. 流体特性属于层流范围内, 可以假设为平面问题进行计算[25,30]. 计算模型和网格划分示意图如图2所示, 模型计算域尺寸为$[-30D,70D]\times [-30D, 30D]$, 间距比选取$L/D=5.0$,双方柱中心点分别为$(-5D, 0)$和$(0, 0)$. 上游方柱静止,下游方柱在$x$和$y$方向均可自由振动,且质量--弹簧--阻尼系统$x$与$y$两个方向自然频率为$f_{\rm n1}=f_{\rm n2}=f_{\rm n}$, 方柱折合质量为$M_{r}=2.0$, $\xi=0.0$(忽略阻尼效应). 边界条件设置如下:进口处采用速度入口:${{u}}_{x}={{U}}_{\infty}=1.0, {{u}}_{y}=0.0$; 出口处采用压力出口:${{p}}=0$;侧向边界均为自由滑移边界:$\partial {{u}}_{x}/\partial y=0.0,{{u}}_{y}=0.0$; 上游方柱表面:${{u}}=0$和${{v}}=0$;下游方柱表面:$u = \dot{X},v\mbox{ = }\dot{Y}$.
图2
图2
计算模型和网格划分示意图
Fig. 2
Schematic of the computational domain and computational mesh
2.2 网格独立性验证
表1 上游静止方柱--下游方柱双自由度尾激振动问题网格独立性验证($U_{\rm r}=5.0, Re=200$)
Table 1
 |
3 计算结果分析
3.1 动力响应分析
图3
图3
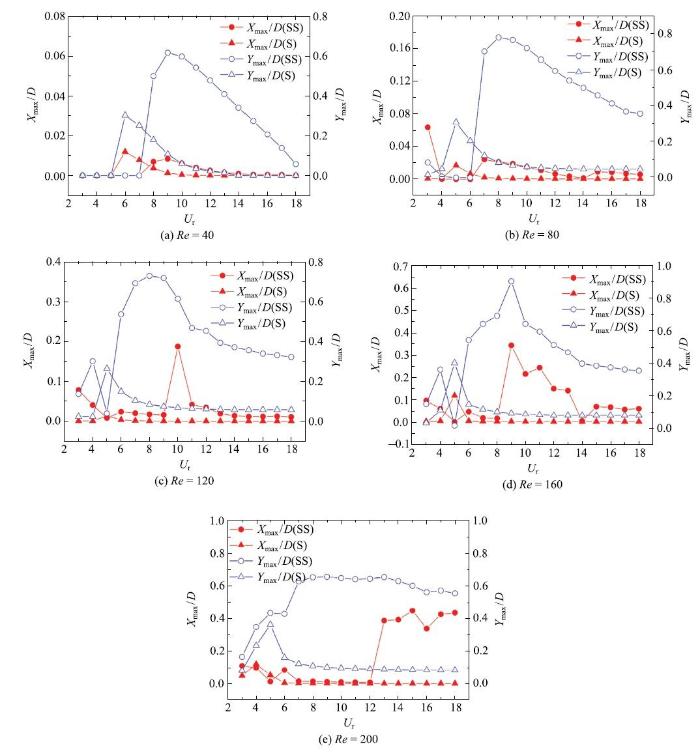
不同雷诺数工况下, 下游方柱与单方柱最大振幅随折减速度的变化
Fig. 3
The relationships between the maximum vibrating amplitude and reduced velocity for the downstream square cylinder and the single square one at different $Re$
当$Re \le 80$时, 随折减速度的增加,方柱体结构两个方向运动特性的变化规律几乎一致,横流方向振动幅度明显大于顺流方向, 如图3(a)与图3(b)所示. $U_{\rm r}$较小时, S工况的振动强于SS工况. 然而, 当$U_{\rm r} \ge8~(Re=40)$与$U_{\rm r} \ge 7~(Re=80)$时, 与S工况相比,SS工况的横流方向振幅会出现明显的增大,说明尾激振动效应对结构的影响增强. 当$Re=40$时,SS工况$Y_{\max}$/$D$最大值达到了$0.61~(U_{\rm r}=9)$,而S工况的$Y_{\max}/D$最大值仅为0.3~($U_{\rm r}=6$),两者之间相差了一倍多. 另外, 当$Re=80$时,SS工况$Y_{\max}$/$D$最大值达到了0.76 ($U_{\rm r}=9$),比S工况增大了1.5倍. 值得注意的是:折减速度较小时(3$\le U_{\rm r}\le 7, Re=40$; 4$\le U_{\rm r} \le 6, Re=80$),下游方柱体结构几乎没有发生振动, 主要由于下游方柱后面的尾流模态处于稳定状态, 尾流区没有发生涡脱落现象,从而抑制了下游方柱的振动, 如图4所示.Han等[31]也报道过类似的现象.
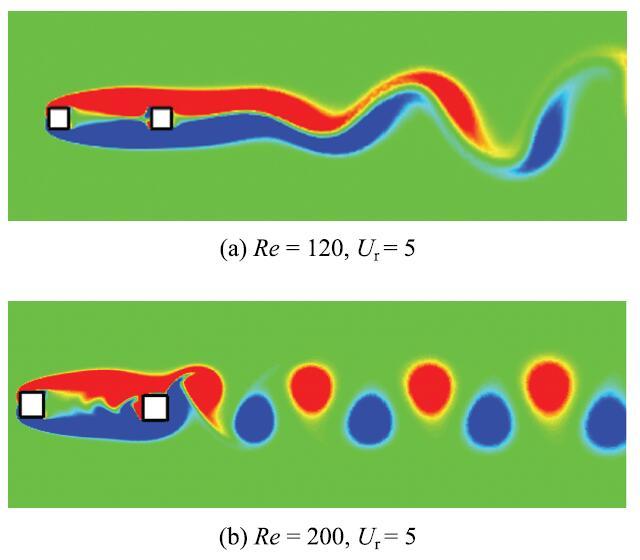
当$Re>80$时, 随着雷诺数的增大, 上游方柱尾流会增强,导致尾激振动效应变得更加强烈. 单方柱振幅曲线的变化较小,然而下游方柱体结构的振动响应发生了较大的变化,尤其是在顺流方向会产生较大的振动. 同时,两个方向发生较大振动的区域均会随雷诺数的增加而扩大. 另外, $U_{\rm r}>8$工况下, 随折减速度的增加, 横流向振幅下降速度减慢,如 图3(c) $\sim $图3(e)所示. 值得注意的是, 当$Re=200,U_{\rm r}=5$时,下游方柱体在横流方向的振幅明显大于其他两个雷诺数工况,这种现象主要是由双方柱之间间隙流与尾流特性变化产生的, 如图5所示.Wang等[28]和Jaiman等[30]也报道过类似的现象.随雷诺数的增加,串列布置双方柱体流场分布会发生改变:当$Re=120$与160时,双方柱之间的流场呈现出稳定状态, 柱间模态为"单钝体模式",但随着尾流不断向下游发展, 旋涡在距离结构较远处发生脱落,这种尾流模态被称为"2S$^{\ast }$"模态. 与传统的2S模态相比,该模态下所对应的结构受到上游方柱尾流"屏蔽"作用以及自身旋涡脱落较远的影响,振动相当微弱. 然而, 当$Re=200$时, 间隙流会发生周期性变化,同时下游方柱近尾流区会呈现出2S泄涡模式,结构与流场之间的耦合作用增强使得结构振幅增大. 另外, $Re=160$,$U_{\rm r}=11$工况下, 单方柱系统两个方向的振幅曲线已趋于稳定.所对应的力和位移时程曲线均呈现为标准的正弦函数形式,柱体振动十分微弱, 如图6(a)所示. 在不同的运动周期内,尾流模态均为稳定的2S模态. 而对于双方柱工况, 由图3(d)可得, 在尾激振动效应作用下, 下游方柱顺流向振幅较大,结构在两个自由度方向均产生剧烈振动. 这可能是由于该工况下,双方柱系统所对应的力和位移时程曲线均为"调制"模式,结构运动周期较长, 如图6(b)所示.上游方柱脱落的旋涡在两柱体间隙区域充分发展,形成完整的涡街并与下游方柱脱落的旋涡相互作用,导致双柱系统的尾流形态会随着振幅的变化呈现出较大的差异,流场的复杂化反过来引起结构的剧烈振动. 另外,在相邻两个"调制"周期的过渡区域内(i时刻), 结构振幅变化较大.上游方柱脱落的旋涡正面撞击下游方柱, 并在其两侧分离成两个小旋涡,使得近尾流区域的尾流模态呈现出2P模态.而远尾流区域旋涡的分布较为紊乱, 呈现出不规则形状.随着振幅的增加(ii时刻), 远尾流区域的旋涡分布逐渐规则,尾流发展趋于 稳定.
图4
图4
当$Re=80, U_{\rm r}=5$时, 瞬时涡量图
Fig. 4
Instantaneous vorticity at $Re=80$and $U_{\rm r}=5$
图5
图6
图6
$Re=160$, $U_{\rm r}=11$时, 下游方柱与单方柱运动位移时程曲线及其对应时刻的瞬时涡量图
Fig. 6
Time-history curve of displacement and instantaneous vorticity for the downstream square cylinder and the single square one at $Re=160$, $U_{\rm r}=11$
3.2 频率分析
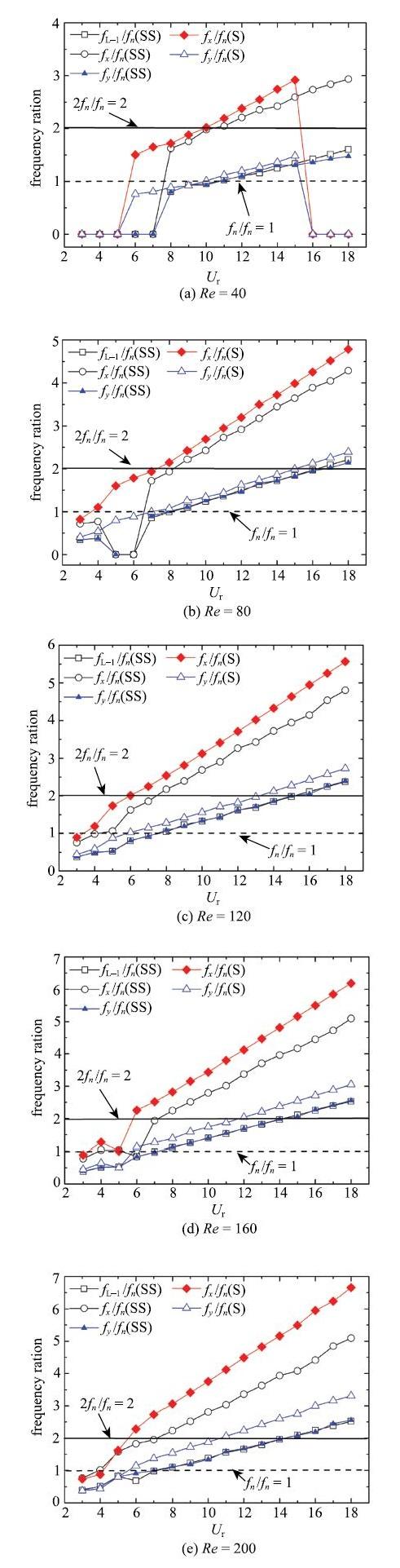
图7分别给出了不同雷诺数下,单方柱的振动频率、串列布置双方柱中上游方柱的升力系数频率和下游方柱的振动频率随折减速度的变化情况.图中相关参数的定义如下:$f_{\rm n}$是系统固有频率;$f_{x}$与$f_{y}$分别是方柱体在$x$和$y$方向的振动频率; $f_{L -1}$是上游方柱体升力系数的频率, 即涡脱落频率.
图7
图7
不同雷诺数下, 下游方柱和单方柱的频率比随折减速度的变化
Fig. 7
The relationships between the frequency ratio and reduced velocity for the downstream square cylinder and the single square one at different $Re$
由图7可得, 由于S工况和SS工况发生振动所对应的内在激励机制发生变化,导致频率特性也会随之改变. 对于SS工况而言, 当$Re \le 80$时,当结构的 振动频率接近于固有频率(横流向)或者两倍固有频率(顺流向)时,结构振幅增大. 当$Re>80$时, 在顺流向, 当3$\le U_{\rm r} \le $4时,当振动频率($f_{x})$接近于固有频率($f_{\rm n})$时,下游方柱振动幅度小幅增大. 但随着折减速度的增大,尾流效应对结构振动响应的影响明显增强, 折减速度较大($U_{\rm r}=10,Re=120$; $9 \le U_{\rm r} \le 13, Re=160$; $13 \le U_{\rm r} \le 18, Re=200$)时, 下游方柱也能发生较大振幅的振动. 另一方面,在横流向, 随着雷诺数的增加,双方柱系统的互扰效应主要以尾流效应为主. 在$f_{y}$/$f_{\rm n}>1$的折减速度范围内($U_{\rm r}>8$),下游方柱的横流向振动频率均接近于上游方柱的涡脱落频率,使得该范围内结构的振动幅度明显增大. 特别地,由于受到自身固有频率以及上游方柱尾流涡干扰的共同作用, 下游方柱在7$\le U_{\rm r} \le 9$范围内达到横流向振幅最大值.
当$Re \le 80$时,串列双方柱系统中上游方柱的涡脱落频率与下游方柱的振动频率在3$\le U_{\rm r} \le 7~(Re=40), 5 \le U_{\rm r} \le 6~(Re=80)$范围内均会出现等于零的情况,说明下游方柱体结构没有发生振动,且间隙流与尾流场区域均未形成卡门涡街, 柱体间流场模态呈稳态,如图4所示. 当$Re=40$时, 单方柱工况在3$\le U_{\rm r} \le 5$、16$\le U_{\rm r} \le $18的范围内也会发生类似的现象. 另一方面,随着折减速度的增加,下游方柱横流向振动频率($f_{y})$逐渐接近于固有频率($f_{\rm n})$,发生频率锁定现象[32], 锁定区间分别为9$\le U_{\rm r} \le 12~(Re=40)$和7$\le U_{\rm r} \le 10~(Re=80)$,导致结构振幅达到最大值, 如图7(a)与图7(b)所示.
当$Re>80$时,不同工况下结构的振动频率与涡脱落频率随折减速度的变化情况基本一致.雷诺数的变化对单方柱工况振幅响应的影响相对较小,锁定现象的发生会引起结构振幅的增大. 特别地, 当$Re=160$, $U_{\rm r}=5$时, 单方柱系统横流方向达到振幅最大值,但所对应的振动频率与固有频率的比值小于1,发生"软锁定"现象[33]. 对于双方柱工况, $U_{\rm r}=3\sim4$
范围内也发生了同样的现象. 另一方面, 随着雷诺数的增加,双方柱工况尾流效应加强,下游方柱的振动频率接近于上游方柱的涡脱落频率,使得两个方向发生大振幅响应的区域逐渐扩大,且对应的振幅值与低雷诺数工况相比明显增大, 与3.1节描述一致.值得注意的是, 在$Re=200, U_{\rm r}=6$工况下,下游方柱的振动频率($f_{y})$远离上游方柱体涡脱落频率($f_{L - 1})$,从而导致下游方柱振动响应增长速度减弱.
3.3 运动轨迹
图8
图8
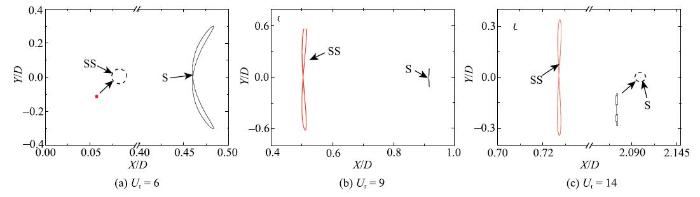
$Re=40$时, 下游方柱和单方柱的运动轨迹随折减速度的变化
Fig. 8
$X$-$Y$trajectories of the downstream square cylinder and the single square one under different reduced velocities at $Re=40$
图9
图9
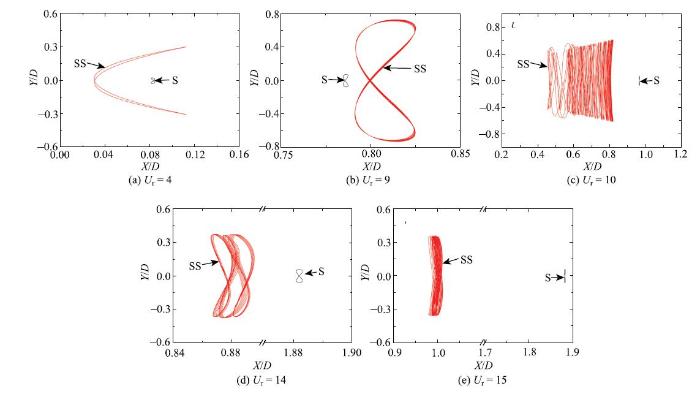
$Re=80$时, 下游方柱和单方柱的运动轨迹随折减速度的变化
Fig. 9
$X$-$Y$trajectories of the downstream square cylinder and the single square one under different reduced velocities at $Re=80$
图10
图10
$Re=120$时, 下游方柱和单方柱的运动轨迹随折减速度的变化
Fig. 10
$X$-$Y$trajectories of the downstream square cylinder and the single square one under different reduced velocities at $Re=120$
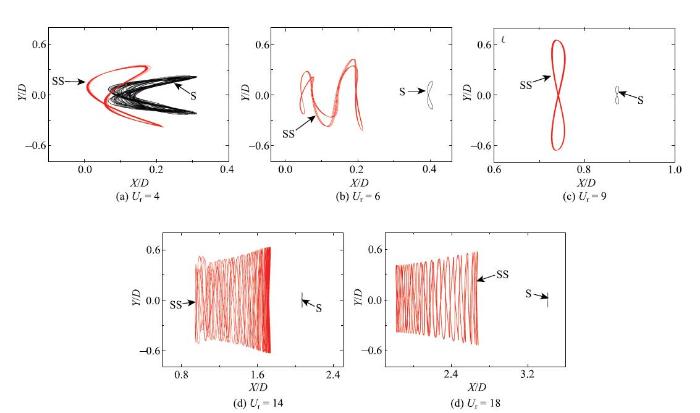
当$Re>80$时, 随着雷诺数的增加, 流场特性变得更加复杂,诱发下游方柱运动轨迹随折减速度的变化较大. 共振区间外,下游方柱主要以规则形状运动. 值得注意的是, 部分工况下($Re=160,U_{\rm r}=6; Re=200, U_{\rm r}=4$),下游方柱的"8"字形运动轨迹不再沿$y=0$对称,而是呈现出"8"字上部分大于下部分的非对称形式(见图11(b), 图12(a)),造成这种现象的原因可能是流场的复杂化使得从下游方柱的上下两侧流出的旋涡结构呈现出非对称分布,相关流场分析详见第4节. 共振区间内, 随着折减速度的增加,下游方柱的运动逐渐呈现出"调制"模式, 且周期较长,使得结构先以"8"字形运动, 然后逐渐转变为不规则形状. 特别地,当$Re=120, U_{\rm r}=14$时,下游方柱出现了类似于串联"双8"字形的运动轨迹.与其他雷诺数工况相比, 当$Re=200$时, 由于雷诺数较大,流场特性更加复杂, 导致下游方柱在大多数工况下均以不规则形状运动.
图11
图11
$Re=160$时, 下游方柱和单方柱的运动轨迹随折减速度的变化
Fig. 11
$X$-$Y$trajectories of the downstream square cylinder and the single square one under different reduced velocities at $Re=160$
图12
图12
$Re=200$时, 下游方柱和单方柱的运动轨迹随折减速度的变化
Fig. 12
$X$-$Y$trajectories of the downstream square cylinder and the single square one under different reduced velocities at $Re=200$
图13
图13
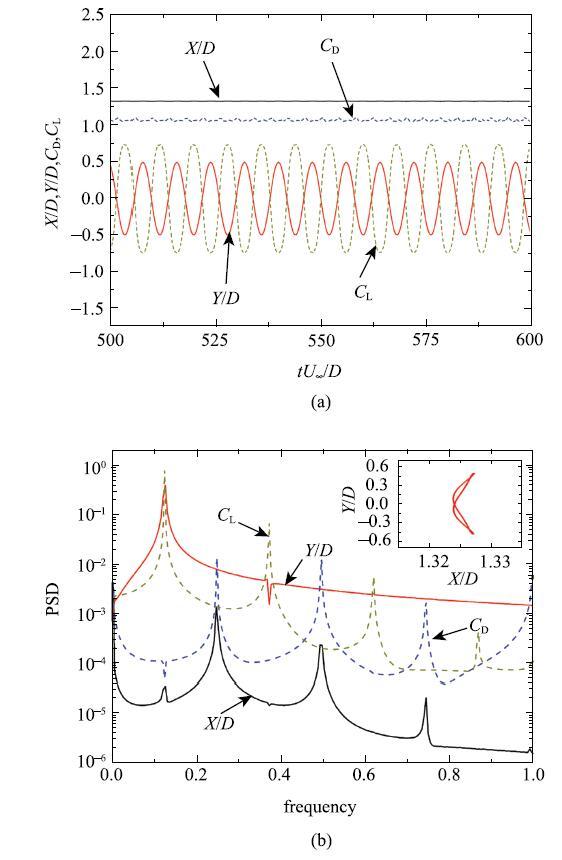
当$Re=80, U_{\rm r}=14$时, 流体力系数及位移的时程曲线和能量谱密度(PSD)
Fig. 13
Time history of the flow force coefficients ($C_{\rm D}$, $C_{\rm L})$and displacements ($X/D$, $Y/D)$and power spectral density (PSD) functions at $Re=80$and $U_{\rm r }=14$
图14
图14
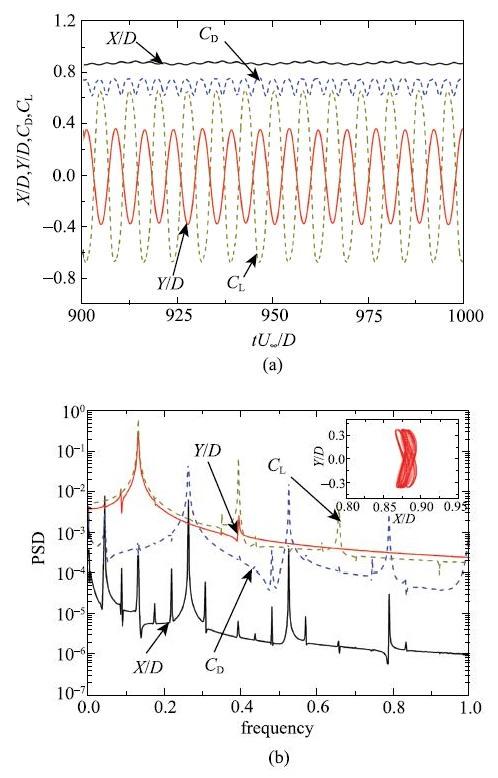
当$Re=120, U_{\rm r}=14$时, 流体力系数及位移的时程曲线和能量谱密度(PSD)
Fig. 14
Time history of the flow force coefficients ($C_{\rm D}$, $C_{\rm L})$and displacements ($X/D$, $Y/D)$and power spectral density (PSD) functions at $Re=120$and $U_{\rm r} =14$
当$Re=80, U_{\rm r}=14$时,{\ziju{0.02}下游方柱的升力系数时程曲线($C_{\rm L})$和位移时程曲线($Y/D)$呈反相,能量从结构流向流体会使得结构动能减少,导致其振动幅度相比振幅极值有所减弱, 如图3(b)所示. 另一方面,阻力系数时程曲线($C_{\rm D})$呈非规则形状,对能量在流体与固体之间的转递有较大影响,使得结构顺流向振动十分微弱. 由PSD曲线可知,下游方柱体结构横流方向位移能量谱密度曲线以一阶频率为主,二阶频率能量分布较小, 同时顺流方向会出现多阶频率. 另外,$X/D$曲线主频是$Y/D$曲线主频的两倍,使得下游方柱以竖直"双8"字形轨迹运动.
当$Re=120, U_{\rm r}=14$时,下游方柱的时程曲线及其相位特征与$Re=80$时类似.
见图14由PSD曲线可知,下游方柱体结构横流方向位移能量谱密度曲线只有两个峰值,并且以一阶频率为主. 然而, 顺流方向会出现多个峰值,并且一阶频率和二阶频率的能量十分接近,使得下游方柱的运动轨迹呈现出类似于串联"双8"字图形.
4 涡动力机理
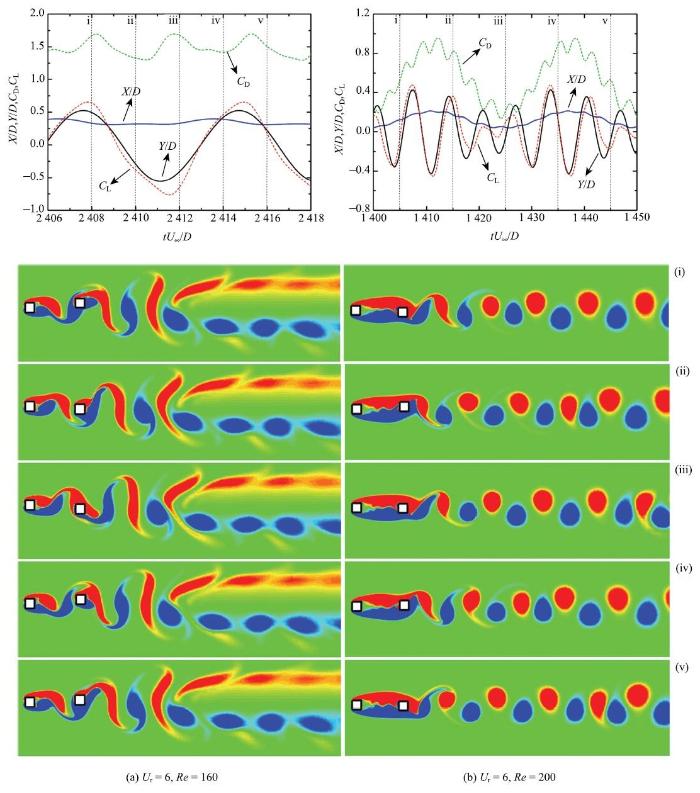
为了分析不同雷诺数工况下,串列双方柱系统中上游静止方柱的尾流与下游双自由度振动方柱之间尾激振动的作用机理,图15分别给出了$U_{\rm r}=6, Re=160$和200工况下,串列双方柱系统的运动位移时程曲线及其对应时刻(i$\sim $v)的瞬时涡 量图.
由图可知, 当$Re=160$时, 上游方柱剪切层重附着在下游方柱表面,并与其自身脱落的旋涡相互作用, 使得尾流区旋涡长度较长,并呈现出非对称的尾流形式. 随着涡街不断向下游发展,上下表面脱落的旋涡会发生分离, 转变为双行涡街,且上行涡的强度弱于下行涡.旋涡分离的过程中上行涡会分裂成一大一小两个子旋涡并分开排布在上下两侧,使得远尾流区域尾流模态中下行涡呈现出对涡与单涡交替出现的模式.另外, 随着上行涡不断向下游发展, 能量发生耗散, 使得涡流强度减弱,旋涡中心和四周的涡量梯度明显减小.流场的变化使得下游方柱运动位移时程曲线均呈现为不规则的形状,对应的横流向位移和升力系数的时程曲线呈同相分布,能量从流体流向结构, 引起方柱横流向剧烈振动, 如图15(a)所示.下游方柱与流场之间耦合作用的变化过程如下:当方柱从最上方位置开始向下运动时(i时刻),下游方柱下表面新形成的旋涡正充分发展, 并在结构右下方形成吸压区,促进下游方柱加速向下并减速向左运动.当下游方柱即将运动到最下方位置时(ii时刻),上行涡已完全脱落并开始形成新的旋涡,而上游方柱的尾流恰好运动到下游方柱下表面,并与下游方柱充分发展的下行涡相互结合, 即将从下游柱体表面脱落,使得下游方柱向下减速运动. 随着尾流涡街的进一步发展,上游方柱新形成的上行涡向后运动并到达下游方柱上表面,与下游方柱的尾流结合成一个更大的旋涡. 另一方面,下游方柱的下行涡逐渐脱落, 并在下表面形成新的旋涡.柱体上侧和后侧分别形成三个吸压包,导致下游方柱向右上方运动(iii$\sim $iv时刻). 到v时刻,流场的流动形态与i时刻基本一致.
图15
图15
不同雷诺数工况下, 下游方柱运动位移时程曲线及其对应时刻的瞬时涡量图
Fig. 15
Time-history curve of displacement of the downstream square cylinder and instantaneous vorticity at different $Re$
5 结论
基于半隐式CBS流体有限元方法与动网格技术相结合的分区流固耦合计算方法,对固定方柱后双自由度振动方柱的尾激振动问题进行了研究,着重分析了雷诺数和折减速度对尾激振动动力响应的影响,并与单方柱工况进行了对比. 主要结论总结如下:
(1)折减速度和雷诺数对单方柱振幅影响较小, 随雷诺数的增大,单方柱结构仅在少数折减速度工况下出现单共振现象.然而对下游方柱振幅的影响较大, 当$Re \le 80$时,下游方柱仅在横流方向发生共振. 当$Re>80$时,在折减速度较大的区间会出现双共振现象,并且发生较大振幅的区域也会增大.
(2)随着雷诺数的增大, 双方柱系统互扰效应会发生转变. 当$Re \le 80$时, 下游方柱的大幅振动主要发生在振动频率与固有频率接近的范围内,振动响应以涡激振动为主导. 当$Re>80$时, 随着雷诺数的增加,尾激振动的影响逐渐增强,下游方柱的振动响应受到结构固有频率与上游方柱涡脱落频率的共同作用.
(3)在不同雷诺数和折减速度工况下, 单方柱的运动轨迹均为"8"字形.然而, 下游方柱的运动轨迹比较复杂. 当$Re \le 80$时,下游方柱的运动轨迹呈现出"8"字形以及竖直"双8"字形等.当$Re>80$时, 运动轨迹在多个工况会出现不规则形状.
(4)不同雷诺数和折减速度工况下,单方柱系统的尾流模态主要呈现为标准的2S模态.而双柱系统的尾流模态以及尾激振动机理受雷诺数和折减速度的影响较大.尾流涡结构随流场的变化出现2P和2T以及非对称涡街等多种不同的模式.由于流场产生较大的变化, 使得下游方柱体运动明显加剧.
参考文献
Vortex-induced vibrations
Circular cylinder wakes and vortex-induced vibrations
An overview of modeling and experiments of vortex-induced vibration of circular cylinders
不同截面形状柱体流致振动的CFD数值模拟
CFD numerical simulation of flow-induced vibration with different cross-section cylinder
基于ALE有限元法的流固耦合强耦合数值模拟
A partitioned strong coupling algorithm for fluid-structure interaction using arbitrary lagrangian-eulerian finite element formulation
Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number
Flow-induced vibrations of square and rectangular cylinders at low Reynolds number
Effect of mass ratio on free vibrations of a square cylinder at low Reynolds numbers
Free vibration of a square cylinder at low Reynolds numbers
Fluid--structure interaction of a square cylinder at different angles of attack
The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack
Three-dimensional wake transition of a square cylinder
Flow interference between a stationary cylinder and an elastically mounted cylinder arranged in proximity
错列角度对双圆柱涡激振动影响的数值模拟研究
Numerical study of staggered angle on the vortex-induced vibration of two cylinders
The role of wake stiffness on the wake-induced vibration of the downstream cylinder of a tandem pair
Numerical investigation of wake induced vibrations of cylinders in tandem arrangement at subcritical Reynolds numbers
Interaction dynamics of upstream vortex with vibrating tandem circular cylinder at subcritical Reynolds number
Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region
Flow-induced vibration of a circular cylinder subjected to wake interference at low Reynolds number
On the effect of spacing on the vortex-induced vibrations of two tandem cylinders
Flow-induced vibration of three unevenly spaced in-line cylinder in cross-flow
小间距比下串列双圆柱涡激振动数值模拟研究:振动响应和流体力
Numerical simulations for VIVs of two tandem cylinders with small spacing ratios: Vibration responses and hydrodynamic forces
Flow induced vibrations of a sharp edge square cylinder in the wake of a circular cylinder
Vibrations of a square cylinder submerged in a wake
Flow past two tandem square cylinders vibrating transversely in phase
Flow characteristics and dynamic responses of a rear circular cylinder behind the square cylinder with different side lengths
Wake-induced vibrations of an elastically mounted cylinder located downstream of a stationary larger cylinder at low Reynolds numbers
平面剪切来流作用下串列布置三圆柱流致运动特性研究
Study of flow-induced motion characteristics of three tandem circular cylinders in planar shear flow
A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow
Wake-induced vibrations of a circular cylinder behind a stationary square cylinder using a semi-implicit characteristic-based split scheme
Frequency lock-in is caused by coupled-mode flutter
Finite element study of vortex-induced cross-flow and in-line oscillations of a circular cylinder at low Reynolds numbers