力学学报, 2019, 51(5): 1273-1284 DOI: 10.6052/0459-1879-18-321

研究综述

青光眼发病机理--筛板变形研究进展 1)

张婷*,†, 李龙*,†, 宋凡,*,†,2)

* 中国科学院力学研究所非线性力学国家重点实验，北京 100190

† 中国科学院大学，北京 100049

PATHOGENETIC MECHANISMS OF GLAUCOMA------RESEARCH PROCESS ON THE DEFORMATION OF LAMINA CRIBROSA 1)

Zhang Ting*,†, Li Long*,†, Song Fan,*,†,2)

* The State Key Laboratory of Nonlinear Mechanics， Institute of Mechanics， Chinese Academy of Sciences， Beijing 100190， China

† University of Chinese Academy of Sciences， Beijing 100049，China

通讯作者: 2)宋凡，研究员，主要研究方向：生物、仿生材料及超高温材料的结构与性能. E-mail:songf@lnm.imech.ac.cn

收稿日期: 2019-09-29   网络出版日期: 2019-09-18

基金资助: 1)国家重点研发计划项目.  2016YFA0501601
中国科学院战略性先导科技专项(B)类.  XDB22040102
国家自然科学基金项目资助..  11472285

Received: 2019-09-29   Online: 2019-09-18

作者简介 About authors

摘要

青光眼是世界上第一大不可逆致盲眼病.其病变与眼内压直接相关,控制眼内压是目前控制青光眼发展的唯一有效途径,但发病的确切机制尚未明确.现已证实,青光眼的原发部位是巩膜筛板：由筛板前后分别承受的眼内压与颅内压产生的压力差会导致筛板结构与形态发生变化,进而挤压穿过筛板的视觉神经,造成视觉神经损伤,产生不可逆的视觉损失.因此,青光眼的发病机理与筛板的力学特性及其周围的力学环境密切相关.自从筛板被确定为青光眼视神经损害的原发部位,筛板便成为该领域的研究热点.其中,通过建立筛板力学模型,研究眼内压与颅内压作用下筛板的受力变形,进而分析筛板变形对视神经的损伤,有助于揭示青光眼视神经损伤机制及青光眼的发病机理.本文将从相关实验、理论和计算以及临床等方面介绍青光眼发病机理中筛板变形的研究进展以及目前存在的问题.

关键词： 青光眼 ; 筛板 ; 变形 ; 视神经损伤 ; 力学模型

Abstract

Glaucoma is the first cause of irreversible blinding eye disease in the world. Glaucomatous optic nerve damage is directly associated with the intraocular pressure, and tight control of intraocular pressure is still the only therapeutic approach available for the treatment of glaucoma, while the pathogenesis of glaucoma remains unknown. It has now been confirmed that the primary site of glaucoma is the lamina cribrosa: the pressure difference between the intraocular pressure and intracranial pressure respectively exerted on the anterior and posterior surfaces of lamina cribrosa can cause the change in the structure and morphology of lamina cribrosa, then the deformation of lamina cribrosa squeezes the optic nerves passing through the lamina cribrosa to make their damages; and finally, the damages produce irreversible visual loss. As a result, the pathogenesis of glaucoma is essentially associated with the mechanical properties of lamina cribrosa and mechanical environment surrounding the lamina cribrosa. Since lamina cribrosa was identified as the primary site of glaucomatous optic nerve damage, it has become the hot spot of glaucomatous optic nerve damage research. As an effective method, we can study the deformation of lamina cribrosa under the effect of intraocular pressure and intracranial pressure by developing mechanical model of lamina cribrosa, and analyze the effect of the deformation of lamina cribrosa on the optic nerve damage. This method has helped us to reveal the mechanism of glaucomatous optic nerve damage and the pathogenesis of glaucoma to some extent. This review will introduce the research progress and the present existing problems on the deformation of lamina cribrosa during glaucoma from the related experimental, theoretical, computational and clinical aspects.

Keywords： glaucoma ; lamina cribrosa ; deformation ; optic nerve injury ; mechanical model

PDF (21642KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张婷, 李龙, 宋凡. 青光眼发病机理--筛板变形研究进展 1). 力学学报[J], 2019, 51(5): 1273-1284 DOI:10.6052/0459-1879-18-321

Zhang Ting, Li Long, Song Fan. PATHOGENETIC MECHANISMS OF GLAUCOMA------RESEARCH PROCESS ON THE DEFORMATION OF LAMINA CRIBROSA 1). Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(5): 1273-1284 DOI:10.6052/0459-1879-18-321

引言

现代医学理论和技术的发展,使眼科疾病的治疗水平得到了极大的提高,白内障、角膜病等大多数可致盲眼病最终得到了有效的治疗.青光眼(glaucoma),由于其对视神经造成的损害不可修复,成为 世界上第一大不可逆的致盲眼病[1-2].据联合国对2020年世界人口和世界各地流行病预测,到2020年全世界青光眼的患病人数将达到近8000万[3].我国是青光眼病高发国家. 根据青光眼的流行病学调查, 我国原发性青光眼的患病率为0.11% $\sim $1.66%.随着年龄的增长发病率也越来越高：40岁以上为1% $\sim $2%,65岁以上高达4% $\sim $7%.由此推算,我国青光眼患病人数超过800万[4-5].更为严重的是,大量青光眼患者在患病初期,由于没有症状或者症状表现不明显,很容易被忽视.据调查,在发达国家有50%的青光眼患者并不知道自己患有青光眼. 而在发展中国家该数据甚至高达90%.由于患者的视觉功能在青光眼疾病发展到晚期时已经被损害,使其无法逆转.

青光眼发病的核心问题是: 将视觉信号传输到大脑的视神经突触细胞的损伤, 造成了不可逆的视觉损失[1].虽然青光眼具 体发病原因尚不明确,但青光眼发病进程已被证实与高眼内压有很强的关联性[6-7].因此,不管是药物干预还是手术治疗,降低眼内压是目前缓解青光眼发病进程的唯一有效方法[1,8-9]. 已有实验证实,青光眼的损伤原发部位是筛板(lamina cribrosa, LC)[10]. 目前大部分关于青光眼发病原因和进程的研究均围绕高眼内压引起的筛板变形和损伤展开[11-13].

1 眼内压、颅内压及筛板

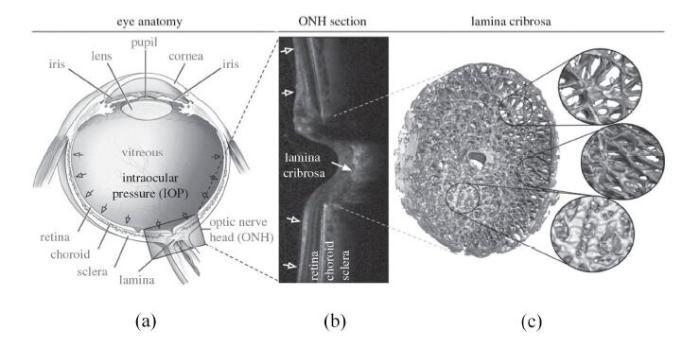
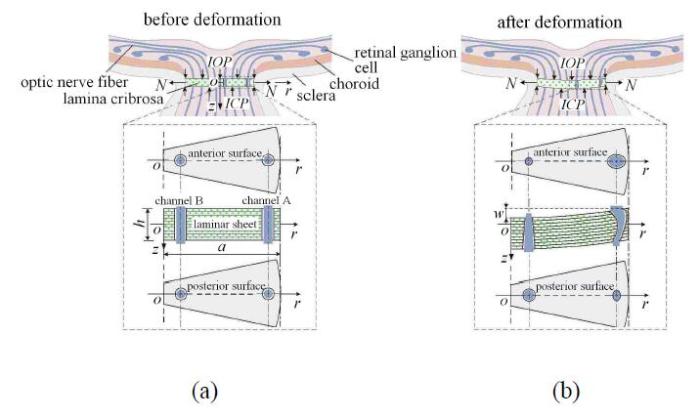
眼球结构如图1(a)所示. 眼内压是眼球内容物作用于眼球壁的压力(intraocular pressure,IOP).维持正常视功能的眼内压称为正常眼内压,约为10 $\sim $21,mmHg (1,mmHg=133.28,Pa). 正常情况下,房水生成率与房水排除率处于动态平衡状态,以维持正常眼内压.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   眼球及视乳头筛板结构图[1]

Fig. 1   Structure of eyeball,optic nerve head (ONH) section and lamina cribrosa[1]


筛板位于眼球后方,是胶原纤维与筛孔中包含的视网膜神经节细胞轴突和神经胶质细胞等神经组织组成的复杂结构[14],如图1所示.其结构主要由十余层连续的纤维薄板构成,筛板周边与巩膜相连,血管和神经纤维从筛孔中穿过. 筛板半径约为0.76 $\sim $1.14,mm,平均半径为0.95,mm,厚度约为0.24 $\sim $0.36,mm,平均厚度为0.3,mm[15-17].筛板的主要作用包括：(1)支撑将视觉信号从视网膜传输到大脑的视神经节的神经突触;(2)使视网膜中心动脉和静脉穿入、穿出眼内空间;(3)调节眼内压(12 $\sim $15,mmHg)和视神经通道内组织压力(7 $\sim $10,mmHg)之间的压力差.筛板主要由睫状后动脉的分支供血,因此血液从筛板的外部边缘进入内部[18].

青光眼病人的眼内压升高会导致筛板后凸,形成病理凹陷,直接挤压从筛孔通过的视神经纤维,使视神经细胞轴浆运输阻滞于筛板区, 轴突蛋白生成和转运减少,导致细胞代谢受损,以致视神经死亡[10,19].

在人体中,筛板处于两个具有不同压力的腔隙之间,其前方承受眼球内的压力,即眼内压,而后方承受颅内蛛网膜下腔的压力,即颅内压(intracranial pressure,ICP). 它们形成的压差构成了筛板的主要力学环境.由于颅内压相对稳定,正常的颅内压在人侧卧位时约为9 $\sim $10,mmHg[15],因此,研究中多涉及眼内压或眼内压与颅内压压差的变化, 很少单独提及颅内压[20-21].事实上,眼内压与颅内压存在相互关联. Quigley[22]提出眼内压与颅内压的关系为

$$ {ICP} = \left\{\begin{matrix}{ll} {IOP}/ 2 ,, &amp; {\rm for} \ {IOP} < 20,{\rm mmHg} \\ 10,{\rm mmHg},, & {\rm for} \ {IOP} \geqslant 20,{\rm mmHg} \end{matrix} \right. $$

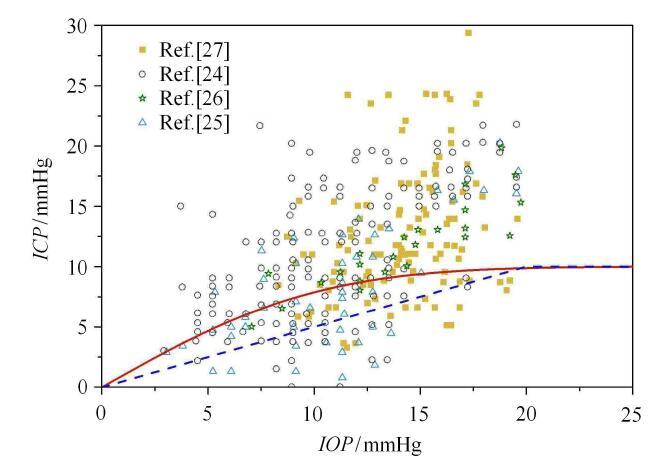
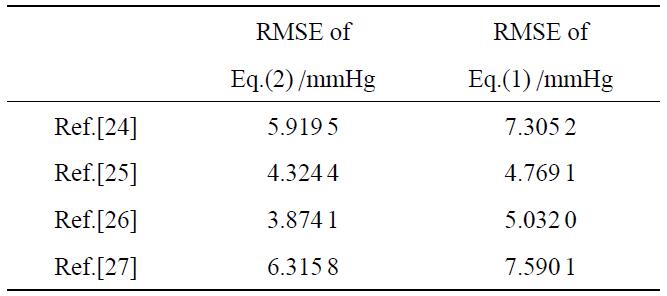
尽管这个关系式已被证明很好地反映了眼内压和颅内压之间的联系,但在建立青光眼发病机制的相关理论模型时,在$IOP = 20$,mmHg处关系式(1)会产生如导数不存在的一系列异常现象,这与眼内压和颅内压均由人体内连续的流体产生的生理规律不符合. 为克服这个缺陷,Tian等[23]其修正为

$${ICP} = 10 \cdot {\rm erf} (0.088 \cdot {IOP}) $$

其中,${\rm erf} (\xi ) = (2 /{\sqrt \pi }) \int_0^\xi {\rm e}^{ - \eta ^2} \eta$为误差函数. 该修正不仅弥补了Quigley[22]提出的关系式的缺陷(图2),而且与临床试验更加吻合(表1).

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   IOP与ICP的关系. 其中,虚线与实线分别表示由 式(1)与式(2)得到的理论结果,实验数据[24-27]则由不同的符号表示

Fig. 2   The relations between IOP and ICP. The broken line stands for Eq.(1), the solid line expresses Eq.(2), and different figurate points indicate the different experimental data from Refs.[24-27]


表1   基于式(1)与式(2)的理论结果相对于实验数据的均方根误差[24-27]

Table 1  The RMSE of Eqs.(1) and (2) with respect to the experiments [24-27]

新窗口打开| 下载CSV


2 筛板变形研究

开角型青光眼的视觉区域损失和视盘凹陷的特征被认为与筛板内视神经纤维的损伤有关[28]. 目前普遍认为,眼内压升高会改变筛板内部结构[19, 29],并且将视神经细胞轴浆运输阻滞于筛板内[30-32]. Maumenee等[33]曾提出,视神经轴突的损伤是由于筛板挤压视神经束产生的机械压力造成的. 验证该假设的关键在于研究在高眼内压下筛板的力学响应.

2.1 筛板组织变化

通过视神经乳头中心区域的显微照片,Yan等[28]对筛板进行了形态学检测,并测量了筛板尺度,发现眼内压升高在引起筛板变形的同时,并不会使筛板厚度发生改变.在此研究中,通过形态测定的方法使筛板的整体形状和内部结构固定.实验组和对照组分别在50,mmHg和5,mmHg载荷下对筛板加压,进行急性实验(acuteexperiment),以研究眼内压对正常视神经乳头的影响,如图3(a).在实验24,h后,虽然50,mmHg压力下筛板中心的凹陷程度(图3(c))明显大于5,mmHg压力下筛板中心的凹陷程度(图3(b)),但是二者的筛板厚度接近,即筛板在变形过程中厚度几乎不变.通过更高倍率的筛板组织显微图片发现,50,mmHg压力下筛板上结缔组织(图3(d))与5,mmHg压力下筛板结缔组织(图3(e))相比,出现了更多数目明显的横向裂纹.上述实验结果表明,眼内压在使筛板变形的过程中,并不改变其厚度;筛板边缘剪切应力在筛板变形中起主导作用,该剪切应力通过挤压视神经纤维束,使筛板上结缔组织产生横向裂纹,造成视觉区域的损失.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   (a)固定在巩膜上的筛板(实线)示意图[28]. (b)与(c)表示在5,mmHg与50,mmHg荷载下,变形后的筛板和视神经乳头;(d)与(e)表示在5,mmHg与50,mmHg荷载下,筛板结缔组织结构图

Fig. 3   (a) Schematic view of the lamina cribrosa (solid lines) showing surrounding sclera overlain by retina[28]. Overview of the optic nerve head region from a normal human eye fixed at (b) 5,mmHg and (c) 50,mmHg; Lamina cribrosa of normal human eye fixed at (d) 5,mmHg and (e) 50,mmHg


另外,Bellezza等[34]通过将正常猴子和患青光眼猴子的筛板固定在不同眼内压下进行急性实验,现患有早期青光眼的猴子筛板发生了塑性形变,这说明在视神经乳头周围的结缔组织受到了损伤. Zeimer等[35]和Coleman等[36]通过测量、比较眼内压升高或者降低条件下,正常眼内和青光眼患病眼内筛板上视神经乳头前表面的位置,发现青光眼患病眼内视神经乳头位置随着视力的下降位移增大,间接反映出筛板位置的改变.而Levy等[37]则发现,筛板在接近巩膜的位置位移最小,中心区域位移最大,这一差距引起了筛板上的结缔组织对视神经轴突的剪切.

2.2 筛孔结构变形

筛板是巩膜上的一个特殊的区域,视神经轴突通过筛板上的孔洞------筛孔穿出眼球.在过去三十年中,筛孔已成为很多临床和组织病 理学研究的焦点[38].通过对人眼球视神经乳头周围筛孔的解剖发现,在筛板的上下边缘部分,由于有更多数量的视神经轴突在这一区域穿过,使得筛孔的平均尺寸也较大[39].进一步研究表明,在筛板的上下边缘部分,由于筛孔较大、结缔组织较薄,穿过这一部分的视神经也更易受到损伤[40-41].此外,筛孔形状的变化与青光眼的严重程度有关：正常的筛孔几乎是圆形的,青光眼的筛孔会被拉长,这会引起视觉区域的损 伤[42-44].

Quigley等[45]以机械压迫假说为基础,提出眼内压升高可能导致筛板和穿过其中的神经纤维发生的变化,从而解释视神经束承受的压迫,如图4所示. 虽然Tian等[46]近期给出了理论证明,然而,至今仍未获得实验证实.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   眼内压升高可能导致的筛板和穿过其中的神经纤维(NF)的改变[45]

Fig. 4   Schematic representation of the changes of lamina cribrosa and nerve fibers (NF) caused by elevated IOP[45]


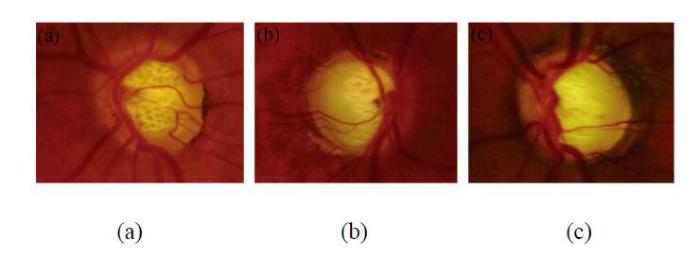
通过对青光眼患者眼底照相观察视神经盘,Tezel等[38]将筛孔形状分为3种：圆形(circular),椭圆形(oval)和有细沟的椭圆(striate),如图5所示.对高眼内压青光眼患者和正常眼内压青光眼患者的长期观察发现,这些青光眼患者可见的筛孔中,仅有7.7%是圆形的,而椭圆形筛孔和有细沟的筛孔所占比例分别为66.7%和25.6%.对比筛孔的初始形态和随后拍摄到的形态,发现青光眼病人眼内筛孔,2.6%由圆形变为椭圆形,7.7%由椭圆形变为有细沟的椭圆.在研究期间,一些患者的筛孔被拉长而变得更加细长. 同时视神经束受损加重的患者,可见的筛孔数目增多.对于单个筛孔,形状被拉长导致面积减小,而由于可见筛孔的增多,筛孔总面积增大,这些现象均伴随着神经束损伤的加剧以及青光眼病情的加重.在后续的观察发现,筛孔形状的拉长仅出现在部分患者眼中,其原因或许与治疗中减低病人眼内压从而使筛板受到的压力减小有关.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   3种筛孔的形状 (a)圆形, (b)椭圆形, (c)带细沟的椭圆形[38]

Fig. 5   Classification of lamina cribrosa pore shape. The shapes of the lamina cribrosa pores are qualitatively classified as (a) circular, (b) oval and (c) striate[38]


通过对青光眼病人和正常人眼内筛板进行光协调性体层摄影术(optical coherence tomography,OCT)扫描,Shoji等[47]获得了筛板的三维图像,并进行逐层比较,分析了筛孔的延伸率指标(elongation indices,EIs)与深度的关系. 研究发现,在筛板前表面上的筛孔延伸率指标最大,且在青光眼病人中更为明显.青光眼病人筛板上部(superior)和下部(inferior)受到更大的压力和弯曲,因此,这些部分的筛孔比其他部分的筛孔延伸率指标要大,且结缔组织的密度变小.这些现象表明,在筛孔延伸率大的区域,筛孔的变形使穿过其中的视神经纤维束受到了更大的不均匀的压力,筛孔的延伸率与青光眼的发病进程有关.

2.3 筛板局部变形的不均匀性

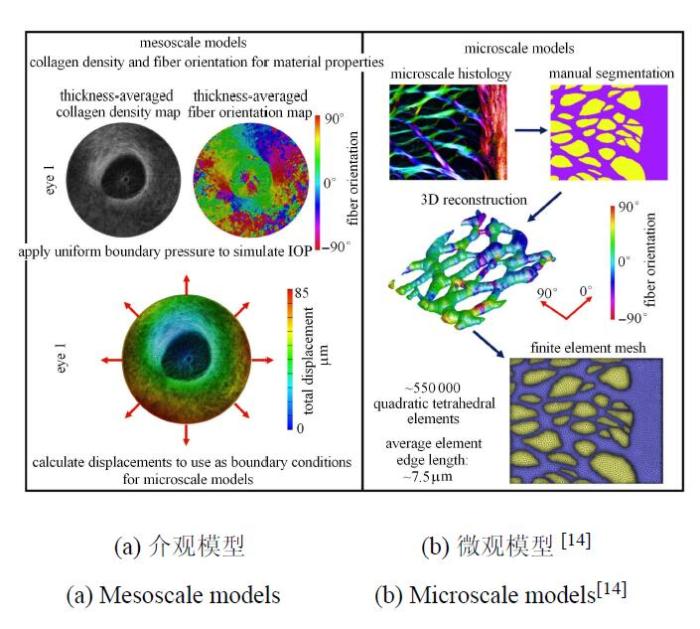
目前,研究者对眼内压升高引起筛孔变形挤压神经组织,从而导致青光眼发病这一观点已有广泛共识.Voorhees等[14]为了研究筛板的微结构和力学性能变化对视神经纤维的影响,对羊筛板的纤维定向性进行了扫描,并使用有限元的方法进行了建模和力学分析(图6).研究结果显示,在眼内压引起的筛板变形中,神经组织的应变很大且不均匀,筛板不同位置受到的应变差异也很大.筛板结缔组织的刚度和非线性影响了神经组织的应变,而神经组织的刚度和结缔组织的各向异性的影响并不明显.相比筛板中心的筛孔,筛板边缘的筛孔应变要大得多.该结果说明在筛板边缘的筛孔,其中的神经组织承受了非常大的剪切变形.通过研究眼内压对筛板上神经组织变形的影响,有助于理解青光眼的发病病理假说------视神经的损伤是眼内压引起的力学损伤.其中,值得注意的是,一些筛孔周围的组织表现出明显的应力集中现象,这一现象在靠近巩膜的筛板部分尤为明显.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   筛板的跨尺度建模

Fig. 6   Multiscale modeling approach


在不同眼内压作用下,Sigal等[48]通过对比、计算筛板平面内变形,分析了筛板内应变的分布和对称性.研究结果表明,筛板 最大挠度和最大拉伸变形发生在中心位置,最大压缩变形发生在筛板边缘处.挠度最大处与形变最大处并不相同,而最大拉伸、最大压缩、最大剪切均发生在不同位置.同时,在筛板的一些区域上,形变在一些筛孔附近高度集中,即发生了应力集中(图7).

图 7

新窗口打开| 下载原图ZIP| 生成PPT

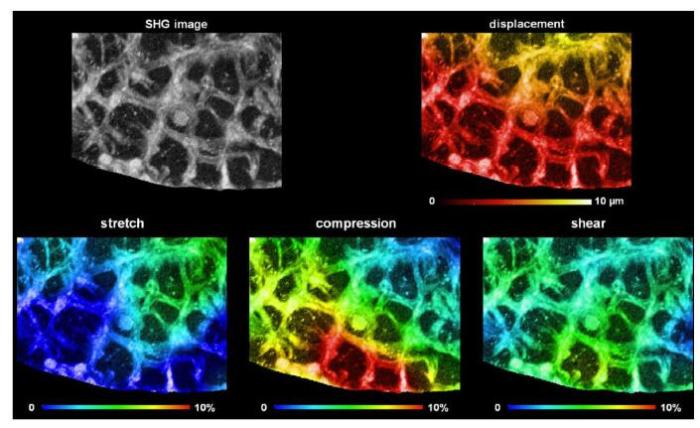
图 7   眼内压由10,mmHg增大到45,mmHg对筛板局部的影响.其中,第1行对比了筛板挠度变化. 第2行由左到右分别为筛板拉伸变形、压缩变形以及剪切变形[48]

Fig. 7   Detail of the biomechanical effects of IOP from 10,mmHg to 45,mmHg. The panels show the structure of the LC in the SHG image (top left), as well as the SHG image colored by the magnitudes of displacement (top right),stretch (bottom left), compression (bottom center), or shear (bottom right)[48]


Tran等[49]使用OCT技术,对不同眼内压和颅内压灵长类动物活体内筛板拍照并进行图像分析,分别研究了眼内压和颅内压对筛板的作用. 结果表明,眼内压和颅内压对筛板的作用都是局部集中、非线性且非单调变化的.压力改变引起的筛板拉伸或压缩变形有时甚至超过20%.眼内压和颅内压的改变对筛板拉压变形的影响不同：眼内压升高使筛板拉伸变形增大,颅内压升高引起筛板压缩变形程度增大.通过实验观测,Midgett等[50]指出,筛板边缘处的剪应力要大于筛板中心位置的剪应力,筛板应变在局部位置较高,而这些区域可能是视神经乳头受损的位置.

3 筛板变形的力学模型

筛板本身尺寸较小(半径约为0.76$\sim $1.14,mm)[37,51],且位于眼球后部,结构相对复杂,在临床和实验中观察难度较大.因此,筛板力学模型的建立对研究和理解眼内压在青光眼发病机制中的作用十分重要.

通过确定边界条件和测试力学参数,建立力学模型是当前理解筛板力学性能非常有效的方法.建立筛板的力学模型,目前主要考虑以下几点：(1)筛板材料的本构关系,其中主要涉及材料属性(弹性或粘性)以及相应力学参数的确定;(2)筛板与巩膜接触边界条件,其主要包括简支、固支或是附加扭转约束边界条件等;(3)筛板中是否存在预应力.

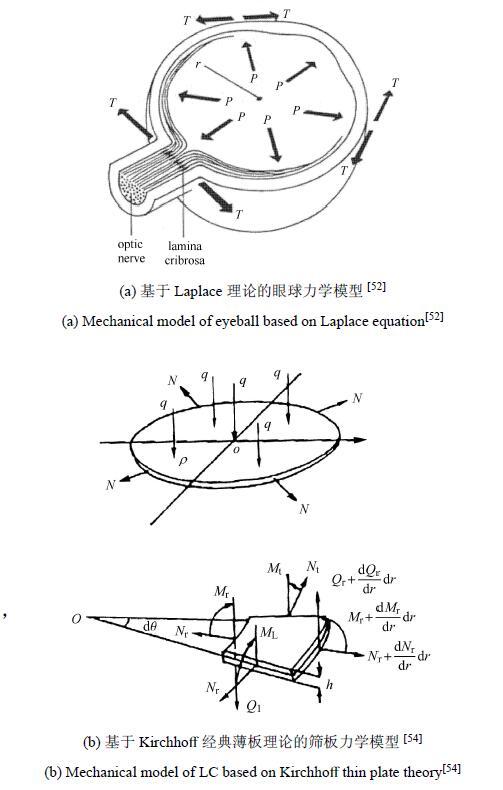
3.1 基于拉普拉斯理论的薄膜模型

早期青光眼研究的理论模型假定眼球弹性且性质均一(图8(a)),根据拉普拉斯公式(Laplace)进行计算[52-53],即

$$IOP = {2N} {R_S }$$

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   两种理论模型

Fig. 8   Two theoretical models


其中,$R_{S}$为眼球半径,$N$为巩膜张力.实际上,筛板在高眼内压载荷作用下,其变形包括拉伸、压缩甚至剪切[48],该薄膜模型由于忽略了筛板的厚度以及抗弯刚度且只能承受张力,因此并不适用于解决筛板问题.根据筛板的受力状态,板理论模型更适合解决筛板问题.

3.2 弹性薄板小变形模型

文献[54]将筛板视为受到巩膜拉力$N$和横向轴对称载荷的各向同性弹性圆板(图8(b)),根据弹性力学的Kirchhoff经典薄板小变形理论,建立了筛板的首个力学模型,并得到筛板的变形挠度

$$w\left( r \right) = \dfrac{q}{2N}\left[ {\dfrac{R^2 - r^2}{2} - \dfrac{I_0\left( {\sqrt {N /D} R} \right) - I_0 \left( {\sqrt {N/D} r} \right)}{\sqrt {N /D} I_1 \sqrt {N/ D} R}R} \right] $$

其中,筛板的抗弯刚度$D = Eh^{3}/[12(1-\mu^{2})]$,$E$为筛板的弹性模量,$h$为筛板厚度,$R$为筛板半径, $\mu $为泊松比, 横向载荷$q = IOP-ICP$,$I_{0}$, $I_{1}$为贝塞尔函数.在该理论模型中,文献[54]将升高的眼内压转化为横向载荷$q$和巩膜拉力$N$两个随之增大的力学载荷,提供了青光眼视神经机械损伤学说的生物力学依据.结果表明,眼内压升高会导致筛板位移增大,筛板的两个结构参数------厚度和半径,是影响筛板力学性能的主要因素：厚度影响筛板抗弯刚度,厚度越小,筛板位移越大;半径越大,筛板位移越大.

然而,在排除了筛板几何参数对结果影响的前提下,文献[54]的理论模型所得的挠度$w$相比于实验测量结果[37]误差较大(图9).例如,当眼内压$IOP = 25$,mmHg和70,mmHg时,该理论模型结果与实验值之间的误差分别超过20%与25%.因此,该理论模型结果并不能合理体现筛板变形状态,从而影响由此获得的其他力学参量的精确性.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   筛板理论模型计算挠度$w$结果与实验结果对比[46]

Fig. 9   The deflections of the center of the LC with IOP variation, which derive from the different mechanical models and experiment[46]


3.3 弹性薄板大变形模型

为解决小变形模型中筛板刚度较大的问题,Edwards等[55]将筛板视为弹性薄板,基于薄板大挠度弯曲理论,结合筛板、巩膜的生理特征参 数[56-57],建立了筛板固定边界圆板模型.通过理论分析,获得了筛板挠度$w$与筛板中心处最大挠度$w_{\max}$之间的关系

$$w = w_{\max } \left( {1 - \dfrac{r^2}{R^2}} \right)\left( {1 -k\dfrac{r^2}{R^2}} \right) (5)$$

其中,$k < 1$表示校正因子.研究结果表明,筛板挠度与其厚度成反比,筛板厚度增大时,筛板中心最大挠度相应减小;眼内压升高,筛板变形加剧;筛板边缘剪应力和剪应变最大.与Kirchhoff薄板小变形理论模型[54]相比,大变形理论模型[55]得到的筛板抗弯刚度要小很多.在排除了筛板几何参数对结果影响的前提下,大挠度模型所得到的挠度$w$与实验结 果[37]相差较大(图9).例如,当眼内压$IOP = 25$,mmHg和70,mmHg时,该理论模型结果与实验值之间的误差分别超过25%与30%.因此,Kirchhoff薄板大变形理论模型也不能合理体现筛板变形状态. 实际上,与筛板厚度(平均厚度300,$\mu$m)相比,筛板挠度远小于其厚度($h /w > 10$),大挠度弯曲理论假设并不成立,因此不适用于解决筛板变形问题.

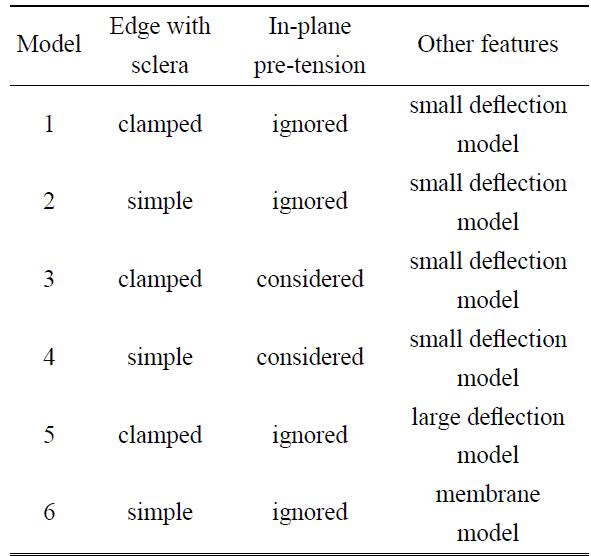
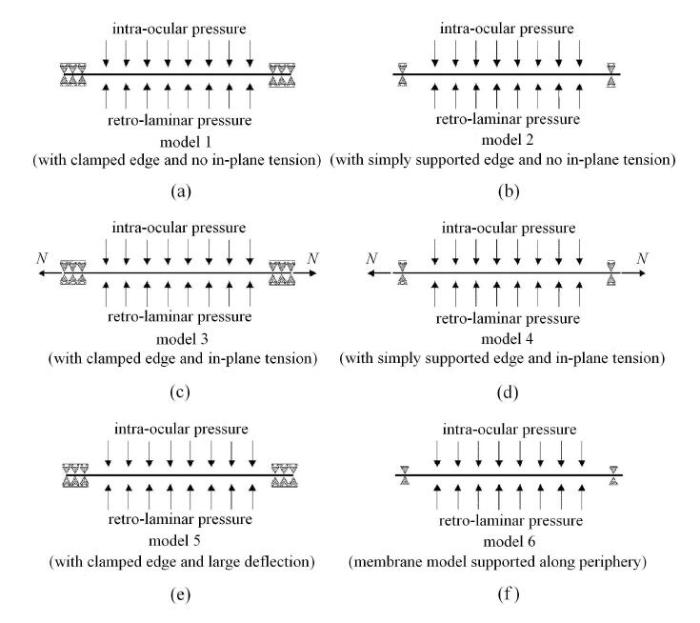
由3.2节与3.3节小结结果分析发现,以Kirchhoff薄板理论建立的力学模型[54-55]与实验测量[37]的筛板位移数据相差较大,并不能对筛板变形进行合理的力学性能分析.

3.4 基于弹性薄板理论的六种模型

在建立筛板模型过程中,边界条件的选择将对研究结果的正确性起到至关重要的影响. Newson等[58]基于Kirchhoff薄板理论,考虑了不同边界条件对计算结果的影响,建立了6种不同的筛板模型(图10,表2),分别计算了各模型筛板应力、应变的分布以及变形情况.

通过对比几种不同边界条件的理论模型的计算结果发现,采用夹支边界考虑巩膜预拉力的小变形薄板模型(模型3)与有限元方法计算结果最为接 近[58]. 同时,在相同几何参数条件下,将该结果(模型3)与两组筛板变形实验测量结果也十分接 近[37, 59]. 因此,对于筛板变形问题,采用夹支边界且考虑巩膜预拉力的小变形薄板模型,最为接近实际问题.

表2   6种不同的筛板边界条件

Table 2  Six boundary conditions of LC models

新窗口打开| 下载CSV


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   6种不同的筛板边界模型[58]

Fig. 10   Free body diagrams of the modeling idealizations in models 1-6 [58]


3.5 基于弹性薄板理论和血流动力学的流固耦合模型

Guidoboni等[18,60-61]在经典薄板理论模型[54]的基础上,提出了生物力学和血流动力学相耦合的筛板模型.该模型将筛板视为多孔固体弹性网络,血管则视为有血流通过的孔洞(图11),血液为牛顿流体.基于此模型,Guidoboni等[18,60-61]研究了眼内压升高和不同的边界约束条件对筛板内应力分布、血液通量和血流速度的影响.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   筛板区域视神经乳头、血管解剖图及其受力示意图[60]

Fig. 11   Left: anatomy of the central retinal vessels, right: schematic representation of the mathematical model[60]


Guidoboni等[18, 60-61]将筛板区域视为由充满血液的弹性微元体组成的流固耦合体,其组成与坐标和时间有关. 在此基础上,将零位移边界和考虑巩膜张力的夹支混合边界条件分别代入该模型,并进行数值迭代计算. 研究结果显示,巩膜张力随着眼内压的升高而增大,混合边界所得的数值结果大于零位移边界所得的数值结果. 与实验测量结果[28]对比发现,混合边界条件下筛板模型变形更接近真实情况. 此外,眼内压升高会造成筛板内等效应力增大,血液通量和血流速度减小. 筛板边缘的应力在高眼内压环境下会发生明显的增长,该部分的组织也更易受到损伤.

综上所述,基于拉普拉斯理论的薄膜模型仅能分析筛板承受张力的变形,忽略了筛板的厚度以及抗弯刚度,因此并不适用于解决筛板问题.筛板的层间剪切是视神经损伤的主要成因之一.然而,基于Kirchhoff经典薄板理论小变形模型、大变形模型以及流固耦合模型[18, 54-55, 58,60-61]由于其采用了直法线假设,从而使得该类力学模型不能分析筛板的横向剪切变形,限制了该力学模型的进一步应用.同时,一般薄板理论要求厚度与直径的比值小于0.1,而筛板厚度(0.24 $\sim $0.36,mm)与直径(半径约0.76 $\sim $1.14,mm)[37, 51]比值约在0.11 $\sim $0.24之间,造成采用基于Kirchhoff薄板理论的力学模型得到的结果与实验测量值误差较大.为了更深入地研究筛板变形,阐释 青光眼的发病机理,基于Reissner板理论的小变形模型近期被用于该领域的研究中.

3.6 Reissner板理论小变形模型

Tian等[46]将筛板视为小变形薄板,考虑了眼内压和颅内压对筛板的共同影响,应用Reissner板小变形理论对筛板受力变形进行力学分析.Reissner板理论对Kirchhoff薄板理论进行了修正,摒弃了直法线的基本假定,引入了板的横向剪切变形,其适用范围从薄板扩大到了中厚板.

在该模型中,筛板被视为边界受到面内拉力$N$的夹支圆板(图12).与Kirchhoff经典薄板理论所得结果相比,Reissner板理论模型[46]所得结果,更为接近实验结果(图9)[37]：当眼内压$IOP =25$,mmHg与70,mmHg时,该理论模型结果与实验测量值之间的误差仅为5%和10%.与Kirchhoff经典薄板理论小变形模型[54]和大变形模型[55]中筛板抗弯刚度过大、过小两种情况不同,该理论模型更能合理反映筛板变形. 更重要的是,该模型得到了筛板的剪应变

$$\gamma _{rz} = - \dfrac{3qa}{Gh^3(1 + \dfrac{N}{C})}\left( {\dfrac{h^2}{4} -z^2} \right)\dfrac{I_1 \left( {\dfrac{k}{a}r} \right)}{I_1 \left( k \right)} $$

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   基于Reissner板理论的筛板变形模型[46]

Fig. 12   Schematic representation of the biomechanical model of the LC based on Reissner's plate theory[46]


由上式可以得到,剪应变在筛板中面处最大,沿厚度方向$z$呈抛物型分布,并由筛板中心向筛板边缘处增大.

Tian等[46]的模型首次将筛板的剪切变形引入青光眼发病机制的研究中,取得了与已有实验[37,51]相一致的结果. 其次,通过计算筛板上筛孔的变形和筛板层间剪切变形,从理论上验证了Quigley等[16,45]的视神经乳头机械损伤假说.同时,该模型考虑了颅内压对筛板变形以及视神经损伤的影响,提出了一种在正常眼内压下青光眼可能的发病机理.该研究有利于加深对青光眼发病机制的理解,可进一步为青光眼的临床治疗提供新的方向.

3.7 有限元方法的应用

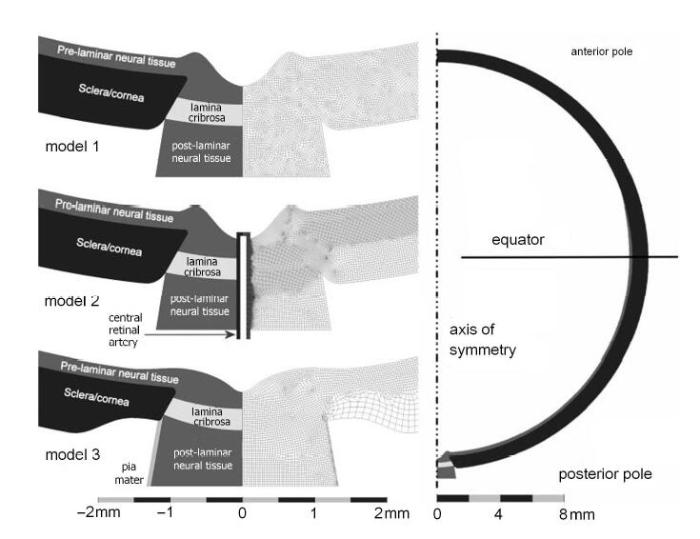
随着计算机的发展,有限元数值模拟方法已被用于计算、研究筛板的受力与变形[8-11, 48, 62-70].Bellezza等[62]采用有限元方法建立了13个理想化的眼球后巩膜壳三维几何模型,用于研究筛板变形与由眼内压造成的视乳头应力之间的关系.随后,Sigal等[48,63-67]通过建立包含筛板、筛板前后神经组织、巩膜、软脑膜及视网膜中央血管的有限元模型(图13),研究了筛板的应力、应变与变形,进而分析了视乳头的组织特性与生物力学特性,发现视乳头在与周边生物力学结构与组织协作下,可稳定地应对外界压力的变化.Yang等[69]利用有限元方法分析了在眼内压急剧增加时慢性青光眼的猴眼视神经乳头和筛板.发现筛板与巩膜可通过局部压缩变薄、伸展以及变形来弱化眼内压急剧增加对视乳头的影响.祁昕征等[68]建立了包含筛板、视网膜和脉络膜的视乳头组织三维模型.结合光相干断层扫描仪与有限元计算模型,分析了不同眼压下视网膜、脉络膜和筛板的厚度变化,通过与实验比较,证明了利用有限元法可对眼底各组织在高眼压下的形态变化进行预测的可行性.有限元方法的应用已为我们提供了大量关于筛板应力、应变与形变信息,便于我们理解青光眼的发病机理.但是由于筛板微结构的复杂性(如筛板中视神经通道(筛孔)和微板层尺寸小、结构缠结),严重地影响了有限元方法在筛板变形和损伤分析领域中的应用,如何获取更为精确的变形和受力状态,对有限元法提出了挑战.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   视乳头区域有限元计算模型[67]

Fig. 13   Finite element modeling of the optic nerve head region[67]


4 研究展望尽管

Tian等[46]给出了较为合理的筛板力学理论模型,但在与青光眼发生、发展密切相关的筛板变形研究中,仍有许多问题亟待解决. 首先,筛板是由胶原纤维组成的复杂网状结构,虽然可将其视为弹性圆板,但筛板上存在200 $\sim $400个筛孔,它们的存在在筛板变形中引起的应力集中问题,是青光眼发病机制研究中不容忽视的问题.在此前许多研究 中[14,49-50],提到了筛板上变形的不均匀性以及筛孔周围的高应力现象,这些现象对研究筛板变形如何引起视神经乳头损伤十分重要,而目前尚未提出明确的理论. 其次,筛板的层间横向剪切变形是视神经损伤的主要成因之一.筛板是由胶原纤维组成的复杂网状弹性结构,约可分为10层,在剪应力的作用下各层发生错动,其具体形式尚不明确.此外,目前关于筛板变形的研究主要集中在筛板自身在高眼压作用下的组织和结构变化,对于筛板变形引起的视神经乳头损伤机制研究较少,变形后的筛板如何挤压、损伤视神经乳头以及筛板变形对视神经血液循环的影响等问题仍无定论.最后,在临床上,杯盘比(视杯直径与视盘直径之比,$C /D$),是判断视神经损伤程度的重要诊断依据,正常人眼杯盘比为0.3 $\sim $0.6.青光眼患病眼杯盘比大于0.6,而在目前已有的理论研究中,无论是Kirchhoff薄板理论模型还是Reissner板理论模型,筛板杯盘比均在0.6左右且并不会随眼压升高而改变. 因此,对于青光眼患病眼的杯盘比为何会增大,仍没有合理的理论能够解释.同时,随着计算机科学的发展,借助图像识别和人工智能技术进行疾病诊断已得到应用.研究如何将光相干断层扫描(OCT)影像、眼压、杯盘比、视野与人工智能技术结合对青光眼进行诊断[71-75],不仅能够对临床青光眼的诊疗带来革命性的影响,还会带来巨大的社会经济效应.

参考文献

Girard MJA, Strouthidis NG, Desjardins A , et al.

In vivo optic nerve head biomechanics: Performance testing of a three-dimensional tracking algorithm

Journal of the Royal Society Interface, 2013,10(87):20130459

[本文引用: 5]

Thylefors B, Negrel AD, Pararajasegaram R , et al.

Global data on blindness

Bulletin of the World Health Organization, 1995,73(1):115-121

[本文引用: 1]

Quigley HA, Broman AT .

The number of people with glaucoma worldwide in 2010 and 2020

British Journal of Ophthalmology, 2006,90(3):262-267

[本文引用: 1]

徐亮, 张莉, 夏翠然 等.

北京农村及城市特定人群原发性闭角型青光眼的患病率及其影响因素

中华眼科杂志, 2005,41(1):8-14

[本文引用: 1]

( Xu Liang, Zhang Li, Xia Cuiran , et al.

The prevalence and its effective factors of primary angle-closure glaucoma in def ined populations of rural and urban in Beijing

Chinese Journal of Ophthalmology, 2005,41(1):8-14 (in Chinese))

[本文引用: 1]

王小中, 张国梅, 归锦纹 等.

121697人健康体检中青光眼的筛查结果分析

实用防盲技术, 2008,3(1):10-13

[本文引用: 1]

( Wang Xiaozhong, Zhang Guomei, Gui Jinwen , et al.

Analysis of screening for glaucoma in health check-up for 121697 people

Department of Ophthalmology, 2008,3(1):10-13 (in Chinese))

[本文引用: 1]

Leske MC, Wu SY, Hennis A , et al.

Risk factors for incident open-angle glaucoma

Ophthalmology, 2008,115(1):85-93

[本文引用: 1]

Sommer A, Tielsch JM, Katz J , et al.

Relationship between intraocular pressure and primary open angle glaucoma among white and black Americans: The Baltimore Eye Survey

Archives of Ophthalmology, 1991,109(8):1090-1095

[本文引用: 1]

Heijl A, Leske MC, Bengtsson B , et al.

Reduction of intraocular pressure and glaucoma progression - Results from the early manifest glaucoma trial

Archives of Ophthalmology, 2002,120(10):1268-1279

[本文引用: 2]

Maier PC, Funk J, Schwarzer G , et al.

Treatment of ocular hypertension and open angle glaucoma: Meta-analysis of randomised controlled trials

British Medical Journal, 2005,331(7509):134-136B

[本文引用: 1]

Quigley HA, Addicks EM, Green WR , et al.

Optic nerve damage in human glaucoma: II. The site of injury and susceptibility to damage

Archives of Ophthalmology, 1981,99(4):635-649

[本文引用: 2]

Sigal IA, Ethier CR .

Biomechanics of the optic nerve head

Experimental Eye Research, 2009,88(4):799-807

[本文引用: 2]

Quigley HA .

Reappraisal of the mechanisms of glaucomatous optic nerve damage. Eye-Transactions of the Ophthalmological Societies of the

United Kingdom, 1987,1:318-322

Kim YN, Shin JW, Sung KR .

Relationship between progressive changes in lamina cribrosa depth and deterioration of visual field loss in glaucomatous eyes

Korean Journal of Ophthalmology: KJO, 2018,32(5):470-477

[本文引用: 1]

Voorhees AP, Jan NJ, Sigal IA .

Effects of collagen microstructure and material properties on the deformation of the neural tissues of the lamina cribrosa

Acta Biomaterialia, 2017,58:278-290

[本文引用: 3]

Berdahl JP, Allingham RR, Johnson DH .

Cerebrospinal fluid pressure is decreased in primary open-angle glaucoma

Ophthalmology, 2008,115(4):763-768

[本文引用: 2]

Quigley HA, Addicks EM .

Regional differences in the structure of the lamina cribrosa and their relation to glaucomatous optic nerve damage

Archives of Ophthalmology, 1981,99(1):137-143

[本文引用: 1]

Jonas JB, Berenshtein E, Holbach L .

Anatomic relationship between lamina cribrosa, intraocular space,and cerebrospinal fluid space

Investigative Ophthalmology & Visual Science, 2003,44(12):5189-5195

[本文引用: 1]

Causin P, Guidoboni G, Harris A , et al.

A poroelastic model for the perfusion of the lamina cribrosa in the optic nerve head

Mathematical Biosciences, 2014,257:33-41

[本文引用: 5]

Quigley HA, Addicks EM, Green WR .

Optic nerve damage in human glaucoma: III. Quantitative correlation of nerve fiber loss and visual field defect in glaucoma, ischemic neuropathy, papilledema, and toxic neuropathy

Archives of Ophthalmology, 1982,100(1):135-146

[本文引用: 2]

Wang B, Tran H, Smith MA , et al.

In-vivo effects of intraocular and intracranial pressures on the lamina cribrosa microstructure

Plos One, 2017,12(11):e0188302

[本文引用: 1]

Johannesson G, Eklund A, Linden C .

Intracranial and intraocular pressure at the lamina cribrosa: Gradient effects

Current Neurology and Neuroscience Reports, 2018,18(4):25

[本文引用: 1]

Quigley HA ,

Pathophysiology of optic nerve in glaucoma//McAllister JA, Wilson RP, Eds. Glaucoma. Butterworths,

London, 1986, 30-53

[本文引用: 2]

Tian H, Du R, Song F .

A modified relation between the intraocular and intracranial pressures

Theoretical and Applied Mechanics Letters, 2016,6(3):148-150

[本文引用: 1]

Spentzas T, Henricksen J, Patters AB , et al.

Correlation of intraocular pressure with intracranial pressure in children with severe head injuries

Pediatric Critical Care Medicine, 2010,11(4):593-598

[本文引用: 4]

Lashutka MK, Chandra A, Murray HN , et al.

The relationship of intraocular pressure to intracranial pressure

Annals of Emergency Medicine, 2004,43(4):585-591

Sajjadi SA, Harirchian MH, Sheiklibahaei N , et al.

The relation between intracranial and intraocular pressures: Study of 50 patients

Annals of Neurology, 2006,59(4):867-870

Li Z, Yang YX, Lu Y , et al.

Intraocular pressure $vs$intracranial pressure in disease conditions: A prospective cohort study (Beijing iCOP study)

BMC Neurology, 2012,12:66

[本文引用: 4]

Yan DB, Coloma FM, Metheetrairut A , et al.

Deformation of the lamina cribrosa by elevated intraocular pressure

British Journal of Ophthalmology, 1994,78(8):643-648

[本文引用: 5]

Emery JM, Landis D, Paton D , et al.

The lamina cribrosa in normal and glaucomatous human eyes

Transactions American Academy of Ophthalmology and Otolaryngology, 1974,78(2):O290-O297

[本文引用: 1]

Quigley HA, Anderson DR .

The dynamics and location of axonal transport blockade by acute intraocular pressure elevation in primate optic nerve

Investigative Ophthalmology, 1976,15(8):606-616

[本文引用: 1]

Minckler DS, Bunt AH, Klock IB .

Radioautographic and cytochemical ultrastructural studies of axoplasmic transport in the monkey optic nerve head

Investigative Ophthalmology & Visual Science, 1978,171(1):33-50

Anderson DR, Hendrick A .

Effect of intraocular pressure on rapid axoplasmic transport in monkey optic nerve

Investigative Ophthalmology, 1974,13(10):771-783

[本文引用: 1]

Maumenee AE .

Causes of optic nerve damage in glaucoma: Robert N. Shaffer Lecture

Ophthalmology, 1983,90(7):741-752

[本文引用: 1]

Bellezza AJ, Rintalan CJ, Thompson HW , et al.

Deformation of the lamina cribrosa and anterior scleral canal wall in early experimental glaucoma

Investigative Ophthalmology & Visual Science, 2003,44(2):623-637

[本文引用: 1]

Zeimer RC .

The relation between glaucomatous damage and optic nerve head mechanical compliance

Archives of Ophthalmology, 1989,107(8):1232-1234

[本文引用: 1]

Coleman AL, Quigley HA, Vitale S , et al.

Displacement of the optic nerve head by acute changes in intraocular pressure in monkey eyes

Ophthalmology, 1991,98(1):35-40

[本文引用: 1]

Levy NS, Crapps EE .

Displacement of optic nerve head in response to short-term intraocular pressure elevation in human eyes

Archives of Ophthalmology, 1984,102(4):782-786

[本文引用: 9]

Tezel G, Trinkaus K, Wax MB .

Alterations in the morphology of lamina cribrosa pores in glaucomatous eyes

British Journal of Ophthalmology, 2004,88(2):251-256

[本文引用: 4]

Radius RL, Gonzales M .

Anatomy of the lamina cribrosa in human eyes

Archives of Ophthalmology, 1981,99(12):2159-2162

[本文引用: 1]

Dandona L, Quigley HA, Brown AE , et al.

Quantitative regional structure of the normal human lamina cribrosa: A racial comparison

Archives of Ophthalmology, 1990,108(3):393-398

[本文引用: 1]

Jonas JB, Mardin CY, Schlotzerschrehardt U , et al.

Morphometry of the human lamina cribrosa surface

Investigative Ophthalmology & Visual Science, 1991,32(2):401-405

[本文引用: 1]

Susanna R .

The lamina cribrosa and visual field defects in open-angle glaucoma. Canadian Journal of Ophthalmology-Journal Canadien D

Ophtalmologie, 1983,18(3):124-126

[本文引用: 1]

Miller KM, Quigley HA .

Comparison of optic disc features in low-tension and typical open-angle glaucoma

Ophthalmic Surgery and Lasers, 1987,18(12):882-889

Miller KM, Quigley HA .

The clinical appearance of the lamina cribrosa as a function of the extent of glaucomatous optic nerve damage

Ophthalmology, 1988,95(1):135-138

[本文引用: 1]

Quigley HA, Flower RW, Addicks EM , et al.

The mechanism of optic nerve damage in experimental acute intraocular pressure elevation

Investigative Ophthalmology & Visual Science, 1980,19(4):505-517

[本文引用: 4]

Tian HJ, Li L, Song F .

Study on the deformations of the lamina cribrosa during glaucoma

Acta Biomaterialia, 2017,55:340-348

[本文引用: 9]

Shoji T, Kuroda H, Suzuki M , et al.

Glaucomatous changes in lamina pores shape within the lamina cribrosa using wide bandwidth, femtosecond mode-locked laser OCT

Plos One, 2017,12(7):17

[本文引用: 1]

Sigal IA, Grimm JL, Jan NJ , et al.

Eye-specific IOP-induced displacements and deformations of human lamina cribrosa

Investigative Ophthalmology & Visual Science, 2014,55(1):1-15

[本文引用: 6]

Tran H, Grimm J, Wang B , et al.,

Mapping in-vivo optic nerve head strains caused by intraocular and intracranial pressures//Larin KV, Sampson DD, Eds. Optical Elastography and Tissue Biomechanics IV,Proceedings of SPIE - The International Society for Optical Engineering,

Bellingham, 2017,10067

[本文引用: 2]

Midgett DE, Pease ME, Jefferys JL , et al.

The pressure-induced deformation response of the human lamina cribrosa: Analysis of regional variations

Acta Biomaterialia, 2017,53:123-139

[本文引用: 2]

Sigal IA, Flanagan JG, Ethier CR .

Factors influencing optic nerve head biomechanics

Investigative Ophthalmology & Visual Science, 2005,46(11):4189-4199

[本文引用: 3]

Szczudlowski K .

Glaucoma hypothesis: Application of the law of Laplace

Medical Hypotheses, 1979,5(4):481-485

[本文引用: 1]

Cahane M, Bartov E .

Axial length and scleral thickness effect on susceptibility to glaucomatous damage: A theoretical model implementing Laplace's law

Ophthalmic Research, 1992,24(4):280-284

[本文引用: 1]

Dongqi H, Zeqin R .

A biomathematical model for pressure-dependent lamina cribrosa behavior

Journal of Biomechanics, 1999,32(5):579-584

[本文引用: 8]

Edwards ME, Good TA .

Use of a mathematical model to estimate stress and strain during elevated pressure induced lamina cribrosa deformation

Current Eye Research, 2001,23(3):215-225

[本文引用: 5]

Jones IL, Warner M, Stevens JD .

Mathematical modelling of the elastic properties of retina: A determination of Young's modulus

Eye, 1992,6:556-559

[本文引用: 1]

Woo SLY, Schlegel WA, Kobayashi AS , et al.

Nonlinear material properties of intact cornea and sclera

Experimental Eye Research, 1972,14(1):29-39

[本文引用: 1]

Newson T, El-Sheikh A .

Mathematical modeling of the biomechanics of the lamina cribrosa under elevated intraocular pressures. Journal of Biomechanical Engineering-Transactions of the

Asme, 2006,128(4):496-504

[本文引用: 5]

Yan DB, Flanagan JG, Farra T , et al.

Study of regional deformation of the optic nerve head using scanning laser tomography

Current Eye Research, 1998,17(9):903-916

[本文引用: 1]

Guidoboni G, Harris A, Cassani S , et al.

Intraocular pressure, blood pressure, and retinal blood flow autoregulation: A mathematical model to clarify their relationship and clinical relevance

Investigative Ophthalmology & Visual Science, 2014,55(7):4105-4118

[本文引用: 6]

Guidoboni G, Harris A, Carichino L , et al.

Effect of intraocular pressure on the hemodynamics of the central retinal artery: A mathematical model

Mathematical Biosciences and Engineering, 2014,11(3):523-546

[本文引用: 4]

Bellezza AJ, Hart RT, Burgoyne CF .

The optic nerve head as a biomechanical structure: Initial finite element modeling

Investigative Ophthalmology & Visual Science, 2000,41(10):2991-3000

[本文引用: 2]

Sigal IA, Bilonick RA, Kagemann L , et al.

The Optic Nerve Head as a Robust Biomechanical System

Investigative Ophthalmology & Visual Science, 2012,53(5):2658-2667

[本文引用: 1]

Sigal IA, Flanagan JG, Lathrop KL , et al.

Human Lamina Cribrosa Insertion and Age

Investigative Ophthalmology & Visual Science, 2012,53(11):6870-6879

Sigal IA, Grimm JL .

A Few Good Responses: Which mechanical effects of IOP on the ONH to study?

Investigative Ophthalmology & Visual Science, 2012,53(7):4270-4278

Sigal IA, Grimm JL, Schuman JS , et al.

A method to estimate biomechanics and mechanical properties of optic nerve head tissues from parameters measurable using optical coherence tomography

IEEE Transactions on Medical Imaging, 2014, 33(5): 1381-1389

Sigal IA, Flanagan JG, Tertinegg I, et al.

Finite element modeling of optic nerve head biomechanics

Investigative Ophthalmology & Visual Science, 2004,45(12):4378-4387

[本文引用: 3]

祁昕征, 魏超, 杨佳燕 等.

三维有限元模型力学分析可预测视乳头的形状变化

中国组织工程研究, 2013,17(50):8712-8718

[本文引用: 1]

( Qi Xinzheng, Wei Chao, Yang Jiayan , et al.

Shape variation of optic nerve head by mechanical analysis using three-dimensional finite element model

Chinese Journal of Tissue Engineering Research, 2013,17(50):8712-8718 (in Chinese))

[本文引用: 1]

Yang HL, Downs JC, Sigal IA , et al.

Deformation of the normal monkey optic nerve head connective tissue after acute IOP elevation within 3-D histomorphometric reconstructions

Investigative Ophthalmology & Visual Science, 2009,50(12):5785-5799

[本文引用: 1]

Schwaner SA, Kight AM, Perry RN , et al.

A methodology for individual-specific modeling of rat optic nerve head biomechanics in glaucoma. Journal of Biomechanical Engineering-Transactions of the

ASME, 2018,140(8):084501

[本文引用: 1]

张秀兰, 李飞 .

人工智能与青光眼:机遇与挑战

中华实验眼科杂志, 2018,36(4):245-247

[本文引用: 1]

( Zhang Xiulan, Li Fei .

Artificial intelligence and glaucoma: Opportunities and challenges

Chinese Journal of Experimental Ophthalmology, 2018,36(14):245-247 (in Chinese))

[本文引用: 1]

Singh A, Dutta MK , ParthaSarathi M, et al.

Image processing based automatic diagnosis of glaucoma using wavelet features of segmented optic disc from fundus image

Computer Methods and Programs in Biomedicine, 2016,124:108-120

Li ZX, He YF, Keel S , et al.

Efficacy of a deep learning system for detecting glaucomatous optic neuropathy based on color fundus photographs

Ophthalmology, 2018,125(8):1199-1206

Muhammad H, Fuchs TJ, De Cuir N , et al.

Hybrid deep learning on single wide-field optical coherence tomography scans accurately classifies glaucoma suspects

Journal of Glaucoma, 2017,26(12):1086-1094

Niwas SI, Lin WS, Bai XL , et al.

Automated anterior segment OCT image analysis for angle closure glaucoma mechanisms classification

Computer Methods and Programs in Biomedicine, 2016,130:65-75

[本文引用: 1]

/

〈 〉