引言
国内外对于曲梁建模仿真的主要研究内容为结构静力学、自由振动、屈曲与稳定性分析和动力学响应方面.如DiRe[8]应用Timoshenko剪切梁理论,推导出由弹性砖块与非线性砂浆层耦合的剪切曲梁单元,建立了平面砌体拱模型,分析了拱的静力学变形并通过实验验证了模型的正确性.Bediz等[9]利用切比雪夫谱方法分析了在混合边界条件下任意横截面形式的三维曲梁弯曲,拉伸和扭转模态.宋郁明等[10]基于Timoshenko梁的几何方程和物理方程推导出圆弧曲梁的振动微分方程,将圆弧的曲率半径趋于无穷大,则圆弧梁的振动微分方程退化为直线梁的振动微分方程,得出了曲梁面内振动与面外振动互不耦合的结论.Stoykov[11]采用Euler-Bernoulli梁理论推导出了在极坐标系框架下的Green-Lagrangian应变张量,通过Ritz法离散偏微分方程,分析研究了半圆形曲梁的屈曲分叉点和相应的二次分枝点.基于Kirchhoff理论胡玉佳等[12]采用欧拉角来描述曲梁横截面的空间位姿建立了三维空间曲梁的控制方程,采用三层坐标系法解决欧拉角的奇异性问题,通过数值算例证明了该方法能有效地解决空间曲梁大变形动力学建模问题.张建书等[13]通过计入应力刚化效应的变形项导出柔性曲梁的变形能表达式,对大范围运动的曲梁进行应力刚化效应的特征值分析.潘科琪等[14]通过Lagrange插值函数构建了四节点曲梁单元,对比研究发现当直接采用曲梁单元离散曲梁和采用直梁单元逼近曲梁,曲梁单元只需要较少数量即可收敛,并与ADAMS的计算结果对比验证了该曲梁模型的正确性.
但是这类文献中并没有研究集中质量、旋转角速度和曲梁的初始曲率对旋转曲梁动力学特性的影响,以及分析旋转曲梁模态特性中的频率转向和振型切换现象.文献[15]表明集中质量大小以及旋转角速度的快慢将会对旋转直梁的模态特性产生较大的影响,所以本文提出一种基于绝对节点坐标法(ANCF)的旋转柔性曲梁新模型,用以研究集中质量和旋转角速度对旋转曲梁动力学特性的影响.
精准的曲梁建模是深入研究旋转曲梁动力学行为的关键.绝对节点坐标法(ANCF)是可资使用的一种优秀方法.由于ANCF是斜率矢量描述,对于梁截面与中心线垂直的Euler-Bernoulli梁问题能很好地解决[16],但是伴随着描述截面横向和纵向变形的插值函数不一致所导致的剪切闭锁问题一直制约着ANCF的发展,所以针对ANCF直梁单元的优化建模主要集中在解决单元的剪切闭锁问题[17-20].另外一个热点方向就是构造高阶梁单元,如Orzechowski等[21]利用高阶插值函数推导出了梁截面可以变形的三维高阶ANCF直梁单元,该梁单元可以准确描述梁拉伸、弯曲、扭转耦合的变形模式并且证明了该高阶梁单元可以有效地捕捉到梁截面的翘曲变形和消除了泊松闭锁问题.相较于直梁单元,曲梁由于有初始曲率,因此对其应变描述会更加复杂.刘铖等[22]推导了曲梁的Green-Lagrangian应变,根据该应变导出了曲梁的应变能,与传统的ANCF梁单元的应变能有细微的差距,通过算例证明了该单元能有效应用于静力学和动力学计算.Sugiyama等[23]应用Hellinger-Reissner变分原理,构造了ANCF杂交剪切曲梁单元,并计算了圆环的固有频率和Hub-beam系统的动力学响应,但是剪切曲梁的高跨比跟Euler-Bernoulli梁相当,不能很好地说明该剪切梁单元能处理高跨比比较大的剪切梁.陈渊钊等[24]在ANCF曲梁模型中引入径向点插值函数(radial pointinterpolation method,RPIM),使用RPIM描述曲梁的位移场,通过算例说明该方法比传统的ANCF精度更高.ANCF还可用于旋转系统的动力学特性分析,如赵将等[25],章孝顺等[15]分别基于ANCF薄板单元和直梁单元分析了旋转柔性薄板和旋转柔性直梁动力学特性中的频率转向和振型切换问题.近年来也有许多学者用ANCF分析非线性接触问题,如兰朋等[26]提出完备化ANCF薄板单元和参考节点的概念建立了车体与钢板弹簧之间的刚柔耦合动力学模型,过佳雯等[27],王庆涛等[28]基于ANCF直梁单元分别建立了考虑含芯拧绞绳中绳股内的线接触模型和弹塑性梁的多区域接触模型.另外,由于ANCF是纯Lagrange描述,因此其应用范围也可以延伸到流体力学领域[29-32].
本文的研究目的是研究集中质量、旋转角速度和初始曲率对于旋转曲梁动力学特性的影响,以及分析旋转曲梁模态特性中的频率转向和振型切换问题.为此,本文基于绝对节点坐标法,从连续介质力学的Green-Lagrangian应变和曲线曲率的精确表达式出发,利用{$\delta$}函数和中心刚体与悬臂曲梁之间的固支边界条件,建立了带集中质量的旋转柔性曲梁动力学模型.通过悬臂曲梁的纯弯曲测试和旋转柔性曲梁的动力学仿真结果分别验证了本文所提出曲梁单元的收敛性和动力学模型的正确性.进一步应用D'Alembert原理,将旋转曲梁等效为带离心力的无旋转曲梁,并借助Newton-Raphson迭代获得等效静力平衡状态下的绝对节点坐标列阵,将其代入通过线性摄动处理获得的系统特征方程,并以此为基础分析研究了集中质量、旋转角速度和初始曲率对曲梁动力学特性的影响.最后本文以旋转直梁的频率转向和振型切换为基础,分析了曲梁的频率转向和振型切换问题.
1 曲梁刚柔耦合动力学建模
1.1 物理描述
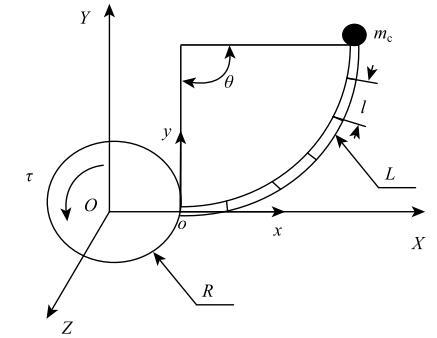
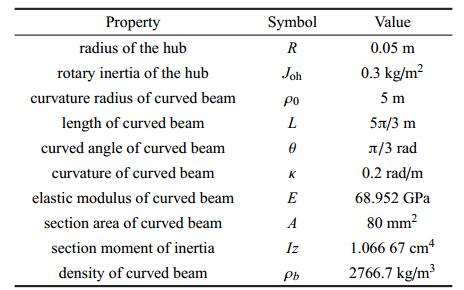
如图1所示,考虑附加集中质量的中心刚体柔性曲梁系统,中心刚体为圆盘,半径为$R.$柔性曲梁曲率半径远大于横截面高度,横截面与中轴线垂直并且关于中轴线对称,不计横截面转动惯量与剪切效应.柔性曲梁总弧长为$L$,曲梁两端点对应的夹角为曲梁弧度角$\theta$,集中质量位于曲梁弧长端点处且大小为$m_{c}$,作用在中心刚体上的力矩为$\tau$使中心刚体柔性曲梁系统绕着$OZ$轴做转动,惯性坐标系为$OXY$,浮动坐标系$oxy$如图固结在中心刚体上.
图1
图1
带集中质量的中心刚体柔性曲梁示意图
Fig. 1
Configuration of hub-curved beam with concentrated mass
1.2 动力学方程推导
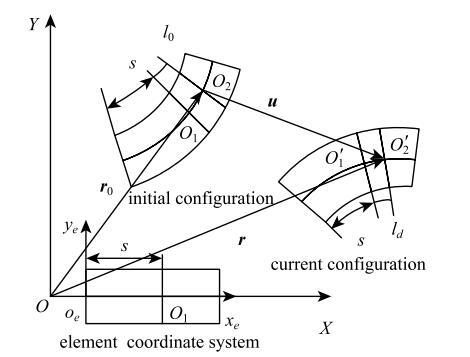
对柔性曲梁进行有限单元离散,将曲梁等分为$n$个曲梁单元,变形前后的曲梁单元如图2所示, $o_{e}x_{e}y_{e}$为曲梁单元坐标系,$l=L/n$为曲梁单元的长度. 对于一维二节点的曲梁单元,其变形如图2所示, 梁单元中轴线上任意一点$O_{1}$的全局绝对位置矢量$r$为 \begin{equation} \label{eq1} r = \left[ {{\begin{array}{*{20}c} {r_1 } \\ {r_2 } \\ \end{array} }} \right] = \left[ {{\begin{array}{*{20}c} {a_0 + a_1 s + a_2 s^2 + a_3 s^3} \\ {b_0 + b_1 s + b_2 s^2 + b_3 s^3} \\ \end{array} }} \right] = {Ne}(1) \end{equation} 式中,$r_{1}$,$r_{2}$分别为$X$,$Y$方向上的绝对位置坐标,$e$为曲梁单元在惯性坐标系$OXY$下的绝对节点坐标列阵,$N$为曲梁单元的形函数 \begin{equation} \label{eq2} N = \left[ {{\begin{array}{*{20}c} {n_1 } & 0 & {n_2 l} & 0 & {n_3 } & 0 & {n_4 l} & 0 \\ 0 & {n_1 } & 0 & {n_2 l} & 0 & {n_3 } & 0 & {n_4 l} \\ \end{array} }} \right](2) \end{equation}其中 \begin{equation} \label{eq3} \left. {{\begin{array}{l} {n_1 = 1-3\xi ^2 + 2\xi ^3} \\ {n_2 = \xi-2\xi ^2 + \xi ^3} \\ {n_3 = 3\xi ^2-2\xi ^3} \\ {n_4 =-\xi ^2 + \xi ^3} \\ \end{array} }} \right\}(3) \end{equation} 式中,$\xi =s/l$,$s$为图2曲梁单元未变形时中轴线上任意一点在单元坐标系下的弧坐标, $l$为曲梁单元未变形时中轴线的弧长. 曲梁单元在惯性坐标系下的绝对节点坐标列阵可表示为
$$\begin{align*} &e = [{\begin{array}{*{20}c} {r^{T}} |_{s = 0} & r_s^{T} |_{s = 0} & r^{T} |_{s = l} & r_s^{T} |_{s = l} \\ \end{array} }]^{T}= \\ &\qquad \left[ {{\begin{array}{*{20}c} {e_1 } & {e_2 } & {e_3 } & {e_4 } & {e_5 } & {e_6 } & {e_7 } & {e_8 } \\ \end{array} }} \right]^{T}(4)\end{align*}$$
其中曲梁单元节点中的绝对位置坐标为 \begin{equation} \label{eq5} \left.\begin{array}{ll} e_1 = r_1 |_{s = 0}, & e_2 = r_2 |_{s = 0} \\ e_5 = r_1 |_{s = l}, & e_6 = r_2 |_{s = l}\\ \end{array}\right\}(5) \end{equation} 曲梁单元节点中的绝对位置斜率为 \begin{equation} \label{eq6} \left.\begin{array}{ll} e_3 = \left.\dfrac{\partial r_1 }{\partial s}\right|_{s = 0}, & e_4 = \left.\dfrac{\partial r_2 }{\partial s}\right|_{s = 0} e_7 = \left.\dfrac{\partial r_1 }{\partial s}\right|_{s = l},& e_8 = \left.\dfrac{\partial r_2 }{\partial s}\right|_{s = l}\\ \end{array}\right\}(6) \end{equation} 梁单元的动能可以表示为 \begin{equation} \label{eq7} T_e = \frac{1}{2}\int_V {\rho _{b} \dot{r}^{T}\dot{r}{d}V = \frac{1}{2}\dot {e}^{T}M_e \dot{e}}(7) \end{equation} 其中$M_e$为曲梁单元的质量阵,可表示为 \begin{equation} \label{eq8} M_e = \int_0^l {\rho _{b} AN\left( s \right)^{T}N\left( s \right){d}s}(8) \end{equation} 式中,$\rho_{b}$和$A$分别为曲梁单元未变形时的密度和横截面积.
设$q$为曲梁总的绝对节点坐标列阵,$B_{e}$为曲梁单元节点坐标列阵对应总体绝对节点坐标列阵中的布尔定位矩阵. $q$和$B_{e}$则有式(9)所表示的关系 \begin{equation} \label{eq9} e = B_e q(9) \end{equation} 因此整根曲梁的动能可以表示为 \begin{equation} \label{eq10} T_{b} = \sum\limits_{e = 1}^n {T_e = \frac{1}{2}\dot {q}^{T}M_b \dot{q}}(10) \end{equation} 其中$M_{b}$为曲梁的总质量阵 \begin{equation} \label{eq11} M_{b} = \sum\limits_{e = 1}^n {B_e^{ T} M_e B_e }(11) \end{equation}
图2
图2
曲梁单元初始构型,即时构型示意图
Fig. 2
Curved beam element in initial and current configuration
当在柔性曲梁任意位置附加集中质量时,附加集中质量可以等效为单位长度上的质量线密度函数, 可以用$\delta$函数表示为 \begin{equation} \label{eq12} \rho _{c} = M_{c} \delta \left( {\bar {s}-a} \right)(12) \end{equation} 其中,$M_{ c}$为集中质量的数值,$\bar{s}$为曲梁中心轴线上任意一点的弧坐标, $a$为集中质量位于曲梁上某个位置所对应的弧坐标 \begin{equation} \label{eq13} a = \sum\limits_{i = 1}^{k-1} {l_i + \Delta l}, \quad k = 1,2,\cdots, n(13) \end{equation} 其中,$k$为集中质量所在曲梁单元在总单元里的编号,$\Delta l$为集中质量所在单元的位置距离单元坐标系原点的弧长距离. 附加集中质量的动能表达式可表示为
$$\begin{align*} & T_{c} = \frac{1}{2}\int_0^L {\rho _{c} \dot {r}^{T}\dot {r}{d}x}=\\ &\qquad\frac{1}{2}m_{c} \dot{e}_k^{T} N^{ T}\left( {\Delta l} \right)N\left( {\Delta l} \right)\dot {e}_k(14)\end{align*} $$
式(14)中,$e_{k}$为集中质量所位于的曲梁单元的绝对节点坐标列阵.
设$B_{k}$为集中质量所位于的曲梁单元绝对节点坐标列阵对应总体节点坐标列阵中的布尔定位矩阵, 则可以将(14)式改写为
$$\begin{align*} & T_{c} = \frac{1}{2}M_{c} \dot {e}_k^{T} N^{T}\left( {\Delta l} \right)N\left( {\Delta l} \right)\dot{e}_k=\\ &\qquad \frac{1}{2}m_c \dot {q}^{T}B_k^{T} N^{T}\left( {\Delta l} \right)N\left( {\Delta l} \right)B_k q=\\ &\qquad \frac{1}{2}\dot {q}^{T}M_c \dot {q}(15)\end{align*} $$
其中$M_{c}$为集中质量矩阵,可表示为 \begin{equation} \label{eq16} M_{c} = m_{c} B_k^{T} N^{ T}\left( {\Delta l} \right)N\left( {\Delta l} \right)B_k(16) \end{equation}
圆盘绕$OZ$轴转动的动能可以表示为 \begin{equation} \label{eq17} T_h = \frac{1}{2}J_{oh} \dot {\theta }_{h}^2 = \frac{1}{2}J_{oh} \omega _{h}^2(17) \end{equation} 其中,$\theta_{h}$和$\omega _{ h}$分别为圆盘的转过的角度和圆盘的角速度,$J_{ oh}$为圆盘的转动惯量.
考虑圆盘与曲梁之间的固支边界条件, 可以将曲梁与圆盘连接处的第一个节点坐标列阵用圆盘转过的角度$\theta _{h}$表示 \begin{equation} \label{eq18} \left. {{\begin{array}{l} {e_1 = R\cos \theta _h } \\ {e_2 = R\sin \theta _h } \\ {e_3 = \cos \theta _{h}} \\ {e_4 = \sin \theta _{h}} \\ \end{array} }} \right\}(18) \end{equation} 因此可以将圆盘角速度的平方用曲梁第一个单元中的绝对节点坐标列阵中的分量表示为 \begin{equation} \label{eq19} \omega _{h} ^2 = \frac{(\dot {e}_1^2 + \dot {e}_2^2 )}{R^2}(19) \end{equation} 设$B_{ h}$为圆盘与曲梁连接处的节点坐标($e_{1},e_{2})$对应总体节点坐标列阵中的布尔定位矩阵. 因此可以将圆盘的动能用总体绝对节点坐标列阵重新表示成
$$\begin{align*} & T_{h} = \frac{1}{2}J_{oh} \frac{(\dot {e}_1^2 + \dot {e}_2^2 )}{R^2} = \frac{1}{2}\frac{J_{oh} }{R^2}\dot {q}^{T}B_{h}^{T} B_{h} \dot {q}=\\ &\qquad\frac{1}{2}\dot {q}^{T}M_{oh} \dot {q}(20)\end{align*} $$
式(20)中$M_{oh}$为圆盘对应的质量矩阵 \begin{equation} \label{eq21} M_{oh} = \frac{J_{oh} }{R^2}B_{ h}^{T} B_{h}(21) \end{equation}
分别将式(10)、式(17)和式(20)相加即可到附加集中质量的旋转柔性曲梁总动能
$$\begin{align*} & T = T_{b} + T_{c} + T_{h} = \frac{1}{2}\dot{q}^{T}M_{b} \dot{q} +\\ &\qquad \frac{1}{2}\dot {q}^{T}M_{c} \dot {q} + \frac{1}{2}\dot {q}^{T}M_{oh} \dot {q} = \frac{1}{2}\dot{q}^{T}M\dot{q}(22)\end{align*} $$
其中,$M$和$q$分别为系统的总质量阵和总绝对节点坐标列阵,$M$可表示为 \begin{equation} \label{eq23} M = M_{b} + M_{c} + M_{ oh}(23) \end{equation}
$$\begin{align*} & \left( {l_{d}} \right)^2-\left( {l_0 } \right)^2 = { d}r^{T}{d}r-{d}r_0 ^{T}{d}r_0= \\ &\qquad {d}s^{T}\left[ {\left( {\frac{\partial r}{\partial s}} \right)^{T}\left( {\frac{\partial r}{\partial s}} \right)-\left( {\frac{\partial r_0 }{\partial s}} \right)^{T}\left( {\frac{\partial r_0 }{\partial s}} \right)} \right]{d}s(24)\end{align*} $$
将式(24)改写为 \begin{equation} \label{eq25} \left( {l_{d} } \right)^2-\left( {l_0 } \right)^2 = 2{d}s^{T}\varepsilon _0 {d}s(25) \end{equation} 式(25)中的$\varepsilon _{0}$为曲梁中线的Green-Lagrangian应变,用曲梁单元的绝对节点坐标列阵可以表示为
$$\begin{align*} & \varepsilon _0 = \frac{1}{2}\left( {\left( {\frac{\partial r}{\partial s}} \right)^{T}\left( {\frac{\partial r}{\partial s}} \right)-\left( {\frac{\partial r_0 }{\partial s}} \right)^{T}\left( {\frac{\partial r_0 }{\partial s}} \right)} \right)=\\ &\qquad \frac{1}{2}\left( {e^{T}N_{s}^{T} N_{s}e-e_0^{T} N_{s}^{T} N_{ s} e_0 } \right)(26)\end{align*} $$
其中$e_{0}$为描述曲梁单元初始构型的绝对节点坐标列阵.
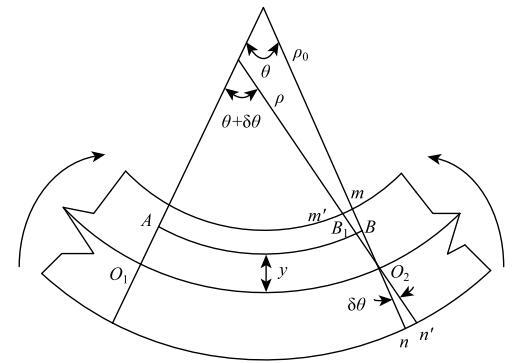
假设梁横截面$mn$绕着与中性轴交点$O_{2}$逆时针旋转了$\delta \theta$变成了$m'n'$,则变化的曲率如图3所示,可表示为 \begin{equation} \label{eq27} \bar {\kappa } = \frac{1}{\rho }-\frac{1}{\rho _0 }(27) \end{equation} 其中,$\rho _{0}$和$\rho $分别为曲梁单元中轴线横截面转动前后的曲率半径.
根据横截面转动前后共用同一中心轴线可以推导出 \begin{equation} \label{eq28} \rho \left( {\theta + \delta \theta } \right) = \rho _0 \theta(28) \end{equation} 将式(28)经过变换可得 \begin{equation} \label{eq29} \frac{1}{\rho }-\frac{1}{\rho _0 } = \frac{\delta \theta }{\rho _0 \theta }(29) \end{equation} 结合式(27)和式(29)可得 \begin{equation} \label{eq30} \bar {\kappa } = \frac{\delta \theta }{\rho _0 \theta }(30) \end{equation}
图3
图3
梁单元截面变形前后示意图
Fig. 3
Schematic of beam element section before and after deformation
由于横截面$mn$转动有一转角$\delta \theta $,距中性层为$y$的任意纤维层的弯曲应变为 \begin{equation} \label{eq31} \varepsilon _\kappa = \frac{\Delta AB}{AB} = \frac{BB_1 }{AB} = -\frac{y\delta \theta }{\left( {\rho _0-y} \right)\theta }(31) \end{equation} 根据本文假设:曲梁的横截面高度远小于曲梁的曲率半径$\rho$,则可以将式(31)简化为 \begin{equation} \label{eq32} \varepsilon _\kappa =-\frac{y\delta \theta }{\rho _0 \theta } =-\bar {\kappa }y(32) \end{equation}
根据文献[33]关于曲线曲率的精确表达式,将曲梁变化的曲率$\bar {\kappa }$用曲梁单元全局位移矢量$r$对弧坐标$s$的偏导数表示
$$\begin{align*} &\bar {\kappa } = \frac{\dfrac{\partial r}{\partial s}\times \dfrac{\partial ^2r}{\partial s^2}}{\left| {\dfrac{\partial r}{\partial s}} \right|^3}-\frac{\dfrac{\partial r_{0} }{\partial s}\times \dfrac{\partial ^2r_{0} }{\partial s^2}}{\left| {\dfrac{\partial r_{0} }{\partial s}} \right|^3} = \frac{r_{ss}^{T} \tilde{I}r_{s}}{f^3}-\frac{r_{0ss}^{T} \tilde{I}r_{0s} }{f_0^3 }=\\ &\qquad \frac{r_{s}^{T} \tilde {I}^{T}r_{ss} }{f^3}-\frac{r_{0s}^{T} \tilde {I}^{T}r_{0ss} }{f_0^3 } = \frac{e^{ T}\varGamma e}{f^3}-\frac{e_0^{T} \varGamma e_0 }{f_0^3 }(33)\end{align*} $$
其中,$\tilde {I} = \left[ {{\begin{array}{*{20}c} 0 & {-1} \\ 1 & 0 \\ \end{array} }} \right]$,$\varGamma = \dfrac{1}{2}\left( {N_{ss}^{T} \tilde {I}N_{ s} + N_{s}^{T} \tilde {I}^{T}N_{ss} } \right)$,
$$f = \left| {\dfrac{\partial r}{\partial {s}}} \right| = \sqrt {\left( {\dfrac{\partial r}{\partial {s}}} \right)^{T}\left( {\dfrac{\partial r}{\partial {s}}} \right)}, ~f_{0} = \left| {\dfrac{\partial r_{0} }{\partial {s}}} \right| = \sqrt {\left( {\dfrac{\partial r_{0} }{\partial {s}}} \right)^{T}\left( {\dfrac{\partial r_{0} }{\partial {s}}} \right)}.$$
将式(33)代入式(32), 并结合式(32)和式(26)可以得出用单元节点坐标列阵$e$表示的曲梁非中线任意一点的应变
$$\begin{align*} & \varepsilon _x = \varepsilon _0-y\bar {\kappa } = \frac{1}{2}\left( {e^{T}N_{s}^{T} N_{s} e-e_{0}^{T} N_{s}^{T} N_{s} e_{0} } \right) -\\ &\qquad y\left( {\frac{e^{T}\varGamma e}{f^3}-\frac{e_0^{T} \varGamma e_0 }{f_0^3 }} \right)(34) \end{align*}$$
根据本文假设:柔性曲梁横截面关于中轴线对称,且不计横截面转动惯量与剪切效应,则$ \int_A {y{d}A = 0} $和$ \int_A {y^2{d}A = I_z } $,因此曲梁单元弹性力所做的虚功可以表示为
$$\begin{align*} & \delta W_e =-\int_V {\sigma _x \delta \varepsilon _x } {d}V =-\int_V {E\varepsilon _x \delta \varepsilon _x } {d}V=\\ &\qquad-\left( {\int_0^l {EA\varepsilon _0 \delta \varepsilon _0 {d}x + \int_0^l {EI_z \bar {\kappa }\delta \bar {\kappa }{d}x} } } \right)(35) \end{align*}$$
其中,$E$为曲梁的弹性模量,$V$为曲梁单元的体积, $A$和$Iz$分别为曲梁横截面面积和曲梁横截面惯性矩.
曲梁单元的广义弹性力可以表示为
$$\begin{align*} & Q_e = \frac{\delta W_e }{\delta e^{T}} =-\int_0^l EA\mathop{\varepsilon _0}\limits_{=\!\!\!=\!\!\!=\!\!\!=\!\!\!=\!\!\!=} N_{s}^{T} N_{s} e{d}x-\\ &\qquad \int_0^l {EI_z \mathop{\bar{\kappa}}\limits_{=\!\!\!=}\cdot \left( {2\frac{\varGamma }{f^3}-3\frac{e^{T}\varGamma e}{f^5}N_{s}^{T} N_{s}} \right)e{ d}x}(36)\end{align*} $$
其中,当式(36)中的下划线项采用直梁形式的初始节点坐标列阵时, 该式自动退化为文献[29]所表示的ANCF直梁形式的弹性力表达式.
将单元的广义弹性力向量组装即可到曲梁总的广义弹性力列阵 \begin{equation} \label{eq37} Q_a = \sum\limits_{e = 1}^n {B_e^{T} Q_e }(37) \end{equation} 则整根曲梁弹性力所做的虚功可以表示为 \begin{equation} \label{eq38} \delta W_{f} = \delta q^{T}Q_a(38) \end{equation}
若在中心刚体上施加一力矩$\tau $,则该力矩所作的虚功可表示为 \begin{equation} \label{eq39} \delta W_\tau = \tau \delta \theta _{ h}(39) \end{equation} 圆盘转过的虚角度$\delta \theta _{ h}$可以根据边界条件转化成用绝对节点坐标的虚位移形式表示, 对式(18)中的$e_{3}$和$e_{4}$求变分可得 \begin{equation} \label{eq40} \sin \theta _{h} \delta \theta _{h} =-\delta e_3(40) \end{equation} \begin{equation} \label{eq41} \cos \theta _{h} \delta \theta _{h} = \delta e_4(41) \end{equation} 分别将式(18)中的第四式乘以式(40),式(18)中的第三式乘以式(41),然后相加可得 \begin{equation} \label{eq42} \delta \theta _{h} =-e_4 \delta e_3 + e_3 \delta e_4(42) \end{equation} 将式(42)用绝对节点坐标列阵的形式可以表示为 \begin{equation} \label{eq43} \delta \theta _{h} = \delta e^{ T}\left[ {{\begin{array}{*{20}c} 0 & 0 & {-e_4 } & {e_3 } & 0 & 0 & 0 & 0 \\ \end{array} }} \right]^{T}(43) \end{equation} 将式(43)代入式(39)即可得到用节点坐标列阵和作用在刚体上的广义力矩表示的力矩虚功 \begin{equation} \label{eq44} \delta W_\tau = \tau \delta \theta _{h} = \delta e^{T}Q_{{h}\tau }(44) \end{equation} 其中广义力矩表示为 \begin{equation} \label{eq45} Q_{{h}\tau } = \left[ {{\begin{array}{*{20}c} 0 & 0 & {-e_4 \tau } & {e_3 \tau } & 0 & 0 & 0 & 0 \\ \end{array} }} \right]^{T}(45) \end{equation}
设$B_{j}$为式(45)对应总体广义力矩列阵的布尔定位矩阵,则可将作用在刚体上的广义力矩转换成总的广义力矩列阵 \begin{equation} \label{eq46} Q_\tau = B_j^{T} Q_{{h}\tau }(46) \end{equation} 因此作用在中心刚体上的力矩所作虚功可以用总的广义力矩列阵重新表示成 \begin{equation} \label{eq47} \delta W_\tau = \delta q^{T}Q_\tau(47) \end{equation}
将式(23)、式(38)、式(47)代入D'Alembert-Lagrange微分变分原理 \begin{equation} \label{eq48} \delta W_f + \delta W_\tau-\delta q^{ T}M\ddot{q} = 0(48) \end{equation} 并且考虑圆盘与曲梁之间的固支连接边界条件,将其转化成约束方程$\varPhi (q,t)=0$,即 \begin{equation} \label{eq49} \left. {{\begin{array}{l} {e_1^2 + e_2^2 = R^2} \\ {e_1 = Re_3} \\ {e_2 = Re_4} \\ \end{array} }} \right\}(49) \end{equation} 通过Lagrange乘子法,把式(49)代入(48)当中,所得的方程与约束方程联立求解, 即可得到描述系统动力学特性的指标\!-3(Index-3)形式的微分、代数方程组(DAEs) \begin{equation} \label{eq50} \left. {{\begin{array}{l} {M\ddot{q} + \varPhi _q^{T} \lambda-Q = 0} \\ {\varPhi \left( {q,t} \right) = 0} \\ \end{array} }} \right\}(50) \end{equation} 式中,$M$为系统的质量矩阵即式(23),$Q$为系统的广义力列阵 \begin{equation} \label{eq51} Q = Q_\tau + Q_a(51) \end{equation} 本文采用广义$\alpha$法[34]求解该微分代数方程组.
2 悬臂曲梁的纯弯曲测试和旋转柔性曲梁的动力学响应分析
为了验证本文曲梁单元的收敛性和旋转柔性曲梁模型的正确性, 仿真计算了在集中力偶作用下悬臂曲梁的纯弯曲变形和考虑了刚柔耦合效应的旋转柔性曲梁动力学响应, 其中动力学响应与文献[14]进行了对比研究.
2.1 算例1:悬臂曲梁的纯弯曲测试
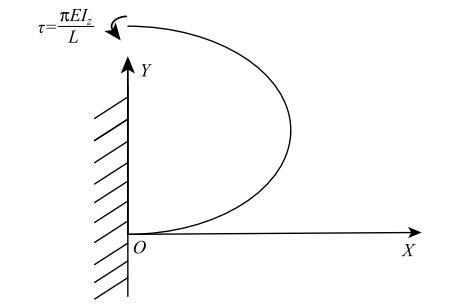
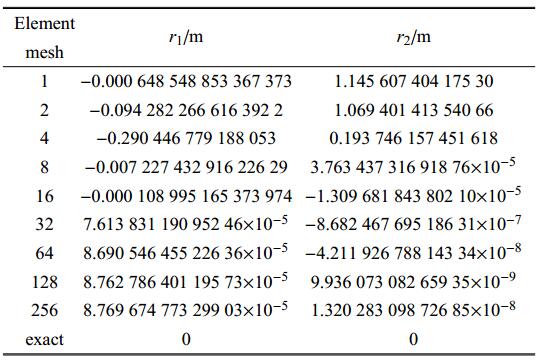
如图4所示的弧度角为$\pi $的悬臂曲梁模型,在其上端施加一个大小为$\pi EIz/L$,方向为沿着$OZ$轴的力偶矩,悬臂曲梁的弹性模量$E=68.895~2$ GPa,横截面面积$A=2.5$ cm$^{2}$,截面惯性矩$Iz=0.133~33$ cm$^{4}$, 参照文献[35]在力偶矩作用下悬臂梁的转角公式为 \begin{equation} \label{eq52} \theta _B = \frac{\tau L}{EI_z }(52) \end{equation} 其中$\theta _{B}$为曲梁端点转过的角度. 将本算例的力偶矩代入上式可知悬臂曲梁端点转过的角度为$\pi $,结合悬臂曲梁原始的弧度角为$\pi $,可知悬臂曲梁会弯成一个整圆,因此端点自由端坐标为(0,0).
图4
图4
弧度角为$\pi$的悬臂曲梁模型
Fig. 4
Cantilever curved beam model with radian angle of $\pi$
表1 悬臂曲梁在力偶矩作用下自由端的位置坐标
Table 1
 |
2.2 算例2:刚柔耦合动力学仿真
中心刚体和曲梁的物理参数如表2所示,假定作用在中心刚体上的外力矩可表示为下式 \begin{equation} \label{eq53} \tau = \left\{ {{\begin{array}{ll} 10\sin \left( {2\pi t} \right), & 0 \le t \le 2~{s} \\ 0, & t > 2~{s} \\ \end{array} }} \right.(53) \end{equation} 由于动力学方程(50)里的$q$是绝对位移,这不便于观察曲梁的变形,我们将绝对位移$q$转换到浮动坐标系$oxy$下. $\theta _{ h}$为浮动坐标系相对于惯性坐标系转过的角度,即圆盘转过的角度, $M_{T}$为浮动坐标系关于惯性坐标系的坐标转换阵, $u_{1}$和$u_{2}$分别为曲梁端点在浮动坐标系下的纵向和横向变形,则$u_{1}$和$u_{2}$可以表示为
$$\begin{align*} & M_{T} = \left[ {{\begin{array}{*{20}c} {\cos \theta _{h}} & {\sin \theta _{h}} \\ {-\sin \theta _{h}} & {\cos \theta _{h}} \\ \end{array} }} \right](54)\\ &\left[ {{\begin{array}{*{20}c} {u_1 } \\ {u_2 } \\ \end{array} }} \right] = M_{T} \left[ {{\begin{array}{*{20}c} {r_1 \left( L \right)} \\ {r_2 \left( L \right)} \\ \end{array} }} \right]-\left[ {{\begin{array}{*{20}c} {R + \rho _0 \cos \theta } \\ {\rho _0-\rho _0 \cos \theta } \\ \end{array} }} \right](55)\end{align*} $$
仿真计算时同样把柔性曲梁划分为20个和40个单元.
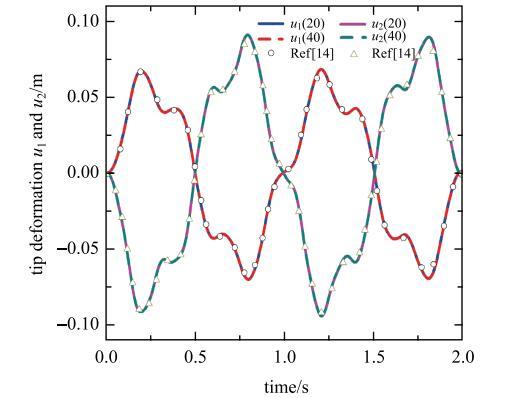
图5为旋转柔性曲梁端点纵向变形和横向变形随时间变化的历程图, 对比文献[14]可以看出本文模型在刚柔耦合动力学模型的求解上也具有良好的正确性, 而且曲梁划分单元数为20和40时所得的曲梁端点动力学响应几乎是一致的, 说明采用20个曲梁单元所得的动力学响应解答已经收敛而且足够精确. 从图5中可以看出曲梁端点的纵向变形与横向变形存在着反向关系,当一方增大,另一方就减小, 这是因为曲梁整体变形过程中存在着由横向变形引起的纵向缩短项,这是文献[14]未曾提及的, 这体现在高次耦合模型[5]和曲率纵向变形效应模型[6]中的具体形式就是需要加入由横向变形引起的纵向缩短项才能正确计算大变形梁的变形, 而ANCF采用了空间向量描述其位置,所以直接包含了该项,这也是ANCF能描述和计算大变形运动的一大原因.
图5
图5
曲梁端点纵向变形和横向变形随时间变化
Fig. 5
The tip longitudinal and transverse deformation of the curved beam varies with time
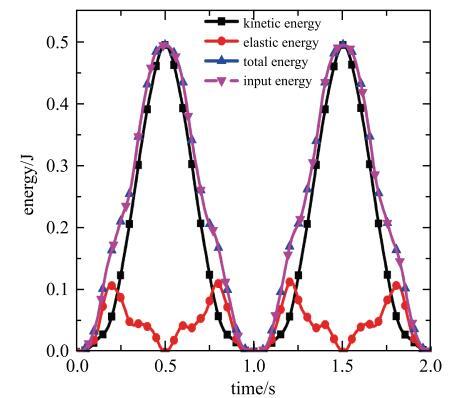
图6
结合算例1和算例2所得的单元划分结果,本文在仿真后续算例时,统一将柔性曲梁划分为20个单元.
3 旋转曲梁的动力学特性分析
由于第1部分导出的曲梁动力学方程(50)是通过约束方程的形式施加圆盘角速度变量, 且动力学方程中的绝对节点坐标列阵是建立在惯性$OXY$下. 为了便于分析系统模态,假设圆盘是匀速转动, 同时将绝对节点坐标列阵建立在浮动坐标系$oxy$下, 通过D'Alembert原理将圆盘角速度变量转换成离心力的形式施加到柔性曲梁上, 将匀速转动的柔性曲梁系统等效成便于分析的无旋转柔性曲梁加离心力的形式.
假设柔性旋转曲梁的绕$OZ$轴做匀速转动,角速度为$\omega _{h}$,因此梁上任意一点$O_{1}$点距离原点$O$的离心力可以表示为 \begin{equation} \label{eq56} F_{ce} = \rho _b A\omega _h^2 \left( {\left[ {{\begin{array}{*{20}c} R \\ 0 \\ \end{array} }} \right] + N\left( s \right)\bar {e}} \right)(56) \end{equation} 其中,$\bar {e}$为曲梁单元在浮动坐标系$oxy$下的绝对节点坐标列阵.
曲梁单元离心力所做的虚功可以表示为
$$\begin{align*} & \delta W_{ce} = \int_0^l {\delta r^{T} \cdot \left[ {\rho A\omega _{h}^2 \left( {\left[ {{\begin{array}{*{20}c} R \\ 0 \\ \end{array} }} \right] + N\left( s \right)\bar {e}} \right)} \right]} {d}s =\\ &\qquad \rho _{b} A\omega _{h}^2 R\delta \bar {e}^{T}\int_0^l {N_1^{T} {d}s} + \omega _{h}^2 \delta \bar {e}^{T}M_e \bar {e}(57)\end{align*} $$
其中,$N_{1}$为曲梁单元形函数$N$中的第一行. 因此曲梁单元的广义离心力为 \begin{equation} \label{eq58} Q_{ce} = \rho _{b} A\omega _{h}^2 R\int_0^l {N_1^T {d}s} + \omega _{h}^2 M_e \bar {e}(58) \end{equation} 相应地可以得出集中质量的广义离心力 \begin{equation} \label{eq59} Q_{cc} = \omega _{h}^2 am_{c} N_1^{T} \left( {\Delta l} \right) + \omega _{h}^2 M_{c} \bar {e}_{k}(59) \end{equation} 将曲梁单元和集中质量的广义离心力组装 \begin{equation} \label{eq60} Q_{c} = \sum\limits_{i = 1}^n {B_i^{ T} Q_{ce} + B_k^{T} Q_{cc} }(60) \end{equation}
由此可以得到用总的广义离心力列阵$Q_{ c}$和总的绝对节点坐标列阵$q$表示的离心力所作的虚功 \begin{equation} \label{eq61} \delta W_{c} = \delta q^{T}Q_{ c}(61) \end{equation}
分别将式(23)、式(38)、式(61)代入D'Alembert-Lagran-ge微分变分原理, 并且考虑固支端的边界条件即可得到带集中质量的无旋转柔性曲梁动力学方程 \begin{equation} \label{eq62} M\ddot {q} = Q_{c} + Q_{ a}(62) \end{equation}
为了得到更普遍性的数值仿真计算结果,下面引入无量纲参数 \begin{equation} \label{eq63} \left.\begin{array}{l} \alpha = \dfrac{m_{c}}{\rho _{b} AL},\beta = \dfrac{a}{L},\gamma = \dfrac{\omega _h }{\omega ^\ast },\delta = \dfrac{R}{L},\zeta = \dfrac{\bar {s}}{L} \\ \mu = \sqrt {\dfrac{AL^2}{I_z }} ,K = \kappa _{0} L \\ \end{array}\right\}(63) \end{equation} 式中,$\omega ^\ast = \sqrt {\dfrac{EI_z }{\rho _b AL^4}} $ 为Euler-Bernoulli梁固有的频率参数,$a$,$A$,$\rho _{ b}$,$L$,$R$,$\bar {s}$,$Iz$,$\kappa _{0}$分别为集中质量位于曲梁上某个位置所对应的弧坐标,曲梁横截面的面积,曲梁的材料密度, 曲梁的总弧长,刚性圆盘的半径,曲梁上任意一点的弧坐标,曲梁横截面的惯性矩,曲梁的初始曲率. $\alpha $,$\beta $,$\gamma $,$\delta $,$\zeta $分别为集中质量比,集中质量位置比,圆盘角速度比,中心刚体半径比和无量纲长度比. $\mu$为曲梁的长细比,$K$为曲梁的无量纲初始曲率. 本文由于集中质量一直位于曲梁端点,因此$\beta =1$,并使曲梁的长细比$\mu =70$.
通过上述无量纲量将方程(62)转化为无量纲形式 \begin{equation} \label{eq64} \bar{M}\mathop{\bar{q}}\limits^{~\cdot\cdot} = \bar {Q}_{c} + \bar {Q}_{a}(64) \end{equation} 为了求解旋转柔性梁在匀角速度为$\omega _{h} $下的特征值问题,需要将方程(64)线性化处理,得到系统的摄动方程 \begin{equation} \label{eq65} \bar {M}\delta \mathop{\bar {q}}\limits^{~\cdot\cdot} + \bar {K}_{T} \left( {\bar {q}_{a} } \right)\delta \bar {q} = 0(65) \end{equation} 其中,$\bar {q}_{a}$ 为柔性曲梁在离心力作用下静平衡位置的构型,需要通过Newton-Raphson迭代求解静平衡方程 \begin{equation} \label{eq66} \bar{Q}_{a} + \bar {Q}_{c} = 0(66) \end{equation} $\bar{K}_{T}$为系统静平衡位置的切线刚度矩阵 \begin{equation} \label{eq67} \bar{K}_{T} =-\left( {\frac{\partial \bar {Q}_{c}}{\partial \bar {q}} + \frac{\partial \bar {Q}_{a}}{\partial \bar {q}}} \right)(67) \end{equation} 假设式(65)的解为 \begin{equation} \label{eq68} \delta \bar{q} = A\bar{e}^{{ j}\omega t}(68) \end{equation} 将式(68)代入式(65)式可得到该等效系统的广义特征方程 \begin{equation} \label{eq69} \left( {\bar {K}_T-\omega ^2\bar {M}} \right)A = 0(69) \end{equation} 通过上式即可求得该等效系统无量纲固有圆频率和模态振型.
3.1 无量纲角速度、初始曲率和集中质量对曲梁固有圆频率的影响
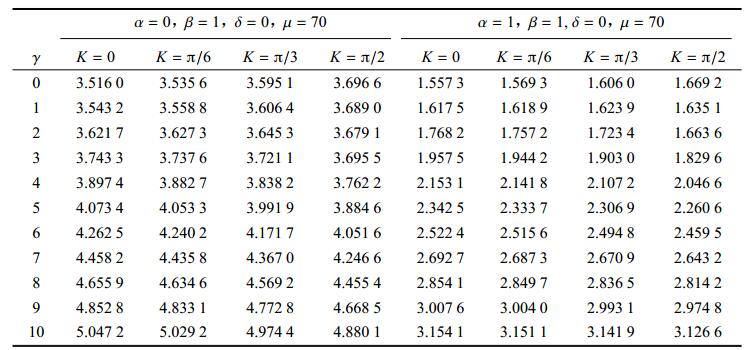
从表3可以看出随着无量纲角速度的增大,旋转柔性曲梁的第一阶固有圆频率呈上升趋势, 因为离心力的引入使结构总体刚度变大,由此可以观察到动力刚化效应. 当系统无量纲角速度$\gamma = 0$时,即系统为静止状态,横向对比可以发现,随着曲梁弧度角的增大,曲梁的固有圆频率呈现细微的上升. 纵向对比可以发现,随着无量纲角速度的增大,第一阶无量纲频率总体呈上升趋势, 但是随着曲梁初始曲率增大的情况下,曲梁固有圆频率上升的幅值减小. 有集中质量的柔性曲梁的第一阶无量纲固有频率跟比无集中质量的柔性曲梁固有频率相比明显减小了, 这是因为在保持曲梁刚度不变的情况下,集中质量的引入会极大增加曲梁质量阵中的某些数值, 从而导致曲梁的第一阶无量纲固有圆频率大幅度下降.
表3 旋转曲梁第一阶弯曲无量纲固有圆频率
Table 3
 |
3.2 曲梁的频率转向
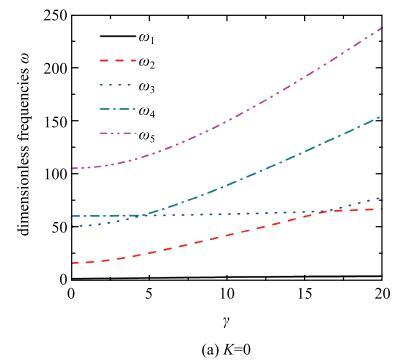
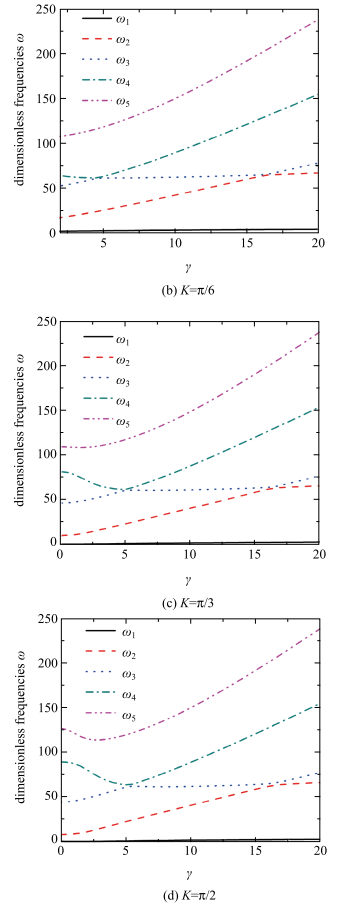
图7为曲梁在不同无量纲初始曲率$K =0$,$\pi/6$,$\pi/3$,$\pi /2$下,且无量纲集中质量比$\alpha =1$,中心刚体的半径比$\delta =0$,集中质量的位置比$\beta=1$, 曲梁前五阶固有圆频率随着无量纲角速度变化的曲线图. 从图7中可以看到频率转向的现象,当无量纲初始曲率分别为$K=0$,$\pi /6$,$\pi/3$,$\pi /2$时,曲梁的第三和第四阶固有圆频率分别会在无量纲角速度$\gamma =4.5$,4.6,5.05,5.41附近转向,第二和第三阶固有圆频率会在无量纲角速度$\gamma =16.5$,16.6,16.66,16.75附近又发生一次转向. 这说明初始曲率变化并不会显著地影响曲梁频率转向的位置,但会使频率转向位置稍微偏后.
从图8中,我们也能看出初始曲率主要影响曲梁第一个频率转向点以前无量纲固有圆频率的值. 随着无量纲角速度变大,曲梁的无量纲初始曲率$K=0$,$\pi /2$时的曲梁频率迹线已经重合,说明曲梁的无量纲初始曲率在无量纲角速度比较小时对曲梁频率影响比较大, 当无量纲角速度变大以后对旋转柔性曲梁固有圆频率影响不大.
图7
图7
曲梁前五阶无量纲固有圆频率随无量纲角速度变化曲线($\alpha =1$,$\beta =1$,$\delta =0$,$\mu =70$)
Fig. 7
The first five order dimensionless natural frequencies with dimensionless angular velocity of the curved beam ($\alpha =1$, $\beta =1$, $\delta =0$, $\mu =70$)
图7
图7
曲梁前五阶无量纲固有圆频率随无量纲角速度变化曲线($\alpha =1$,$\beta =1$,$\delta =0$,$\mu =70$) (续)
Fig. 7
The first five order dimensionless natural frequencies with dimensionless angular velocity of the curved beam ($\alpha =1$, $\beta =1$, $\delta =0$, $\mu =70$) (continued)
图8
图8
不同无量纲曲率下曲梁前五阶无量纲固有圆频率随无量纲角速度变化曲线对比($\alpha =1$,$\beta =1$,$\delta =0$,$\mu =70$,$K=0$,$\pi/2$)
Fig. 8
Contrast of the first five order dimensionless natural frequencies with dimensionless angular velocity of the curved beam under different dimensionless curvatures ($\alpha =1$, $\beta =1$, $\delta =0$, $\mu =70$, $K=0$, $\pi/2$)
图9
图9
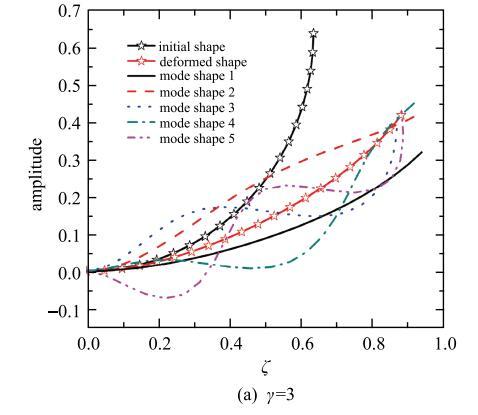
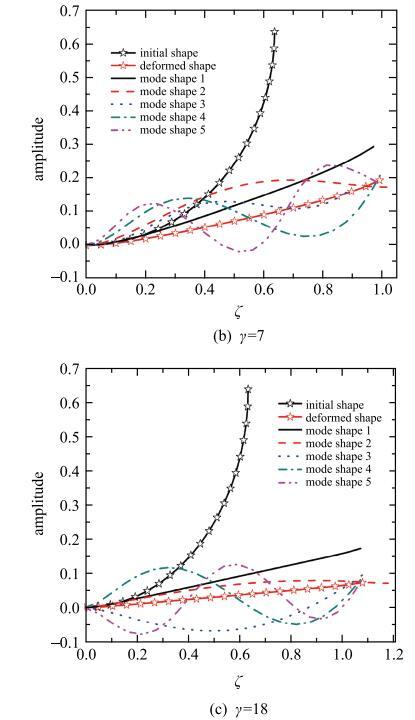
无量纲角速度$\gamma =3$,7,18曲梁静平衡位置构型图($K=\pi/2$)
Fig. 9
Configuration of static equilibrium position of the curved beam with dimensionless angular velocity $\gamma =3$, 7, 18($K=\pi/2$)
3.3 直梁与曲梁频率转向导致的模态振型差异
图10为初始无量纲初始曲率$K=0$时,在无量纲角速度$\gamma= 3$,7,18下的直梁模态振型图. 其中,中心刚体的半径比$\delta = 0$,无量纲集中质量比$\alpha =1$,集中质量的位置比$\beta =1$. 从图10(a)看出,当无量纲角速度$\gamma= 3$时,直梁的前三阶模态振型为弯曲振型,第四阶模态振型为拉伸振型,第五阶模态振型为弯曲振型, 而图10(b)当无量纲角速度$\gamma = 7$时,直梁的前两阶模态振型为弯曲振型,第三阶模态振型为拉伸振型,第四、五阶模态振型为弯曲振型. 可知在$\gamma = 3$和$\gamma = 7$之间直梁的第三阶和第四阶模态振型发生切换,这显然对应了图7(a)当无量纲角速度$\gamma=4.5$ 时直梁第三阶和第四阶频率迹线发生了转向. 从图10(c)可以得到当无量纲角速度$\gamma = 18$时,可以发现直梁的第一阶模态振型为弯曲振型,而第二阶模态振型为拉伸振型,第三、四、 五阶模态振型为弯曲振型,这时直梁的第二阶和第三阶模态振型又发生了切换, 这显然又对应了图7(a)当无量纲角速度$\gamma = 16.5$时直梁的第二和第三阶频率迹线发生了转向. 从中我们可以得知,当随着无量纲角速度增大,直梁的拉伸模态振型会逐渐提前.
图10
图10
直梁前5阶振型 ($\alpha=1$,$\beta =1$,$\delta =0$,$\mu =70$,$K=0$)
Fig. 10
The first five mode shapes of the straight beam ($\alpha = 1$, $\beta =1$, $\delta =0$, $\mu =70$, $K=0$)
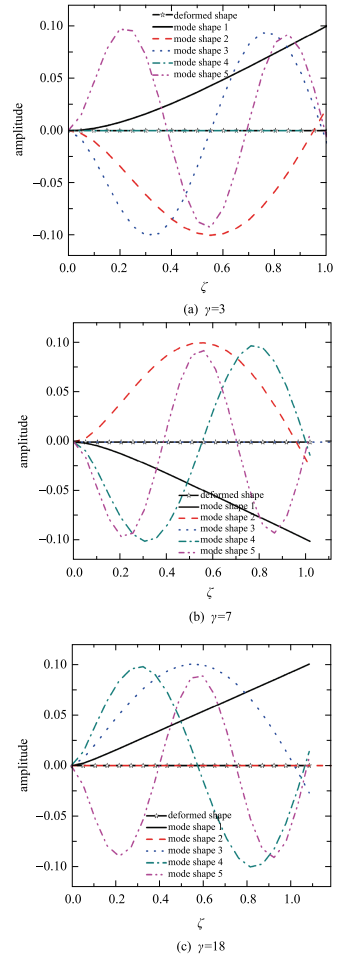
下文研究初始无量纲初始曲率$K$不为0时的曲梁模态振型,以初始无量纲曲率$K =\pi/2$,集中质量比$\alpha =1$,中心刚体的半径比$\delta = 0$,集中质量的位置比$\beta =1$为例进行对比研究. 图11为在无量纲角速度$\gamma =3$,7,18下的曲梁模态振型图. 对比图10和图11可以看出,和直梁的拉伸模态振型与弯曲模态振型分开不同, 曲梁的拉伸和弯曲模态振型是耦合在一起,但是仍旧可以发现曲梁频率迹线转向所导致的模态振型切换. 从图11(a)可以看出,当无量纲角速度$\gamma =3$时,曲梁前三阶模态振型为弯曲变形占主导,第四阶模态振型为拉伸变形占主导, 因为除了第一阶模态振型,第二、三阶模态振型并没有偏离曲梁变形后端点过多的位置. 从图11(b)可以看出,当无量纲角速度为$\gamma = 7$时,曲梁的第三阶模态振型很明显的变成了拉伸变形占主导,第四阶为弯曲变形占主导的模态振型. 这与图7(d)无量纲角速度$\gamma = 5.41$时曲梁第三阶和第四阶频率迹线发生了转向是对应的. 从图11(c)可以看出,无量纲角速度为$\gamma = 18$时,曲梁的第二阶模态振型为拉伸变形占主导,第三阶模态振型变成弯曲变形占主导. 这又与图7(d)对应,当$\gamma =16.75$时曲梁的第二和第三阶频率迹线发生转向. 综上可得出,随着无量纲角速度增大,曲梁拉伸变形占主导的模态振型也逐渐提前.
图11
图11
曲梁前五阶振型 ($\alpha =1$,$\beta =1$,$\delta = 0$,$\mu =70$,$K=\pi /2$)
Fig. 11
The first five mode shapes of the curved beam ($\alpha =1$, $\beta =1$, $\delta =0$, $\mu =70$, $K=\pi/2$)
图11
图11
曲梁前五阶振型 ($\alpha =1$,$\beta =1$,$\delta = 0$,$\mu =70$,$K=\pi /2$) (续)
Fig. 11
The first five mode shapes of the curved beam ($\alpha =1$, $\beta =1$, $\delta =0$, $\mu =70$, $K=\pi/2$) (continued)
4 结论
为了分析集中质量、旋转角速度和曲梁的初始曲率对旋转曲梁动力学特性的影响, 以及研究旋转曲梁模态特性中的频率转向和振型切换问题,本文基于绝对节点坐标法推导出曲梁单元, 并以此建立了带集中质量的旋转柔性曲梁动力学模型, 根据悬臂曲梁的纯弯曲测试和旋转柔性曲梁的动力学仿真结果分别验证了本文所提出曲梁单元的收敛性和动力学模型的正确性, 通过对旋转曲梁的动力学特性研究可得以下结论.
(1)随着无量纲旋转角速度的增大,曲梁的固有圆频率会增大, 集中质量的引入会极大地降低系统固有圆频率.
(2)曲梁的无量纲初始曲率只有当无量纲角速度比较小时对曲梁固有圆频率影响较大,随着无量纲角速度的增大, 曲梁会拉伸成一根直梁,从而曲梁的频率特性与直梁的频率特性相近.
(3)通过对曲梁频率转向和振型切换的研究可得:随着无量纲角速度的增大, 曲梁拉伸变形占主导的模态振型会提前.
参考文献
直升机旋翼动力学优化浅析
Analysis of helicopter rotor dynamic optimization
直升机桨叶动力分析的综合离散法
Synthetic discrete method for dynamic analysis of helicopter blades
风力机旋转叶片的刚柔耦合动力学响应特性分析
Dynamic response characteristics analysis of rigid-flexible coupling of wind turbine rotating blade
大型卫星天线系统固有模态的有限元分析
The modal analysis for satellite-large space antenna system with finite element
大变形旋转柔性梁的一种高次刚柔耦合动力学模型
对在平面内做大范围转动的中心刚体-柔性梁系统的刚柔耦合建模理论进行了深入研究,建立了系统的高次耦合动力学模型. 该动力学模型考虑了柔性梁横向弯曲变形和纵向伸长变形,且在纵向位移中计及由于横向变形而引起的纵向缩短项,即非线性耦合变形项,并保留了与非线性耦合项相关的一些高阶项,最终得到了系统的高次刚柔耦合动力学方程. 由此得到的动力学方程不仅能适用于柔性梁的小变形问题,也同样适用于大变形问题,弥补了一次近似耦合模型在处理柔性梁大变形问题上的不足. 通过与绝对节点坐标法以及一次近似耦合模型的对比验证了高次耦合模型的正确性.
A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation
对在平面内做大范围转动的中心刚体-柔性梁系统的刚柔耦合建模理论进行了深入研究,建立了系统的高次耦合动力学模型. 该动力学模型考虑了柔性梁横向弯曲变形和纵向伸长变形,且在纵向位移中计及由于横向变形而引起的纵向缩短项,即非线性耦合变形项,并保留了与非线性耦合项相关的一些高阶项,最终得到了系统的高次刚柔耦合动力学方程. 由此得到的动力学方程不仅能适用于柔性梁的小变形问题,也同样适用于大变形问题,弥补了一次近似耦合模型在处理柔性梁大变形问题上的不足. 通过与绝对节点坐标法以及一次近似耦合模型的对比验证了高次耦合模型的正确性.
考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
<p>对在平面内做大范围转动的中心刚体柔性梁系统的动力学进行了研究,建立了考虑大变形效应的系统刚柔耦合动力学模型,并进行了动力学仿真.该动力学模型不但考虑了柔性梁横向弯曲变形和纵向变形(包含轴向拉伸变形和横向弯曲变形而引起的纵向缩短项),还考虑了纵向变形对曲率的影响,称为曲率纵向变形效应.在以往的研究中,柔性梁的横向弯曲变形能往往直接使用柔性梁横向弯曲变形来表达,并没有考虑纵向变形的影响.为了考虑柔性梁纵向变形对横向弯曲变形能的影响,在浮动坐标系下使用柔性梁参数方程形式的精确曲率公式来计算柔性梁的弯曲变形能.在此基础上建立了基于浮动坐标系的考虑曲率纵向变形效应的刚耦合动力学模型.论文给出了数值仿真算例,验证了本文所建的动力学模型既能适用于柔性梁的小变形问题,又能适用于大变形问题,且较现有高次刚柔耦合动力学模型更加适用于大变形问题的处理.论文还通过与能处理柔性梁大变形问题的绝对节点坐标法的比较,验证了模型的正确性.</p>
Rigid-flexible coupling dynamic modeling and simulation with the longitudinal deformation induced curvature effect for a rotating flexible beam under large deformation
<p>对在平面内做大范围转动的中心刚体柔性梁系统的动力学进行了研究,建立了考虑大变形效应的系统刚柔耦合动力学模型,并进行了动力学仿真.该动力学模型不但考虑了柔性梁横向弯曲变形和纵向变形(包含轴向拉伸变形和横向弯曲变形而引起的纵向缩短项),还考虑了纵向变形对曲率的影响,称为曲率纵向变形效应.在以往的研究中,柔性梁的横向弯曲变形能往往直接使用柔性梁横向弯曲变形来表达,并没有考虑纵向变形的影响.为了考虑柔性梁纵向变形对横向弯曲变形能的影响,在浮动坐标系下使用柔性梁参数方程形式的精确曲率公式来计算柔性梁的弯曲变形能.在此基础上建立了基于浮动坐标系的考虑曲率纵向变形效应的刚耦合动力学模型.论文给出了数值仿真算例,验证了本文所建的动力学模型既能适用于柔性梁的小变形问题,又能适用于大变形问题,且较现有高次刚柔耦合动力学模型更加适用于大变形问题的处理.论文还通过与能处理柔性梁大变形问题的绝对节点坐标法的比较,验证了模型的正确性.</p>
高速旋转柔性梁刚柔耦合动力学分析
基于一次近似理论对绕纵轴高速旋转的柔性梁进行动力学分析,考虑了轴向与横向振动之间的耦合作用以及由偏心产生的离心力作用;采用Hamilton原理导出了旋转柔性梁在恒定转速下动力学方程,并采用假设模态法对所得动力学方程进行分析,得出恒定转速下柔性梁一次近似模型与零次近似模型动力学响应。二者对比表明柔性梁在低速旋转时刚柔耦合项影响较小,可以忽略,可采用零次近似模型;而在高速旋转时刚柔耦合项影响较大,不可以忽略,应采用一次近似模型以得到较为精确的结果。<br>
Rigid-flexible coupled dynamic analysis for a high-speed spinning flexible beam
基于一次近似理论对绕纵轴高速旋转的柔性梁进行动力学分析,考虑了轴向与横向振动之间的耦合作用以及由偏心产生的离心力作用;采用Hamilton原理导出了旋转柔性梁在恒定转速下动力学方程,并采用假设模态法对所得动力学方程进行分析,得出恒定转速下柔性梁一次近似模型与零次近似模型动力学响应。二者对比表明柔性梁在低速旋转时刚柔耦合项影响较小,可以忽略,可采用零次近似模型;而在高速旋转时刚柔耦合项影响较大,不可以忽略,应采用一次近似模型以得到较为精确的结果。<br>
A multiscale force-based curved beam element for masonry arches
A spectral-Tchebychev solution for three-dimensional dynamics of curved beams under mixed boundary conditions
圆弧曲梁振动微分方程推导及振动特性分析
Derivation of vibration differential equation and analysis of vibration properties about ARC-curved beam
Buckling analysis of geometrically nonlinear curved beams
Large deformation analysis of composite spatial curved beams with arbitrary undeformed configurations described by Euler angles with discontinuities and singularities
大运动曲梁应力刚化效应特征值分析
Eigenvalue analysis of stress stiffening effect for large moving beam
Geometric nonlinear dynamic analysis of curved beams using curved beam element
Modal characteristics of a rotating flexible beam with a concentrated mass based on the absolute nodal coordinate formulation
基于绝对节点坐标法的大变形柔性梁几种动力学模型研究
<p>对在平面内大范围转动的大变形柔性梁动力学进行了研究, 基于绝对节点坐标法建立了一种新的大变形柔性梁的非线性动力学模型. 该动力学模型中考虑了柔性梁的轴向拉伸变形和横向弯曲变形, 利用Green-Lagrangian应变张量计算柔性梁的轴向应变及应变能, 利用曲率的精确表达式计算柔性梁的横向弯曲变形能. 运用拉格朗日恒等式给出了柔性梁横向弯曲变形能新的表达式, 该变形能表达式更加简洁, 通过新的变形能表达式得到了新的弹性力模型, 由此得到的动力学方程可以精确地描述柔性梁的几何大变形问题. 通过与高次耦合模型以及ANSYS中BEAM188非线性梁单元模型的比较, 验证了本模型在计算大变形时的正确性以及高次耦合模型在处理大变形问题时的不足. 进一步研究发现, 新的广义弹性力模型可以适当地简化, 给出了两种简化模型, 根据不同模型的计算效率以及计算精度的比较确定了不同模型的适用范围.</p>
Several dynamic models of a large deformation flexible beam based on the absolute nodal coordinate formulation
<p>对在平面内大范围转动的大变形柔性梁动力学进行了研究, 基于绝对节点坐标法建立了一种新的大变形柔性梁的非线性动力学模型. 该动力学模型中考虑了柔性梁的轴向拉伸变形和横向弯曲变形, 利用Green-Lagrangian应变张量计算柔性梁的轴向应变及应变能, 利用曲率的精确表达式计算柔性梁的横向弯曲变形能. 运用拉格朗日恒等式给出了柔性梁横向弯曲变形能新的表达式, 该变形能表达式更加简洁, 通过新的变形能表达式得到了新的弹性力模型, 由此得到的动力学方程可以精确地描述柔性梁的几何大变形问题. 通过与高次耦合模型以及ANSYS中BEAM188非线性梁单元模型的比较, 验证了本模型在计算大变形时的正确性以及高次耦合模型在处理大变形问题时的不足. 进一步研究发现, 新的广义弹性力模型可以适当地简化, 给出了两种简化模型, 根据不同模型的计算效率以及计算精度的比较确定了不同模型的适用范围.</p>
A two-dimensional shear deformable beam element based on the absolute nodal coordinate formulation
A geometrically exact beam element based on the absolute nodal coordinate formulation
Structural and continuum mechanics approaches for a 3D shear deformable ANCF beam finite element: Application to static and linearized dynamic examples
基于绝对节点坐标法的二维剪切梁精确曲率建模
对二维剪切梁单元进行研究,利用平面旋转场理论推导了精确曲率模型.采用几何精确梁理论构建了剪切梁单元弹性力矩阵.通过绝对节点坐标方法建立了系统的非线性动力学方程,提出基于旋转场曲率的二维剪切梁单元,并分别引入经典二维剪切梁单元和基于位移场曲率的二维剪切梁单元进行比较研究.首先,静力学分析证明了所提模型的正确性;其次,特征频率分析验证了模型可与理论解符合,收敛精度高,并且能准确地预测单元固有频率对应的振型;最后,在非线性动力学问题上,通过与ANSYS结果对比分析,证明了该模型可有效处理柔性大变形问题,并且与经典二维剪切梁单元相比具有缓解剪切闭锁的优势.因此,本文提出的基于旋转场曲率的二维剪切梁单元在处理几何非线性问题中具有较大的应用潜力.
Accurate curvature model of planar shear deformable beam based on absolute nodal coordinate formulation
对二维剪切梁单元进行研究,利用平面旋转场理论推导了精确曲率模型.采用几何精确梁理论构建了剪切梁单元弹性力矩阵.通过绝对节点坐标方法建立了系统的非线性动力学方程,提出基于旋转场曲率的二维剪切梁单元,并分别引入经典二维剪切梁单元和基于位移场曲率的二维剪切梁单元进行比较研究.首先,静力学分析证明了所提模型的正确性;其次,特征频率分析验证了模型可与理论解符合,收敛精度高,并且能准确地预测单元固有频率对应的振型;最后,在非线性动力学问题上,通过与ANSYS结果对比分析,证明了该模型可有效处理柔性大变形问题,并且与经典二维剪切梁单元相比具有缓解剪切闭锁的优势.因此,本文提出的基于旋转场曲率的二维剪切梁单元在处理几何非线性问题中具有较大的应用潜力.
Analysis of warping deformation modes using higher order ANCF beam element
New spatial curved beam and cylindrical shell elements of gradient-deficient absolute nodal coordinate formulation
A curved beam element in the analysis of flexible multi-body systems using the absolute nodal coordinates.
Dynamic analysis of rotating curved beams by using absolute Nodal coordinate formulation based on radial point interpolation method
Modal Analysis of a rotating thin plate via absolute nodal coordinate formulation
完备化ANCF薄板单元及在钢板弹簧动力学建模中的应用
The completed form of elastic model for ANCF thin plate element and its application on dynamic modeling of the leaf spring
含芯拧绞绳非线性弯曲动力学特性分析与研究
Analysis of the cored stranded wire rope on the nonlinear bending dynamic characteristics
Contact dynamics of elasto-plastic thin beams simulated via absolute nodal coordinate formulation
A total lagrangian ANCF liquid sloshing approach for multibody system applications
Nonlinear finite element analysis of liquid sloshing in complex vehicle motion scenarios
ANCF analysis of the crude oil sloshing in railroad vehicle systems
基于拉格朗日描述的罐车内液体晃动模拟
Liquid sloshing simulating in railway tank car based on total Lagrangian approach
Convergence of the generalized- $\alpha $, scheme for constrained mechanical systems