细分曲面边界元法的黏附吸声材料结构拓扑优化分析
TOPOLOGY OPTIMIZATION ANALYSIS OF ADHESIVE SOUND ABSORBING MATERIALS STRUCTURE WITH SUBDIVISION SURFACE BOUNDARY ELEMENT METHOD
中图分类号: O343.2
文献标识码: A
通讯作者:
收稿日期: 2018-12-29
网络出版日期: 2019-05-18
版权声明: 2019 力学学报期刊社 所有
基金资助:
展开
摘要
等几何分析采用样条基函数构造几何模型和实施变量近似,实现了计算机辅助设计和辅助工程的无缝连接,并已广泛应用于弹性力学、电磁场和位势问题等领域.然而直接采用等几何方法难以构造复杂模型,限制了该方法在大规模实际工程问题上的应用.细分曲面法可用于克服这一问题,该方法对传统模型的离散网格进行细分和拟合操作,构造出极限光滑曲面,连续性更高,对复杂结构的适用性更强.该方法主要有以下优点:(1)适用于任意拓扑结构;(2)数值计算稳定;(3)实施简单;(4)局部细化与连续性控制.由于该方法在复杂结构模型构造方面具有较强的灵活性和便利性,已被广泛应用于航空航天、汽车、动画、游戏制作等建模领域.将细分曲面法与边界元法相结合进行结构声学分析,几何场与物理场均采用箱样条基函数进行插值近似.以黏附吸声材料结构的声散射问题为例,建立吸声材料分布拓扑优化数学模型,并采用移动渐进线算法进行设计变量更新,最终获得最优材料分布.
关键词:
Abstract
Isogeometric analysis (IGA) realizes the seamless integration of CAD and CAE by using spline basis functions to represent geometric models and implement the numerical analysis, and is widely used in elastic mechanics, electromagnetic field, potential problem and other fields. However, it is difficult to construct directly a complex structure by using IGA. The subdivision surface method can be used to subdivide and fit the discrete mesh of a traditional model in order to construct smooth surfaces. Such a method is suitable for complicated problems. This method has the following advantages: (1) It is suitable for any topological structure; (2) The numerical calculation is stable; (3) It is simple to implement; (4) Local refinement and continuity control. Because of its flexibility and convenience in the construction of complex structural models, this method has been widely used in aerospace, automobile, animation, game making and other modeling fields. The subdivision surface method (SSM) and the boundary element method (BEM) were integrated to perform structural acoustic analysis. The box-spline interpolation of SSM was used for both geometric interpolation and physical interpolation, achieving high-order approximation of the structural surface and physical field. The acoustic scattering of the structure of adhesive sound absorption materials was taken as an example to test the effectiveness of the algorithm. The above analysis was combined with the method of moving asymptotes (MMA) algorithm to conduct a topological optimization of the distribution of sound absorption materials. In this study, the adjoint variable method and the acoustic BEM were used to analyze the sensitivity of the distribution of sound absorption materials on the surface of the structure. Each update of design variables brings small changes in the layout of sound absorbing materials, and ultimately the optimal solution is obtained. The resulting solvers provide an efficient computational tool for topology optimization design. The proposed algorithm is then applied to some numerical examples to illustrate the potential for engineering optimization design.
Keywords:
引 言
采用细分曲面法,能够将任意拓扑结构的不连续离散网格构建成整体光滑曲面,克服了采用NURBS[1]方法建模时遇到的曲面片拼接困难的问题.细分曲面法的实质是采用一定的细分规则对多边形网格重复进行细分处理,直到达到细分收敛极限.基本思路是:(1)根据结构模型的初始控制网格类型,选取不同的细分方法进行细分操作,如Catmull-Clark模式[2]、Doo-Sabin模式[3]、Loop模式[4]、Butterfly模式[5]和$\sqrt3$模式[6]等;(2) 通过细分操作,得到新一级网格信息;(3)重复细分操作直至达到细分收敛极限,最后进行拟合操作获得极限光滑曲面.该方法目前已被广泛应用于卡通动画、3D打印、计算机图形学和工程曲面建模[7]等领域中.在工程数值分析中,Cirak等[8-9]首次将细分曲面与有限元法相结合,进行薄壳结构的动力学响应分析.
边界单元法[10]是一种半解析的数值方法,该方法只需在结构表面进行网格离散和数值分析,具有降维计算和高计算精度的优点,且相对于有限元法更适合处理无限域、半无限域和断裂等问题[11-13].虽然边界元法有这些优点,但也有一些难以克服的缺点,比如形成的系数矩阵是非对称的满阵,导致存储量和计算量都非常大;形成的边界积分方程含有奇异积分项,直接决定了边界元方法的计算精度.实际上,采用快速多极算法[14-15]可有效提高计算效率和降低内存占有量.另外,针对边界积分方程中存在的高阶奇异性问题,牛忠荣等[16]和高效伟等[17]分别提出半解析算法和径向积分法对奇异积分进行精确求解.
将细分曲面与边界元相结合,能自适应获得满足不同精度要求的细分层次网格信息,省去了前处理中耗时耗力的模型重复离散过程.覃先云等[18 -20]提出了基于参数曲面的边界面法.Liu等[21]将细分曲面法与耦合有限元和边界元法相结合进行薄壳结构声振耦合问题求解.本文将细分曲面法与边界元法相结合,进行黏附吸声材料结构的声学散射[22]分析.实际上,黏附吸声材料虽然已经被广泛使用,但由于工业设计的诸多要求限制,如结构的重量、尺寸和成本造价等,通常难以在结构表面进行全覆盖.因此,在给定的材料体积约束下获得降噪效果最优的材料分布是非常有实际工程意义的.
优化问题[23]通常可以采用梯度算法进行求解,此类方法收敛快且效果好,但是前提是需要目标函数的梯度信息.因此对目标函数进行敏感度分析是优化分析重点之一.敏感度分析的常用方法包括有限差分法[24]和解析法(如直接微分法[25]和伴随变量法[2-27].有限差分法需要对目标函数作大量的差分运算,计算量和设计变量的数目成正比.而直接微分法需要先计算出中间变量的梯度,随后根据链式法则计算出目标函数的梯度值.当出现多个设计变量时,其效率明显降低.伴随变量法则通过引入和设计变量无关的伴随变量避免了计算中间变量的梯度,更适合求解具有多个设计变量的优化问题.例如,Denli和Sun[28]对圆柱壳结构进行优化,采用伴随法进行灵敏度分析;Chen等[29]分析了二维等几何方法的吸声材料的拓扑优化;Zhao等[30]讨论了有限元与边界元耦合方法的材料拓扑优化问题.因此,本文采用伴随变量法,进行结构表面吸声材料分布的敏感度分析,并结合MMA[31](移动渐进线)算法进行吸声材料分布的拓扑优化分析.最后,通过若干数值算例验证所提方法的可靠性和有效性.
1 细分曲面法
本文采用Loop细分方法[4]对初始三角形网格进行细分处理.在细分过程中每个母三角形单元划分成4个子三角形单元(1-4分裂),重复细分直至得到逼近型极限曲面.该方法优点是收敛速度快,且所生成的极限曲面在非奇异点处$c^2$连续,在奇异点处$c^1$连续.
1.1 Loop细分规则
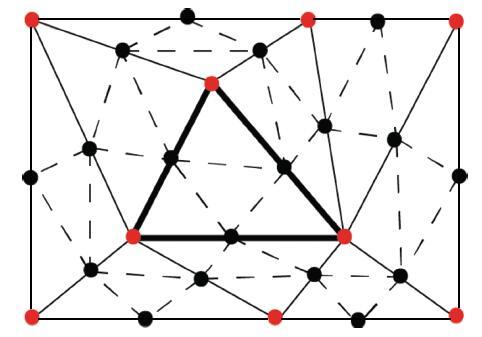
Loop细分过程为:Loop细分采用的是1-4三角形分裂模式,首先需要确定每次细分后生成的新顶点和单元的位置和编号.如图1所示,红色节点为初始网格点,黑色节点为一次细分后生成的新的中间节点(单元边中点).
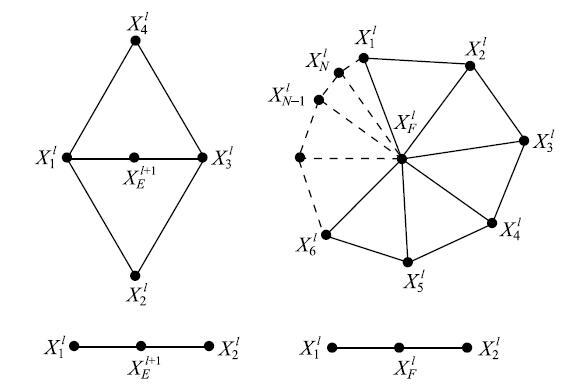
然后分两种情况计算生成新顶点坐标:(1)细分过程中在原始网格边上插入的中间节点$X_E$;(2)细分后由原始网格顶点映射得到新顶点$X_F $,如图2所示.具体插值计算表达式如下.
(1) 边界边中间顶点
$$X_E^{l{ + }1} = \frac{1}{2}(X_1^l + X_2^l) (1)$$
内部边中间顶点
$$X_E^{l{ + }1} = \frac{1}{8}(3X_1^l + 3X_3^l +X_2^l + X_4^l ) (2)$$
(2) 边界端点生成新顶点
$$X_F^{l{ + }1} = \frac{1}{8}(X_1^l + X_2^l) + \frac{3}{4}X_F^l (3)$$
内部端点生成新顶点
$$\left.\begin{array}{l} X_F^{l + 1} = (1 - Nw)X_F^l + w\sum\limits_{i = 1}^N {X_i^l } \\ w = \dfrac{1}{N}\left[ {\dfrac{5}{8} - \left( {\dfrac{3}{8} + \dfrac{1}{4}\cos\dfrac{2\pi }{N}} \right)^2} \right] \end{array}\right\} (4)$$
式中,$l$是细分级数,$w$是权值,$N$是价数(相邻点个数).基于上述计算理论,对两个共边三角形进行一次细分操作,如图3所示.
1.2 细分后的曲面拟合分析
1.2.1 规则单元块的拟合
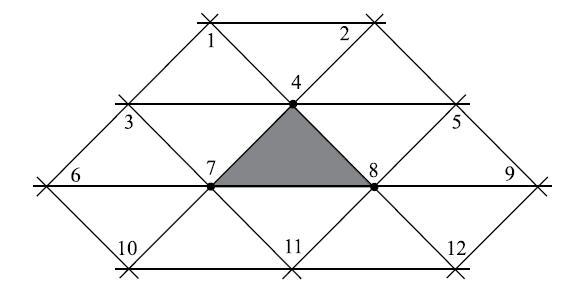
对细分极限网格进行拟合操作,可构造出极限光滑曲面.3个顶点价数都等于6的三角形单元叫做规则单元.对规则单元进行拟合操作,首先需对该单元及周边与其相关联的单元顶点按图4重新编号,图中黑色单元为被拟合单元.将拟合单元中3个顶点的编号分别设定为4,7和8,第一条边$l_{47}$的两个对顶点编号设定为3和8,边$l_{34}$的两个对顶点编号为1和7、边$l_{37} $的两个对顶点编号为6和4.同理可由第二条边$l_{78} $和第三条边$l_{84}$得到编号为11,10,12,5,9和2这些顶点.最终可获得规则三角形单元12个控制点对应的全局编号.
规则三角形单元在局部参数坐标系下的映射曲面形状表达如下
$$X(v,w) =\sum\limits_{i = 1}^{12} {B(v,w)X_i } (5)$$
式中,$B(v,w)$是箱样条基函数, $X_i$是规则单元控制点坐标向量,参数域满足下式
$${\varGamma }= \left\{{(v,w)\left| {v \in (0,1),w \in (0,1 - v)} \right.}\right\} (6)$$
采用面积坐标表示三角形参数空间域,由于基函数在每个参数的最大次数是4次,因此该拟合面是通过4次箱样条插值计算得到的.对于规则单元,基函数显式表达,请见文献[32].
1.2.2 不规则单元块的拟合
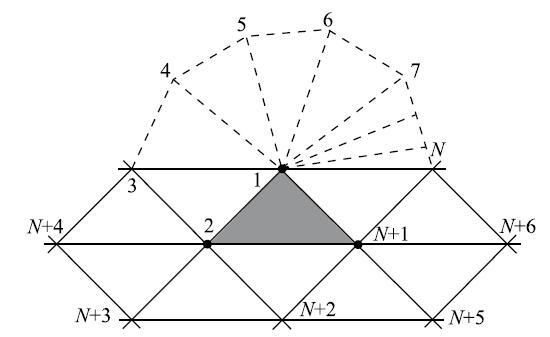
初始网格中可能存在价数$N \ne\mbox{6}$的不规则顶点,包含不规则顶点的单元称作不规则单元.在对不规则三角形单元进行曲面拟合时,首先需要对该单元及与其相关联邻近单元的顶点重新编号,如图5所示.设定该拟合单元中3个顶点的编号分别为1,2和$N +1$,然后根据每条边的对顶点信息获得图5中局部编号为$N + 2$,$N +3$,$N + 4$,$N + 5$和$N + 6$顶点的全局编号.另外,对于不规则顶点1的处理需特殊对待.由边$N$找到编号为3的顶点,之后通过边$l_{13}$找到顶点4、由边$l_{14} $找到顶点5,依此类推直至找到顶点$N$.通过此类操作,最终可获得不规则三角形单元$N + 6$个控制点的全局编号.
图5 不规则三角形单元控制网格顶点排序$N + 6$
Fig. 5 Control vertex patch of irregular triangular elements $(N+6)$
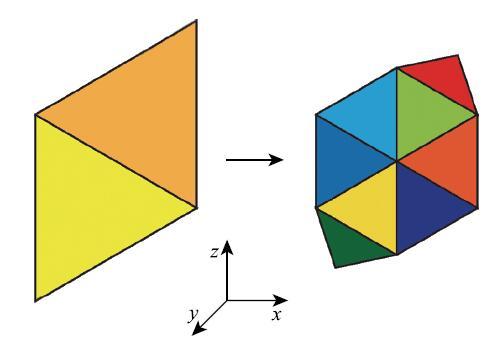
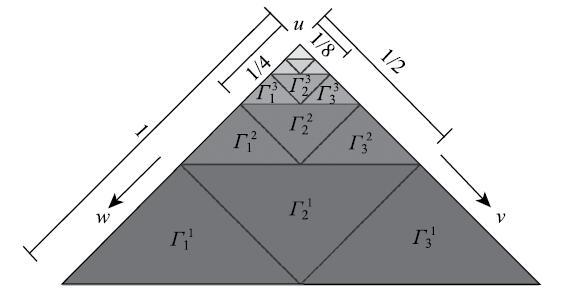
由于不规则单元的基函数隐式表达,因此在对该类单元进行拟合操作前需做特殊处理.采取的方法是通过对该单元进行重复细分,一次细分生成4个子三角形单元,其中3个不包含原始不规则顶点的子单元为规则单元,另外一个为不规则单元.当原始参数域内的拟合点落在规则子单元上,则采用规则插值算法得到该点的曲面映射点坐标.当原始参数域内的拟合点落在不规则子单元上,则进一步对该不规则子单元进行细分,直至使该拟合点落在规则的子单元上,如图6所示.
1.3 实际模型演示
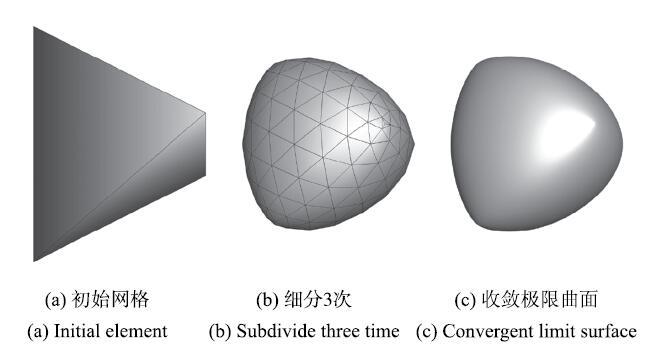
通过3DMax,Maya和Catia等三维设计软件构建初始网格模型,然后根据需要对网格进行全局或局部细分,构造出光滑模型.在图7中,初始网格模型是一个四面体结构,图7(b)和图7(c)分别为细分3次和细分收敛极限模型,可见随着细分次数的增加, 四面体每个面由于权值的影响往里收缩,面片以4倍的速率增大,四面体的表面逐渐变得光滑,最终达到极限收敛状态,更多复杂模型细分结果见图8.
2 细分曲面边界元法
考虑以下控制声波域的亥姆霍兹方程
$$\nabla ^2p(x) + k^2p(x) = 0,\quad \forall x \in \varOmega (7)$$
式中,$\nabla ^2$为拉普拉斯算子,$p$为声压,$k = \omega/c$为波数,$\omega $为圆频率,$c$为波速.使用格林第二等式变换并将域内点$x$逼近边界,可以得到点$x$处的边界积分方程
$$ c(x)p(x) + \int_\varGamma {\dfrac{\partial G(x,y)}{\partial { n}(y)}p(y){\rm d}\varGamma (y) = } $$
$$\quad \int_\varGamma{G(x,y)q(y){\rm d}\varGamma (y) + p_i (x)} (8)$$
式中,$x$是源点,$y$是场点,${ n}(y)$为点$y$处外法线向量,$q(y) = {\partial p(y)} /{\partial { n} (y)}$. 对于三维声场问题,格林函数$G(x)$及其法向导数分别为
$$G(x,y) = \dfrac{\mbox{e}^{{\rm i}kr}}{4\pi r}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$
$$ \dfrac{\partial G(x,y)}{\partial { n} (y)} = -\frac{\mbox{e}^{{\rm i}kr}}{4\pi r^2}(1 -\mbox{i}kr)\dfrac{\partial r}{\partial { n} (y)} (9)$$
式中,$r = \left| {x - y} \right|$表示源点和场点间的距离.为了模拟结构表面粘附吸声材料的吸声特性,引入阻抗边界条件,如下
$$q(y) = \frac{\partial p(y)}{\partial { n} (y)}\mbox{= i}{\kern 1pt} k\beta (y)p(y) (10)$$
式中,$\beta(y)$表示在场点$y$处的归一化声导纳,将上式代入到边界积分方程中可得到
$$c(x)p(x) + \int_\varGamma {\left[ {\frac{\partial G(x,y)}{\partial{ n} (y)} - \mbox{i}k\beta (y)G(x,y)} \right]} p(y){\rm d}\varGamma (y) = p_i (x) (11)$$
使用配点法离散上式,得到如下表达
$$ c(x)p(x) = \sum\limits_{m = 1}^{N_e } {\sum\limits_{n = 1}^{N + 6}{\mbox{i}k\beta _n^m (y(v,w))} } p_n^m (y(v,w))\cdot~~~~~~~$$
$$\int_{\varGamma _m } {\varPhi _n }(y(v,w))G(x,y(v,w)){\rm d}\varGamma _m - ~~~~~~~~~~~~$$
$$\sum\limits_{m = 1}^{N_e } {\sum\limits_{n = 1}^{N + 6}{p_n^m (y(v,w)){\kern 1pt} } } \cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$
$$\int_{\varGamma _m } {\varPhi _n } (y(v,w))\frac{\partial G(x,y(v,w))}{\partial { n} (y(v,w))}{\rm d}\varGamma _m + p_i(x) (12)$$
式中,$\varPhi _n $是插值形函数,采用的是Loop细分的箱样条基函数.$N + 6$表示积分单元$\varGamma _m $周边相关联单元顶点数.假设导纳在单元上为常量,集合所有配点处的离散方程,可得到如下表达式
$$({ H} - { { GB}}){ p} = { p}_{\rm i} (13)$$
式中,${ H}$和${ G}$是边界元系数矩阵,${ p}$是声压向量,${ p}_{\rm i} $是配点处入射波向量,${ B}$为导纳矩阵,可表示为
$${ B} = \mbox{i}k\left[{{\begin{array}{*{20}c} {\beta _1 } & &\\& \ddots &\\&& {\beta _{N_e } } \\\end{array} }} \right] (14)$$
3 基于细分曲面边界元法的优化分析
3.1 优化问题定义
在给定吸声材料体积约束条件下,优化问题可表示为
$$\left. \begin{array}{llll} \min & \varPi = { p}_{\rm f}^{\rm H} { p}_{\rm f} \\ \mbox{s.t.}&\sum\limits_{e = 1}^{N_e }{\rho _e v_e - f_{\rm v} } \sum\limits_{e = 1}^{N_e } {v_e \le 0} \\ &0 \le \rho _{\min } \le \rho _e \le 1 \end{array}\right\} (15) $$
式中,${ p}_{\rm f} $表示考察点处的声压向量,$({\kern 1pt}{\kern 1pt} {\kern 1pt} )^{\rm H}$表示向量的共轭转置. $\rho _e$和$v_e$分别表示单元$e~(e = 1,2,\cdots,N_e )$的变密度和体积.$f_{\rm v} $表示体积分数约束,$\rho _{\min }$为计算中避免奇异值的下限. 声压${ p}_{\rm f}$可通过域内积分方程计算
$${ p}_{\rm f} = - ({ H}_{\rm f} -{ G}_{\rm f} { B}){ p} + { p}_{\rm f}^i (16)$$
式中,矩阵${ H}_{\rm f}, { G}_{\rm f}$和向量${ p}_{\rm f}^i $与式(13)中对应项含义相同,不同之处在于此时源点位于域外.
3.2 设计敏感度分析
由于采用基于梯度的优化算法求解优化问题,因此需要计算目标函数的梯度信息,本文将使用伴随变量法进行敏感度计算.由式(13)和式(16),目标函数可以表达为
$$ \begin{array}{lll} \varPi = \varPi ({ p}_{\rm f} ) + \lambda _1^{\rm T} \left[ {({ H} - { {GB}}){ p} - { p}_i } \right]+\\ \quad \lambda _2^{\rm T} \left[ {{ p}_{\rm f} + ({ H}_{\rm f} - { G}_{\rm f} { B}){ p} - { p}_{\rm f}^i } \right] \\ \end{array} (17)$$
式中,$\lambda _1^{\rm T} $和$\lambda _2^{\rm T}$为任意选取的伴随向量. 直接对上式微分可得
$$ \dfrac{\partial {\varPi} }{\partial \rho _e } = \dfrac{\partial {{ p}}_{\rm f}^{\rm H} }{\partial \rho _e }{{ p}}_{\rm f} + {{ p}}_{\rm f}^{\rm H} \dfrac{\partial {{ p}}_{\rm f} }{\partial \rho _e } + \dfrac{\partial { \lambda} _1^{\rm T} }{\partial \rho _e }\left[ {({{ H}} - { {GB}}){ { p}} - {{ p}}_i } \right]\mbox{ + } ~~~~~~$$ $$\dfrac{\partial { \lambda} _2^{\rm T} }{\partial \rho _e }\left[ {{{ p}}_{\rm f} + ({{ H}}_{\rm f} - {{ G}}_{\rm f} {{ B}}){{ p}} - {{ p}}_{\rm f}^{\rm i} } \right]+~~~~~~~~~~~~~~~~~~~~~$$
$${ \lambda} _1^{\rm T} \Big[\left(\dfrac{\partial {{ H}}}{\partial \rho _e } \!-\! \frac{\partial {{ G}}}{\partial \rho _e }{{ B}} \!-\! {{ G}}\frac{\partial {{ B}}}{\partial \rho _e }\right){{ p}} \!+\!\left({{ H}} - { {GB}}\right)\frac{\partial {{ p}}}{\partial \rho _e } -\! $$
$$\dfrac{\partial {{ p}}_i }{\partial \rho _e } \Big]\mbox{ + } { \lambda} _2^{\rm T} \Big[ \dfrac{\partial {{ p}}_{\rm f} }{\partial \rho _e } \!+\! \left(\dfrac{\partial {{ H}}_{\rm f} }{\partial \rho _e } - \dfrac{\partial {{ G}}_{\rm f} }{\partial \rho _e }{{ B}} - {{ G}}_{\rm f} \dfrac{\partial {{ B}}}{\partial \rho _e }\right){{ p}} +$$
$$({{ H}}_{\rm f} - {{ G}}_{\rm f} {{ B}})\dfrac{\partial {{ p}}}{\partial \rho _e } - \frac{\partial {{ p}}_{\rm f}^{\rm i} }{\partial \rho _e } \Big] ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (18) $$
式中, $({{ H}} - {{ {GB}}}){{ p}} - {{ p}}_i \mbox{ = }{\bf 0}$和${{ p}}_{\rm f} + ({{ H}}_{\rm f} - {{ G}}_{\rm f} {{ B}}){ p} - {{ p}}_{\rm f}^{\rm i} \mbox{ = }{\bf 0}$. 由于边界元系数矩阵仅由几何信息决定,和本文考虑的设计变量无关,因此${\partial {{ G}}} /{\partial \rho _e }$,${\partial {{ H}}} / {\partial \rho _e }$,${\partial { G}_{\rm f}} /{\partial \rho _e }$和${\partial {{ H}}_{\rm f} } /{\partial \rho _e }$都为零. 此外,本文考虑的声激励和设计变量无关,${\partial {{ p}}_{\rm i} } /{\partial \rho _e }$和${\partial {{ p}}_{\rm f}^{\rm i} } /{\partial \rho _e }$同样为零. 因此,式(18)可简化为
$$ \dfrac{\partial \varPi }{\partial \rho _e } = \frac{\partial {{ p}}_{\rm f}^{\rm H} }{\partial \rho _e }{{ p}}_{\rm f} + {{ p}}_{\rm f}^{\rm H} \frac{\partial {{ p}}_{\rm f} }{\partial \rho _e } + { \lambda} _1^{\rm T} \left[ {({{ H}} - {{ {GB}}})\dfrac{\partial { p}}{\partial \rho _e } - {{ G}}\dfrac{\partial {{ B}}}{\partial \rho _e }{{ p}}} \right]\mbox{ + } $$
$$ { \lambda} _2^{\rm T} \left[ {\dfrac{\partial {{ p}}_{\rm f} }{\partial \rho _e } + ({{ H}}_{\rm f} - {{ G}}_{\rm f} {{ B}})\dfrac{\partial {{ p}}}{\partial \rho _e } - {{ G}}_{\rm f} \dfrac{\partial {{ B}}}{\partial \rho _e }{{ p}}} \right]~~~~~~~ (19)$$
利用复数的性质,上式可进一步写为
$$\dfrac{\partial \varPi }{\partial \rho _e } = - \Re \left({ \lambda} _1^{\rm T} { { G}}\dfrac{\partial {{ B}}}{\partial \rho _e }{{ p}} + { \lambda} _2^{\rm T} {{ G}}_{\rm f} \dfrac{\partial {{ B}}}{\partial \rho _e }{{ p}}\right) +~~~~~~~$$
$$ \Re \left[ {({ \lambda} _2^{\rm T} + 2{{ p}}_{\rm f}^{\rm H} )\dfrac{\partial {{ p}}_{\rm f} }{\partial \rho _e }} \right]\mbox{ + } ~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$
$$\Re \left\{ {\left[ {{ \lambda} _1^{\rm T} ({{ H}} - {{ {GB}}}) + { \lambda} _2^{\rm T} ({{ H}}_{\rm f} - {{ G}}_{\rm f} {{ B}})} \right]\dfrac{\partial {{ p}}}{\partial \rho _e }} \right\} (20)$$
式中,$\Re $表示取复数的实部. 正如前面所提,伴随向量${ \lambda}_1^{\rm T} $和${ \lambda }_2^{\rm T}$可任意选取,使其满足以下方程
$$\left.{\begin{array}{l} { \lambda} _2^{\rm T} + 2{{ p}}_{\rm f}^{\rm H} = {\bf 0} \\ { \lambda} _1^{\rm T} {{({ H}}} - {{ {GB})}} + { \lambda} _2^{\rm T} {{({ H}}}_f - {{ G}}_f {{ B)}} = {\bf 0} \end{array}} \right\} (21)$$
该方程可以采用GMRES[33]迭代求解.由于该伴随方程和设计变量无关,因此只需求解一次,这也是伴随变量法适用于多设计变量问题的原因.最后,目标函数对设计变量的导数可表示为
$$\frac{\partial \varPi }{\partial \rho _e } = - \Re \left({ \lambda} _1^{\rm T} {{ G}}\frac{\partial {{ B}}}{\partial \rho _e }{{ p}} + { \lambda} _2^{\rm T} {{ G}}_f \frac{\partial {{ B}}}{\partial \rho _e }{{ p}}\right) (22) $$
式中,${ \lambda} _1^{\rm T} {{ G}}$可以由快速多极算法(FMM)计算得到.当场点数目远小于配点的数目时,${ \lambda}_1^{\rm T} {{ G}}_f$计算量并不大,否则可同样使用FMM加速计算.
3.3 导纳模型
根据Delany-Bazley-Miki[34]模型,得到材料的归一化阻抗表达
$$\overline z = 1 + 0.069~9\left(\frac{f}{\sigma }\right)^{ - 0.632} +\mbox{0.107~~1i}\left(\frac{f}{\sigma }\right)^{ - 0.632} (23)$$
式中,$\sigma $是材料的流阻率$({{\rm N }\cdot {\rm s}} /{{\rm m}^4})$,$f$是频率(Hz). 对应归一化导纳值为
$$\beta _0{ =}\frac{1}{\overline {z}} (24)$$
根据SIMP[35](固体各向同性材料惩罚化)方法,单元导纳可插值为
$$\beta _e = \beta _0 \rho _e^\eta (25)$$
式中,$\eta $为惩罚因子.其作用是使得中间密度向0或1逼近,一般取值为3.尽管SIMP方法能够惩罚中间密度,最终结果仍可能出现灰色单元,本文将采用Heaviside[36]函数对中间密度值进行二次惩罚,以克服这一问题.
3.4 设计变量更新法
本文将采用移动渐近线方法(MMA)求解优化问题,迭代收敛准则为
$${change} = \frac{\left| {\varPi ^{i + 1} - \varPi ^i} \right|}{\varPi ^i}< \tau (26)$$
式中,$\varPi ^i$表示目标函数在第$i$次迭代时的值,优化过程如下
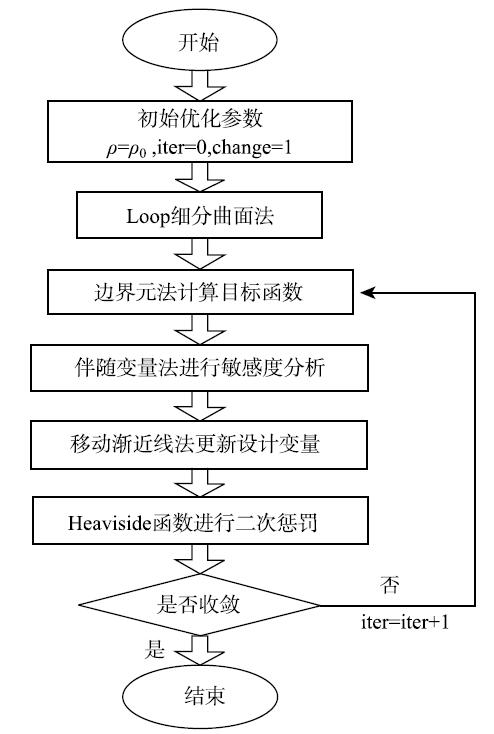
4 数值算例分析
4.1 BeTSSi-Sub薄壁艇模型
为了验证所提优化算法的可靠性,本文将对复杂结构表面吸声材料的分布进行优化设计.分析结构采用2002年的世界数字仿真大会上提供的BeTSSi-Sub薄壁艇模型.平面波沿$x$轴正向传播,入射波幅值为1.0 Pa. 艇壁厚度取0.05 m.坐标原点位于艇艏与艇体连接处截面圆圆心,$x$轴正方向由艇艏指向艇艉,优化目标为最小化点(60,0, 0)处的声压幅值. 结构离散为13~128个三角形单元,如图9所示
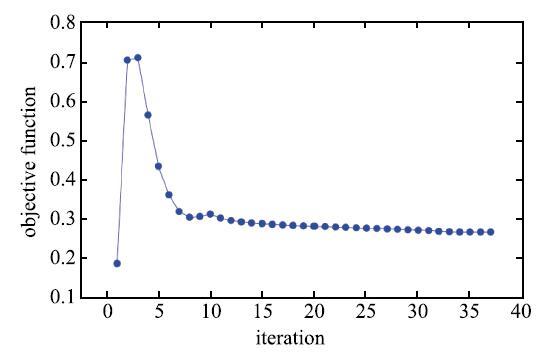
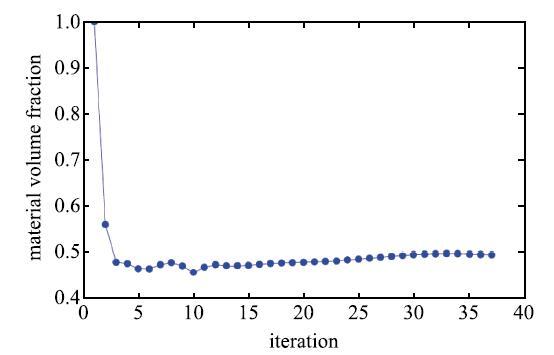
首先考虑潜艇在平面波沿着$x$轴正方向入射情况下,吸声材料的优化分布问题.激励频率为50 Hz,体积比约束设定为0.5.优化过程中目标函数和材料的体积分数变化趋势分别如图10和图11所示.
图11 材料体积分数比随迭代步变化
Fig. 11 The change of material volume fraction with iteration step
可以看出第一步(初始情况)对应的目标函数值最小,这是由于我们选择全覆盖为初始设计.随后由于材料体积约束的作用,体积分数急剧降低,导致了目标函数也急剧增大,随后优化算法根据目标函数敏感度不断寻优,目标函数随之下降,最终于第37步收敛.
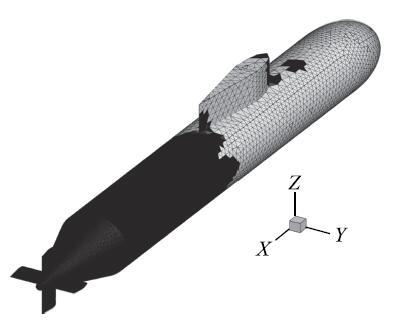
优化后的吸声材料分布和对应的声压分布分别如图12和图13所示.我们可以看出最终拓扑分布中几乎不存在中间密度状态单元存在,这说明采用的方法能够给出清晰的0-1分布.
图12 50 Hz时潜艇表面吸声材料的最优分布
Fig. 12 The optimal distribution of sound absorption materials on submarine surface at 50 Hz
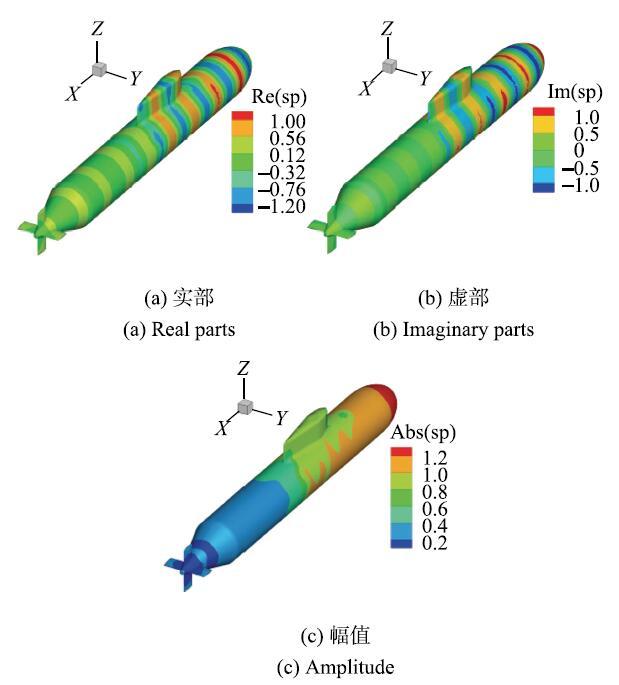
图13 吸声材料最优分布时声压的分布
Fig. 13 Distribution of acoustic pressure with optimal distribution of sound absorbing materials
为了考察激励频率对最优分布的影响,我们随后给出了激励频率分别为10,100,150和200Hz时潜艇表面吸声材料的优化分布,体积比约束仍然设定为0.5,结果如图14所示.可以看出,不同激励频率下的最优分布有所不同,这说明吸声材料的最优分布具有频率依赖性.这是由于频率变化,波长也随着变化,导致声波干涉情况发生变化,吸声材料的分布也需要发生相应的改变.此外,随着频率的升高,优化结果中吸声材料的分布就显得更加零散.
图14 不同频率下潜艇表面吸声材料的最优分布
Fig. 14 The optimal distribution of sound absorption materials on submarine surface at different excitation frequencies
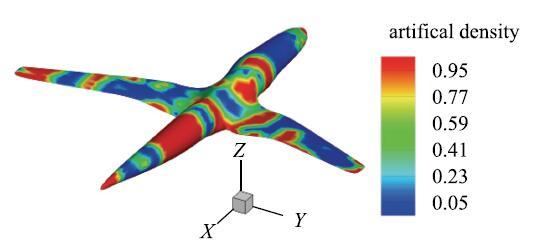
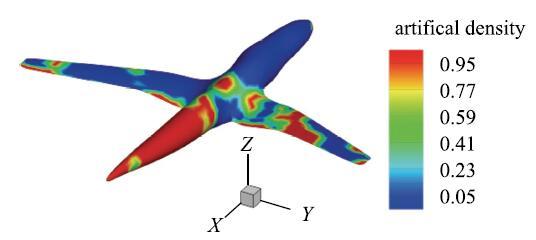
4.2 飞行器模型
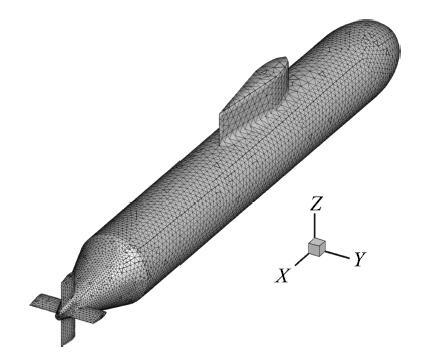
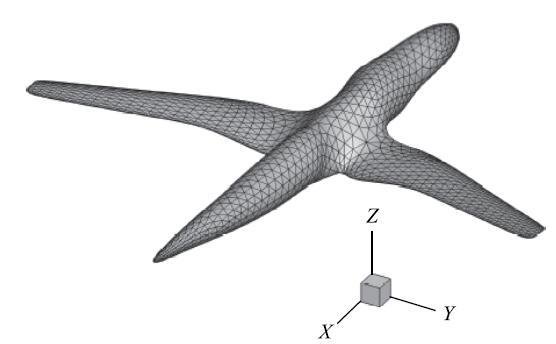
飞行器模型同样采用三角形单元进行离散,初始网格由324个单元构成.使用Loop细分法对初始模型进行两次细分操作,得到含有5184个单元和2530个节点的网格模型,如图15所示.
我们同样考虑飞行器在平面波入射情况下,吸声材料的优化分布问题.激励频率为100 Hz,体积比约束设定为0.5.
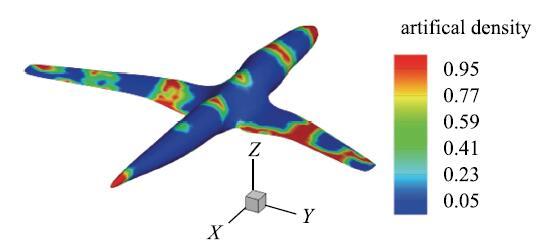
优化后的吸声材料分布和对应的声压级分布分别如图16和图17所示.同样可以看出,最终拓扑分布中几乎不存在着中间密度状态单元.此外,由于结构较为复杂,我们采用三角形单元离散,最终的网格模型并非完全对称,所以得到的优化结构也存在着一些不对称的地方,这是由于离散网格模型的局限性导致的,因此在对对称结构进行优化时选择对称部分作为优化分析对象是一个较好的方法.需要说明的是,尽管得到的优化分布不是完全对称,但这并不意味着失去了意义,只要优化方法能够给出一套较为粗略的预设计方案,就能够为后续的精细设计提供基础和借鉴价值.
图16 100 Hz时飞行器表面吸声材料的最优分布
Fig. 16 The optimal distribution of sound absorption materials on aircraft surface at 100 Hz
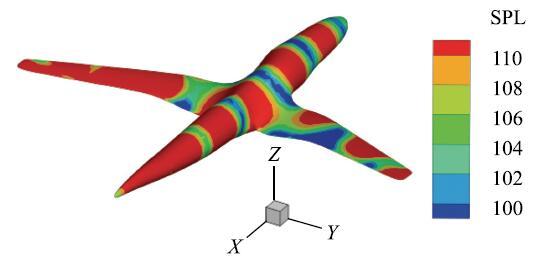
图17 吸声材料最优分布时声压级的分布
Fig. 17 Distribution of acoustic pressure level at optimal distribution of sound absorbing materials
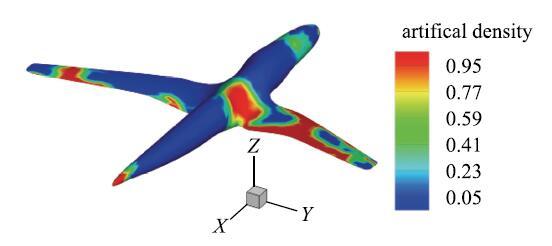
这里同样考察了激励频率对最优分布的影响,分别给出了激励频率为50,150和200Hz时飞行器表面吸声材料的优化分布,体积比约束仍然设定为0.5,结果如图18$\sim$图20所示.
图18 50 Hz时飞行器表面吸声材料的最优分布
Fig. 18 The optimal distribution of sound absorption materials on aircraft surface at 50 Hz
图19 150 Hz时飞行器表面吸声材料的最优分布
Fig. 19 The optimal distribution of sound absorption materials on aircraft surface at 150 Hz
图20 200 Hz时飞行器表面吸声材料的最优分布
Fig. 20 The optimal distribution of sound absorption materials on aircraft surface at 200 Hz
5 结论
本文采用细分曲面边界元法结合SIMP变密度法对结构表面吸声材料的分布进行优化设计.引入介质导纳参数,借助SIMP插值模型建立了介质导纳参数和吸声材料单元相对密度之间的关系;建立以吸声材料单元相对密度为设计变量,以吸声材料的体积为约束的拓扑优化数学模型,最终给出了在吸声材料体积限制下的最优分布算法.通过对潜艇和飞行器模型的吸声材料分布优化算例,验证了所提方法的可行性和有效性,同时证明了该方法可推广到复杂工程应用中.优化分析的结果显示吸声材料的最优分布是具有频率依赖性的.
The authors have declared that no competing interests exist.
参考文献
| [1] |
Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement .
The concept of isogeometric analysis is proposed. Basis functions generated from NURBS (Non-Uniform Rational B-Splines) are employed to construct an exact geometric model. For purposes of analysis, the basis is refined and/or its order elevated without changing the geometry or its parameterization. Analogues of finite element h- and p-refinement schemes are presented and a new, more efficient, higher-order concept, k-refinement, is introduced. Refinements are easily implemented and exact geometry is maintained at all levels without the necessity of subsequent communication with a CAD (Computer Aided Design) description. In the context of structural mechanics, it is established that the basis functions are complete with respect to affine transformations, meaning that all rigid body motions and constant strain states are exactly represented. Standard patch tests are likewise satisfied. Numerical examples exhibit optimal rates of convergence for linear elasticity problems and convergence to thin elastic shell solutions. A k-refinement strategy is shown to converge toward monotone solutions for advection鈥揹iffusion processes with sharp internal and boundary layers, a very surprising result. It is argued that isogeometric analysis is a viable alternative to standard, polynomial-based, finite element analysis and possesses several advantages.
|
| [2] |
Iso-geometric finite element analysis based on catmull-clark subdivision solids .
We present a volumetric iso-geometric finite element analysis based on Catmull-Clark solids. This concept allows one to use the same representation for the modeling, the physical simulation, and the visualization, which optimizes the design process and narrows the gap between CAD and CAE. In our method the boundary of the solid model is a Catmull-Clark surface with optional corners and creases to support the modeling phase. The crucial point in the simulation phase is the need to perform efficient integration for the elements. We propose a method similar to the standard subdivision surface evaluation technique, such that numerical quadrature can be used.Experiments show that our approach converges faster than methods based on tri-linear and tri-quadratic elements. However, the topological structure of Catmull-Clark elements is as simple as the structure of linear elements. Furthermore, the Catmull-Clark elements we use are C2-continuous on the boundary and in the interior except for irregular vertices and edges.
|
| [3] |
Behaviour of recursive division surfaces near extraordinary points .
The behaviour of the limits surface defined by a recursive division construction can be analysed in terms of the eigenvalues of a set of matrices. This analysis predicts effects actually observed, and leads to suggestions for the further improvement of the method.
|
| [4] |
A survey of curve and surface methods in CAGD .
ABSTRACT CAGD - short for Computer Aided Geometric Design - is concerned with the approximation and representation of curves and surfaces that arise when these objects have to be processed by a computer. Designing curves and surfaces plays an important role in the construction of quite different products such as car bodies, ship hulls, airplane fuselages and wings, propeller blades, shoe insoles, bottles, etc, etc, but also in the description of geological, physical and even medical phenomena. In this survey we mainly present methods for the generation of curves and surfaces, not for subsequent operations such as viewing, intersections, etc. Also not covered are generation methods that construct curves and surfaces from other such objects, such as fillet curves/surfaces, offset curves/surfaces etc.
|
| [5] |
A butterfly subdivision scheme for surface interpolation with tension control . |
| [6] |
$\sqrt 3 $-subdivision . |
| [7] |
Durup$\imath $nar F. Three-dimensional Scene Representations: Modeling, Animation, and Rendering Techniques. Three-Dimensional Television . |
| [8] |
Subdivision surfaces: a new paradigm for thin-shell finite-element analysis . |
| [9] |
Shape optimisation with multiresolution subdivision surfaces and immersed finite elements .
We develop a new optimisation technique that combines multiresolution subdivision surfaces for boundary description with immersed finite elements for the discretisation of the primal and adjoint problems of optimisation. Similar to wavelets, multiresolution surfaces represent the domain boundary using a coarse control mesh and a sequence of detail vectors. Based on the multiresolution decomposition efficient and fast algorithms are available for reconstructing control meshes of varying fineness. During shape optimisation the vertex coordinates of control meshes are updated using the computed shape gradient information. By virtue of the multiresolution editing semantics, updating the coarse control mesh vertex coordinates leads to large-scale geometry changes and, conversely, updating the fine control mesh coordinates leads to small-scale geometry changes. In our computations we start by optimising the coarsest control mesh and refine it each time the cost function reaches a minimum. This approach effectively prevents the appearance of non-physical boundary geometry oscillations and control mesh pathologies, like inverted elements. Independent of the fineness of the control mesh used for optimisation, on the immersed finite element grid the domain boundary is always represented with a relatively fine control mesh of fixed resolution. With the immersed finite element method there is no need to maintain an analysis suitable domain mesh. In some of the presented two and three-dimensional elasticity examples the topology derivative is used for introducing new holes inside the domain. The merging or removing of holes is not considered.
|
| [10] |
|
| [11] |
轴对称薄壁结构自由振动的边界元分析 .
采用双互易法分析薄壁轴对称结构自由振动的特征频率以及特征模态.首先,采用径向基函数插值域积分里的位移,利用双互易法将域积分转化为子午面边界的积分.然后,将边界物理量、基本解和特解展开为傅里叶级数,沿环向积分后得到的边界积分方程可用于轴对称结构带体积力问题和受非对称载荷的动力学分析,其积分域为轴对称结构子午面边界上的线积分,进一步降低了问题的维度和离散的难度.文章详细探讨了源点处于对称轴的特殊情况,根据基本解和特解的退化形式,针对无体积力和有体积力分别给出了处理奇异矩阵的方案.对于薄壁结构,采用双曲正弦变换处理近奇异积分有效提高积分精度.最后将双互易法和双曲正弦变化应用于薄壁轴对称结构带体积力的静力学和自由振动分析.数值结果表明,文章提出的处理奇异矩阵的方法能够有效处理源点处于对称轴的情况;当圆筒厚高比为10-3,边界元计算的特征频率的相对误差为10-3,且优于有限元的结果.
Free vibration analysis of thin-walled axisymmetric structures with boundary element method .
采用双互易法分析薄壁轴对称结构自由振动的特征频率以及特征模态.首先,采用径向基函数插值域积分里的位移,利用双互易法将域积分转化为子午面边界的积分.然后,将边界物理量、基本解和特解展开为傅里叶级数,沿环向积分后得到的边界积分方程可用于轴对称结构带体积力问题和受非对称载荷的动力学分析,其积分域为轴对称结构子午面边界上的线积分,进一步降低了问题的维度和离散的难度.文章详细探讨了源点处于对称轴的特殊情况,根据基本解和特解的退化形式,针对无体积力和有体积力分别给出了处理奇异矩阵的方案.对于薄壁结构,采用双曲正弦变换处理近奇异积分有效提高积分精度.最后将双互易法和双曲正弦变化应用于薄壁轴对称结构带体积力的静力学和自由振动分析.数值结果表明,文章提出的处理奇异矩阵的方法能够有效处理源点处于对称轴的情况;当圆筒厚高比为10-3,边界元计算的特征频率的相对误差为10-3,且优于有限元的结果.
|
| [12] |
一种模拟大规模高频声场的双层奇异边界法 .
大规模高频声场的数值模拟是一项非常有计算挑战性的课题. 为了解决传统边界型离散方法由于全局支撑的满阵限制, 不易应用于大规模高频声场模拟的计算瓶颈, 本文提出了一种用于模拟大规模高频声场的双层奇异边界法. 在该方法中, 通过引入双层结构, 细网格上的全局支撑的满阵被转化为局部支撑的大规模稀疏矩阵, 传统奇异边界法模拟大规模问题时所面临的高计算量以及过度存储需求遂得以解决. 其次, 双层奇异边界法仅通过粗网格评估远场作用, 且独立于特定的插值核函数. 相较于快速多级方法, 该方法具有更强的适应性和灵活性, 且多层结构使该方法具有一定的预调节作用, 非常适合求解具有大规模、高秩、高条件数特点的高频波矩阵. 在其后的散射球模型算例中, 双层奇异边界法配置10万个节点, 成功模拟了无量纲波数高达160的声散射问题. 在对于人头模型的声散射特性分析中, 双层奇异边界法比COMSOL软件计算速度快了约78.13%. 当配置8万个节点时, 双层奇异边界法成功模拟了频率高达25 kHz 的工况, 该频率已远远超出了人耳的听力极限.
A dual-level singular boundary method for large-scale high frequency sound field analysis .
大规模高频声场的数值模拟是一项非常有计算挑战性的课题. 为了解决传统边界型离散方法由于全局支撑的满阵限制, 不易应用于大规模高频声场模拟的计算瓶颈, 本文提出了一种用于模拟大规模高频声场的双层奇异边界法. 在该方法中, 通过引入双层结构, 细网格上的全局支撑的满阵被转化为局部支撑的大规模稀疏矩阵, 传统奇异边界法模拟大规模问题时所面临的高计算量以及过度存储需求遂得以解决. 其次, 双层奇异边界法仅通过粗网格评估远场作用, 且独立于特定的插值核函数. 相较于快速多级方法, 该方法具有更强的适应性和灵活性, 且多层结构使该方法具有一定的预调节作用, 非常适合求解具有大规模、高秩、高条件数特点的高频波矩阵. 在其后的散射球模型算例中, 双层奇异边界法配置10万个节点, 成功模拟了无量纲波数高达160的声散射问题. 在对于人头模型的声散射特性分析中, 双层奇异边界法比COMSOL软件计算速度快了约78.13%. 当配置8万个节点时, 双层奇异边界法成功模拟了频率高达25 kHz 的工况, 该频率已远远超出了人耳的听力极限.
|
| [13] |
大规模边界元模态分析的高效数值方法 .
随着大规模快速边界元计算技术的发展,在复杂结构的动态设计、振动与噪声分析中愈来愈多地采用边界元法,因此求解大规模边界元特征值问题、进行复杂结构和声场模态分析,成为工程应用中一个十分重要,但却极具挑战性的课题,目前国际上还没有十分有效的数值方法.本文针对边界元法中典型的非线性特征值问题,提出了一种通用、高效的数值解法,称为基于预解矩阵采样的Rayleigh-Ritz投影法,记为RSRR.首先,通过求解一系列频域边界元问题来构造特征向量搜索空间,进而可以采用Rayleigh-Ritz投影,将原问题转化为一个可以采用现有方法求解的小规模缩减特征值问题;其次,为了降低Rayleigh-Ritz投影过程的计算量,基于解析函数的Cauchy积分公式,构造了边界元系数矩阵的插值近似方法,以及缩减特征值问题系数矩阵的快速计算方法,给出了插值项数的估计策略;最后,将RSRR与声学快速边界元法结合,应用于大规模吸声结构的复模态分析.数值算例表明,RSRR方法能够可靠地求出给定频段内的全部特征值和特征向量,具有计算效率高、精度高、通用等优点.
An efficient numerical method for large-scale modal analysis using boundary element method .
随着大规模快速边界元计算技术的发展,在复杂结构的动态设计、振动与噪声分析中愈来愈多地采用边界元法,因此求解大规模边界元特征值问题、进行复杂结构和声场模态分析,成为工程应用中一个十分重要,但却极具挑战性的课题,目前国际上还没有十分有效的数值方法.本文针对边界元法中典型的非线性特征值问题,提出了一种通用、高效的数值解法,称为基于预解矩阵采样的Rayleigh-Ritz投影法,记为RSRR.首先,通过求解一系列频域边界元问题来构造特征向量搜索空间,进而可以采用Rayleigh-Ritz投影,将原问题转化为一个可以采用现有方法求解的小规模缩减特征值问题;其次,为了降低Rayleigh-Ritz投影过程的计算量,基于解析函数的Cauchy积分公式,构造了边界元系数矩阵的插值近似方法,以及缩减特征值问题系数矩阵的快速计算方法,给出了插值项数的估计策略;最后,将RSRR与声学快速边界元法结合,应用于大规模吸声结构的复模态分析.数值算例表明,RSRR方法能够可靠地求出给定频段内的全部特征值和特征向量,具有计算效率高、精度高、通用等优点.
|
| [14] |
FEM/wideband FMBEM coupling for structural--acoustic design sensitivity analysis .
A coupling algorithm based on the finite element method (FEM) and the wideband fast multipole boundary element method (wideband FMBEM) is proposed for acoustic fluid–structure interaction simulation and structural–acoustic design sensitivity analysis by using the direct differentiation method. The wideband fast multipole method (FMM), which is developed by combining the original FMM and the diagonal form FMM, is used to accelerate the calculation of the matrix–vector products in boundary element analysis. The iterative solver generalized minimal residual method is applied to accelerate the calculation of the solution to the linear system of equations. The FEM/wideband FMBEM algorithm makes it possible to predict the effects of arbitrarily shaped vibrating structures on the sound field numerically. Numerical examples are presented to demonstrate the validity and efficiency of the proposed algorithm.
|
| [15] |
基于有限元与宽频快速多极边界元的二维流固耦合声场分析 .
采用有限元/快速多极边界元法进行水下弹性结构的辐射和散射声场分析。Burton-Miller法用于解决传统单Helmholtz边界积分方程在求解外边界值问题时出现的非唯一解的问题。该文采用GMRES和快速多极算法加速求解系统方程。针对传统快速算法在高频处效率低和对角式快速算法在低频处不稳定这一问题,该文通过结合这两种快速算法形成宽频快速算法来克服。同时该文通过观察不同参数条件设置下,宽频快速多极法得到的数值结果在计算精度和计算时间上的变化,得到最优的参数组合值。最后通过数值算例验证该文算法的正确性和有效性。
FEM/Wideband FMBEM coupling analysis for two dimensional acoustic fluid-structure interaction problems .
采用有限元/快速多极边界元法进行水下弹性结构的辐射和散射声场分析。Burton-Miller法用于解决传统单Helmholtz边界积分方程在求解外边界值问题时出现的非唯一解的问题。该文采用GMRES和快速多极算法加速求解系统方程。针对传统快速算法在高频处效率低和对角式快速算法在低频处不稳定这一问题,该文通过结合这两种快速算法形成宽频快速算法来克服。同时该文通过观察不同参数条件设置下,宽频快速多极法得到的数值结果在计算精度和计算时间上的变化,得到最优的参数组合值。最后通过数值算例验证该文算法的正确性和有效性。
|
| [16] |
二维边界元法高阶元几乎奇异积分半解析算法 .
<p>针对边界元法中高阶单元中几乎奇异积分计算难题,解剖了二维边界元法高阶单元的几何特征,定义源点相对高阶单元的接近度。将高阶单元上奇异积分核函数用近似奇异函数逼近,从而分离出积分核中主导的奇异函数部分,其奇异积分核分解为规则核函 数和奇异核函数两项积分之和。规则核函数用常规高斯数值积分,再对奇异核函数积分导出解析公式,从而建立了一种新的半解析法,用于高阶边界单元上几乎强奇异和超奇异积分计算。给出3个算例,采用边界元法高阶单元的半解析法计算了弹性力学薄体结构和近边界点位移/应力,并与线性边界元正则化算法结果作了比较,结果表明提出的二次元的半解析算法更加有效。特别是分析薄体结构,采用正则化算法的线性边界元分析比有限元有显著优势,而用提出的二次边界元半解析算法分析比其线性元的有效接近度又减小了4个量级。</p>
A new semi-analysis algorithm of nearly singular integrals in high order boundary element analysis of 2D elasticity .
<p>针对边界元法中高阶单元中几乎奇异积分计算难题,解剖了二维边界元法高阶单元的几何特征,定义源点相对高阶单元的接近度。将高阶单元上奇异积分核函数用近似奇异函数逼近,从而分离出积分核中主导的奇异函数部分,其奇异积分核分解为规则核函 数和奇异核函数两项积分之和。规则核函数用常规高斯数值积分,再对奇异核函数积分导出解析公式,从而建立了一种新的半解析法,用于高阶边界单元上几乎强奇异和超奇异积分计算。给出3个算例,采用边界元法高阶单元的半解析法计算了弹性力学薄体结构和近边界点位移/应力,并与线性边界元正则化算法结果作了比较,结果表明提出的二次元的半解析算法更加有效。特别是分析薄体结构,采用正则化算法的线性边界元分析比有限元有显著优势,而用提出的二次边界元半解析算法分析比其线性元的有效接近度又减小了4个量级。</p>
|
| [17] |
边界元中计算任意高阶奇异线积分的直接法 .
提出了一种精确计算任意高阶奇异曲线积分的直接计算法.首先将曲线单元上的各种几何量用投影线上的几何量来表示,然后通过幂级数展开和解析的方法显式地消除了积分的奇异性.还导出了计算等参坐标对局部直角坐标偏导数的表达式.由于这种方法涉及到的是总体尺度间的坐标变换,操作起来直观明了,可以处理二维问题边界元分析中出现的任意高阶奇异边界积分.最后用具体算例验证该方法的正确性.
A direct method for evaluating line integrals with arbitrary high order of singularities .
提出了一种精确计算任意高阶奇异曲线积分的直接计算法.首先将曲线单元上的各种几何量用投影线上的几何量来表示,然后通过幂级数展开和解析的方法显式地消除了积分的奇异性.还导出了计算等参坐标对局部直角坐标偏导数的表达式.由于这种方法涉及到的是总体尺度间的坐标变换,操作起来直观明了,可以处理二维问题边界元分析中出现的任意高阶奇异边界积分.最后用具体算例验证该方法的正确性.
|
| [18] |
基于参数曲面三维势问题的边界面法 .
This work presents a new implementation of the boundary element method (BEM), here called the boundary face method (BFM). The conventional BEM uses the standard elements for boundary integration and approximation of the geometry, and thus introduces errors of geometry. In this paper, the boundary faces of the geometry are discretized by patches in parametric space. Both boundary integration and variable approximation are also performed in the parametric space. The geometric data at Gaussian integration points, such as the coordinates, the Jacobians and the out normals are calculated directly from the faces rather than from elements, and thus no geometric error will be introduced. The BFM has real potential to seamlessly interact with CAD software, because its implementation can be directly based on a CAD model through its Brep data. Numerical examples for 3D potential problems demonstrate that the new method provides not only more accurate results than the conventional BEM, but also a new way toward automatic simulation, as simulations can be greatly simplified with our method.
A boundary face method for 3D potential problems based on parametric surface .
This work presents a new implementation of the boundary element method (BEM), here called the boundary face method (BFM). The conventional BEM uses the standard elements for boundary integration and approximation of the geometry, and thus introduces errors of geometry. In this paper, the boundary faces of the geometry are discretized by patches in parametric space. Both boundary integration and variable approximation are also performed in the parametric space. The geometric data at Gaussian integration points, such as the coordinates, the Jacobians and the out normals are calculated directly from the faces rather than from elements, and thus no geometric error will be introduced. The BFM has real potential to seamlessly interact with CAD software, because its implementation can be directly based on a CAD model through its Brep data. Numerical examples for 3D potential problems demonstrate that the new method provides not only more accurate results than the conventional BEM, but also a new way toward automatic simulation, as simulations can be greatly simplified with our method.
|
| [19] |
A dual interpolation boundary face method for elasticity problems, European Journal of Mechanics -A/ |
| [20] |
A double-layer interpolation method for implementation of BEM analysis of problems in potential theory .
A double-layer interpolation method (DLIM) is proposed to improve the performance of the boundary element method (BEM). In the DLIM, the nodes of an element are sorted into two groups: (i) nodes inside the element, called source nodes, and (ii) nodes on the vertices and edges of the element, called virtual nodes. With only source nodes, the element becomes a conventional discontinuous element. Taking into account both source and virtual nodes, the element becomes a standard continuous element. The physical variables are interpolated by continuous elements (first-layer interpolation), while the boundary integral equations are collocated at the source nodes only. We further established additional constraint equations between source and virtual nodes using a moving least-squares (MLS) approximation (second-layer interpolation). Using these constraints, a square coefficient matrix of the overall system of linear equations was finally achieved. The DLIM keeps the main advantages of MLS, such as significantly alleviating the meshing task, while providing much better accuracy than the traditional BEM. The method has been used successfully for solving potential problems in two dimensions. Several numerical examples in comparison with other methods have demonstrated the accuracy and efficiency of our method.
|
| [21] |
Isogeometric FEM-BEM coupled structural-acoustic analysis of shells using subdivision surfaces .
Abstract: We introduce a coupled finite and boundary element formulation for acoustic scattering analysis over thin shell structures. A triangular Loop subdivision surface discretisation is used for both geometry and analysis fields. The Kirchhoff-Love shell equation is discretised with the finite element method and the Helmholtz equation for the acoustic field with the boundary element method. The use of the boundary element formulation allows the elegant handling of infinite domains and precludes the need for volumetric meshing. In the present work the subdivision control meshes for the shell displacements and the acoustic pressures have the same resolution. The corresponding smooth subdivision basis functions have the $C^1$ continuity property required for the Kirchhoff-Love formulation and are highly efficient for the acoustic field computations. We validate the proposed isogeometric formulation through a closed-form solution of acoustic scattering over a thin shell sphere. Furthermore, we demonstrate the ability of the proposed approach to handle complex geometries with arbitrary topology that provides an integrated isogeometric design and analysis workflow for coupled structural-acoustic analysis of shells.
|
| [22] |
Controlling sound with acoustic metamaterials .
Acoustic metamaterials can manipulate and control sound waves in ways that are not possible in conventional materials. Metamaterials with zero, or even negative, refractive index for sound offer new possibilities for acoustic imaging and for the control of sound at subwavelength scales. The combination of transformation acoustics theory and highly anisotropic acoustic metamaterials enables precise control over the deformation of sound fields, which can be used, for example, to hide or cloak objects from incident acoustic energy. Active acoustic metamaterials use external control to create effective material properties that are not possible with passive structures and have led to the development of dynamically reconfigurable, loss-compensating and parity鈥搕ime-symmetric materials for sound manipulation. Challenges remain, including the development of efficient techniques for fabricating large-scale metamaterial structures and converting laboratory experiments into useful devices. In this Review, we outline the designs and properties of materials with unusual acoustic parameters (for example, negative refractive index), discuss examples of extreme manipulation of sound and, finally, provide an overview of future directions in the field.
|
| [23] |
Design of absorbing material distribution for sound barrier using topology optimization .
A topology optimization approach based on the boundary element method (BEM) and the optimality criteria (OC) method is proposed for the optimal design of sound absorbing material distribution within sound barrier structures. The acoustical effect of the absorbing material is simplified as the acoustical impedance boundary condition. Based on the solid isotropic material with penalization (SIMP) method, a topology optimization model is established by selecting the densities of absorbing material elements as design variables, volumes of absorbing material as constraints, and the minimization of sound pressure at reference surface as design objective. A smoothed Heaviside-like function is proposed to help the SIMP method to obtain a clear 0鈥1 distribution. The BEM is applied for acoustic analysis and the sensitivities with respect to design variables are obtained by the direct differentiation method. The Burton鈥揗iller formulation is used to overcome the fictitious eigen-frequency problem for exterior boundary-value problems. A relaxed form of OC is used for solving the optimization problem to find the optimal absorbing material distribution. Numerical tests are provided to illustrate the application of the optimization procedure for 2D sound barriers. Results show that the optimal distribution of the sound absorbing material is strongly frequency dependent, and performing an optimization in a frequency band is generally needed.
|
| [24] |
Adjoint sensitivity analysis and optimization of hysteretic dynamic systems with nonlinear viscous dampers .
In this paper we discuss the adjoint sensitivity analysis and optimization of hysteretic systems equipped with nonlinear viscous dampers and subjected to transient excitation. The viscous dampers are...
|
| [25] |
A wideband fast multipole boundary element method for three dimensional acoustic shape sensitivity analysis based on direct differentiation method .
78 A wideband fast multipole boundary element approach for 3D acoustic shape sensitivity analysis. 78 Boundary integral equations of sensitivity coefficients based on Burton–Miller's method. 78 Analytical evaluation of hypersingular integrals for constant element for efficient treatment. 78 Demonstrations of accuracy and efficiency of the approach through numerical examples.
|
| [26] |
Design sensitivity analysis for a sequential structural-acoustic problem . |
| [27] |
Topology optimization of bounded acoustic problems using the hybrid finite element-wave based method . |
| [28] |
Structural-acoustic optimization of sandwich cylindrical shells for minimum interior sound transmission .
This paper presents an optimization study of cylindrical sandwich shells to minimize the transmitted sound into the interior induced by the exterior acoustic excitations. The boundary elements and finite elements are, respectively, used to model the interior and exterior acoustics and the vibration of the shell. The design parameters of the optimization are the reinforcement angles of the orthotropic composite materials of the skins and core. The sensitivity analysis of the objective function with respect to the design variables is computed by the adjoint-variable technique. The optimizations of the shell at a single frequency and in a band of frequencies are investigated. From the promising optimization results it is seen that the reinforcement angles in the composite sandwich layers are effective structural design parameters to minimize the sound transmission into the interior without giving up the structural rigidity, particularly at low frequencies where the structural damping is not effective.
|
| [29] |
An isogeometric approach two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution . |
| [30] |
Minimization of sound radiation in fully coupled structural-acoustic systems using FEM-BEM based topology optimization .
A topology optimization approach is proposed for the optimal design of bi-material distribution on underwater shell structures. The coupled finite element method (FEM) / boundary element method (BEM)...
|
| [31] |
The method of moving asymptotes-a new method for structural optimization . |
| [32] |
Exact evaluation of Loop subdivision surfaces at arbitrary parameter values
Abstract In this paper we disprove the belief widespread within the computer graphics community that Catmull-Clark subdivision surfaces cannot be evaluated directly without explicitly subdividing. We show that the surface and all its derivatives can be evaluated in terms of a set of eigenbasis functions which depend only on the subdivision scheme and we derive analytical expressions for these basis functions. In particular, on the regular part of the control mesh where Catmull-Clark surfaces are bi-cubic B-splines, the eigenbasis is equal to the power basis. Also, our technique is both efficient and easy to implement. We have used our implementation to compute high quality curvature plots of subdivision surfaces. The cost of our evaluation scheme is comparable to that of a bi-cubic spline. Therefore, our method allows many algorithms developed for parametric surfaces to be applied to Catmull-Clark subdivision surfaces. This makes subdivision surfaces an even more attractive tool for free-form surface modeling. 1
|
| [33] |
适合于求解边界元方程组的GMRES算法的实用化和并行化研究 .
为了将GMRES算法应用于大型边界元方程组的求解,采用预条件技术和重正交技术相结合的方法实现了该算法的实用化,然后在实用化的基础上针对迭代算法具有良好并行性的特点,研究了该算法在网络机群环境下的并行化技术.数值试验和分析表明所用的这些技术是行之有效的,对于提高求解速度和增大求解问题的规模是有意义的.
Study on the utilization and parallelization of the GMRES algorithm for BEM systems solution .
为了将GMRES算法应用于大型边界元方程组的求解,采用预条件技术和重正交技术相结合的方法实现了该算法的实用化,然后在实用化的基础上针对迭代算法具有良好并行性的特点,研究了该算法在网络机群环境下的并行化技术.数值试验和分析表明所用的这些技术是行之有效的,对于提高求解速度和增大求解问题的规模是有意义的.
|
| [34] |
Predicting the sound absorption of natural materials: Best-fit inverse laws for the acoustic impedance and the propagation constant .
Natural materials are becoming a valid option for sound absorption treatments. In particular, among them, natural fibers have received increasing attention given their good thermal insulation properties, lack of harmful effects on health, and availability in large quantities. This paper discusses an inverse method to predict the acoustical properties of nine natural fibers. Six vegetative fibers: kenaf, wood, hemp, coconut, straw, and cane; one animal fiber, sheep wool; recycled cardboard; and granular cork are investigated. The absorption coefficient and the flow resistance for samples of different thickness have been measured. Moving from the Delany-Bazley model, this study compares the impedance tube results with the theoretically predicted ones. Then, using a least-square fit procedure based on the Nelder-Mead method, the coefficients that best predict both the acoustic impedance and the propagation constant laws are calculated. The inverse approach used in this paper allows to determine different physical parameters and to obtain formulas to include the investigated natural fibers in software modelling for room acoustics applications.
|
| [35] |
基于SIMP插值模型的渐进结构优化方法 .
在传统渐进结构优化算法(ESO)及带惩罚的变密度法(SIMP)的基础上,本文提出将二者相结合的基于SIMP插值模型的渐进结构优化算法。该方法通过缩小传统ESO算法中的进化步长,从而缩小了由于进化步长过大而导致的敏度评估误差,使得ESO算法在合理性及通用性上获得了较大改善。数值算例表明,该方法在保持了常规ESO方法的优点的同时,拥有更高的稳定性和可靠性。
SIMP-based evolutionary structural optimization method for topology optimization .
在传统渐进结构优化算法(ESO)及带惩罚的变密度法(SIMP)的基础上,本文提出将二者相结合的基于SIMP插值模型的渐进结构优化算法。该方法通过缩小传统ESO算法中的进化步长,从而缩小了由于进化步长过大而导致的敏度评估误差,使得ESO算法在合理性及通用性上获得了较大改善。数值算例表明,该方法在保持了常规ESO方法的优点的同时,拥有更高的稳定性和可靠性。
|
| [36] |
Volume preserving nonlinear density filter based on heaviside functions .
To prevent numerical instabilities and ensure manufacturability, restrictions should be applied in topology optimization. In this paper, a volume preserving density filter based on Heaviside functions is presented. Different from earlier Heaviside density filters, this filter is volume preserving, which ensures efficiency and stability in optimization. The new filter is compared with four other filters through a compliance minimization problem.
|

/
| 〈 |
|
〉 |