平面剪切来流作用下串列布置三圆柱流致运动特性研究1)
STUDY OF FLOW-INDUCED MOTION CHARACTERISTICS OF THREE TANDEM CIRCULAR CYLINDERS IN PLANAR SHEAR FLOW1)
中图分类号: O357.1
文献标识码: A
通讯作者:
收稿日期: 2018-12-24
网络出版日期: 2019-05-18
版权声明: 2019 力学学报期刊社 所有
基金资助:
展开
摘要
基于四步半隐式特征线分裂算子有限元方法,对Re=100时,剪切来流作用下串列三圆柱体双自由度流致振动问题进行了数值计算. 首先,与现有文献结果进行对比验证该方法的正确性. 然后,着重分析剪切率、固有频率比和折减速度三个关键参数对串列三圆柱体结构流致动力响应及流场特性的影响. 数值计算结果表明:剪切率、固有频率比与折减速度对结构振幅和运动轨迹的影响较大. 随剪切率的增大,上游圆柱最大振幅的变化与单圆柱工况类似. 中下游圆柱最大振幅会增大且会出现双向共振现象,同时,发生共振响应区域会扩大. 随固有频率比的增大,上游圆柱顺流向锁定区间范围会减小,而中下游圆柱双向锁定区间会扩大. 另一方面,均匀来流作用下,结构运动轨迹以"8"字形和不规则形状为主. 随剪切率的增大,锁定区间内运动轨迹会由"8"字形转变为"雨滴"形. 在大剪切率与高固有频率比工况下,中游圆柱体结构运动轨迹会出现"双雨滴"形状. 最后,通过对流场特性的分析,揭示了剪切来流作用下串列三圆柱结构流致运动响应的内在机理.
关键词:
Abstract
Flow-induced motions of three elastically mounted circular cylinders subjected to the planar shear flow in tandem arrangement at $Re =100$ were numerically investigated by using semi-implicit characteristics-based split (CBS) finite element algorithm. Firstly, the results are compared with the existing data in the literature to verify the accurateness of the method. Then, the influence of some key parameters, such as shear ratio ($k$), natural frequency ratio ($r$) and reduced velocity ($U_{\rm r}$) on the characteristics of flow-induced dynamic responses and flow field of three circular cylinders with tandem arrangement was analyzed. The numerical results show that the shear ratio, natural frequency ratio and reduced velocity play an important role in the amplitude and trajectory of motion. The change of maximum amplitude of the upstream cylinder is similar to that of an isolated cylinder case with the increasing of $k$. The maximum amplitudes of the midstream and downstream cylinders increase, and the dual resonance is observed. Meanwhile, the increasing of $k$ causes the extension of the resonance region. With the increasing of $r$, the lock-in region of the upstream cylinder reduces in the in-line direction. However, for the midstream and downstream ones, the dual-lock-in region broadens. On the other hand, the prominent $X-Y$ trajectories of three circular cylinder resemble figure-eight shape and irregular one in the uniform flow. With the change of $k$, the motion orbit transforms from figure-eight to the raindrop shape in the lock-in region. In the larger shear ratio and higher natural frequency ratio case, the dual-raindrop is observed in the $X-Y$ vibrating trajectory of the midstream cylinder. Finally, the flow-induced motion mechanism of three tandem circular cylinders exposed to planar shear flow is revealed according to the analysis of the characteristic of the flow field.
Keywords:
引 言
当流体经过弹性支撑柱体结构时,在其两侧会产生交替的旋涡脱落,导致结构在横流向和顺流向脉动力的作用下发生振动. 当振动频率接近于自身固有频率时,柱体会发生"锁定现象",诱发结构的共振破坏,带来灾难性的后果. 因此,有关涡激振动的防治问题一直是研究者们所关注的热点之一,并取得了一系列成果[1-4]. 随着计算机性能的提升与数值计算理论的完善,有限元方法凭借其计算效率高、适用性强、便于处理复杂非线性边界问题等优势在流体动力学计算方面逐渐得到广泛的应用[5-7].
在实际工程中,海洋立管、桥梁拉索、高层建筑等都以结构群的形式出现,并且按照排布方式的不同大致可划分错列[8-10]、并列[11-12]、串列[13-19]及阵列式[20-21]等. Papaioannou等[13]将不同间距比工况下串列双圆柱系统的涡激振动响应与单圆柱工况进行对比,得出:间距比较小时,上游圆柱的锁定区间范围明显扩大且对应的最大振幅增大,而超过临界间距比后,上游圆柱的振幅响应基本不受下游圆柱的影响. 李朋等人[14]对前后排列海洋立管进行了实验研究,指出超过锁振区间后,柱体之间的干涉作用使得上游立管振幅减小趋势比单管工况缓慢. Prasanth等[15]对${Re}=100$, $L =5.5 D$ ($D$为结构特征尺寸)时串列布置双圆柱的涡激振动问题进行了数值模拟,发现在上游圆柱尾流的影响下,下游圆柱在两个方向的振幅会显著增大. Mysa等[16]对亚临界雷诺数下上游静止圆柱的尾流对下游圆柱单自由度流致振动的影响进行了数值模拟,重点指出折减速度较大时,诱发结构大幅振动的机制转变为尾激振动,并分析了其内在机理. 与双圆柱问题相比,三圆柱体结构的涡激振动问题会更加复杂. Yu等[17]通过研究发现与串列双圆柱工况相比,三圆柱系统的振动响应更加剧烈,横流向最大振幅提高了25%. 同时,结构振动响应接近于"混乱"状态,导致运动轨迹大多呈现为不规则形状. Mahmoud和Atef[18]对串列布置三圆柱系统的流致振动问题进行了研究,着重分析了上中游两静止圆柱体间距比的变化对下游圆柱体动力响应及其流场特性的影响. Chen等[19]研究了不同间距比工况下串列三圆柱系统单自由度流致振动问题,系统分析了间距比对三圆柱体结构流致动力响应的影响,并揭示了流体与结构之间相互作用的力学机理.
另一方面,一些学者对非均匀来流作用下柱体流致振动问题开展了相关研究,主要可概括为Poiseuille管道流[22-23]、周期性来流[24-25]及剪切来流[26-31]三种形式.目前,关于平面剪切来流方面的研究成果多集中于单圆柱体结构.对于剪切来流作用下结构的涡激振动问题,由于来流速度随空间发生变化,柱体周边流场的差异会使得结构的受力及运动与均匀来流工况相比更加复杂. 黄智勇等[26]对${Re}=2000 \sim5000$范围内,平面剪切来流作用下单圆柱体涡激振动问题进行了数值模拟,发现"剪切率锁定区间",且锁定区间的范围随雷诺数的增大而扩大. Zhang等[27]与Tu等[28]发现在低雷诺数工况下,随剪切率的增大,发生共振的区域会扩大.最近,Gsell等[29]对不同来流工况下(剪切率$\beta =0\sim 0.4$),单圆柱体结构的涡激振动问题进行了数值模拟.当剪切率较大时($\beta =0.4$),圆柱体顺流向的振幅可以达到2$D$,超过横流向最大振幅1.3$D$.然而,与均匀来流工况下相同,当柱体数量增多时,流场会随着来流速度差与结构的运动逐渐呈现为不规则性.Tu等[30]综合考虑了间距比、剪切率与折减速度3个关键参数对串列双圆柱体流致振动响应的影响,发现剪切率的变化对顺流向振幅的影响大于横流向振幅. 剪切来流作用下,双圆柱系统以不规则形状运动的范围扩大.另外,成功捕捉到了"T+P"尾流模态.由此可见,在实际工程中,呈串列布置的工程结构随柱体数量的增多以及影响参数的改变往往会使得系统的流固耦合特性更加复杂,如何更安全合理的选取柱体结构群的数量与布置及相关参数,在一定程度上避免涡激振动引起的危害是工程设计中需要重点考虑的问题之一.通过串列双圆柱系统来推断多柱体结构群的涡激振动问题会具有相当大的不确定性.目前,对串列三圆柱体涡激振动问题的研究并不完善.
综上所述,本文基于四步半隐式特征线分裂算子有限元方法,对剪切来流作用下串列布置三圆柱系统双自由度流致振动问题进行了数值模拟,主要分析了剪切率、固有频率比、折减速度三个关键参数对结构动力响应、流场特性的影响及其内在机理,为实际工程应用提供参考依据.
1 数值方法
1.1 流体控制方程
基于任意$\!$-$\!$-$\!$拉格朗日欧拉(ALE)描述下的不可压缩黏性流体的N-S方程,其无量纲形式为
$\dfrac{\partial {\pmb u}_i }{\partial x_i } = {\bf 0} (1)$
$\dfrac{\partial {\pmb u}_i }{\partial t} + {\pmb c}_j \dfrac{\partial {\pmb u}_i }{\partial x_j } = - \dfrac{\partial {\pmb p}}{\partial x_i } + \dfrac{1}{Re}\dfrac{\partial ^2{\pmb u}_i }{\partial x_j \partial x_j } (2)$
式中,$t$为时间; ${\pmb u}_{i}$和${\pmb p}$分别为流体速度和压力;$x_{i}$和$x_{j}$分别为$i$, $j$方向的空间坐标;${\pmb c}_{j} ={\pmb u}_{j}-{\pmb w}_{j}$,其中${\pmb c}_{j}$为流体相对于网格移动速度的对流速度,${\pmb w}_{j}$为网格移动速度.
雷诺数${Re}={\pmb U}_{\rm c}D/v$,其中${\pmb U}_{\rm c}$和$D$分别为流场中心线($y=0$)处的特征速度和特征尺寸,$v$为流体动力黏性系数.
1.2 四步半隐式CBS稳定化流体有限元
本文采用时间分裂算法,并引入两个辅助速度${\pmb u}_{i}^{1}$与${\pmb u}_{i}^{2}$,将流体控制方程转变为4个方程,具体分裂步骤如下
$\dfrac{{\pmb u}_i^1 - {\pmb u}_i^{(n)} }{\Delta t} = - {\pmb u}_j^{(n)} \dfrac{\partial {\pmb u}_i^{(n)} }{\partial X_j } + \dfrac{\Delta t}{2}{\pmb u}_m^{(n)} \dfrac{\partial }{\partial X_m }\left( {{\pmb u}_j^{(n)} \dfrac{\partial {\pmb u}_i^{(n)} }{\partial X_j }} \right) (3)$
$\dfrac{\partial ^2{\pmb p}^{\left( {n + 1} \right)}}{\partial X_i^2 } = \dfrac{1}{\Delta t}\dfrac{\partial {\pmb u}_i^1 }{\partial X_i } (4)$
$\dfrac{{\pmb u}_i^2 - {\pmb u}_i^1 }{\Delta t} = - \dfrac{\partial {\pmb p}^{n + 1}}{\partial X_i } (5)$
$\dfrac{{\pmb u}_i^{\left( {n + 1} \right)} - {\pmb u}_i^2 }{\Delta t} = \dfrac{1}{Re}\dfrac{\partial ^2{\pmb u}_i^{\left( {n + 1} \right)} }{\partial X_j \partial X_j } (6)$
由于CBS算法可以运用同阶插值与低阶单元对流场速度与压力进行近似,故采用三角形T3单元对流场域进行网格划分.每个单元内速度 和压力的离散格式表达式为
$$ {\pmb u}_i = \sum_{I = 1}^3 {N_I } {\pmb u}_{iI} \,, \ \ {\pmb p} = \sum_{I = 1}^3 {N_I } {\pmb p}_I (7) $$
式中,${\pmb u}_{iI}$和${\pmb p}_{I}$分别是速度和压力的节点值,$N_{I}$ ($I=1,2,3$)是单元的3个形函数.
将形函数代入式(3) $\sim$式(6)中,然后根据标准Galerkin方法进行有限元空间离散,得到如下的有限元计算格式
${\pmb A}_{IJ} \dfrac{{\pmb u}_{iJ}^1 - {\pmb u}_{iJ}^{(n)} }{\Delta t} = - \left( {{\pmb B}_{IJ}^{(n)} + {\pmb C}_{S,IJ}^{(n)} } \right) {\pmb u}_{iJ}^{(n)} (8)$
${\pmb D}_{IJ} {\pmb P}_J^{\left( {n + 1} \right)} = - \dfrac{1}{\Delta t}{\pmb E}_{iIJ} {\pmb u}_{iJ}^1 (9)$
${\pmb A}_{IJ} \dfrac{{\pmb u}_{iJ}^2 - {\pmb u}_{iJ}^1 }{\Delta t} = - {\pmb E}_{iIJ} {\pmb P}_J^{\left( {n + 1} \right)} (10)$
$\left( {{\pmb A}_{IJ} + \dfrac{\Delta t}{Re}{\pmb D}_{IJ} } \right) {\pmb u}_{iJ}^{\left( {n + 1} \right)} = {\pmb A}_{IJ} {\pmb u}_{iJ}^2 (11)$
式中相关参数张量表达式为
$\left.\begin{matrix} {\pmb A}_{IJ} = \int_\varOmega {N_I } N_J \varOmega \ \ {\pmb B}_{IJ}^{(n)} = \int_\varOmega {N_I } {\pmb u}_j^{(n)} \dfrac{\partial N_J }{\partial X_j } \varOmega \\ {\pmb C}_{S,IJ}^{(n)} = \dfrac{\Delta t}{2}\int_\varOmega {\dfrac{\partial N_I }{\partial X_m }} {\pmb u}_m^{(n)} {\pmb u}_j^{(n)} \dfrac{\partial N_J }{\partial X_j }\varOmega \\ {\pmb D}_{IJ} = \int_\varOmega {\dfrac{\partial N_I }{\partial X_i }} \dfrac{\partial N_J }{\partial X_i }\varOmega \,, \ \ {\pmb E}_{iIJ} = \int_\varOmega {N_I \dfrac{\partial N_J }{\partial X_i }} \varOmega \\\end{matrix} \right\}$
在已知$t^{(n)}$时刻的速度场${\pmb u}_{i}^{(n)}$和压力场${\pmb p}^{(n)}$的前提下,四步半隐式CBS有限元方法计算$t^{(n + 1)}$时刻结果的计算步骤为:先计算辅助速度${\pmb u}_{i}^{1}$;再求解压力场${\pmb p}^{(n + 1)}$;接着计算辅助速度${\pmb u}_{i}^{2}$;最后修正速度场得到${\pmb u}_{i}^{(n + 1)}$.
1.3 固体控制方程
弹性支撑圆柱结构运动体系可假设为质量$\!$-$\!$-$\!$阻尼$\!$-$\!$-$\!$弹簧系统,考虑双自由度运动的结构控制方程量纲归一化形式为
$\ddot {\pmb X} + \dfrac{4\pi \xi }{{\pmb U}_{{\rm r},x} }\dot{\pmb X} + \dfrac{4\pi ^2}{{\pmb U}_{{\rm r},x}^2 }X = \dfrac{{\pmb C}_{\rm D} }{2m_{\rm r} } (13)$
$\ddot {\pmb Y} + \dfrac{4\pi \xi }{{\pmb U}_{{\rm r},y} }\dot{\pmb Y} + \dfrac{4\pi ^2}{{\pmb U}_{{\rm r},y}^2 }Y = \dfrac{{\pmb C}_{\rm L} }{2m_{\rm r} } (14)$
式中,$\ddot {\pmb X}$, $\dot{\pmb X}$, ${X}$分别为结构顺流向加速度、速度和位移;$\ddot{Y}$, $\dot{Y}$, ${Y}$分别为结构横流向加速度、速度和位移; $\xi $ 为结构阻尼系数,为了得到最大结构位移响应,取 $\xi =0$;${U}_{{\rm r}, x}={U}_{\rm c}/(f_{n, x}D)$和${U}_{{\rm r},y} ={U}_{\rm c}/(f_{n, y}D)$分别为$x$方向(顺流向)与$y$方向(横流向)折减速度,其中$f_{n, x}$和$f_{n,y}$分别为弹性支撑圆柱体结构的顺流向和横流向自然频率;${\pmb C}_{\rm D}=2{\pmb F}_{\rm D}\rho {\pmb U}_{c}^{2}D$和${\pmb C}_{\rm L}=2{\pmb F}_{\rm L}\rho {\pmb U}_{c}^{2}D$分别为阻力系数和升力系数,其中${F}_{\rm D}$和${\pmb F}_{\rm L}$分别为作用于结构上的阻力与升力;$m_{\rm r}=m/(\rho D^{2})$为结构折合质量,其中$m$为单位长度结构质量, $\rho $为流体密度.
1.4 网格更新
为了避免网格失效的问题,本文通过求解Laplace方程得到每个动网格节点位移,其边值问题表达式如下[32]
$$ \dfrac{\partial ^2\left[ {\left( {1 + \tau } \right) {\pmb S}_i } \right]}{\partial x_j \partial x_j } = {\bf 0}\,, \ \ {\pmb S}_i = {\pmb g}_i \left| {_{\varGamma _{\rm m }} } \right.\,, \ \ {\pmb S}_i = {\bf 0}\left| {_{\varGamma _{\rm f }} } \right. (15) $$
式中, ${\pmb S}_{i}$为网格节点$i$方向位移;$\varGamma _{\rm m }$和$\varGamma _{\rm f }$分别为网格动边界和固定边界;${\pmb g}_{i}$是运动边界上的节点位移; $\tau $ 是网格形变控制参数.
1.5 流固耦合计算步骤
本文采用分区迭代方法求解流固耦合问题,并运用Fortran语言编制了相应的数值计算程序,详细的计算框架如下.
(1) 求解流体控制方程:运用基于四步半隐式CBS稳定化有限元方法求解流体控制方程(1)和(2),获得$t^{(n + 1)}$时刻流场速度与压力,从而得到流体作用于结构上的流体力.
(2) 求解固体控制方程:将流体力($C_{\rm D}$, $C_{\rm L}$)施加到结构,以Newmark-$\beta $时间积分方法求解结构运动控制方程 (13)和(14),得到$t^{(n + 1)}$时刻结构的动力响应.
(3) 网格更新:采用标准Galerkin有限元方法求解Laplace方程,获得网格节点位移及网格速度,并更新网格坐标.
(4) 返回第一步开始计算$t^{(n + 2)}$时刻,并循环至系统达到稳定为止.
1.6 算例验证
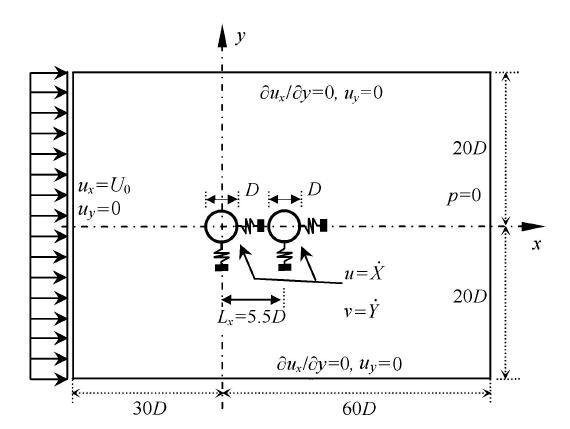
为了验证本文所用数值方法的可靠性,选取文献[9]在均匀来流作用下,串列布置双圆柱体结构两自由度流致振动问题进行验证.计算域尺寸为$[-30D, 60D]\times [-20D, 20D]$,上游圆柱(upstream cylinder, UC)和下游圆柱(downstream cylinder,DC)的圆心位置分别为($0, 0$)与($5.5D, 0$),如图1所示. 边界条件设置如下:入口处采用速度入口:${u}_{x}={\pmb U}_{0}$,${\pmb u}_{y}={\bf 0}$;出口处采用压力出口:${\pmb p}={\bf0}$;上下边界均为自由滑移边界:$\partial {\pmb u}_{x}/\partial y={\bf 0}$, ${\pmb u}_{y}={\bf0}$;圆柱表面均采用无滑移边界:${\pmb u}_{x}={\pmb u}_{y}={\bf 0}$.其他参数如下:${Re}=100$,$m_{r}=10$,不考虑结构阻尼的影响.对于弹性支撑圆柱体结构,可简化为质量$\!$-$\!$-$\!$弹簧系统模型,圆柱表面速度为$u = \dot {X}$, $v = \dot {Y}$.由图2可知,不同折减速度工况下,本文所计算的双圆柱体结构振动位移统计结 果($X_{\rm rms}/D$,$Y_{\max}/D$)与文献[9]中的结果吻合较好,本文数值方法的可靠性与适用性得到了验证.
图2 串列双圆柱涡激振动振幅随折减速度$U_{\rm r}$变化的对比
Fig. 2 The comparisons of the variation of vibration amplitudes with $U_{\rm r}$
2 问题描述
2.1 计算模型
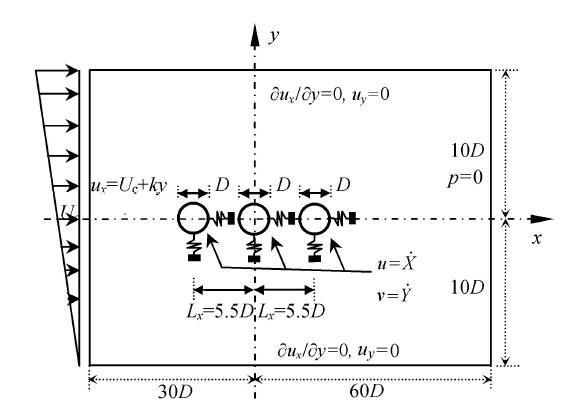
基于上述方法,对串列三圆柱体双自由度流致振动问题进行数值模拟研究,主要参数为:雷诺数${Re}=100$,质量比$m_{\rm r} =2.0$, 间距比$L_{x} =5.5 D$,为了考虑剪切率、固有频率比与折减速度3个关键参数对串列三圆柱体结构流致振动响应的影响,参数取值分别为来流剪切率$k=0$, 0.05, 0.1,固有频率比$r=f_{n, x}/f_{n, y} =1.0$, 1.5, 2.0,折减速度$U_{\rm r}={ U}_{\rm c}/(f_{n,x}D)=3\sim 21$. 计算域尺寸为$[-30D, 60D]\times [-10D, 10D]$,上游圆柱(upstream cylinder,UC)、中游圆柱(midstream cylinder, MC)和下游圆柱(downstream cylinder, DC)的圆心位置分别为$(-5.5D, 0)$, (0,0)与($5.5D, 0$),本文计算域堵塞率$B=5%$,如图3所示. 入口速度为 ${\pmb u}_{x}={\pmb U}_{\rm c}+ky$, ${\pmb u}_{y}=0$, 其中${\pmb U}_{\rm c}=1.0$;其他边界条件均与1.6节所描述的内容一致.
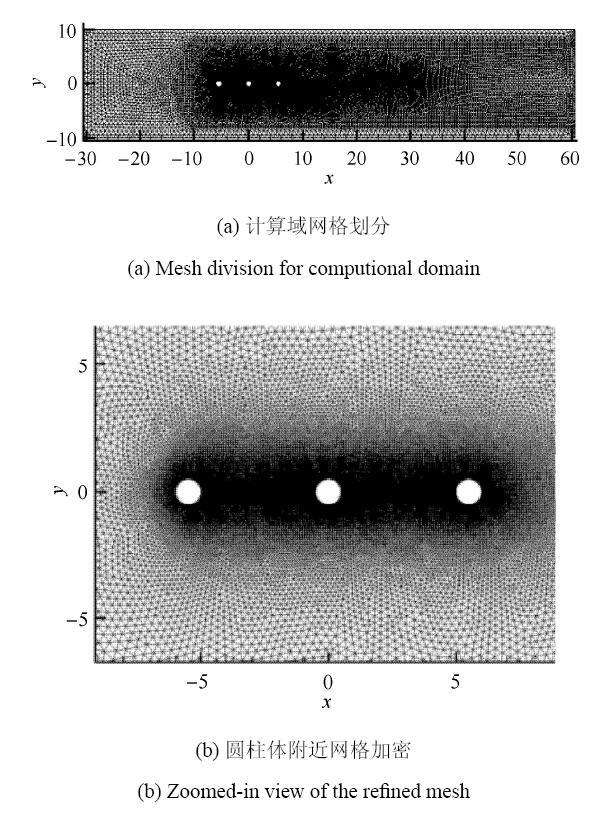
2.2 网格划分
流场计算域采用非结构化三角形网格进行划分,其中圆柱附近及尾流区域进行网格加密处理,如图4所示. 为了消除因网格质量对计算结果可能带来的影响,对网格进行独立性验证. 由表1可知,与粗网格GI相比,网格GII的$X_{\max}/D$与$Y_{\max}/D$的计算结果最大变化率分别为3.00%和4.39%;与密网格GIII相比,其最大变化率分别下降为0.91%和0.85%,数值波动明显减小.若采用网格GIII进行计算,虽能获得最高的计算精度,但是计算总耗时会大幅增大,计算效率降低.综上所述,本文所有算例采用的网格密度和分 布情况与GII类似,无量纲计算步长$\Delta t =0.002$.
表1 网格独立性验证:串列布置三圆柱计算结果 (${Re}=100$, $k=0$, $r=1.0$, $ U_{\rm r} =5.5$)
Table 1 Grid independence test: the results for the three circular cylinders in the tandem arrangement at ${Re}=100$, $k=0$, $r=1.0$, $ U_{\rm r} =5.5$
 |
3 计算结果与分析
本文分析了不同剪切率、固有频率比与折减速度工况下串列三圆柱体结构体系双自由度流致振动振幅特性、频率特性、运动轨迹的变化情况. 为了方便分析,将整个折减速度区间划分为若干个子区域.
3.1 振幅特性
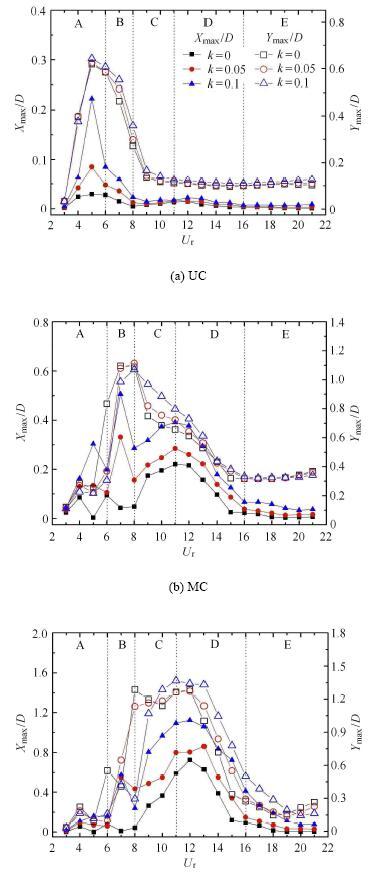
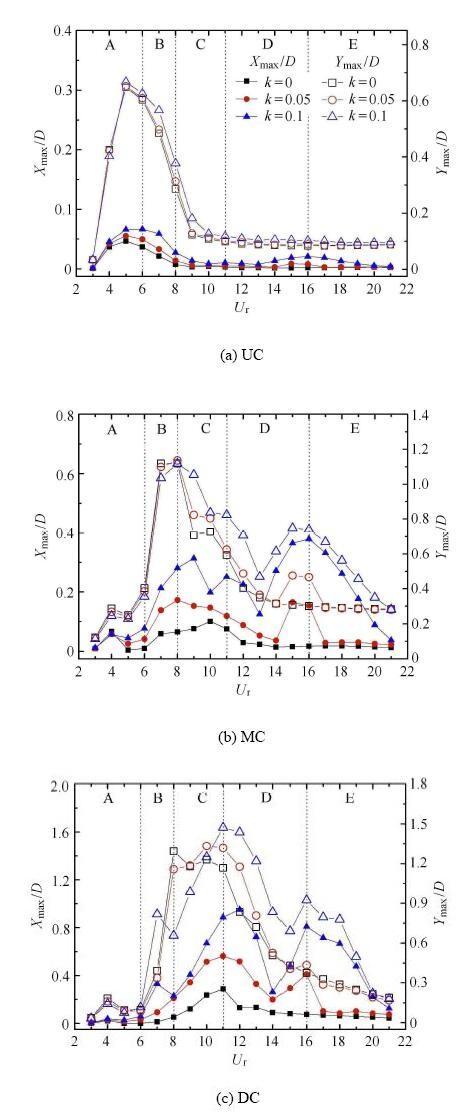
由于圆柱体之间的空间较大,导致下游圆柱对上游圆柱尾流发展的影响较小. 图5给出当$r=1.0$时,不同剪切率工况下,串列三圆柱体 结构体系在$x$, $y$两个自由度方向最大振幅随折减速度的变化情况.由图可知,随剪切率的增大,三圆柱体发生较大振幅的区域均会扩大.另外,上游圆柱在顺流向的振幅受剪切率变化的影响较大,然而横流向振幅受其影响较小,与文献[30]报道的结果类似.与上游圆柱相比,中下游两圆柱体在两个方向发生大振幅的区域明显扩大.
图5 不同剪切率工况下,$x$, $y$两个方向最大振幅随折减 速度的变化($r =1.0$)
Fig. 5 The variation of the maximum vibrating amplitudes with reduced velocity under different shear ratios ($r =1.0$)
当$r=1.0$时,UC的动力响应与单圆柱工况一致,横流向最大振幅随折减速度的变化曲线分为"初始分支"、"上端分支"和"下端分支" 3个部分,与文献[28]中的描述一致. 随折减速度的增大,UC的振幅先增大,在$U_{\rm r}=5$达到峰值后,逐渐减小最后趋于稳定,如图5(a)所示.
相对于UC,MC的最大振幅曲线呈现出较大的不规则性,如图5(b)所示,在区域A$\sim$C范围内,$X_{\max}/D$存在多个极值点.随剪 切率的增大,$X_{\max}/D$普遍增大,而$Y_{\max}/D$仅在区域C范围内出现明显的增大,当$3 \leqslant U_{\rm r}\leqslant 7$时,$Y_{\max}/D$随剪切率的增加而减小.随折减速度的具体变化趋势如下:在区域A$\sim$C内,$X_{\max}/D$出现多次跳跃:当$k =0$,$U_{\rm r}=5$时,MC在顺流向的振动十分微弱. 这可能是由UC脱落的尾流涡街对MC的"屏蔽"作用造成的. 均匀来流作用下,当$U_{r}= 11$时MC达到顺流向最大振幅值0.22. 然而,剪切来流作用下,当$U_{\rm r}=7$时,MC顺流向的振幅会达到第一个峰值$X_{\max}/D =0.33$ ($k =0.05$)和0.51($k =0.1$). 同时,当$U_{\rm r}=11$时,会达到另一个峰值$X_{\max}/D =0.28$ ($k =0.05$)和0.39 ($k =0.1$).另一方面,对于横流向振幅而言,随折减速度的增大,$Y_{\max}/D$先增大,最大振幅为1.11 ($k =0.05$,$U_{\rm r}=8$),然后减小并趋于稳定. 值得注意的是,在$k =0.0$与$U_{\rm r}=6$工况下,$Y_{\max}/D$为0.83,是剪切来流工况的2.7倍.由图5(c)可知,DC的最大振幅随折减速度的变化趋势与MC基本相同. 但是,在区域A$\sim$C范围内DC的振幅波动性相对较小.具体描述如下:在区域A, B范围内,均匀来流作用下,$X_{\max}/D$在零附近波动,振动相当微弱.剪切来流作用下,$X_{\max}/D$逐渐增大并在$U_{\rm r} =7$工况时达到第一个极大值点.在区域C$\sim$E范围内,$X_{\max}/D$随折减速度增大至最大振幅,最大值为1.12 ($k =0.1$,$U_{\rm r}=12$),后不断减小并趋于稳定. 大多数工况下,$X_{\max}/D$随剪切率的增大而增大. 另一方面,在$U_{\rm r}=3\sim9$范围内,$Y_{\max}/D$曲线随剪切率的变化存在较大的差异性. 特别是,当$U_{\rm r}=6$时,均匀来流工况下,DC在横流向的振幅会达到极大值0.55,远远大于剪切来流工况,与MC类似.这可能是该工况下中上游圆柱涡脱落与DC横流向运动之间时机的差异造成的. 当$U_{\rm r}=8$时,均匀来流作用下,DC达到横流向最大振幅1.29. 然而,随剪切率的增大振幅减小,在$k=0.1$工况下$Y_{\max}/D$减小至0.29.这可能是因为剪切来流作用下,由于三圆柱体上下表面存在流速差,导致流场分布特性发生变化. 剪切来流作用下,当$k=0.1$,$U_{\rm r} =11$时,DC达到横流向的最大振幅1.27.
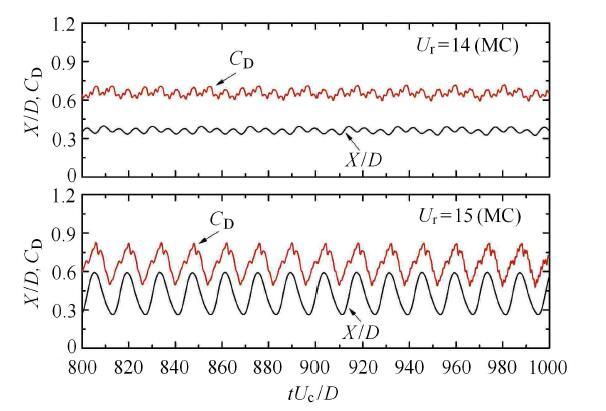
当$r =1.5$时,三圆柱体振幅曲线会出现两个大振幅区域,且顺流向的最大振幅明显减小. 由图6可知,振幅随折减速度变化的 趋势如下:与$r=1.0$工况相比,在区域A, B范围内,UC顺流向振幅受剪切率的影响减弱,当$U_{\rm r} \geqslant 13$后,$X_{\max}/D$会再次出现小幅增大. 另外,$U_{\rm r} =5$工况下,横流向最大振幅为0.67 ($k =0.1$). 不同剪切率 工况下,MC振幅曲线随折减速度的变化趋势基本一致,并在区域A, B内的波动性较小. 值得注意的是,当$k =0.05$时, 在$U_{\rm r} =15$, 16工况下,$X_{\max}/D$突然增大至较大值0.16. 由图7可知,MC顺流向的运动位移曲线与阻力系 数时程曲线从反相($U_{\rm r} =14$)转变为同相($U_{\rm r} =15$),能量从流体传向结构,MC获得更多的动能而发生剧 烈振动,使得该工况下的振幅远远大于$U_{\rm r} =14$工况. 然而,当$k =0.1$时,$X_{\max}/D$在$U_{\rm r} =13$工 况下减小至极小值后,在UC尾流影响下会出现第二个大振幅区域,峰值为0.38 ($U_{\rm r} =16$). 另一方面,$Y_{\max}/D$曲 线的变化趋势和$X_{\max}/D$类似,横流向最大振幅为1.14 ($k =0.05$,$U_{\rm r} =8$). 对于DC,与$r =1.0$工况相比,第一 个大振幅平台的范围有所减小. 振幅曲线变化趋势与MC基本一致,两个大振幅区域拐点位置分别出现在$U_{\rm r} =14$ ($X_{\max}/D$)和$U_{\rm r} =15$ ($Y_{\max}/D$)工况下. 值得注意的是,当$U_{\rm r} =8$时,随剪切率的增大,下游 圆柱体振幅变化趋势和与$r =1.0$工况时一致.
图6 不同剪切率工况下,$x$, $y$两个方向最大振幅随折减速度的变化($r =1.5$)
Fig. 6 The variation of the maximum vibrating amplitudes with reduced velocity under different shear ratios ($r =1.5$)
图7 不同折减速度工况下,顺流向位移($X/D$)与阻力系数($C_{\rm D}$)时程曲线($k =0.05$, $ r =1.5$)
Fig. 7 Time history of streamwise displacements ($X/D)$ and the drag coefficients ($C_{\rm D})$ at different reduced velocities ($k =0.05$, $ r =1.5$)
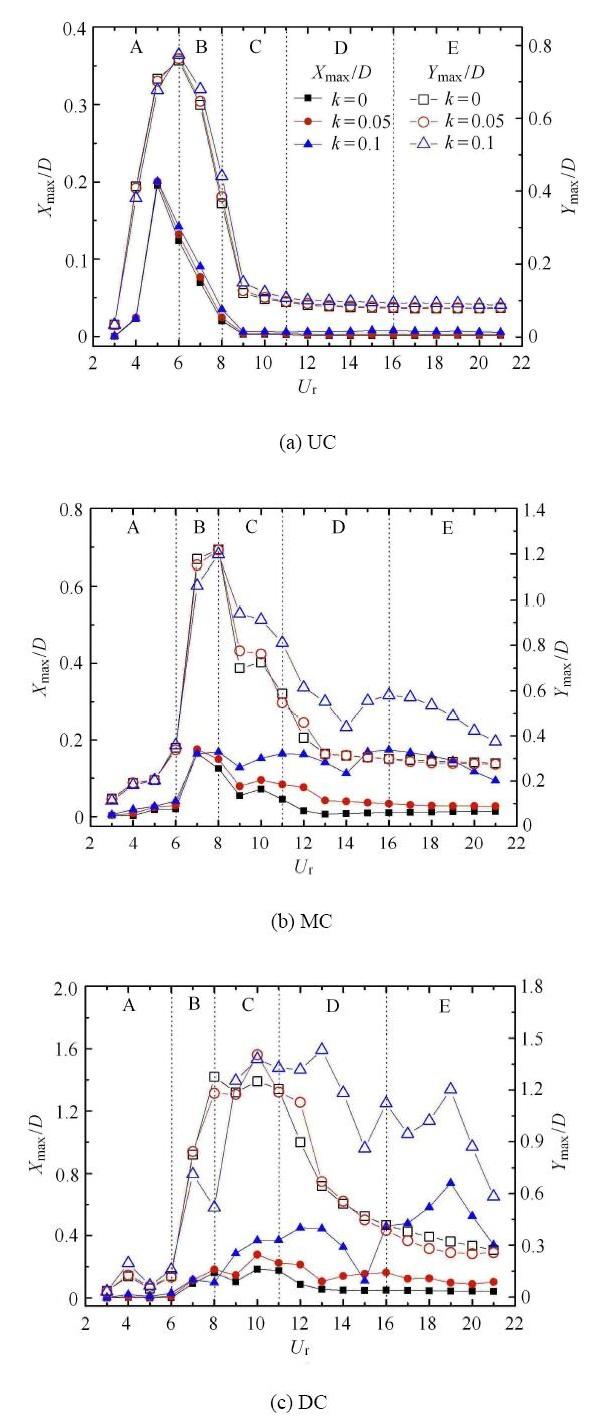
当$r=2.0$时,大折减速度范围内,振幅值会减小. 然而,在$k=0.1$工况下,DC流致振动响应明显增强.由图8可知,大多数工况 下,三圆柱在$x$,$y$方向的振幅随折减速度的变化趋势与$r=1.5$工况下基本一致,主要区别在于:不同剪切率工况下,UC顺流向最大振幅明显增大,振幅曲线随折减速度同步变化.$U_{\rm r}=6$工况下,达到横流向最大振幅,最大值为0.77 ($k=0.1$).与UC相比,随固有频率比的增大,MC顺流向最大振幅持续减小,且仅在$k=0.1$工况下出现振幅再次增大,拐点出现于$U_{\rm r}=14$工况.另一方面,当$k=0$和0.05时,MC横流向振幅曲线基本重合,并在区域C$\sim$E范围内普遍小于大剪切率工况($k =0.1$).对于DC,$k =0.1$工况下,在区域D, E范围内仍产生剧烈振动:当$U_{\rm r}=13$时,达到横流向最大振幅1.43后,$Y_{\max}/D$值在$U_{\rm r}=15$工况下减小至极小值0.86,随后再次增大并在0.9$\sim$1.2范围内不断跳跃.
图8 不同剪切率工况下,$x$, $y$两个方向最大振幅随折减速度的变化($r =2.0$)
Fig. 8 The variation of the maximum vibratin amplitudes with reduced velocity under different shear ratios ($r =2.0$)
3.2 频率特性
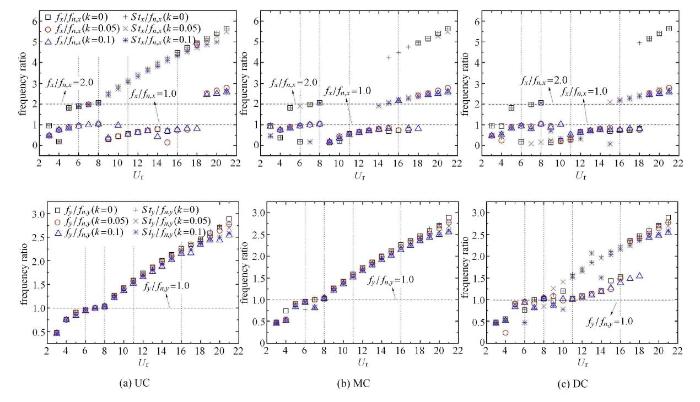
图9$\sim$图11分别给出了不同工况下,串列布置三圆柱系统$x$、$y$两个方向自身振动频率($f_{x}$和$f_{y}$)与涡脱落频率(${St}_{x}$和${St}_{y}$)随折减速度的变化情况.
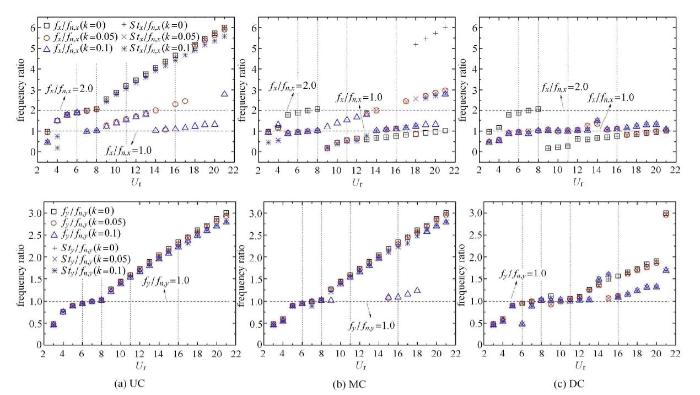
图9 不同剪切率工况下,$x, y$两个方向频率比随折减速度的变化($r =1.0$)
Fig. 9 The variation of frequency ratios with reduced velocities under different shear ratios ($r =1.0$)
当$r =1.0$时,在区域B范围内,均匀来流作用下,UC顺流向振动频率远离固有频率,仅发生横流向锁定现象.剪切来流作用下, UC则会发生双向锁定. 另外,除了受到固有频率的影响外,柱体运动还会被其自身涡脱落干扰.在顺流向,大多数工况下,UC振动频率基本偏离自身涡脱落频率,而在横流向则恰好相反.当UC振动频率接近固有频率时,其横流向振幅会取得较大值,当超过共振区间时,UC振幅减小并趋于稳定,此时其横流向振动频率接近于涡脱落频率,说明UC自身固有频率对其产生剧烈振动的影响强于尾流涡干扰.与UC相比,MC锁定区间会扩大,如图9(b)所示,在区域D, E内,3种剪切率工况下,均会发生单向共振.另外,涡脱落频率对MC的影响明显强于UC,区域C范围内,在振动频率偏离固有频率的情况下MC顺流向振幅仍随折减速度的增加而增大.值得注意的是,在横流向振动频率、自身固有频率和涡脱落频率三者相等的工况下,MC会达到横流向最大振幅,如图5(b)所示.另外,当$U_{\rm r} =7$时,剪切来流作用下,MC振动频率和固有频率几乎重合,导致顺流向振幅出现跳跃并达到最大值.对于DC而言,双向锁定区域进一步扩大到区域B, C内,如图9(c)所示.在大振幅区域内,DC振动频率基本偏离自身尾流涡脱落频率,说明旋涡脱落对DC横流向振幅的影响较小,DC发生大幅振动主要与其自身固有频率有关.值得注意的是,在大折减速度工况下,由于横流向振动频率均接近于自身涡脱落频率,中下游圆柱横流向振幅最终会稳定于一个较大值.
当$r =1.5$时,剪切来流工况下,在大折减速度范围内,三圆柱体均会出现锁定现象,振幅也出现两个峰值.由图10(a)可知,在 区域B范围内,$k =0.1$工况下,UC发生双向锁定现象,但在$k=0$和0.05工况下,UC仅在横流向发生共振,在顺流向振动频率接近于两倍固有频率. 另外,当$k =0.1$时,$14 \leqslant U_{r} \leqslant 17$范围内,UC顺流向振动频率再次接近固有频率,引起振幅的小幅增大.由于尾流效应增强,中下游圆柱发生共振的区域明显扩大. 与$r=1.0$工况相比,MC振动频率响应主要区别在于,当$k =0.1$时,MC在区域D,E范围内会发生双向锁定,从而引起振幅再次增大,出现两个峰值,如图10(b)所示,另外,涡脱落频率对MC振幅的影响明显减小. 值得注意的是,当$k =0.05$时,MC振动频率在$U_{\rm r} =15 \sim16$工况下接近于固有频率,结构发生共振,使得其振幅出现极大值,如图6(b)所示.与MC相比,均匀来流作用下,DC横流向锁定区间扩大到区域B, C范围内.然而,剪切来流作用下,DC在区域B$\sim$D范围内均会发生双向锁定,如图10(c)所示.在区域E范围内,DC仅在顺流向发生锁定现象,与3.1节所描述的内容完全一致. 另外,与$r=1.0$时不同,不同工况下,DC振动频率均接近于自身涡脱落频率.
图10 不同剪切率工况下,$x$、$y$两个方向频率比随折减速度的变化($r =1.5$)
Fig. 10 The variation of frequency ratios with reduced velocitiesunder different shear ratios ($r =1.5$)
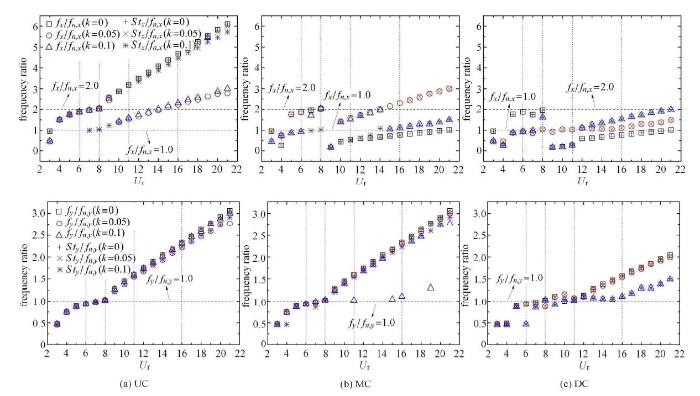
图11 不同剪切率工况下,$x$, $y$两个方向频率比随折减速度的变化($r =2.0$)
Fig. 11 The variation of frequency ratios with reduced velocities under different shear ratios ($r =2.0$)
当$r =2.0$时,相对于低固有频率比工况,三圆柱系统顺流向频率锁定区间的范围明显减小,如图11所示.随$r$的增大,剪切率 的变化对结构振动频率的影响增大.中下游两圆柱的存在会影响UC尾流的涡脱落,使得其顺流向振动频率基本偏离固有频率.特别是,在区域B内,UC的振动频率为固有频率的两倍,并获得了较大的振幅.这说明,当固有频率比较大时,顺流向振动频率为两倍基频时也能引起UC剧烈振动.对于MC而言,在区域B内,随固有频率比的增大,MC顺流向振动频率在不同剪切率工况下逐渐接近于两倍固有频率,并能诱发较大的振幅,与UC类似,如图11(b)所示. 另外,在区域D, E内,在$k=0.1$工况下MC会发生双向共振,使得结构出现振幅再次增大现象. DC频率特性与$r =1.5$工况下基本一致.
3.3 运动轨迹
图12给出了不同固有频率比与剪切率工况下,三圆柱体结构体系相对运动轨迹随折减速度的变化情况.均匀来流作用下,柱体运动轨迹大 都关于中心线($y =0$)对称.然而,剪切来流作用下,来流速度梯度引起圆柱上下两侧尾流的不对称分布,导致运动轨迹不再呈现出对称性.
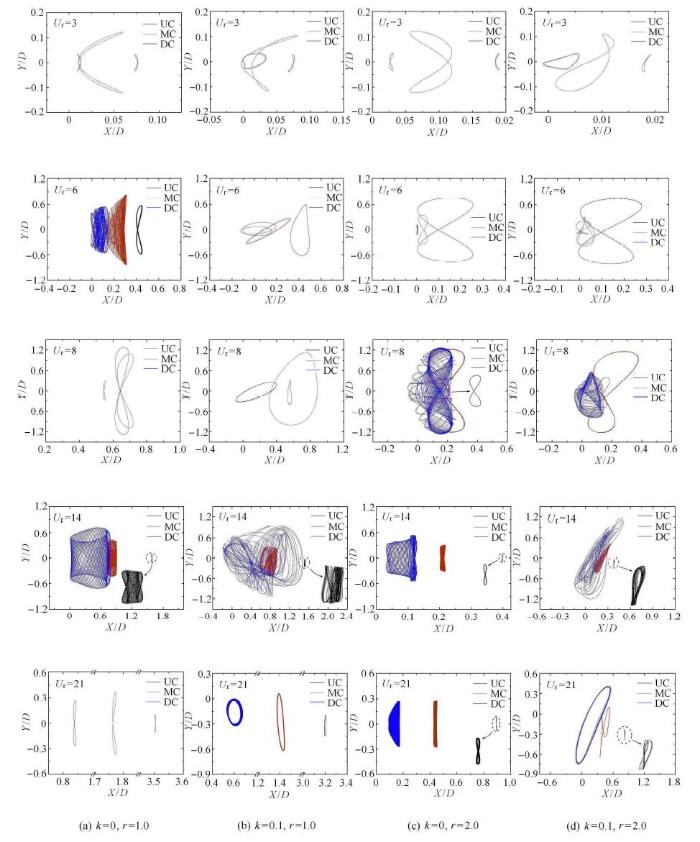
图12 不同工况下,运动轨迹随折减速度的变化
Fig. 12 The variation of $X$-$Y$ trajectories with reduced velocities at different cases
由于上游圆柱体受中下游圆柱体影响较小,运动轨迹基本与单圆柱工况类似:均匀来流作用下,以对称"8"字形为主,随固有频率比的增大,在共振区域内,UC顺流向振幅明显增大,导致"8"字形运动轨迹相对更为饱满. 剪切来流作用下,当$r=1.0$时,运动轨迹在共振区间内主要为"雨滴"形,随$U_{r}$的增大,运动轨迹呈现出不规则性,超过锁定区间后,逐渐恢复为"雨滴"形. 但当$r=2.0$时,剪切率的变化对UC运动轨迹影响较小.在共振区范围内,UC运动轨迹仍以"8"字形为主,然而,在非共振区域内,结构会发生不规则形状周期性运动.由于受到上游圆柱尾流的影响,中下游两圆柱体运动相对更为复杂.对于MC而言,在均匀来流工况下,运动轨迹仍然以"8"字形和不规则形状为主.在剪切来流作用下,MC运动轨迹则存在较大的差异. 当$r =1.0$时,MC主要以"椭圆"形和不规则形状运动.尤其在小折减速度工况下,运动轨迹出现了"三环"形状. 在较大的固有频率比工况下($r =2.0$),当$U_{\rm r}$较小时,MC的运动轨迹大多呈不规则的"8"字形,随着$U_{\rm r}$的增大,其运动轨迹会呈现出不规则性.值得注意的是,当$U_{\rm r} =6.0$时,MC的运动轨迹出现了"双雨滴"形状.对于DC而言,均匀来流工况下,其运动轨迹仍然以"8"字形和不规则形状为主,与MC基本一致.在剪切来流作用下,DC主要以"8"字形与"椭圆"形运动.
为了分析剪切率对中游圆柱体运动轨迹影响的内在机理,本节给出了在$k =0$和0.1两种不同剪切率工况下, MC位移($X/D$,$Y/D$)及流 体力系数($C_{\rm D}$, $C_{\rm L}$)的能量谱密度图(PSD) 分别如图13和图14所示.
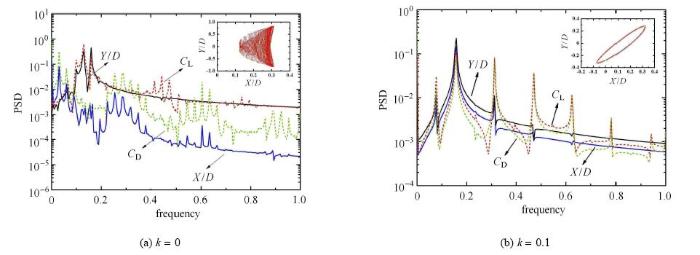
图13 不同剪切率工况下,MC流体力系数及位移的能量谱密度图($r =1.0$, $U_{\rm r} =6$)
Fig. 13 Power spectral density (PSD) of the flow force coefficients($C_{\rm D}$, $C_{\rm L})$ and displacements ($X/D$, $Y/D)$ of midstream cylinder under different shear ratios ($r =1.0$, $U_{\rm r} =6$
图14 不同剪切率工况下,MC流体力系数及位移的能量谱密度图($r =2.0$, $U_{\rm r} =6$)
Fig. 14 Power spectral density (PSD) of the flow force coefficients ($C_{\rm D}$, $C_{\rm L})$ and displacements ($X/D$, $Y/D)$ of midstream cylinder under different shear ratios ($r =2.0$, $U_{\rm r} =6$)
固有频率比$r =1.0$工况下,当$k =0$时,$X/D$与$C_{d}$的能量谱密度曲线中出现了"多频"现象,显著影响了能量在流体与结构之间的传递,从而使得MC在顺流向的运动变得复杂.同时,MC横流向位移与升力系数的PSD曲线均出现两个相近的主频,相互重合且能量分布较大. 当$k=0.1$时,MC横流向运动明显减弱,运动轨迹转变为"椭圆"形,如图13(b)所示.在文献[28]对单圆柱体涡激振动研究中也发现了类似现象. MC在两个方向的力和位移频谱曲线基本重合.以一阶主频为主,其他次频能量分布较小,使得运动轨迹呈现出"椭圆"形.
随$r$的增大,MC两个方向位移PSD曲线与相对应的流体力PSD曲线完全重合. 顺流向$X/D$与$C_{\rm D}$的频率值是横流向$Y/D$ 与$C_{\rm L}$的频率值的两倍,导致中游圆柱体以"8"字形运动,如图14(a)所示.一些学者也报道过类似的现象[28,33].
剪切率的增大对MC位移及流体力系数的PSD曲线特性的影响显著. 尤其是顺流向,$C_{\rm D}$曲线的波动性会显著增加.同时,$C_{\rm D}$频率能量分布较大且比$X/D$大一个数量级,导致MC以"双雨滴"形状运动,如图14(b)所示.
4 涡动力机理
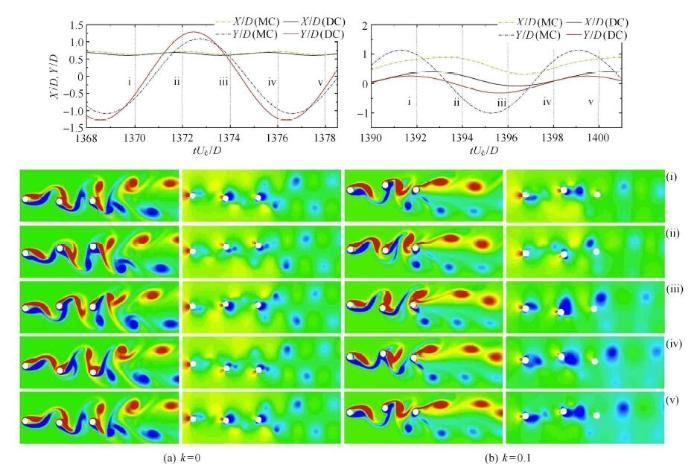
通过对三圆柱体流致运动周围流场瞬时压力场与涡量场的变化进行分析,揭示结构运动响应发生变化的内在机理.图15分别为$r =1.0$,$U_{\rm r} =8$工况下,不同来流作用下下游圆柱体的运动位移时程曲线以及所对应时刻(i$\sim$v)的涡量场云图和瞬态压力场云图.由图可知,由于圆柱体之间的间隙足够大,MC对UC尾流发展几乎没有阻碍作用,导致UC周围的流场分布以及运动响应特性与单圆柱工况一致. 另外,随着来流特性的变化,三圆柱体与流场之间的耦合作用也会发生改变.
图15 不同剪切率工况下,MC与DC运动位移时程曲线图及对应不同时刻涡量场云图和瞬态压力场云图($r =1.0$,$U_{\rm r} =8$)
Fig. 15 Time-history curve of displacement of midstream and downstream cylinders under different shear ratio cases and vorticity contours and instantaneous pressure contours at different times ($r =1.0$, $U_{\rm r} =8$)
均匀来流作用下,UC脱落的旋涡从MC表面附近向后传播,与MC自身脱落的旋涡相互融合共同作用,在MC表面以及近尾流区域形成较强的吸压区,从而引起结构发生大幅度振动,如图15(a)所示.
同时,MC的尾流对DC的作用,导致MC与DC两者运动基本呈现出同步同向状态.三圆柱体与流场之间相互作用的变化过程如下:MC即将从下往上运动到平衡位置时(i时刻),从UC表面脱落的上行涡达到MC的上侧并与其正在发展的尾流相互融合,同时,在MC的后上方区域形成了较强的吸压区导致其往右上加速运动.另一方面,DC下行涡已完全脱落并会逐渐与MC下表面脱落的旋涡结合成一个大旋涡.然而,DC上行涡正在逐渐发展,在DC后侧形成较强的吸压区使得结构向右上方加速运动.此时,从MC上表面脱落的旋涡恰好到达DC的上侧,两圆柱体的旋涡即将结合,但距离较远影响较小.MC与DC位于即将运动到最上方位置时(ii时刻),MC上行涡基本发展充分,并与UC尾流结合形成了一个旋涡.同时,MC下行涡的强度逐渐增大,导致在MC后下方区域会出现两个吸压包,在前上方区域出现了正压区,在流场压力的作用下使得MC减速向左上方运动.另外,DC上行涡也已发展充分即将脱落,同时,其下行涡的强度得到进一步发展,导致DC周围的压力分布及其运动状态与MC基本一致.iii时刻,MC与DC的上行涡已脱落,下行涡开始逐渐发展,使得其周围的流场分布以及运动状态与i时刻相反. iv时刻,MC与DC的下行涡发展充分即将脱落,同时上行涡的强度逐渐增大,导致圆柱体结构减速向下运动与ii时刻相反. v时刻,流场分布特性与圆柱体运动状态与i时刻一致.
随来流剪切率的增大,UC的尾流涡街会呈现出非对称性,其周围压力的分布也会发生较大的变化,影响UC的运动状态,进一步对MC与DC周围流场特性及运动响应产生影响,如图15(b)所示.三圆柱体与流场之间相互作用的变化过程如下:i时刻,MC上行涡已发展充分并脱落,同时,下行涡在后表面开始形成,导致其迎流面受到正压的作用,背流面则受到负压的作用.另一方面,MC的尾流从DC的上下两侧通过,抑制了DC尾流涡街的发展,使得旋涡尺寸增大并在远尾流区域发生脱落,减弱了DC的运动幅度.ii时刻,MC尾流强度增大,在其上下表面形成了吸力区,导致MC向下减速运动.此时,MC的尾流逐渐靠近DC,并在其左上方形成吸压区,导致DC加速向左与减速向下运动.iii时刻,MC上表面的旋涡逐渐发展并与UC尾流开始融合,在其右上方形成较大的吸压区.同时,MC的尾流到达了DC后上方,并在该区域形成吸压区.iv时刻,UC尾流与MC上行涡即将融合成一个旋涡,在MC背流面下方区域出现了较大的吸压区,导致其减速向上运动.v时刻,流场分布及结构运动状态与i时刻基本类似.
5 结 论
基于四步半隐式特征线分裂算子有限元方法,对不同来流作用下串列布置三圆柱双自由度结构体系流致振动问题进行了数值模拟,着重分析了剪切率、固有频率比与折减速度的变化对结构振动响应特性及流场分布的影响,并阐述了其内在力学机理. 主要结论如下:
随剪切率、固有频率比与折减速度的改变,上游圆柱体的振动幅度变化规律与单圆柱工况类似. 然而,3个参数对中下游两个圆柱体振动幅度的影响较大. 固有频率比较小时,剪切率的变化会使得中下游两个圆柱体发生双向共振现象. 随固有频率比的增大($r$=1.5),在剪切来流作用下,中下游两个圆柱体在$x$,$y$方向的振幅会出现两个峰值. 当$k$=0.1,$r$=2.0时,在大折减速度范围内,中下游两个圆柱体在$x$,$y$方向的振幅均会保持较大值.
中下游两个圆柱体的运动频率与结构固有频率一致的区域会随剪切率的增大而扩大,发生较大振幅的区域也会扩大. 值得注意的是,在运动频率、结构固有频率与涡脱落频率三者相等的工况下,中游圆柱体结构的振幅会达到峰值.
均匀来流作用下,串列三圆柱体结构运动轨迹主要为"8"字形和不规则形状. 然而,剪切来流作用下,运动轨迹会出现"8"字、"雨滴"和不规则形状. 值得注意的是,中游圆柱体会以"雨滴"、"双雨滴"和"三环"形轨迹运动.
上游圆柱体尾流对中游圆柱体动力响应特性的影响强于中游圆柱体尾流对下游圆柱体的影响. 剪切来流作用下,由于流场存在流速差导致涡量场与压力场特性发生变化,进一步会影响三圆柱体结构的动力响应特性.
The authors have declared that no competing interests exist.
参考文献
| [1] |
Vortex shedding from oscillating bluff bodies .
Experimental and analytical work on vortex shedding from bluff bodies (BB) and the resulting oscillation is reviewed for the period 1972-1982, considering BBs of various shapes. Topics discussed include fixed BBs, oscillations and motion equation of a flexibly mounted BB, free and forced vibrations, the influence of BB motion on vortex shedding, and model predictions of vortex-induced oscillation using nonlinear oscillation theory and flow-field computations. Photographs and graphs of experimental data are provided.
|
| [2] |
Vortex-induced vibrations . |
| [3] |
An overview of modeling and experiments of vortex-induced vibration of circular cylinders .
This paper reviews the literature on the mathematical models used to investigate vortex-induced vibration (VIV) of circular cylinders. Wake-oscillator models, single-degree-of-freedom, force–decomposition models, and other approaches are discussed in detail. Brief overviews are also given of numerical methods used in solving the fully coupled fluid–structure interaction problem and of key experimental studies highlighting the nature of VIV.
|
| [4] |
A review of recent studies on vortex-induced vibrations of long slender cylinders .
This paper reviews the progress made during the past decade on vortex-induced vibration (VIV) of long slender cylindrical structures. When the aspect ratio, which is defined as the ratio of length to diameter for cylindrical structures, is large enough (10 2鈥10 3), some unexpected phenomena occur, e.g., dual resonance, multi-mode vibration, unsteady lock-in, the third and higher harmonic fluid forces and traveling wave dominant response, as summarized in this paper. In addition, a brief outline is given of numerical methods used in predicting the response of long slender cylinder undergoing VIV.
|
| [5] |
Benchmark problems for incompressible fluid flows with structural interactions .
Various methods of analysis for the solution of fluid flows with structural interactions have been proposed in the literature, and new techniques are being developed. In these endeavors, to advance the field, thorough evaluations of the procedures are necessary. To help in establishing such evaluations, we present in this paper the solutions of some benchmark problems. The results can be used to evaluate existing and new formulations of incompressible fluid flows with structural interactions.
|
| [6] |
Characteristic-based split (CBS) finite element method for incompressible viscous flow with moving boundaries .
This paper gives an insight into the existing ALE (arbitrary Lagrangian Eulerian)-CBS (characteristic-based split) method and proposes an alternative CBS scheme for incompressible viscous flow with moving boundaries. First, the existing CBS scheme in ALE framework is reformulated from the Navier-Stokes (NS) equations in Eulerian description, and its advantages and drawbacks are discussed. Then, the classical semi-implicit CBS scheme is combined with the segment spring analogy method, and a new CBS solution procedure in Eulerian framework is developed for moving mesh. By the proposed CBS scheme, the influence of the mesh velocity in the existing ALE-CBS method is circumvented, and the extension of the existing CBS schemes and programs for fixed boundary problems to moving boundary problems seems to be more convenient. Finally, two moving boundary problems, namely the broken dam problem and the flow around an oscillating circular cylinder are presented. Numerical results from the proposed CBS scheme agree very well with available results in literature and show a slightly higher accuracy than those from the existing ALE-CBS method. Combined with other classical CBS schemes involving compressibility, turbulence, viscoelasticity, etc. and suitable moving mesh techniques, the proposed CBS solution procedure could be applied widely to the moving boundary problems in engineering.
|
| [7] |
基于ALE有限元法的流固耦合强耦合数值模拟 .A partitioned strong coupling algorithm for fluid-structure interaction using arbitrary lagrangian-eulerian finite element formulation . |
| [8] |
Vortex-induced vibrations of three staggered circular cylinders at low Reynolds numbers .
Vortex-induced vibrations of three staggered circular cylinders are investigated via two-dimensional finite element computations. All the cylinders are of equal diameter (D) and are mounted on elastic supports in both streamwise (x61) and transverse (y61) directions. The two downstream cylinders are placed symmetrically on either side of the upstream body at a streamwise gap of 5D, with the vertical distance between them being 3D. Flow simulations are carried out for Reynolds numbers (Re) in the range of Re = 60-160. Reduced mass (m*) of 10 is considered and the damping is set to zero value. The present investigations show that the upstream cylinder exhibits initial and lower synchronization response modes like an isolated cylinder does at low Re. Whereas for both the downstream cylinders, the upper lock-in branch also appears. The initial and the upper modes are characterized by periodic oscillations, while the lower lock-in branch is associated with nonperiodic vibrations. The 2S mode of vortex shedding i...
|
| [9] |
Vortex-induced vibration of two circular cylinders at low Reynolds number .
Vortex-induced vibration of a pair of equal-sized circular cylinders in tandem and staggered arrangements in laminar flow regime is investigated. A stabilized finite element method is utilized to carry out the computations in two dimensions. Both cylinders are free to oscillate in transverse as well as in-line directions. The Reynolds number, based on the free-stream speed, , and the diameter, , of the cylinders is 100. To encourage high amplitude of oscillation the structural damping is set to zero and cylinders of low nondimensional mass are considered (=10). The computations are carried out for various values of reduced speed of the oscillator (2??15). The cylinders are separated by 5.5 in the streamwise direction. They are separated by 0.7 in the cross-flow direction to study the effect of stagger. The downstream cylinder lies in the wake of the upstream one and experiences an unsteady inflow. The upstream cylinder in both tandem and staggered arrangement responds qualitatively similarly to a single cylinder. Compared to an isolated cylinder, a small increase in transverse oscillation amplitude of the upstream cylinder is observed due to the presence of the downstream cylinder. In both arrangements, the downstream cylinder shows very large amplitude transverse oscillations comparable to that of a single cylinder at higher Re. In the staggered arrangement, very large streamwise oscillations of the downstream cylinder are observed. Compared to an isolated cylinder, the synchronization range for the two-cylinder arrangement is larger. The downstream cylinder in the staggered arrangement undergoes two types of motion: an orbital motion at most of the studied, and figure-of-eight motion for a small range of . In the tandem arrangement, only the figure-of-eight motion is observed. The stagger in the arrangement of the two cylinders is found to have a significant effect on the flow.
|
| [10] |
错列角度对双圆柱涡激振动影响的数值模拟研究 .
为研究错列角度α对双圆柱涡激振动问题的影响,采用自主研发的基于CIP(constrained interpolation profile)方法的数值模型,对雷诺数Re=100、错列角度α=0?~90?(间隔15?)的等直径双圆柱涡激振动问题进行数值模拟.模型在笛卡尔网格系统下建立,采用具有三阶精度的CIP方法求解N-S(Navier--Stokes)方程,采用浸入边界法处理流--固耦合问题,避免了任意拉欧方法下的网格畸变和重叠动网格技术中的大量信息交换问题,保证了模型的计算效率.重点分析不同错列角度α上下游圆柱的升阻力系数、位移响应、涡脱频率和尾涡模态等.结果表明:折合速度Ur=2.0~3.0时,上下游圆柱升阻力随错列角度的增大基本呈单调增大的趋势;Ur=5.0~8.0时,随错列角度的增大,上下游圆柱阻力变化较小,升力呈"上凸"趋势,在α=15?~30?取得最大值;Ur=10.0~13.0时,随错列角度的增大,上下游圆柱阻力变化较小,升力呈"下凹"趋势,在α=30?~45?取得最小值,且柱体横流向振幅和升力没有明显的对应关系.最后,结合尾涡模态对以上规律的成因进行分析.研究结果可为相关海洋工程设计提供参考.
Numerical study of staggered angle on the vortex-induced vibration of two cylinders .
为研究错列角度α对双圆柱涡激振动问题的影响,采用自主研发的基于CIP(constrained interpolation profile)方法的数值模型,对雷诺数Re=100、错列角度α=0?~90?(间隔15?)的等直径双圆柱涡激振动问题进行数值模拟.模型在笛卡尔网格系统下建立,采用具有三阶精度的CIP方法求解N-S(Navier--Stokes)方程,采用浸入边界法处理流--固耦合问题,避免了任意拉欧方法下的网格畸变和重叠动网格技术中的大量信息交换问题,保证了模型的计算效率.重点分析不同错列角度α上下游圆柱的升阻力系数、位移响应、涡脱频率和尾涡模态等.结果表明:折合速度Ur=2.0~3.0时,上下游圆柱升阻力随错列角度的增大基本呈单调增大的趋势;Ur=5.0~8.0时,随错列角度的增大,上下游圆柱阻力变化较小,升力呈"上凸"趋势,在α=15?~30?取得最大值;Ur=10.0~13.0时,随错列角度的增大,上下游圆柱阻力变化较小,升力呈"下凹"趋势,在α=30?~45?取得最小值,且柱体横流向振幅和升力没有明显的对应关系.最后,结合尾涡模态对以上规律的成因进行分析.研究结果可为相关海洋工程设计提供参考.
|
| [11] |
Free-stream turbulence effects on vortex-induced vibration of two side-by-side elastic cylinders . |
| [12] |
Vortex-induced vibration of two elastically coupled cylinders in side-by-side arrangement .
Vortex-induced vibration (VIV) of two elastically coupled circular cylinders in side-by-side arrangement is investigated numerically. The Reynolds-averaged Navier鈥揝tokes equations are solved by the finite element method for simulating the flow and the equation of motion is solved for calculating the vibration. The mass ratio (the ratio of the mass of the cylinder to the displaced fluid mass) is 2 and the Reynolds number is 5000 in the simulations. Simulations are carried out for one symmetric configuration (referred to be Case A) and one asymmetric configuration (referred to be Case B). In both Case A and Case B, the primary response frequencies of the two cylinders are found to be the same both inside and outside the lock-in regimes. Five response regimes are found in both cases and they are the first-mode lock-in regime, the second-mode lock-in regime, the sum-frequency lock-in regime and two transition regimes. When the vibration is transiting from the first- to the second-mode lock-in regimes, the vibration of each cylinder contains both first- and the second-mode natural frequencies, and the vibrations are usually irregular. In the transition regime between the second-mode lock-in and the sum-frequency lock-in regimes, the response frequencies of both cylinders increases with an increase in the reduced velocity until they are close to the sum of the two natural frequencies. In both cases, the lower boundary reduced velocity of the total lock-in regime (the sum of the five lock-in regimes) is about 3 and the upper boundary reduced velocity is about 11 times the first-to-second-mode natural frequency ratio.
|
| [13] |
On the effect of spacing on the vortex-induced vibrations of two tandem cylinders .
A spectral element method using Jacobi polynomial bases is employed to study the vortex-induced oscillations of two identical elastically mounted cylinders in tandem arrangement. Three different cylinder spacings, /=2.5, 3.5 and 5.0, are examined in order to identify the effect of spacing on the two-degree-of-freedom oscillations of the cylinders. Computations were conducted in two space dimensions (2-D)鈥攁n assumption that is expected to be valid for the Reynolds number, =160, considered. The single cylinder case is also examined at the same flow and structural parameters for reference and comparison. A widening of the range of the response region of the upstream cylinder is observed when the cylinder spacing is decreased. The synchronization curves of the upstream cylinder display a shift on the reduced velocity (R) axis depending on the spacing. The maximum oscillation amplitude of the downstream cylinder increases when the cylinders are brought to a distance that the flow around the corresponding stationary system displays reattachment. There are three significant frequencies at the spectral responses: the shedding frequency of the stationary tandem system (N). The energy input of the flow on each cylinder is studied in terms of the line integral of the hydrodynamic force yielding the work, the phase angle between force and displacement at the prominent spectral frequency, and finally the lift in phase with velocity.
|
| [14] |
干涉对海洋立管涡激振动影响实验研究 .
文章进行了干涉对海洋立管涡激振动影响的实验研究,实验分为立管前后排列和并肩排列两部分。立管间距为3-10倍直径,模型材料采用有机玻璃,长1.5 m,外径18 mm,壁厚2 mm,边界条件均为铰接,外流速分别从0.3-0.8 m/s,每级增加0.1 m/s。通过在立管表面粘贴应变计获得动态应变数据,分别从立管的横向动态响应、振幅、频率等方面对前后排列、并肩排列立管以及和单独立管的实验数据进行对比研究。结果表明,当有外流通过时,立管会受到其他立管尾流的影响,漩涡脱落引起的振动由于间距及排列方式的不同而显著不同,使得立管的动力特性、动力响应以及漩涡的脱落形式同单个立管相比均有较大的变化。
Li Xiaoming et al. Experimental investigation of vortex-induced vibration of marine risers with interference .
文章进行了干涉对海洋立管涡激振动影响的实验研究,实验分为立管前后排列和并肩排列两部分。立管间距为3-10倍直径,模型材料采用有机玻璃,长1.5 m,外径18 mm,壁厚2 mm,边界条件均为铰接,外流速分别从0.3-0.8 m/s,每级增加0.1 m/s。通过在立管表面粘贴应变计获得动态应变数据,分别从立管的横向动态响应、振幅、频率等方面对前后排列、并肩排列立管以及和单独立管的实验数据进行对比研究。结果表明,当有外流通过时,立管会受到其他立管尾流的影响,漩涡脱落引起的振动由于间距及排列方式的不同而显著不同,使得立管的动力特性、动力响应以及漩涡的脱落形式同单个立管相比均有较大的变化。
|
| [15] |
Flow-induced oscillation of two circular cylinders in tandem arrangement at low Re .
Results are presented for flow-induced vibrations of a pair of equal-sized circular cylinders of low nondimensional mass ( m * = 10) in a tandem arrangement. The cylinders are free to oscillate both in streamwise and transverse directions. The Reynolds number, based on the free-stream speed and the diameter of the cylinders, D is 100 and the centre-to-centre distance between the cylinders is 5.5 D. The computations are carried out for reduced velocities in the range 2 ≤ U * ≤ 15. The structural damping is set to zero for enabling maximum amplitudes of oscillation. A stabilized finite element method is utilized to carry out the computations in two dimensions. Even though the response of the upstream cylinder is found to be qualitatively similar to that of an isolated cylinder, the presence of a downstream cylinder is found to have significant effect on the behaviour of the upstream cylinder. The downstream cylinder undergoes very large amplitude of oscillations in both transverse and streamwise directions. The maximum amplitude of transverse response of the downstream cylinder is quite similar to that of a single cylinder at higher Re beyond the laminar regime. Lock-in and hysteresis are observed for both upstream and downstream cylinders. The downstream cylinder undergoes large amplitude oscillations even beyond the lock-in state. The phase between transverse oscillations and lift force suffers a 180 66 jump for both the cylinders almost in the middle of the synchronization regime. The phase between the transverse response of the two cylinders is also studied. Complex flow patterns are observed in the wake of the freely vibrating cylinders. Based on the phase difference and the flow patterns, the entire flow range is divided into five sub-regions.
|
| [16] |
Interaction dynamics of upstream vortex with vibrating tandem circular cylinder at subcritical Reynolds number .
react-text: 347 We present an active feedback blowing and suction (AFBS) procedure via model reduction for unsteady wake flow and the vortex-induced vibration (VIV) of circular cylinders. The reduced-order model (ROM) for the AFBS procedure is developed by the eigensystem realization algorithm (ERA), which provides a low-order representation of the unsteady flow dynamics in the neighbourhood of the... /react-text react-text: 348 /react-text [Show full abstract]
|
| [17] |
Flow-induced vibrations of in-line cylinder arrangements at low Reynolds numbers .
The present study numerically explores the limiting two degrees of freedom (streamwise and transverse) free oscillation response of three circular cylinders, placed in an in-line configuration subjected to a uniform cross flow at low Reynolds numbers. Three identical cylinders with a low mass ratio (m68=4/π) and zero damping are considered. The spacing between the cylindersL/Dis equal to 4. The reduced velocityUris varied from 2 to 13 for two values of the Reynolds number (Re=100andRe=150). For comparison purposes, the free oscillation responses of an isolated cylinder and a tandem cylinder pair under the same conditions are also evaluated. The results show that the dynamic behaviors of three in-line cylinders are significantly different from those of the tandem cylinder pair. While the maximum transverse oscillation amplitude increases by about 25%, there is now a very large streamwise oscillation amplitude (AX/D≈1.3), comparable to those in the transverse direction. They appear atUr>9. The frequency responses of the triple cylinder case are much richer; in particular, at higherUr. There is a clear low frequency component which is most evident in the streamwise direction. Many of the displacement trajectories of the triple cylinder case can almost be described as “bounded random movements”. The associated phase portraits and the Poincaré maps show that the dynamical characteristics of the triple cylinder configuration are considerably richer than those of the tandem cylinder pair. Even at such low Re, the free oscillations of three in-line cylinders already seem to approach a chaotic response. In particular, there is evidence that the fluid–structure system approaches to chaos via the quasi-periodic route. Due to such much more complex dynamical characteristics, it is therefore highly risky to predict the free oscillation behaviors of multiple in-line cylinders by extrapolating those of the tandem cylinder pair.
|
| [18] |
Flow-induced vibration of three unevenly spaced in-line cylinder in cross-flow .
The flow over three cylinders arranged in-line with uneven spacing in cross-flow is numerically investigated at a Reynolds number of 200. The center-to-center distance between the upstream and the most downstream cylinder was kept constant at 4 diameters. The distance between the inline centers of the upstream and middle cylinders ( x x mathContainer Loading Mathjax ) was studied in the range of 1.05 to 2.95 diameters. The flow structure around the cylinders shows two distinctive patterns of vortex shedding, one of which occurs at x=1.60 x = 1 . 60 mathContainer Loading Mathjax and 1.80 diameters, and causes significantly higher oscillating lift and mean drag forces with a lower value of Strouhal number. At these middle cylinder locations, the shear layer reattaches on the downstream cylinder and results in vortex formation in the gap between the middle and downstream cylinders. On the other hand, at all other locations of the middle cylinder the shear layer does not reattach on the downstream cylinder. Moreover, when the middle cylinder is located at x=1.60 x = 1 . 60 mathContainer Loading Mathjax or 1.80 diameters, the vortex formation length is shorter and the vorticity in the downstream vortex street is higher than the case when the middle cylinder is located at all other locations. To understand the effect of these distinctive flow features on the flow-induced vibration response of the most downstream cylinder, the coupling between the flow field and the cylinder motion is numerically modeled. As the reduced velocity is increased, the oscillation amplitude of the downstream cylinder increases to its maximum at lock-in, then it starts to decrease similar to the case of a single cylinder. However, the oscillation amplitude reaches a higher value than that observed for the case of vortex-induced vibration of both a single cylinder and two tandem cylinders. Moreover, significant oscillation amplitude is pertained at high reduced velocities with dependency on the uneven spacing between the cylinders. The frequency of oscillations increases at different rates in three different ranges of reduced velocities, indicating different energy transfer mechanisms. Although the frequency of vibration is shifted away from the structure resonance frequency at high reduced velocities, the significant amplitude of oscillations is attributed to the interaction of two opposing mechanisms that occur when the cylinder is at different positions in the cycle. The wide range of reduced velocities at which the cylinder vibrates with a significant amplitude makes the configuration of three in-line cylinders a good candidate for flow energy harvesting.
|
| [19] |
Vortex-induced vibrations of three tandem cylinders in laminar cross-flow: Vibration response and galloping mechanism .
Vortex-induced vibrations (VIV) of three tandem cylinders are numerically studied using the immersed boundary method. Cylinders are free to vibrate in the cross-flow direction. The Reynolds number is Re =100 Re = 100 mathContainer Loading Mathjax and the reduced velocity is U r =36580 U r = 3 65 80 mathContainer Loading Mathjax . Six spacing ratios are selected in the range L∕D=1.2655.0 L ∕ D = 1 . 2 65 5 . 0 mathContainer Loading Mathjax . The mass ratio is m 65 =2.0 m 65 = 2 . 0 mathContainer Loading Mathjax , while the damping ratio is set as zero for achieving large vibration amplitudes. The characteristics of the vibration amplitude, drag and lift forces, lift frequency, phase difference between displacement and lift, and the wake patterns are discussed. It is found that, in the case with small L∕D L ∕ D mathContainer Loading Mathjax , large-amplitude vibrations of the cylinders are excited due to strong wake-cylinder interference. However, in the cases with large L∕D L ∕ D mathContainer Loading Mathjax , the vibration responses of the upstream cylinder resemble those of an isolated cylinder indicating vanishing interference from the downstream cylinders. While, the two downstream cylinders attain large vibration amplitudes even at high reduced velocities. A wake pattern, T+S, i.e. the cylinders alternately shed triple vortices and a single vortex in a vibration cycle, is observed. This wake pattern is caused by the asymmetric vibration of the cylinders and transverse dislocation of the equilibrium positions. With increasing L∕D L ∕ D mathContainer Loading Mathjax , two different vibration patterns are observed: wake-induced galloping (WG) for the small- L∕D L ∕ D mathContainer Loading Mathjax case ( L∕D=1.2 L ∕ D = 1 . 2 mathContainer Loading Mathjax ) and vortex-induced vibration (VIV) for the moderate- to large- L∕D L ∕ D mathContainer Loading Mathjax cases ( L∕D=1.5655.0 L ∕ D = 1 . 5 65 5 . 0 mathContainer Loading Mathjax ). The major characteristic feature of WG, distinct to VIV, are the divergent vibrations of the cylinders with the increasing reduced velocity. The mechanism of WG is elucidated by analyzing the complex but stable interactions between vortices and cylinders. Three pivotal factors are identified: the ‘perfect’ timing between vortex-shedding and cylinder motion, the transverse dislocation of the equilibrium positions, and the low and decreasing vibration frequency.
|
| [20] |
耦合四圆柱涡激振动的力特性及水动能获取分析 .
涡激振动是一种常见的流固耦合现象,结构物振幅较大时,可利用涡激振动从海洋流中或河流中获取能量。论文通过流固双向耦合数值方法,模拟均匀来流下,弹性支撑刚性连接的耦合四圆柱在不同横向和流向间距比下的横向涡激振动。分析横向和流向间距比对该耦合结构涡激振动时的压力和升力特性及获取能量和能量密度的影响。结果表明:各种组合间距比下,上端两圆柱的升力系数均值CL与下端两圆柱的CL关于CL=0对称,压力系数幅值Ap关于θ =180o对称,但其升力系数均方根值却近似相等;获取的水动能及能量密度随着组合间距比的增加先增加,随后获取能量增加缓慢,而能量密度却不断减少,因此选择合理的横向和流向间距比可从单位水体的海洋流或河流中获取更多的水动能。<br>
Force characteristics and hydrokinetic energy harvesting for VIV of four coupling-linked cylinders .
涡激振动是一种常见的流固耦合现象,结构物振幅较大时,可利用涡激振动从海洋流中或河流中获取能量。论文通过流固双向耦合数值方法,模拟均匀来流下,弹性支撑刚性连接的耦合四圆柱在不同横向和流向间距比下的横向涡激振动。分析横向和流向间距比对该耦合结构涡激振动时的压力和升力特性及获取能量和能量密度的影响。结果表明:各种组合间距比下,上端两圆柱的升力系数均值CL与下端两圆柱的CL关于CL=0对称,压力系数幅值Ap关于θ =180o对称,但其升力系数均方根值却近似相等;获取的水动能及能量密度随着组合间距比的增加先增加,随后获取能量增加缓慢,而能量密度却不断减少,因此选择合理的横向和流向间距比可从单位水体的海洋流或河流中获取更多的水动能。<br>
|
| [21] |
Flow-induced vibrations of four circular cylinders with square arrangement at low Reynolds numbers .
Flow-induced vibrations (FIV) of four identical circular cylinders placed in a square arrangement are numerically investigated. Modeled as a spring-damping system subjected to uniform flows, each cylinder is allowed to freely oscillate with equal natural frequencies in the inline and transverse directions. The spacing ratio, LID, remains 5, where L is the central distance of any two adjacent cylinders and D the cylinder diameter. The Reynolds numbers are chosen as Re=80 and 160. The incidence angle of the incoming uniform flow is alpha=0 degrees. The mass ratio for each cylinder is M-r=6.0 and the reduce velocity, U-r, varies from 3 to 14. The coupled system is numerically resolved by a semi-implicit characteristics-based split (CBS) finite element algorithm under the arbitrary Lagrangian-Eulerian description. The calculated results are analyzed in detail. In particular, some intrinsic mechanisms are interpreted on the cylinder responses and the wake patterns. The unsymmetrical figures of "8" and "O", and other irregular figures are observed in the cylinders' X-Y trajectories. Besides the "4S" wake pattern, the "2P+2S" pattern is discovered herein. The "dual-resonance" phenomenon, which indicates the cylinders' synchronizations occurring in both the inline and transverse directions, is detected in this work. (C) 2014 Elsevier Ltd. All rights reserved.
|
| [22] |
Poiseuille flow-induced vibrations of two cylinders in tandem .
Laminar flows past two tandem cylinders which are free to move transversely in a parallel-wall channel were studied numerically by the lattice Boltzmann method. With fixed Reynolds number Re=100, blockage ratio β=1/4 and structural damping ξ=0, the effect of streamwise separation between two cylinders at a range of S/D=[1.1, 10] on the motions of cylinders and fluids was studied for both mass ratios of m(68)=1 and m(68)=0.1. A variety of distinct vibration regimes involving periodic, quasi-periodic and non-periodic vibrations with corresponding flow patterns were observed. A detailed analysis of the vibration amplitudes, vibration frequencies and relative equilibrium positions for both mass ratios demonstrated that as S/D increases, the interaction of the two cylinders first enhances and then reduces. In the strong coupling regime, both cylinders oscillate periodically around the centerline of the channel with large vibration amplitudes and high vibration frequencies. By comparing with the case of an isolated cylinder, a further study indicated that the gap flow plays an important role in such a dynamic system, and the vortex cores formation behind the front cylinder causes the interaction of the cylinders decouple rapidly. Based on the present observations, such a dynamic model system can be considered as a novel type of vortex-induced vibrations (VIV) and is expected to find applications in fluid mixing and heat transfer.
|
| [23] |
Poiseuille flow-induced vibrations of two tandem circular cylinders with different mass ratios .
Flow-induced vibrations of two tandem circular cylinders with different mass ratios confined between two parallel walls are numerically studied via a lattice Boltzmann method. With fixed Reynolds number Re = 100 and blockage ratio尾= 1/4, the effects of mass ratiom*= [0.0625, 16] and streamwise separation between two cylindersS/D= [1.125, 10] on the cylinder motions and vortex wake modes are investigated. A variety of distinct cylinder motion regimes involving the symmetric periodic vibration, biased quasi-periodic vibration, beating vibration, and steady regimes, with the corresponding wake structures, e.g., two rows of alternately rotating vortices, a single row of same-sign vortices, and steady wake, are observed. For each current case, the cylinder motion type is exclusive and in the binary oscillation regime, both cylinders always vibrate at a common primary frequency. The lighter cylinder usually oscillates at a larger amplitude than the heavier one, while the heavier cylinder undergoes larger lift force than the lighter one. The lift force and cylinder displacement always behave as an out-of-phase state. In the gap-interference region, large-amplitude oscillations could be produced extensively and in the wake-interference region, the cylinder motions and fluid flows are mainly dependent on the upstream cylinder. When the separation is large enough, both cylinders behave as two isolated ones. The mechanisms for the excitations of cylinder vibrations have also been analysed.
|
| [24] |
Numerical investigation of vortex-induced virbration of circular cylinder in transverse direction in oscillatory flow .
78 Response is strongly dependent on reduced velocity. 78 The vibration mode changes in time frequently. 78 The vibration frequency depends on the number of vortices shedding from the circular cylinder. 78 Wavelet analysis can identify the variations in both frequency and amplitude with time.
|
| [25] |
正弦振荡来流下柔性立管涡激振动发展过程 .
<p>在风浪流的作用下,海洋浮式结构物将带动悬链线立管在水中作周期性往复运动,从而在立管运动方向上产生相对振荡来流,这种振荡来流将激励立管悬垂段发生“间歇性” 的涡激振动. 在海洋工程水池中对一个4m 长的立管微段进行模型试验研究,以探索相对振荡来流作用下立管涡激振动产生的机理及其发展的物理过程. 试验通过振荡装置带动模型作正弦运动来模拟不同最大约化速度<em>U</em><sub><em>R</em></sub><sub>max</sub>、不同<em>KC</em>(Keulegan-Carpenternumber)的相对振荡来流,利用光纤应变片测量立管涡激振动响应. 结合模态分析方法处理试验数据得到位移响应时历,继而提出相对振荡来流下柔性立管涡激振动发展的3 个阶段:建立阶段、锁定阶段以及衰减阶段. 并进一步总结了最大约化速度<em>U</em><sub><em>R</em></sub><sub>max</sub>,<em>KC</em> 对涡激振动发展过程的影响规律. 最终获得不同最大约化速度<em>U<sub>R</sub></em><sub>max</sub>下,涡激振动各发展阶段随KC 所占时间分布比例图.</p>
Xu Yuwang et al. VIV developing process of a flexible cylinder under oscillatory flow .
<p>在风浪流的作用下,海洋浮式结构物将带动悬链线立管在水中作周期性往复运动,从而在立管运动方向上产生相对振荡来流,这种振荡来流将激励立管悬垂段发生“间歇性” 的涡激振动. 在海洋工程水池中对一个4m 长的立管微段进行模型试验研究,以探索相对振荡来流作用下立管涡激振动产生的机理及其发展的物理过程. 试验通过振荡装置带动模型作正弦运动来模拟不同最大约化速度<em>U</em><sub><em>R</em></sub><sub>max</sub>、不同<em>KC</em>(Keulegan-Carpenternumber)的相对振荡来流,利用光纤应变片测量立管涡激振动响应. 结合模态分析方法处理试验数据得到位移响应时历,继而提出相对振荡来流下柔性立管涡激振动发展的3 个阶段:建立阶段、锁定阶段以及衰减阶段. 并进一步总结了最大约化速度<em>U</em><sub><em>R</em></sub><sub>max</sub>,<em>KC</em> 对涡激振动发展过程的影响规律. 最终获得不同最大约化速度<em>U<sub>R</sub></em><sub>max</sub>下,涡激振动各发展阶段随KC 所占时间分布比例图.</p>
|
| [26] |
均匀平面剪切流作用下圆柱体的涡激振动 .
对二维平面均匀剪切流作用下,弹性支撑圆柱体在横向和流向运动的涡激振动进行了数值模拟.数值计算实现了雷诺数在[2000,5000]内,圆柱体在不同剪切率[0.01,0.05]条件下的涡激振动.圆柱体的横向振幅、运动轨迹、振动频率和升力系数及位移时历曲线的计算结果表明,对于不同的雷诺数,存在剪切率的“锁定区间”.雷诺数较小时,剪切率的锁定区间较小,随着雷诺数的增加,剪切率的锁定区间增大.在剪切率的锁定区间内,横向振幅增大,脱离剪切率锁定区问后,横向振幅迅速下降.计算结果发现圆柱体的运动轨迹可以完全不同于普遍认可的“8”形轨迹,在剪切率锁定区间内圆柱体运动轨迹似“小雨点”的外形,这是在平面横向剪切流条件下得到的圆柱体运动的新轨迹.
Vortex-induced vibration of a cylinder in uniform planar shear flow .
对二维平面均匀剪切流作用下,弹性支撑圆柱体在横向和流向运动的涡激振动进行了数值模拟.数值计算实现了雷诺数在[2000,5000]内,圆柱体在不同剪切率[0.01,0.05]条件下的涡激振动.圆柱体的横向振幅、运动轨迹、振动频率和升力系数及位移时历曲线的计算结果表明,对于不同的雷诺数,存在剪切率的“锁定区间”.雷诺数较小时,剪切率的锁定区间较小,随着雷诺数的增加,剪切率的锁定区间增大.在剪切率的锁定区间内,横向振幅增大,脱离剪切率锁定区问后,横向振幅迅速下降.计算结果发现圆柱体的运动轨迹可以完全不同于普遍认可的“8”形轨迹,在剪切率锁定区间内圆柱体运动轨迹似“小雨点”的外形,这是在平面横向剪切流条件下得到的圆柱体运动的新轨迹.
|
| [27] |
An in-depth study on vortex-induced vibration of a circular cylinder with shear flow .
To investigate the in-depth mechanism of vortex-induced vibration of a circular cylinder with shear flow, in this paper, with the use of exponential-polar coordinate attached on the moving cylinder, the stream function-vorticity equations of vortex-induced vibration, the initial/boundary conditions and distribution of hydrodynamic force together with cylinder motion equation in shear flow are deduced, the hydrodynamic force consists of inertial force, the vortex-induced force and viscous damping force. Similarly, the cylinder motion equation with virtual mass is induced where the virtual mass consists of the cylinder mass, the potential added mass and the apparent added mass induced by viscosity. Our numerical results revealed that there are three factors affecting fluid-structure interactions from the fixed cylinder to its steady vibration: The first is the vortex shedding where one side shear layer of cylinder strengthens with the effect of the dominated vortex. The second is the vibration of cylinder which pushes the fluid on the pressure side and pumps that on the suction side. The third is the vortexes strengthen in one side and weaken in the other side together with the shift of front stagnation point with the effect of background vortex which is generated by shear flow. The character of vortex-induced vibration in shear flow are affected by the above three factors.
|
| [28] |
Flow-induced vibration on a circular cylinder in planar shear flow .
In this paper, the flow-induced vibrations of an elastically mounted circular cylinder subjected to the planar shear flow with the 1-DOF (only transverse direction) and 2-DOF (in-line and cross-flow directions) movements are studied numerically in the laminar flow (Re=150). Based on a characteristic-based-split (CBS) finite element method, the numerical simulation is conducted, and is verified through the benchmark problem of the uniform flow past an elastically mounted circular cylinder. The computation is carried out for lower reduced mass of Mr=2.0 and the structural damping ratio is set to zero to maximize the vortex-induced response of the cylinder. The effects of some key parameters, such as shear rate (k=0.0鈥0.1), reduced velocity (Ur=3.0鈥12.0) and natural frequency ratio (r=1.0鈥2.0), on the characteristics of vortex-induced vibration (VIV) responses are studied. The results show that, in the 1-DOF system, the frequency synchronization region extends with the increasing of k. The shear rate greatly affects the phase portraits, which shift from the double-valued type to the single-valued one. On the other hand, in the 2-DOF system, the increasing of k causes the extension of the single-resonant region and dual-resonant one at the lower natural frequency ratios. While at the higher natural frequency ratios, the change of k only expands the single-resonant region in the transverse direction. The predominant vortex shedding patterns are 2S and P+S modes. Finally, the interaction between vortex and cylinder as well as the mechanism of flow-induced vibration in planar shear flow are revealed. The phase between the force and its corresponding displacement changes from out-of-phase to in-phase and the higher harmonic forces appear with the increasing of shear rate, resulting in the energy transferring from the fluid to the structure and then the dynamic response of the cylinder intensifying.
|
| [29] |
Vortex-induced vibrations of a cylinder in planar shear flow . |
| [30] |
Flow-induced vibrations of two circular cylinders in tandem with shear flow at low Reynolds number .
61The VIV of two tandem cylinders in shear flow are numerically investigated at Re=160.61The dynamic responses of two tandem cylinders in shear flow are investigated.61TheX–Ytrajectories of both cylinders subjected to shear flow are investigated.61The WIV mechanism of both cylinders in planar shear flow is revealed.
|
| [31] |
不同剪切率来流作用下柔性圆柱涡激振动数值模拟 .
采用浸入边界法对细长柔性圆柱在线性剪切流条件下的涡激振动进行三维数值模拟.细长柔性圆柱振动采用三维索模型模拟,其两端铰接,质量比为6,长细比为50,无量纲顶张力为496.来流为线性剪切流,剪切率从0到0.024变化,最大雷诺数为250.研究发现:剪切流作用下柔性立管横流向振动表现为驻波模式,而顺流向振动表现为行波与驻波混合模式.随着剪切率增大,振动频谱呈现多频响应,振动能量逐渐向低频转移.阻力系数平均值随着展向变化,脉动阻力系数和升力系数的均方根值均表现为"双峰"模式.流固能量传递系数沿立管轴向的分布表明,振动激励区集中于高流速区,而振动阻尼区多位于低流速区.剪切率较小时,圆柱的泻涡为平行交叉模式;剪切率较大时,圆柱的泻涡为倾斜泻涡模式,且由于泻涡频率沿立管轴向变化,尾流发生涡裂现象,形成泻涡频率不同的胞格结构.
Numerical simulation of vortex-induced vibration of a flexible cylinder exposed to shear flow at different shear rates .
采用浸入边界法对细长柔性圆柱在线性剪切流条件下的涡激振动进行三维数值模拟.细长柔性圆柱振动采用三维索模型模拟,其两端铰接,质量比为6,长细比为50,无量纲顶张力为496.来流为线性剪切流,剪切率从0到0.024变化,最大雷诺数为250.研究发现:剪切流作用下柔性立管横流向振动表现为驻波模式,而顺流向振动表现为行波与驻波混合模式.随着剪切率增大,振动频谱呈现多频响应,振动能量逐渐向低频转移.阻力系数平均值随着展向变化,脉动阻力系数和升力系数的均方根值均表现为"双峰"模式.流固能量传递系数沿立管轴向的分布表明,振动激励区集中于高流速区,而振动阻尼区多位于低流速区.剪切率较小时,圆柱的泻涡为平行交叉模式;剪切率较大时,圆柱的泻涡为倾斜泻涡模式,且由于泻涡频率沿立管轴向变化,尾流发生涡裂现象,形成泻涡频率不同的胞格结构.
|
| [32] |
An adaptive mesh rezoning scheme for moving boundary flows and fluid-structure interaction .
Arbitrary Lagrangian–Eulerian (ALE) techniques provide a general framework for solving moving boundary flows and fluid–structure interaction problems. ALE formulations allow freedom of prescribing the fluid mesh velocity which can be independent of the velocity of the fluid particles. A major challenge in ALE descriptions lies in developing mesh moving techniques to update the fluid mesh and map the moving domain in a rational way. Exploiting the notion of arbitrary mesh velocity for the fluid domain, we have developed an adaptive mesh rezoning technique for structured and unstructured meshes. The method has been applied to meshes composed of triangles, quadrilaterals, as well as an arbitrary combination of these two element types in the computational domain. This feature of the proposed scheme is very attractive from practical problem solving viewpoint in that it allows kinematically complex problems to be handled effectively. A variety of test cases are shown that involve single and/or multiple moving objects. Embedding the mesh rezoning scheme in our flow solver, we also present some representative simulations of flows over moving meshes.
|
| [33] |
Resonant vibrations of bluff bodies cause multivortex shedding and high frequency forces .
A flexibly mounted circular cylinder in cross-flow, with natural frequencies in the inline and transverse directions having a ratio close to 2:1, exhibits drastic changes in the vortex structures in its wake, the frequency content of the fluid forces, and the orbital shape of its resulting motions. Stable multivortex patterns form in the cylinder wake, associated with large high-frequency force components.
|

/
| 〈 |
|
〉 |