基于滑移速度壁模型的复杂边界湍流大涡模拟1)
(中国科学院力学研究所非线性力学国家重点实验室,北京 100190);(中国科学院大学工程科学学院,北京 100049)
LARGE-EDDY SIMULATION OF FLOWS WITH COMPLEX GEOMETRIES BY USING THE SLIP-WALL MODEL1)
中图分类号: O357
文献标识码: A
通讯作者:
收稿日期: 2019-01-28
网络出版日期: 2019-05-18
版权声明: 2019 力学学报期刊社 所有
基金资助:
展开
摘要
采用滑移速度壁模型实现了浸入边界方法与壁模型相结合的大涡模拟.本文首先分别采用平衡层模型和非平衡壁模型对周期山状流进行数值模拟,以考查在壁模型中考虑切向压力梯度的作用.数值结果表明,流场的压力对本文所采用的壁模型形式并不敏感,但是考虑切向压力梯度可以显著改进壁面摩擦力的计算结果,并且能够准确的预测强压力梯度区以及分离区内的流动平均统计特性.不考虑压力梯度效应的平衡层模型显著低估了壁面摩擦力的分布,同时无法准确预测分离区内的平均速度剖面.非平衡模型的修正项正比于切向压力梯度和壁面法向距离,因此在强压力梯度区或者网格较粗时,计算得到的平均压力和摩擦力分布以及流动的低阶统计量均与参考的实验和计算结果吻合.在此基础上,通过回转体绕流的大涡模拟考查了该方法用于模拟高雷诺数壁湍流的适用性,非平衡壁模型可以准确地捕捉流动的物理结构并较准确地预测其水动力学特性.结果表明,将浸入边界方法与非平衡滑移速度壁模型相结合的大涡模拟,有望成为数值模拟复杂边界高雷诺数壁湍流的工具.
关键词:
Abstract
A slip-wall model is combined with the immersed boundary method for large-eddy simulation of flows with complex geometries. Firstly, large eddy simulation of flows over periodic hills are conducted to evaluate the effects of the tangential pressure gradient in wall model. Both the equilibrium stress balance model which based on the assumption of an equilibrium boundary-layer and the non-equilibrium wall model, in which the pressure gradient blend into the simplified thin boundary-layer equations and the RANS-like eddy viscosity in both the procedure of computing the wall-shear stress and reconstructing the wall-slip velocity, are utilized for comparison. The numerical results show that the pressure coefficient is not sensitive to the types of wall model which we considered, especially the strong pressure gradient in front of the hill crest is well catched by both models. However, when taking into account the tangential pressure gradient, the non-equilibrium wall model is superior to the equilibrium one for its ability to improve the prediction of the wall-shear stress and flow separation. When the equilibrium stress balance model is used, the wall-shear stress is heavily under-predicted and remarkable discrepancies of the mean velocity profiles can also be seen in the recirculation region. By comparison, the correction of the non-equilibrium wall model is proportional to both the tangential pressure gradient and the normal distance away from the wall, thus the hydrodynamic coefficients and the mean flow statistics are all in good agreement with the references even on very coarse grids. Secondly, large-eddy simulation of flow around an axisymmetric body is conducted to assess the applicability of current method when applied to high Reynolds number wall-bounded turbulent flows. The flow structures and the hydrodynamic characteristics are well predicted by the non-equilibrium wall model. This work confirms that the immersed boundary method in combination with the non-equilibrium slip-wall model is a possible and promising way to deal with turbulent flows which have complex geometries.
Keywords:
引 言
随着计算机性能的提升以及计算资源的丰富,大涡模拟方法在科学研究领域和工业界受到广泛关注[1-4],但是复杂边界高雷诺数壁湍流仍然是大涡模拟应用于工程流动的重要挑战[5-7]. 当基于流动积分尺度和平均速度的雷诺数$Re\sim O\left( {10^6} \right)$时,超过99{%}的计算网格点将用于解析边界层内区的流动[8-9]. 为了降低计算所需的网格量,通常采用壁模型$^{[8-13]}$来模化高雷诺数湍流的近壁区流动.
壁面应力模型是一种常见的壁模型[8-10]. 该模型为大涡模拟提供应力边界条件,从而修正壁面附近的动量通量. 壁面应力模型可以大致分为平衡层模型和双层模型两大类[14-16]. 其中平衡层模型主要是在平衡层假设下根据湍流近壁区平均速度的对数律或幂律,建立壁面切应力与切向速度之间的函数关系. 该类模型形式简单,但是通常难以准确计算复杂边界流动的壁面切应力[9]. 双层模型则是一种微分方程形式的壁模型,通常在湍流近壁区嵌入一套细网格,并在细网格上求解薄边界层方程,以提供大涡模拟所需的应力边界条件[17-19]. 相比于平衡层模型,双层模型可以反映湍流近壁流动的非平衡特性,但是需要求解微分方程,实现过程相对复杂. 最近Duprat等[20] 通过考虑压力梯度对近壁涡黏系数的影响,给出了近壁区切向速度的近似表达式. 该方法考虑了薄边界层方程非平衡项中压力梯度的影响,并且不需要求解微分方程. 上述壁模型已经被成功地应用于贴体网格方法中. 近年来,随着超级计算机与复杂边界湍流数值模拟的发展,壁模型与浸入边界方法的结合正逐步引起关注.
浸入边界方法是一种非贴体网格方法[21].它通过动量方程中的体积力项反映边界对流动的影响,可以基于笛卡尔网格模拟具有复杂几何形状及运动边界的流动.该方法已经被成功地应用于不同状态的层流[21-23]以及中等雷诺数的湍流[24-25]数值模拟中.将浸入边界方法与壁模型相结合是模拟具有复杂几何边界的高雷诺数壁湍流的有效途径[26].在浸入边界方法中,由于几何边界通常与流场计算网格(欧拉网格)不重合并且其影响是通过控制方程的体积力来体现,因此难以直接施加应力边界条件[27].目前壁模型与浸入边界方法相结合的主要思路是在壁面外的近壁区重构速度,以匹配壁模型所对应的速度剖面,从而计算大涡模拟动量方程的等效体积力.该思路由Tessicini 等[28]首先提出,他们采用近壁边界层模型来构建等效体积力.其中大涡模拟方程求解至壁面外的第二层欧拉网格并为壁模型提供边界条件.壁面外第一层欧拉网格上的速度则通过求解简化的薄边界层方程来重构,并以此计算大涡模拟动量方程的体积力.这种思路被不同形式的壁模型所采用. Choi等[29]通过近壁区平均速度的幂律来重构壁面外第一个欧拉网格点上的速度,并对其进行修正以满足速度剖面的高阶连续条件.Roman 等[27]直接采用对数率重构速度,此外通过调整雷诺平均形式的涡黏系数来修正壁面附近的动量通量.Cristallo 和 Verzicco[26]提出了一种改进思路,他们建议将大涡模拟方程求解至壁面外的第一层欧拉网格上,而壁模型则用于计算壁面摩擦力.这等价于在壁面重构滑移速度,并为边界层外区的大涡模拟提供准确的壁面切应力.根据他们的描述,该方法可以改进Tessicini 等[28]的计算结果.在壁面重构滑移速度的思路在Ji 等[30]所提出的迭代直接力方法中被采用.他们通过近壁区速度的幂律来计算壁面切应力,并以此重构壁面滑移速度来构建等效体积力.
目前针对浸入边界方法与壁模型相结合的大涡模拟研究仍然是开放性的问题,其所采用的壁模型均是基于平衡层假设.该假设在流动面临分离或强压力梯度时并不成立,因此这类壁模型不能反映近壁区流动的非平衡特性.Duprat等[20]基于贴体网格方法提出非平衡壁模型的数值结果表明,在壁模型中仅考虑切向压力梯度的影响可以明显改进壁模型对流动分离及强压力梯度区的预测结果.本文工作将Duprat等[20]的思路用于构建壁面滑移速度,以实现浸入边界方法与非平衡壁模型相结合的大涡模拟.
本文工作通过周期山状流的大涡模拟考查了在壁模型中考虑切向压力梯度的作用.进一步的对高雷诺数的回转体绕流进行大涡模拟并分析其水动力特性.其中湍流近壁区流动通过Duprat等[20]提出的非平衡壁模型来模化,而浸入边界方法中的等效体积力则通过重构壁面滑移速度[31]来计算.
本文内容安排如下:第1节介绍基于浸入边界方法的大涡模拟控制方程与数值方法;第2节介绍将浸入边界方法与壁模型相结合的方法;第3节介绍周期山状流以及回转体绕流大涡模拟的主要结果;第4节将对本文工作进行总结.
1 数值方法
1.1 控制方程及其离散
本文求解滤波后不可压缩流动的Navier-Stokes (N-S) 方程组
$$\frac{\partial \tilde {u}_i }{\partial x_i } = 0\tag{1}\\ $$
$$\frac{\partial \tilde {u}_i }{\partial t} + \frac{\partial \tilde {u}_i \tilde {u}_j }{\partial x_j } = - \frac{1}{\rho }\frac{\partial \tilde {p}}{\partial x_i } + \nu \frac{\partial ^2\tilde {u}_i }{\partial x_j \partial x_j } - \frac{\partial \tilde {\tau }_{ij} }{\partial x_j }\mbox{ + }f_i\tag{2} $$
其中, $\tilde {u}_i \left( {i = 1,2,3} \right)$和$\tilde{p}$分别表示滤波后的速度分量和压力, $f_i \left( {i = 1,2,3}\right)$为浸入边界方法中的等效体积力. $\nu $和$\rho$分别为流体运动学黏性系数和密度.文中采用涡黏假设来封闭动量方程中的亚格子应力\begin{equation}\label{eq3} \tilde {\tau }_{ij} = - 2\nu _t \tilde {S}_{ij} +\frac{1}{3}\tilde {\tau }_{kk} \delta _{ij} \tag{3}\end{equation}式中, $\tilde {S}_{ij} $为根据滤波速度计算所得的应变率张量.亚格子涡黏系数$\nu _t $通过WALE模型[32]确定
$$\nu _t = C_{\rm w}^2 \bar {\varDelta }^2\frac{\left( {\tilde {S}_{ij}^d \tilde {S}_{ij}^d } \right)^{3 / 2}}{\left( {\tilde {S}_{ij} \tilde {S}_{ij} } \right)^{5 / 2} + \left( {\tilde {S}_{ij}^d \tilde {S}_{ij}^d } \right)^{5 / 4}}\tag{4}$$
$$\tilde {S}_{ij}^d = \frac{1}{2}\left( {\tilde {g}_{ij}^2 + \tilde {g}_{ji}^2 } \right) - \frac{1}{3}\delta _{ij} \tilde {g}_{kk}^2 \tag{5}$$
$$\tilde {g}_{ij} = \frac{\partial \tilde {u}_i }{\partial x_j }\tag{6} $$
式(4)中滤波尺度$\bar{\varDelta }$取为欧拉网格宽度,模型常数$C_{\rm w} $取为0.6.
采用投影方法求解不可压缩流动方程组(1)和(2),具体求解步骤如下
$$\frac{\tilde {u}_i^{\ast } - \tilde {u}_i^n }{\Delta t} = rhs^{n + 1 / 2} - \frac{\partial \tilde {p}^n}{\partial x_i } + f_i^{n + 1 / 2}\tag{7}$$
$$\tilde {u}_i^{n + 1} = \tilde {u}_i^\ast - \Delta t\frac{\partial \delta p}{\partial x_i }\tag{8}$$
$$\frac{\partial ^2\delta p}{\partial x_i \partial x_i } = \frac{1}{\Delta t}\frac{\partial \tilde {u}_i^\ast }{\partial x_i }\tag{9}$$
$$ \tilde {p}^{n + 1} = \tilde {p}^n + \delta p\tag{10} $$
其中,上标$n$表示当前时间步,$\tilde {u}_i^\ast$为中间步的预估速度分量,右端项$rhs$包含对流、扩散项与亚格子应力项,$\delta p$为压力修正项. 体积力项$f_i^{n + 1 / 2}$的计算过程将在1.2节详细讨论.本文采用二阶的中心差分格式离散空间导数,采用二阶的Adams-Bashforth格式进行时间推进.控制方程的详细求解过程及计算程序在不同状态流动中的验证结果可以参考文献[33,34,35].
1.2 浸入边界方法
本文采用Vanella和Baralas[36]提出的直接力方法来计算等效体积力.其中体积力的计算在表征几何边界的拉格朗日网格上进行.欧拉与拉格朗日网格间物理量的插值通过移动最小二乘方法来实现.
作用于欧拉网格上的体积力$f_i^{n + 1 / 2} $可表示为
\begin{equation} \label{eq11} f_i^{n + 1 / 2} = W_{ij} F_j^{n + 1 / 2} , {i,j = 1,2,3} \tag{11} \end{equation}
其中, $W_{ij} $为权函数. 拉格朗日网格上的体积力$F_i^{n + 1 / 2}$可以通过式(12)计算
\begin{equation} \label{eq12} F_j^{n + 1 / 2} = \frac{U_j^{\rm b} - \hat {U}_j^{\ast {\ast }} }{\Delta t}, {j = 1,2,3} \tag{12} \end{equation}
式中, $U_j^{\rm b} $为边界拉格朗日网格上的目标速度. $\hat {U}_j^{\ast\ast}$
$为该网格上的预估速度并可以由其周围欧拉网格上的速度插值得到
\begin{equation} \label{eq13} \hat {U}_j^{\ast {\ast }} = W_{ji} \hat {u}_i^{\ast {\ast }} ,\quad {i,j = 1,2,3}\tag{13} \end{equation}
其中, $\hat {u}_i^{\ast{\ast }}$为欧拉网格上的预估速度,由方程(7)在不考虑体积力$f_i^{n + 1 / 2}$时计算得到
\begin{equation} \label{eq14} \hat {u}_i^{\ast {\ast }} = \tilde {u}^n + \Delta t\left( {rhs^{n + 1 / 2} - \frac{\partial \tilde {p}^n}{\partial x_i }} \right)\tag{14} \end{equation}
2 浸入边界方法与壁模型的结合
以壁面滑移速度的形式将大涡模拟壁模型与浸入边界方法相结合.由于壁模型主要用于计算壁面切应力和重构壁面滑移速度,而流场计算的欧拉网格与几何边界通常并不重合,因此将模型方程以及流动物理量投影到局部正交的坐标系下.近壁区流动速度${ {{u}}}$可以在该局部坐标系下沿切向和法向分解为[29]
$$ { {{u}}} = { {{u}}}_{{\rm w}} + u_\eta { {{e}}}_{{\eta}} + u_\xi { {{e}}}_{{\xi }}\tag{15} $$
其中${ {{e}}}_{{\eta}} $和${ {{e}}}_{{\xi }} $分别为局部坐标系下的法向和切向单位矢量,$u_\eta $和$u_\xi $分别为局部的法向和切向速度. 文中主要研究几何边界为静止状态的流动问题,因此边界的运动速度${ {{u}}}_{{\rm w}} $设置为零.
采用如下方式构造壁面滑移速度来计算等效体积力.该方法在湍流近壁区内维持切向速度的线性分布并同时满足流动控制体内的积分动量守恒.壁面上的切向速度$u_{\xi ,{\rm S}} $和法向速度$u_{\eta ,{\rm S}}$可以分别表示为[31]
$$u_{\xi ,{\rm S}} = u_{\xi ,{\rm P}} - \frac{\delta _{\rm P} }{\left( {\nu \mbox{ + }\nu _{\rm t} } \right)}\left( {\frac{\tau _{\rm w} }{\rho } + S\delta _{\rm P} } \right)\tag{16}$$
$$u_{\eta ,{\rm S}} = 0\tag{17}$$
式(16)中$u_{\xi ,{\rm P}}$为壁模型与大涡模拟交界面(本文定义为匹配面)上的切向速度. $u_{\xi,{\rm P}} $可从大涡模拟的流场在匹配面上插值得到. $\delta _{\rm P}$为匹配面距离壁面的法向距离,$\nu _{\rm t} $为涡黏系数.右端项$S$为薄边界层方程中的非平衡项(见式(18)).该项的具体形式以及壁面摩擦力$\tau _{\rm w}$的求解过程将在以下内容中进行详细介绍.本文中匹配面距离壁面的法向距离设置为$2\Delta h(\Delta h$为欧拉网格宽度),而移动最小二乘插值的模板半宽为$1.2\Delta h$.因此在匹配面上的插值操作并不涉及到边界内部的固体点,并同时可以避免在边界和匹配面插值的相互干扰.
本文采用Duprat等[20]提出的壁模型来计算壁面切应力,从而重构壁面滑移速度.在局部坐标系下,边界层内区流动的切向动量方程为[17-19]
\begin{equation} \label{eq16} \frac{\partial }{\partial \eta }\left[ {\left( {\nu \mbox{ + }\nu _{\rm t} } \right)\frac{\partial { { {u}}}}{\partial \eta } \cdot { { {e}}}_{{\xi}} } \right] = S\tag{18} \end{equation}
其中,$S = \dfrac{1}{\rho }\nabla \bar {P}_{\rm m} \cdot { {{e}}}_{{\xi}} + \dfrac{\partial { {{u}}}}{\partial t} \cdot{ {{e}}}_{{\xi }} + \left( {{ { {u}}} \cdot \nabla }\right){ {{u}}} \cdot { {{e}}}_{{\xi }} $,$\bar {P}_{\rm m}$表示匹配面上的滤波压力,可以由大涡模拟插值得到并且在边界层内区沿法向保持为常数.
方程(18)是关于切向速度的偏微分方程,可以在边界层内区直接求解,其中下壁面满足无滑移边界条件,上边界的边界条件则由大涡模拟提供.仿照Wang和Moin的工作[19],本文主要考虑模型方程的两种简化形式:
(1) $S = 0$,对应于平衡层模型(文中标记为EB模型);
(2) $S = 1 / \rho \left( {\nabla \bar {P}_{\rm m} \cdot { {{e}}}_{{ \xi }} } \right)$,即右端项仅考虑切向压力梯度引起的非平衡效应(文中标记为NEB模型).
在这两种情况下,将动量方程沿法向积分可以得到壁面摩擦力的解析表达式[19]
\begin{equation} \label{eq17} \tau _{\rm w} = {\rho }\left( {u_{\xi ,{\rm P}} - S\int_0^{\delta _{\rm P} } {\frac{\eta {\rm d}\eta }{\nu + \nu _{\rm t} }} } \right)\bigg/ {\int_0^{\delta _{\rm P} } {\frac{{\rm d}\eta }{\nu + \nu _{\rm t} }} }\tag{19} \end{equation}
Duprat 等[20] 对van Driest公式[37]进行修正,以考虑切向压力梯度对近壁涡黏的影响
$$\frac{\nu_{\rm t}}{\nu } = \kappa \eta ^\ast \left[ {\alpha + \eta ^\ast \left( {1 - \alpha } \right)^{\frac{3}{2}}} \right]^\beta \left( {1 - {\rm e}^{ - \frac{\eta ^\ast }{1 + \alpha ^3A}}} \right)^2\tag{20} $$
其中壁面单位定义为$\eta ^\ast = \eta u_{\tau {p}} / \nu (\eta $为距离壁面的法向距离). 特征速度$u_{\rm \tau p}= \sqrt {u_\tau ^2 + u_{\rm p}^2 } $,其中$u_\tau$为摩擦速度,$u_{\rm p} = \left| {\left( {\nu / \rho }\right)\left( {\nabla \bar {P}_{\rm m} \cdot { {{e}}}_{ { \xi}} } \right)} \right|^{1 / 3}$用于表征切向压力梯度的影响.参数$\alpha = u_\tau ^2 / u_{\rm\tau p}^2$可以定量衡量壁面切应力与切向压力梯度的相对大小.模型参数设置为$\kappa = 0.41$,$\beta = 0.78$,$A = 18$20.
引入上述形式的涡黏衰减函数,方程(19)是关于壁面切应力的超越方程.为便于求解,在计算当前时刻的壁面切应力时,右端项的涡黏系数则根据方程(20)利用上一时间步的壁面切应力来计算[19].
上述形式的壁模型最终被简化为代数模型.由该模型计算壁面切应力以重构壁面滑移速度,并由此构建等效体积力,从而实现大涡模拟壁模型与浸入边界方法的结合.
3 结果与讨论
本文分别采用NEB模型$\bigg(S = 1 / \rho \left( {\nabla \bar{P}_{\rm m} \cdot { {{e}}}_{ { \xi }} }\right)\bigg)$以及EB模型($S = 0,\alpha =1)$,在周期山状流和回转体绕流中实现了浸入边界方法与滑移速度壁模型相结合的大涡模拟,并通过不同模型计算结果的对比考查了在构造壁模型时考虑切向压力梯度的作用.
3.1 周期山状流
本文通过周期山状流的大涡模拟考查在壁模型中考虑压力梯度的作用.该流动具有复杂的几何边界,流动沿流向具有压力梯度并且伴随分离、再附等复杂的流动现象,是验证大涡模拟壁模型的标准算例.Breuer等[38] 对该流动进行了详尽的实验和数值模拟研究.他们通过PIV实验对宽广雷诺数范围内的周期山状流进行定量的测量分析,并进一步的采用基于贴体网格的直接数值模拟以及壁面解析的大涡模拟对该雷诺数范围内的流动进行细致的研究.他们的数值和实验对比结果被广泛用作周期山状流数值模拟的参考数据库.本文选择了其中雷诺数最高的一个算例为本文大涡模拟的参考对象.
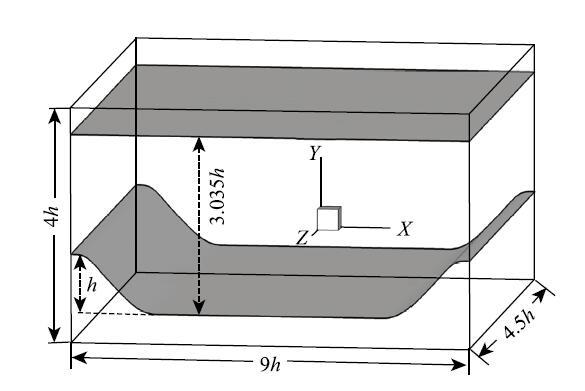
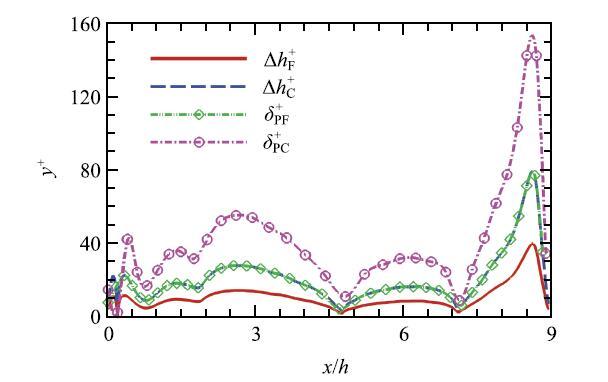
大涡模拟的雷诺数$Re_h = U_{\rm b} h / \nu = 10~595$,其中$U_{b} $和$h$分别为整体流动的平均速度以及山峰高度.图1中给出了周期山状流的几何构型与计算域的示意图,流向、法向和展向的计算域分别为$L_x= 9h$,$L_y = 4h$以及$L_z = 4.5h$.其中,槽道的最大高度为$3.035h$,计算域法向边界的位置根据网格尺度进行调整以保证与欧拉网格不重合.流场的计算在两种不同尺度的均匀笛卡尔网格上进行,其中细网格宽度$\Delta h = h / 32$,该网格尺度与Temmerman 等[39]壁面模化大涡模拟中的近壁贴体网格尺度一致. 粗网格的宽度$\Delta h =h /16$,该算例的总网格量仅为Breuer等[38]壁面解析大涡模拟的5{%}.以壁面单位无量纲化后的欧拉网格尺度以及匹配面的位置沿山状壁面的分布见图2.注意文中匹配面距离壁面的法向距离设置为$\delta _{\rm p} = 2\Delta h$,在粗网格下无量纲化后的匹配面位置最远已经达到$\delta _{\rm p}^+ \approx 160$. 计算过程中的壁模型同时施加在山状流的上、下壁面.流向及展向均设置为周期性边界条件,计算域的法向边界则为自由滑移边界条件.周期山状流采用定流量的方式驱动,即在流场每一瞬时根据入口截面的流量确定相应的压力梯度,并将其施加于全场以驱动流体运动.本文在施加NEB模型时考虑了该驱动力的影响,模型中的压力梯度为流场计算得到的压力梯度与瞬时流场的驱动压力梯度之和.数值模拟中的初始流场发展30个"流过"时间,物理量的统计时间则为50个"流过"时间.
图1 周期山状流的几何构型与计算域示意图
Fig. 1 Schematic illustration of the periodic hills configuration and definition of the computational domain
图2 周期山状流中以壁面单位无量纲化后的欧拉网格尺度以及匹配面的位置沿下壁面的分布.字符"C"和"F"分别代表粗细两种不同的欧拉网格,字符"P"则表示匹配面上的拉格朗日点
Fig. 2 Non-dimensional resolution of the uniform grids and wall-dista- nces of the matching points along the lower wall for the flow over periodic hills. The letters "C" and "F" represent the coarse and fine grids, respectively, and the letter "P" represents the probe point on the matching surface
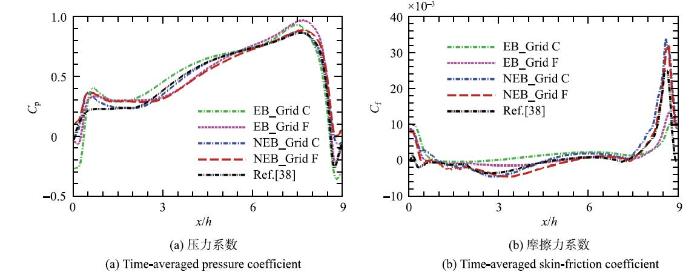
图3中给出了周期山状流下壁面的平均压力系数$C_{\rm p}$和平均摩擦力系数$C_{\rm f} $的分布.从图3(a)中的压力系数分布可以看出,除了在山峰后方的分离泡内(${x /}h <4.5)$产生微小偏差外,两种壁模型的预测结果与参考结果整体吻合,尤其是可以准确地捕捉山峰前方(${x/ }h\! >\! 8.0)$伴随流动加速而形成的顺压梯度.不同形式的壁模型在不同网格上的计算结果基本一致,这说明流场压力的计算结果对本文所采用的壁模型形式并不敏感.而对比图3(b)中关于壁面摩擦力的计算结果则可以发现,同一模型在不同网格上的计算结果已经收敛,但是预测结果的准确性则明显依赖于模型形式.NEB模型的计算结果与参考结果吻合较好,尤其是可以准确捕捉山峰前方(${x/ }h \!>\! 8.0)$伴随强压力梯度而形成的摩擦力峰值.而EB模型的计算结果则整体较为平缓,并且在山峰附近严重低估了摩擦力的峰值.该结果表明在壁模型中考虑切向压力梯度项可以明显的改进壁面切应力的计算结果.
图3 周期山状流下壁面的平均压力系数$C_{\rm p} $和平均摩擦力系数$C_{\rm f} $的分布,其中字符"C"和"F"分别代表粗细两种不同的欧拉网格
Fig. 3 Distribution of the time-averaged (a) pressure and (b) skin-friction coefficients along the lower wall for the flow over periodic hills. Grid "C" and "F" represent the coarse and fine grids, respectively
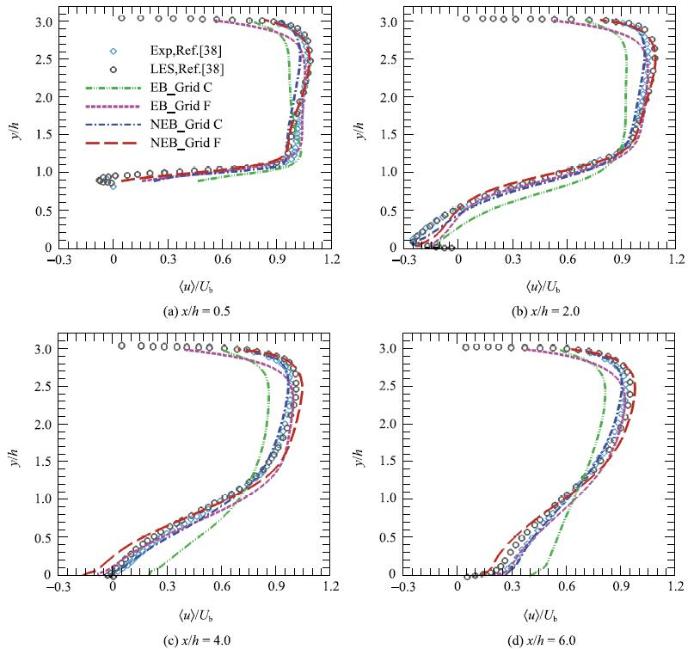
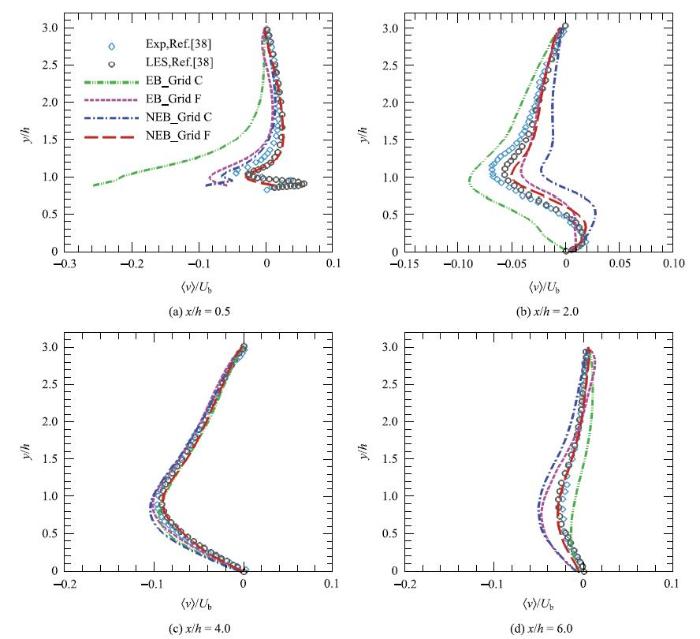
图4中给出了周期山状流不同位置处的流向平均速度剖面的结果.在细网格上,不同形式的壁模型都可以较为准确的预测速度分布.但是NEB模型的计算结果稍微优于EB模型,尤其在靠近上下壁面的区域.NEB模型的优势在粗网格上表现的更为明显.此时,EB模型显著高估了下壁面附近的流向平均速度,同时由于截面等流量的限制高估了上壁面附近的速度.与此相反,NEB模型在粗网格上计算得到的流向平均速度则与细网格上一致并与参考结果非常吻合.
图4 周期山状流不同流向位置处的流向平均速度剖面.其中空心圆及菱形符号分别为Breuer 等[
Fig. 4 The mean streamwise velocity profiles at different locations. The experimental (circles) and wall-resolved LES simulation (diamonds) results by Breuer et al[
图5中给出了不同流向位置处的法向平均速度的分布结果.可以看出,EB模型即使在细网格上的预测结果在分离点附近($x / h =0.5)$以及回流区内($x / h =2.0)$与参考结果呈现出明显的偏差,粗网格上的结果偏离得更加明显.而NEB模型在不同网格上的预测结果趋于收敛,并且即使在粗网格上的计算结果仍然与参考结果吻合.这表明考虑压力梯度的非平衡壁模型可以有效模拟周期山状流分离点附近以及回流区内的平均流动.
图5 周期山状流不同流向位置处的法向平均速度剖面.其中各曲线与符号的代表意义与
Fig. 5 The mean normal velocity profiles at different locations. Symbols and lines labeled as in
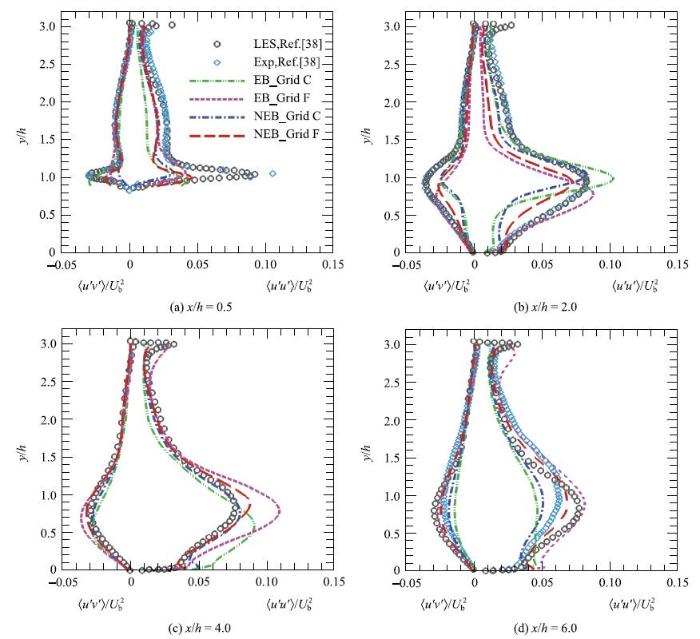
不同流向位置处的流向脉动速度方差以及雷诺切应力的分布见图6.不同形式的壁模型计算得到的结果一致.两种模型均可以准确预测流动附着后($x / h \ge4.0)$的雷诺应力分布,但是在分离点附近($x / h = 0.5)$以及回流区($x/ h =2.0)$的分离泡内均低估了速度脉动以及雷诺切应力,并且随着网格的加密结果并没有明显改善.导致这种差异的一种可能原因是NEB模型中没有考虑对流项的影响.下文回转体绕流的算例中存在类似的现象. Larsson等[6]以及Frere等[40]指出由于压力梯度与对流项同量级,在壁模型中不能仅考虑压力梯度项而忽略对流效应.在NEB模型中考虑对流项的影响可能有助于减少误差.另一个可能的原因是在分离点附近和回流区的涡黏系数已不满足关系式(20).Bose和Moin[41]认为回流区内的速度剖面采用线性函数分布即可.壁模型的计算结果与参考结果在分离点和回流区内的这种差异现象,在Temmerman等[39]基于贴体网格以及Chang等[42]基于浸入边界方法的壁面模化大涡模拟中同样存在.在分离点和回流区的下游,EB模型和NEB模型均可以给出较为准确的结果,这是因为此部分区域的脉动量由剪切层的演化所主导,受壁模型的影响较小.
图6 周期山状流不同流向位置处的流向速度脉动方差及雷诺切应力的剖面.其中各曲线与符号的代表意义与
Fig. 6 The resolved fluctuation of the streamwise velocity and the Reynolds shear stress at different locations. Symbols and lines labeled as in
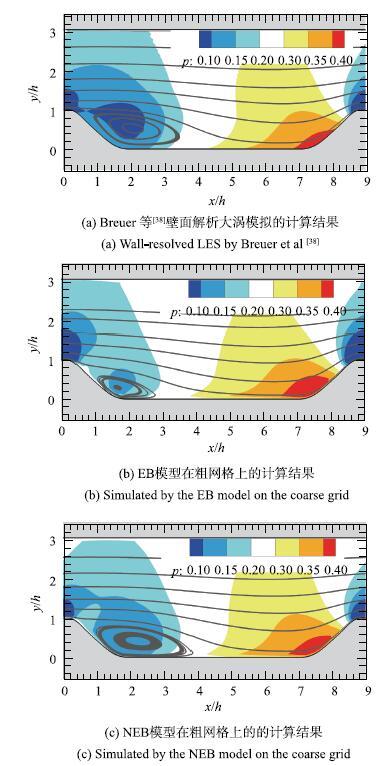
图7中给出了粗网格上不同模型计算得到的平均压力分布以及平均流场的流线图.通过与Breuer等[38]的壁面解析大涡模拟的结果对比可以发现,不同模型均可以较好的预测平均压力的分布.但是EB模型预测的分离泡相对更小且更薄,流动分离的较晚同时再附的较早,而NEB模型在粗网格上的计算结果仍然与参考结果保持一致.
图7 周期山状流的平均压力分布以及平均流动的流线图
Fig. 7 Distribution of pressure and streamlines of the mean flow
通过图3$\sim$图7中与参考结果的对比可以看出计算结果对网格尺度以及模型形式的依赖性.相比于EB模型,NEB模型具有明显优势,尤其在计算壁面摩擦力以及预测流动分离及再附方面.EB模型基于平衡边界层假设,该假设在强压力梯度以及分离区内并不成立.而对于NEB模型,简化薄边界层方程的右端项以及涡黏衰减函数均考虑了切向压力梯度的影响,并将其同时用于计算壁面摩擦力以及重构壁面滑移速度,部分反映了近壁流动的非平衡特性.从壁面滑移速度(式(16))和壁面切应力(式(18))的表达式中可以看出,非平衡壁模型的修正项正比于切向压力梯度$\left({\nabla \bar {P}_{\rm m} \cdot {e}_\xi }\right)$和壁面法向距离$\delta _{\rm P} $.因此在强压力梯度区或者网格较粗时,该模型仍然可以准确的预测流动的水动力特征以及平均统计特性.
3.2 回转体绕流
为检验浸入边界方法结合滑移速度壁模型模拟工程流动的潜力,本文进一步对高雷诺数回转体绕流进行大涡模拟并分析其水动力特性.该流动的几何构型为无附体的DARPA SUBOFF模型[43],是研究潜航器绕流的标准模型之一.
轴对称的艇体结构主要由钝型的艏部、圆柱形的中间艇体以及收缩的舰尾组成,其中艇长$L$与截面最大直径$D$的比例约为$8.6$.
回转体绕流的雷诺数(基于艇身长度$L$以及来流速度$U_\infty)$为$1.2\times 10^6$. 其中大涡模拟计算域(流向$\times $法向$\times $展向)为$\left[ { - 2.6D,23.2D} \right]\times \left[ {-4.3D,4.3D} \right] \times \left[ { - 4.3D,4.3D}\right]$[44]. 计算采用的均匀欧拉网格尺度为$\Delta h = D /32$,对应于艇体平行段流动的无量纲壁面单位约为$\Delta h^ + \approx225$. 该算例的计算网格量仅为相同状态下Posa等[44]全附体回转体绕流壁面解析的大涡模拟的1/50.流动的攻角与偏航角均设置为零.在计算域的入口边界给定均匀的来流速度,出口为对流边界条件,侧面边界则设置为自由滑移边界条件.本文分别采用EB与NEB模型来模化回转体近壁区的流场.
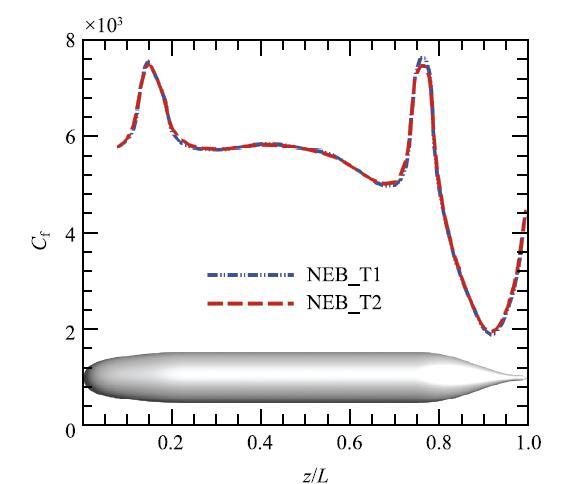
本次计算主要关注钝体绕流的平均水动力特性. 根据Posa等[44]对相同状态下全附体的回转体绕流的壁面解析大涡模拟的研究结果,采用如下方法统计平均值:待流动发展完成后,平均量的统计时长为流动由入口流至出口的时间(对应于流动3次流过艇体的时间),对这种轴对称的流动,统计量的计算同时在时间及周向进行平均.本文测试了不同统计时长对结果的影响,如图8所示.当统计时间为一次流过艇体的时间时,艇体表面的平均摩擦力系数已经收敛,因此本文后继关于平均量的统计结果均基于一次流过艇体的时间计算得到.
图8 NEB模型计算得到的回转体子午线上的平均摩擦系数分布.其中T1的统计时间为流动一次流过计算域的时间,T2为一次流过艇体的时间
Fig. 8 Distributions of the time-averaged skin-friction coefficients at the meridian plane predicted by the NEB model. T1 and T2 are the times of flow past the computational domain and the axisymmetric body, respectively
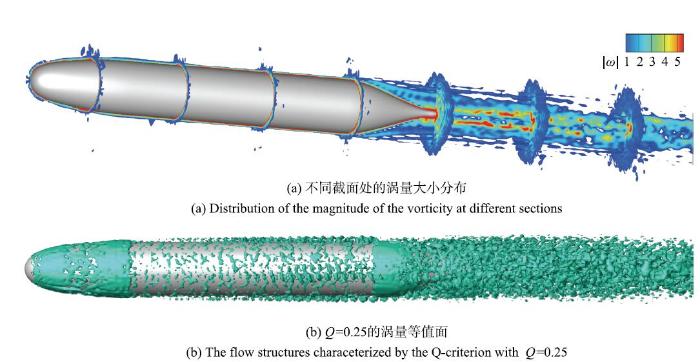
由NEB模型计算得到的瞬时流场结构如图9所示.图9(a)中给出了流向不同截面位置处以及展向中心截面处的涡量大小的分布云图,揭示了附着于回转体表面的边界层向下游发展的演化过程以及流动尾迹结构的特征.流动经由艏部因几何扩张而加速形成湍流边界层,艇体平行段流动近似为平板边界层流动,而尾部流动则由于几何的收缩而发生减速,并导致边界层变厚.展向中心截面上艇体尾部的涡量分布结果表明流动并未发生明显的分离,这与Huang等[45]的实验观测以及Posa等[44]壁面解析的大涡模拟结果一致.边界层在回转体尾部脱出形成亏损的尾迹并使得涡量集中分布于尾迹截面的中心区域.由Q准则显示的小尺度涡结构见图9(b).
图9 由NEB模型计算得到的回转体绕流的瞬时流场结构
Fig. 9 Instantaneous flow structures predicted by the NEB wall model
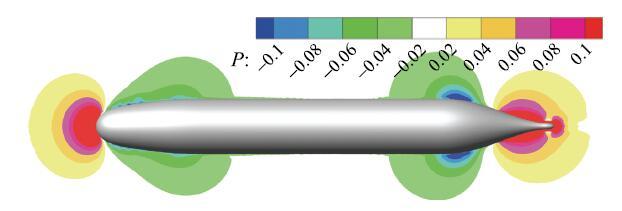
回转体表面边界层流动的演化历程同样可以由图10中心截面上的平均压力分布来揭示.流动在艏部前缘的驻点区形成高压,向后因边界层加速发展对应于压力向下游的递减.平行段的压力近似维持为常数,使得该区域的近壁流动表现出与零压力梯度平板边界层相似的特性.而尾部则由于几何曲率的变化,边界层减速、变厚并形成明显的逆压梯度.
图10 由NEB模型计算得到的回转体绕流中心截面($z = 0)$处的平均压力分布云图
Fig. 10 Instantaneous fields of the mean pressure (predicted by the NEB model) at the symmetric plane ($z = 0)$
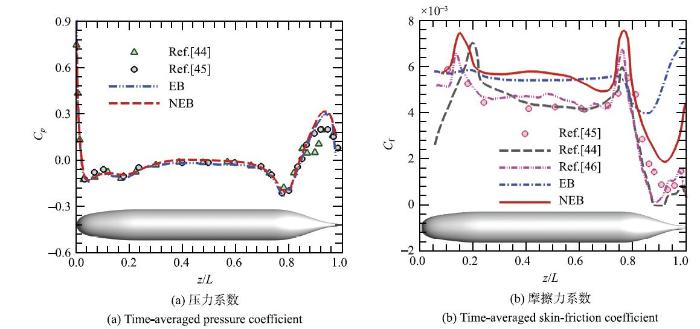
图11中给出了由不同模型计算得到的平均压力系数和摩擦力系数沿壁面子午线的分布.从图11(a)可以看出,两种形式的壁模型均可以准确的预测壁面压力,尤其是能够准确地捕捉回转体艏部及尾部的压力梯度.而对比图11(b)中的计算结果则可以发现两种模型均高估了壁面摩擦力,但是NEB模型的预测结果仍优于EB模型.NEB模型的计算结果与参考结果整体上定性吻合. 尤其是在艏部扩张段($x /D < 0.2)$流动加速的顺压区以及尾部收缩段($x / D>0.75)$流动减速的强逆压梯度区,NEB模型可以较准确地捕捉摩擦力的峰值.而EB模型计算得到的摩擦力系数曲线沿艇体变化比较缓慢,在强压力梯度区的预测结果与参考结果呈现出明显的偏差并且未能捕捉到尾部收缩段摩擦力的峰值.两种形式的壁模型均可以准确的计算压力分布,而非平衡壁模型则可以改进壁面摩擦力的计算结果,这与在周期山状流中观察到的现象一致.
图11 回转体绕流中心截面子午线上的平均压力系数$C_{\rm p} $和平均摩擦力系数$C_{\rm f} $的分布
Fig. 11 Distribution of the time-averaged (a) pressure and (b) skin-friction coefficients at the meridian plane
图11(b)中同样给出了直接基于壁面应力构造等效体积力的模拟方法计算结果[46].可以看出,该方法可以更准确地预测壁面切应力.值得注意的是,该方法采用与滑移速度壁模型相同的方式计算壁面切应力,区别在于与浸入边界方法相结合的方式.滑移速度壁模型通过壁面切应力重构切向滑移速度,法向速度则满足壁面无穿透条件,然后以此构建壁面上的等效体积力.而在直接由壁面切应力构建等效体积力的方法中,壁面切应力直接转化为体积力的形式施加在壁面外附近的代理层上,并隐含了法向速度的影响.根据Bae等[47]的研究工作,法向穿透速度有助于改善流场脉动量的计算结果.另外,在近壁区流动的模型方程中,仅考虑切向压力梯度所引起的非平衡效应.Larsson等[6]以及Frere等[40]则指出,由于压力梯度项与对流项近似平衡,因此薄边界层方程中的压力梯度项与对流项必须同时考虑或忽略.本文下一步的工作将综合考虑上述因素,并对回转体绕流的水动力学特性以及流场尾迹结构特征进行更细致的研究.
4 总结与结论
本文采用滑移速度壁模型构建等效体积力,实现了浸入边界方法与壁模型相结合的大涡模拟.分别采用平衡层模型以及考虑切向压力梯度的非平衡壁模型,在周期山状流以及回转体绕流中对比考查了在壁模型中考虑压力梯度的作用.
本文首先在雷诺数为$10~595$的周期山状流中检验了两种壁模型模拟复杂几何边界的湍流分离流动的能力.数值结果表明,流场压力对壁模型的形式并不敏感,但是考虑切向压力梯度可以显著改进壁面摩擦力的计算结果,并且能够准确的预测强压力梯度区以及分离区内流动的平均统计特性.由于平衡边界层假设在强压力梯度以及分离区内并不成立,平衡层模型显著低估了壁面摩擦力,并且难以准确预测该区域内的平均速度剖面.非平衡壁模型在薄边界层方程中考虑了切向压力梯度的影响.在重构壁面滑移速度和计算壁面切应力时的修正项正比于压力梯度和壁面法向距离.因此在流动的强压力梯度区以及网格较粗时,计算得到的平均压力以及摩擦力分布、平均速度剖面以及脉动统计量均与参考的实验和计算结果吻合.在此基础上,本文对雷诺数为$1.2\times10^6$的回转体绕流进行大涡模拟,以考查该方法应用于高雷诺数壁湍流的适用性.非平衡壁模型可以准确的捕捉典型的流动结构,壁面压力的计算结果与参考结果吻合.与平衡层模型相比,可以更好地预测壁面摩擦力沿艇体的分布,尤其是能够捕捉到艇体尾部的摩擦力峰值.该结果再次证明在壁模型中考虑压力梯度可以改进壁面摩擦力的计算结果.
本文工作表明,将浸入边界方法与考虑压力梯度的大涡模拟非平衡壁模型相结合,有望提升其模拟具有复杂几何边界的高雷诺数壁湍流的能力,并且在降低计算量的同时预测流动的平均统计特性.
The authors have declared that no competing interests exist.
参考文献
| [1] |
飞机尾涡演变及快速预测的大涡模拟研究 .
随着我国人民生活水平的提高,航空运输的重要性与日俱增,航班延误问题也日益严重.尾流间隔(保障后机不受前机尾流影响的最小安全间隔)是制约机场效率的关键因素.针对这一工程应用问题,采用大涡模拟方法研究飞机尾涡在大气中的演变特性.研究工作首先发展了飞机尾涡演变的大涡模拟方法,将自适应网格技术应用于飞机尾涡演变的大涡模拟,大幅减少所需的网格量,提高计算效率.提出了升力面尾涡生成方法,在不增加计算量的情况下实现了尾涡卷起过程和远场衰减的组合模拟.在系列算例分析研究基础上,创建了基于大涡模拟计算结果的尾流间隔快速预测系统.该系统可以根据实时大气风场和进出港的前后飞机机型,快速预测并输出所需的尾流间隔.经过与场地测试数据比较表明,在北京市2014年的平均风速条件下,本系统预测的尾流间隔可在现有标准基础上缩减7%~50%,能够有效提高机场容量.
Large eddy simulation on the evolution and the fast-time prediction of aircraft wake vortices .
随着我国人民生活水平的提高,航空运输的重要性与日俱增,航班延误问题也日益严重.尾流间隔(保障后机不受前机尾流影响的最小安全间隔)是制约机场效率的关键因素.针对这一工程应用问题,采用大涡模拟方法研究飞机尾涡在大气中的演变特性.研究工作首先发展了飞机尾涡演变的大涡模拟方法,将自适应网格技术应用于飞机尾涡演变的大涡模拟,大幅减少所需的网格量,提高计算效率.提出了升力面尾涡生成方法,在不增加计算量的情况下实现了尾涡卷起过程和远场衰减的组合模拟.在系列算例分析研究基础上,创建了基于大涡模拟计算结果的尾流间隔快速预测系统.该系统可以根据实时大气风场和进出港的前后飞机机型,快速预测并输出所需的尾流间隔.经过与场地测试数据比较表明,在北京市2014年的平均风速条件下,本系统预测的尾流间隔可在现有标准基础上缩减7%~50%,能够有效提高机场容量.
|
| [2] |
高亚声速湍流喷流气动噪声数值分析 .
<p>为适应航空噪声管制规定要求,发动机喷流噪声控制成为目前气动声学研究中的重要课题,预测分析喷流噪声辐射并揭示其产生机理将为噪声控制奠定基础.采用高精度并行LES(large eddy simulation)方法计算分析马赫数0.9高亚声速喷流的湍流演化和气动噪声现象.首先,仔细验证喷流LES湍流场计算保真性,并分析流场中不同尺度涡结构的演化形态.其次,利用可穿透面FW-H(Ffowcs Williams and Hawkings)方法外推喷流近场声源数据获得精确声辐射远场,进而分析声场主导声模态特性.最后,通过分析声源机制、分离声模态等方法研究势流核末端大尺度拟序涡运动演化形成的低波数波包在噪声主导声模态产生中的重要作用.数值结果表明LES结合可穿透面FW-H方法可精确预测高亚声速喷流的流场及声场特征,且数值分析揭示涡环对并形成的大尺度拟序结构在喷流中心线上沿径向融合,产生了在远场低方位角占优的主导声模态,并构成强指向性声场,噪声峰值方位角约为30°.</p>
Numerical investigation of noise of a high subsonic turbulent jet .
<p>为适应航空噪声管制规定要求,发动机喷流噪声控制成为目前气动声学研究中的重要课题,预测分析喷流噪声辐射并揭示其产生机理将为噪声控制奠定基础.采用高精度并行LES(large eddy simulation)方法计算分析马赫数0.9高亚声速喷流的湍流演化和气动噪声现象.首先,仔细验证喷流LES湍流场计算保真性,并分析流场中不同尺度涡结构的演化形态.其次,利用可穿透面FW-H(Ffowcs Williams and Hawkings)方法外推喷流近场声源数据获得精确声辐射远场,进而分析声场主导声模态特性.最后,通过分析声源机制、分离声模态等方法研究势流核末端大尺度拟序涡运动演化形成的低波数波包在噪声主导声模态产生中的重要作用.数值结果表明LES结合可穿透面FW-H方法可精确预测高亚声速喷流的流场及声场特征,且数值分析揭示涡环对并形成的大尺度拟序结构在喷流中心线上沿径向融合,产生了在远场低方位角占优的主导声模态,并构成强指向性声场,噪声峰值方位角约为30°.</p>
|
| [3] |
大涡模拟在内燃机中应用的研究进展 .
<p>大涡模拟 能够以比较合理的计算成本, 提供更多详细的湍流信息, 故近年来已经广泛地应用于科学和工程领域, 并也成为内燃机缸内湍流流动与燃烧过程模拟计算的最有潜力的数值方法.综合现有研究成果, 对内燃机中大涡模拟的研究进展和模拟方法进行了比较全面的评述.介绍了大涡模拟的基本概念、方法、亚网格模型,着重讨论了内燃机缸内冷态流场、燃油喷雾过程以及两相液雾湍流燃烧大涡模拟的国内外研究进展.最后论述了大涡模拟在内燃机应用中当前需要解决的问题及其发展趋势.</p>
Large eddy simulation for internal combustion engines: progress and prospects .
<p>大涡模拟 能够以比较合理的计算成本, 提供更多详细的湍流信息, 故近年来已经广泛地应用于科学和工程领域, 并也成为内燃机缸内湍流流动与燃烧过程模拟计算的最有潜力的数值方法.综合现有研究成果, 对内燃机中大涡模拟的研究进展和模拟方法进行了比较全面的评述.介绍了大涡模拟的基本概念、方法、亚网格模型,着重讨论了内燃机缸内冷态流场、燃油喷雾过程以及两相液雾湍流燃烧大涡模拟的国内外研究进展.最后论述了大涡模拟在内燃机应用中当前需要解决的问题及其发展趋势.</p>
|
| [4] |
高速列车头型长细比对气动噪声的影响 .
高速列车的头尾车外形对气动噪声具有重要的影响.工程实践中随着车速的增加,车辆头部越来越细长,日本高速磁悬浮列车实践中甚至出现了具有极端长细比的头部形状.本文以讨论头型长细比对列车气动噪声的影响规律为出发点,应用非线性声学求解器(NLAS)和FW–H声学比拟法的混合算法,在3种运行速度下对基于CRH380A高速列车头型概化的4种不同头型长细比的模型车的气动噪声进行了数值模拟.给出了不同头型长细比列车的流场特征、气动阻力和气动噪声.结果表明,列车的气动总阻力随头型长细比的增大而减小,且头型长细比对列车总气动阻力的影响随运行速度的增加而增强.而头型长细比对气动噪声的影响呈现出较为复杂的影响,并不存在单调的影响关系;综合考虑气动阻力和气动噪声,长细比最大的头型综合性能较优,但差异并不显著,因此在不考虑微气压波等因素的条件下,简单增加车头长细比并不一定能带来明显的气动噪声性能提升.
Study on the influence of the slenderness ratio of high-speed train on the aerodynamic noise .
高速列车的头尾车外形对气动噪声具有重要的影响.工程实践中随着车速的增加,车辆头部越来越细长,日本高速磁悬浮列车实践中甚至出现了具有极端长细比的头部形状.本文以讨论头型长细比对列车气动噪声的影响规律为出发点,应用非线性声学求解器(NLAS)和FW–H声学比拟法的混合算法,在3种运行速度下对基于CRH380A高速列车头型概化的4种不同头型长细比的模型车的气动噪声进行了数值模拟.给出了不同头型长细比列车的流场特征、气动阻力和气动噪声.结果表明,列车的气动总阻力随头型长细比的增大而减小,且头型长细比对列车总气动阻力的影响随运行速度的增加而增强.而头型长细比对气动噪声的影响呈现出较为复杂的影响,并不存在单调的影响关系;综合考虑气动阻力和气动噪声,长细比最大的头型综合性能较优,但差异并不显著,因此在不考虑微气压波等因素的条件下,简单增加车头长细比并不一定能带来明显的气动噪声性能提升.
|
| [5] |
Grid-point requirements for large eddy simulation: Chapman's estimates revisited .
Resolution requirements for large eddy simulation (LES), estimated by Chapman [AIAA J. Vol. 17, p. 1293 (1979)], are modified using accurate formulae for high Reynolds number boundary layer flow. This correction indicates that the number of grid points (N) required for wall-modeled LES is proportional to Re/ 7 , but a wall-resolving LES requires N ~Re3 / 7 , where L is the flat-plate length in the streamwise direction. The number of grid points required for the flow over an aircraft using LES with and without modeling the viscous wall region is estimated: the number of grid points for the wall-modeled LES is one to three orders of magnitude smaller than that for the wall-resolving LES, indicating the practical importance of wall modeling in LES for high Reynolds number flows.
|
| [6] |
Large eddy simulation with modeled wall-stress: recent progress and future directions . |
| [7] |
采用RANS/LES混合方法研究分离流动 .
采用结合湍流模式和大涡模拟(LES)的混合方法数值模拟Aerospatial A-profile翼型以及细长椭球体大迎角分离流动.该类混合方法比较适于模拟分离流动:近壁区附体流动采用湍流模式,而远离物面分离区域内的大尺度运动则用LES方法.通过计算和实验结果的对比,混合方法切实可行并具有很大的发展潜力.
Simulation of separation flows with RANS/LES hybrid methods .
采用结合湍流模式和大涡模拟(LES)的混合方法数值模拟Aerospatial A-profile翼型以及细长椭球体大迎角分离流动.该类混合方法比较适于模拟分离流动:近壁区附体流动采用湍流模式,而远离物面分离区域内的大尺度运动则用LES方法.通过计算和实验结果的对比,混合方法切实可行并具有很大的发展潜力.
|
| [8] |
Wall-layer models for large-eddy simulations . |
| [9] |
Wall-layer models for large-eddy simulations .
The numerical simulation of high Reynolds number flows is hampered by model accuracy if the Reynolds-averaged Navier鈥揝tokes (RANS) equations are used, and by computational cost if direct or large-eddy simulations (LES) that resolve the near-wall layer are employed. The cost of a calculation scales like the Reynolds number to the power 3 for direct numerical simulations, or 2.4 for LES, making the resolution of the wall layer at high Reynolds number infeasible even with the most advanced computers. In LES, an attractive alternative to compute high- flows is the use of wall-layer models, in which only the outer layer is resolved, while the near-wall region is modeled. Three broad classes of approaches are presently used: bypassing this region altogether using wall functions, solving a separate set of equations in the near-wall region, weakly coupled to the outer flow, or simulating the near-wall region in a global, Reynolds-averaged, sense. These approaches are discussed and their ranges of applicability are highlighted. Various unresolved issues in wall-layer modeling are presented.
|
| [10] |
Wall-modeled large-eddy simulation for complex turbulent flows .
This paper focuses on numerical and practical aspects associated with a parallel implementation of a two-layer zonal wall model for large-eddy simulation (LES) of compressible wall-bounded turbulent flows on unstructured meshes. A zonal wall model based on the solution of unsteady three-dimensional Reynolds-averaged Navier–Stokes (RANS) equations on a separate near-wall grid is implemented in... [Show full abstract]
|
| [11] |
Aeroacoustic prediction of a multi-element airfoil using wall-modeled large-eddy simulation .
react-text: 324 Engineers charged with making jet aircraft quieter have long dreamed of being able to see exactly how turbulent eddies produce sound, and this dream is now coming true with the advent of large-eddy simulation. Two obvious challenges remain: validating the large-eddy-simulation codes at the resolution required to see the fluid-acoustic coupling, and the interpretation of the massive data sets... /react-text react-text: 325 /react-text [Show full abstract]
|
| [12] |
Reynolds-stress-constrained large-eddy simulation of wall-bounded turbulent flows .
In the traditional hybrid RANS/LES approaches for the simulation of wall-bounded fluid turbulence, such as detached-eddy simulation (DES), the whole flow domain is divided into an inner layer and an outer layer. Typically the Reynolds-averaged Navier鈥揝tokes (RANS) equations are used for the inner layer, while large-eddy simulation (LES) is used for the outer layer. The transition from the inner-layer solution to the outer-layer solution is often problematic due to the lack of small-scale dynamics in the RANS region. In this paper, we propose to simulate the whole flow domain by large-eddy simulation while enforcing a Reynolds-stress constraint on the subgrid-scale (SGS) stress model in the inner layer. Both the algebraic eddy-viscosity model and the one-equation Spalart鈥揂llmaras (SA) model have been used to constrain the Reynolds stress in the inner layer. In this way, we improve the LES methodology by allowing the mean flow of the inner layer to satisfy the RANS solution while small-scale dynamics is included. We validate the Reynolds-stress-constrained large-eddy simulation (RSC-LES) model by simulating three-dimensional turbulent channel flow and flow past a circular cylinder. Our model is able to predict mean velocity, turbulent stress and skin-friction coefficients more accurately in turbulent channel flow and to estimate the pressure coefficient after separation more precisely in flow past a circular cylinder compared with the pure dynamic Smagorinsky model (DSM) and DES using the same grid resolution. Furthermore, the computational cost of the RSC-LES is almost the same as that of DES.
|
| [13] |
近壁湍流的降阶模型及其应用 .
由条带和流向涡的循环再生构成的近壁自维持过程(self-sustaining process,SSP)是壁湍流产生和维持的重要机制.文章通过对最小槽道的直接数值模拟(direct numerical simulation,DNS)获得近壁自维持过程的流场数据,采用正规正交分解法(proper orthogonal decomposition,POD)对该数据进行分析,获得了不同流向和展向尺度的特征模态,通过将Navier-Stokes方程在这些模态上进行投影,得到近壁自维持过程的降阶模型,并采用DNS数据对降阶模型的预测能力进行了评价.该模型被初步应用于大涡模拟近壁模型的构造.
Reduced-order model for near-wall turbulence and its application .
由条带和流向涡的循环再生构成的近壁自维持过程(self-sustaining process,SSP)是壁湍流产生和维持的重要机制.文章通过对最小槽道的直接数值模拟(direct numerical simulation,DNS)获得近壁自维持过程的流场数据,采用正规正交分解法(proper orthogonal decomposition,POD)对该数据进行分析,获得了不同流向和展向尺度的特征模态,通过将Navier-Stokes方程在这些模态上进行投影,得到近壁自维持过程的降阶模型,并采用DNS数据对降阶模型的预测能力进行了评价.该模型被初步应用于大涡模拟近壁模型的构造.
|
| [14] |
|
| [15] |
湍流大涡数值模拟进展 .
本文简要陈述湍流大涡数值模拟的原理、优点,着重讨论湍流大涡数值模拟方法的关键问题及其可能解决的途径,包括脉动的过滤、亚格子模型、近壁模型和标量湍流的大涡数值模拟中的特殊问题.文章强调大涡数值模拟中亚格子应力的本质是可解尺度湍流和不可解尺度湍流动量间的输运,并以作者最近提出的新型亚格子模型说明发展亚格子模型的正确途径.文章最后提出湍流大涡数值模拟近期需要迫切解决的问题和其他具有挑战性的方向.
Progress in large eddy simulation of turbulent flows .
本文简要陈述湍流大涡数值模拟的原理、优点,着重讨论湍流大涡数值模拟方法的关键问题及其可能解决的途径,包括脉动的过滤、亚格子模型、近壁模型和标量湍流的大涡数值模拟中的特殊问题.文章强调大涡数值模拟中亚格子应力的本质是可解尺度湍流和不可解尺度湍流动量间的输运,并以作者最近提出的新型亚格子模型说明发展亚格子模型的正确途径.文章最后提出湍流大涡数值模拟近期需要迫切解决的问题和其他具有挑战性的方向.
|
| [16] |
大涡模拟的壁模型及其应用 .
大涡模拟是研究湍流的非定常特性的重要方法.但解析壁面层的大涡模拟所需的计算量与直接数值模拟相当,是大涡模拟在高雷诺数壁湍流数值模拟中所面临的主要困难.解析壁面层所需的网格尺度与壁面黏性长度同量级,是引起壁湍流大涡模拟计算量增加的主要原因.壁模型通过模化近壁流动避免了完全解析壁面层,可以显著地降低壁湍流大涡模拟的计算量,是克服上述困难的有效方法.本文介绍了大涡模拟壁模型的主要类型;详细讨论了常用的壁面应力模型,特别是平衡层模型和双层模型的构建思路和特点;基于近壁流动的特征讨论了应力边界条件的必要性和适用性;指出了壁面应力模型的局限性以及考虑非平衡效应修正的各种方法;讨论了壁面应力模型的研究历史、最新进展和发展趋势,给出了常用的壁面应力模型的分支与发展关系图;并基于Werner-Wengle模型实现了周期山状流的大涡模拟.
Wall-model for large-eddy simulation and its applications .
大涡模拟是研究湍流的非定常特性的重要方法.但解析壁面层的大涡模拟所需的计算量与直接数值模拟相当,是大涡模拟在高雷诺数壁湍流数值模拟中所面临的主要困难.解析壁面层所需的网格尺度与壁面黏性长度同量级,是引起壁湍流大涡模拟计算量增加的主要原因.壁模型通过模化近壁流动避免了完全解析壁面层,可以显著地降低壁湍流大涡模拟的计算量,是克服上述困难的有效方法.本文介绍了大涡模拟壁模型的主要类型;详细讨论了常用的壁面应力模型,特别是平衡层模型和双层模型的构建思路和特点;基于近壁流动的特征讨论了应力边界条件的必要性和适用性;指出了壁面应力模型的局限性以及考虑非平衡效应修正的各种方法;讨论了壁面应力模型的研究历史、最新进展和发展趋势,给出了常用的壁面应力模型的分支与发展关系图;并基于Werner-Wengle模型实现了周期山状流的大涡模拟.
|
| [17] |
Approximate wall boundary conditions in the large-eddy simulation of high Reynolds number flow. Flow,
The near-wall regions of high Reynolds numbers turbulent flows must be modelled to treat many practical engineering and aeronautical applications. In this review we examine results from simulations of both attached and separated flows on coarse grids in which the near-wall regions are not resolved and are instead represented by approximate wall boundary conditions. The simulations use the dynamic Smagorinsky subgrid-scale model and a second-order finite-difference method. Typical results are found to be mixed, with acceptable results found in many cases in the core of the flow far from the walls, provided there is adequate numerical resolution, but with poorer results generally found near the wall. Deficiencies in this approach are caused in part by both inaccuracies in subgrid-scale modelling and numerical errors in the low-order finite-difference method on coarse near-wall grids, which should be taken into account when constructing models and performing large-eddy simulation on coarse grids. A promising new method for developing wall models from optimal control theory is also discussed.
|
| [18] |
Two-layer approximate boundary conditions for large-eddy simulations .
Abstract A new method to model the effect of the solid boundaries on the rest of the flowfield in large-eddy simulations is proposed. The filtered Navier-Stokes equations are solved up to the first computational point. From there to the wall, a simplified set of equations is solved, and an estimate of the instantaneous wall shear stress required to impose boundary conditions is obtained. Computations performed for the plane channel, square duct, and the rotating channel flow cases gave improved results compared with existing models. The additional computing time required by the model is on the order of 10-15% of the overall computing time. The mean flow quantities and low-order statistics, which are of primary interest in engineering calculations, are in very good agreement with the reference data available in the literature.
|
| [19] |
Dynamic wall modeling for large-eddy simulation of complex turbulent flows .
The efficacy of large-eddy simulation (LES) with wall modeling for complex turbulent flows is assessed by considering turbulent boundary-layer flows past an asymmetric trailing-edge. Wall models based on turbulent boundary-layer equations and their simpler variants are employed to compute the instantaneous wall shear stress, which is used as approximate boundary conditions for the LES. It is demonstrated that, as first noted by Cabot and Moin [Flow Turb. Combust.63, 269 (2000)], when a Reynolds-averaged Navier鈥揝tokes type eddy viscosity is used in the wall-layer equations with nonlinear convective terms, its value must be reduced to account for only the unresolved part of the Reynolds stress. A dynamically adjusted mixing-length eddy viscosity is used in the turbulent boundary-layer equation model, which is shown to be considerably more accurate than the simpler wall models based on the instantaneous log law. This method predicts low-order velocity statistics in good agreement with those from the full LES with resolved wall-layers, at a small fraction of the original computational cost. In particular, the unsteady separation near the trailing-edge is captured correctly, and the prediction of surface pressure fluctuations also shows promise.
|
| [20] |
A wall-layer model for large eddy simulations of turbulent flow with/out pressure gradient .
In this work, modeling of the near-wall region in turbulent flows is addressed. A new wall-layer model is proposed with the goal to perform high-Reynolds number large-eddy simulations of wall bounded flows in the presence of a streamwise pressure gradient. The model applies both in the viscous sublayer and in the inertial region, without any parameter to switch from one region to the other. An analytical expression for the velocity field as a function of the distance from the wall is derived from the simplified thin-boundary equations and by using a turbulent eddy coefficient with a damping function. This damping function relies on a modified van Driest formula to define the mixing-length taking into account the presence of a streamwise pressure gradient. The model is first validated by a priori comparisons with direct numerical simulation data of various flows with and without streamwise pressure gradient and with eventual flow separation. Large-eddy simulations are then performed using the present wall model as wall boundary condition. A plane channel flow and the flow over a periodic arrangement of hills are successively considered. The present model predictions are compared with those obtained using the wall models previously proposed by Spalding, Trans. ASME, J. Appl. Mech 28, 243 (2008) and Manhart et al., Theor. Comput. Fluid Dyn. 22, 243 (2008) . It is shown that the new wall model allows for a good prediction of the mean velocity profile both with and without streamwise pressure gradient. It is shown than, conversely to the previous models, the present model is able to predict flow separation even when a very coarse grid is used.
|
| [21] |
Immersed boundary methods . |
| [22] |
Immersed boundary methods for simulating fluid-structure interaction .
Fluid鈥搒tructure interaction (FSI) problems commonly encountered in engineering and biological applications involve geometrically complex flexible or rigid bodies undergoing large deformations. Immersed boundary (IB) methods have emerged as a powerful simulation tool for tackling such flows due to their inherent ability to handle arbitrarily complex bodies without the need for expensive and cumbersome dynamic re-meshing strategies. Depending on the approach such methods adopt to satisfy boundary conditions on solid surfaces they can be broadly classified as diffused and sharp interface methods. In this review, we present an overview of the fundamentals of both classes of methods with emphasis on solution algorithms for simulating FSI problems. We summarize and juxtapose different IB approaches for imposing boundary conditions, efficient iterative algorithms for solving the incompressible Navier鈥揝tokes equations in the presence of dynamic immersed boundaries, and strong and loose coupling FSI strategies. We also present recent results from the application of such methods to study a wide range of problems, including vortex-induced vibrations, aquatic swimming, insect flying, human walking and renewable energy. Limitations of such methods and the need for future research to mitigate them are also discussed.
|
| [23] |
A coupled FDM-FEM method for free surface flow interaction with thin elastic plate .
AbstractA partitioned approach by the coupling finite difference method (FDM) and the finite element method (FEM) is developed for simulating the interaction between free surface flow and a thin elastic plate. The FDM, in which the constraint interpolation profile method is applied, is used for solving the flow field in a regular fixed Cartesian grid, and the tangent of the hyperbola for interface capturing with the slope weighting scheme is used for capturing free surface. The FEM is used for solving structural deformation of the thin plate. A conservative momentum-exchange method, based on the immersed boundary method, is adopted to couple the FDM and the FEM. Background grid resolution of the thin plate in a regular fixed Cartesian grid is important to the computational accuracy by using this method. A virtual structure method is proposed to improve the background grid resolution of the thin plate. Both of the flow solver and the structural solver are carefully tested and extensive validations of the coupled FDM鈥揊EM method are carried out on a benchmark experiment, a rolling tank sloshing with a thin elastic plate.
|
| [24] |
An embedded-boundary formulation or large-eddy simulation of turbulent flows interacting with moving boundaries .
A non-boundary-conforming formulation for simulating complex turbulent flows with dynamically moving boundaries on fixed Cartesian grids is proposed. The underlying finite-difference solver for the filtered incompressible Navier鈥揝tokes equations is based on a second-order fractional step method on a staggered grid. To satisfy the boundary conditions on an arbitrary immersed interface, the velocity field at the grid points near the interface is reconstructed using momentum forcing without smearing the sharp interface. The concept of field-extension is also introduced to treat the points emerging from a moving solid body to the fluid. Laminar flow cases and large-eddy simulations (LES) are presented to demonstrate the formal accuracy and range of applicability of the method. In particular, simulations of laminar flow induced by the harmonic in-line oscillation of a circular cylinder in quiescent fluid, and from a transversely oscillating cylinder in a free-stream are presented and compared to reference simulations and experiments. LES of turbulent flow over a traveling wavy wall and transitional flow through a bileaflet prosthetic heart valve are also shown. All results are in very good agreement with reference results in the literature.
|
| [25] |
A ghost-cell immersed boundary method for large eddy simulation of flows in complex geometries .
An efficient ghost-cell immersed boundary (IB) method is proposed for large eddy simulations of three-dimensional incompressible flow in complex geometries. In the framework of finite volume method, the Navier芒聙聯Stokes equations are integrated using an explicit time advancement scheme on a collocated mesh. Since the IB method is known to generate an unphysical velocity field inside the IB that violates the mass conservation of the cells near the IB, a new IB treatment is devised to eliminate the unphysical velocity generated near the IB and to improve the pressure distribution on the body surface. To validate the proposed method, both laminar and turbulent flow cases are presented. In particular, large eddy simulations were performed to simulate the turbulent flows over a circular cylinder and a sphere at subcritical Reynolds numbers. The computed results show good agreements with the published numerical and experimental data.
|
| [26] |
Combined immersed boundary/ large-eddy-simulations of in compressible three dimensional complex flows.
In this paper we show how the Immersed Boundary (IB) method can be used with the Large-Eddy-Simulation (LES) to compute moderately high Reynolds number flows in complex geometric configurations. The resulting combination gives an easy-to-use, inexpensive and accurate technique which can be an important step towards the application of computational fluid dynamics (CFD) to industrially relevant problems. This paper aims at describing the main features of the method, some of the important drawbacks and possible solutions. Several representative examples are discussed in order to show the flexibility and the range of the applicability of this technique.
|
| [27] |
A simple wall-layer model for large eddy simulation with immersed boundary method .
A wall-layer model is proposed for large eddy simulation of high Reynolds number turbulent flows in conjunction with immersed boundaries. The model is based on two main steps: the reconstruction of the velocity field at the first grid point off the immersed body and the modelization of the actual wall shear stress at the immersed boundary through imposition of a Reynolds averaged Navier鈥揝tokes-like eddy viscosity obtained by means of analytical considerations. The model is tested in a turbulent plane channel flow with walls reproduced by immersed boundaries considering both Cartesian and curvilinear grids. Even with coarse and distorted grids the proposed methodology is able to reproduce accurately both first- and second-order turbulent statistics.
|
| [28] |
Wall modeling for large-eddy simulation using an immersed boundary method. |
| [29] |
An immersed boundary method for complex incompressible flows .
An immersed boundary method for time-dependent, three-dimensional, incompressible flows is presented in this paper. The incompressible Navier鈥揝tokes equations are discretized using a low-diffusion flux splitting method for the inviscid fluxes and second-order central-differences for the viscous components. Higher-order accuracy achieved by using weighted essentially non-oscillatory (WENO) or total variation diminishing (TVD) schemes. An implicit method based on artificial compressibility and dual-time stepping is used for time advancement. The immersed boundary surfaces are defined as clouds of points, which may be structured or unstructured. Immersed-boundary objects are rendered as level sets in the computational domain, and concepts from computational geometry are used to classify points as being outside, near, or inside the immersed boundary. The velocity field near an immersed surface is determined from separate interpolations of the components tangent and normal to the surface. The tangential velocity near the surface is constructed as a power-law function of the local wall normal distance. Appropriate choices of the power law enable the method to approximate the energizing effects of a turbulent boundary layer for higher Reynolds number flows. Five different flow problems (flow over a circular cylinder, an in-line oscillating cylinder, a NACA0012 airfoil, a sphere, and a stationary mannequin) are simulated using the present immersed boundary method, and the predictions show good agreement with previous computational and experimental results. Finally, the flow induced by realistic human walking motion is simulated as an example of a problem involving multiple moving immersed objects.
|
| [30] |
A novel iterative direct-forcing immersed boundary method and its finite volume applications .
We present a novel iterative immersed boundary (IB) method in which the body force updating is incorporated into the pressure iterations. Because the body force and pressure are solved simultaneously, the boundary condition on the immersed boundary can be fully verified. The computational costs of this iterative IB method is comparable to those of conventional IB methods. We also introduce an improved body force distribution function which transfers the body force in the discrete volume of IB points to surrounding Cartesian grids totally. To alleviate the demanding computational requirements of a full-resolved direct numerical simulation, a wall-layer model is presented. The accuracy and capability of the present method is verified by a variety of two- and three-dimensional numerical simulations, ranging from laminar flow past a cylinder and a sphere to turbulent flow around a cylinder. The improvement of the iterative IB method is fully demonstrated and the influences of different body force distribution strategies is discussed.
|
| [31] |
|
| [32] |
Subgrid-scale stress modelling based on the square of the velocity gradient tensor.
A new subgrid scale model is proposed for Large Eddy Simulations in complex geometries. This model which is based on the square of the velocity gradient tensor accounts for the effects of both the strain and the rotation rate of the smallest resolved turbulent fluctuations. Moreover it recovers the proper y 3 near-wall scaling for the eddy viscosity without requiring dynamic procedure. It is also shown from a periodic turbulent pipe flow computation that the model can handle transition.
|
| [33] |
A hydrodynamic stress model for simulating turbulence/particle interactions with immersed boundary methods . |
| [34] |
Direct and Large-Eddy Simulation X .
Reflects the state of the art of numerical simulation of transitional and turbulent flows and provides a forum for discussion of developments in simulation techniques and understanding of flow physics.
|
| [35] |
Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations .
In the present study a methodology to perform large-eddy simulations around complex boundaries on fixed Cartesian grids is presented. A novel interpolation scheme which is applicable to boundaries of arbitrary shape, does not involve special treatments, and allows the accurate imposition of the desired boundary conditions is introduced. A method to overcome the problems associated with the computation of the subgrid scale terms near solid boundaries is also discussed. A detailed study on the accuracy and efficiency of the method is carried out for the cases of Stokes flow around a cylinder in the vicinity of a moving plate, the three-dimensional flow around a circular cylinder, and fully developed turbulent flow in a plane channel with a wavy wall. It is demonstrated that the method is second-order accurate, and that the solid boundaries are mimicked “exactly” on the Cartesian grid within the overall accuracy of the scheme. For all cases under consideration the results obtained are in very good agreement with analytical and numerical data.
|
| [36] |
A moving-least-squares reconstruction for embedded-boundary formulations .
Not Available
|
| [37] |
On turbulent flow near a wall . |
| [38] |
Flow over periodic hills - numerical and experimental study in a wide range of Reynolds numbers .
The paper presents a detailed analysis of the flow over smoothly contoured constrictions in a plane channel. This configuration represents a generic case of a flow separating from a curved surface with well-defined flow conditions which makes it especially suited as benchmark case for computing separated flows. The hills constrict the channel by about one third of its height and are spaced at a distance of 9 hill heights. This setup follows the investigation of Fr02hlich et al. [Fr02hlich J, Mellen CP, Rodi W, Temmerman L, Leschziner MA. Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions. J Fluid Mech 2005;526:19–66] and complements it by numerical and experimental data over a wide range of Reynolds numbers. We present results predicted by direct numerical simulations (DNS) and highly resolved large-eddy simulations (LES) achieved by two completely independent codes. Furthermore, these numerical results are supported by new experimental data from PIV measurements. The configuration in the numerical study uses periodic boundary conditions in streamwise and spanwise direction. In the experimental setup periodicity is achieved by an array of 10 hills in streamwise direction and a large spanwise extent of the channel. The assumption of periodicity in the experiment is checked by the pressure drop between consecutive hill tops and PIV measurements. The focus of this study is twofold: (i) Numerical and experimental data are presented which can be referred to as reference data for this widely used standard test case. Physical peculiarities and new findings of the case under consideration are described and confirmed independently by different codes and experimental data. Mean velocity and pressure distributions, Reynolds stresses, anisotropy-invariant maps, and instantaneous quantities are shown. (ii) Extending previous studies the flow over periodic hills is investigated in the wide range of Reynolds numbers covering 100 81 Re 81 10 , 595. Starting at very low Re the evolution and existence of physical phenomena such as a tiny recirculation region at the hill crest are documented. The limit to steady laminar flow as well as the transition to a fully turbulent flow stage are presented. For 700 81 Re 81 10 , 595 turbulent statistics are analyzed in detail. Carefully, undertaken DNS and LES predictions as well as cross-checking between different numerical and experimental results build the framework for physical investigations on the flow behavior. New interesting features of the flow were found.
|
| [39] |
Investigation of wall-function approximations and subgrid-scale model in large eddy simulation of separated flow in a channel with streamwise periodic constrictions .
Large eddy simulations are presented for the flow in a periodic channel segment, which is laterally constricted by hill-shaped obstructions on one wall, having a height of 33% of the unconstricted channel. The Reynolds number, based on channel height, is 21,560. Massive separation thus arises on the hills鈥 leeward sides, the length of which is about 50% of that of the periodic segment. After reattachment, the flow is allowed to recover over about 30% of the segment length before being strongly accelerated over the windward side of the next hill. The principal challenge of this flow arises from the separation on the curved hill surface and the fact that the reattachment point, and hence the whole flow, are highly sensitive to the separation process. Simulations were performed with three grids, six subgrid-scale models and eight practices of approximating the near-wall region in simulations on the two coarser grids. These were supported by wall-resolved and wall-function simulations for fully-developed channel flow. The principal objective is to identify the sensitivity of the predictive accuracy to resolution and modelling issues. Coarse-grid simulations are judged by reference to data derived from two independent highly-resolved simulations obtained over identical meshes of close to 5 million nodes. Similarly, coarser-grid simulations were also performed with the two codes to enhance confidence in the results. The principal message emerging from the simulations is that grid resolution, especially in the streamwise direction around the mean separation position, has a very strong influence on the reattachment behaviour and hence the whole flow. This has serious implications for even more challenging high-Reynolds-number cases in which separation occurs from gently curved surfaces. The near-wall treatment, including the details of the numerical implementation of the wall laws, is also shown to be influential, most prominently on the coarsest grid. The application of the no-slip conditions at the wall at which separation occurs is found to cause substantial errors, especially in conjunction with poor streamwise resolution, even if the wall-nearest grid nodes are within the semi-viscous sublayer, in the range 5??15. The sensitivity to subgrid-scale modelling is shown to be more modest, with those models returning relatively low subgrid-scale viscosity giving the closest accord with the highly-resolved simulation.
|
| [40] |
High Reynolds number airfoil: from wall-resolved to wall-modeled LES.
This paper presents an in-depth study, using wall-resolved Large-Eddy Simulation (wrLES), of a high Reynolds number airfoil in a near-stall condition. The flow around the NACA4412 airfoil, a widely...
|
| [41] |
A dynamic slip boundary condition for wall-modeled large-eddy simulation .
Wall models for large-eddy simulation (LES) are a necessity to remove the prohibitive resolution requirements of near-wall turbulence in high Reynolds turbulent flows. Traditional wall models often rely on assumptions about the local state of the boundary layer (e.g., logarithmic velocity profiles) and requirea prioriprescription of tunable model coefficients. In the present study, a slip velocity boundary condition for the filtered velocity field is obtained from the derivation of the LES equations using a differential filter. A dynamic procedure for the local slip length is additionally formulated making the slip velocity wall model free of anya priorispecified coefficients. The accuracy of the dynamic slip velocity wall model is tested in a series of turbulent channel flows at varying Reynolds numbers and in the LES of a National Advisory Committee for Aeronautics (NACA) 4412 airfoil at near-stall conditions. The wall-modeled simulations are able to accurately predict mean flow characteristics, including the formation of a trailing-edge separation bubble in NACA 4412 configuration. The validation cases demonstrate the effectiveness of this wall-modeling approach in both attached and separated flow regimes.
|
| [42] |
Simulations of laminar and turbulent flows over periodic hills with immersed boundary method .
Laminar and turbulent flows over periodic hills are investigated with an immersed boundary method to mimic the curved geometry of the hill within the Cartesian framework. Here, turbulence is modeled through large eddy simulation with and without wall models. For laminar flows examined, flow over periodic hill separates earlier and reattaches later with the increase of Reynolds number. For turbulent flow simulations, Reynolds numbers from 2800 to 10595 are investigated. Predictions without wall models, i.e. assuming linear velocity profile at the wall, return better results both in mean and turbulence quantities, especially for the axial velocity at Reynolds number being 2800 and 5600. The good performance may lay in the fact that at these lower Reynolds numbers, the adopted grid resolves partly the near wall region. Predictions with wall models show a faster recovery of the recirculation zone and excessive diffusive transport across the shear layer. Among the wall models, turbulent boundary layer equation performs marginally better.
|
| [43] |
Geometric Characteristics of the DARPA SUBOFF Models. |
| [44] |
A numerical investigation of the wake of an axisymmetric body with appendages .
We report wall-resolved large-eddy simulations of an axisymmetric body of revolution with appendages. The geometry is that of the DARPA SUBOFF body at 0 yaw angle and a Reynolds number equal to (based on the free-stream velocity and the length of the body). The computational grid, composed of approximately 3 billion nodes, is designed to capture all essential flow features, including the turbulent boundary layers on the surface of the body. Our results are in good agreement with measurements available in the literature. It is shown that the wake of the body is affected mainly by the shear layer from the trailing edge of the fins and the turbulent boundary layer growing along the stern, while the influence of the wake of the sail is minimal. In agreement with the reference experiments, a bimodal behaviour for the turbulent stresses is observed in the wake. This is due to the displacement of the maximum of turbulent kinetic energy away from the wall along the surface of the stern, where the boundary layer is subjected to strong adverse pressure gradients. The junction flows, produced by the interaction of the boundary layer with the leading edge of the fins, enhance this bimodal pattern, feeding additional turbulence in the boundary layer and the downstream wake. The evolution of the wake towards self-similarity is also investigated up to nine diameters downstream of the tail. We found the mean flow approaches this condition, while its development is delayed by the wake of the appendages, especially by the flow coming from the tip of the fins. However, the width of the wake and its maximum momentum deficit follow the expected power-law behaviour on the side away from the sail. The second-order statistics, on the other hand, are still far from self-similarity, which is consistent with experimental observations in the literature.
|
| [45] |
|
| [46] |
Wall-modeling for large-eddy simulation of flows around an axisymmetric body using the diffuse-interface immersed boundary method. |
| [47] |
Turbulence intensities in large-eddy simulation of wall-bounded flows .
Log-layer mismatch refers to a chronic problem found in wall-modeled large-eddy simulation (WMLES) or detached-eddy simulation, where the modeled wall-shear stress deviates from the true one by approximately 15%. Many efforts have been made to resolve this mismatch. The often-used fixes, which are generally ad hoc, include modifying subgrid-scale stress models, adding a stochastic forcing, and... [Show full abstract]
|

/
| 〈 |
|
〉 |