油气井密封结构的变形与失效行为研究进展1)
A REVIEW ON THE DEFORMATION AND FAILURE OF SEALS IN OILFIELD1)
中图分类号: TE25
文献标识码: A
通讯作者:
收稿日期: 2019-03-19
网络出版日期: 2019-05-18
版权声明: 2019 力学学报期刊社 所有
基金资助:
展开
摘要
在今后相当长一个时期,石油和天然气依然是人类的主要能源.油气井密封是油气开采中最重要的作业之一,在水平钻井、水力压裂等最新的油气开采技术中发挥着重要的作用,促进了页岩气等非常规油气开采的发展.密封质量会直接影响油气井的安全和生产效率,密封元件的失效可造成严重的环境污染和生命财产损失.因此,深入理解密封元件的失效行为,对于油气井安全评估具有重要意义.水泥和可溶胀高弹体密封是两种最主要的密封方式.水泥密封已有百余年历史,溶胀式高弹体密封则是一种相对较新的密封技术.本文介绍这两种油气井密封结构变形与失效行为的国内外最新研究进展.首先,介绍固井水泥环固化过程中的应力演化、生产作业导致的应力、水泥环的失效模式和失效判据方面的研究进展;然后,介绍溶胀式高弹体封隔器的基本原理、力学理论、测试方法、失效模式及失稳等方面的研究进展.
关键词:
Abstract
Oil and gas will still be the major energy resource of human in a long period. Sealing is one of the most important operations in oil and gas exploitation, which plays an essential role in horizontal drilling and hydraulic fracturing, booming the exploitation of unconventional oil and gas like shell gas. The quality of sealing is critical to the performance and safety of wells. The deformation and failure of seals may lead to severe environmental pollution, losses of life and property. Therefore, it is important to study the mechanical behavior of seals in oilfields systematically and deeply for safety assessment as well as better sealing of wells. Cement and swellable elastomers are the most widely used sealing materials in oilfield. Well cementing has been developed for more than 100 years. While swellable elastomeric packer is relatively new. In this review, we present the recent advances in the studies of the deformation and failure of cement sheath and swellable packers. The first part focuses on the cement sheath, including stress evolution during the solidification process and production stage, failure modes, and failure criteria. In the second part, emphasis is placed on the work principle, basic theory, test method, failure modes and instability of swellable packers.
Keywords:
引 言
能源是人类社会的命脉.据美国能源情报署估计,2040年世界能源总需求将从2012年的$5.79\times10^{17}$ kJ增长到$8.60\times 10^{17}$ kJ,增长约48%.尽管新能源和核能快速增长,但届时石油和天然气依然是主要能源[1].需求促进了油气产业和相关技术的发展,如水平钻井技术[2]、水力压裂技术[3-7]、新型密封材料和工具[8-9]的开发等.
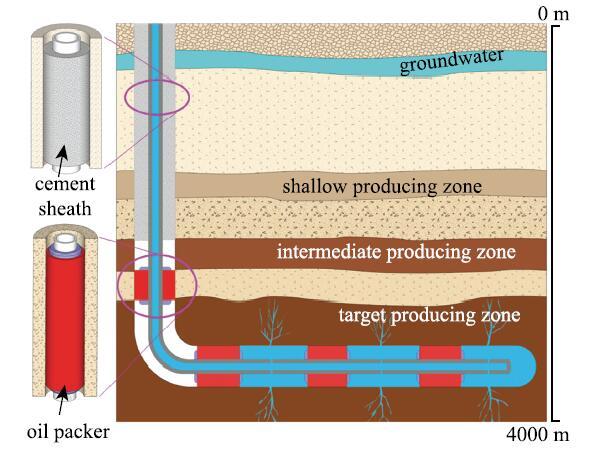
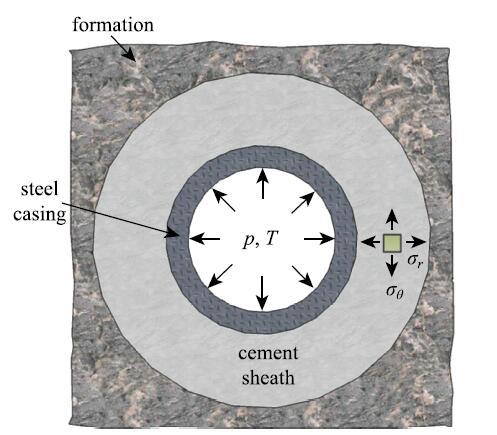
油气开采是一个复杂的系统工程.在正式生产前,需要通过探测、钻井、固井、完井等作业,来建立油气采集的工作条件.在油气井的整个生命周期中,良好密封是确保安全和生产效率的重要条件[9-10].油气井的密封元件主要包括水泥环和高弹体封隔器两种,如图1所示.由于低成本、低渗透率、易固化的特点,水泥被广泛用来密封井壁和套管间的环形空间.水泥环的主要功能是提供层位封隔(即阻止不同地层层位的流体互相连通)、支撑套管、防止套管腐蚀等.溶胀式高弹体封隔器是一种相对较新的密封工具,具有成本低、操作简便、自动密封、封隔压力大等优点,可用于水力压裂、辅助固井、储层改造、阻水、防砂等作业,甚至可以替代固井[11].密封结构失效会降低生产效率,甚至造成严重的环境污染和生命财产损失.在很长一段时间内,油气井密封主要由经验主导,缺少系统、量化研究.这可能是由于早期的油气井深度较浅,地质环境比较简单,人们的主要精力放在如何提高固井效率等方面,没有过多地关注密封元件的力学性能、寿命等问题.然而,随着开采时间推移,浅层油气资源越来越少[12-13],人们不得不考虑页岩、深海和极地的非常规油气资源开发[14].
近年来,在高温、高压、深水等极端环境中运行的油气井数量快速增加[15-16],这对密封元件的可靠性提出了更高要求.另外,二氧化碳的深埋存储等其他应用对地下深井的密封效果和生命周期也提出了更严苛要求[17].实践表明,目前的密封作业不能提供理想的封隔效果,即使初始密封良好,但后续生产作业中仍可能发生泄漏.例如,2000---2012年美国宾州开发的油气井中有6.2%的非常规油气井和1.0% 的常规油气井发生甲烷泄漏[18].水力压裂法开采页岩气使浅层地下水中的甲烷含量明显上升[19]. 更重要的是,油气井密封失效后难以补救.因此,系统深入研究油气井密封元件的失效机理,对于油气井密封的安全性评估、密封材料的选择、密封器件的设计等具有重要意义.
本文介绍油气井密封结构失效行为的国内外研究进展,首先简要介绍固井水泥环中的应力、失效模式和失效判据, 然后重点介绍溶胀式高弹体封隔器这种相对较新的密封结构的溶胀、变形、断裂、弹性泄漏及其应用等.
1 固井水泥环密封
固井作业开始于1903年[10].油气井钻探到一定深度后,下入套管,并在套管和井眼之间注入水泥浆,这一过程称为固井.当水泥浆固化后,水泥环、套管以及井壁胶结在一起,阻止水层、油层和气层的互相连通,从而起到层位封隔的作用.随着油气井深度的增加,钻井过程中可能需要多次固井.经过百余年的发展,固井技术有了明显进步,主要包括水泥品种的丰富、固井工具的改良、固井作业的自动化和精确控制等.
固井水泥由两部分组成:基本水泥和外加剂.煅烧后的水泥主要含有四种成分:硅酸三钙($3\mbox{CaO} \cdot\mbox{SiO}_2 )$、硅酸二钙($2\mbox{CaO} \cdot \mbox{SiO}_2)$、铝酸三钙($3\mbox{CaO} \cdot \mbox{Al}_2 \mbox{O}{}_3)$和铁铝酸四钙($4\mbox{CaO} \cdot \mbox{Al}_2 \mbox{O}_3 \cdot\mbox{Fe}_2 \mbox{O}_3 )$.当与水混合时,这些成分和水发生复杂的物理和化学反应.刚开始反应速率较低,水泥浆能在一定时间内保持流动性,固井作业可以在这一时间窗口内完成.之后反应加速,快速生成大量水合硅酸钙凝胶(C-S-Hgel),水泥浆固化,强度逐渐增大.固化后的水泥成分主要是水合硅酸钙和氢氧钙石[10].
由基本水泥形成的水泥浆的应用范围非常有限.为了满足不同油气井深度和地层特性的要求,需要在水泥中添加外加剂,主要有促凝剂、缓凝剂、降失水剂、消泡剂、防气窜剂、分散剂、填充剂和增重剂等.外加剂不超过水泥总重量的5%,但对油井水泥的性能有重要的影响,除了能改变水泥浆的流变学特性、固化时间等短期性能以确保固井成功率,还能影响水泥环的长期力学性质,如弹性模量、泊松比、抗拉抗压强度等.这些参数对水泥环的封隔能力和使用寿命有重要影响[20-21].
1.1 水泥固化过程中的应力演化
固井水泥受到套管和井壁的约束,在固化过程中和固化之后都处于复杂的应力状.当水泥环中的应力增大到某一临界值时,水泥环可能发生破坏,失去层位封隔能力,甚至造成大的灾难.因此,分析水泥环中的应力及其演化,对预测与预防水泥环的失效有重要作用.下面简要介绍水泥环在固化过程中的应力演化.
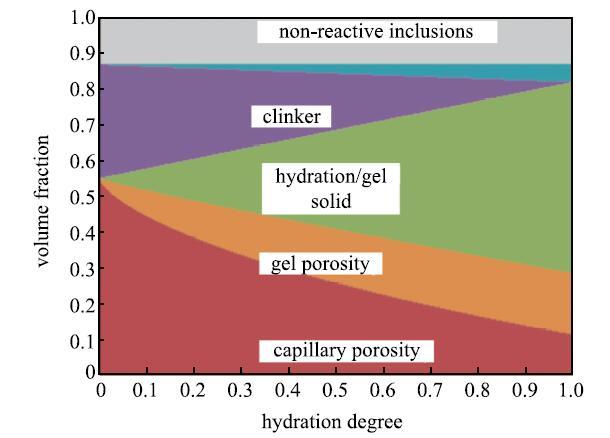
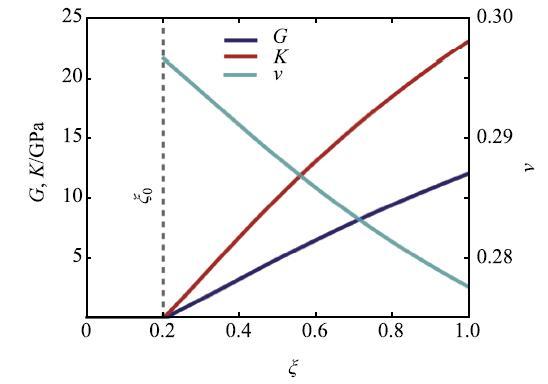
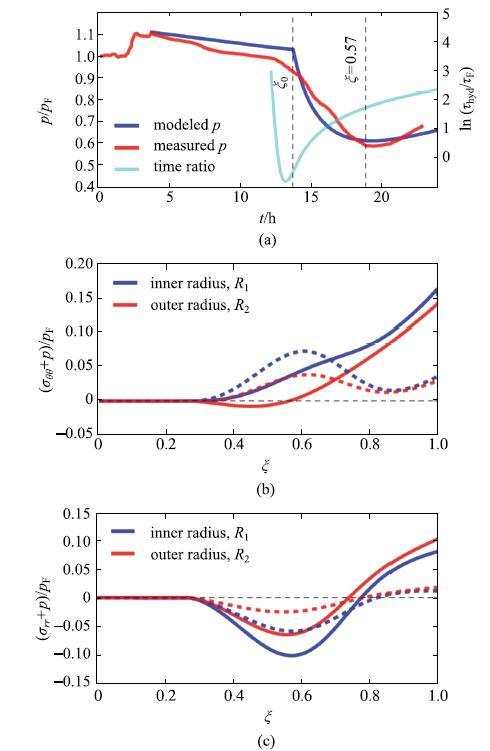
水泥固化是一个复杂的化学--力学过程.研究表明[22-24],随着固化程度的增加,水泥熟料逐渐减少,生成的水合硅酸钙凝胶和氢氧钙石逐渐增加(图2),并不断长大,互相粘接在一起形成紧密的三维多孔结构.水泥浆从不可压缩流体逐渐转变为可压缩多孔固体,其弹性模量($G$和$K)$随着固化程度的增加而不断增大,而泊松比($\nu $)逐渐降低(图3).水化反应的生成物体积通常小于反应物的体积,导致水泥在固化过程中产生体积收缩[22-23].由于套管和井壁的约束,水泥环无法自由收缩而产生内应力,并随着固化程度增加而变化(图4).
图2 水泥固化过程中各组分体积分数随固化程度的变化[
Fig. 2 The relation between the volume fractions in hydrating cement and the degree of hydration[
图3 水泥固化过程中的力学参数随固化程度($\xi )$的演化[
Fig. 3 The evolution of mechanical properties with the degree of hydration[
图4 水泥环中的 (a) 孔隙压力,(b) 等效环向应力和 (c) 等效径向应力随固化程度的变化. 实线表示硬岩层(40 GPa);虚线表示软岩层 (5 GPa) [
Fig. 4 (a) The pore pressure, (b) effective hoop stress and (c) effective radial stress are plotted as functions of the degree of hydration. The solid lines are for stiff formation (40 GPa); dashed lines are for soft formation (5 GPa)[
多孔弹性模型能很好地描述水泥的力学性能[24-26],Ulm等[27-29]利用多尺度均匀化方法预测了水泥的力学参数随固化程度的变化关系.在此基础上利用多孔弹性模型推导出了水泥环中的孔隙压力和等效应力在固化过程中的演化规律$^{[22\mbox{-}23,30]}$.在达到临界固化程度之前,水泥浆的黏度变化很小,尚不具备强度,其孔隙压力几乎不变(图4(a)),等效应力为零(图4(b)和图4(c)).当超过临界固化程度后,水化反应速率显著提高,孔隙压力先急速降低,然后逐渐平稳并在固化完成前轻微恢复.孔隙压力的变化速率主要受水化反应速率的影响.
从图4(b)可见,岩层的弹性模量对水泥环中的等效环向应力影响较大.对于两种不同模量的岩层,孔隙压力的降低使得水泥环/套管界面处($R_{1})$的等效环向应力进入拉伸状态.对于硬岩层,水泥环与岩层界面处($R_{2})$的等效环向应力短暂进入压缩状态,然后变为拉伸状态;而对于软岩层,$R_{2}$处的等效环向应力一直处于拉伸状态.固化结束后,硬岩层对应的水泥环等效环向应力要远大于软岩层情况,且水泥环内径处的等效环向应力一直大于外径处的等效环向应力.因此,水泥环和套管界面处最容易萌生拉伸裂纹.
水泥环中的等效径向应力对孔隙压力的变化非常敏感.随着孔隙压力的降低,等效径向应力进入压缩状态.当孔隙压力降到极小值时,等效径向压应力达到最大.随后,孔隙压力缓慢升高,水泥环中的等效径向压力逐渐减小,并最终变为拉应力.这是因为在水化反应初期水泥环没有足够的强度,等效应力主要受孔隙压力变化的影响.在固化后期,水泥环强度逐渐增大,水泥环中的应力状态主要受控于水泥的体积收缩、套管及岩层的约束强度.同样,等效径向应力大小也强烈依赖于岩层的弹性模量.当固化完成后,水泥环中的等效应力不再变化,处于"冻结"状态,通常被称为初始应力.如果水泥体积收缩过大,即使没有施加任何作业压力,水泥环也可能因为初始应力过高而破坏$^{[22\mbox{-}23,30\mbox{-}31]}$.
1.2 生产作业阶段水泥环中的应力
如前所述,水泥在固化过程中会产生初始应力.在后续生产作业中,套管压力和温度的变化还会引入新的应力.此外,地应力、地下流体压力等也会影响水泥环的应力状态.因此,要精确预测和分析固井水泥环的应力是非常复杂和困难的.但是,在线弹性条件下,各种因素造成的应力可以线性叠加.因此,对于特定井况,可以找出主要影响因素,再叠加得到最终应力.下面分析最主要的两个因素:套管压力和温度变化引起的应力[32].
理想状态下,套管、水泥环和岩层可以简化为三个同心圆环(图5),各层可当作是均匀各向同性材料.套管内的压力可能因为井下环境或生产作业而变化,进而造成水泥环中应力状态的变化.通常情况下,可忽略套管内压力随井深的变化,即可将问题简化为平面应变问题,由弹性力学中的经典拉梅问题求解.
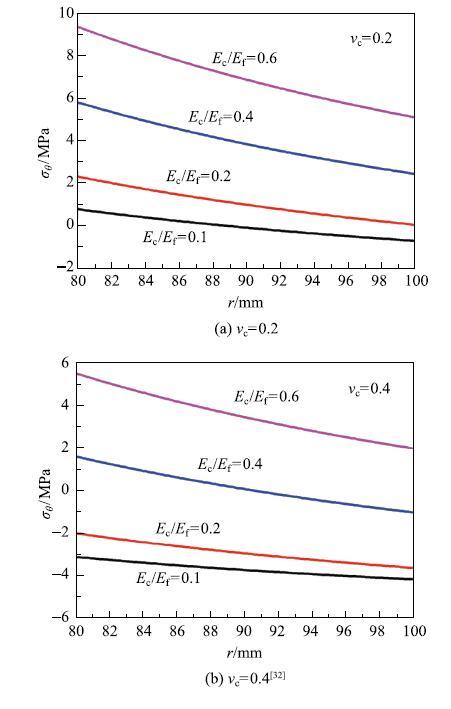
固化水泥的抗拉强度远低于其抗压强度,因此水泥环对拉应力更敏感.当套管内压力增大时,水泥环中的径向应力始终为压应力.环向应力的分布如图6所示[32],在水泥环与套管界面处最大,在水泥环/岩层界面处降低.因此,在水泥环与套管界面处最容易萌生拉伸裂纹.如果降低水泥与岩层模量比($E_{\rm c}/E_{\rm f})$,水泥环中的环向拉应力随之降低,并有可能从拉变为压.同时水泥泊松比的提高也能有效降低拉应力.当套管压力降低时,环向拉应力会减小甚至变为压应力,而径向应力可能变为拉应力.此时,水泥环、套管及岩层的界面可能因为拉应力而失去粘接,形成微环隙.
图6 水泥环在套管内压作用下的环向应力分布
Fig. 6 The hoop stress in the cement sheath under inner pressure
井下高温环境和套管内温度变化是造成水泥环应力变化的另一个主要原因.随着油气井深度增加,岩层温度可达300[16].同时,射孔、水力压裂和蒸汽增产等井下作业也会引起温度和压力的极大变化,例如,蒸汽增产用到的蒸汽温度在200$\sim$300[33].与套管内压力变化造成的应力不同,温度变化造成的应力是瞬态的,如作业温度快速周期变化,则温度应力可能会随时处于动态变化中.
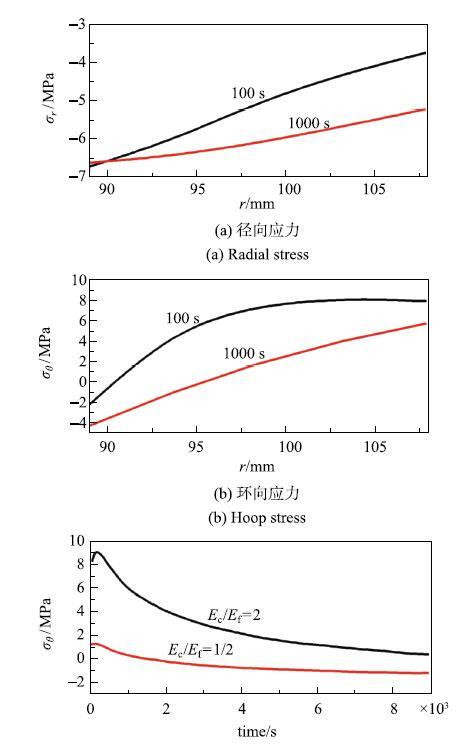
图7显示了套管内温度升高造成的应力变化[20].当温度升高100$^\circ$F (55.6℃) 100s之后,水泥环中的径向应力为压应力.环向应力在水泥环与套管界面附近为压应力,在水泥环/岩层界面附近为拉应力.这是由于水泥环的不均匀膨胀造成的,在温度升高后的较短时间内,水泥环内的温度梯度较大,内层温度高,膨胀应变大.其膨胀受到外侧膨胀较小区域的约束,因此产生压应力.外侧区域受到内侧膨胀的驱动,而产生拉应力.随着时间的延长,水泥环内的温度分布更加均匀,相应的热应力分布也更加均匀.径向压缩应力增大,环向拉伸应力降低. 从图7(a)和图7(b)可以看出,环向应力为危险应力,特别是水泥环/岩层界面附近的环向应力最有可能导致拉伸裂纹的出现.图7(c) 显示了水泥环/岩层界面处的环向应力随时间的变化.在温度升高后的瞬间,界面处的环向应力直接达到非常高的拉应力水平,短暂继续升高后逐渐降低.从图中可以看出拉应力的水平同样受水泥/岩层模量比的强烈影响,当$E_{c}/E_{\rm f}$ 由2降低到1/2时,界面处的最大应力从9MPa左右大幅降低到约1.4MPa,并且环向应力迅速由拉伸应力变为压缩应力.这表明模量较小的水泥环有可能抵抗更高的温度变化.
1.3 固井水泥环的失效模式与失效判据
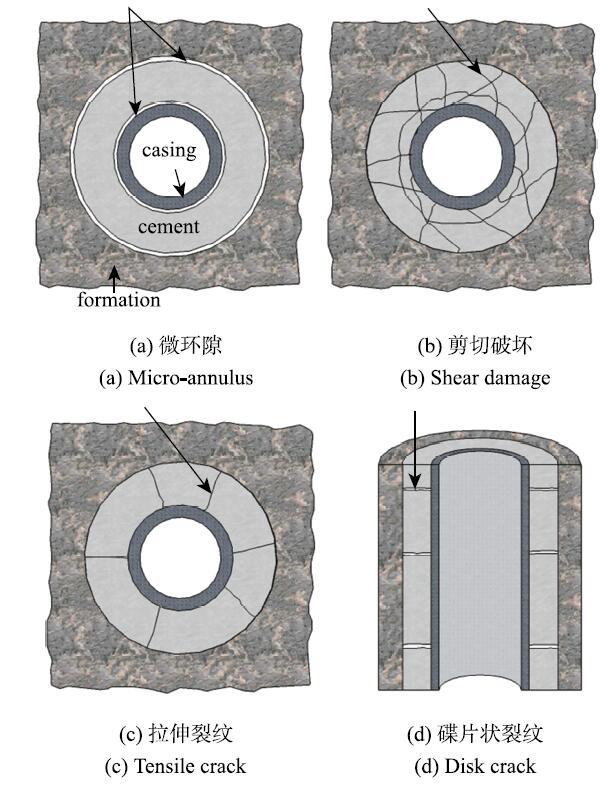
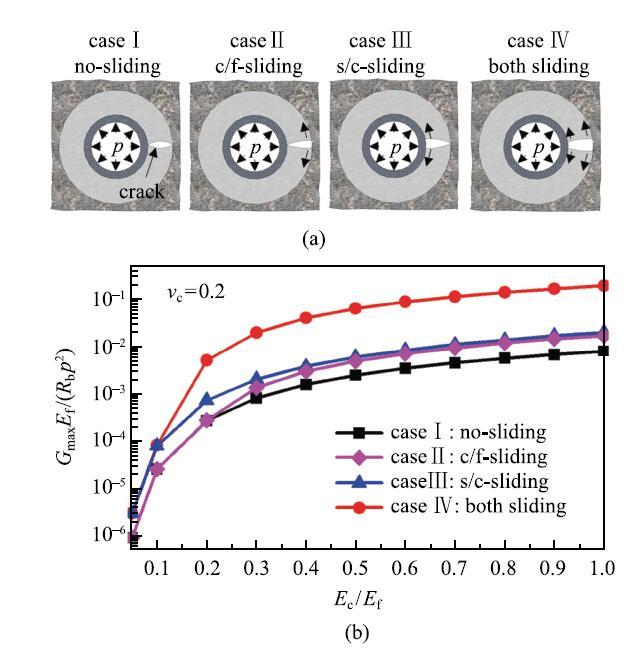
上一节讨论了水泥环中的应力演化和影响因素.当水泥环中的应力超过安全阈值时,水泥环可能发生多种形式的破坏$^{[21,34\mbox{-}36]}$,可总结为四种:(1)微环隙,(2)剪切破坏,(3)拉伸裂纹,(4)碟片状裂纹,如图8所示.
水泥环在固化过程中会收缩,套管内压力或温度突然降低也会导致套管收缩,从而导致径向应力变为拉伸状态.水泥环、套管以及岩层的结合强度一般小于其自身强度,因此容易在界面处产生拉伸微裂纹,形成微环隙,特别是在水泥环和套管界面处.这是因为水泥环中的径向拉应力在该界面处达到最大值,且水泥环和金属套管的粘接强度很弱.如果固井之前没有将钻井泥浆清理干净,则会进一步降低界面强度,促进微环隙萌生[37].当压应力超过某一临界值时,水泥环发生剪切破坏,形成网络状的剪切带(图8(b)).当环向拉应力过大时,水泥环中产生放射状的张开型裂纹(图8(c)).拉伸裂纹可能贯穿水泥环厚度,并在高度方向上传播上千米.碟片状裂纹主要是由于水泥收缩产生轴向拉应力而引起的,以一定间隔分布在油气井高度方向.微环隙和水泥环内的轴向拉伸裂纹给流体提供了沿高度方向上运移的通道,造成层位封隔的失效,需要在水泥环设计和安全评估中予以重点关注.
目前,工程中采用的强度分析方法[20-21]不考虑水泥环中的缺陷,利用线弹性力学计算其中的应力场,并利用强度准则来确定水泥环破坏的临界条件.这种方法常被用来确定已有水泥环能承受的临界工作状态,或者为已知的井下环境和作业条件设计能满足功能要求的水泥环.该方法适用于预测水泥环的剪切破坏.但对于微环隙、拉伸裂纹和碟片状裂纹等张开型裂纹,水泥环经常在远低于强度的条件下破坏,强度理论不再适用于预测这些失效模式.Ulm等[31]采用断裂力学预测裂纹在水泥环中的径向扩展.Wang等[32]研究了裂纹沿轴向扩展的临界条件,提供了一个判断水泥环状态的临界安全准则.该准则不需要测量水泥环中初始裂纹的状态,只依赖于材料的性质和作业条件.
选择合理的失效判据,对准确预测水泥环的失效,建立可靠的设计模型具有重要意义.下面列出几种常见失效模式的失效判据.
(1) 剪切失效. Mohr-Coulomb 准则常被用来预测水泥环的受压剪切破坏
\begin{equation} \label{eq1} \tau _{\rm f} = c + \sigma \tan \varphi\tag{1} \end{equation}
式中,$\tau _{\rm f}$为水泥的抗剪强度,$\sigma$为剪切滑动面上的法向应力,$c$为材料内聚力,$\varphi $为材料内摩擦角.
(2) 径向裂纹.
拉伸裂纹最容易萌生于水泥环/套管界面处,当裂纹沿径向扩展时,裂纹的张开位移$\delta$是位置$r$的函数(图9),裂尖的能量释放率为[30]
\begin{equation} \label{eq2} G = \frac{1}{2}\frac{{\rm d}}{{\rm d}h}\int_0^h {\sigma _\theta \left( r \right)\delta \left( r \right){\rm d}r}\tag{2} \end{equation}
式中,$\sigma _\theta \left( r\right)$为同样外载荷条件下,完好水泥环中的环向应力.裂纹张开位移可由有限元法或格林函数法求得. 裂纹扩展的临界条件为$G =\varGamma _{\rm c}$,式中$\varGamma _{\rm c}$为固化水泥的断裂能,其大小可由实验测量得到[38].
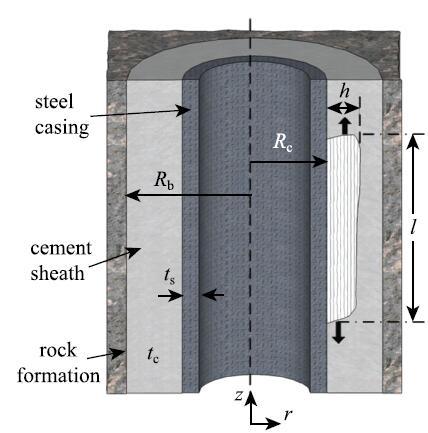
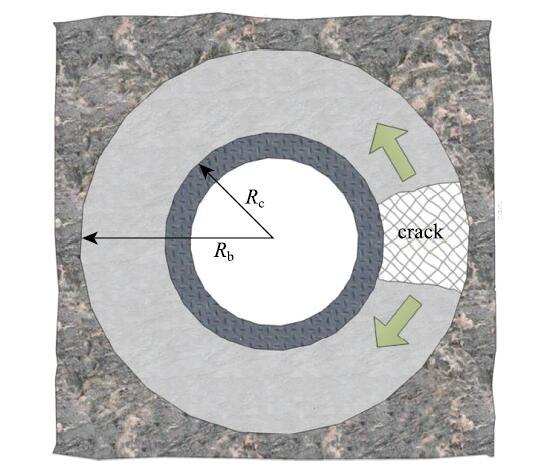
(3) 隧穿(轴向)裂纹.固井水泥环的高度通常在几百米甚至几千米的尺度范围内,在固井作业和水泥浆固化过程中,不可避免地会在水泥环中造成各种缺陷.这些缺陷随机分布在水泥环中,当外载荷达到某一临界值时,一些缺陷可能会开始扩展,形成一条大裂纹.水泥环中的裂纹可能沿着径向向外扩展,也可能沿着轴向扩展,是一个复杂的三维问题.但是,裂纹沿径向扩展只会造成水泥环局部的破坏,不会对其层位封隔功能造成严重的影响.而裂纹沿着油气井轴向的扩展才会让其失去某一段或者整体的层位封隔功能.Wang等[32]将这种沿着油气井高度方向扩展的裂纹称为"隧穿裂纹"(图10).
图10 隧穿(轴向)裂纹示意图[
Fig. 10 Schematic of a tunneling crack in the cement sheath[
隧穿裂纹的能量释放率 $G$定义为裂纹沿着高度方向扩展单位面积时,系统应变能的减少量.在其他条件都固定时,隧穿裂纹的能量释放率随着裂纹长度 $l$ 增大.当$l/h >2$时,隧穿裂纹达到稳态扩展阶段,即能量释放率不再随着$l$变化[39].在这一阶段裂尖能量释放率为[40]
\begin{equation} \label{eq3} G = \frac{1}{2h}\int_0^h {\sigma _\theta \left( r \right)\delta \left( r \right){\rm d}r}\tag{3} \end{equation}
这样就可以将复杂的三维问题转化为求解两个平面应变问题.
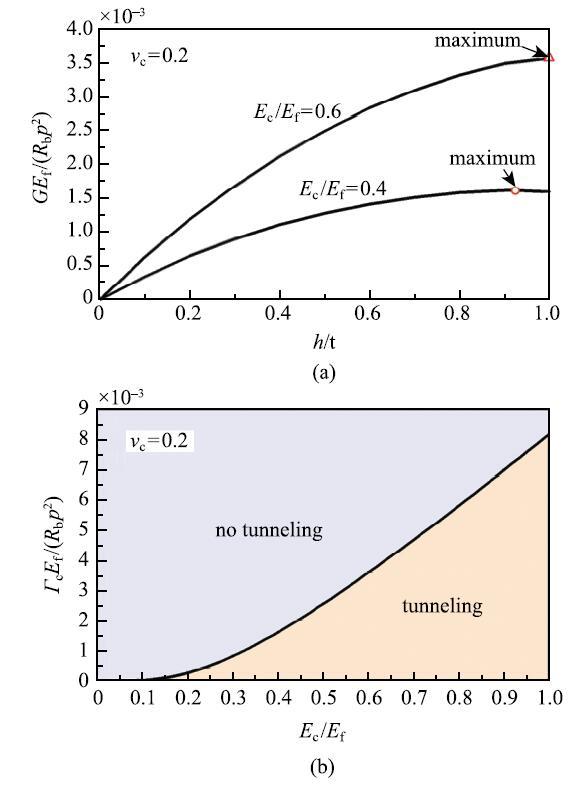
从式(3)可见,在其他参数固定情况下,裂尖能量释放率是裂纹宽度$h$的函数,如图11(a)所示.如果能量释放率的最大值小于材料的断裂能,则裂纹不会沿油井高度方向扩展;以水泥/岩层模量比为横坐标,无量纲断裂能为纵坐标,可得水泥环的安全/失效状态图,如图11(b)所示. 断裂临界条件将该平面分成两部分,一是安全区 (notunneling),即图中浅紫色部分,在这一区域任何尺寸的初始裂纹都不可能沿着水泥环高度方向扩展;二是潜在失效区(tunneling),即图中右下角土黄色部分,在这一区域,水泥环中的某些初始裂纹的能量释放率可能会超过材料的断裂能,从而扩展成隧穿裂纹,导致层位封隔的失效.
图11 (a)无量纲能量释放率和裂纹宽度的关系,(b)水泥环的安全与失效区域图[
Fig. 11 (a) The normalized energy release rate as a function of the normalized width of the tunnel, (b) failsafe diagram in the plane with axes of the normalized Young's modulus and normalized fracture energy of the cement[
(4) 微环隙. 微环隙的能量释放率比较容易确定[31]
\begin{equation}\label{eq4} G = \frac{1}{2}\sigma _r \delta _{\rm i}\tag{4}\end{equation}
式中,$\sigma _r $为完好结构在界面处的径向应力,$\delta _{\rm i}$为界面处的微环隙张开位移. 但是,微环隙的界面断裂能难以确定.一是水泥、套管及岩层的粘结强度难以测量,二是界面强度受到固井工艺、泥浆清理程度等多个因素的影响.
(5) 碟片状裂纹.根据水泥环的几何特性,碟片状裂纹最可能的扩展路径如图12所示,其裂尖能量释放率为
\begin{equation} \label{eq5} G = \frac{1}{R_{\rm b}^2 - R_{\rm c}^2 }\int_{R_{\rm c} }^{R_{\rm b}} {\sigma _z \delta \left( r \right)r{\rm d}r}\tag{5}\end{equation}
式中$\delta _z $为$z$方向的裂纹张开位移.当能量释放率达到水泥断裂能时,裂纹开始扩展.
1.4 影响水泥环失效的关键参数
研究表明,水泥环的完整性不仅和水泥本身的性能密切相关,还和岩层、套管的力学性能以及几何参数相关$^{[20,23, 35]}$.在工程中套管和岩层的相关参数基本上都是确定的,能够通过设计以改善水泥环长期完整性的参数主要有以下几个:
(1) 水泥/岩层模量比. 从图6和图7(c) 可见,当$E_{\rm c}/E_{\rm f}$降低时,套管压力和温度变化导致的拉应力会显著降低,从而降低裂纹扩展驱动力(图11(a)).工程中也发现,利用泡沫水泥等低模量水泥可提高油气井的长期层位封隔能力[41].但是,Petersen[22]的研究表明,在水泥固化阶段,坚硬岩层会使水泥环内产生较大的初应力,容易造成水泥环失效.油气井所处岩层的力学性能变化范围很大,其模量变化范围为1$\sim$30GPa [20].因此,单一水泥不能满足所有需求,需根据特定井下环境选择合适的水泥.
(2) 水泥泊松比. 随着固井水泥的成分变化,其泊松比可在0.1$\sim$0.4范围内调节[36].常规水泥的泊松比较小,通过添加橡胶颗粒等可提高其不可压缩性和泊松比值.如图7所示,高泊松比有助于降低环向拉应力水平,甚至促使拉应力变为压应力,从而降低产生拉伸裂纹的几率.因此,水泥--橡胶复合材料是比较理想的固井材料[8].
(3) 界面强度.水泥环、套管以及井壁的粘结强度直接影响微环隙的萌生和扩展.同时,界面滑移对水泥环内拉伸裂纹的扩展也有重要的影响[32].如图13所示,当界面脱粘滑移时,隧穿裂纹的能量释放率显著上升.水泥环两侧的界面中,水泥环与套管界面的影响更大.因此,界面粘接强度对水泥环的层位封隔能力至关重要.但是在油气井中,由于油基钻井液的污染,水泥环、套管以及井壁的粘接强度通常比较弱,甚至被泥饼直接隔离开,从而失去接触[37].可见,泥浆清理工作对于提高水泥环的承载能力有重要作用.
图13 水泥环和套管以及岩层的界面力学性能对隧穿裂纹能量释放率的影响[
Fig. 13 The effect of interfacial sliding on the energy release rate of tunneling crack[
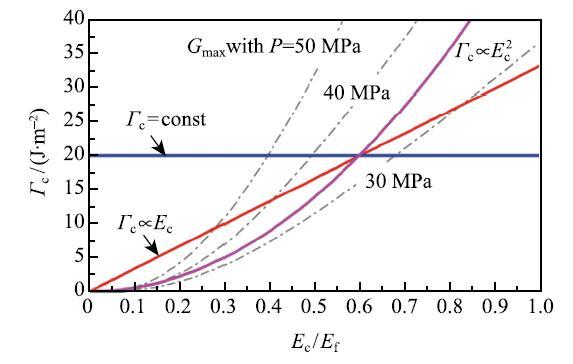
(4) 断裂韧性.在以前研究中,许多人认识到了水泥模量对水泥环安全性的重要影响[16, 20-21, 36].降低固化水泥的模量有助于降低拉伸裂纹的能量释放率,即减小裂纹扩展驱动力.但是,人们却忽略了影响裂纹扩展临界条件的另一个重要因素:水泥的断裂韧性,即水泥材料抵抗裂纹扩展的能力.材料的模量和断裂韧性是耦合在一起的两个参数,当水泥模量降低时,其断裂能往往也会随之下降[38].因此,降低水泥的弹性模量并不一定能提高水泥环的安全性,需要考虑水泥的断裂能和弹性模量之间的关系.Wang等[32]考虑了三种简单的关系,如图14所示:断裂能为常数;断裂能随模量线性变化;断裂能是模量的二次函数.虚线为对应于套管内压力$p = 30$,40 和50 MPa的最大能量释放率.当断裂能为常数时,降低水泥模量能有效提高其临界载荷,但当断裂能是模量的二次函数时,降低水泥模量对其承载能力影响不大.若断裂能随模量下降更快,则降低模量甚至有可能降低其承载能力.
图14 水泥的断裂能和模量之间的关系对其完整性的影响[
Fig. 14 The correlation between the fracture energy and elastic modulus of cement and its effect on the integrity of cement sheath[
2 溶胀式高弹体封隔
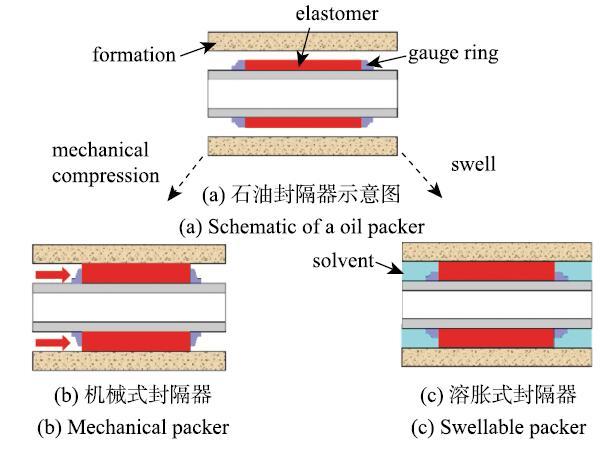
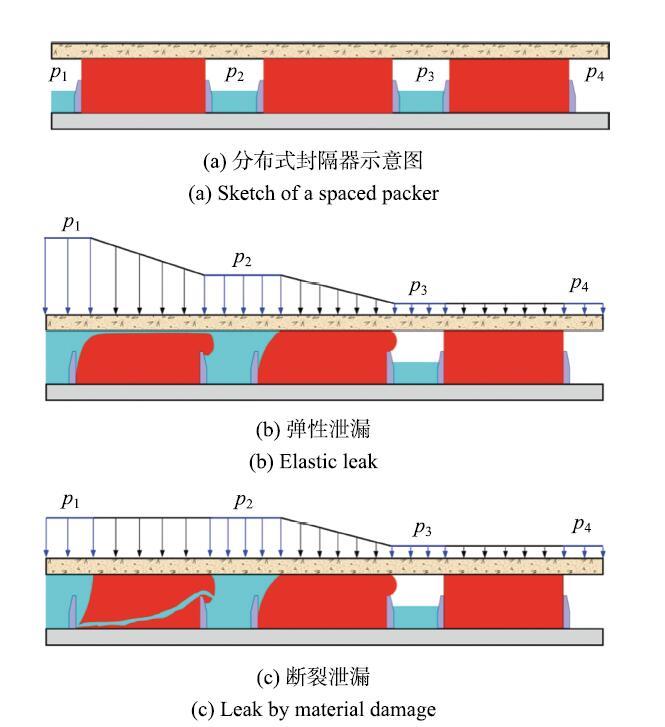
高弹体封隔器是油气开采中另一种重要的密封工具.传统高弹体封隔器利用橡胶材料作为密封元件,通过机械挤压使橡胶径向膨胀而实现密封[9],如图15(a)和图15(b)所示. 其缺点是操作复杂,能够密封的环空尺寸和压力差有限.前已述及,水泥密封已有百余年历史.相比之下,溶胀式高弹体密封则是最新发展起来的密封技术,2001年第一次被应用到工程实践中[42].溶胀式封隔器采用亲水或亲油的高弹体聚合物作为密封元件[43-44],当高弹体遇到井下液体(油或水)之后吸收这些液体发生体积膨胀并和井壁接触,建立一定的接触压力(图15(c)),这一过程可能需要数周至数月,取决于高弹体的材料性质、封隔器的几何尺寸和井下环境(井下温度、流体性质、井壁渗透率等).与机械式封隔器相比,溶胀式封隔器具有成本低、结构简单、操作简便、封隔空间大、封隔压力高等优点.特别是当井壁受流体冲刷尺寸变大时,高弹体能继续溶胀弥补井眼尺寸的变化,维持密封状态.这些优点使其在油气工程中迅速得到了广泛应用,2010年左右已有超过两万个溶胀式封隔器被用到世界各地的油气井中[42],现已成为最主要的封隔工具.本节重点介绍溶胀式封隔器这一新的封隔工具,综述其溶胀、变形和破坏的基本理论,测试方法和失效模式.
图15 高弹体封隔器的结构及工作原理示意图
Fig. 15 Schematic of the structures and work principles of elastomeric seals
2.1 高弹体密封的失效模式及实验方法
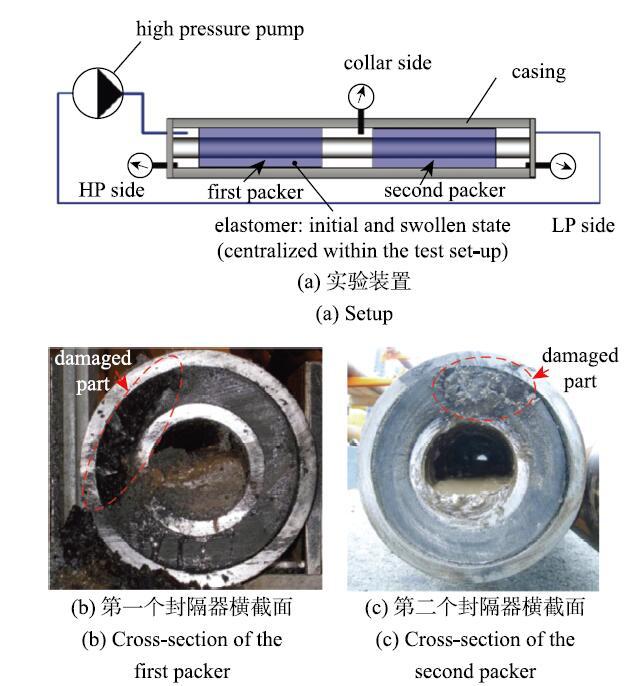
在井下作业中,高弹体封隔器需要阻止其两端的流体互相流通,并维持一定的压力差.例如,多级水力压裂中高弹体封隔器两端需要承受约70MPa的流体压力差[45].当流体压力超过封隔器的承载能力时,高弹体密封元件会因变形过大或断裂而导致封隔器的泄漏.由于高弹体封隔器在几百到上千米深的井下工作,工程人员无法实时观测封隔器的变形和泄漏情况.为此,工程中主要采用全尺寸模型来测试封隔器在流体压力下的响应[43, 45]. Nijhof等[45]在实验室中测试了两个串联的溶胀式封隔器在高压流体作用下的泄漏和破坏情况,测试装置如图16所示.利用金属套管模拟井壁,将两个5 m长的封隔器串联放置在两层套管之间,等待一段时间使高弹体聚合物溶胀并和外侧套管接触,建立起一定的接触压力.封隔器左侧连接高压泵并逐渐加压,3个压力计实时监测两端和封隔器之间的压力,在左侧高压作用下,两个封隔器相继发生泄漏.之后实验人员锯开套管,观察封隔器的失效模式.在第一个封隔器中观察到一个贯穿整个密封元件长度的通道,通道内橡胶被破坏成小颗粒并随高压液体流出,其他部分保持完好,在金属隔环约束下保持在原处(图16(b)).对于第二个封隔器,仅在高压一侧发现橡胶局部破坏,在整个长度方向上,绝大部分材料没有发现破坏的迹象(图16(c)).这种方法耗时长,需要复杂的高压设备,价格昂贵.该实验装置也无法实时观察高弹体密封元件的变形和破环情况,只能在实验结束之后通过切割试件观察其破坏后的状态.
针对这一问题,Druecke等[46]利用硅橡胶制作了微型封隔器,并采用透明实验装置实时观察密封材料在流体压力作用下的变形、破坏和泄漏,实验观察到的破坏模式,如图17所示.图17(a)是聚二甲基硅氧烷橡胶(PDMS)微型封隔器,从泄漏过后的封隔器可以看出,在封隔器两端靠近金属隔环处,材料有轻微破坏,但是其他部分材料仍保持完整.在液体压力的作用下,另一种硅橡胶封隔器 (图 17(b))经历了非常大的变形,且有很大一部分材料被挤出低压端的金属隔环,碎成了许多小碎片,最终发生泄漏.
图17 溶胀式封隔器模型的两种失效模式[
Fig. 17 Two failure modes of mini swellable packers[
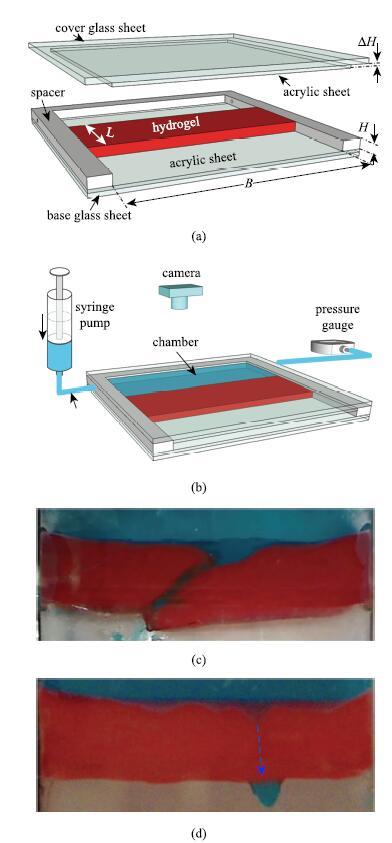
Wang等[47-48]采用了相似方法设计了一套透明实验装置,如图18所示,并利用水凝胶作为模型材料,其弹性模量比高弹体模量低了3个数量级,测试中相应的流体压力也降低了3个数量级,极大地降低了实验难度和实验成本.因此,可以利用简单的桌面实验装置进行测量.在该装置中,将水凝胶底部粘接到透明亚克力板上,两端粘接到一块U型垫片上,当垫片和盖玻片粘接到一起时,水凝胶被预压缩,以建立接触压力.水凝胶和顶部亚克力板之间没有粘接,上下两块玻璃为水凝胶提供刚性约束.水凝胶、亚克力板和垫片形成了一个密封腔体,如图18(b)所示,并通过塑料导管和注射泵以及压力计相连.
图18 透明桌面实验装置和利用该装置观察到的两种失效模式[
Fig. 18 Transparent desktop setup, and two failure modes observed by using this setup[
实验中注射泵以恒定的速率向腔体内注射水,并记录注射体积$Q_{\rm i}$和压力$p$. 同时利用数码相机记录水凝胶的变形和泄漏.Wang等[47-48]观察到断裂泄漏和弹性泄漏两种失效模式,并系统研究了几何参数和材料参数对临界泄漏压力的影响.
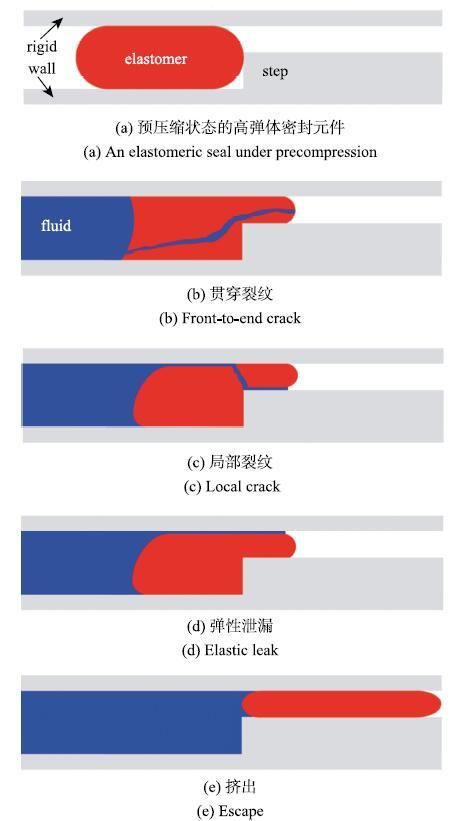
根据文献及作者的研究结果,可将高弹体密封元件的失效模式总结为图19所示的几种形式.高弹体材料被约束在两块刚性体之间,旁边的台阶阻止高弹体大变形,并防止高弹体脱离密封位置.当向高弹体一侧施加流体压力时,高弹体变形,并向低压一侧挤出.当流体压力增加到一定程度时,高压端可能萌生一条裂纹,并沿长度方向贯穿高弹体(图19(b)),从而形成一条流体泄漏通道.或者在台阶附近出现裂纹,将挤出的材料切掉,而其他部分保持完好(图19(c)).这两种失效模式在传统的橡胶密封圈也被观察到[49].
高弹体密封元件还可能在不发生任何破坏的情况下泄漏(图19(d)).
流体沿着高弹体和约束刚体之间的界面泄漏.这种模式被称为弹性泄漏,即密封元件仅因为高弹体的弹性大变形而发生泄漏[47].如果高弹体周围的约束不足,密封元件甚至有可能被挤出密封位置而泄漏(图19€).每种失效模式对应一定的临界压力,其中最低的临界压力决定了其失效模式.
2.2 高弹体封隔器的溶胀
高弹体聚合物由大量的单体通过共价键交联聚合形成三维的网状结构.当高弹体聚合物和液体接触时,高分子上的某些官能基团(如亲水性基团、亲油性基团)就会促使液体中与其亲近的小分子(溶剂)进入到高分子网络内部,导致高弹体溶胀变形,直到在外载荷和周围的化学势共同作用下达到平衡状态.高分子聚合物和溶剂小分子的集合体被称为弹性凝胶.
当凝胶承受的外力发生变化时,在短时间内,溶剂小分子还来不及在高分子网络内迁移,但是新的应力平衡状态已经建立,这一过程只涉及到高分子网络构型的改变,凝胶形状发生改变,但是体积不变;在长时间内,溶剂小分子在高分子网络中会重新分布,使得凝胶的形状和体积都发生变化,当时间足够长时,凝胶和外界机械载荷以及周围溶剂的化学势都达到平衡状态[50-51].可见,凝胶溶胀是一个复杂的热力学过程,文献[52,53,54]在热力学框架内,建立了考虑大变形和溶剂扩散的理论模型,Liu等[55]对这一理论作了系统综述,下面予以简单介绍.
取参考状态下体积为${\rm d}V( X)$的微元体作为研究对象,并忽略惯性和动能的影响,溶剂分子在高弹体网络内的扩散过程可由以下一系列方程决定:
(1) 变形梯度. 在初始构型中,一个物质点的坐标为$X$.在时间$t$,材料变形到现时状态,物质点$X$的坐标变为$X$.方程$x( X,t)$描述了聚合物网络的变形历史,材料的变形状态可用形变张量来表示,其表达式为
\begin{equation} \label{eq6} F_{iK} \left( { X,t} \right) = \frac{\partial x_i \left( { X,t} \right)}{\partial X_K }\tag{6} \end{equation}
(2) 溶剂分子守恒方程.假设在溶胀过程中没有化学反应发生,因此溶剂分子的总量应该守恒,则凝胶内部满足关系
\begin{equation} \label{eq7} \frac{\partial C\left( { X,t} \right)}{\partial t} + \frac{\partial J_K \left( { X,t} \right)}{\partial X_K } = r\left( { X,t} \right)\tag{7} \end{equation}
表面满足关系
\begin{equation} \label{eq8} J_K \left( { X,t} \right)N_K \left( X \right) = - i\left( { X,t} \right)\tag{8} \end{equation}
式中,$J_{K}( X, t)$为凝胶内溶剂分子的名义通量,$r( X,t) {\rm d}V( X)$为单位时间内注入材料微元体的溶剂分子数目,$i( X,t){\rm d}A( X)$为单位时间内从单元表面进入的分子数目.
(3) 力平衡方程. 在微元体内满足
\begin{equation} \label{eq9} \frac{\partial s_{iK} }{\partial X_K } + B_i = 0\tag{9} \end{equation} 在边界上满足 \begin{equation} \label{eq10} s_{iK} N_K = T_i\tag{10} \end{equation}
其中,$s_{iK}$为名义应力,$B_{i}$和$T_{i}$分别为施加在单元上的体力和面力在$i$方向上的分量.
(4) 局部平衡条件.当凝胶在达到溶胀平衡状态之前,凝胶中不同的材料单元处于非平衡状态,相邻的材料单元之间存在化学式梯度,会驱动液体分子在凝胶内扩散.虽然凝胶在溶胀过程中整体上处于非平衡状态,但是凝胶内部的材料微元体可以认为处于平衡状态中.这是因为流体的扩散是一个非常缓慢的过程.材料的惯性可以忽略,材料微元内部的黏弹性过程有足够的时间松弛,微元体内部的液体分子也有足够的时间和周围的化学势平衡.因此有
\begin{equation} \label{eq11} s_{iK} = \frac{\partial W\left( { F,C} \right)}{\partial F_{iK} }\tag{11} \end{equation} \begin{equation} \label{eq12} \mu = \frac{\partial W\left( { F,C} \right)}{\partial C}\tag{12} \end{equation}
式中,$W( F,C)$为凝胶的自由能密度函数,$\mu $为溶剂的化学势.需要说明的是,除了本节外,本文其他部分的$\mu $代表材料的剪切模量.
(5) 扩散动力学方程. 在现时构形中,扩散通量$j$与化学势$\mu$的关系为[56]
\begin{equation} \label{eq13} j_i = - \frac{cD}{kT}\frac{\partial \mu }{\partial x_i }\tag{13} \end{equation}
式中,$c$为现时构形中单位体积内的溶剂分子数量,$D$为扩散系数,$k$为玻尔兹曼常数,$T$为热力学温度.
(6) 不可压缩条件. 假设凝胶中的所有分子都是不可压缩的.因此,凝胶的体积等于纯高分子网络的体积加上吸收的溶剂的体积,则有
\begin{equation} \label{eq14} 1 + \nu C = \det \left( F \right)\tag{14} \end{equation}
(7) 应变能密度函数.凝胶的自由能来自于两种分子过程:高分子网络的拉伸变形和高分子网络与液体小分子的混合.根据Flory和Rehner[57]的理论,自由能函数可以采用如下的形式
\begin{equation} \label{eq15} W\left( { F,C} \right) = W_{\rm s} \left( F \right) + W_{\rm m} \left( C \right)\tag{15} \end{equation}
拉伸网络的自由能函数$W_{\rm s}( F)$可采用常用的高分子聚合物的自由能函数[58-63].对于凝胶,通常采用Flory模型[64]来代表其形变自由能
\begin{equation} \label{eq16} W_{\rm s} = \frac{1}{2}NkT\left[ {F_{iK} F_{iK} - 3 - 2\lg \left( {\det \left( F \right)} \right)} \right]\tag{16} \end{equation}
除Flory模型外,还有Neo-Hooken模型[58]、Gent模型[59]、Mooney-Rivlin模型[60-61]、Ogden模型[62]、Arruda-Boyce模型[63]等.不同材料模型对不同应变区域的应力应变关系描述精度有所不同,因此需要根据具体问题,选用合适的材料模型.如果考虑材料的黏弹性和Mullins效应,则需要新的材料模型[65-66].常用的混合自由能函数为[67-68]
\begin{equation} \label{eq17} W_{\rm m} \left( C \right) = - \frac{kT}{\nu }\left[ {\nu C\log \left( {1 + \frac{1}{\nu C}} \right) + \frac{\chi }{1 + \nu C}} \right]\tag{17} \end{equation}
其中,$\chi $为无量纲参数. 当$\chi <0$时,混合能驱动液体进入凝胶内部;当$\chi> 0$时,混合能驱动液体从凝胶内部向外扩散.
基于上述方程,以及具体问题的边界条件和初始条件,可以确定高弹体溶胀的控制方程,模型中的相关参数可以通过实验测量得到[69-70].但是,由于封隔器的构型和边界条件比较复杂,难以得到简单的解析解.通常做法是将这些材料模型植入到有限元软件中,通过数值计算来预测封隔器建立密封状态的时间和接触压力的变化过程[71-76].
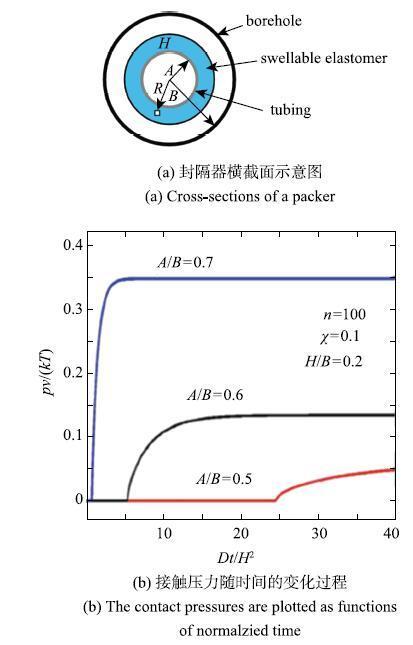
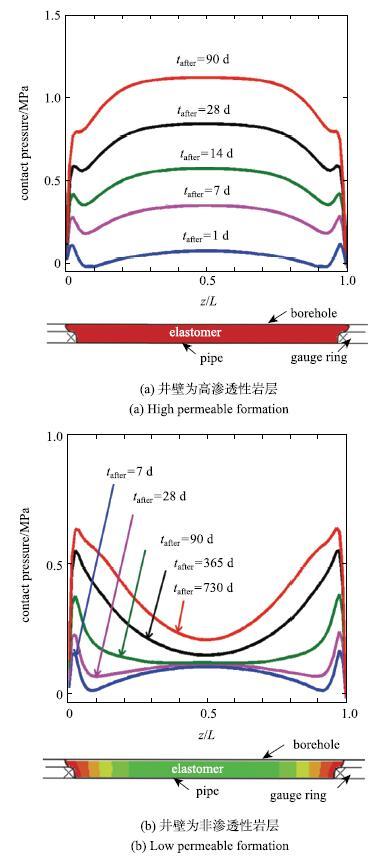
Cai等[73]采用平面应变模型,即假设高弹体聚合物沿着套管轴向均匀溶胀,计算了高弹体封隔器的溶胀过程,如图20所示.当井眼尺寸和高弹体厚度比一定时,封隔器和井壁之间的初始间隙越小,高弹体就越早和井壁接触,并且接触压力越大.Lou和Chester[76]采用Chester等[75]开发的ABAQUS用户子程序,计算了高弹体封隔器的溶胀过程中,密封元件长度方向的接触压力分布随时间的变化过程.在计算中,他们采用了可渗透性和非渗透性两种不同的岩层边界条件.结果表明,当井壁被设定为可渗透性岩层时,溶胀较快,最大接触压力在封隔器的中部,如图21所示.当岩层不具有渗透性时,聚合物溶胀相当缓慢,且最大接触压力在高弹体两端接近金属隔环处,这说明中间部分的材料没有充分溶胀,密封效果比较差.由多孔弹性理论[50-51]可知,当岩层具有渗透性时,高弹体靠近井壁的界面能够接触井下流体,溶剂分子主要从井壁向内侧扩散,高弹体溶胀的特征时间尺度为$t~H^{2}/D$,其中$H$为高弹体的厚度,$D$为溶剂在高弹体中的扩散系数.当井壁不具有渗透性或渗透率很低时,高弹体只有靠近金属隔环处与井下流体接触,溶剂分子主要从高弹体元件两端向中间扩散,高弹体溶胀的特征时间为$t~L^{2}/D$,其中$L$为高弹体元件的长度.对于高弹体封隔器,$L$远大于$H$.可见,井壁的渗透性以及封隔器的长度对于封隔器的溶胀速度和最后的封隔效果有非常重要的影响.这也说明以前实验中利用金属或玻璃套管模拟井壁具有一定的局限性,不能模拟高渗透性岩层情况.
图20 利用平面应变模型计算封隔器中的高弹体材料的溶胀过程[
Fig. 20 Swelling process of elastomer in a swellable packer under plane strain condition[
图21 高弹体封隔器长度方向的接触压力分布示意图[
Fig. 21 The distribution of contact pressure along the length of a packer[
2.3 高弹体封隔器的变形
当高弹体和井壁或者外侧套管壁接触并建立一定接触压力后,能够阻止封隔器两端的流体向另一侧流动,并维持一定的压力差.在一侧高压作用下,高弹体会变形,且随着流体压力的增大而增大.当压力差到达临界值后,封隔器会由于高弹体变形过大或断裂而泄漏.
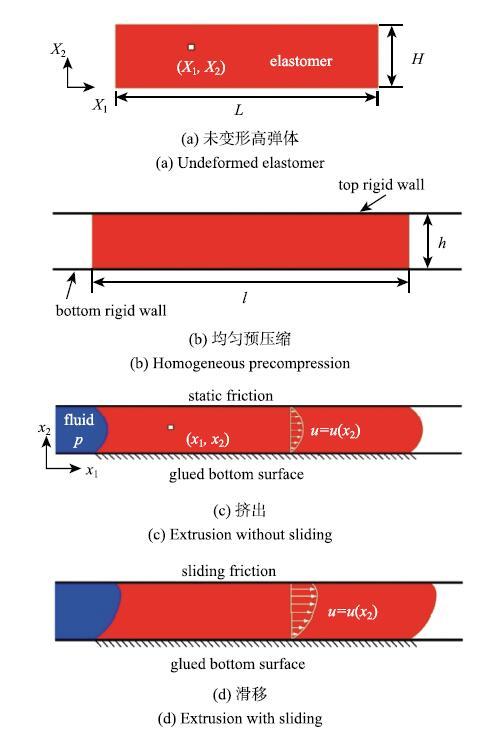
Wang等[48]建立了一个高弹体密封的理论模型.该模型能完整描述高弹体密封元件在流体压力下的挤出变形,高弹体和刚性墙界面的相对滑动,裂纹的萌生和传播过程.如图22所示,考虑一块初始长度为$L$,高度为$H$,厚度为$B$的高弹体.假设高弹体沿厚度方向均匀变形,因此只用考虑其一个截面,这可简化为平面应变问题.高弹体被放置于两块刚性墙之间,并被压缩至高度为$h$,长度为$l$.由于高弹体的不可压缩性,$LH = lh$,其延伸率$\lambda = h/H =L/l$,可作为表征高弹体预压缩程度量.为了获得显式理论解,Wang等[48]假设高弹体在预压缩过程中变形均匀.预压缩之后,高弹体和底面刚性墙粘接.由于材料不可压缩,任何均匀的静水压力不会对其变形有影响.高弹体沿着其长度方向承受一定的压力差,如图22(c)所示,高弹体左侧的液体压力相对于环境压力为$p$,右侧为环境压力.当流体压力较小时,高弹体和顶部刚性墙之间的静摩擦力阻止两者相对滑动,高弹体仅发生挤出变形.当流体压力较大时,高弹体相对于顶部刚性墙滑移,如图22(d)所示.
图22 高弹体密封元件受预压缩后在流体压力作用下的变形和滑动示意图[
Fig. 22 The extrusion and sliding of a piece of precompressed elastomer under fluid pressure[
密封元件在流体压力下的响应过程也需要利用状态变量来描述.由于材料变形的非均匀性,密封元件的变形状态不能用某一点的应变状态来描述.模型中用高弹体的挤出体积$Q$,即高弹体穿过某一竖直平面的体积,来代表其变形状态.对于不可压缩材料,$Q$ 沿$x_{1}$方向处处相等.$p-Q$曲线,即流体压力--挤出体积曲线,能客观描述一个密封元件的力学行为,且容易在实验中测量.
高弹体和刚性墙之间的摩擦力阻止两者的相对滑动,且影响密封元件的封隔能力.模型中假设滑动摩擦力$\tau$为常数,这常用于复合材料模型中[77],并且和凝胶类材料的摩擦实验结果相符合[78-79].
在模型中,高弹体的变形场仅是$x_{2}$的函数,并适用于不可压缩材料.对于溶胀式封隔器,短时间内的变形可以忽略其多孔弹性,当做是不可压缩的.采用Neo-Hookean材料模型,可得$p-Q$关系为
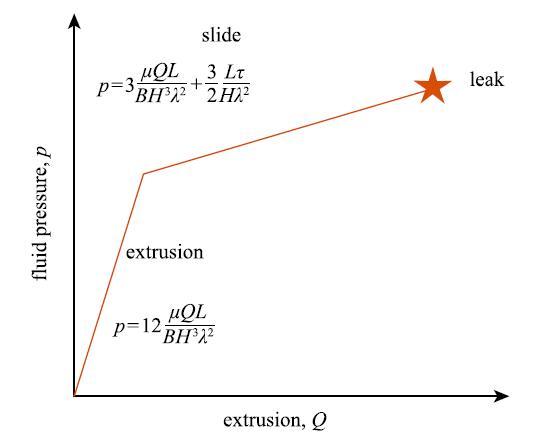
\begin{equation} \label{eq18} p = \left\{ {{\begin{array}{ll} 12\dfrac{\mu QL}{BH^3\lambda ^2}, & p < \dfrac{2L\tau }{H\lambda ^2} \\[3mm] 3\dfrac{\mu QL}{BH^3\lambda ^2} + \dfrac{3}{2}\dfrac{L\tau }{H\lambda ^2}, & p > \dfrac{2L\tau }{H\lambda ^2}\\ \end{array} }} \right.\tag{18} \end{equation}
式中$p = {2L\tau }/{\left( {H\lambda ^2}\right)}$为界面滑移的临界条件. 如果$p < {2L\tau }/{\left({H\lambda ^2} \right)}$,则界面无相对滑移,$u\left( h \right) =0$,界面静摩擦力$\sigma _{12} \left( h \right) = { - pH\lambda ^2}/{\left( {2L} \right)}$. $p > {2L\tau }/{\left( {H\lambda ^2}\right)}$时,滑动摩擦力为常数,$\sigma _{12} \left( h \right) = -\tau $. $p-Q$为双线性关系,如图23所示.当高弹体界面开始滑动时,斜率发生变化. 剪切模量$\mu $影响两个阶段的斜率,界面滑动摩擦力影响滑动阶段直线的截距.滑动阶段的直线随着$Q$线性增加,直到开始泄漏.
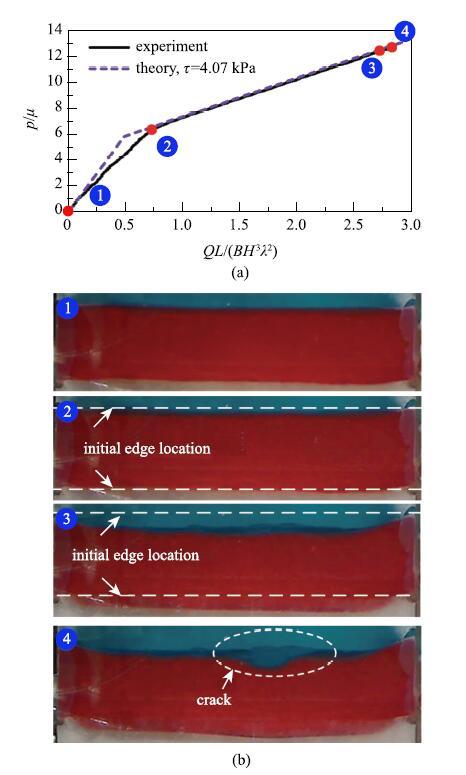
理论上高弹体的挤出体积$Q$等于注入密封腔体内的液体体积$Q_{\rm i}$,但是采用如图18所示的实验装置时,塑料导管在液体压力下也会膨胀,因此部分注入的液体体积,$Q_{\rm s}$,被消耗在了导管中,注入密封腔体的水的体积$Q = Q_{\rm i}-Q_{\rm s}$.实验测量和理论预测的$p-Q$曲线的比较如图24(a)所示,两者吻合较好.相应的变形过程如图24(b)所示,当流体压力比较小时(①-②),几乎观察不到水凝胶的变形;而当流体压力比较大时(②-③),水凝胶在液体压力驱动下向下滑动,直到水凝胶发生断裂(④).这一过程与理论模型假设一致.
图24 理论预测和实验测量的$p-Q$曲线比较;(b)水凝胶的变形和破坏过程[
Fig. 24 (a) Comparison between the theoretical prediction and experimental measurement on $p-Q$ relation; (b) The deformation and fracture of a hydrogel sample[
2.4 高弹体封隔器的泄漏
如第2.1节所述,当流体压力达到临界值时,高弹体密封元件可能会出现多种形式的泄漏.若不考虑隔环的影响,主要有断裂泄漏和弹性泄漏两种模式[47-48].下面介绍两种泄漏模式.
(1) 断裂泄漏.
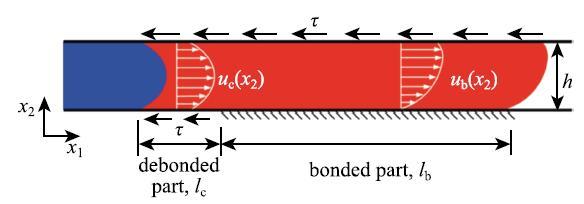
实验中观察到的断裂泄漏过程比较复杂[48],可以分成两个阶段:第一阶段在密封元件高压端底部附近产生一条裂纹,该裂纹平行于底部刚性墙向前传播;第二阶段该裂纹转换成一条垂直于底面的裂纹,贯穿整个密封元件.Wang等[48]分析了第一阶段裂纹传播的临界条件,理论模型如图25所示,一条裂纹位于高弹体高压一侧靠近底部的地方,长度为$l_{\rm c}$.
除了裂尖附近和高弹体两端附近,断裂区域和未断裂区域的位移场均独立于$x_{1}$.利用平衡方程和边界条件可以得到两个区域的位移场,并进一步计算出裂尖能量释放率.当能量释放率达到材料的断裂能时,裂纹开始扩展.利用该临界条件可得裂纹扩展时的临界流体压力[48]
\begin{equation} \label{eq19} p_f = \frac{\sqrt 6 }{\lambda }\sqrt {\frac{\varGamma \mu }{H}} \frac{L}{H} + \frac{2\tau L}{H\lambda ^2}\tag{19} \end{equation}
Wang等[48]系统测试了材料参数和几何参数对临界泄漏压力的影响,几何参数的影响如图26所示,可见理论预测与实验非常吻合.说明该模型能较好预测断裂泄漏的临界条件,对高弹体封隔器的设计能提供一定的指导.
图26 临界泄漏压力和几何参数的关系.黑点为实验结果,紫线为理论预测[
Fig. 26 The relations between leak pressures and geometrical parameters. Solid dots are experimental results, purple lines are theoretical predictions[
(2) 弹性泄漏.
人们将发生泄漏的封隔器从井下回收进行观察,发现一些出现泄漏的封隔器并没有发生任何破坏,或仅在靠近金属隔环的地方有轻微的破坏,绝大部分都保持完好.这困扰了技术人员很长一段时间:在材料没有破坏的情况下,井下流体是如何穿过高弹体封隔元件而泄漏的?
在经典密封理论[49]中,高弹体密封元件被放置在需要密封的两块配件之间,并被压缩一定的位移,如图27(a)所示.
图27 (a)$\sim$(c) 经典密封理论和 (d)$\sim$(f) 弹性泄漏原理示意图
Fig. 27 Schematics of (a)$\sim$(c) classical sealing theory and (d)$\sim$(f) elastic leak
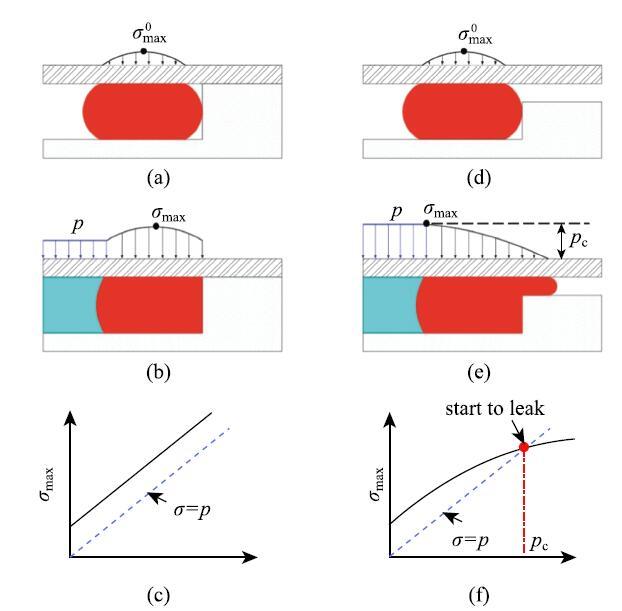
高弹体和相邻配件之间的接触面上建立起一定的接触压力分布,此时的最大接触压力记为$\sigma_{\max }^0 $.在理想状况下,两个配件的配合面之间的间隙足够小,高弹体元件被约束在密封槽内,不会被挤出.由于高弹体的剪切模量较小,容易变形,而体积模量远大于剪切模量,不容易被压缩.因此当密封腔体内的压力增加为$p$时,相当于在高弹体周围增加了大小为$p$的静水压力,如图27(b)所示,最大接触压力变为
\begin{equation} \label{eq20} \sigma _{\max } = \sigma _{\max }^0 + p\tag{20} \end{equation}
式中,$\sigma _{\max }$和流体压力$p$的关系如图27 (c)所示,可见最大接触压力大于流体压力.在这种状况下,密封腔体内的流体没办法穿过密封元件和相邻配合面间的界面而泄漏.因此,不管流体压力增加到多大,都不会发生泄漏.
实际上,两个配件的结合面不可能完美接触,会存在一定的间隙,如图27(d)所示.在传统密封装置中,可以通过尽量提高加工精度来减小间隙量,从而降低材料挤出效应带来的影响.但是,对于高弹体石油封隔器,其初始直径需要小于井眼直径以便于将封隔器放入井下预定位置.同时,井下密封环境在作业之前是很难预测的,如井眼尺寸的变化、金属隔环的损坏等.因此,金属隔环和井壁间的间隙是不可避免的.针对传统高弹体密封元件,人们已经给出了密封元件的接触压力分布和材料挤出效应对接触压力的影响[80-82],但是对接触压力的变化和泄漏之间的联系还缺乏深入的理解.Liu等[47]实时观察了弹性泄漏过程,如图28所示,并阐释了弹性泄漏的机理,如图27(d)$\sim$图27(f)所示.在不考虑界面摩擦和黏附力的情况下,当高弹体被预压缩时,会在高弹体和相邻接合面间建立一定的接触压力,此时的最大接触压力为$\sigma _{\max }^0 $,位于接触面的中间位置.当左侧流体压力$p$开始增大时,接触压力也会随之增大.但是,由于高弹体存在一定的变形空间,部分材料被挤入右边两个接合面间的间隙里,材料变形导致接触压力增加的速度小于流体压力的增加速度,如图27(f)所示,且最大接触压力的位置向左侧移动.当流体压力增加到临界值$p_{\rm c}$时,最大接触压力等于流体压力,其位置移动到最左侧.此时如果有一小滴流体因扰动而进入配合界面时,就会在逐渐减小的接触压力作用下穿过整个接触面而泄漏.因此,发生弹性泄漏的临界条件为
\begin{equation} \label{eq21} p_{\rm c} = \sigma _{\max }\tag{21} \end{equation}
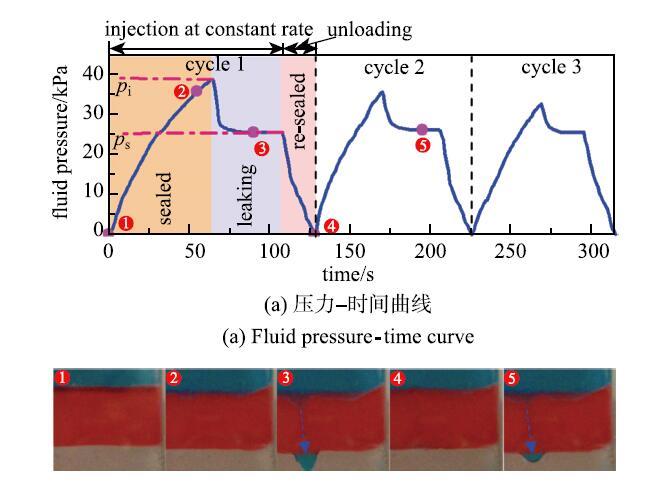
由于界面摩擦力和黏附力的影响,流体压力达到某一峰值$p_{\rm i}$后开始泄漏,如图28所示,泄漏瞬间流体压力迅速降低并维持在平台$p_{\rm s}$.这是因为泄漏到达稳态阶段后,界面之间形成了稳定的流体通道,界面摩擦力和黏附力的影响消失.在泄漏过程中密封元件仍然能维持其临界压力差,与理论模型相比,$p_{\rm s} = p_{\rm c}$. 如果流体压力一旦小于$p_{\rm s}$,泄漏就会立即停止.当重新加载时,泄漏峰值压力略有降低,但平台压力$p_{\rm s}$基本不变.这说明除了初始泄漏压力会受到摩擦力和黏附力等非弹性因素的影响,在稳态阶段,泄漏过程是纯弹性,可逆的.
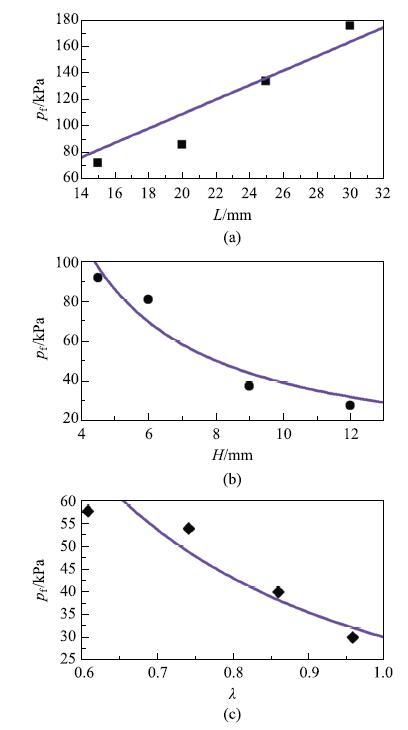
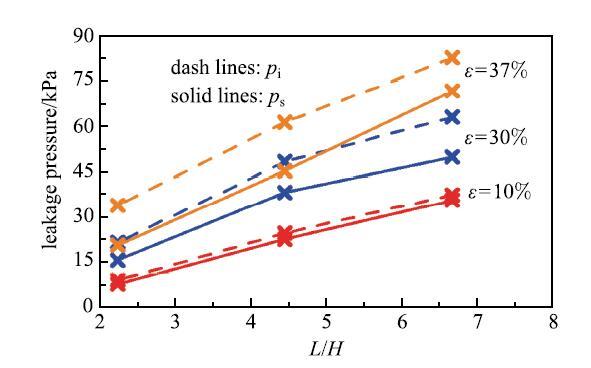
实验发现,该临界条件在一定范围内不受流体注入速度的影响,只跟密封元件的材料和几何参数有关.因此,弹性泄漏问题可以转化为一个纯弹性边值问题,只需要对高弹体进行分析,通过弹性理论得到该临界条件,就可以确定该密封元件发生弹性泄漏的临界压力.实验发现,临界压力随着密封元件的长度几乎线性增长,随着预压缩应变的增大而增大(图29),即增加密封元件的长度或者提高初始接触压力就可以提高密封元件的封隔能力.
图29 几何参数对泄漏压力的影响[
Fig. 29 Effects of geometric parameters on the leak pressure[
2.5 弹性泄漏的应用
为了提高封隔器的封隔能力,一种直观的方法就是增大高弹体元件的长度,称之为连续设计.然而,随着长度的增大,制造和运输将变得困难,成本也随之大幅度上升.此外,过长的封隔器在下井作业中被卡住的风险也会明显增加.如2.2节所述,当井壁渗透性较差时,封隔器中间部分的高弹体达到溶胀平衡所需时间会随着高弹体长度的增长而显著增加.另一种方法是将若干个较短的封隔器串联在套管上,称之为分布式设计,如图30(a) 所示. 相对于连续设计,分布式设计可以避免连续设计中的上述问题.更重要的是,这种设计可以使封隔器设计模块化.连续设计要根据需要封隔的压力差来调整高弹体的长度,使得封隔器设计和生产变得非常复杂.而分布式设计可设计生产标准封隔元件,实际应用中可根据需要封隔的压力差来选择串联的封隔器个数.
当串联封隔器间的间隙充满不可压缩流体时(例如水),需要封隔的压力差就可以几乎均匀的分布在各个封隔器上.在这种情况下,相对于弹性元件总长一样的连续封隔器,分布式封隔器理论上能够承受更大的压力差,因为在分布式封隔器中有更多的金属隔环来约束弹性体的变形.然而,实际情况中井下流体大部分是高度可压缩的,例如天然气、油气混合物等[83-84],因此加载于封隔器一侧的高压不能被传递到后面的封隔器上,只有高压端的第一个封隔器承受压力差.当第一个封隔器破坏后,后面的封隔器--跟着接连失效.
Wang等[85]提出可以利用弹性泄漏来提高分布式封隔器的封隔能力,并通过实验进行了验证.当若干个串联的封隔器完成初始密封后,两个封隔器间的空隙充满了液/气混合物,如图30(a) 所示.假设第一个封隔器左侧的液体以恒定流速注入,液体压力$p_{1}$会随之增大. 在初始阶段,液体压力主要施加在第一个封隔器上.因为中间液/气混合物是高度可压缩的,第一个封隔器的弹性体变形对流体挤压所造成的压力变化可以忽略不计.如果串联的封隔器发生弹性泄漏,当第一个封隔器两端的压力差 $p_{1}$-- $p_{2}$达到临界值后,第一个封隔器中的高弹体和井壁会在局部失去接触,形成一个很窄的泄漏通道.这种弹性泄漏是由于高弹体的弹性变形造成的,没有材料破坏,在泄漏过程中封隔器左右两侧仍能保持恒定的压力差.泄漏的液体注入两个封隔器中间的空隙, $p_{2}$开始增加,第二个封隔器开始承压并发生弹性变形,如图30(b) 所示.$p_{1}$ 随着 $p_{2}$ 进一步升高,直到 $p_{2}$达到某一临界值开始泄漏.可以设想,如果有更多封隔器串联在一起,随着后面封隔器逐步被激发承载,所有的封隔器能够均匀的承担外加压力,所承载的压力总和 $p_{1 }$能够上升到更高的水平.
然而,如果单个封隔器的失效模式为断裂泄漏时,串联封隔器无法提高封隔能力.同弹性泄漏一样,在初始阶段,液体压力$p_{1}$主要施加在第一个封隔器上,但是当第一个封隔器发生泄漏后,压力分布和弹性泄漏中的情况会变得完全不一样,如图30(c)所示.材料断裂会形成永久性泄漏通道,第一个封隔器不能再继续承担任何压力差,即$p_{1}=p_{2}$,所有的外加压力全部施加在第二个封隔器上,直到第二个封隔器同样发生断裂破坏.在这种情况下,不管有多少个封隔器串联在一起,在任何时刻都只有其中一个封隔器承载着绝大部分的外加压力,封隔器会从高压端依次破坏,达不到提高封隔能力的目的.
2.6 高弹体封隔器中的失稳现象
软材料在溶胀或外力作用下,会出现多种失稳现象,如曲屈、褶皱、折痕、凸脊、指形失稳等.这些现象及其力学机理已被广泛研究[86-94].人们观察了凝胶或高弹体的失稳现象,并进行了理论解释[88],以避免失稳带来的灾害[95-98],甚至利用可控的失稳形成预先设计的复杂图形,进行结构的自组装和制造[99-102].
在溶胀过程中和工作压力作用下,高弹体密封元件也会出现多种失稳现象.Druecke等[46]观察到高弹体在受约束溶胀时会产生非均匀形变,形成向前突出的尖端(图31).在流体压力的作用下,密封元件也会出现周期或局部的失稳(图32)[47].这些失稳会造成局部大变形,可能会对临界泄漏压力产生重要影响.如图32所示,弹性泄漏通道都在失稳变形的尖端产生.但是,到目前为止还没有任何研究考虑失稳对高弹体泄漏的影响,需要在未来的研究中予以考虑.
图31 高弹体封隔器溶胀过程中的失稳现象[
Fig. 31 Instability formed in the swelling of an elastomeric packer[
3 小 结
油气井密封在油气开采中具有重要作用.特别是对于深海或页岩油/气开采,急需具有更好可控性、更高封隔能力的密封器件来保证作业安全,同时降低开采成本以提高经济效益.本文综述了水泥和高弹体油气井密封结构的变形与失效行为的最新研究进展,包括水泥环固化过程中的应力演化、生产作业导致的应力、水泥环的失效模式和失效判据,高弹体封隔器的实验方法、失效模式、溶胀、变形、断裂、弹性泄漏及其应用等.
总的来说,水泥密封历史悠久且研究相对较充分,溶胀式高弹体密封则是一种新技术且逐渐得到了学术和工程界的重视.相比之下,人们对溶胀式高弹体封隔器设计及相关的基础理论研究尚不充分,影响高弹体封隔器力学性能的关键参数和失效机理还缺乏系统、深入的理解,不足以对越来越具有挑战性的工程设计提供有效的指导,还有很多重要的基础问题需要进一步研究.
力学是工程科学,在国家重大需求和国民经济主战场中发挥了并且还将继续发挥十分重要的作用.学科交叉是一种趋势,力学与其他学科交叉的例子很多.希望本文能为促进力学与其他学科的交叉提供参考.
The authors have declared that no competing interests exist.
参考文献
| [1] |
International energy outlook |
| [2] |
Horizontal directional drilling: Profile of an emerging industry . |
| [3] |
Hydraulic fracturing: The fuss, the facts, the future . |
| [4] |
An Overview of Hydraulic Fracturing and Other Formation Stimulation Technologies for Shale Gas Production .
|
| [5] |
Hydraulic fracturing: History of an enduring technology .
|
| [6] |
基于离散裂缝的多段压裂水平井数值试井模型及应用 .URL 摘要
水平井压裂技术已经成为开发低渗透油气藏、页岩气藏和致密气场等非常规油气藏的关键技术.基于离散裂缝模型,对裂缝进行简化,建立了二维多段压裂水平井有限导流裂缝数值试井模型,利用有限元方法求解模型,获得多段压裂水平井试井理论曲线和压力场特征.分析表明:多段压裂水平井的试井理论曲线一共分为7个阶段:井筒储存段、裂缝线性流段、裂缝–地层双线性流段、裂缝干扰段、地层线性流段、系统径向流段和边界作用段,其中裂缝–地层双线性流段和裂缝干扰段是其典型特征.分析了裂缝数量、裂缝间距、裂缝不对称、裂缝不等长和裂缝部分缺失等因素对试井理论曲线的影响,结果表明:裂缝数量和裂缝间距对试井理论曲线的影响最大.较多的裂缝、较大裂缝间距、对称的裂缝和等长的裂缝有利于降低压裂水平井井底的流动阻力,提高产能.将建立的数值试井模型应用于四川盆地一口多段压裂水平井的压力恢复测试的数值试井解释,结果表明:本文建立的模型可以较好地拟合压力恢复测试数据,可以获得裂缝的导流能力和裂缝长度,为压裂效果评价和压裂设计提供指导.
A numerical well test model for multi-fractured horizontal wells based on discrete-fracture model and its application .URL 摘要
水平井压裂技术已经成为开发低渗透油气藏、页岩气藏和致密气场等非常规油气藏的关键技术.基于离散裂缝模型,对裂缝进行简化,建立了二维多段压裂水平井有限导流裂缝数值试井模型,利用有限元方法求解模型,获得多段压裂水平井试井理论曲线和压力场特征.分析表明:多段压裂水平井的试井理论曲线一共分为7个阶段:井筒储存段、裂缝线性流段、裂缝–地层双线性流段、裂缝干扰段、地层线性流段、系统径向流段和边界作用段,其中裂缝–地层双线性流段和裂缝干扰段是其典型特征.分析了裂缝数量、裂缝间距、裂缝不对称、裂缝不等长和裂缝部分缺失等因素对试井理论曲线的影响,结果表明:裂缝数量和裂缝间距对试井理论曲线的影响最大.较多的裂缝、较大裂缝间距、对称的裂缝和等长的裂缝有利于降低压裂水平井井底的流动阻力,提高产能.将建立的数值试井模型应用于四川盆地一口多段压裂水平井的压力恢复测试的数值试井解释,结果表明:本文建立的模型可以较好地拟合压力恢复测试数据,可以获得裂缝的导流能力和裂缝长度,为压裂效果评价和压裂设计提供指导.
|
| [7] |
基于孔与裂隙网络模型的平行微裂隙对驱油的影响规律研究 .
认识双重多孔介质中油水两相微观渗流机制是回答形成什么类型的裂隙网络可提高油藏采收率的关键. 微裂隙的分布可以提高多孔介质的绝对渗透率,但对于基质孔隙中的流体介质,微裂隙的存在会引起多孔介质中局部流体压力和流场的变化,导致局部流动以微裂隙流动为主,甚至出现窜流现象,降低驱油效率. 本文基于孔与裂隙双重网络模型,在网络进口设定两条平行等长且具有一定间隔的微裂隙,分析微裂隙的相对间隔(微裂隙之间距离/喉道长度)和微裂隙相对长度(微裂隙长度/喉道长度)对于微观渗流特征的影响. 结果表明:随微裂隙相对长度的增加,出现驱油效率逐渐降低,相对渗透率曲线中的油水共渗区水饱和度和等渗点增加,油水两相的共渗范围减小等现象;随着微裂隙之间相对间隔增大,周围越来越多的基质孔穴间的压力差减小,在毛管压力的限制下,驱替相绕过这些区域,而导致水窜现象.
Effect of parallel micro-fractures on flooding based on pore-fracture network model .
认识双重多孔介质中油水两相微观渗流机制是回答形成什么类型的裂隙网络可提高油藏采收率的关键. 微裂隙的分布可以提高多孔介质的绝对渗透率,但对于基质孔隙中的流体介质,微裂隙的存在会引起多孔介质中局部流体压力和流场的变化,导致局部流动以微裂隙流动为主,甚至出现窜流现象,降低驱油效率. 本文基于孔与裂隙双重网络模型,在网络进口设定两条平行等长且具有一定间隔的微裂隙,分析微裂隙的相对间隔(微裂隙之间距离/喉道长度)和微裂隙相对长度(微裂隙长度/喉道长度)对于微观渗流特征的影响. 结果表明:随微裂隙相对长度的增加,出现驱油效率逐渐降低,相对渗透率曲线中的油水共渗区水饱和度和等渗点增加,油水两相的共渗范围减小等现象;随着微裂隙之间相对间隔增大,周围越来越多的基质孔穴间的压力差减小,在毛管压力的限制下,驱替相绕过这些区域,而导致水窜现象.
|
| [8] |
Stimuli-responsive cement-reinforced rubber .
In this work, we report the successful development of a cement鈥搑ubber reactive composite with reversible mechanical properties. Initially, the composite behaves like rubber containing inert filler, but when exposed to water, it increases in volume and reaches a stiffness that is intermediate between that of hydrogenated nitrile butadiene rubber (HNBR) and hydrated cement, while maintaining a relatively large ductility characteristic of rubber. After drying, the modulus increases even further up to 400 MPa. Wet/drying cycles prove that the elastic modulus can reversibly change between 150 and 400 MPa. Utilizing attenuated total reflection Fourier transform infrared spectroscopy), we demonstrate that the high pH produced by the hydration of cement triggers the hydrolysis of the rubber nitrile groups into carboxylate anions. Thus, the salt bridges, generated between the carboxylate anions of the elastomer and the cations of the filler, are responsible for the reversible variations in volume and elastic modul...
|
| [9] |
The evolution of the role of openhole packers in advanced horizontal completions: From novel technology to a critical key to success . |
| [10] |
|
| [11] |
Deployment of swelling elastomer packers . |
| [12] |
The end of cheap oil .
Not Available
|
| [13] |
Global oil & gas depletion: An overview . |
| [14] |
页岩气高效开采的力学问题与挑战 .
页岩气是指赋存于富含有机质泥页岩中以吸附和游离状态为主要存在方式的天然气,中国资源量丰富,地域分布广泛.页岩气开采能缓解我国常规油气产量不足、煤化石燃料引起环境污染等问题,已成为中国绿色能源开发的重要领域.尽管北美页岩气"革命"取得了成功,目前也仅有预期产量5%~15%的采收率.与北美地区相比,中国页岩气埋藏深,赋存条件差,自然丰度低,因此,高效开采面临更多的困难和挑战.近年来,围绕国家重大能源战略需求,瞄准技术发展前沿,学术界和工业界联合对页岩气高效开采的关键科学和技术问题展开研究.本文结合近三年四川、重庆地区的页岩气试验区块遇到的新问题,针对中国未来3500 m以下深部开采的新挑战,如地质沉积、裂缝发育构造不同、上覆压力增加、水平应力场变化等新问题,介绍和总结了目前中国页岩气高效开采面临的力学科学问题,主要包括多重耦合下的安全优质钻完井力学理论和方法、水力压裂体积改造和多尺度缝网形成机制、多尺度渗流力学特性与解吸附机理等."深部页岩气高效开采"的研究面向国家重大能源需求,科学意义重大,工程背景明确,需要工程力学、石油工程、地球物理、化学工程和环境工程等多学科专家合作,开展理论研究、物理模拟、数值模拟及现场试验等综合应用基础研究,取得高效开采页岩油气理论与技术的突破.学科交叉是研究页岩气高效开采问题、突破技术瓶颈的桥梁,只有力学与石油工程、地球科学等学科实现深度交叉融合,才能更加有效地推动页岩油气等非常规油气资源的开发.
Problems and challenges of mechanics in shale gas efficient exploitation .
页岩气是指赋存于富含有机质泥页岩中以吸附和游离状态为主要存在方式的天然气,中国资源量丰富,地域分布广泛.页岩气开采能缓解我国常规油气产量不足、煤化石燃料引起环境污染等问题,已成为中国绿色能源开发的重要领域.尽管北美页岩气"革命"取得了成功,目前也仅有预期产量5%~15%的采收率.与北美地区相比,中国页岩气埋藏深,赋存条件差,自然丰度低,因此,高效开采面临更多的困难和挑战.近年来,围绕国家重大能源战略需求,瞄准技术发展前沿,学术界和工业界联合对页岩气高效开采的关键科学和技术问题展开研究.本文结合近三年四川、重庆地区的页岩气试验区块遇到的新问题,针对中国未来3500 m以下深部开采的新挑战,如地质沉积、裂缝发育构造不同、上覆压力增加、水平应力场变化等新问题,介绍和总结了目前中国页岩气高效开采面临的力学科学问题,主要包括多重耦合下的安全优质钻完井力学理论和方法、水力压裂体积改造和多尺度缝网形成机制、多尺度渗流力学特性与解吸附机理等."深部页岩气高效开采"的研究面向国家重大能源需求,科学意义重大,工程背景明确,需要工程力学、石油工程、地球物理、化学工程和环境工程等多学科专家合作,开展理论研究、物理模拟、数值模拟及现场试验等综合应用基础研究,取得高效开采页岩油气理论与技术的突破.学科交叉是研究页岩气高效开采问题、突破技术瓶颈的桥梁,只有力学与石油工程、地球科学等学科实现深度交叉融合,才能更加有效地推动页岩油气等非常规油气资源的开发.
|
| [15] |
|
| [16] |
Options for high-temperature well stimulation . |
| [17] |
Cement sheath integrity for CO$_{2}$ storage -- an integrated perspective .
Two types of mechanisms could lead to loss of cement-sheath integrity: mechanical and chemical degradations. However, chemical degradation by CO2 does not seem to be a real threat when the cement sheath is initially without default. Hence, it is important to understand the mechanical mechanisms that could lead to loss of cement-sheath integrity before and during CO2 sequestration. This is with this objective that Total has developed an integrated perspective whereby all events in the life of the well, are scrutinized. The description of this perspective is the objective of this paper.
|
| [18] |
Assessment and risk analysis of casing and cement impairment in oil and gas wells in pennsylvania, 2000--2012 . |
| [19] |
Increased stray gas abundance in a subset of drinking water wells near marcellus shale gas extraction .
Horizontal drilling and hydraulic fracturing are transforming energy production, but their potential environmental effects remain controversial. We analyzed 141 drinking water wells across the Appalachian Plateaus physiographic province of northeastern Pennsylvania, examining natural gas concentrations and isotopic signatures with proximity to shale gas wells. Methane was detected in 82% of drinking water samples, with average concentrations six times higher for homes <1 km from natural gas wells (P = 0.0006). Ethane was 23 times higher in homes <1 km from gas wells (P = 0.0013); propane was detected in 10 water wells, all within approximately 1 km distance (P = 0.01). Of three factors previously proposed to influence gas concentrations in shallow groundwater (distances to gas wells, valley bottoms, and the Appalachian Structural Front, a proxy for tectonic deformation), distance to gas wells was highly significant for methane concentrations (P = 0.007; multiple regression), whereas distances to valley bottoms and the Appalachian Structural Front were not significant (P = 0.27 and P = 0.11, respectively). Distance to gas wells was also the most significant factor for Pearson and Spearman correlation analyses (P < 0.01). For ethane concentrations, distance to gas wells was the only statistically significant factor (P < 0.005). Isotopic signatures (delta C-13-CH4, delta C-13-C2H6, and delta H-2-CH4), hydrocarbon ratios (methane to ethane and propane), and the ratio of the noble gas He-4 to CH4 in groundwater were characteristic of a thermally postmature Marcellus-like source in some cases. Overall, our data suggest that some homeowners living < 1 km from gas wells have drinking water contaminated with stray gases.
|
| [20] |
|
| [21] |
Use of finite element analysis to engineer the cement sheath for production operations . |
| [22] |
Chemo-poro-elastic fracture mechanics of wellbore cement liners: The role of eigenstress and pore pressure on the risk of fracture. [Master Thesis] . |
| [23] |
Early-age stress and pressure developments in a wellbore cement liner: Application to eccentric geometries .
his paper introduces a predictive model for the stress and pressure evolutions in a wellbore cement liner at early ages. A pressure state equation is derived that observes the coupling of the elastic changes of the solid matrix, the eigenstress developments in the solid and porespaces, and the mass consumption of water in course of the reaction. Here, the transient constitution of the solid volume necessitates advancing the mechanical state of the poroelastic cement skeleton incrementally and at constant hydration degree. Next, analytic function theory is employed to assess the localization of stresses along the steel–cement (SC) and rock–cement (RC) interfaces by placing the casing eccentrically with respect to the wellbore hole. Though the energy release rate due to complete debonding of either interface is only marginally influenced by the eccentricity, the risk of evolving a microcrack along the thick portion of the sheath is substantially increased. Additionally, it is observed that the risk of microannulus formation is principally affected by the pressure rebound, which is engendered by the slowing reaction rate and amplified for rock boundaries with low permeability.
|
| [24] |
Is concrete a poromechanics materials? --- a multiscale investigation of poroelastic properties .
There is an ongoing debate, in Concrete Science and Engineering, whether cementitious materials can be viewed as poromechanics materials in the sense of the porous media theory. The reason for this debate is that a main part of the porosity of these materials manifests itself at a scale where the water phase cannot be considered as a bulk water phase, but as structural water; in constrast to water in the gel porosity and the capillary porosity. The focus of this paper is two-fold: (1) to review the microstructure of cementitious materials in the light of microporomechanics theory by starting at the scale where physical chemistry meets mechanics, and which became recently accessible to mechanical testing (nanoindentation):(2) to provide estimates of the poroelastic properties (drained and undrained stiffness, Biot coefficient, Biot modulus, Skempton coefficient) of cementitious materials (cement paste, mortar and concrete) by means of advanced homogenization techniques of microporomechanics. This combined experimental-theoretical microporomechanics approach allows us to deliver a blueprint of the elementary poroelastic properties of all cementitious materials, which do not change from one cementitious material to another, but which are intrinsic properties. These properties result from the intrinsic gel porosity of low density and high density C-S-H, which yield a base Biot coefficient of 0.61< b 810.71 and a Skempton coefficient of B =0.20–0.25. While the base Biot coefficient decreases gradually at larger scales, because of the addition of non-porous solid phases (Portlandite,..., aggregates), it is shown that the Skempton coefficient is almost constant over 3–5 orders of magnitude.
|
| [25] |
Experimental chemo-mechanics of early-age fracture properties of cement paste .
Abstract The risk of early-age fracture of cementitious materials in ever more challenging environments provides a unique opportunity to employ an experimental chemo-mechanical platform to develop functional relations between hydration degree, fracture and strength properties, assessed by isothermal calorimetry, micro-scratching, splitting and microindentation on white cement paste at various curing ages from 7 h to 28 days. We show that the modulus, tensile strength, fracture toughness and energy all evolve with a natural logarithmic dependence on the hydration degree. These trends are linked to the densification of the material during the hydration process, explained by compaction mechanics and free volume theory. We show that while the fracture process zone size is essentially constant during the hydration process, the ductility of the material, quantified by M/H, decreases, and is consistent with the evolution of Kc/H. Both quantities provide a convenient way to experimentally assess the fracture sensitivity of early-age cement-based materials.
|
| [26] |
Poromechanical behaviour of hardened cement paste under isotropic loading .
The poromechanical behaviour of hardened cement paste under isotropic loading is studied on the basis of an experimental testing program of drained, undrained and unjacketed compression tests. The macroscopic behaviour of the material is described in the framework of the mechanics of porous media. The poroelastic parameters of the material are determined and the effect of stress and pore pressure on them is evaluated. Appropriate effective stress laws which control the evolution of total volume, pore volume, solid volume, porosity and drained bulk modulus are discussed. A phenomenon of degradation of elastic properties is observed in the test results. The microscopic observations showed that this degradation is caused by the microcracking of the material under isotropic loading. The good compatibility and the consistency of the obtained poromechanical parameters demonstrate that the behaviour of the hardened cement paste can be indeed described within the framework of the theory of porous media.
|
| [27] |
|
| [28] |
The nanogranular nature of C--S--H .
Despite its ubiquitous presence as binding phase in all cementitious materials, the mechanical behavior of calcium-silicate-hydrates (C-S-H) is still an enigma that has deceived many decoding attempts from experimental and theoretical sides. In this paper, we propose and validate a new technique and experimental protocol to rationally assess the nanomechanical behavior of C-S-H based on a statistical analysis of hundreds of nanoindentation tests. By means of this grid indentation technique we identify in situ two structurally distinct but compositionally similar C-S-H phases heretofore hypothesized to exist as low density (LD) C-S-H and high density (HD) C-S-H, or outer and inner products. The main finding of this paper is that both phases exhibit a unique nanogranular behavior which is driven by particle-to-particle contact forces rather than by mineral properties. We argue that this nanomechanical blueprint of material invariant behavior of C-S-H is a consequence of the hydration reactions during which precipitating C-S-H nanoparticles percolate generating contact surfaces. As hydration proceeds, these nanoparticles pack closer to center on-average around two characteristic limit packing densities, the random packing limit (eta=64%) and the ordered face-centered cubic (fcc) or hexagonal close-packed (hcp) packing limit (eta=74%), forming a characteristic LD C-S-H and HD C-S-H phase. [All rights reserved Elsevier]
|
| [29] |
Multiscale strength homogenization: Application to shale nanoindentation. [Master Thesis] . |
| [30] |
Radial fracture in a three-phase composite: Application to wellbore cement liners at early ages .
Abstract Little understanding exists between the early-age stress developments in a wellbore cement sheath and its risk of impairment. During hydration, the cement morphology and pore-pressure changes induce eigenstresses in the solid and pore volumes. Utilizing these stresses as the driving mechanism of fracture, this paper formalizes the inspection of a radial crack in an elastic cement sheath constrained by an inner steel casing and an outer rock formation. The solution is constructed in the framework of analytic function theory and seeks the Green鈥檚 function for an edge dislocation in the intermediate cement phase. A dislocation pile-up along the line of fracture constructs a singular integral equation for the crack opening displacement derivative, from which the energy release rate is readily deduced. Under the uniform development of eigenstresses, the stiffness ratios of steel-to-cement and rock-to-cement generally predict the crack to initiate along the steel-cement interface. Here, the impacts of (i) a rigid bond and (ii) a sliding interface with no shear are assessed. This leads to the primary result of the paper: the potential for radial fracture is substantially mitigated by ensuring the shear connection between the steel casing and the cement sheath.
|
| [31] |
|
| [32] |
Crack tunneling in cement sheath of hydrocarbon well . |
| [33] |
The study on composition changes of heavy oils during steam stimulation processes .
Using the heavy oils obtained from Liaohe oilfields in China, we have conducted the aquathermolysis reaction in laboratory at 240 degree C. The results showed that Liaohe heavy oils have been undergoing visbreaking in the process of steam-drive and steam stimulation. After reaction with steam, the viscosity of the heavy oil was reduced by 28-42 % and the amount of the saturated and aromatic hydrocarbons increased, while resin and asphaltene decreased. The gas partition chromatography showed that the accumulated amount of carbon numbers increased, after reaction, the accumulated amount of carbon numbers less than C//2//0 are 38.79-53.92 % , and before reaction they are 13.30-20.92 % . The results provided the basic data for heavy oil recovery by in situ catalytic method in production of heavy oil in oilfields.
|
| [34] |
An innovative methodology for designing cement-sheath integrity exposed to steam stimulation .
|
| [35] |
Evaluation of cement systems for oil and gas well zonal isolation in a full-scale annular geometry .
Loss of zonal isolation in a wellbore can be caused by mechanical failure ofthe cement or by development of a microannulus. However, behavior of thesealant is driven by specific boundary conditions such as rock properties.Large-scale laboratory testing of the cement sheath in an annular geometry anda confined situation was performed to simulate various downhole stressconditions and evaluate the behavior of several sealants. Failure modes of thecement sheath were determined as a function of cement mechanical properties,loading parameters, and boundary conditions. Results were used to validate ananalytical model that predicts cement-sheath failure.
|
| [36] |
Cement sheath stress failure . |
| [37] |
Experimental and numerical study of drilling fluid removal from a horizontal wellbore .
After a well has been drilled, the drilling fluid should be removed and replaced with either cement and/or completion fluids. For effective zonal isolation and optimum hydrocarbon production during the life of the well, the entire drilling fluid should be removed from the annulus. Cement and completion fluids are sensitive to drilling fluid contamination, and even a thin layer of oil-based drilling fluid could prevent the cement from bonding to the formation and the casing. In addition, for optimum hydrocarbon production, the cement sheath must be able to withstand the stresses throughout the life of the well.
|
| [38] |
The scratch test for strength and fracture toughness determination of oil well cements cured at high temperature and pressure .
Recent advances in scratch test analysis provide new ways to relate measured scratch test properties not only to strength properties but fracture properties of materials as well. Herein, we present an application of such tools to oil well cements cured at high temperatures and pressures. We find a concurrent increase of strength and toughness of different oil well cement baseline formulations which we relate to the water-to-binder ratio for a series of cementitious materials prepared with cement and silica flour. The scratch test thus emerges as a self-consistent technique for both cohesive–frictional strength and fracture properties that is highly reproducible, almost non-destructive, and not more sophisticated than classical compression tests, which makes this ‘old’ test highly attractive for performance-based field applications.
|
| [39] |
Microcracks tunneling in brittle matrix composites driven by thermal expansion mismatch . |
| [40] |
Mixed mode cracking in layered materials .
This chapter describes the mixed mode cracking in layered materials. There is ample experimental evidence that cracks in brittle, isotropic, homogeneous materials propagate such that pure mode I conditions are maintained at the crack tip. An unloaded crack subsequently subject to a combination of modes I and II will initiate growth by kinking in such a direction that the advancing tip is in mode I. The chapter also elaborates some of the basic results on the characterization of crack tip fields and on the specification of interface toughness. The competition between crack advance within the interface and kinking out of the interface depends on the relative toughness of the interface to that of the adjoining material. The interface stress intensity factors play precisely the same role as their counterparts in elastic fracture mechanics for homogeneous, isotropic solids. When an interface between a bimaterial system is actually a very thin layer of a third phase, the details of the cracking morphology in the thin interface layer can also play a role in determining the mixed mode toughness. The elasticity solutions for cracks in multilayers are also elaborated.
|
| [41] |
McDermott JR, Langlinais JC, et al. Foamed cement job successful in deep HTHP offshore well . |
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
Large elastic deformation as a mechanism for soft seal leakage .
Experiments were performed to visualize,in situ, the deformation and leakage of soft seals under differential pressure. Two annular seals and a flat, rectangular seal were investigated in the experiments. The observations show that large, nonuniform elastic deformation precedes seal leakage. A corresponding finite element model for a rectangular solid seal shows that large deformation leads to a decrease in the compressive sealing stress between the seal and the surface against which it seals. The predicted flow path for the model is qualitatively similar to the flow path observed in the experiments. A leakage mechanism in which nonuniform elastic deformation leads to seal leakage is proposed.
|
| [47] |
Elastic leak of a seal .DOI URL [本文引用: 10] 摘要
Abstract An elastomeric seal may leak by elastic deformation without any material damage. We describe elastic leak using a theoretical model, and watch a seal deform and leak using a transparent experimental setup. The elastomer seals the fluid by forming contact with surrounding hard materials. As the fluid pressure increases, the contact stress also increases but not as much. When the fluid pressure surpasses the contact stress, the elastomer and the hard materials lose contact in some region, forming a leaking path. The critical fluid pressure for elastic leak depends on the geometry and constraint of the seal, but is insensitive to the rate at which the fluid is injected. Our study points to the significance of elastic deformation in modes of failure that also involve material damage.
|
| [48] |
Extrusion, slide, and rupture of an elastomeric seal .DOI URL [本文引用: 21] 摘要
Elastomeric seals are essential to two great technological advances in oilfields: horizontal drilling and hydraulic fracturing. This paper describes a method to study elastomeric seals by using the pressure-extrusion curve (i.e., the relation between the drop of pressure across a seal and the volume of extrusion of the elastomer). Emphasis is placed on a common mode of failure found in oilfields: leak caused by a crack across the length of a long seal. We obtain an analytical solution of large elastic deformation, which is analogous to the Poiseuille flow of viscous liquids. We further obtain analytical expressions for the energy release rate of a crack and the critical pressure for the onset of its propagation. The theory predicts the pressure-extrusion curve using material parameters (elastic modulus, sliding stress, and fracture energy) and geometric parameters (thickness, length, and precompression). We fabricate seals of various parameters in transparent chambers on a desktop, and watch the seals extrude, slide, rupture and leak. The experimentally measured pressure-extrusion curves agree with theoretical predictions remarkably well. 漏 2016 Elsevier Ltd
|
| [49] |
|
| [50] |
Poroelastic relaxation indentation of thin layers of gels .
We develop a method of poroelastic relaxation indentation (PRI) to characterize thin layers of gels. The solution to the time-dependent boundary-value problem is obtained in a remarkably simple form, so that the force-relaxation curve obtained by indenting a gel readily determines all the poroelastic constants of the gel—the shear modulus, Poisson’s ratio, and the effective diffusivity. The method is demonstrated with a layer of polydimethylsiloxane immersed in heptane.
|
| [51] |
Viscoelasticity and poroelasticity in elastomeric gels .
An elastomeric gel is a mixture of a polymer network and a solvent. In response to changes in mechanical forces and in the chemical potential of the solvent in the environment, the gel evolves by two concurrent molecular processes: the conformational change of the network, and the migration of the solvent. The two processes result in viscoelasticity and poroelasticity, and are characterized by two material-specific properties: the time of viscoelastic relaxation and the effective diffusivity of the solvent through the network. The two properties define a material-specific length. The material-specific time and length enable us to discuss macroscopic observations made over different lengths and times, and identify limiting conditions in which viscoelastic and poroelastic relaxations have either completed or yet started. We formulate a model of homogeneous deformation, and use several examples to illustrate viscoelasticity-limited solvent migration, where the migration of the solvent is pronounced, but the size of the gel is so small that the rate of change is limited by viscoelasticity. We further describe a theory that evolves a gel through inhomogeneous states. Both infinitesimal and finite deformation are considered.
|
| [52] |
A theory of coupled diffusion and large deformation in polymeric gels .
A large quantity of small molecules may migrate into a network of long polymers, causing the network to swell, forming an aggregate known as a polymeric gel. This paper formulates a theory of the coupled mass transport and large deformation. The free energy of the gel results from two molecular processes: stretching the network and mixing the network with the small molecules. Both the small molecules and the long polymers are taken to be incompressible, a constraint that we enforce by using a Lagrange multiplier, which coincides with the osmosis pressure or the swelling stress. The gel can undergo large deformation of two modes. The first mode results from the fast process of local rearrangement of molecules, allowing the gel to change shape but not volume. The second mode results from the slow process of long-range migration of the small molecules, allowing the gel to change both shape and volume. We assume that the local rearrangement is instantaneous, and model the long-range migration by assuming that the small molecules diffuse inside the gel. The theory is illustrated with a layer of a gel constrained in its plane and subject to a weight in the normal direction. We also predict the scaling behavior of a gel under a conical indenter.
|
| [53] |
A coupled theory of fluid permeation and large deformations for elastomeric materials .
An elastomeric gel is a cross-linked polymer network swollen with a solvent (fluid). A continuum-mechanical theory to describe the various coupled aspects of fluid permeation and large deformations (e.g., swelling and squeezing) of elastomeric gels is formulated. The basic mechanical force balance laws and the balance law for the fluid content are reviewed, and the constitutive theory that we develop is consistent with modern treatments of continuum thermodynamics, and material frame-indifference. In discussing special constitutive equations we limit our attention to isotropic materials, and consider a model for the free energy based on a Flory–Huggins model for the free energy change due to mixing of the fluid with the polymer network, coupled with a non-Gaussian statistical–mechanical model for the change in configurational entropy—a model which accounts for the limited extensibility of polymer chains. As representative examples of application of the theory, we study (a) three-dimensional swelling-equilibrium of an elastomeric gel in an unconstrained, stress-free state; and (b) the following one-dimensional transient problems: (i) free-swelling of a gel; (ii) consolidation of an already swollen gel; and (iii) pressure-difference-driven diffusion of organic solvents across elastomeric membranes.
|
| [54] |
A theory for species migration in a finitely strained solid with application to polymer network swelling .
We present a theory for the behavior of a solid undergoing two interdependent processes, a macroscopic or mechanical process due to the deformation of the solid and a microscopic or chemical process due to the migration of a chemical species through the solid. The principle of virtual power is invoked to deduce the basic balances of the theory, namely the mechanical force balance and the transport balance for the chemical species. In combination with thermodynamically consistent constitutive relations, these balances generate the basic equations of the theory. Keeping in mind applications involving the swelling of polymer networks by liquids, a specialization of the theory is presented and applied to study the influences of mechanical and chemical interactions on equilibrium states and diffusive dynamical processes. It is shown that the possibility of a mechanically induced phase transition is governed by two parameters: the Flory interaction parameter and a parameter given by the product between the number of cross-linked units per unit reference volume and the molecular volume of the liquid molecule. As for diffusion, it is shown that the theory is able to describe the pressure-induced diffusion in swollen membranes.
|
| [55] |
Advances in mechanics of soft materials: A review of large deformation behavior of hydrogels .
Hydrogels possess magnificent properties which may be harnessed for novel applications. However, this is not achievable if the mechanical behaviors of hydrogels are not well understood. This paper aims to provide the reader with a bird's eye view of the mechanics of hydrogels, in particular the theories associated with deformation of hydrogels, the phenomena that are commonly observed, and recent developments in applications of hydrogels. Besides theoretical analyses and experimental observations, another feature of this paper is to provide an overview of how mechanics can be applied.
|
| [56] |
|
| [57] |
Statistical mechanics of cross-linked polymer networks II. Swelling .
A model is proposed for the structure of a cross‐linked network, such as exists in a vulcanized rubber, which is amenable to statistical treatment. Expressions are derived for the structural entropy of the network, and for the entropy change on deformation. The latter is in agreement with the relationship derived by Wall and others by a different treatment.
|
| [58] |
|
| [59] |
A new constitutive relation for rubber . |
| [60] |
A theory of large elastic deformation .
It is postulated that (A) the material is isotropic, (B) the volume change and hysteresis are negligible, and (C) the shear is proportional to the traction in simple shear in a plane previously deformed, if at all, only by uniform dilatation or contraction. It is deduced that the general strain‐energy function,W, has the formW=G4∑i=13(λi611λi)2+H4∑t=13(λi2611λi2),where the λi's are the principal stretches (1+principal extension),Gis the modulus of rigidity, andHis a new elastic constant not found in previous theories. The differences between the principal stresses are σi[minus]σi=λi68W/68λi[minus]λi68W/68λi. Calculated forces agree closely with experimental data on soft rubber from 400 percent elongation to 50 percent compression.
|
| [61] |
Large elastic deformations of isotropic materials. I. Fundamental concepts.
The mathematical theory of small elastic deformations has been developed to a high degree of sophistication on certain fundamental assumptions regarding the stress-strain relationships which are obeyed by the materials considered. The relationships taken are, in effect, a generalization of Hooke’s law— ut tensio , sic vis . The justification for these assumptions lies in the widespread agreement of experiment with the predictions of the theory and in the interpretation of the elastic behaviour of the materials in terms of their known structure. The same factors have contributed to our appreciation of the limitations of these assumptions.
|
| [62] |
Large deformation isotropic elasticity - on the correlation of theory and experiment for incompressible rubberlike solids.
Many attempts have been made to reproduce theoretically the stress-strain curves obtained from experiments on the isothermal deformation of highly elastic 'rubberlike' materials. The existence of a strain-energy function has usually been postulated, and the simplifications appropriate to the assumptions of isotropy and incompressibility have been exploited. However, the usual practice of writing the strain energy as a function of two independent strain invariants has, in general, the effect of complicating the associated mathematical analysis (this is particularly evident in relation to the calculation of instantaneous moduli of elasticity) and, consequently, the basic elegance and simplicity of isotropic elasticity is sacrificed. Furthermore, recently proposed special forms of the strain-energy function are rather complicated functions of two invariants. The purpose of this paper is, while making full use of the inherent simplicity of isotropic elasticity, to construct a strain-energy function which: (i) provides an adequate representation of the mechanical response of rubberlike solids, and (ii) is simple enough to be amenable to mathematical analysis. A strain-energy function which is a linear combination of strain invariants defined by φ (α)=(a1α+a2α+a3α-3)/α is proposed; and the principal stretches a1,a2 and a3 are used as independent variables subject to the incompressibility constraint a1a2a3=1. Principal axes techniques are used where appropriate. An excellent agreement between this theory and the experimental data from simple tension, pure shear and equibiaxial tension tests is demonstrated. It is also shown that the present theory has certain repercussions in respect of the constitutive inequality proposed by Hill (1968a, 1970b).
|
| [63] |
A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials .
Aconstitutive model is proposed for the deformation of rubber materials which is shown to represent successfully the response of these materials in uniaxial extension, biaxial extension, uniaxial compression, plane strain compression and pure shear. The developed constitutive relation is based on an eight chain representation of the underlying macromolecular network structure of the rubber and the non-Gaussian behavior of the individual chains in the proposed network. The eight chain model accurately captures the cooperative nature of network deformation while requiring only two material parameters, an initial modulus and a limiting chain extensibility. Since these two parameters are mechanistically linked to the physics of molecular chain orientation involved in the deformation of rubber, the proposed model represents a simple and accurate constitutive model of rubber deformation. The chain extension in this network model reduces to a function of the root-mean-square of the principal applied stretches as a result of effectively sampling eight orientations of principal stretch space. The results of the proposed eight chain model as well as those of several prominent models are compared with experimental data of Treloar (1944, Trans. Faraday Soc. 40, 59) illustrating the superiority, simplicity and predictive ability of the proposed model. Additionally, a new set of experiments which captures the state of deformation dependence of rubber is described and conducted on three rubber materials. The eight chain model is found to model and predict accurately the behavior of the three tested materials further confirming its superiority and effectiveness over earlier models.
|
| [64] |
|
| [65] |
A constitutive model for soft materials incorporating viscoelasticity and mullins effect .
Soft materials including elastomers and gels are widely used in applications of energy absorption, soft robotics, bioengineering, and medical instruments. For many soft materials subject to loading and unloading cycles, the stress required on reloading is often less than that on the initial loading, known as Mullins effect. Meanwhile, soft materials usually exhibit rate-dependent viscous behavior. Both effects were recently reported on a new kind of synthesized tough gel, with capability of large deformation, high strength, and extremely high toughness. In this work, we develop a coupled viscoelastic and Mullins-effect model to characterize the deformation behavior of the tough gel. We modify one of the elastic components in Zener model to be a damageable spring to incorporate the Mullins effect and model the viscous effect to behave as a Newtonian fluid. We synthesized the tough gel described in the literature (Sun et al., Nature 2012) and conducted uniaxial tensile tests and stress relaxation tests. We also investigated the two effects on three other soft materials, polyacrylate elastomer, Nitrile-Butadiene Rubber, and polyurethane. We find that our presented model is so robust that it can characterize all the four materials, with modulus ranging from a few tens of kilopascal to megapascal. The theory and experiment for all tested materials agree very well. Copyright 漏 2017 by ASME.
|
| [66] |
A phenomenological model for shakedown of tough hydrogels under cyclic loads . |
| [67] |
Thermodynamics of high polymer solutions .
Scitation is the online home of leading journals and conference proceedings from AIP Publishing and AIP Member Societies
|
| [68] |
Solutions of long chain compounds .
Scitation is the online home of leading journals and conference proceedings from AIP Publishing and AIP Member Societies
|
| [69] |
Swellable elastomers under constraint . |
| [70] |
Kinetics of swelling under constraint .
Swellable elastomers are used to seal flow channels in oilfield operations. After sealing, the elastomers are constrained triaxially, and a contact load builds up between the elastomers and surrounding rigid materials. For these applications, the ability to predict the evolution of the contact load is important. This work introduces an experimental setup to measure the contact load as a function of time. The experimental data are well represented by a simple time-relaxation equation derived from the linear poroelastic theory, enabling a determination of the effective diffusivity of solvent inside the elastomers.
|
| [71] |
Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load .
A network of polymers can imbibe a large quantity of a solvent and swell, resulting in a gel. The swelling process can be markedly influenced by a mechanical load and geometric constraint. When the network, solvent, and mechanical load equilibrate, inside the gel the chemical potential of the solvent is homogeneous, but the concentration of the solvent and the deformation of the network can be inhomogeneous. We use the chemical potential of the solvent and the deformation gradient of the network as the independent variables of the free-energy function, and show that the boundary value problem of the swollen gel is equivalent to that of a hyperelastic solid. We implement this approach in the finite-element package, ABAQUS, and analyze examples of swelling-induced deformation, contact, and bifurcation. Because commercial software like ABAQUS is widely available, this work may provide a powerful tool to study complex phenomena in gels.
|
| [72] |
Inhomogeneous and anisotropic equilibrium state of a swollen hydrogel containing a hard core .
A polymer network can imbibe water from environment and swell to an equilibrium state. If the equilibrium is reached when the network is subject to external mechanical constraint, the deformation of the network is typically anisotropic and the concentration of water inhomogeneous. Such an equilibrium state in a network constrained by a hard core is modeled here with a nonlinear differential equation. The presence of the hard core markedly reduces the concentration of water near the interface and causes high stresses.
|
| [73] |
Force generated by a swelling elastomer subject to constraint .
When an elastomer imbibes a solvent and swells, a force is generated if the elastomer is constrained by a hard material. The magnitude of the force depends on the geometry of the constraint, as well as on the chemistry of the elastomer and solvent. This paper models an elastomer crosslinked on the exterior surface of a metallic tubing. The elastomer then imbibes a solvent and swells. After the swollen elastomer touches the wall of the borehole, a significant amount of time is needed for the solvent in the elastomer to redistribute, building up the sealing pressure to the state of equilibrium. The sealing pressure and the sealing time are calculated in terms of the geometric parameters (i.e., the thickness of the elastomer and the radii of the tubing and borehole), the number of monomers along each polymer chain of the elastomer, and the affinity between the elastomer and the solvent.
|
| [74] |
A thermo-mechanically coupled theory for fluid permeation in elastomeric materials: Application to thermally responsive gels .
An elastomeric gel is a cross-linked polymer network swollen with a solvent, and certain gels can undergo large reversible volume changes as they are cycled about a critical temperature. We have developed a continuum-level theory to describe the coupled mechanical deformation, fluid permeation, and heat transfer of such thermally responsive gels. In discussing special constitutive equations we limit our attention to isotropic materials, and consider a model based on a Flory–Huggins model for the free energy change due to mixing of the fluid with the polymer network, coupled with a non-Gaussian statistical–mechanical model for the change in configurational entropy—a model which accounts for the limited extensibility of polymer chains. We have numerically implemented our theory in a finite element program. We show that our theory is capable of simulating swelling, squeezing of fluid by applied mechanical forces, and thermally responsive swelling/de-swelling of such materials.
|
| [75] |
A finite element implementation of a coupled diffusion-deformation theory for elastomeric gels .
The theory of Chester and Anand (2011) for fluid diffusion and large deformations of elastomeric gels is implemented as a user-defined element (UEL) subroutine in the commercial finite element software package ABAQUS. A specialized form of the constitutive equations and the governing partial differential equations of the theory are summarized, and the numerical implementation is described in detail. To demonstrate the robustness of the numerical implementation a few illustrative numerical simulation examples for axisymmetric, plane strain, and three-dimensional geometries are shown. For educational purposes, and also to facilitate the numerical implementation of other coupled multiphysics theories, the source code for the UEL is provided as an online supplement to this paper.
|
| [76] |
Kinetics of swellable packers under downhole conditions .
Swellable packers have been widely employed in various oil-field applications. Examples include zonal-isolation, water shut-off, and multi-stage fracturing. Key factors required for these applications are how fast the packer can seal the borehole as well as how fast a certain amount of contact pressure can build up. These factors, which are generally measured from full-scale packer tests, can be estimated through numerical simulations together with lab-scale experiments. In this work, we have developed a three-dimensional continuum level model and simulation capability to study the behavior of swellable packers affected by various downhole conditions. Such conditions include the borehole type, i.e., permeable or non-permeable borehole, and downhole uncertainties, i.e., variations of borehole size and borehole temperature, which are studied systematically through numerical simulations.
|
| [77] |
Models of fiber debonding and pullout in brittle composites with friction .
Models for the debonding of a fiber embedded in a brittle matrix are proposed and analyzed. Attention is restricted to systems having a residual compressive stress acting across the fiber/matrix interface. Debonding, as well as pullout after the fiber breaks, is accompanied by frictional sliding. Fiber—matrix interaction is modeled by a cylindrical cell with two sets of boundary conditions: one modeling an isolated fiber—matrix unit and the other a matrix containing an array of unidirectional fibers. The elastic properties of the fiber are taken to be transversely isotropic about the fiber axis, while the matrix is assumed to be isotropic. The debonding process is treated within the framework of fracture mechanics as a mode 2 crack. Two idealizations of friction are considered: a constant friction stress independent of normal compression across the interface, and Coulomb friction. Approximate closed form solutions to the model are presented. These are assessed using results from an accurate numerical analysis.
|
| [78] |
Friction of gels. 3. Friction on solid surfaces .
Frictions of several kinds of hydrogels, poly(vinyl alcohol) gel, gellan gel, poly(2-acrylamido-2-methylpropanesulfonic acid) gel, and its sodium salt gel, sliding on glass plates as well as on Teflon plates have been investigated both in air and in water. The frictional force and its dependencies on the load are quite different depending on the chemical structures of the gels, surface properties of the opposing substrates, and the measurement condition. The gel friction is explained in terms of interface interaction, either attractive or repulsive, between the polymer chain and the solid surface. Surface adhesion between glass particles and gels measured by atomic force microscopy showed a good correlation with the friction, which supports the polymer repulsion鈭抋dsorption model proposed by authors.
|
| [79] |
Effect of surface tension on the adhesion between a rigid flat punch and a semi-infinite neo-Hookean half-space .
We study the effect of surface stress on the retraction of a rigid flat circular punch adhering to an incompressible neo-Hookean half space using a large deformation finite element model (FEM). The effect of surface stress is determined by the dimensionless elasto-capillary number,ω=σ/(Ea), whereσis the isotropic solid-air interface surface stress which we shall called surface tension,Eis the small strain Young’s modulus andais the radius of punch. Adhesion of the punch to the half space is characterized by work of adhesionWad. Within the range of retraction displacement of this work (less or equal to the punch radius), the stiffness of the system is insensitive to retraction displacement and depends only on the elasto-capillary number. In general, surface tension increases the slope of load-displacement curve or the stiffness of the system. For a given work of adhesion, the pull-off force (displacement) increases (decreases) with surface tension. Our results show that the apparent contact angle is not 90 degrees, as predicted by linear elastic theory, but varies from 20 to 180 degrees and is very sensitive toωwhen it is near zero. This result can be potentially used to measure solid surface tension.
|
| [80] |
Stress fields in a compressed unconstrained elastomeric o-ring seal and a comparison of computer predictions and experimental results .
A finite element stress analysis computer program, FEMALES (an acronym for Finite Element Mechanical Analysis of Large Elastic Strain), has been written at the University of Bologna, Italy. It was developed specifically for the analysis of large deformations in elastomeric materials. In this paper the program is reviewed for use in elastomeric sealing applications. The principle of operation of the program is described, and its performance is compared with experimental and analytical results for the case of an O-ring compressed between flat plates. The comparison is divided into two parts: a comparison of stress-related parameters and a comparison of displacement-related parameters. Also, two main methods for specifying elastic material properties are considered: firstly an elaborate method which involves a range of measurements from elastomer specimens, and secondly another known as the neo-Hookean model which only requires estimates of Young's modulus and the bulk modulus. In this particular application it was found that the two models gave similar results. This supports the use of the simpler model, since the materials data can be very readily obtained. The overall conclusion drawn from the work was that FEMALES is a workable system that produces results in good agreement with experiment. This gives confidence in its use and development for more complicated geometries, and as such it should become a useful tool for seal design and assessment.
|
| [81] |
Geometry and contact pressure of an o-ring mounted in a seal groove .
Abstract This paper gives equations that are useful in engineering practice to determine the geometry, the contact pressure, and the force of the contact pressure of an O-ring mounted in a seal groove loaded and unloaded by the sealed pressure. The equations were verified in line with the present state of the art in this field and taking into account modem analytical methods. The information on the geometry, the contact pressure, and the force of the contact pressure is useful in resolving the problems of leak tightness, friction, leakage, durability, and also design of the O-ring seals.
|
| [82] |
Analytical study of the extrusion of rectangular elastomeric seals for linear hydraulic actuators.
ABSTRACT Rectangular elastomeric seals used on reciprocating piston rods in high-pressure hydraulic actuators often suffer from extrusion damage at the low-pressure side of the actuators. The extrusion takes place at the narrow clearance between the rod and the actuator, where the seal develops a ‘nip’ under conditions of high sealed pressure and/or high friction with the rod, which is amplified in the absence of a back-up ring. This form of strain can lead to permanent damage of the seal and impair the sealing performance of the system. This paper deals with the modelling of this kind of seal extrusion. Algebraic equations were developed to describe the shape and contact pressure of the extruded part of the seal with the rod. A study is presented about the effects of various operating parameters on the extent of seal extrusion in order to minimize the risks of damage. It was found that only the use of a back-up ring can adequately cancel the seal extrusion mechanism.
|
| [83] |
|
| [84] |
|
| [85] |
Elastic leak for a better seal . |
| [86] |
Instability of a compressed elastic film on a viscous layer .
A flat, compressed elastic film on a viscous layer is unstable. The film can form wrinkles to reduce the elastic energy. A linear perturbation analysis is performed to determine the critical wave number and the growth rate of the unstable modes. While the viscous layer has no effect on the critical wave number, its viscosity and thickness set the time scale for the growth of the perturbations. The fastest growing wave number and the corresponding growth rate are obtained as functions of the compressive strain and the thickness ratio between the viscous layer and the elastic film. The present analysis is valid for all thickness range of the viscous layer. In the limits of infinitely thick and thin viscous layers, the results reduce to those obtained in the previous studies.
|
| [87] |
Swelling instability of surface-attached gels as a model of soft tissue growth under geometric constraints .
The purpose of this work is to provide a theoretical analysis of the mechanical behavior of the growth of soft materials under geometrical constraints. In particular, we focus on the swelling of a gel layer clamped to a substrate, which is still the subject of many experimental tests. Because the constrained swelling process induces compressive stresses, all these experiments exhibit surface instabilities, which ultimately lead to cusp formation. Our model is based on fixing a neo-Hookean constitutive energy together with the incompressibility requirement for a volumetric, homogeneous mass addition. Our approach is developed mostly, but not uniquely, in the plane strain configuration. We show how the standard equilibrium equations from continuum mechanics have a similarity with the two-dimensional Stokes flows, and we use a nonlinear stream function for the exact treatment of the incompressibility constraint. A free energy approach allows the extension both to arbitrary hyperelastic strain energies and to additional interactions, such as surface energies. We find that, at constant volumetric growth, the threshold for a wavy instability is completely governed by the amount of growth. Nevertheless, the determination of the wavelength at threshold, which scales with the initial thickness of the gel layer, requires the coupling with a surface effect. Our findings, which are valid in proximity of the threshold, are compared to experimental results. The proposed treatment can be extended to weakly nonlinearities within the aim of the theory of bifurcations.
|
| [88] |
Analytical solutions of polymeric gel structures under buckling and wrinkle .
One of the unique properties of polymeric gel is that the volume and shape of gel can dramatically change even at mild variation of external stimuli. Though a variety of instability patterns of slender and thin film gel structures due to swelling have been observed in various experimental studies, many are not well understood. This paper presents the analytical solutions of swelling-induced instability of various slender and thin film gel structures. We have adopted the well developed constitutive relation of inhomogeneous field theory of a polymeric network in equilibrium with a solvent and mechanical load or constraint with the incremental modulus concept for slender beam and thin film gel structures. The formulas of buckling and wrinkle conditions and critical stress values are derived for slender beam and thin film gel structures under swelling-induced instability using nonlinear buckling theories of beam and thin film structures. For slender beam structure, we construct the stability diagram with the distinct stable and unstable zones. The critical slenderness ratio and corresponding critical stresses are provided for different dimensionless material parameters. For thin film gel structures, we consider the thin film gel on an elastic foundation with different stiffness. The analytical solutions of critical stress and corresponding wrinkle wavelength, as well as buckling condition (or critical chemical potential) are given. These analytical solutions will provide a guideline for gel structure design used in polymeric gels MEMS and NEMS structures such as sensors and actuators. More importantly, the work provides a theoretical foundation of gel structure buckling and wrinkle, instability phenomena are different from normal engineering or material buckling.
|
| [89] |
Creasing instability of elastomer films .
The creasing instability of elastomer films under compression is studied by a combination of experiment and numerical simulation. Experimentally, we attach a stress-free film on a much thicker and stiffer pre-stretched substrate. When the substrate is partially released, the film is uniaxially compressed, leading to formation of an array of creases beyond a critical strain. The profile of the folded surface is extracted using confocal fluorescence microscopy, yielding the depths, spacings, and shapes of creases. Numerically, the onset and development of creases are simulated by introducing appropriately sized defects into a finite-element mesh and allowing the surface of the film to self-contact. The measurements and simulations are found to be in excellent agreement.
|
| [90] |
Creases and wrinkles on the surface of a swollen gel .
Consider a layer of a gel attached to a rigid substrate, immersed in a solvent, and swelling in the thickness direction. The flat surface of the gel remains stable if the swelling ratio is small, but becomes unstable if the swelling ratio is large. While creases have been commonly observed, wrinkles have also been observed under certain conditions. We compare the critical conditions for the onset of creases and wrinkles by using a nonlinear field theory of gels. The critical swelling ratio for the onset of creases is calculated by using a finite element method, and that for wrinkles is calculated by using an analytical method. We find that the critical swelling ratio for the onset of creases is significantly lower than that for wrinkles.
|
| [91] |
Bifurcation diagrams for the formation of wrinkles or creases in soft bilayers .
Abstract Subject to compression, elastic materials may undergo bifurcation of various kinds. A homogeneous material forms creases, whereas a bilayer consisting of a stiff film and a compliant substrate forms wrinkles. Here, we show several new types of bifurcation behavior for bilayers consisting of films and substrates of comparable elastic moduli. Depending on the ratios of moduli and thicknesses of the two materials, the critical strain for the onset of creases can be either smaller or larger than that for the onset of wrinkles. When the critical strain for the onset of creases is lower than that of wrinkles, creases can be subcritical or supercritical. When the critical strain for the onset of wrinkles is lower than that of creases, wrinkles can further channel to creases at a strain much lower than the critical strain for the onset of creases in a homogeneous material. Experiments, conducted with bilayer polydimethylsiloxane (PDMS) structures subject to compressive loading, show that the different types of bifurcation behavior agree with the theoretical predictions.
|
| [92] |
Digital instability of a confined elastic meniscus .
Thin soft elastic layers serving as joints between relatively rigid bodies may function as sealants, thermal, electrical, or mechanical insulators, bearings, or adhesives. When such a joint is stressed, even though perfect adhesion is maintained, the exposed free meniscus in the thin elastic layer becomes unstable, leading to the formation of spatially periodic digits of air that invade the elastic layer, reminiscent of viscous fingering in a thin fluid layer. However, the elastic instability is reversible and rate-independent, disappearing when the joint is unstressed. We use theory, experiments, and numerical simulations to show that the transition to the digital state is sudden (first-order), the wavelength and amplitude of the fingers are proportional to the thickness of the elastic layer, and the required separation to trigger the instability is inversely proportional to the in-plane dimension of the layer. Our study reveals the energetic origin of this instability and has implications for the strength of polymeric adhesives; it also suggests a method for patterning thin films reversibly with any arrangement of localized fingers in a digital elastic memory, which we confirm experimentally.
|
| [93] |
Bulk elastic fingering instability in hele-shaw cells .
We demonstrate experimentally the existence of a purely elastic, nonviscous fingering instability which arises when air penetrates into an elastomer confined in a Hele-Shaw cell. Fingers appear sequentially and propagate within the bulk of the material as soon as a critical strain, independent of the elastic modulus, is exceeded. Key elements in the driving force of the instability are the confinement of the gel and its adhesion to the plates of the cell, which result in a considerable expense of elastic energy during the growth of the air bubble.
|
| [94] |
Fluid-driven fingering instability of a confined elastic meniscus .
When a fluid is pumped into a cavity in a confined elastic layer, at a critical pressure, destabilizing fingers of fluid invade the elastic solid along its meniscus (Saintyves, Dauchot, and Bouchaud, 2013). These fingers occur without fracture or loss of adhesion and are reversible, disappearing when the pressure is decreased. We develop an asymptotic theory of pressurized highly elastic layers trapped between rigid bodies to explain these observations, with predictions for the critical fluid pressure for fingering, and the finger wavelength. We also show that the theory links this fluid-driven fingering with a similar transition driven instead by transverse stretching of the elastic layer. We further verify these predictions by using finite-element simulations on the two systems which show that, in both cases, the fingering transition is first-order (sudden) and hence has a region of bistability. Our predictions are in good agreement with recent observations of this elastic analog of the classical Saffman-Taylor interfacial instability in hydrodynamics.
|
| [95] |
Charge localization instability in a highly deformable dielectric elastomer .
This paper shows that a highly deformable capacitor made of a soft dielectric and two conformal electrodes can switch between two states discontinuously, by a first-order transition, as the total charge varies gradually. When the total charge is small, it spreads evenly over the area of the capacitor, and the capacitor deforms homogeneously. When the total charge is large, it localizes in a small region of the capacitor, and this region thins down preferentially. The capacitor will survive the localization without electrical breakdown if the area of the electrode is small. Such a bistable system may lead to useful devices.
|
| [96] |
Electro-mechanical coupling bifurcation and bulging propagation in a cylindrical dielectric elastomer tube .
This paper explores the critical and post-bulging bifurcation of a cylindrical dielectric elastomer (DE) tube undergoing finite deformation under electro-mechanical coupling loading. Explicit expressions for the critical conditions of electro-mechanical bifurcation are derived by using a simplified mathematical method. The post-bifurcation path is comprehensively investigated by specifying the material model as ideal dielectric elastomer. In the post-bifurcation analysis, we analytically establish conditions for the phase coexistence of steady propagation and analyze the physical implications. We demonstrate a global instability under force or voltage control and a localized instability under volume or charge control. Cylindrical tube experiments have been carried out under electro-mechanical coupling loading to verify the theoretical predictions. Good agreements on the critical conditions as well as the post-bifurcation path are obtained. This work characterizes the bifurcation mechanism of rubber-like materials under complex coupling loading.
|
| [97] |
Anomalous bulging behaviors of a dielectric elastomer balloon under internal pressure and electric actuation .
When a clamped membrane of elastomer is subject to a lateral pressure, it bulges into a hemispherical balloon. However, for a clamped membrane of dielectric elastomer (DE) under a lateral pressure as well as a voltage through the thickness, it may bulge into a regular hemispherical balloon or an irregular shape. This work focuses on the anomalous bulging behaviors (i.e. the irregular bulging shape) of a DE balloon under electromechanical coupling loading. The full set of the equilibrium configurations of the DE balloon is theoretically derived within the framework of thermodynamics, based on which we find that with the increase of the applied voltage, the pressure-volume relationship changes from the single-N shape for the case of purely mechanical loading to a double-N shape, where five or more equilibrium configurations exist including both regular and irregular bulging shapes. Through stability analysis we find that the anomalous bulging is a common behavior for the DE balloon under electromechanical coupling loading and all types of irregular bulging shapes can be achieved by following carefully designed loading paths. Besides, the irregular bulging region usually has the largest local strain which may initiate the failure of the DE membrane. Guided by the theoretical analysis, we conducted experiments on a DE balloon under the internal pressure and electrical actuation. Typical irregular shapes were successfully observed and the entire evolution of the shape changing agrees very well with theoretical predictions. These findings enrich understandings of highly nonlinear behaviors for soft materials under electromechanical coupling loading.
|
| [98] |
Nonlinear vibration of dielectric elastomer incorporating strain stiffening .
Due to the strain-stiffening of polymer chains, a membrane of dielectric elastomer (DE) can reach two different stable equilibrium states under a static electrical load. In this paper, a theoretical model is developed to investigate the strain-stiffening effect on the nonlinear vibration of a circular DE membrane subjected to electro-mechanical loading. Free vibration, steady parametric excitation and chaos of the DE membrane undergoing large deformation are studied respectively. We find that after a small perturbation the DE membrane vibrates steadily around the two stable stretches and two natural frequencies exist for the same loading condition. With the increase of initial perturbation energy, the amplitude鈥揻requency response of free vibration shows a transition from behaving like a soft spring to a hard spring attributed to strain-stiffening effect. When driven by a sinusoidal voltage, the DE membrane can resonate at multiple frequencies of excitation around small and large stable equilibrium states respectively. Variation of the sinusoidal voltage may induce a sudden change from steady vibration to chaos and the critical conditions for the transition are numerically calculated.
|
| [99] |
Controlled 3d buckling of silicon nanowires for stretchable electronics .
Silicon (Si) nanowire (NW) coils were fabricated on elastomeric substrates by a controlled buckling process. Si NWs were first transferred onto prestrained and ultraviolet/ozone (UVO)-treated poly(dimethylsiloxane) (PDMS) substrates and buckled upon release of the prestrain. Two buckling modes (the in-plane wavy mode and the three-dimensional coiled mode) were found; a transition between them was achieved by controlling the UVO treatment of PDMS. Structural characterization revealed that the NW coils were oval-shaped. The oval-shaped NW coils exhibited very large stretchability up to the failure strain of PDMS (鈭104% in our study). Such a large stretchability relies on the effectiveness of the coil shape in mitigating the maximum local strain, with a mechanics that is similar to the motion of a coil spring. Single NW devices based on coiled NWs were demonstrated with a nearly constant electrical response in a large strain range. In addition to the wavy shape, the coil shape represents an effective archite...
|
| [100] |
Harnessing snap-through instability in soft dielectrics to achieve giant voltage-triggered deformation . |
| [101] |
Controlled mechanical buckling for origami-inspired construction of 3d microstructures in advanced materials .
Abstract On page 2629, Y. Zhang, J. A. Rogers, and co-workers introduce an approach that exploits controlled mechanical buckling for reversible, autonomic origami assembly of 3D structures across material classes from soft polymers to brittle inorganic semiconductors, and length scales from nanometers to centimeters. This approach provides access to 3D architectures with a broad range of topologies.
|
| [102] |
Mechanical self-assembly of a strain-engineered flexible layer: Wrinkling, rolling, and twisting .
Self-shaping of curved structures, especially those involving flexible thin layers, has attracted increasing attention because of their broad potential applications in e.g. nanoelectromechanical/micro-electromechanical systems (NEMS/MEMS), sensors, artificial skins, stretchable electronics, robotics, and drug delivery. Here, we provide an overview of recent experimental, theoretical, and computational studies on the mechanical self-assembly of strain-engineered thin layers, with an emphasis on systems in which the competition between bending and stretchingenergy gives rise to a variety ofdeformations,such as wrinkling, rolling, and twisting. We address the principle of mechanical instabilities, which is often manifested in wrinkling or multistability of strain-engineered thin layers. The principles of shape selection and transition in helical ribbons are also systematically examined. We hope that a more comprehensive understanding of the mechanical principles underlying these rich phenomena can foster the development of new techniques for manufacturing functional three- dimensional structures on demand for a broad spectrum of engineering applications.
|

/
| 〈 |
|
〉 |