引 言
在海洋地震工程领域,需要关注海底地震波的传播[1-2]及海底地震作用下结构的安全性问题[3-6],其响应分析涉及流固耦合问题.总体上,流固耦合从机理上可分为两类:一类是耦合作用仅仅发生在流体和固体介质的交界面上,由界面协调条件引入的[7-16];另一类是流固两相混合在一起,难以明显分开,其耦合效应通过描述问题的微分方程来体现,如描述饱和多孔介质的Biot方程[17-18].在海洋工程中,海床土一般为饱和土,通过Biot方程进行描述,属于第二类流固耦合,海水与饱和海床之间的耦合、海水与结构(或基岩)间的耦合、以及饱和海床土与基岩(或结构)之间的耦合属于第一类流固耦合.因此,海洋工程中的流固耦合问题十分复杂,计算较为困难.若采用现行方法,需不同分析模块之间进行交互耦合[19].
图1
1 基本理论
1.1 一般饱和多孔介质情形
饱和多孔介质的固相平衡方程
液相平衡方程
相容方程(考虑初始孔压和初始体应变为零时)
其中,${\bf{L}}_{\rm s}$和${\bf{L}}_{\rm w}$为微分算子矩阵;${{ {\sigma }'}}$为有效应力矢量,$\tau$为平均孔压,以拉为正;$P$为孔隙水压,以压为正;${{U}}$和${{u}}$分别为液相和固相的位移矢量,${{\dot {U}}}$和${{\dot {u}}}$为速度,${{\ddot {U}}}$和${{ \ddot {u}}}$为加速度;$\rho _{\rm s}$和$\rho _{\rm w}$分别为固相和液相的密度,$\beta$为孔隙率,$b = {\beta ^2\mu _0 } / k_0$,$k_0$为流体渗透系数,$\mu _0$为动黏度系数;$E_{\rm w}$为流体的体变模量,$e^{\rm s}$和$e^{\rm w}$分别为固相和液相的体应变,${{e}}$为固相的应变矢量.${\bf{L}}_{\rm s}$和${\bf{L}}_{\rm w}$分别为
Dirichlet边界条件
Neumann边界条件
其中,${{\bar {u}}}$和${{\bar {U}}}$分别为在边界上给定的固相和液相位移.${{\bar {\sigma }}}$和$\bar {P}$分别为边界上固相平均应力和真实孔压的给定值;${{n}}$为沿边界外法线的方向矢量,${{\hat {n}}}$为由方向导数组成的矩阵,其形式如下
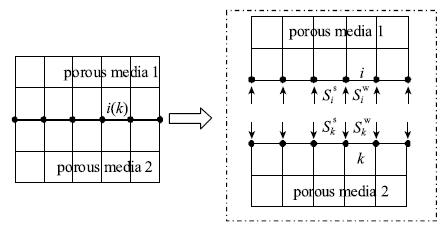
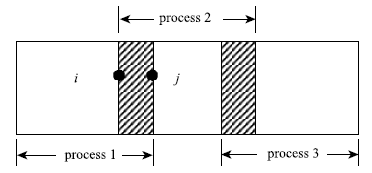
对方程(1)和(2)采用伽辽金方法离散,考虑边界条件,可得任一结点i的解耦运动平衡方程为[28]
其中,${{M}}_{{\rm s}i}$和${{M}}_{{\rm w}i}$分别为集中在i节点上的固相质量和液相质量;${{F}}_i^{\rm s}$和${{F}}_i^{\rm w}$分别为集中在节点i的固、液相本构力;${{ T}}_i^{\rm s}$和${{T}}_i^{\rm w}$分别为集中在节点i的固、液相黏性阻力;${{S}}_i^{\rm s}$和${{S}}_i^{\rm w}$分别作用在节点i的固、液相边界力.在同一介质内,由于所有位移和应力都连续,通过单元界面作用在它们之上的应力大小相等、方向相反,在单元组装的过程中,内部节点的${{S}}_i^{\rm s}$和${{S}}_i^{\rm w}$均为零.它们由下面的式子计算得到
图2
其中
此时,${{S}}_i^{\rm s}$和${{S}}_i^{\rm w}$为介质二作用在界面点i上的界面力,${{\bar {S}}}_k^{\rm s}$和${{\bar {S}}}_k^{\rm w}$为介质一作用在界面点k上的界面力,它们之间的关系由如下界面连续条件[30]确定
其中,式(13c)中的${k}'$为阻滞系数,这里假设两种介质的孔隙完全连通,${k}' = 0$.另外,假设系统的初始值为零,则式(13d)、式(13e)中的速度可换成位移和加速度,本文的推导中采用这一假设.将式(7)和式(10)中x方向的方程相加,考虑到式(13d)和式(13b),以及${ {\hat {n}}} =-{{ \bar{\hat {n}}}}$,有
这即是通常的单元组装后,节点k的x方向平衡方程.同理,可得节点k的y方向固相方程如下
这里以水平成层介质为例,则方向导数$n_x = n_y =-\bar {n}_x =-\bar {n}_y = 0$,$n_z =-\bar {n}_z = 1$,由式(9h)、式(12h)可知,$S_{ix}^{\rm w} = S_{iy}^{\rm w} = 0$ ,$\bar {S}_{ix}^{\rm w} = \bar {S}_{iy}^{\rm w} = 0$.因此,i点和k点在x,y方向的液相方程如下
取式(7)、式(8)、式(10)、式(11)式的z方向方程相加,考虑到$n_x = n_y =-\bar {n}_x =-\bar {n}_y = 0$,$n_z =-\bar {n}_z = 1$,由式(13a)可知,$S_{iz}^{\rm s} + S_{iz}^{\rm w} + \bar {S}_{kz}^{\rm s} + \bar {S}_{kz}^{\rm w} = 0$,故可得
将式(8)乘以$\bar {\beta }$,加上式(11)乘以$\beta$,取z方向的方程.由式(9h)、式(12h)和式(13c)可知,$\bar {\beta }S_{iz}^{\rm w} + \beta \bar {S}_{kz}^{\rm w} = 0$,故可得
将式(13e)代入式(20)和式(21),消去$\ddot {u}_{iz}$、$\ddot {U}_{iz}$,整理得
其中
式(24d)中,附加的$\varepsilon$为一非常小的量,其作用是避免饱和多孔介质退化到流体和固体情形时,分母为零.联立式(22)、式(23),可解得
式(14)~式(19),以及式(25)和式(26)可采用时步积分求解。本文采用如下显式积分格式
其中,上标$p$表示$t = p\Delta t$时刻.对式(14)~式(19)以及式(25)和式(26)式采用上述时步积分格式,可得
得到$\bar {u}_{kx}^{(p + 1)}$,$\bar {u}_{ky}^{(p + 1)}$,$\bar {u}_{kz}^{(p + 1)}$,$\bar {U}_{kz}^{(p + 1)}$后,由式(13d)和式(13e)可进一步求得$u_{ix}^{(p + 1)}$,$u_{iy}^{(p + 1)}$,$u_{iz}^{(p + 1)}$,$U_{iz}^{(p + 1)}$
因此,由式(29)可得界面点i和k的响应.
1.2 特殊情形
1.2.1 流体-饱和土情形
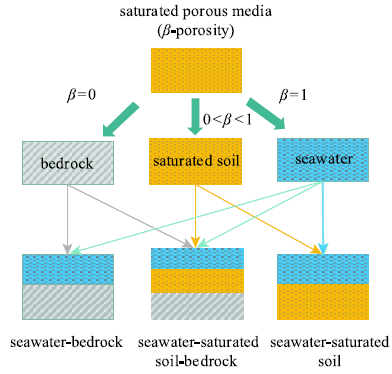
考虑饱和土上覆流体情形.此时,图2中介质二为饱和多孔介质,介质一为流体,$\beta = 1$,${{M}}_{{\rm s}i} = {\bf 0}$.考虑无黏的理想流体,动黏度系数为零,则$b = 0$,${{T}}_i^{\rm s} = {\bf 0}$,${{T}}_i^{\rm w} = {\bf 0}$;不存在固相,固相骨架模量可取为零,则${{F}}_i^{\rm s} = {\bf 0}$,${{S}}_i^{\rm s} = {\bf 0}$;由此,式(7)自动满足,式(8)退化为如下理想流体方程
因此,饱和多孔介质方程可以用来分析理想流体的动力响应.
流体-饱和土界面连续条件为[28]
由动力方程式(10)、式(11)、式(30)以及界面连续条件式(31),按2.1节的方法,可得界面点的运动方程如下
其中
将$\beta = 1$,${{M}}_{{\rm s}i} = {\bf 0}$,${{F}}_i^{\rm s} = {\bf 0}$,${{ T}}_i^{\rm s} = {\bf 0}$,${{T}}_i^{\rm w} = {\bf 0}$,${{F}}_i^{\rm s} = {\bf 0}$,${{ S}}_i^{\rm s} = {\bf 0}$代入式(24)和式(29),可分别得到式(33)和式(32).因此流体-饱和土耦合情形是两种不同多孔介质耦合情形的特例,可直接由1.1节中的理论进行分析.
1.2.2 饱和土-干基岩情形
图2中的介质二若为不透水的基岩,不存在液相,则$\bar {\beta } = 0$,${{\bar {M}}}_{{\rm w}k} = {\bf 0}$;液相体积模量和固液之间的黏性力取为零,则${{\bar {F}}}_k^{\rm w} = {\bf 0}$,${{\bar {T}}}_k^{\rm w} = {\bf 0}$,${{\bar {T}}}_k^{\rm s} = {\bf 0}$,${{\bar {S}}}_k^{\rm w} = {\bf 0}$,方程(11)自动满足,式(10)退化为如下干基岩方程
因此,饱和多孔介质方程可以用来分析干基岩的动力响应.
饱和土-干基岩界面条件为[30]
由动力方程式(7)、式(8)、式(34)以及界面连续条件(35)式,按2.1节的方法,可得界面点的运动方程如下
其中
将$\bar {\beta } = {\bf 0}$,${{\bar {M}}}_{{\rm w}k} = {\bf 0}$,${{\bar {F}}}_k^{\rm w} = {\bf 0}$,${{\bar {T}}}_k^{\rm w} = {\bf 0}$,${{\bar {T}}}_k^{\rm s} = {\bf 0}$,${{\bar {S}}}_k^{\rm w} = {\bf 0}$代入式(24)和式(29),可分别得到式(37)和式(36).因此饱和土-干基岩耦合情形也是两种不同多孔介质耦合情形的特例,可直接由2.1节中的理论进行分析.
1.2.3 流体-干基岩情形
此时,图2中介质一为理想流体,介质二为干基岩.按前述参数取值,运动方程分别退化为式(30)和式(34).流体-干基岩界面连续条件为(不透水)
由动力方程(30)和(34)以及界面连续条件式(38),可得界面点的运动方程如下
其中
同样,将$\beta = 1$,${{M}}_{{\rm s}i} = {\bf 0}$,${{F}}_i^{\rm s} = {\bf 0}$,${{T}}_i^{\rm s} = {\bf 0}$,${{T}}_i^{\rm w} = {\bf 0}$,${{S}}_i^{\rm s} = {\bf 0}$,以及$\bar {\beta } = {\bf 0}$,${{\bar {M}}}_{{\rm w}k} = {\bf 0}$,${{\bar {F}}}_k^{\rm w} = {\bf 0}$,${{\bar {T}}}_k^{\rm w} = {\bf 0}$,${{\bar {T}}}_k^{\rm s} = {\bf 0}$,${{\bar {S}}}_k^{\rm w} = {\bf 0}$代入式(24)和式(29),可分别得到式(40)和式(39).因此,流体-干基岩耦合情形同样是两种不同多孔介质耦合情形的特例.
综上可知,流体、固体、饱和多孔介质之间的耦合均可统一在同一理论框架进行分析.
1.3 实施方法
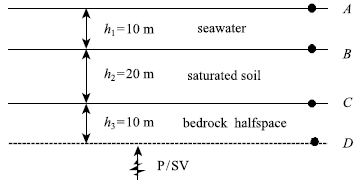
图3
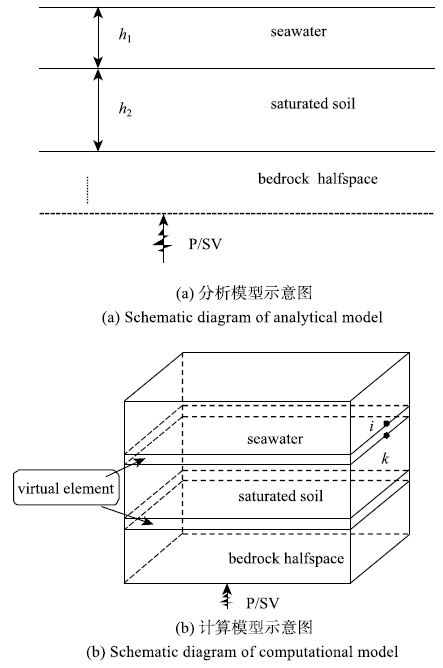
另外,对于复杂地形,或有散射体(如海工结构)存在的情形,需要通过有限元等数值方法进行求解.因此,我们对图3(a)所示的问题采用本文提出的有限元方法求解,计算模型如图3(b)所示,在侧面和底面采用多次透射人工边界[22],用于模拟无限域.在边界上采用传递矩阵方法得到的自由场作为波动输入.海水-饱和海床-基岩体系中,内部点(除人工边界点和界面点外的其余节点)及界面点的响应计算,均采用统一的饱和多孔介质方程和不同饱和多孔介质间界面点的计算方法,即2.1节中的理论方法.具体实施时,在界面处设置一层"虚单元",该单元的材料参数为零.这样,对于内部点的响应,按饱和多孔介质显式有限元方法计算;对于界面点的响应,没有界面连续条件约束的某些方向(对于文中所述情形,为x和y方向的液相等),其响应计算与内部点一样.对于有连续条件的方向,仅需每时步在节点对(如图3(b)中i和k点)之间传递节点本构力和位移.基于此,编制了相应的三维有限元计算程序,以实现本文方法.
2 算例验证
采用如下线弹性本构
其中,$E_{\rm u}$和$E_{\rm b}$分别为不排水和排水时饱和多孔介质的压缩模量,$E_{\rm w}$为孔隙流体的压缩模量,$k_0$为渗透系数.
图4
表1 材料参数表
Table 1
| Media | Prosity yS | 仲 | Ps/(kg.m_3) | Pw/(kg.m_3) | V | G/MPa | Ew/GPa | M/GPa | a | k0 / ^m2 |
|---|---|---|---|---|---|---|---|---|---|---|
| seawater | 1 | 0 | 0 | 1000 | 0.49 | 0 | 2.25 | 2.25 | 1 | 1 |
| saturated soil | 0.26 | 0.001 | 2000 | 1000 | 0.49 | 83.2 | 2.25 | 4.78 | 0.697 | 10_7 |
| bedrock | 0 | 0 | 2500 | 0 | 0.2 | 480 | 0 | — | 0 | 0 |
2.1 海水-干土情形
图5
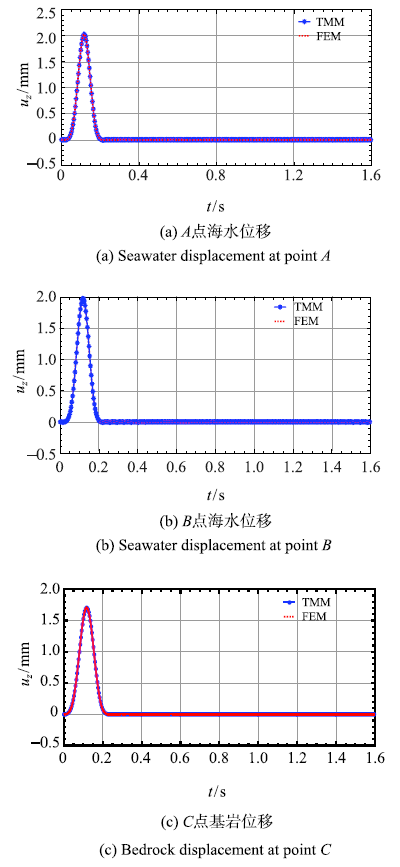
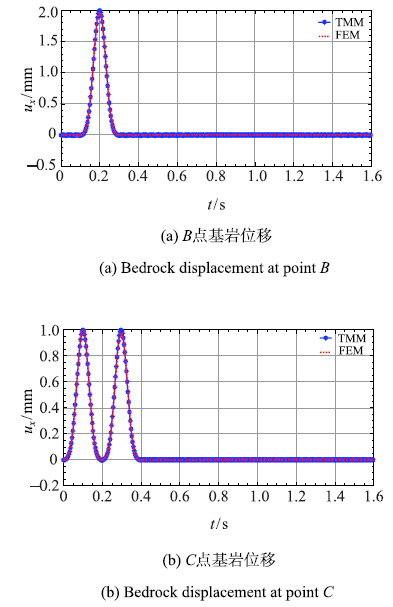
图6
图6
P波入射时海水-基岩系统的位移响应
Fig.6
Displacement of seawater-bedrock system for P wave incidence
图7
图7
SV波入射时海水-基岩系统的位移响应
Fig.7
Displacement of seawater-bedrock system for SV wave incidence
2.2 海水-饱和土情形
图8
图9
图9
P波入射时海水-饱和土系统的位移响应
Fig.9
Displacement of seawater-saturated soil system for P wave incidence
图10
图10
SV波入射时海水-饱和土系统的位移响应
Fig.10
Displacement of seawater-saturated soil system for SV wave incidence
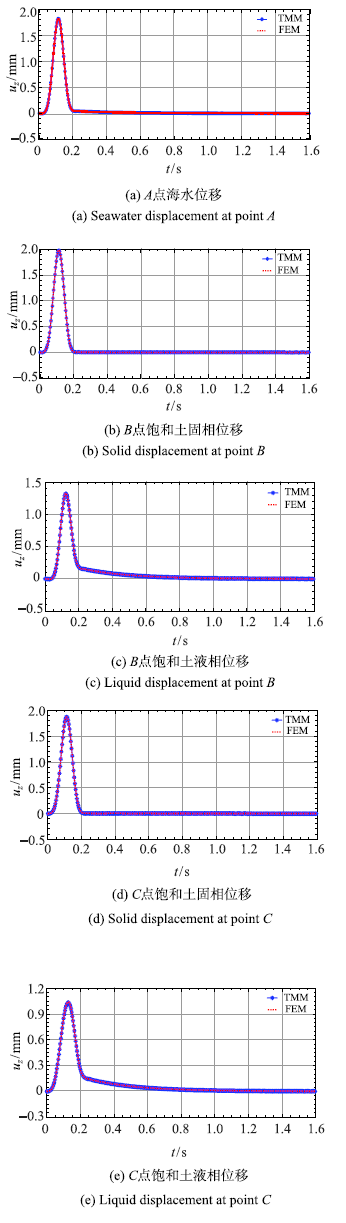
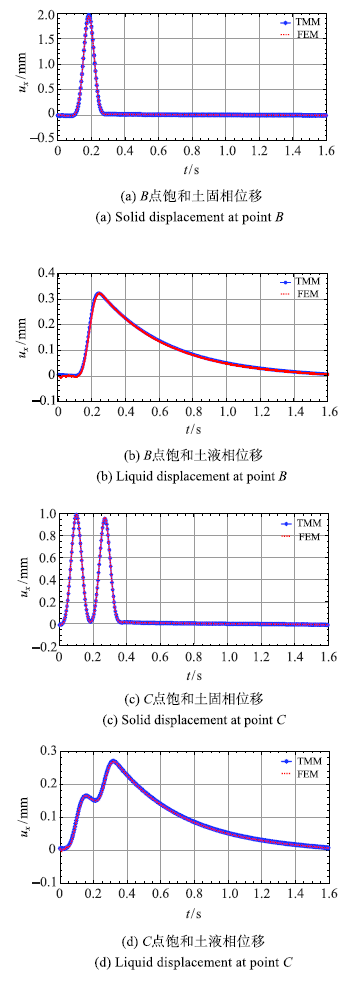
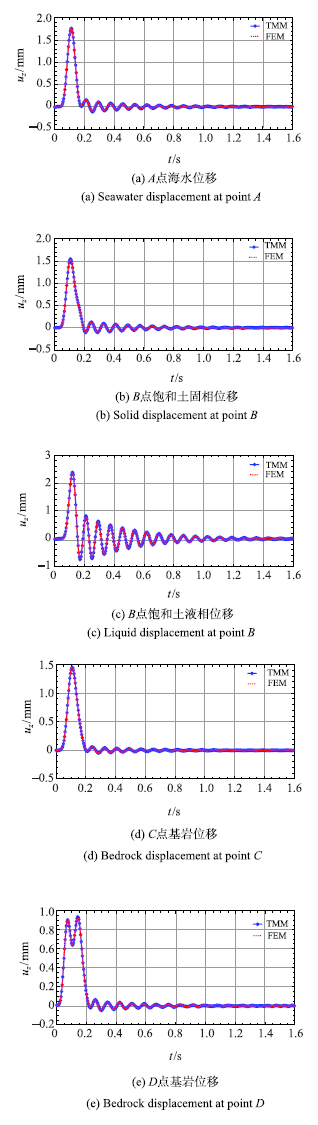
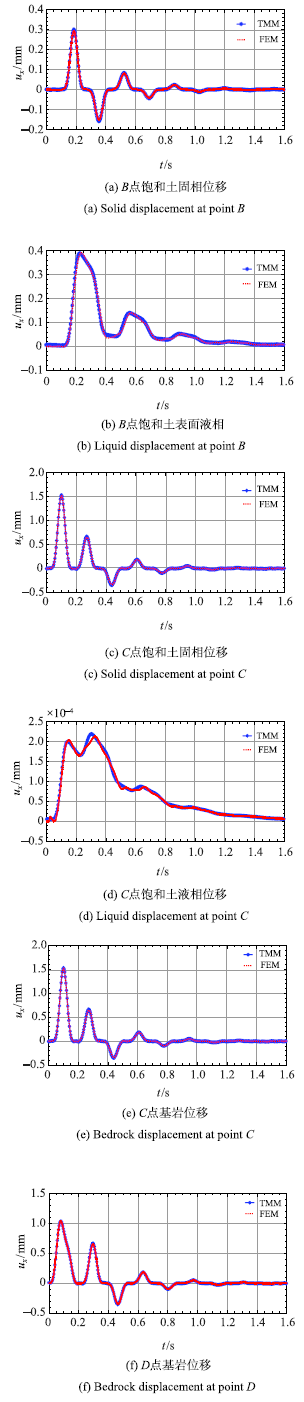
2.3 海水-饱和海床-基岩情形(并行算例)
图11
图12
图13
图13
P波入射时海水-饱和土-基岩体系的位移响应
Fig.13
Displacement of seawater-saturated soil-bedrock system for P wave incidence
图14
图14
SV波入射时海水-饱和土-基岩体系的位移响应
Fig.14
Displacement of seawater-saturated soil-bedrock system for SV wave incidence
通过上述三个算例,验证了本文统一计算框架的有效性,以及并行计算的可行性.
3 结 论
本文将理想流体、固体、饱和多孔介质之间的耦合分析纳入到统一计算框架,建立了集中质量显式有限元求解方法,并编制了相应的三维并行分析程序.分析了半无限海水-饱和海床、海水-弹性基岩、海水-饱和海床-弹性基岩三种情形在P-SV波垂直入射时的动力响应,通过与传递矩阵方法得到的结果进行对比,验证了该统一计算框架的有效性以及并行计算的可行性.
文中的算例采用线弹性本构,但公式推导只涉及本构力,可以适用于非线性情形.界面点的精度与内域点一致,取决于有限元空间离散精度和时步积分格式的精度,可以采用其他格式满足所需精度要求.文中算例未出现失稳现象,但耦合计算格式的稳定性需另做讨论.另外,本文只考虑了水平成层情形,通过考虑界面的方向导数,该方法可以推广到复杂海底地形情形,结合并行技术,可以模拟大规模海底地震动问题以及海水-海床-结构体系的地震响应问题,也可为海洋声学及海洋地震勘探提供正演分析方法.
参考文献
FDM Simulation of seismic-wave propagation for an aftershock of the 2009 Suruga Bay earthquake: Effects of ocean-bottom topography and seawater layer
ABSTRACT Feasibility studies on simulating seismic-wave propagation in media for a suboceanic earthquake, including both land and ocean-bottom topographies and a seawater layer, are scarce. Some of the conventional staggered-grid finite-difference method (FDM) simulations use a simplified structure model without a seawater layer and with a flat ocean-bottom topography. In this study, we apply our heterogeneity, oceanic layer, and topography scheme (HOT)-FDM and a 3D structure model including land and ocean-bottom topographies, a seawater layer, and a fluid-solid boundary condition to an aftershock (M-w 5.8) of the 2009 Suruga Bay earthquake. We attempt to reproduce observations at seismic stations near the coast and then simulate waveforms in the ocean-bottom stations. Our results show that a large difference between the cases with and without topographies can be seen in the coda part after the S wave in the simulated waveforms in terms of amplitudes and elongations. The synthetic waveforms in the model with topographies are in agreement with the observed waveforms. Our results also show that a significant difference in the amplification of the coda part between the cases with and without the seawater layer can be found at the ocean-bottom stations. This coda part is the S-and Rayleigh-wave propagation associated with the ocean and the underlying sediment layers. Our results show that a realistic model with topographies and a seawater layer is needed in FDM simulations in order to precisely reproduce observed waveforms or predict seismic motion for a suboceanic earthquake.
Study on the effect of the oceanic water layer on strong ground motion simulations
We studied the effect of the oceanic water layer on strong ground motion simulations. Source faults of subduction zone earthquakes, such as the Nankai-Tonankai earthquake, West Japan, are situated in the offshore area, under a thick water layer. The necessity of including the oceanic water layer in the velocity model for simulations employing the finite difference method is debated by many researchers, and consideration given to the possibility of neglecting by this layer, which would reduce the computation time and stabilize the calculations. Although the oceanic water layer has a low velocity and density, it can affect surface wave generation. In this study, for demonstration purposes, we calculated and compared strong ground motions from three source fault models, placed into the boundary between the crust and subducting plate, where source rupture of the Tonankai earthquake is expected. Simulations were made for two realistic three-dimensional velocity models: without and with the oceanic water layer. The model without the oceanic water layer was constructed simply by subtracting the depth of the oceanic layer from the depth of all velocity interfaces under the ocean. This procedure keeps the thickness of the layers (oceanic sediments, surface low-velocity layer, upper crust, and lower crust) the same as in the model with the oceanic layer and reduces simulation errors. Simulations were made for the set of sites on a line across the subduction zone and directed to the Osaka basin. The results show that the water layer has a strong effect on the fundamental mode of the Rayleigh wave, which can be generated by the shallow (approx. 5 km) source. Considering that all asperities of the expected Nankai-Tonankai earthquake are deep (> 10 km), we conclude that the effect of the water layer can be neglected for ground motions at land sites.
Seismic response of poroelastic seabed and composite breakwater under strong earthquake loading
Abstract 61 ” as the governing equation for porous seabed foundation, the seismic response of a composite breakwater and its porous seabed foundation under the seismic wave recorded in the Japan 311 off the pacific coast of Tohoku earthquake (M L =029.0) is investigated using a FEM numerical model. The numerical results indicate that the seismic response of composite breakwater is very strong in the earthquake process. The amplification of the input seismic wave occurs both in seabed foundation and composite breakwater; and this amplification is positively related to the buried depth of points. The horizontal seismic response is much strong than the vertical seismic response. The seismic wave induced excess pore pressure and effective stresses in seabed foundation vibrates; the vibration amplitude is also positively related to the buried depth of points. Under strong seismic loading, the surface region of seabed foundation could liquefy. The parametric study shows that the young’s modulus of seabed foundation has significant effect on the seismic response of composite breakwater.
Seismic response of fluid-structure interaction of undersea tunnel during bidirction earthquake
Seismic behaviors of a floating submerged tunnel with a rectangular cross-section
61Two-dimensional seismic behaviors of a submerged floating tunnel (SFT) are examined.61The effects of seawater upon the seismic behaviors of an SFT system are investigated.61The depth of the ocean water is one of the important factors for the SFT system.61Behaviors of the SFT system are affected by the location of the tunnel in the water.61The energy absorption by seabed influences the dynamic responses of the SFT system.
LeTallec P. Load and motion transfer algorithms for fluid/structure interaction problems with non-matching discrete interfaces: Momentum and energy conservation, optimal discretization and application to aeroelasticity
Two effcient staggered algorithms for serial and parallel solution of three-dimensional nonlinear transient aeroelastic problems
Partitioned procedures and staggered algorithms are often adopted for the solution of coupled fluid/structure interaction problems in the time domain. In this paper, we overview two sequential and parallel partitioned procedures that are popular in computational nonlinear aeroelasticity, and address their limitation in terms of accuracy and numerical stability. We propose two alternative serial and parallel staggered algorithms for the solution of coupled transient aeroelastic problems, and demonstrate their superior accuracy and computational efficiency with the flutter analysis of the AGARD Wing 445.6. We contrast our results with those computed by other investigators and validate them with experimental data.
Provably second-order time-accurate loosely-coupled solution algorithms for transient nonlinear computational aeroelasticity
A methodology for designing formally second-order time-accurate and yet loosely-coupled partitioned procedures for the solution of nonlinear fluid tructure interaction (FSI) problems on moving grids is presented. Its key components are a fluid time-integrator that is provably second-order time-accurate on moving grids, the midpoint rule for advancing in time the solution of the structural dynamics equations of motion, a second-order structure predictor for bypassing the inner-iterations encountered in strongly-coupled solution procedures, and a carefully designed algorithm for time-integrating the motion of the fluid-mesh. Following this methodology, two different loosely-coupled schemes are constructed for the solution of transient nonlinear FSI problems and proved to be second-order time-accurate. Three-dimensional numerical results pertaining to the simulation of the aeroelastic response to a gravity excitation of a complete F-16 configuration are also presented. In addition to confirming the theoretical results discussed in this paper, these numerical results highlight a very stable behavior of the designed loosely-coupled partitioned procedures.
Finite element developments for general fluid flows with structural interactions
The objective in this paper is to present some developments for the analysis of Navier-Stokes incompressible and compressible fluid flows with structural interactions. The incompressible fluid is discretized with a new solution approach, a flow-condition-based interpolation finite element scheme. The high-speed compressible fluids are solved using standard finite volume methods. The fluids are fully coupled to general structures that can undergo highly non-linear response due to large deformations, inelasticity, contact and temperature. Particular focus is given on the scheme used to couple the fluid media with the structures. The fluids can also be modelled as low-speed compressible or slightly compressible media, which are important models in engineering practice. Some solutions obtained using ADINA are presented to indicate the analyses that can be performed
Performance of partitioned procedures in fluid-structure interaction
Partitioned simulations of fluid–structure interaction can be solved for the interface’s position with Newton–Raphson iterations but obtaining the exact Jacobian is impossible if the solvers are “black boxes”. It is demonstrated that only an approximate Jacobian is needed, as long as it describes the reaction to certain components of the error on the interface’s position. Based on this insight, a quasi-Newton coupling algorithm with an approximation for the inverse of the Jacobian (IQN-ILS) has been developed and compared with a monolithic solver in previous work. Here, IQN-ILS is compared with other partitioned schemes such as IBQN-LS, Aitken relaxation and Interface-GMRES(R).
Numerical methods for fluid-structure Interaction-A review
The interactions between incompressible fluid flows and immersed structures are nonlinear multi-physics phenomena that have applications to a wide range of scientific and engineering disciplines. In this article, we review representative numerical methods based on conforming and non-conforming meshes that are currently available for computing fluid-structure interaction problems, with an emphasis on some of the recent developments in the field. A goal is to categorize the selected methods and assess their accuracy and efficiency. We discuss challenges faced by researchers in this field, and we emphasize the importance of interdisciplinary effort for advancing the study in fluid-structure interactions.
Partitioned solver for strongly coupled fluid-structure interaction
In this work a fluid-structure interaction solver is developed in a partitioned approach using block Gauss-Seidel implicit scheme. Finite volume method is used to discretize the fluid flow problem on a moving mesh in an arbitrary Lagrangian-Eulerian formulation and by using an adaptive time step. The pressure-velocity coupling is performed by using the PIMPLE algorithm, a combination of both SIMPLE and PISO algorithms, which permits the use of larger time steps in a moving mesh. The structural elastic deformation is analyzed in a Lagrangian formulation using the St. Venant-Kirchhoff constitutive law, for non-linear large deformations. The solid structure is discretized by the finite volume method in an iterative segregated approach. The automatic mesh motion solver is based on Laplace smoothing equation with variable mesh diffusion. The strong coupling between the different solvers and the equilibrium on the fluid-structure interface are achieved by using an iterative implicit fixed-point algorithm with dynamic Aitken's relaxation method. The solver, which is called vorflexFoam, is developed using the open source C++ library OpenFOAM. The solver is validated on two different benchmarks largely used in the open literature. In the first one the structural deformation is induced by incompressibility. The second benchmark consists on a vortex excited elastic flap in a Von Karman vortex street. Finally, a more complex case is studied including two elastic flaps immersed in a pulsatile flow. The present solver detects accurately the interaction between the complex flow structures generated by the flaps and the effect of the flaps oscillations between each other. (c) 2012 Elsevier Ltd. All rights reserved.
Parallel coupling numerics for partitioned fluid-structure interaction simulations
Within the last decade, very sophisticated numerical methods for the iterative and partitioned solution of fluid tructure interaction problems have been developed that allow for high accuracy and very complex scenarios. The combination of these two aspects ccuracy and complexity emands very high computational grid resolutions and, thus, high performance computing methods designed for massively parallel hardware architectures. For those architectures, currently used coupling methods, which mainly work with a staggered execution of the fluid and the structure solver, i.e., the execution of one solver after the other in every outer iteration, lead to severe load imbalances: if the flow solver, e.g., scales on a very large number of processors but the structural solver does not due to its limited amount of data and required operations, almost all processors assigned to the coupled simulations are idle during the execution of the structure solver. We propose two new iterative coupling methods that allow for the simultaneous execution of flow and structure solvers. In both cases, we show that pure fixed-point iterations based on the parallel execution of the solvers do not lead to good results, but the combination of parallel solver execution and so-called quasi-Newton methods yields very efficient and robust methods. Those methods are known to be very efficient also for the stabilization of critical scenarios solved with the standard staggered solver execution. We demonstrate the competitive convergence of our methods for various established benchmark scenarios. Both methods are perfectly suited for use with black-box solvers because the quasi-Newton approach uses solely input and output information of the solvers to approximate the effect of the unknown Jacobians that would be required in a standard Newton solver.
preCICE-A fully parallel library for multi-physics surface coupling
In the emerging field of multi-physics simulations, we often face the challenge to establish new connections between physical fields, to add additional aspects to existing models, or to exchange a solver for one of the involved physical fields. If in such cases a fast prototyping of a coupled simulation environment is required, a partitioned setup using existing codes for each physical field is the optimal choice. As accurate models require also accurate numerics, multi-physics simulations typically use very high grid resolutions and, accordingly, are run on massively parallel computers. Here, we face the challenge to combine flexibility with parallel scalability and hardware efficiency. In this paper, we present the coupling tool preCICE which offers the complete coupling functionality required for a fast development of a multi-physics environment using existing, possibly black-box solvers. We hereby restrict ourselves to bidirectional surface coupling which is too expensive to be done via file communication, but in contrast to volume coupling still a candidate for distributed memory parallelism between the involved solvers. The paper gives an overview of the numerical functionalities implemented in preCICE as well as the user interfaces, i.e., the application programming interface and configuration options. Our numerical examples and the list of different open-source and commercial codes that have already been used with preCICE in coupled simulations show the high flexibility, the correctness, and the high performance and parallel scalability of coupled simulations with preCICE as the coupling unit.
An added-mass partition algorithm for fluid-structure interactions of compressible fluids and nonlinear solids
We describe an added-mass partitioned (AMP) algorithm for solving fluid–structure interaction (FSI) problems involving inviscid compressible fluids interacting with nonlinear solids that undergo large rotations and displacements. The computational approach is a mixed Eulerian–Lagrangian scheme that makes use of deforming composite grids (DCG) to treat large changes in the geometry in an accurate, flexible, and robust manner. The current work extends the AMP algorithm developed in Banks et al. [1] for linearly elasticity to the case of nonlinear solids. To ensure stability for the case oflightsolids, the new AMP algorithm embeds an approximate solution of a nonlinear fluid–solid Riemann (FSR) problem into the interface treatment. The solution to the FSR problem is derived and shown to be of a similar form to that derived for linear solids: the state on the interface being fundamentally an impedance-weighted average of the fluid and solid states. Numerical simulations demonstrate that the AMP algorithm is stable even for light solids when added-mass effects are large. The accuracy and stability of the AMP scheme is verified by comparison to an exact solution using the method of analytical solutions and to a semi-analytical solution that is obtained for a rotating solid disk immersed in a fluid. The scheme is applied to the simulation of a planar shock impacting a light elliptical-shaped solid, and comparisons are made between solutions of the FSI problem for a neo-Hookean solid, a linearly elastic solid, and a rigid solid. The ability of the approach to handle large deformations is demonstrated for a problem of a high-speed flow past a light, thin, and flexible solid beam.
Extended ALE Method for fluid-structure interaction problems with large structural displacements
Standard Arbitrary Lagrangian-Eulerian (ALE) methods for the simulation of fluid-structure interaction (FSI) problems fail due to excessive mesh deformations when the structural displacement is large. We propose a method that successfully deals with this problem, keeping the same mesh connectivity while enforcing mesh alignment with the structure. The proposed Extended ALE Method relies on a variational mesh optimization technique, where mesh alignment with the structure is achieved via a constraint. This gives rise to a constrained optimization problem for mesh optimization, which is solved whenever the mesh quality deteriorates. The performance of the proposed Extended ALE Method is demonstrated on a series of numerical examples involving 2D FSI problems with large displacements. Two way coupling between the fluid and structure is considered in all the examples. The FSI problems are solved using either a Dirichlet-Neumann algorithm, or a Robin-Neumann algorithm. The Dirichlet-Neumann algorithm is enhanced by an adaptive relaxation procedure based on Aitken's acceleration. We show that the proposed method has excellent performance in problems with large displacements, and that it agrees well with a standard ALE method in problems with mild displacement.
Theory of propagation of elastic waves in a fluid-saturated porous solid
Mechanics of deformation and acoustic propagation in porous media
A unified treatment of the mechanics of deformation and acoustic propagation in porous media is presented, and some new results and generalizations are derived. The writer's earlier theory of deformation of porous media derived from general principles of nonequilibrium thermodynamics is applied. The fluid﹕olid medium is treated as a complex physicalヽhemical system with resultant relaxation and viscoelastic properties of a very general nature. Specific relaxation models are discussed, and the general applicability of a correspondence principle is further emphasized. The theory of acoustic propagation is extended to include anisotropic media, solid dissipation, and other relaxation effects. Some typical examples of sources of dissipation other than fluid viscosity are considered.
Wave propagation near a fluid-solid interface: A spectral-element approach
A 2D finite-element scheme for fluid-solid-acoustic interactions and its application to human phonation
We present a recently developed approach for the modeling of fluid–solid–acoustic interaction problems. For the efficient numerical solution of the coupled three-field problem we apply the finite-element method. The mechanical and the acoustic fields are approximated by a standard Galerkin scheme. A residual-based stabilization method is chosen for the fluid field. The interaction of the Eulerian fluid field with the Lagrangian mechanical field is based on the Arbitrary-Lagrangian–Eulerian (ALE) method and is iteratively coupled in a strong sense. The solid–acoustic interaction is based on continuum mechanics, and the fluid–acoustic coupling on Lighthill’s analogy. The new steps of our scheme are verified through validation examples. Finally, a fluid–solid–acoustic simulation of the human phonation process is presented based on a realistic model.
考虑水-饱和土场地-结构耦合时的沉管隧道地震反应分析
用理想流体介质模拟水层、流体饱和多孔介质模拟饱和土地层,在理 想流体介质与流体饱和多孔介质相连接边界的连续条件基础上,结合已有的对理想流体介质、流体饱和多孔介质进行动力反应分析的显式有限元方法,并考虑地层与 结构的动力相互作用,建立了进行水与场地、结构耦合动力分析的方法.利用该方法对沉管隧道的地震响应进行了研究,重点分析了水深、地质条件等因素对沉管隧 道地震反应的影响,并从中得出了一些可供相关人员进行沉管隧道抗震分析时参考的结论.
Seismic Response analysis of immersed tube tunnels considering water saturated soil site structure coupling
用理想流体介质模拟水层、流体饱和多孔介质模拟饱和土地层,在理 想流体介质与流体饱和多孔介质相连接边界的连续条件基础上,结合已有的对理想流体介质、流体饱和多孔介质进行动力反应分析的显式有限元方法,并考虑地层与 结构的动力相互作用,建立了进行水与场地、结构耦合动力分析的方法.利用该方法对沉管隧道的地震响应进行了研究,重点分析了水深、地质条件等因素对沉管隧 道地震反应的影响,并从中得出了一些可供相关人员进行沉管隧道抗震分析时参考的结论.
透射边界条件在波动谱元模拟中的实现:二维波动
将邢浩洁和李鸿晶提出的多次透射公式(multi-transmitting formula,MTF)的谱元格式应用于均匀介质中线弹性SH波动问题的谱元模拟.假定紧邻人工边界的一层谱单元为具有直线边界的四边形单元,以保证每个人工边界节点都唯一对应一条指向内域的离散网格线.人工边界节点在某时刻的位移由该离散网格线上的节点在前若干时刻的位移确定,按照MTF谱元格式进行计算.通过平面波以一定角度传播的外源问题算例和点源脉冲自由扩散的内源问题算例,验证了方法的可行性以及对实际复杂波动问题的适用性.通过不同类型初值问题算例,在时域内分析了插值多项式阶次、人工波速和透射阶次三个参数对反射误差的影响.结果表明:插值多项式阶次较高的格式会表现出更好的精度,但总体上对反射误差的影响较小;人工波速对反射误差具有显著影响,当人工波速小于介质物理波速时反射误差较大,而当人工波速等于或稍大于介质物理波速时反射误差处于较低水平;透射阶次对反射误差具有决定性影响,表现在不失稳的情形下提高透射阶次能够迅速降低反射误差,但内源问题从三阶MTF开始出现飘移失稳,外源问题从二阶MTF开始出现轻微的飘移失稳.
Implementation of multi-transmitting boundary condition for wave motion simulation by spectral element method: Two dimension case
将邢浩洁和李鸿晶提出的多次透射公式(multi-transmitting formula,MTF)的谱元格式应用于均匀介质中线弹性SH波动问题的谱元模拟.假定紧邻人工边界的一层谱单元为具有直线边界的四边形单元,以保证每个人工边界节点都唯一对应一条指向内域的离散网格线.人工边界节点在某时刻的位移由该离散网格线上的节点在前若干时刻的位移确定,按照MTF谱元格式进行计算.通过平面波以一定角度传播的外源问题算例和点源脉冲自由扩散的内源问题算例,验证了方法的可行性以及对实际复杂波动问题的适用性.通过不同类型初值问题算例,在时域内分析了插值多项式阶次、人工波速和透射阶次三个参数对反射误差的影响.结果表明:插值多项式阶次较高的格式会表现出更好的精度,但总体上对反射误差的影响较小;人工波速对反射误差具有显著影响,当人工波速小于介质物理波速时反射误差较大,而当人工波速等于或稍大于介质物理波速时反射误差处于较低水平;透射阶次对反射误差具有决定性影响,表现在不失稳的情形下提高透射阶次能够迅速降低反射误差,但内源问题从三阶MTF开始出现飘移失稳,外源问题从二阶MTF开始出现轻微的飘移失稳.
三维一致粘弹性人工边界及等效粘弹性边界单元
基于粘弹性人工边界推导了三维一致粘弹性人工边界单元的刚度及阻尼矩阵,利用单元矩阵等效原理采用普通有限单元构造了等效粘弹性边界单元来模拟三维粘弹性边界。均匀半空间算例与成层半空间算例证明三维粘弹性边界单元具有与集中粘弹性人工边界相近的精度,并且施加更为简便。
Three-dimensional uniform viscoelastic artificial boundary and equivalent viscoelastic boundary element
基于粘弹性人工边界推导了三维一致粘弹性人工边界单元的刚度及阻尼矩阵,利用单元矩阵等效原理采用普通有限单元构造了等效粘弹性边界单元来模拟三维粘弹性边界。均匀半空间算例与成层半空间算例证明三维粘弹性边界单元具有与集中粘弹性人工边界相近的精度,并且施加更为简便。
波动问题中流体介质的动力人工边界
无限域流体介质的波动辐射效应是影响海域工程动力反应的重要因素,人工边界是实现此类开放系统近场波动问题数值分析的有效方法.基于位移格式的流体波动理论推导开放域流体介质的人工边界,分别给出一维、二维和三维空间中平面波、柱面波和球面波的流体介质动力人工边界条件,其中一维平面波动人工边界为经典的黏性边界,二维柱面波、三维球面波的人工边界处节点应力与节点速度和加速度成正比,可等效为由阻尼与质量系统构成的人工边界条件.讨论相应的数值模拟技术,给出流体介质动力人工边界在ANSYS软件平台的具体实现方法.近场流体介质动力反应问题的算例表明,所发展的流体动力人工边界对于轴对称波动与非轴对称波动在近场有限域截断处的透射吸收作用的模拟计算精度均较为良好,说明此流体介质人工边界具有较高的可靠性与实用性.所发展的流体介质动力人工边界可较为方便地与大型商用有限元软件结合,可为包括海域地形和海岛在内的海域工程的动力分析提供一定的方法借鉴.
BaoXin, Tan Hui, et al. Dynamical artificial boundary for fluid medium in wave motion problems
无限域流体介质的波动辐射效应是影响海域工程动力反应的重要因素,人工边界是实现此类开放系统近场波动问题数值分析的有效方法.基于位移格式的流体波动理论推导开放域流体介质的人工边界,分别给出一维、二维和三维空间中平面波、柱面波和球面波的流体介质动力人工边界条件,其中一维平面波动人工边界为经典的黏性边界,二维柱面波、三维球面波的人工边界处节点应力与节点速度和加速度成正比,可等效为由阻尼与质量系统构成的人工边界条件.讨论相应的数值模拟技术,给出流体介质动力人工边界在ANSYS软件平台的具体实现方法.近场流体介质动力反应问题的算例表明,所发展的流体动力人工边界对于轴对称波动与非轴对称波动在近场有限域截断处的透射吸收作用的模拟计算精度均较为良好,说明此流体介质人工边界具有较高的可靠性与实用性.所发展的流体介质动力人工边界可较为方便地与大型商用有限元软件结合,可为包括海域地形和海岛在内的海域工程的动力分析提供一定的方法借鉴.
关于传递矩阵法分析饱和成层介质响应问题的讨论
<p>水平成层土体的地震响应分析(自由场分析)是地震工程领域地震波散射问题的前提基础,由于饱和多孔方程的复杂性,以往的研究大多集中于干土情形,对于饱和土情形的研究相对较少.而实际工程中,地下水位以下,土体孔隙中充满流体,应考虑饱和多孔介质模型.基于Biot多孔介质模型,考虑饱和土中固液相对运动引起的衰减,采用Thomson-Haskell传递矩阵方法得到了饱和成层土体在地震波入射情形时的稳态反应,经傅里叶反变换,可得到时域暂态反应.通过SV波从基岩入射至上覆饱和土层的数值算例,验证了该方法的有效性.发现和初步阐明了计算中出现的两类违背因果律(即响应先于输入)的现象:(1)当SV波入射角度大于导致基岩中反射P波为非均匀波的临界角时,会使得计算结果违背因果律.因此,当入射角超过临界角时,非均匀波的表示尚需进一步完善;(2)由于P2波的衰减,当与稳态波衰减有关的渗透率、土层厚度、入射波频率等参数导致衰减系数超过计算机表示精度时,会出现结果违背因果律现象,并据此得到了满足因果律的参数范围,该范围可作为实际计算时的一个上界.该工作为采用传递矩阵法分析水平饱和土层自由场响应提供了指导依据,且地下水位以上可采用干土模型,水位以下采用饱和土模型,更符合实际情形.</p>
Discussion on the matrix propagator method to analyze the response od saturated layered media
<p>水平成层土体的地震响应分析(自由场分析)是地震工程领域地震波散射问题的前提基础,由于饱和多孔方程的复杂性,以往的研究大多集中于干土情形,对于饱和土情形的研究相对较少.而实际工程中,地下水位以下,土体孔隙中充满流体,应考虑饱和多孔介质模型.基于Biot多孔介质模型,考虑饱和土中固液相对运动引起的衰减,采用Thomson-Haskell传递矩阵方法得到了饱和成层土体在地震波入射情形时的稳态反应,经傅里叶反变换,可得到时域暂态反应.通过SV波从基岩入射至上覆饱和土层的数值算例,验证了该方法的有效性.发现和初步阐明了计算中出现的两类违背因果律(即响应先于输入)的现象:(1)当SV波入射角度大于导致基岩中反射P波为非均匀波的临界角时,会使得计算结果违背因果律.因此,当入射角超过临界角时,非均匀波的表示尚需进一步完善;(2)由于P2波的衰减,当与稳态波衰减有关的渗透率、土层厚度、入射波频率等参数导致衰减系数超过计算机表示精度时,会出现结果违背因果律现象,并据此得到了满足因果律的参数范围,该范围可作为实际计算时的一个上界.该工作为采用传递矩阵法分析水平饱和土层自由场响应提供了指导依据,且地下水位以上可采用干土模型,水位以下采用饱和土模型,更符合实际情形.</p>
土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
数值模拟是解决土-结构动力相互作用问题的重要手段,而合理地实现地震波动输入直接影响地震作用下土-结构动力相互作用问题数值模拟的精度。波动法是目前常用的地震动输入方法之一,该方法将输入地震动转化为人工边界上的等效荷载,相较于其他地震动输入方法,波动法模拟精度高,但实施上相对复杂。从有限元模型入手,推导了采用波动法确定等效输入地震荷载的另一种形式,以此为基础,提出了一种在人工边界上实现地震动输入的新方法。新方法通过对土-结构有限元模型中由包含人工边界节点的单元组成的子结构施加自由场位移时程并进行动力分析,直接获得可实现地震波动有效输入的等效荷载,然后将等效输入地震荷载施加在土-结构模型的人工边界节点上,从而完成土-结构动力相互作用问题分析中地震动输入和地震反应计算。与原有波动法相比,新方法避免了需分别计算人工边界上自由场应力和由引入人工边界条件带来的附加力,以及需要根据不同人工边界面确定荷载的作用方向等较为复杂的处理过程,具有等效地震荷载计算简便、地震动输入过程更易于实施的特点。采用竖直入射和斜入射地震波动作用下的弹性半空间和成层半空间地震反应算例验证了新方法的有效性。
The seismic wave input method for soil-structure dynamic interaction analysis based on the substructure of artificial boundaries
数值模拟是解决土-结构动力相互作用问题的重要手段,而合理地实现地震波动输入直接影响地震作用下土-结构动力相互作用问题数值模拟的精度。波动法是目前常用的地震动输入方法之一,该方法将输入地震动转化为人工边界上的等效荷载,相较于其他地震动输入方法,波动法模拟精度高,但实施上相对复杂。从有限元模型入手,推导了采用波动法确定等效输入地震荷载的另一种形式,以此为基础,提出了一种在人工边界上实现地震动输入的新方法。新方法通过对土-结构有限元模型中由包含人工边界节点的单元组成的子结构施加自由场位移时程并进行动力分析,直接获得可实现地震波动有效输入的等效荷载,然后将等效输入地震荷载施加在土-结构模型的人工边界节点上,从而完成土-结构动力相互作用问题分析中地震动输入和地震反应计算。与原有波动法相比,新方法避免了需分别计算人工边界上自由场应力和由引入人工边界条件带来的附加力,以及需要根据不同人工边界面确定荷载的作用方向等较为复杂的处理过程,具有等效地震荷载计算简便、地震动输入过程更易于实施的特点。采用竖直入射和斜入射地震波动作用下的弹性半空间和成层半空间地震反应算例验证了新方法的有效性。
两相介质近场波动模拟的解耦方法,
本文将求解近场波动问题的一种解耦技术推广到两相介质,得到了一种求解两相介质近场波动问题的直接解耦方法,包括集中质量有限元模型、时域显式积分格式和局部人工边界条件. 首先应用加权残数法,并依据波动模拟的精度要求,得到了两相介质集中质量有限元模型. 然后,结合两相介质中波动的衰减特性,实现了透射边界在两相介质近场波动中的运用. 最后,通过数值实验,并与解析解对比,验证了本文方法的有效性.
Decoupling method for near-field wave simulation of two-phase media
本文将求解近场波动问题的一种解耦技术推广到两相介质,得到了一种求解两相介质近场波动问题的直接解耦方法,包括集中质量有限元模型、时域显式积分格式和局部人工边界条件. 首先应用加权残数法,并依据波动模拟的精度要求,得到了两相介质集中质量有限元模型. 然后,结合两相介质中波动的衰减特性,实现了透射边界在两相介质近场波动中的运用. 最后,通过数值实验,并与解析解对比,验证了本文方法的有效性.
The effect of boundaries on wave propagation in a liquid-filled porous solid: V. Transmission across a plane interface
The effect of boundaries on wave propagation in a liquid-filled porous solid: VII. Surface waves in a half-space in the presence of a liquid layer
Transmission of elastic waves through a stratified solid media
The transmission of a plane elastic wave at oblique incidence through a stratified solid medium consisting of any number of parallel plates of different material and thickness is studied theoretically. The matrix method is used to systematize the analysis and to present the equations in a form suitable for computation.
The dispersion of surface waves on multilayered media
A matrix formalism developed by W. T. Thomson is used to obtain the phase velocity dispersion equations for elastic surface waves of Rayleigh and Love type on multi-layered solid media. The method is used to compute phase and group velocities of Rayleigh waves for two assumed three-layer and one two-layer model of the earth's crust in the continents. The computed group velocity curves are compared with published values of the group velocities at various frequencies of Rayleigh waves over continental paths. The scatter of the observed values is larger than the difference between the three computed curves. It is believed that not all of this scatter is due to observational errors but probably represents a real horizontal heterogeneity of the continental crusts. (Author)