引 言
在工程应用中,管道一般会受到外界的约束作用,以维持系统稳定性或限制其振动幅值.这些约束大体可以分为单点约束[8]和 分布式约束[9]两类.单点约束是指管道在长度方向上某点有约束,如固定端约束[8];分布式约束是指管道在长度方向上的较大范围有约束,如弹性地基约束[9]. 随着工作时间的变长,某些约束可能会发生松动.对于分布式的松动约束,管道外壁与约束间可能存有间隙,此时管道在内部流体力激励下可能会与松动约束发生碰撞.关于运动约束作用下输液管的非线性振动问题,国内外学者做了一系列的研究工作. 例如,Païdoussis等[8, 10]从实验和理论两方面详细研究了悬臂输液管在单点松动约束下的非线性振动,探讨了立方非线性弹簧力和修正三线性弹簧力对管道振动的分岔行为和混沌运动的影响;Jin[11]从理论上分析了悬臂输液管受到单点非线性弹性支承时管道的稳定性和非线性响应;Xu等[12]研究了端部有集中质量和立方非线性约束悬臂输液管的分岔行为;Hassan等[13-14]揭示了在格条状运动约束下悬臂输液管的非线性动力学行为,并提出一种碰撞模型来研究管道与约束间的碰撞行为,该模型考虑了管道与约束之间接触形式的不同,并初步提出了分布式碰撞约束的概念;Wang等[15]建立了三维悬臂输液管受到平行板型和圆环型单点约束下的平面和非平面非线性振动行为,讨论了在不同系统参数下这两种约束对管道的平面和空间运动的影响.
以上关于松动约束下悬臂输液管稳定性和非线性振动问题的研究报道中,均假设管内流速恒定不变;在此情形下,当管内流速小于临界流速时($u_0 < u_{\rm cr} )$,系统是稳定的,不会发生颤振失稳.但是,如果管内流体具有周期变化的脉动特性时,系统可能在流速低于临界值时发生参数共振而引起结构失稳.金基铎等[16-17]给出了两端简支输液管的参数共振区域,分析了共振频率和脉动频率之间的关系,并以实验方式系统地研究了两端简支输液管的参数共振问题,实验所得结果与理论分析结果定性一致[18];Panda等[19]借助多尺度法深入分析了脉动内流激励下两端简支输液管的内共振行为,得到了各参数下系统的幅频响应曲线;Wang[20]研究了具有单点约束两端简支管的参数振动和分岔行为;张紫龙等[21]考虑地基的剪切效应、非线性刚度和黏滞阻尼的影响,研究了弹性地基上输液管的受迫振动与参数共振;李云东等[22]采用数值方法求解了脉动内流下悬臂输液管的参数振动问题,还分析了弹性地基对管道振动行为的影响;Ni等[23]应用多尺度法从理论上分析了输流曲管在脉动内流激励下的面内和面外共振行为,得到了管道受一定的脉动平均流速和脉动幅值下产生共振的激励频率区间.对于管内流速大于临界流速的情形($u_0 > u_{\rm cr} )$,也有相关研究人员开展了一系列研究工作.毛晓晔等[24-25]应用高阶多尺度法首次研究了超临界流速输液管在3:1内共振条件下的稳态幅频响应;陈树辉等[26]采用多元L-P方法分析了轴向运动梁横向非线性振动的内共振,揭示了很多复杂而有趣的非线性振动特有的现象,结果表明多元L-P方法的数值结果在小振幅时与IHB法的结果一致,需指出的是,轴向运动梁和输液管是两种相近的动力学系统,其振动控制方程都含有科氏力项和离心力项;张艳雷[27]系统地对超临界流速下输液管的横向非线性参数共振动力学行为进行了大量研究,着重发展多尺度法分析管道的次谐波共振、超谐波共振和组合共振.
还应指出的是,以上关于非线性输液管参数共振的研究报道,侧重于探究单点松动约束力或分布式线性弹簧力的影响.
1 理论模型
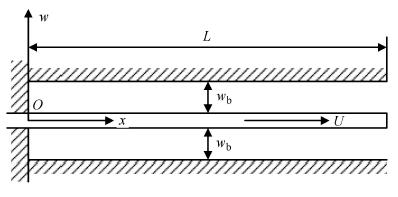
考虑如图1所示的悬臂输液管模型,其总长度为$L$. 标记x为沿管道轴线方向的位置坐标,$w\left( {x,t} \right)$为管道的横向位移. 在沿管道轴线方向上具有分布式运动约束,管道外壁与约束的间隙为$w_{\rm b}$.管道的弯曲刚度为$EI$,管材的黏弹性系数为$E^\ast$,单位长度上管道和管内流体的质量分别为M和M.假设管内流速($U)$为随时间有简谐变化分量的脉动形式;重力加速度记为g.
图1
图1
具有分布式运动约束的悬臂输液管模型示意图
Fig.1
Schematic of a cantilever pipe conveying fluid subjected to distributed motion constraints
不失一般性,该输液管模型的无量纲非线性运动方程可写成[10]
式中的无量纲参数定义如下
$$ \xi = \frac{x}{L} , \quad \eta = \frac{w}{L} ,\quad \tau = \sqrt {\frac{EI}{m + M}} \frac{t}{L^2} \\ u = \sqrt {\frac{M}{EI}} LU , \quad \alpha = \sqrt {\frac{EI}{m + M}} \frac{E^\ast }{L^2} \\ \beta = \frac{M}{m + M} , \quad \gamma = \frac{m + M}{EI}L^3g $$
对于随时间有周期变化的脉动流,假定其流速为$u = u_0 \left( {1 + \sigma \sin \omega \tau } \right)$,其中$u_0$为平均流速,$\sigma$为脉动幅值,$\omega$为脉动频率.
本文分别采用立方非线性弹簧模型和修正三线性弹簧模型来描述管道受到的分布式约束力[10],这两种模型下的无量纲约束力$f\left(\eta \right)$可分别表示为
(1)立方非线性模型
(2)修正三线性模型
式中,$\kappa _{\rm c}$和$\kappa _{\rm t}$分别表示立方非线性模型和修正三线性模型的无量纲刚度系数,d为管道外壁与约束间的无量纲间隙,且定义为$d = {w_{\rm b} } L$. 从修正三线性模型约束力的"力——位移曲线"可知[30],当管道的横向位移w小于间隙d时,约束力为零;反之,管道和约束间有碰撞力.
运动方程(1)可采用Galerkin方法进行离散;因此,可令
其中,基函数$\varphi _j \left( \xi \right)$为悬臂梁的归一化模态函数,$q_j \left( \tau \right)$为广义时间坐标,$N$为参与计算的模态截断数. 将解形式(4)代入非线性运动方程中,利用模态 函数的正交性,将离散方程整体左乘模态函数$\varphi _i \left( \xi \right)$,并在$ \left[ {0, 1} \right]$区间关于$ \xi$对方程进行积分即可得到关于广义坐标$q_j \left( \tau \right)$的非线性微分方程组
式中,${\pmb q} = \left[ {{\pmb q}_1 ,{\pmb q}_2 ,\ldots ,{\pmb q}_N } \right]^{\rm T}$,$\dot{\pmb q} = \left[ { \dot {\pmb q}_1 ,\dot{\pmb q}_2 ,\ldots ,\dot{\pmb q}_N } \right]^{\rm T}$和$ \ddot{\pmb q} = \left[ { \ddot{\pmb q }_1 , \ddot{\pmb q }_2 ,\cdots , \ddot{\pmb q }_N } \right]^{\rm T}$分别表示管道离散后的广义位移、速度和加速度列向量;${\pmb M }$,${\pmb C}$,${\pmb K}$和${\pmb f}\left( {\pmb q} \right)$分别表示离散化系统的质量矩阵、阻尼矩阵、刚度矩阵和非线性运动约束力向量;${\pmb g}_1 \left( {{\pmb q},\dot{\pmb q}} \right)$,${\pmb g}_2 \left( {{\pmb q},\dot{\pmb q}} \right)$和${\pmb g}_3 \left( {{\pmb q},\dot{\pmb q}} \right)$为考虑管道变形时产生的几何非线性项,其具体形式可参考文献[29]. 这些非线性项可进一步写成
其中,$\alpha _{ijkl}$,$\beta _{ijkl}$和$\gamma _{ijkl}$分别为各非线性项中关于广义坐标乘积的系数矩阵元素. 为便于应用龙格库塔积分格式,引入状态向量${\pmb z} = \left[ {{\pmb q};{\pmb p}} \right]$(其中${\pmb p}= \dot{\pmb q})$,二阶常微分方程组(5)可转化成如下形式的一阶状态方程
上式中各系数矩阵具有如下形式
为便于利用Floquet理论研究线性系统在脉动内流作用下的稳定性区域,首先不考虑系统的非线性项(${\pmb F}$和${\pmb G})$,得到相应的线性化系统
从文献[29]可知,质量矩阵、阻尼矩阵和刚度矩阵因脉动内流的影响均随时间作周期性变化,故矩阵${\pmb A}\left( \tau \right)$是一个与时间有关的周期函数,即${\pmb A}\left( {T + \tau } \right) = {\pmb A}\left( \tau \right)$,其中$T$为脉动内流的一个脉动周期. 根据方程(9)的形式,可假设其基本解为${\pmb Z}\left( \tau \right)$,由于${\pmb A}\left( {T + \tau } \right) = {\pmb A}\left( \tau \right)$,故${\pmb Z}\left( {T + \tau } \right)$也是方程(9)的解. 由此可知,${\pmb Z}\left( \tau \right)$和${\pmb Z}\left( {T + \tau } \right)$之间有如下关系
其中,$ \bar{\pmb A}\left( \tau \right)$可由方程(9)经过数值积分得到. 利用方程(10)的周期性关系,积分初始条件可设定为单位矩阵元素的形式,即
因此,对方程(9)进行数值积分得到的矩阵$\left[ {{\pmb Z}_1 \left( {T + \tau } \right),{\pmb Z}_2 \left( {T + \tau } \right), \cdots ,{\pmb Z}_{2n} \left( {T + \tau } \right)} \right]$即为$ \bar {\pmb A}\left( \tau \right)$. 接下来考虑矩阵$ \bar{\pmb A}\left( \tau \right)$的特征值,如果其所有特征值的绝对值均小于1,则线性系统(9)是稳定的,反之则不稳定.
下面将主要研究在脉动内流激励下管道的参数共振,讨论不同激励频率下管道的共振区域,以及引入分布式运动约束时管道的响应随脉动频率的变化规律,探究系统的共振频率与脉动频率之间的关系.
2 线性系统的参数共振稳定性
当管内流体具有脉动特性时,流体的平均流速($u_0 )$、脉动幅值($\sigma )$以及脉动频率($\omega )$会影响线性系统的稳定性,还可改变非线性系统的分岔路径及动力学响应.本文除了分析线性系统的参数共振行为外,还将研究分布式运动约束(模拟为立方非线性或修正三线性弹簧)下管道的非线性共振响应问题. 为了描述管道与单点松动约束之间的非线性碰撞力,Païdoussis经过大量实验研究和理论分析,提出了方非线性和修正三线性弹簧模型[8,10],并借助实验数据拟合出了两种模型对应的碰撞力参数取值.本文将直接采用文献[10]中关于输液管和碰撞力模型的参数取值$\alpha = 0.005$,$\beta = 0.213$,$\gamma = 26.75$,$\kappa _c = 10^5$,$\kappa _t = 5.6\times 10^6$,$d = 0.044$.
对于定常流(恒定流速)的情形,由文献[29]可知,系统在式(12)所给参数取值下发生颤振失稳的临界流速为$u_{\rm cr} = 8.05$. 下面拟着重分析平均流速低于$u_{\rm cr}$时管道系统的参数共振问题.为此,本文分别选取低于临界流速的两个不同大小的平均流速值$u_0 = 6$或$u_0 = 7$,以及3个不同大小的脉动幅值($\sigma = 0.2$,$0.4$或$0.6)$分别进行计算. 计算分析时,以脉动频率($\omega)$为主要控制变量,探究系统的稳定性和动力响应随脉动频率变化时的演化规律.为将系统的参数共振行为同固有频率进行关联,首先计算出输液管在定常流速$u = u_0 = 6$或$u = u_0 = 7$时的固有频率,其结果如表1所示.
表1 两个不同流速值下输液管的前四阶无量纲固有频率
Table 1
| Natural | First order Second order Third order Fourth order | |||
|---|---|---|---|---|
| frequency | ^1 | ^2 | 以3 | ^4 |
| U0 = 6 | 6.27 | 17.64 | 52.00 | 104.60 |
| U0 = 7 | 2.78 | 16.84 | 46.14 | 98.47 |
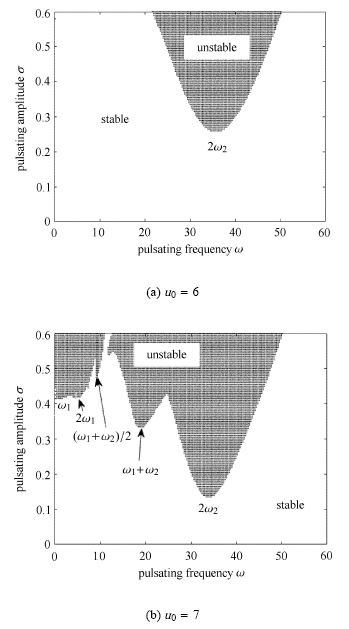
基于Floquet理论,可以方便地得到线性系统在脉动内流作用下的稳定性参数区域,其结果如图2所示. 从图2(a)所示关于$u_0 = 6$的计算结果可知,输液管系统的共振区域主要出现在二阶固有频率附近;当$\sigma = 0.2$时,输液管系统不会发生参数共振;在脉动幅值逐渐增大至$\sigma = 0.6$的过程中,系统发生共振的频率范围随之增大. 图2(b)所示关于$u_0 = 7$的共振区域同$u_0 = 6$的结果相比有明显增大;当脉动幅值较大时,在$\left[ {0, 60} \right]$的频率范围内,共振行为在第一阶和第二阶固有频率附近均表现出较强的参与性. 从图2(b)还可看到,在$\sigma = 0.2$时系统出现了较小频率范围内的共振区间,在$\sigma = 0.4$时有两个共振区间,而当$\sigma = 0.6$时系统在较宽频率范围均出现了共振.
图2
图2
两个平均流速取值下输液管系统的参数共振区域
Fig.2
Parametric resonance regions of the pipe system under two mean flow velocities
3 非线性系统的参数共振响应
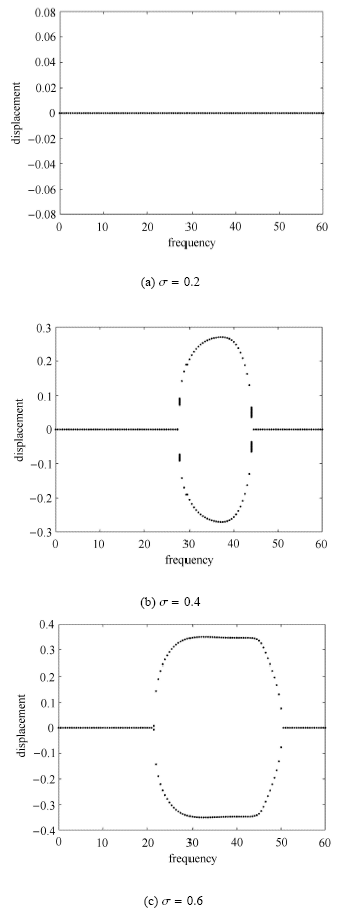
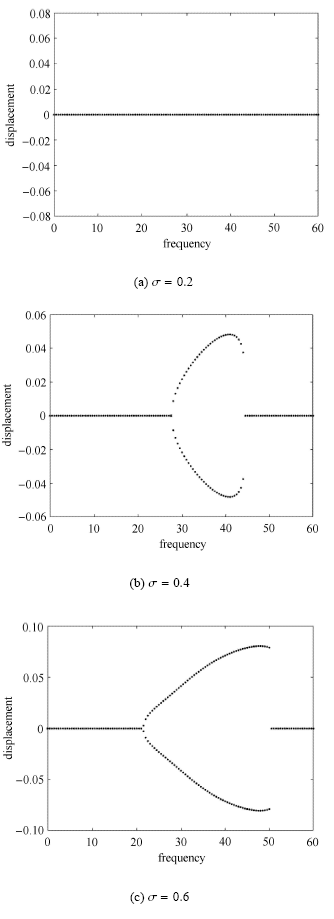
首先考虑没有运动约束的情形,计入系统的几何非线性因素(方程(7)中的${\pmb G})$. 图3给出了$u_0 = 6$时以脉动频率为控制参数、振动幅值为纵坐标的3个分岔图,分别对应于3个不同的$\sigma$取值. 从图3可知,当脉动幅值为$\sigma = 0.2$时,管道振动位移为0,这表示输液管系统是稳定的,在所研究的频率范围内不会发生参数共振;这与前面线性系统的共振分析结果是一致的. 当$\sigma = 0.4$和$\sigma = 0.6$时,系统分别在$27.5 \leqslant \omega \leqslant 44$和$21.5 \leqslant \omega \leqslant 50$的频率范围内发生共振,在分岔图中表现为非零的幅值;在这两个脉动频率的共振参数区间内,其非线性响应同样和前面线性系统的共振分析结果相吻合. 对比输液管系统的固有频率和脉动频率可知,此时系统发生了两倍于第二阶固有频率的主共振($\omega \approx 2\omega _2 )$.
图3
图3
没有运动约束时管道自由端位移在不同脉动幅值下随脉动频率变化的分岔图 ($u_0 = 6)$
Fig.3
Bifurcation diagrams for the tip displacement under various pulsating amplitudes without motion constraints ($u_0 = 6)$
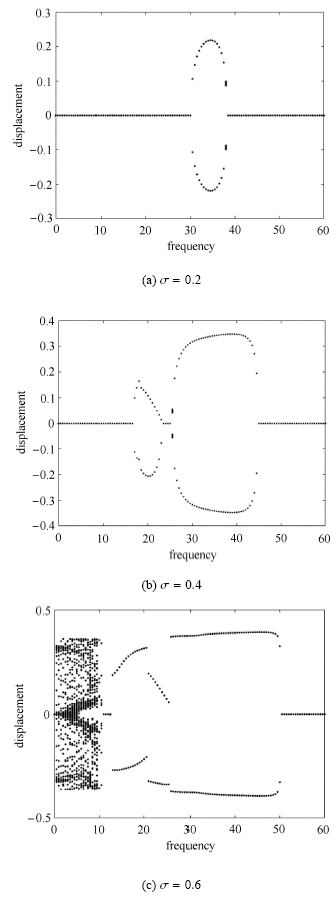
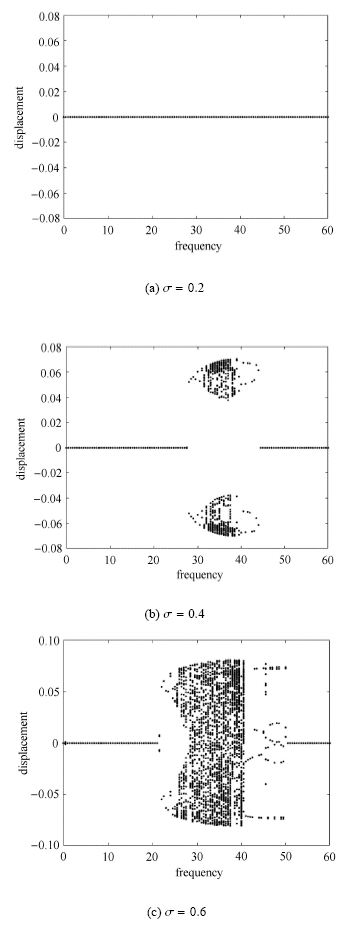
当平均流速$u_0 = 7$时,图4的分岔图显示输液管在$\sigma = 0.2$时已发生了参数共振,出现了非零振动幅值.结合图2(b)给出的 不稳定区域可知,此时的共振仍是两倍于第二阶固有频率的主共振($\omega \approx 2\omega _2 )$.当$\sigma = 0.4$时,图4(b)给出的分岔图表明系统出现了两个共振区间;根据文献[31]和图2(b)的稳定性分析结果可知,此时系统在$25.5 \leqslant \omega \leqslant 45$范围内发生了$\omega \approx 2\omega _2$的参数共振,而在$16.5 \leqslant \omega \leqslant 23$范围内则发生一阶和二阶模态的组合共振($\omega \approx \omega _1 + \omega _2 )$. 当$\sigma = 0.6$时,从图2(b)可以看到:系统在较宽频率范围内都发生了共振行为;这和图4(c)绘制的分岔图是吻合的. 然而,$\sigma =0.6$时系统的非线性动态响应行为较复杂,在较小脉动频率条件下表现为复杂运动形态;随着脉动频率值的增大,管道在$11 \leqslant \omega \leqslant 50$范围内表现为周期运动,其周期运动幅值在某些脉动频率值处有显著的跳跃现象.
图4
图4
没有运动约束时管道自由端位移在不同脉动幅值下随脉动频率变化的分岔图 ($u_0 = 7)$
Fig.4
Bifurcation diagrams for the tip displacement under various pulsating amplitudes without motion constraints ($u_0 = 7)$
接下来分析分布式立方非线性弹簧约束力下输液管的非线性动态响应问题. 图5和图6分别给出了两种不同平均流速下管道自由端位移随流速脉动频率变化的分岔图. 从图5关于$u_0 = 6$的计算结果可知,立方非线性约束力作用下管道振动的分岔图定性上与图3是一致的,但是管道振动的位移幅值变小很多. 另外,图5(b)和图5(c)给出的分岔路径均在某一脉动频率值附近出现了幅值跳跃现象. 从图6(c)关于$u_0 = 7$且$\sigma = 0.6$的分岔图可以看到,管道发生复杂运动行为(如混沌运动、多周期运动和概周期运动)的脉动频率范围变宽很多,这与没有立方非线性约束力的结果(图4(c))有显著不同. 这一结果表明,当管内流速的波动幅值较大时(如$\sigma = 0.6)$,管道的动力学行为对外界非线性约束力表现得更加敏感,呈现出多样化的运动形态.
图5
图5
立方非线性模型下管道自由端位移在不同脉动幅值下随脉动频率变化的分岔图 ($u_0 = 6)$
Fig.5
Bifurcation diagrams for the tip displacement under various pulsating amplitudes with cubic motion constraints ($u_0 = 6)$
图6
图6
立方非线性模型下管道自由端位移在不同脉动幅值下随脉动频率变化的分岔图($u_0 = 7)$
Fig. 6
Bifurcation diagrams for the tip displacement under various pulsating amplitudes with cubic motion constraints ($u_0 = 7$)
文献[10]曾指出,修正三线性弹簧模型可更好地模拟松动约束的作用力.因此,本文最后将分析修正三线性弹簧约束力作用下管道的非线 性共振响应行为,其计算结果如图7和图8所示.从图7和图8给出的分岔图来看,即使对于中等大小的$\sigma$ 值,管道的共振响应也可表现为复杂的运动形态(见图7(b)和图8(b)). 当$\sigma = 0.6$时,即使对于$u_0 = 6$的情形也可诱发管道出现复杂的共振响应行为(见图7(c)).还应指出,对于修正三线性弹簧模型,管道与约束间的碰撞力与管道实时的位移值有关:当管道位移值小于间隙值时,碰撞力为零;当管道位移值超过间隙值时,管道和运动约束发生碰撞,即出现了强的非线性约束力.
图7
图7
修正三线性模型下管道自由端位移在不同脉动幅值下随脉动频率变化的分岔图 ($u_0 = 6)$
Fig.7
Bifurcation diagrams for the tip displacement under various pulsating amplitudes with trilinear motion constraints ($u_0 = 6)$
图8
图8
修正三线性模型下管道自由端位移在不同脉动幅值下随脉动频率变化的分岔图($u_0 = 7)$
Fig.8
Bifurcation diagrams for the tip displacement under various pulsating amplitudes with trilinear motion constraints ($u_0 = 7)$
修正三线性模型与立方非线性模型的计算结果呈现出较大的差异性,主要是由于立方非线性模型有很大的缺陷:在管道位移很小的情况下,管道和约束之间也有相互作用力.与此显著不同的是,修正三线性模型只有当管道位移达到间隙值时才与约束发生相互作用,产生一个从无到有的突变的约束力,使得管 道的瞬时响应也发生较大的变化.因此,正如文献[10]所指出的,修正三线性模型可更好地描述松动约束力的实际情况.
图9
图9
修正三线性模型下管道发生混沌运动的相轨迹图和庞加莱映射 ($u_0 = 6$,$\sigma = 0.4$,$\omega = 35$)
Fig.9
Phase portrait and Poincaré map for the pipe system with trilinear motion constraints ($u_0 = 6$,$\sigma = 0.4$,$\omega = 35$)
4 结 论
本文基于悬臂输液管道的非线性动力学模型,引入立方非线性和修正三线性弹簧模型来描述分布式运动约束的非线性力,给出了脉动内流激励下管道的非线性振动微分方程,研究了因流速周期性变化引起的参数共振行为,揭示了输液管系统丰富的动力学现象. 研究结果表明,输液管的稳定性参数区域和非线性复杂响应与平均流速、流速脉动幅值和流速脉动频率密切相关. 在所分析的脉动频率范围内,输液管主要表现为在两倍于第二阶固有频率附近的参数共振. 对于立方非线性约束模型,管道的参数共振响应多表现为简单的周期-1运动,但在平均流速较大且脉动幅值较大时可诱发出复杂的运动行为. 对于修正三线性约束模型,输液管系统的参数共振响应除了简单的周期-1运动外,在较宽的系统参数范围内均可出现包括混沌在内的复杂运动形态.
参考文献
Non-linear dynamics of a fluid-conveying cantilevered pipe with a small mass attached at the free end
悬臂输流管道的运动分岔现象和混沌运动
研究受约束悬臂输流管道的稳定性和运动分岔问题.在静态与动态失稳区域边界上的一个交叉点附近,用理论分析的方法详细研究了该系统可能发生的复杂运动和运动分岔现象.在动态失稳区域内发现了输流管道的概周期运动和由于概周期运动环面破裂而导致混沌的现象.理论分析结果与数值模拟结果相吻合.
Bifurcations and chaotic motions of a cantilevered pipe conveying fluid
研究受约束悬臂输流管道的稳定性和运动分岔问题.在静态与动态失稳区域边界上的一个交叉点附近,用理论分析的方法详细研究了该系统可能发生的复杂运动和运动分岔现象.在动态失稳区域内发现了输流管道的概周期运动和由于概周期运动环面破裂而导致混沌的现象.理论分析结果与数值模拟结果相吻合.
Bifurcations in nonlinear models of fluid-conveying pipes supported at both ends
Stationary bifurcations in several nonlinear models of fluid conveying pipes fixed at both ends are analyzed with the use of Lyapunov–Schmidt reduction and singularity theory. Influence of the gravitational force, curvature and vertical elastic support on various properties of bifurcating solutions are investigated. In particular the conditions for occurrence of supercritical and subcritical bifurcations are presented for the models of Holmes, Thurman and Mote, and Paidoussis.
Non-linear dynamics of supported pipe conveying pulsating fluid-I. Subharmonic resonance
In this paper the non-linear behavior of supported pipes conveying pulsating fluid is examined in the vicinity of subharmonic resonance. The method of averaging is used to yield a set of autonomous equations when the parametric excitation frequency is twice the natural frequency of the system. The autonomous, averaged equations are then used to examine the bifurcation behavior of the system. It is found that the trivial solution lts for the stability boundaries and bifurcation paths are obtained. Numerical values of these results are plotted for pinned-pinned and clamped-clamped pipes.
Non-linear dynamics of supported pipe conveying pulsating fluid-II. Combination resonance
In this paper the work presented in [N. Sri Namchchivaya, Int. J. Non-linear Mech. 24, 185 196 (1989)] is extended to study the non-linear behavior of supported pipes conveying pulsating fluid in the presence of combination resonance. The method of averaging is used to obtain a set of autonomous equations. It is found that the trivial solution of the averaged equation loses stability through a Hopf bifurcation giving rise to a periodic solution. Explicit results for the bifurcating solutions are obtained locally and globally. In addition a numerical scheme is also used to verify these results. It is found that various results obtained using different techniques agree in their common regions of validity. Numerical values of these results are evaluated for pinned-pinned and clamped-clamped pipes.
Chaotic oscillations of the autonomous system of a constrained pipe conveying fluid
Experiments have shown that a cantilevered pipe conveying fluid, the limit-cycle motions of which (beyond the Hopf bifurcation) interact with motion-limiting non-linear constraints, exhibits region of chaotic motions. In this paper the planar dynamics of the flexible pipe system are examined theoretically by means of a two-degree-of-freedom (four-dimensional) analytical model, exploring the existence of chaotic oscillations in the parameter space of this autonomous system. Calculations of the Lyapunov exponents, phase portraits of the oscillation, bifurcation diagrams and Poincar maps establish definitively the existence of chaotic motions. The route to chaos is shown to be via period-doubling bifurcations. The effect of some key parameters on the chaotic regions is investigated.
Effect of a viscoelastic foundation on the dynamic stability of a fluid conveying pipe
Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid: A full nonlinear analysis
In this paper, the planar dynamics of a nonlinearly constrained pipe conveying fluid is examined numerically, by considering the full nonlinear equation of motions and a refined trilinear-spring model for the impact constraints ompleting the circle of several studies on the subject. The effect of varying system parameters is investigated for the two-degree-of-freedom ( N =2) model of the system, followed by less extensive similar investigations for N =3 and 4. Phase portraits, bifurcation diagrams, power spectra and Lyapunov exponents are presented for a selected set of system parameters, showing some rather interesting, and sometimes unexpected, results. The numerical results are compared with experimental ones obtained previously. It is found that in the parameter space that includes N , there exists a subspace wherein excellent qualitative, and reasonably good ( N =2) to excellent ( N =4) quantitative agreement with experiment. In the latter case, excellent agreement is not only obtained in the threshold flow velocities ( u ) for the key bifurcations, but the inclusion of the nonlinear terms improves agreement with experiment in terms of amplitudes of motion and by capturing features of behaviour not hitherto predicted by theory.
Stability and chaotic motions of a restrained pipe conveying fluid
The stability and dynamics of a cantilevered pipe conveying fluid with motion-limiting constraints and an elastic support have been investigated. Attention was concentrated on the behaviour of the system in the region of dynamic instability, and several motions were found by using the method of numerical simulations. The effect of the spring constant and some other parameters on the dynamics of the system was also investigated. It is shown that chaotic motions can occur in this system in a certain region of parameter space.
Bifurcations of a cantilevered pipe conveying steady fluid with a terminal nozzle
This paper studies interactions of pipe and fluid and deals withbifurcations of a cantilevered pipe conveying a steady fluid,clamped at one end andhaving a nozzle subjected to nonlinear constraints at the free end.Either the nozzleparameter or the flow velocity is taken as a variable parameter.The discrete equationsof the system are obtained by the Ritz-Galerkin method.The static stability isstudied by the Routh criteria.The method of averaging is employed to investigatethe stability of the periodic motions.A Runge-Kutta scheme is used to examine theanalytical results and the chaotic motions.Three critical values are given.The firstone makes the system lose the static stability by pitchfork bifurcation.The secondone makes the system lose the dynamical stability by Hopf bifurcation.The thirdone makes the periodic motions of the system lose the stability by doubling-periodbifurcation.
A simulation of the turbulence response of heat exchanger tubes in lattice-bar supports
Tube failures due to excessive flow-induced vibrations are a major concern with regards to the operation of heat exchangers in nuclear power and chemical process plants. Among the possible excitation mechanisms, turbulence-induced forces have a persistent effect and thus are an important factor in determining the long-term reliability of heat exchangers. Impact forces which occur when tube/support collisions take place play a vital role in determining tube wear. To address this issue, a tube/support interaction model was implemented in an in-house finite element program and validated against three published examples. Pseudo-forces in conjunction with modal superposition were utilized in solving the nonlinear equations of motion of loose tubes in lattice-bar supports. Time-domain simulations of the nonlinear response of the tube are presented to determine the effect of various tube and support parameters on the vibratory characteristics of the systems. Special attention was paid to the effect of increased clearance on the response of tubes in lattice-bar supports. The tube response, impact force and contact ratio were analysed and represented in dimensionless form. The dimensionless parameters developed proved effective in collapsing the data pertaining to different flow velocities over single curves. These are useful in identifying the roles of several key variables in altering tube dynamics. Moreover, these parameters may also be used to scale the results to account for differences in geometrical and material properties.
A new tube/support impact model for heat exchanger tubes
Heat exchanger tubes are often loosely supported at intermediate points by plates or flat bars. Flow-induced vibrations result in fretting wear tube damage due to impacting and rubbing of tubes against their supports. Prediction of tube response relies on modelling the nonlinear tube/support interaction. The evaluated response is used to predict the resultant wear damage using experimentally measured wear coefficients. An accurate prediction of impact forces and work rate is therefore paramount. The analytical models available in the open literature generally assume tube/support contact occurs at a single point. In this paper, a computational algorithm is proposed to describe tube/support impact considering a finite support width. The new model provides a means of representing tube/support contact as a combination of edge and segmental contact. The proposed model utilizes a distributed contact stiffness to describe the segmental contact. The formulation also incorporates a stick/slip friction model. The model developed is utilized to simulate the dynamics of loosely supported tubes.
Non-planar responses of cantilevered pipes conveying fluid with intermediate motion constraints
两端铰支输流管道在脉动内流作用下的稳定性和参数共振
研究了两端铰支输流管道在脉动内流作用下的参数共振问题。用平均法导出了失稳判据和3 种参数共振区域的边界曲线方程,并据此讨论了系统参数对不稳定区域的影响。用数值方法分析了各种参数共振的响应曲线,其存在区域以及响应频率与脉动流频率之间的关系。研究结果发现,组合共振区域内发生两种不同的拟周期运动和组合周期运动, 而且第1 振型次谐波共振曲线延伸到组合共振区域。因此,在同一脉动频率下存在可发生多种不同运动(第1 振型次谐波振动、拟周期振动和组合周期振动等) 的参数区域。
Stability and parametric resonances of a pinned-pinned pipe conveying pulsating fluid
研究了两端铰支输流管道在脉动内流作用下的参数共振问题。用平均法导出了失稳判据和3 种参数共振区域的边界曲线方程,并据此讨论了系统参数对不稳定区域的影响。用数值方法分析了各种参数共振的响应曲线,其存在区域以及响应频率与脉动流频率之间的关系。研究结果发现,组合共振区域内发生两种不同的拟周期运动和组合周期运动, 而且第1 振型次谐波共振曲线延伸到组合共振区域。因此,在同一脉动频率下存在可发生多种不同运动(第1 振型次谐波振动、拟周期振动和组合周期振动等) 的参数区域。
Parametric resonances of supported pipes conveying pulsating fluid
In this paper, the stability and parametric resonances of supported pipes conveying pulsating fluid are studied via numerical methods. According to the stability criterion derived, the effect of physical parameters of the system on the regions of three parametric resonances is discussed. The amplitude requency response curves of the parametric resonances and their frequency characteristics are investigated through numerical simulations. The results obtained show that several motions can take place in the region of combination resonance, including quasiperiodic and combined periodic motions. There exist some regions of overlap between the regions of the different resonances, and hence different types of steady state response may occur at the same value of the exciting frequency in these regions of overlap. This phenomenon may lead to sudden changes in motion from one steady state response to another.
两端固定输流管道参数共振的实验研究
用实验方法研究了两端固定输流 管道在脉动内流作用下的参数共振问题。所设计的实验系统合理有效,基本符合进行参数共振实验的设计目的。对三种合成管道在几个不同的平均流速和脉动流作用 下做了多次重复实验获得了第一振型1/2次谐波参数共振相关实验数据,实验结果与理论结果在定性上一致。本文还对可能引起定量误差的原因做了较详细的分 析。通过实验观察,得到以下结论:(1)当平均流速达到一定值时,两端固定管道在一定的脉动流振幅和脉动频率下会产生第一振型1/2次谐波参数共振。脉动 流振幅越大,发生参数共振的频率范围也越大。当脉动流振幅小于一定值时,不再发生参数共振。(2)平均流速越大,发生参数共振所需要的脉动流频率就越小。 平均流速大小对于能否出现1/2次谐波参数共振、共振区域大小、形状以及位置都有很重要的影响。在其它条件一定的情况下,低频脉动时平均流速越大管道越容 易失稳。以上观察到的现象与理论分析中得到的结果是一致的。
Experiments on parametric resonance of clamped-clamped pipes conveying fluid
用实验方法研究了两端固定输流 管道在脉动内流作用下的参数共振问题。所设计的实验系统合理有效,基本符合进行参数共振实验的设计目的。对三种合成管道在几个不同的平均流速和脉动流作用 下做了多次重复实验获得了第一振型1/2次谐波参数共振相关实验数据,实验结果与理论结果在定性上一致。本文还对可能引起定量误差的原因做了较详细的分 析。通过实验观察,得到以下结论:(1)当平均流速达到一定值时,两端固定管道在一定的脉动流振幅和脉动频率下会产生第一振型1/2次谐波参数共振。脉动 流振幅越大,发生参数共振的频率范围也越大。当脉动流振幅小于一定值时,不再发生参数共振。(2)平均流速越大,发生参数共振所需要的脉动流频率就越小。 平均流速大小对于能否出现1/2次谐波参数共振、共振区域大小、形状以及位置都有很重要的影响。在其它条件一定的情况下,低频脉动时平均流速越大管道越容 易失稳。以上观察到的现象与理论分析中得到的结果是一致的。
Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances
ABSTRACT In this paper, the nonlinear planar vibration of a pipe conveying pulsatile fluid subjected to principal parametric resonance in the presence of internal resonance is investigated. The pipe is hinged to two immovable supports at both ends and conveys fluid at a velocity with a harmonically varying component over a constant mean velocity. The geometric cubic nonlinearity in the equation of motion is due to stretching effect of the pipe. The natural frequency of the second mode is approximately three times the natural frequency of the first mode for a range of mean flow velocity, resulting in a three-to-one internal resonance. The analysis is done using the method of multiple scales (MMS) by directly attacking the governing nonlinear integral-partial-differential equations and the associated boundary conditions. The resulting set of first-order ordinary differential equations governing the modulation of amplitude and phase is analyzed numerically for principal parametric resonance of first mode. Stability, bifurcation, and response behavior of the pipe are investigated. The results show new zones of instability due to the presence of internal resonance. A wide array of dynamical behavior is observed, illustrating the influence of internal resonance.
A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid
In this paper, the non-linear dynamics of simply supported pipes conveying pulsating fluid is further investigated, by considering the effect of motion constraints modeled as cubic springs. The partial differential equation, after transformed into a set of ordinary differential equations (ODEs) using the Galerkin method with =2, is solved by a fourth order Runge utta scheme. Attention is concentrated on the possible motions of the system with a higher mean flow velocity. Phase portraits, bifurcation diagrams and power spectrum diagrams are presented, showing some interesting and sometimes unexpected results. The analytical model is found to exhibit rich and variegated dynamical behaviors that include quasi-periodic and chaotic motions. The route to chaos is shown to be via period-doubling bifurcations. Finally, the cumulative effect of two non-linearities on the dynamics of the system is discussed.
非线性弹性地基上悬臂输流管的受迫振动
<FONT face=Verdana>本文综合考虑地基的剪切效应、非线性刚度和粘滞阻尼的影响,建立了非线性Pasternak地基上输流管的运动控制方程。基于Galerkin法研究了基础激励作用下非线性弹性地基上悬臂输流管的非线性动力学行为,着重讨论了基础激励和地基剪切刚度对系统动力学特性的影响。结果表明:系统在基础激励作用下具有非常复杂的动态响应,包括多种形式的周期、概周期和混沌运动;地基的剪切刚度对系统的动态特性有重要影响,随着地基剪切刚度的增大,在基础激励参数区域内系统的概周期和混沌运动窗口逐渐减小,当地基剪切刚度足够大时,系统将始终处于周期运动状态。<BR></FONT>
Forced vibration of a cantilever fluid-conveying pipe on nonlinear elastic foundation
<FONT face=Verdana>本文综合考虑地基的剪切效应、非线性刚度和粘滞阻尼的影响,建立了非线性Pasternak地基上输流管的运动控制方程。基于Galerkin法研究了基础激励作用下非线性弹性地基上悬臂输流管的非线性动力学行为,着重讨论了基础激励和地基剪切刚度对系统动力学特性的影响。结果表明:系统在基础激励作用下具有非常复杂的动态响应,包括多种形式的周期、概周期和混沌运动;地基的剪切刚度对系统的动态特性有重要影响,随着地基剪切刚度的增大,在基础激励参数区域内系统的概周期和混沌运动窗口逐渐减小,当地基剪切刚度足够大时,系统将始终处于周期运动状态。<BR></FONT>
非线性弹性地基上悬臂管道的参数振动
本文首先建立了非线性弹性地基上悬臂输流管在振荡流作用下的运动方程,应用Galerkin方法将运动控制偏微分方程离散成常微分方程组。采用数值方法着重讨论了平均流速、脉动幅值、脉动频率和地基剪切刚度等参数对系统动力学行为的影响。 结果表明:以平均流速为分岔参数系统会出现拟周期运动,然后是周期运动, 接着出现混沌运动;以脉动幅值为分岔参数系统发生周期2,周期4,周期8,然后进入混沌运动;以脉动频率为分岔参数系统先发生拟周期运动,然后在二阶次谐波附近发生混沌运动。另外,地基剪切刚度对系统地周期运动和混沌有抑制作用,随着剪切刚度增大,系统从混沌状态演化到周期状态,直至稳态。 <br>
Parametric vibration of a cantilevered pipe conveying pulsating fluid on a nonlinear elastic foundation
本文首先建立了非线性弹性地基上悬臂输流管在振荡流作用下的运动方程,应用Galerkin方法将运动控制偏微分方程离散成常微分方程组。采用数值方法着重讨论了平均流速、脉动幅值、脉动频率和地基剪切刚度等参数对系统动力学行为的影响。 结果表明:以平均流速为分岔参数系统会出现拟周期运动,然后是周期运动, 接着出现混沌运动;以脉动幅值为分岔参数系统发生周期2,周期4,周期8,然后进入混沌运动;以脉动频率为分岔参数系统先发生拟周期运动,然后在二阶次谐波附近发生混沌运动。另外,地基剪切刚度对系统地周期运动和混沌有抑制作用,随着剪切刚度增大,系统从混沌状态演化到周期状态,直至稳态。 <br>
In-plane and out-of-plane dynamics of a curved pipe conveying pulsating fluid
Abstract This paper investigates the in-plane and out-of-plane dynamics of a curved pipe conveying fluid. Considering the extensibility, von Karman nonlinearity, and pulsating flow, the governing equations are derived by the Newtonian method. First, according to the modified inextensible theory, only the out-of-plane vibration is investigated based on a Galerkin method for discretizing the partial differential equations. The instability regions of combination parametric resonance and principal parametric resonance are determined by using the method of multiple scales (MMS). Parametric studies are also performed. Then the differential quadrature method (DQM) is adopted to discretize the complete pipe model and the nonlinear dynamic equations are carried out numerically with a fourth-order Runge utta technique. The nonlinear dynamic responses are presented to validate the out-of-plane instability analysis and to demonstrate the influence of von Karman geometric nonlinearity. Further, some numerical results obtained in this work are compared with previous experimental results, showing the validity of the theoretical model developed in this paper.
3:1内共振下超临界输液管受迫振动响应
首次研究了超临界流速输液管在3∶1内共振条件下的稳态幅频响应.考虑超临界速度引起的管道屈曲位形,建立描述连续体非线性振动的偏微分-积分方程.通过Galerkin截断方法,将连续体方程离散化.对于同时含有平方与立方非线性的多自由度系统,发展高阶多尺度法建立可解性条件.稳态幅频响应曲线揭示了内共振条件下,不同模态间能量的转移.最后,数值仿真结果验证了近似解析分析的有效性.
Forced vibration responses of supercritical fluid-conveying pipes in 3:1 internal resonance
首次研究了超临界流速输液管在3∶1内共振条件下的稳态幅频响应.考虑超临界速度引起的管道屈曲位形,建立描述连续体非线性振动的偏微分-积分方程.通过Galerkin截断方法,将连续体方程离散化.对于同时含有平方与立方非线性的多自由度系统,发展高阶多尺度法建立可解性条件.稳态幅频响应曲线揭示了内共振条件下,不同模态间能量的转移.最后,数值仿真结果验证了近似解析分析的有效性.
Steady-state response of a fluid-conveying pipe with 3:1 internal resonance in supercritical regime
The forced vibration response of the pipe conveying fluid, with 3:1 internal resonance, is studied here for the first time. The straight equilibrium configuration becomes bent while the velocity of the fluid exceeds the critical value. As a result, the original mono-stable system transforms to a bi-stable system. Critical excitation which can cause global responses is solved out from the potential equation of the unperturbed system. The condition of 3:1 internal resonance is established after the partial differential equation is discretized. Global bifurcations are studied in simulation ways. By the method of multiple scales, local responses around the bent configuration are investigated. The analytical results are verified by simulations. Responses at the second mode bifurcate out another branch near the resonance frequency. It is very different with the triply harmonic responses without internal resonance. The triply harmonic response is a resonant excitation to the second mode. Responses will change largely with the detuning relationship between these two modes. Influences of the excited amplitude are also studied. Based on the analytical method, critical excited conditions of jumping and hysteretic phenomena are determined. The responses will have up- and down-bifurcations in the special region.
轴向运动梁非线性振动内共振研究
采用多元L-P方法分析轴向运动梁横向非线性振动的内共振. 首先根据哈密顿原理建立轴向运动梁的横向振动微分方程, 然后利用Galerkin方法分离时间和空间变量,再采用多元L-P方法进行求解. 推导了内共振条件下频率-振幅方程的求根判别式. 理论分析发现内共振与强迫力的振幅有关, 而且可以从理论上决定这一界乎不同内共振的强迫力振幅的临界值. 典型算例获得了轴向运动梁横向非线性振动内共振复杂的频率-振幅响应曲线, 揭示了很多复杂而有趣的非线性振动特有的现象. 多元L-P方法的数值结果, 在小振幅时与IHB法的结果一致.
On internal resonance of nonlinear vibration of axially moving beams
采用多元L-P方法分析轴向运动梁横向非线性振动的内共振. 首先根据哈密顿原理建立轴向运动梁的横向振动微分方程, 然后利用Galerkin方法分离时间和空间变量,再采用多元L-P方法进行求解. 推导了内共振条件下频率-振幅方程的求根判别式. 理论分析发现内共振与强迫力的振幅有关, 而且可以从理论上决定这一界乎不同内共振的强迫力振幅的临界值. 典型算例获得了轴向运动梁横向非线性振动内共振复杂的频率-振幅响应曲线, 揭示了很多复杂而有趣的非线性振动特有的现象. 多元L-P方法的数值结果, 在小振幅时与IHB法的结果一致.
Nonlinear impacting oscillations of pipe conveying pulsating fluid subjected to distributed motion constraints
Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints
ABSTRACT In this paper, the nonlinear dynamics of a cantilevered pipe conveying fluid interacting with two support walls on both sides is first investigated. The main goal of this study is to explore how the dynamics of a cantilevered pipe will perform in the presence of two support walls along the pipe axis. The interacting force is defined as impact in order to simulate the impacting effects for a pipe with various flow velocities. The impact force is modeled either by a cubic spring or by a trilinear spring. The nonlinear equations of motion are discretized via Galerkin method, and the discretized equations are solved by using a fourth-order Runge-Kutta method. Results show that the pipe would periodically impact the walls when the flow velocity is just beyond the critical value. When the flow velocity is sufficiently higher, however, the pipe may behave different patterns of contacting the walls, such as point contact and segments contact. Periodic, quasi-periodic motions, as well as chaotic oscillations are observed in such a pipe system.
Nonlinear dynamics of cantilevered pipes conveying fluid: Towards a further understanding of the effect of loose constraints
The nonlinear dynamics of a fluid-conveying cantilevered pipe with loose constraints placed somewhere along its length is investigated. The main objective of this study is to determine the effects of several geometrical and physical parameters of the loose constraints on the characteristics and behavior of pipes conveying fluid. Based on the full nonlinear equation of motion, the dynamical behavior of the pipe system is investigated. Phase portraits and bifurcation diagrams are constructed for a selected set of system parameters. Typical results are firstly compared to numerical ones reported previously and excellent agreement is obtained. Then, the threshold flow velocities for several key bifurcations including pitchfork, period doubling, chaos, and sticking behaviors are predicted, showing that in many cases, the gap size, stiffness, and asymmetry of the loose constraints have remarkable effects on the nonlinear responses of the cantilevered pipe conveying fluid. For a pipe system with small/large constraint gap sizes, small constraint stiffness, or large constraint offset, some of the complex dynamical behaviors including chaos and period-doubling bifurcations would disappear, at least in the flow velocity range of interest.
Nonlinear analysis of the parametric resonances of a planar fluid-conveying cantilevered pipe
This paper deals with the nonlinear dynamics and the stability of cantilevered pipes conveying fluid, where the fluid has a harmonic component of flow velocity, assumed to be small, superposed on a constant mean value. The mean flow velocity is near the critical value for which the pipe becomes unstable by flutter through a Hopf bifurcation. The partial differential equation is transformed into a set of ordinary differential equations (ODEs) using the Galerkin method. The equations of motion contain nonlinear inertial terms, and hence cannot be put into standard form for numerical integration. Various approaches are adopted to tackle the problem: (a) the centre manifold theory applied on the set of non-autonomous equations, followed by the normal form method, yielding both the principal and the fundamental resonances; (b) a perturbation method via which the nonlinear inertial terms are removed by finding an equivalent term using the linear equation; the system is then put into first-order form and integrated using a Runge-Kutta scheme; (c) a finite difference method based on Houbolt's scheme, which leads to a set of nonlinear algebraic equations that is solved with a Newton-Raphson approach; (d) periodic solutions and stability boundaries are obtained using an incremental harmonic balance method as proposed by S. L. Lau. Using the four methods, the dynamics of the pipe conveying fluid are investigated in detail. For example, the effects of (i) the forcing frequency, (ii) the perturbation amplitude, and (iii) the flow velocity are considered. Particular attention is paid to the effect of the nonlinear terms. These results are compared with experiments undertaken in our laboratory, utilizing elastomer pipes conveying water. The pulsating component of the flow is generated by a plunger pump, and the motions are monitored by a noncontacting optical follower system. It is shown analytically, numerically and experimentally, that periodic and quasiperiodic oscillations can exist, depending on the parameters.