引 言
对于类橡胶材料本构模型的研究有很多[4-5].这些模型大致可以被分为两大类:第一类是基于微观统计力学,这类模型从材料的微观结构出发,假设材料是由随机分布的分子链组成,比如三链模型[6],四链模型[7-8],八链模型[9],以及Full-network模型[10];第二类是基于唯象模型的研究,这类模型应用连续介质力学方法,假设弹性势是由伸长比或者伸长比构成的不变量组成,从实验数据出发,再确定弹性势中的各种参数[11-15].除此之外,近年来还涌现了许多基于黏——超弹性理论的类橡胶材料本构模型[16-18].邹广平等[19]利用参数分离的方法对弹簧——金属丝网橡胶进行本构建模.王宝珍和胡时胜[20]根据类橡胶材料(猪肝)从准静态到高应变下的力学特征,通过将两部分简单相加的方法进行建模.谈炳东等[21]根据纤维增强复合材料连续介质力学理论,提出了各向异性超弹性本构模型,并能很好地预测0$^\circ$~45$^{\circ}$各向异性力学性能.
Mullins效应的力学机理十分复杂,涉及到大变形、非线性变形以及应力软化效应,因此用模型去模拟Mullins效应将变得十分困难.尽管如此,还是有很多科研工作者在这些方面做了大量的工作[1,22].Simo[23]在基于变形梯度的弹性势中加入了一个表征损伤的量,用来解释类橡胶材料应力软化过程中出现的分子链破坏,微结构损伤.在此基础上,根据引入量演化方程的不同,提出了各种不同的结 果[23-27];Mullins等[28-29]提出了不同的方法,他们将橡胶内部区域分为两大类,分别是"硬区"和"软区",材料的变形主要是在"软区"产生.一旦应力达到某一个程度,那么"硬区"将会向"软区"转化,由此产生材料应力软化.
以上研究成果很多都可以模拟Mullins效应,但是都存在着不同的缺陷. 微结构模型的参数往往需要迭代求解,计算量大;唯象模型往往需要引入没有物理意义的隐式参数.因此,本文的目的是通过显式的方法建立一个多轴、可压缩的应变能函数,其在加载状态下可以精确匹配单轴拉伸和压缩、等双轴拉伸和压缩、以及平面应变3个基准实验,同时在卸载状态下也能模拟材料应力软化现象.材料在加载——卸载的循环中,模型可以自动产生应力——应变关系滞回圈.
1 带有耗散的多轴可压缩弹性势
表1 物理量符号
Table 1
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| F | deformation gradient | B | left Cauchy Green tensor |
| 山 | stretch | h | logarithmic strain |
| T | Kirchoff stress | a | Cauchy stress |
| J | volume ratio | u | Poisson ratio |
| n | eigenvector | W | potential |
| I | identity tensor | h | deviatoric logarithmic strain |
| hi | lateral logarithmic | K | energy dissipation |
为了直接从弹性势导出应力应变关系,选择使用对数应变${\pmb h}$,也叫Hencky应变[36]
对数应变与变形梯度的关系为
其中,${\pmb B} = {\pmb F} \cdot {\pmb F}^{\rm T}$,也称为左柯西——格林张量;$\lambda _i , {\pmb n}_i$ ($i = 1$, 2, 3)是材料伸长比(特征值)和特征向量.
1.1 基于对数应变的不变量
根据方程(2)给出3个基本不变量表达
其中,$s =1$, 2, 3.
本文模型可以应对可压缩情况. 因此,体积变化的影响必须考虑, 从对数应变偏量$ \tilde {\pmb h}$
出发,给出3个新的不变量表达为
其中,$s = 1$, 2, 3.
根据方程(3)~(5),得出新的不变量和基本不变量之间的关系为
当材料不可压缩,那么$i_1 = 0$,将其代入方程(6),可以得到对应的不变量相等,即
$$ j_s = i_s$$
其中,$s = 1$, 2, 3.
为了得到符合要求的多轴可压缩弹性势,需要构造3个新的不变量$\gamma _i$ ($i = 1$, 2, 3),其表达式如下
其中,$\gamma _{1}$主要用来控制体积比,若材料不可压缩,变形前后体积不变,则$\gamma _{1} = \ln J = 0$,否则$\gamma _{1} \ne {0}$;$\gamma _{2}$在单轴拉伸和压缩、等双轴拉伸和压缩、平面应变的情况下恰好可以转化成对数应变或者其线性关系;$\gamma _{3}$主要用来控制变形模式,使得多轴弹性势在对应的情况下可以分别转化为单轴拉伸和压缩、等双轴拉伸和压缩、以及平面应变的单轴弹性势. 其具体的推导过程将在后文中给出.
1.2 单轴弹性势
为了得出单轴拉伸压缩和平面应变情况下的单轴弹性势.首先给出在各自情况下的单轴应力——应变关系,然后通过积分得到对应的弹性势.和之前研究不一样的是,这里的应力——应变关系和弹性势依赖于新引入的标量$\kappa$,该标量表示在加载——卸载过程中出现的能量耗散大小,其具体方程将在后面的内容中给定.
为了处理可压缩情况,在这里给出泊松比的表达. 假设应力方向对数应变为$h$,侧向对数应变为$h_l$,则泊松比$\upsilon$定义为
在不可压缩情况下$\upsilon = 0.5$;一般情况下,泊松比的范围为$ 0 < \upsilon < 0.5$.
1.2.1 单轴拉伸和压缩
在单轴拉伸和压缩情况下,假设对数应变和应力的关系为
为了简化问题,假设$\kappa$和$h$相互独立,对方程(9)积分,得到单轴拉伸和压缩情况下的弹性势为
1.2.2 平面应变
平面应变实验描述如下:对一个六面体橡胶块,固定一个方向的变形,在另一个方向拉伸,最后一个方向自由. 假设加载方向应力为$\tau _{\rm p}$,应变为$h$,固定方向应力为$\tau _{\rm pf}$,给定其两个方向的应力——应变关系为
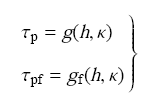
在该变形模式下,只有在载荷方向做功,因此得到应变能弹性势为
1.3 多轴可压缩弹性势
根据方程(1), 需要给出弹性势标量函数
的具体形式. 通过1.1节构造的3个不变量$\gamma _i$ (方程(8)),$i = 1$,2,3,可以将方程(13)简化为
根据方程(1)和(15),结合方程(8),可以得到
其中
式中,$ \tilde {\pmb h}$是对数应变偏量,${\pmb I}$如表1所示,是单位二阶张量. 张量${\pmb I}, \tilde {\pmb h}, \mathop{\pmb h}\limits^{\smile }$之间相互正交
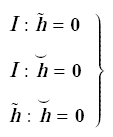
因此,可以将${\pmb I}, \tilde {\pmb h}, \mathop{\pmb h}\limits^{\smile }$作为对数应变张量的3个基.
根据文献[32],利用Hermite插值方法,可以得到新的多轴可压缩弹性势为
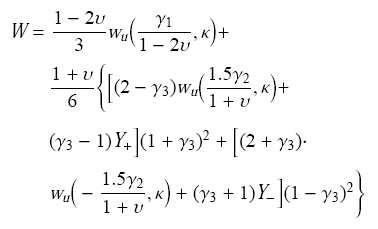
其中,$Y_ + ,Y_-$分别为$\left. {\frac{\partial W}{\partial \gamma _3 }} \right|_{\gamma _{3} = 1}$和$\left. {\frac{\partial W}{\partial \gamma _3 }} \right|_{\gamma _{3} =-1}$的值,给定为
方程(19)~(20)给定了一个可以处理Mullins效应的多轴可压缩弹性势. 其在单轴拉伸和压缩,以及平面应变的情况下,通过方程(16)可以自动退化到方程(10)和(12). 除此之外,由于等双轴拉伸和单轴拉伸存在这对应关系[33],只要给出符合条件的形函数,任意类橡胶材料的3个基准实验都能精确匹配;同时还可以匹配和预测橡胶Mullins效应产生的应力软化效应.
2 新弹性势预测基准实验
为了证明方程(19)~ (20)提出的弹性势符合要求,必须给出其在3个基准实验下的变形行为.注意在单轴情况下,伸长比和对数应变存在关系
2.1 单轴拉伸和压缩
假设在单轴拉伸或压缩情况下,基尔霍夫应力张量为
对数应变张量为
式中,$h$,$h_l$分别为拉伸方向应变和侧向应变. 根据方程(4),(8),(23)和(9),可得到
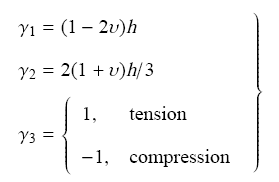
结合方程(24)和(21),可得到体积比与伸长比关系为
同时将方程(24)代入 方程(19), 可以得到弹性势变成
对方程(26)求导, 最终得到的应力应变关系为$\tau _u = f(h, \kappa )$和方程 (10)对应.
2.2 等双轴拉伸和压缩
等双轴拉伸和压缩情况下,假设拉伸方向应力为$\tau _e$,则基尔霍夫应力张量为
假设应力方向对数应变为$h$,则不受力方向的对数应变为$\frac{-h}{\upsilon }$,对数应变张量为
根据方程(4),(28)和(8),可得到
同样的方法,可以得到体积比与伸长比关系
弹性势变成
在等双轴拉伸情况下,对以下方程求导
得到应力——应变关系为
2.3 平面应变
平面应变情况下,假设拉伸方向应力为$\tau _{\rm p}$,固定端应力为$\tau _{\rm pf}$,基尔霍夫应力为
拉伸方向对数应变$h$,自由端方向应变$h_{\rm f}$,两者关系为
根据方程(35),对数应变为
根据前面类似的方法,可推导得到
为了简化推导,在此变形模式下,橡胶几乎不可压缩,因此得
将方程(38)代入方程(19),可得到
基于不可压缩的假设,在平面应变情况下,对数应变偏量变成
方程(17)变成
方程(16)中的$\frac{\partial W}{\partial \gamma _2 }$和$\frac{\partial W}{\partial \gamma _{3} }$可以通过张量运算关系
得到,其结果为
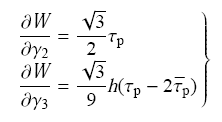
将方程(40), (41), (43), (38)代入方程(16), 结合方程(20),最终得到$\tau _{\rm p} = g(h, \kappa )$, 以及$\tau _{{\rm pf}} = g_{\rm f} (h, \kappa)$. 这个结果与方程(12)对应.
通过推导,我们可以得出结论:由方程(19)~(20)构成的多轴不可压缩弹性势,在单轴拉伸和压缩,平面应变情况下,应力——应变关系能自动退化到各自形函数(方程(10)和(12))形式,单轴压缩的应力——应变关系,只要给出泊松比,就能通过方程(33)给定.
和前面研究不同的是,本文3个形函数,也就是方程方程(10)和(12),全都依赖于表征软化效应的耗散量$\kappa$. 耗散量的演化方程和对模型的具体影响,将在下文详细描述.
3 带有软化效应的形函数
本章将给出方程(10)和(12)的显式表达式,使得方程(19)和(20)给出的应力——应变关系不仅可以精确匹配3个基准实验,还可以模拟Mullins效应产生的滞回圈.
3.1 Mullins效应滞回圈
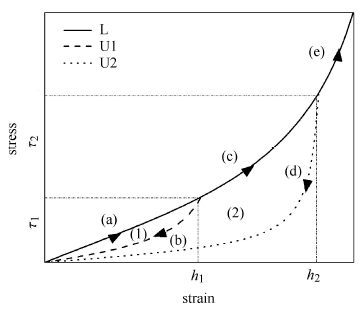
图1所示为Mullins效应滞回圈. 图中横坐标表示应变,纵坐标表示应力. 类橡胶材料的应变随着应力的增大而增大,其加载曲线L沿着(a)-(c)-(e)方向. 如果当应力达到$\tau _{1}$时,开始卸载,材料由于Mullins效应产生软化,不会沿着原路径(a)返回,而是沿着图中U1路线((b)曲线)回到原点,形成一个滞回圈(1);当材料在应力达到$\tau _{2}$时卸载,那么同样地,应力——应变曲线将沿着图中U2路线((d)曲线)返回到原点,而不是沿着原路径(c)-(a)返回,形成另一个滞回圈(2).
图1
根据图1,可以得出Mullins效应滞回圈存在以下3个特点:第一,卸载曲线和加载曲线往往不重合,且卸载曲线一般在加载曲线下方;第二,不同的卸载应力下,卸载曲线往往也不重合. 一般地,卸载应力越大,材料软化就越严重;第三,Mullins效应滞回圈面积的物理意义是加载——卸载后,产生的能量耗散,卸载点应力越大,其耗散的能量就越大.
基于以上思路,假设应变从0加载到$h_{\rm m}$后,开始卸载,那么加载产生的能量设为$\kappa _{\rm m}$,且
其中,$\bar {f}(h)$表示加载的应力——应变曲线. 而$h_{\rm m} = f^{-1}(\tau _{\rm m} )$,$h = f^{-1}(\tau )$是$\tau = f(h)$的反函数. 如果$h_{\rm m}$很小,接近0,那么材料软化的程度就很小,能量耗散$\kappa$与$\kappa _{\rm m}$之比$\kappa / \kappa _{\rm m}$接近为0;若$h_{\rm m}$很大,材料软化非常巨大,那么$\kappa / \kappa _{\rm m}$接近为1. 所以$\kappa / \kappa _{\rm m}$的取值范围
由此我们假设耗散$\kappa$随着卸载点应力$\tau _{\rm m}$的变化规律为
式中,$\tau _r$和M是可调参数. 当$\tau _{\rm m} = \tau _{\rm r}$时,$\kappa = \frac{\kappa _{\rm m} }{2}$;参数M表示$\kappa$随着$\tau _{\rm m}$变化的速度.
3.2 单轴拉伸和压缩
在前面研究工作的基础上,给定单轴拉伸和压缩情况下的形函数为
$$ f(h,\kappa ) = \frac{1}{2}(1 + \chi )\bar {f}(h) + \frac{1}{2}(1-\chi )\tilde {f}(h,\kappa ) (47) $$
其中,$\chi = \frac{\dot {h}}{\left| \dot {h} \right|}$,可得
将方程(48)代入方程(47), 可得
$\bar {f}(h)$表示加载应力——应变形函数,根据前面的研究,给定其形式为
只要给出合适的参数$E_0$,$h_{10} h_{20}$和$\alpha _0$,那么加载部分的应力——应变曲线就能自动产生.
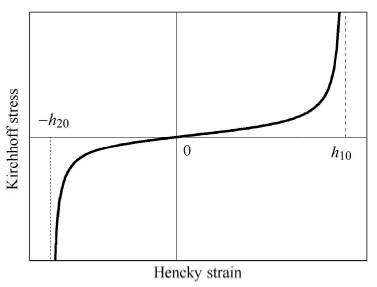
关于这几个参数在形函数中的意义如图2所示.杨氏模量$E_0$控制应变很小情况下的曲线斜率;参数$\alpha _0$控制当曲线接近边界的应力大小,$\alpha _0$越大,那么接近边界的时候,应力就越大,反之,应力则越小;$h_{10}$和$h_{20}$控制两条边界线的位置,其值越大,则表示材料达到钢化效应的时候变形就越大.
图2
$\tilde {f}(h, \kappa )$表示卸载曲线的应力——应变曲线,其形式给定为
式中,$E(\kappa )$,$h_1 (\kappa )$,$h_2 (\kappa )$和$\alpha (\kappa )$随着耗散$\kappa$的变化而变化,因此不同的卸载点卸载,其卸载曲线必然不重合.
3.3 等双轴拉伸压缩和平面应变
根据方程(33)和(47),可以推导得到等双轴拉伸和压缩的形函数
只要单轴拉伸和压缩的相关参数给定,泊松比给定,那么等双轴拉伸和压缩的应力——应变关系就能确定.
平面应变的应力应变形函数,通过类似的方法可得
其中,$\bar {g}(h)$,$\tilde {g}(h,\kappa )$,$\bar {g}_{\rm f} (h)$和$\tilde {g}_{\rm f} (h,\kappa)$分别表示载荷方向加载,卸载曲线和固定端方向加载,卸载曲线. 具体形式为
同样地,我们需要给出参数$h_{{\rm p}0}$,$\alpha _{ \rm p0}$和$\alpha _{ \rm pf0}$,以及$h_{\rm p} (\kappa )$,$\alpha _{\rm p} (\kappa )$和$\alpha _{\rm pf} (\kappa)$随耗散$\kappa$的变化规律.
4 数值模拟
本章将介绍新模型在3个基准实验和加载——卸载情况下产生的模拟结果,同时将其与对应的实验结果作比较并预测,证明本文方法的有效性.
4.1 基准实验模拟
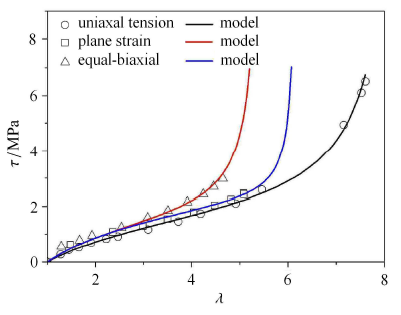
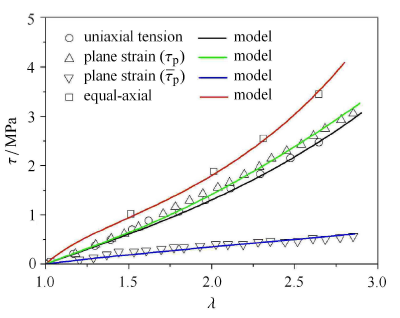
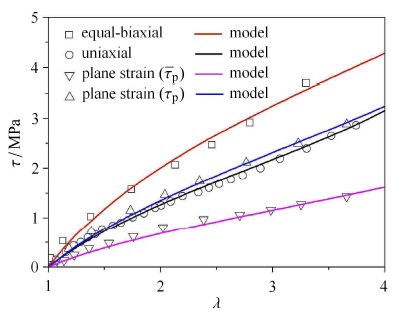
基准实验包括单轴拉伸压缩、等双轴拉伸以及平面应变拉伸,其应力——应变形函数通过方程(47)、(52)以及(53)给出.将应变$h = \ln \lambda$代入到方程,在加载情况下,3个方程分别退化为
表2 匹配基准实验的模型参数数值
Table 2
图3
图4
图5
4.2 Mullins效应滞回圈模拟
模拟Mullins效应产生的滞回圈,除了给出参数$E_0$,$\alpha _0$,$h_{10}$,$h_{20}$,$\upsilon$,$\alpha _{\rm p0}$,$\alpha _{\rm pf0}$和$h_{\rm p}$以外,还需要给出$E(\kappa )$,$h_1 (\kappa )$,$h_2 (\kappa )$,$\alpha(\kappa )$,和$h_{\rm p} (\kappa )$以及$\alpha _{\rm p} (\kappa )$和$\alpha _{\rm pf} (\kappa )$的变化规律.
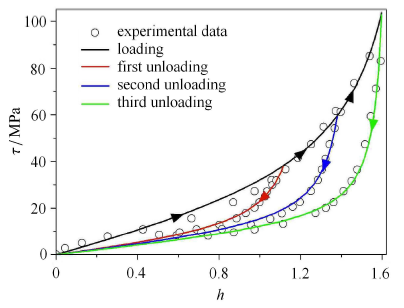
取Mullins和Tobin[40]的实验进行对比. 由于文献中所做的实验是单轴拉伸,因此需要给出的参数包括:$E_0$,$\alpha _0$,$h_{10}$和$h_{20}$(在加载状态下),$E(\kappa )$,$h_1 (\kappa )$,$h_2 (\kappa )$和$\alpha(\kappa )$(在卸载状态下).
方程(46)中,参数给定为:$m = 5.7\times 10^{-3}$,$\tau _{\rm r} = 83.6$MPa. 第1~3次卸载的卸载应力分别是: 38.2 MPa, 59.5 MPa和 102.8 MPa. 卸载状态的参量随着$\kappa$变化的规律如下
式中,$h_2 (\kappa )$影响的是压缩情况,在拉伸情况下,几乎不随耗散的变化而变化,本文给定为
表3 匹配Mullins 和Tobin[40] 中Mullins 效应的模型参数数值(加载)
Table 3
| E0/MPa | a0 | 々10 | 乃20 |
|---|---|---|---|
| 25 | 0.35 | 1.85 | 10 |
表4 匹配Mullins 和Tobin[40] 中Mullins 效应的模型参数数值(卸载)
Table 4
| No | Km | K | h1(K) | 乃 2(k) | E (k) | a(K) |
|---|---|---|---|---|---|---|
| 1st | 18.4 | 6.9 | 1.26 | 10 | 12 | 0.27 |
| 2nd | 31.0 | 14.2 | 1.47 | 10 | 11 | 0.22 |
| 3rd | 47.8 | 26.5 | 1.64 | 10 | 10 | 0.17 |
将参数代入方程(51),(53)和(54),得到模型结果和试验结果的对比如图6所示.
图6
4.3 Mullins效应滞回圈预测
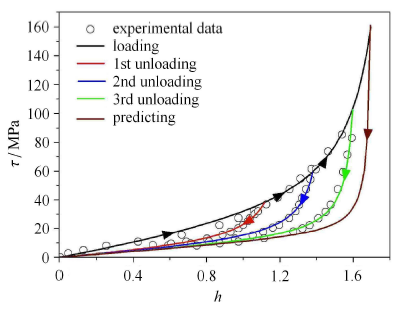
在4.2节分析的基础上,继续以文献[37]的实验为基础,进行卸载曲线预测分析. 预测点取卸载应力$\tau _{\rm m} =164.5$ MPa,此时$\kappa _{\rm m} = 61.11$代入到方程(46),得到
将耗散$\kappa$代入到方程(58)~(61),得到结果如表5所示.
表5 预测文献[37] 中Mullins 效应的模型参数数值(加载)
Table 5
| Km | K | h1(K) | h2(K) | E (k) | a(K) |
|---|---|---|---|---|---|
| 61.1 | 43.7 | 1.71 | 10 | 10 | 0.094 |
将表中的参数代入方程(47),就能得到预测的曲线结果,4.2节模型匹配的结果和4.3节模型预测的结果对比如图7所示.
图7
5 结 论
本文通过显式、直接的方法给出了一个多轴可压缩应变能函数,能模拟类橡胶材料三个基准实验,同时可以模拟并预测Mullins效应软化产生的应力——应变关系滞回圈.
本文方法的优势在于一下四点:第一,没有引入任何隐式参数,所有的量都可以显式表达,计算量大大减少;第二,可以适用于类橡胶材料的普遍情况(包括不可压缩和可压缩);第三,本模型并非局限于一种橡胶或者一种实验,对于所有类橡胶材料都能适应,并且能至少模拟三个基准实验;第四,对于类橡胶材料在加载——卸载情况下产生的的应力——应变滞回效应,可以通过模型给出,并能准确匹配和预测.
参考文献
Softening of rubber by deformation
Effect of stretching on the properties of rubber
Permanent set in vulcanized rubber
Comparison of hyperelastic models for rubber-like materials
Constitutive models of rubber elasticity: A review
Statistical theory of networks of Non-Gaussianflexible chains
Network structure and the elastic properties of vulcanizedrubber
network structure and the elastic properties of vulcanized rubber.
Stress-strain data for vulcanised rubber under varioustypes of deformation
http://xlink.rsc.org/?DOI=tf9444000059
A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials
Aconstitutive model is proposed for the deformation of rubber materials which is shown to represent successfully the response of these materials in uniaxial extension, biaxial extension, uniaxial compression, plane strain compression and pure shear. The developed constitutive relation is based on an eight chain representation of the underlying macromolecular network structure of the rubber and the non-Gaussian behavior of the individual chains in the proposed network. The eight chain model accurately captures the cooperative nature of network deformation while requiring only two material parameters, an initial modulus and a limiting chain extensibility. Since these two parameters are mechanistically linked to the physics of molecular chain orientation involved in the deformation of rubber, the proposed model represents a simple and accurate constitutive model of rubber deformation. The chain extension in this network model reduces to a function of the root-mean-square of the principal applied stretches as a result of effectively sampling eight orientations of principal stretch space. The results of the proposed eight chain model as well as those of several prominent models are compared with experimental data of Treloar (1944, Trans. Faraday Soc. 40, 59) illustrating the superiority, simplicity and predictive ability of the proposed model. Additionally, a new set of experiments which captures the state of deformation dependence of rubber is described and conducted on three rubber materials. The eight chain model is found to model and predict accurately the behavior of the three tested materials further confirming its superiority and effectiveness over earlier models.
A Non-Gaussian theory for rubber in biaxial strain II: Optical properties
The model used is essentially that used in Part I, modified by the introduction of anisotropic optical properties associated with the chain links. Equations are derived for the differences of principal polarizabilities for the biaxially strained network. These are evaluated by numerical computa02tion, as in part I. The variations of polarizability differences with strain are found to follow a very similar pattern to the corresponding principal stresses. Comparisons are made also with the Gaussian optical theory and with a simplified ‘3-chain’ non-Gaussian model analogous to that of James & Guth. The theory predicts one important effect not derivable from the simpler theories.
A theory of large elastic deformation
It is postulated that (A) the material is isotropic, (B) the volume change and hysteresis are negligible, and (C) the shear is proportional to the traction in simple shear in a plane previously deformed, if at all, only by uniform dilatation or contraction. It is deduced that the general strain‐energy function,W, has the formW=G4∑i=13(λi611λi)2+H4∑t=13(λi2611λi2),where the λi's are the principal stretches (1+principal extension),Gis the modulus of rigidity, andHis a new elastic constant not found in previous theories. The differences between the principal stresses are σi[minus]σi=λi68W/68λi[minus]λi68W/68λi. Calculated forces agree closely with experimental data on soft rubber from 400 percent elongation to 50 percent compression.
Large elastic deformations of isotropic materials II. Some uniqueness theorems for pure, homogeneous deformation
The equilibrium of a cube of incompressible, neo-Hookean material, under the action of three pairs of equal and oppositely directed forces f1,f2,f3, applied normally to, and uniformly distributed over, pairs of parallel faces of the cube, is studied. It is assumed that the only possible equilibrium states are states of pure, homogeneous deformation. It is found that (1) when the stress components in the deformed cube are specified, the corresponding equilibrium state is uniquely determined (this is shown in section 6 of Part I). (2) When the three pairs of equal and oppositely directed forces f1,f2and f3are specified, (a) the corresponding equilibrium state is uniquely determined, provided that one or more of the forces f1,f2and f3is negative, i.e. is a compressional force, or, if they are all positive, provided that f1f2f3< (1/3E)3, where 1/3E is the constant of proportionality between the stress and strain components (analogous to the rigidity modulus of the classical theory of small elastic deformations of isotropic materials). (b) If f1,f2and f3are all positive and f1f2f3> (1/3E)3, then the equilibrium state is not necessarily uniquely determined. The number of equilibrium states which exist depends on the values of f1,f2,f3and 1/3E. The actual state of deformation which is obtained depends in general on the order in which the forces are applied. In the cases (1) and (2a), it is shown that the unique equilibrium state is one of stable equilibrium. In case (2b), it is shown that the possible equilibrium states are of eight different types. Two of these are mutually exclusive. Of these eight types of equilibrium state, four are inherently unstable. Of the other four types, one is inherently stable. The three remaining types of equilibrium state are not necessarily unique; i.e. more than one equilibrium state of each type may correspond to specified values of f1,f2and f3. However, if one or more equilibrium states of a particular type exists, then at least one of them is stable. If f1= f2= f3= f, then there is a unique state of stable equilibrium, provided that f < 1/3E. If 1/3E < f < (1/4)1/3E, then there are three states of stable equilibrium, none of which is identical with the undeformed state of the cube. If (1/4)1/3E < f < 2/3E, there are four states of stable equilibrium, one of which is identical with the undeformed state of the cube. If f > 2/3E, then there is only one state of stable equilibrium, and this is identical with the undeformed state of the cube.
A new constitutive relation for rubber
Characterization of elastic properties of carbon-black-filled rubber vulcanizats
Large deformation isotropic elasticity on the correlation of theory and experiment for incompressible rubberlike solids
Many attempts have been made to reproduce theoretically the stress-strain curves obtained from experiments on the isothermal deformation of highly elastic 'rubberlike' materials. The existence of a strain-energy function has usually been postulated, and the simplifications appropriate to the assumptions of isotropy and incompressibility have been exploited. However, the usual practice of writing the strain energy as a function of two independent strain invariants has, in general, the effect of complicating the associated mathematical analysis (this is particularly evident in relation to the calculation of instantaneous moduli of elasticity) and, consequently, the basic elegance and simplicity of isotropic elasticity is sacrificed. Furthermore, recently proposed special forms of the strain-energy function are rather complicated functions of two invariants. The purpose of this paper is, while making full use of the inherent simplicity of isotropic elasticity, to construct a strain-energy function which: (i) provides an adequate representation of the mechanical response of rubberlike solids, and (ii) is simple enough to be amenable to mathematical analysis. A strain-energy function which is a linear combination of strain invariants defined by φ (α)=(a1α+a2α+a3α-3)/α is proposed; and the principal stretches a1,a2 and a3 are used as independent variables subject to the incompressibility constraint a1a2a3=1. Principal axes techniques are used where appropriate. An excellent agreement between this theory and the experimental data from simple tension, pure shear and equibiaxial tension tests is demonstrated. It is also shown that the present theory has certain repercussions in respect of the constitutive inequality proposed by Hill (1968a, 1970b).
A visco-hyperel-astic constitutive model for rubber-like materials: A rate-dependent relaxation time scheme
A three-dimensional visco-hyperelastic constitutive model is developed to describe the rate-dependent behavior of rubber-like materials at large deformations. The model encompasses a hyperelastic part which uses the “Exp–Ln” strain energy function to characterize the equilibrium response and a viscous part capturing the rate sensitivity using a hereditary integral form which links the overstress to the history of stored strain energy. A physically consistent rate-dependent relaxation time scheme is introduced which reduces the number of required material parameters and also facilitates the calibration process. The proposed model is verified using various uniaxial experimental data in different rate ranges. Furthermore, the model is incorporated via VUMAT in ABAQUS/Explicit to examine its performance in three-dimensional deformations. To this end, finite element analysis of an elastomeric bushing is performed and the results are compared to those of experiment. It is then concluded that, the proposed constitutive relations are quite efficient in predicting the behavior of rubber-like materials in different states of deformation and also in wide ranges of strain rate.
帘线/橡胶复合材料各向异性黏——超弹性本构模型
<p>帘线/橡胶复合材料广泛应用于轮胎等重要工程领域,为了描述其在服役条件下的大变形、非线性、各向异性和高应变率等材料力学行为,基于纤维增强复合材料连续介质力学理论,提出了一种考虑应变率效应的帘线/橡胶复合材料各向异性黏-超弹性本构模型. 该模型中单位体积的应变能被解耦为便于参数识别的基体等容变形能、帘线拉伸变形能、剪切应变能和黏性应变能四部分. 给出了模型参数的确定方法,并通过拟合文献中单轴拉伸、偏轴拉伸实验数据,得到了模型参数. 利用该模型预测了不同加载和变形条件下的力学行为,并将预测结果与实验结果对比分析. 结果表明, 考虑黏性模型和不考虑黏性模型对不同应变率变形条件下的预测结果相差很大,且考虑黏性模型的预测结果与实验结果吻合很好. 因此,与不考虑黏性模型相比,所提出的各向异性黏-超弹性本构模型能更好地表征帘线/橡胶复合材料在大变形、高应变率条件下的力学特性.</p>
An anisotropic visco-hyperelastic constitutive model for cord-rubber composites
<p>帘线/橡胶复合材料广泛应用于轮胎等重要工程领域,为了描述其在服役条件下的大变形、非线性、各向异性和高应变率等材料力学行为,基于纤维增强复合材料连续介质力学理论,提出了一种考虑应变率效应的帘线/橡胶复合材料各向异性黏-超弹性本构模型. 该模型中单位体积的应变能被解耦为便于参数识别的基体等容变形能、帘线拉伸变形能、剪切应变能和黏性应变能四部分. 给出了模型参数的确定方法,并通过拟合文献中单轴拉伸、偏轴拉伸实验数据,得到了模型参数. 利用该模型预测了不同加载和变形条件下的力学行为,并将预测结果与实验结果对比分析. 结果表明, 考虑黏性模型和不考虑黏性模型对不同应变率变形条件下的预测结果相差很大,且考虑黏性模型的预测结果与实验结果吻合很好. 因此,与不考虑黏性模型相比,所提出的各向异性黏-超弹性本构模型能更好地表征帘线/橡胶复合材料在大变形、高应变率条件下的力学特性.</p>
短纤维增强三元乙丙橡胶横观各向同性黏-超弹性本构模型
短纤维增强三元乙丙橡胶包覆薄膜,是一种应用于固体火箭发动机缠绕包覆装药的新型复合材料.为了描述其在工作过程中受振动、冲击等载荷作用时的力学行为,基于黏弹性理论和纤维增强连续介质力学理论,提出了一种考虑应变率强化效应的横观各向同性黏--超弹本构模型.模型中应变能函数被分解为超弹性应变能和黏性应变能,其中超弹性应变能包括表征各向同性的橡胶基体应变能和表征各向异性的纤维拉伸应变能,黏性应变能采用表征橡胶和纤维黏性响应的宏观唯象模型.选取表征各应变能的函数形式,经过数学变换、替代、叠加,求解确定最终的应力应变形式,明确模型参数获取的具体步骤,将预测结果与实验结果对比分析,准确性较高.研究表明:该模型能有效预测材料在低应变率下纤维方向为045的非线性率相关力学特性;模型形式易于实现有限元开发,对固体火箭发动机装药结构完整性分析具有参考价值.
A transversely isotropic visco-hyperelastic constitutive model for short fiber reinforced EPDM
短纤维增强三元乙丙橡胶包覆薄膜,是一种应用于固体火箭发动机缠绕包覆装药的新型复合材料.为了描述其在工作过程中受振动、冲击等载荷作用时的力学行为,基于黏弹性理论和纤维增强连续介质力学理论,提出了一种考虑应变率强化效应的横观各向同性黏--超弹本构模型.模型中应变能函数被分解为超弹性应变能和黏性应变能,其中超弹性应变能包括表征各向同性的橡胶基体应变能和表征各向异性的纤维拉伸应变能,黏性应变能采用表征橡胶和纤维黏性响应的宏观唯象模型.选取表征各应变能的函数形式,经过数学变换、替代、叠加,求解确定最终的应力应变形式,明确模型参数获取的具体步骤,将预测结果与实验结果对比分析,准确性较高.研究表明:该模型能有效预测材料在低应变率下纤维方向为045的非线性率相关力学特性;模型形式易于实现有限元开发,对固体火箭发动机装药结构完整性分析具有参考价值.
弹簧-金属丝网橡胶组合减振器迟滞力学模型及实验研究
金属丝网橡胶材料是一种完全由金属丝编织成的多孔复合材料,与传统螺旋卷制金属橡胶材料相比,其改进了成型工艺,剔除了制备过程中大量的手工工艺干扰,提高机械化程度,重合度更高,拥有更稳定的力学性能.由于金属丝网橡胶材料具有承载能力高、阻尼大、耐高温、耐低温、耐老化、抗油抗腐蚀等优良特性,在很多方面强于传统橡胶,多用于航空航天、船舶、军事武器等军工工业.弹簧—金属丝网橡胶组合减振器具有可设计刚度和较高承载能力,但因其具有复杂的非线性迟滞特性,目前相关材料的本构模型还难以准确描述其力学特性.本文在弹簧—金属丝网橡胶组合减振器静态迟滞力学性能实验的基础上,结合其干摩擦阻尼迟滞特性,提出了一种迟滞力学性能理论模型.根据减振器迟滞实验恢复力—位移曲线特点,利用参数分离的方法将迟滞曲线分解为弹性恢复力和干摩擦阻尼力,分别建模求解等效刚度和干摩擦阻尼系数,以此建立了组合减振器理论模型,并与实验结果进行对比及进行误差分析,验证了理论模型的准确性.
Hysteresis mechanical model and experimental study of spring metal-net rubber combination damper
金属丝网橡胶材料是一种完全由金属丝编织成的多孔复合材料,与传统螺旋卷制金属橡胶材料相比,其改进了成型工艺,剔除了制备过程中大量的手工工艺干扰,提高机械化程度,重合度更高,拥有更稳定的力学性能.由于金属丝网橡胶材料具有承载能力高、阻尼大、耐高温、耐低温、耐老化、抗油抗腐蚀等优良特性,在很多方面强于传统橡胶,多用于航空航天、船舶、军事武器等军工工业.弹簧—金属丝网橡胶组合减振器具有可设计刚度和较高承载能力,但因其具有复杂的非线性迟滞特性,目前相关材料的本构模型还难以准确描述其力学特性.本文在弹簧—金属丝网橡胶组合减振器静态迟滞力学性能实验的基础上,结合其干摩擦阻尼迟滞特性,提出了一种迟滞力学性能理论模型.根据减振器迟滞实验恢复力—位移曲线特点,利用参数分离的方法将迟滞曲线分解为弹性恢复力和干摩擦阻尼力,分别建模求解等效刚度和干摩擦阻尼系数,以此建立了组合减振器理论模型,并与实验结果进行对比及进行误差分析,验证了理论模型的准确性.
猪肝动态力学性能及本构模型研究
在交通事故中,腹部器官常因冲击载荷作用而受到伤害,严重时甚至危及生命.肝损伤是腹部损伤中最为常见的一种,致死率很高,了解肝脏的动态力学性能对于事故中肝脏的损伤评估及防护设计有着重要的意义.从新鲜的猪肝组织中取肝实质部分制作试样,利用英斯特朗材料试验机对其进行两种加载率(0.004 s~(-1),0.04 s~(-1))和两种加载方向(垂直肝脏表面和平行于肝脏表面)的准静态压缩试验,并压缩至破坏.利用改进的分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)实验装置沿平行于肝脏表面方向进行三种高应变率(1 300 s~(-1),2 400 s~(-1),4 500 s~(-1))的动态压缩试验.结果表明:所有应变率下的猪肝压缩应力应变曲线都呈非线性凹向上特征,初始阶段应力值很低,应变约30%后应力幅值显著增大;准静态压缩时,两种应变率(0.004 s~(-1),0.04 s~(-1))和两种加载方向下肝脏组织破坏应力和破坏应变等力学性能无显著不同,平均破坏应变为48%,平均破坏应力为0.45 MPa.高应变率下肝脏组织的流动应力明显高于准静态下的流动应力,表现出一定的率敏感性.采用Yeoh型超弹性本构模型描述猪肝组织准静态力学性能,基于黏超弹性模型理论,提出了一个能描述肝脏组织从低应变率到高应变率范围力学性能的率相关本构模型,该模型与实验结果有很好的一致性.
Research on dynamic mechanical response and constitutive model of porcine liver
在交通事故中,腹部器官常因冲击载荷作用而受到伤害,严重时甚至危及生命.肝损伤是腹部损伤中最为常见的一种,致死率很高,了解肝脏的动态力学性能对于事故中肝脏的损伤评估及防护设计有着重要的意义.从新鲜的猪肝组织中取肝实质部分制作试样,利用英斯特朗材料试验机对其进行两种加载率(0.004 s~(-1),0.04 s~(-1))和两种加载方向(垂直肝脏表面和平行于肝脏表面)的准静态压缩试验,并压缩至破坏.利用改进的分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)实验装置沿平行于肝脏表面方向进行三种高应变率(1 300 s~(-1),2 400 s~(-1),4 500 s~(-1))的动态压缩试验.结果表明:所有应变率下的猪肝压缩应力应变曲线都呈非线性凹向上特征,初始阶段应力值很低,应变约30%后应力幅值显著增大;准静态压缩时,两种应变率(0.004 s~(-1),0.04 s~(-1))和两种加载方向下肝脏组织破坏应力和破坏应变等力学性能无显著不同,平均破坏应变为48%,平均破坏应力为0.45 MPa.高应变率下肝脏组织的流动应力明显高于准静态下的流动应力,表现出一定的率敏感性.采用Yeoh型超弹性本构模型描述猪肝组织准静态力学性能,基于黏超弹性模型理论,提出了一个能描述肝脏组织从低应变率到高应变率范围力学性能的率相关本构模型,该模型与实验结果有很好的一致性.
短纤维增强 EPDM 包覆薄膜超弹性本构模型
短纤维增强三元乙丙橡胶(EPDM)包覆薄膜用于一种新型缠绕包覆工艺,主要解决复杂构型自由装填药柱外表面可靠性包覆问题.为了描述其在固体火箭发动机工作过程中产生的大变形、非线性和各向异性等力学行为,根据纤维增强复合材料连续介质力学理论,提出了各向异性超弹性本构模型.该模型中单位体积的应变能函数被解耦成两部分:表征各向同性的橡胶基体应变能和表征各向异性的纤维拉伸应变能,通过引入纤维方向对纤维应变能进行修正,给出了通过单轴拉伸、偏轴拉伸实验数据获取模型参数的具体方法.研究结果表明,该模型能够很好地预测材料在纤维方向045时的各向异性力学特性,并将预测结果与实验数据对比,误差在5%以下.所建立的各向异性超弹性本构模型准确性高、易于实现数值开发,在一定程度上能够为固体火箭发动机的装药结构完整性分析提供理论依据.
Hyperelastic constitutive model for short fiber reinforced EPDM inhibitor film
短纤维增强三元乙丙橡胶(EPDM)包覆薄膜用于一种新型缠绕包覆工艺,主要解决复杂构型自由装填药柱外表面可靠性包覆问题.为了描述其在固体火箭发动机工作过程中产生的大变形、非线性和各向异性等力学行为,根据纤维增强复合材料连续介质力学理论,提出了各向异性超弹性本构模型.该模型中单位体积的应变能函数被解耦成两部分:表征各向同性的橡胶基体应变能和表征各向异性的纤维拉伸应变能,通过引入纤维方向对纤维应变能进行修正,给出了通过单轴拉伸、偏轴拉伸实验数据获取模型参数的具体方法.研究结果表明,该模型能够很好地预测材料在纤维方向045时的各向异性力学特性,并将预测结果与实验数据对比,误差在5%以下.所建立的各向异性超弹性本构模型准确性高、易于实现数值开发,在一定程度上能够为固体火箭发动机的装药结构完整性分析提供理论依据.
A review on the Mullins effect
The Mullins effect remains a major challenge in order to provide good mechanical modeling of the complex behavior of industrial rubber materials. It has been forty years since Mullins [Mullins L. Softening of rubber by deformation. Rubber Chem Technol 1969;42:339 62.] wrote his review on the phenomenon and still no general agreement has been found either on the physical source or on the mechanical modeling of this effect. Therefore, we reviewed the literature dedicated to this topic over the past six decades. We present the experimental evidences, which characterize the Mullins softening. The phenomenon is observed in filled rubbers and crystallizing pure gum. Then, the phenomenological models dedicated to fit the mechanical behavior of rubbers undergoing some Mullins softening are studied. To overcome the limit of a descriptive phenomenological modeling, several authors looked for a physical understanding of the phenomenon. Various theories have been proposed, but none of them has been supported unanimously. Nonetheless, these theories favor the emergence of physically based mechanical behavior laws. We tested some of these laws, which show little predictive abilities since the values of their parameters either cannot be measured experimentally or do not compare well with the physical quantities they are linked to.
On a fully three-dimensional finite-strain viscoelastic damage model: Formulation and computational aspects
A fully three-dimensional finite-strain viscoelastic model is developed, characterized by: (i) general anisotropic response, (ii) uncoupled bulk and deviatoric response over any range of deformations, (iii) general relaxation functions, and (iv) recovery of finite elasticity for very fast or very slow processes; in particular, classical models of rubber elasticity (e.g. Mooney-Rivlin). Continuum damage mechanics is employed to develop a simple isotropic damage mechanism, which incorporates softening behavior under deformation, and leads to progressive degradation of the storage modulus in a cyclic test with increasing amplitude (Mullins' effect). A numerical integration procedure is proposed which trivially satisfies objectivity and bypasses the use of midpoint configurations. The resulting algorithm can be exactly linearized in closed form, and leads to symmetric tangent moduli. Quasi-incompressible response is accounted for within the context of a three-field variational formulation of the Hu-Washizu type.
Discontinuous and continuous damage evolution in Ogden-type large-strain elastic materials
Superimposed finite elastic-viscoelastic-plastoelastic stress response with damage in filled rubbery polymers. Experiments, modeling and algorithmic implementation
On damage modeling for elastic and viscoelastic materials at large strain
Geometrical and different physical nonlinearities have to be taken into account in order to model elastomeric material. In the present contribution, a novel approach of rubber elasticity is introduced. The approach considers the topological constraints as well as the limited extensibility of network chains in filled rubber. Subsequently, a formulation of finite viscoelastic damage is derived. With this description at hand, softening effects as well as time and frequency dependency of the material can be characterized. The goal of the present paper is twofold. Firstly, the constitutive formulations are introduced. Moreover, computational aspects are stressed. The shown approaches are presented in a format ready for a finite element implementation.
A finite elastic-viscoelastic-elastoplastic material low with damage: Theoretical and numerical aspects
The present work is concerned with the theoretical formulation and numerical implementation of a new isotropic finite elastic–viscoelastic–elastoplastic material law with Mullins’ damage for rubber-like materials based on a set of dissipation inequalities published recently by the first author. A phenomenological model consisting of an elastic, an elastoplastic branch and N viscoelastic branches connected in parallel is exploited. The total free energy and the total stress are additively decomposed into three parts corresponding to the three types of branches. The damage effect is assumed to act on the three types of branches homogeneously and isotropically. According to the dissipation inequalities the evolution equations of the viscoelastic and elastoplastic branches are directly formulated in terms of the corotational rates of the internal elastic logarithmic strains. It is proved that in the present constitutive setting the internal elastic logarithmic strains are coaxial to the total and trial elastic logarithmic strains. The present theoretical and algorithmic formulations provide an alternative geometric representation of the same constitutive model outlined in [J. Mech. Phys. Solids 48 (2000) 323]. The numerical simulations show that the present material law gives predictions agreeing quite well with the experimental observations and numerical simulations issued in (loc. cit.).
Theoretical model for the elastic behavior of filler reinforced vulcanized rubbers
Constitutive model for stretch-induced softening of the stress-stretch behavior of elastomeric materials
Elastomeric materials experience stretch-induced softening as evidenced by a pre-stretched material exhibiting a significantly more compliant response than that of the virgin material. In this paper, we propose a fully three-dimensional constitutive model for the observed softening of the stress-strain behavior. The model adopts the Mullins and Tobin concept of an evolution in the underlying hard and soft domain microstructure whereby the effective volume fraction of the soft domain increases with stretch. The concept of amplified strain is then utilized in a mapping of the macroscopic deformation to the deformation experienced by the soft domain. The strain energy density function of the material is then determined from the strain energy of the soft domain and thus evolves as the volume fraction of soft domain evolves with deformation. Comparisons of model results for cyclic simple extension with the experimental data of Mullins and Tobin show the efficacy of the model and suggest that an evolution in the underlying soft/hard domain microstructure of the elastomer captures the fundamental features of stretch-induced softening. Model simulations of the cyclic stress-strain behavior and corresponding evolution in structure with strain for uniaxial tension, biaxial tension and plane strain tension are also presented and demonstrate three-dimensional features of the constitutive model
Mullins effect in swollen rubber: Experimental investigation and constitutive modelling
Apart from the well-known hyperelastic and large stress-strain behavior in dry rubber, the inelastic responses such as hysteresis and Mullins effect are also observed when a dry rubber is cyclically loaded. The former is given by different loading and unloading paths in a cycle, while the latter corresponds to the significant decrease in stress between two successive cycles, particularly between the first and second loading. The Mullins effect or the stress-softening effect disappears after several cycles of loading, i.e. five cycles for the materials used in the present study. A number of models describing the Mullins effect in dry rubber are available in the literature. Nevertheless, works focusing on the Mullins effect in swollen rubbers are less common. Therefore, the experimental investigation and modelling of Mullins effect in swollen rubbers are addressed in the present study. For this purpose, mechanical tests were conducted in order to probe the Mullins effect in swollen rubbers under cyclic loading conditions. Furthermore, the pseudo-elastic model [Ogden, R.W. & Roxburgh, D. G., 1999. A pseudo-elastic model for the Mullins effect in filled rubber. Proc. Roy. Soc. A. 455, 2861-2877] is considered and extended in order to account for swelling level. Results show that the proposed model is qualitatively in good agreement with experimental observations. (C) 2013 Elsevier Ltd. All rights reserved.
A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber
Stress softening during initial loading cycles, known as the Mullins effect, and the residual strain upon unloading are not accounted for when the mechanical properties of rubber are represented in terms of a strain-energy function, i.e. if the material is modelled as hyperelastic. In this paper we first describe some experimental results that illustrate stress softening in particle-reinforced rubber together with associated residual strain effects. In particular, the results show how the stress softening and residual strain change with the magnitude of the applied strain. Then, on the basis of these data a constitutive model is derived to describe this behaviour. The theory of pseudo-elasticity is used for this model, the basis of which is the inclusion of two variables in the energy function in order separately to capture the stress softening and residual strain effects. The dissipation of energy, i.e. the difference between the energy input during loading and the energy returned on unloading is also accounted for in the model by the use of a dissipation function, which evolves with the deformation history.
Constitutive modeling of the anisotropic behavior of Mullins softened filled rubbers
Original constitutive modeling is proposed for filled rubber materials in order to capture the anisotropic softened behavior induced by general non-proportional pre-loading histories. The hyperelastic framework is grounded on a thorough analysis of cyclic experimental data. The strain energy density is based on a directional approach. The model leans on the strain amplification factor concept applied over material directions according to the Mullins softening evolution. In order to provide a model versatile that applies for a wide range of materials, the proposed framework does not require to postulate the mathematical forms of the elementary directional strain energy density and of the Mullins softening evolution rule. A computational procedure is defined to build both functions incrementally from experimental data obtained during cyclic uniaxial tensile tests. Successful comparisons between the model and the experiments demonstrate the model abilities. Moreover, the model is shown to accurately predict the non-proportional uniaxial stress-stretch responses for uniaxially and biaxially pre-stretched samples. Finally, the model is efficiently tested on several materials and proves to provide a quantitative estimate of the anisotropy induced by the Mullins softening for a wide range of filled rubbers.
An explicit,direct approach to obtaining multiaxial elastic potentials which exactly match data of four benchmark tests for incompressible rubberlike materials-Part 1: Incompressible deformations
Multiaxial strain energy functionsof rubberlike materials: An explicit approach based on polynomial interpolation
New multi-axial constitutive mod-dels for large elastic deformation behaviors of soft up to breaking
A hyperelastic model is proposed to characterize large elastic deformation behaviours of soft solids. Novelties in four respects are incorporated in this model, namely, (i) general compressible deformations may be treated and, accordingly, the usually-assumed incompressibility constraint and associated issues may be bypassed; (ii) applicability for all kinds of material samples may be automatically ensured, in the sense that any given test data for three deformation modes may be exactly fitted, including uniaxial, equi-biaxial and plane-strain extension; (iii) model parameters of direct physical meanings may be provided to characterize both strain-stiffening and softening effects; and (iv) breaking behaviour may be simulated. Numerical results for model validation are in good agreement with Treloar classic data for rubbers and with extensive data for various kinds of polymer gels.
Hencky's logarithmic strain and dual stress-strain and strain-stress relations isotropic finite hyperelasticity
It has been known that the Kirchhoff stress tensor τ and Hencky’s logarithmic strain tensor h may be useful in formulations of isotropic finite elasticity and elastoplasticity. In this work, a straightforward proof is presented to demonstrate that, for an isotropic hyperelastic solid, the just-mentioned stress–strain pair τ and h are derivable from two dual scalar potentials with respect to each other. These results establish a simple, explicit dual formulation of isotropic finite hyperelasticity. As a result, they supply a complete solution to the problem of finding out the inverted stress–strain relation for isotropic hyperelastic solids, raised by J.A. Blume [Int. J. Non-linear Mech. 27 (1992) 413]. Moreover, an explicit form of such an inverted hyperelastic stress–strain relation is derived in terms of the powers I, τ and τ2.
The properties of rubber in pure homogeneous strain
Measurements are reported on the relationship between the principal stresses t1 and t2 and the corresponding extension ratios lambda 1 and lambda 2 in the general biaxial strain of a rubber sheet. The resulting data are shown to be consistent with the Valanis-Landel hypothesis, according to which the strain energy W is a separable function w( lambda ) of the principal extension ratios. The formulation of the series for lambda (dw/d lambda ) in terms of strain invariants I1 and I2 enables delta W/ delta I1 and delta W/ delta I2 to be accurately calculated for any values of I1 and I2. It is concluded that both delta W/ delta I1 and delta W/ delta I2 are functions of both I1 and I2. The results confirm the conclusions of earlier workers that the empirical Mooney constants derived from uniaxial extension or compression bear no direct relation to the values of delta W/ delta I1 and delta W/ delta I2.
Biaxial strain testing of extremely soft polymer gels
We present a biaxial tensile tester to characterize the nonlinear stress–strain behavior of extremely soft polymer gels with very low shear moduli, of the order of 102Pa, under general (equal and unequal) biaxial strain. Stretching of gel sheet specimens in a solvent bath can avoid finite self-weight bending deformations that have precluded biaxial tensile experiments with such extremely soft gels. General biaxial strain covers a wide range of physically accessible deformations in contrast to the conventional uniaxial strain that is only a special one among them. We have used this tensile tester to examine the biaxial stress–strain relations of two types of hydrogel with water contents of more than 95 wt%, namely “chemical gels” with covalent cross-links and “physical gels” with noncovalent cross-links (microcrystallites acting as cross-links). Biaxial data provide a definite basis for the discussion of the differences in the nonlinear elasticities of these hydrogels at very low network concentrations. In particular, the biaxial data for fully swollen chemical gels reveal that the exceptional agreement of the data in a wide range of uniaxial strain with predictions of the simplest rubber elasticity model (ideal gas model), which has long been known, is superficial because the model evidently fails to describe the biaxial data. This new biaxial tester will be a powerful tool for the full characterization of the large deformation behavior of extremely soft materials, including biological soft tissues.
Theoretical model for the elastic behavior offiller-reinforced vulcanized rubbers