引 言
帽型梁是常用的吸能结构,其吸能性能的提升设计是备受关注的问题[1-3]. 目前,性能提升设计的手段主要包括设计截面形状[4-6]和轴向结构特征[7-8]、增加和设计内部填充[9-11]等.近期研究表明,通过合理设计厚度分布,薄壁管结构可在冲击变形时产生理想的变形模式,具有更优的结构性能.设计和发现最优厚度分布形式成为关注热点,出现了大量的相关研究工作[12-16].孙光永等[14]提出了指数描述型厚度变化的功能梯度结构设计方案;李光耀等[15]提出了用NURBS曲线描述柔性轧制差厚板的厚度,通过等几何分析优化得到最优构型;Mozumder等[16]利用HCA优化方法设计了薄壁耐撞性结构的壁厚分布.这些方法获得的结构往往具有复杂的厚度分布方式,传统工艺很难实现,需要发展适应制造工艺的厚度分布设计方法.
针对柔性轧制工艺的薄壁结构厚度分布设计,就是要寻找合适的分段方式、各段厚度及过渡区的厚度分布,以实现冲击吸能性能最优.由于帽型梁冲击性能分析是一个高度非线性的问题,直接以能量吸收最大化为设计目标构建优化模型,需要大量的分析,计算量大.因此,需要发展基于某种设计准则的优化模型,以减少分析次数.本文以应变能密度均匀分布为吸能最优设计准则,根据元胞自动机方法的思想实现应变能密度的均匀分布.利用粒子群算法对优化迭代过程进行过滤规整,使结构满足轧制特点.本文采用了较为准确的轧制过渡区厚度描述方式,与实际工艺成型的柔性轧制结构更为接近.
本文以广泛应用于汽车结构的帽型梁横向冲击过程为研究对象,考虑结构可由轧制工艺手段得到的含不同过渡区的轧制板制成,寻找其最优构型.文章以直线型与多项式型的过渡区为例,说明了该优化策略的可行性,并基于该策略实现了基于轧制板工艺的帽型梁结构构型的快速优化设计.
1 基于柔性轧制工艺的帽型梁结构设计
帽型梁由上方U型冲压板与下方平板两部分组成.两块板通过螺栓连接等连接工艺连接而成.为实现制备变厚度分布的帽型梁结构,可采用柔性轧制板作为基板材料,通过加工成形得到所需的结构件.因此,上下两块板都可以是单向变厚度柔性轧制板.
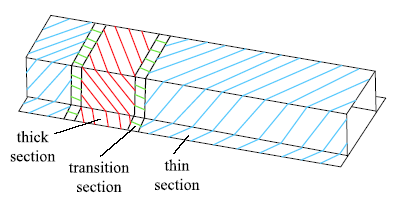
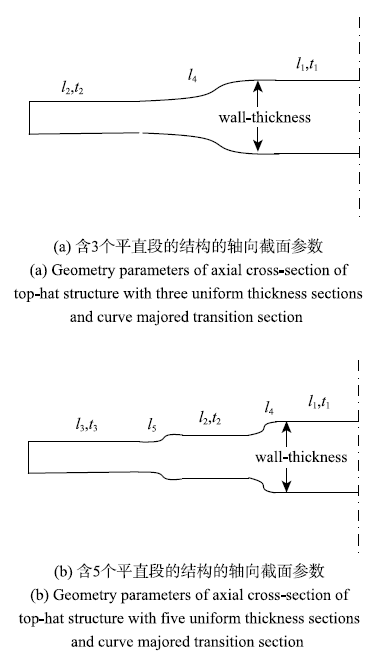
柔性轧制工艺首先通过冷轧机轧制出周期性变厚度带材,然后对整块板材进行退火处理、矫直矫平、按需可控裁剪,获得含过渡区的分段变厚度板材.因此,本文采用的柔性轧制板也应满足该特征,即板厚度变化方向上,柔性轧制板分为平直段与过渡段.为适应工艺特征,我们给出结构设计如图1所示,结构由平直段和过渡段组成.
图1
图1
基于柔性轧制工艺的轴向变厚度帽型梁结构
Fig.1
Axial variable thickness top-hat beam based on flexible rolling process
2 受横向冲击帽型梁的优化模型
薄壁结构在受到冲击载荷时,往往会发生大变形,其变形模式与冲击载荷的方向及结构本身相关.对于等厚度帽型薄壁梁结构的横向冲击问题,可以预见在结构的中部具有较大的塑性变形.而对于采用变厚度柔性轧制工艺获得的变厚度帽型梁结构,由于该结构由不同厚度的柔性轧制板制成,因此可以通过设计合理的壁厚分布改变特定工况下结构的变形模式,以获得更优的结构性能.
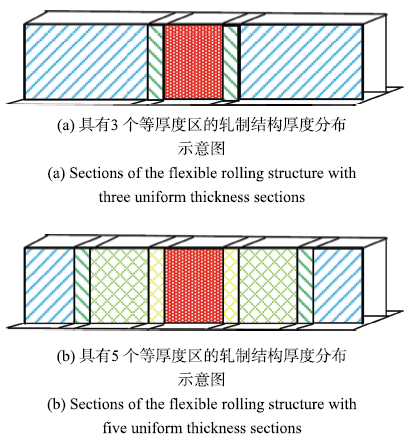
针对帽型梁结构的横向冲击过程,我们认为该结构合理的壁厚分布为结构沿轴向变厚度分布,且不同厚度分区之间由过渡区连接而成.两种不同的轧制结构设计方案及厚度分布情况如图2所示.
图2
图2
两种可能的薄壁梁轧制结构设计方案
Fig.2
Two possible thickness design schemes of thin-walled beam
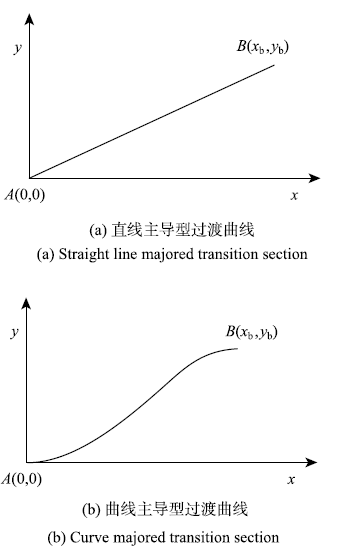
柔性轧制板结构中,平直段分区之间由连续的过渡区域连接而成.考虑两种常用的过渡区描述形式如图3所示.
图3
对于该帽型薄壁梁结构进行优化设计,就是要寻找结构合理的分区长度、厚度及过渡区形式,使得其具有最优的结构性能.该优化问题对应的优化列式为
式中, $f(t)$为结构的性能评价指标,$M_{\rm Total}$为初始结构的总质量,$\rho $}为材料的密度,$t$为具有上下限约束的结构厚度分布,A为结构面内的面积微元,有限元分析中亦可认为是shell单元的面积.
在结构耐撞性性能评价中,主要的评价指标包括结构的能量吸收(EA)、相对能量吸收(SEA)、结构的峰值冲击力(PCF)、平均冲击力(MCF),及结构对保护对象的保护能力(HIC)等.依据不同的使用工况,应选择不同的性能评价指标.作为冲击吸能结构,结构的SEA值越大则性能越好.针对上述受横向冲击的帽型薄壁梁结构,以冲击吸能SEA为优化目标进行结构耐撞性优化时,若优化变量设为结构的厚度分布,则优化列式可以写为
上式即本文考虑的受横向冲击帽型梁的优化模型.
3 基于HCA的受冲击轧制结构的优化流程
在上节的非线性冲击优化问题中,由于目标函数不能显式地表达,因此优化问题的敏度求解困难,很难用常规优化方法求解.为解决此类问题,Patel等[24]、Tovar等[25]等指出以应变能密度均匀分布为目标的混合元胞自动机(HCA)与结构的能量吸收最大化具有相关性,可应用于结构耐撞性拓扑优化中[26-30].HCA方法是一种适用于动力学拓扑优化的方法,该方法通过改变结构内单元的密度,以实现结构内材料的最优分布.其中,单元密度更新过程中,考虑了相邻单元对目标单元的影响.因此,对于文中待求的结构能量吸收优化问题,我们采用HCA准则方法来获取优化变量的优化方向,从而实现结构拓扑的迭代更新与优化.图4所示即为典型的HCA优化结构[30].
图4
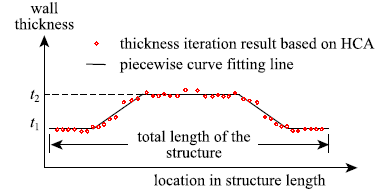
然而,HCA方法迭代得到的结构是连续变厚度的,变厚度轧制工艺获得的结构形式为厚度单向变化的,且结构分为平直区与过渡区.因此,针对轧制结构进行优化时,需要在上述HCA优化方法中引入轧制工艺条件约束.这里,我们提出在HCA迭代过程中采用过滤的方式,将连续变厚度结构转化为符合轧制约束的结构,如图5所示.
图5
图5
基于HCA迭代得到的厚度分布及分段拟合曲线示意图
Fig.5
Thickness distribution in axial direction of variable thickness structure
在寻找合适的轧制约束时,我们借鉴曲线拟合的思想,将HCA迭代得到的厚度分布作为测量值,轧制曲线上对应点为拟合值,采用误差估计中常用的$R_{\rm MSE}$作为评价二者之间近似程度的指标.因此,寻找合适的轧制结构几何描述的问题,即等同于求解一个最小化$R_{\rm MSE}$的问题. 其中$R_{\rm MSE}$的表达式如下
式中, $x_i $及$y_i$分别为结构长度方向上单元的位置及厚度,由HCA方法迭代得到;$\overline {x_i } $及$\overline {y_i } $为对应的拟合曲线上的点的坐标及厚度.$n$为结构长度方向的单元数. 对于本问题,$x_i \mbox{ = }\overline {x_i } $,且$n$为定值,故求式(3)的最小值,亦等同于求下式的最小值
因此,只要给定图5所示的分段拟合曲线的方程形式(轧制结构的分段长度分区数),通过求解一个最小化$M_{\rm SE}$的问题,即可找到符合轧制约束的结构,从而实现优化迭代过程中的工艺约束.
本工作采用PSO智能算法来寻找最优的拟合曲线.PSO算法中,单个粒子的描述参量为分段曲线各段的长度与厚度,目标函数为轧制面拟合的均方差(MSE).可以通过PSO智能算法较快速地找到每次HCA厚度迭代对应的分段拟合曲线.
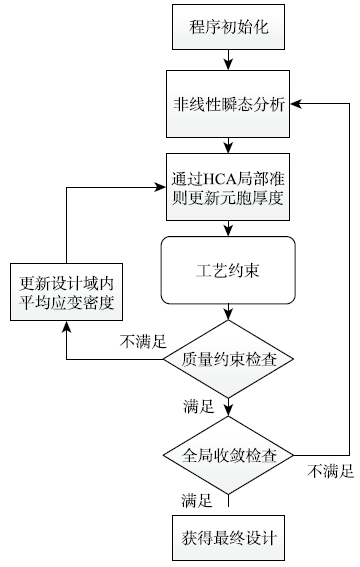
因此,我们建立了一种冲击条件下寻找轧制结构最优厚度分布及各段分区长度的策略.该策略根据应变能分布均匀的目标需求,自动调整结构参数,通过迭代的方式找到最优构型.对应的优化流程如图6所示.
图6
图6
基于轧制工艺约束的HCA优化过程
Fig.6
Optimization flow of hybrid cellular automata with flexible rolling process constraint
4 受横向冲击的帽型梁结构的厚度优化
图7
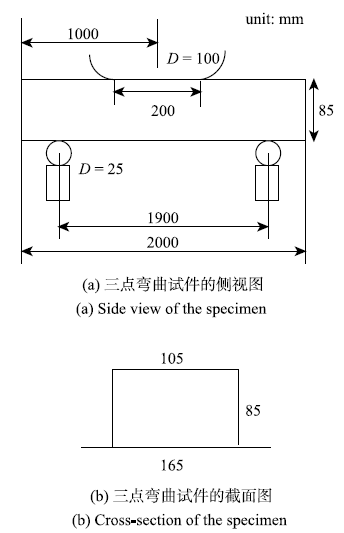
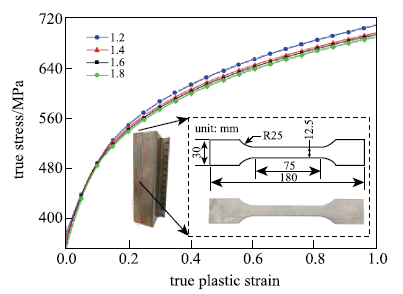
为探究一般的轧制型帽型梁结构横向冲击时的最优构型,我们将上述结构进行简化,考虑工程轧制结构的横向冲击吸能.最终以图8所示的三点弯曲梁结构为例. 梁的总长度为2000 mm,初始板厚 为1.4 mm,梁的横截面几何参数如图所示.在三点弯曲试验中,下方支座为圆柱形,半径为25 mm;支座间的距离为1900 mm. 上方刚性冲头为恒定速度0.6 m/s向下施压,总位移为60 mm.
图8
图8
三点弯曲帽型梁模型及部分参数
Fig.8
geometry parameters of the top-hat specimen under three point bending
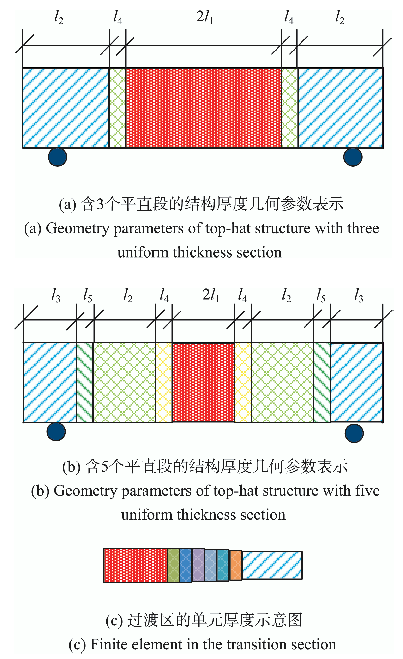
对于该横向冲击帽型梁结构,我们认为合理的轧制结构为平直段分段数为3段或者5段.针对这两种情况进行优化设计.鉴于模型的对称性,厚度分布也设为对称分布.结构的模型厚度示意图及设计变量(分区长度及厚度)的设定如图9所示.
图9
图9
帽型梁结构厚度分布的几何参数与有限元处理
Fig.9
Geometry parameters of the top-hat beam and the finite element in the transition section
图10
模型中,轧制板在同一截面内具有相同的厚度.对于不同厚度的板厚区域,有限元中给定截面属性时需要对厚度与材料属性进行离散化.结构厚度若超出实验结果的范围,则采用插值法得到.通过对离散单元给定不同的厚度值来近似连续变厚度的情况.
图11
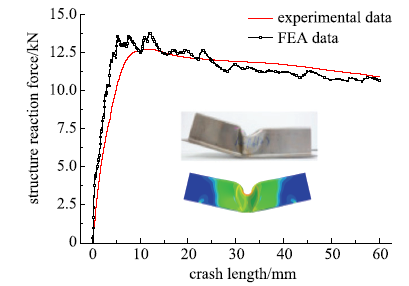
有限元分析与实验得到的结构冲击峰值力分别为13.782 kN与12.720 kN,误差为8.35%;结构的能量吸收分别为685.7 J与679.9 J,误差为0.85%.可见,利用上述有限元参数设置进行薄壁结构冲击性能仿真具有相当的可信性.
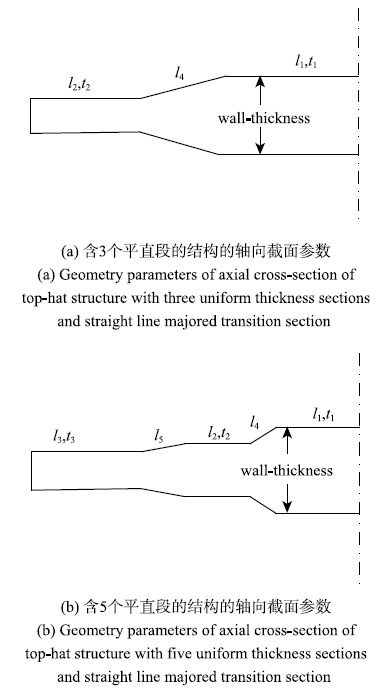
4.1 带直线型过渡区的柔性轧制板结构设计
图12
图12
带直线型过渡区的结构参数示意图
Fig.12
Geometry parameters of TRB top-hat structure with straight line majored transition section
将轧制方向的连续分布厚度按照有限元网格的密度等效为离散的厚度分布形式,即可利用前述优化列式进行结构优化分析.我们令柔性轧制板的等厚度区的厚度取值范围为0.8~2.4 mm.采用前文提到的HCA方法对该结构进行优化设计.轧制约束受实际工艺水平决定,针对本例,设定过渡区形式为直线过渡,过渡区长度为10 mm以内.为加快PSO智能算法的收敛速度,初始全局解设定为轧制结构的各个分段等长,厚度为结构初始厚度1.4 mm.对粒子初始状态的选取时,考虑可能的实际分段情况,每个粒子对应的分段长度为10$\sim $100 mm,厚度为0.8$\sim $ 2.4 mm.对于5个平直段分区的设计方案,轧制结构中的两个平直区厚度相等时,即退化为3个分区的设计方案.
通过迭代得到的最优结构参数及能量吸收如表1所示.其中结构编号1为3个等厚区的设计,结构编号2为5个等厚区的设计.
表1 优化后的直线过渡型轧制结构的几何参数
Table 1
| Structure | Geometry | h,h丨 | l4丨 | ,2,t2 丨 | hi | h,hl |
|---|---|---|---|---|---|---|
| label | parameter | mm | mm | mm | mm | mm |
| 1 | length | 250 | 60 | 690 | — | — |
| thickness | 1.536 | — | 1.346 | — | — | |
| 2 | length | 320 | 90 | 170 | 100 | 320 |
| thickness | 1.827 | — | 1.418 | — | 0.975 |
表2 含直线型过渡轧制结构优化方案的能量吸收
Table 2
| Structure label | Energy absorption" | SEA|(kJkg-1) |
|---|---|---|
| 1 | 528.5 | 0.1092 |
| 2 | 703.1 | 0.1453 |
表3 含直线型过渡轧制结构优化方案的厚度分布及变形模式
Table 3
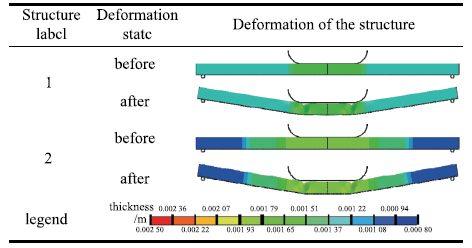 |
4.2 带多项式型过渡区的柔性轧制板结构设计
考虑帽型梁轧制结构的等厚度为3段与5段的两种情况.我们假定各等厚度段之间为多项式形式的过渡区,如图13所示.
图13
图13
带多项式型过渡区的结构参数示意图
Fig.13
Geometry parameters of axial cross-section of top-hat structure with curve majored transition section
式中 x轴零点为结构最左侧. 图13(b)对应的结构厚度分布方程同理.采用式(2)的优化列式,PSO曲面拟合的参数设置与上节相同.
表4 优化后曲线过渡型轧制结构的几何参数
Table 4
| Structure label | Geometry parameter | h,hl mm | l4 / mm | h,t2l mm | hi mm | h,hl mm |
|---|---|---|---|---|---|---|
| 3 | length | 250 | 40 | 710 | — | — |
| thickness | 1.532 | 1.350 | — | — | ||
| 4 | length | 330 | 100 | 170 | 70 | 330 |
| thickness | 1.813 | 1.403 | 70 | 0.975 |
表5 含曲线型过渡轧制结构优化方案的能量吸收
Table 5
 |
表6 含曲线型过渡轧制结构优化方案的厚度分布及变形模式
Table 6
 |
同时,对比过渡区为曲线时的优化结果与过渡区为直线时的结果,二者也非常接近.
4.3 优化结果分析与对比
利用本文提出的优化方法,可以得到吸能性能相比初始结构更优的结构构型.在本文的算例中,考虑工艺限制,过渡区的长度上限设为10 mm.以上述优化构型的能量吸收性能为评价指标,对各个结构性能进行对比,如表7所示.
表7 不同帽型梁优化后模型吸能性能对比
Table 7
| Promotion | ||||
|---|---|---|---|---|
| Structure label | Description | Energy absorption/J | SEA/(kJ.kg-1) | (compared with original structure)/% |
| 0 | uniform | 447.9 | 0.09253 | 0.00 |
| three uniform | ||||
| 7 | section and linear transition | 528.5 | 0.1092 | 18.0 |
| five uniform | ||||
| 8 | section and linear transition | 703.1 | 0.1453 | 57.0 |
| three uniform | ||||
| 9 | section and curve transition | 527.6 | 0.1090 | 17.8 |
| five uniform | ||||
| 10 | section and curve transition | 697.7 | 0.1441 | 55.8 |
从优化结果来看,上述算例达到最优构型时,结构的过渡区长度达到了上限值.同时,相对于直线过渡区,曲线过渡区在与等厚度区连接处更为平缓,但是过渡区内部的斜率变化更大.文中含直线过渡区结构的优化结果更优.为充分发挥曲线过渡区的优势,可以考虑改进工艺,从而适当加大过渡区的长度.
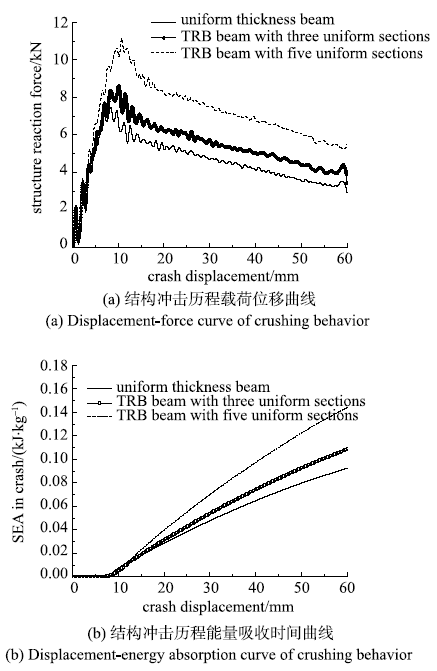
图14为不同优化柔性轧制板结构的冲击历程位移-结构反力曲线及结构冲击历程位移-{\ziju{-0.04}单位质量的能量吸收SEA曲线.可以看到,采用本文所提的优化方法得到的优化构型具有较好的能量吸收性能.其中,含多项式型过渡区的轧制结构其能量吸收性能更优.
图14
图14
不同优化模型得到的轧制成型帽型梁结构的冲击历程曲线
Fig.14
Crushing behavior of different optimized top-hat beam
对于文中提出的PSO-HCA方法,由于是针对非线性结构响应进行优化,因此迭代过程容易陷入局部解.本例最终得到的优化解相对于迭代历程中的其他结构具有较优的性能.
通过帽型梁结构横向受载情况下的结构位移-反力图,可以发现该结构在受冲击过程中反力首先会出现一个峰值力,之后有一个平台力阶段.我们知道,对于耐撞性结构来说,峰值力也是评价结构性能的一个重要指标.因此,对于重视峰值力性能的结构,采用柔性轧制板进行设计时需要引起注意.
4.4 结构变形模式与结构吸能关系的讨论
为探究不同轧制结构参数对结构性能的影响,本文选取了如下所示的若干组结构几何参数,对相应的薄壁帽型梁结构进行冲击吸能仿真.
表8 基于经验设计方案的曲线过渡型轧制结构的几何参数
Table 8
| Structure | Geometry | h,hl | 14/ | h,hl | Isl | h, hi |
|---|---|---|---|---|---|---|
| label | parameter | mm | mm | mm | mm | mm |
| 0 | length | — | — | — | — | — |
| thickness | 1.4 | 1.4 | ||||
| 5 | length | 600 | 100 | 300 | — | — |
| thickness | 2.5 | 0.8 | ||||
| 6 | length | 450 | 100 | 450 | — | — |
| thickness | 2.0 | 0.8 | ||||
| 7 | length | 120 | 100 | 410 | 100 | 270 |
| thickness | 2.5 | 1.4 | 0.8 | |||
| 8 | length | 270 | 100 | 260 | 100 | 270 |
| thickness | 2.0 | 1.4 | 0.8 | |||
| 9 | length | 300 | 60 | 640 | — | — |
| thickness | 1.8 | 1.2 | ||||
| 10 | length | 150 | 40 | 490 | 10 | 310 |
| thickness | 1.8 | 1.388 | 1.2 |
表9 经验设计方案在冲击载荷下的能量吸收与比能量吸收
Table 9
| Structure label | Energy absorption/J | SEA/(kJkg-1) |
|---|---|---|
| 0 | 447.9 | 0.092 53 |
| 5 | 225.6 | 0.046 61 |
| 6 | 277.7 | 0.057 37 |
| 7 | 536.5 | 0.110 80 |
| 8 | 560.1 | 0.115 70 |
| 9 | 443.8 | 0.091 70 |
| 10 | 467.6 | 0.096 60 |
表10 经验设计方案的结构的厚度分布及冲击变形
Table 10
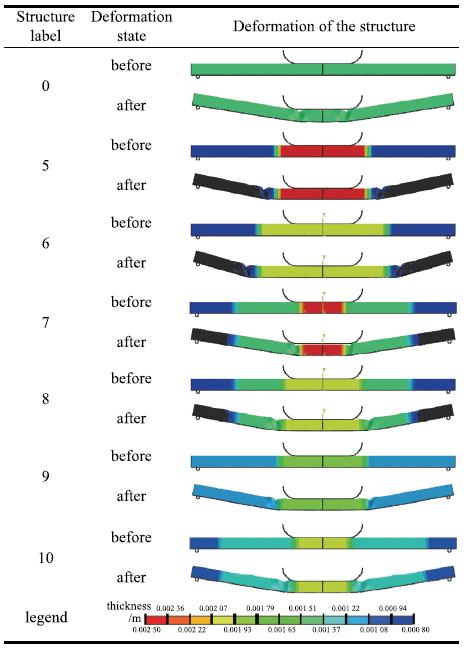 |
有限元分析结果表明,结构的能量吸收与结构冲击载荷下的变形模式密切相关.通过经验设计在结构的中部进行加厚,并不能很好地实现增加结构能量吸收的目的.在上述不同参数的设计方案中,结构发生主要大变形的位置可以大致分为两类,分别为在冲头位置与在薄板厚度过渡位置产生大变形.
结构大变形的位置与结构的几何参数密切相关.同时,为保证结构内部尽量多的位置进行有效的变形吸能,结构加厚的区域厚度并非越大越好.虽然给定了结构的厚度上下限为0.8~2.5 mm,但是优化结果的厚度值并没有达到上下限约束.因为过渡区在结构内占比较小,若结构厚度变化过大,将导致过渡位置的刚度过于不连续,从而在此处发生较大变形,不利于结构整体的能量吸收.然而,利用经验设计减小各分区厚度上下限差值的设计方案并没能得到较好的结果,这是因为最优性能的结构的各个几何参数是相关的.因此,相比于经验设计,本文所提供的方法能较为容易地获得轧制结构分区各段的最优长度与厚度值.
5 结 论
对于基于轧制工艺的帽型薄壁梁结构,具有分段变厚度、并在分段间含梯度过渡层的结构形式的特征.对这类薄壁帽型梁结构的厚度优化可有效提升结构的吸能性能.
(1)本文提出带过滤的HCA方法,能针对轧制工艺的特点进行厚度的合理调控,优化结构的厚度分布,实现结构的最优设计.该方法可用于多轧制区、不同轧制区形式的轧制结构优化.本文针对直线型过渡区与三次函数型过渡区轧制帽型梁轧,利用上述方法找到了最优分段厚度、长度及过渡方式.
(2)对于薄壁冲击结构,在冲击位置进行结构加厚(加强)能提升结构的冲击性能.然而通过经验设计的方式很难找到合理的结构厚度分布形式.
(3)过渡区描述形式不同的轧制结构,通过优化得到的最终构型的性能也不同.本文按照轧制工艺的需要对过渡区的长度进行约束.最终算例表明,二者差距很小;直线型过渡形式要比曲线型过渡形式优化得到的最优构型具有更优的耐撞性能.
(4)在结构厚度的优化调配过程中,不同的厚度分布会出现不同的冲击变形模式.因此,在实际工程应用中,结构的加强方案需要考虑设计方案的稳健性.
参考文献
A theoretical analysis for the quasi-static axial crushing of top-hat and double-hat thin-walled sections
A theoretical analysis, using superfolding elements (SE), has been carried out to determine the mean crushing loads for the quasi-static axial loading of top-hat and double-hat, spot-welded mild steel sections. The theoretical predictions compare favourably with experimental results reported in a companion article and with the experimental and numerical predictions of other authors.
Experimental study into the energy absorbing characteristics of top-hat and double-hat sections subjected to dynamic axial crushing
## TULIP Type: Articles/Papers (Journal) ##
On design of hybrid material double-hat thin-walled beams under lateral impact
61Hybrid material beam proposed as vehicle bumper to reduce pedestrian injury.61Quasi-static and dynamic three points bending tests of the hybrid beam.61Hybrid beam has better crashworthiness than its homogeneous counterparts.61Parametric study and multiobjective optimization of both types of beams.
Quasi-static axial compression of thin-walled tubes with different cross-sectional shapes
Recently more attention has been paid to the energy absorption capability of novel structures in the retrofit of impact or blast protection structure. As the most versatile components, thin-walled metal tubes with different cross-sections are used and specifically explored by many researchers. One method for improving crashworthiness performance under quasi-static axial crushing is to vary the cross-sectional shape with only convex polygons. As an alternative, it is also necessary to develop tubes with concave polygon sections. In this paper, four types of geometries are studied experimentally. They are hexagon, octagon, 12-sided and 16-sided star, respectively. Experimental data are then compared with those predicted from FE simulations using ABAQUS. It is shown that the experimental and the corresponding numerical results are in agreement with each other. The increase in the number of inward corners demonstrates a promising improvement in energy absorption, but to a certain extent. It is found that the 12-sided star shape has the best energy absorption capability when D/t ratio is less than 50, where D is notional diameter and t is the thickness. The 16-sided star shape performed poorly compared to the others studied.
Dynamic axial crush analysis and design optimization of a square multi-cell thin-walled tube with lateral variable thickness
In this paper, we proposed a strategy to improve the energy absorption efficiency of a square multi-cell tube by designing the lateral wall thickness distribution. We uniformly arranged the walls so that we could vary the thickness of the walls while forming a square multi-cell tube. Explicit formulations for predicting the mean crushing force of the multi-cell tube under axial compression were derived based upon the Super Folding Element method. The energy absorption capacities of a variety of typical square multi-cell tubes with different lateral thickness distribution were obtained by theoretical and numerical analysis. The predicting results of the formulations have good agreement with the numerical simulation performed by explicit non-linear finite element method. The theoretical and numerical results showed that the energy absorption capacities could be improved by modifying the lateral thicknesses of the multi-cell tube. The optimization based on a surrogate model and the explicit prediction formulations was carried out to find the optimal lateral thickness distribution of 3鈥椻3 square multi-cell tube. We found that the tube has better energy absorption properties when the material is concentrated in the center of the cross-section. Based on the optimization results, a non-convex multi-corner multi-cell square tube with lateral variable thickness was proposed that resulted in a 48.3% improvement in energy absorption capacity compared with traditional uniform thickness multi-cell tube.
Experimental and numerical investigation on bending collapse of embedded multi-cell tubes
Energy absorption of axially compressed thin-walled square tubes with patterns
The paper suggests the introduction of patterns to the surface of conventional thin-walled square tubes to improve the energy absorption capacity under axial compressive loads. A quasi-static axial crushing analysis has been conducted numerically by the nonlinear explicit finite element code LS-DYNA. Two types of patterns constructed using the basic pyramid elements were introduced. Type A pattern was aimed at triggering the extensional mode for relatively thin square tubes whereas type B pattern was intended to develop new collapse mode capable of absorbing more energy during collapse. A total of 30 tubes with a length of 12002mm, thickness 1.202mm and widths of 40 or 6002mm were simulated. Numerical results showed that all tubes with type A patterns developed the extensional collapse mode instead of the symmetric collapse mode and absorbed about 15–32.5% more energy than conventional thin-walled square tubes with a mass increase less than 5%. Meanwhile, a new collapse mode named octagonal collapse mode was observed for tubes with type B pattern and the energy absorption of tubes developing this mode increased by 54–93% compared with the conventional tube. The influence of various configurations of the patterns on the deformation and energy absorption of the tubes was also discussed. The paper opens up a new avenue in design of high energy absorption components.
The effect of different shapes of holes on the crushing characteristics of aluminum square windowed tubes under dynamic axial loading
Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models
Despite the rapid growth of computing power and continuing advancements in numerical techniques, significant complexity exists when applying traditional sensitivity based optimization to such highly nonlinear problems as crashworthiness design. As a major alternative, surrogate modeling techniques have proven considerably effective. However the challenge remains how to determine the most suitable surrogate scheme for modeling nonlinear responses and conducting optimization. This paper presents a comparative study on the different surrogate models, such as polynomial response surface (PRS), Kriging (KRG), support vector regression (SVR) and radial basis function (RBF), which have been widely used for a variety of engineering problems, thereby gaining insights into their relative performance and features in computational modeling and design. In this study, a foam-filled tapered thin-walled structure is exemplified. Both the gradient and non-gradient algorithms, specifically sequential quadratic programming (SQP) and particle swarm optimization (PSO), are used for these abovementioned four surrogate models, respectively. The design results demonstrate that simultaneous use of different surrogate models can be essential for both gradient and non-gradient optimization algorithms because they may generate different outcomes in the crashworthiness design.
Axial compression of foam-filled thin-walled circular tubes
The effect of low density polyurethane foam on the axial crushing of thin-walled ( D/ t>600) circular metal tubes is studied under quasi-static and dynamic loading conditions. The mode of deformation of the tube is found to change from irregular diamond crumpling to axisymmetric bellows folding due to the filler. Assuming the axisymmetric mode of crushing and using the model of foam recently developed ( M.F. Ashby, Metals Trans. 14A, 1755 1769, 1983), the behaviour is analysed. Theoretical predictions agree well with experiments. Numerical results show that there is an optimum foam density which produces a maximum specific energy absorption of the filled cylinders.
Crashworthiness analysis and multi-objective design optimization of a novel lotus root filled tube (LFT)
Theoretical, numerical, and experimental study on laterally variable thickness (LVT): Multi-cell tubes for crashworthiness
61Present a LFGT multi-cell tube.61Establish finite element modeling of LFGT multi-cell tube and conduct experimental validation.61Explore the influence of the thickness gradient on the crashworthiness of the LFGT tubes.61Establish the theoretical model to predict the mean crushing force of the LFGT multi-cell tubes.
Energy absorption mechanics for variable thickness thin-walled structures
This paper introduces axial functionally graded thickness (AFGT) and lateral functionally graded thickness (LFGT) to thin-walled square structures separately, and then investigates their crashworthiness theoretically, numerically, experimentally under axial crushing load. The quasi-static axial crush experiments and the corresponding finite element models are first conducted to analysis the deformation mode and crushing force for uniform thickness (UT), AFGT and LFGT square tube under the same mass. Then, theoretical models predicting the mean crushing forces of AFGT and LFGT square tubes are established. The results show that both theoretical solutions and numerical results for FGT tubes agree well with the experimental results. Energy absorption characteristics between FGT and UT square tubes with same mass are compared based on the validated numerical models, which shows that AFGT square tube can effectively reduce the initial peak force compared to UT square tube while LFGT square tube remarkably surpasses the UT square tube in specific energy absorption ( SEA ) under axial crushing. Furthermore, parametric studies are performed to investigate the effects of gradient thickness variation on the energy absorption characteristics of AFGT and LFGT square tubes. The results again demonstrate that both AFGT and LFGT square tubes can improve the crashworthiness of thin-walled square tubes.
Crashing analysis and multiobjective optimization for thin-walled structures with functionally graded thickness
61Propose a novel functionally graded thickness thin-walled structure for crashworthiness.61Compare the crashworthiness of functionally graded thickness thin-walled structure with uniform thickness thin-walled structure.61Perform multiobjective optimization design for functionally graded thickness thin-walled structure.
Accurate analysis and thickness optimization of tailor rolled blanks based on isogeometric analysis
Combined isogeometric analysis (IGA) and shape optimization, this paper provides a method that can accurately analyze Tailor Rolled Blanks (TRB) and optimize its thickness profile continuously. While
Cost and mass optimization for crashworthiness design of shell-based structure using hybrid cellular automata
//Abstract The hybrid cellular automaton (HCA) method has been successfully applied to nonlinear transient topology sizing optimization for crashworthiness design. This method utilizes the cellular automata (CA) computing paradigm and nonlinear transient finite element analyses (FEA). In earlier efforts, the HCA algorithm has been used to develop an effcient methodology for synthesizing sheet metal structures with optimal material thickness distribution under a dynamic loading event using a thickness based topology sizing optimization. In thickness based topology optimization, the objective is to redistribute element thickness to meet the desired performance constraints. The objective in crashworthiness design is to generate energy absorbing structures which can be obtained by uniformly distributing internal energy density (IED). In this paper, the HCA algorithm is utilized to do simultaneous thickness and cost optimization for structures suitable to be manufactured by the tailor welded blank (TWB) technology for significant mass savings. The sheet metal structure can have different material parts, and the optimum distribution of the material and thickness is obtained to meet the desired performance using nonlinear transient analysis. This methodology is used to tackle complicated problems that involve dynamic events, such as impacts and collisions. The existing commercial thickness optimization tools utilize models under static loading conditions because of the complexities associated with dynamic/impact loading and they are not suitable for design with multiple material and thickness distribution simultaneously. The HCA based thickness optimization algorithm employs nonlinear transient analysis (via LS-Dyna) to capture material and geometric nonlinearities that occur during a dynamic crash event. Therefore by applying this method to impact problems, the resulting structure will account for all phenomena involved. The effectiveness of the algorithm is demonstrated using a at plate and C-section rail example problem subjected to single or multiple dynamic impact loading. The structures synthesized by the HCA algorithm are able to meet the manufacturing as well as performance constraints. 2009 by the American Institute of Aeronautics and Astronautics, Inc.
A review on tailored blanks--Production, applications and evaluation
Tailored Blanks is the collective for semi-finished sheet products which are characterised by a local variation of the sheet thickness, sheet material, coating or material properties. With these adaptions the tailored blanks are optimised for a subsequent forming process or the final application. In principle four different approaches can be distinguished to realise tailored blanks: joining materials with different grade, thickness or coating by a welding process (tailor welded blanks), locally reinforcing the blank by adding a second blank (Patchwork blanks), creating a continuous variation of the sheet thickness via a rolling process (tailor rolled blanks) and adapting the material properties by a local heat treatment (tailor heat treated blanks). The major advantage of products made from tailored blanks in comparison to conventional products is a weight reduction. This paper covers the state of the art in scientific research concerning tailored blanks. The review presents the potentials of the technology and chances for further scientific investigations.
Multi-objective topology optimization of a vehicle door using multiple material tailor-welded blank (TWB): technology
A tailor welded blanks design of automotive front rails by esl optimization for crash safety and lightweighting
Fatigue behavior of tailor (laser)-welded blanks for automotive applications
The drive towards weight reduction in the automotive industry has led to the use of tailor-welded blanks (TWBs) for structural applications. This work is aimed at evaluating the fatigue behavior of the TWBs having different thickness combinations and compositions with and without zinc coating. The results showed that TWBs made from zinc-coated/galvanized steels exhibited a lower fatigue limit as compared with the TWB combination from uncoated bare metals. This was attributed to the intergranular cracking in the galvanized TWBs caused by the presence of zinc penetrating beneath the sheet surface. The fracture surface of the uncoated TWB was basically characterized by the fatigue striations.
Analysis of clamping mechanism for tailor welded blank forming
Manufacturing of sheet metal parts from tailor rolled blanks
A review on the rolling technology of shape flat products
This paper offers a review of rolling technology of shape flat products. The demands for the shape flat products are increasing quickly in the market of structural material. Some of them are so new th
Crashworthiness design using a hybrid cellular automaton algorithm
//
Topology optimization using a hybrid cellular automaton method with local control rules
Topology optimization for crashworthiness of thin-walled structures under axial impact using hybrid cellular automata
Although topology optimization is well established in most engineering fields, it is still in its infancy concerning highly non-linear structural applications like vehicular crashworthiness. One of the approaches recently proposed and based on Hybrid Cellular Automata is modified here such that it can be applied for the first time to thin-walled structures. Classical methods based on voxel techniques, i.e., on solid three-dimensional volume elements, cannot derive structures made from thin metal sheets where the main energy absorption mode is related to plastic buckling, folding and failure. Because the main components of car structures are made from such thin-walled beams and panels, a special approach using SFE CONCEPT was developed, which is presented in this paper.
A hybrid cellular automaton-bi-directional evolutionary optimization algorithm for topological optimization of crashworthiness
Crashworthiness optimization of automotive parts with tailor rolled blank
Tailor rolled blank (TRB) as an advanced manufacturing process developed recently has broad application prospects in automotive and aerospace industries for its significant advantages in better load-carrying ability and lighter mass. TRB is a typical custom product, whose performance is closely related to its thickness variation, thus how to obtain the optimal thickness variation of a TRB part becomes a challenging task, especially for crashworthiness design. To address this issue, an optimization method based on the variation of wall thickness is presented to maximize the energy absorption capacity of TRB parts. Firstly, finite element (FE) models of two typical automotive parts, TRB top-hat column and TRB bumper beam, are established and validated through crushing experiments. Then a heuristic optimization method is proposed based on the general assumption that more mass enables to absorb more energy. The elemental energy density is used to optimize structural thickness distribution of geometrical and material nonlinear structures. Numerical results demonstrate the capability and effectiveness of the proposed optimization method for achieving the best thickness layout of automotive TRB parts for crashworthiness.
Topology optimization for crashworthiness of thin-walled structures under axial crash considering nonlinear plastic buckling and locations of plastic hinges
基于元胞自动机的变厚度薄壁梁侧向耐撞性优化设计方法
薄壁结构是汽车等运载工具的重要防护装置,除了其轴向防撞能力外,侧向耐撞性能分析与提升方式也非常重要。研究基于薄壁结构厚度合理分布的侧向耐撞性能提升方式和建立基于元胞自动机的变厚度薄壁梁侧向耐撞性优化方法。以汽车B柱受力环境和性能要求为设计需求,首先利用所建立的方法给出了连续变厚度的薄壁梁厚度分布设计,其性能较常规的等厚度薄壁梁最大侵入位移大幅下降(下降82%),验证了变厚度设计的有效性;然后,考虑单向变厚度便于柔性轧制工艺制成TRB,给出了轴向连续变厚度薄壁梁的厚度分布设计,该设计较等厚度梁最大侵入位移下降73%;与连续变厚度梁相比,在侵入位移降低量略小的情况下,实现了可制造性。设计实例表明本文提出的连续变厚度设计能够有效提高侧向耐撞性能,所建立的方法能够获得合理的厚度分布设计,是有效的耐撞性优化设计方法。
A hybrid cellular automata based method of variable thickness thin-walled beam for crashworthiness optimization under lateral impact
薄壁结构是汽车等运载工具的重要防护装置,除了其轴向防撞能力外,侧向耐撞性能分析与提升方式也非常重要。研究基于薄壁结构厚度合理分布的侧向耐撞性能提升方式和建立基于元胞自动机的变厚度薄壁梁侧向耐撞性优化方法。以汽车B柱受力环境和性能要求为设计需求,首先利用所建立的方法给出了连续变厚度的薄壁梁厚度分布设计,其性能较常规的等厚度薄壁梁最大侵入位移大幅下降(下降82%),验证了变厚度设计的有效性;然后,考虑单向变厚度便于柔性轧制工艺制成TRB,给出了轴向连续变厚度薄壁梁的厚度分布设计,该设计较等厚度梁最大侵入位移下降73%;与连续变厚度梁相比,在侵入位移降低量略小的情况下,实现了可制造性。设计实例表明本文提出的连续变厚度设计能够有效提高侧向耐撞性能,所建立的方法能够获得合理的厚度分布设计,是有效的耐撞性优化设计方法。
Bending characteristics of top-hat structures through tailor rolled blank (TRB) process
Tailor rolled blank top-hat (TRBTH) structure, as a relatively new thin-walled configuration, was proposed in this study to better balance the crashworthiness and lightweight requirements, which was featured in a thicker wall thickness in the critical load-bearing areas and a thinner wall thickness in the other regions. To capture the non-uniform material properties and thickness variation of the TRBTH structure accurately, a more realistic finite element (FE) modeling technique was first developed and validated experimentally. It was found that the corresponding FE simulation results agreed well with the testing results. Second, the bending characteristics of TRBTH and uniform thickness top-hat (UTTH) structure with the equal mass were compared through the typical three-point and four-point bending conditions. It was revealed that the TRBTH had a higher bending resistance, which allowed absorbing more transverse crushing energy. Third, the detailed numerical analyses were performed for the bending deformation to explore the crushing advantages of the TRBTH structure more comprehensively. It was divulged that the TRBTH structures engaged more material to participate in deformation than the UTTH counterpart under the transverse loading. Finally, a parametric study was conducted to investigate the effects of the thickness distribution and length of thick zone on the three-point and four-point bending characteristics; and it was found that these structural parameters could affect the crashworthiness of TRBTH structure significantly in a form of different deformation patterns. For this reason, the bending characteristics can be further improved by optimizing the TRB parameters, making it more suitable for being an effective energy absorber.