引 言
微细颗粒的分离技术现已广泛应用于生命科学、环境监测、食品分析等领域[1-3],尤其是使用微流控技术来分离微颗粒,常见的分离方法有流体动力分离、介电泳分离、声波分离等[4-6],其中介电泳分离技术是一种相对温和的方法,因其具有可以通过电场轻松操控微粒、没有生物标记、分离效率高等 优点而广受关注[7-9].介电泳分离是指利用非均匀电场极化并操纵微流道中的微粒,使其按特定方向运动,从而达到分离的目地[10-11].能够被介电泳分离的微粒往往具有一定柔性,比如细胞[12]、DNA等微米和亚微米尺度下呈现电中性的微小流体或颗粒,因其在运动过程中会产生形变,并同时受到流场和电场的综合作用,所以运动过程非常复杂.采用单一的计算方法对柔性微粒介电泳分离过程进行模拟存在很大的挑战,本文尝试结合有限单元法和格子玻尔兹曼方法处理这一问题,以期深入了解柔性微粒的分离机制和变形特征.
自1951年由Phol发现悬浮液中电中性微粒在非均匀电场中会产生移动的介电泳现象以来,介电泳技术和场流技术结合的介电泳——场流分离技术(dielectrophoresis field flow fraction,DEP-FFF)在细胞等微粒的分离技术方面得到了广泛应用并获得诸多进展[13-16].除用实验来探索微流控分离机制和设计微流控芯片外,数值模拟方法也是研究微流控技术的一个重要手段.下文将简单介绍介电泳分离芯片的仿真研究现状,为了阐述充分,一些其他相关微流控芯片的仿真方法也将适当说明.目前关于微流控芯片的仿真研究主要分为两类手段,一类是宏观的数值计算,如用有限单元法和有限差分法等来模拟计算.Ai等[17]利用任意拉格朗日——欧拉法分析了介电泳力对不同直径 的聚苯乙烯微粒运动轨迹的影响.陈琰等[18]使用有限元法对单个微粒在受到介电泳力作用下的运动轨迹进行了模拟. 曾议等[19]利用有限差分法模拟了微流控芯片中的微粒浓度变化过程. 王伟等[20]采用有限单元法模拟了微藻微粒和聚苯乙烯微粒进行分离过程. 有限单元等宏观仿真方法优点在于算法成熟,求解步骤系统化、标准化,能够应用于各种场合,然而介电泳分离过程属 于典型的多相流动,系统中涉及微米级的颗粒,采用宏观仿真方法存在一定难度,而且微粒的自然形变很难求解.
另一类介电泳分离的数值计算方向是微观仿真,目前微尺度颗粒模拟常用的仿真方法有分子动力学(molecular dynamics, MD)[21-23]、格子玻尔兹曼(lattice Boltzmann method, LBM)[24-25]和耗散微粒动力学(dissipative particle dynamics, DPD)[26-27]等.如陈君等[28]采用格子玻尔兹曼方法模拟了微颗粒的布朗运动,Fu等[29]模拟了微液滴内部的反应混合行为,皆模拟出与理论基本一致的仿真结果.但是,介电泳分离芯片包含数十微米宽的流道,而且其长度可达数百毫米,微粒同时受到流场和电场的综合作用,微观仿真方法无论在时间和空间尺度上都无法完全覆盖. 考虑到以上问题,多尺度模拟是解决柔性微粒介电泳分离仿真的有效方案.
本文将对介电泳分离过程进行有限单元——格子玻尔兹曼的多尺度耦合计算.格子玻尔兹曼方法是一种基于介观尺度的动力学计算方法,相比于其他传统的计算方法,具备流体相互作用描述简单、复杂边界易于设置、易于并行计算等优势.另外,通过有限单元法求解微粒在电场作用下产生的介电泳力,可大大提高计算效率.最终实现介电泳分离过程中多相流动、微粒轨迹追踪和变形的多尺度耦合求解.
1 介电泳分离原理
图1
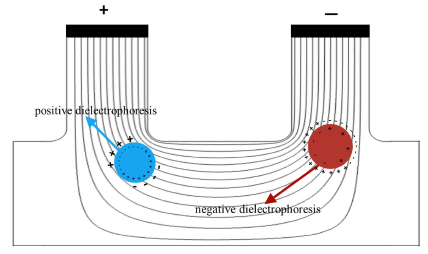
介电泳分离原理其实质是研究不同微粒在微流道内的运动轨迹并对其加以操纵. 微粒在流道内同时受到流场和电场的综合作用,流场主要是给微粒提供一个横向迁移的动力,而电场主要是给微粒提供一个偏转的力,最后微粒在流场和电场综合作用下实现分离的目的. 因此微粒在介电泳分离过程中主要求解流体、电场和微粒运动方程. 流体的流动用Navier-Stokes(N-S)方程描述
式中,${\pmb u}$为流体速度矢量,$\rho$为密度,${\pmb P}$为压力,$ \mu $为动力黏度. 流体所受外加的电场力,可用体积电荷密度$\rho _{\rm e}$和电场强度${\pmb E}$进行计算. 其体积电荷密度计算公式为
式中,$ {z}_{ i}$为i种微粒的离子价,$e$为电子电量(1.6× 10$^{-19 }$ C),$ {n}_{ i}$为单位体积内离子数. 芯片中电场强度的分布是根据拉普拉斯方程求解
式中,$\varphi$为外加电势,电场强度可用电势梯度计算${\pmb E} =-\nabla \varphi$.
介电泳分离过程中,微粒是在流场和电场的综合作用下运动的,主要受到介电泳力、拖曳力、浮力的作用. 微粒的运动轨迹则通过牛顿方程求解
式中,$m_i$为微粒的质量,${\pmb v}_i$为微粒的运动速度,${\pmb F}_{\rm B}$为布朗力,$ {\pmb F}_{\rm D}$为拖曳力,${\pmb F}_{\rm DEP}$为微粒所受到的介电泳力. 布朗力的计算公式
式中,$\zeta$为高斯分布随机变量(标准正态分布),$k_{\rm B}$为玻尔兹曼常数,${T}$为绝对温度,$r_{\rm m}$为微粒外半径. 拖拽力的计算公式
式中,$\tau _{\rm m}$为微粒所受到的切应力.
根据等效偶极矩理论,微粒在介质溶液中受到的平均介电泳力为
式中,$\varepsilon$为介电常数,$\varepsilon _0$ 为溶液的相对介电常数,${real}$为Clausius-Mossotti因子,$\varepsilon _{\rm f}^\ast$为介质溶液的复相对介电常数,$\varepsilon _{\rm p}^\ast$为微粒的复相对介电常数,对于交变电场,复介电常数$\varepsilon ^\ast$为
式中,$\sigma$为电导率,$\omega$为电场频率.在实际的分离过程中,微粒的空间位置是在不断变化的,因此介电泳力也是随时间和空间变化的,故求解介电泳力则需耦合求解流场、电场和微粒运动的方程.
如果将微粒看作是刚性微粒,则联立 式(1)、式(3)、式(4),采用有限单元等宏观方法,结合离散 模型(dispersed phased model, DPM),就可以对流场和微粒运动进行计算.然而实际分离过程中的细胞等生物微粒,往往具有较强的柔性,不能当作刚性微粒处理.格子玻尔兹曼等微观方法,易于描述微粒的自然变形,但微粒同时受流场和变化电场的作用,完全采用微观方法对电场及电泳力进行求解,计算效率非常低,且电势的控制方程为椭圆方程,而格子玻尔兹曼法适于求解双曲型方程,因此用格子玻尔兹曼法求解电势方程可能会存在难以收敛等问题[31].本文将采用有限单元——格子玻尔兹曼法的耦合方法来模拟介电泳技术下的微粒分离过程,并利用分步耦合的方式进行计算.先通过有限单元法求解微粒在电场作用下产生的介电泳力,然后将其匹配到采用格子玻尔兹曼法计算的流场中,进行流体和微粒的多相流动、轨迹追踪和微粒变形的求解.
2 介电泳分离的多尺度仿真模型
2.1 介电泳分离模型
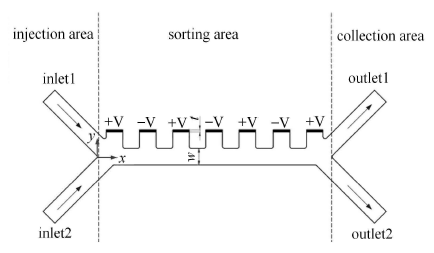
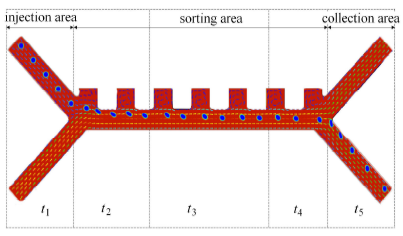
不失一般性,本文针对一款经典的介电泳分离芯片进行计算,该款芯片分离效率可达98%,具体参见文献[15].芯片的主要结构如图2,该芯片主要用于细胞的分离,芯片大概分为三个功能区:左边两条倾斜流道区为"注入区域",中间结合电极的流道为"分离区域",右边两条倾斜流道区为"收集区域". 在inlet1,inlet2处分别注入含有微粒的悬浮液和不含有微粒的悬浮液(缓冲液),微粒流经"分离区域"时,在介电泳力和流体流动的共同作用下把不同大小的微粒分离开来,最后不同大小的微粒分别从outlet1和outlet2中流出实现分离的目的.主要工作参数为:整体尺寸约825μM×320μm,流道宽度w=40μm,分离的微粒直径为12μm. Inlet1注入流速为0.135m/s,inlet2流速为0.854m/s,流体具体参数如表1.电极按图2所示,电压U=70V,电源频率为100kHz,电极厚度为d =0.2μm.
表1 介电泳分离芯片流体参数植
Table1
| Parameter | Unit | Parameter value |
|---|---|---|
| inlet1 | m/s | 0.135 |
| inlet2 | m/s | 0.854 |
| outlet1 | Pa | 0 |
| outlet2 | Pa | 0 |
| pc | kg/m3 | 1.0x103 |
| v | Pa-s | 1.0x103 |
图2
表2 微粒模型参数值
Table 2
| Parameter | Unit | Parameter value |
|---|---|---|
| dc | pm | 12 |
| pc | kg/m3 | 1050 |
| v | Pa/s | 5.0x10-3 |
| a | N/m | 9.57x10-4 |
| S/m | 0.31 | |
| £p | 59 | |
| S/m | 1.0x10-6 | |
| £m | 4.44 | |
| r | nm | 9 |
图3
图3
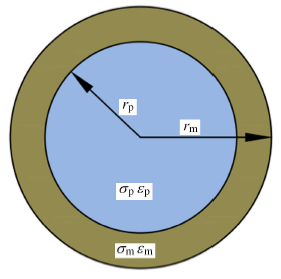
微粒模型图微粒介电模型$r = r_{\rm m}-r_{\rm p}$
Fig.3
Dielectrophoretic model of particle$r = r_{\rm m}-r_{\rm p}$
在第一步的有限元计算中,不考虑微粒的变形,将其简化为刚性球形颗粒. 采用DPM模型进行流场和电场的耦合计算,获得电场分布结果,并利用 式(8)计算出微粒的介电泳力,随后将其耦合到格子玻尔兹曼法型的微粒相上,从而模拟出芯片内微粒的变形和分离轨迹.
2.2 格子玻尔兹曼计算方法
式中,$f_i$为粒子的概率分布函数,${\pmb e}_i$为粒子的速度集矢量,${\pmb\Omega }_i$为碰撞算子,$b$为格点数. 本文采用的二维的D2Q9格子模型[43]($b=9$),在格子模型上,式(9)可按下式进行离散计算
式中,${\pmb u}({\pmb x},t)$和${\pmb u}^{\rm eq}({\pmb x},t)$表示动量矢量,${\pmb u} = ( u_{0}$,$u_{1}$,$u_2, \cdots, u_{ n} )^{\rm T}$,松弛矩阵${\pmb S }$是一个对角矩阵. 速度和动量空间的映射可以通过线性变换实现
式中,${\pmb M}$为装换矩阵. 其松弛时间和运动黏度关系如下[46]
式中,$\upsilon$为运动黏度,$c_{\rm s}$为声速,$\tau$ 为松弛时间.因此多松弛格式来描述微粒的碰撞过程时,其运输方程为
式中,${\pmb\Omega}$表示碰撞矩阵,$f_{\rm i}^{\rm eq}$表示经过碰撞后的平衡态分布函数,由于在速度空间中碰撞步骤难以实现,但是碰撞过程在动量空间中较为容易实现. 因此上述方程可转变为
平衡态分布函数$f_{\rm i}^{\rm eq}$采用麦克斯韦——波尔兹曼(Maxwell-Boltzmann)分布来近似表示,即
式中,$\omega _{\rm i}$为保持各向同性而建立的加权常数,$\delta$为Kronecker脉冲采样函数,$\alpha,\beta$ 为方程中出现的向量的不同空间分量. 经过上述处理,宏观流场中的流体参数,包括密度$\rho$和速度${\pmb u}$等,可以利用分布函数的各阶统计矩进行计算
3 仿真结果及分析
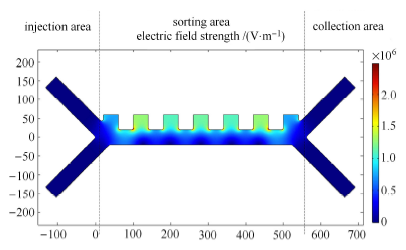
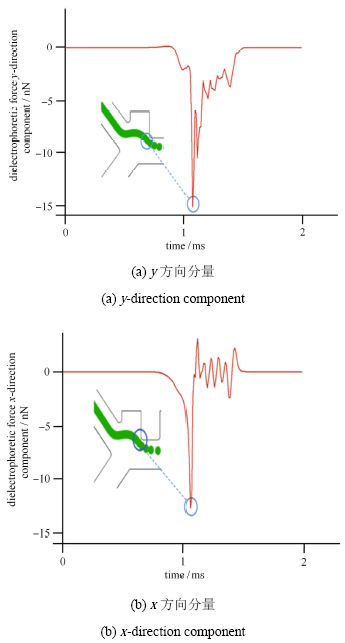
3.1 电场及微粒介电泳力分析
图4
图5
3.2 微粒轨迹分析
利用有限元计算得到的电场分布和介电泳力,施加于格子玻尔兹曼模型的微粒相上,进行微粒轨迹和变形的计算. 同样设置inlet1, inlet2为速度入口,outlet1, oulet2为压力出口,壁面处利用bounce-back方法设置非滑移边界.根据平均流速,为保证计算精确度,每隔1.0×10$^{-5}$ s,根据粒子所处的空间位置,更新一次粒子所受的介电泳力,求解出微粒在流场和电场作用下的形变和运动情况.
图6
图6
无介电泳力作用下微粒的运动轨迹
Fig.6
The trajectories of particles under without dielectrophoresis force
其次,对有介电泳力作用时微粒的运动轨迹进行分析,如图7所示,同样,该轨迹图也是由多个时刻下微粒轨迹图组成. 把整个轨迹图分为5个时段,从图中可以看到,微粒在"分离区域"运动中的$t_2$时段内,微粒在流道上部流层运动,$t_3$时段内,微粒在流道中部偏上流层运动,$t_4$时段内,微粒在流道中部偏下流层.故与无介电泳力作用时不同的是微粒进入"分离区域"后,在介电泳力的作用下,微粒逐步从流道上部流层向流道中下部流层运动,最终随中下部流层流动至收集出口,实现微粒分离.
图7
图7
介电泳力作用下微粒的运动轨迹
Fig.7
The trajectories of particles under dielectrophoresis force
3.3 微粒的形变分析
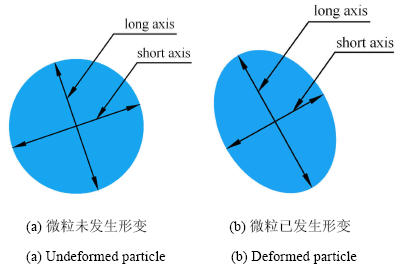
由于微粒形变会影响微粒分离效果和分离精确度,所以我们对微粒在整个芯片内部流道中的运动情况进行分析,发现微粒在运动的过程当中会发生形变. 为直观的分析微粒形变,定义一个能够衡量微粒形变量大小的参数,本文称为形变率,$\eta =$ 微粒长径/微粒短径,如图8所示.$\eta$值越大,则说明微粒形变量越大,反之则说明微粒形变量越小,我们规定$\eta = 1$时微粒未发生形变,此时微粒为圆形.
图8
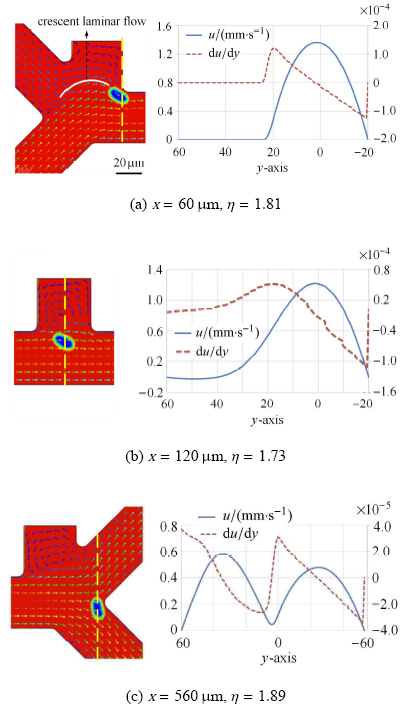
对结果进行分析发现,微粒处在不同的区域的形变量不一样,微粒在芯片各区域的形变率如图9所示,微粒形变量较大的位置发生在芯片左边两条流道交汇处、"分离区域"流道上部流层和右边流道分叉处.
图9
在该3个区域中分别选取一个位置说明微粒的形变情况,其具体形变情况如图10(a)~图10(c)所示,通过测量计算发现这3个位 置的微粒形变率$\eta$分别达到了:1.81, 1.73,1.89,而其他部分的微粒形变全都小于1.6,这表明微粒在这3个区域内的形变量是最大的.对于芯片左边两流道交汇处的微粒形变而言,由于微粒悬浮液入口流道处的速度小于缓冲液入口流道,当两股流体在"Y"形流道处汇流后,流速大的缓冲液挤压流速小的微粒悬浮液后,使两股流体的混合液在汇流处呈现出"月牙"形流层,见图10(a).当微粒顺着月牙形流层运动时,微粒在两股不同流速流体的剪切、挤压下运动至芯片边界附近,边界对流体流动产生阻碍作用进一步加剧了微粒的形变,最终微粒被拉长为椭圆形状. 在边界附近,由于流体黏滞作用,流速较低,但是剪切变形速率u/y较 高[47-49]因此微粒受到的剪切力较大,使其产生较大变形,不同位置的流速分布和剪切变形速率,如图10所示.
图10
图10
微粒典型形变位置和剪切变形速率
Fig.10
Typical deformation position of the particle and the shear deformation rate
4 结 论
介电泳分离过程牵涉到多种物理场、多种物相以及微粒变形等复杂因素,采用单一的计算方法对其进行模拟存在很大的挑战. 本文结合有限单元和格子玻尔兹曼方法,对柔性微粒在介电泳分离芯片中的运动过程进行了多尺度计算,既满足了计算的效率要求,又能够对微粒的轨迹和变形情况进行精确描述.
利用此方法,通过分步耦合的方式模拟了一款经典介电泳分离芯片中的多相流动. 首先通过有限单元法计算了微粒在电场作用下产生的介电泳力,发现介电泳力受电场变化率和流道几何形状的影响. 随后将介电泳力匹配到格子玻尔兹曼模型中,进行流体和微粒运动的计算. 对微粒运动轨迹与介电泳力之间的关系进行了分析,探讨了微粒变形的情况及其影响因素,发现微粒的变形主要与流体剪切作用有关. 本文提出的多尺度耦合方法,有望解决微流体模拟中一些关键问题,为微流控芯片的设计提供参考.
参考文献
基于微流控芯片的核酸检测技术
核酸检测,作为一种分子诊断技术,包括核酸提取、扩增和检测,对微生物分析、医学诊断、及时就医等起着根本性的作用。目前核酸检测存在工作量大、成本高、而且耗时长等问题,显著影响了其在诊断中的应用。微流控芯片技术以及侧向流层析试纸条,具有制作成本低、设备小型化、分析速度快、灵敏度高等特点,且结果可传送给最终用户,在医疗诊断中具有巨大的发展潜力。鉴于前人的相关研究成果,本文首先介绍了微流控技术在核酸检测中的意义,其次介绍了以微流控芯片为平台的核酸提取技术、扩增技术,以及核酸检测技术,在文章最后展望了将核酸的提取、扩增、检测技术集成到一个微装置中的可行性。
Nucleic acid detection techniques based on microfluidic chip
核酸检测,作为一种分子诊断技术,包括核酸提取、扩增和检测,对微生物分析、医学诊断、及时就医等起着根本性的作用。目前核酸检测存在工作量大、成本高、而且耗时长等问题,显著影响了其在诊断中的应用。微流控芯片技术以及侧向流层析试纸条,具有制作成本低、设备小型化、分析速度快、灵敏度高等特点,且结果可传送给最终用户,在医疗诊断中具有巨大的发展潜力。鉴于前人的相关研究成果,本文首先介绍了微流控技术在核酸检测中的意义,其次介绍了以微流控芯片为平台的核酸提取技术、扩增技术,以及核酸检测技术,在文章最后展望了将核酸的提取、扩增、检测技术集成到一个微装置中的可行性。
微流控芯片技术在生命科学领域的研究进展
经过十几年的发展,微流控芯片技术已经成为21世纪最为重要的前沿技术之一.现已广泛应用于生命科学,环境监测、食品分析等领域,与传统检测方法相比,其具有高灵敏度、高通量、样品和试剂耗量小等优点.本文将微流控芯片技术在生命科学领域的研究进展从基因检测、蛋白质组学研究和细胞分析三方面做一综述.
Research progress of microfluidic chip technology in the field of life science
经过十几年的发展,微流控芯片技术已经成为21世纪最为重要的前沿技术之一.现已广泛应用于生命科学,环境监测、食品分析等领域,与传统检测方法相比,其具有高灵敏度、高通量、样品和试剂耗量小等优点.本文将微流控芯片技术在生命科学领域的研究进展从基因检测、蛋白质组学研究和细胞分析三方面做一综述.
微流控技术对细胞微环境的模拟及应用研究
<p>细胞微环境是一个多因素组成的、时空可变的复杂集合,对细胞的行为和功能发挥起着决定性作用。但传统的细胞生物学研究方法很难在体外为细胞提供这样一个复杂的、微尺度的生长环境,致使许多体外研究结果与在体情况相差甚远。近年来,微流控技术与细胞培养技术的结合为细胞微环境的模拟和控制提供了可能。文章通过提炼微环境的重要参数及其特征,介绍微流控技术是如何满足这些参数的需求,探讨了微流控技术在体外模拟细胞微环境的可行性,并总结了近年来该技术在微环境体外模拟研究中取得的成果,对微流控技术在细胞微环境构建中的发展方向和应用前景进行了展望。</p>
Simulation and application of microfluidic technology to cell microenvironment
<p>细胞微环境是一个多因素组成的、时空可变的复杂集合,对细胞的行为和功能发挥起着决定性作用。但传统的细胞生物学研究方法很难在体外为细胞提供这样一个复杂的、微尺度的生长环境,致使许多体外研究结果与在体情况相差甚远。近年来,微流控技术与细胞培养技术的结合为细胞微环境的模拟和控制提供了可能。文章通过提炼微环境的重要参数及其特征,介绍微流控技术是如何满足这些参数的需求,探讨了微流控技术在体外模拟细胞微环境的可行性,并总结了近年来该技术在微环境体外模拟研究中取得的成果,对微流控技术在细胞微环境构建中的发展方向和应用前景进行了展望。</p>
Density-gradient-free microfluidic centrifugation for analytical and preparative separation of nanoparticles
Sedimentation and centrifugation techniques are widely applied for the separation of biomolecules and colloids but require the presence of controlled density gradients for stable operation. Here we present an approach for separating nanoparticles in free solution without gradients. We use microfluidics to generate a convective flow perpendicular to the sedimentation direction. We show that the hydrodynamic Rayleigh aylor-like instability, which, in traditional methods, requires the presence of a density gradient, can be suppressed by the Poiseuille flow in the microchannel. We illustrate the power of this approach by demonstrating the separation of mixtures of particles on the nanometer scale, orders of magnitude smaller than the micrometer-sized objects separated by conventional inertial microfluidic approaches. This technique exhibits a series of favorable features including short analysis time, small sample volume, limited dilution of the analyte, limited interactions with surfaces as well as the poss...
基于介电电泳的粒子分离微流控芯片的研究
文中制备了一种用于粒子分离的介电电泳微流控芯片,利用粒子介电性质不同实现粒子批量、高效分离.采用MEMS工艺,由光刻有电极的ITO玻璃基底和PDMS微通道制备而成.在此基础上,测定了当缓冲溶液的电导率为1 μS/cm、交流信号电压为10 V时聚苯乙烯小球和酵母菌的正负介电泳响应,确定了两种微粒的分离条件:酵母菌细胞在1 ~ 50 kHz时表现负介电泳响应,50 kHz~5 MHz时表现正介电泳响应,50 kHz为交叉频率;聚苯乙烯小球在1 kHz~5 MHz始终表现负介电泳响应.选取10 V、5 MHz交流电压信号作为分离条件,对直径均为5μm的聚苯乙烯小球和酵母菌进行了分离,分离效率达到92.4%.
Study on particle separation of microfluidic chip based on dielectrophoresis
文中制备了一种用于粒子分离的介电电泳微流控芯片,利用粒子介电性质不同实现粒子批量、高效分离.采用MEMS工艺,由光刻有电极的ITO玻璃基底和PDMS微通道制备而成.在此基础上,测定了当缓冲溶液的电导率为1 μS/cm、交流信号电压为10 V时聚苯乙烯小球和酵母菌的正负介电泳响应,确定了两种微粒的分离条件:酵母菌细胞在1 ~ 50 kHz时表现负介电泳响应,50 kHz~5 MHz时表现正介电泳响应,50 kHz为交叉频率;聚苯乙烯小球在1 kHz~5 MHz始终表现负介电泳响应.选取10 V、5 MHz交流电压信号作为分离条件,对直径均为5μm的聚苯乙烯小球和酵母菌进行了分离,分离效率达到92.4%.
微流控芯片细胞捕获分离方法概述
: 细胞捕获分离是免疫学、诊断检测、病理研究等学科经常用到的生物学实验方法.近年来,微流控芯片平台的细胞捕获分离方式花样繁多,层出不穷,它具有可快速检测、所需样本量少、节约试剂、成本低廉等优势.本文主要对近年来多种微流控细胞捕获分离的方法,以免疫捕获分离和无标签细胞分离两类对其进行介绍.免疫捕获分离是较为传统的细胞捕获分离方式,它的特异性好、捕获分离后的细胞纯度较高.无标签细胞分离是近几年热门发展的技术手段,它采用物理学与生物学相结合的方式,能较好地保持细胞的完整性和生物活性.细胞捕获分离在微流控平台的应用虽然发展迅速,但其在工业化生产和微型化整合等方面还存在一些问题,只有解决生产问题,细胞捕获分离在微流控平台的应用才真正具有实际价值,可以真正作为一种技术手段用于日常的实验操作和医学检测中.就目前而言,细胞捕获分离在微流控芯片中仍具有很大的发展前景.
Microfluidic chips for cell capturing and separation
: 细胞捕获分离是免疫学、诊断检测、病理研究等学科经常用到的生物学实验方法.近年来,微流控芯片平台的细胞捕获分离方式花样繁多,层出不穷,它具有可快速检测、所需样本量少、节约试剂、成本低廉等优势.本文主要对近年来多种微流控细胞捕获分离的方法,以免疫捕获分离和无标签细胞分离两类对其进行介绍.免疫捕获分离是较为传统的细胞捕获分离方式,它的特异性好、捕获分离后的细胞纯度较高.无标签细胞分离是近几年热门发展的技术手段,它采用物理学与生物学相结合的方式,能较好地保持细胞的完整性和生物活性.细胞捕获分离在微流控平台的应用虽然发展迅速,但其在工业化生产和微型化整合等方面还存在一些问题,只有解决生产问题,细胞捕获分离在微流控平台的应用才真正具有实际价值,可以真正作为一种技术手段用于日常的实验操作和医学检测中.就目前而言,细胞捕获分离在微流控芯片中仍具有很大的发展前景.
Simultaneous on-chip DC dielectrophoretic cell separation and quantitative separation performance characterization
Through integration of a MOSFET-based microfluidic Coulter counter with a dc-dielectrophoretic cell sorter, we demonstrate simultaneous on-chip cell separation and sizing with three different samples including 1) binary mixtures of polystyrene beads, 2) yeast cells of continuous size distribution, and 3) mixtures of 4T1 tumor cells and murine bone marrow cells. For cells with continuous size distribution, it is found that the receiver operator characteristic analysis is an ideal method to characterize the separation performance. The characterization results indicate that dc-DEP separation performance degrades as the sorting throughput (cell sorting rate) increases, which provides insights into the design and operation of size-based microfluidic cell separation.
DC dielectrophoresis separation of marine algae and particles in a microfluidic chip
AbstractThis paper reports a microfluidic method of continuous separation of marine algae and particles by DC dielectrophoresis. The locally non-uniform electric field is generated by an insulating PDMS triangle hurdle fabricated within a PDMS microchannel. Both the particles and algae are subject to negative DEP forces at the hurdle where the gradient of local electric-field strength is the strongest. The DEP force acting on the particle or the algae depends on particles’ or algae’s volume, shape and dielectric properties. Thus the moving particles and algae will be repelled to different streamlines when passing the hurdle. In this way, combined with the electroosmotic flow, continuous separation of algae of two different sizes, and continuous separation of polystyrene particles and algae with similar volume but different shape were achieved. This first demonstration of DC DEP separation of polystyrene particles and algae with similar sizes illustrates the great influence of dielectric properties on particle separation and potentials for sample pretreatment.
基于介电泳原理的三明治式微流控芯片
根据介电泳的工作原理,利用粒子介电性质的不同设计了基于双层微电极结构的芯片模型,实现了介电性质不同的粒子的断续分离。采用COMSOL软件仿真并分析了芯片内部的电场强度和介电泳力的分布;对比二维微流控芯片和三明治式微流控芯片,发现三明治式微流控芯片可以克服电场强度在通道高度方向上的衰减。用三明治式微流控芯片进行粒子的断续分离,与二维微流控芯片进行实验对比,结果显示,在酵母菌细胞与聚苯乙烯小球的断续分离实验中,三明治式微流控芯片的分离效率为95.2%,比二维微流控芯片的分离效果好、分离效率高。
Sandwiched microfluidic chip based on the principle of dielectrophoresis
根据介电泳的工作原理,利用粒子介电性质的不同设计了基于双层微电极结构的芯片模型,实现了介电性质不同的粒子的断续分离。采用COMSOL软件仿真并分析了芯片内部的电场强度和介电泳力的分布;对比二维微流控芯片和三明治式微流控芯片,发现三明治式微流控芯片可以克服电场强度在通道高度方向上的衰减。用三明治式微流控芯片进行粒子的断续分离,与二维微流控芯片进行实验对比,结果显示,在酵母菌细胞与聚苯乙烯小球的断续分离实验中,三明治式微流控芯片的分离效率为95.2%,比二维微流控芯片的分离效果好、分离效率高。
一种力——电协同驱动的细胞微流控培养腔理论模型
细胞培养液在微流控生物反应器中受到外界物理场(如压力梯度或者电场)作用流动而产生流体剪应力,并进一步刺激种子细胞调控其内部基因的表达,从而促进细胞的分化和生长,这个过程在自然生命组织内的微管中亦是如此.考虑到细胞培养微腔隙中液体流动行为很难实验量化测定,理论建模分析是目前可行的研究手段.因此建立了矩形截面的细胞微流控培养腔理论模型,将外部的物理驱动场(压力梯度与电场)与培养腔内液体的流速、切应力和流率联系起来,分别得到了压力梯度驱动(pressure gradient driven,PGD)、电场驱动(electric field driven,EFD)及力–电协同驱动(pressure-electricity synergic driven,P-ESD)三种驱动方式下的液体流动理论模型.结果表明该理论模型与现有的实验结果基本一致,即力–电协同作用下的解答为压力梯度驱动和电场驱动结果的叠加.细胞培养腔内的流体流速、剪应力及流率幅值均正比于外部物理场强幅值,但随着压力梯度驱动载荷频率的增大而减小,随着电场驱动频率的变化不明显.在压力梯度驱动作用下,细胞贴壁处的切应力随着腔高的增大而线性增大,流率则随着腔高的增大而非线性增大,而电场驱动下的结果不受腔高的影响.生理范围内的温度场变化对压力和电场驱动的结果影响不大.另外,在引起细胞响应的流体切应力水平,电场驱动能提供较大的切应力幅值而压力梯度驱动则能提供较大的流率幅值.该理论模型的建立为细胞微流控生物反应器实验系统的设计及参数优化提供理论参考,同时也为力–电刺激细胞生长、分化机理的研究的提供基础.
A theoretical microfluidic flow model for the cell culture chamber under the pressure gradient and electric field driven loads
细胞培养液在微流控生物反应器中受到外界物理场(如压力梯度或者电场)作用流动而产生流体剪应力,并进一步刺激种子细胞调控其内部基因的表达,从而促进细胞的分化和生长,这个过程在自然生命组织内的微管中亦是如此.考虑到细胞培养微腔隙中液体流动行为很难实验量化测定,理论建模分析是目前可行的研究手段.因此建立了矩形截面的细胞微流控培养腔理论模型,将外部的物理驱动场(压力梯度与电场)与培养腔内液体的流速、切应力和流率联系起来,分别得到了压力梯度驱动(pressure gradient driven,PGD)、电场驱动(electric field driven,EFD)及力–电协同驱动(pressure-electricity synergic driven,P-ESD)三种驱动方式下的液体流动理论模型.结果表明该理论模型与现有的实验结果基本一致,即力–电协同作用下的解答为压力梯度驱动和电场驱动结果的叠加.细胞培养腔内的流体流速、剪应力及流率幅值均正比于外部物理场强幅值,但随着压力梯度驱动载荷频率的增大而减小,随着电场驱动频率的变化不明显.在压力梯度驱动作用下,细胞贴壁处的切应力随着腔高的增大而线性增大,流率则随着腔高的增大而非线性增大,而电场驱动下的结果不受腔高的影响.生理范围内的温度场变化对压力和电场驱动的结果影响不大.另外,在引起细胞响应的流体切应力水平,电场驱动能提供较大的切应力幅值而压力梯度驱动则能提供较大的流率幅值.该理论模型的建立为细胞微流控生物反应器实验系统的设计及参数优化提供理论参考,同时也为力–电刺激细胞生长、分化机理的研究的提供基础.
Lattice Boltzmann method: Fundamentals and engineering applications with computer codes
Introducing the Lattice Boltzmann Method in a readable manner, this book provides detailed examples with complete computer codes. It avoids the most complicated mathematics and physics without scarifying the basic fundamentals of the method.Mohamad, A A
Multi-step dielectrophoresis for separation of particles
A new concept for separation of particles based on repetitive dielectrophoretic trapping and release in a flow system is proposed. Calculations using the finite element method have been performed to envision the particle behavior and the separation effectiveness of the proposed method. As a model system, polystyrene beads in deionized water and a micro-flow channel with arrays of interdigited electrodes have been used. Results show that the resolution increases as a direct function of the number of trap-and-release steps, and that a difference in size will have a larger influence on the separation than a difference in other dielectrophoretic properties. About 200 trap-and-release steps would be required to separate particles with a size difference of 0.2%. The enhanced separation power of dielectrophoresis with multiple steps could be of great importance, not only for fractionation of particles with small differences in size, but also for measuring changes in surface conductivity, or for separations based on combinations of difference in size and dielectric properties.
Separation of platelets from other blood cells in continuous-flow by dielectrophoresis field-flow-fractionation
We present a microfluidic device capable of separating platelets from other blood cells in continuous flow using dielectrophoresis field-flow-fractionation. The use of hydrodynamic focusing in combination with the application of a dielectrophoretic force allows the separation of platelets from red blood cells due to their size difference. The theoretical cell trajectory has been calculated by numerical simulations of the electrical field and flow speed, and is in agreement with the experimental results. The proposed device uses the so-called “liquid electrodes” design and can be used with low applied voltages, as low as 10 Vpp. The obtained separation is very efficient, the device being able to achieve a very high purity of platelets of 98.8% with less than 2% cell loss. Its low-voltage operation makes it particularly suitable for point-of-care applications. It could further be used for the separation of other cell types based on their size difference, as well as in combination with other sorting techniques to separate multiple cell populations from each other.
Determination of the surface tension of biological cells using the freezing front technique
The freezing front technique for solid surface tension measurements was used to obtain the surface tensions of glutaraldehyde-fixed human erythrocytes, and fresh human lymphocytes and grnulocytes in aqueous media. The results agree well with the values obtained by other methods and indicate that the freezing front technique is sufficiently sensitive to detect small differences (of the order of 0.1 ergs/cm 2 ) in surface tension. This property, along with a number of applications for which it is uniquely suited makes the freezing front technique an important new approach to the measurement of the surface tensions of biological cells and of small particles in general.
DC electrokinetic particle transport in an L-shaped microchannel
Electrokinetic transport of particles through an L-shaped microchannel under DC electric fields is theoretically and experimentally investigated. The emphasis is placed on the direct current (DC) dielectrophoretic (DEP) effect arising from the interactions between the induced spatially nonuniform electric field around the corner and the dielectric particles. A transient multiphysics model is developed in an arbitrary Lagrangian-Eulerian (ALE) framework, which comprises the Navier-Stokes equations for the fluid flow and the Laplace equation for the electrical potential. The predictions of the DEP-induced particle trajectory shift in the L-shaped microchannel are in quantitative agreement with the obtained experimental results. Numerical studies also show that the DEP effect can alter the angular velocity and even the direction of the particle's rotation. Further parametric studies suggest that the L-shaped microfluidic channel may be utilized to focus and separate particles by size via the induced DEP effect.
微粒受介电泳力作用运动的仿真研究
在外加交变电场作用下,介电液中的粒子将极化产生介电泳力。此外,粒子还将受到重力、布朗运动以及液体的粘滞阻力等作用。粒子运动遵循牛顿运动定律,分别模拟粒子从90、50和10μm高度处释放的运动情况,并以90μm高度处释放为例分析了粒子运动速度的变化。结果表明,粒子运动速度可由初始释放时的静止状态增大至10-3 m/s数量级。随着释放高度的降低,粒子到达电极的运动时间减小,可由90μm释放时的11.2s缩短至10μm释放时的0.15s。
Simulation of particle motion caused by dielectrophoretic force
在外加交变电场作用下,介电液中的粒子将极化产生介电泳力。此外,粒子还将受到重力、布朗运动以及液体的粘滞阻力等作用。粒子运动遵循牛顿运动定律,分别模拟粒子从90、50和10μm高度处释放的运动情况,并以90μm高度处释放为例分析了粒子运动速度的变化。结果表明,粒子运动速度可由初始释放时的静止状态增大至10-3 m/s数量级。随着释放高度的降低,粒子到达电极的运动时间减小,可由90μm释放时的11.2s缩短至10μm释放时的0.15s。
一种微流控系统仿真的新方法
针对复杂的大规模微流控芯片,提出了一种新的通用微流控系统行为模拟方法,计算芯片中由压力驱动的,线性和非线性的,静态和动态的溶液、溶质传输。对芯片中溶液/溶质传输的对流-扩散方程进行了分析,定义新的节点变量,抽象出系统集总模型,通过空间离散化处理,考虑了管壁柔性对模型参数的影响,建立毛细管传输的数值模型。新方法可以避免复杂解析解的求解,计算时间短。利用Verilog-AMS语言实现了模型建立和求解,开发了具体应用程序,对自制微流控开关梯度发生器及脉冲编码调制器进行模拟和分析,通过对比仿真和实验结果,验证了方法的有效性。
A new simulation method for microfluidic systems
针对复杂的大规模微流控芯片,提出了一种新的通用微流控系统行为模拟方法,计算芯片中由压力驱动的,线性和非线性的,静态和动态的溶液、溶质传输。对芯片中溶液/溶质传输的对流-扩散方程进行了分析,定义新的节点变量,抽象出系统集总模型,通过空间离散化处理,考虑了管壁柔性对模型参数的影响,建立毛细管传输的数值模型。新方法可以避免复杂解析解的求解,计算时间短。利用Verilog-AMS语言实现了模型建立和求解,开发了具体应用程序,对自制微流控开关梯度发生器及脉冲编码调制器进行模拟和分析,通过对比仿真和实验结果,验证了方法的有效性。
Permeation Process of small molecules across lipid membranes studied by molecular dynamics simulations
The transport of small molecules across a phospholipid membrane is studied by molecular dynamics simulations. The effects of size, hydrophobicity, and asphericity of the penetrants on the permeation process are investigated. For this purpose, permeability coefficients of oxygen and ammonia are computed using an inhomogeneous solubility-diffusion model and compared to the previously computed results of the permeation of water. Furthermore, solubility and diffusion data are computed for a series of Lennard-Jones particles that differ in size and shape. The results are discussed within the framework of the four-region model and are especially related to the free volume characteristics of the membrane. It is concluded that the free energy of solvation mainly determines the shape of the permeation resistance profile. For hydrophobic particles the membrane interior will act as a trap instead of a barrier. Moderately hydrophilic and hydrophilic penetrants experience the largest resistance to permeation in the dense part of the lipid tail region. This region is therefore most important in discriminating between various penetrants.
分子动力学模拟技术在生物分子研究中的进展
在当今科学探索中,分子动力学模拟作为实验的辅助,替代甚至引导,有越来越大的重性。在这篇综述里,我们概括介绍了分子模拟领域的发展历史,特别是专注于近期的进展,包括新的分子力场,增强采样技术以及在研究生物分子体系方面的最新成果。
Recent developments in using molecular dynamics simulation techniques to study biomolecules
在当今科学探索中,分子动力学模拟作为实验的辅助,替代甚至引导,有越来越大的重性。在这篇综述里,我们概括介绍了分子模拟领域的发展历史,特别是专注于近期的进展,包括新的分子力场,增强采样技术以及在研究生物分子体系方面的最新成果。
Glycan binding and specificity of viral influenza neuraminidases by classical molecular dynamics and replica exchange molecular dynamics simulations
Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using Lattice Boltzmann method
61MHD nanofluid forced convection in a porous cavity is investigated.61LBM is applied to solve this three dimensional problem.61Nusselt number is an enhancing function of Darcy and Reynolds numbers.61Nusselt number is a decreasing function of Hartmann number.
Multiscale particle-based modeling of flowing platelets in blood plasma using dissipative particle dynamics and coarse grained molecular dynamics
We developed a multiscale particle-based model of platelets, to study the transport dynamics of shear stresses between the surrounding fluid and the platelet membrane. This model facilitates a more accurate prediction of the activation potential of platelets by viscous shear stresses ne of the major mechanisms leading to thrombus formation in cardiovascular diseases and in prosthetic cardiovascular devices. The interface of the model couples coarse-grained molecular dynamics (CGMD) with dissipative particle dynamics (DPD). The CGMD handles individual platelets while the DPD models the macroscopic transport of blood plasma in vessels. A hybrid force field is formulated for establishing a functional interface between the platelet membrane and the surrounding fluid, in which the microstructural changes of platelets may respond to the extracellular viscous shear stresses transferred to them. The interaction between the two systems preserves dynamic properties of the flowing platelets, such as the flipping motion. Using this multiscale particle-based approach, we have further studied the effects of the platelet elastic modulus by comparing the action of the flow-induced shear stresses on rigid and deformable platelet models. The results indicate that neglecting the platelet deformability may overestimate the stress on the platelet membrane, which in turn may lead to erroneous predictions of the platelet activation under viscous shear flow conditions. This particle-based fluid tructure interaction multiscale model offers for the first time a computationally feasible approach for simulating deformable platelets interacting with viscous blood flow, aimed at predicting flow induced platelet activation by using a highly resolved mapping of the stress distribution on the platelet membrane under dynamic flow conditions.
耗散微粒动力学模拟方法在软物质体系研究中的一些进展与应用
软物质是指处于固体和理想流体之间的复杂态物质,主要包括聚合物、表面活性剂、液晶、胶体悬浮液、以及生物大分子等。软物质能够对外界微小的作用产生强烈的非线性响应,并展现出丰富的有序自组装相态。作为一种新颖的模拟技术,耗散粒子动力学方法非常适合在介观尺度上对软物质体系的复杂行为进行合理的描述。本文对耗散粒子动力学模拟方法的发展及一些应用进行了系统评述。耗散粒子动力学模拟方法体现了分子动力学与格子Boltzmann模型的优点,通过与其它理论模型(如Flory-Huggins理论、Smoothed particle hydrodynamics模型等)相结合,该方法能够在介观尺度上有效地研究聚合物熔体和溶液体系、生物膜及囊泡体系以及胶体悬浮液等体系的行为。这些研究结果,对新材料的研发、特殊材料的制备、以及材料加工条件的选择具有十分重要的科学意义和实际应用价值。
Progress and applications of dissipative particle dynamics simulation method in soft matters
软物质是指处于固体和理想流体之间的复杂态物质,主要包括聚合物、表面活性剂、液晶、胶体悬浮液、以及生物大分子等。软物质能够对外界微小的作用产生强烈的非线性响应,并展现出丰富的有序自组装相态。作为一种新颖的模拟技术,耗散粒子动力学方法非常适合在介观尺度上对软物质体系的复杂行为进行合理的描述。本文对耗散粒子动力学模拟方法的发展及一些应用进行了系统评述。耗散粒子动力学模拟方法体现了分子动力学与格子Boltzmann模型的优点,通过与其它理论模型(如Flory-Huggins理论、Smoothed particle hydrodynamics模型等)相结合,该方法能够在介观尺度上有效地研究聚合物熔体和溶液体系、生物膜及囊泡体系以及胶体悬浮液等体系的行为。这些研究结果,对新材料的研发、特殊材料的制备、以及材料加工条件的选择具有十分重要的科学意义和实际应用价值。
Simulation of reactive mixing behaviors inside micro-droplets by a lattice Boltzmann method
The Villermaux/Dushman competing parallel reactions are modeled into a multiphase/multicomponent lattice Boltzmann method (LBM) to theoretically investigate the interplay between mixing and reactions in droplet-based microfluidics. To quantify the mixing and reaction efficiency inside the droplets, the standard deviation mathContainer Loading Mathjax representing the pure mixing performance without reaction and the segregation index Xs reflecting mixing index with simultaneous chemical reactions are calculated based on the simulation results. The results show that the species transport can be evidently intensified by matching the flow recirculation and the appropriate initial distribution of reactants. We further demonstrate that the reaction selectivity could be improved by tuning droplet flow conditions or adding internal baffles to arbitrarily adjust the position of recirculation inside droplet.
Studies of particle levitation in a dielectrophoretic field-flow fraction-based microsorter
Abstract We study particle levitation in a dielectrophoretic field-flow fraction DEP-FFF flow sorter by using theoretical and numerical meth- ods. By balancing DEP forces with gravitational and buoyant forces, one can obtain the analytical solution for the particle levitation height. Nu- merical simulation is carried out and used to compare with the analytical prediction. One can find that there exists a maximum particle levitation height at a specific electrode width d for each applied voltage. The maximum levitation height happens at hp/d=0.95. The particle behaviors can be discussed based on the ratio between levitation height hp and the width of electrode d. When levitation height is higher than hp/d 0.6, simulation results show excellent agreement less than 2% error with the first-order approximated analytical solution. When levitation height is between 0.43hp/d0.6, the results start to show the large discrepancies more than 2% error between simulation and the first- order approximated analytical solution. A higher order theoretical solution has to be considered for this situation. When levitation height is hp/d 0.43, particles will stick on the bottom wall. Approximate theoretical solution is no longer applicable. 2009 Society of Photo-Optical Instrumentation
Research progress on microfluidic chip of cell separation based on dielectrophoresis
As for the separation of cell or particles by microfluidic chip based on dielectrophoretic field-flow-fractionation (DEP-FFF), the height of the cell location depends on the equilibrium of DEP and sedimentation (Fsed) forces, and the cells with different size would locate at different height, subject to different flow rate and separate to different outlets finally.
DC electrokinetic particle transport in an L-shaped microchannel
Electrokinetic transport of particles through an L-shaped microchannel under DC electric fields is theoretically and experimentally investigated. The emphasis is placed on the direct current (DC) dielectrophoretic (DEP) effect arising from the interactions between the induced spatially nonuniform electric field around the corner and the dielectric particles. A transient multiphysics model is developed in an arbitrary Lagrangian-Eulerian (ALE) framework, which comprises the Navier-Stokes equations for the fluid flow and the Laplace equation for the electrical potential. The predictions of the DEP-induced particle trajectory shift in the L-shaped microchannel are in quantitative agreement with the obtained experimental results. Numerical studies also show that the DEP effect can alter the angular velocity and even the direction of the particle's rotation. Further parametric studies suggest that the L-shaped microfluidic channel may be utilized to focus and separate particles by size via the induced DEP effect.
Review article-dielectrophoresis: Status of the theory, technology, and applications
A review is presented of the present status of the theory, the developed technology and the current applications of dielectrophoresis (DEP). Over the past 10 years around 2000 publications have addressed these three aspects, and current trends suggest that the theory and technology have matured sufficiently for most effort to now be directed towards applying DEP to unmet needs in such areas as biosensors, cell therapeutics, drug discovery, medical diagnostics, microfluidics, nanoassembly, and particle filtration. The dipole approximation to describe the DEP force acting on a particle subjected to a nonuniform electric field has evolved to include multipole contributions, the perturbing effects arising from interactions with other cells and boundary surfaces, and the influence of electrical double-layer polarizations that must be considered for nanoparticles. Theoretical modelling of the electric field gradients generated by different electrode designs has also reached an advanced state. Advances in the technology include the development of sophisticated electrode designs, along with the introduction of new materials (e.g., silicone polymers, dry film resist) and methods for fabricating the electrodes and microfluidics of DEP devices (photo and electron beam lithography, laser ablation, thin film techniques, CMOS technology). Around three-quarters of the 300 or so scientific publications now being published each year on DEP are directed towards practical applications, and this is matched with an increasing number of patent applications. A summary of the US patents granted since January 2005 is given, along with an outline of the small number of perceived industrial applications (e.g., mineral separation, micropolishing, manipulation and dispensing of fluid droplets, manipulation and assembly of micro components). The technology has also advanced sufficiently for DEP to be used as a tool to manipulate nanoparticles (e.g., carbon nanotubes, nano wires, gold and metal oxide nanoparticles) for the fabrication of devices and sensors. Most efforts are now being directed towards biomedical applications, such as the spatial manipulation and selective separation/enrichment of target cells or bacteria, high-throughput molecular screening, biosensors, immunoassays, and the artificial engineering of three-dimensional cell constructs. DEP is able to manipulate and sort cells without the need for biochemical labels or other bioengineered tags, and without contact to any surfaces. This opens up potentially important applications of DEP as a tool to address an unmet need in stem cell research and therapy.
Time evolution of a two-dimensional model system. I. Invariant states and time correlation functions
This paper is the first one of a series devoted to the study of a particularly simple two鈥恉imensional system of classical particles. The model is presented and some general feautres of it are established. We prove that, among states without correlations between particles with different velocities, there is a unique time invariant state with given density and hydrodynamic velocity. This ``equilibrium state'' is studied in detail. In particular its ergodic and mixing properties are investigated. We propose an approximation in order to estimate the asymptotic part of the time correlation functions and show that the long time tail is ruled by the ``hydrodynamic'' behavior of the model, namely by the evolution of the long wavelength perturbations.
Lattice-gas automata for the Navier-Stokes equation
Lattice gas hydmdynamics in two and three dimensions
Use of the Boltzmann equation to simulate lattice gas automata
An alternative to the lattice-gas automata (LGA) for the investigation of hydrodynamic properties is proposed, i.e., the lattice gas is modeled with a Boltzmann equation. It is found that this approach completely eliminates the statistical noise connected with the usual lattice-gas simulations and thus permits simulations that demand much less computer time. This technique is estimated to be more efficient that the LGA for intermediate to low Reynolds numbers (less than about 100).
Lattice-gas automata for the NavierStokes equation
Use of the Boltzmann equation to simulate lattice-gas automata
An alternative to the lattice-gas automata (LGA) for the investigation of hydrodynamic properties is proposed, i.e., the lattice gas is modeled with a Boltzmann equation. It is found that this approach completely eliminates the statistical noise connected with the usual lattice-gas simulations and thus permits simulations that demand much less computer time. This technique is estimated to be more efficient that the LGA for intermediate to low Reynolds numbers (less than about 100).
用多松弛格子Boltzmann方法模拟三维水击波
旨在探索用多松弛格子Boltzmann方法模拟多维水击波的可行性.采用三维方法模拟了一维水电站简单管水击现象,得到准确的直接水击和间接水击过程,证明其能准确模拟压力波传播与反射特性;模拟了二维拐角衍射,得到与其他方法吻合的结果;详细分析了断波撞击三维台阶产生的反射和衍射现象,获得合理的压力分布.研究表明:多松弛格子Boltzmann方法稳定性好,精度较高,能够准确模拟水击波的传播、反射和衍射,可推广到实际问题研究中.
Three-dimensional simulation of water hammer wave by multiple-relaxtion-time lattice Boltzmann method
旨在探索用多松弛格子Boltzmann方法模拟多维水击波的可行性.采用三维方法模拟了一维水电站简单管水击现象,得到准确的直接水击和间接水击过程,证明其能准确模拟压力波传播与反射特性;模拟了二维拐角衍射,得到与其他方法吻合的结果;详细分析了断波撞击三维台阶产生的反射和衍射现象,获得合理的压力分布.研究表明:多松弛格子Boltzmann方法稳定性好,精度较高,能够准确模拟水击波的传播、反射和衍射,可推广到实际问题研究中.
MRT-LBM analysis of acoustic streaming in standing waves between two-dimensional flat plates
Acoustic streaming generated by standing waves between two-dimensional flat plates is analyzed based on multiple relaxation time lattice Boltzmann method(MRT-LBM).Simulation results are in good agreement with approximate analytical solutions of Rayleigh streaming.Effects of viscosity and width between two plates on acoustic streaming in standing waves are studied.Dimensionless velocity distributions of x component with different viscosity at x=L/4 and dimensionless velocity distributions of y component with different viscosity at x=L/2,and effects of widths on boundary layer vortex thickness and formation progress of acoustic streaming in standing waves are revealed.It demonstrates availability of MRT-LBM model in simulating acoustic streaming in standing waves.
Lattice Boltzmann Method and Its Applications in Engineering
非牛顿流体固粒悬浮流的若干问题
非牛顿流体固粒悬浮流具有广泛的应用背景,其特殊的流动属性使其成为一些新兴技术领域的核心突破点.同时,该流动又比较复杂,即便是在低固粒浓度的情况下,非牛顿流体特性也会对整个系统的微结构产生重要的影响,从而进一步影响固粒的运动.本文给出了非牛顿流体方程、固粒运动方程和非牛顿流体固粒悬浮流的特征参数,分析了这些参数的作用;阐述了单个固粒在管道中的径向移动、多固粒的相互作用和聚集、多固粒形成的链状结构以及非圆球固粒运动等方面的研究成果、结果分析以及尚未解决的问题,并对以上问题进行了总结和展望,给出了需要深入研究的具体问题和内容,旨在为进一步的研究提供参考和依据.
Review of some researches on suspension of solid particle in non-newtonian fluid
非牛顿流体固粒悬浮流具有广泛的应用背景,其特殊的流动属性使其成为一些新兴技术领域的核心突破点.同时,该流动又比较复杂,即便是在低固粒浓度的情况下,非牛顿流体特性也会对整个系统的微结构产生重要的影响,从而进一步影响固粒的运动.本文给出了非牛顿流体方程、固粒运动方程和非牛顿流体固粒悬浮流的特征参数,分析了这些参数的作用;阐述了单个固粒在管道中的径向移动、多固粒的相互作用和聚集、多固粒形成的链状结构以及非圆球固粒运动等方面的研究成果、结果分析以及尚未解决的问题,并对以上问题进行了总结和展望,给出了需要深入研究的具体问题和内容,旨在为进一步的研究提供参考和依据.
椭圆颗粒在剪切流中旋转特性的数值研究
研究颗粒在流体剪切作用下的运动特性是理解和预测颗粒悬浮流流动行为的关键.当流体的惯性不能忽略时,颗粒的运动往往变得非常复杂.本文采用格子Boltzmann方法对中等雷诺数下椭圆颗粒在剪切流中的旋转运动进行了模拟.首先,研究了雷诺数(0<Re≤170)的影响,结果表明当雷诺数低于临界值时,颗粒以周期性的方式旋转,角速度最小时对应的长轴方向随着雷诺数的增大而逐渐远离水平方向,而且这一倾角与雷诺数呈分段线性关系;当雷诺数大于临界值时,椭圆形颗粒最终保持静止状态,且静止时的转角与雷诺数呈幂函数关系,雷诺数越大,转角越小,椭圆的长轴越远离水平位置.其次,研究了椭圆颗粒的长短轴之比α(1≤α≤10)的影响,结果表明颗粒旋转的周期与α呈幂函数关系,α越大,颗粒旋转周期越小.此外,当α超过临界值时,颗粒也在水平位置附近保持静止状态,此时的转角与α也呈幂函数关系,α越大,转角越小.研究还发现,当雷诺数较大时椭圆颗粒在旋转过程中会产生过冲现象.
Numerical study on the rotation of elliptical particle in shear flow
研究颗粒在流体剪切作用下的运动特性是理解和预测颗粒悬浮流流动行为的关键.当流体的惯性不能忽略时,颗粒的运动往往变得非常复杂.本文采用格子Boltzmann方法对中等雷诺数下椭圆颗粒在剪切流中的旋转运动进行了模拟.首先,研究了雷诺数(0<Re≤170)的影响,结果表明当雷诺数低于临界值时,颗粒以周期性的方式旋转,角速度最小时对应的长轴方向随着雷诺数的增大而逐渐远离水平方向,而且这一倾角与雷诺数呈分段线性关系;当雷诺数大于临界值时,椭圆形颗粒最终保持静止状态,且静止时的转角与雷诺数呈幂函数关系,雷诺数越大,转角越小,椭圆的长轴越远离水平位置.其次,研究了椭圆颗粒的长短轴之比α(1≤α≤10)的影响,结果表明颗粒旋转的周期与α呈幂函数关系,α越大,颗粒旋转周期越小.此外,当α超过临界值时,颗粒也在水平位置附近保持静止状态,此时的转角与α也呈幂函数关系,α越大,转角越小.研究还发现,当雷诺数较大时椭圆颗粒在旋转过程中会产生过冲现象.
Cell death: Critical control points
Programmed cell death is a distinct genetic and biochemical pathway essential to metazoans. An intact death pathway is required for successful embryonic development and the maintenance of normal tissue homeostasis. Apoptosis has proven to be tightly interwoven with other essential cell pathways. The identification of critical control points in the cell death pathway has yielded fundamental insights for basic biology, as well as provided rational targets for new therapeutics.
蛋白质物理改性的研究进展
蛋白质是食品中的重要组分之一,其功能特性对食品的品质至关重要。蛋白质改性主要包括化学法、酶法、物理法以及基因工程等。相对于其他改性方法,蛋白质的物理改性方法具有廉价、安全、处理时间短以及对产品营养性能影响较小等优点。而新兴的物理改性方法又具有低能耗、低温处理、产品品质高以及低消耗等优点。本文介绍了超高压、脉冲电场、超声、辐照、微波和射频处理等几种新的物理改性方法以及改性对蛋白功能性的影响,以及各种方法亟需解决的问题等。目前,新兴的物理改性方法还处于实验室阶段,未广泛应用于食品工业中,并且关于部分方法改性机理研究较少,研究材料种类较少,还需进一步扩展相关知识从而为蛋白质改性加工提供新思路。
Research progress on physical modification methods of protein
蛋白质是食品中的重要组分之一,其功能特性对食品的品质至关重要。蛋白质改性主要包括化学法、酶法、物理法以及基因工程等。相对于其他改性方法,蛋白质的物理改性方法具有廉价、安全、处理时间短以及对产品营养性能影响较小等优点。而新兴的物理改性方法又具有低能耗、低温处理、产品品质高以及低消耗等优点。本文介绍了超高压、脉冲电场、超声、辐照、微波和射频处理等几种新的物理改性方法以及改性对蛋白功能性的影响,以及各种方法亟需解决的问题等。目前,新兴的物理改性方法还处于实验室阶段,未广泛应用于食品工业中,并且关于部分方法改性机理研究较少,研究材料种类较少,还需进一步扩展相关知识从而为蛋白质改性加工提供新思路。