微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义.
蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响.
1 模型与方法
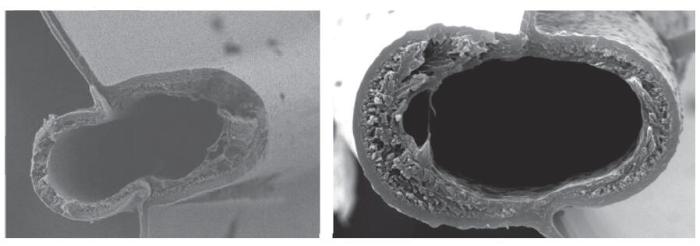
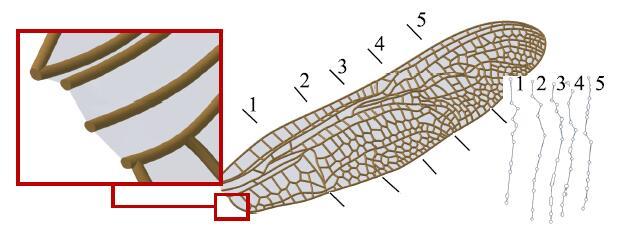
蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果.
图1 蜻蜓前翅横截面褶皱...
Fig. 1 The cross section of corrugated dragonfly forewing...
图2 翅脉横截面结构...
Fig. 2 The cross section of veins...
1.1 模型的简化
为了降低建模的难度,根据已有研究[35 -36 ]对蜻蜓前翅做如下的简化:
(1)忽略前翅翅脉和翅膜沿展向和弦向的尺寸变化,翅脉和翅膜的尺寸取平均值;
(2)忽略极微小皱褶以及皱褶内部结构的影响,忽略翅脉形状的细微变化,将蜻蜓前翅的翅脉形状简化为圆管,圆管状翅脉的外径为0.18mm,内径为0.145 mm,翅膜的厚度为4 $\mu$m;
(3)忽略前翅翅脉和翅膜的材料属性(弹性模量、泊松比等)沿展向和弦向的变化,根据文献[37 ],采用翅脉的平均弹性模量3800MPa,泊松比0.25,翅膜的平均弹性模量1500MPa,泊松比0.15,前翅的平均密度为1200 kg/m$^{3}$;
(4)忽略蜻蜓躯干以及后翅对褶皱前翅气动特性的影响.
1.2 模型的建立
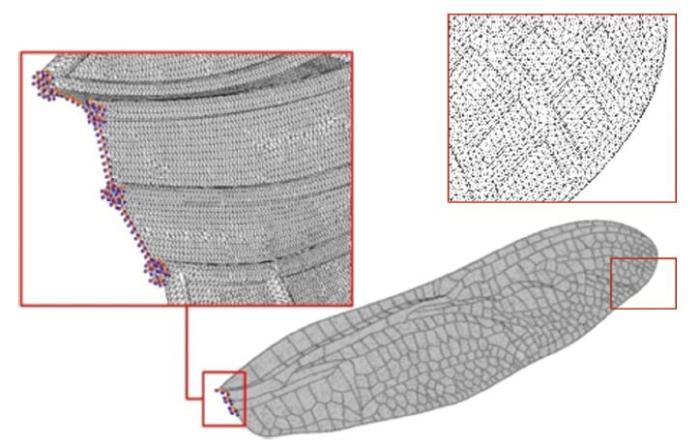
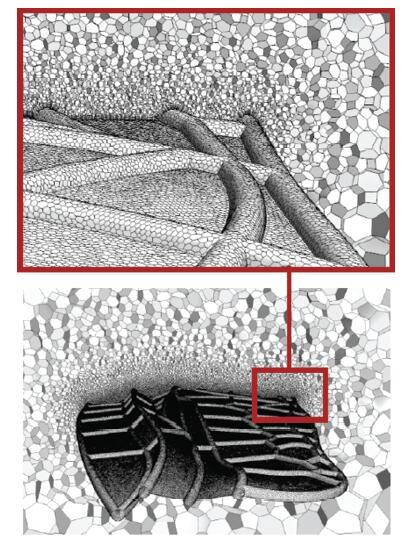
利用三维建模软件CATIA,通过逆向工程的方法,将高清蜻蜓前翅数码图片导入CATIA,利用样条曲线拟合纵横交错的翅脉,建立蜻蜓前翅的轮廓,然后填充轮廓形成翅膜曲面,根据实际测量皱褶结构深度和夹角的数据,偏转与之相对应翅膜面,翅脉和翅膜的空间分布形成前翅上的皱褶结构,赋予翅膜厚度和翅脉的形状与尺寸,翅膜镶嵌在圆管状翅脉上,最终建立蜻蜓三维褶皱前翅的CFD模型和CSD模型分别如图3 和图4 所示.有限元分析时,翅脉和翅膜采用均质的实体单元,因此前翅CSD模型的翅脉是由厚度为0.035mm的空心圆管构成,而CFD模型的翅脉为实心圆管,其他尺寸参数以及空间构型与前翅的CFD模型一致.
图3 蜻蜓褶皱前翅CFD模型...
Fig. 3 CFD model of the corrugated dragonfly forewing...
图4 蜻蜓褶皱前翅CSD模型...
Fig. 4 CSD model of the corrugated dragonfly forewing...
1.3 模型的验证
为了验证蜻蜓三维褶皱前翅模型的准确性,对此模型进行模态分析,与弯艳玲[38 ]通过三维激光扫描技术建立的蜻蜓三维褶皱前翅模型进行对比.真实前翅翼根处的翅脉和翅膜是固定在蜻蜓躯体上的,因此在模态分析时,将前翅翼根处的翅脉和翅膜设置为固定约束,如图5 所示,所有在翼根处的网格节点被设置为固定约束,约束此网格节点的所有自由度.蜻蜓前翅CSD模型有限元网格如图5 所示,翅脉和翅膜都采用均质的实体单元.
图5 有限元分析边界条件及网格...
Fig. 5 Boundary conditions and grids of finite element analysis...
模态分析的结果如表1 所示,结果表明蜻蜓前翅的主要模态(一阶模态,二阶模态和三阶模态)与弯艳玲的结果差别不大,因弯艳玲建立的蜻蜓前翅是通过激光扫描系统建立的精确模型,对比本文建立的蜻蜓三维褶皱前翅模型前三阶模态频率,其最大相对误差在10%以下,说明建立的此模型能保证足够的精度.
如图6 所示,蜻蜓褶皱前翅的振型云图表明,第一阶振型以沿展向的弯曲变形为主,第二阶振型是以前翅中轴线的扭转变形为主,第三阶振型则是弯曲扭转耦合,蜻蜓褶皱前翅的振形云图得出的结果与弯艳玲的结论一致,蜻蜓在飞行过程中,翅膀的运动形式主要是扑动和扭转,与之对应的三阶模态振型按照一阶为弯曲、二阶扭转和三阶为弯扭耦合的方式变化,符合自然界蜻蜓前翅的规律.
图6 蜻蜓褶皱前翅前三阶模态图...
Fig. 6 The modal of corrugated dragonfly forewing...
1.4 耦合控制方程
在流固耦合交界面处,应满足流体与固体的应力($\tau$)、位移($d$)、热流量($q$)、温度($T$) 等变量的守恒,即需满足如下方程
$$\left.\begin{array}{lll}n_{ f}\tau_{ f}=n_{ s}\tau_{ f} d_{ f}=d_{ s} q_{ f}=q_{ s} T_{ f}=T_{ s}\end{array}\right\}$$
其中,下标f 表示流体,下标s 表示固体.
1.5 模型网格
建立外流域,前翅的翼根处所在的平面为对称面,前翅的边界条件为壁面,湍流模型采用的是$k$-$\omega$ SST低雷诺数模型.采用非结构网格离散计算域,对于非结构网格,目前常用的网格形式有四面体网格、八面体网格以及笛卡尔网格,在相同条件下,笛卡尔的网格数量最少,其次为八面体网格,但由于笛卡尔网格无法适用于网格变形技术--动网格技术,因此用于柔性前翅的CFD网格采用适用动网格技术且高效的八面体网格对计算域进行离散.为使计算的结果不依赖于网格选取,对蜻蜓前翅CFD模型分别设置了3套不同大小的计算网格:第一套网格的蜻蜓前翅表面网格尺寸为0.04 mm;第二套网格为 0.03mm;第三套网格为0.02 mm.计算结果表明,使用第一套和第二套网格计算得到蜻蜓前翅的升力系数相对误差为14.9%,第二套和第三套网格的相对误差为4.7%.在权衡计算的准确性和计算时间后,最终选用第二套网格,如图7 所示,即蜻蜓前翅尺寸为0.03mm. 固体求解时有限元网格如图5 所示,蜻蜓前翅的表面为流固耦合交界面.
图7 前翅周围网格局部图...
Fig. 7 Grids of the corrugateddragonfly forewing...
1.6 算例验证
选用第二套网格,计算了平板在$Re$=10 000时攻角($\alpha)$介于0$^\circ$~10$^\circ$(间隔2$^\circ$)下的升力系数($C_{l}$),与Kesel的实验结果对比如图8 所示.从图8 中可以看出,平板的升力系数数值计算值与实验值基本相近,表明此网格能够保证足够的精度.
图8 数值计算平板的升力系数与Kesel[17 ]的实验结果对比图...
Fig. 8 Comparison between the numerical and the experimental lift coefficient of Kesel[17 ] ...
2 结果与讨论
为揭示蜻蜓滑翔时气动力对前翅的影响,分别计算了$Re$=2500时蜻蜓前翅攻角介于0$^\circ\!\!\sim$25$^\circ$(攻角间隔为5$^\circ$)之间,在滑翔时因空气作用力使前翅产生的变形和应力.
2.1 滑翔时柔性蜻蜓前翅的气动特性
对比刚性和柔性蜻蜓褶皱前翅在滑翔时不同攻角下的气动特性差异,气动特性的差异主要根据升力系数($C_{ l}$)、阻力系数($C_{ d}$)和升阻比($C_{ l}/C_{d}$)来判定,刚性和柔性前翅的气动特性比较如表2 所示,其中负值表示柔性前翅比刚性前翅的气动特性差,正值表示柔性前翅的的气动特性优于刚性前翅.在0$^\circ\!\!\sim$25$^\circ$攻角范围内,与刚性前翅相比,柔性减小了前翅的升力系数,同时也减小了阻力系数.
与刚性前翅相比,随着攻角的增大,柔性前翅升力系数的减少量逐渐减小,而阻力系数则相反,柔性前翅阻力系数的减少量随攻角的增加逐渐增大.在10$^\circ$攻角以下时,刚性前翅的升阻比高于柔性前翅,而当攻角继续增大时,则柔性前翅的升阻比高于刚性前翅.因此攻角的变化决定了柔性能否改善蜻蜓前翅的气动特性,只有在大攻角(大于10$^\circ$)时,蜻蜓的柔性翅膀有助于改善其气动特性.
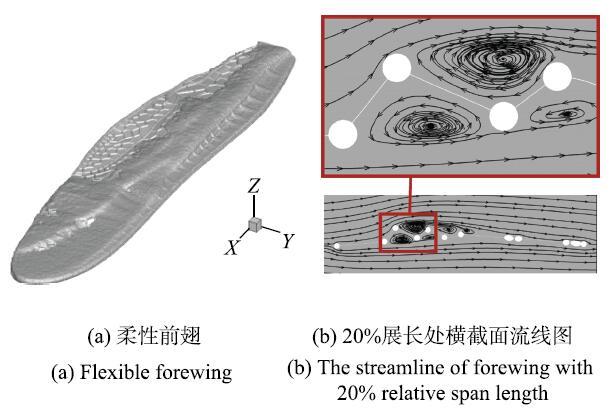
如图9 所示,蜻蜓前翅褶皱被许多涡填充,褶皱上表面凹槽内的驻留涡沿顺时针旋转,下表面凹槽内的驻留涡沿逆时针旋转,这与Rees[19 ]的实验结果一致,且涡主要分布在蜻蜓前翅前缘区域起伏较大的褶皱处,因此褶皱结构能够滞留涡.
图9 攻角为0$^\circ$时柔性前翅的涡量图及流线图...
Fig. 9 The vortex and streamline of flexible forewing at 0$^\circ$angles of attack...
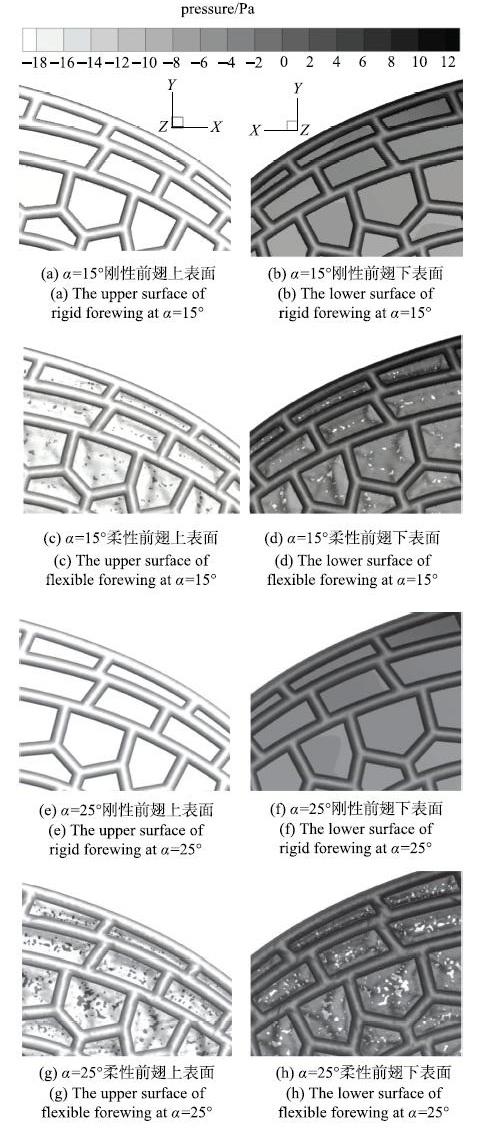
如图10 所示,对比刚性和柔性褶皱前翅的压力云图,柔性前翅的翅膜由于气动力的作用,其表面变得凹凸不平,上表面的低压区出现相对更高的压力分布,下表面高压区出现相对更低的压力分布,对比图10 (d)和图10 (h),攻角为25$^\circ$时这种差别更为明显.翅膜的上下表面压力差相较于刚性前翅的翅膜有所降低,更低的压力差意味着翅膀所受的合力更小,合力的分量之一--阻力也更小,因此柔性前翅的阻力系数比刚性前翅的低,攻角为25$^\circ$时阻力系数的减小量比攻角为15$^\circ$时的更大.
柔性前翅翅膜的上下表面压力差相较于刚性前翅的翅膜有所降低,更低的压力差意味着翅膀所受的合力更小,合力的分量之一--升力也更小,数值模拟的结果也显示在0$^\circ\sim$25$^\circ$攻角时,柔性前翅的升力系数比刚性前翅小,但从表2 中攻角为5$^\circ$时柔性前翅比刚性前翅的升力系数减小5.21%,到攻角为25$^\circ$时柔性前翅比刚性前翅的升力系数减小0.19%,这是因为与攻角为5$^\circ$时蜻蜓柔性前翅的前缘涡相比,攻角为25$^\circ$时,柔性前翅的前缘翅脉处存在比刚性前翅更强的前缘涡,如图11 所示.刚性前翅的前缘脉为圆管状,而柔性前翅的前缘脉产生变形,成类圆管状,如图11 (d)所示,变形后的前缘脉诱导出更强的前缘涡.攻角为25$^\circ$时,前缘涡的存在使蜻蜓柔性前翅能够保持与刚性前翅相当的升力系数,但由于柔性前翅具有更低的阻力系数,相较于刚性蜻蜓前翅,柔性使得前翅气动特性得到改善,升阻比提高3.15%.
图10 不同攻角时不同属性的褶皱前翅翅尖处压力云图...
Fig. 10 The pressure of corrugated forewing on wingtipwith different properties at different angles of attack...
图11 不同攻角时不同属性60%展长处横截面的涡量图对比...
Fig. 11 The vortex of the cross sections with differentproperties at different angles of attack shown below at 0.6$l_{rel}$, where $l_{ rel}$ is the relative span length...
2.2 蜻蜓前翅的变形与应力
基于CFD/CSD的双向流固耦合计算方法,数值求解$Re$=2500时0$^\circ\!\!\sim$25$^\circ$攻角(间隔5$^\circ$)蜻蜓滑翔时前翅在流场中受气动载荷后的变形和应力.蜻蜓柔性褶皱前翅在0$^\circ\!\!\!\sim$25$^\circ$攻角(间隔5$^\circ$)时最大变形值依次为:0.1694,1.265,2.169,2.602,2.721,2.910,单位为mm;柔性褶皱前翅最大应力值依次为:1.602,9.537, 16.24,19.76,20.82,22.34,单位为MPa.变形和应力总体上随着攻角的增大而增大,攻角10$^\circ$以后,变形和应力增长率减小,特别是攻角在15$^\circ$和25$^\circ$之间,变形和应力增大,但增幅不大,此攻角范围内褶皱前翅在流场中表现为升力系数变化也不明显,与此时蜻蜓前翅出现大范围的流动分离有关.
如图12 所示,在攻角为0$^\circ$时蜻蜓柔性褶皱前翅的最大变形位于靠近后缘的翅尖处,而攻角为5$^\circ\sim$25$^\circ$时前翅的最大变形位于翅尖处,柔性只是增加了垂直于蜻蜓前翅平面方向上的变形,但并没有使前翅发生扭转,即柔性对蜻蜓褶皱前翅的攻角的影响很小.如图10 和图11 所示,翅脉和翅膜因空气作用力产生变形,翅膜受气动载荷后表面成凹凸不平状,从而改变了蜻蜓柔性前翅的上下表面压力差.翅脉受气动载荷后由圆管状变成类圆管状,变形后的前缘翅脉,改变了柔性前翅的前缘涡强度.
图12 不同攻角($\alpha )$下柔性前翅的变形(单位:m) ...
Fig. 12 The deformation(unit: m) of flexible dragonfly forewingat different angles of attack ($\alpha )$ ...
蜻蜓柔性褶皱前翅最大应力位置在翼根处,如图13 所示,攻角为0$^\circ$时最大应力位置位于第五根横脉上表面,而攻角为5$^\circ$~25$^\circ$时蜻蜓前翅的最大应力位于第三根横脉上表面.随着攻角的逐渐增大,应力的分布发生变化,在第三根横脉和第五根横脉的根部出现了最大应力,而第三根横脉和第五根横脉都处于蜻蜓前翅褶皱的的上凸部分,应力主要集中于此区域,因此褶皱上凸部分承受蜻蜓滑翔时前翅的主要载荷.
图13 不同攻角($\alpha )$下柔性前翅翼根部的应力(单位:Pa)云图...
Fig. 13 The stress(unit: Pa) of flexible forewing at differentanglesof attack ($\alpha )$ ...
2.3 蜻蜓前翅的气动响应
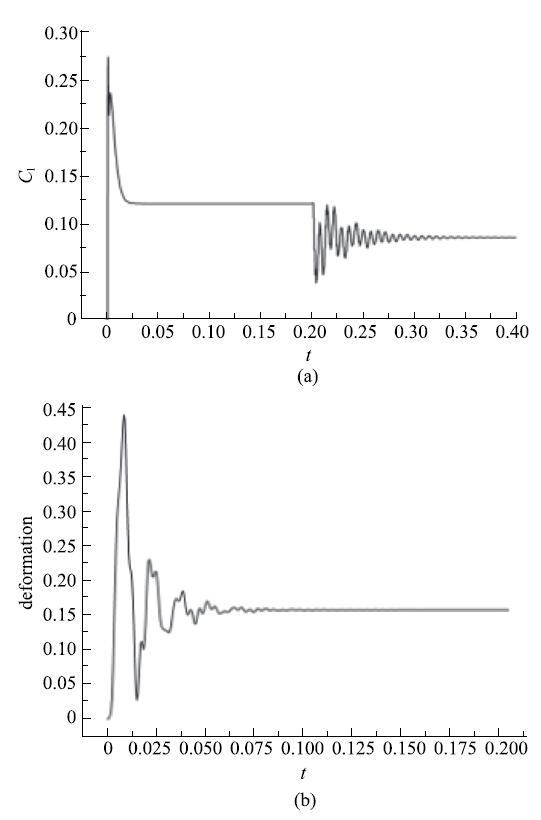
首先数值模拟蜻蜓刚性褶皱前翅的流场,在刚性前翅周围流场稳定后,改变前翅的属性,赋予前翅材料,基于CFD/CSD双向流固耦合数值计算开始,此时前翅将产生变形,刚性褶皱前翅的数值模拟相当于为流固耦合加载了一个稳定的初始流场.如图14 (a)所示,在蜻蜓前翅周围流场稳定后,褶皱前翅的升力系数趋于稳定,其升力系数为0.1247,此时前翅属性为刚性.当将前翅属性由刚性改变为柔性时,在受到气动载荷后,蜻蜓柔性前翅出现振动,如图14 (b)所示,在变形响应曲线中的表现为变形出现震荡,但震 荡的幅值逐渐减小最终稳定,前翅的升力
图14 攻角0$^\circ$蜻蜓前翅气动响应图...
Fig. 14 The pneumatic response of corrugated dragonfly forewingat0$^\circ$ angles of attack...
系数波动一段时间后趋于稳定,且稳定后的升力系数比刚性褶皱前翅的更小.即蜻蜓前翅在受气动载荷以后,出现振动并在很短的时间内(约0.125s)趋于稳定,不至于因长时间的振动而破坏翅膀的结构,使翅膀产生疲劳损坏,减少翅膀的寿命.在蜻蜓前翅的气动响应中,翅膀表现出优异的抗扰动能力和极强的稳定性.
3 结 论
蜻蜓在滑翔飞行时,三维褶皱刚性前翅和柔性前翅相比,在小攻角(小于10$^\circ$)时刚性前翅的气动特性优于柔性前翅,继续增大攻角,柔性前翅的气动特性则优于刚性前翅.蜻蜓扑翼飞行时,翅膀的攻角变化幅度大且频率高,而蜻蜓柔性翅膀的气动特性同时还受攻角变化的影响,因此蜻蜓扑翼飞行时,柔性也是其不能忽略的特性.
蜻蜓滑翔过程中,褶皱结构能够滞留涡,柔性前翅在翅尖处产生了垂直于翅膀所在平面方向上的最大变形,而没有发生扭转,翼根处受到应力最大,褶皱上凸部分承受蜻蜓滑翔时前翅的主要载荷.蜻蜓柔性前翅受气动载荷后产生变形,表现为翅脉和翅膜的外形改变以及整个前翅弯曲变形.翅膜的外形改变,其上下表面压力差相较于刚性前翅减小了,从而柔性前翅的升力和阻力也减小了.但在大攻角时,柔性前翅由于外形改变的前缘脉,诱导出比刚性前翅更强的前缘涡,维持了柔性前翅的升力,使柔性前翅的升力减少量变小,因此大攻角时柔性对蜻蜓褶皱前翅的气动特性的改善约3%.蜻蜓褶皱前翅在受气动载荷后,气动响应时间短,表现出优异的力学性能.本研究有助于解释蜻蜓翅膀优秀的功能表现,对仿生扑翼飞行器的柔性机翼设计有一定的参考意义.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
刘强 , 刘周 , 白鹏 等 . 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
. 力学学报 , 2016 , 48 (2 ): 269 -277
URL
[本文引用: 1]
(Liu Qiang Liu Zhou Bai Peng et al .Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at low Reynolds number
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (2 ): 269 -277 (in Chinese))
URL
[本文引用: 1]
[2]
孟令兵 , 昂海松 , 肖天航 . 柔性翼微型飞行器流固耦合数值模拟
. 南京航空航天大学学报 , 2013 , 45 (5 ): 621 -627
(Meng Lingbing Ang Haisong Xiao Tianhang Numerical simulation of fluid-structure interaction for flexible wing MAV
. Journal of Nanjing University of Aeronautics & Astronautics , 2013 , 45 (5 ): 621 -627 (in Chinese))
[3]
Lian Y Wei S Viieru D et al .Membrane wing aerodynamics for micro air vehicles
. Progress in Aerospace Sciences , 2003 , 39 (6 ): 425 -465
[4]
AIAA . Computational modeling of highly flexible membrane wings in micro air vehicles
. AIAA Paper2006 -1661 , 2006
[5]
Jaiman RK Jiao X Geubelle PH et al .Conservative load transfer along curved fluid-solid interface with non-matching meshes
. Journal of Computational Physics , 2006 , 218 (1 ): 372 -397
[6]
Lian Y Wei S . Three-dimensional fluid-structure interactions of a membrane wing for micro air vehicle applications
. AIAA Paper2003 -1726 , 2003
[本文引用: 1]
[7]
Mueller TJ. Fixed and flapping wing dynamics for MAV applications
. AIAA Progress in Astron and Aeron, Massachusetts : AIAA Press , 2001 : 195
[本文引用: 1]
[8]
Liu H Kawachi K A numerical study of insect flight
. Journal of Computational Physics , 1998 , 146 (1 ): 124 -156
[9]
Rayner JMV A new approach to animal flight mechanics
. Journal of Experimental Biology , 1979 , 80 (1 ): 17 -54
[本文引用: 1]
[10]
Hu Z Deng XY Aerodynamic interaction between forewing and hindwing of a hovering dragonfly
. Acta Mechanica Sinica , 2014 , 30 (6 ): 787 -799
URL
[本文引用: 1]
[11]
Kwok M Mittal R Experimental investigation of the aerodynamics of a modeled dragonfly wing section
. Bulletin of Faculty of Engineering Toyama University , 2005 , 5 (1 ): 50 -53
[本文引用: 2]
[12]
Noda R Nakata T Liu H Effects of wing deformation on aerodynamic performance of a revolving insect wing
. Acta Mechanica Sinica , 2014 , 30 (6 ): 819 -827
URL
[本文引用: 1]
[13]
Hamamoto M Ohta Y Hara K et al .Application of fluid--structure interaction analysis to flapping flight of insects with deformable wings
. Advanced Robotics , 2007 , 21 (1-2 ): 1 -21
[本文引用: 1]
[14]
Hamamoto M Ohta Y Hara K et al .Free-flight analysis of dragonfly hovering by fluid--structure interaction analysis based on an arbitrary Lagrangian--Eulerian method
. Advanced Robotics , 2013 , 27 (9 ): 657 -666
[本文引用: 1]
[15]
孟令兵 , 昂海松 , 肖天航 . 基于CFD/CSD方法的蜻蜓柔性翼气动特性分析
. 航空动力学报 , 2014 , 29 (9 ): 2063 -2069
[本文引用: 1]
(Meng Lingbing Ang Haisong Xiao Tianhang Analysis of aerodynamic characteristics of a flexible wing of dragonfly based on CFD/CSD method
. Journal of Aerospace Power , 2014 , 29 (9 ): 2063 -2069 (in Chinese))
[本文引用: 1]
[16]
郝淑文 . 低雷诺数下柔性膜扑翼气动特性的流固耦合分析. [博士论文]
. 北京:北京理工大学 , 2015
[本文引用: 1]
(Hao Shuwen Fluid-structure interaction of unsteady aerodynamic of membrane flapping wings at low reynolds number. [PhD Thesis]
. Beijing: Beijing Institute of Technology , 2015 (in Chinese))
[本文引用: 1]
[17]
Kesel AB Aerodynamic characteristics of dragonfly wing sections compared with technical aerofoils
. Journal of Experimental Biology , 2000 , 203 : 3125 -3135
[本文引用: 3]
[18]
Vargas A Mittal R Dong H A computational study of the aerodynamic performance of a dragonfly wing section in gliding flight
. Bioinspiration & Biomimetics , 2008 , 3 (2 ): 026004
[本文引用: 1]
[19]
Rees CJC Form and function in corrugated insect wings
. Nature , 1975 , 256 (5514 ): 200 -203
[本文引用: 2]
[20]
Meng XG Sun M Aerodynamic effects of wing corrugation at gliding flight at low Reynolds numbers
. Physics of Fluids , 2013 , 25 (7 ): 071905
[本文引用: 1]
[21]
Zhang Z Yin Y Zhong Z et al .Aerodynamic performance of dragonfly wing with well-designed corrugated section in gliding flight
. Computer Modeling in Engineering & Sciences , 2015 , 109 (3 ): 285 -302
[本文引用: 1]
[22]
Dompreh KA Eghan MJ Kotsedi L et al .Comprehensive optical study of the dragonfly Aeshna cyanea, transparent wing
. Optics Communications , 2013 , 297 (12 ): 176 -181
[本文引用: 1]
[23]
赵红晓 , 仲政 . 蜻蜓翅膀的力学研究进展
. 力学季刊 , 2009 , 30 (3 ): 398 -404
[本文引用: 1]
(Zhao Hongxiao Zhong Zheng Research advance in mechanical research of dragonfly wings
. Chinese Quarterly of Mechanics , 2009 , 30 (3 ): 398 -404 (in Chinese))
[本文引用: 1]
[24]
Okamoto M Yasuda K Azuma A Aerodynamic characteristics of the wings and body of a dragonfly
. Journal of Experimental Biology , 1996 , 199 (2 ): 281 -294
[本文引用: 1]
[25]
孙茂 . 昆虫飞行的空气动力学
. 力学学报 , 2015 , 45 (2 ): 1 -28
[本文引用: 1]
(Sun Mao Aerodynamics of inset flight
. Chinese Journal of Theoretical and Applied Mechanics , 2015 , 45 (2 ): 1 -28 (in Chinese))
[本文引用: 1]
[26]
Hertel H. Structure Form , Movement . New York: Reinhold Publishing Corporation , 1966
[27]
Wootton RJ Newman ADJS An approach to the mechanics of pleating in dragonfly wings
. Journal of Experimental Biology , 1986 , 125 (1 ): 361 -372
[28]
Newman DJS The functional wing morphology of some. [PhD Thesis]
. Odonata: University of Exeter , 1983
[29]
Antonia BK Ute P Werner N Biomechanical aspects of the insect wing: an analysis using the finite element method. Computers in Biology and Medicine}. 1998 , 28 : 423 -437
[30]
陈应龙 . 蜻蜓翅膀微结构与力学行为的仿生分析研究. [博士论文]
. 北京:清华大学 , 2012
(Chen Yinglong Bionicresearch on the relation between the multi-scaled structure and microstructure and mechanical behavior of dragonfly wing. [PhD Thesis]
. Beijing: Tsinghua University , 2012 (in Chinese))
[31]
Dong HB Christopher K Liang ZX et al .An integrated analysis of a dragonfly in free flight//Proceedings of 28th
AIAA Applied Aerodynamics Conference , 2010 : 4390 -4400
[本文引用: 1]
[32]
Tong J Zhao YR Sun JY et al .Nanomechanical properties of the stigmaof dragonfly Anax parthenope julius Brauer
. Journal of Materials Science , 2007 , 42 (8 ):2894 -2898
URL
[本文引用: 1]
[33]
Ren HH Wang XS Li XD et al .Effects of dragonfly wing structure on the dynamic per formances
. Journal of Bionic Engineering , 2013 , 10 (1 ): 28 -38
URL
[34]
Jongerius SR Lentink D Structural analysis of a dragonfly wing
. Experimental Mechanics , 2010 , 50 (9 ): 1323 -1334
URL
[本文引用: 1]
[35]
Sudo S Tsuyuki K Ikohagi T et al .A study on the wing structure and flapping behavior of a dragonfly. JSME International Journal Series C Mechanical Systems,
Machine Elements and Manufacturing , 1999 , 42 (3 ): 721 -729
[本文引用: 2]
[36]
李秀娟 . 蜻蜓翅膀功能特性力学机制的仿生研究. [博士论文]
.吉林:吉林大学 , 2013
[本文引用: 2]
(Li Xiujuan Bionic investigation on mechanical mechanism of dragonfly wings functional characteristics. [PhD Thesis]
. Jilin: Jilin University , 2013 (in Chinese))
[本文引用: 2]
[37]
Shahnazi R Pariz N Kamyad AV Adaptive fuzzy output feedback control for a class of uncertain nonlinear systems with unknown backlash-like hysteresis
. Communications in Nonlinear Science & Numerical Simulation , 2010 , 15 (8 ): 2206 -2221
URL
[本文引用: 1]
[38]
弯艳玲 . 蜻蜓翅翼三维空间结构的动力学与疲劳寿命研究. [博士论文]
. 吉林:吉林大学 , 2010
[本文引用: 2]
(Wan Yanling Dynamics and fatigue life of three-dimensional structure of dragonfly wings. [PhD Thesis]
. Jilin: Jilin University , 2010 (in Chinese))
[本文引用: 2]
低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
1
2016
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
1
2016
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
Membrane wing aerodynamics for micro air vehicles
2003
Computational modeling of highly flexible membrane wings in micro air vehicles
2006
Conservative load transfer along curved fluid-solid interface with non-matching meshes
2006
Three-dimensional fluid-structure interactions of a membrane wing for micro air vehicle applications
1
2003
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
Fixed and flapping wing dynamics for MAV applications
1
2001
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
A numerical study of insect flight
1998
A new approach to animal flight mechanics
1
1979
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
Aerodynamic interaction between forewing and hindwing of a hovering dragonfly
1
2014
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
Experimental investigation of the aerodynamics of a modeled dragonfly wing section
2
2005
... 微型飞行器低雷诺数飞行时,由于机翼表面的层流附面层难以维持,气流不易稳定,导致其存在失速迎角小和抗阵风性能差等缺点[1 -6 ],而昆虫飞行时能克服低雷诺数($Re$)的气动局限性,实现高稳定性和低能耗的飞行.研究表明,昆虫柔性翅膀的变形是其用来克服低雷诺数飞行时气动局限性的主要方式之一[7 -9 ].有昆虫界战斗机之称的蜻蜓,作为自然界最优秀的飞行者之一[10 ],其翅膀上没有神经和肌肉,所以蜻蜓对翅膀的主动控制相对较少,在飞行过程中的蜻蜓翅膀的变形是被动的,变形的大小取决于翅膀本身的结构和材料的属性以及所受气动力的分布情况[11 ],研究蜻蜓柔性翅膀的变形对其气动特性的影响,对微型扑翼飞行器的设计具有一定的指导 意义. ...
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Effects of wing deformation on aerodynamic performance of a revolving insect wing
1
2014
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Application of fluid--structure interaction analysis to flapping flight of insects with deformable wings
1
2007
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Free-flight analysis of dragonfly hovering by fluid--structure interaction analysis based on an arbitrary Lagrangian--Eulerian method
1
2013
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
基于CFD/CSD方法的蜻蜓柔性翼气动特性分析
1
2014
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
基于CFD/CSD方法的蜻蜓柔性翼气动特性分析
1
2014
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
低雷诺数下柔性膜扑翼气动特性的流固耦合分析. [博士论文]
1
2015
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
低雷诺数下柔性膜扑翼气动特性的流固耦合分析. [博士论文]
1
2015
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Aerodynamic characteristics of dragonfly wing sections compared with technical aerofoils
3
2000
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
... 数值计算平板的升力系数与Kesel[17 ]的实验结果对比图... ...
... Comparison between the numerical and the experimental lift coefficient of Kesel[17 ] ... ...
A computational study of the aerodynamic performance of a dragonfly wing section in gliding flight
1
2008
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Form and function in corrugated insect wings
2
1975
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
... 如图9 所示,蜻蜓前翅褶皱被许多涡填充,褶皱上表面凹槽内的驻留涡沿顺时针旋转,下表面凹槽内的驻留涡沿逆时针旋转,这与Rees[19 ]的实验结果一致,且涡主要分布在蜻蜓前翅前缘区域起伏较大的褶皱处,因此褶皱结构能够滞留涡. ...
Aerodynamic effects of wing corrugation at gliding flight at low Reynolds numbers
1
2013
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Aerodynamic performance of dragonfly wing with well-designed corrugated section in gliding flight
1
2015
... 蜻蜓飞行过程中柔性翅膀的变形是一个流固耦合问题[12 ],目前国内外对蜻蜓柔性翅膀进行了相关的研究,Hamamoto等[13 -14 ]基于有限元分析方法处理蜻蜓悬停时的流固耦合问题,结果表明柔性翅膀的变形对其气动特性具有较小的影响.孟令兵等[15 ]基于计算流体力学/计算结构力学(computational fluiddynamics,CFD/computational structuralmechanics,CSD)方法对蜻蜓扑翼飞行时柔性翅膀的变形进行了数值模拟,结果显示柔性翅膀的变形降低了阻力,并增大推力,提高了蜻蜓的飞行性能,但其建立的模型实际上为具有蜻蜓翅膀外轮廓的平板.郝淑文[16 ]利用Matlab软件建立了适合于求解柔性膜扑翼气动特性的流固耦合整体法求解程序,分析了刚性和柔性蜻蜓翅膀模型前飞时动态变形的瞬时、时均气动响应,但此翅膀模型忽略了翅脉、翅膜以及褶皱等重要结构.以上研究只考虑了柔性翅膀的变形,而褶皱是蜻蜓翅膀上最为显著的结构之一,文献[11 ,17 -18 ]对蜻蜓褶皱翼的研究表明,与平板相比,褶皱翼有比平板具有更高的升阻比;而Rees[19 ]、Meng等[20 ]对蜻蜓褶皱翼的研究则表明,褶皱翼的升阻比低于平板;Zhang等[21 ]的研究结果显示,蜻蜓褶皱翼的升阻比低于平板,通过改变褶皱的起皱幅度可显著改善其气动效能,使褶皱翼的升阻比高于平板.在蜻蜓实际飞行中,皱褶与柔性翅膀的变形同时存在,两者共同作用下对蜻蜓翅膀气动特性的影响如何?本文基于真实的蜻蜓前翅,根据前人对蜻蜓前翅的实际测量数据和研究成果,经过适当的简化,构建出有褶皱结构的蜻蜓三维前翅CFD模型和CSD模型,基于CFD/CSD双向耦合的计算方法,对蜻蜓三维柔性褶皱前翅的变形问题展开研究,以期揭示蜻蜓滑翔时柔性对褶皱前翅气动特性的影响. ...
Comprehensive optical study of the dragonfly Aeshna cyanea, transparent wing
1
2013
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
蜻蜓翅膀的力学研究进展
1
2009
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
蜻蜓翅膀的力学研究进展
1
2009
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
Aerodynamic characteristics of the wings and body of a dragonfly
1
1996
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
昆虫飞行的空气动力学
1
2015
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
昆虫飞行的空气动力学
1
2015
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
An approach to the mechanics of pleating in dragonfly wings
1986
The functional wing morphology of some. [PhD Thesis]
1983
蜻蜓翅膀微结构与力学行为的仿生分析研究. [博士论文]
2012
蜻蜓翅膀微结构与力学行为的仿生分析研究. [博士论文]
2012
An integrated analysis of a dragonfly in free flight//Proceedings of 28th
1
2010
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
Nanomechanical properties of the stigmaof dragonfly Anax parthenope julius Brauer
1
2007
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
Effects of dragonfly wing structure on the dynamic per formances
2013
Structural analysis of a dragonfly wing
1
2010
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
A study on the wing structure and flapping behavior of a dragonfly. JSME International Journal Series C Mechanical Systems,
2
1999
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
... 为了降低建模的难度,根据已有研究[35 -36 ]对蜻蜓前翅做如下的简化: ...
蜻蜓翅膀功能特性力学机制的仿生研究. [博士论文]
2
2013
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
... 为了降低建模的难度,根据已有研究[35 -36 ]对蜻蜓前翅做如下的简化: ...
蜻蜓翅膀功能特性力学机制的仿生研究. [博士论文]
2
2013
... 蜻蜓翅膀的巧妙结构是其卓越的飞行能力的主要原因[22 ],蜻蜓翅膀主要由厚度很薄且透明的翅膜(厚度2~5$\mu $m)[23 ]、对翅膜起连接和支撑作用的翅脉组成.Okamoto等[24 ]对蜻蜓前翅的数据采集表明,前翅横截面的形状呈褶皱状,褶皱实际为翅脉和翅膜的空间分布所形成的蜻蜓翅膀上显著的结构,主要表现为翅膜的下凹和上凸,翅脉位于翅膜下凹位置的底端或上凸位置的顶峰,如图1 所示.研究表明,褶皱能提高蜻蜓翅膀的稳定性和整体结构刚度,减小翅膀的耗材[25 -31 ].翅脉结构精巧,是蜻蜓翅膀的主要承载结构,在力学性能中发挥了关键作用[32 -34 ].如图2 所示,不同位置的翅脉形状不尽相同,但大体外形类似于圆管,而且为中空结构,这种结构有利于减轻蜻蜓翅膀的结构重量[35 ],缓释蜻蜓飞行中的交变应力[36 ],在建立蜻蜓褶皱前翅CFD和CSD模型时,相关的简化则是基于以上研究成果. ...
... 为了降低建模的难度,根据已有研究[35 -36 ]对蜻蜓前翅做如下的简化: ...
Adaptive fuzzy output feedback control for a class of uncertain nonlinear systems with unknown backlash-like hysteresis
1
2010
... (3)忽略前翅翅脉和翅膜的材料属性(弹性模量、泊松比等)沿展向和弦向的变化,根据文献[37 ],采用翅脉的平均弹性模量3800MPa,泊松比0.25,翅膜的平均弹性模量1500MPa,泊松比0.15,前翅的平均密度为1200 kg/m$^{3}$; ...
蜻蜓翅翼三维空间结构的动力学与疲劳寿命研究. [博士论文]
2
2010
... 为了验证蜻蜓三维褶皱前翅模型的准确性,对此模型进行模态分析,与弯艳玲[38 ]通过三维激光扫描技术建立的蜻蜓三维褶皱前翅模型进行对比.真实前翅翼根处的翅脉和翅膜是固定在蜻蜓躯体上的,因此在模态分析时,将前翅翼根处的翅脉和翅膜设置为固定约束,如图5 所示,所有在翼根处的网格节点被设置为固定约束,约束此网格节点的所有自由度.蜻蜓前翅CSD模型有限元网格如图5 所示,翅脉和翅膜都采用均质的实体单元. ...
... Frequency comparison of the corrugated dragonfly forewing
Model Model 1 Model 2 Model 3 Ref.[38 ] 63.75 Hz 220.85 Hz 284.52 Hz present 57.76 Hz 226.79 Hz 284.00 Hz relative error 9.40% 2.69% 0.18%
如图6 所示,蜻蜓褶皱前翅的振型云图表明,第一阶振型以沿展向的弯曲变形为主,第二阶振型是以前翅中轴线的扭转变形为主,第三阶振型则是弯曲扭转耦合,蜻蜓褶皱前翅的振形云图得出的结果与弯艳玲的结论一致,蜻蜓在飞行过程中,翅膀的运动形式主要是扑动和扭转,与之对应的三阶模态振型按照一阶为弯曲、二阶扭转和三阶为弯扭耦合的方式变化,符合自然界蜻蜓前翅的规律. ...
蜻蜓翅翼三维空间结构的动力学与疲劳寿命研究. [博士论文]
2
2010
... 为了验证蜻蜓三维褶皱前翅模型的准确性,对此模型进行模态分析,与弯艳玲[38 ]通过三维激光扫描技术建立的蜻蜓三维褶皱前翅模型进行对比.真实前翅翼根处的翅脉和翅膜是固定在蜻蜓躯体上的,因此在模态分析时,将前翅翼根处的翅脉和翅膜设置为固定约束,如图5 所示,所有在翼根处的网格节点被设置为固定约束,约束此网格节点的所有自由度.蜻蜓前翅CSD模型有限元网格如图5 所示,翅脉和翅膜都采用均质的实体单元. ...
... Frequency comparison of the corrugated dragonfly forewing
Model Model 1 Model 2 Model 3 Ref.[38 ] 63.75 Hz 220.85 Hz 284.52 Hz present 57.76 Hz 226.79 Hz 284.00 Hz relative error 9.40% 2.69% 0.18%
如图6 所示,蜻蜓褶皱前翅的振型云图表明,第一阶振型以沿展向的弯曲变形为主,第二阶振型是以前翅中轴线的扭转变形为主,第三阶振型则是弯曲扭转耦合,蜻蜓褶皱前翅的振形云图得出的结果与弯艳玲的结论一致,蜻蜓在飞行过程中,翅膀的运动形式主要是扑动和扭转,与之对应的三阶模态振型按照一阶为弯曲、二阶扭转和三阶为弯扭耦合的方式变化,符合自然界蜻蜓前翅的规律. ...