颗粒材料是一种普遍存在于自然界中的物质,在生产生活方面得到了广泛的应用,如土木水利工程、化学工程、食品加工工程等领域.在水工结构工程中,土石坝中的堆石料、心墙防渗土料、位于坝基的土质覆盖层均是典型的颗粒材料,这类材料的应力变形性质将直接影响工程的安全;而岩土工程中的土质边坡、软土地基与基础、地下工程等都迫切需要土体颗粒材料的稳定性研究.无论是筑坝颗粒类材料、还是覆盖层土料或是边坡土质,从本质上讲都是岩土类摩擦耗散型颗粒材料,属于不连续介质,其宏微观的力学机制在某种程度上是相通的.
对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的.
颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析.
颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制.
本文将基于颗粒材料真三轴离散元数值试验结果,分析三维应力路径下颗粒材料的宏微观力学响应,并通过组构张量特征及强弱接触体系划分研究,对颗粒体系三维宏微观特征的统一性及强弱接触体系对宏观应力张量的贡献进行深入探讨.
1 颗粒体系的微观结构
1.1 微观结构定义
从宏观角度来看,颗粒体系属于连续介质,描述其基本特征的量为应力张量${\boldsymbol{\sigma}}$与应变张量${\boldsymbol{\varepsilon }}$.当研究对象为代表体积元(representative volume element,RVE)时,其在微观层面包含有不可计数的颗粒,颗粒之间相互接触、滑移、转动,表现出了不连续\特性.
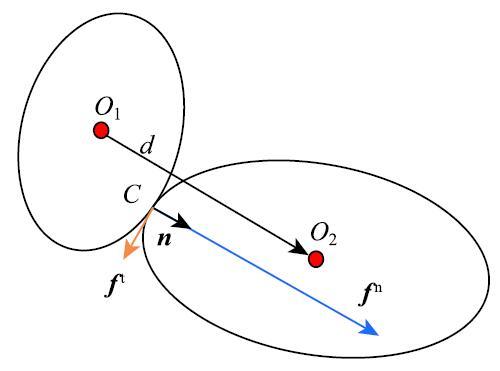
对于两个颗粒固体之间特定的接触,一般存在接触法向\textbf{n}}、枝向量\textbf{d}}、法向接触力\textbf{f }}$^{n}$、切向接触力\textbf{f}}$^{t}$等基本属性(如图1 所示).其中,接触法向、枝向量为接触的几何特性,接触法向是颗粒间接触方向的单位向量,枝向量为接触两颗粒几何中心之间的位置差,接触法向和枝向量属于对颗粒接触的方向及长度的量化指标;而法向和切向接触力则是该接触的力学表征,是两颗粒间接触力在接触法向和切向方向的分量.图1 为两个任意颗粒的接触示意,$O_{1}$和$O_{2}$为颗粒的中心点,两颗粒接触于点$C$,法向接触力 和切向接触力分别为\textbf{f }}$^{n}$和\textbf{f }}$^{t}$.
图1 颗粒之间的接触表征...
Fig. 1 Contact characterization between particles
配位数(coordinationnumber)为颗粒与周边固体的接触数目,颗粒体系内的平均配位数是颗粒材料的最基本、最直接的微观标量指标.一般而言,当颗粒体系的平均配位数较大时,其内部结构较为稳定;而平均配位数减小则意味着颗粒体系变得松散或者各向异性程度增加,将有可能引起局部化或者全局化的失稳破坏.平均配位数一般定义为$$Z = \frac{{2{N_{c}}}}{{{N_{p}}}}\tag1$$ 式中,$N_{c}$为体系内的总接触数目,$N_{p}$为颗粒总数.
1.2 微观研究手段
探究材料的微细观结构,着重于对材料内部的接触、孔隙、颗粒形状、颗粒位移等进行采集和分析,进而研究颗粒材料微观、细观层面的形态学特征、几何学特征和能量特征,目前主要有物理试验和数值试验两方面.在物理试验方面,国内外学者主要通过研发新型设备,发展微观观测手段,并提取不同试验条件下颗粒材料的内在结构信息,目前常用的观测手段有光弹试验、扫描电镜观测、X射线透视仪观测、X射线衍射仪观测、计算机X射线断层成像(computedtomography,CT)技术扫描、数字图像相关(digital imagecorrelation,DIC)技术成像、立体摄影、激光散斑法等[32 -36 ].
除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ].
2 离散元数值试验
2.1 数值试样与三维应力路径
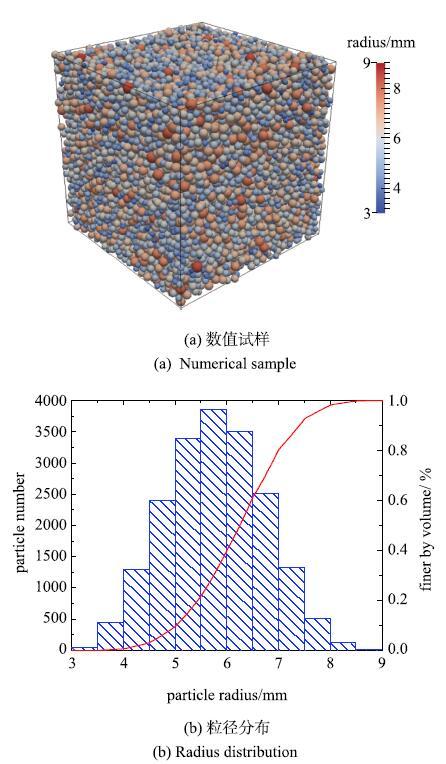
采用19436个圆球颗粒组成的颗粒集合体进行真三轴数值试验,试样及粒径分布如图2 所示.为了避免由制样产生的初始各向异性,首先在试样的各个方向采用位移控制等速地压缩试样直至目标大小,然后给试样施加三向等压应力直至达到预定的围压值.颗粒间接触模型采用Hertz-Mindlin模型,并采用转动摩擦系数反映材料的抗转动特性,颗粒的弹性模量取为65GPa,泊松比取为0.12,滑动摩擦系数和转动摩擦系数分别为0.4和0.05.
图2 数值计算条件...
Fig.2 Numerical conditions
在真三轴数值试验中,一般采用中主应力系数$b$或应力罗德角$\theta _b$反映3个主应力之间的关系
$$ b = \frac{{{\sigma _2}-{\sigma _3}}}{{{\sigma_1}-{\sigma _3},}}\tan {\theta _\sigma } = \dfrac{{\sqrt3 b}}{{2-b}}\tag1$$
式中,中主应力系数$b$反映的是3个主应力大小之间的差异,其取值范围为$0 < b<1$;应力罗德角$ \theta _\sigma = \arctan [\sqrt 3 (\sigma _2 -\sigma _3 ) / (2\sigma _1-\sigma _2-\sigma _3)]$,为主应力空间第一主应力和偏应力分量夹角. 当$b = 0$时,$\sigma_2 = \sigma _3 $,应力罗德角$\theta _\sigma \mbox{ =}0$,试样处于三轴压缩状态;当$b = 1$时,$\sigma _2 = \sigma _1$,应力罗德角$\theta _\sigma \mbox{ = }\pi /3$,试样处于三轴拉伸状态.本文进行的真三轴数值试验的$b$值分别取为0.0,0.25,0.5,0.75和1.0.
通过控制周期性边界的移动速率来控制试验各个方向应力的大小,进行两种类型的三轴试验,即等$p$等$b$试验与等$\sigma_3 $等$b$试验,其应力路径如图3 所示.
图3 真三轴试验应力路径...
Fig.3 Stress paths under true triaxial tests
2.2 峰值状态与临界状态
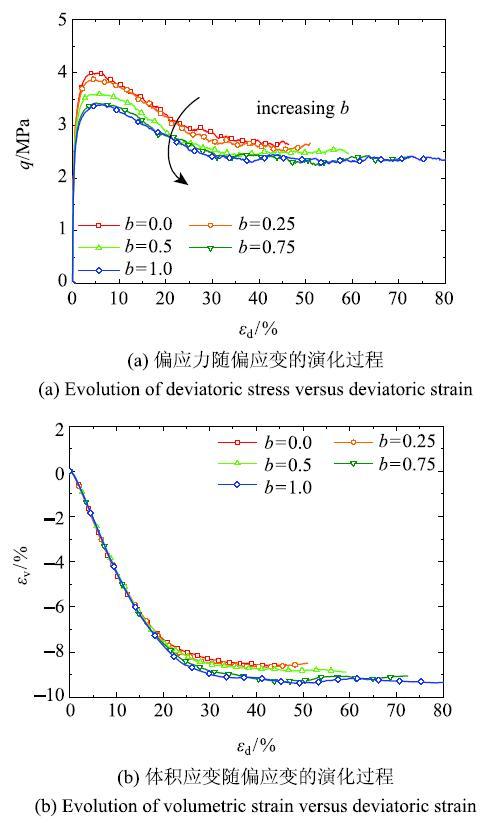
限于篇幅,本文仅列出围压为4 MPa的等$p$等$b$真三轴数值试验结果.图4 为各试样加载过程中,偏应力与体积应变随偏应变的演化过程.各试样在偏应变$\varepsilon _{d}$约为5{%}处,偏应力均达到峰值;在加载后期,试样的应力状态、体积应变均不再变化,因此可以认为各试样均达到了临界状态.随着中主应力系数$b$的增大,峰值及临界状态对应的偏应力减小,而体积应变的演化过程则近似唯一,不同中主应力系数$b$对应的试样均产生了明显的剪胀.
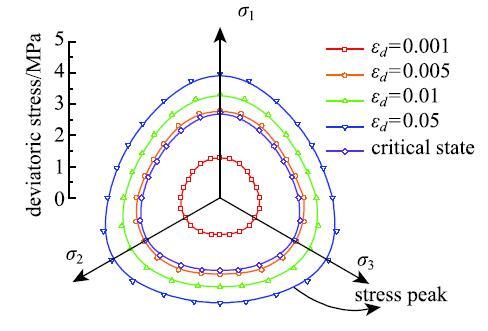
不同偏应变条件下,三维应力在$\pi$平面内呈现出不同大小的三角锥形,如图5 所示.一般而言三维应力路径下峰值状态和临界状态的应力比可以采用Lade-Duncan准则[44 ]和Matsuoka-Nakai准则[45 ]确定,也可以采用角隅函数近似模拟不同路径下的峰值和临界强度[16 ].图5 所示的三维应力特征符合真三轴试验的一般规律.
图4 真三轴条件下的应力应变曲线
Fig.4 Stress-strain relationship under true triaxial loading condition
图5 $\pi $平面内的应力演化过程...
Fig.5 Stress evolution at $\pi $ plane
采用不同围压、不同控制方式的真三轴数值试验数据绘制临界状态线(criticalstate line, CSL),如图6 所示.可以发现真三轴条件下的宏观临界状态线是唯一的,三维应力路径下宏观临界状态的唯一性已从理论研究[31 ]、数值试验[23 ]中得到了证实.
图6 临界状态线...
Fig.6 Critical state line
2.3 微观标量特征
从微观结构考量,分析配位数和接触力的分布特征,如图7 和图8 所示.
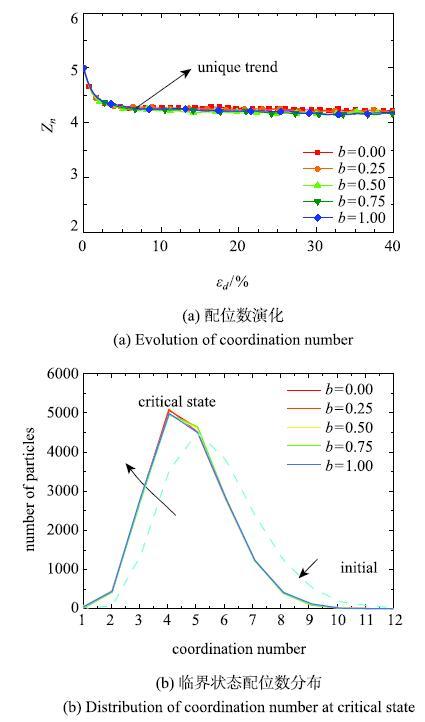
由图7 (a)可知,试样在各加载路径下的平均配位数随偏应变的演化规律一致,该细观结构量基本呈现出路径无关的特性;加载过程中,平均配位数出现了骤减,以使试样的接触状态能够适应加载的各向异性;试样达到临界状态后,其配位数基本保持不变.结合图7 (b)中配位数的分布情况,可以看出从初始状态到临界状态,配位数的众数发生了左移,试样的平均接触数有所减小.配位数能够在一定程度上反映试样内部的体积变化,配位数越高,则颗粒之间的相互作用更加紧密,因而颗粒周边的孔隙会减小;反之,配位数越低,颗粒周边则更容易产生较大的孔隙结构而产生体积膨胀.因此,从配位数角度来看,颗粒集合体在真三轴应力条件下的临界状态体积应变或是孔隙比与围压的关系是唯一的.
图7 配位数演化与分布...
Fig.7 Evolution and distribution of coordination number
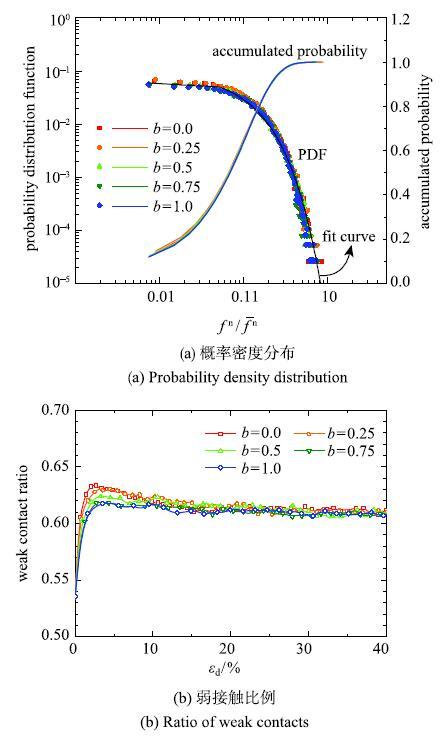
图8 临界状态接触力特征...
Fig.8 Contact force characteristics at critical state
Radjai等[24 ]发现了颗粒体系中的法向接触力可以根据其均值分为强接触系统和弱接触系统两部分:对于接触力大于均值的强接触系统,其分布概率密度函数呈指数下降,而弱接触力的概率密度则是幂律而变化的.围压为4MPa的试样加载到临界状态时,不同应力路径对应的试样内部法向接触力的概率密度分布及累积概率密度分布如图8 所示.可以发现,中主应力系数$b$对临界状态下的接触力分布几乎没有影响,同一横轴对应的数据点基本都集中在一个狭窄的区域.考虑试样在加载过程中的弱接触比例(图8 (b),这里取小于平均接触力的接触占系统总接触数的比例)的演化规律,可以发现在加载过程中试样的弱接触比例的变化趋势与中主应力系数$b$有关,在峰值点附近,中主应力系数$b$越小,试样内部的弱接触比例越高;但是到临界状态后,该比例趋于一致.
3 三维组构张量及强接触系统
3.1 接触组构张量定义
接触法向\textbf{n}}是颗粒接触最基本的特征,根据接触法向的空间的分布规律,可以定义接触法向概率密度函数$f$(\textbf{n}}).考虑接触的某一特征属性$g$(如接触力、枝向量长度等)在接触法向域内的分布特性,令$g$(\textbf{n}})代表\textbf{n}}方向该属性的均值,则其在所有方向的均值可定义为
$$\left\langle {g({\boldsymbol{n}})} \right\rangle =\int\limits_\varOmega {g({\boldsymbol{ n})f({\boldsymbol{ n}})}{{d}}}\varOmega \tag2$$
对于接触法向概率密度而言,其在域内所有方向的均值为1. Kanatani[46 ]基于布丰投针的方向问题,给出了一般化的接触法向概率密度的解析式
$$f({\boldsymbol{n}}) = \frac{1}{Q}[1 + {D_{ij}}{n_i}{n_j} +{D_{ijkl}}{n_i}{n_j}{n_k}{n_l} + \cdots]\tag3$$
即接触法向概率密度函数与$2m(m$为正整数,$m=1,2,3,\cdots)$阶张量${D_{{i_1}{i_2}\cdots{i_{2m}}}}$ 有关.三维条件下,$Q$取值为4$\pi$},张量${D_{{i_1}{i_2}\cdots{i_{2m}}}}$ 可表示为
$${D_{{i_1}{i_2}\cdots{i_{2m}}}}{{ = }}\frac{{2(2m) +1}}{{{2^{2m}}}}\left( \begin{array}{c}2(2m)\\2m\end{array} \right){2^{2m}}N_{{i_1}{i_2}\cdots{i_{2m}}}'\tag4$$
式中,${D_{{i_1}{i_2}\cdots{i_{2m}}}}$为2$m$阶组构张量的偏张量,组构张量${D_{{i_1}{i_2}\cdots{i_{2m}}}}$可以采用接触法向2$m$个分量积的平均值表示
$$N_{{i_1}{i_2}\cdots{i_{2m}}}^{} = \frac{1}{{{N_c}}}\sum\limits_{c =1}^{{N_c}} {n_{{i_1}}^cn_{{i_2}}^c\cdots n_{{i_{2m}}}^c} \tag5$$
一般而言,二阶的组构张量已经足够描述颗粒材料的接触各向异性,Oda[47 ]定义了适用于岩土颗粒材料的组构张量$\boldsymbol{\varPhi}$并给出了接触概率密度函数$f$(\textbf{n}})的数学表达式
$${\varPhi _{ij}} = \frac{1}{{{N_c}}}\sum\limits_{c \in {N_c}} {{n_i}{n_j}} = \int_\varOmega {f(n)} {n_i}{n_j}{d}\varOmega\tag6\\ f(n) = \frac{1}{{4\pi }}(1 + a_{ij}^c{n_i}{n_j})\tag7$$
式(8)为三维条件下的概率密度分布,参考式(5),组构的各向异性张量$a^c$可以写成 $$a_{ij}^c = \frac{{15}}{2}a_{ij}^{}\tag8$$式中,张量$a$为组构张量$\varPhi $的偏张量.
为进一步区分强弱接触系统的特性,引入一个阈值 $\zeta $,表示为法向接触力与其平均值$\bar f^n$ 的比值. 令子集 $S_{\zeta }$为平均法向接触力大于$\zeta \bar f^{n}$的接触的集合,则该子集对应的组构张量则定义为
$$\varPhi _{ij}^\zeta= \frac{1}{{N_c^\zeta }}\sum\limits_{c \in {S_\zeta }}{{n_i}{n_j}} \tag9$$
3.2 组构张量与应力张量
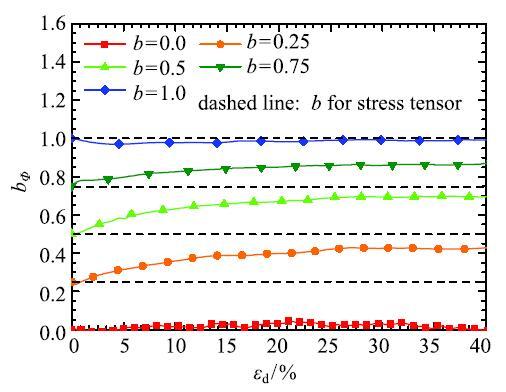
应力张量的中主应力系数与罗德角呈线性关系,描述了三个应力主值直接的差异.类比于应力张量的中主应力系数,组构张量的不同主值之间的差异系数可以表示为$${b_\varPhi } = \frac{{{\varPhi _2}-{\varPhi _3}}}{{{\varPhi _1}-{\varPhi_3}}}\tag10$$ 式中, $\varPhi _{i}$为组构张量的主值.图9 给出了$b_{\varPhi }$在不同的三维应力加载路径下的演化过程.由于采用的三轴试验为等$p$等$b$路径,故加载过程中应力的中主应力系数$b$是恒定不变的(图9 中虚线所示).对于非对称的三维应力路径($b$分别为0.25,0.5以及0.75),其组构的主值差异系数要高于中主应力系数.
图9 $b_{\varPhi }$随偏应变的演化曲线...
Fig.9 Evolution of $b_{\varPhi }$ along deviatoric strain$$K = {\boldsymbol{s}}:{\boldsymbol{ a}}\tag11$$
组构偏张量与应力偏张量的第一联合不变量在某一平均应力的临界状态条件下的三维应力空间内是与加载路径无关的[23 ,48 ],该不变量表示为
式中, ${\boldsymbol{s}}$为应力张量$\sigma $的偏张量.
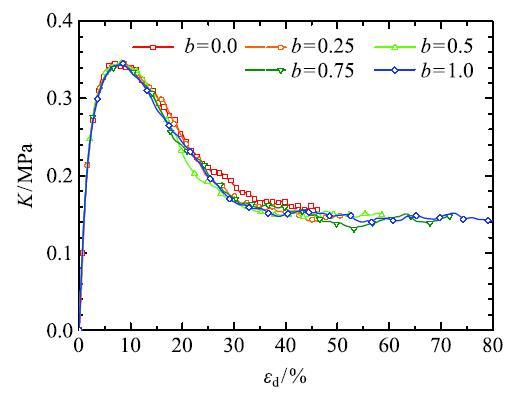
组构张量和应力张量的第一联合不变量$K$随剪应变的演化关系如图10 所示.可以发现,$K$值的演化过程不随应力路径的变化而变化,均在相同的剪应变处达到峰值,然后逐渐同步下降直至临界状态出现.在偏应力的演化过程(图4 )中,不同应力路径对应的曲线形状相似但具有不同的峰值和临界状态值,说明在三维加载应力路径下,应力的特征值具有相似性而非唯一性.而图10 则在应力张量与组构张量的联合不变量$K$中体现了三维空间加载的唯一演化过程.$K$值在临界状态下与试样的平均压力相关[23 ],而在本文的研究中进一步发现了在考虑单一平均压力加载的条件下,$K$值的唯一性不仅体现在临界状态,而且体现在三维加载的全\过程.
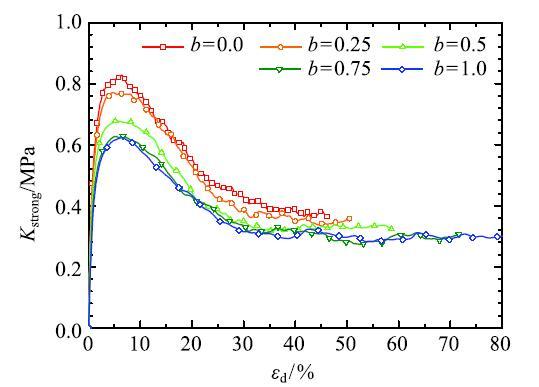
仅考虑强接触系统(取$\zeta =1)$时,其组构张量与应力张量的联合不变量$K_{strong}$的演化趋势却与偏应变存在非唯一的关系,如图11 所示.强接触系统的组构张量与应力张量的联合不变量与三维应力加载路径相关,且类似于偏应力的演化规律.这进一步说明了强接触系统与总接触系统之间的组构张量对宏观应力的贡献是不同的,强接触系统能够反映应力张量的不变量特性与三维强度准则,总接触系统则与宏观应力张量之间存在某种"互补"关系,二者的内积(即第一联合不变量)在三维空间内特定的偏应变条件下具有绝对的唯一性.
图10 组构与应力张量的联合不变量$K$的演化过程...
Fig.10 Evolution of joint invariant $K$ (between fabric tensor and stress tensor)
图11 强接触系统组构与应力张量的联合不变量$K_{strong$的演化过程\\
Fig.11 Evolution of joint invariant $K_{strong }$(between fabric tensor of strong contact system and stress tensor)
3.3 组构偏值及强弱接触体系的划分
偏张量的第二不变量可用来量化组构各向异性,令$a$为组构张量\textbf{$\varPhi$}的偏张量,则其第二不变量计算如下 $$a = \sqrt {\dfrac{3}{2}a:a} \tag12$$
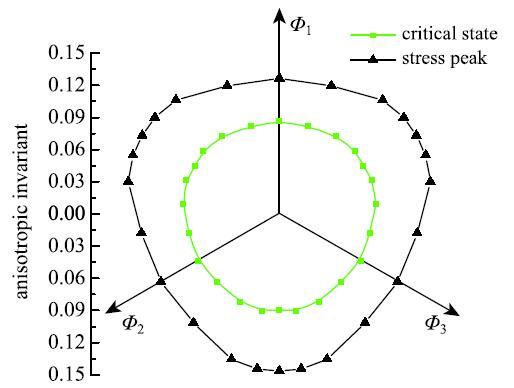
图12 为峰值状态和临界状态条件下组构张量\textbf{$\varPhi$}}的各向异性不变量(anisotropy invariant,即$a)$在$\pi$}平面内的分布情况, 其形状与应力张量在$\pi$}平面内的形状呈相反的趋势,这也进一步说明了组构张量与应力张量的"互补"关系.
图12 峰值状态与临界状态的组构张量各向异性不变量...
Fig.12 Anisotropy invariants of fabric tensor at $\pi $ plane for stress peak and critical state
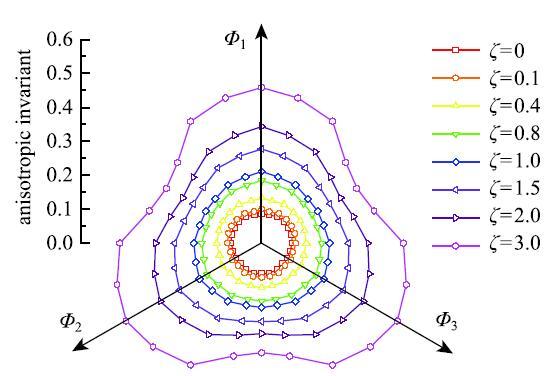
在前述的分析中,强弱接触体系的划分采用了传统的平均接触力,即$\zeta$=1.为了区分不同阈值划分的强接触系统组构张量的区别,图13 给出了不同阈值判定的强接触系统临界状态下$a$值在$\pi$}平面内的分布. 可以看出,不同$\zeta$值对应于不同的形状的临界面,且在$\zeta $为0.8$\sim$1.5时,其形状与应力张量在$\pi$}平面内的分布高度相似(图5 ). 当$\zeta$$<$0.8时,其形状类似于图13 ,体系内部存在大量对组构几何特性影响显著的弱接触,因此不能完全体现宏观的应力不变量三维临界状态特征;当$\zeta$$>$1.5时,组构张量的形状趋于畸形,这是由于此时系统内部的接触较少,强接触之间的联系较少,不能形成有效的微观结构来支撑整体的外荷载,尤其是对于三轴拉伸情况,$\zeta$$>$1.5时的$a$值在呈现出凹陷的趋势.
图13 临界状态下不同强接触系统组构张量偏值在$\pi $平面内的分布...
Fig.13 Deviatoric invariant of fabric tensor for different strong contact systems at $\pi $ plane
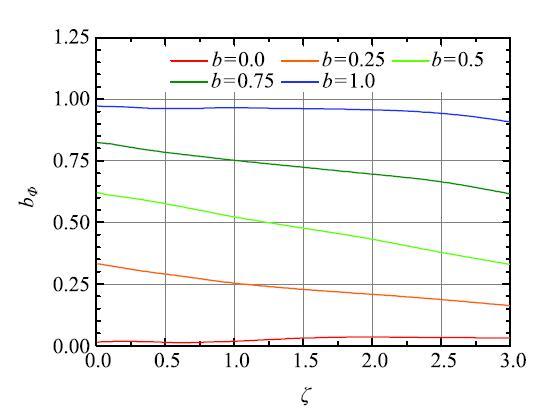
考虑不同强接触系统组构张量的主值差异,图14 为临界状态下不同$\zeta$值对应的强接触系统的$b_{\varPhi }$.除轴对称加载路径外,$b_{\varPhi }$随着$\zeta$的增大而减小,当$\zeta $为1或者略大于1时,$b_{\varPhi}$恰好为宏观应力张量的$b$值.因此,从三维张量主值的差异来看,大多数文献[24 ,25 ]中推荐强接触系统采用$\zeta$ = 1的值是合理的.结合本节前述分析,强弱接触系统的分界线可能存在一个取值范围,当0.8$\le \zeta \le$1.5时,组构与应力的共轴性、组构的各向异性等均基本能反映宏观的应力状态,但采用$\zeta$=1来划分强弱接触体系更为简单有效。
图14 临界状态下$b_{\varPhi }$与$\zeta $的关系...
Fig.14 Relationship between $b_{\varPhi }$ and $\zeta $ at critical state
4 结论与展望
本文采用离散元方法,进行了颗粒材料多种应力路径下的真三轴试验,并对等$p$等$b$应力路径的真三轴试验进行了多重的宏微观分析,重点研究了三维应力路径下颗粒体系的组构张量特性和强弱接触系统,具体结论如下:
(1)颗粒体系偏应力峰值状态和临界状态下的偏应力在不同的三维应力路径下存在差异,体积应变、临界状态线、配位数分布以及接触力分布等宏微观指标与加载路径无关;
(2)三维应力路径下组构张量与应力张量存在非共轴性,但二者的联合不变量在整个三维加载过程中的演化表现出独立于加载路径的一致性;
(3)强接触系统的组构张量更能反映宏观应力张量的特征,其主值差异系数、各向异性不变量等张量特征值与应力张量一致;强弱接触体系的组构张量对颗粒体系宏观响应的贡献不同,其分界点存在一定取值范围,但采用平均接触力较为简单合理.本文的研究结论中关于组构张量及强弱接触体系的三维分析得到的初步结论,有助于进一步理解颗粒体系内部的结构特征.在后续的研究中,作者拟从强弱接触体系的组构特征入手,辅以必要的物理试验,从微观层面出发分析模拟颗粒体系的本构行为.此外,颗粒形态对于颗粒体系的力学行为也有不可忽略的影响,本文所得的结论及颗粒体系后续的研究应在不同形态的颗粒体系中进行进一步分析与验证,使颗粒力学相关的体系更为完善.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
李广信 . 高等土力学 . 北京 : 清华大学出版社 , 2004
[本文引用: 1]
(Li Guangxin . Advanced Soil Mechanics. Beijing : Tsinghua University Presss , 2004 (in Chinese))
[本文引用: 1]
[2]
程展林 , 丁红顺 , 吴良平 . 粗粒土试验研究
. 岩土工程学报 , 2007 , 29 (8 ): 1151 -1158
URL
(Cheng Zhanlin Ding Hongshun Wu Liangping Experimental study on mechanical behaviour of granular material
. Chinese Journal of Geotechnical Engineering , 2007 , 29 (8 ): 1151 -1158 (in Chinese))
URL
[3]
黄茂松 , 姚仰平 , 尹振宇 等 .土的基本特性及本构关系与强度理论研究进展//中国土木工程学会全国土力学及岩土工程学术大会 , 2015
[本文引用: 1]
(Huang Maosong Yao Yangping Yin Zhenyu et al .Progress in the study of elementary mechanical behaviors, constitutive modeling and failure criterion of soils//The 12th National Conference on Soil Mechanics and Geotechnical Engineering of
China Civil Engineering Society , 2015 (in Chinese))
[本文引用: 1]
[4]
Darve F Laouafa F Instabilities in granular materials and application to landslides. Mechanics of Cohesive-frictional
Materials , 2000 , 5 (8 ): 627 -652
[本文引用: 1]
[5]
Nicot F Darve F A micro-mechanical investigation of bifurcation in granular materials
. International Journal of Solids & Structures , 2007 , 44 (20 ): 6630 -6652
URL
[6]
Nicot F Darve F The H-microdirectional model: Accounting for a mesoscopic scale
. Mechanics of Materials , 2011 , 43 (12 ): 918 -929
URL
[7]
Small M Walker D M Tordesillas A et al .Characterizing chaotic dynamics from simulations of large strain behavior of a granular material under biaxial compression
. Chaos: An Interdisciplinary Journal of Nonlinear Science , 2013 , 23 (1 ): 013113
[8]
Zhou W Liu J Ma G et al .Macroscopic and microscopic behaviors of granular materials under proportional strain path: A DEM study
. International Journal for Numerical and Analytical Methods in Geomechanics , 2016 , 40 (18 ): 2450 -2467
[本文引用: 1]
[9]
钱建固 , 黄茂松 . 轴对称状态下土体剪切带触发形成的分叉理论
. 岩土工程学报 , 2003 , 25 (4 ): 400 -404
URL
[本文引用: 1]
(Qian Jiangu Huang Maosong Bifurcation of soils at inception of shear band under axisymmetric conditions
. Chinese Jounal of Geotechnical Engineering , 2003 , 25 (4 ): 400 -404 (in Chinese))
URL
[本文引用: 1]
[10]
Drescher A Jong GDJD Photoelastic verification of a mechanical model for the flow of a granular material
. Journal of the Mechanics & Physics of Solids , 1972 , 20 (5 ): 337 -340
[本文引用: 2]
[11]
王雨婷 . 摩擦特性对颗粒材料宏细观力学特征的影响. [硕士论文]
. 武汉: 武汉大学 , 2017
[本文引用: 2]
(Wang Yuting The influence of friction properties on macro-mechanical characteristics of granular materials. [Master Thesis]
. Wuhan: Wuhan University , 2017 (in Chinese))
[本文引用: 2]
[12]
钱劲松 , 陈康为 , 张磊 . 粒料固有各向异性的离散元模拟与细观分析
. 力学学报 , 2018 , 50 (5 ): 1041 -1050
(Qian Jinsong Chen Kangwei Zhang Lei Simulation and micro-mechanics analysis of inherent anisotropy of granular by distinct element method
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (5 ): 1041 -1050 (in Chinese))
[13]
熊迅 ,李天密 ,马棋棋 等 . 石英玻璃圆环高速膨胀碎裂过程的离散元模拟
. 力学学报 ,2018 , 50 (3 ): 622 -632
URL
(Xiong Xun Li Tianmi Ma Qiqi et al .Discrete element simulations of the high velocity expension and fragmentation of qartz glass rings
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (3 ): 622 -632 (in Chinese))
URL
[14]
周博 , 黄润秋 , 汪华斌 等 . 基于离散元法的砂土破碎演化规律研究
. 岩土力学 , 2014 , 35 (9 ): 2709 -2716
(Zhou Bo Huang Ruiqiu Wang Huabin et al .Study of evolution of sand crushability based on discrete elements method
. Rock & Soil Mechanics,} 2014 , 35 (9 ): 2709 -2716 (in Chinese))
[15]
刘嘉英 , 马刚 , 周伟 等 . 抗转动特性对颗粒材料分散性失稳的影响研究
. 岩土力学 , 2017 , 38 (5 ): 1472 -1480
(Liu Jiaying Ma Gang Zhou Wei et al .Impact of rotation resistance on diffuse failure of granular materials
. Rock & Soil Mechanics , 2017 , 38 (5 ): 1472 -1480 (in Chinese))
[16]
刘嘉英 , 马刚 , 周伟 等 . 基于离散元的颗粒材料三维临界状态与剪胀特性研究
. 水利学报 , 2017 , 48 (9 ): 1107 -1117
[本文引用: 4]
(Liu Jiaying Ma Gang Zhou Wei et al .Three-dimensional critical state and dilatancy of granular materials based on DEM
. Journal of Hydraulic Engineering , 2017 , 48 (9 ): 1107 -1117 (in Chinese))
[本文引用: 4]
[17]
周伟 , 刘东 , 马刚 等 . 基于随机散粒体模型的堆石体真三轴数值试验研究
. 岩土工程学报 , 2012 , 34 (4 ): 748 -755
URL
[本文引用: 3]
(Zhou Wei Liu Dong Ma Gang et al .Numerical simulation of true triaxial tests on mechanical behaviors of rockfill based on stochastic granule model
. Chinese Journal of Geotechnical Engineering , 2012 , 34 (4 ): 748 -755 (in Chinese))
URL
[本文引用: 3]
[18]
Zhou W Ma G Chang X et al .Influence of particle shape on behavior of rockfill using a three-dimensional deformable DEM
. Journal of Engineering Mechanics , 2013 , 139 (12 ): 1868 -1873
URL
[19]
Ma G Zhou W Ng TT et al .Microscopic modeling of the creep behavior of rockfills with a delayed particle breakage model
. Acta Geotechnica , 2015 , 10 (4 ): 481 -496
[20]
Ma G Regueiro RA Zhou W et al .Role of particle crushing on particle kinematics and shear banding in granular materials
. Acta Geotechnica , 2018 (6 ): 1 -18
[本文引用: 1]
[21]
Rothenburg L Bathurst RJ Analytical study of induced anisotropy in idealized granular materials
. Géotechnique , 1989 , 39 (4 ): 601 -614
[本文引用: 1]
[22]
Chantawarangul K Numerical simulations of three-dimensional granular assemblies. [Ph D Thesis]. University,
of Waterloo , 1993
[本文引用: 1]
[23]
Zhao J Guo N Unique critical state characteristics in granular media considering fabric anisotropy
. Geotechnique , 2013 , 63 (8 ): 695 -704
URL
[本文引用: 5]
[24]
Radjai F Jean M Moreau JJ et al .Force Distributions in Dense Two-Dimensional Granular Systems
. Physical Review Letters , 1996 , 77 (2 ): 274 -277
[本文引用: 3]
[25]
Radjai F Wolf DE Jean M et al .Bimodal character of stress transmission in granular packings
. Physical Review Letters , 1998 , 80 (1 ): 61 -64
[本文引用: 2]
[26]
张敏 , 许成顺 , 杜修力 等 . 中主应力系数及应力路径对砂土剪切特性影响的真三轴试验研究
. 水利学报 , 2015 , 46 (9 ): 1072 -1079
URL
[本文引用: 1]
(Zhang Min Xu Chengshun Du Xiuli et al .True triaxial experimental research on shear behaviors of sand under different intermediate principal stresses and different stress paths
. Journal of Hydraulic Engineering , 2015 , 46 (9 ): 1072 -1079 (in Chinese))
URL
[本文引用: 1]
[27]
Huang X Hanley KJ O'Sullivan C et al . DEM analysis of the influence of the intermediate stress ratio on the critical-state behaviour of granular materials
. Granular Matter , 2014 , 16 (5 ): 641 -655
URL
[28]
Ma G Chang X L Zhou W et al .Mechanical response of rockfills in a simulated true triaxial test: A combined FDEM study
. Geomechanics & Engineering , 2014 , 7 (3 ): 317 -333
[29]
Zhou W Liu J Ma G et al . Three-dimensional DEM investigation of critical state and dilatancy behaviors of granular materials
. Acta Geotechnica , 2017 , 12 (3 ): 1 -14
[30]
姚仰平 , 张民生 , 万征 等 . 基于临界状态的砂土本构模型研究
. 力学学报 , 2018 , 50 (3 ): 589 -598
URL
(Yao Yangping Zhang Minsheng Wan Zheng et al .Constitutive model for sand based on the critical state
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (3 ): 589 -598 (in Chinese))
URL
[31]
Li X S Dafalias Y F Anisotropic critical state theory: Role of fabric
. Journal of Engineering Mechanics , 2012 , 138 (3 ): 263 -275
URL
[本文引用: 3]
[32]
白冰 , 周健 . 扫描电子显微镜测试技术在岩土工程中的应用与进展
. 电子显微学报 , 2001 , 20 (2 ): 154 -160
[本文引用: 1]
(Bai Bing Zhou Jian Application and progress of scanning electron microscopy testing technology in geotechnical engineering
. Journal of Chinese Electron Microscopy Society , 2001 , 20 (2 ): 154 -160 (in Chinese))
[本文引用: 1]
[33]
Yang J Yang ZX Li XS Quantifying and modelling fabric anisotropy of granular soils
. Géotechnique , 2008 , 58 (4 ): 237 -248
[34]
Hall SA Bornert M Desrues J et al .Discrete and continuum analysis of localised deformation in sand using X-ray CT and volumetric digital image correlation
. Géotechnique , 2010 , 60 (5 ): 11 -20
[35]
程展林 , 左永振 , 丁红顺 . CT技术在岩土试验中的应用研究
. 长江科学院院报 , 2011 , 28 (3 ): 33 -38
URL
(Chen Zhanlin Zuo Yongzhen Ding Hongshun Application research of CT technology in geotechnical experiment
. Journal of Yangtze River Scientific Research Institute , 2011 , 28 (3 ): 33 -38 (in Chinese))
URL
[36]
姜景山 , 程展林 , 左永振 等 . 粗粒土CT三轴流变试验研究
. 岩土力学 , 2014 (9 ): 2507 -2514
[本文引用: 1]
(Jiang Jinshan Cheng Zhanlin Zuo Youzhen et al .CT triaxial rheological test on coarse-grained soils. Rock & Soil Mechanics , 2014 (9 ): 2507 -2514 (in Chinese))
[本文引用: 1]
[37]
徐小敏 . 砂土液化及其判别的微观机理研究. [博士论文]
. 杭州: 浙江大学 , 2012
[本文引用: 2]
(Xu Xiaomin Study on the micromechanism of sand liquefaction and its evalution. [PhD Thesis]
. Hangzhou: Zhejiang University , 2012 (in Chinese))
[本文引用: 2]
[38]
戴北冰 , 杨峻 , 周翠英 . 松砂不稳定行为的数值模拟研究
. 岩土工程学报 , 2013 , 35 (9 ): 1737 -1745
URL
[本文引用: 1]
(Dai Beibing Yang Jun Zhou Cuiying Numerical study on instability behavior of sand
. Chinese Journal of Geotechnical Engineering , 2013 , 35 (9 ): 1737 -1745 (in Chinese))
URL
[本文引用: 1]
[39]
Sibille L Hadda N Nicot F et al .Granular plasticity, a contribution from discrete mechanics
. Journal of the Mechanics & Physics of Solids , 2015 , 75 : 119 -139
[本文引用: 1]
[40]
Latham JP Munjiza A Garcia X et al .Three-dimensional particle shape acquisition and use of shape library for DEM and FEM/DEM simulation
. Minerals Engineering , 2008 , 21 (11 ): 797 -805
URL
[本文引用: 1]
[41]
Zhou W Yang L Ma G et al .Macro-micro responses of crushable granular materials in simulated true triaxial tests
. Granular Matter , 2015 , 17 (4 ): 497 -509
[42]
Alaei E Mahboubi A A discrete model for simulating shear strength and deformation behaviour of rockfill material, considering the particle breakage phenomenon
. Granular Matter , 2012 , 14 (6 ): 707 -717
URL
[43]
Yuan C Chareyre B Darve F Pore-scale simulations of drainage in granular materials: Finite size effects and the representative elementary volume
. Advances in Water Resources , 2015 , 95 : 109 -124
[本文引用: 1]
[44]
Lade PV Duncan JM Elasto-plastic stress-strain theory for cohesionless soil
. ASCE Journal of the Geotechnical Engineering Division , 1975 , 101 (1 ): 1037 -1053
[本文引用: 1]
[45]
Matsuoka H Nakai T Relationship among Tresca, Mises, Mohr-Coulomb and Matsuoka-Nakai failure criteria
. Soils & Foundations , 2008 , 25 (4 ): 123 -128
[本文引用: 1]
[46]
Kanatani K I Stereological determination of structural anisotropy
. International Journal of Engineering Science , 1984 , 22 (5 ): 531 -546
[本文引用: 1]
[47]
Oda M Fabric tensor for discontinuous geological materials
. Soils and Foundations , 1982 , 22 (4 ): 96 -108
[本文引用: 1]
[48]
Li XS Dafalias YF Dissipation consistent fabric tensor definition from DEM to continuum for granular media
. Journal of the Mechanics and Physics of Solids , 2015 , 78 : 141 -153
[本文引用: 1]
1
2004
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
1
2004
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
Progress in the study of elementary mechanical behaviors, constitutive modeling and failure criterion of soils//The 12th National Conference on Soil Mechanics and Geotechnical Engineering of
1
2015
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
Progress in the study of elementary mechanical behaviors, constitutive modeling and failure criterion of soils//The 12th National Conference on Soil Mechanics and Geotechnical Engineering of
1
2015
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
Instabilities in granular materials and application to landslides. Mechanics of Cohesive-frictional
1
2000
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
A micro-mechanical investigation of bifurcation in granular materials
2007
The H-microdirectional model: Accounting for a mesoscopic scale
2011
Characterizing chaotic dynamics from simulations of large strain behavior of a granular material under biaxial compression
2013
Macroscopic and microscopic behaviors of granular materials under proportional strain path: A DEM study
1
2016
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
轴对称状态下土体剪切带触发形成的分叉理论
1
2003
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
轴对称状态下土体剪切带触发形成的分叉理论
1
2003
... 对岩土类颗粒材料力学特性的研究,主要通过土力学中土工测试的方法得到土体的强度和变形特性,进而建立合理的本构模型以描述岩土体宏观的连续介质特征.然而粗粒土、砂土等类型的岩土材料属于非关联弹塑性材料,是由大量粒径不等、形状不同的土石颗粒以不同的排列方式堆积而成,颗粒间没有黏聚力,高压下存在颗粒破碎,力学性质看似简单实则复杂,表现出的应力应变关系通常具有非线性、弹塑性、压硬性和剪胀性、应变硬化与应变软化、各向异性以及应力路径相关性等[1 - 3 ].在失稳破坏时,还存在液化、应变局部化等多种模式,涉及分岔与混沌问题[4 - 9 ].因此,若要对这类摩擦性颗粒材料建立一个统一的完备的本构模型,是极具挑\战的. ...
Photoelastic verification of a mechanical model for the flow of a granular material
2
1972
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
摩擦特性对颗粒材料宏细观力学特征的影响. [硕士论文]
2
2017
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
摩擦特性对颗粒材料宏细观力学特征的影响. [硕士论文]
2
2017
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
石英玻璃圆环高速膨胀碎裂过程的离散元模拟
2018
石英玻璃圆环高速膨胀碎裂过程的离散元模拟
2018
抗转动特性对颗粒材料分散性失稳的影响研究
2017
抗转动特性对颗粒材料分散性失稳的影响研究
2017
基于离散元的颗粒材料三维临界状态与剪胀特性研究
4
2017
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
... 不同偏应变条件下,三维应力在$\pi$平面内呈现出不同大小的三角锥形,如图5 所示.一般而言三维应力路径下峰值状态和临界状态的应力比可以采用Lade-Duncan准则[44 ]和Matsuoka-Nakai准则[45 ]确定,也可以采用角隅函数近似模拟不同路径下的峰值和临界强度[16 ].图5 所示的三维应力特征符合真三轴试验的一般规律. ...
基于离散元的颗粒材料三维临界状态与剪胀特性研究
4
2017
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
... 不同偏应变条件下,三维应力在$\pi$平面内呈现出不同大小的三角锥形,如图5 所示.一般而言三维应力路径下峰值状态和临界状态的应力比可以采用Lade-Duncan准则[44 ]和Matsuoka-Nakai准则[45 ]确定,也可以采用角隅函数近似模拟不同路径下的峰值和临界强度[16 ].图5 所示的三维应力特征符合真三轴试验的一般规律. ...
基于随机散粒体模型的堆石体真三轴数值试验研究
3
2012
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
基于随机散粒体模型的堆石体真三轴数值试验研究
3
2012
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
Influence of particle shape on behavior of rockfill using a three-dimensional deformable DEM
2013
Microscopic modeling of the creep behavior of rockfills with a delayed particle breakage model
2015
Role of particle crushing on particle kinematics and shear banding in granular materials
1
2018
... 颗粒材料往往是孔隙和颗粒固体共同构成的复杂体系,从材料内部的微观颗粒和接触到宏观的连续介质,颗粒材料涉及多个层次的结构体系,具有典型的多尺度特征.各个尺度之间相互联系与影响,决定了颗粒材料的宏观力学上的强度和变形等特性.从微观角度出发,探索颗粒材料本质属性,并建立起多重尺度结构之间的合理联系,有利于合理地描述颗粒材料的宏观本构行为.目前由于试验设备的完善及微观观测手段的发展,使对物理试验中材料的微细观结构的演化探究成为可能,如许多学者通过光弹试验研究颗粒材料内部的力链结构[10 ].此外,不连续数值模拟方法得到了广泛应用,如离散单元法(discreteelement method, DEM) [11 -16 ]、连续-离散耦合分析方法(combined finite and discreteelement method, FDEM) [17 -20 ]. 与有限元方法(finiteelement method, FEM)、有限差分方法(finite difference method,FDM)等不同,这类离散数值方法通过建立微观离散体之间的接触本构关系,并基于一定的运动学定律,对大量微观颗粒构成的集合进行显式计算并统计分析. ...
Analytical study of induced anisotropy in idealized granular materials
1
1989
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
Numerical simulations of three-dimensional granular assemblies. [Ph D Thesis]. University,
1
1993
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
Unique critical state characteristics in granular media considering fabric anisotropy
5
2013
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
... 采用不同围压、不同控制方式的真三轴数值试验数据绘制临界状态线(criticalstate line, CSL),如图6 所示.可以发现真三轴条件下的宏观临界状态线是唯一的,三维应力路径下宏观临界状态的唯一性已从理论研究[31 ]、数值试验[23 ]中得到了证实. ...
... 组构偏张量与应力偏张量的第一联合不变量在某一平均应力的临界状态条件下的三维应力空间内是与加载路径无关的[23 ,48 ],该不变量表示为 ...
... 组构张量和应力张量的第一联合不变量$K$随剪应变的演化关系如图10 所示.可以发现,$K$值的演化过程不随应力路径的变化而变化,均在相同的剪应变处达到峰值,然后逐渐同步下降直至临界状态出现.在偏应力的演化过程(图4 )中,不同应力路径对应的曲线形状相似但具有不同的峰值和临界状态值,说明在三维加载应力路径下,应力的特征值具有相似性而非唯一性.而图10 则在应力张量与组构张量的联合不变量$K$中体现了三维空间加载的唯一演化过程.$K$值在临界状态下与试样的平均压力相关[23 ],而在本文的研究中进一步发现了在考虑单一平均压力加载的条件下,$K$值的唯一性不仅体现在临界状态,而且体现在三维加载的全\过程. ...
Force Distributions in Dense Two-Dimensional Granular Systems
3
1996
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... Radjai等[24 ]发现了颗粒体系中的法向接触力可以根据其均值分为强接触系统和弱接触系统两部分:对于接触力大于均值的强接触系统,其分布概率密度函数呈指数下降,而弱接触力的概率密度则是幂律而变化的.围压为4MPa的试样加载到临界状态时,不同应力路径对应的试样内部法向接触力的概率密度分布及累积概率密度分布如图8 所示.可以发现,中主应力系数$b$对临界状态下的接触力分布几乎没有影响,同一横轴对应的数据点基本都集中在一个狭窄的区域.考虑试样在加载过程中的弱接触比例(图8 (b),这里取小于平均接触力的接触占系统总接触数的比例)的演化规律,可以发现在加载过程中试样的弱接触比例的变化趋势与中主应力系数$b$有关,在峰值点附近,中主应力系数$b$越小,试样内部的弱接触比例越高;但是到临界状态后,该比例趋于一致. ...
... 考虑不同强接触系统组构张量的主值差异,图14 为临界状态下不同$\zeta$值对应的强接触系统的$b_{\varPhi }$.除轴对称加载路径外,$b_{\varPhi }$随着$\zeta$的增大而减小,当$\zeta $为1或者略大于1时,$b_{\varPhi}$恰好为宏观应力张量的$b$值.因此,从三维张量主值的差异来看,大多数文献[24 ,25 ]中推荐强接触系统采用$\zeta$ = 1的值是合理的.结合本节前述分析,强弱接触系统的分界线可能存在一个取值范围,当0.8$\le \zeta \le$1.5时,组构与应力的共轴性、组构的各向异性等均基本能反映宏观的应力状态,但采用$\zeta$=1来划分强弱接触体系更为简单有效. ...
Bimodal character of stress transmission in granular packings
2
1998
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 考虑不同强接触系统组构张量的主值差异,图14 为临界状态下不同$\zeta$值对应的强接触系统的$b_{\varPhi }$.除轴对称加载路径外,$b_{\varPhi }$随着$\zeta$的增大而减小,当$\zeta $为1或者略大于1时,$b_{\varPhi}$恰好为宏观应力张量的$b$值.因此,从三维张量主值的差异来看,大多数文献[24 ,25 ]中推荐强接触系统采用$\zeta$ = 1的值是合理的.结合本节前述分析,强弱接触系统的分界线可能存在一个取值范围,当0.8$\le \zeta \le$1.5时,组构与应力的共轴性、组构的各向异性等均基本能反映宏观的应力状态,但采用$\zeta$=1来划分强弱接触体系更为简单有效. ...
中主应力系数及应力路径对砂土剪切特性影响的真三轴试验研究
1
2015
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
中主应力系数及应力路径对砂土剪切特性影响的真三轴试验研究
1
2015
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
DEM analysis of the influence of the intermediate stress ratio on the critical-state behaviour of granular materials
2014
Mechanical response of rockfills in a simulated true triaxial test: A combined FDEM study
2014
Three-dimensional DEM investigation of critical state and dilatancy behaviors of granular materials
2017
Anisotropic critical state theory: Role of fabric
3
2012
... 颗粒材料宏观上的复杂物理力学性质,是其微观结构的几何、拓扑、力学等统计特征决定的.基于颗粒间接触的组构张量(fabrictensor)自提出以来,已大量应用于岩土类颗粒材料的应力变形分析中:如Rothenburg和Bathurst[21 ]、Chantawarungal[22 ]分别推导了二维和三维条件下的应力-接触力-组构(stress-force-fabric)关系;Zhao和 Guo[23 ]研究了三维条件下颗粒体系内组构张量和应力张量的共轴性.颗粒体系内的接触体系存在强弱之分,一般以平均接触力为界,Radjai等[24 -25 ]针对二维颗粒体系的接触统计特征,研究了强弱接触体系的概率密度分布及其对应力张量的影响.真三轴应力路径能够反映颗粒材料的真实状态.三维应力路径下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件[16 -17 ,26 - 31 ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... ].此时颗粒体系的组构、强弱接触体系与宏观响应之间呈现出更复杂的联系[31 ],需要从微观层面进行更为细致的分析,进而研究三维应力路径下颗粒体系的应力变形机制. ...
... 采用不同围压、不同控制方式的真三轴数值试验数据绘制临界状态线(criticalstate line, CSL),如图6 所示.可以发现真三轴条件下的宏观临界状态线是唯一的,三维应力路径下宏观临界状态的唯一性已从理论研究[31 ]、数值试验[23 ]中得到了证实. ...
扫描电子显微镜测试技术在岩土工程中的应用与进展
1
2001
... 探究材料的微细观结构,着重于对材料内部的接触、孔隙、颗粒形状、颗粒位移等进行采集和分析,进而研究颗粒材料微观、细观层面的形态学特征、几何学特征和能量特征,目前主要有物理试验和数值试验两方面.在物理试验方面,国内外学者主要通过研发新型设备,发展微观观测手段,并提取不同试验条件下颗粒材料的内在结构信息,目前常用的观测手段有光弹试验、扫描电镜观测、X射线透视仪观测、X射线衍射仪观测、计算机X射线断层成像(computedtomography,CT)技术扫描、数字图像相关(digital imagecorrelation,DIC)技术成像、立体摄影、激光散斑法等[32 -36 ]. ...
扫描电子显微镜测试技术在岩土工程中的应用与进展
1
2001
... 探究材料的微细观结构,着重于对材料内部的接触、孔隙、颗粒形状、颗粒位移等进行采集和分析,进而研究颗粒材料微观、细观层面的形态学特征、几何学特征和能量特征,目前主要有物理试验和数值试验两方面.在物理试验方面,国内外学者主要通过研发新型设备,发展微观观测手段,并提取不同试验条件下颗粒材料的内在结构信息,目前常用的观测手段有光弹试验、扫描电镜观测、X射线透视仪观测、X射线衍射仪观测、计算机X射线断层成像(computedtomography,CT)技术扫描、数字图像相关(digital imagecorrelation,DIC)技术成像、立体摄影、激光散斑法等[32 -36 ]. ...
Quantifying and modelling fabric anisotropy of granular soils
2008
Discrete and continuum analysis of localised deformation in sand using X-ray CT and volumetric digital image correlation
2010
粗粒土CT三轴流变试验研究
1
... 探究材料的微细观结构,着重于对材料内部的接触、孔隙、颗粒形状、颗粒位移等进行采集和分析,进而研究颗粒材料微观、细观层面的形态学特征、几何学特征和能量特征,目前主要有物理试验和数值试验两方面.在物理试验方面,国内外学者主要通过研发新型设备,发展微观观测手段,并提取不同试验条件下颗粒材料的内在结构信息,目前常用的观测手段有光弹试验、扫描电镜观测、X射线透视仪观测、X射线衍射仪观测、计算机X射线断层成像(computedtomography,CT)技术扫描、数字图像相关(digital imagecorrelation,DIC)技术成像、立体摄影、激光散斑法等[32 -36 ]. ...
粗粒土CT三轴流变试验研究
1
... 探究材料的微细观结构,着重于对材料内部的接触、孔隙、颗粒形状、颗粒位移等进行采集和分析,进而研究颗粒材料微观、细观层面的形态学特征、几何学特征和能量特征,目前主要有物理试验和数值试验两方面.在物理试验方面,国内外学者主要通过研发新型设备,发展微观观测手段,并提取不同试验条件下颗粒材料的内在结构信息,目前常用的观测手段有光弹试验、扫描电镜观测、X射线透视仪观测、X射线衍射仪观测、计算机X射线断层成像(computedtomography,CT)技术扫描、数字图像相关(digital imagecorrelation,DIC)技术成像、立体摄影、激光散斑法等[32 -36 ]. ...
砂土液化及其判别的微观机理研究. [博士论文]
2
2012
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
... ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
砂土液化及其判别的微观机理研究. [博士论文]
2
2012
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
... ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
松砂不稳定行为的数值模拟研究
1
2013
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
松砂不稳定行为的数值模拟研究
1
2013
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
Granular plasticity, a contribution from discrete mechanics
1
2015
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
Three-dimensional particle shape acquisition and use of shape library for DEM and FEM/DEM simulation
1
2008
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
Macro-micro responses of crushable granular materials in simulated true triaxial tests
2015
A discrete model for simulating shear strength and deformation behaviour of rockfill material, considering the particle breakage phenomenon
2012
Pore-scale simulations of drainage in granular materials: Finite size effects and the representative elementary volume
1
2015
... 除了物理试验中微细观观测手段外,采用计算机进行不连续数值分析研究颗粒材料的微细观结构也在近几十年得到了长足进步.这类方法的基本思想是将不连续介质离散化为独立的单元,通过对各个独立结构之间的相互作用进而对整体的力学性质进行分析研究.对于岩土类颗粒材料,颗粒离散单元法(discrete element method,DEM)得到了广泛应用,一般而言,离散单元法中的独立单元为颗粒或者块体结构,具有一定的微观几何形状,单元之间通过一定的接触判断发生相互作用,其力和位移之间的关系遵循经典的牛顿运动定律.离散单元法中各组成单元之间可以相对运动,并且不需要满足位移连续和变形协调等条件,模拟条件近似于颗粒材料离散本质,有助于复杂力学问题的求解,如有限变形、非线性应力应变关系、弹塑性耦合等[37 ].目前颗粒离散元法为研究岩土颗粒材料常用的数值手段,将砂土、粗粒土等颗粒材料简化为球形或者圆盘形状,虽然与实际情况有所偏差,但是已经能够基本描述岩土类颗粒材料的应力变形特征,其基本规律较为符合光弹试验结果[10 ].颗粒离散元法能够很好地再现摩擦性颗粒材料的剪胀、液化、剪切带以及临界状态等特性[8 ,11 ,16 -17 ,23 ],并且可重复性高,适用于多种复杂的边界条件,能够容易地获得颗粒的接触、运动等信息,在探究材料的微细观结构方面优势突出.如戴北冰等[38 ]针对松散砂土的不稳定行为和静态液化现象,开展了多组的双轴剪切试验离散元数值模拟,从宏微观的角度研究了松砂不稳定行为的各种影响因素及其发生机理.徐小敏[37 ]分析了砂土静态液化及动力液化条件下的微观机理.Sibille等[39 ]基于离散元结果采用微观的二阶功理论,对颗粒材料的发生静态液化时的接触破坏点分布进行了分析.经过不断改进后,颗粒离散元法也能够对颗粒形状、颗粒破碎、颗粒间黏聚力、液桥力等特性进行表征与研究[40 - 43 ]. ...
Elasto-plastic stress-strain theory for cohesionless soil
1
1975
... 不同偏应变条件下,三维应力在$\pi$平面内呈现出不同大小的三角锥形,如图5 所示.一般而言三维应力路径下峰值状态和临界状态的应力比可以采用Lade-Duncan准则[44 ]和Matsuoka-Nakai准则[45 ]确定,也可以采用角隅函数近似模拟不同路径下的峰值和临界强度[16 ].图5 所示的三维应力特征符合真三轴试验的一般规律. ...
Relationship among Tresca, Mises, Mohr-Coulomb and Matsuoka-Nakai failure criteria
1
2008
... 不同偏应变条件下,三维应力在$\pi$平面内呈现出不同大小的三角锥形,如图5 所示.一般而言三维应力路径下峰值状态和临界状态的应力比可以采用Lade-Duncan准则[44 ]和Matsuoka-Nakai准则[45 ]确定,也可以采用角隅函数近似模拟不同路径下的峰值和临界强度[16 ].图5 所示的三维应力特征符合真三轴试验的一般规律. ...
Stereological determination of structural anisotropy
1
1984
... 对于接触法向概率密度而言,其在域内所有方向的均值为1. Kanatani[46 ]基于布丰投针的方向问题,给出了一般化的接触法向概率密度的解析式 ...
Fabric tensor for discontinuous geological materials
1
1982
... 一般而言,二阶的组构张量已经足够描述颗粒材料的接触各向异性,Oda[47 ]定义了适用于岩土颗粒材料的组构张量$\boldsymbol{\varPhi}$并给出了接触概率密度函数$f$(\textbf{n}})的数学表达式 ...
Dissipation consistent fabric tensor definition from DEM to continuum for granular media
1
2015
... 组构偏张量与应力偏张量的第一联合不变量在某一平均应力的临界状态条件下的三维应力空间内是与加载路径无关的[23 ,48 ],该不变量表示为 ...