串联式叉型滞后簇发振荡及其动力学机制1)
江苏大学土木工程与力学学院,江苏镇江 212013
SERIES-MODE PITCHFORK-HYSTERESIS BURSTING OSCILLATIONS AND THEIR DYNAMICAL MECHANISMS1)
中图分类号: O322
文献标识码: A
版权声明: 2019 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
作者简介: 2) 韩修静,副教授,主要研究方向:动力学与控制. E-mail:xjhan@mail.ujs.edu.cn
展开
摘要
簇发振荡是自然界和科学技术中广泛存在的快慢动力学现象,其具有与通常的振荡显著不同的特性.根据不同的动力学机制可将其分为多种模式,例如,点-点型簇发振荡和点-环型簇发振荡等.叉型滞后簇发振荡是由延迟叉型分岔诱发的一类具有简单动力学特性的点-点型簇发振荡.研究以多频参数激励Duffing系统为例,旨在揭示一类与延迟叉型分岔相关的具有复杂动力学特性的簇发振荡,即串联式叉型滞后簇发振荡.考虑了一个参激频率是另一个的整倍数情形,利用频率转换快慢分析法得到了多频参数激励Duffing系统的快子系统和慢变量,分析了快子系统的分岔行为.研究结果表明,快子系统可以产生两个甚至多个叉型分岔点;当慢变量穿越这些叉型分岔点时,形成了两个或多个叉型滞后簇发振荡;这些簇发振荡首尾相接,最终构成了所谓的串联式叉型滞后簇发振荡.此外,分析了参数对串联式叉型滞后簇发振荡的影响.
关键词:
Abstract
Bursting oscillations is a spontaneous physical phenomenon existing in natural science, which has various patterns according to their dynamical regimes. For instance, bursting of point-point type means bursting patterns related to transition behaviors among different equilibrium attractors. Pitchfork-hysteresis bursting, induced by delayed pitchfork bifurcation, is a kind of point-point type bursting pattern showing simple dynamical characteristics. The present paper takes the Duffing system with multiple-frequency parametric excitations as an example in order to reveal bursting patterns, related to delayed pitchfork bifurcation, showing complex characteristics, i.e., the series-mode pitchfork-hysteresis bursting oscillations. We considered the case when one excitation frequency is an integer multiple of the other, obtained the fast subsystem and the slow variable of the Duffing system by frequency-transformation fast-slow analysis, and analyzed bifurcation behaviors of the fast subsystem. Our study shows that two or multiple pitchfork bifurcation points can be observed in the fast subsystem, and thus two or multiple pitchfork-hysteresis bursting patterns are created when the slow variable passes through these points. In particular, the pitchfork-hysteresis bursting patterns are connected in series, and as a result, the so-called series-mode pitchfork-hysteresis bursting oscillations are generated. Besides, the effects of parameters on the series-mode pitchfork-hysteresis bursting oscillations are analyzed. It is found that the damping of the system and the maximum excitation amplitude show no qualitative impact on corresponding dynamical mechanisms, while the smaller one may lead to vanish of busting oscillations. Our findings reveal the road from simple dynamical characteristics of point-point type bursting oscillation related to complex one, thereout, a complement and expansion for nowadays bursting dynamics is obtained.
Keywords:
簇发振荡,即大幅振荡与小幅振荡交错演变的复杂振荡模式,最早见于Belousov-Zhabotinsky化学反应系统[1-3].自Hodgkin和Huxley[4]构建两时间尺度模型再现了实验中所观测到的神经纤维的簇放电活动,多时间尺度复杂动力学行为,特别是其中的簇发振荡,逐渐受到广泛关注[5- 7].随后,簇发振荡作为自然科学中存在的自发物理现象在众多领域相继被报道[8-9].例如,激光焊接中通过无源电探针对等离子体电信号的功率谱及频域分析得到的等离子体振荡特性[10],在欧洲核子研究中心的大型强子对撞机实验中观测到的强子物质温度的周期振荡[11],神经系统中实现信息处理及生物功能的电活动[12],气候数据中的复杂振荡行为[13],输电塔和塔线的耦合振荡[14-15]等等.
在各种簇发振荡模式中,"点-点"型簇发振荡是一大类较为简单的簇发振荡,它的产生与系统在两个或多个平衡点吸引子之间的相互转迁有关[16-17].而这种转迁通常由鞍结分岔和亚临界Hopf分岔等分岔模式诱发,由此形成了具有不同动力学机制的"点-点"型簇发振荡,例如"fold/fold"型[18- 20]和"subH/subH"型[21-23].此外,系统在不同平衡点之间的转迁亦可由延迟分岔加以调控.因而,可以得到与延迟分岔相关的各种"点-点"型簇发振荡[24-26].最近,文献[27]探讨了一类具有复杂动力学特性的"点-点"型簇发振荡.研究发现,与折分岔相关的S形平衡点滞后曲线的上、下稳定支在一定的条件下能够发生连续的"弯折",其特征是在上、下稳定支中出现了多个"极值点".这一特征使簇发的准静态过程产生振荡,并由此揭示了与折分岔相关的具有简单动力学特性的"点-点"型簇发振荡通向复杂性的道路.
\begin{equation} \label{eq1} \left.{\begin{array}{l} \dot {x} = y \\ \dot {y} = \beta _1 \cos (\omega _1 t)x-[1 + \beta _2 \cos (\omega _2 t)]x^3-\delta y \\ \end{array}}\right\} \end{equation}
其中$\beta _1 \cos (\omega _1 t)$和$\beta _2 \cos (\omega _2 t)$均是慢变周期参数激励. 当仅含慢变参数激励$\beta _1 \cos (\omega _1 t)$时,系统1})能够产生"叉型滞后"簇发振荡[30],这是一种与延迟叉型分岔相关的简单的"点-点"型簇发振荡模式. 本文以系统1})为例,围绕多频参数激励下的簇发动力学问题,旨在揭示与延迟叉型分岔相关的复杂的"点-点"型簇发振荡,即所谓的"串联式叉型滞后簇发振荡". 我们将说明,多频参数激励会导致系统1})的快子系统其分岔行为的复杂化,例如产生多个叉型分岔点. 特别地,每一个叉型分岔点可以诱发一个简单的"叉型滞后"簇发振荡,它们首尾相接形成了具有复杂动力学特性的"串联式叉型滞后簇发振荡".
1 串联式叉型滞后簇发振荡
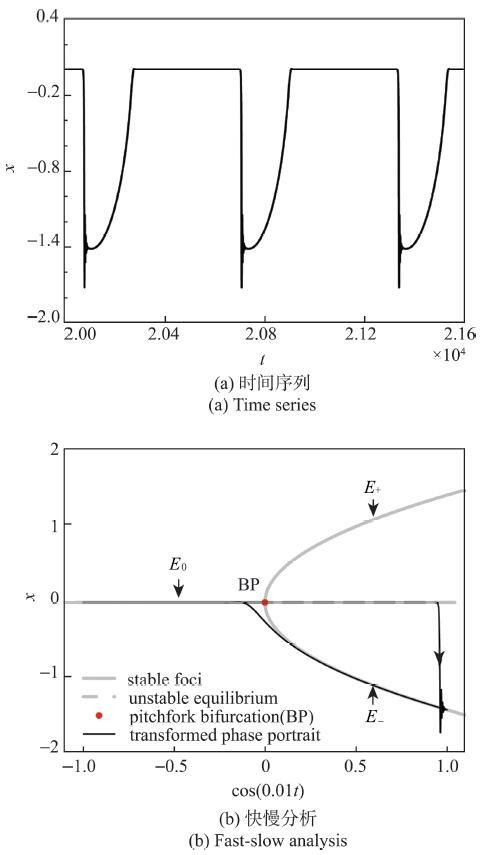
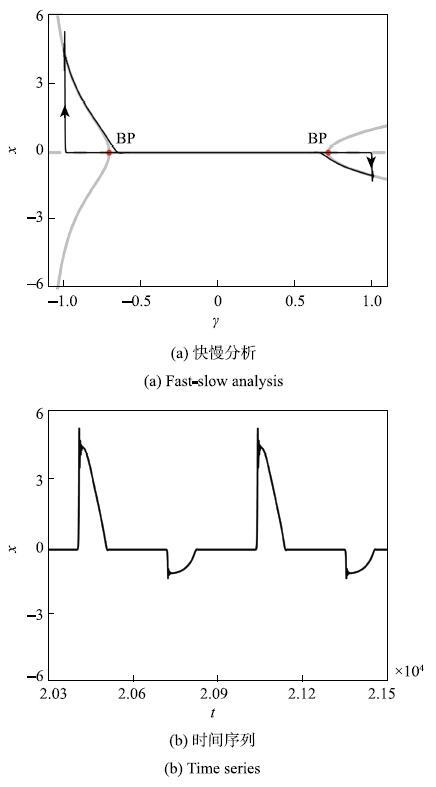
图1(a)给出了$\beta _2 = 0$,即系统1})在慢变周期参数参数激励$\beta _1 \cos (\omega _1 t)$作用下的簇发振荡. 由于参数激励$\beta _1 \cos (\omega _1 t)$的频率较低,与系统的固有频率相比存在量级差异,因此, 此时的系统1})是频率两尺度非线性系统,其中低频激励$\beta _1 \cos (\omega _1 t)$可视为慢变量,而快子系统是$\dot {x} = y, ~\dot {y} = \gamma x-x^3-\delta y$,其中$\gamma $是控制参数. 当慢变量$\beta _1 \cos (\omega _1 t)$增大并穿越该快子系统的叉型分岔点$\gamma = 0$时,出现了延迟叉型分岔现象,并进一步形成了不稳定的平衡点与稳定平衡点之间的滞后(hysteresis). 这正是"叉型滞后"簇发振荡产生的重要原因,见图1(b).
图1 "叉型滞后"簇发振荡.系统参数固定在$\delta = 0.6$,$\beta _1 = 2.0$,$\beta _2 = 0$,$\omega _1 = 0.01$,$\omega _2 = 0.01$...
Fig. 1 The pitchfork-hysteresis bursting oscillations. The system parameters are fixed at $\delta = 0.6$,$\beta _1 = 2.0$,$\beta _2 = 0$,\\ $\omega _1 = 0.01$ and $\omega _2 = 0.01$...
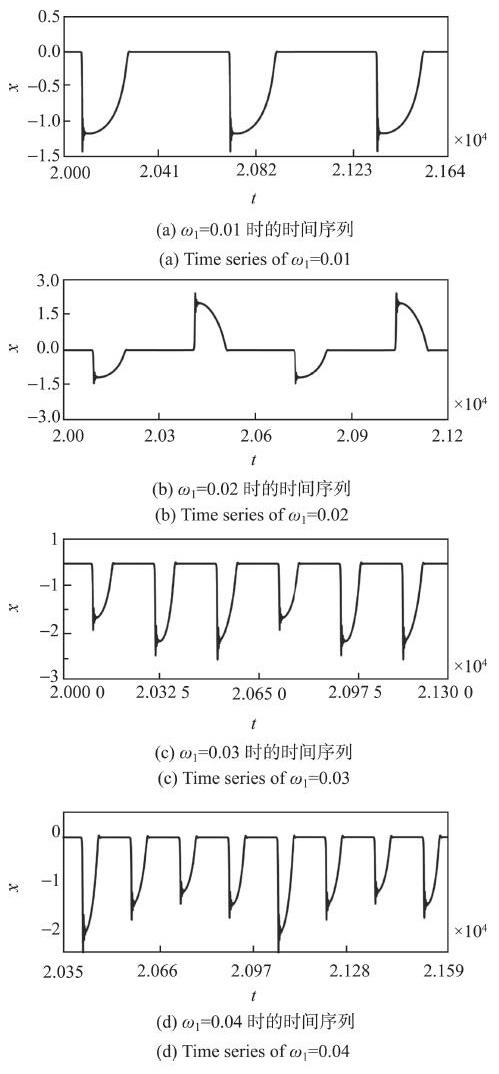
当系统1})在低频参数激励$\beta _1 \cos (\omega _1 t)$和$\beta _2 \cos (\omega _2 t)$的联合作用下时,"叉型滞后"簇发振荡将呈现出复杂的动力学特性. 特别地,在簇发振荡的每一周期演化中,可以观测到两个甚至多个与准静态过程相交替的大幅振荡. 例如,对于固定的$\delta = 0.6$,$\beta _1 = 2.0$,$\beta _2 = 0.5$,$\omega _2 = 0.01$,图2给出了随着$\omega _1 $增大时的一组簇发振荡模式:当$\omega _1 = \omega _2 = 0.01$时,系统产生了与图1中相似的簇发振荡模式(见图2(a));然而,当$\omega _1 = 2\omega _2 = 0.02$时,在簇发振荡的每一周期中,大幅振荡的数量从1个变成了2个(见图2(b));当$\omega _1 = 3\omega _2 = 0.03$时,大幅振荡的数量进一步变成了3个(见图2(c));当$\omega _1 = 4\omega _2 = 0.04$时,大幅振荡的数量又变成了4个(见图2(d)). 综上所述,当$\omega _1 $是$\omega _2 $的整倍数时,在簇发振荡的每一周期中,大幅振荡的数量等于频率比$\omega _1 / \omega _2 $. 需要指出的是,这种类似的簇发振荡以及上述所描述的演化规律在很大的参数范围内均可观测到.
图2 系统从(a)"叉型滞后"簇发振荡向(b-d)"串联式叉型滞后"簇发振荡的转迁...
Fig.2 Transition from "pitchfork-hysteresis" bursting oscillations (a) to "series-mode pitchfork-hysteresis" bursting oscillations (b-d) ...
图3
Fig.3 Fast-slow analysis of the bursting oscillations in
通过频率转换快慢分析法[31]探讨以图2为代表的簇发振荡的动力学机制. 所谓的频率转换快慢分析法是指根据各慢变激励的频率关系,通过De公式将含有两个及以上的慢变激励(即慢变量)的频域两尺度快慢系统转化为仅含一个慢变激励的快慢系统进行分析的思想方法. 由于转化后的快慢系统仅含一个慢变量,因此可接着采用经典的快慢分析法[6]对其进行分析,进而可以揭示原系统中的簇发动力学.
首先,考虑图2(a)中的簇发振荡. 由于此时系统具有相同的激励频率,故可将慢变激励$\cos (\omega t)$视为慢变量,其中$\omega = \omega _1 = \omega _2 $. 基于此,可得快子系统
\begin{equation} \label{eq2} \left. {\begin{array}{l} \dot {x} = y \\ \dot {y} = \beta _1 \gamma x-(1 + \beta _2 \gamma )x^3-\delta y \\ \end{array}} \right\} \end{equation}
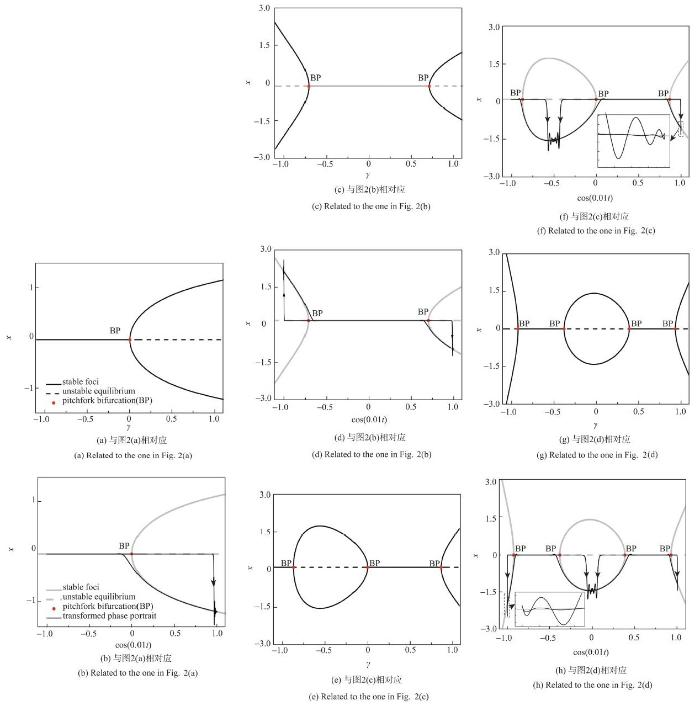
其中,$\gamma $是控制参数,而参数$\beta _{1,2} $和$\delta $与图2(a)中的相同. 图3(a)给出了快子系统2})关于控制参数$\gamma $的分岔图:一个叉型分岔点(记为BP)发生于$\gamma = 0$. 在图3(b)中,与图2(a)相对应的转换相图被叠加到分岔图之上,由此说明了图2(a)中的簇发振荡亦属于"叉型滞后",一种简单的簇发振荡模式.
接着,分析图2(b)中的簇发振荡. 注意到此时$\omega _1 = 2\omega _2 $,因此按照频率转换快慢分析法,可将$\cos (\omega _2 t)$视为慢变量. 此外,由于$\cos (\omega _1 t) = 2[\cos (\omega _2 t)]^2 - 1$,故可得快子系统
$$\left. {\begin{array}{l} \dot {x} = y \\ \dot {y} = \beta _1 (2\gamma ^2-1)x-(1 + \beta _2 \gamma )x^3-\delta y \\ \end{array}} \right\}(3) $$
其中,$\gamma $是控制参数,其他参数与图2(b)中的相同.如图3(c)所示,此时的快子系统呈现出两个叉型分岔点(均记为BP). 当慢变量$\cos (\omega _2 t)$穿越这两个分岔点时,分别形成了"叉型滞后"簇发振荡;它们首尾相接构成了图2(b)所示的"串联式叉型滞后"簇发振荡(见图3(d)).
然后,揭示图2(c)中的簇发振荡. 根据频率关系$\omega _1 = 3\omega _2 $,选取$\cos (\omega _2 t)$为慢变量. 同时,注意到$\cos (\omega _1 t) = 4[\cos (\omega _2 t)]^3-3\cos (\omega _2 t)$,故可得快子系统
$$ \left. {\begin{array}{l} \dot {x} = y \\ \dot {y} = \beta _1 (4\gamma ^3-3\gamma )x-(1 + \beta _2 \gamma )x^3 - \delta y \\ \end{array}} \right\}(4) $$
其中,$\gamma $是控制参数,其他参数与图2(c)中的相同. 此时,快子系统产生了3个叉型分岔点(见图3(e)).每个叉型分岔点对应着一个简单的"叉型滞后"簇发振荡(见图3(f)), 由此得到了图2(c)所示的包含3个简单簇发的"串联式叉型滞后"簇发振荡.
最后,探讨图2(d)中的簇发振荡. 采用上述类似的分析方法可知,慢变量是$\cos (\omega _2 t)$,快子系统是
$$ \left. {\begin{array}{l} \dot {x} = y \\ \dot {y} = \beta _1 (1-8\gamma ^2 + 8\gamma ^4)x-(1 + \beta _2 \gamma )x^3-\delta y \\ \end{array}} \right\}(5) $$
其中,$\gamma $是分岔参数,其他的参数同图2(d).此时的快子系统产生了4个叉型分岔点, 而这是诱发图2(d)所示的包含4个简单簇发的"串联式叉型滞后"簇发振荡的重要原因,见图3(g)和图3(h).
综上所述,延迟叉型分岔的数量的不断增多,导致了如图2所示的簇发振荡, 其大幅振荡数量的不断增多;其中,延迟时间的长短决定了时间序列中出现的跳跃区间的大小. 需要说明的是,延迟叉型分岔的延迟时间可以按照文献[32,33]给出的方法严格加以分析. 然而,由于分析的复杂性且与本文的主题相悖,故在此不作探讨.
另一方面,当延迟分岔行为结束之后,轨线便向非零稳定支转迁. 注意到这里的非零稳定支是"焦点",因此轨线"盘旋"地向非零支转迁,从而产生了相应的振荡现象. 特别地,根据文献[34]的结论,易知,在本文所考虑的参数范围内,非零稳定支总是"焦点";因此, 这种振荡行为(或强或弱)总是存在的(例如,见图3(f)和图3(h)).
2 参数对簇发振荡的影响
注意到阻尼$\delta (\delta > 0)$和激励振幅$\beta _{1,2} $是系统1})的参数,因此这些参数的变化可能会引起"串联式叉型滞后"簇发振荡的定性变化. 本部分重点分析参数对固定频率下的"串联式叉型滞后"簇发振荡的影响,以此揭示"串联式叉型滞后"簇发振荡的转迁.
首先,考虑$\delta $对"串联式叉型滞后"簇发振荡的影响. 经分析容易知道,快子系统其稳定的平衡点可以是焦点和结点,这与参数$\delta $有关[30]. 然而,平衡点的稳定性和分岔与$\delta $无关. 因此,$\delta $的变化无法引起"串联式叉型滞后"簇发振荡的定性改变.
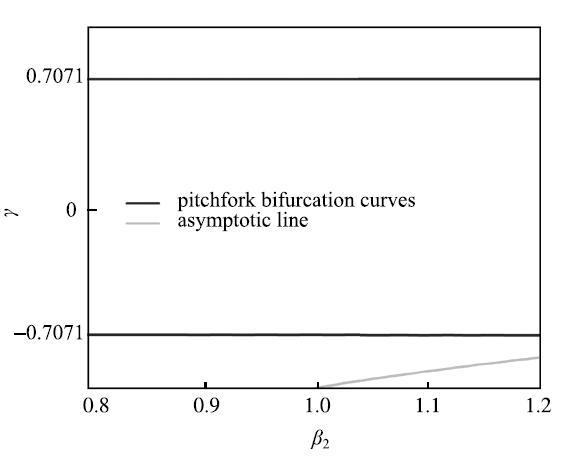
接下来,探讨激励振幅对"串联式叉型滞后"簇发振荡的影响. 作为一个例子,我们考虑图2(b)中的"串联式叉型滞后"簇发振荡. 首先分析$\beta _2 $对簇发动力学的影响. 图4给出了快子系统(3)关于$\gamma $和$\beta _2 $的两参数分岔集,其中$\delta $和$\beta _1 $的值固定不变,即与图2(b)中的相同. 如图所示,当$\beta _2 < 1$(例如$\beta _2 = 0.9$,见图5(a)时,由于快子系统(3)只含有两个叉型分岔点, 故而只能得到如图2(b)所示的由两个简单簇发形式组成的"串联式叉型滞后"簇发振荡(见图5(b)). 因此,图2(b)给出的是系统在$\beta _2 < 1$时的簇发振荡的典型代表.
图4 快子系统(3)在参数平面$(\beta _2 ,\gamma )$上的分岔集...
Fig.4 Bifurcation sets of the fast subsystem (3) on parameter plane $(\beta _2 ,\gamma )$ ...
图5 当$\beta _2 = 0.9$时,系统(1)中的"串联式叉型滞后"簇发振荡...
Fig.5 "Series-mode pitchfork-hysteresis" bursting oscillations of system (1) for $\beta _2 = 0.9$...
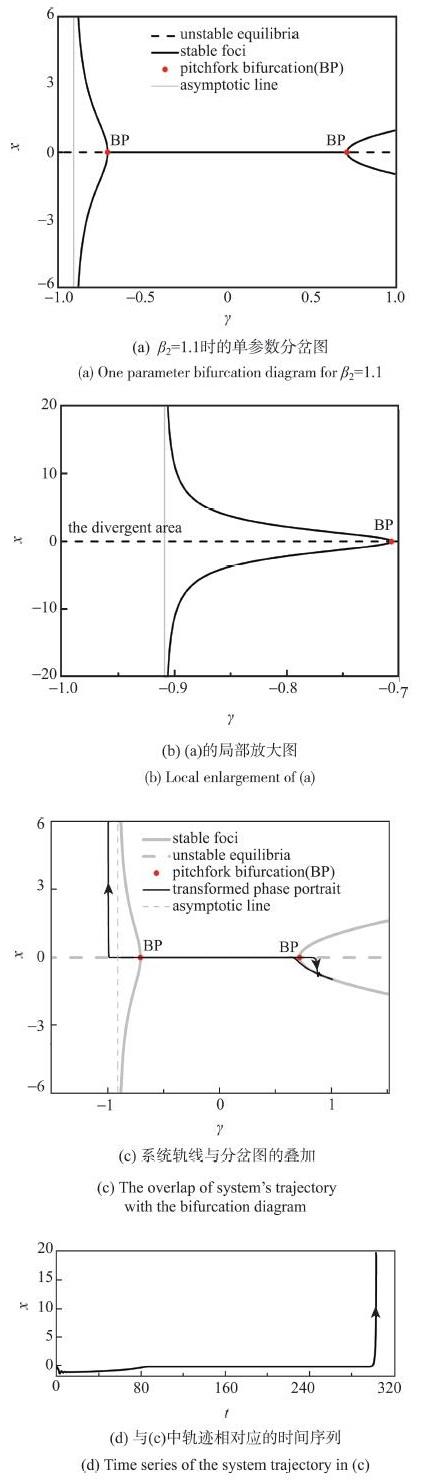
图6 "渐近线"的存在将导致簇发振荡的消失...
Fig.6 The existence of asymptotic line leads to the disappearance of bursting oscillations...
当$\beta _2 > 1$时,如图4所示,快子系统(3)出现了第3条分岔曲线,即与分岔值为负的叉型分岔相关的非零平衡点曲线的"渐近线"$1 + \beta _2 \gamma = 0$. 渐近线的存在定性地改变了快子系统(3)的动力学行为,因而会对簇发振荡产生重要影响. 图6(a)和图6(b)给出了$\beta _2 = 1.1$时快子系统(3)在"渐近线"附近的动力学行为. 可以看到,当控制参数$\gamma $接近临界值$\gamma _{c} =-0.909~ 1$时,由$BP_ - $生成的两条非零平衡点曲线变得越发陡峻,并沿着"渐近线"$\gamma _{c} =-0.909~1$向远处延伸;当$\gamma $达到临界值$\gamma _{c} =-0.909~1$时,非零平衡点消失. 由此,在"渐近线"的左侧形成了一个发散区域$[-1,\gamma _{c} ]$. 当轨线处于该区域时,系统向无穷远处演化. 注意到,这里的慢变量是$\cos (\omega _2 t)$,它必能进入发散区域$[ - 1,\gamma _{c} ]$. 因此,当$\beta _2 > 1$时,簇发振荡将会消失(见图6(c)和图6(d)).
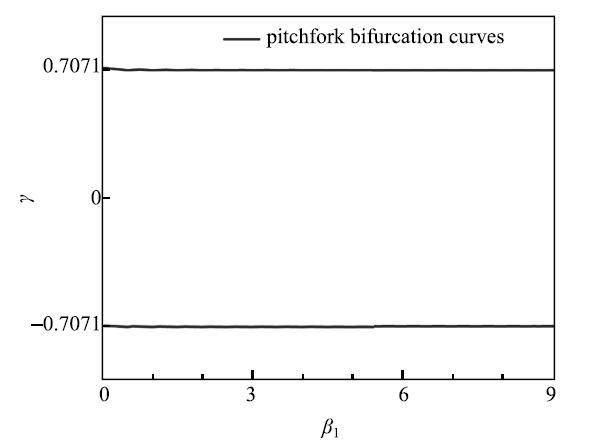
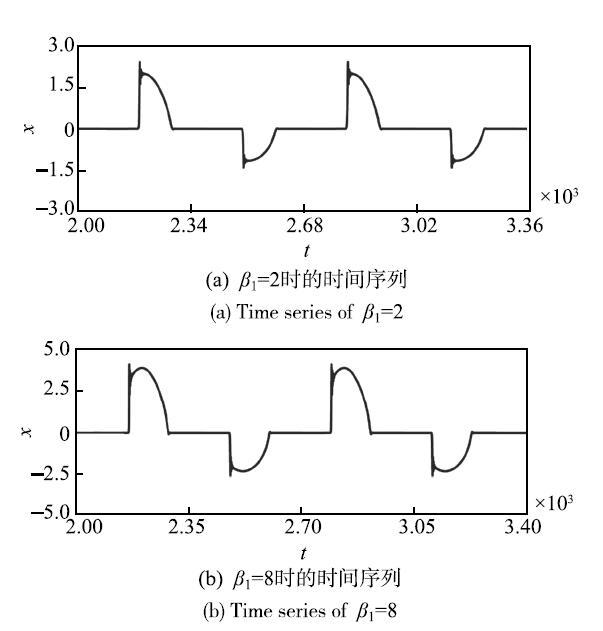
最后,分析振幅$\beta _1 $对图2(b)所示的簇发振荡的影响. 图7给出了快子系统(3)在参数平面$(\beta _1 ,\gamma )$上的分岔集,其余参数的取值同图2(b). 如图所示,在较大的参数范围内只有两条叉型分岔曲线$\gamma _{BP} = \pm 0.707~1$,因此在所考虑的参数范围内,系统只能产生与这两个叉型分岔相关的簇发振荡模式.从这一点来看,$\beta _1 $的变化对簇发动力学没有定性的影响(例如,见图8).
图7 参数平面$(\beta _1 ,\gamma )$上的分岔集...
Fig.7 Bifurcation sets on parameter plane $(\beta _1 ,\gamma )$ ...
图8 不同$\beta _1 $下的簇发振荡,其他参数同
Fig.8 Bursting oscillations related to different values of$\beta _1 $, where the other parameters are the same as in
3 结 论
研究了多频参数激励Duffing系统的簇发动力学,揭示了与延迟叉型分岔相关的复杂的"点-点型"簇发振荡,即"串联式叉型滞后簇发振荡". 研究表明,多频参数激励能够导致快子系统其叉型分岔点数量的不断增多;当慢变量穿越这些分岔点时,先后形成了多个"叉型滞后簇发振荡". 这些簇发振荡的动力学行为虽然较为简单,但它们首尾相接,构成了具有复杂动力学特性的"串联式叉型滞后簇发振荡". 进一步的分析表明,"串联式叉型滞后簇发振荡"其大幅振荡的数量与参数激励的频率比有关. 我们的研究揭示了"点-点型"簇发振荡通向复杂性的道路,即多频参数激励诱发的叉型分岔点数量的不断增多. 此外,探讨了参数对"叉型滞后簇发振荡"的影响. 结果表明,$\beta _2 $的不断增大会导致"渐进线"的出现,由此形成了一个发散区域,并最终导致簇发振荡的消失;系统参数$\delta $会对平衡点的类型产生影响,但不会影响平衡点的稳定性及分岔,而$\beta _1 $等其他系统参数对簇发动力学没有定性影响.
The authors have declared that no competing interests exist.
参考文献
| [1] |
Periodical process of oxidation of malonic acid solution . |
| [2] |
Oscillatory clusters in the periodically illuminated, spatially extended Belousov-Zhabotinsky reaction. Phys. Rev .
|
| [3] |
The prehistory of the Belousov-Zhabotinsky oscillator. J. Chem . |
| [4] |
Discussion: Electrical excitability of cells, theory and experiment: Review of the Hodgkin-Huxley foundation and an update. Bull. Math . |
| [5] |
Neural excitability, spiking and bursting. Int. [J]. |
| [6] |
Ordinary and Partial Differential Equations . |
| [7] |
Sector-delayed-Hopf-type mixed-mode oscillations in a prototypical three-time-scale model . |
| [8] |
Chaotic bursting in semiconductor lasers . |
| [9] |
An experimental study of slow passage through Hopf and pitchfork bifurcations in a parametrically driven nonlinear oscillator. Commun. Nonlinear Sci. Numer . |
| [10] |
Analysis of plasma oscillations by electrical detection in Nd:YAG laser welding. J Mater. Process . |
| [11] |
Temperature oscillations and sound waves in hadronic matter . |
| [12] |
神经系统信息处理和异常功能的复杂动力学 .Complex dynamics of the nervous system for information processing and abnormal functions . |
| [13] |
Mixed mode oscillations in a conceptual climate model . |
| [14] |
Two-degree-of-freedom inclined cable galloping-Part 1: General formulation and solution for perfectly tuned system . |
| [15] |
Nonlinear inelastic responses of transmission tower-line system under downburst wind. Eng . |
| [16] |
由多平衡态快子系统所诱发的簇发振荡及机理 .Bursting oscillations as well as the bifurcation mechanism induced by fast subsystem with multiple balances . |
| [17] |
多平衡态下簇发振荡产生机理及吸引子结构分析 .Mechanism of bursting oscillations with multiple equilibrium states and the analysis of the structures of the attractors . |
| [18] |
Mixed-mode oscillations in a nonlinear time delay oscillator with time varying parameters . |
| [19] |
非对称型簇发振荡吸引子结构及其机理分析. 物理学报, 2017, 66(11): 35-45 (Wu Tianyi, Chen Xiaoke, Zhang Zhengdi, et al. Structures of the asymmetrical bursting oscillation attractors and their bifurcation mechanisms .
|
| [20] |
Different types of bursting calcium oscillations in non-excitable cells . |
| [21] |
Symmetric bursting of focus-focus type in the controlled Lorenz system with two time scales. Phys. Lett . |
| [22] |
周期激励下Hartley模型的簇发及分岔机制 .Bursting phenomena as well as the bifurcation mechanism in periodically excited Hartley model . |
| [23] |
Hopf-bifurcation-delay-induced bursting patterns in a modified circuit system. Commun. Nonlinear Sci. Numer . |
| [24] |
反馈时滞对van der Pol振子张弛振荡的影响 .Delay effect on the relaxation oscillations of a van der Pol oscillator with delayed feedback . |
| [25] |
A heterogenous Cournot duopoly with delay dynamics: Hopf bifurcations and stability switching curves .
|
| [26] |
Stability and bifurcation analysis in the coupled HR neurons with delayed synaptic connection. Nonlinear . |
| [27] |
Turnover of hysteresis determines novel bursting in Duffing system with multiple-frequency external forcings. Int. [J]. |
| [28] |
The Duffing Equation: Nonlinear Oscillators and Their Behaviour . |
| [29] |
Dynamics of a time delayed Duffing oscillator. Int. [J]. |
| [30] |
Delayed bifurcations to repetitive spiking and classification of delay-induced bursting . |
| [31] |
Fast-slow analysis for parametrically and externally excited systems with two slow rationally related excitation frequencies . |
| [32] |
Slow passage through a pitchfork bifurcation . |
| [33] |
Adiabatic dynamical systems and hysteresis . |
| [34] |
Bursting oscillations in Duffing's equation with slowly changing external forcing . |

/
| 〈 |
|
〉 |