非齐次边界条件下轴向运动梁的非线性振动1)
NONLINEAR VIBRATIONS OF AXIALLY MOVING BEAMS WITH NONHOMOGENEOUS BOUNDARY CONDITIONS1)
中图分类号: O323
文献标识码: A
通讯作者:
版权声明: 2019 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
作者简介: 2) 张登博,博士研究生,主要研究方向:非线性动力学与振动控制. E-mail:zhangdengbo2009@163.com;
展开
摘要
轴向运动系统的横向非线性振动一直是国内外研究的热点课题之一.目前相关研究大都是针对齐次边界条件的.但是在工程实际中,非齐次边界条件更为常见,而针对非齐次边界条件的研究相对较少.为深入研究非齐次边界条件对轴向运动系统横向非线性振动的影响,本文以轴向变速运动黏弹性Euler梁为例,引入由黏弹性引起的非齐次边界条件,同时还引入由轴向加速度引起的径向变化张力,建立梁横向振动的积分-偏微分型运动方程,并导出了相应的非齐次边界条件.采用直接多尺度法分析了梁的次谐波参数共振.由可解性条件得到了梁的稳态响应,并根据Routh-Hurvitz判据确定了系统稳态响应的稳定性.通过数值例子讨论了黏弹性系数,轴向运动速度,轴向速度脉动幅值和非线性系数对幅频响应的影响,并详细对比分析了非齐次边界条件和齐次边界条件对幅频响应的影响.结果表明:随着黏弹性系数的增大,非齐次边界条件下的零解失稳区域和稳态响应幅值比齐次边界条件下的失稳区域和幅值大,非齐次边界条件对高阶次谐波参数共振的影响更加显著.最后,引入微分求积法来验证直接多尺度法的近似解结果.
关键词:
Abstract
The transverse nonlinear vibration of the axial moving system has become one of the hot subjects at home and abroad. At present, most of the related studies are on the homogeneous boundary conditions. However, the nonhomogeneous boundary conditions are more common in the engineering practice. There are relatively few publications on the axial moving system with homogeneous boundary conditions. In order to study the effect of nonhomogeneous boundary conditions on the transverse nonlinear vibration of an axial moving beam, the nonlinear parametric vibrations of an axially accelerating viscoelastic Euler beam under nonhomogeneous boundary conditions are studied in this paper. The variable tension caused by the axial acceleration is introduced. A nonlinear integro-partial-differential equation and corresponding nonhomogeneous boundary conditions of an axially accelerating viscoelastic beam are presented. The effects of nonhomogeneous boundary conditions are highlighted. The method of multiple scales is used to establish the solvability conditions. The steady-state response of the beam was obtained from the solvability condition. According to the Routh-Hurvitz criterion, the stability of the response was determined. Some numerical examples are introduced to demonstrate the effect of the viscoelastic coefficient, mean speed, axial speed fluctuation amplitude, nonlinear coefficient, and the nonhomogeneous boundary conditions on the steady-state response. The larger viscoelastic coefficient leads to the smaller instability interval of the trivial solutions and the smaller stable steady-state response amplitude especially for the second mode. The instability interval and the stable steady-state response amplitude with the nonhomogeneous boundary conditions are larger than that with the homogeneous boundary conditions. The differential quadrature scheme is introduced to confirm the approximate analytical results. The numerical results show reasonable agreement with the approximate analytical results.
Keywords:
在工程实际及生活中,轴向运动系统广泛存在于电子工程、军事、机械、土木、纺织以及航空航天工程中.电梯缆绳、动力传送带、空中缆车索道、磁带和纸带等都可以简化为轴向运动系统.由于传输速度的存在,轴向运动系统会产生较大的横向振动从而引起有害的振动和噪声.
国内外众多学者[1 -4]对轴向运动系统横向振动的问题进行了一系列研究.Chen等[5]利用Galerkin法研究了轴向运动黏弹性梁的高维非线性动.Yang等[6]利用平均法研究了轴向运动黏弹性Timoshenko梁的动态稳定性.Sahoo等[7]分析了轴向运动梁的动态稳定性、分叉以及稳态响应.胡璐等[8]研究了黏性流体环境下V 型悬臂梁结构流固耦合振动特性.详细分析了不同流体黏度、V型梁角度及尺寸变化对耦合系统振动特性的影响. Ghayesh等[9 -10]分别研究了轴向运动Euler梁和Timoshenko梁的非线性振动.吕海玮等[11]研究了轴向运动软夹层梁的横向振动.Chen等[12]通过Rayleigh-Ritz法建立了轴向运动悬臂梁的高效动力学模型,研究了轴向运动梁的频率响应特性.Chen等[13]采用多元L-P方法分析轴向运动梁的非线性振动.Li等[14]讨论和比较了在低频和高频次谐波参数共振下轴向运动黏弹性夹层梁的非线性幅频响应、不稳定边界和动态响应.Wang等[15]通过直接多尺度法和Galerkin法研究了轴向运动超弹性梁的非线性参数振动,研究发现改变泊松比和弹性模量的大小会导致系统软硬特性发生变化.陈树辉等[16]引入多元L-P法分析了内共振下轴向运动梁的非线性振动. Lü等[17]分析了变速度下轴向运动黏弹性夹层梁非线性参数振动.Hua等[18-19]分别利用Galerkin法和有限元法研究了悬臂梁的自激振动和内压作用下轴向运动梁的动力学特性.Kelleche等[20]研究了轴向运动黏弹性梁的动态稳定性.基于Timoshenko梁理论和电磁场理论,胡宇达等[21]研究了轴向运动导电导磁梁的磁弹性耦合振动.唐有绮等[22]引入了由轴向加速度引起的径向变化张力,研究了径向变张力对轴向运动Timoshenko梁的影响.
研究者发现,以往研究轴向运动体系大都是采用齐次边界条件.但是,在工程实际中,非齐次边界条件更为普遍,而目前关于非齐次边界条件的研究相对较少.Tang等[23]运用直接多尺度法研究了非齐次边界条件下轴向运动黏弹性Euler梁的固有频率、稳态响应及其稳定性.Zhang等[24]引入非齐次边界条件研究了轴向运动黏弹性Euler梁的动态稳定性.Tang等[25]利用直接多尺度法和微分求积法分析了非齐次边界条件对面内运动板的组合参数共振和次谐波参数共振的动态稳定性的影响.他们的研究发现,非齐次边界条件对失稳边界的影响非常小.现有文献还未发现非齐次边界条件对轴向运动梁的非线性振动产生显著影响
本文研究了轴向加速黏弹性Euler梁的非线性参数振动,引入由黏弹性引起的非齐次边界条件和取决于轴向加速度的轴向变化张力,给出了轴向加速黏弹性Euler梁的非线性控制方程和非齐次边界条件.适当取定参数,得到了系统的稳态响应曲线以及黏弹性系数和非齐次边界条件对稳态响应的影响.最后,通过微分求积方法对近似解析方法进行了数值验证.
1 控制方程
考虑横截面面积为$A$,密度为{$\rho$},弹性模量为$E$,惯性矩为$I$,支承两端间距为$L$,黏弹性系数为{$\alpha$},初始轴力为$P_{0}$,横向位移为$v(x$,$t)$的均匀Euler梁以变速度{$\varGamma $}($t)$沿轴向运动.采用广义Hamilton原理可以得到轴向加速运动Euler梁的动力学方程[24]和相应的非齐次边界条件
$$\rho A\left( {v,_{tt} + 2\varGamma v,_{xt} + \varGamma ^2v,_{xx}} \right) -\left[ P_0 + \eta \rho A\varGamma ^2 +\right.\\ \left. \left( {x-L} \right)\rho A\dot {\varGamma }\right]v,_{xx} + k_{ s} v + I\left[ Ev,_{xxxx} +\right.\ \left. \alpha \left( v,_{xxxxt} + \var Gammav,_{xxxxx} \right) \right]-\frac{EA}{}v,_{xx} \int_0^L {v,_x^2{ d}x} = 0\tag{1} $$
$$ label{eq2}\left. v \right|_0^L = 0,\;\;\left. {I\left[{Ev,_{xx} + \alpha \left( {v,_{xxt} + \varGamma v,_{xxx} }\right)} \right]} \right|_0^L = 0\tag{2}$$
式中,{$\eta $}为支撑刚度参数,其变化区间为[0,1]. $k_{s}$为地基刚度. 对于两端简支的边界条件,其横向位移为零,弯矩为零.当黏弹性本构关系采用Kelvin模型并取物质时间导数时,精确的边界条件为式(2)(非齐次边界条件). 非齐次边界条件式(2)中考虑了黏弹性的影响.但是,在以往的研究中,为了简化计算,仅仅在控制方程当中考虑黏弹性本构,而边界条件依然采用弹性本构时的边界条件(齐次边界条件),即边界条件式(2)中{$\alpha$}=0.
引入无量纲参数
\begin{equation}\left.\label{eq3}\begin{array}{l} v \leftrightarrow \frac{v}{\sqrt \varepsilon L},\;\;x\leftrightarrow \frac{x}{L},\;\;t \leftrightarrow \frac{t}{L}\sqrt{\frac{P_0 }{\rho A}}\\[3mm] \gamma = \varGamma \sqrt {\frac{\rho A}{P_0 }} ,\;\;\kappa = 1- \eta , \;\; k_{ f} = \sqrt {\frac{EI}{P_0 L^2}} \\[3mm] k_{ s} \leftrightarrow \frac{k_{ s} L^2}{P_0},\;\;\alpha \leftrightarrow \frac{\alpha I}{\varepsilon L^3\sqrt{\rho AP_0 } },\;\;k_{ N} = \sqrt {\frac{EA}{P_0}} \\ \end{array}\right\}\tag{3}\end{equation}
式中,{$\varepsilon $}为无量纲参数.因此,化简后的无量纲形式的运动方程和非齐次边界条件为
$$ v,_{tt} + 2\gamma v,_{xt} + \left[ {\kappa \gamma ^2 -\left( {x-1} \right)\dot {\gamma }-1} \right]v,_{xx} + k_{f}^2 v,_{xxxx} + k_{ s} v=\ \frac{1}{2}\varepsilon k_{ N}^2 v,_{xx} \int_0^1{v,_x^2 { d}x}-\varepsilon \alpha \left( {v,_{xxxxt} + \gamma v,_{xxxxx} } \right) \tag{4}$$
$$\label{eq5} \left. v \right|_0^1 = 0,\;\;\left. {\left[ {k_{f}^2 v,_{xx} + \varepsilon \alpha \left( {v,_{xxt} + \gamma v,_{xxx} } \right)} \right]} \right|_0^1 = 0\tag{5}$$
设无量纲化的轴向运动速度在平均速度附近做周期正弦脉动
\begin{equation}\label{eq6} \gamma = \gamma _0 + \varepsilon \gamma _1 \sin \left({\omega t} \right)\tag{6}\end{equation}
式中,{$\gamma $}$_{0}$为平均速度,{$\varepsilon\gamma $}$_{1}$为轴向速度脉动的振幅.应用直接多尺度方法,设式(4)的一阶近似解为
\begin{equation}\label{eq7} v\left( {x,t;\varepsilon } \right) = v_0 \left( {x,T_0,T_1 } \right) + \varepsilon v_1 \left( {x,T_0 ,T_1 } \right) +O\left( {\varepsilon ^2} \right)\tag{7}\end{equation}
式中,$T_{0}$={$\tau $} 和$T_{1}$={$\varepsilon$T}$_{0}$.将式(6)和式(7)代入式(4)和式(5),分离{$\varepsilon$}$^{0}$和{$\varepsilon $}$^{1}$阶量得
$$ v_0,_{T_0 T_0 } + 2\gamma _0 v_0 ,_{xT_0 } \!+\! \left( {\kappa\gamma _0^2-1} \right)v_0 ,_{xx} \!+ k_{ f}^2 v_0 ,_{xxxx}\!+ k_{ s} v_0 = 0~~~~~~\tag {8a}$$
$$\label{eq9} {v_0 } |_{x =0}^{x = 1} = 0,\;\;\left. {v_0 ,_{xx} } \right|_{x = 0}^{x = 1} =0\tag{8b}$$
$$v_1 ,_{T_0 T_0 } + 2\gamma _0 v_1 ,_{xT_0 } + \left( {\kappa\gamma _0^2 -1} \right)v_1 ,_{xx} + k_{ f}^2 v_1 ,_{xxxx} =\ \qquad -2v_0 ,_{T_0 T_1 }-2\gamma _0 v_0 ,_{xT_1 } -\alpha ( v_0 ,_{xxxxT_0 } +\\\gamma _0 v_0 ,_{xxxxx} ) + \frac{1}{2}k_{ N}^2v_0 ,_{xx} \int_0^1 {v_0,_x^2 { d}x} \tag{9a}$$
$$\left.{\begin{array}{ccc}-\left( {1-x} \right)\omega \gamma _1 \cos (\omega t)v_0 ,_{xx} -2\gamma _1 \sin (\omega t)\cdot\\ \qquad \left( {v_0 ,_{xT_0 } + \kappa \gamma _0 v_0 ,_{xx} }\right) {v_1 } |_{x = 0}^{x = 1} \!=\! 0\ { [ {k_{ f}^2v_1 ,_{xx} + \alpha( {v_0 ,_{xxT_0 } \!+\! \gamma _0 v_0 ,_{xxx} })} ]} |_{x = 0}^{x = 1}\! =\! 0\end{array}}\right\}\tag{9b}$$
2 次谐波参数共振
考虑速度的脉动频率{$\omega $}在2{$\omega$}$_{n}$附近变化[26-28]
\begin{equation}\label{eq12} \omega = 2\omega _n + \varepsilon \sigma\tag{10}\end{equation}
式中,{$\sigma $}为调谐参数. 线性派生系统(8a)的解可设为
$$v_0 \left( {x,T_0 ,T_1 } \right) =\ \qquad\varphi _n \left( x \right)A_n \left( {T_1 } \right){e}^{{ i}\omega _n T_0 }{ + }\varphi _l \left( x \right)A_l\left( {T_1 } \right){ e}^{{ i}\omega _l T_0 } +cc \tag{11}$$
式中,{$\varphi $}$_{n}(x)$和{$\varphi$}$_{l}(x)$为模态函数;$A_{n}$ ($T_{1})$和$A_{l}$($T_{1})$为待定的复函数;{$\omega $}$_{n}$和{$\omega$}$_{l}$为第$n$和第$l$阶固有频 率[24].{cc}表示等式右端前两项的复数共轭.
将式(10)和式(11)代入式(9a),且将式中三角函数转换为指数函数,得到
$$v_1 ,_{T_0 T_0 } + 2\gamma _0 v_1 ,_{xT_0 } + \left( {\kappa\gamma _0^2 -1} \right)v_1 ,_{xx} + k_{ f}^2 v_1 ,_{xxxx} + k_{ s} v_1 = \\ \qquad -\bigg[ {2\zeta _0 \dot {A}_n } + \alpha \zeta _1 A_n+ \gamma _1 \zeta _2 \bar {A}_n { e}^{{ i}\sigma T_1 } -\frac{1}{2}k_{ N}^2 \zeta _3A_n^2 \bar {A}_n -\\ \qquad { k_{ N}^2 \zeta _4 A_l A_n \bar {A}_l } \bigg]{e}^{{ i}\omega _n T_0 }-\bigg[ {2\xi _0 \dot {A}_l + \alpha\xi _1 A_l } -\frac{1}{2}k_{ N}^2 \xi _2 A_l^2 \bar {A}_l -\\ \qquad { k_{ N}^2 \xi _3 A_n A_l \bar {A}_n } \bigg]{e}^{{ i}\omega _l T_0 } + cc + NST \tag12$$
式中,{NST}表示久期项.
\begin{equation}\left.\label{eq15}\begin{array}{l} \zeta _0 = { i}\omega _n \varphi _n + \gamma _0 {\varphi}'_n \\\zeta _2 = \left[ {\left( {1-x} \right)\omega _n -i\kappa \gamma _0 } \right]\bar {{\varphi}"}_n-\omega _n \bar {{\varphi }'}_n \zeta _1 = { i}\omega _n {{\varphi }"_n}" + \gamma _0{{\varphi }"_n}"' \zeta _3 = 2{\varphi }"_n \int_0^1{{\varphi }'_n {\bar {\varphi }}'_n { d}x} +{\bar {\varphi }}"_n \int_0^1 {{\varphi }'^2_n { d}x} \\[2mm] \zeta _4 = {\varphi }"_l \int_0^1 {{\varphi }'_n {\bar{\varphi }}'_l { d}x} + {\varphi }"_n \int_0^1 {{\varphi }'_l\bar {{\varphi }'}_l { d}x + } \bar {{\varphi }"}_l\int_0^1 {{\varphi }'_l {\varphi }'_n { d}x} \\[2mm] \xi _0 = { i}\omega _l \varphi _l + \gamma _0 {\varphi}'_l ,\;\;\xi _1 = { i}\omega _l{{\varphi }"_l}" + \gamma _0 {{\varphi }"_l}"' \\[2mm] \xi _2 = 2{\varphi }"_l \int_0^1 {{\varphi }'_l {\bar{\varphi }}'_l { d}x} + {\bar{\varphi }}"_l \int_0^1 {{\varphi }'^2_l { d}x} \\[2mm] \xi _3 = {\varphi }"_l \int_0^1 {{\varphi }'_n {\bar{\varphi }}'_n { d}x} + {\varphi }"_n \int_0^1 {{\varphi }'_l\bar {{\varphi }'}_n { d}x + } \bar {{\varphi }"}_n\int_0^1 {{\varphi }'_l {\varphi }'_n { d}x} \\ \end{array}\!\!\right\}\tag{13}\end{equation}
为求解非齐次边界条件,假定$v_{1}(x$, $T_{0}$, $T_{1})$有形式为
$$ \label{eq16} v_1 \left( {x,T_0 ,T_1 } \right) = \psi _n \left({x,T_1 } \right){ e}^{{ i}\omega _n T_0 } +\\ \qquad \psi_l \left( {x,T_1 } \right){ e}^{{ i}\omega _l T_0 } +N\left( {x,T_0 ,T_1 } \right) + cc\tag{14}$$
式中,$N(x$, $T_{0}$, $T_{1})$表示久期项.
将式(14)代入式(12)并按系数exp(i{$\omega$}$_{n}T_{0})$和exp(i{$\omega $}$_{l}T_{0})$分离变量,引入内积[29]得到
$$\left\langle {\left( {k_{ s}-\omega _n^2 } \right)\psi _n +2{ i}\gamma _0 \omega _n \psi _n ,_x + \left( {\kappa \gamma_0^2-1} \right)\psi _n ,_{xx} }+ \right.\\ \qquad \left. { k_{ f}^2 \psi _n ,_{xxxx} ,\varphi _n } \right\rangle =\ \qquad \bigg\langle {- \bigg( {2\zeta _0 \dot {A}_n + \alpha \zeta _1 A_n + \gamma _1\zeta _2\bar {A}_n { e}^{{ i}\sigma T_1 }} }-\\ \qquad { { \frac{1}{2}k_{ N}^2 \zeta _3 A_n^2 \bar {A}_n- k_{ N}^2 \zeta _4 A_l A_n \bar {A}_l } \bigg),\varphi _n }\bigg\rangle \tag{15a}$$
$$\bigg\langle \left( {k_{ s}-\omega _l^2 } \right)\psi _l +2{ i}\gamma _0 \omega _l \psi _l ,_x + \left( {\kappa \gamma_0^2-1} \right)\psi _l ,_{xx} +\ \qquad k_{ f}^2 \psi _l,_{xxxx} ,\phi _l \bigg\rangle = \bigg\langle -\bigg( 2\xi _0\dot {A}_l + \alpha \xi _1 A_l-\frac{1}{2}k_{ N}^2\xi _2 A_l^2 \bar {A}_l -\\ \qquad k_{ N}^2 \xi _3 A_n A_l \bar {A}_n \bigg),\phi _l\bigg\rangle \tag{15b}$$
引入非齐次边界条件(9b)得到
$$\left. {\alpha A_n \gamma _0\varphi _n ,_{xxx} \bar {\varphi }_n ,_x } \right|_0^1 =\bigg\langle {-\bigg( {2\zeta _0 \dot {A}_n + \alpha \zeta_1 A_n + \gamma _1 \zeta _2 \bar {A}_n { e}^{{ i}\sigma T_1 }} } -\\ \qquad { { \frac{1}{2}k_{ N}^2 \zeta _3 A_n^2 \bar {A}_n- k_{ N}^2 \zeta _4 A_l A_n \bar {A}_l } \bigg),\varphi _n }\bigg\rangle \tag{16a}$$
$$\left. {\alpha A_n \gamma _0 \phi _l ,_{xxx} \bar {\phi }_l ,_x} \right|_0^1 = \bigg\langle -\bigg( 2\xi _0 \dot {A}_l + \alpha\xi _1A_l-\\ \qquad \frac{1}{2}k_{ N}^2 \xi _2 A_l^2 \bar {A}_l-k_{N}^2 \xi _3 A_n A_l \bar {A}_n \bigg),\phi _l \bigg\rangle\tag{16b}$$
根据可解性条件得到
$$ \label{eq21} \dot {A}_n + \alpha\zeta _1 A_n + \gamma _1 \zeta _2 \bar {A}_n { e}^{{i}\sigma T_1 }{ + }k_{ N}^2 \zeta _3 A_n^2 \bar {A}_n +k_{ N}^2 \zeta _4 A_l A_n \bar {A}_l = 0\\ \tag{17a}$$
$$\label{eq22} \dot {A}_n + \alpha \xi _1 A_n { + }k_{ N}^2\xi _2 A_n^2 \bar {A}_n { + }k_{ N}^2 \xi _3 A_n A_l \bar{A}_n = 0\tag{17b}$$
其中
$\begin{equation}\left.\label{eq23}\begin{array}{l} \zeta _1 \leftrightarrow \frac{ \int_0^1 {\zeta _1 \bar{\varphi }_n { d}x} + \left. {\gamma _0 \varphi _n ,_{xxx} \bar{\varphi }_n ,_x } \right|_0^1 }{ \int_0^1 {2\zeta _0 \bar{\varphi }_n { d}x} }\\[3mm]\zeta _2 \leftrightarrow \frac{\int_0^1 {\zeta _2 \bar {\varphi }_n { d}x} }{ \int_0^1{2\zeta _0 \bar {\varphi}_n { d}x} }\\[3mm] \zeta _3 \leftrightarrow-\frac{ \int_0^1 {\zeta _3 \bar{\varphi }_n { d}x} }{ \int_0^1 {4\zeta _0 \bar {\varphi }_n{ d}x} },\;\;\;\zeta _4 \leftrightarrow-\frac{ \int_0^1{\zeta _4 \bar {\varphi }_n { d}x} }{ \int_0^1 {2\zeta _0\bar {\varphi}_n { d}x} }\\[3mm] \xi _1 \leftrightarrow \frac{\int_0^1 {\xi _1 \bar{\varphi }_l { d}x} + \left. {\gamma _0 \varphi _l ,_{xxx} \bar{\varphi }_l ,_x } \right|_0^1 }{ \int_0^1 {2\xi_0 \bar {\varphi }_l { d}x} } \\[3mm] \zeta _2 \leftrightarrow-\frac{ \int_0^1 {\xi _2 \bar{\varphi }_l { d}x} }{ \int_0^1 {4\xi _0 \bar {\varphi }_l{ d}x} },\;\;\;\;\xi _3 \leftrightarrow-\frac{ \int_0^1{\xi _3 \bar {\varphi }_l { d}x} }{ \int_0^1 {2\xi _0 \bar{\varphi }_l{ d}x} } \\ \end{array}\right\}\tag{18}\end{equation}$
对于给定的参数,经数值计算表明{$\zeta$}$_{1}$和{$\xi $}$_{1}$是正实数;{$\zeta$}$_{2}$是复数;{$\zeta $}$_{3}$,{$\zeta$}$_{4}$,{$\xi $}$_{2}$和{$\xi $}$_{3}$是负虚数.式(17b)的解随着时间的延长会呈$E$指数形式衰减为零.这就说明,第$l$阶模态对系统初始阶段有短期的影响,但是对第$n$阶模态参数共振稳态响应没有影响.因此,式(17a)简化为
\begin{equation}\label{eq24} \dot {A}_n + \alpha \zeta _1 A_n + \gamma _1 \zeta _2\bar {A}_n { e}^{{ i}\sigma T_1 }{ + }k_{ N}^2 \zeta_3 A_n^2 \bar {A}_n = 0\tag{19}\end{equation}
把式(17a)写成极坐标形式
\begin{equation}\label{eq25} A_n = \alpha _n \left( {T_1 } \right){ e}^{{i}\beta _n \left( {T_1 } \right)}\tag{20}\end{equation}
式中,{$\alpha $}$_{n}$和{$\beta$}$_{n}$是$T_{1}$的实函数,分别对应第$n$阶模态的幅值和相角.将式(20)代入式(19),并分离结果中的实部和虚部,导出
$$\label{eq26} \alpha _n ,_{T_1 } = \alpha _n \left[ {\gamma _1\left( {\zeta _2^{ I} \sin \theta-\zeta _2^{ R} \cos\theta } \right)-\alpha \zeta _1 } \right]\tag{21}$$
$$\label{eq27} \alpha _n \beta _n ,_{T_1 } =-\alpha _n \left[{k_{ N}^2 \zeta _3 \alpha _n^{ 2} + \gamma _1 \left( {\zeta_2^{ R} \sin \theta + \zeta _2^{ I} \cos \theta } \right)}\right]\tag{22}$$
式中,{$\theta $}={$\sigma$T}$_{1}$$-$2{$\beta$}$_{n}$,上标R和I分别表示对应参数的实部和虚部. 显然式(19)有零解.假设还有非零解存在,对于稳态响应,振幅和新的相位角应该为常数
$$\label{eq28} 0 = \gamma _1 \left( {\zeta _2^{ I} \sin \theta -\zeta _2^{ R} \cos \theta } \right)-\alpha \zeta _1\tag{23}$$
$$label{eq29} \sigma =-2\left[ {k_{ N}^2 \zeta _3 \alpha_n^{ 2} + \gamma _1 \left( {\zeta _2^{ R} \sin \theta +\zeta _2^{ I} \cos \theta } \right)} \right]\tag{24}$$
联立式(23)和式(24)消去相位角{$\theta$},得到次谐波参数共振的稳态响应幅值为
\begin{equation}\label{eq30} \alpha _{n1,2} = \sqrt {\frac{-\sigma \pm 2\sqrt{\gamma _1^2 \left| {\zeta _2 } \right|^2-\left( {\alpha \zeta_1 } \right)^2} }{2k_{ N}^2 \zeta _3^{ I} }}\tag{25}\end{equation}
由式(25)可得系统存在稳态解的条件为
$$\label{eq31} \alpha \le {\gamma _1 \left| {\zeta _2 } \right|}
\mathord{\left/ {\vphantom {{\gamma _1 \left| {\zeta _2 } \right|}
{\zeta _1 }}} \right. \kern-\nulldelimiterspace} {\zeta _1 }
\tag{26}$$
$$\label{eq32} \sigma \ge \sigma _{1,2} = \pm 2\sqrt {\gamma _1^2
\left| {\zeta _2 } \right|^2-\left( {\alpha \zeta _1 }
\right)^2}\tag{27} $$
由式(21)和式(22)得到
$$\label{eq33} \alpha _n ,_{T_1 } =\alpha _n \left[ {\gamma _1 \left( {\zeta _1^{ I} \sin \theta -\zeta _2^{ R} \cos \theta } \right)-\alpha \zeta _1 }\right]\tag{28}$$
$$label{eq34} \theta ,_{T_1 } = \sigma { + 2}k_{ N}^2 \zeta_3 \alpha _n^{ 2} + 2\gamma _1 \left( {\zeta _2^{ R} \sin\theta + \zeta _2^{ I} \cos \theta } \right)\tag{29}$$
非零解的稳定性由方程组(28)和(29)确定。因此,方程组(28)和(29)右端函数的Jacobi矩阵为
\begin{equation}\label{eq35} J{ = }\left[ {{\begin{array}{*{20}c} 0 \hfill & {-\alpha _{n1,2} \left( {0.5\sigma + k_{ N}^2 \zeta _3\alpha _{n1,2}^{ 2} } \right)} \hfill \\ {{ 4}k_{ N}^2 \zeta _3 \alpha _{n1,2} } \hfill & {-2\alpha \zeta_1 } \hfill \\\end{array} }} \right]\tag{30}\end{equation}
Jacobi矩阵的特征方程为
\begin{equation}\label{eq36} \lambda ^2 + 2\alpha \zeta _1 \lambda + 2k_{ N}^2\zeta _3 \left( {\sigma + 2k_{ N}^2 \zeta _3 \alpha_{n1,2}^{ 2} } \right)\alpha _{n1,2}^{ 2} = 0\tag{31}\end{equation}
由Routh-Hurwitz判据可得其稳态响应的稳定性.由此可知,第一个非零解总是不稳定的,第二个非零解总是稳定的.
为研究零解的稳定性,我们把式(19)转化为自治方程,引入变换
\begin{equation}\label{eq37} A_n = \left[ {p\left( {T_1 } \right) + { i}q\left({T_1 } \right)} \right]{ e}^{0.5{ i}\sigma T_1 }\tag{32}\end{equation}
其中$p$和$q$是$T_{1}$的实函数。将式(32)代入式(19),并分离结果的实部和虚部,得到
\begin{equation}\label{eq38}\left.\begin{array}{l} \dot {p}_1 =-\left( {\alpha \zeta _1 + \gamma _1 \zeta _2^{ R} } \right)p_1+ \left( {0.5\sigma-\gamma _1 \zeta _2^{ I} } \right)q_1 +\\\qquad k_{ N}^2 \zeta_3 q\left( {p^2 + q^2} \right) \\ \dot {q}_1 =-\left( {0.5\sigma + \gamma _1 \zeta _2^{ I} } \right)p_1 -\left( {\alpha \zeta _1-\gamma _1 \zeta _2^{ R} } \right)q_1\\\qquad-k_{ N}^2\zeta _3 p\left( {p^2 + q^2} \right) \\ \end{array}\right\}\tag{33}\end{equation}
式(33)右端的Jacobi矩阵的特征方程为
\begin{equation}\label{eq39} \left[ {{\begin{array}{*{20}c} {-\left( {\alpha \zeta _1 + \gamma _1 \zeta _2^{ R} } \right)-\lambda }\hfill & {\left( {0.5\sigma-\gamma _1 \zeta _2^{ I} } \right)} \hfill \\ {-\left( {0.5\sigma + \gamma _1 \zeta _2^{ I} } \right)} \hfill & {-\left({\alpha \zeta _1-\gamma _1 \zeta _2^{ R} } \right)-\lambda } \hfill \\\end{array} }} \right] = 0\tag{34}\end{equation}
由其特征方程的行列式可求得零解的稳定性的条件为
\begin{equation}\label{eq40} \left| {\gamma _1 } \right| < \sqrt {\frac{0.25\sigma^2 + \alpha ^2\zeta _1^2 }{\left| {\zeta _2 } \right|^2}}\tag{35}\end{equation}
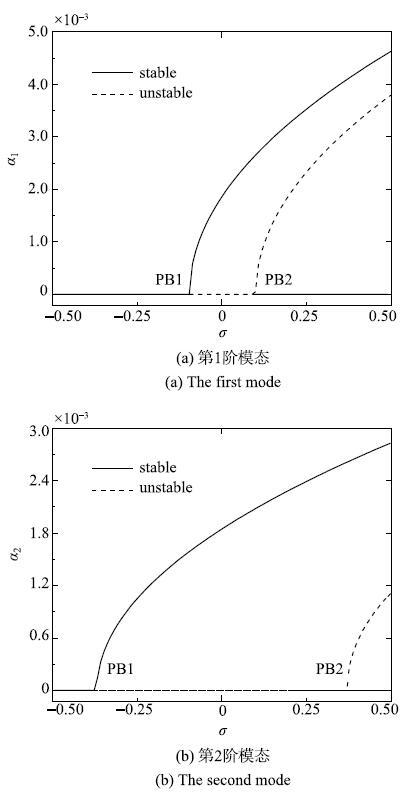
给定$L$=1.0 m,$E$=3.0$\times $10$^{10}$ Pa,$A$=0.04$\times $0.03m$^{2}$, {$\rho $}=7680kg/m$^{3}$和$P_{0}$=6.75$\times $10$^{4}$N,由式(3)可解得相应的无量纲参数$k_{ f}$=0.2,$k_{s}$=0.72,$k_{ N}$=23.094~01. 若考虑{$\kappa$}=0.5,{$\gamma $}$_{0}$=0.86,{$\alpha$=}1.0$\times $10$^{-5}$和{$\gamma$}$_{1}$=0.03,图1给出了Euler梁在发生次谐波参数共振时前两阶模态的稳态幅频特性曲线及稳定性情况.此时,Euler梁的稳态响应有两种解:零解和非零解.其中实线表示稳定解;点线表示非稳定解.从图1可以看出,非零解曲线向右偏,呈现为硬特性.对于第一阶次谐波参数共振,当{$\sigma $ }$<$ {PB1}({$\sigma$}=$-$0.102 83)时,系统有且仅有一个稳定的零解. 当{$\sigma $ }=PB1时,系统发生超临界叉式分岔. 当{$\sigma$}通过点{PB1},系统由一个稳定的零解分岔为一个不稳定的零解和一个稳定的非零解(即稳定的极限环). 当{$\sigma $ }= {PB2} ({$\sigma$}=0.102 83)时,系统发生次临界叉式分岔. 继续增大{$\sigma$},系统不稳定的零解分岔为一个稳定的零解和一个不稳定的非零解(即不稳定的极限环).此时系统由两个稳定解.对于第二阶次谐波参数共振,点{PB1}对应{$\sigma $}=$-$0.39101,点{PB2}对应{$\sigma $}=0.391 01.
图1 前两阶模态次谐波参数共振响应曲线...
Fig. 1 The stable and unstable responses of the first two modes
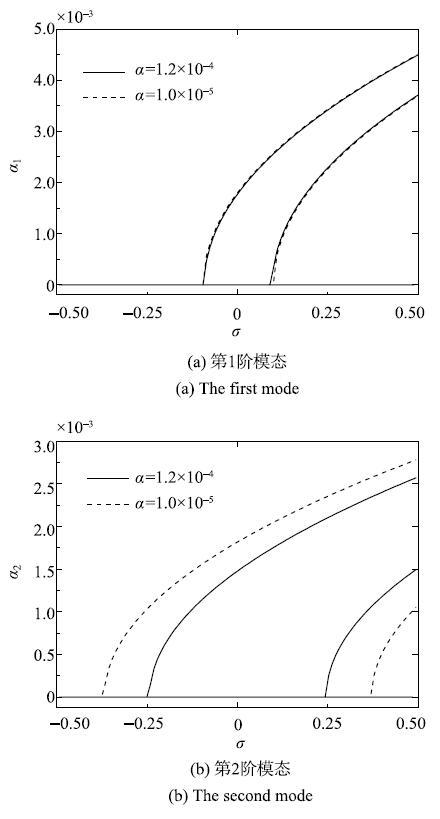
给定{$\kappa $}=0.5, $k_{ f}$=0.2, $k_{ s}$=0.72,{$\gamma $}$_{ 0}$=0.86, {$\gamma $}$_{1}$=0.03和$k_{ N}$=23.09401,图2给出了黏弹性系数对系统稳态幅频特性曲线的影响.其中实线表示{$\alpha $=}1.2$\times $10$^{ -4}$;点线表示{$\alpha $=}1.0$\times $10$^{-5}$.图2表明零解失稳区域随黏弹性系数增大而减小,黏弹性系数对高阶次谐波参数共振的影响更为显著.由于黏弹性本构的引入,根据黏性形变的不可逆性,系统的振动能量会持续耗散,提高了系统的长期振动过程中的稳定性.
图2 不同黏弹性系数对前两阶模态响应曲线的影响...
Fig. 2 The effect of the viscoelastic coefficients on the Stable and unstable responses of the first two modes
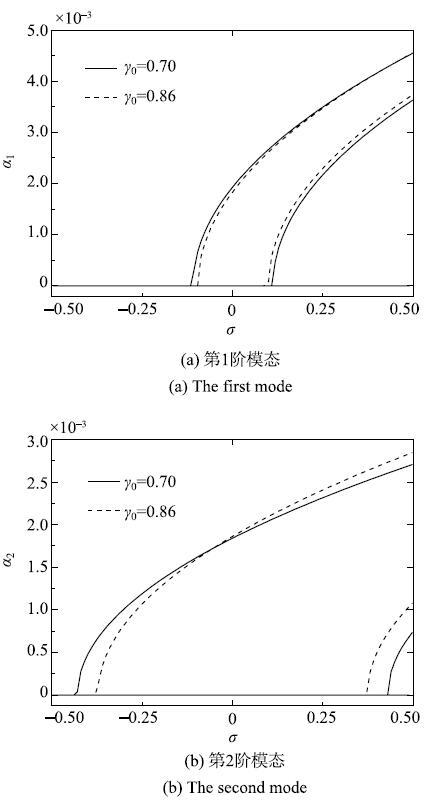
给定{$\kappa $}=0.5, $k_{ f}$=0.2, $k_{ s}$=0.72,{$\gamma $}$_{ 0}$=0.86, {$\alpha $}=1.0$\times$10$^{-5}$, $k_{ N}$=23.094 01和{$\gamma$}$_{1}$=0.03,图3给出了轴向平度速度对系统稳态幅频特性曲线的影响.其中实线表示{$\gamma $}$_{0}$=0.70;点线表示{$\gamma$}$_{0}$=0.86.图3表明轴向平度速度对高阶次谐波参数共振的零解失稳区域影响更为显著,高阶次谐波参数共振的非零响应幅值对平均速度有较高的敏感性.
图3 不同轴向平均速度对前两阶模态响应曲线的影响...
Fig. 3 The effect of the mean speeds on the stable and unstable responses of the first two modes
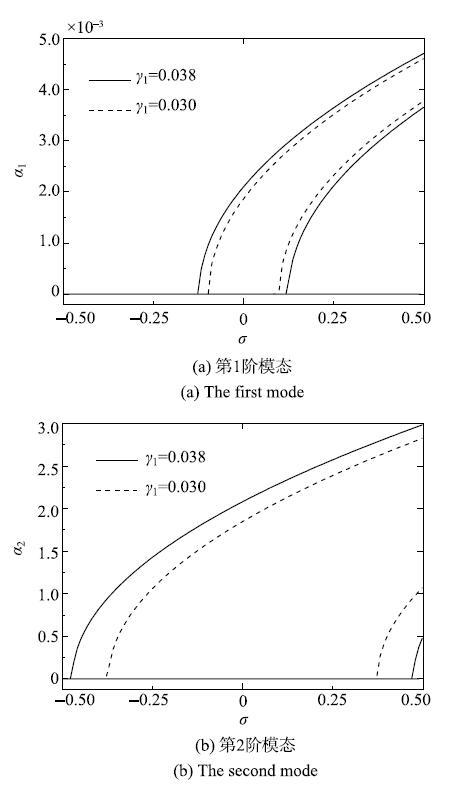
给定{$\kappa$}=0.5,$k_{f}$=0.2,$k_{s}$=0.72,{$\gamma$}$_{0}$=0.86,$k_{N}$= 23.094~01和{$\alpha$=}1.0$\times $10$^{ -5}$,图4给出了速度脉动幅值对系统稳态幅频特性的影响.其中实线表示{$\gamma$}$_{1}$=0.038;点线表示{$\gamma $}$_{1}$=0.03.从图4可以看出,速度脉动幅值对零解失稳区域的影响与黏弹性系数和轴向平均速度相反,对高阶次谐波参数共振更加敏感.
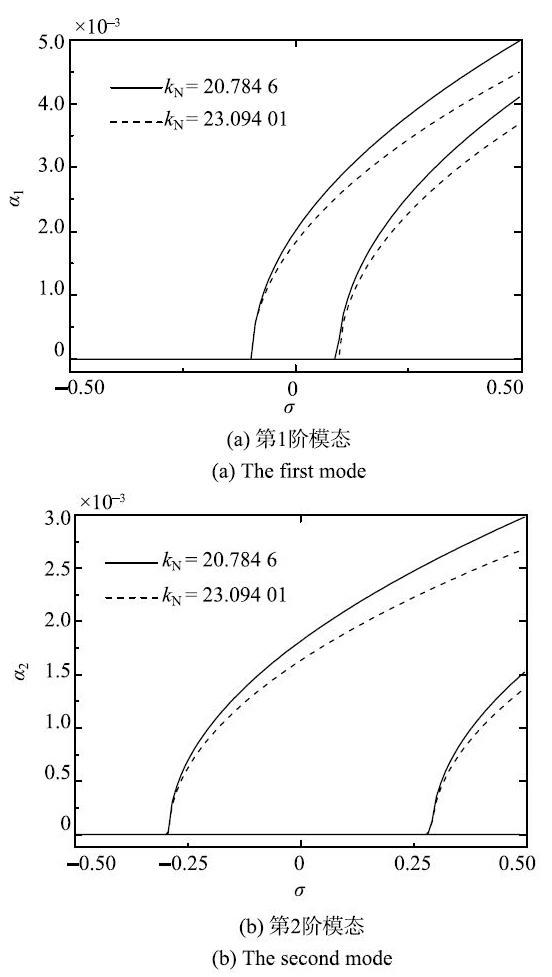
给定{$\kappa $}=0.5, $k_{ s}$=0.72, {$\gamma$}$_{0}$=0.86, {$\gamma $}$_{1}$=0.03和{$\alpha$=}1.0$\times $10$^{ -5}$,图5给出了不同非线性系数对系统稳态幅频特性曲线的影响.其中实线表示$k_{ f}=$0.18和$k_{ N}=$20.784 6;虚线$k_{f}=$0.2和$k_{ N}=$23.094 01.从图5可以看出,对于较小的非线性系数,次谐波参数共振非零响应幅值随调谐参数的增大而快速 增大.
图4 不同速度脉动幅值对前两阶模态响应曲线的影响...
Fig. 4 The effect of the axial speed fluctuation amplitudes on the stable and unstable responses of the first two modes
图5 不同非线性系数对前两阶模态响应曲线的影响...
Fig. 5 The effect of the nonlinear coefficients on the stable and unstable responses of the first two modes
3 数值验证
本节引入微分求积法[30-33]对以上近似解析解进行数值验证.Euler梁的计算区域为$x \in $[0,1]. $x$方向的网点数为$N$.令{$\varepsilon $}=1. 通过微分求积法将控制方程(4)离散为
$$\ddot {v}_i + \sum\limits_{k = 1}^N {\left( {2\gammaA_{ik}^{\left( 1 \right)} + \alpha \tilde {A}_{ik}^{\left( 4\right)} } \right)\dot {v}_k } +k_{ s} v_i+ \\ \qquad \sum\limits_{k = 1}^N {\left\{ {\left[ {\kappa \gamma ^2 \!-\! \left( {x_i \!-\!1} \right)\dot {\gamma } \!-\! 1} \right]\tilde {A}_{ik}^{\left( 2\right)} + k_{ f}^2 \tilde {A}_{ik}^{\left( 4 \right)}\! +\!\alpha \gamma \tilde{A}_{ik}^{\left( 5 \right)} } \right\}v_k } -\ \qquad \frac{1}{2}k_{ N}^2 \sum\limits_{k = 1}^N {\tilde {A}_{ik}^{\left( 2\right)} v_k } \sum\limits_{g = 1}^N {I_g \left( {\sum\limits_{k =1}^N {A_{gk}^{\left( 1 \right)} v_k } } \right)^2} \; = 0 \tag{36}$$
式中,$ {i = 2,3, \cdots ,N-1}$,积分的加权系数$I_{g}$为

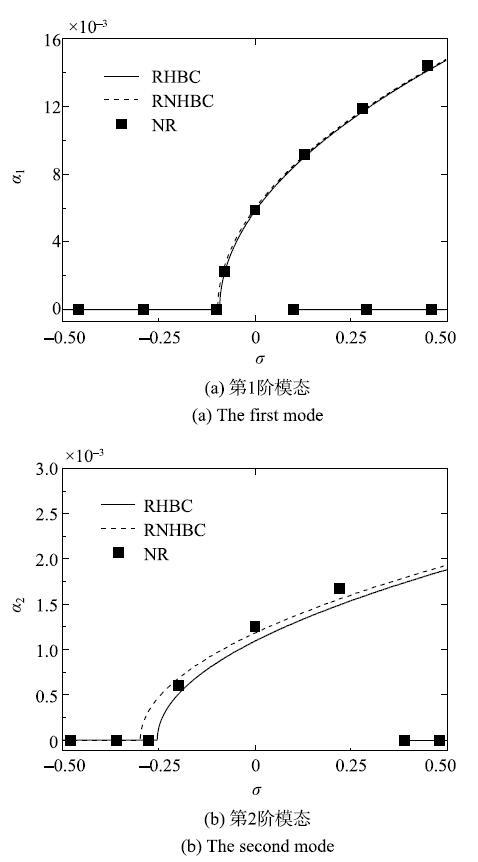
给定式中的$N$=17, {$\kappa $}=0.5, $k_{ f}$=0.2, $k_{s}=$0.72, {$\gamma $}$_{0}$=0.86, $k_{ N}$=23.094~01,{$\gamma $}$_{1}$=0.03和{$\alpha $=}1.0$\times$10$^{-5}$,图6给出了不同方法下系统稳态幅频特性曲线的对比.其中圆点表示齐次边界条件下的幅频特性曲线;实线表示非齐次边界条件下的幅频特性曲线;方点表示数值解.在此组参数下,从图6可以看出,第一和第二阶次谐波参数共振中,数值解和近似解析解在定性上有着相同的趋势,在定量上也吻合得较好.
图6 不同方法下前两阶模态响应曲线的对比...
Fig. 6 The comparison for the analytical and numerical results sf the stable steady-state responses
给定$N$=17, {$\kappa $}=0.5, $k_{ f}$=0.2, $k_{s}$=0.72, {$\gamma $}$_{0}$=0.86, $k_{ N}$=23.094 01,{$\gamma $}$_{1}$=0.03和{$\alpha $=}0.0001,图7给出了不同方法下系统稳态幅频特性曲线的对比.其中实线表示齐次边界条件下的幅频特性曲线;虚线表示非齐次边界条件下的幅频特性曲线;方点表示数值解.对比图6和图7可以看出,随着黏弹性系数的增大,不同边界条件下的系统稳态幅频特性曲线呈现出显著的差异.从图7可以看出,第一阶次谐波参数共振中数值解和近似解析解差别较小,而对于第二阶次谐波参数共振,数值解和近似解析解在定性上有相同的趋势,定量上有些差别.不同边界条件下的系统稳态幅频特性曲线呈现出显著的 差异.
图7 不同方法下前两阶模态响应曲线的对比...
Fig. 7 The comparison for the analytical and numerical results of the stable steady-state responses
4 结论
本文运用直接多尺度法和微分求积法研究了轴向变速运动黏弹性Euler梁的横向非线性参数振动,得到了次谐波参数共振时的幅频特性曲线,以及判断了其稳定性.~考虑了黏弹性系数对系统的稳态响应曲线的影响.研究发现,黏弹性系数和轴向平均速度的增大导致零解失稳区域减小.速度脉动幅值的增大导致零解失稳区域增大.非线性系数对非零响应的幅值影响较大,非线性系数减小,非零响应幅值随调谐参数的增大而快速增大.
同时着重对比分析了非齐次边界条件和齐次边界条件对稳态幅频特性曲线的影响.发现当黏弹性系数非常小时,两种边界条件下的稳态幅频特性曲线差别很小,同时和数值解也吻合得较好.但是,随着黏弹性系数增大,两种边界条件下的稳态幅频特性曲线的差异明显变大,同时和数值解在定性上有相同的趋势,在定量上有些差别.特别是第二阶模态,数值差异非常明显.因此,在轴向运动系统中存在黏弹性的情况下,若忽略非齐次边界条件对系统稳态幅频特性曲线的影响,可能会导致稳态响应分析不准确.
The authors have declared that no competing interests exist.
参考文献
| [1] |
大变形轴向运动梁的精确动力学模型 .Exact dynamic model of axially moving beam with large deformation . |
| [2] |
平带系统非线性振动实验研究 .
Experimental study on nonlinear vibration of flat-belt system .
|
| [3] |
轴向受压运动梁横向振动特性的数值分析 .Numerical analysis of free vibration of an axially moving beam under compressive load . |
| [4] |
凸肩叶片的非线性振动特性与运动分岔 .Nonlinear vibratory characteristics and bifurcations of shrouded blades . |
| [5] |
Nonlinear dynamics of higher dimensional system for an axially accelerating viscoelastic beam . |
| [6] |
Dynamic stability of axially accelerating timoshenko beams: Averaging method . |
| [7] |
Parametric and internal resonances of an axially moving beam with time-dependent velocity . |
| [8] |
黏性流体环境下Ⅴ型悬臂梁结构流固耦合振动特性研究 .Analysis of flexural vibration of V-shaped beams immersed in viscous fluids . |
| [9] |
Sub- and super-critical nonlinear dynamics of a harmonically excited axially moving beam . |
| [10] |
Nonlinear vibrations and stability of an axially moving Timoshenko beam with an intermediate spring support . |
| [11] |
轴向运动软夹层梁横向振动分析 .Analysis of transverse vibration of axially moving soft sandwich beam . |
| [12] |
轴向移动悬臂梁高效动力学建模及频率响应分析 .An efficient dynamic modeling of an axially moving cantilever beam and frequency response analysis . |
| [13] |
Multidimensional lindstedt-poincaré method for nonlinear vibration of axially moving beams . |
| [14] |
Nonlinear forced vibration and stability of an axially moving viscoelastic sandwich beam . |
| [15] |
Nonlinear vibration of axially accelerating hyperelastic beams . |
| [16] |
轴向运动梁非线性振动内共振研究 .On internal resonance of nonlinear vibration of axially moving beams . |
| [17] |
Non-linearly parametric resonances of an axially moving viscoelastic sandwich beam with time-dependent velocity . |
| [18] |
The self-excited vibrations of an axially retracting cantilever beam using the Galerkin method with fitted polynomial basis functions . |
| [19] |
Dynamic analysis of an axially moving beam subject to inner pressure using finite element method . |
| [20] |
Stability of an axially moving viscoelastic beam . |
| [21] |
轴向运动导电导磁梁的磁弹性振动方程 .Magneto-elastic vibration equations for axially moving conductive and magnetic beams . |
| [22] |
轴向变速黏弹性Timoshenko梁的非线性振动 .Nonlinear vibrations of axially acceleratiing viscoelastic Timoshenko beams . |
| [23] |
Parametric and internal resonance of axially accelerating viscoelastic beams with the recognition of longitudinally varying tensions . |
| [24] |
Irregular instability boundaries of axially accelerating viscoelastic beams with 1:3 internal resonance . |
| [25] |
Dynamic stability of axially accelerating viscoelastic plates with longitudinally varying tensions . |
| [26] |
Dynamic stability in parametric resonance of axially accelerating viscoelastic Timoshenko beams . |
| [27] |
轴向运动梁和面内平动板横向振动的建模与分析. [博士论文] .
Transverse vibrations of axially moving beams and in-plane translating plates: Modeling and analysis. [PhD Thesis] .
|
| [28] |
Stability analysis and numerical confirmation in parametric resonance of axially moving viscoelastic plates with time-dependent speed . |
| [29] |
Solvability condition in multi-scale analysis of gyroscopic continua . |
| [30] |
用微分求积法分析轴向移动黏弹性梁的非平面非线性振动 .Using DQM to analyze the nonplanar nonlinear vibrationa of an axially moving viscoelastic beam . |
| [31] |
数值仿真轴向运动黏弹性梁非线性参激振动 .
Numerical investigation into nonlinear parametric resonance of axially moving accelerating viscoelastic beams .
|
| [32] |
The differential quadrature method in computational mechanics: A review .
|
| [33] |
Implementing multiple boundary conditions in the DQ solution of higher-order PDE's: Application to free vibration of plates . |

/
| 〈 |
|
〉 |