基于中间构形的大变形弹塑性模型
武汉大学土木建筑工程学院,武汉430072
A LARGE DEFORMATION ELASTOPLASTIC MODEL BASED ON THE INTERMEDIATE CONFIGURATION
中图分类号: O33
文献标识码: A
版权声明: 2019 力学学报期刊社 力学学报期刊社 所有
作者简介:
作者简介: 1) 陈明祥,教授,主要研究方向:材料宏观本构关系.E-mail: mxchen@whu.edu.cn
展开
摘要
在大变形弹塑性本构理论中,一个基本的问题是弹性变形和塑性变形的分解.通常采用两种分解方式,一是将变形率(或应变率)加法分解为弹性和塑性两部分,其中,弹性变形率与Kirchhoff应力的客观率通过弹性张量联系起来构成所谓的次弹性模型,而塑性变形率与Kirchhoff应力使用流动法则建立联系;另一种是基于中间构形将变形梯度进行乘法分解,它假定通过虚拟的卸载过程得到一个无应力的中间构形,建立所谓超弹性-塑性模型.研究了基于变形梯度乘法分解并且基于中间构形的大变形弹塑性模型所具有的若干性质,包括:在不同的构形上,塑性旋率的存在性、背应力的对称性、塑性变形率与屈服面的正交性以及它们之间的关系.首先,使用张量函数表示理论,建立了各向同性函数的若干特殊性质,并导出了张量的张量值函数在中间构形到当前构形之间进行前推后拉的简单关系式.然后,基于这些特殊性质和关系式,从热力学定律出发,建立模型在不同构形上的数学表达,包括客观率表示的率形式和连续切向刚度等,从而获得模型所具有的若干性质.最后,将模型与4种其他模型进行了比较分析.
关键词:
Abstract
In the large deformation elastoplastic constitutive theory, a basic problem is the decomposition of elastic deformation and plastic deformation. In the usual case, two decomposition methods are adopted. One method is to decompose deformation rate (or strain rate) into elastic and plastic parts. Among them, the elastic deformation rate and the objective rate of Kirchhoff stress are linked by elastic tensors, and by using this way, a sub-elastic model can be established. In the mean time,the plastic deformation rate is related to Kirchhoff stress by using flow law. Another method is to decompose the deformation gradient tensor based in the intermediate configuration. It is supposed that by considering the virtual unloading process, an unstressed intermediate configuration can be obtained and the so-called hyperelastic-plastic model can be established. In this paper, a large number of properties of a large deformation elastoplastic model which is based on the deformation gradient multiplicative decomposition are studied, and the model is built in the intermediate configuration. These properties include: in different configurations, the existence of the plastic spin rate; the symmetry of back stress; the orthogonality of plastic deformation rate and yield surface; and the relationships between plastic spin rate, back stress, plastic deformation rate and yield surface. First of all, by using the tensor function representation theorem which is in the appendix, some special properties of the isotropic function are obtained and some formula relationships are established, and some simple relationships of tensor value function between the intermediate configuration and the current configuration are derived. Secondly, based on these properties and relationships, and in combination with the laws of thermodynamics, the mathematical expression of the model in different configurations is established, which consists of objective rate representation and continuous tangential stiffness. Thus, some properties of the large deformation elastoplastic model based on the intermediate configuration are obtained. Finally, the model is compared and analyzed with the four models.
Keywords:
大变形弹塑性本构理论中,一个基本的问题是弹性变形和塑性变形的分解[1- 2]. 通常采用两种分解方式,一是将变形率(或应变率)加法分解为弹性和塑性两部分,其中, 弹性变形率与Kirchhoff应力的客观率通过弹性张量联系起来构成所谓的次弹性模型, 而塑性变形率与Kirchhoff应力使用流动法则建立联系[3];另一种是基于中间构形将变形梯度进行乘法分解[4-5],它假定通过虚拟的卸载过程得到一个无应力的中间构形,建立所谓超弹性-塑性模型. 基于变形率加法分解的次弹塑性模型本质上是小变形弹塑性理论的直接扩展, 由于它采用率形式的次弹性模型描述弹性变形,在弹性阶段的应力循环中存在非物理的能量耗散, 另一方面,次弹性模型通常采用Jaumann应力客观率和Green-Naghdi率[6],在分析简单剪切变形会导致违背物理的应力振荡,对于某些特殊的应力率, 比如"基于对数应力率的弹性率",剪切变形会导致应力振荡的问题确实可以被解决, 使用基于对数应力率的弹性率方程还可以精确可积等同于无耗散超弹性方程, 此时无能量耗散,另外,应力振荡也取决于材料的硬化参数[2];基于乘法分解的超弹塑性模型,由于其丰富的物理内涵和简单的数学形式, 得到广泛的应用,然而,存在主要的问题是乘法分解中叠加转动的非唯一性等问题[7- 8]. 为了消除中间构形的影响,一些文献提出了各种不同的分解. Nemat-Nasser [9]首次提出了一个关于变形梯度的唯一且对弹性转动和塑性转动不附加任何假定的分解$ F = V^{ e} Q U^{ p}$,其中,$ V^{ e}$是弹性左伸长张量,是$ U^{ p}$右塑性伸长张量,$ Q$是转动张量;Schieck 和\Stumpf [10]提出一个不同的确定性分解$ F = Q\hat { U}^{ e} U^{ p}$,其中$\hat { U}^{ e}$是旋转后拉的右伸长张量,Ghavam与Naghdabadi [11]提出$ F = V^{ e} \varLambda ^{ p} Q^{ p}R$,其中\textbf{\textit{R}}是变形梯度极分解中的转动张量,$ \varLambda ^{ p}$和$ Q^{ p}$分别是塑性伸长和塑性转动,Heidari等[12]提出的分解是$ F = V^{ e}F^{ ep}$,其中,$ F^{ ep}$是Euler塑性变形梯度.
本文集中讨论基于变形梯度乘法分解$ F = F^{ e} F^{p}$而且基于中间构形的大变形弹塑性模型,目的是,弄清模型应所具有的若干性质;它们在当前构形上的数学表示;以及与其他模型之间的比较.首先,使用张量函数表示理论,建立各向同性函数的若干特殊性质,由此建立张量的张量值函数在中间构形到当前构形之间进行前推后拉的简单关系式;然后,在中间构形上,从热力学定律出发并结合各向同性函数的特殊性质,建立模型的数学表达;再应用导出的前推后拉关系式,方便地得到有限元分析所需要的模型在当前构形上的数学表示,包括客观率表示的率形式和连续切向刚度等;最后,将模型与4种其它模型进行比较分析, 这4种模型分别是(1)Moran\等[13]基于塑性旋率为零假定的模型;(2)Heidari\等[12]基于不同分解的模型,(3)基于Jaumann共旋客观率的次弹性模型,(4)基于对数率的模型.
张量运算符号规定如下:黑体代表张量,$\left( \cdot \right)^{T}$和$\left( \cdot \right)^{ -1}$分别代表张量的转置和求逆,$\left( \cdot \right)^{ - {T}}$代表先求逆再求转置(或先求转置再求逆变,因两者顺序可以交换而不影响结果),${tr}\left( \cdot \right)$ 代表张量的求迹运算,对于任意张量$S$和$ T$,$ {ST}$代表它们之间的点积$ S_{{ik}} T_{{kj}}$,符号"$ \otimes $"代表张量并乘${ {S} \otimes {T}} = S_{{ij}} T_{{kl}}$,符号"$:$"代表张量之间的双点积$ {S}: {T} = S_{{ij}}T_{{ij}} $或$ {\mathbb{C}: S} = \mathbb{C}_{{ijkl}} {S}_{{kl}}$,$\left( \cdot \right)_{,S}$代表相对\textbf{\textit{S}}求偏导数,符号"sym"代表将非对称张量对称化${sym}\left( T \right) = \dfrac{1}{2}\left( { T + T^{T}} \right)$,运算$ S\boxtimes T$定义为$S\boxtimes T: A = {SA}^{ T} T$或${S\boxtimes T} = {S}_{{il}} {T}_{{jk}} $.
1 运动关系
\begin{equation}\label{eq1} {F} = {F}^{e}{F}^{p} \tag{1}\end{equation}
式中${{ F}}^{ e}$是弹性变形梯度,${ F}^{p}$是塑性变形梯度,Green应变可表示为
\begin{equation}\label{eq2} E = \frac{1}{2}\left( {{ F}^{ T}{ F} - I}\right)= { F}^{ pT}\bar { E}^{ e}{ F}^{ p} + E^{ p} \tag{2}\end{equation}
式中
\begin{equation}\label{eq3} \bar { E}^{ e} = \frac{1}{2}\left( {\bar {
C}^{ e} - I} \right),\quad \bar { C}^{ e} = { F}^{ eT}{ F}^{ e} \tag{3}\end{equation}
\begin{equation} \label{eq4} E^{ p} = \frac{1}{2}\left( { C^{ p} - I} \right),\quad C^{ p} = { F}^{ pT}{ F}^{ p} \tag{4} \end{equation}
当前构形上的速度梯度为
\begin{equation}\label{eq5} l = \dot { F} F^{ - 1} = \dot { F}^{e} F^{ e-1} + F^{ e}\dot { F}^{ p} F^{ p- 1} F^{ e - 1} = l^{ e} + l^{ p} \tag{5}\end{equation}
式中$ l^{ e}$和$ l^{p}$分别为弹性速度梯度和塑性速度梯度
\begin{equation}\label{eq6} l^{ e} = \dot { F}^{ e} F^{ e -1},\quad l^{ p} = F^{ e}\bar { L}^{ p}F^{ e - 1} \tag{6}\end{equation}
式中$\bar { L}^{p}$是中间构形上的塑性速度梯度
\begin{equation}\label{eq7} \bar { L}^{ p} = \dot { F}^{ p} F^{p - 1} \tag{7}\end{equation}
将$ l^{ e}$和$ l^{p}$的对称部分和反对称部分分别定义为相应的变形率和旋率,即有
\begin{equation}\label{eq8} d^{ e} = \frac{1}{2}\left( { l^{ e} + l^{ eT}} \right),\quad w^{ e} = \frac{1}{2}\left( {l^{ e} - l^{ eT}} \right) \tag{8}\end{equation}
\begin{equation}\label{eq9} d^{ p} = \frac{1}{2}\left( { l^{ p} + l^{ pT}} \right),\quad w^{ p} = \frac{1}{2}\left( {l^{ p} - l^{ pT}} \right) \tag{9}\end{equation}
类似地,将${ l}^{ e}$和$ l$从当前构形分别通过${F}^{ e - 1}\left( \cdot \right){ F}^{e}$混合型后拉到中间构形,定义中间构形上的弹性变形梯度$\bar {L}^{ e}$和速度梯度$\bar { L}~^{[15-16],有
$$\bar { L}^{ e} = { F}^{ e - 1} l^{e}{ F}^{ e} = { F}^{ e - 1}\dot { F}^{ e}\tag{10}\\ \bar { L} = { F}^{ e - 1} l{ F}^{ e} = {F}^{ e - 1}\dot {{ F}}^{ e} + \dot {{ F}}^{p}F^{ p - 1} = \bar { L}^{ e} + \bar { L}^{ p}\tag{11}$$
定义中间构形上的塑性变形率和物质旋率为
\begin{equation}\label{eq12} \bar { D}^{ p} = \frac{1}{2}\left( {\bar {L}^{ p} + \bar { L}^{ pT}} \right),\quad \bar {W}^{ p} = \frac{1}{2}\left( {\bar { L}^{ p} - \bar {L}^{ pT}} \right) \tag{12}\end{equation}
采用同样的方式可定义中间构形上的变形率$\bar {D}$和物质旋率$\bar { W}$以及弹性变形率$\bar { D}^{e}$和弹性物质旋率$\bar { W}^{e}$,因此有率的加法分解\begin{equation}\label{eq13} \bar { D} = \bar { D}^{ e} + \bar {D}^{ p},\quad \bar { W} = \bar { W}^{ e} + \bar {W}^{ p} \tag{13}\end{equation}
2 本构方程
2.1 中间构形上的本构方程
使用定义式(6)和定义式(3),并考虑到第二P-K应力$S$和Kirchhoff应力$ \tau$的对称性,参考构形中单位体积的变形功率可写成
$$S:\dot { E} = \tau : l = { tr}\left({ \tau \dot {{ F}}^{ e}{ F}^{ e - 1}} \right) +{ tr}\left( { \tau { F}^{ e}\bar { L}^{ p}{F}^{ e - 1}} \right) =\\ \qquad \bar { S}:\dot {\bar { E}}^{ e} + \varSigma:\bar { L}^{ p} \tag{14}$$
式中最后等式右边两项分别是弹性变形功率和塑性变形功率,而
$\bar { S} = { F}^{ e - 1} \tau { F}^{ e- T} = { F}^{ p} S{ F}^{ pT}\tag{15}$
$ \varSigma = { F}^{ eT}\tau { F}^{ e - T} = \bar{ C}^{ e}\bar { S} \tag{16}$
分别是中间构形上的第二P-K应力和Mandel应\力[17],后者一般为不对称张量.
假定处于恒温状态,单位体积的自由能密度可表示为
\begin{equation}\label{eq17} \psi = \psi \left( {\bar { E}^{ e}, \xi }\right) \tag{17}\end{equation}
式中\textbf{$\xi$}是内变量,它可以是张量和标量,也可以是两者的组合.热力学第二定律表述为耗散率应大于零,即
\begin{equation}\label{eq18} S:\dot { E} - \dot {\psi } \ge 0 \tag{18}\end{equation}
将式(14)和式(17)一起代入并整理,得
\begin{equation}\label{eq19} \left( {\bar { S} - \frac{\partial \psi }{\partial\bar { E}^{ e}}} \right):\dot {\bar { E}}^{ e} + \varSigma :\bar { L}^{ p} + \frac{\partial \psi }{\partial\xi }\dot {\xi } \ge 0 \tag{19}\end{equation}
采用Coleman和Noll[18]和 Coleman和Gurtin[19
]的方法,得超弹性本构关系为
\begin{equation}\label{eq20} \bar { S} = \frac{\partial \psi }{\partial \bar{ E}^{ e}} = 2\frac{\partial \psi \left( {\bar { C}^{e}, \xi } \right)}{\partial {{\bar { C}^{ e}}}} \tag{20}\end{equation}
Mandel假设屈服函数为
\begin{equation}\label{eq21} f\left( { \varSigma ,\xi } \right) = 0 \tag{21}\end{equation}
进一步地建立最大耗散假定(Lubliner [20 ]})$,即
\begin{equation}\label{eq22} ( \varSigma - \varSigma^0): \bar{ L}^{p} \le 0 \tag{22}\end{equation}
上式对于任意满足${f}\left( {\varSigma ^0,\xi } \right) \le0$的$ \varSigma ^0$和$\xi $.
由此导出正交流动法则
\begin{equation}\label{eq23} \bar{ L}^{ p} = \dot {\lambda} \frac{\partial f}{\partial \varSigma} \tag{23}\end{equation}
以及Kuhn-Tucker 条件
$$\dot {\lambda } \ge 0;~ f\left( { \tau ,\xi } \right) \le 0;~\dot {\lambda }f\left( { \tau ,\xi } \right) = 0$$
2.2 与中间构形刚体叠加转动的相关性
当中间构形的叠加刚体转动$\bar { Q}$时,变形梯度为
\begin{equation}\label{eq24} { F}^{ e\ast } = { F}^{ e}\bar {Q}^{ T},\quad { F}^{ p\ast }= \bar { Q} { F}^{p} \tag{24}\end{equation}
其他主要物理量将按下列式子变化
$$\bar { C}^{ e\ast } = \bar { Q}\bar { C}^{e}\bar { Q}^{ T},\quad \bar { S}^\ast = \bar { Q}\bar{ S}\bar { Q}^{ T} \tag{25}\\ \varSigma ^\ast = \bar { C}^{ e * }\bar { S}^* = Q \varSigma Q^{ T},\quad \bar { D}^{ p\ast } = Q\bar { D}^{ p}{ Q}^{T} \tag{26}\endalign$$
设内变量由一个对称二阶张量$\alpha $和一个标量$k$组成$\xi =\{\alpha,k\}$,例如在运动硬化描述中,二阶张量内变量就是背应力张量,进一步地,假定自由能可分解为弹性和塑性两部分之和
\begin{equation}\label{eq27} \psi = \psi ^{ e}\left( {\bar { C}^{ e}}\right)+ \psi ^{ p}\left( {\bar { \alpha },k} \right)\tag{27}\end{equation}
而屈服函数表示为
\begin{equation}\label{eq28} {f}\left( { \varSigma,\bar { \alpha },{k}}\right) = 0 \tag{28}\end{equation}
要消除乘法分解中叠加转动的非唯一性,就要求
$\psi ^{ e}\left( {\bar { C}^{ e}} \right) = \psi^{ e}\left( {\bar { C}^{ e\ast }} \right) = \psi ^{e}\left( { Q\bar { C}^{ e} Q^{ T}} \right)\tag{29}$
${f}\left( { \varSigma,\bar { \alpha },{k}} \right) =f\left( {\varSigma ^\ast,\bar { \alpha }^\ast ,{k}^\ast }\right) = {f}\left( { Q \varSigma Q^{ T}, Q\bar{ \alpha } Q^{ T},{k}} \right) \tag{30}$
上面已要求$\bar { \alpha }^\ast = Q\bar { \alpha }{Q}^{ T}$,即要求背应力\textbf{$ \alpha$}相对中间构形的转动是客观的,能像第二P-K应力$\bar {S}$和Mandel应力$ \varSigma$一样变换,这可通过在建立其率形式演化方程中使用客观率来实现.再结合式(20)、式(23)和式(A1),所以有
(1) $\psi $是$\bar { C}^{ e}$的各向同性函数,从而有$\bar{ S}$是$\bar { C}^{ e}$的各向同性函数,与$\bar {C}^{ e}$共主轴,Mandel应力$\varSigma = \bar { C}^{e}\bar { S}$对称,也与$\bar { C}^{e}$共主轴;也就是说,要消除乘法分解中叠加转动的非唯一性,需要要求:材料具有初始各项同性.另外,当乘法分解弹塑性表述可被包含为对数率弹塑性表述的特殊情形,在此情形叠加转动的非唯一性可予以消除[21-22].
(2) $f$必须是$ \varSigma $和$\bar {\alpha}$的各向同性函数,若考虑运动硬化,$f$通常表示为$\varSigma -\bar {\alpha }~(\bar {\alpha}$为背应力)的各向同性函数,$\bar { L}^{ p}$也是$\varSigma- \bar {\alpha }$的各向同性函数,由于$\bar { \alpha}$已假设对称,则$\bar { L}^{ p}$对称,于是,塑性旋率应为零
\begin{equation}\label{eq31} \bar { W}^{ p} = 0 \tag{31}\end{equation}
Eidel与Gruttmann[23]通过假定屈服只取决于相对应力$\varSigma - \bar {\alpha}$的对称部分而得到式(31),实际上,由于Mandel应力为对称张量,只需要像上面那样假定背应力$\bar{ \alpha }$对称即可. Moran等[13]曾将当前构形上的塑性变形率和塑性旋率逆变型后拉到中间构形定义为中间构形上的塑性变形率和塑性旋率
\begin{equation}\label{eq32} \bar { D}_{ MOS}^{ P} = { F}^{eT}{ d}^{ p}{ F}^{ e} = \frac{1}{2}\left( {\bar {C}^{ e}\bar { L}^{ p} + \bar { L}^{ pT}\bar {C}^{ e}} \right) \tag{32}\end{equation}
\begin{equation}\label{eq33} \bar { W}_{ MOS}^{ P} = { F}^{ eT}{w}^{ p}{ F}^{ e} = \frac{1}{2}\left( {\bar { C}^{e}\bar { L}^{ p} - \bar { L}^{ pT}\bar { C}^{e}} \right) \tag{33}\end{equation}
他们假定
\begin{equation}\label{eq34} \bar { W}_{ MOS}^{ P} = 0\left( {\Leftrightarrow { w}^{ p} = 0} \right) \tag{34}\end{equation}
式(33) $\bar { W}^{ p} = 0$和式(34) $ w^{ p} = 0$的含义并不相同,前者是以中间构形作为参照,而后者本质上是以当前构形作为参照.若不考虑各向异性硬化,内变量仅为标量,按照上面的分析,$\bar {L}^{ p}$应对称且与$ \varSigma $共主轴,从而与$\bar {C}^{ e}$共主轴,$\bar { C}^{ e}\bar { L}^{p}$为对称张量,式(31)和式(34)同时成立.
2.3 当前构形上的本构方程
定义弹性左Cauchy-Green变形张量
\begin{equation}\label{eq35} b^{ e} = F^{ e} F^{ eT}\tag{35}\end{equation}
求物质时间导数,并考虑到式(6),得
\begin{equation}\label{eq36} \dot { b}^{ e} = l^{ e} b^{ e}+ b^{ e} l^{ eT} = {lb}^{ e} + b^{e} l^{ T} + {\cal L}_v b^{ e} \tag{36}\end{equation}
式中${\cal L}_v b^{ e}$是$ b^{ e}$的Lie导数,为
\begin{equation}\label{eq37} {\cal L}_v b^{ e} = F\left( { F^{ -1} b^{ e} F^{ - T}} \right)^ \cdot F^{ T}\tag{37}\end{equation}
在各向同性弹性情况下,将基于中间构形的本构方程式(20)和式(23),直接使用$F^{ e}\left( \cdot \right) F^{ e -1}$混合型前推到当前构形可得到当前构形的本构方程.
首先讨论弹性本构方程式(20)的混合型前推. 使用式(3b)和式(35),得$F^{ e}\bar { C}^{ e} F^{ e-1} = b^{e}$,再使用式(A10)和式(15),得
$F^{ e}\frac{\partial \psi ^{ e}\left( {\bar {C}^{ e}} \right)}{\partial \bar { C}^{ e}} F^{ e -1} = \frac{\partial \psi ^{ e}\left( { b^{ e}}\right)}{\partial b^{ e}} \tag{38}$
$F^{ e}\bar { S} F^{ e-1} = \tau b^{ e - 1}\tag{39}$
所以,式(20)按照$ F^{ e}\left( \cdot \right) F^{e-1}$的混合型前推变为
\begin{equation}\label{eq40} \tau = 2\frac{\partial \psi ^{ e}}{\partial b^{ e}} b^{ e} \tag{40}\end{equation}
$\psi ^{ e}$是$ b^{e}$的各向同性函数,结合式(A1)和式(40),$ \tau $也是$ b^{e}$的各向同性函数,且两者共主轴,还有
$\tau b^{ e} = b^{ e} \tau\tag{41{ a}}$
$\frac{\partial \psi ^{e}}{\partial b^{ e}} b^{ e} = b^{e}\frac{\partial \psi ^{ e}}{\partial b^{ e}}\tag{41{ b}}$
借助式(41b),弹性变形功率可表示为
\begin{equation}\label{eq42} \frac{\partial \psi ^{ e}}{\partial b^{e}}:\dot { b}^{ e} = \frac{1}{2}{ tr}\left( { b^{ e- 1} \tau \dot { b}^{ e}} \right) = \tau :\left({\frac{1}{2}\dot { b}^{ e} b^{ e - 1}} \right)\tag{42}\end{equation}
下面讨论流动法则式(23)的$ F^{ e}\left( \cdot \right)F^{ e - 1}$混合型前推. 使用式(37)、式(35)、式(7)和式(1),得
\begin{equation}\label{eq43} \frac{1}{2} F^{ e}\left( {\bar { L}^{ P}+ \bar { L}^{ PT}} \right) F^{ e - 1} = F^{e}\bar { D}^{ P} F^{ e - 1} = - \frac{1}{2}{\cal L}_v b^{ e} b^{ e - 1} \tag{43}\end{equation}
式(43)两边双点积就得塑性变形功率,因为与式(16)和式(31)结合有
\begin{equation}\label{eq44} \tau :\left( { - \frac{1}{2}{\cal L}_{v} b^{ e} \cdot b^{ e - 1}} \right) = { tr}\left( {\tau F^{ e}\bar { D}^{ P} F^{ e - 1}} \right) = \varSigma :\bar { L}^{ p} \tag{44}\end{equation}
将定义在中间构形上的Mandel应力式(16)前推,考虑到式(41a),得
$F^{ e} \varSigma F^{ e - 1} = b^{e} \tau b^{ e - 1} = \tau \tag{45{ a}}$
$F^{ e} \varSigma ^{ T} F^{ e - 1} = \tau\tag{45{ b}}$
使用式(A10)和式(45),得
\begin{equation}\label{eq46} F^{ e}\frac{\partial f\left( { \varSigma,\bar { \alpha }} \right)}{\partial \varSigma } F^{ e- 1} = \frac{\partial f\left( { \tau , \alpha }\right)}{\partial \tau } \tag{46}\end{equation}
式中$ \alpha $是当前构形上的背应力
\begin{equation}\label{eq47} \alpha = F^{ e}\bar { \alpha }F^{ e - 1} \tag{47}\end{equation}
为非对称张量. 使用式(A10)、式(45b)和式(47),则有
$$F^{ e}\left( {\dfrac{\partial f\left( {\varSigma ,\bar { \alpha }} \right)}{\partial \varSigma }}\right)^{ T} F^{ e - 1} = \\ \left( { F^{ e - T}\dfrac{\partial f\left( {\varSigma ,\bar {\alpha }} \right)}{\partial \varSigma }F^{ eT}} \right)^{ T} = \left( {\dfrac{\partial f\left( {\tau , \alpha ^{ T}} \right)}{\partial \tau }}\right)^{ T} \tag{48}$$
所以,流动法则式(23)按照$ F^{ e}\left( \cdot \right)F^{ e - 1}$的混合型前推就是
\begin{equation}\label{eq49} - \frac{1}{2}{\cal L}_v b^{ e} b^{ e - 1} = \frac{1}{2}\dot {\lambda }\left({\frac{\partial f\left( { \tau , \alpha } \right)}{\partial \tau } + \left( {\frac{\partial f\left( { \tau , \alpha^{ T}} \right)}{\partial \tau }} \right)^{ T}} \right)\tag{49}\end{equation}
或者,对式(23)直接进行$ F^{ e}\left( \cdot \right) F^{e - 1}$混合型前推,使用定义式(6b)和式(46),得
\begin{equation}\label{eq50} l^{ p} = \dot {\lambda }\frac{\partial f\left({ \tau , \alpha } \right)}{\partial \tau } \tag{50}\end{equation}
若$\bar { L}^{P}$对称,比如在运动硬化模型中,见式(31)前的讨论,于是,$\bar {L}^{ P} = \bar { D}^{P}$,结合式(43)和式(46),流动法则的前推式(49)则简化为
\begin{equation}\label{eq51} - \frac{1}{2}{\cal L}_v b^{ e} b^{ e - 1} = \dot {\lambda }\frac{\partial f\left( { \tau , \alpha } \right)}{\partial \tau }\tag{51}\end{equation}
式(50)仍然保持不变.
式(36)两边点乘$\dfrac{1}{2} b^{ e -1}$并整理,或者,在式(10)、式(11)和式(43)的帮助下,将式(35)采用$F^{ e}\left( \cdot \right) F^{ e -1}$混合型前推到当前构形,得
\begin{equation}\label{eq52} \frac{1}{2}\left( { l + b^{ e} l^{T} b^{ e - 1}} \right) = \frac{1}{2}\dot { b}^{ e}b^{ e - 1} + \left( { - \frac{1}{2}{\cal L}_v b^{ e}b^{ e - 1}} \right) \tag{52}\end{equation}
使用$ \tau$双点积式(52)的两边,右边两项分别为弹性变形功率和塑性变形功率,见式(42)和式(44),所以左边为总的变形功率.从一定意义上说,式(52)可看作是变形率的弹塑性分解.
2.4 与中间构形叠加刚体转动相关性的进一步讨论
在中间构形的叠加刚体转动下,使用式(43),式(24)和式(7),得
$$\left( { - \dfrac{1}{2}{\cal L}_{v} b^{ e} \cdot b^{ e - 1}} \right)^ * = \dfrac{1}{2} F^{ e * }\left( {\bar { L}^{ p\ast } + \bar { L}^{ p\ast T}} \right) F^{ e * - 1} =\dfrac{1}{2} F^{ e}\left( \bar { L}^{ p} + \bar { L}^{ pT} \right) F^{ e - 1} = - \dfrac{1}{2}{\cal L}_{v} b^{ e} \cdot b^{ e - 1} \tag{53}$$
考虑到定义在当前构形的$ b^{e}$和\textbf{\textit{l}}与中间构形叠加转动无关,再结合上式给出的不变性结果,于是,$- \dfrac{1}{2}{\cal L}_{v} b^{ e} \cdot b^{ e -1}$和$\dot { b}^{e}$都与中间构形的选取无关,因此,模型消除了中间构形叠加转动的非唯一性.
Heidari等[12]将变形梯度分解为
\begin{equation}\label{eq54} F = V^{ e} F^{ ep} \tag{54}\end{equation}
式中$ V^{ e}$是弹性左伸长张量,继而使用$ V^{ e}(b^{ e})$建立了式(40)表示的超弹性本构方程以及如下的塑性流动法则
\begin{equation}\label{eq55} D^{ ep}= \dot{\lambda} \frac{\partial f}{\partial \tau} \tag{55}\end{equation}
式中$ D^{ ep}\!=\! ( L^{ ep} + L^{epT})/2$,而$ L^{ ep} \!=\! \dot { F}^{ ep} F^{ep - 1}$,$f\left( { \tau , \alpha ,k} \right) \!=\! 0$.式(54)定义的分解实际上是将式(1)分解所得的中间构形进行刚体转动$\bar{ Q} = R^{e}$,上面已一般性表明,模型式(49)消除了中间构形叠加转动的非唯一性,因此,模型式(55)与模型式(49)等价.下面对其等价性进行具体直接的讨论. 当中间构形产生$\bar { Q} = R^{ e}$刚体转动,按照式(24),有
\begin{equation}\label{eq56} F^{ e\ast } = V^{ e}, F^{ p\ast }= R^{ e} F^{ p}, F = V^{ e} F^{ p\ast} \tag{56}\end{equation}
在带"*"的中间构形上,流动法则(23)变为
\begin{equation}\label{eq57} {\bar { L}^{ p*}} = \dot \lambda\frac{{\partial {{f}}}}{{\partial { \varSigma ^ * }}} \tag{57}\end{equation}
式中屈服函数$f$满足式(30)的要求. 考虑到式(25),有
\begin{equation}\label{eq58} \varSigma ^ * = \bar { C}^{ e * }\bar {S}^* = V^{ e} \tau V^{ e - 1} \tag{58}\end{equation}
根据前面的分析,$ V^{ e}( b^{ e})$和$ \tau$共主轴,根据式(97),\$ \varSigma ^ * = \tau$,此外,就仅考虑运动硬化而言,$\bar { L}^{ p\ast}$对称;因此(57)可写成
\begin{equation}\label{eq59} {\bar { D}^{ p*}} = \dot \lambda\frac{{\partial {{f}}}}{{\partial \tau }} \tag{59}\end{equation}
其中,屈服函数$f\left( { \tau - \alpha ,{k}} \right) = 0$.对照式(54)和式(56),$\bar { D}^{ p\ast }$与Heidari等[12]中的$ D^{ ep}$一致,因此,等价性得到具体证明.
3 率形式与切向模量
3.1 使用弹性变形率
任意张量场$ T$的共旋率使用上标"$\nabla $"代表,定义为
\begin{equation}\label{eq60} T^\nabla = \dot { T} - \varOmega T - T \varOmega ^{ T} \tag{60}\end{equation}
在各向同性弹性下,结合式(A12)和定义式(60),弹性本构方程(40)可写成任意共旋率的形式
\begin{equation}\label{eq1} { \tau }^\nabla = \frac{\partial { \tau}}{\partial { b}^{ e}}:{ b}^{ e\nabla} =2\frac{\partial }{\partial { b}^{ e}}\left( {\frac{\partial\psi ^{ e}}{\partial { b}^{ e}}{ b}^{ e}}\right):{ b}^{ e\nabla} \tag{61}\end{equation}
下面将证明式(61)可使用Kirchhoff应力的Jaumman率$ \tau ^{\nablaJ}$和弹性变形率\textbf{\textit{d}}$^{ e}$表示为
\begin{equation}\label{eq2} \tau ^{\nabla J} = { C}^{J}: { d}^{ e} - w^{ p} \tau - \tau w^{ pT} \tag{62}\end{equation}
式中${ C}^{J}$是空间弹性张量
\begin{equation}\label{eq3} { C}^{J} = 2\frac{\partial }{\partial b^{e}}\left( {\frac{\partial \psi ^{ e}}{\partial b^{e}} b^{ e}} \right):\left( { b^{ e}\boxtimes I + I\boxtimes b^{ e}} \right) \tag{63}\end{equation}
当不考虑塑性旋率即$ w^{ p} =0$时,本构方程式(62)同通常采用的次弹性模型形式上相同,不过,这里的弹性张量不是常张量,而是取决于左Cauchy-Green变形张量.
结合定义式(60)和式(36),得\textbf{\textit{b}}$^{e}$的任意共旋率
\begin{equation}\label{eq4} b^{ e\nabla } = d^{ e} b^{ e} + b^{ e} d^{ e} - \left( { \varOmega - w^{e}} \right) b^{ e} - b^{ e}\left( { \varOmega - w^{ e}} \right)^{ T} \tag{64}\end{equation}
而\textbf{$ \tau $}的任意共旋率可表示为
\begin{equation}\label{eq5} \tau ^\nabla = \tau ^{\nabla {J}} - \left({ \varOmega - w} \right) \tau - \tau \left( {\varOmega - w} \right)^{ T} \tag{65}\end{equation}
$$\dfrac{\partial \tau }{\partial b^{ e}}:\left[{ - \left( { \varOmega - w^{ e}} \right) b^{ e}- b^{ e}\left( { \varOmega - w^{ e}} \right)^{T}} \right] =- \left( { \varOmega - w^{ e}} \right) \tau- \tau \left( { \varOmega - w^{ e}} \right)^{ T}\tag{66}$$
将式(64)和式(65)一起代入式(61),并考虑到式(66),得式(62).
流动法则式(50)还可写成
\begin{equation}\label{eq7} d^{ p} = \dot {\lambda }{ sym}\left({f_{\tau } } \right) \tag{67}\end{equation}
式中塑性因子可表示为
\begin{equation}\label{eq8} \dot {\lambda } = \frac{1}{{E}_{ p} }\left({\frac{\partial f}{\partial \tau }: \tau ^{\nabla {J}}}\right) \tag{68}\end{equation}
最终,率形式的本构方程可表示为
\begin{equation}\label{eq9} \tau ^{\nabla {J}} = { C}_{ ep}^{J} :{ d}- w^{ p} \tau - \tau w^{ pT} \tag{69}\end{equation}
式中弹塑性切线模量${ C}_{ ep} $
\begin{equation}\label{eq10} { C}_{ ep}^{J} = { C}^{J} - \frac{\left({{ C}^{J} :{ sym}\left( {f_{,\tau } } \right)} \right)\otimes \left( {{ sym}\left( {f_{,\tau } } \right):{ C}^{J}} \right)}{{E}_{ p} + { sym}\left( {f_{,\tau } }\right):{ C}^{J}:{ sym}\left( {f_{,\tau } } \right)}\tag{70}\end{equation}
Moran等[13]直接使用中间构形上应力和变形率建立的本构方程,导出切线模量,然后前推到当前构形,过程和运算相对比较复杂.而且,他们为简便起见,还假定$ w^{ P} = 0~(\bar {W}_{ MOS}^{ P} =0)$,使用式(50),这相当于在本文模型中假定当前构形中背应力张量$\alpha$对称,这时,塑性变形率与屈服面正交,但是,后拉到中间构形上的背应力$\bar{ \alpha}$将不对称,塑性旋率不为零,塑性变形率与屈服面也不正交.本文在前面的讨论中,假定中间构形中背应力张量$ \alpha$对称,从而中间构形上的塑性旋率$\bar { W}^{ P} = 0$,塑性变形率与屈服面正交. 所以,本文讨论的模型与Moran等[13]在有关背应力和塑性旋率的假设方面不同,不过,若不考虑各向异性硬化,则两者一致,为
\begin{equation}\label{eq11} \tau ^{\nabla {J}} = { C}_{ ep}^{J} :{d},\quad { C}_{ ep}^{J} = { C}^{J} - \frac{\left( {{C}^{J} : f_{,\tau } } \right) \otimes \left( { f_{,\tau }:{ C}^{J} } \right)}{{E}_{ p} + f_{,\tau } :{C}^{J}: f_{,\tau } } \tag{71}\end{equation}
若进一步仅考虑弹性变形为小变形的情况,且针对Neo-Hook超弹性材料,由于该材料的超弹性张量在小弹性变形下近似为通常次-弹性模型所采用的各向同性弹性张量,流动法则简化为$d^{ p} = \dot {\lambda } f_{,\tau }$,所以本文模型给出的结果将与基于Jaumann共旋客观率的次-弹性模型基本一致.
3.2 使用对数应变的弹性对数率
空间对数应变和空间弹性对数应变分别定义为
\begin{equation}\label{eq12} h = \ln V = \frac{1}{2}\ln b,\quad h^{ e} = \ln V^{ e} = \frac{1}{2}\ln b^{ e}\tag{72}\end{equation}
Xiao等[24 -25]引入了对数率的概念,使得变形率可表示为对数应变的对数率
\begin{equation}\label{eq13} d = h^{\log },\quad h^{\log } = \dot {h} - \varOmega ^{\log } h - h \varOmega ^{\log { T}} \tag{73}\end{equation}
式中$ \varOmega^{\log }$是对数旋率,为
\begin{equation}\label{eq14} \varOmega^{ log} = { w} + \sum\limits_{i=1}^3 {\sum\limits_{j \ne i}^3 {\left( {\frac{\lambda _{j}^2 +\lambda _i^2 }{\lambda _{j}^2 - \lambda _i^2 } + \frac{1}{\ln\lambda _i - \ln \lambda _{j} }} \right){d}_{ij} { n}_i \otimes{ n}_j } } \tag{73}\end{equation}
式中$\lambda _i$是弹性主伸长,$n_{i}(i=1,2,3)$是3个Euler\主轴.
根据定义,$ h^{ e}$和$ d^{e}$是以中间构形作为变形的参照所得的对数应变和变形率,类似于式(73)和式(74),引入弹性对数率的概念,使得弹性变形率可表示为弹性对数应变的弹性对数率
\begin{equation}\label{eq15} { d}^{ e} = { h}^{ e, e\log },\quad h^{ e, e\log } = \dot { h}^{ e} - { \varOmega} ^{e\log }{ h}^{ e} - h^{ e}{ \varOmega} ^{ e\logT } \tag{75}\end{equation}
式中$ \varOmega^{ e\log}$是弹性对数旋率,系将对数旋率定义式(74)中的变形量用相应的弹性变形量替换所得,为
$$\varOmega ^{ e\log } = { w}^{ e} +\dl\sum\limits_{i= 1}^3 \dl\sum\limits_{j \ne i}^3 \left(\dfrac{\left( {\lambda _{j}^{ e} } \right)^2 + \left( {\lambda_i^{ e} } \right)^2}{\left( {\lambda _{j}^{ e} } \right)^2 -\left( {\lambda _i^{ e} } \right)^2} + \right.\left. \dfrac{1}{\ln \lambda _i^{ e} - \ln \lambda_{j}^{ e} } \right){d}_{ij}^{ e} n_i^{ e} \otimes n_j^{ e} \tag{76}$$
弹性本构方程式(40)可以用对数应变等价表示为
\begin{equation}\label{eq17} \tau = \frac{\partial \psi }{\partial h^{e}} \tag{77}\end{equation}
写成共旋率的形式是
\begin{equation}\label{eq18} { \tau} ^{\log } = { C}^{\log}: h^{e,\log } \tag{78}\end{equation}
式中
\begin{equation}\label{eq19} { C}^{\log } = \frac{\partial ^2\psi }{\partial h^{ e}\partial h^{ e}} \tag{79}\end{equation}
\begin{equation}\label{eq20} d - h^{ e,\log } = \dot {\lambda}\frac{\partial f}{\partial \tau } \tag{80}\end{equation}
使用式(A12),式(68)给出的塑性因子又可表示为
\begin{equation}\label{eq21} \dot {\lambda } = \frac{1}{{E}_{ p} }\left({\frac{\partial f}{\partial \tau }: \tau ^{\log }} \right)\tag{81}\end{equation}
最终,本构方程可表示为
\begin{equation}\label{eq22} \tau ^{\log } = { C}_{ ep}^{\log } : d\tag{82}\end{equation}
式中弹塑性模量${ C}_{ ep}^{\log } $
\begin{equation}\label{eq23} { C}_{ ep}^{\log } = { C}^{\log } -\frac{\left( {{ C}^{\log } : f_{,\tau } } \right) \otimes\left( { f_{,\tau } :{ C}^{\log } } \right)}{{E}_{ p} + f_{,\tau } :{ C}^{\log } : f_{,\tau } } \tag{83}\end{equation}
本文模型若采用上述过程,可得
\begin{equation}\label{eq24} \tau ^{\log } = { C}_{ ep}^{\log } : d +\left( {\varOmega ^{\log } - \varOmega ^{ e\log }}\right) h^{ e} + h^{ e}\left( {\varOmega ^{\log T} - \varOmega ^{ e\log T}} \right) \tag{84}\end{equation}
\begin{equation}\label{eq25} { C}_{ ep}^{\log } = { C}^{\log } -\frac{\left( {{ C}^{\log } :{ sym}\left( { f_{,\tau } }\right)} \right) \otimes \left( {{ sym}\left( { f_{,\tau } }\right):{ C}^{\log } } \right)}{{E}_{ p} + { sym}\left({ f_{,\tau } } \right):{ C}^{\log } :{ sym}\left( {f_{,\tau } } \right)} \tag{85}\end{equation}
式(84)与对数率模型相比,则多出对数旋率与弹性对数旋率之差引起的项.
4 算例
本文算例讨论下面几种大变形弹塑性分解模型:(1) Moran等[13]基于塑性旋率为零假定的模型(Moran模型);(2)本文提出的基于中间构形的大变形弹塑性模型(RFM模型);(3)基于Xiao等[24-27]提出的塑性流动法则(80)建立的大变形弹塑性模型.对于基于Jaumann共旋客观率的次-弹性模型,由于当弹性变形很小时,和之前模型结果将是一致的,在本文中,算例从略.算例选择简单剪切问题,如图1所示,图中初始构形的正方形边长为单位长度.
对于本文的RFM模型,模型选取如下:
(1)对于弹性部分,使用Neo-Hookean超弹性模\型[28],它的能量函数为
\begin{equation}\label{eq26} W_0 = \frac{1}{2}\mu \left( {I^{ Ce} - 3} \right)- \mu \ln J^{ e} + \frac{1}{2}\lambda \left( {\ln J^{ e}}\right)^2 \tag{86}\end{equation}
其中,$\mu $和$\lambda $是Lam\'{e}常数,$I^{Ce}$是右Cauchy-Green弹性变形张量$ C^{e}$的第一不变量,$J^{ e}$是弹性变形的体积比.Neo-Hookean超弹性本构关系是
\begin{equation}\label{eq27} \tau = \mu \left( { b^{ e} - I} \right)+ \lambda \left( {\ln J^{ e}} \right) I \tag{87}\end{equation}
(2)塑性屈服函数选取为
\begin{equation}\label{eq28} f = f\left( { \tau , \alpha ,\zeta } \right) =\sqrt {3\hat {J}_2 } - Y\left( \xi \right) \tag{88}\end{equation}
其中,$\hat {J}_2 $是等效应力$\hat { \tau } = \tau - \alpha $的偏应力第二不变量
\begin{equation}\label{eq29} \hat {J}_2 = \frac{1}{2}\hat { \tau }':\hat {\tau }' \tag{89}\end{equation}
其中,$\hat { \tau }'$是$\hat { \tau }$的偏量部分.内变量使用下面的式子定义
\begin{equation}\label{eq30} \dot {\xi } = \dot {\bar {\varepsilon }}^{ p} =\left( {\frac{2}{3} d^{ p}: d^{ p}}\right)^{\frac{1}{2}} \tag{90}\end{equation}
塑性模量定义为
\begin{equation}\label{eq31} E_{ p} = \frac{\partial Y}{\partial \xi } \tag{91}\end{equation}
屈服面硬化函数假设为指数函数
\begin{equation}\label{eq32} Y = \tau _{ s0} + \left( {\tau _{ s1} - \tau_{ s0} } \right)\left( {1 - { e}^{ - C_{ iso} \xi }}\right) \tag{92}\end{equation}
从而
\begin{equation}\label{eq33} E_{ p} = C_{ iso} \left( {\tau _{ s1} - \tau_{ s0} } \right){ e}^{ - C_{ iso} \xi } \tag{93}\end{equation}
对于背应力,选取Armstrong--Frederick模型[29-30],背应力演化公式为
\begin{equation}\label{eq34} \bar { \alpha }^{\nabla J} = C_{ kin} \bar {D}^{ p} - C_{ non} \xi \bar { \alpha } \tag{94}\end{equation}
其中,$C_{ kin} $为背应力的运动硬化系数;$C_{ non}$为动态恢复项,用于描述背应力的非线性特征.
对于Moran模型和Xiao模型,为了和本文的模型进行对比,选取弹性模型和塑性模型和本文一样的,选取相应合适的背应力模型.对于Moran等[13]基于塑性旋率为零假定的模型,背应力演化公式为
\begin{equation}\label{eq35} \alpha ^{\nabla J} = C_{ kin} d^{ p} -C_{ non} \xi \alpha \tag{95}\end{equation}
对于基于Xiao[24- 27]提出的塑性流动法则(80)建立的大变形弹塑性模型,背应力演化公式为
\begin{equation}\label{eq36} \alpha ^{\nabla \log } = C_{ kin} d^{p} - C_{ non} \xi \alpha \tag{96}\end{equation}
本文选取下列的参数:弹性模型参数:$\lambda = 78$ GPa,\linebreak$\mu=78$ GPa;塑性模型参数:$C_{ iso} =5/3$,$\tau _{ s0} =285.6$ MPa,$\tau _{ s1} = 680.0$ MPa;背应力模型参数:$C_{kin} = 20.0$ MPa,$C_{ non} = 0.2$.
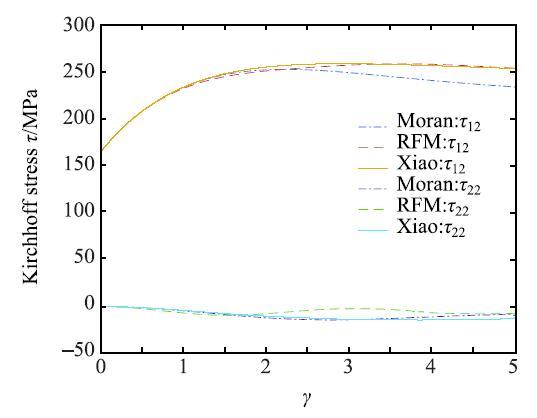
如图2所示,给出了当剪切位移$0 \le \gamma \le 5$时,应力分量$\tau_{22} ,\tau _{12} $的结果.
图2 Kirchhoff应力分量$\tau _{11} ,\tau_{12} $和剪切位移$\gamma$的关系曲线...
Fig. 2 The relation curve of Kirchhoff stress component $\tau_{11} ,\tau _{12} $ and shear displacement $\gamma $...
弹性变形部分很小,大约在$\gamma = 0.0021$时,开始产生塑性变形.在塑性变形部分,各种模型的结果略有不同,当$\gamma > 2$时,Moran模型的$\tau _{22} ,\tau _{12}$相比RFM模型和Xiao模型,产生了一定的差异;RFM模型和Xiao模型的结果很接近.
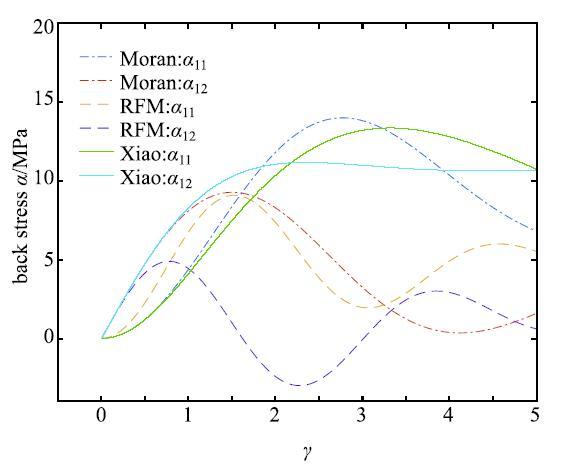
如图3所示,给出了当剪切位移$0 \le \gamma \le5$时,背应力分量$\alpha _{11} ,\alpha _{12} $的结果.当剪切变形$\gamma $约为0.1的时候,背应力是一致的,当$\gamma >0.1$时,背应力产生了一定的差别.
图3 背应力分量$\alpha _{11} ,\alpha_{12} $和剪切位移$\gamma$的关系曲线...
Fig. 3 The relation curve of back stress component $\alpha_{11},\alpha _{12} $ and shear displacement $\gamma $...
5 结论
本文所讨论的基于中间构形的模型,具有如下结论:
(1)在等向硬化的情况下,无论是中间构形还是当前构形,塑性旋率均为零,塑性变形率均与屈服面正交.
(2)在运动硬化的情况下,在中间构形上,若假定背应力对称,则塑性旋率为零,塑性变形率与屈服面正交,但前推到当前构形则有,背应力不对称,塑性旋率不为零,塑性变形率与屈服面也不正交,只是塑性变形梯度与屈服面正交.反过来,在当前构形上,若假定背应力对称,则当前构形的塑性旋率为零,塑性变形率与屈服面正交,但后拉到中间构形,中间构形上的背应力不对称,塑性旋率不为零,塑性变形率与屈服面也不正交.
(3)无论是等向硬化还是运动硬化的情况,与将弹性变形梯度假设为对称的伸长张量的模型给出一致的结果.
(4)在假定当前构形上的塑性旋率为零的情况下,与通常基于变形率加法分解的次弹塑性模型形式上相同,只是所采用弹性张量不是常张量,而是取决于左Cauchy-Green变形张量.
与对数率模型相比,则多出由对数旋率与弹性对数旋率之差引起的项.
The authors have declared that no competing interests exist.
参考文献
| [1] |
|
| [2] |
大变形弹塑性本构理论的几个基本问题 .Some fundamental problems in elastic-plastic constitutive theory of finite deformation . |
| [3] |
Elasticity and Plasticity of Large Deformations . |
| [4] |
Elasto-plastic deformation at finite strain . |
| [5] |
Concerning elastic and plastic components of deformation . |
| [6] |
Caveats concerning conjugate stress and strain measures for frame indifferent anisotropic elasticity . |
| [7] |
Decomposition of strain measures and their rates in finite deformation elastoplasticity . |
| [8] |
On finite deformation elasto-plasticity . |
| [9] |
Certain basic issues in finite-deformation continuum plasticity . |
| [10] |
Deformation analysis for finite elastic-plastic strains in a lagrangean-type description . |
| [11] |
Hardening materials modeling in finite elastic--plastic deformations based on the stretch tensor decomposition . |
| [12] |
An Eulerian multiplicative constitutive model of finite elastoplasticity . |
| [13] |
Formulation of implicit finite element methods for multiplicative finite deformation plasticity . |
| [14] |
|
| [15] |
Equations constitutives et directeurs dans les milieux plastiques et viscoplastiques . |
| [16] |
Micromechanics of crystals and polycrystals . |
| [17] |
Plasticité Elassique et Viscoplasticité. Vienna-New York: |
| [18] |
The Thermodynamics of Elastic Materials with Heat Conduction and Viscosity. The Foundations of Mechanics and Thermodynamics. Berlin, |
| [19] |
Thermodynamics with internal state variables .
|
| [20] |
Normality rules in large-deformation plasticity . |
| [21] |
A consistent finite elastoplasticity theory combining additive and multiplicative decomposition of the stretching and the deformation gradient . |
| [22] |
The integrability criterion in finite elastoplasticity and its constitutive implications . |
| [23] |
Elastoplastic orthotropy at finite strains: Multiplicative formulation and numerical implementation . |
| [24] |
Logarithmic strain, logarithmic spin and logarithmic rate . |
| [25] |
Hypoelasticity model based upon the logarithmic stress rate . |
| [26] |
Elastoplasticity beyond small deformations . |
| [27] |
Hencky's logarithmic strain and dual stress--strain and strain--stress relations in isotropic finite hyperelasticity . |
| [28] |
A review of methods to characterize rubber elastic behavior for use in finite element analysis . |
| [29] |
A mathematical representation of the multiaxial Bauschinger effect . |
| [30] |
On the theoretical and numerical modelling of Armstrong--Frederick kinematic hardening in the finite strain regime . |
| [31] |
Theory of representations for tensor functions-A unified invariant approach to constitutive equations .
|
| [32] |
各向同性张量函数的导数 .
The derivative of an isotropic tensor .
|
| [33] |
连续介质力学中某些物理量的近似和大变形弹塑性定义的比较. [博士论文] .
The approximation of some variables and the comparison of elasto-plastic large deformation definitions in continuum mechanics. [PhD Thesis] .
|

/
| 〈 |
|
〉 |