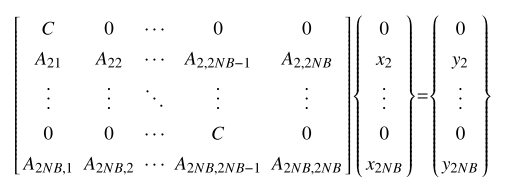轴对称薄壁结构自由振动的边界元分析1)
北京大学工学院力学与工程科学系,北京 100871
FREE VIBRATION ANALYSIS OF THIN-WALLED AXISYMMETRIC STRUCTURES WITH BOUNDARY ELEMENT METHOD1)
中图分类号: O34
文献标识码: A
版权声明: 2019 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
作者简介: 2) 陈永强,副教授,主要研究方向:计算力学、固体力学.E-mail: chenyq@pku.edu.cn
展开
摘要
采用双互易法分析薄壁轴对称结构自由振动的特征频率以及特征模态.首先,采用径向基函数插值域积分里的位移,利用双互易法将域积分转化为子午面边界的积分.然后,将边界物理量、基本解和特解展开为傅里叶级数,沿环向积分后得到的边界积分方程可用于轴对称结构带体积力问题和受非对称载荷的动力学分析,其积分域为轴对称结构子午面边界上的线积分,进一步降低了问题的维度和离散的难度.文章详细探讨了源点处于对称轴的特殊情况,根据基本解和特解的退化形式,针对无体积力和有体积力分别给出了处理奇异矩阵的方案.对于薄壁结构,采用双曲正弦变换处理近奇异积分有效提高积分精度.最后将双互易法和双曲正弦变化应用于薄壁轴对称结构带体积力的静力学和自由振动分析.数值结果表明,文章提出的处理奇异矩阵的方法能够有效处理源点处于对称轴的情况;当圆筒厚高比为$10^{-3}$,边界元计算的特征频率的相对误差为$10^{-3}$,且优于有限元的结果.
关键词:
Abstract
The dual reciprocity method(DRM) is extended to study the eigenvalue and eigenmode of thin-walled axisymmetric structures. First the displacement in the domain integral can be approximated by a set of radial basis functions and the domain integral can be converted to the boundary using DRM. Then the displacement and the traction can be expanded as Fourier series and integrate along the circumferential direction. The obtained boundary integral equation can be used for analysis of elastostatics of axisymmetric structure distributed body force and elastodynamics subject to asymmetric loading. The special case of the source point on the axis of symmetry is discussed in detail. New schemes are suggested for dealing with singular matrices for cases with and without body force respectively according to the degenerate form of the fundamental solution and the particular solution. For the thin walled structure, the sinh transformation is applied to improve the accuracy of evaluation of the nearly singular integrals. The developed project has been used to analyze elastostatics with body force and the free vibration of the thin axisymmetric structures. Numerical results indicate that the proposed method for dealing with singular matrices can effectively deal with the situation where the source point is on the axis of symmetry. and when the thickness ratio reaches $10^{-3}$, the relative error of the results can approach $10^{-3}$, which is better than those of FEM.
Keywords:
薄壁结构是工程中比较常见的结构,如火箭的整流罩、飞机涂层等.在火箭发射过程中,随机振动环境会影响结构失效,因此研究薄壁结构的动力学响应对于卫星发射等领域具有重要的现实意义.在建模过程中,航天器的部分结构常等效为柱壳、圆锥体等薄壁轴对称结构.边界元法因其降维等优点已被广泛应用到弹性动力学分析,边界元法求解弹性动力学问题主要有以下3种:利用与时间有关的基本解建立边界积分方程,即时域边界元法[1-4];通过Laplace变换等积分变换转变为椭圆型问题求解,即频域边界元法[5-7];另外还可通过双互易法[8]、径向积分法[9]等利用弹性静力学基本解求解弹性动力学问题.时域边界元法需对时间进行积分,存储量和计算量比较大.Yao等[10]提出了一种新的弹性动力学时空域边界积分方程,公式和核函数更简单,计算量和需要存储起来反复使用的方程系数的量都显著减少.频域边界元法的基本解形式复杂,且频率耦合在基本解中,会造成计算效率低等问题.因此,本文采用双互易法建立边界积分方程进行弹性体的自由振动分析.
双互易法最先由Nardini等[11]提出,利用互易性原理和径向基函数将域积分转化为边界积分,因此,边界积分方程中可利用弹性静力学的基本解计算带体积力问题和弹性动力学问题.Park等[12]利用双互易法对轴对称弹性体受重力、离心力等常规体积力进行了分析.Javaran等[13 -15]采用高斯函数、傅里叶级数、球Hankel函数等不同的径向基函数进行了2D和3D弹性动力学分析.Fahmy等[16]利用双三次B样条函数将双互易法扩展于各向异性功能梯度材料的最优形状设计中.双互易法还被推广应用于裂纹分析[17-18]和非线性、非均质问题[19-20].采用双互易法计算弹性体自由振动的特征频率,特征频率与离散后形成的系数矩阵解耦,可以通过迭代高效地求出特征频率及相应的特征模态.Wang等[21-22]利用双互易法分析了空心圆柱的自由振动,但未考虑近奇异积分,对于薄壁结构计算精度低.
本文考虑薄壁结构近奇异积分的影响,利用双互易法和傅里叶级数展开,推导了几何轴对称结构受非对称载荷的弹性动力学的边界积分方程,其积分域为子午面边界的积分,进一步降低了问题的维度和离散的难度.对于薄壁结构出现的近奇异积分,本文采用双曲正弦变化进行处理,有效提高近奇异积分的精度,并应用于计算薄壁轴对称结构自由振动的特征频率及其相应模态,具有降低计算规模和高精度的优点.
对于源点处于对称轴这种特殊情况,系数矩阵会出现奇异性,本文根据基本解和特解的退化形式,针对无体积力和有体积力的情况分别给出了处理奇异矩阵的方案,并通过数值算例验证本文提出的处理奇异矩阵的方法的有效性.
1 轴对称结构的边界积分方程
1.1 三维问题的边界积分方程
弹性体自由振动的平衡方程
$$\sigma _{ij,j} + f_i = 0\tag{1}$$
式中,$f_i$ 考虑为惯性力
$${f_i} = \rho {\omega ^2}{u_i}\tag{2}$$
式中$\omega$为弹性体做简谐振动的固有圆频率. 采用3DKelvin解$U^\ast_{ki}(p;q)$作为权函数,其中$p$为源点,$q$为场点,利用互易性原理,可以得到方程(1)的等效积分形式[23]
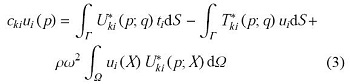
方程(3)的最后一项含有域积分,如果在域内划分单元会失去边界元法降维的优势,利用双互易法可将域积分转化为边界积分.采用径向基函数$F_{il}^J(X,\xi^J)$的线性组合对方程(3)域积分中的位移进行插值
$$u_i \left( X \right) = F_{il}^J \left( {X,\xi ^J} \right)\alpha_l \left( {\xi ^J} \right)\tag{4}$$
式中,$\alpha _l $是对应基函数的系数. 寻找特定的位移场$\psi _{il}^j $和相应的应力张量$\sigma _{ik}^p $ 满足以下平衡方程
$$\sigma_{ik,k}^p + \rho \omega ^2F_{il}^J \left( {X,\xi ^J} \right)\alpha_l \left( {\xi ^J} \right) = 0\tag{5}$$
与$\sigma _{ik}^p $相应的位移特解$u_i^p \left( X \right)$和面力特解$t_i^p(X)$可表达为如下形式
$$\left.\begin{array}{ll} {u_i^p \left( X \right) = \rho \omega ^2\psi _{il}^J \left( {X,\xi ^J}\right)\alpha _l \left( {\xi ^J} \right)}\\ {t_i^p \left( X \right) = \rho \omega ^2p_{il}^J \left( {X,\xi ^J}\right)\alpha _l \left( {\xi ^J} \right)}\end{array}\right\}\tag{6}$$
式中,$p_{il}^J(X, \xi^J) = \sigma _{ilj}^p{n_j}$为面力.于是,方程(3)右端的域积分项可以用应力特解的梯度表示,并再利用一次互易性原理,可以得到
$$\int_\varOmega u_i U_{ki}^{\ast } {d}\varOmega = \alpha _l\int_\varOmega U_{ki}^\ast F_{il}{d}\varOmega =\\ \qquad-\alpha _l \int_\varOmega U_{ki}^\ast \sigma_{il,j} {d}\varOmega = \alpha _l \Bigg( c_{ki} \psi _{il}-\\ \qquad\int_\varGamma U_{ki}^\ast \left( {p;q} \right)p_{il} {d}S + \int _\varGamma T_{ki}^\ast \left( {p;q} \right)\psi _{il} {d}S \Bigg)\tag{7}$$
把方程(7)代入方程(3),可得到弹性体自由振动的边界积分方程[11]
$$c_{ki}{u_i}\left( p \right) = \int_\varGamma U_{ki}^{{*}}\left( {p;q} \right){t_i}{d}S-\\ \qquad \int_\varGamma T_{ki}^{{*}}\left( {p;q} \right){u_i}{d}S + \rho {\omega ^2}\Bigg(c_{ki}u_i^p-\\ \qquad \int_\varGamma U_{ki}^{{*}}\left( {p;q}\right)t_i^p{d}S + \int_\varGamma T_{ki}^{{*}}\left( {p;q}\right)u_i^p{d}S\Bigg)\tag{8} $$
从方程(8)可以看出,采用双互易法得到的弹性动力学的边界积分方程中,频率$\omega$ 与基本解是解耦的,这使得在迭代求解的时候,系数矩阵(积分)只需要计算一次;而对于采用频域边界元法求解,频率$\omega$ 耦合在基本解中,每迭代一次就需要重新计算积分.因此本文采用双互易法求解特征频率效率更高.
双互易法需要通过径向基函数对体积力进行插值,本文主要采用多项式形式的径向基函数[24]
$$F_{il} = \left( {A + r} \right)\delta _{il}\tag{9}$$
其中,$A$ 为任意常数,$r$ 为源点$x$ 到插值点$\xi ^J$之间的距离,对应的位移特解$\psi _{il} $ 和面力的特解$p_{il} $分别为
$$\psi _{il} = \left( {D_1 A + D_2 r} \right)\delta _{il}r^2 + \left( {D_3 A + D_4 r} \right)r_i r_l\tag{10}$$
$$p_{il} = r_i n_l \left( {S_1 A + S_2 r} \right) + r_l n_i \left({S_3 A +S_4 r} \right)+\\ \quad~r_n \left[ {\delta _{ik} \left( {S_3 A + S_4 r} \right) +S_5 \frac{r_i r_l }{r}} \right]\tag{11} $$
其中
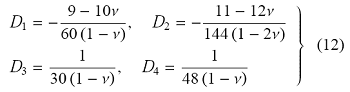
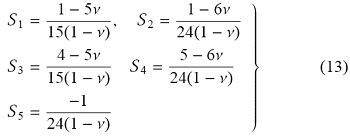
Park[12]针对径向基函数$F_{il} = \mu \left( {C_1}-{C_2}r\right)\delta_{il}$给出了面力和位移的特解,本文选取的径向基函数式(9)与其类似,因此本文的特解参考了Park的文献.
1.2 轴对称结构的边界积分方程
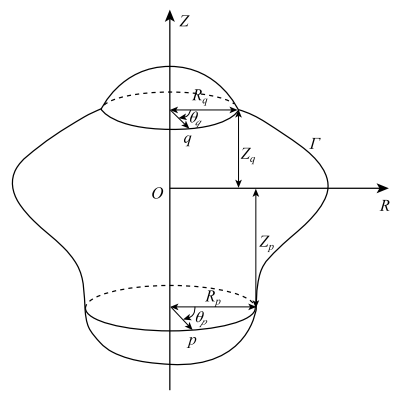
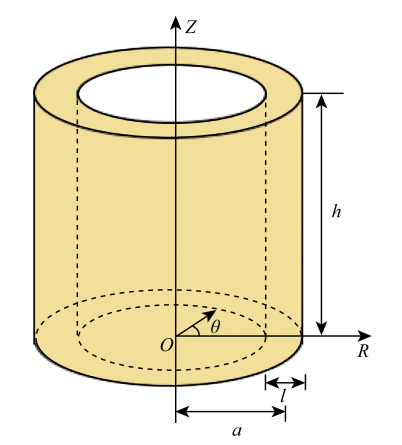
对于轴对称结构,如图1 所示,采用柱坐标系$(R, \theta,Z)$描述,现将三维情况下的边界积分方程转化为几何轴对称下的边界积分方程(暂不考虑有体积力的情况),首先需将直角坐标系下表达的物理量转为用柱坐标系表达(以位移为例)
$$\left\{\begin{array}{c}u_1\\u_2\\u_3\end{array} \right\} = \left[ \begin{array}{ccc}\cos \theta _q &-\sin \theta _q & 0\\\sin\theta _q & \cos\theta _q & 0\\0 & 0 & 1\end{array} \right]\left\{\begin{array}{c}u_r\\u_\theta\\u_z\end{array} \right\}= T\left( \theta _q\right) u\tag{14}$$
其中,$T\left(\theta \right)$ 为转换矩阵,对于直角坐标系下的基本解$U^\ast$有如下转换
$$ U = { {T\left( {{\theta _p}} \right)} ^{T}}U^\ast {T\left( {{\theta _q}} \right)} \tag {15}$$
图1 轴对称结构示意图...由于其载荷不一定对称,需将边界上的物理量及基本解沿着$\theta$方向进行傅里叶级数展开[
Fig. 1 Axisymmetric structure
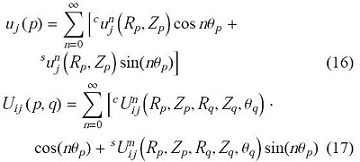
其中,$R_x,\theta_x$和$Z_x$分别表示点$x$在柱坐标系下的径向、环向和轴向坐标,$i,j$ 代表$R,\theta,Z$方向,$n$为环向波数,$n=0$即为纯对称情况(载荷也是轴对称的),上标$c$和$s$分别表示与$\cos\theta$和$\sin\theta$相关的项. $^cU^n_{ij}$和$^sU^n_{ij}$为傅里叶展开系数
$$\left.\begin{array}{l}{{}_{}^cU_{ij}^n = \dfrac{1}{\pi }\int_0^{2\pi }{U_{ij}}{{cos}}(n{\theta _p}){d}{\theta_p}}\\[3mm]{{}_{}^sU_{ij}^n = \dfrac{1}{\pi}\int_0^{2\pi }{U_{ij}}{{sin}}(n{\theta _p}){d}{\theta _p}}\end{array}\right\}\tag {18}$$
对面力也可以做类似的傅里叶级数展开,将展开后的表达式代入无体积力的边界积分方程,且有${d}S=R_q{d}\theta{d}\varGamma,\varGamma$为轴对称结构子午面的边界,由于$\cos n\theta_p$ 和$\sinn\theta_p$是线性无关的,可得以下两个方程
$${c_{ij}}{}_{}^cu_j^n = \int_\varGamma ^{}\mathop \sum \limits_{m = 0}^\infty \bigg[ {\int_{-\pi }^\pi{}_{}^cU_{ij}^n{{\cos}}(m{\theta _q}){d}{\theta_q}}\cdot{}_{}^ct_j^m +\\ {\int_{-\pi }^\pi{}_{}^cU_{ij}^n{{sin}}(m{\theta _q}){d}{\theta_q}{}_{}^st_j^m}\bigg]{R_q}{d}\varGamma- \\ \qquad \int_\varGamma \mathop \sum \limits_{m = 0}^\infty\bigg[ {\int_{-\pi }^\pi {}_{}^cT_{ij}^n{{cos}}(m{\theta_q}){d}{\theta_q}{}_{}^cu_j^m} +\\ \qquad \int_{-\pi }^\pi {}_{}^cT_{ij}^n{{sin}}(m{\theta_q}){d}{\theta _q}{}_{}^su_j^m \bigg]{R_q}{d}\varGamma\tag {19}$$
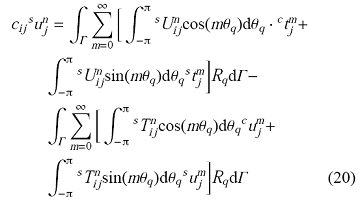
令$\theta=\theta_q-\theta_p$,代入式(18)可得
$$\left.\begin{array}{l}{}_{}^cU_{ij}^n = \dfrac{1}{\pi }\int_0^{2\pi} U_{ij} \left({{cos}}(n{\theta _q}){{cos}}(n\theta) +{{sin}}(n{\theta _q}){{sin}}(n\theta) \right){d}\theta\\{}_{}^sU_{ij}^n = \dfrac{1}{\pi }\int_0^{2\pi}{U_{ij}} \left({{sin}}(n{\theta _q}){{cos}}(n\theta) -{{cos}}(n{\theta _q}){{sin}}(n\theta) \right){d}\theta\end{array}\right\}\tag {21}$$
将式(21)代入式(19)和式(20)中,利用三角函数的正交性,可进行如下简化
$$\mathop \sum \limits_{m = 0}^\infty \int_0^{2\pi}{}_{}^cU_{ij}^n{{cos}}(m{\theta _q}){d}{\theta _q} = \mathop \sum \limits_{m = 0}^\infty \dfrac{1}{\pi}\cdot\\ \qquad \int_0^{2\pi} \int_0^{2\pi} {U_{ij}}\big[ {{cos}}(n{\theta _q}){{cos}}(n\theta)+\\ \qquad {{sin}}(n{\theta _q}){{sin}}(n\theta) \big]{cos}(m{\theta _q}){d}{\theta _q}{d}\theta= \\ \qquad\int_0^{2\pi} U_{ij}{{cos}}(n\theta) {d}\theta =U_{ij}^{nc}\tag {22}$$
$$ \mathop \sum \limits_{m = 0}^\infty \int_0^{2\pi}{}_{}^cU_{ij}^n{{sin}}(m{\theta _q}){d}{\theta _q} =\mathop \sum \limits_{m = 0}^\infty \dfrac{1}{\pi }\cdot\\ \qquad\int_0^{2\pi} \int_0^{2\pi} {U_{ij}}\big[ {{{cos}}(n{\theta _q}){{cos}}(n\theta) }+\\ \qquad {{sin}}(n{\theta _q}){{sin}}(n\theta) \big]{{sin}}(m{\theta _q}){d}{\theta _q}{d}\theta= \\ \qquad \int_0^{2\pi} {U_{ij}}{{sin}}(n\theta) {d}\theta= U_{ij}^{ns}\tag {23}$$
将式(22)和式(23)代入式(19)和式(20)简化后可得
$$ c_{ij}{}_{}^cu_j^n = \int_\varGamma \left[ {U_{ij}^{nc}{}_{}^ct_j^n + U_{ij}^{ns}{}_{}^st_j^n} \right]{R_q}{d}\varGamma-\\ \qquad \int_\varGamma\left[T_{ij}^{nc}{}_{}^cu_j^n +T_{ij}^{ns}{}_{}^su_j^n\right]{R_q}{d}\varGamma\tag {24}$$
$$ {c_{ij}}{}_{}^su_j^n=\int_\varGamma \left[ {U_{ij}^{nc}{}_{}^st_j^n-U_{ij}^{ns}{}_{}^ct_j^n} \right]{R_q}{d}\varGamma +\\ \qquad \int_\varGamma \left[ {T_{ij}^{nc}{}_{}^su_j^n -T_{ij}^{ns}{}_{}^cu_j^n} \right]{R_q}{d}\varGamma\tag {25}$$
其中
$$\left.\begin{array}{*{20}{l}} {\left[ {U_{ij}^{nc}} \right] =\left[ {\begin{array}{*{20}{c}}{U_{RR}^{nc}}&0&{U_{RZ}^{nc}}\\0&{U_{\theta \theta }^{nc}}&0\\{U_{ZR}^{nc}}&0&{U_{ZZ}^{nc}}\end{array}} \right]}\\{\,\left[ {U_{ij}^{ns}} \right] = \left[ {\begin{array}{*{20}{c}}0&{U_{R\theta }^{ns}}&0\\{U_{\theta R}^{ns}}&0&{U_{\theta Z}^{ns}}\\0&{U_{Z\theta }^{ns}}&0\end{array}} \right]}\end{array}\right\}\tag {26}$$
根据$[U^{nc}_{ij}]$和$[U^{ns}_{ij}]$零元素的位置,可以进一步得到对称部分和反对称部分的边界积分方程.
对称部分
$${c_{ij}}\bar{u}_j^n = \int_\varGamma \left({\bar{U}_{ij}^n{{\bar t}_j}-\bar{T}_{ij}^n{{\bar u}_j}}\right){R_q}{d}\varGamma \tag {27}$$
反对称部分
$${c_{ij}}\overline {\overline{u}}_j^n = \int_\varGamma \left(\overline {\overline {U}} _{ij}^n{{\overline {\overline t} }_j}-\overline {\overline {T}} _{ij}^n{{\overline {\overline u}} _j} \right){R_q}{d}\varGamma \tag {28}$$其中
$$\left.\begin{array}{*{20}{l}}{\overline{u}_i^n = {{\left[ {u_R^{n{{c}}}\,u_\theta ^{ns}\,u_Z^{nc}} \right]}^{T}}}\\[3mm]{\overline {\overline {u}} _i^n = {{\left[ {u_R^{ns}\,u_\theta^{nc}\,u_Z^{ns}} \right]}^{T}}}\end{array}\right\}\tag {29}$$
$$\left.\begin{array}{*{20}{l}} {\left[ {\bar U_{ij}^n} \right] = \left[{\begin{array}{*{20}{c}}{U_{RR}^{nc}}&{U_{R\theta }^{ns}}&{U_{RZ}^{nc}}\\{-U_{\theta R}^{ns}}&{U_{\theta \theta }^{nc}}&{-U_{\theta Z}^{ns}}\\{U_{ZR}^{nc}}&{U_{Z\theta }^{ns}}&{U_{ZZ}^{nc}}\end{array}} \right]}\\{\,\left[ {\overline {\overline U} _{ij}^n} \right] = \left[{\begin{array}{*{20}{c}}{U_{RR}^{nc}}&{-U_{R\theta }^{ns}}&{U_{RZ}^{nc}}\\{U_{\theta R}^{ns}}&{U_{\theta \theta }^{nc}}&{U_{\theta Z}^{ns}}\\{U_{ZR}^{nc}}&{-U_{Z\theta }^{ns}}&{U_{ZZ}^{nc}}\end{array}} \right]}\end{array}\right\}\tag {30}$$
矩阵$\overlineU^n_{ij}$和$\overline{\overline{U}}^n_{ij}$中元素的表达式为
$$\left.\begin{array}{*{20}{c}}{U_{ij}^{nc} = \int_0^{2\pi } {U_{ij}}{{cos}}(n\theta) {d}\theta}\\[3mm]{U_{ij}^{ns} = \int_0^{2\pi} {U_{ij}}{{sin}}(n\theta) {d}\theta }\end{array}\right\}\tag {31}$$
其中, $i$和$j$代表$R,\theta$和$Z$,$\overline{(\cdot)}$和$\overline{\overline{(\cdot)}}$分别表示对称和反对称情况.对于有体积力情况,将体积力和特解也做类似傅里叶级数展开,代入边界积分方程(8)中,利用三角函数的正交性化简,可得轴对称结构带体积力情况的边界积分方程.
对称部分
$$ {{c_{ij}}\bar u_j^n = \int_\varGamma\left( {\bar U_{ij}^n\bar t_j^n-\bar T_{ij}^n\bar u_j^n} \right){R_q}{d}\varGamma }\\ \qquad{\left[ {{c_{ij}}\bar \psi _{jl}^J-\int_\varGamma \left({\bar U_{ij}^n\bar p_{jl}^J-\bar T_{ij}^n\bar \psi _{jl}^J}\right){R_q}{d}\Gamma } \right]\alpha _l^J}\tag {32}$$
反对称部分
$${c_{ij}}\overline {\overline u} _j^n = \int_\varGamma \left( {\overline {\overline U} _{ij}^n\overline {\overline t} _j^n-\overline {\overline T} _{ij}^n\overline {\overline u} _j^n} \right){R_q}{d}\varGamma \\ \qquad {\left[ {{c_{ij}}\overline {\overline \psi } _{jl}^J -\int_\varGamma \left( {\overline {\overline U} _{ij}^n\overline{\overline p} _{jl}^J-\overline {\overline T} _{ij}^n\overline{\overline \psi } _{jl}^J} \right){R_q}{d}\varGamma }\right]\alpha _l^J}\tag {33}$$
方程(32)和方程(33)即为定义在轴对称结构子午面边界上的边界积分方程;$\overline{U^n_{lj}}$以及$\overline{\overline{U^n_{lj}}}$称为轴对称问题的位移基本解.由于该基本解是Kelvin基本解沿着环向$\theta$进行了积分得到的,环向波数$n=0$的基本解[23](以位移为例)
$$ U_11=\dfrac{A}{aR_p R_q} \Big\{[4H(1-\nu)-(R_q^2+R_p^2 )]K-\\ \qquad[C^2 (3-4\nu)+H(Z_q^2-Z_p^2 )/r^2 ]E\Big\}\\ \qquad U_{12}=\dfrac{A}{aR_p}(Z_q-Z_p )\left(-K+\dfrac{F}{r^2}E\right)\\ \qquad U_{21}=\dfrac{A}{aR_q}(Z_q-Z_p )\left(K-\dfrac{F}{r^2}E\right)\\ \qquad U_{22}=\dfrac{2A}{a}\left[(3-4\nu)K+\dfrac{(Z_q-Z_p)^2}{r^2 E}\right]\tag {34}$$
其中,$K$和$E$分别表示第一类和第二类完全椭圆积分.对轴对称结构子午面的边界$\varGamma$进行离散,可将轴对称情况下的边界积分方程转化为线性方程组
$$ {{H^n}} {{u^n}}- {{G^n}} {{t^n}} = \\ \qquad {\left( { {{H^n}} {{P^n}} -{{G^n}} {{\Psi ^n}} } \right) {{\alpha ^n}} }\tag {35}$$
上式中的未知系数可利用方程(4)将$\alpha$反解出来,即
$$\alpha = F^{-1}f\tag{36}$$
将式(2)和式(36)代入式(35)可得 $$H^n u^n-G^n t^n= \rho {\omega ^2}M^n u^n\tag 37$$ 其中$M = \left( H^nP^n-G^n\Psi ^n \right){F^n}^{-1}$.
本文采用Wang等[21]提出的扩充矩阵的方法,将边界上的位移和面力分为未知量$\{x\}$和已知量$\{y\}$,通过在$[M]$矩阵中位移已知对应的自由度上增加$\{0\}$列,使得以下方程中矩阵$\overline{M}$和$\widetilde{M}$的大小与矩阵$A$和$B$一样
$$\left( A -{\rho _s}{\omega ^2} {\bar{M}} \right)\left\{ x \right\} = \left( B -\rho {\omega ^2} \tilde {M} \right)\left\{ y \right\}\tag{38}$$
对于自由振动问题,给定的位移和面力一般为0,即$y={\bf0}$,代入方程(38)可进一步得到$$ A x = \rho {\omega^2}\bar{M} x \tag 39$$上式为一般的特征值求解,可求解出$\omega$.
2 单元上的数值积分
2.1 奇异积分
轴对称结构的基本解中含有两类完全椭圆积分分别为
$$ K\left(m,\dfrac{\pi}{2}\right)=\int_0^{\pi/2}\dfrac{1}{\left(1-{m^2}{{si}}{{{n}}^2}\theta\right)^{0.5}}{d}\theta\\ E\left({m,\frac{\pi }{2}}\right)=\int_0^{\pi/2}\left(1-{m^2}{{si}}{{{n}}^2}\theta\right)^{0.5}{d}\theta \tag {40}$$
其中
$$m = \dfrac{{2\sqrt {{R_p}{R_q}} }}{{\sqrt {{{\left( {{R_p}+ {R_q}} \right)}^2} + {{\left( {{Z_q}-{Z_p}} \right)}^2}}}}\tag {41}$$
$$ K = {{ln}}4 + \mathop \sum \limits_{i = 1}^n {a_i}{{\left( {1-{m^2}} \right)}^i} + \\ \qquad{{ln}}\left(\dfrac{1}{{1-{m^2}}}\right)\left[\frac{1}{2}+\mathop\sum\limits_{i =1}^n{b_i}\left({1-{m^2}}\right)^i\right]\tag {42}$$
$$ {E = 1 + \mathop \sum \limits_{i = 1}^n {c_i}{{\left( {1-{m^2}} \right)}^i} + }\\ \qquad {{{ln}}\left( {\frac{1}{{1-{m^2}}}} \right) {\mathop\sum \limits_{i = 1}^n {d_i}{{\left( {1-{m^2}} \right)}^i}} }\tag {43}$$
其中,$a_i, b_i, c_i, d_i$是展开后各项的系数,$n$是展开的项数;一般认为,$n$取到5,展开的截断误差可以达到${10^{-8}}^{[25].当源点处于被积单元上时,会出现$\lnr$型的奇异积分,本文采用对数型高斯公式进行处理[23].对于面力基本解中出现的$1/r$型强奇异积分($H$矩阵主对角块元素),如果直接计算其柯西主值积分,需要将被积函数进行泰勒展开,公式繁琐,本文采用简单特解间接求出:轴向方向采用刚体位移法,径向方向采用静水压等简单特解法[25].
轴向方向
$${\left[ {\begin{array}{*{20}{c}}{{H_{RZ}}}\\{{H_{ZZ}}}\end{array}} \right]_{ii}} = -\mathop \sum \limits_{{j = 1}\atop {j \ne i} }^n {\left[ {\begin{array}{*{20}{c}}{{H_{RZ}}}\\{{H_{ZZ}}}\end{array}} \right]_{ij}}\tag {44}$$
径向方向
$$ {{{\left[ {\begin{array}{*{20}{c}}{{H_{RR}}} 0\\{{H_{ZR}}} 0\end{array}} \right]}_{ii}}{{\left[ {\begin{array}{*{20}{c}}{u_R^*}\\0\end{array}} \right]}_i} = \mathop \sum \limits_{{j = 1}\atop {j \ne i} }^n {{\left[ {\begin{array}{*{20}{c}}{{H_{RZ}}}\\{{H_{ZZ}}}\end{array}} \right]}_{ij}}-}\\ \qquad \mathop \sum \limits_{ {j = 1}\atop {j \ne i} }^n {{\left[{\begin{array}{*{20}{c}}{{H_{RR}}}&{{H_{RZ}}}\\{{H_{ZR}}}&{{H_{ZZ}}}\end{array}} \right]}_{ij}}{{\left[ {\begin{array}{*{20}{c}}{u_R^*}\\{u_Z^*}\end{array}} \right]}_j}-\\ \qquad {{\left[ {\begin{array}{*{20}{c}}0 {{H_{RZ}}}\\0 {{H_{ZZ}}}\end{array}} \right]}_{ii}}{{\left[ {\begin{array}{*{20}{c}}0\\{u_Z^*}\end{array}} \right]}_i}\tag {45}$$
2.2 近奇异积分
对于薄壁结构,从方程(42)和(43)可以看出,当源点$p$ 和场点$q$比较接近的时候,$K$和$E$会出现$\ln r$ 型的近奇异积分.对于近奇异积分,这里采用双曲正弦变换[26-27]来处理
$$\xi =a + b{{sinh}\left( {{k_1}s + {k_2}} \right)}\tag {46}$$
该变换的雅可比为
$$\frac{{{d}\xi }}{{{d}s}} = b{k_1}{{cosh}}\left({{k_1}s + {k_2}} \right)\tag {47}$$
是源点到单元投影点的局部坐标,$b$是源点到单元的最短距离, $k_1$ 和$k_2$ 的取值使得积分区间仍保持为$[-1,1]$
$$\left.\begin{array}{*{20}{l}}{{k_1}{{ = }}\dfrac{1}{2}\left[ {{{arcsinh}}\left({\dfrac{{1 + a}}{b}} \right) + {{arcsinh}}\left( {\dfrac{{1 -a}}{b}} \right)}\right]}\\[3mm]{{k_2}{{ = }}\dfrac{1}{2}\left[ {{{arcsinh}}\left({\dfrac{{1 + a}}{b}} \right)-{{arcsinh}}\left( {\dfrac{{1 -a}}{b}} \right)} \right]}\end{array}\right\}\tag {48}$$
双曲正弦变换的作用是将高斯点向近奇异点附近汇聚,并使得变换的雅可比${d}\xi/{d}s$随着近奇异性越强而越趋于0 (但不等于0).
3 对称轴的处理
3.1 无体积力情况
当源点或场点处于对称轴上,有$R_p=0$或$R_q=0$时,即$m=0$,代入式(40)得$K=E=\pi/2$,因基本解中$R_p$和$R_q$出现在分母上所以不能直接使用式(34),位移基本解和面力基本解的退化形式[28]
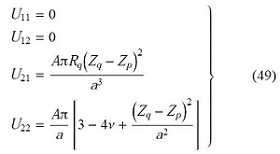
$$\left.\begin{array}{*{20}{l}}T_{11}=0\\T_{12}=0\\{T_{21}} = \dfrac{{2G\pi A}}{{{a^3}}}\left\{ {{R_q}\left[ {{2\nu -1} -\dfrac{{3{{\left( {{Z_q}-{Z_p}}\right)}^2}}}{{{C^2}}}} \right]{n_2}} \right.-\\\qquad\left. { \left( {{Z_q}-{Z_p}} \right)\left[ {2\left( {1 +\nu } \right)-\dfrac{{3{{\left( {{Z_q}-{Z_p}}\right)}^2}}}{{{C^2}}}} \right]{n_1}} \right\}\\{T_{22}} = \dfrac{{2GA\pi}}{{{a^3}}}\left\{ {\left( {{Z_q} -{Z_p}} \right)\left[ { {2\nu -1} } \right.} \right.- \\\qquad\left. {\left. {\dfrac{{3{{\left( {{Z_q}-{Z_p}}\right)}^2}}}{{{C^2}}}} \right]{n_2} + {R_q}\left[ { {2\nu-1}-\dfrac{{3{{\left( {{Z_q}-{Z_p}}\right)}^2}}}{{{C^2}}}} \right]{n_1}}\right\}\end{array}\right\}\tag{50}$$
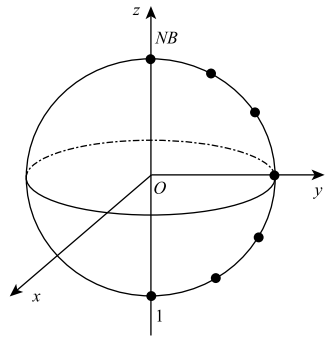
从退化形式可以看出,径向方向的位移基本解$(U_{11,U_{12})$和面力基本解$(T_{11,T_{12})$都为0(对称轴上径向方向的位移和面力为0). 如图2所示,$NB$为边界节点数,第1个点和第$NB$个点处于对称轴上, 其对应的径向方向的自由度分别为1和$2NB-1$,在形成的系数矩阵$G$和$H$中第1行和第$2NB-1$行都为0, 矩阵是奇异的,直接求解会失败.由于对称轴上径向位方向的位移和面力为0,本文在出现[0]行的对角线上添加一个不为0的常数$C$进行求解,如图3所示.
以上给出了源点或场点处于对称轴上$(m=0)$基本解的退化形式及其处理方法.当源点和场点重合时$R_p=R_q$且$Z_p=Z_q(m=1)$,从式(40)和式(41)可以看出,第一类完全椭圆积分$K$是奇异的,但事实上在对边界单元进行积分时,积分的高斯点并没有取至$-1$和1(线性单元),因此并不会出现源点和场点重合的情况.但对于有体积力的情况,采用径向基函数对域积分里的物理量插值时(式(4))会出现$X=\xi_J$的情况,径向基函数及相应的位移特解和面力特解需要进一步退化.
3.2 有体积力情况
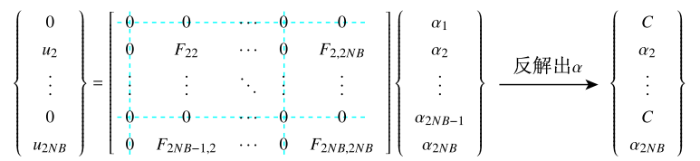
对于有体积力情况类似,当源点或场点处于对称轴上有$R_p=0$或$R_q=0$,即$m=0$时,Park等[12]给出了位移特解$\psi$和面力特解$p$的退化形式,本文选取的插值基函数与其类似,因此将参数$D_1\sim D_4$和$S_1\simS_5$替换成本文的式(12)和式(13)即可.从退化形式可以看出插值基函数$F_{11}=0,F_{12}=F_{21}=0$,因此方程(36)中$F$矩阵的第1行和第1列、第$NB-1$行和第$NB-1$列都为0,矩阵是奇异的,方程(36)中不能直接对$F$ 矩阵求逆. 从方程(4)可以看出,当$F$矩阵的第1列为0时(对称轴上径向位移$u_1=0$),$\alpha_1$可取任意常数$C$,因此本文将$F$矩阵所有0行和0列去掉,再进行求逆,过程如图4所示.
4 数值算例
4.1 实心球旋转
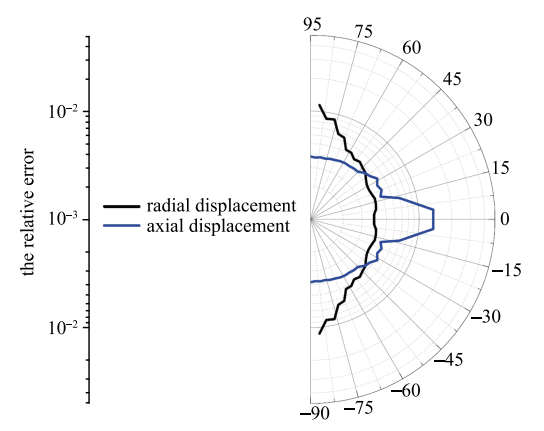
为了验证本文提出的处理奇异矩阵方法的有效性,本算例考虑一个实心球以圆频率$\omega=1$rad/s绕$z$轴旋转,如图2 所示,弹性模量$E=10^9$Pa,泊松比$\nu=0.3$,密度$\rho=10^3$kg/m$^3$,体积力$f_R=\rho\omega^2 u_R$,总共采用21个边界节点,图5给出了径向和轴向位移的相对误差沿子午面边界(母线)的分布.该问题在球坐标$(\rho, \theta,\varphi)$系下的径向位移解析解为[29]
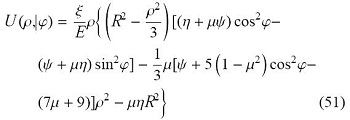
其中, $\eta = -5{\mu ^2} + \mu + 12$,$\psi = -5{\mu ^2} -6\mu + 3$,$\xi = \dfrac{{\lambda {\omega ^2}}}{{5\left( {7 +5\mu } \right)\left( {1-\mu } \right)}}$,$R$是球的半径,$\lambda, \mu$是拉梅系数.
图5 径向位移和轴向位移沿母线的相对误差分布...
Fig.5 The distribution of relative error of radial and axial displacement along the generator
从图5可以看出,采用21个节点计算得到的径向和轴向的相对误差在$10^{-3}$量级,径向位移在球的上下极点误差最大,轴向位移在球维度为0附近误差最大,大约为$1\times10^{-2}$.球的上下极点处于对称轴上,验证了本文提出的处理奇异矩阵的方法的正\确性.
4.2 空心圆筒自由振动
空心圆筒的高为$h$,平均半径为$a$,如图6所示,剪切模量和密度分别为$\mu$和$\rho=10^3$kg/m$^3$,弹性模量$E=10^3$ Pa,泊松比$\nu=0.3$. 圆筒两端自由.由于对称性,这里只取圆筒的一半来分析:在$z=h/2$处固定$z$方向的位移,得到关于$z=h/2$对称的模态;在$z=h/2$处固定$r,\theta$方向的位移,得到关于$z=h/2$反对称的模态[30].这里定义了3个无量纲参数:$H = h/a,L = l/a,\omega ' = \omegaa/\sqrt {\mu /\rho } ,$ 考虑以下3种情况.
(1)首先考虑常规圆筒$(H=1,L=10^{-3})$时的自由振动时环向波数$n=0,1,2$的特征频率及相应的特征模态($NB$表示边界节点数,$NI$表示内部节点数),将边界元法的结果与有限元(FEM)和高精度的级数解(SSR)对比;
(2) 然后考虑薄壁圆筒$(H=1, L=10^{-3})$时的自由振动.将边界元法的结果与有限元和高精度的级数解对比;
(3)最后将圆筒的厚高比$L/H$从1.4降到$10^{-3}$,考虑圆筒厚高比对特征频率的影响.
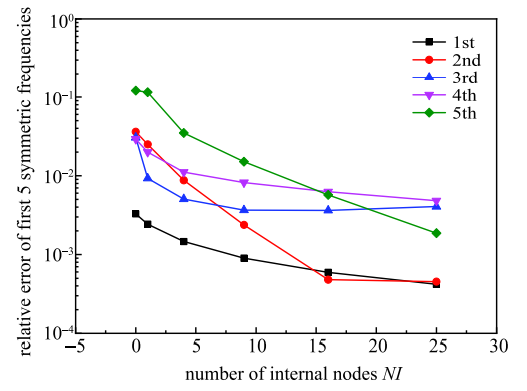
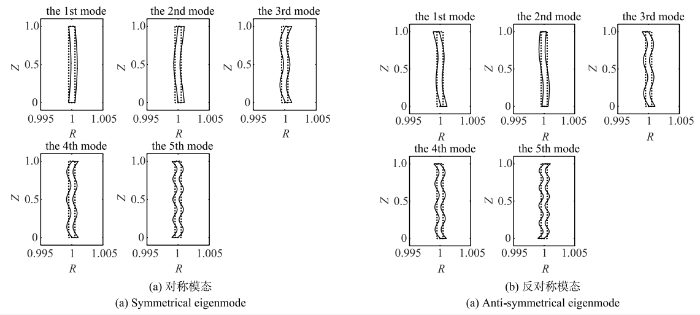
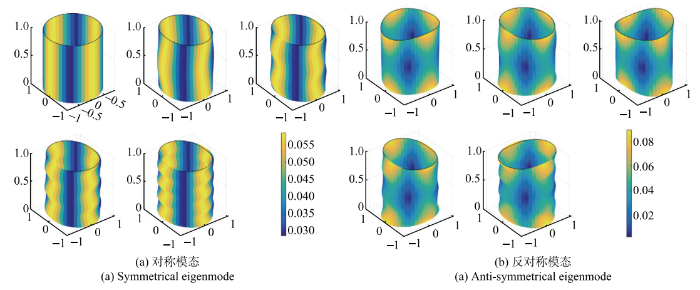
===表1和表2分别给出了常规圆筒$(H=1,L=1.4)$环向波数$n=0$时采用边界元法、有限元法(FEM)和高精度的级数解(SSR)得到的前五阶对称和反对称的特征频率,边界元法的单元数从8个增加至32个,总共采用25个内部节点,表中的相对误差是以高精度的级数解为精确解,采用32个边界单元得到的数值解的相对误差,可以看出边界元法采用很少的单元相对误差就可以达到$10^{-3}$,边界元法得到的结果优于FEM.表2和图7 给出了$n=0$ (纯对称)时相应的对称模态和反对称模态. 表3给出了前300阶对称的特征频率,可以看出,随自由度(nod)增加,前300阶特征频率趋于收敛.表4 和表5 分别给出了环向波数$n=1$和$n=2$低阶的对称及反对称频率,由于没有级数解作为对比,本文将边界元得到的解与有限元作了对比,根据边界元解的收敛趋势,FEM的结果偏高. 图8给出了前五阶对称的特征频率的相对误差(以级数解作为精确解)随内部节点数的变化,可以看出,增加少量的内部节点可以有效加快特征频率特别是高阶频率的收敛速度.
表1 环向波数w = 0常规圆筒前五阶对称频率(# = 25).
Table 1 The first 5 symmetrical frequency of the general hollow
| cylinder with n = | 0(N/ = | 25) | ||||
|---|---|---|---|---|---|---|
| Order | NB = 8 | NB = 16 | NB = 32 | fem[31] | ssr[32] | Relative error/10-3 |
| 1 | 1.813 56 | 1.814 15 | 1.814 44 | 1.816 1 | 1.815 2 | 0.41 |
| 2 | 4.238 10 | 4.255 90 | 4.257 07 | 4.262 2 | 4.259 0 | 0.44 |
| 3 | 4.569 28 | 4.587 09 | 4.587 85 | 4.608 5 | 4.569 3 | 4.00 |
| 4 | 5.165 48 | 5.21211 | 5.221 00 | 5.257 2 | 5.245 0 | 4.60 |
| 5 | 5.842 22 | 5.651 44 | 5.646 73 | 5.708 9 | 5.636 2 | 1.80 |
表2 环向波数w = 0常规圆筒前五阶反对称频率(M = 25)
Table 2 The first 5 anti-symmetrical frequency of the general hollow cylinder with n = 0 (N = 25)
| Order | NB = 8 | NB = 16 | NB = 32 | fem[31] | ssr[32] | Relative error /10-3 |
|---|---|---|---|---|---|---|
| 1 | 1.053 79 | 1.051 43 | 1.051 41 | 1.0529 | 1.0522 | 0.75 |
| 2 | 3.190 02 | 3.130 20 | 3.126 04 | 3.1339 | 3.1296 | 1.10 |
| 3 | 3.987 52 | 3.956 86 | 3.954 27 | 3.968 0 | 3.953 1 | 0.29 |
| 4 | 5.784 93 | 5.712 80 | 5.707 17 | 5.711 5 | 5.689 3 | 3.10 |
| 5 | 6.276 04 | 5.868 76 | 5.832 29 | — | — | — |
表3 环向波数n= 0常规圆筒高阶对称频率
Table 3 The high order symmetrical frequency of the general hollow cylinder with n = 0
| Nod | 10th | 50th | 100th | 150th | 200th | 300th |
|---|---|---|---|---|---|---|
| 850 | 9.038 598 9 | 24.444 439 | 36.248 822 | 45.450 729 | 55.389 133 | 75.967 757 |
| 1122 | 9.036 501 3 | 24.441 012 | 35.981 287 | 46.046 117 | 54.695 635 | 74.334 159 |
| 1522 | 9.036 523 7 | 24.438 609 | 35.976 340 | 46.046 351 | 54.683 062 | 74.246 037 |
| 2322 | 9.036 535 1 | 24.438 314 | 35.975 216 | 46.046 477 | 54.682 184 | 74.199900 |
| 3122 | 9.036 538 8 | 24.438 263 | 35.974922 | 46.046 492 | 54.682 054 | 74.197708 |
| 3922 | 9.036 540 6 | 24.438 240 | 35.974777 | 46.046 495 | 54.681 993 | 74.197958 |
表4 环向波数n=1常规圆筒前五阶对称和反对称频率
Table 4 The first 5 symmetrical and anti-symmetrical frequency of the general hollow cylinder with n = 1
 |
表5 环向波数n=2常规圆筒前五阶对称和反对称频率
Table 5 The first 5 symmetrical and anti-symmetrical frequency ofthe general hollow cylinder with n = 2
 |
图7 $n=0$常规圆筒前五阶模态($R$为径向,$Z$为轴向) ...
Fig.7 The first 5 eigenmodes of the general hollow cylinder with $n=0$ ($R$ is adial direction, $Z$ is axial direction)
图8 前五阶对称特征频率随内部节点数的变化$(n=0)$ ...
Fig.8 The variation of first 5 symmetrical frequency with thenumber of internal nodes $(n=0)$
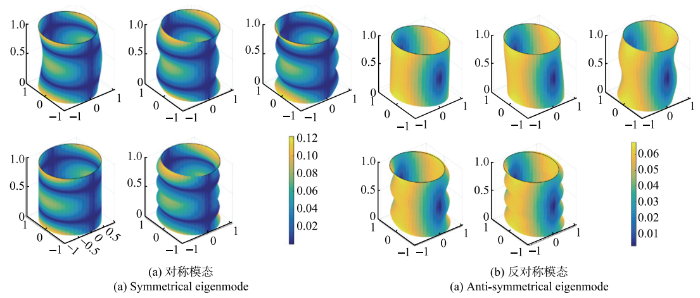
考虑薄壁圆筒$(H=1,L=10^{-3})$ 时的自由振动.表6和表7给出了薄壁圆筒$(H=1,L=10^{-3})$环向波数$n=0$时采用边界元法、有限元法(FEM)和高精度的级数解(SSR)得到的前五阶对称和反对称的特征频率.表7和 图9 给出了环向波数$n=0$ 时相应的对称模态和反对称模态.边界元法的单元数从24个增加至404个,总共采用27个内部节点,可以看出由于薄壁圆筒低阶特征频率特别密集,所以采用较多的单元才能准确捕捉其特征根.表6给出了采用404个边界单元的相对误差,大约在$10^{-3}$ 量级. 表8和表9分别给出了薄壁圆筒环向波数$n=1$和$n=2$低阶的对称及反对称频率,与FEM相比结果偏低.表8、图10 和表9、图11 分别给出了薄壁圆筒$n=1$和$n=2$对称及反对称模态.
表6 环向波数n = 0 薄壁圆筒前5 阶对称频率
Table 6 The first 5 symmetrical frequency of the thin hollow cylinder with n = 0
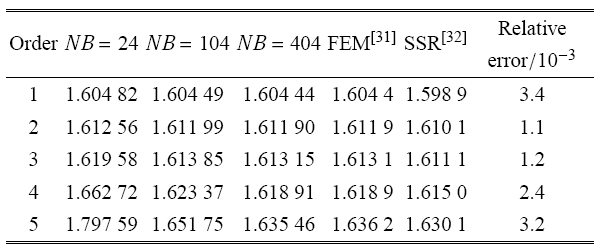 |
表7 环向波数n = 0 薄壁圆筒前5 阶反对称频率
Table 7 The first 5 anti-symmetrical frequency of the thin hollow cylinder with n = 0
 |
表8 环向波数n = 1 薄壁圆筒对称及反对称频率
Table 8 The first 5 symmetrical and anti-symmetrical frequency of the thin hollow cylinder with n = 1
 |
表9 环向波数n = 2 薄壁圆筒对称及反对称频率
Table 9 The first 5 symmetrical and anti-symmetrical frequency of the thin hollow cylinder with n = 2
 |
图9 $n=0$薄壁圆筒前五阶模态...
Fig.9 The first 5 symmetrical and anti-symmetrical eigenmodesof the thin hollow cylinder with $n=0$
图10 薄壁圆筒前五阶模态...
Fig.10 The first 5 symmetrical and anti-symmetrical eigenmodes of the thin hollow cylinder with $n=1$
图11 $n=2$薄壁圆筒前五阶模态...
Fig.11 The first 5 symmetrical and anti-symmetrical eigenmodes of the thin hollow cylinder with $n=2$
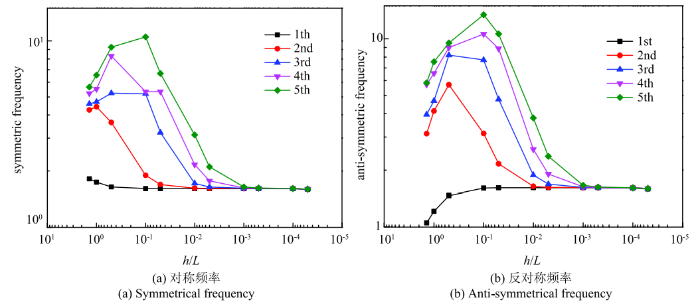
最后考虑$h/L$从1.4减小至$10^{-5}$量级时,薄壁圆筒特征频率的变化,图12给出了前五阶对称频率和反对称频率随着$h/L$减小的变化,其中(a)图为对称频率,(b)图为反对称频率.从图中可以看出当圆筒的厚高比低于$10^{-2}$时,圆筒低阶的频率几乎不变.
图12 环向波数$n=0$ 时前五阶特征频率随的变化...
Fig.12 The variation of the first 5 symmetrical frequency of $n=0$ with thickness ratio $h/L$
5 结论
本文采用双互易边界元法和傅里叶级数展开计算轴对称结构自由振动时对称以及反对称的特征频率,由于只需要在轴对称结构子午面边界上划分单元,因此大大降低了离散的难度和计算量.采用少量单元得到的圆筒特征频率的相对误差在$10^{-3}$量级以内,且数值结果表面通过增加几个内部节点就可以有效提高高阶频率的精度.本文采用少量的自由度计算了高阶的特征频率,在给出的算例中,选取约2000自由度可以得到前300阶特征频率的收敛解.
对于节点处于对称轴这种特殊情况,本文通过基本解和特解的退化形式,发现系数矩阵存在奇异性,通过对称轴上物理量的性质分别对无体积力和有体积力情况提出了处理奇异矩阵的方法,最后通过数值算例验证了该方法的有效性.
本文采用了双曲正弦变换处理近奇异积分,可以高精度的求解薄壁结构的特征频率以及特征模态,在本文算例中,圆筒厚度与高度比值为$10^{-3}$ 时,求得的特征频率的相对误差也在$10^{-3}$ 量级以内.数值结果表明当圆筒的厚高比小于$10^{-3}$时,圆筒的特征频率几乎不变.
The authors have declared that no competing interests exist.
参考文献
| [1] |
A direct formulation and numerical solution of the general transient elastodynamic problem. I . |
| [2] |
A direct formulation and numerical solution of the general transient elastodynamic problem. II .
|
| [3] |
A bem investigation on the influence of underground cavities on the seismic response of canyons .
|
| [4] |
On a way to save memory when solving time domain boundary integral equations for acoustic and vibroacoustic applications . |
| [5] |
Multi-domain bem for two-dimensional problems of elastodynamics . |
| [6] |
Dynamic crack analysis in piezoelectric solids under time-harmonic loadings with a symmetric galerkin boundary element method .
|
| [7] |
Spectral bem for the analysis of wave propagation and fracture mechanics . |
| [8] |
Axisymmetric free-vibration problems by boundary element method. Journal of Applied Mechanics-Transactions of the |
| [9] |
Radial integration bem for vibration analysis of two- and three-dimensional elasticity structures . |
| [10] |
A new time domain boundary integral equation and efficient time domain boundary element scheme of elastodynamics. Cmes-Computer Modeling in Engineering & |
| [11] |
A new approach to free vibration analysis using boundary elements . |
| [12] |
A bem formulation for axisymmetric elasticity with arbitrary body force using particular integrals . |
| [13] |
A dual reciprocity bem approach using new fourier radial basis functions applied to 2d elastodynamic transient analysis . |
| [14] |
The solution of elastostatic and dynamic problems using the boundary element method based on spherical hankel element framework .
|
| [15] |
The dual reciprocity method applied to free vibrations of 2d structures using compact supported radial basis functions . |
| [16] |
Shape design sensitivity and optimization of anisotropic functionally graded smart structures using bicubic b-splines drbem . |
| [17] |
复杂载荷三维裂纹分析双重边界元法 .Dual BEM for sif analyses of 3D structures with complex loads . |
| [18] |
Dynamic analysis of three-dimensional polycrystalline materials using the boundary element method . |
| [19] |
非线性泊松问题的拟线性化边界积分方法研究 .A study of boundary integral method for a type of nonlinear problem based on generalized quasilinearlization theory . |
| [20] |
A collocation and least squares p-singular boundary method without fictitious boundary . |
| [21] |
Free-vibration of axisymmetric solids by bem using particular integrals . |
| [22] |
Generalized Axisymmetric Elastodynamic Analysis by |
| [23] |
|
| [24] |
A new approach to free-vibration analysis using boundary elements . |
| [25] |
The Boundary Integral Equation Method in |
| [26] |
The sinh transformation for evaluating nearly singular boundary element integrals over high-order geometry elements . |
| [27] |
A sinh transformation for evaluating nearly singular boundary element integrals . |
| [28] |
The boundary integral equation method in axisymmetric stress analysis problems . |
| [29] |
匀速旋转实心圆球的弹性力学解 .Elastic mechanics solution to rotative medicine globe . |
| [30] |
|
| [31] |
Natural frequencies of free finite-length circular-cylinders . |
| [32] |
Vibrations of free hollow circular cylinders . |

/
| 〈 |
|
〉 |