格子Boltzmann方法模拟多孔介质惯性流的边界条件改进1)
A LATTICE BOLTZMANN SIMULATION OF FLUID FLOW IN POROUS MEDIA USING A MODIFIED BOUNDARY CONDITION1)
中图分类号: O351.3
文献标识码: A
版权声明: 2019 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
作者简介: 2) 程志林, 博士研究生, 主要研究方向:多孔介质孔隙尺度流体模拟. E-mail:zhilin_cheng1992@163.com
展开
摘要
格子Boltzmann方法可以有效地模拟水动力学问题,边界处理方法的选择对于可靠的模拟计算至关重要.本文基于多松弛时间格子Boltzmann模型开展了不同边界条件下,周期对称性结构和不规则结构中流体流动模拟,阐述了不同边界条件的精度和适用范围. 此外,引入一种混合式边界处理方法来模拟多孔介质惯性流, 结果表明:对于周期性对称结构流动模拟,体力格式边界条件和压力边界处理方法是等效的,两者都能精确地捕捉流体流动特点; 而对于非周期性不规则结构,两种边界处理方法并不等价,体力格式边界条件只适用于周期性结构;由于广义化周期性边界条件忽略了垂直主流方向上流体与固体格点的碰撞作用,同样不适合处理不规则模型;体力-压力混合式边界格式能够用来模拟周期性或非周期性结构流体流动,在模拟多孔介质流体惯性流时,比压力边界条件有更大的应用优势,可以获得更大的雷诺数且能保证计算的准确性.
关键词:
Abstract
The lattice Boltzmann method has been considered as an effective method for the simulation of hydrodynamic flows. Handling the boundary condition accurately in simulation is extremely essential for a reliable study. In this paper, a multiple relaxation time lattice Boltzmann model with different boundary conditions was applied to mimic the flows in periodically symmetric and irregular structures. The scope of application and accuracy for different boundary conditions in various geometries was investigated. In addition, a hybrid boundary treatment method was introduced to simulate the non-Darcy flow in porous media, the simulation results of which were also compared to the results obtained using pressure boundary condition. The results show that for the symmetric and periodic flow simulation, both the body force and the pressure driven boundary treatments are perfectly equivalent and both can accurately capture the flow characteristics. While for the fluid flow in irregular structures, the body force and pressure boundary conditions are not equivalent, and the body force one has limited use and can only be applied to periodic structures. This implies that one must be cautious of the reliability of modeling when conducting model validation with simple structures. It seems that the regular structures could be inadequate to validate the modeling, which depends on the research issues, i.e., the flow patterns in what kinds of structures. Furthermore, the generalized periodic boundary condition proposed by previous authors combines periodic density momentum with a pressure gradient in one dimension is also not appropriate to conduct flow simulation in irregular models since this method ignores the effect of asymmetric obstacles in the direction perpendicular to the main streamlines. Moreover, the hybrid boundary condition can be used to perform flow simulations not only in periodic structures but also the irregular ones. In particular, for the inertial flow of fluids in porous media, the relatively high Reynolds number can be achieved readily with the hybrid boundary condition. For the pressure driven boundary condition, the pressure gradient comes from the density difference between the inlet and outlet. To provide a higher Reynolds number, it is necessary to implement a great density contrast in inlet and outlet nodes. However, this approach is inconsistent with physical situation and causes undesirable errors in simulation. All in all, the hybrid boundary condition has greater advantages over the pressure boundary condition.
Keywords:
多孔介质水动力学问题的研究一直是许多行业的研究热点,具有重要的研究意义[1-6].格子Boltzmann方法(lattice Boltzmann method,LBM)作为一种介观模拟方法, 以动理学Boltzmann方程为基础, 通过求解流体粒子的分布函数,进而统计平均得到流体的宏观量, 如密度、速度和压力等.LBM程序编制简单, 边界容易处理,是一种极具潜力的方法. 一般而言,模型边界格点的分布函数是未知的,选择适当的边界处理方法对模拟计算的准确性和稳定性至关重要.常见的边界条件包括体力格式的周期性边界条件(bodyforce, BF)、密度差压力驱动边界条件(densitydifference, DD)和速度边界条件等.
BF边界条件由于形式简单,且计算区域内流体格点的分布函数都是已知的,不需要对边界格点进行额外的处理,因而得到了广泛的应用.Chukwudoize和Tyagi[7]基于单松弛时间(single relaxation time,SRT)LBM采用BF边界条件研究了粗糙度对体心立方体结构中流体惯性流的影响. Arabjamaloei和Ruth[8]探讨了流体惯性力作用对多孔介质渗透率的影响,并通过实验对模拟结果进行了验证. 此后,Kakouei等[9]分别利用BF和DD边界条件研究了气体在真实多孔介质中的达西流和惯性流动,研究结果表明,由于进出口较大的密度差使得DD边界处理格式不适合处理流体惯性流,而采用BF边界条件能够得到正确的结果. 此外,Zhao等[10-11]利用BF边界条件开展了多孔介质单相流和多相流模拟.尽管一些学者[12-14]怀疑BF边界条件的适用性,认为BF边界条件只能严格应用于流动截面不变的Poiseuille流.然而, 该观点并没有得到有效的论证,BF边界条件的适用范围需要进一步调查.
此外,当LBM被应用于多孔介质非达西流动(惯性流)模拟时,为了达到惯性流动阶段, 需要获得较大的雷诺数$Re$;通常的做法是增大压力梯度, 提高流体流速. 在LBM中,流体压力梯度与模型进出口的密度差直接相关,增大密度差能够获得更大的压力梯度,Kakouei等[9]采用DD边界条件研究多孔介质非达西流,发现表观渗透率随着$Re$的增大而增大,这显然与理论不符. 而Newman和Yin[15],Chai等[16]以及Sukop等[17]用类似的处理方法成功地模拟了多孔介质流体惯性流,造成这一现象的原因需要进一步澄清.
本文首先简要介绍了LBM基本理论,之后分别了模拟了不同边界条件,流体在周期对称性结构和不规则结构下的流动情况,讨论了不同边界条件的精度和适用性. 此外,通过引入一种混合式边界处理方法来模拟多孔介质非达西流,并探讨了这种边界条件的适用范围及优势,解释了不同学者采用DD边界条件取得互相矛盾结论的原因.
1 LBM方法
1.1 MRT-LBM模型
原始形式的Boltzmann方程不能直接求解, 最常用的求解方法是BGK(Bhatnagar-Gross-Krook)近 似[18], 即SRT-LBM,该模型满足质量、动量和能量守恒.另一种方法为多松弛时间模型(multiple relaxation time, MRT),与SRT-LBM相比使用了多个松弛时间的碰撞算子, 在矩空间中执行碰撞步.该模型会带来额外的计算量(增加约30 %)[19-20],但松弛参数选取更自由且数值稳定高已被广泛应用于多孔介质单相流和多相流模拟当中.本文采用MRT-LBM对二维多孔介质进行流体模拟和分析,其碰撞项可以表示为
$${{ f}}\left( {{{ x}} + c{{ e}}\Delta t,t + \Delta t} \right)-{{ f}}\left( {{{ x}},t} \right) =- \left( {{{ M}}^{-1}{{ {SM}}}} \right)( {{ f}}\left({{{ x}},t} \right) - {{ f}}^{ eq}\left( {{{ x}},t} \right)) + {{ M}}^{-1}\left( {{{ I}} -\frac{1}{2}{{ S}}} \right){{ M\bar {F}}}(1)$$
式中${{ f}}({{ x}},t)$为$t$时刻位于${x}$处流体粒子的分布函数; $c$为格子速度, 一般取为1; ${e}$为离散速度, 对于D2Q9模型, 可以表示为[21]
$${{ e}} =\left( {{\begin{array}{*{20}c} 0 & 1 & 0 & {-1} & 0 & 1 & { -1} & {-1} & 1 0 & 0 & 1 & 0 & {-1} & 1 & 1 & {-1} & {-1} \end{array} }} \right)(2)$$
平衡分布函数${{ f}}^{ eq}\left( {{{ x}},t}\right)$表示为[21]
$$f_i^{ eq} = \rho W_i \left[ {1 +\frac{3}{c^2}\left( {{{ e}}_i \cdot {{ u}}} \right) +\frac{9}{2c^4}\left( {{ e}_i \cdot {{ u}}} \right)^2 -\frac{3}{2c^2}{ u}^2} \right](3)$$
式中, 权系数$W_i $表示为
$$W_i = \left\{ {\begin{array}{lll} 4/9,&i = 1 1/9,&i = 2, 3, 4,5 1/{36},&i = 6,7,8,9 \end{array}} \right.(4)$$
流体密度和速度分别通过式(5)和式(6)计算得到
$$\rho = \sum\limits_i{f_i }(5)$$
$$\rho {{ u}} =\sum\limits_i {{{ e}}_i f_i } + \frac{\Delta t}{2}\rho {{F}}(6)$$
上式中${{ F}}$为外力; 此外, 式(1)中${M}$为转换矩阵, 参照文献[22,23]取值为
${ S}$为对角松弛矩阵, 可以表示为
$${{ S}} = \mbox{diag}\left[ {s_1 ,\mbox{ }s_2 ,\mbox{ }s_3,\mbox{ }s_4 ,\mbox{ }s_5 ,\mbox{ }s_6 ,\mbox{ }s_7 ,\mbox{ }s_8,\mbox{ }s_9 } \right](8)$$
式中各参数取为[24]: $s_1 =s_4 = s_6 = 1.0$, $s_2 = 1.64$, $s_3 = 1.54$, $s_5 = s_7 = 1.2$,$s_8 = s_9 = 1 /\tau $; 其中松弛因子$\tau$与流体的动力黏度$v$和格子声速$c_{ s}(= c/{\sqrt 3 })$有关,关系如下
$$v = c_{ s}^2 \left( {\tau-0.5} \right)\Delta t(9)$$
式(1)中${ I}$为单位矩阵, 外力项${{\bar {F}}}$采用Guo等[22]提出的处理格式, 其表达式为
$${{\bar {F}}}_i = \rho W_i \left[ {\frac{3}{c^2}\left( {{ e}_i \cdot{{ F}}} \right) + \frac{9}{c^4}\left( {{ e}_i \cdot {{u}}} \right)\left( {{{ e}}_i \cdot { F}} \right) -\frac{3}{c^2}{{ u}} \cdot {{ F}}} \right](10)$$
1.2 边界条件
本文主要涉及4种边界格式, 现简要介绍各边界条件的基本原理.
BF周期性边界条件假设流体粒子从模型出口离开流场时,下一时间步又从入口重新进入流场,因此BF边界条件中流体满足质量和动量守恒.假设在$x$方向流动存在周期$L$, 则有
$$\rho \left( {x,t} \right) = \rho \left( {x + L,t}\right)~~~~~{(11a)}$$
$$\rho {{ u}}\left( {x,t} \right) =\rho {{ u}}\left( {x + L,t} \right){(11b)}$$
流体粒子的分布函数可表示为
$$f_i \left( {x,t + \Delta t} \right) =f_i \left( {x + L,t} \right)(12)$$
DD压力边界条件采用Guo等[25]提出的非平衡外推格式进行处理,主要原理是将边界格点上的未知分布函数分为平衡态部分和非平衡态部分,其中平衡态部分计算公式为
$$f_i^{ eq} \left( {x_a ,t} \right) = f_i^{ eq} \left( {\rho _{ in},u_{ in} } \right)(13)$$
式中, $u_{ in} = u_{x_b }$为邻近格点的速度, $x_b = x_a + c_i \Delta t$. $\rho _{ in}$为入口处流体格点的密度; 非平衡态部分等于$x_b$处的非平衡分布函数.综上可得边界格点的分布函数可表示为
$$f_i \left( {x_a ,t} \right) = f_i^{ eq} \left[ {\rho _{ in},u\left( {x_b ,t} \right)} \right] + \left[ {f_i \left( {x_b ,t}\right)-f_i^{ eq} \left( {x_b ,t} \right)} \right](14)$$
对于某些涉及周期性速度场和非周期性压力场的流动问题,显然式(11)无法同时满足. 据此,Kim和Pitsch[26]提出了一种广义化周期性边界(generalizedperiodic boundary condition, GPBC)来解决这一问题,其主要思想是将式(11)修正为
$$p\left( {x,t} \right) = p\left( {x + L,t} \right) + \Delta p{(15a)}$$ $${{ u}}\left( {x,t} \right) = {{u}}\left( {x + L,t} \right) {(15b)}$$
式(15)严格满足质量和动量守恒,GPBC边界处理方法同样将边界流体格点的分布函数分为平衡态和非平衡部分,需要说明的是GPBC边界格点为真实进出口边界的外的虚拟格点, 如图1所示.
图 1 GPBC边界进出口格点示意图[
Fig. 1 The diagram of inlet and outlet nodes for generalizedperiodic boundary condition[
对于平衡态部分有
$$f_i^{ eq} \left( {x_0 ,t} \right) = f_i^{ eq} \left( {p_{ in} ,u_N }\right)~~~~~{(16a)}$$
$$f_i^{ eq} \left( {x_{N + 1} ,t}\right) = f_i^{ eq} \left( {p_{ out} ,u_1 }\right){(16b)}$$
式中$u_1 $和$u_N$分别为模型进出口边界的速度, $p_{ in} $和$p_{ out}$分别为进出口边界的压力; 非平衡态部分直接由式(17)计算得到,详细的介绍见文献${[5, 26].
$$f_i^{ neq} \left( {x_0 ,t} \right) = f_i^{neq} \left( {x_N ,t}\right)~~~{(17a)}$$
$$f_i^{ neq} \left( {x_{N + 1} ,t} \right) = f_i^{neq} \left( {x_1,t} \right){(17b)}$$
本文受传统计算流体动力学(computational fluid dynamics,CFD)边界处理方法的启发, 引入一种混合式边界处理格式,该方法同时结合了外力驱动边界格式和进出口压力差驱动格式.主要实现思想是:考虑到外力驱动边界格式,其模型进出口一般周期性处理;而BFDD边界格式是在外力驱动(BF)边界条件的基础上增加了对进出口的处理,并设定了一定的密度差, 也就是将DD边界条件加到了BF边界处理中,此时模型进出口不再按照周期性处理. 该边界条件在实施时,只需要在DD边界处理过程中增加一外力项即可,论文后续称之为BFDD边界条件.
2 结果与讨论
本部分模拟了不同边界条件下, 周期对称性结构和不规则结构内流体流动,探讨了不同边界条件的适用性, 并分析了产生异常结果的原因. 此外,通过引入一种混合式边界处理方法, 模拟了较高Re下多孔介质流体惯性流,并与传统边界处理方法结果进行了对比分析.
2.1 周期性结构流动模拟
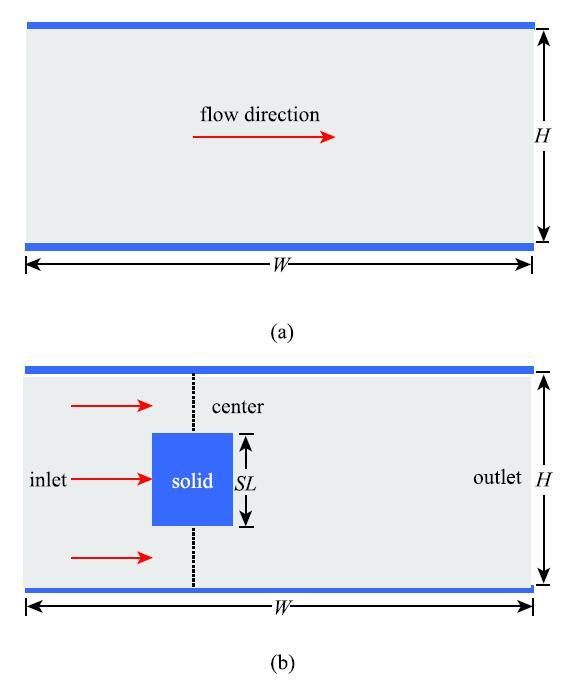
由于平板Poiseuille流动模式简单且存在解析解已被广泛地应用于LBM模型验证[27- 30].本文选用该模型以及方柱绕流(如图2所示)来探讨BF边界条件和DD边界条件的适用范围.平板 Poiseuille 流动假设流体受压差驱动呈层流流动,垂直于流动方向截面的流体流速可根据下式计算
$$u\left( y \right) = \frac{G^\ast }{2\mu }\left( {\frac{H^2}{4} -y^2} \right)(18)$$
其中, $u(y)$为流体的速度, $G^\ast$为压力梯度, $\mu $为流体的动力黏度, $H$为平板的高度.
采用第二部分介绍的 D2Q9 MRT-LBM模拟平板Poiseuille流,模型参数和结果均采用格子单位. 基本参数设为: $H$ =23, 33, 43 lu,$W$ =100 lu, $\rho $=1, $c$=1, $\Delta t$=1, 运动黏度$\upsilon $=1/6 lu$\cdot $ts$^{-2}$,其与式(10)中动力黏度换算关系为: $\upsilon = \mu/\rho $; lu(Lattice unit)和ts分别代表格子长度和时间步长.模型上下边界采用标准反弹格式, 对于DD边界条件,进出口采用压力边界非平衡外推格式, 详细介绍见文献${[25].而BF边界条件, 模型进出口采用周期性边界条件,模拟中施加的外力平行于水平方向, 垂直方向上为0.两种边界条件压力梯度相同, 即$G^\ast $=1.0$\times $10$^{-5}$.需要说明的是, 为了满足壁面无滑移条件,本文涉及的体力格式边界模拟中, 流固边界处格点外力项均设置为0. 此外,DD边界条件需要调节进出口的密度差来达到需要的压力梯度,进出口的密度($\rho _{ in} $和$\rho _{ out} )与压力梯度关系,见式(19); 而BF边界条件中外力$F$大小通过给定的压力梯度转化计算得到,见式(20)
$$G^\ast = c_{ s}^2 \frac{\rho _{ in}-\rho _{ out} }{W} (19)$$
$$F = {G^\ast }/\rho (20)$$
$$\frac{\sqrt {\dl\sum {\left[ {u\left( t \right)-u\left( {t-1000}\right)} \right]^2} } }{\sqrt {\dl\sum {u\left( t \right)^2} } } <10^{-8}(21)$$
图 2 周期性结构 (a) 平板Poiseuille流动; (b) 方柱绕流...
Fig. 2 Periodic structures: (a) two dimensional plate Poiseuille flow; (b) flow around a square in a channel...
模拟收敛条件, 见式(21). 如不加说明,本文接下来所有模拟均采用该收敛准则,流固边界格点均采用标准反弹格式处理.
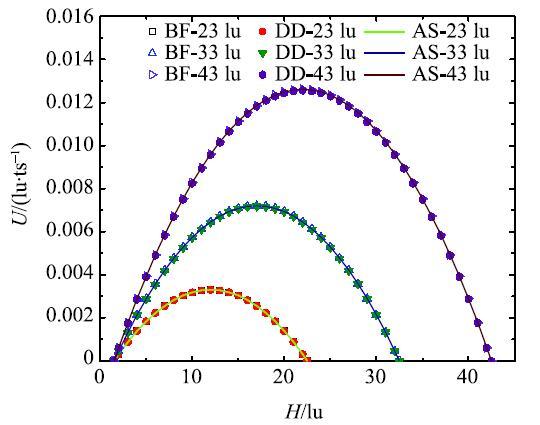
图3为不同高度平板分别在BF和DD边界条件下流速剖面分布. 可以看出,BF和DD边界条件模拟结果与解析解(analytical solution, AS)非常一致,说明BF和DD边界条件均能反映平板Poiseuille流动特点,两种边界条件是等效的.
图 3 解析解及BF和DD边界条件下流体在不同通道高度下速度剖面对比...
Fig. 3 Comparison of analytical solutions and the velocity profiles for the two parallel plates with different heights under BF and DD boundary conditions...
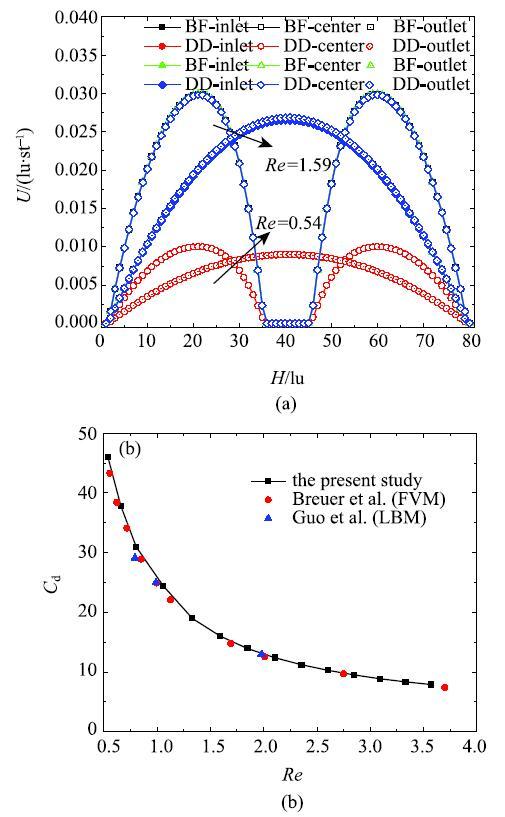
方柱绕流模拟中设置模型宽度、高度和方柱大小分别为500,80和10 lu, 方柱位于模型三分之一位置处,这与Guo等[31]和Breuer等[32]采用的模型一致.分别采用BF和DD边界条件模拟了$Re$为0.54和1.59条件下,模型进出口和方柱中线处的速度剖面, 结果如图4(a)所示.可以发现在不同边界条件下,模型进出口及中央流速分布几乎完全一致,说明两种边界格式在处理流体绕流模拟中是完全等效的.此外, 本节计算了$Re$处于0.5~4.0之间时方柱绕流的曳力系数($C_{ d})$, 见图4(b).本文结果与Guo等[31]和Breuer等[32]的模拟结果吻合,反映了本文代码的可靠性. 需要说明的是,曳力系数的计算采用了Mei等[33]提出的动量交换法;另外,本节只是为了对比BF和DD边界下周期性结构流体流动差异,因此只模拟了较低雷诺数条件下的流动.
结合上述平板Poiseuille流动模拟结果可知,当模型为周期性对称结构且流动充分发展时,两种边界处理方法可以得到一致的结果,这与之前学者的结论一致[4-5]. 实际上,BF边界条件有着严格的使用条件, 文章接下来将对其进行阐述.
2.2 倾斜平板流动模拟
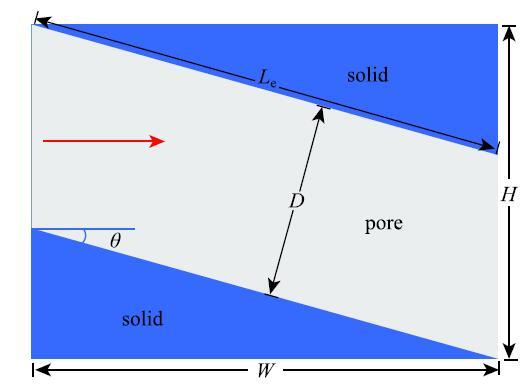
本节将对比不同边界条件下非周期性结构中流动模拟结果.以倾斜毛管流动为例, 如图5所示. 假设流体在毛管内符合Poiseuille流,模型渗透率存在解析解, 可以表示为[34]$$K = \frac{D^3W}{12HL_e }(22)$$式中, $K$为渗透率, lu$^{2}$; $D$为毛管直径, lu;$L_{e}$为毛细管实际长度, lu; 其余参数与上文定义一致.
图 4 (a)BF和DD边界条件下方柱绕流进出口及中央速度剖面对比; (b)曳力系数$C_{ d}$随雷诺数$Re$的变化...
Fig. 4 (a) Comparison of the velocity profiles for inlet,center and outlet of the channel under BF and DD boundaryconditions; (b) The variation in the drag coefficients as afunction of Reynoldsnumber...
图 5 倾斜毛管流动示意图...
Fig. 5 The configuration for fluid flow in the inclined Capillary tube...
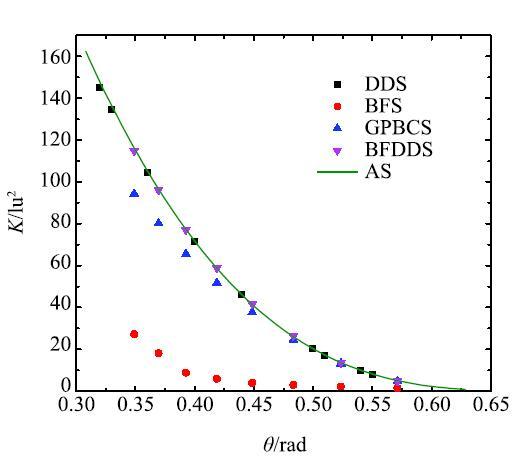
设定模型长度和宽度为120和100 lu, 流体密度和黏度设定与上文一致,不同边界条件下压力梯度$G^\ast $均为6.2$\times $10$^{-6}$.为了使模拟更稳定且边界条件更方便实施, 在进出口添加了缓冲区域.倾斜毛管模拟所得渗透率可以通过达西定律求得, 固定模型宽度和高度,通过改变倾斜角(最大为$\arctan \left( {H /W} \right))$,得到毛管在不同条件下模拟结果, 如图6所示.可以明显看出DD边界条件结果与解析解吻合得很好,而BF边界条件模拟结果出现了异常; 随着倾斜角的减小,模拟解与解析解偏离越来越大. 由此说明,BF周期性边界条件与DD边界在模拟非周期性不规则结构时两者并不等效,BF边界条件不适合应用于此类模拟研究. 理论上,压差驱动的流动模拟与直接赋予流体格点等效压力梯度的方式是等效的,因此BF边界条件过去被许多学者应用与多孔介质包括达西流、惯性流和微尺度流动流动模拟中[7-9, 11, 35]. 事实上, 过去就有学者[12-14]认为BF边界条件有着严格的使用条件,然而这一观点很少被提及且没有得到有效论证. 另一方面, 由于二维或三维Poiseuille流这类流动存在解析解, 在开展LBM流动模拟时,研究者大多会采用这类结构进行模型验证,因此往往掩盖了BF边界条件的缺陷. 通过模拟结果可以看出,BF边界条件确实不适用于非周期性结构中,显然也不适用于真实多孔介质结构.
图 6 不同边界不同倾斜角毛管渗透率与解析解对比...
Fig. 6 Comparison of analytical permeability and simulatedpermeability for the inclined tube with different $\theta $under different boundary conditions...
本文利用GPBC同样进行了倾斜管流动模拟, 参数设置与上述一致.可以发现, GPBC模拟结果随着模型渗透率的增大误差也越来越大,说明GPBC边界同样不适合模拟不规则结构,主要原因是GPBC边界条件只处理了主流线方向上流体的密度和分布函数,而忽略了垂直主流方向的流动.Gräser和Grimm[14]提出了一种自适应广义周期性边界条件来消除垂直主流方向上固体格点对流体的抑制作用,但处理过程中需要迭代计算, 无疑增加了计算量且破坏了LBM的并行性,因此难以推广应用.
BFDD边界条件倾斜管流体模拟结果见图6, 可以发现BFDD与DD边界条件类似,模拟结果均与解析解吻合. 值得一提的是,这种边界处理方法在传统有限元或有限体积法求解N-S方程的CFD模拟中被广泛应用,而在LBM中却鲜有提及. 通过模拟结果可以发现,BFDD边界格式在LBM中同样是合 理的.
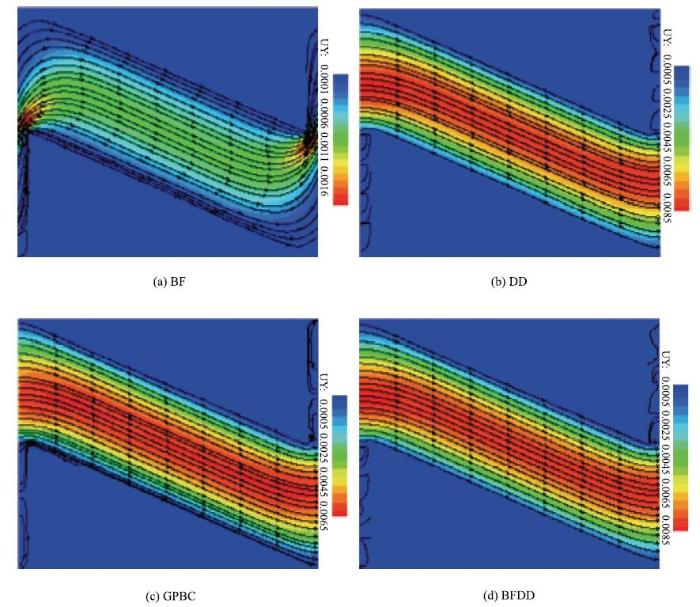
为了更直观地论述不同边界处理方法在倾斜管流动模拟中的适用性,绘制了倾斜角为$\pi$/8时不同边界条件下模型流场图, 见图7.可以看出, 由于BF边界下进出口按照周期性处理,流体从出口流出后又流回入口, 模型的流线发生了巨大的变化,管内最大速度出现在进出口, 显然这与真实情况不符;DD和BFDD边界条件下毛管内流场分布几乎一致,管内流体符合Poiseuille流动规律, 此外缓冲区域存在少许无效流线,这是由于流体格点与缓冲区域碰撞反弹所致, 对整体流动几乎没有影响;GPBC边界条件下, 模型流场基本与DD和BFDD一致,区别在于其进出口依然是按照周期性处理,因此在缓冲区域GPBC边界的流线分布与前两种边界处理并不一致. 此外,GPBC边界下流场最大速度(0.006 5)要小于DD和BFDD边界下最大速度(0.0085), 因此模拟所得渗透率要小于理论值.
图 7 不同边界条件下毛管倾斜角$\theta $为$\pi$/8时流场示意图...
Fig. 7 The schematic for fluid flow in the inclined capillarytube of which $\theta $ is $\pi$/8 under different boundaryconditions...
过对比不同边界条件下模拟倾斜管流动模拟结果发现,只有DD和BFDD边界条件能够精确地反映这类不规则几何模型的流动特点.需要说明的是, 为了确保流动属于蠕动流范畴($Re\ll 1$),上述模拟中施加的压力梯度都比较小,此时BFDD与DD边界条件相比并无优势.接下来将通过模拟多孔介质内高速非达西流,来阐释BFDD边界处理方法的优势.
2.3 多孔介质流体流动模拟
多孔介质流动模拟一般可以采用求解广义化N-S方程的LBM模型或者孔隙尺度LBM模型进行研究,两者详细介绍见文献[36]. 本文均采用孔隙尺度模型,即模型只包括不可渗透固体格点和流体格点. 根据$Re$的大小,可以将流动划分为3种模式:蠕动流(达西流)、层流惯性流(非达西流)和湍流.达西流可以通过式(23)进行描述, 式中$K_{ d}$为达西渗透率,lu$^{2}$; 随着多孔介质内流速的增大, 流体惯性作用不可忽略,此时流速与压力梯度不再呈线性关系, 一般可以通过添加惯性项,即Forchheimer方程[37]来描述非达西流, 见式(24)
$$-\nabla p = \frac{\mu }{K_{ d} }U~~~~~~~~~~~~(23)$$
$$-\nabla p = \frac{\mu }{K_{ d} }U + \beta \rho U^2(24)$$
式中, $\beta$为非达西系数, lu$^{-1}$;式(24)可以变换为[38-39]
$$\frac{1}{K^\ast } = \frac{K_{ d}}{K_{ app} } = 1 +Fo(25)$$
式(25)中, $K^\ast $为无量纲渗透率;$K_{ app} $为表观渗透率, lu$^{2}$; $Fo$为Forchheimer数,可以表示为$Fo\mbox{ = }\dfrac{\beta K_{ d} {Re}}{d}$; ${Re} =\dfrac{\rho Ud}{\mu }$, $d$为特征长度, lu.
通常来讲, 湍流现象很少出现在多孔介质流动中,本文只讨论前两种情况来评价BFDD和DD边界条件的适用性.本节所用的多孔介质 (图8所示)模型宽度和高度都为201 lu,孔隙度为0.61; 流动区域内由80个随机颗粒填充, 粒径为16 lu.采用BFDD和DD边界条件, 不断增大压力梯度以获得更大的$Re$,使流体流动从蠕动流转变为惯性流. 需要说明的是, 本节LBM流动模拟中,流体运动黏度设为0.1 lu$\cdot $ts$^{-2}$,这样一方面可以保证计算的稳定性,另一方面可以更容易地获得较大的$Re$, 其他参数设置与上文一致.
然而BFDD边界条件的实施涵盖了DD和BF边界格式,需要考虑两种边界条件提供的压力梯度的配比问题. 具体来讲,假设流动问题为蠕动流, 那么只实施DD边界条件是合适的;若在较高雷诺数条件下,DD边界条件由于高密度差问题会造成严重的压缩效应,那么此时应用BFDD边界格式. 因此,BFDD边界格式中BF和DD边界条件提供的压力梯度具体比例与雷诺数有关.针对此,基于本文所用多孔介质开展了一系列关于边界条件配比的惯性流动模拟,结果如图9和图10所示.
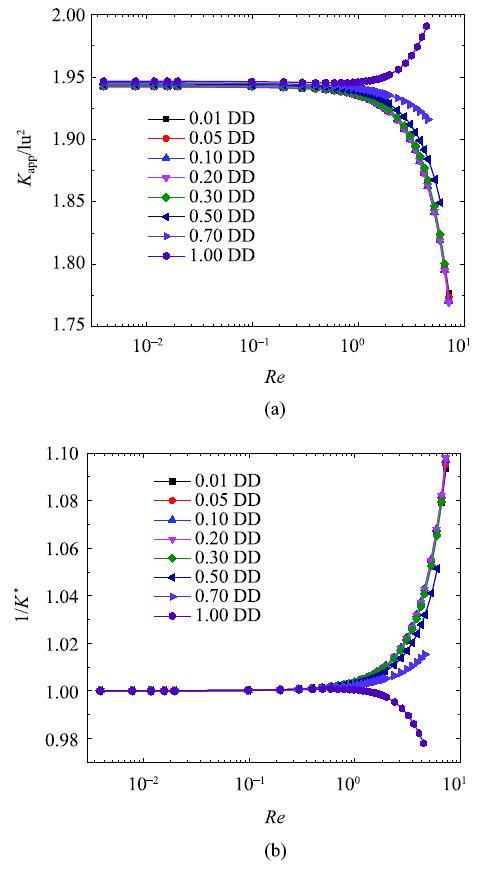
图 9 \不同边界条件配比对模拟结果的影响;(a)和(b)分别为表观渗透率和无量纲渗透率倒数随雷诺数的变化...
Fig. 9 The effect of the assignment of boundary conditions onthe simulated results; (a) and (b) denotes the variation ofapparent permeability and inverse dimensionless permeability as a functionof Reynolds number...
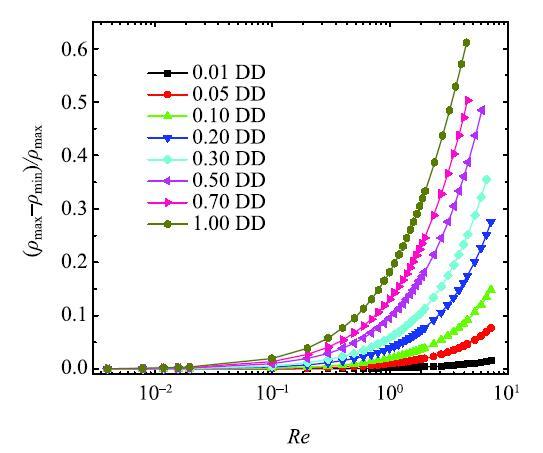
图 10 多孔介质非达西渗流阶段不同边界条件下进出口密度差与雷诺数关系...
Fig. 10 Variation of density difference of inlet and outletwith the increased Reynolds number under different boundaryconditions when transforming into the non-Darcy regime...
图9为不同边界配比下1/$K^{\ast }$和$K_{ app}$随$Re$变化趋势,图例表示DD边界条件提供的压力梯度占总压力梯度的比重, 1.00DD表示总压力梯度完全由DD边界格式供给, 即DD边界格式.可以看出在$Re<0.3$时, 流动仍处于蠕动流,两种边界条件下模型渗透率几乎不变, 达西渗透率约为1.945 lu$^{2}$;两种边界条件下模拟所得渗透率相差不大, 可以忽略不计.随着$Re$的不断增大, 蠕动流逐渐向惯性流过渡, 由式(25)可知,模型表观渗透率会小于达西渗透率,主要是由于流体惯性力作用造成的黏性耗散所致[40].从图中可以看出, BFDD边界条件处理方法能够精确地反映这一特征,而DD边界处理方法只在低雷诺数流动阶段有效, 随着雷诺数的增大,表观渗透率反而出现了增大, 这与Kakouei等[9]的研究结果一致,他们利用BF边界条件对其进行修正, 显然是不合理的.使用DD边界条件出现异常的主要原因是流体所需的压力梯度由进出口的密度差确定,较高的雷诺数必然需要更高的压力梯度, 即更大的密度差,这显然与真实物理情况不符且会带来较大的压缩效应,可见DD边界条件并不适合用来研究多孔介质惯性流. 此外,假如继续增大压力梯度, DD边界处理会造成计算不稳定最终发散;而由于BFDD边界格式压力梯度由两部分组成,可以通过低密度差加较大体力的方法获得更大的压力梯度,因此可以模拟更大$Re$下的流动, 如图9所示.然而在DD边界条件占比为0.50和0.70时, 由于进出口的密度差仍然较高,造成的压缩效应使得模拟结果在较高雷诺数下出现了偏差.当DD边界条件占比小于0.3时,不同配比条件下模拟结果呈现出了非常一致的趋势.可见DD边界配比在小于0.3时, 模拟结果与边界分配比大小并无关联. 此外,从1/$K^{\ast }$随$Re$的变化趋势同样可以看出,在较大雷诺数流动模拟中, BFDD边界处理方法比DD边界具有更大的优势.
当流动从蠕动流逐渐进入非达西渗流阶段,不同边界配比条件下流体密度差与$Re$关系, 如图10所示. 图中$\rho_{\max } $和$\rho _{\min } $分别为流体最大和最小密度.正如上述所言, DD边界处理中压力梯度来源于进出口的密度差,可以看出密度差随着$Re$不断增大, 最终接近0.7,而马赫数与密度变化存在正相关关系,较大的密度差会产生较大的压缩效应. 相反DD边界配比小于0.3时,即使在较大雷诺数下, 最大密度差都未超过0.36,因此精确地捕捉到了惯性段流动特征. 综合以上分析可知,在使用BFDD边界条件时,一个较小的进出口密度差分配附加一个较大的体力梯度可以保证模拟的正确实施.
另一方面根据$Re$的定义, 在其他条件不变的情况下,增大模型的特征长度同样可以获得更大的雷诺数.因此通过增加计算区域来提高网格密度,利用DD边界条件或者速度边界条件也能够精确地呈现多孔介质非达西流动特征,见文献${[15, 17]. 此外,通过采用不可压LBM模型也能捕捉到非达西流动特征[16].本文及文献${[9]采用DD边界条件模拟结果出现的异常理论上可以通过提高网格分辨率来获得正确结果.然而这种方法会不可避免使得计算量成倍增加,而BFDD边界处理方法能够用更小的计算量来达到研究目的. 此外,本文旨在阐述不同边界条件的适用性, 以及BFDD边界处理方法的优越性,因而未考虑模型网格分辨率问题以及松弛时间对计算的影响.未来研究多孔介质非达西流动,需要考虑网格分辨率及松弛时间对模拟结果的影响,计算所得的非达西系数也应进行验证.
3 结论
本文基于MRT-LBM分别开展了不同边界条件下,周期对称性结构和不规则结构中流动模拟,分析了不同边界条件的精度和适用性.引入一种混合式边界处理方法来模拟多孔介质非达西流, 取得如下结论:
(1) 对于周期性对称结构流动模拟, BF和DD边界处理方法两者是等效的,都可以精确地捕捉流体流动特点.
(2) 对于非周期性不规则结构, BF和DD边界处理方法是不等价的,BF边界条件只适用于周期性结构. 同样,GPBC边界条件不适合处理不规则模型.提出的混合式BFDD边界条件能够用来模拟周期性或非周期性结构流体流动.
(3) 当模拟多孔介质内流体惯性流时, 在较小网格分辨率时,DD边界条件不适合用来开展此类研究,进出口过大的密度差会造成较大的压缩效应, 使得模型计算不稳定,模拟结果出现异常;BFDD边界格式中压力梯度由进出口密度差和体力两部分组成,在同等条件下, 较DD边界条件有着明显的优势,可以获得更大的雷诺数且能够正确捕捉多孔介质惯性流特征.
The authors have declared that no competing interests exist.
参考文献
| [1] |
页岩气高效开采的力学问题与挑战 .Problems and challenges of mechanics in shale gas efficient exploitation . |
| [2] |
低渗透煤层气藏中气-水两相不稳定渗流动态分析 .Dynamic analysis on gas-water two-phase unsteady seepage flow in low-permeable coalbed gas reservoirs . |
| [3] |
多孔介质壁面剪切湍流速度时空关联的研究 .Space-time correlations of fluctuating veloctuating in porous wall-bounded turbulent shear flows . |
| [4] |
Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers . |
| [5] |
The Lattice Boltzmann Method: Principles and Practice . |
| [6] |
Nanoscale simulation of shale transport properties using the lattice Boltzmann method: Permeability and diffusivity . |
| [7] |
Pore scale inertial flow simulations in 3-D smooth and rough sphere packs using lattice Boltzmann method . |
| [8] |
Numerical study of inertial effects on permeability of porous media utilizing the lattice Boltzmann method . |
| [9] |
Cessation of Darcy regime in gas flow through porous media using LBM: Comparison of pressure gradient approaches . |
| [10] |
Relative permeability of two immiscible fluids flowing through porous media determined by lattice Boltzmann method . |
| [11] |
Pore scale characteristics of gas flow in shale matrix determined by the regularized lattice Boltzmann method . |
| [12] |
Implementation aspects of 3D lattice-BGK: Boundaries, accuracy, and a new fast relaxation method . |
| [13] |
Pressure boundary condition of the lattice Boltzmann method for fully developed periodic flows .
|
| [14] |
Adaptive generalized periodic boundary conditions for lattice Boltzmann simulations of pressure-driven flows through confined repetitive geometries . |
| [15] |
Lattice Boltzmann simulation of non-Darcy flow in stochastically generated 2D porous media geometries . |
| [16] |
Non-Darcy flow in disordered porous media: A lattice Boltzmann study . |
| [17] |
Evaluation of permeability and non-Darcy flow in vuggy macroporous limestone aquifer samples with lattice Boltzmann methods . |
| [18] |
A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems . |
| [19] |
Multiple--relaxation--time lattice Boltzmann models in three dimensions . |
| [20] |
Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability . |
| [21] |
Lattice BGK models for Navier-Stokes equation . |
| [22] |
Discrete lattice effects on the forcing term in the lattice Boltzmann method . |
| [23] |
Multirelaxation-time interaction-potential-based lattice Boltzmann model for two-phase flow . |
| [24] |
Study of immiscible displacements in porous media using a color-gradient-based multiphase lattice Boltzmann method . |
| [25] |
Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method . |
| [26] |
A generalized periodic boundary condition for lattice Boltzmann method simulation of a pressure driven flow in a periodic geometry . |
| [27] |
微尺度振荡Couette流的格子Boltzmann模拟 .Guo ZhaoLi. Lattice Boltzmann modeling of microscale oscillating Couette flow . |
| [28] |
基于格子Boltzmann方法的页岩气微观流动模拟 .
Microscale shale gas flow simulation based on lattice Boltzmann method .
|
| [29] |
Gas transport in self-affine rough microchannels of shale gas reservoir .
|
| [30] |
The effect of pore structure on non-Darcy flow in porous media using the lattice Boltzmann method . |
| [31] |
Lattice-BGK simulation of a two-dimensional channel flow around a square cylinder . |
| [32] |
Accurate computations of the laminar flow past a square cylinder based on two different methods: lattice-Boltzmann and finite-volume . |
| [33] |
Force evaluation in the lattice Boltzmann method involving curved geometry . |
| [34] |
Numerical study on the tortuosity of porous media via lattice Boltzmann method . |
| [35] |
Prediction of non-Darcy coefficients for inertial flows through the castlegate sandstone using image-based modeling . |
| [36] |
Lattice Boltzmann model for incompressible flows through porous media . |
| [37] |
Wasserbewegung durch boden, Z. Ver. Deutsch , |
| [38] |
On the derivation of the Forchheimer equation by means of the averaging theorem . |
| [39] |
A criterion for non-Darcy flow in porous media . |
| [40] |
Inertial effects on fluid flow through disordered porous media . |

/
| 〈 |
|
〉 |