后临界湍流区间内旋转薄壳结构振动演化与作用机制实测研究1)
南京航空航天大学航空宇航学院,南京210016
EVOLUTION CHARACTERISTIC AND WORKING MECHANISM ANALYSIS OF ROTATING THIN-WALLED STRUCTURES IN POST-CRITICAL TURBULENT INTERVAL BASED ON FIELD MEASUREMENT1)
中图分类号: TU279.7$^+$41
文献标识码: A
版权声明: 2019 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
作者简介: 2)柯世堂,教授,主要研究方向:风工程与结构工程.E-mail: keshitang@163.com
展开
摘要
载荷的时变特征可能会对结构振动强度和能量作用机理产生重要影响,火/核电厂最重要的大型建筑结构均为典型的旋转薄壳结构(如冷却塔、烟囱等).为揭示后临界湍流区间内旋转薄壳结构的振动演化特征及其作用机制,实测了后临界雷诺数($Re\ge $3.5$\times $10$^{6}$)条件下8座典型旋转薄壳结构的振动响应.首先,在对实测响应进行降噪滤波处理后进行了不同时距的信号非平稳识别,基于非平稳分析模型对响应的时变均值和极值估计进行研究,并基于多尺度小波变换的演化谱方法开展了响应的频域演变特性研究.在此基础上,探讨了结构风振响应的共振分量占比及其效应,识别了结构的自振频率和阻尼比,并以结构基频为划分依据分别讨论了不同旋转薄壳结构的阻尼作用机制.研究结果表明:(1)旋转薄壳结构在后临界湍流区间内风致振动响应表现为强度非平稳、频率平稳的演化特性;(2)后临界湍流区间内的旋转薄壳结构的风振问题应区分准静力作用点与共振激发点分别进行研究,不同共振激发点的功率谱分布形式较为相近,而准静力作用点的功率谱分布规律差异较大;(3)共振激发点的振动能量分布呈现明显的分段趋势,基于本文大量实测分析结果回归得出适用于共振激发点的三阶段共振谱表达式;(4)借助本文提出的等效阻尼比概念拟合出此类结构的阻尼比预测公式,论证了目前工程中通用的5%阻尼比取值的不合理性.
关键词:
Abstract
Recent study found that the time-varying characteristic of the load may have a significant effect on the vibrational strength and energy mechanism. The most important structures in fire/nuclear power plants (such as cooling towers, chimneys, etc.) are all typical rotating thin-walled structures. To reveal the vibration evolution characteristic and working mechanism of thin-walled structures in post-critical turbulent interval, the vibration responses of eight typical rotating thin-walled structures of high Reynolds number flow ($Re \ge $3.5$\times $10$^6$) are measured. Firstly, non-stationary identifications of signals with different time intervals are performed after depressing and filtering noise. The time-varying mean and extreme estimation of response are studied based on non-stationary analysis model. Besides, the frequency domain evolution characteristics are studied based on evolution spectrum method. On this basis, proportion of resonance component in wind-induced response and its effect are discussed. Then, self-resonant frequency and damping ratio of the structures are identified, and the damping mechanism of different rotating thin-walled structures is studied. The evolution characteristic and working mechanism are revealed as follows. (1) The wind-induced vibration response of the rotating thin-shell structure in post-critical turbulent interval is characterized by stable frequency evolution characteristics and non-stationary evolution characteristics in intensity aspect; (2) The wind-induced vibration problem of rotating thin-walled structures in post-critical turbulent interval should be studied as quasi-static and resonance excitation points separately. The vibration energy distributions of resonance excitation points at different regions of the cooling tower were similar, but the PSD functions of quasi-static points were dramatically different from each other; (3) Vibration energy distribution of the resonant excitation points showed a phased trend, and the proposed resonance spectral expression takes three variation stages of responses into account and achieves high prediction accuracy; (4) With the concept of equivalent damping ratio proposed in this paper, the damping ratio prediction formula is proposed. More importantly, these analysis results show that resonance effects and non-stationary effects on wind-induced effects of rotating thin-walled structures in post-critical turbulent interval are generally notable, and the irrationality of 5% damping ratio value commonly used in the current project for this type of rotating thin-walled structure has been demonstrated.
Keywords:
旋转薄壳结构在随机载荷作用下的共振现象一直是振动力学研究的经典问题之一,诸如火/核电厂中最为重要的构筑物(如冷却塔、烟囱等)均为典型的旋转薄壳结构[1].随着国家能源战略转型暨电力领域"上大压小"等政策的普遍实施,电力工业正朝着"巨型化"方向发展.根据Zdravkovich的研究工作,当雷诺数达到3.5$\times$10$^{6}$以上时,圆柱绕流中的旋涡脱落重新规则化,此时的雷诺数区间被定义为后临界区间[2].同小尺寸薄壳结构的振动问题相比,火/核电厂中的巨型旋转薄壳结构普遍处于后临界湍流区间内,当旋涡周期性脱落的频率与结构自振频率接近时,结构将发生远大于静力作用的共振响应,极大改变结构的振动特性.作为火/核电厂最重要的构筑物,一旦此类旋转薄壳结构在复杂湍流的作用下发生破坏事故,造成的人员伤亡和环境破坏不堪设想[3].因此,如何有效地识别后临界湍流区间内旋转薄壳结构的振动演化特性,合理预测结构的动力响应具有重要的学术意义和工程应用价值.
目前,针对旋转薄壳结构在后临界湍流区间下的振动研究主要基于气弹模型测振试验或刚体模型测压试验与有限元分析相结合的手段[4-7]. 例如,文献[4]从应力波传播的角度出发,研究了圆截面薄壳结构在非稳态轴向载荷作用下的结构动态响应.文献[5]在考虑Green--Lagrange应变的基础上,基于刚体测压风洞试验结果探讨了电厂冷却塔在随机风载荷下的振动特性,研究中采用了改进的加工硬化塑性混凝土模型描述此类壳体结构的双轴应力状态.文献[6]基于气弹模型测振试验获取了旋转薄壳结构的动态位移响应,分析了结构风振响应的组成成分.文献[7]基于刚体测压试验和有限单元法进行了冷却塔壳体随机风振响应分析,研究了结构阻尼比对冷却塔风振响应的影响.然而,上述研究的研究工作均在亚临界($300 \le Re<3.0\times$10$^{5})$或后临界(3.0$\times $10$^{5}\le Re<3.5\times$10$^{6})$区间开展,未充分考虑后临界湍流区间内的载荷特征.旋转薄壳结构的圆截面特征导致其对雷诺数效应异常敏感[8],文献[9]研究指出基于风洞试验无法完全真实反映壳体结构风效应的非平稳特征,现场实测成为研究此类问题最直接有效的技术手 段[10].
目前,关于后临界湍流区间内薄壳结构的实测研究大多聚焦于表面风压实测[11],关于结构风致振动的实测研究开展的相对较少,较有代表性的有Winney[12]和Górski[13]分别对不同巨型旋转薄壳结构进行了动态响应现场实测.Winney[12]对某高114m的中型冷却塔进行了动态响应现场实测,识别了结构的的模态参数,其研究成果对此类结构动力分析模型的建立具有较大参考价值.Górski[13]识别了某295m薄壁烟囱的阻尼比,其分析结果与我国相关规范[14]给出的参考取值差异较大,Górski识别的阻尼比均处于1%以下的区间,这一研究结果值得引起重视.遗憾的是,上述研究均未有效地进行系列现场实测研究,研究结果仅针对某一特定工程的旋转薄壳结构获得,因此其研究结论的普适性有待讨论.此外,已有学者开展了后临界湍流风场内结构荷载演化特性的实测研究,结果表明结构的荷载非平稳特征十分显著,对大跨度悬索桥梁等结构振动的影响不容忽视[15-16].然而,目前针对旋转薄壳结构在后临界湍流区间内振动演化特性及其对结构安全性影响的研究迄今尚未系统开展.
鉴于此,本文以实际大气边界层中的巨型旋转薄壳结构为工程背景,选取我国8座各具代表性的高耸旋转薄壳冷却塔为现场测试目标,获取了实际雷诺数条件下此类旋转薄壳结构的振动响应信号.着重探讨了非平稳特征对结构振动响应在幅域和频域的影响规律,研究了结构风振响应的共振效应,建立适用于此类结构的响应谱分析模型.此后,采用多种模态识别方法得到结构的主要模态参数,分别讨论不同旋转薄壳结构的阻尼作用机制.上述工作不仅有助于提升对旋转薄壳结构振动特性的基本认识,亦可以作为实际工程研究的参考依据.
1 实测工作介绍
1.1 测试目标选取
目前新建的电厂大型冷却塔一般高180 m左右,底部直径可达160m,此时雷诺数一般为10$^{7}\sim$10$^{8}$数量级[9],然而它的壳体厚度一般仅为分米级,为典型的旋转薄壳结构,其振动问题是目前旋转薄壳结构中最为棘手的工程应用问题[17-19].因此,本文将电厂大型冷却塔结构作为研究旋转薄壳结构的代表,综合考虑结构尺寸和所处流场特征等因素,从全国上百座类似结构中遴选出8座各具代表性的电厂冷却塔进行现场实测.其中,结构高度从80 m到190 m不等,基本风压包括0.35 kN/m$^{2}$,0.45kN/m$^{2}$和0.55kN/m$^{2}$等,反映了不同结构特征和外部条件,8座测试塔主要参数见表1所
表1 测试塔主要参数列表
Table 1 Main parameters of 8 measured targets
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| year of construction | 2015 | 1989 | 2015 | 2014 | 2013 | 2006 | 2015 | 2015 |
| tower arrangement | five towers | five towers | single towers | single tower | three towers | three towers | two towers | single tower |
| height/m | 182.0 | 150.0 | 179.0 | 180.0 | 126.7 | 80.0 | 190.0 | 180.0 |
| thickness/m | 0.22 〜1.20 | 0.21 〜0.74 | 0.26 〜1.85 | 0.34 〜1.85 | 0.19 〜1.50 | 0.15 〜0.55 | 0.28 〜1.40 | 0.35〜2.30 |
| throat diameter/m | 78.0 | 66.0 | 98.6 | 109.6 | 58.6 | 34.4 | 84.0 | 102.0 |
| concrete grade | C35 | C30 | C40 | C40 | C40 | C30 | C45 | C40 |
| reference wind pressure/(kN.m-2) | 0.35 | 0.35 | 0.35 | 0.55 | 0.55 | 0.55 | 0.45 | 0.55 |
| images |  | |||||||
1.2 现场实测
现场测试仪器主要包括低频加速度传感器、动态信号采集仪、信号传输导线和风速风向采集仪等.测试采用的加速度传感器为美国PCB压电式低频加速度传感器,灵敏度范围为900~1100mV/g, 频响范围可达0.025~800 Hz,具有极强的抗干扰能力.信号采集仪为DH5927动态信号测试分析系统,可实现实时控制、采集、存储和分析等功能.综合考虑结构固有频率分布特点和可能存在的非平稳特征,现场测试的最终选取采样频率为20Hz.
为防止将测点布置在结构振动时位移为零的不动点,测试前基于有限元单元方法建立了结构数值仿真模型并进行动力特性分析.现场实测中沿塔筒子午向和环向布设足够数量的测点,以塔C为例给出测点布置示意图及现场图(图1).
测试塔所处区域的风场来流信息(风速和风向)由当地气象站协助采集,与结构风振响应信号同步进行.各测试塔均选择具有一定代表性的强风工况(10 min平均风速大于10m/s)的响应数据进行后续分析,最终获得系列实际后临界湍流情况下的结构风振响应.
2 风振特性
2.1 实测数据
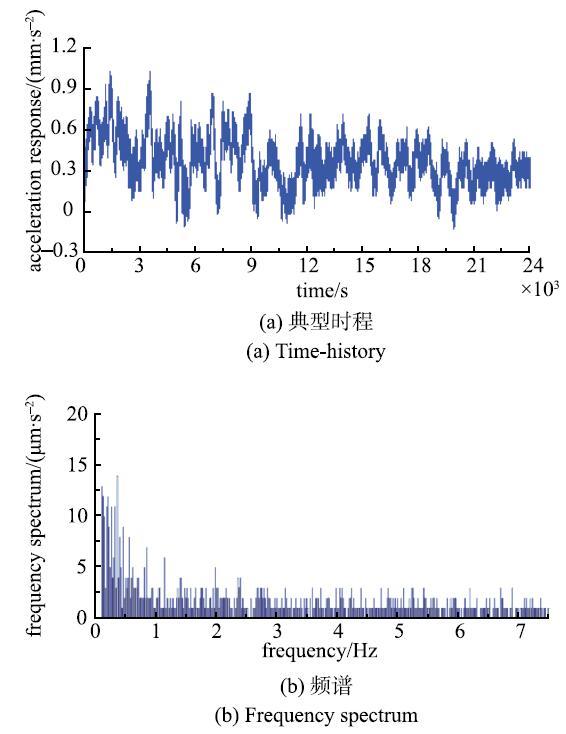
图2给出了典型实测加速度信号及其直接处理得到的频谱分布图(节选自塔C测点3-1).从时域分布可以看出,加速度时程呈现出一定的非平稳特征,而从频域分布上可以发现振动信号呈现明显的多模态参与特征.环境激励下获取的振动信号中不可避免地混有一定的高频干扰信号,同时由于结构自身频率分布密集,直接采用实测数据进行分析易产生虚假模态及模态缺失等问题.
图2 典型测点实测响应信号时程曲线及频谱图...
Fig. 2 Time-history and frequency spectra of measured responseattypical measuring point...
由于实测信号中存在的响应混叠现象和奇异值现象,首先对实测响应信号进行了基于小波变换模极大值法[20]的降噪处理.通过综合对比滤波结果的均方根误差、信噪比和信号的光滑性,最终选择了bior6.8小波基函数对实测信号进行2层小波分解(图3),可有效过滤结构响应中的高频干扰信号.
图3 测点实测加速度响应滤波前后对比...
Fig. 3 Comparison of acceleration responses before and afterthe smoothing...
2.2 非平稳特征
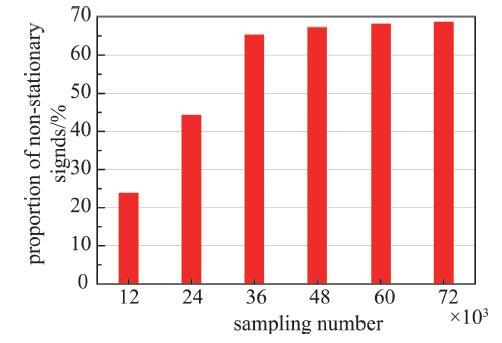
对于非线性信号分析而言,信号尺度的选择 尤为重要,基于轮次检验法[21]进行采样点数$N$= 12 000,24000,36 000,48 000,60 000和72 000等情况下的信号非平稳检验,分别对应样本时长为10,20,30,40,50和60 min.以塔C为例,列举了不同信号尺度下非平稳信号占比(即未通过非平稳检验的信号占全部有效信号的比例),如图4所示.随着识别样本数的增加,风振响应的非平稳信号逐渐增多,当识别长度达到36000个采样点之后, 非平稳信号占比趋于稳定.因此,后续分析中的样本点数如无特别说明均取为36 000.
图4 不同信号尺度下风振响应非平稳信号占比...
Fig. 4 Proportion of non-stationary signals under different signal scales...
当不考虑响应非平稳特性时,结构响应$R(t)$被分解为恒定的均值$\bar{R}$和脉动成分$r(t)$.实际上,后临界湍流区间内旋转薄壳结构的风振响应呈现出显著的非平稳特性,此时$R(t)$应被分解为一个随时间变化的趋势项(即时变平均值)$\bar{R}^{\ast}(t)$和一个零均值的脉动分量$r^{\ast }(t)^{[8],即
$$R(t){{ = }}{\overline R ^{{*}}}(t){{ +}}{r^*}(t){-1mm}(1)$$
相应的,基于非平稳分析模型的响应NS根方差$\textit{\sigma}$$_{r}^{\ast }$为[15]$${\sigma _r}^{{*}}{{ = }}\sqrt {\frac{1}{T}\int_0^T{{r^*}^2(t){ d}t} } (2)$$式中,$T$为样本采样时长.
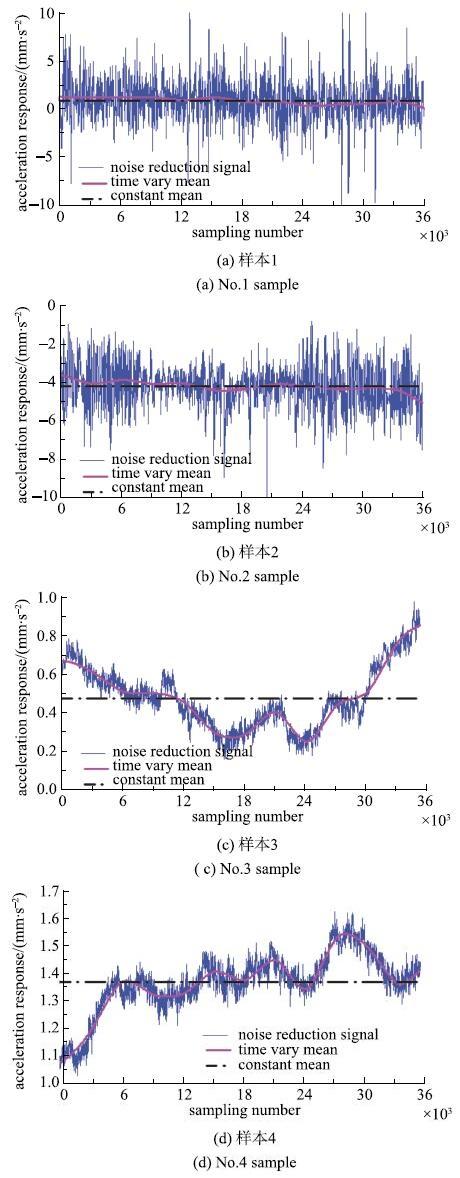
基于多尺度小波分析技术[22]提取了响应的时变平均值$\bar{R}^{\ast}(t)$,部分典型测点响应的时变均值和常数均值如图5所示(节选自塔C测点1-1/2-1/3-1/4-1).图中,样本1的趋势项平均值为0.925 mm/s$^{2}$,常数均值为0.932mm/s$^{2}$,其他测点的趋势项平均值与常数项均十分接近,表明本文提取时变趋势项的合理性.响应趋势项均呈现一定的时变特性,样本2由于自身振幅较小,其时变特征表现的更为显著.
图5 典型测点响应时变均值与常数均值对比...
Fig. 5 Comparison between time-vary mean and constant mean ofsometypical measuring points...
以塔C为例,列举给出未考虑非平稳特征时的响应极值估计误差,如表2所示.结合更多实测数据分析表明,后临界湍流区间内旋转薄壳结构的风振效应表现出显著的非平稳特征,基于平稳分析模型对此类结构的振动特性进行极值估计会造成一定程度的偏差,误差可高达50%以上.
响应功率谱密度可以直观地反映结构振动的能量分布规律,而演变功率谱(即演化谱)可用于描述功率谱密度在一定时段内的变化规律,是刻画非平稳随机过程的能量分布规律的主要参量[23],以在时域和频域都具有较好局部性的Morlet小波作为小波变换的基函数.
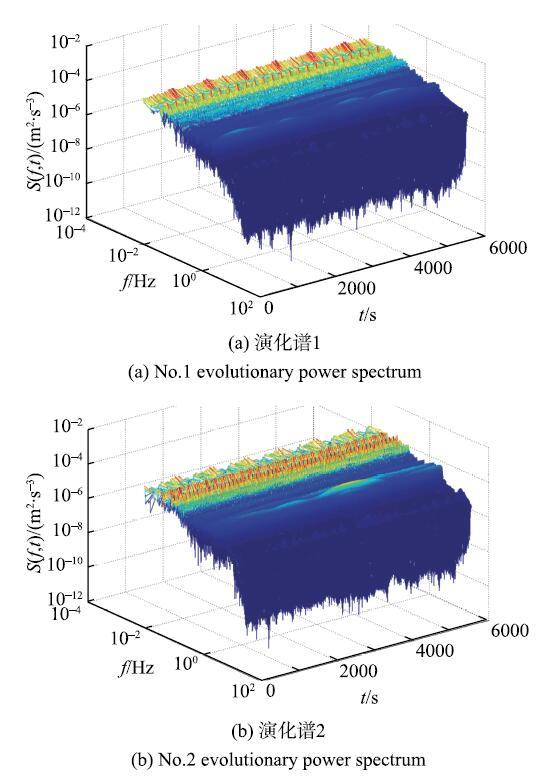
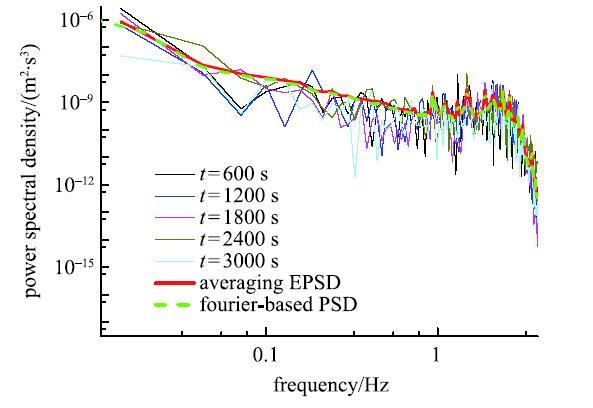
图6列举给出部分典型测点的响应演变功率谱示意图(节选自塔C),分别从时域和频域2个方面刻画了结构振动能量的变化.图7给出了EPSD在不同时间点的切片图,并与均一化的EPSD和基于FFT的功率谱进行对比.由图可知,虽然响应时程信号表现出较强的非平稳性,但从频域刻画的信息发现,此类旋转薄壳结构在后临界湍流区间内的振动能量频率成分无明显变化,参与振动的结构固有模态并未随时间的推移发生明显改变.结合更多测点演化谱分析结果,结果均表明旋转薄壳结构在后临界湍流区间内的风振响应表现为强度非平稳、频率平稳的演化特性.
图6 部分典型测点演化功率谱...
Fig. 6 Evolutionary power spectrum of some typical measuring points...
表2 未考虑非平稳特征的响应极值估计误差
Table 2 Extreme value estimation error of non-stationary features is not considered
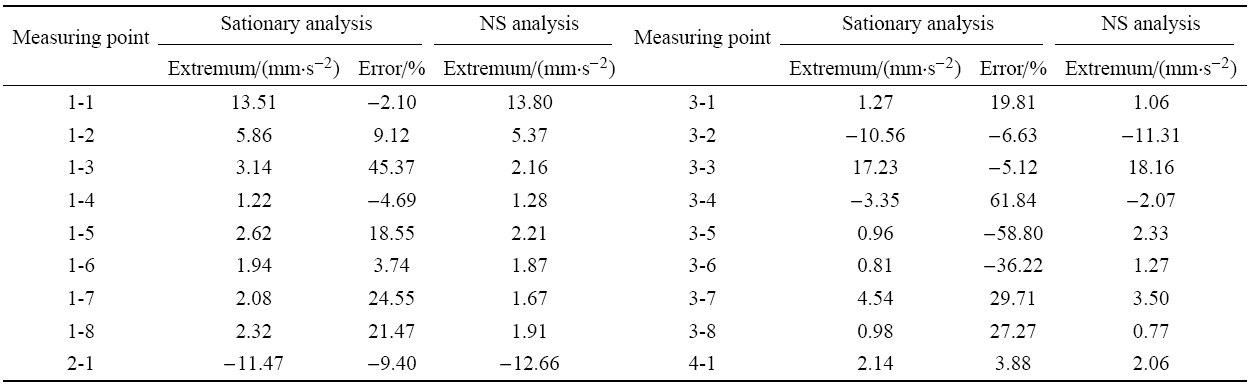 |
图7 EPSD时间切片谱、均一化的EPSD和基于FFT的功率谱对比...
Fig. 7 Comparison of the spectrum snapshots of EPSD and the traditional Fourier-based PSD...
2.3 共振效应
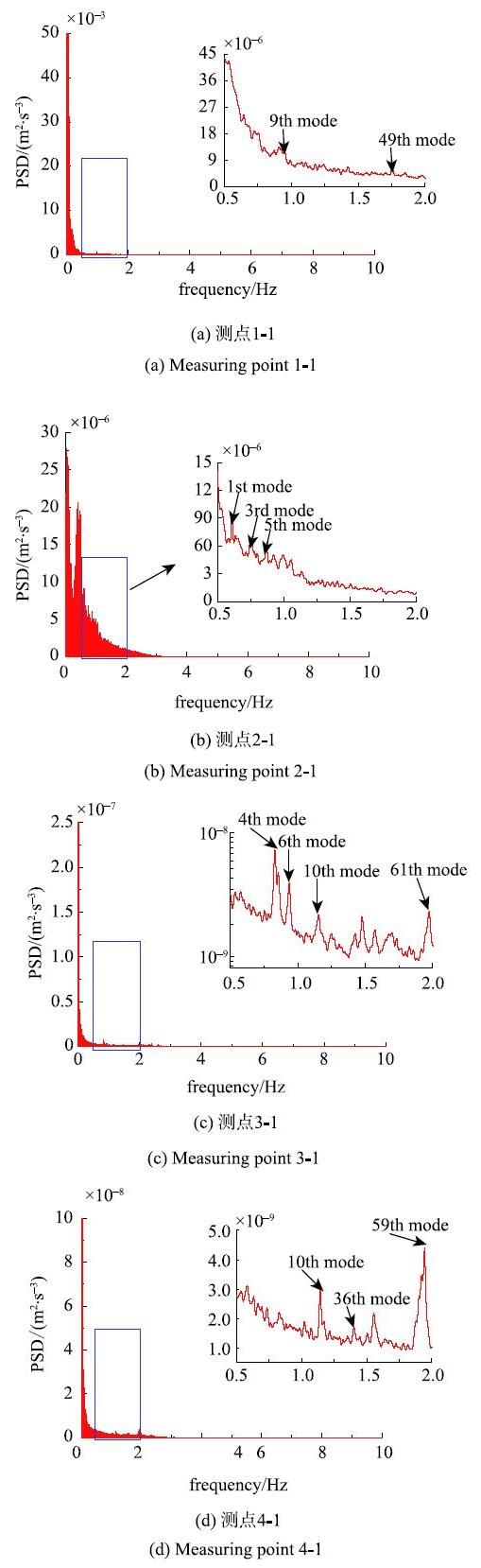
结构风振响应的频率平稳演化特性,为进一步分析结构测点实测功率谱密度函数提供了便利,以塔C为例,列举给出了部分典型测点实测风振响应功率谱密度函数(均一化EPSD),如图8所示.分析
图8 部分典型测点实测风振响应功率谱密度函数...
Fig. 8 Power spectrum density of wind-induced responses at some typical points...
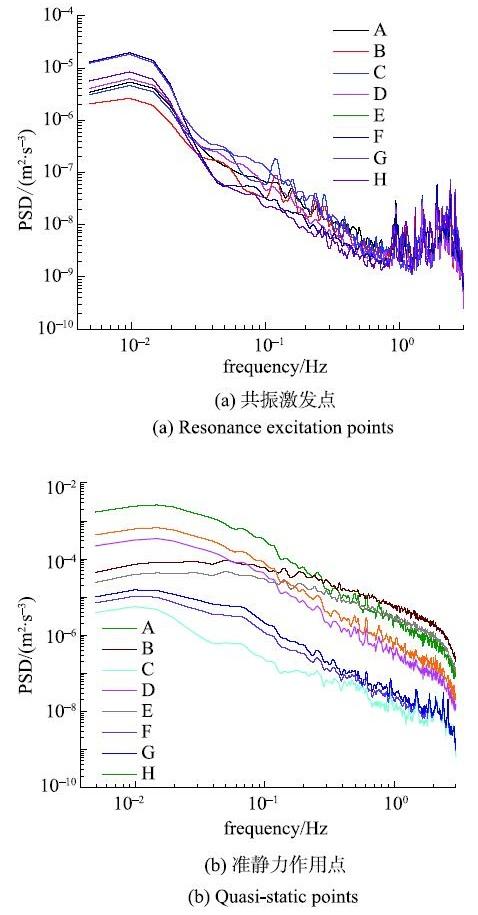
可知,(1)风致共振响应被限制在一个狭窄的频率段,从0Hz开始到2 Hz已经下降到非常低的水平; (2)不同高度测点的响应功率谱密度分布规律差异较大,靠近喉部区域的测点2-1,其能量主要由前几阶共振模态和背景分量贡献;(3)其余几个高度测点的能量主要由背景分量贡献,表现于各阶模态共振分量均较小,且前几阶模态共振分量与高阶模态分量相当,甚至更小.更多的环向测点响应谱分析结果表明,大型冷却塔这类巨型旋转薄壳结构,不同测点处的功率谱分布规律差异较显著,对于后临界湍流区间内的旋转薄壳结构应区分准静力作用区与共振激发区分别进行研究.
参考已有冷却塔共振分量研究[24]给出的计算标准,冷却塔响应共振分量占比按下式计算
$${\lambda _r} = \sum\limits_{i = {f_1}}^{5} {{S_{{RR}}}}\bigg/\sum\limits_{f = 0}^{5} {{S_{{RR}}}}(3)$$
式中,$S_{{RR}}$为冷却塔风振响应的概率密度函数值,$f_{1}$为结构基频.
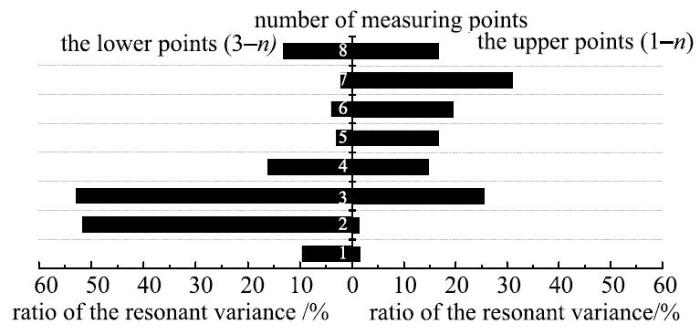
以塔C为例,给出了壳体第一层和第三层测点的共振分量占比,如图9所示.纵坐标为环向8个测点的编号,横坐标表示共振分量对风振响应的贡献比例.比较可惜的是,由于风振响应信号均为实测得到,壳体来流风向在测量过程中并非始终一致,因此无法从图中划分出明确的迎风面和背风面等区域.但从图中可以发现,共振分量对间冷塔风振响应的贡献程度与所处的环向角度密切相关,波动性较大,从理论上分析这应与来流风载荷在不同环向区域的脉动程度差异较大有关.
图9 壳体第一层和第三层环向测点共振分量占比...
Fig. 9 Comparison of resonance component proportion at the 1st and the 3rd layer...
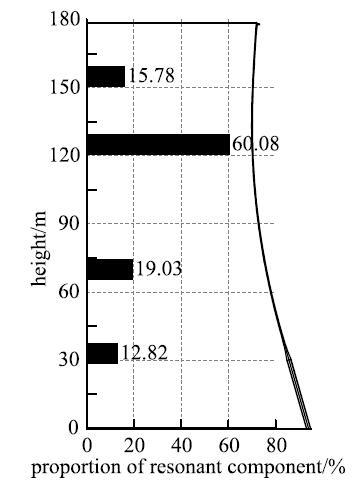
统计塔C不同高度处测点共振分量占比的平均值,如图10所示.距离塔顶刚性环较近的第一层测点和位于下环梁和支柱交界处的第四层测点的共振分量占比均较小,分别仅为15.78%和12.82%.位于塔筒中下部的第三层测点和喉部附近的第二层测点受共振分量影响较大,喉部测点共振分量占比甚至达到60%以上.
图10 壳体不同高度测点共振分量占比示意图...
Fig. 10 Resonance component proportion at different heights ofthetower shell...
分别列举了不同塔型典型准静力作用点与共振激发点响应信号功率密度分布曲线,如图11所示.由图可知,不同共振激发点的功率谱分布规律较为接近,可归纳总结出具有普适性的响应谱计算公式;而准静力作用点的功率谱密度函数与测点所在位置和当时所处的风向等因素相关,不同测点功率谱密度函数的分布规律差异较大.
图11 准静力作用点与共振激发点响应谱分布图...
Fig. 11 Spectral of the resonance excitation points and quasi-static points...
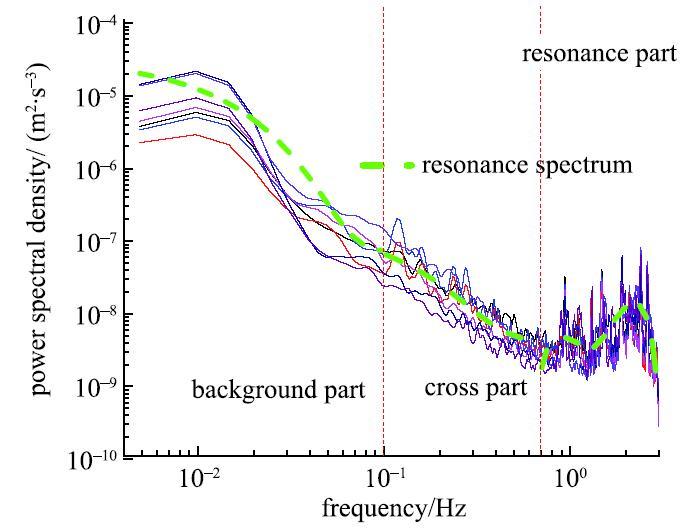
综合对比不同共振激发点的功率谱密度函数,回归分析得到适用于后临界湍流区间内旋转薄壳结构共振激发点的响应功率谱计算公式,即共振谱表达式. 将共振谱分三段表达,即:①背景分量为主阶段功率谱$S_{ b}(f)$,②交叉项分量为主阶段功率谱$S_{ c}(f)$,③共振分量为主阶段功率谱$S_{ r}(f)$,分别对应式(4)~式(6)
$${S_{ b}}(f) = {a_1} + \frac{{{a_2}{a_3}^f +{a_4}{a_5}^f}}{2},\quad {0~{{Hz}}<f}\le 0.1~{{Hz}}\tag{4}$$
$${S_{ c}}(f) = {b_1} + {b_2}\left(\frac{{\exp ({b_3}f) -1}}{{{b_3}}}\right),{0.1~{{Hz}}<f \le 0.7~{{Hz}}} \tag{5}$$
$${S_{ r}}(f) = {c_0} + {c_1}f + {c_2}{f^2} + {c_3}{f^3} +{c_4}{f^4} + {c_5}{f^5}, \qquad\quad {f>0.7~{{Hz}}}\tag{6}$$
式中,$f$为频率,$a_{i}$,$b_{i}$和$c_{i}$为拟合系数,见表3$\sim $表5所示.
表3 共振谱背景分量为主阶段功率谱表达式系数
Table 3 Fitting coefficients of power spectrum section dominated by background component
| ai | a2 | a3 | a4 | a5 |
|---|---|---|---|---|
| 6.480 26x | 3.024 58x | 8.476 91x | 2.911 85x | 2.530 95x |
| 10-8 | 10-5 | 10-47 | 10-5 | 10-40 |
表4 共振谱交叉项分量为主阶段谱表达式系数
Table 4 Fitting coefficients of power spectrum section dominated by cross term
| b1 | b2 | b3 |
|---|---|---|
| 1.705 62x10-7 | -1.802 91x10-6 | -10.809 71 |
表5 共振谱共振分量为主阶段功率谱表达式系数
Table 5 Fitting coefficients of power spectrum section dominated by resonance component
| C0 | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| -1.582 82x 5.747 81x | -7.667 72x 4.780 52x | -1.387 80x | 1.510 27x | ||
| 10-7 | 10-7 | 10-7 | 10-7 | 10-7 | 10-8 |
图12给出了共振谱回归曲线与实际多测点功率谱密度曲线的对比示意图.由图可知,实测值较均匀地分布于回归曲线附近,回归公式有较好的预测效果.
图12 共振谱与实际功率谱对比示意图...
Fig. 12 Comparison of resonance spectrum and actual power spectrum...
3 阻尼作用机制
3.1 模态参数识别
由前述分析知,旋转薄壳结构在后临界湍流区间内的风振响应在频域表现出平稳的演化特性,这也为进一步识别得到此类结构的关键阻尼参数提供便利.作为结构动力分析的重要动力特性参数,对于大尺度无限自由度结构而言,合理的阻尼比取值对于结构动力分析结果的准确性至关重要.近年来结构的模态参数识别算法发展迅速,目前应用较广的有随机减量法(简称RDT)[21]和易卜拉欣时域方法(简称ITD)[25]等.单一识别方法均可能存在丢失模态或虚假模态的情况,为确保不丢失模态以及模态参数识别的正确性,本文采用两阶段时域识别方法,首先采用随机减量法和自然激励法[26](简称NExT)从实测响应中提取结构的自由响应曲线或互相关函数.在此基础上,结合ITD、STD[27]和ARMA[28]方法进行模态参数识别.
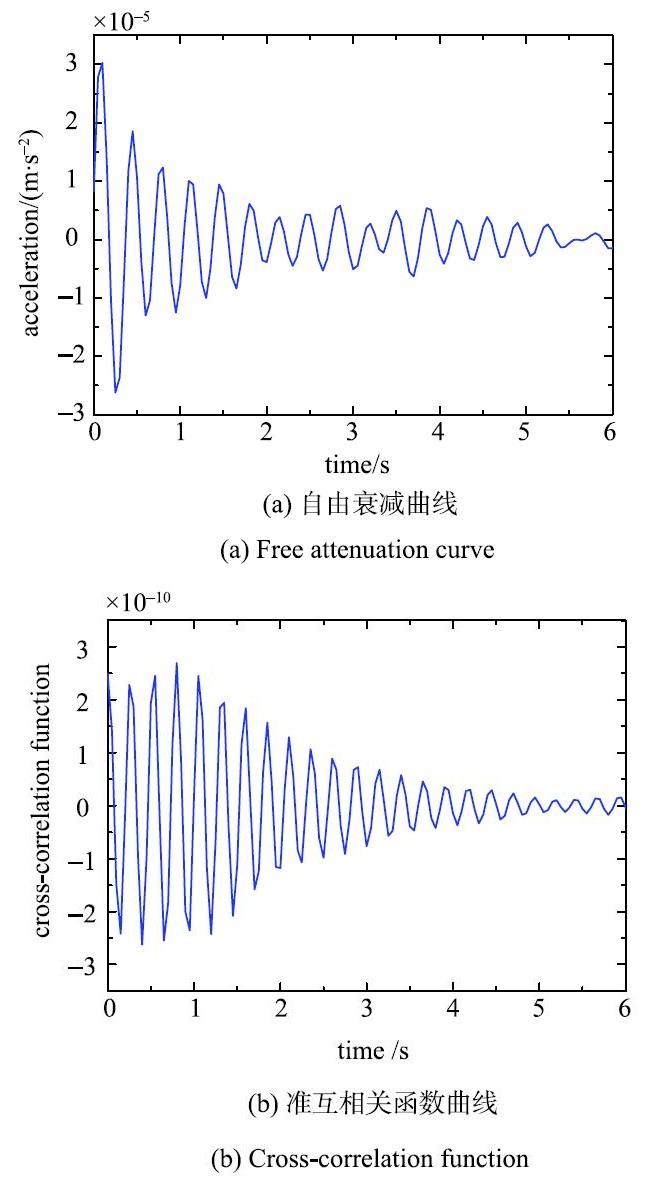
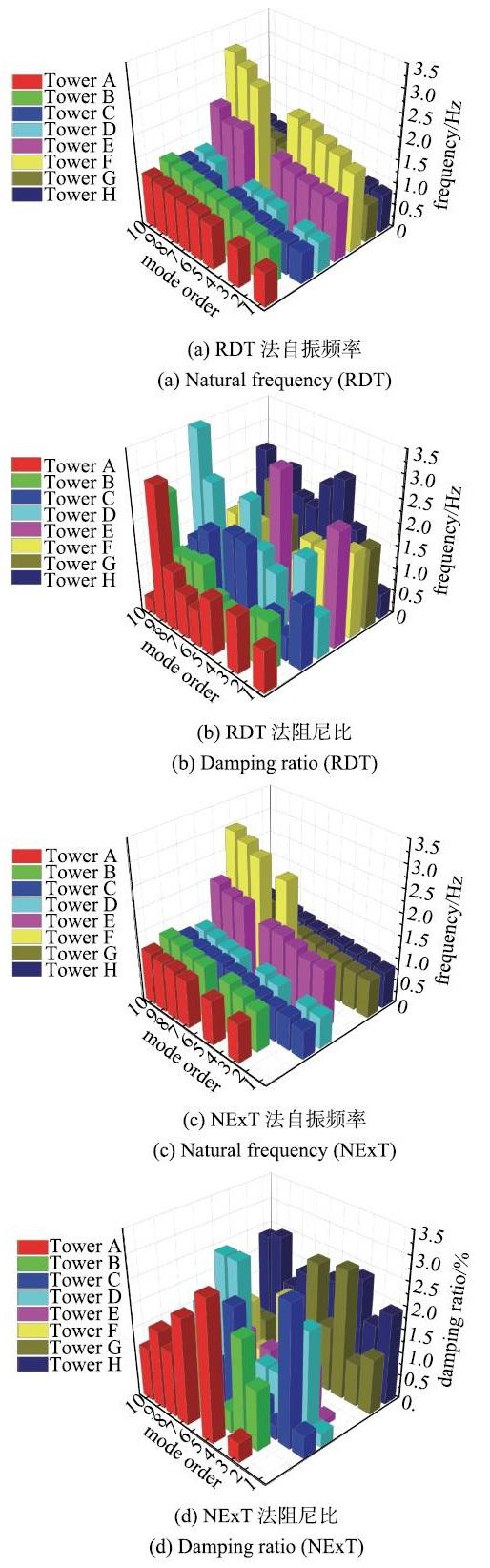
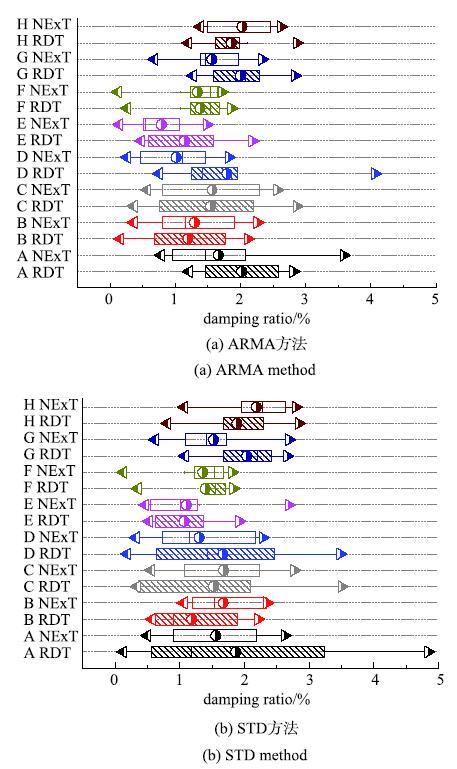
首先采用随机减量法对滤波后的信号进行预处理,剔除响应中的强迫振动部分获取了结构自由振动衰减曲线,再以测点4-1作为参考点,采用自然激励技术得到结构两点之间的互相关函数代替脉冲响应函数.图13给出的典型预处理加速度响应曲线有效过滤了频率分量中的强迫振动成分,经预处理后的信号呈现出平滑地衰减趋势.图14列举了基于前处理+ITD方法识别得到的结构前10阶自振频率和阻尼比.由图可知,采用不同模态识别方法获得的前10阶频率结果基本一致,多种识别方法可有效解决单一方法产生的模态丢失问题.此外,汇总给出了多种模态识别方法得到的前10节阻尼比箱式图(图15),图中左右两点为最值,
图14 基于前处理+ITD方法识别得到的结构模态识别前10阶结果...
Fig. 14 Identification results of the first 10 order based on ITD method...
图15 不同识别方法得到的前10阶阻尼比箱式图...
Fig. 15 Box plot of the first 10 order damping ratio based on different methods...
中间长方形上沿代表概率分布为75%的取值,下沿代表概率分布为25%的取值,圆点为平均值.与频率识别结果的高度吻合不同,不同识别方法得到的结构阻尼比离散性较大,但前10阶阻尼比识别结果中97.9%的数值小于3%.值得注意的是,本文分析结果与Winney[12]针对此类旋转薄壳结构的实测阻尼比均明显较规范[14]阻尼比5%小,Górski[13]对烟囱的阻尼比识别结果亦小于5%,第一阶阻尼比仅为0.6%左右.分析其原因,一方面是由于旋转薄壳结构与建筑结构构型差异显著,其内部不存在隔墙等联系构件;此外,本文和上述实测研究的旋转薄壳结构的振动均处于弹性范围内,结构变形尚未进入塑性阶段.
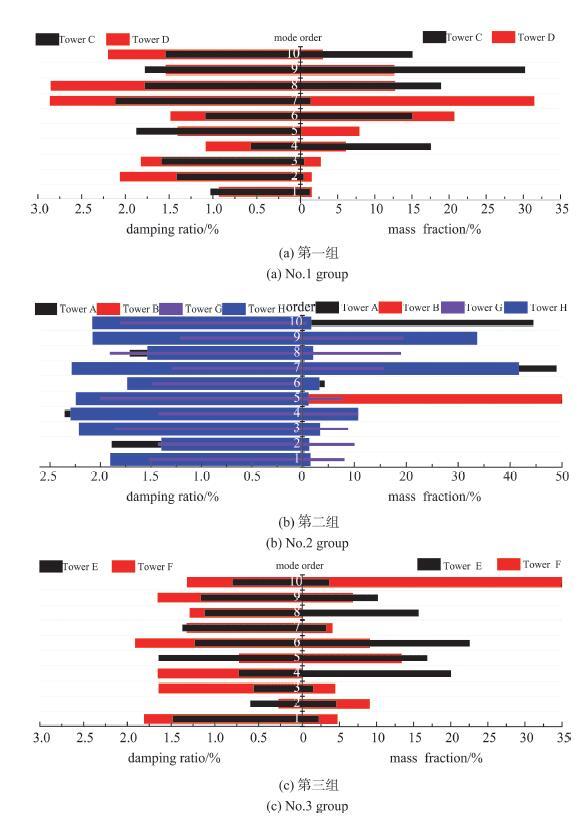
3.2 结构基频的影响
按结构基频将本文实测旋转薄壳结构分为以下三个组别:(1)第一组结构的基频均小于0.7Hz,包括塔C和塔D;(2)第二组基频在处于0.7$\sim $1.0Hz,包括塔A、塔B、塔G和塔H;(3)第三组基频高于1.0Hz,包括测试塔E和塔F.图16分别给出了三组测试塔的前10阶阻尼比及对应的振型参与系数.由图可知,前10阶振型对不同旋转薄壳结构整体振动的贡献程度差异显著,第二组测试塔的质量参与分布更具有代表性,表现出个别振型的主导作用明显,振型参与系数主要集中在了某一阶或者某两阶振型.
图16 测试塔前10阶振型参与系数及阻尼比...
Fig. 16 The first 10 order mass participation factors anddampingratio...
3.3 等效阻尼比的提出
根据本文分析和相关研究结果可定性判定,5%阻尼比取值对后临界湍流区间内的巨型旋转薄壳结构不尽合理,进行结构风振计算的阻尼比取值应小于这一数值.为定量地给出阻尼比取值建议,借鉴振型组合思想[29-30]将结构振型参与系数作为对应模态阻尼比的附加权重值,得到结构的等效阻尼比.计算公式如下
$${\xi _{{{eq}}}} = \sum\limits_{i = 1}^n {{\eta _i}} {\xi_i}(7)$$
式中,\textit{$\xi $}$_{{eq}}$为等效阻尼比(%);\textit{$\eta$}$_{i}$为第$i$阶模态的振型参与系数所占的百分比;\textit{$\xi$}$_{,i}$为第$i$阶模态阻尼比(%);$n$为识别得到自振频率和阻尼比阶数.
基于上述方法给出了8座测试塔等效阻尼比,如表6所示.不同测试结构的等效阻尼比分布在1.13%~2.16%之间,均小于规范阻尼比5%,与规范值的最大相对误差达到77.4%.
为方便对阻尼比取值进行估计,基于8座测试塔实测得到的前10阶模态阻尼比,以基率$f$为变量回归得到结构前10阶模态阻尼比的拟合 公式
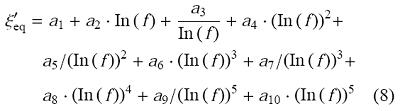
式中,\textit{$\xi$}$_{eq}^{'}$为等效阻尼比的估算值,单位为%;$a_{i}$($i=1,2,\cdots$,10)为拟合系数,如表7所示.拟合公式与原始数据的确定系数为0.99,与实测值吻合较好.
表6 测试冷却塔等效阻尼比
Table 6 Equivalent damping ratios of measured cooling towers
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| Equivalent damping ratios/% | 1.84 | 1.34 | 1.42 | 2.10 | 1.13 | 1.20 | 1.54 | 2.16 |
4 结论
本文实测了后临界湍流区间内多个旋转薄壳结构的风振响应,分析了实际雷诺数条件下结构响应的时域和频域演化特性.在此基础上,系统研究了结构响应的共振效应和阻尼作用机制.主要涉及现场实测、信号处理、数理统计、演化谱估计、极值计算和模态识别等内容,得到如下主要结论:
(1)后临界湍流区间内旋转薄壳结构的风振响应表现出强烈的非平稳特征,未考虑非平稳特性对响应的极值估计影响较大,但振动能量频率成分随时间变化较小,参与振动的结构固有模态未发生明显改变;结构振动表现为强度非平稳、频率平稳的演化特性;
(2)后临界湍流区间内旋转薄壳结构的振动应区分共振激发区与准静力作用区,不同准静力作用点的功率谱分布差异较大,而共振激发点的功率谱分布较为相近;本文针对性地提出了适用于共振激发点的风振响应共振谱表达式,通过分段考虑响应功率谱的三个变化阶段,具有良好的预测效果;
(3)后临界湍流区间内旋转薄壳结构的薄弱区域共振分量占比可达60%以上,上下端部增强区域的共振分量占比低至10%水平,其余大多数区域的共振分量占比处于20%左右;采用合理的阻尼比取值进行结构动力计算对后临界湍流区间内旋转薄壳结构的安全设计意义重大;
(4)后临界湍流区间内旋转薄壳结构的阻尼作用机制十分复杂,采用多种模态识别方法虽有效解决了模态丢失问题,但识别阻尼比的取值规律呈现出显著的离散分布特征,借鉴振型组合思想提出等效阻尼比概念,8座测试目标的等效阻尼比处于1%~2.5%,最终提出此类结构的阻尼比预测公式.
The authors have declared that no competing interests exist.
参考文献
| [1] |
Damage, deterioration and the long-term structural performance of cooling-tower shells: A survey of developments over the past 50 years . |
| [2] |
Flow around circular cylinders-volume 1: Fundamentals . |
| [3] |
The influence of self-excited forces on wind loads and wind effects for super-large cooling towers . |
| [4] |
Localization of dynamic buckling patterns of cylindrical shells under axial impact . |
| [5] |
Nonlinear behavior and ultimate load bearing capacity of reinforced concrete natural draught cooling tower shell . |
| [6] |
大型双曲冷却塔气弹模型风洞试验和响应特性 .Wind tunnel test on aeroelastic model of large hyperbolic cooling towers and features of wind-induced response . |
| [7] |
双冷却塔布置与山地环境风干扰作用效应研究 .Study on interference effect of cooling towers under condition of tower-tower and hilly surroundings . |
| [8] |
串列双圆柱流致振动的数值模拟及其耦合机制 .Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanisms . |
| [9] |
A Comparative study of stationary and non-stationary wind models using field measurements . |
| [10] |
Aspects of the dynamic wind-induced response of structures and codification . |
| [11] |
高超临界雷诺数区间内二维圆柱绕流的实测研究 .Field measurements on flow past a circular cylinder in transcritical Reynolds number regime . |
| [12] |
The modal properties of model and full scale cooling towers, |
| [13] |
Investigation of dynamic characteristics of tall industrial chimney based on GPS measurements using random decrement method . |
| [14] |
|
| [15] |
Extreme value of typhoon-induced non-stationary buffeting response of long-span bridges . |
| [16] |
大跨度斜拉桥非线性振动模型与理论研究进展 .Review on nonlinear vibration and modeling of large span cable-stayed bridge . |
| [17] |
Tests on microconcrete model of hyperbolic cooling tower . |
| [18] |
超空泡运动体圆柱薄壳的非线性动力屈曲分析 .The nonlinear dynamic buckling analysis of a thin-walled cylindrical shell of supercavitating vehicles . |
| [19] |
柔性圆柱涡激振动流体力系数识别及其特性 .Identification and characteristics of hydrodynamic coefficients for a flexible cylinder undergoing vortex-induced vibration . |
| [20] |
Spectral-temporal filtering of ndt data using wavelet transform modulus maxima . |
| [21] |
Random data: Analysis and measurement procedures . |
| [22] |
Ten lectures on wavelets . |
| [23] |
Evolutionary spectra estimation using wavelets . |
| [24] |
Wind loading on cooling towers . |
| [25] |
Random decrement technique for modal identification of structures . |
| [26] |
Structural nonlinearity identification using perturbed eigen problem and ITD modal analysis method . |
| [27] |
Identification and monitoring of modal parameters in aircraft structures using the natural excitation technique (NExT) combined with the eigensystem realization algorithm (ERA) . |
| [28] |
Signals & Systems (2nd ed.) . |
| [29] |
ARMA model parameter estimation based on the equivalent MA approach . |
| [30] |
Effects of concrete cracking on the earthquake response of gravity dams . |

/
| 〈 |
|
〉 |