力学学报  2019 , 51 (1): 103-110 https://doi.org/10.6052/0459-1879-18-211

流体力学

基于PIV技术分析颗粒在湍流边界层中的行为1)

高天达*, †, 孙姣*, †, **, 范赢*, †, 陈文义*, †, 2), , 轩瑞祥*, †

*河北工业大学过程装备与控制工程系,天津 300130
†河北工业大学工程流动与过程强化研究中心,天津 300130
**天津大学机械学院力学系,天津 300350

PIV EXPERIMENTAL INVESTIGATION ON THE BEHAVIOR OF PARTICLES IN THE TURBULENT BOUNDARY LAYER1)

Gao Tianda*, †, Sun Jiao*, †, **, Fan Ying*, †, Chen Wenyi*, †, 2), , Xuan Ruixiang*, †

*Department of Process Equipment and Control Engineering, Hebei University of Technology, Tianjin 300130, China
†Research Center of Engineering Fluid and Process Enhancement, Hebei University of Technology, Tianjin 300130, China
**Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin 300350, China

中图分类号:  O357.5$^+$2

文献标识码:  A

版权声明:  2019 力学学报期刊社 力学学报期刊社 所有

基金资助:  1) 国家自然科学基金资助项目(11572357,11602077).

作者简介:

作者简介: 2) 陈文义,教授,主要研究方向：实验流体力学. E-mail:cwy63@126.com

展开

摘要

采用粒子图像测速技术(particle image velocimetry,PIV)在平板湍流边界层内开展实验研究,对比颗粒相及单相液体的平均速度剖面、湍流强度、雷诺应力等湍流统计量,分析颗粒在湍流边界层中的行为.利用空间多尺度局部平均涡量的概念提取壁湍流发卡涡展向涡头(顺向涡)并统计其数量规律,得到不同法向位置处顺向涡周围流向脉动速度及流线的空间拓扑结构,比较分析顺向涡发展程度及周围的湍流相干结构.结果发现：与清水工况相比,颗粒相湍流边界层的缓冲层变薄、对数律区下移,湍流强度得到增强,雷诺应力在对数律区有所增大;颗粒的流向脉动速度在展向涡周围的分布与清水工况不同,颗粒能够被流体展向涡周围的猝发过程有效传递;颗粒相的顺向涡涡核较大,且随着法向位置的升高逐渐发展完整,涡和条带在流向上拉伸得更长;同时发现在两种工况下,顺向涡的左下方始终存在一个逆向涡,颗粒相逆向涡的形成弱于单相流体;两种工况下的顺向涡数量均随着法向位置的升高而减少,最后逐渐趋于稳定.

关键词： 两相流 ; 粒子图像测速 ; 湍流边界层 ; 空间多尺度局部平均涡量 ; 顺向涡

Abstract

The particle image velocimetry (PIV) is used to conduct experimental research in the solid-liquid two-phase plane turbulent boundary layer. The turbulence statistics such as the average velocity profile, turbulence intensity and Reynolds stress of the particle phase and single-phase clean water are compared to analyze the behavior of the particles in the turbulent boundary layer. The concept of multi-scale spatial locally-averaged vortices is utilized to extract the spatial topologies of the spanwise vortex head and the statistic of the prograde vortex is acquired. From that, the spatial topologies of the fluctuating velocity and streamlines around the prograde vortex at different normal positions can be obtained. The degree of development of the prograde vortex and the surrounding turbulence coherence structure can be compared and analyzed. The results show that compared with the clean water conditions, the buffer layer of the turbulent boundary layer of the particle phase becomes thinner, the logarithmic region moves downward, the turbulence intensity is enhanced, and the Reynolds stress in the logarithmic law region is increased. The fluctuating velocity of the particle phase is different from the clear water condition around the vortex, and the particles can be effectively transferred by the burst process around the spanwise vortex. The particle-laden flow has a large prograde vortex core and develops as the normal position rises. The vortex and the band stretch longer in the flow direction. At the same time, it is found that there is always a retrograde vortex in the lower left of the prograde vortex under both conditions, and the formation of retrograde vortex in the particle-laden flow is weaker than that of single-phase fluids. The number of prograde vortices in both conditions decreases with the increase of the normal position, and finally gradually stabilizes.

Keywords： two-phase flow ; PIV ; turbulent boundary layer ; multi-scale spatial locally-averaged vortices ; prograde vortex

0

PDF (21929KB) 元数据 多维度评价 相关文章 收藏文章

本文引用格式 导出 EndNote Ris Bibtex

高天达, 孙姣, 范赢, 陈文义, 轩瑞祥. 基于PIV技术分析颗粒在湍流边界层中的行为1)[J]. 力学学报, 2019, 51(1): 103-110 https://doi.org/10.6052/0459-1879-18-211

Gao Tianda, Sun Jiao, Fan Ying, Chen Wenyi, Xuan Ruixiang. PIV EXPERIMENTAL INVESTIGATION ON THE BEHAVIOR OF PARTICLES IN THE TURBULENT BOUNDARY LAYER1)[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(1): 103-110 https://doi.org/10.6052/0459-1879-18-211

液固两相流常见于日常的生产生活中,如化工单元操作、沙石水力输运和污水处理等.与液固两相流相关的基础问题一直是科研的热点[1 -4],其中颗粒如何在液固两相湍流边界层内运动是研究的重要问题之一.液固两相流中颗粒的运动行为直接受流体的作用,同时又反作用于流体[5- 11].颗粒周围的局部流场受颗粒的影响较大,尤其是颗粒周围的涡结构.涡的无规则运动引起物质、动量、能量的扩散输运,在化工过程的传热传质方面有着十分重要的意义.因此对颗粒与液固两相湍流边界层内涡结构的研究十分重要.

Muste等[12]利用DLDV技术对明渠悬浮流动中的流体相与颗粒相进行了测量,发现沉积物颗粒的平均速度低于水的平均速度.Righetti等[13]在平板湍流边界层中进行实验,发现在湍流边界层中近壁相干结构挟带着颗粒做抬升或下扫运动,并且发生了显著的动量交换.Wang等[14-15]对颗粒在垂直平板边界层内的规律进行了研究,发现在边界层内部,颗粒速度大于流体相速度,粒子流的边界层厚度小于流体相的边界层厚度.王汉封等[16]运用PIV技术对充分发展的水平槽道内稀疏湍流两相流中的颗粒行为进行了定量研究.发现槽道下壁面附近,向上运动颗粒的概率大于向下运动的颗粒,两者概率的差异随着法向距离的增大而减小.Sumer等[17-18]对近壁区的颗粒运动进行了测量,发现颗粒做下降运动时的法向速度大于其做上升运动时的法向速度,据此他们推测颗粒是受湍流猝发事件影响的.Li等[19]运用双向耦合的欧拉-拉格朗日点粒子方法研究平板湍流边界层,发现颗粒的流向脉动速度大于流体的流向脉动速度,法向和展向脉动速度则小于流体的脉动速度,且粒子法向和展向脉动速度随粒子斯托克斯数增长而下降.Vinkovic等[20]对稀疏湍流通道内的颗粒行为进行了直接数值模拟,发现被喷射事件包围的颗粒会远离壁面.Marchioli等[21]发现颗粒通过近壁区的扫掠事件在低速条带中聚集,而颗粒通过近壁区喷射事件从壁面区域转移到外区,只有具有明显空间相干性的喷射与扫掠事件才能有效地传递粒子.吴文权和黄远东[22-23]应用离散涡方法计算了两种 {St}的泥沙粒子在圆柱绕流场中的运动,结果表明液固两相流中颗粒运动与旋涡存在有明确的相关性.Dritselis等[24]对垂直湍槽流近壁区域颗粒与流体相互作用机理进行直接数值模拟和拉格朗日粒子追踪,重点研究了颗粒对于近壁区相干结构的影响.发现在单向流和液固两相流中,近壁区中以准流向涡结构为主,无论是颗粒自身运动还是跟随流体运动,都会产生一个反向力矩,从而削弱准流向涡的运动尺度及强度,抑制流场湍动强度.Richter等[25]利用直接数值模拟结合拉格朗日点粒子方法来研究库特流(Couetteflow)中不同雷诺数下颗粒和边界层中发卡涡的相互作用.研究证明,发卡涡由于颗粒相的存在被削弱,并且随着雷诺数的增大削弱程度也在逐渐增大.陈启刚等[26]利用基于二维平面流场的涡结构模式匹配方法对明渠湍流中的涡结构进行了分析,发现涡结构的密度和涡量沿水深逐渐减小,且顺向涡的平均流场具有典型的发夹涡群特征.Hambleton等[27]在对边界层外区的逆向涡进行线性随机估计时发现,顺向涡的左下角常会伴随一个逆向涡.苏健等[28]在利用高时间分辨率粒子图像测速技术(TRPIV)研究超疏水壁面湍流边界层中展向涡的空间分布特征时发现逆向涡对顺向涡的进一步发展起抑制作用.Kaftori等[29-30]实验研究了壁湍流中固体颗粒的运动.证实壁相干结构是影响湍流中固体边界附近颗粒运动以及沉积和夹带的主要因素;发现壁湍流中的颗粒行为与漏斗形旋涡的主要基础结构相一致.

综上所述,前人的研究多集中在液固两相湍流边界层内的速度差异以及喷射、扫掠等相干结构上,对颗粒形成的涡结构研究较少.对涡结构的深入理解对工程中的传质传热,节能减阻有重要的意义.因此本文从涡的角度揭示液固两相湍流边界层内液相与固相之间的关系,突破单点测量的局限性,利用粒子图像测速技术\!(PIV)\!对清水工况和加入颗粒条件下平板湍流边界层进行研究,采用空间多尺度局部平均涡量的概念提取壁湍流展向涡涡头平面结构,通过对比分析颗粒相与单液相的平均速度剖面、湍流度、雷诺应力等统计量及顺向涡结构,获得液固两相湍流边界层中颗粒运动与液相流场之间的关系,为颗粒在液固两相湍流边界层内的运动规律提供参考.

1 实验设备与参数

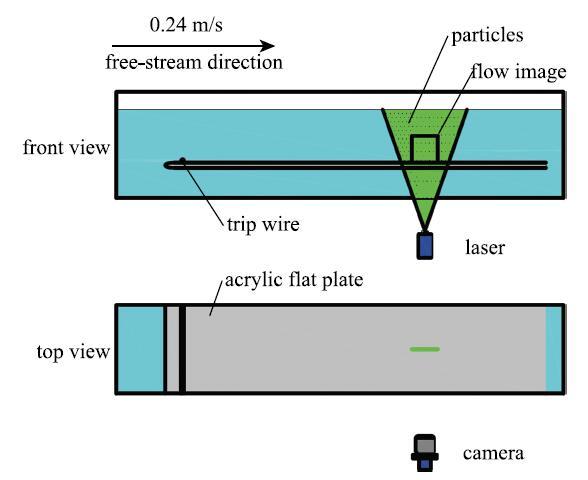
实验在河北工业大学PIV流体力学实验室中型低速循环水槽中进行,其背景湍流度小于0.8%,实验装置如图1所示.水槽实验段长为2600 mm,宽为500 mm,高为600 mm. 平板长为2200mm,宽为500 mm,厚为15 mm. 平板水平放置在距水槽底部250mm处,并通过调节后缘板将平板表面沿流向的静压力梯度调节至接近于零,平板前端为8:1椭圆修形;为获得充分发展的湍流边界层在距平板前缘100mm位置添加直径5 mm的拌线.实验过程中通过调节变频器使得水槽的自由来

显示原图| 下载原图ZIP| 生成PPT

图1   实验装置示意图...

Fig. 1   Schematic diagram of the experimental facility

流速度为$U_{\infty }=0.24$m/s;实验环境温度为20\textcelsius ,此时水的密度$\rho _{ f} =998~{{ kg}}/{{ m}^{ 3}}$;水的运动黏度$\nu = 1.006~{{mm}^{ 2}}/ { s}$. 清水组边界层名义厚度为59mm,摩擦雷诺数$Re_\tau = 645$. 实验选用20 $\mu$m的聚苯乙烯作为流场示踪剂,颗粒相选用直径$d_{ p} = 140~{\mu m}$的聚苯乙烯颗粒,颗粒密度$\rho _{ p} = 1050~{\mbox{kg}}/{{ m}^{ 3}}$. 通过拍摄视窗观测其粒子浓度满足PIV工作要求.颗粒雷诺数$Re_{ p} = {d_{ p} u_{ p} }/ \nu =0.077$,式中$u_{ p} = {gd^2_{ p} \left( {\rho _{ p} -\rho _{ f} } \right)}/ ({18\mu })$为颗粒沉降速度, {$\mu$}为水的动力黏度. 颗粒Stokes数$St = {\tau _{ p} }/ {\tau _{f} = 0.137}$,式中$\tau _{ p} = {\rho _{ p} d_{ p}^2 }/({18\mu })$为颗粒对流体的响应时间,$\tau _{ f} = \nu /{u_\ast^2 }$为流体流动特征时间.根据牛顿迭代法求得本实验的壁面摩擦速度$u_\ast = 0.0~110~{ m}/{ s}$.

数据采集采用德国Lavision公司的PIV系统,激光器型号为LPY700,双脉冲激光最高频率为100Hz,最大能量100 mJ,相机为4MX相机(像素为2048$\times$2048),最大采样频率为180 Hz. 本次实验激光器能量为100mJ,图像采集模式为双帧双曝,图像采集频率为60 Hz,曝光时间为1000$\mu $s,每种工况采集样本量为16 000张,图像视野实际大小约为100mm$\times $100 mm(流向$\times$法向),利用系统自带的Davis系统对原始图像用互相关算法处理,查询窗口像素设置为32$\times$32,重叠率为75%,得到的瞬时速度场有256$\times$256(流向$\times $法向)个速度矢量.

本文分两组实验,第一组为仅含示踪粒子的清水对照组,说明加入颗粒前流场情况的同时也表示加入颗粒后,不考虑颗粒影响的液相场情况;第二组为仅含140 $\mu $m聚苯乙烯颗粒的实验组.对实验组的处理,参考液固双流体模型[31],即在动力学规律上考虑颗粒相与流体相的耦合作用,但在数学处理上采用连续介质假设按连续相处理.清水组与颗粒组进行比较,可以清楚地分析出颗粒在液相流场作用下的运动行为.

2 湍流基本统计量分析

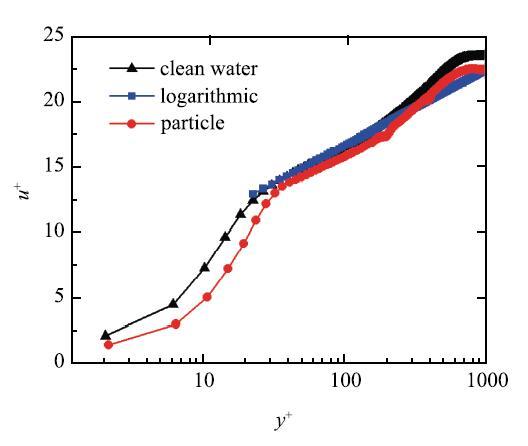
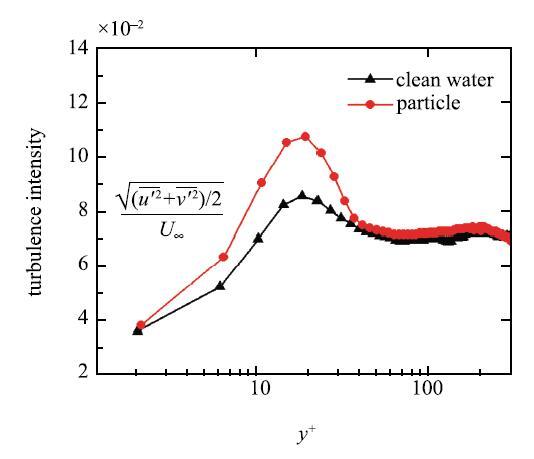
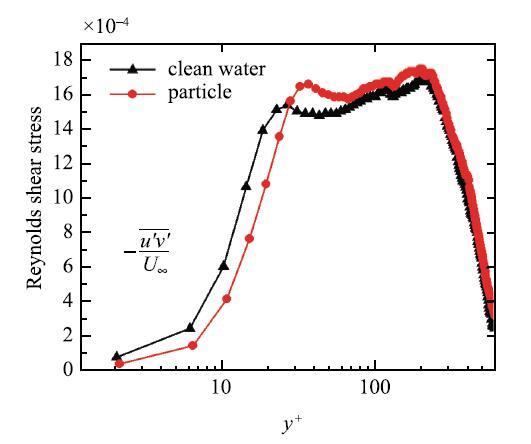
对两种工况下得到的实验数据进行处理,图2所示为平均速度剖面,横轴距壁面无量纲距离为$y^ + = {yu_\ast }/ \nu$,纵轴流向无量纲速度为$u^ + = u/ {u_\ast }$.从图中可知在整个检测区域内,颗粒组的无量纲速度均小于清水组的无量纲速度,这与Muste[12]的结论是一致的,这是由于颗粒与周围流体相之间存在一定的滑移速度,造成了颗粒相运动的落后.相较于清水组,颗粒组的缓冲层更薄,对数律区内移.图3所示为湍流度分布曲线,颗粒组的湍流度强于清水组.分析知粒子由于惯性在被流体加速后会更易维持脉动状态.图4所示为雷诺切应力分布曲线,雷诺应力

显示原图| 下载原图ZIP| 生成PPT

图2   流向平均速度剖面图...

Fig. 2   Streamwise mean velocity profiles

显示原图| 下载原图ZIP| 生成PPT

图3   湍流度分布曲线...

Fig. 3   Distribution of the normal turbulence intensity

显示原图| 下载原图ZIP| 生成PPT

图4   雷诺切应力分布曲线...

Fig. 4   Distribution of the Reynolds shear stress

表征由脉动引起的穿越单位面积的动量输运率.颗粒组对数律区的雷诺切应力比清水组大.说明颗粒在流场内的动量输运率得到提高.颗粒组与清水组湍流统计量沿壁面距离变化的趋势相吻合,说明颗粒运动的主要动量来源是液相流场.发现颗粒组与清水组相比在不同壁面区域中湍流统计量数值变化的程度不同,这可能与不同壁面区域中的湍流结构有关.

3 发卡涡展向涡头的检测

相干结构在湍流边界层中扮演着重要的角色,为了研究颗粒相与湍流边界层中相干结构相互作用的影响,需要从瞬时速度场中识别提取大尺度展向涡结构[32],本文利用空间多尺度局部平均涡量[33]的概念来提取完整的展向涡结构.

流向脉动速度沿法向的局部平均结构函数为

$$\delta u_y \left( {x_0 ,y_0 ,l_y } \right) = \overline {u\left({x_0 ,y_0 + y} \right)} _{y \in \left[ {0,l_y } \right]} -\overline {u\left( {x_0 ,y_0-y} \right)} _{y \in \left[ {0,l_y }\right]} \tag{1}$$

法向脉动速度沿流向的局部平均结构函数为

$$\delta \nu _x \left( {x_0 ,y_0 ,l_x } \right) = \overline {\nu\left( {x_0 + x,y_0 } \right)} _{x \in \left[ {0,l_x } \right]} -\overline {\nu \left( {x_0-x,y_0 } \right)} _{x \in \left[{0,l_x } \right]}\tag{2}$$

湍涡的定义为

\begin{equation}\label{eq1} \overline {\omega \left( {x_0 ,y_0 ,l_x ,l_y }\right)} = \delta \nu _x \left( {x_0 ,y_0 ,l_x } \right) -\delta u_y \left( {x_0 ,y_0 ,l_y } \right)\tag{3}\end{equation}

其中,$\overline {\omega \left( {x_0 ,y_0 ,l_x ,l_y } \right)}$作为二者之差,表示在$\left( {x_0 ,y_0 } \right)$空间位置,流向尺度$l_x$、法向尺度$l_y$的一个展向湍涡.

湍流边界层中存在大量不规则的涡结构,因此可在$x-y$平面检测出大量发卡涡展向涡头,即顺向涡结构.实验检测了流场中顺向涡中心,即负的极值点.根据上式定义的局部涡量计算公式,现定义检测函数为

$$\begin{array}{l} D (x,y) = \\ \left\{ \begin{array}{l} 1,\quad \overline {\omega \left( {x,y} \right)} < 0 \\1,\quad \overline {\omega \left( {x-1,y} \right)} > \overline{\omega \left( {x,y} \right)} ~\& ~\overline {\omega \left( {x +1,y} \right)} > \overline{\omega \left( {x,y} \right)} \\1, \quad \overline {\omega \left( {x,y-1} \right)} > \overline{\omega \left( {x,y} \right)} ~\&~ \overline {\omega \left( {x,y +1}\right)} > \overline{ \omega({x,y} ) }\\ 0,\quad { otherwise} \\\end{array} \right. \\\end{array}\tag{4}$$

其中,$D\left( {x,y} \right)$为顺向涡中心识别函数.一旦涡心被检测到,各物理量在一定尺度范围内的空间相位平均拓扑计算公式为

当$D\left( {x^\ast \left( m \right),y^\ast \left( m\right)} \right) = 1$

\begin{equation}\label{eq2} f\left( {x_{ L} ,y_{ L} } \right) =\frac{1}{N}\sum\limits_{m = 1}^N {f\left( {x^\ast \left( m \right)+ x_{ L} ,y^\ast \left( m \right) + y_{ L} } \right)}\tag{5}\end{equation}

式中$\left( {x^\ast \left( m \right),y^\ast \left( m \right)}\right)$表示第$m$次检测到的展向涡心位置,$x_L \in \left[ { -\dfrac{L_x }{2},\dfrac{L_x }{2}} \right]$,$y_L \in \left[ { -\dfrac{L_y }{2},\dfrac{L_y }{2}} \right]$,$L_{x}$和$L_{y}$分别为流向和法向所截取区域的尺度.为包含涡及涡周围流场的完整信息,本文$L_{x}$,$L_{y}$分别取64,32倍矢量间距,检测出的展向涡个数用$N$表示.

3.1 流向脉动速度

近壁区的速度场由高低速流体交替构成,低速流体远离壁面的过程称为"喷射",而高速流体冲向壁面的过程称为"扫掠",二者合称湍流的猝发过程,猝发过程对雷诺应力有很大的贡献.

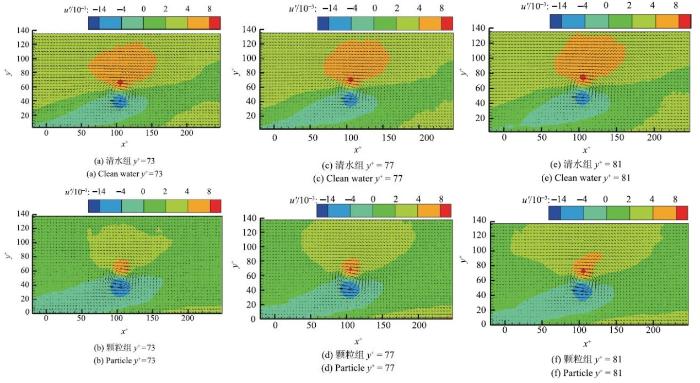
图5为清水对照组和颗粒实验组在$x-y$平面内(法向位置依次是$y^{ +}$=73,$y^{ + }$=77,$y^{ +}$=81)顺向涡周围流向脉动速度空间平均拓扑结构分布.云图很好的展现了展向涡周围流场分布特征：展向涡的下方分布着低速流体($u'<0$的区域),展向涡上方分布着高速流体($u'>0$的区域).从图中脉动速度矢量方向可以

显示原图| 下载原图ZIP| 生成PPT

图5   不同检测中心法向位置展向涡周围流向脉动速度分布云图...

Fig. 5   Contours of the streamwise fluctuating velocity aroundspanwise vortex at different normal position of testing center

明显地看到低速流体正在远离壁面,逐渐向外喷射,而高速流体则对应地下扫,即"扫掠"事件.由图5可见,展向涡周围区域的猝发过程能够有效地传递粒子,且颗粒的流向脉动速度在展向涡上方的高速区域数值整体减小,在下方低速区域数值整体增大.这是由于颗粒本身具有惯性,当近壁颗粒随喷射过程转移时,不会立即加速到高速区域的流向脉动速度;而随扫掠事件转移到低速区域的远壁颗粒,仍然保持较高的动量.

3.2 顺向涡$\alpha $角的对比

图6分别为清水对照组和颗粒实验组在$x-y$平面内(法向位置依次是$y^{ +}=73$,$y^{ + }=77$,$y^{ +}=81$)检测到的展向涡头顺向涡结构[34].从图中看出展向涡头顺向涡的法向尺度随着壁面法向距离的增大而变大,且逐渐发展成圆形,这与Elsinga等[35]的结论一致.从图中还可以看出顺向涡周围的流线绕涡心以顺时针方向旋转,在涡心的上游下方,低速流体与高速流体相遇形成驻点.用过驻点的切线与水平方向夹角表示顺向涡发展的充分性,用$\alpha$角表示. 清水组和颗粒组$\alpha$角均是随着法向距离的增大而增大;在相同法向距离上,颗粒组的$\alpha$角总是小于清水组;这说明颗粒在随流体运动的同时,由于自身

显示原图| 下载原图ZIP| 生成PPT

图6   展向涡周围流线分布图...

Fig. 6   Distributions of streamline around spanwise vortex

惯性,产生的涡和条带在流向上拉伸得更长.进一步分析图6,发现随着壁面距离增大,在顺向涡的左下方逐渐形成一个逆向涡,且距离壁面越远,逆向涡形成的越完整,位置越向左偏离顺向涡的正下方;逆向涡上剪切层与顺向涡下剪切层的相互作用,阻碍了发卡涡附近区域的猝发过程.颗粒组在壁面距离更远的地方才有逆向涡生成,说明流体相形成的逆向涡只有发展到一定程度后才能改变颗粒的运动方式.当$y^{ + }>73$后,观察到颗粒组逆向涡逐渐形成.

3.3 顺向涡数量随法向的变化

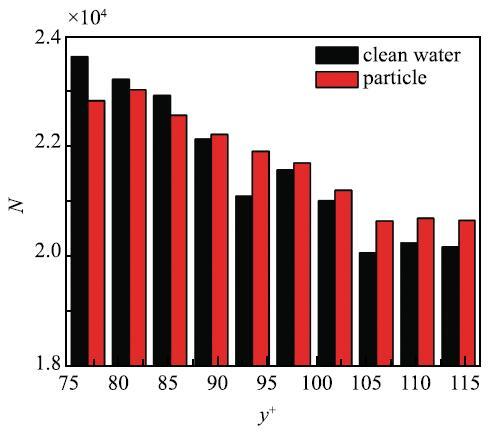
图7是两种工况条件下检测到的顺向涡数量沿法向分布规律,由图可知,顺向涡的数量随法向距离的增加而减小,且逐渐趋于稳定,这与陈启刚等[26]的结论是一致的.

显示原图| 下载原图ZIP| 生成PPT

图7   顺向涡数目沿法向分布规律...

Fig. 7   Distributions of the number of prograde vortex along\\normal-wall positions

4 结论

本文利用粒子图像测速技术分别对清水和颗粒工况下的平板湍流边界层瞬时速度场进行测量,得到了平均速度剖面、湍流度、雷诺应力等统计量,分析了两种工况条件下的发卡涡展向涡头(顺向涡)及逆向涡结构,得到了以下结论：

(1)与清水组相比,颗粒组的无量纲速度均小于清水组,湍流度得到加强并且雷诺切应力在对数律区增大.

(2)展向涡周围的湍流相干结构能够有效地传递粒子.与清水组相比,颗粒组流向脉动速度绝对值大的区域面积更多,颗粒组发卡涡附近的湍流猝发强度更大.

(3)展向涡能够有效地挟带颗粒运动. 通过比较$\alpha$角,颗粒组提取出的涡和条带在流向上拉伸得更长;颗粒组逆向涡的形成较单相流体缓慢.说明流体挟带颗粒需要一定的能量积累,且挟带的颗粒与流体相之间存在滑移.

(4)在两种工况下,顺向涡的数量均随着法向位置的升高而减少,最后逐渐趋于稳定.

The authors have declared that no competing interests exist.

参考文献

[1] 岳湘安. 液-固两相流基础. 北京: 石油工业出版社, 1996

[本文引用: 1]     

(Yue Xian'an, Foundation of Liquid-solid Two-phase Flow. Beijing: Petroleum Industry Press, 1996(in Chinese))

[本文引用: 1]     

[2] 白静, 方红卫, 何国建等.

细颗粒泥沙净冲刷和输移的大涡模拟研究

.力学学报, 2017, 49(1): 65-74

URL     

(Bai Jing, Fang Hongwei, He Guojian, et al.

Numerical simulation of erosion and transport of fine sediments by large eddy simulation

. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(1): 65-74(in Chinese))

URL     

[3] Gore RA, Crowe CT.

Effect of particle size on modulating turbulent intensity

. International Journal of Multiphase Flow, 1989, 15(2): 279-285

[4] 张培杰,林建忠.

非牛顿流体固粒悬浮流的若干问题

. 力学学报, 2017, 49(3): 543-549

URL      [本文引用: 1]     

(Zhang Peijie, Lin Jianzhong.

Review of some researches on suspension of solid particle in non-Newtonian fluid

. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 543-549(in Chinese))

URL      [本文引用: 1]     

[5] 王殿常, 禹明忠, 王兴奎.

明槽水流中颗粒运动特性的试验研究

. 应用基础与工程科学学报, 2000, 8(3): 301-309

[本文引用: 1]     

(Wang Dianchang, Yu Mingzhong, Wang Xingkiu.

Experimental study on particle movement characteristics in water flow in open channel

. Journal of Applied Basic and Engineering Sciences, 2000, 8(3): 301-309(in Chinese))

[本文引用: 1]     

[6] 陈荣前, 聂德明.

椭圆颗粒在剪切流中旋转特性的数值研究

. 力学学报, 2017, 49(2): 257-267

URL     

(Chen Rongqian, Nie Deming.

Numerical study on the rotation of an elliptical particle in shear flow

. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 257-267(in Chinese))

URL     

[7] 刘青泉.

水-沙两相流的激光多普勒分相测量和试验研究

. 泥沙研究, 1998(2): 72-80

(Liu Qingquan.

LDV measurments and experimental study of water and sediment two-phase flow

. Sediment Research, 1998(2): 72-80(in Chinese))

[8] 禹明忠.

PTV技术和颗粒三维运动规律的研究. [博士论文]

. 北京: 清华大学, 2002

(Yu Mingzhong.

Study on PTV technique and 3-D movement of particles. [PhD Thesis]

. Beijing: Tsinghua University, 2002(in Chinese))

[9] 宋晓阳, 及春宁, 许栋.

明渠湍流边界层中颗粒的运动与分布

. 力学学报, 2015, 47(2): 231-241

URL     

(Song Xiaoyang, Ji Chunning, Xu Dong.

Distribution and motion of particles in the turbulent boundary layer of channel flow

. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 231-241(in Chinese))

URL     

[10] 林建忠, 王灿星.

研究两相流中固粒对流体湍动特性影响的新方法

. 工程热物理学报, 1997(4): 497-501

(Lin Jianzhong, Wang Canxing.

A new method of studying the effect of particles on the turbulent properties

. Journal of Engineering Thermophysics, 1997(4): 497-501(in Chinese))

[11] Deshmukh A, Vasava V, Patankar A, et al.

Particle velocity distribution in a flow of gas-solid mixture through a horizontal channel

. Powder Technology, 2016, 298: 119-129

[本文引用: 1]     

[12] Muste M, Patel VC.

Velocity profiles for particles and liquid in open-channel flow with suspended sediment

. Journal of Hydraulic Engineering, 1997, 123(9): 742-751

[本文引用: 2]     

[13] Righetti M, Romano GP.

Particle-fluid interactions in a plane near-wall turbulent flow

. Journal of Fluid Mechanics, 2004, 505(505): 93-121

[本文引用: 1]     

[14] Wang J, Levy EK.

Particle motions and distributions in turbulent boundary layer of air-particle flow past a vertical flat plate

. Experimental Thermal & Fluid Science, 2003, 27(8):845-853

URL      [本文引用: 1]     

[15] Wang J, Levy EK.

Particle behavior in the turbulent boundary layer of a dilute gas-particle flow past a flat plate

. Experimental Thermal & Fluid Science, 2006, 30(5): 473-483

URL      [本文引用: 1]     

[16] 王汉封, 栗晶, 柳朝晖等.

水平槽道内气固两相湍流中颗粒行为的PIV实验研究

. 实验流体力学, 2012, 26(1): 38-44

[本文引用: 1]     

(Wang Hanfeng, Li Jing, Liu ZH, et al.

PIV experimental study of particle behavior in gas-solid two-phase turbulence in a horizontal channel

. Experimental Fluid Mechanics, 2012, 26(3): 38-44(in Chinese))

[本文引用: 1]     

[17] Sumer BM, Deigaard R.

Particle motions near the bottom in turbulent flow in an open channel. Part 2

. Journal of Fluid Mechanics, 2006, 109(109): 311-337

[本文引用: 1]     

[18] Sumer BM, Oguz B.

Particle motions near the bottom in turbulent flow in an open channel

. Journal of Fluid Mechanics, 2006, 86(1): 109-127

[本文引用: 1]     

[19] Li D, Luo K, Fan J.

Particle statistics in a two-way coupled turbulent boundary layer flow over a flat plate

. Powder Technology, 2017, 305: 250-259

[本文引用: 1]     

[20] Vinkovic I, Doppler D, Lelouvetel J, et al.

Direct numerical simulation of particle interaction with ejections in turbulent channel flows

. International Journal of Multiphase Flow, 2011, 37(2): 187-197

URL      [本文引用: 1]     

[21] Marchioli C, Soldati A.

Mechanisms for particle transfer and segregation in a turbulent boundary layer

. Journal of Fluid Mechanics, 2002, 468(468): 283-315

[本文引用: 1]     

[22] 吴文权, 黄远东.

液固两相流中流体旋涡对固体粒子运动影响的数值研究

. 工程热物理学报, 1999, 20(3): 365-369

URL      [本文引用: 1]     

(Wu Wenquan, Huang Yuandong.

A numerical study of the effect of fluid vortex on solid particle motion in liquid-solid two-phase flow

. Journal of Engineering Thermophysics, 1999, 20(3): 365-369(in Chinese))

URL      [本文引用: 1]     

[23] 黄远东, 吴文权.

非定常不稳定液固两相流动中旋涡对颗粒运动影响的数值研究

. 水科学进展, 2002, 13(1): 1-8

URL      [本文引用: 1]     

(Huang Yuandong, Wu Wenquan.

Numerical study of the effect of vortices on particle motion in unsteady and unstable liquid-solid two-phase flow

. Advances in Water Science, 2002, 13(1): 1-8(in Chinese))

URL      [本文引用: 1]     

[24] Dritselis CD, Vlachos NS.

Numerical study of educed coherent structures in the near-wall region of a particle-laden channel flow

. Physics of Fluids, 2008, 20(5): 69

[本文引用: 1]     

[25] Richter DH, Sullivan PP.

Modification of near-wall coherent structures by inertial particles

. Physics of Fluids, 2014, 26(10): 407-432

[本文引用: 1]     

[26] 陈启刚, 李丹勋, 钟强等.

基于模式匹配法的明渠紊流涡结构分析

. 水科学进展, 2013, 24(1): 95-102

URL      [本文引用: 2]     

(Chen Qigang, Li Danxun, Zhong Qiang, et al.

Analysis of turbulent eddy structure in open channel based on pattern matching method

. Progress in Water Science, 2013, 24(1): 95-102(in Chinese))

URL      [本文引用: 2]     

[27] Hambleton WT, Hutchins N, Marusic I.

Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer

. Journal of Fluid Mechanics, 2006, 560(560): 53-64

[本文引用: 1]     

[28] 苏健, 田海平, 姜楠.

逆向涡对超疏水壁面减阻影响的TRPIV实验研究

. 力学学报, 2016, 48(5): 1033-1039

URL      [本文引用: 1]     

(Su Jian, Tian Haiping, Jiang Nan.

TRPIV experimental investigation of the effect of retrograde vortex on drag-reduction mechanism over superhydrophobic surfaces

. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(5): 1033-1039(in Chinese))

URL      [本文引用: 1]     

[29] Kaftori D, Hetsroni G, Banerjee S.

Particle behavior in the turbulent boundary layer. I. Motion, deposition, and entrainment

. Physics of Fluids, 1995, 7(5): 1095-1106

[本文引用: 1]     

[30] Kaftori D, Hetsroni G, Banerjee S.

Particle behavior in the turbulent boundary layer. II. Velocity and distribution profiles

. Physics of Fluids, 1995, 7(5): 1107-1121

[本文引用: 1]     

[31] Elghobashi S.

On predicting particle-laden turbulent flows

. Applied Scientific Research, 1994, 52(4): 309-329

[本文引用: 1]     

[32] 姜楠, 管新蕾, 于培宁.

雷诺应力各向异性涡黏模型的层析TRPIV测量

. 力学学报, 2012, 44(2): 213-221

URL      [本文引用: 1]     

(Jiang Nan, Guan Xinlei, Yu Peining.

Tomography TRPIV measurement of the anisotropic eddy viscosity model of Reynolds stress

. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(2): 213-221(in Chinese))

URL      [本文引用: 1]     

[33] 姜楠, 于培宁, 管新蕾.

湍流边界层相干结构空间拓扑形态的层析TRPIV测量

. 航空动力学报, 2012, 27(5): 1113-1121

[本文引用: 1]     

(Jiang Nan, Yu Peining, Guan Xinlei.

Tomographic TRPIV measurement of spatial topological morphology of coherent structures in turbulent boundary layer

. Journal of Aeronautical Power, 2012, 27(5): 1113-1121(in Chinese))

[本文引用: 1]     

[34] Adrian RJ, Meinhart CD, Tomkins CD.

Vortex organization in the outer region of the turbulent boundary layer

. Journal of Fluid Mechanics, 2000, 422(422): 1-54

[本文引用: 1]     

[35] ElsingA GE, Marusic I.

Lifetimes of flow topology in a turbulent boundary layer

. Physics of Fluids, 2010, 22(1): 457-82

[本文引用: 1]     

/

〈 〉