航天事业的发展关乎国家战略利益与安全,运载火箭、民用空间基础设施、空间宽带互联网、在轨维护与服务系统、载人航天与探月工程、深空探测等已经成为国家创新管理、资源环境保护、提供信息服务以及培育新兴产业不可或缺的重点产品和重大航天工程.围绕经济社会发展和国家安全重大需求,《中国制造2025重点领域技术路线图》选择十大战略产业实现重点突破,力争到2025年处于国际领先地位或国际先进水平,其中重型运载火箭、高定位精度卫星平台、高性能有效载荷、深空探测器以及相关地面设备等航天重大装备是我国由"航天大国"向"航天强国"转变的高端装备.
随着航天重大工程的逐步实施,航天器正朝着超高速、超大尺度、多功能的方向发展,其面临的发射和运行环境也更加恶劣.大型柔性航天器发射过程中的主/被动隔振与减振、在轨运行中航天器及其有效载荷的动态响应、航天器柔性结构的振动及其控制、结构振动与飞行器姿态的混合控制等问题越来越复杂且难于处理;航天器结构的大型化和柔性化(如大阵面天线和大挠性航天器等)也对其地面试验和半实物仿真提出了挑战.
按照研究对象间的相互关系,航天器动力学与控制可分为跨航天器动力学与控制、航天器系统级动力学与振动控制以及航天器部件级动力学与振动控制.黄文虎等[1 ]详细总结了2012年以前国内外在涉及上述三个方面的相关研究方向上取得的成果.本文在对大型柔性航天器涉及的若干动力学与振动控制问题及其研究现状进行详细综述的基础上,提炼出航天动力学与振动控制领域亟待解决的若干基础科学问题,包括多刚柔体系统动力学建模与模型降阶、复杂结构状态空间模型构建方法与能控性、航天器姿态运动与大型柔性结构振动的混合控制律设计等,并指出其未来发展方向.
1 大型柔性航天器涉及的动力学与振动控制问题
航天器动力学与控制问题涉及跨航天器(星箭耦合、空间分离、空间交会、空间对接、绳系卫星等)动力学与控制,航天器系统级动力学与控制(如轨道稳定性、姿态稳定性与控制、姿轨控耦合、航天器结构振动、多刚/柔体系统振动与稳定、航天器隔振与减振、热气弹多场耦合等)以及航天器部件的动力学与控制(部件结构展开、锁定、空间碎片高速撞击、贮箱晃动、贮箱液固耦合、有效载荷隔振等),详细内容见文献[1 ].孟光等[2 ]从航天器发射、在轨运行、地面仿真和试验等方面阐述了近年来航天重大工程中出现的动力学问题,内容涉及耦合动力学、空气动力学、多体动力学、结构动力学以及试验力学等.这里着重阐述大型柔性航天器发射和在轨运行以及天地一体化科学实验装置中存在的振动、振动控制、结构振动与姿轨控耦合等问题,覆盖理论分析、数值仿真以及实验模拟等诸多方面.
1.1 航天器发射过程中的主/被动振动控制
航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ].
以减小航天器发射时所承受的环境载荷为目标,对卫星支架或适配器进行结构设计,或在适配器与星箭界面之间加装隔振平台的方法称为整星隔振.与土木、机械等工程领域中结构或仪器设备的隔振方法一样,整星隔振也分为被动隔振、主动隔振、半主动隔振以及主被动一体化隔振.20世纪90年代初,美国加州空间管理局(CSA)工程公司开始针对小型运载火箭和小卫星开展整星隔振和抗冲性能研究,探索整星隔振的可行性, 并进行整星隔振器的设计和性能分析.
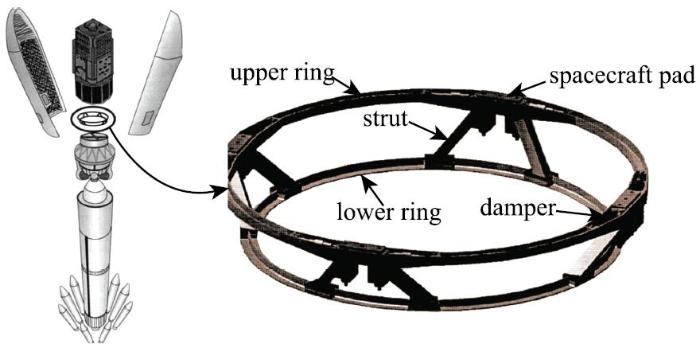
针对中小型运载火箭与3t左右的航天器之间振动隔离问题,美国CSA工程公司和美国空间研究实验室(Air Force Research Laboratory)设计了用以替代原适配器的整星被动隔振系统(见图1 ),试验结果表明其隔振效果良好[6 ].
图1 运载火箭与具备隔振性能的适配器...
Fig. 1 Launch vehicle and adapter with performance of vibration isolation...
CSA 工程公司根据美国轨道科学公司(Orbital Sciences Corporation, OSC) 提供的卫星和火箭有限元模型和发射阶段的环境载荷,设计了由一组单向被动减振器组成的整星隔振系统,以隔离卫星的轴向 振动,并已成功完成数次卫星发射任务. 为了隔离火箭的横向振动,CSA 工程公司尝试采用一组多向Softride Multiflex 减振器组成整星隔振系统(见图2 ),隔离卫星的轴向和横向振动[7 ].
图2 多向减振器整星隔振系统...
Fig. 2 Whole-Satellite vibration isolation system with SoftRide MultiFlex...
传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ]
除了与结构振动密切相关外,主动隔振技术的发展还依赖于微电子、自动控制、信号处理和计算机等技术的发展.近年来,主动隔振技术日趋成熟,其研究对象己经从单自由度系统发展到多自由度系统,由简单线性系统发展到复杂非线性系统;控制系统从SISO发展到MMO;振动方向也由单方向振动发展到多方向耦合振动.2003年美国 Honeywell 公司研制的ELVIS隔振系统,在隔离纵向振动的同时,可以较好地控制航天器摇晃模态响应,但系统复杂尚处于试验研究阶段.Hood 技术公司与华盛顿大学联合研制的六轴主动隔振平台采用立方Stewart平台结构,其6个支腿由电磁音圈作动器并联软弹簧组成,采用柔性铰链与上下平台连接,它在隔离基座振动的同时具有调姿与定位功能[13 ].比利时布鲁塞尔自由大学Marneffe等[14 ]提出用一个电磁感应系统替代机械结构,构造具有Maxwell阻尼单元的张弛隔振器,其隔振效果甚至优于用分散天棚控制器构成的主动隔振器,其隔振平台仍然采用立方Stewart 平台结构.Zhang等[15 ]采用压电堆设计了整星隔振的主被动一体化隔振平台,采用非概率可靠性理论研究了隔振系统的可靠性,数值分析和实验测试的结果表明了隔振的有效性.Yang等[16 ]研究六支腿Stewart平台的解耦条件,将六轴振动控制系统解耦,并设计了分散力反馈控制器,采用数值算例说明了其控制方法的有效性.
哈尔滨工业大学飞行器动力学与振动控制团队设计并改进了电磁作动器的磁路结构,建立了六支腿Stewart电磁隔振平台的动力学方程,通过加权函数的适当选取,针对外部扰动和噪声环境下的星箭系统提出鲁棒控制器设计方案;在理论研究的基础上构建了整星主被动一体化隔振系统(见图3 ),使其在保证隔振性能要求的同时,其频率漂移在合理范围[17 ];建立了带基础激励并考虑参数不确定性的Stewart平台的非线性动力学方程,采用$H_\infty $和$\mu$综合控制算法实现了多由度振动控制,并对平台构型进行了优化设计,仿真结果表明在全频段内振动最大衰减可达30 dB[18 ].Tang等[19 ]进一步利用支腿位移为广义坐标建立了装有Stewart隔振平台的有效载荷分散形式的非线性动力学模型,据此提出了分散控制算法,并证明了系统的稳定性.数值仿真和实验研究的结果表明,在5$\sim$10 Hz范围内,对纵横两个方向的共振峰都有很好的削峰效应.
图3 改进的电磁式促动器和电磁式Stewart隔振平台...
Fig. 3 Improved electromagnetic actuator and electromagnetic Stewart vibration isolation platform...
迄今为止,在整星主被动隔振方面已取得了若干卓有成效的研究成果,但大多数的研究都是将隔振对象视为刚体,仅有少部分涉及柔性卫星的主被动隔振研究.事实上,加装隔振平台势必要引起运载火箭-卫星系统的固有特性的改变,对于大型柔性航天器,虽然其空间结构处于收拢状态,也还存在动力学建模、状态空间模型构建、输出信号测量、连接部件的不确定以及安装空间和附加质量的限制等多方面的困难.
1.2 柔性航天器动力学建模
前已述及,对于大型柔性航天器,由于运载工具有效空间的限制,其空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.空间结构的展开过程涉及若干复杂的、尚未解决的动力学与控制问题,例如怎样描述和分析柔性构件大范围运动与弹性变形的相互耦合、众多运动副带来的间隙和碰撞、结构展开与航天器姿态耦合等.为了确保大型柔性空间结构入轨后能够顺利展开并迅速稳定到平衡状态,必须在其设计阶段进行有效的动力学建模和动响应预测,建立可行的展开控制策略,这方面的研究进展可参考胡海岩等[20 ]关于大型网架式可展开空间结构的非线性动力学与控制的综述.
空间结构展开锁定后的尺度可达30$\sim$50 m量级,但要求具有很高的指向精度和1 mm 量级的反射面均方根误差,必须有效控制结构的变形和振动.研究这类大型柔性空间结构展开锁定后的动力学建模与控制问题不能再采用针对早期航天器特征的若干假设,例如,传统航天器往往具有中心刚体平台,根据任务需要加装较小尺度的有效载荷或太阳翼等,是典型的刚柔耦合系统,中心刚体的质量、转动惯量等在航天器整体中所占的比例具有绝对优势.
随着航天技术的进步和航天任务的多样化,要求新一代航天器具备功能强、寿命长等特点[1 ].为了增强航天器的功能,需要搭载多种有效载荷.而为了控制航天器的质量以降低发射成本,这些有效载荷大都是轻质的超大型柔性结构.例如,国际空间站为了具备空间抓取的功能,安装了长达17m的柔性机械臂(见图4 ).
图4 柔性机械臂...
Fig. 4 Flexible manipulators...
高性能和长寿命必然导致航天器对能源需求的增加,从而要求航天器安装更大面积的太阳翼.比如,国际空间站(见图5 )带有多块太阳翼,其翼展达到88m;由波音公司制造的美国宽带全球卫星通信(WGS)系列卫星安装有超大尺度的太阳翼(见图6 ),所提供的能量保证了卫星具有强大的功能-单星的功率和容量相当于现役DSCS-3的10倍;法国Spacebus-4000C2(图7 )和Spacebus-4000C3(图8 )卫星平台安装有超大型的太阳翼,以确保卫星平台拥有杰出的性能.此外,一些新提出的航天器发展方案,比如空间太阳能电站、太阳帆航天器等,主要由大型柔性结构组成,其尺寸、体积和重量在航天器整体中占绝大比例,航天器的平台部分所占比例非常小,甚至可以忽略不计.
图5 国际空间站...
Fig. 5 International space station...
图6 美国宽带全球通信卫星...
Fig. 6 Wideband Global Satcom of USA...
图7 空客-4000...
Fig. 7 Spacebus-4000...
图8 空客-4000 C3...
Fig. 8 Spacebus-4000 C3...
早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性.
蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程.
采用文献[28 ]的方法建立带两个太阳翼的航天器模型的动力学,所得固有频率除前两阶非零频率外,其高阶频率与设计频率相吻合.方柳等[29 ]建立了考虑动力刚化效应的挠性卫星姿态运动与结构振动的耦合动力学方程,采用假设模态进行离散,得到系统的线性动力学模型和动力刚化模型,数值仿真结果表明动力刚化效应会对柔性结构振动产生较大影响.
哈尔滨工业大学深圳研究生院研究空间机器人在抓取空间目标航天器前后的动力学行为,分别建立了带柔性附件空间机器人和它与带柔性附件航天器的大型组合体的动力学模型(见图9 ),发展了相应的数值求解方法,并与采用Adams软件建立的模型及其求解结果进行比较,验证了求解方法的有效性[30 ].郭其威等[31 ]采用子结构模型缩聚方法,将MATLAB软件与NASTRAN集成,用于快速求解含大型柔性附件航天器的系统模态,数值算例表明了方法的有效性,进一步的仿真结果表明:当中心平台的惯性特性不占优时,约束模态与系统模态的频率相差较大.
图9 空间机器人与目标飞行器组合体示意图$^{[30 ]}$ ...
Fig. 9 The schematic diagram of space robot and target vehicle assembly$^{[30 ]}$ ...
由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解.
1.3 柔性航天器姿态运动-结构振动混合控制研究
柔性航天器是典型的刚柔耦合系统,包括刚体运动(姿态机动或轨道机动)和柔性体弹性振动两种运动.柔性航天器的控制主要研究航天器姿态运动-柔性体弹性振动的混合控制,将航天器假定为刚体而进行的姿态控制,忽略了柔性体振动对星体姿态运动的影响,不能直接应用于柔性航天器.Modi[39 ]对1974年以前关于带挠性附件航天器的姿态动力学与控制的研究成果进行了全面综述,认为这类研究是结构动力学、连续介质力学、卫星动力学以及控制理论等的综合性问题. Modi对当时空间探险失败的教训归结为:在大多数情况下,并非设计者缺乏理论分析和数值计算等设计方法,而是由于他们本身根本还未认清姿态动力学与结构挠性相互作用的机理.Likins[40 ]总结了早期航天器姿态动力学与控制研究方面的经验,并指出:活动部件和结构挠性的存在,使得航天器的姿态控制问题必须由结构、动力学和控制三方面的工程师共同解决.为了在体现超大型空间结构的柔性特性的同时,实现简化计算的目的,尹婷婷等[41 ]提出将其简化为空间刚性杆-弹簧组合结构模型,据此建立系统的动力学方程,为实现超大型空间结构的实时反馈控制提供构建状态空间模型的途径.
早期的航天器姿态控制大都采用传统的控制系统设计方法,具有设计简单的优点,但在设计反馈控制律时没考虑系统中存在的结构变形或参数不确定性因素,只依赖于简化抽象出来的状态方程,主要保证闭环系统的带宽远远低于挠性附件频率以避免控制 / 结构相互作用引起的失稳.对于结构频率低、模态密集的现代柔性航天器,要求姿态运动具有较高的指向精度和稳定度等性能,是一个具有相当难度的控制问题.传统控制系统设计方法通过限制控制系统带宽提供鲁棒性,但要以牺牲系统性能为代价,有时甚至无法保证系统自身运行的稳定性,因此无法用于现代柔性航天器.
鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感.
刘伦和曹登庆[47 ]研究以蜂窝夹芯板作为基板的太阳翼, 将其等效为采用三层的层合板(包含蜂窝芯层和上下面板),基于刚柔耦合模态建立了更加符合工程实际的柔性航天器低维高精度离散动力学模型,结合输入成形和比例微分控制,设计了算法简单且适宜于实时控制的姿态机动和结构振动抑制的协同控制器,以保证航天器姿态机动和结构振动的协同控制.Singh等[48 ]在模型参数完全未知的情况下,设计了一个单轴柔性航天器的自适应输出反馈控制器,该控制器类似于反馈线性化控制器,并引入了一种高增益反馈观测器来补偿模型未建模动态特性.
柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响.
2 大型柔性航天器动力学与控制亟待解决的基础科学问题
综上所述,针对大型柔性航天器涉及的动力学与振动控制问题(包括航天器发射过程中的主/被动振动控制,大型柔性结构动力学建模与振动响应分析,大型柔性航天器的结构振动与姿轨控耦合动力学与混合控制等),在动力学建模和动力学特性分析、控制理论与主动振动控制、姿态控制与结构振动抑制等方面已经获得了大量研究成果.为适应大推力火箭发动机及重型运载火箭技术,长寿命、高可靠、高定位精度先进卫星平台技术,高性能、新型有效载荷技术,载人航天及在轨维护与服务关键技术发展的重大需求,无论是振动响应分析、振动隔离、结构振动的主/被动控制,还是姿轨控与结构振动耦合分析都会涉及到复杂结构动力学建模方法的有效性、计算方法的高效率、控制指令的实时性、控制方案的鲁棒性等动力学与控制的基础理论和基础科学问题.以下几方面的基础科学问题是涉及大型柔性航天器动力学与控制的值得重点开展的研究主题.
2.1 大型柔性结构动力学建模与模型降阶
2.1.1 复杂柔性结构的数值建模与模型降阶
为适应大型柔性航天器的动力学建模与振动控制器设计,需要对多体动力学软件架构进行拓展.随着工业界对动力学仿真性能孜孜不倦的追求,多体系统动力学软件架构已经历过大约四代更新.与软件架构直接相关的计算机硬件已具备越来越强的并行计算功能,特别是近年来GPU硬件的迅猛发展,为构建精度高、速度快的新一代仿真软件架构提供了契机.亟待开展的基础科学问题包括:
(1) 完善大变形柔性部件功能并嵌入多体系统动力学框架.传统的多体系统主要由刚体和小变形柔性体两种部件组成,大变形柔性体的动力学建模方法是最近十几年才蓬勃发展起来的.为求解空间多刚柔体系统的动态响应,需要进一步完善大变形柔性体的计算模型,并解决与传统软件的约束库及控制模块的兼容问题.
(2) 多求解器合作仿真的理论基础和算法实现.传统的多体计算程序都是用一个大型的求解器来计算所有自由度的动力学响应,其积分步长容易受到局部高频模块的控制,导致整体仿真计算量过大.多求解器合作仿真的思路是用多个求解器来合作求解一个大型系统,可以真正做到动力学层面的并行化,解决大规模计算量的问题,提高可求解问题的规模.
(3) 针对大型柔性航天器的动态响应求解进行应用层程序设计、开发和优化.以大型柔性航天器的动态响应求解为主要目标,用内核层的部件模块搭建相关系统的应用程序包并进行优化,形成一个集火箭、卫星、空间飞行器等复杂多体系统动力学建模、仿真与控制方法研究于一体的计算仿真平台.
(4) 复杂柔性结构动力学模型的高效降阶方法.采用数值方法(包括绝对节点坐标法、混合坐标法中的有限元离散建模方式、商业有限元软件等)所建立的动力学模型维数很高,当存在铰链非线性和几何非线性时,该类模型不仅计算量大、耗时长,而且极难描绘非线性动力系统丰富的动力学现象.尽管通过对高维有限元模型降维,可以在一定程度上减少计算量,但降维方法的有效性仍然是难以突破的困难问题,急需发展简便有效的降阶(降维)方法.
2.1.2 组合柔性结构的解析建模与模型降阶
大型柔性航天器主要是由桁架、梁、板、壳等子结构通过连接结构组装而成的复杂空间结构,这类柔性航天器具有低频、密频等复杂动力学特性.对于此类航天器而言,如何得到低维高精度的动力学模型是对整个系统的非线性特性进行准确分析的关键.传统的解析方法是针对单一弹性结构(如索、杆、梁、板、壳等)建立的,对于复杂的多刚柔体系统,目前尚无通用的解析建模方法.在没有其他有效建模方法的情况下,通常采用假设模态法建立系统的近似模型,这样的近似方法在处理复杂的空间柔性结构时往往会带来较大误差.哈尔滨工业大学飞行器动力学与控制研究团队提出了针对平面运动的组合结构的全局模态提取方法,并成功地应用于大跨度斜拉桥[55 ]、微机电系统中的静电梳[56 ]、带柔性附件航天器[57 ]等细长柔性组合体的动力学建模,开展了全局模态提取、密频与重频分析以及模态跃迁、系统动态响应分析等一系列研究.全局模态提取方法能够将系统中各构件和部件的振动用全局模态和统一的模态坐标表示,将其应用于柔性体振动位移离散,可得到低维高精度的非线性动力学模型,适用于系统非线性动力学特性分析和控制器设计.尽管全局模态提取方法具有适宜于非线性振动分析和控制器设计等优点,但目前还仅能处理平面运动的索-梁组合结构的动力学建模问题,要用于处理大型柔性航天器(复杂空间柔性组合结构)的动力学建模与振动响应求解,尚有很多基础科学问题需要攻克,包括:
(1) 索-梁组合结构的全局模态提取与非线性振动研究.以求解三维空间中索-梁组合结构的非线性动态响应为目标,将平面内索-梁组合结构的全局模态提取方法拓展至三维空间,用以建立此类结构的低维的非线性动力学模型.这是一个极具挑战性的研究工作,要实现从二维到三维的跨越,不仅需要克服连接结构力与位移匹配条件的建模困难,而且需要处理每个单一索或梁的空间运动的耦合等问题.
(2) 梁-板-壳组合结构动力学建模与模型降阶.迄今为止,尚未见到关于含有板壳的组合结构全局模态的解析求解的报道,急需开展梁-板组合结构、板-壳组合结构以及梁-板-壳组合结构的全局模态提取与非线性振动方程的离散化与降维方法研究,这是求解梁-板-壳组合结构非线性动态响应的重要基础.
此外,虽然在带铰链连接太阳翼(铰接多梁结构)的柔性航天器的全局模态提取方面获得了成功,但现有用于提取索-梁组合结构全局模态的方法尚不能处理一般的多柔体系统的动力学建模问题.当柔性部件快速转动与大变形相互耦合将导致几何非线性问题,比利时学者Brüls等[58 ]提出了多柔体系统"全局模态参数化(global modal parameterization)"的概念以及用于处理快速转动与小变形耦合问题的方法.基于全局模态参数化的概念,Luo等[59 ]研究了采用POD方法和Galerkin映射对由绝对节点坐标法建立的大型柔性多体系统进行降维处理的方法,极大地改善了计算效率.借助Brüls提出的全局模态参数化参数化概念,将现有处理组合结构的全局模态的方法拓展到多柔体系统是一个值得探索的重要课题.
2.2 复杂结构状态空间模型构建与能控性研究
对于复杂结构振动的主动控制,状态空间模型构建和系统的能控性分析是其中的关键环节.虽然结构振动的主动控制已取得若干令人瞩目的成果,但如何实现对复杂结构的在线振动控制仍然是难以攻克的困难问题,目前关于结构主动振动控制的研究报告大多是针对单一结构(如索、梁、板等)给出的.在航天领域,关于整星的主动隔振已取得若干有价值的成果,但实际研究中通常将卫星做简化处理,如考虑成刚体或者由线性弹簧连接的2自由度系统,鲜见有对于实际卫星状态空间模型的构建以及主动隔振的实验研究成果的报道.关于复杂结构状态空间模型的构建,无论是解析方法、有限元法还是实验方法都是个困难问题,而模型的规模和精度则是控制律设计和振动控制是否有效的关键所在.亟待开展的研究基础科学问题包括:
(1) 构建复杂结构状态空间模型的理论方法.对于由螺栓或其他连接部件连接而成的复杂结构(如卫星通过螺栓与适配器连接,适配器又通过螺栓与运载火箭连接),采用解析的方法建模是非常困难的,通常采用有限元方法建立动力学模型.采用有限元方法不仅要克服连接件带来的建模困难,而且需要对有限元模型进行模型修正和降维处理.
(2) 构建复杂结构状态空间模型的实验方法.由于理论建模困难,人们常用实验数据来重构复杂结构的状态空间模型.对于单频激励或者窄带激励,采用实验方法重构的状态空间模型相对精度较高,但对于宽带激励会有较大误差.急需发展相应的重构方法,以获得适合于较宽频带的状态空间模型.
(3) 复杂结构振动控制系统的能控性和能观性.如果已经获得系统的振动方程,则可将其转换成状态空间模型,其能控性和能观性可以直接由其状态空间模型而得到.在未建模的情况下,研究由其控制器数量和控制器安装位置来判断复杂结构振动控制系统的能控性和能观性.
(4) 基于非线性分析的整星主/被动一体化隔振.对加装NES减振器的柔性卫星实验研究结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.将NES减振技术与主动控制结合有望提出用于整星多维隔振的主被动一体化控制技术,以期达到在空间和附加质量等约束条件下的有效 隔振.
2.3 航天器姿态运动与大型柔性结构振动的混合控制律设计
当柔性结构质量和转动惯量超过航天器刚体平台的占比时,航天器姿态运动与其大型柔性结构振动的耦合效应将变得十分突出.一方面,航天器在轨工作时,大型柔性结构的弹性振动易于发生且很难衰减,并显著影响航天器姿态稳定,从而导致航天器工作性能下降.另一方面,航天器进行太阳翼对日定向或者执行某些突发任务时,需要进行快速的姿态机动,此时航天器姿态运动极易激起超大型柔性结构的弹性振动,并反作用于航天器姿态运动,从而导致姿态机动失效.亟待开展的研究基础科学问题包括:
(1) 大型柔性航天器的高效状态空间模型构建.迄今为止的姿态控制律设计大多是针对利用传统建模方法给出的动力学模型进行的,为了克服模型不确定性带来的问题,即使在存在中心(占优)刚体的情况下,也需要进行鲁棒性分析,且计算费时,不利于对航天器姿态运动-柔性结构振动进行实时控制.开展航天器姿态运动与大型柔性结构振动的混合控制,不仅需要获得系统的全局模态,而且要求在低维的状态空间模型中包含系统的非线性信息,以利于开展其非线性系统的鲁棒控制器设计.
(2) 大型柔性航天器姿态机动与结构振动的鲁棒混合控制.结合大型柔性航天器的结构特征,厘清航天器姿态运动与大型柔性结构振动之间的耦联关系,提出既能满足航天器姿态机动要求,又能抑制其柔性结构复杂振动的有效控制方案,是大型柔性航天器结构振动控制与姿态机动研究中必须解决的科学难题.
(3) 大型柔性航天器姿控执行机构与分布于结构的压电促动器的协调控制.对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大尺度柔性结构的振动抑制任务.随着航天器向大型化和柔性化的方向发展,采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用分布式的压电促动器对柔性结构进行振动抑制是必然趋势.对于大型甚至超大型柔性航天器,其姿控执行机构与分布于结构的压电促动器的协调控制律设计仍然是此类航天器设计制造与安全运行的关键问题和亟待开展的重要研究课题.
3 结语
大推力火箭发动机及重型运载火箭,长寿命、高可靠、高定位精度先进卫星平台,高性能、新型有效载荷,载人航天及在轨维护与服务平台等航天重大装备的发展使得航天器朝着超高速、超大尺度、多功能的方向发展.与此同时,航天器发射过程中的振动与主/被动振动控制、在轨运行中大型柔性航天器动力学建模与动态响应分析、结构振动与飞行器姿态的混合控制等问题也变得越来越复杂且难于处理.针对大型柔性航天器发射过程中的振动与隔振,大型柔性航天器在轨运行状态的动力学建模与振动响应分析,大型柔性结构振动与航天器姿轨控耦合动力学与混合控制等航天重大装备中涉及到的动力学与控制问题,提炼出了多刚柔体系统动力学建模与模型降阶、复杂结构状态空间模型构建与能控性研究、航天器姿态运动与大型柔性结构振动的混合控制律设计等航天动力学与控制领域中亟待解决的若干基础科学问题.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
黄文虎 , 曹登庆 , 韩增尧 . 航天器动力学与控制的研究进展与展望
. 力学进展 , 2012 , 42 (4 ): 367 -394
URL
[本文引用: 4]
(HuangWenhu , Cao Dengqing Han Zengyao Advances and trends in dynamics and control of spacecraft
.Advances in Mechanics 2012 , 42 (4 ): 367 -394 (in Chinese))
URL
[本文引用: 4]
[2]
孟光 ,周徐斌 ,苗军 . 航天重大工程中的力学问题
. 力学进展 ,2016 , 46 (6 ): 467 -322
URL
[本文引用: 2]
(Meng Guang Zhou Xubin Miao Jun Mechanical problems in momentous projects of aerospace engineering
. Advances in Mechanics 2016 , 46 : 467 -322 (in Chinese))
URL
[本文引用: 2]
[3]
马兴瑞 ,于登云 ,韩增尧 等 . 星箭力学环境分析与试验技术研究进展
. 宇航学报 , 2006 , 27 (3 ): 323 -331
URL
[本文引用: 1]
(Ma Xingrui Yu Dengyun Han Zengyao et al .Research evolution on the satellite-rocket mechanical environment analysis and test technology
.Journal of Astronautics 2006 , 27 (3 ): 323 -331 (in Chinese))
URL
[本文引用: 1]
[4]
王庆伟 , 谭述君 , 吴志刚 等 . 大型液体火箭姿控与跷振大回路耦合动力学建模与分析
. 力学学报 , 2015 , 47 (5 ): 789 -798
URL
[本文引用: 1]
(Wang Qingwei Tan Shujun Wu Zhigang et al .Dynamic modeling and analysis of large-loop coupled by attitude control and pogo for large liquid rockets
.Chinese Journal of Theoretical and Applied Mechanics 2015 , 47 (5 ): 789 -798 (in Chinese))
URL
[本文引用: 1]
[5]
张军 , 谌勇 , 骆剑 等 . 整星隔振技术的研究现状和发展
. 航空学报 , 2006 , 26 (2 ): 179 -183
URL
[本文引用: 1]
(Zhang Jun Chen Yong Luo Jian et al .Review of the whole-spacecraft isolation techniques
.Acta Aeronauticaet Astronautica Sinica 2006 , 26 (2 ): 179 -183 (in Chinese))
URL
[本文引用: 1]
[6]
Wilke PS Johnson CD Fosness ER Whole-spacecraft passive launch isolation
.Journal of Spacecraft and Rockets , 1998 , 35 (5 ): 690 -694
[本文引用: 1]
[7]
Wilke PS Johnson CD . Recent launches using the softride wholespacecraft vibration isolation system// Proceedings of the AIAA Space 2001 Conference,
Albuquerque,NM , 2001 : AIAA-2001-4078
[本文引用: 1]
[8]
Liu LK Liang L Zheng GT et al .Dynamic design of octo-strut platform for launch stage whole-spacecraft vibration isolation
.Journal of Spacecraft and Rockets , 2005 , 42 (4 ): 654 -662
[本文引用: 1]
[9]
Wang Z Liu LK Zheng GT Optimal design of octo-strut vibration isolation platform
.Journal of Guidance, Control, and Dynamics , 2006 , 29 (3 ): 749 -753
[本文引用: 1]
[10]
Zhang YW Fang B Chen Y Vibration isolation performance evaluation of the discrete whole-spacecraft vibration isolation platform for flexible spacecraft
.Meccanica , 2012 , 47 : 1185 -1195
URL
[本文引用: 1]
[11]
Yang K Zhang YW Ding H et al .Nonlinear energy sink for wholespacecraft vibration reduction
.Journal of Vibration and Acoustics , 2017 , 139 : 021011
[本文引用: 1]
[12]
陆泽琦 ,陈立群 . 非线性被动隔振的若干进展
. 力学学报 , 2017 , 49 (3 ): 550 -564
URL
[本文引用: 1]
(Lu Zeqi Chen Liqun Some recent progresses in nonlinear passive isolations of vibrations
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (3 ): 550 -564 (in Chinese))
URL
[本文引用: 1]
[13]
Thayer D Campbell M Vagners J Six-axis vibration isolation system using soft actuators and multiple sensors
.Journal of Spacecraft and Rockets , 2002 , 39 (2 ): 206 -212
[本文引用: 1]
[14]
Marne_e B Avraam M Deraemaeker A et al . Vibration isolation of precision payloads: A six-axis electromagnetic relaxation isolator
.Journal of Guidance, Control, and Dynamics , 2009 , 32 (2 ): 395 -401
[本文引用: 1]
[15]
Zhang Y Zang J Fang B et al .Dynamic characteristics of integrated active and passive whole-spacecraft vibration isolation platform based on non-probabilistic reliability
.Transactions of the Japan Society for Aeronautical and Space Sciences , 2014 , 57 (5 ): 263 -271
URL
[本文引用: 1]
[16]
Yang X Wu H Li Y et al .Dynamic isotropic design and decentralized active control of a six-axis vibration isolator via Stewart plat form
.Mechanism and Machine Theory , 2017 , 117 : 244 -252
[本文引用: 1]
[17]
Chi W Cao D Wang D et al .Design and experimental study of a VCM-based Stewart parallel mechanism used for active vibration isolation
.Energies , 2015 , 8 : 8001 -8019
[本文引用: 1]
[18]
Wu Y Yu K Jiao J et al .Dynamic isotropy design and analysis of a six-DOF active micro-vibration isolation manipulator on satellites
.Robotics and Computer-Integrated Manufacturing , 2018 , 49 : 408 -425
[本文引用: 1]
[19]
Tang J Cao D Yu T Decentralized vibration control of a VCM-Based Stewart parallel mechanism: simulation and experiments
.Journal of Mechanical Engineering Science , 2018 . DOI: 10.1177/0954406218756941
URL
[本文引用: 1]
[20]
胡海岩 ,田强 ,张伟 等 . 大型网架式可展开空间结构的非线性动力学与控制
. 力学进展 , 2013 , 43 (4 ): 390 -414
URL
[本文引用: 1]
(Hu Haiyan Tian Qiang Zhang Wei et al .Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes
.Advances in Mechanics 2013 , 43 (4 ): 390 -414 (in Chinese))
URL
[本文引用: 1]
[21]
曲广吉 . 航天器动力学技术的发展和挑战
. 强度与环境 , 2003 , 30 (4 ): 1 -6
URL
[本文引用: 1]
(Qu Guangji Development and challenge of spacecraft dynamics technology
.Structure and Environment Engineering 2003 , 30 (4 ): 1 -6 (in Chinese))
URL
[本文引用: 1]
[22]
曲广吉 . 复合柔性结构航天器动力学建模研究
. 中国工程科学 , 1999 , 1 (2 ): 52 -56
URL
[本文引用: 1]
(Qu Guangji Dynamics modeling of spacecraft with composite flexible structures
.Engineering Science 1999 , 1 (2 ): 52 -56 (in Chinese))
URL
[本文引用: 1]
[23]
缪炳祺 ,曲广吉 ,夏邃勤 等 . 关于柔性航天器动力学模型降阶问题
. 中国工程科学 , 2001 , 3 (11 ): 60 -64
URL
[本文引用: 1]
(Liao Bingqi Qu Guangji Xia Suiqin et al .On the order reduction of dynamics models of flexible spacecraft
.Engineering Science 2001 , 3 (11 ): 60 -64 (in Chinese))
URL
[本文引用: 1]
[24]
Mettler E Quadrelli MB Multibody dynamics modeling of segmented booms of the mars express spacecraft
.Journal of Spacecraft and Rockets , 2005 , 42 (3 ): 523 -529
[本文引用: 1]
[25]
蒋建平 ,李东旭 . 带太阳帆板航天器刚柔耦合动力学研究
. 航空学报 , 2006 , 27 (3 ): 418 -422
URL
[本文引用: 1]
(Jiang Jianping Li Dongxu Research on rigid-flexible coupling dynamics of spacecraft with solar panel
.Acta Aeronauticaet Astronautica Sinica 2006 , 27 (3 ): 418 -422 (in Chinese))
URL
[本文引用: 1]
[26]
张越 , 赵阳 , 谭春林 等 . ANCF 索梁单元应变耦合问题与模型解耦
. 力学学报 , 2016 , 48 (6 ): 1406 -1415
URL
[本文引用: 1]
(Zhang Yue Zhao Yang Tan Chunlin et al .The strain coupling problem and model decoupling of ANCF cable/beam element
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (6 ): 1406 -1415 (in Chinese))
URL
[本文引用: 1]
[27]
章孝顺 , 章定国 , 洪嘉振 . 考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
. 力学学报 , 2016 , 48 (3 ): 692 -701
URL
[本文引用: 1]
(Zhang Xiaoshun Zhang Dingguo Hong Jiazhen Rigid-flexible coupling dynamic modeling and simulation with the longitudinal deformation induced curvature e_ect for a rotating flexible beam under large deformation
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (3 ): 692 -701 (in Chinese))
URL
[本文引用: 1]
[28]
和兴锁 ,邓峰岩 ,张烈霞 等 . 大型空间刚柔耦合组合体的动力学建模
. 机械科学与技术 , 2004 , 23 (5 ): 543 -545
URL
[本文引用: 2]
(He Xingsuo Deng Fengyan Zhang Liexia et al .Dynamics modeling of large coupled rigid flexible space platform system
.Mechanical Science and Technology 2004 , 23 (5 ): 543 -545 (in Chinese))
URL
[本文引用: 2]
[29]
方柳 ,刘玉亮 ,赵桂平 . 考虑动力刚化的挠性航天器的动力学建模与分析
. 兵器装备工程学报 , 2017 , 38 (9 ): 67 -72
URL
[本文引用: 1]
(Fang Niu Liu Yuliang Zhao Guiping Dynamic modeling and analysis for flexible spacecraft with dynamic sti_ening
.Journal of Ordnance Equipment Engineering 2017 , 38 (9 ): 67 -72 (in Chinese))
URL
[本文引用: 1]
[30]
Xu W Meng D Chen Y et al .Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft
.Multibody System Dynamics , 2014 , 32 (3 ): 357 -401
URL
[本文引用: 3]
[31]
郭其威 ,吴松 ,刘芳 等 . 航天器柔性附件对整器固有振动特性影响因素及规律分析
. 振动与冲击 , 2016 , 35 (6 ): 187 -191
URL
[本文引用: 1]
(Guo Qiwei Wu Song Liu Fang et al .The e_ect and change rule of spacecraft flexible annex on system natural vibration characteristics
.Journal of Vibration and Shock 2016 , 35 (6 ): 187 -191 (in Chinese))
URL
[本文引用: 1]
[32]
胡海岩 ,田强 ,张伟 等 . 大型网架式可展开空间结构的非线性动力学与控制
. 力学进展 , 2013 , 43 (4 ): 390 -414
URL
[本文引用: 1]
(Hu Haiyan Tian Qiang Zhang Wei et al .Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes
.Advances in Mechanics 2013 , 43 (4 ): 390 -414 (in Chinese))
URL
[本文引用: 1]
[33]
王巍 ,于登云 ,马兴瑞 . 航天器铰接结构非线性动力学特性研究进展
. 力学进展 , 2006 , 36 (2 ): 233 -238
URL
(Wang Wei Yu Dengyun Ma Xingrui Advances and trends of non-linear dynamics of space joint-dominated structure
.Advances in Mechnics 2006 , 36 (2 ): 233 -238 (in Chinese))
URL
[34]
曹登庆 , 初世明 , 李郑发 等 . 空间可展机构非光滑力学模型和动力学研究
. 力学学报 , 2013 , 45 (1 ): 3 -15
URL
[本文引用: 1]
(Cao Dengqing Chu Shiming Li Zhengfa et al .Study on the non-smooth mechanical models and dynamics for space deployable mechanisms
.Chinese Journal of Theoretical and Applied Mechanics 2013 , 45 (1 ): 3 -15 (in Chinese))
URL
[本文引用: 1]
[35]
白争锋 ,赵阳 ,田浩 . 含铰间间隙太阳帆板展开动力学仿真
. 哈尔滨工业大学学报 , 2009 , 41 (3 ): 11 -14
URL
[本文引用: 1]
(Bai Zhengfeng Zhao Yang Tian Hao Dynamics and simulation of deployment for solar panels with hinge clearance
.Journal of Harbin Institute of Technology 2009 , 41 (3 ): 11 -14 (in Chinese))
URL
[本文引用: 1]
[36]
阎绍泽 , 申永胜 , 陈洪彬 . 考虑杆件柔性和铰间隙的可展结构动力学数值模拟
. 清华大学学报(自然科学版) , 2003 , 43 (2 ): 145 -148
URL
[本文引用: 1]
(Yan Shaoze Shen Yongsheng Chen Hongbin Dynamic performance of deployable structures with flexible members and clearance connections
.J Tsinghua Univ (Sci & Tech )2003 , 43 (2 ): 145 -148 (in Chinese))
URL
[本文引用: 1]
[37]
尉飞 ,郑钢铁 . 具有非线性连接的航天器非线性振动分析
. 振动工程学报 , 2009 , 22 (4 ): 329 -334
URL
[本文引用: 1]
(Wei Fei Zheng Gangtie Nonlinear dynamics of spacecraft with nonlinear joints
.Journal of Vibration Engineering 2009 , 22 (4 ): 329 -334 (in Chinese))
URL
[本文引用: 1]
[38]
刘福寿 , 金栋平 . 环形桁架结构径向振动的等效圆环模型
. 力学学报 , 2016 , 48 (5 ): 1184 -1191
URL
[本文引用: 1]
(Liu Fushou Jin Dongping Equivalent circular ring model for the radial vibration analysis of hoop truss structures
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (5 ): 1184 -1191 (in Chinese))
URL
[本文引用: 1]
[39]
Modi VJ Attitude dynamics of satellites with flexible appendagesa brief review
.Journal of Spacecraft and Rockets , 1974 , 11 (11 ): 743 -751
[本文引用: 1]
[40]
Likins P Spacecraft attitude dynamics and control-a personal perspective on early developments
.Journal of Guidance, Control, and Dynamics , 1986 , 9 (2 ): 129 -134
[本文引用: 1]
[41]
尹婷婷 , 邓子辰 , 胡伟鹏 等 . 空间刚性杆-弹簧组合结构轨道、姿态耦合动力学分析
. 力学学报 , 2018 , 50 (1 ): 87 -98
URL
[本文引用: 1]
(Yin Tingting Deng Zichen Hu Weipeng et al .Dynamic modelling and simulation of orbit and attitude coupling problems for structure combined of spatial rigid rods and spring
.Chinese Journal of Theoretical and Applied Mechanics 2018 , 50 (1 ): 87 -98 (in Chinese))
URL
[本文引用: 1]
[42]
Cai GP Hong JZ Yang SX Model study and active control of a rotating flexible cantilever beam
.International Journal of Mechanical Sciences , 2004 , 46 (6 ): 871 -889
URL
[本文引用: 1]
[43]
Cai GP LimCW. Active control of a flexible hub-beam system using optimal tracking control method
.International Journal of Mechanical Sciences , 2006 , 48 (10 ): 1150 -1162
[本文引用: 1]
[44]
Banerjee AK Pedreiro N Singhose WE Vibration reduction for flexible spacecraft following momentum dumping with/without slewing
.Journal of Guidance, Control, and Dynamics , 2001 , 24 (3 ): 417 -427
[本文引用: 1]
[45]
Hu QL Shi P Gao H Adaptive variable structure and commanding shaped vibration control of flexible spacecraft
.Journal of Guidance, Control, and Dynamics , 2007 , 30 (3 ): 804 -815
[本文引用: 1]
[46]
胡军 ,张国琪 ,张志方 等 . 可抑制航天器轨控过程中太阳翼大幅振动的新型轨控方法研究
. 载人航天 , 2011 (2 ): 15 -23
URL
[本文引用: 1]
(Hu Jun Zhang Guoqi Zhang Zhifang et al .New orbit control method to reduce solar panel vibration during orbit maneuvering.Manned Spaceflight , 2011 (2 ): 15 -23 (in Chinese))
URL
[本文引用: 1]
[47]
Lun L Cao DQ Dynamic modeling for a flexible spacecraft with solar arrays composed of honeycomb panels and its proportional- derivative control with input shaper
.Journal of Dynamic Systems, Measurement, and Control-Transactions of the ASME , 2016 , 138 : 081008
[本文引用: 1]
[48]
Singh SN Zhang R Adaptive output feedback control of spacecraft with flexible appendages by modeling error compensation
.Acta Astronautica , 2004 , 54 (4 ): 229 -243
URL
[本文引用: 1]
[49]
Azadi M Fazelzadeh S Eghtesad M et al .Vibration suppression and adaptive-robust control of a smart flexible satellite with three axes maneuvering
.Acta Astronautica , 2011 , 69 (5 ): 307 -322
[本文引用: 1]
[50]
50 Hu QL Sliding mode maneuvering control and active vibration damping of three-axis stabilized flexible spacecraft with actuator dynamics
.Nonlinear Dynamics , 2008 , 52 : 227 -248
URL
[本文引用: 1]
[51]
Hu Q Cao J Zhang Y Robust backstepping sliding mode attitude tracking and vibration damping of flexible spacecraft with actuator dynamics
.Journal of Aerospace Engineering , 2009 , 22 (2 ): 139 -152
[本文引用: 1]
[52]
da Fonseca IM Rade DM Goes LCS Attitude and vibration control of a satellite containing flexible solar arrays by using reaction wheels, and piezoelectric transducers as sensors and actuators
.Acta Astronautica , 2017 , 139 : 357 -366
[本文引用: 1]
[53]
陶佳伟 , 张涛 . 控制受限的挠性航天器姿态机动控制和振动抑制
. 电机与控制学报 ,2018 , 22 (3 ): 105 -113
URL
[本文引用: 1]
(Tao Jiawei Zhang Tao Robust adaptive attitude maneuvering and vibration reducing control of flexible spacecraft with input saturation
.Electric Machines and Control 2018 , 22 (3 ): 105 -113 (in Chinese))
URL
[本文引用: 1]
[54]
袁国平 ,史小平 ,李隆 . 航天器姿态机动的自适应鲁棒控制及主动振动抑制
. 振动与冲击 , 2013 , 32 (12 ): 110 -115
URL
[本文引用: 1]
(Yuan Guoping Shi Xiaoping Li Long Adaptive robust attitude maneuver control of a flexible spacecraft with active vibration suppression
.Journal of Vibration and Shock 2013 , 32 (12 ): 110 -115 (in Chinese))
URL
[本文引用: 1]
[55]
Cao DQ Song MT Zhu WD et al .Modeling and analysis of the inplane vibration of a complex cable-stayed bridge
.Journal of Sound and Vibration , 2012 , 331 (26 ),5685 -5714
URL
[本文引用: 1]
[56]
Song MT Cao DQ Zhu WD Dynamic analysis of a micro-resonator driven by electrostatic combs
.Communications in Nonlinear Science and Numerical Simulation , 2011 , 16 (8 ): 3425 -3442
URL
[本文引用: 1]
[57]
Wei J Cao D Wang L et al .Dynamic modeling and simulation of flexible spacecraft with flexible joints
.International Journal of Mechanical Sciences , 2017 ,130 : 558 -570
[本文引用: 1]
[58]
Brǘls O Duysinx P Golinval JC The global modal parameterization for non-linear model-order reduction in flexible multibody dynamics
.International Journal for Numerical Methods in Engineering , 2007 , 69 (5 ): 948 -977
[本文引用: 1]
[59]
Luo K Hu H Liu C et al .Model order reduction for dynamic simulation of a flexible multibody system via absolute nodal coordinate formulation
.Computer Methods in Applied Mechanics and Engineering , 2017 , 324 : 573 -594 .
[本文引用: 1]
航天器动力学与控制的研究进展与展望
4
2012
... 按照研究对象间的相互关系,航天器动力学与控制可分为跨航天器动力学与控制、航天器系统级动力学与振动控制以及航天器部件级动力学与振动控制.黄文虎等[1 ]详细总结了2012年以前国内外在涉及上述三个方面的相关研究方向上取得的成果.本文在对大型柔性航天器涉及的若干动力学与振动控制问题及其研究现状进行详细综述的基础上,提炼出航天动力学与振动控制领域亟待解决的若干基础科学问题,包括多刚柔体系统动力学建模与模型降阶、复杂结构状态空间模型构建方法与能控性、航天器姿态运动与大型柔性结构振动的混合控制律设计等,并指出其未来发展方向. ...
... 航天器动力学与控制问题涉及跨航天器(星箭耦合、空间分离、空间交会、空间对接、绳系卫星等)动力学与控制,航天器系统级动力学与控制(如轨道稳定性、姿态稳定性与控制、姿轨控耦合、航天器结构振动、多刚/柔体系统振动与稳定、航天器隔振与减振、热气弹多场耦合等)以及航天器部件的动力学与控制(部件结构展开、锁定、空间碎片高速撞击、贮箱晃动、贮箱液固耦合、有效载荷隔振等),详细内容见文献[1 ].孟光等[2 ]从航天器发射、在轨运行、地面仿真和试验等方面阐述了近年来航天重大工程中出现的动力学问题,内容涉及耦合动力学、空气动力学、多体动力学、结构动力学以及试验力学等.这里着重阐述大型柔性航天器发射和在轨运行以及天地一体化科学实验装置中存在的振动、振动控制、结构振动与姿轨控耦合等问题,覆盖理论分析、数值仿真以及实验模拟等诸多方面. ...
... 随着航天技术的进步和航天任务的多样化,要求新一代航天器具备功能强、寿命长等特点[1 ].为了增强航天器的功能,需要搭载多种有效载荷.而为了控制航天器的质量以降低发射成本,这些有效载荷大都是轻质的超大型柔性结构.例如,国际空间站为了具备空间抓取的功能,安装了长达17m的柔性机械臂(见图4 ). ...
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
航天器动力学与控制的研究进展与展望
4
2012
... 按照研究对象间的相互关系,航天器动力学与控制可分为跨航天器动力学与控制、航天器系统级动力学与振动控制以及航天器部件级动力学与振动控制.黄文虎等[1 ]详细总结了2012年以前国内外在涉及上述三个方面的相关研究方向上取得的成果.本文在对大型柔性航天器涉及的若干动力学与振动控制问题及其研究现状进行详细综述的基础上,提炼出航天动力学与振动控制领域亟待解决的若干基础科学问题,包括多刚柔体系统动力学建模与模型降阶、复杂结构状态空间模型构建方法与能控性、航天器姿态运动与大型柔性结构振动的混合控制律设计等,并指出其未来发展方向. ...
... 航天器动力学与控制问题涉及跨航天器(星箭耦合、空间分离、空间交会、空间对接、绳系卫星等)动力学与控制,航天器系统级动力学与控制(如轨道稳定性、姿态稳定性与控制、姿轨控耦合、航天器结构振动、多刚/柔体系统振动与稳定、航天器隔振与减振、热气弹多场耦合等)以及航天器部件的动力学与控制(部件结构展开、锁定、空间碎片高速撞击、贮箱晃动、贮箱液固耦合、有效载荷隔振等),详细内容见文献[1 ].孟光等[2 ]从航天器发射、在轨运行、地面仿真和试验等方面阐述了近年来航天重大工程中出现的动力学问题,内容涉及耦合动力学、空气动力学、多体动力学、结构动力学以及试验力学等.这里着重阐述大型柔性航天器发射和在轨运行以及天地一体化科学实验装置中存在的振动、振动控制、结构振动与姿轨控耦合等问题,覆盖理论分析、数值仿真以及实验模拟等诸多方面. ...
... 随着航天技术的进步和航天任务的多样化,要求新一代航天器具备功能强、寿命长等特点[1 ].为了增强航天器的功能,需要搭载多种有效载荷.而为了控制航天器的质量以降低发射成本,这些有效载荷大都是轻质的超大型柔性结构.例如,国际空间站为了具备空间抓取的功能,安装了长达17m的柔性机械臂(见图4 ). ...
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
航天重大工程中的力学问题
2
2016
... 航天器动力学与控制问题涉及跨航天器(星箭耦合、空间分离、空间交会、空间对接、绳系卫星等)动力学与控制,航天器系统级动力学与控制(如轨道稳定性、姿态稳定性与控制、姿轨控耦合、航天器结构振动、多刚/柔体系统振动与稳定、航天器隔振与减振、热气弹多场耦合等)以及航天器部件的动力学与控制(部件结构展开、锁定、空间碎片高速撞击、贮箱晃动、贮箱液固耦合、有效载荷隔振等),详细内容见文献[1 ].孟光等[2 ]从航天器发射、在轨运行、地面仿真和试验等方面阐述了近年来航天重大工程中出现的动力学问题,内容涉及耦合动力学、空气动力学、多体动力学、结构动力学以及试验力学等.这里着重阐述大型柔性航天器发射和在轨运行以及天地一体化科学实验装置中存在的振动、振动控制、结构振动与姿轨控耦合等问题,覆盖理论分析、数值仿真以及实验模拟等诸多方面. ...
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
航天重大工程中的力学问题
2
2016
... 航天器动力学与控制问题涉及跨航天器(星箭耦合、空间分离、空间交会、空间对接、绳系卫星等)动力学与控制,航天器系统级动力学与控制(如轨道稳定性、姿态稳定性与控制、姿轨控耦合、航天器结构振动、多刚/柔体系统振动与稳定、航天器隔振与减振、热气弹多场耦合等)以及航天器部件的动力学与控制(部件结构展开、锁定、空间碎片高速撞击、贮箱晃动、贮箱液固耦合、有效载荷隔振等),详细内容见文献[1 ].孟光等[2 ]从航天器发射、在轨运行、地面仿真和试验等方面阐述了近年来航天重大工程中出现的动力学问题,内容涉及耦合动力学、空气动力学、多体动力学、结构动力学以及试验力学等.这里着重阐述大型柔性航天器发射和在轨运行以及天地一体化科学实验装置中存在的振动、振动控制、结构振动与姿轨控耦合等问题,覆盖理论分析、数值仿真以及实验模拟等诸多方面. ...
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
星箭力学环境分析与试验技术研究进展
1
2006
... 航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ]. ...
星箭力学环境分析与试验技术研究进展
1
2006
... 航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ]. ...
大型液体火箭姿控与跷振大回路耦合动力学建模与分析
1
2015
... 航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ]. ...
大型液体火箭姿控与跷振大回路耦合动力学建模与分析
1
2015
... 航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ]. ...
整星隔振技术的研究现状和发展
1
2006
... 航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ]. ...
整星隔振技术的研究现状和发展
1
2006
... 航天器在发射过程中需承受极为复杂和严酷的动力学环境[3 ],包括由运载火箭发动机推力产生的近似稳态的加速度环境、由发动机工作和火箭跷振效应产生的低频振动环境、由发动机点火、关机和级间分离产生的瞬态振动环境、由火工装置或其他分离装置产生的爆炸冲击环境以及整流罩外气动噪声通过结构传递的高频随机振动环境等.包括发动机振动和火箭跷振在内的振动载荷通过运载火箭与航天器之间的连接部件(适配器或卫星支架)传递到航天器,从而引发航天器整体以及各部件结构的振动[4 ].由于运载工具有效空间的限制,柔性航天器的空间结构(如太阳能帆板、雷达天线阵列、空间桁架等)不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.尽管大型柔性航天器在发射过程中,其空间结构大都以折叠状态固定,但其为数众多的连接结构也使其对发射的动力学环境提出了更高的要求.改善航天器的振动环境的一个有效的途径是对发射过程中的航天器(整星)进行隔振,它利用被动、主动或主/被动一体化的隔振平台来改造或替代原有的星箭连接适配器,从而达到降低作用于航天器振动载荷的目的.为了对发射阶段的大型柔性航天器进行有效隔振,提高其发射的安全性和可靠性,整星的主/被动振动控制近年来引起了从事航天器动力学与控制的科学家与工程师们的极大重视[5 ]. ...
Whole-spacecraft passive launch isolation
1
1998
... 针对中小型运载火箭与3t左右的航天器之间振动隔离问题,美国CSA工程公司和美国空间研究实验室(Air Force Research Laboratory)设计了用以替代原适配器的整星被动隔振系统(见图1 ),试验结果表明其隔振效果良好[6 ]. ...
Recent launches using the softride wholespacecraft vibration isolation system// Proceedings of the AIAA Space 2001 Conference,
1
2001
... CSA 工程公司根据美国轨道科学公司(Orbital Sciences Corporation, OSC) 提供的卫星和火箭有限元模型和发射阶段的环境载荷,设计了由一组单向被动减振器组成的整星隔振系统,以隔离卫星的轴向 振动,并已成功完成数次卫星发射任务. 为了隔离火箭的横向振动,CSA 工程公司尝试采用一组多向Softride Multiflex 减振器组成整星隔振系统(见图2 ),隔离卫星的轴向和横向振动[7 ]. ...
Dynamic design of octo-strut platform for launch stage whole-spacecraft vibration isolation
1
2005
... 传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ] ...
Optimal design of octo-strut vibration isolation platform
1
2006
... 传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ] ...
Vibration isolation performance evaluation of the discrete whole-spacecraft vibration isolation platform for flexible spacecraft
1
2012
... 传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ] ...
Nonlinear energy sink for wholespacecraft vibration reduction
1
2017
... 传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ] ...
非线性被动隔振的若干进展
1
2017
... 传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ] ...
非线性被动隔振的若干进展
1
2017
... 传统的单向隔振方式无法直接应用于航天器,必须寻求多向隔振方法以隔离由运载火箭传递的纵向和横向的振动.哈尔滨工业大学飞行器动力学与振动控制团队设计出八支腿被动隔振平台,其每个支腿由线性弹簧和阻尼器构成,建立了系统的非线性动力学模型,仿真结果表明八支腿被动隔振平台可以有效地实现振动隔离[8 ];对八支腿隔振平台进行参数分析,并采用遗传算法对隔振平台的隔振效率进行优化,应用柔性卫星隔振的动力学仿真结果表明,通过优化设计,隔振平台可具有优良的隔振效果[9 ];设计出一种圆盒式隔振器,用以代替原适配器,利用纤维增强材料的各向异性很好地提高横纵刚度比,特殊的结构设置凸显了阻尼层的作用,很好地抑制了卫星的振动,改善了卫星的发射环境[10 ].Yang等[11 ]借用非线性能量阱(NES)的设计思想,提出了用于柔性卫星纵向振动抑制的NES减振器,对加装NES减振器的柔性卫星缩比模型采用有限元仿真和实验研究的结果表明,NES减振器可以有效降低基础激励到柔性卫星的振动传递率.有关非线性被动隔振研究的最新进展及其在整星振动抑制方面的研究成果可参见陆泽琦和陈立群的综述[12 ] ...
Six-axis vibration isolation system using soft actuators and multiple sensors
1
2002
... 除了与结构振动密切相关外,主动隔振技术的发展还依赖于微电子、自动控制、信号处理和计算机等技术的发展.近年来,主动隔振技术日趋成熟,其研究对象己经从单自由度系统发展到多自由度系统,由简单线性系统发展到复杂非线性系统;控制系统从SISO发展到MMO;振动方向也由单方向振动发展到多方向耦合振动.2003年美国 Honeywell 公司研制的ELVIS隔振系统,在隔离纵向振动的同时,可以较好地控制航天器摇晃模态响应,但系统复杂尚处于试验研究阶段.Hood 技术公司与华盛顿大学联合研制的六轴主动隔振平台采用立方Stewart平台结构,其6个支腿由电磁音圈作动器并联软弹簧组成,采用柔性铰链与上下平台连接,它在隔离基座振动的同时具有调姿与定位功能[13 ].比利时布鲁塞尔自由大学Marneffe等[14 ]提出用一个电磁感应系统替代机械结构,构造具有Maxwell阻尼单元的张弛隔振器,其隔振效果甚至优于用分散天棚控制器构成的主动隔振器,其隔振平台仍然采用立方Stewart 平台结构.Zhang等[15 ]采用压电堆设计了整星隔振的主被动一体化隔振平台,采用非概率可靠性理论研究了隔振系统的可靠性,数值分析和实验测试的结果表明了隔振的有效性.Yang等[16 ]研究六支腿Stewart平台的解耦条件,将六轴振动控制系统解耦,并设计了分散力反馈控制器,采用数值算例说明了其控制方法的有效性. ...
Vibration isolation of precision payloads: A six-axis electromagnetic relaxation isolator
1
2009
... 除了与结构振动密切相关外,主动隔振技术的发展还依赖于微电子、自动控制、信号处理和计算机等技术的发展.近年来,主动隔振技术日趋成熟,其研究对象己经从单自由度系统发展到多自由度系统,由简单线性系统发展到复杂非线性系统;控制系统从SISO发展到MMO;振动方向也由单方向振动发展到多方向耦合振动.2003年美国 Honeywell 公司研制的ELVIS隔振系统,在隔离纵向振动的同时,可以较好地控制航天器摇晃模态响应,但系统复杂尚处于试验研究阶段.Hood 技术公司与华盛顿大学联合研制的六轴主动隔振平台采用立方Stewart平台结构,其6个支腿由电磁音圈作动器并联软弹簧组成,采用柔性铰链与上下平台连接,它在隔离基座振动的同时具有调姿与定位功能[13 ].比利时布鲁塞尔自由大学Marneffe等[14 ]提出用一个电磁感应系统替代机械结构,构造具有Maxwell阻尼单元的张弛隔振器,其隔振效果甚至优于用分散天棚控制器构成的主动隔振器,其隔振平台仍然采用立方Stewart 平台结构.Zhang等[15 ]采用压电堆设计了整星隔振的主被动一体化隔振平台,采用非概率可靠性理论研究了隔振系统的可靠性,数值分析和实验测试的结果表明了隔振的有效性.Yang等[16 ]研究六支腿Stewart平台的解耦条件,将六轴振动控制系统解耦,并设计了分散力反馈控制器,采用数值算例说明了其控制方法的有效性. ...
Dynamic characteristics of integrated active and passive whole-spacecraft vibration isolation platform based on non-probabilistic reliability
1
2014
... 除了与结构振动密切相关外,主动隔振技术的发展还依赖于微电子、自动控制、信号处理和计算机等技术的发展.近年来,主动隔振技术日趋成熟,其研究对象己经从单自由度系统发展到多自由度系统,由简单线性系统发展到复杂非线性系统;控制系统从SISO发展到MMO;振动方向也由单方向振动发展到多方向耦合振动.2003年美国 Honeywell 公司研制的ELVIS隔振系统,在隔离纵向振动的同时,可以较好地控制航天器摇晃模态响应,但系统复杂尚处于试验研究阶段.Hood 技术公司与华盛顿大学联合研制的六轴主动隔振平台采用立方Stewart平台结构,其6个支腿由电磁音圈作动器并联软弹簧组成,采用柔性铰链与上下平台连接,它在隔离基座振动的同时具有调姿与定位功能[13 ].比利时布鲁塞尔自由大学Marneffe等[14 ]提出用一个电磁感应系统替代机械结构,构造具有Maxwell阻尼单元的张弛隔振器,其隔振效果甚至优于用分散天棚控制器构成的主动隔振器,其隔振平台仍然采用立方Stewart 平台结构.Zhang等[15 ]采用压电堆设计了整星隔振的主被动一体化隔振平台,采用非概率可靠性理论研究了隔振系统的可靠性,数值分析和实验测试的结果表明了隔振的有效性.Yang等[16 ]研究六支腿Stewart平台的解耦条件,将六轴振动控制系统解耦,并设计了分散力反馈控制器,采用数值算例说明了其控制方法的有效性. ...
Dynamic isotropic design and decentralized active control of a six-axis vibration isolator via Stewart plat form
1
2017
... 除了与结构振动密切相关外,主动隔振技术的发展还依赖于微电子、自动控制、信号处理和计算机等技术的发展.近年来,主动隔振技术日趋成熟,其研究对象己经从单自由度系统发展到多自由度系统,由简单线性系统发展到复杂非线性系统;控制系统从SISO发展到MMO;振动方向也由单方向振动发展到多方向耦合振动.2003年美国 Honeywell 公司研制的ELVIS隔振系统,在隔离纵向振动的同时,可以较好地控制航天器摇晃模态响应,但系统复杂尚处于试验研究阶段.Hood 技术公司与华盛顿大学联合研制的六轴主动隔振平台采用立方Stewart平台结构,其6个支腿由电磁音圈作动器并联软弹簧组成,采用柔性铰链与上下平台连接,它在隔离基座振动的同时具有调姿与定位功能[13 ].比利时布鲁塞尔自由大学Marneffe等[14 ]提出用一个电磁感应系统替代机械结构,构造具有Maxwell阻尼单元的张弛隔振器,其隔振效果甚至优于用分散天棚控制器构成的主动隔振器,其隔振平台仍然采用立方Stewart 平台结构.Zhang等[15 ]采用压电堆设计了整星隔振的主被动一体化隔振平台,采用非概率可靠性理论研究了隔振系统的可靠性,数值分析和实验测试的结果表明了隔振的有效性.Yang等[16 ]研究六支腿Stewart平台的解耦条件,将六轴振动控制系统解耦,并设计了分散力反馈控制器,采用数值算例说明了其控制方法的有效性. ...
Design and experimental study of a VCM-based Stewart parallel mechanism used for active vibration isolation
1
2015
... 哈尔滨工业大学飞行器动力学与振动控制团队设计并改进了电磁作动器的磁路结构,建立了六支腿Stewart电磁隔振平台的动力学方程,通过加权函数的适当选取,针对外部扰动和噪声环境下的星箭系统提出鲁棒控制器设计方案;在理论研究的基础上构建了整星主被动一体化隔振系统(见图3 ),使其在保证隔振性能要求的同时,其频率漂移在合理范围[17 ];建立了带基础激励并考虑参数不确定性的Stewart平台的非线性动力学方程,采用$H_\infty $和$\mu$综合控制算法实现了多由度振动控制,并对平台构型进行了优化设计,仿真结果表明在全频段内振动最大衰减可达30 dB[18 ].Tang等[19 ]进一步利用支腿位移为广义坐标建立了装有Stewart隔振平台的有效载荷分散形式的非线性动力学模型,据此提出了分散控制算法,并证明了系统的稳定性.数值仿真和实验研究的结果表明,在5$\sim$10 Hz范围内,对纵横两个方向的共振峰都有很好的削峰效应. ...
Dynamic isotropy design and analysis of a six-DOF active micro-vibration isolation manipulator on satellites
1
2018
... 哈尔滨工业大学飞行器动力学与振动控制团队设计并改进了电磁作动器的磁路结构,建立了六支腿Stewart电磁隔振平台的动力学方程,通过加权函数的适当选取,针对外部扰动和噪声环境下的星箭系统提出鲁棒控制器设计方案;在理论研究的基础上构建了整星主被动一体化隔振系统(见图3 ),使其在保证隔振性能要求的同时,其频率漂移在合理范围[17 ];建立了带基础激励并考虑参数不确定性的Stewart平台的非线性动力学方程,采用$H_\infty $和$\mu$综合控制算法实现了多由度振动控制,并对平台构型进行了优化设计,仿真结果表明在全频段内振动最大衰减可达30 dB[18 ].Tang等[19 ]进一步利用支腿位移为广义坐标建立了装有Stewart隔振平台的有效载荷分散形式的非线性动力学模型,据此提出了分散控制算法,并证明了系统的稳定性.数值仿真和实验研究的结果表明,在5$\sim$10 Hz范围内,对纵横两个方向的共振峰都有很好的削峰效应. ...
Decentralized vibration control of a VCM-Based Stewart parallel mechanism: simulation and experiments
1
2018
... 哈尔滨工业大学飞行器动力学与振动控制团队设计并改进了电磁作动器的磁路结构,建立了六支腿Stewart电磁隔振平台的动力学方程,通过加权函数的适当选取,针对外部扰动和噪声环境下的星箭系统提出鲁棒控制器设计方案;在理论研究的基础上构建了整星主被动一体化隔振系统(见图3 ),使其在保证隔振性能要求的同时,其频率漂移在合理范围[17 ];建立了带基础激励并考虑参数不确定性的Stewart平台的非线性动力学方程,采用$H_\infty $和$\mu$综合控制算法实现了多由度振动控制,并对平台构型进行了优化设计,仿真结果表明在全频段内振动最大衰减可达30 dB[18 ].Tang等[19 ]进一步利用支腿位移为广义坐标建立了装有Stewart隔振平台的有效载荷分散形式的非线性动力学模型,据此提出了分散控制算法,并证明了系统的稳定性.数值仿真和实验研究的结果表明,在5$\sim$10 Hz范围内,对纵横两个方向的共振峰都有很好的削峰效应. ...
大型网架式可展开空间结构的非线性动力学与控制
1
2013
... 前已述及,对于大型柔性航天器,由于运载工具有效空间的限制,其空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.空间结构的展开过程涉及若干复杂的、尚未解决的动力学与控制问题,例如怎样描述和分析柔性构件大范围运动与弹性变形的相互耦合、众多运动副带来的间隙和碰撞、结构展开与航天器姿态耦合等.为了确保大型柔性空间结构入轨后能够顺利展开并迅速稳定到平衡状态,必须在其设计阶段进行有效的动力学建模和动响应预测,建立可行的展开控制策略,这方面的研究进展可参考胡海岩等[20 ]关于大型网架式可展开空间结构的非线性动力学与控制的综述. ...
大型网架式可展开空间结构的非线性动力学与控制
1
2013
... 前已述及,对于大型柔性航天器,由于运载工具有效空间的限制,其空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开,锁定并保持预定的几何构形.空间结构的展开过程涉及若干复杂的、尚未解决的动力学与控制问题,例如怎样描述和分析柔性构件大范围运动与弹性变形的相互耦合、众多运动副带来的间隙和碰撞、结构展开与航天器姿态耦合等.为了确保大型柔性空间结构入轨后能够顺利展开并迅速稳定到平衡状态,必须在其设计阶段进行有效的动力学建模和动响应预测,建立可行的展开控制策略,这方面的研究进展可参考胡海岩等[20 ]关于大型网架式可展开空间结构的非线性动力学与控制的综述. ...
航天器动力学技术的发展和挑战
1
2003
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
航天器动力学技术的发展和挑战
1
2003
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
复合柔性结构航天器动力学建模研究
1
1999
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
复合柔性结构航天器动力学建模研究
1
1999
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
关于柔性航天器动力学模型降阶问题
1
2001
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
关于柔性航天器动力学模型降阶问题
1
2001
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
Multibody dynamics modeling of segmented booms of the mars express spacecraft
1
2005
... 早期的航天器多使用贴身式太阳能电池阵,所带天线尺寸小,柔性附件的转动惯量和质量占整星的比重非常小,一般使用刚体假设对航天器进行建模.针对这类航天器,结构动力学的主要任务是研究航天器结构从设计、研制、试验、发射到在轨飞行、轨道转移和返回着陆全过程的各类结构振动问题,涉及复杂航天器系统级结构和部件级结构的动力学建模、模态分析、系统降阶、线性与非线性振动响应计算与地面试验等,前期的研究成果可参见综述文献[1 -2 ,21 ].曲广吉[22 ]采用混合坐标法和基于伪坐标的拉格朗日方程导出了航天器的动力学方程,采用航天器整体的系统模态(通过模态综合或者求解航天器整体的动力学方程对应的特征值问题)离散柔性结构的位移,获取了系统离散动力学模型;缪炳祺等[23 ]提出采用模态价值分析和内平衡理论对航天器结构动力学系统进行模型降阶,但需要用到航天器整体系统的模态,而非部件模态或附件结构弹性变形模态,实际应用中尚存在困难.Mettler和Quadrelli[24 ]研究火星快车号飞船的天线和形体之间的动力学交互作用时,将天线划分成13个铰链连接的梁段,梁与梁之间用扭簧连接,采用多体系统动力学建立动力学模型,根据数值仿真结果揭示了飞船动力学与天线振动之间的动态相容性. ...
带太阳帆板航天器刚柔耦合动力学研究
1
2006
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
带太阳帆板航天器刚柔耦合动力学研究
1
2006
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
ANCF 索梁单元应变耦合问题与模型解耦
1
2016
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
ANCF 索梁单元应变耦合问题与模型解耦
1
2016
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
1
2016
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
1
2016
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
大型空间刚柔耦合组合体的动力学建模
2
2004
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
... 采用文献[28 ]的方法建立带两个太阳翼的航天器模型的动力学,所得固有频率除前两阶非零频率外,其高阶频率与设计频率相吻合.方柳等[29 ]建立了考虑动力刚化效应的挠性卫星姿态运动与结构振动的耦合动力学方程,采用假设模态进行离散,得到系统的线性动力学模型和动力刚化模型,数值仿真结果表明动力刚化效应会对柔性结构振动产生较大影响. ...
大型空间刚柔耦合组合体的动力学建模
2
2004
... 蒋建平和李东旭[25 ]考虑太阳翼的非线性变形耦合项,使用假设模态离散太阳翼变形,基于Kane方程建立了带太阳翼航天器的一次近似刚柔耦合动力学模型,仿真结果表明,一次近似模型可以准确地预测大角度机动情况下系统的动态行为.张越等[26 ]研究索梁单元应变耦合机理,从能量角度分析应变耦合效应对单元精度的影响,导出了索梁单元的应变解耦模型.章孝顺等[27 ]采用柔性梁参数方程的精确曲率来计算柔性梁的弯曲变形能,建立了更为精确的刚柔耦合动力学模型,用于处理柔性梁大位移运动下的大变形问题.和兴锁等[28 ]使用混合坐标法描述大型刚柔耦合空间组合体的运动,将组合体看作中心体上铰接若干柔性附件,各附件相对于中心体运动,使用拉格朗日方程建立了系统的动力学方程. ...
... 采用文献[28 ]的方法建立带两个太阳翼的航天器模型的动力学,所得固有频率除前两阶非零频率外,其高阶频率与设计频率相吻合.方柳等[29 ]建立了考虑动力刚化效应的挠性卫星姿态运动与结构振动的耦合动力学方程,采用假设模态进行离散,得到系统的线性动力学模型和动力刚化模型,数值仿真结果表明动力刚化效应会对柔性结构振动产生较大影响. ...
考虑动力刚化的挠性航天器的动力学建模与分析
1
2017
... 采用文献[28 ]的方法建立带两个太阳翼的航天器模型的动力学,所得固有频率除前两阶非零频率外,其高阶频率与设计频率相吻合.方柳等[29 ]建立了考虑动力刚化效应的挠性卫星姿态运动与结构振动的耦合动力学方程,采用假设模态进行离散,得到系统的线性动力学模型和动力刚化模型,数值仿真结果表明动力刚化效应会对柔性结构振动产生较大影响. ...
考虑动力刚化的挠性航天器的动力学建模与分析
1
2017
... 采用文献[28 ]的方法建立带两个太阳翼的航天器模型的动力学,所得固有频率除前两阶非零频率外,其高阶频率与设计频率相吻合.方柳等[29 ]建立了考虑动力刚化效应的挠性卫星姿态运动与结构振动的耦合动力学方程,采用假设模态进行离散,得到系统的线性动力学模型和动力刚化模型,数值仿真结果表明动力刚化效应会对柔性结构振动产生较大影响. ...
Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft
3
2014
... 哈尔滨工业大学深圳研究生院研究空间机器人在抓取空间目标航天器前后的动力学行为,分别建立了带柔性附件空间机器人和它与带柔性附件航天器的大型组合体的动力学模型(见图9 ),发展了相应的数值求解方法,并与采用Adams软件建立的模型及其求解结果进行比较,验证了求解方法的有效性[30 ].郭其威等[31 ]采用子结构模型缩聚方法,将MATLAB软件与NASTRAN集成,用于快速求解含大型柔性附件航天器的系统模态,数值算例表明了方法的有效性,进一步的仿真结果表明:当中心平台的惯性特性不占优时,约束模态与系统模态的频率相差较大. ...
... 空间机器人与目标飞行器组合体示意图$^{[30 ]}$ ... ...
... The schematic diagram of space robot and target vehicle assembly$^{[30 ]}$ ... ...
航天器柔性附件对整器固有振动特性影响因素及规律分析
1
2016
... 哈尔滨工业大学深圳研究生院研究空间机器人在抓取空间目标航天器前后的动力学行为,分别建立了带柔性附件空间机器人和它与带柔性附件航天器的大型组合体的动力学模型(见图9 ),发展了相应的数值求解方法,并与采用Adams软件建立的模型及其求解结果进行比较,验证了求解方法的有效性[30 ].郭其威等[31 ]采用子结构模型缩聚方法,将MATLAB软件与NASTRAN集成,用于快速求解含大型柔性附件航天器的系统模态,数值算例表明了方法的有效性,进一步的仿真结果表明:当中心平台的惯性特性不占优时,约束模态与系统模态的频率相差较大. ...
航天器柔性附件对整器固有振动特性影响因素及规律分析
1
2016
... 哈尔滨工业大学深圳研究生院研究空间机器人在抓取空间目标航天器前后的动力学行为,分别建立了带柔性附件空间机器人和它与带柔性附件航天器的大型组合体的动力学模型(见图9 ),发展了相应的数值求解方法,并与采用Adams软件建立的模型及其求解结果进行比较,验证了求解方法的有效性[30 ].郭其威等[31 ]采用子结构模型缩聚方法,将MATLAB软件与NASTRAN集成,用于快速求解含大型柔性附件航天器的系统模态,数值算例表明了方法的有效性,进一步的仿真结果表明:当中心平台的惯性特性不占优时,约束模态与系统模态的频率相差较大. ...
大型网架式可展开空间结构的非线性动力学与控制
1
2013
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
大型网架式可展开空间结构的非线性动力学与控制
1
2013
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
空间可展机构非光滑力学模型和动力学研究
1
2013
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
空间可展机构非光滑力学模型和动力学研究
1
2013
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
含铰间间隙太阳帆板展开动力学仿真
1
2009
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
含铰间间隙太阳帆板展开动力学仿真
1
2009
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
考虑杆件柔性和铰间隙的可展结构动力学数值模拟
1
2003
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
考虑杆件柔性和铰间隙的可展结构动力学数值模拟
1
2003
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
具有非线性连接的航天器非线性振动分析
1
2009
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
具有非线性连接的航天器非线性振动分析
1
2009
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
环形桁架结构径向振动的等效圆环模型
1
2016
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
环形桁架结构径向振动的等效圆环模型
1
2016
... 由于运载器有效空间的限制,太阳能帆板、雷达天线阵列、空间桁架等空间结构不得不以折叠状态固定在载荷舱内,待发射入轨后再逐步展开、锁定并保持预定的几何构形.空间可展机构中绝大部分都可以视为由铰链连接结构,在展开过程中运动副之间不可避免地产生接触和分离,导致空间可展机构具有非光滑力学特征.铰链间隙引起的非光滑振动比光滑动力学系统的振动更为复杂,由于其振动现象在航天工程领域的重要性,关于铰链连接空间结构的非线性振动问题得到了广大国内外学者和工程技术人员的普遍关注[32 -34 ].文献[35 ]研究铰间间隙对太阳帆板展开过程的影响,采用非线性等效弹簧阻尼模型描述铰链间隙的接触碰撞,采用Coulomb摩擦模型描述铰间间隙处的摩擦作用,并将其嵌入到Adams多体系统动力学分析软件中;对一单翼小卫星太阳帆板展开过程进行动力学分析的研究结果表明:铰间间隙对卫星姿态角速度影响较明显,在帆板展开初期由于间隙的存在出现大的抖动,之后姿态角速度围绕理想状态角速度出现明显抖动.关于含铰链间隙的空间结构的非线性振动,从非光滑动力学角度仅能处理2$\sim$3个自由度的非线性系统,对于自由度达到数万量级的空间结构, 这样的分析思路是行不通的,需要寻求某种平均意义下的简化模型或简化分析方法.事实上,由于间隙的存在,使得碰撞时的加速度、运动副反力、平衡力矩等超出理想零间隙时的几倍甚至十几倍[36 ],这方面的研究亟待加强.此外,尉飞和郑钢铁[37 ]提出了计算空间连接结构的频域响应方法,实际计算时仅需选取结构中的非线性自由度、激励自由度和需要关注的自由度,大大地降低计算规模,适合于具有局部非线性的大型有限元模型的计算.刘福寿和金栋平[38 ]将环形桁架结构看作由重复的平面桁架单元构成的环形周期结构,提出周期桁架单元等效梁模型,借此研究环形桁架结构的径向振动,实现了对环形桁架结构的简化处理和近似解析求解. ...
Attitude dynamics of satellites with flexible appendagesa brief review
1
1974
... 柔性航天器是典型的刚柔耦合系统,包括刚体运动(姿态机动或轨道机动)和柔性体弹性振动两种运动.柔性航天器的控制主要研究航天器姿态运动-柔性体弹性振动的混合控制,将航天器假定为刚体而进行的姿态控制,忽略了柔性体振动对星体姿态运动的影响,不能直接应用于柔性航天器.Modi[39 ]对1974年以前关于带挠性附件航天器的姿态动力学与控制的研究成果进行了全面综述,认为这类研究是结构动力学、连续介质力学、卫星动力学以及控制理论等的综合性问题. Modi对当时空间探险失败的教训归结为:在大多数情况下,并非设计者缺乏理论分析和数值计算等设计方法,而是由于他们本身根本还未认清姿态动力学与结构挠性相互作用的机理.Likins[40 ]总结了早期航天器姿态动力学与控制研究方面的经验,并指出:活动部件和结构挠性的存在,使得航天器的姿态控制问题必须由结构、动力学和控制三方面的工程师共同解决.为了在体现超大型空间结构的柔性特性的同时,实现简化计算的目的,尹婷婷等[41 ]提出将其简化为空间刚性杆-弹簧组合结构模型,据此建立系统的动力学方程,为实现超大型空间结构的实时反馈控制提供构建状态空间模型的途径. ...
Spacecraft attitude dynamics and control-a personal perspective on early developments
1
1986
... 柔性航天器是典型的刚柔耦合系统,包括刚体运动(姿态机动或轨道机动)和柔性体弹性振动两种运动.柔性航天器的控制主要研究航天器姿态运动-柔性体弹性振动的混合控制,将航天器假定为刚体而进行的姿态控制,忽略了柔性体振动对星体姿态运动的影响,不能直接应用于柔性航天器.Modi[39 ]对1974年以前关于带挠性附件航天器的姿态动力学与控制的研究成果进行了全面综述,认为这类研究是结构动力学、连续介质力学、卫星动力学以及控制理论等的综合性问题. Modi对当时空间探险失败的教训归结为:在大多数情况下,并非设计者缺乏理论分析和数值计算等设计方法,而是由于他们本身根本还未认清姿态动力学与结构挠性相互作用的机理.Likins[40 ]总结了早期航天器姿态动力学与控制研究方面的经验,并指出:活动部件和结构挠性的存在,使得航天器的姿态控制问题必须由结构、动力学和控制三方面的工程师共同解决.为了在体现超大型空间结构的柔性特性的同时,实现简化计算的目的,尹婷婷等[41 ]提出将其简化为空间刚性杆-弹簧组合结构模型,据此建立系统的动力学方程,为实现超大型空间结构的实时反馈控制提供构建状态空间模型的途径. ...
空间刚性杆-弹簧组合结构轨道、姿态耦合动力学分析
1
2018
... 柔性航天器是典型的刚柔耦合系统,包括刚体运动(姿态机动或轨道机动)和柔性体弹性振动两种运动.柔性航天器的控制主要研究航天器姿态运动-柔性体弹性振动的混合控制,将航天器假定为刚体而进行的姿态控制,忽略了柔性体振动对星体姿态运动的影响,不能直接应用于柔性航天器.Modi[39 ]对1974年以前关于带挠性附件航天器的姿态动力学与控制的研究成果进行了全面综述,认为这类研究是结构动力学、连续介质力学、卫星动力学以及控制理论等的综合性问题. Modi对当时空间探险失败的教训归结为:在大多数情况下,并非设计者缺乏理论分析和数值计算等设计方法,而是由于他们本身根本还未认清姿态动力学与结构挠性相互作用的机理.Likins[40 ]总结了早期航天器姿态动力学与控制研究方面的经验,并指出:活动部件和结构挠性的存在,使得航天器的姿态控制问题必须由结构、动力学和控制三方面的工程师共同解决.为了在体现超大型空间结构的柔性特性的同时,实现简化计算的目的,尹婷婷等[41 ]提出将其简化为空间刚性杆-弹簧组合结构模型,据此建立系统的动力学方程,为实现超大型空间结构的实时反馈控制提供构建状态空间模型的途径. ...
空间刚性杆-弹簧组合结构轨道、姿态耦合动力学分析
1
2018
... 柔性航天器是典型的刚柔耦合系统,包括刚体运动(姿态机动或轨道机动)和柔性体弹性振动两种运动.柔性航天器的控制主要研究航天器姿态运动-柔性体弹性振动的混合控制,将航天器假定为刚体而进行的姿态控制,忽略了柔性体振动对星体姿态运动的影响,不能直接应用于柔性航天器.Modi[39 ]对1974年以前关于带挠性附件航天器的姿态动力学与控制的研究成果进行了全面综述,认为这类研究是结构动力学、连续介质力学、卫星动力学以及控制理论等的综合性问题. Modi对当时空间探险失败的教训归结为:在大多数情况下,并非设计者缺乏理论分析和数值计算等设计方法,而是由于他们本身根本还未认清姿态动力学与结构挠性相互作用的机理.Likins[40 ]总结了早期航天器姿态动力学与控制研究方面的经验,并指出:活动部件和结构挠性的存在,使得航天器的姿态控制问题必须由结构、动力学和控制三方面的工程师共同解决.为了在体现超大型空间结构的柔性特性的同时,实现简化计算的目的,尹婷婷等[41 ]提出将其简化为空间刚性杆-弹簧组合结构模型,据此建立系统的动力学方程,为实现超大型空间结构的实时反馈控制提供构建状态空间模型的途径. ...
Model study and active control of a rotating flexible cantilever beam
1
2004
... 鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感. ...
LimCW. Active control of a flexible hub-beam system using optimal tracking control method
1
2006
... 鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感. ...
Vibration reduction for flexible spacecraft following momentum dumping with/without slewing
1
2001
... 鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感. ...
Adaptive variable structure and commanding shaped vibration control of flexible spacecraft
1
2007
... 鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感. ...
可抑制航天器轨控过程中太阳翼大幅振动的新型轨控方法研究
1
2011
... 鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感. ...
可抑制航天器轨控过程中太阳翼大幅振动的新型轨控方法研究
1
2011
... 鉴于传统控制系统设计的不足,国内外广泛开展了现代控制理论与方法的研究,以达到所要求的系统性能和控制精度.现代柔性航天器姿态控制技术种类多样,如:基于状态空间的最优控制、输入成形、鲁棒控制、变结构控制(滑模控制)、自适应控制等.蔡国平等[42 -43 ]建立了中心刚体-柔性梁系统的有限元动力学模型, 并对比研究了系统零次近似与一次近似模型在转速逐渐增大时的适用性; 基于经典的LQR技术对中心刚体-悬臂梁这一典型刚柔耦合系统进行了最优控制, 该方法可以扩展到同是刚柔耦合系统的柔性航天器姿态控制中. Banerjee等[44 ]将输入成形技术用于产生卸载挠性航天器动量的喷气指令, 这样可以在卸载飞轮动量的同时, 抑制掉挠性结构的振动,并且也不用增加额外的燃料. 胡庆雷等[45 ]将变结构输出反馈控制与输入成形相结合, 并引入自适应律设计了柔性航天器姿态控制和结构振动抑制的控制律, 不仅能够保证闭环系统的稳定性,还能克服参数不确定性和外界扰动,具有很强的鲁棒性. 鉴于航天器轨控过程中可能激起太阳翼等大型挠性部件的大幅振动等原因, 基于被控对象的动力学特点借鉴输入成型控制器设计方法, 胡军等[46 ]给出了两种可适用于任意轨控推力配置系统的新型轨控策略, 用以降低既定轨控任务过程中的太阳翼变形幅度和振动幅度. 在实际应用中,输入成形方法需要使用精确的数学模型来求取脉冲的幅值和作用时刻, 其解对模型具有严重的依赖性,且对模型参数的变化很敏感. ...
Dynamic modeling for a flexible spacecraft with solar arrays composed of honeycomb panels and its proportional- derivative control with input shaper
1
2016
... 刘伦和曹登庆[47 ]研究以蜂窝夹芯板作为基板的太阳翼, 将其等效为采用三层的层合板(包含蜂窝芯层和上下面板),基于刚柔耦合模态建立了更加符合工程实际的柔性航天器低维高精度离散动力学模型,结合输入成形和比例微分控制,设计了算法简单且适宜于实时控制的姿态机动和结构振动抑制的协同控制器,以保证航天器姿态机动和结构振动的协同控制.Singh等[48 ]在模型参数完全未知的情况下,设计了一个单轴柔性航天器的自适应输出反馈控制器,该控制器类似于反馈线性化控制器,并引入了一种高增益反馈观测器来补偿模型未建模动态特性. ...
Adaptive output feedback control of spacecraft with flexible appendages by modeling error compensation
1
2004
... 刘伦和曹登庆[47 ]研究以蜂窝夹芯板作为基板的太阳翼, 将其等效为采用三层的层合板(包含蜂窝芯层和上下面板),基于刚柔耦合模态建立了更加符合工程实际的柔性航天器低维高精度离散动力学模型,结合输入成形和比例微分控制,设计了算法简单且适宜于实时控制的姿态机动和结构振动抑制的协同控制器,以保证航天器姿态机动和结构振动的协同控制.Singh等[48 ]在模型参数完全未知的情况下,设计了一个单轴柔性航天器的自适应输出反馈控制器,该控制器类似于反馈线性化控制器,并引入了一种高增益反馈观测器来补偿模型未建模动态特性. ...
Vibration suppression and adaptive-robust control of a smart flexible satellite with three axes maneuvering
1
2011
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
Sliding mode maneuvering control and active vibration damping of three-axis stabilized flexible spacecraft with actuator dynamics
1
2008
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
Robust backstepping sliding mode attitude tracking and vibration damping of flexible spacecraft with actuator dynamics
1
2009
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
Attitude and vibration control of a satellite containing flexible solar arrays by using reaction wheels, and piezoelectric transducers as sensors and actuators
1
2017
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
控制受限的挠性航天器姿态机动控制和振动抑制
1
2018
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
控制受限的挠性航天器姿态机动控制和振动抑制
1
2018
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
航天器姿态机动的自适应鲁棒控制及主动振动抑制
1
2013
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
航天器姿态机动的自适应鲁棒控制及主动振动抑制
1
2013
... 柔性航天器姿态运动和柔性附件结构振动的混合控制设计的一大趋势是综合各种控制方法的优点,设计出满足控制需求的控制律.采用输入成型进行振动抑制的方法是利用姿控发动机在完成姿态机动的同时对柔性附件的振动进行抑制;对于大型柔性航天器,仅有安装于中心平台的姿控发动机很难完成航天器姿态机动和大型柔性结构的振动抑制任务.在采用姿控发动机对航天器姿态机动进行跟踪控制的同时采用压电促动器对柔性附件进行振动抑制是近期的一个发展方向.Azadi等[49 ]采用压电层作为作动器用于抑制柔性附件的振动,利用Lagrange-Rayleigh-Ritz建立动力模型,设计了满足航天器大角度轨迹跟踪和柔性附件振动抑制要求的自适应鲁棒控制律.针对柔性航天器的大角度姿态机动控制,胡庆雷[50 ]采用假设模态法导出系统的动力学模型,基于滑膜控制理论设计出了非连续姿态控制律,采用压电片作为促动器和传感器进行主动振动控制,其控制律采用了模态速度反馈和应变率反馈,进一步的研究成果可参见文献[51 ].da Fonseca等[52 ]采用有限元方法建立了带柔性太阳翼的航天器的动力学模型,航天器姿态控制主要采用PID技术,基于压电传感器和促动器的主动控制技术应用于太阳翼针对的抑制,分析结果和实验数据表明:姿态机动可能引发太阳翼的振动模态,而太阳翼的振动也会反过来对姿态机动造成影响.针对挠性航天器姿态机动过程中存在模型参数不确定性、外界干扰、执行机构饱和受限及挠性附件振动及挠性模态不易直接测量的问题,陶佳伟和张涛[53 ]提出了一种鲁棒自适应控制方法,数值仿真结果表明所设计的控制器能够严格满足执行机构的饱和约束,在完成姿态机动控制的同时,有效抑制挠性附件振动.袁国平等[54 ]采用自适应鲁棒控制方法设计姿态控制器,主动振动控制器设计则采用$H_{\infty}$状态反馈理论,并且设计时充分考虑了由于忽略挠性附件模型高阶模态所带来的结构不确定性;仿真结果表明所提出的控制方案在对结构振动进行抑制的同时,可有效地降低干扰和转动惯量不确定性对系统性能的影响. ...
Modeling and analysis of the inplane vibration of a complex cable-stayed bridge
1
2012
... 大型柔性航天器主要是由桁架、梁、板、壳等子结构通过连接结构组装而成的复杂空间结构,这类柔性航天器具有低频、密频等复杂动力学特性.对于此类航天器而言,如何得到低维高精度的动力学模型是对整个系统的非线性特性进行准确分析的关键.传统的解析方法是针对单一弹性结构(如索、杆、梁、板、壳等)建立的,对于复杂的多刚柔体系统,目前尚无通用的解析建模方法.在没有其他有效建模方法的情况下,通常采用假设模态法建立系统的近似模型,这样的近似方法在处理复杂的空间柔性结构时往往会带来较大误差.哈尔滨工业大学飞行器动力学与控制研究团队提出了针对平面运动的组合结构的全局模态提取方法,并成功地应用于大跨度斜拉桥[55 ]、微机电系统中的静电梳[56 ]、带柔性附件航天器[57 ]等细长柔性组合体的动力学建模,开展了全局模态提取、密频与重频分析以及模态跃迁、系统动态响应分析等一系列研究.全局模态提取方法能够将系统中各构件和部件的振动用全局模态和统一的模态坐标表示,将其应用于柔性体振动位移离散,可得到低维高精度的非线性动力学模型,适用于系统非线性动力学特性分析和控制器设计.尽管全局模态提取方法具有适宜于非线性振动分析和控制器设计等优点,但目前还仅能处理平面运动的索-梁组合结构的动力学建模问题,要用于处理大型柔性航天器(复杂空间柔性组合结构)的动力学建模与振动响应求解,尚有很多基础科学问题需要攻克,包括: ...
Dynamic analysis of a micro-resonator driven by electrostatic combs
1
2011
... 大型柔性航天器主要是由桁架、梁、板、壳等子结构通过连接结构组装而成的复杂空间结构,这类柔性航天器具有低频、密频等复杂动力学特性.对于此类航天器而言,如何得到低维高精度的动力学模型是对整个系统的非线性特性进行准确分析的关键.传统的解析方法是针对单一弹性结构(如索、杆、梁、板、壳等)建立的,对于复杂的多刚柔体系统,目前尚无通用的解析建模方法.在没有其他有效建模方法的情况下,通常采用假设模态法建立系统的近似模型,这样的近似方法在处理复杂的空间柔性结构时往往会带来较大误差.哈尔滨工业大学飞行器动力学与控制研究团队提出了针对平面运动的组合结构的全局模态提取方法,并成功地应用于大跨度斜拉桥[55 ]、微机电系统中的静电梳[56 ]、带柔性附件航天器[57 ]等细长柔性组合体的动力学建模,开展了全局模态提取、密频与重频分析以及模态跃迁、系统动态响应分析等一系列研究.全局模态提取方法能够将系统中各构件和部件的振动用全局模态和统一的模态坐标表示,将其应用于柔性体振动位移离散,可得到低维高精度的非线性动力学模型,适用于系统非线性动力学特性分析和控制器设计.尽管全局模态提取方法具有适宜于非线性振动分析和控制器设计等优点,但目前还仅能处理平面运动的索-梁组合结构的动力学建模问题,要用于处理大型柔性航天器(复杂空间柔性组合结构)的动力学建模与振动响应求解,尚有很多基础科学问题需要攻克,包括: ...
Dynamic modeling and simulation of flexible spacecraft with flexible joints
1
2017
... 大型柔性航天器主要是由桁架、梁、板、壳等子结构通过连接结构组装而成的复杂空间结构,这类柔性航天器具有低频、密频等复杂动力学特性.对于此类航天器而言,如何得到低维高精度的动力学模型是对整个系统的非线性特性进行准确分析的关键.传统的解析方法是针对单一弹性结构(如索、杆、梁、板、壳等)建立的,对于复杂的多刚柔体系统,目前尚无通用的解析建模方法.在没有其他有效建模方法的情况下,通常采用假设模态法建立系统的近似模型,这样的近似方法在处理复杂的空间柔性结构时往往会带来较大误差.哈尔滨工业大学飞行器动力学与控制研究团队提出了针对平面运动的组合结构的全局模态提取方法,并成功地应用于大跨度斜拉桥[55 ]、微机电系统中的静电梳[56 ]、带柔性附件航天器[57 ]等细长柔性组合体的动力学建模,开展了全局模态提取、密频与重频分析以及模态跃迁、系统动态响应分析等一系列研究.全局模态提取方法能够将系统中各构件和部件的振动用全局模态和统一的模态坐标表示,将其应用于柔性体振动位移离散,可得到低维高精度的非线性动力学模型,适用于系统非线性动力学特性分析和控制器设计.尽管全局模态提取方法具有适宜于非线性振动分析和控制器设计等优点,但目前还仅能处理平面运动的索-梁组合结构的动力学建模问题,要用于处理大型柔性航天器(复杂空间柔性组合结构)的动力学建模与振动响应求解,尚有很多基础科学问题需要攻克,包括: ...
The global modal parameterization for non-linear model-order reduction in flexible multibody dynamics
1
2007
... 此外,虽然在带铰链连接太阳翼(铰接多梁结构)的柔性航天器的全局模态提取方面获得了成功,但现有用于提取索-梁组合结构全局模态的方法尚不能处理一般的多柔体系统的动力学建模问题.当柔性部件快速转动与大变形相互耦合将导致几何非线性问题,比利时学者Brüls等[58 ]提出了多柔体系统"全局模态参数化(global modal parameterization)"的概念以及用于处理快速转动与小变形耦合问题的方法.基于全局模态参数化的概念,Luo等[59 ]研究了采用POD方法和Galerkin映射对由绝对节点坐标法建立的大型柔性多体系统进行降维处理的方法,极大地改善了计算效率.借助Brüls提出的全局模态参数化参数化概念,将现有处理组合结构的全局模态的方法拓展到多柔体系统是一个值得探索的重要课题. ...
Model order reduction for dynamic simulation of a flexible multibody system via absolute nodal coordinate formulation
1
2017
... 此外,虽然在带铰链连接太阳翼(铰接多梁结构)的柔性航天器的全局模态提取方面获得了成功,但现有用于提取索-梁组合结构全局模态的方法尚不能处理一般的多柔体系统的动力学建模问题.当柔性部件快速转动与大变形相互耦合将导致几何非线性问题,比利时学者Brüls等[58 ]提出了多柔体系统"全局模态参数化(global modal parameterization)"的概念以及用于处理快速转动与小变形耦合问题的方法.基于全局模态参数化的概念,Luo等[59 ]研究了采用POD方法和Galerkin映射对由绝对节点坐标法建立的大型柔性多体系统进行降维处理的方法,极大地改善了计算效率.借助Brüls提出的全局模态参数化参数化概念,将现有处理组合结构的全局模态的方法拓展到多柔体系统是一个值得探索的重要课题. ...