倾斜非均匀磁场下导电方管磁流体管流的数值模拟研究1)
杭州电子科技大学机械工程学院,杭州310018
DIRECT NUMERICAL SIMULATION OF MHD FLOW IN CONDUCTING SQUARE DUCTS WITH INCLINED FRINGING MAGNETIC FIELD1)
中图分类号: TL3
文献标识码: A
收稿日期: 2018-08-18
接受日期: 2018-08-18
网络出版日期: 2018-11-18
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
2) 毛洁,教授,主要研究方向:磁流体动力学. E-mail: maojie@hdu.edu.cn
展开
摘要
热核聚变反应堆液态金属包层应用中的一个重要问题是液态金属在导电管中流动和强磁场相互作用产生的额外的磁流体动力学压降.这种磁流体动力学压降远远大于普通水力学压降.美国阿贡国家实验室ALEX研究小组,对非均匀磁场下导电管中液态金属磁流体动力学效应进行了实验研究,其实验结果成为液态金属包层数值验证的标准模型之一.液态金属包层在应用中会受到不同方向的磁场作用,本文以ALEX的非均匀磁场下导电方管中液态金属管流实验中的一组参数为基础,保持哈特曼数、雷诺数和壁面电导率不变,采用三维直接数值模拟的方法,研究了外加磁场与侧壁之间的倾角对导电方管内液态金属流动的速度、电流和压降分布的影响.研究结果表明:沿流向相同横截面上的速度、电流以及压力分布均随磁场的倾斜而同向旋转.倾斜磁场均匀段,横截面上的高速区位于平行磁场方向的哈特曼层和平行层交叉位置,压力梯度随磁场倾角的增大先增大后减小.倾斜磁场递减段,在三维磁流体动力学效应作用下,横截面上的高速射流位置向垂直磁场方向偏移.磁场递减段的三维磁流体动力学压降随磁场倾角的增大而增大.随磁场倾斜,截面上的射流峰值逐渐减小,二次流增强,引发层流向湍流的转捩.
关键词:
Abstract
An essential issue in the application of liquid metal blanks in thermal nuclear fusion reactors is the additional magnetohydrodynamic (MHD) pressure drop caused by the interaction of the liquid metal flow with a strong magnetic field. The additional MHD pressure drop is much higher than hydrodynamic pressure drop. Argonne liquid metal experiment (ALEX) group in Argonne National Laboratory of American studied the MHD effect of Liquid Metal flow in ducts and pipes subjected to a fringing magnetic field by experiments. The experiments were introduced as one of the benchmark cases to test numerical codes for liquid metal blankets. As the liquid metal blankets would be subjected to the magnetic field with different directions, liquid metal flow in a square duct subjected to an inclined fringing magnetic field has been numerically studied in this paper. The model is based on one of the ALEX's experiments. With constant Hartmann number, Reynolds number and wall conductance ratio, the effects of the angle between the magnetic field and the side wall on the velocity, the electric current, and the pressure distribution have been investigated using three-dimensional direct numerical simulation method. The results show that the distribution of the velocity, the electric current and the pressure on the cross section rotates with the increase of the inclination angle of the magnetic field. In the uniform part of the inclined magnetic field, the velocity jets located at the junction corners of the Hartmann layer and the side layer which are parallel to the external magnetic field. The pressure gradient in the part of the uniform magnetic field increases firstly and decreases with the increase of the inclination angle of the magnetic field. In the decreasing part of the inclined magnetic field, the high-speed velocity jet is transferred to another pair of corners due to the three-dimensional MHD effect along the streamwise direction. The three-dimensional MHD pressure drop at the cross-section of the duct increases with the increase of the inclination angle of the magnetic field. Furthermore, the maximum value of the velocity jets decreases, the second flow increases and the laminar-turbulent transition of the duct flow occurs.
Keywords:
引 言
磁流体管道流的研究对热核聚变反应堆液态包层的应用具有重要的意义[1-4].
强磁场作用下液态金属在管道内流动产生的磁流体效应已经在实验[5-8]和数值模拟[9-13]中得到了广泛研究. 美国阿贡国家实验室[14-20]进行了一系列关于磁流体管道流的实验研究,部分实验成为验证数值模拟程序的标准模型.Votyakov等[21]对磁场进行计算分析时发现非均匀磁场影响液态金属的流动状态,提出对边缘磁场下的流体流动状态进行分析时必须考虑流向的场分量.Albets-Chico等 [22-23]采用三维直接数值模拟的方法研究了进入磁场段时液态金属的湍流流动状态,提供了在边缘磁场中湍流衰减的详细信息.Hiromichi等[24]通过数值模拟研究了非均匀磁场对管道内金属流体湍流流动状态的影响,表明雷诺数和壁面电导率保持一致时,侧壁射流强度随哈特曼数的增加而增强,且具有发展为湍流的趋势.Zhou等[25]分别对非均匀磁场作用下的绝缘和导电矩形管道中的流动状态进行分析,提出非均匀磁场是产生三维磁流体压降的原因,但边缘地带的三维压降与管道的导电性无关.Li等[26]对不同哈特曼数下进入非均匀磁场段的导电圆管进行研究,发现均匀层流段速度呈"M型"分布,但向非均匀磁场段过渡时呈现出复杂的三维现象.Yu等[27]通过对不同磁场方向作用下矩形腔内的自然对流进行了数值模拟研究,提出磁场倾角决定流量,在磁场的主导作用下,温度分布没有显著差异,对于不同的纵横比,不同的磁场倾角导致不同的抑制作用.Sarkar等[28]和Seth等[29]研究了旋转系统中倾斜磁场对磁流体管流的影响,发现磁场的霍尔电流和倾斜角度可衰减主流速度,加速二次流.
在磁约束聚变反应堆环境下,会存在磁场与矩形管道壁面存在倾角的情况.采用直接数值模拟的方法对倾斜非均匀磁场作用下,矩形管道中的磁流体流动特性进行数值模拟研究.探究当磁场与管壁存在一定倾角时,均匀磁场和递减磁场作用下导电方管中的速度、电流和磁流体压降等的分布状态.
1 基本控制方程
不可压缩液态金属流体在外加磁场的作用下,忽略感应磁场的无量纲控制方程[30]为
$$\nabla \cdot u = 0 (1)$$$$\label{eq2} \frac{\partial u}{\partial t} + u \cdot\nabla u = - \nabla p + \frac{1}{Re}\nabla ^2 u + N(J\times B) (2)$$$$\label{eq3} J = - \nabla \phi + u\times B (3)$$$$\label{eq4} \nabla ^2\phi = \nabla \cdot ( u\times B) (4)$$
固壁区感应电势控制方程
\begin{equation}\label{eq5} \nabla ^2\phi _{\rm w} = 0\tag{5}\end{equation}
式中,$ u$, $ J$, $ B$, $t$, $P$, $\phi$分别代表速度矢量、感应电流矢量、外加磁场矢量、时间、压力和感应电势,分别用$U_{\rm m} $, $\sigma _{\rm f} U_{\rm m} B_0 $, $B_0 $, $a / U_{\rm m} $,$\rho U_{\rm m} ^2$, $U_{\rm m} B_0 a$进行无量纲化. 其中$U_{\rm m}$为截面流向平均速度;$a$为特征长度;$B_0 $为均匀段磁场强度,$\rho$为流体密度,$\upsilon $为液态金属的运动黏度,$\phi _{\rm w}$为固体区电势. 研究过程中所涉及到的无量纲参数分别是:雷诺数$Re =U_{\rm m} a / \upsilon $代表惯性力与黏性力的比值;相互作用参数$N =\sigma _{\rm f} aB_0^2 / \rho U_{\rm m}$代表洛伦兹力与惯性力的比值;哈特曼数$Ha = B_0 a\sqrt {\sigma_{\rm f} / \rho \upsilon } = \sqrt {Re \cdot N}$,其平方代表洛伦兹力与黏性力比值.另一个重要的无量纲参数为壁面电导率$C = \delta \sigma _{\rm w} /a\sigma _{\rm f} $,式中$\delta $表示固体壁的厚度,$\sigma _{\rm f} $和$\sigma _{\rm w} $分别为流体和固体壁的导电率.
2 数值模型
2.1 计算参数及外加磁场
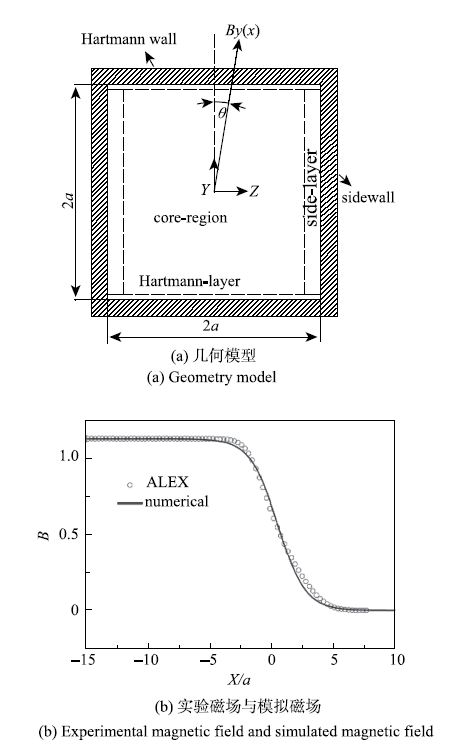
Reed等[17]在1987年发表的非均匀磁场下磁流体流动状态的报告是以ALEX的实验结果为基础,首次揭示了非均匀磁场下液态金属管流的三维磁流体效应.实验中的磁场是由厚0.2 m,宽0.76 m,长1.83m的铁电磁体产生的,磁场两端迅速衰减,中间段为均匀磁场.实验研究中所采用的导电方管的物理模型如图1(a)所示,发表的实验结果仅给出了均匀磁场段和磁场下降段的结果.管道流体区的无量纲几何尺寸为$2a \times 2a \times 15a$, 其中$a =0.043~9\mbox{ m}$,管壁厚度$\delta \mbox{ = }0.15a = 6.585$ mm实验中所采用的金属流体是NaK,其物性参数分别为:密度$\rho =856~{\mbox{kg/}}{\rm m^3}$, 运动黏度 $\upsilon \mbox{ =9.62}\times \mbox{10}^{ - 7}~\rm {m^2}/s\mbox{}$,导电率为 $\sigma _{\rm f} = 2.83\times 10^6~\rm s/m$,固体壁面的导电率为$\sigma _{\rm w} = 1.311\times 10^6~\rm s/m$。本文中仅取导电方管实验中的一组参数为基准,入口平均速度为$U_{\rm m} = 0.339~\rm m/s$,外加最大磁场强度为$B_0 \mbox{ = }1.129$T,相应的无量纲参数为Re = 15 469,Ha = 2900,$C$= 0.07.保持Re,Ha和$C$不变,定义磁场倾斜角度为磁场方向与侧壁之间的夹角为$\theta$,倾角以每5$^\circ$为一组,范围$0^{\circ} \le \theta \le45^{\circ}$,采用三维数值模拟方法研究不同磁场倾角下导电方管中液态金属管流的磁流体效应及流动状态.
首先对实验磁场进行拟合,采用双曲函数来近似模拟ALEX实验中递减磁场段的实验数据.磁场拟合公式为
\begin{equation}\label{eq6} B = B_0 \frac{1 - \tanh\left[ {\gamma \left( {x / a +d} \right)} \right]}{2}\tag{6}\end{equation}
ALEX实验所测得的磁场与拟合函数所得磁场沿流向的分布如图1(b)所示,计算时将磁场$B$分解为$B_y= B \cos \mbox{ }\theta $和$B_z = B \sin \theta $. 式中$B_0$是均匀段磁场强度;$a$是管道特征长度;$\gamma$是磁场的变化因子,用来调节磁场变化的快慢;$d$是坐标修正系数,用来修正磁场的坐标位置.模拟计算中的参数设置为:$\gamma = 0.45, d = - 0.33$。
2.2 边界条件及网格分布
壁面速度为无滑移边界条件,入口给定平均速度为$U_{\rm m}$,出口速度为零梯度. 入口和出口的压力分别设置为零梯度和固定值零.进、出口和固体外壁面的电势设置为$\partial \phi / \partial n =0$,代表无电流流入和流出计算域.流体区与固体区的交界面为电势耦合边界条件,设置为:$\phi _{\rm f} =\phi _{\rm w} $,$\sigma _{\rm f} \left( {\partial \phi _{\rm f} /\partial n} \right) = \sigma _{\rm w} \left( {\partial \phi _{\rm w} /\partial n} \right)$,下标f和w分别代表流体区和固体区.
由于磁流体边界层极薄[31],需要保证哈特曼层有3$\sim$5个网格,侧层内约15个网格,截面网格增长率不超过20%.在流向单位长度均布10个网格,固体域划分为10个网格,节点分布采用单向增长方式.导电方管总网格数为4 200 000.
2.3 数值方法
采用在开源软件OpenFOAM中自主开发的流固耦合低磁雷诺数磁流体求解器对控制方程进行求解.采用四步投影算法求解动量方程和质量连续性方程;采用结构网格同位相容守恒算法求解电势泊松方程、感应电流和洛伦兹力[32],采用边界耦合方法分别求解流、固区感应电势.求解器经过完备的有效性验证 [33].对流项与扩散项及电势项均采用"Gausslinear",时间项采用"backward",以保证空间与时间均达到二阶离散精度.速度、压力和电势的收敛标准分别为10$^{-7}$,10$^{-6}$和10$^{-7}$.计算的时间步长均为10$^{-4}$.
3 结果与讨论
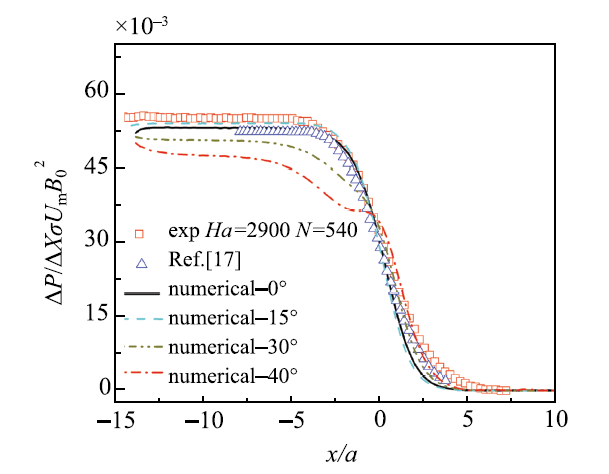
包层的总压降是液态包层设计的关键参数,它决定了整个磁流体循环回路的驱动功率.在非均匀磁场作用下,总压降分为均匀磁场段的完全发展压降和递减磁场段的三维磁流体压降.图2和图3显示了$\theta $ =0$^\circ$时压差的数值模拟结果与实验数据之间以及磁场倾斜时沿流向压差间的比较.
图2 轴向无量纲压力梯度沿流向分布
Fig.2 The dimensionless axial pressure gradient along the flow distribution
图3 横向无量纲横向压差沿流向分布
Fig.3 The dimensionless transverse pressure difference along the flow direction
图2中,$\theta $ =0$^\circ$及实验数据中的轴向无量纲压差均是取侧壁上($y$/$a $=~0,$z$/$a $=~0.9)压力梯度沿流向的分布.倾斜磁场时,侧壁上的无量纲压力梯度以$\theta $ =0$^\circ$为基准,取侧壁上倾斜相应角度后所在位置的数据带入计算进行比较.忽略拟合磁场与实验磁场存在的误差,磁场倾角为0$^\circ$时的数值解与实验值吻合良好,在磁场均匀段,数值解略低于实验值;在无磁场段压力梯度几乎为零,数值解与实验值完全重合,反映出外加磁场会导致磁流体产生远大于普通水力学的磁流体压降.随磁场倾斜,流向无量纲压力梯度整体趋势不变,但在磁场均匀段,$\theta$ = 0$^\circ$时的轴向压差比实验值小3.68%, 而$\theta $= 15$^\circ$时的模拟结果具有最高值. 进入递减磁场,$\theta$ =0$^\circ$的轴向压差比实验值小6.95%,目前发表的结果中磁场下降段和实验相比,误差均较大.
截面上哈特曼壁和平行壁的最大压差沿流向分布如图3所示.在磁场均匀段与无磁场段两个壁面的压差基本为零,而在磁场递减段出现了明显的三维磁流体压降,这是非均匀磁场导致的典型现象.对于导电方管,其数值解与实验值在磁场递减段的压差极大值处出现了较大偏差,原因可能为实验中该位置处于磁极边缘,真实的磁场为三维连续性磁场,而在模拟中只采用了一维双曲函数.通过对磁场倾斜角度进行模拟,发现压差极大值的误差有所减小,$\theta$ = 30$^\circ$时模拟结果的最大值比实验值的最大值高7.2%.且随磁场倾斜,截面横向压差增大.因此研究不同磁场倾角作用下导电方管中的流动状态具有重要意义.
倾斜磁场下整个流场的流动状态分布如图4所示($\theta =45^{\circ})$,可以清晰看出射流的位置由磁场均匀段的BD角在磁场递减段转移到AC角,且在流体流出磁场后,BD处的射流发生了转捩现象.因此将计算域分为倾斜磁场均匀段和倾斜磁场递减段两部分,分别对管道中的速度、电流和压降的分布进行分析,并分别对$\theta=0^{\circ}$,15$^\circ$,30$^\circ$和45$^\circ$的结果作图进行对比分析.
图4 流场内速度分布云图与电流流线图 ($\theta $ = 45$^\circ$)
Fig.4 The colored contours of the velocity distribution and current streamlines along the flow direction ($\theta $ =45$^\circ$)
3.1 倾斜磁场均匀段
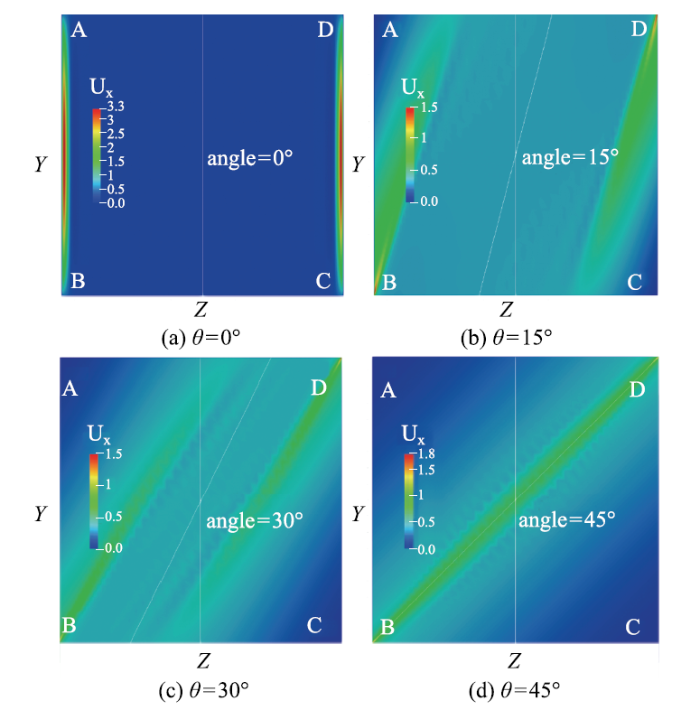
截面$x / a = -10$处,倾斜磁场均匀段的流向速度云图如图5所示,电势云图和电流分布如图6所示.速度分布依然具有明显的高速区和低速区,且高低速分界面与磁场倾斜方向保持平行.在$\theta =0^{\circ}$时,射流出现在侧层内,此位置处电流线与磁场方向几乎平行,洛伦兹力减小,形成射流.磁场倾斜后,电流随之倾斜,在高低电势的交界面电流线方向与磁场方向仍然保持局部平行,故高速区出现在哈特曼壁与侧壁的交界位置.随磁场倾斜后,管道垂直壁面相交处BD位置形成射流,该处射流是由与运动方向一致的洛伦兹力作用产生的.
图5 均匀磁场段横截面上的速度云图($x/a$~= $-$10)
Fig.5 The colored contours of velocity distribution with uniform magnetic field ($x$/$a $= $-$10)
在均匀磁场段,高电势区与低电势区有着明显的分界面,其方向与磁场方向始终保持平行,即电势梯度与磁场方向保持垂直,如图6所示.但只有在$\theta =0^{\circ}$,45$^\circ$时,截面上的电流方向与磁场方向完全垂直;在$5^{\circ}\le \theta \le 45^{\circ}$时,电流沿磁场方向呈反对称分布.受几何形状的影响,角BD处形成电流密集区,尤其在$\theta =45^{\circ}$时,角BD处电流密度最大.
图6 均匀磁场段横截面上的电流流线图与电势云图$(x/a = -10)$
Fig.6 The distribution of electric current streamlines and the colored contours of the electric potential with uniform magnetic field on the plane ($x$/$a $ = $-$10)
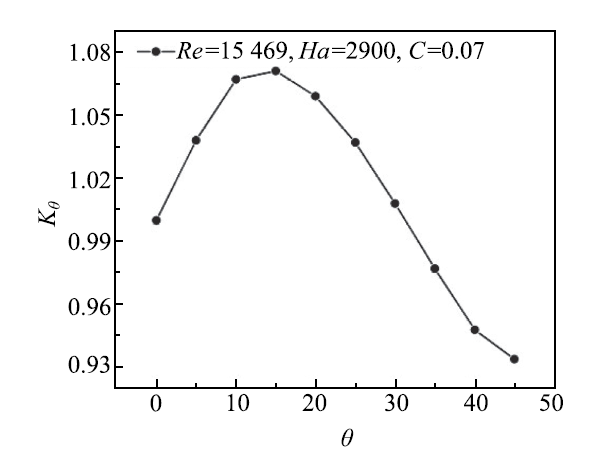
由图3可知,在磁场均匀段,同一截面上的压力值基本一致.取管道中心轴线上的压力梯度进行对比,以$\theta =0^{\circ}$时的压力梯度对其余磁场倾角下的压力梯度进行归一化.即先计算出$\theta = 0^{\circ}$时的流向压力梯度 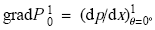
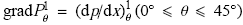
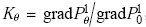
图7 均匀磁场段的流向无量纲压力梯度
Fig.7 The dimensionless pressure gradient along the flow direction with uniform magnetic field
3.2 倾斜磁场递减段
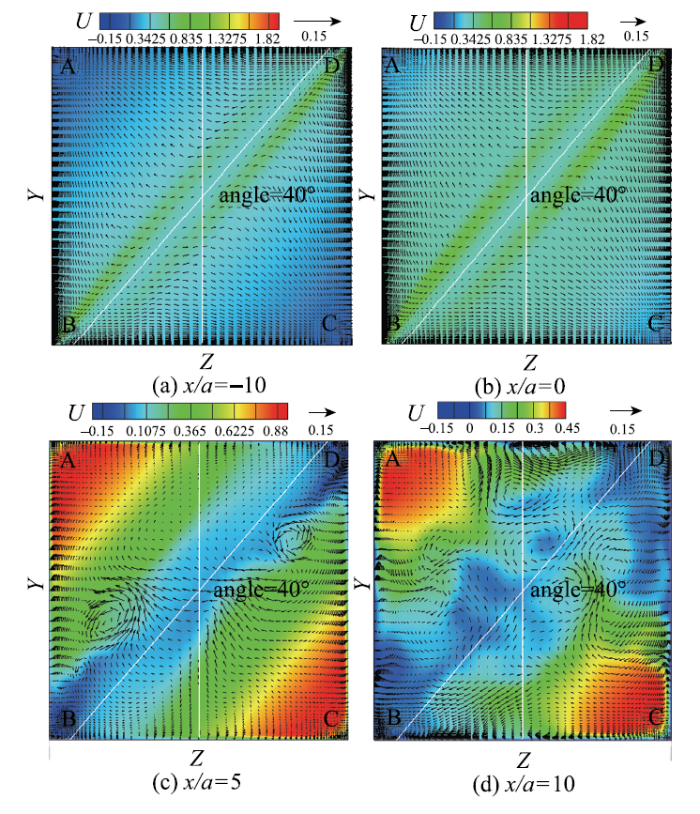
随磁场的递减,在管道出口处,速度分布与磁场均匀段的速度分布完全不同,如图8所示.高速射流区的位置由BD处(图5)转移到AC处,且在$\theta =45^{\circ}$时,截面上的速度呈现出显著的湍流分布.射流出现转移的原因是三维磁流体效应的作用,在磁场递减段,洛伦兹力将管道中心的流体推向管壁方向,随磁场强度的减弱,BD处的正向洛伦兹力急速衰减到零,综合作用下使得BD处的射流消失,AC处形成新的射流.且随着磁场的倾斜,磁流体在流出磁场后出现了层流向湍流的转捩,在数值模拟中,这种转捩首先发生在$\theta= 40^{\circ}$时,如图9所示. 磁场递减段$x$/$a $=0截面横向速度矢量图中并没有涡形成,但在流体流出磁场时,图9(c)中$x$/$a $=~5处截面的横向速度变大,并有两个速度涡形成,图9(d)中$x$/$a$= 10截面的横向速度矢量图中有更多涡形成.由于二次流形成的涡,流向速度在中心位置出现紊乱分布.
图8 出口截面的瞬时流向速度云图$(x/a=10)$
Fig.8 The colored contours of the instantaneous streamwise velocity at the outlet of the duct on the plane($x$/$a $ = 10)
图9 不同截面的流向速度云图和横向速度矢量图($\theta = 40^{\circ})$
Fig.9 The colored contours of the streamwise velocity and the transverse velocity vectors at different cross sections along the flow
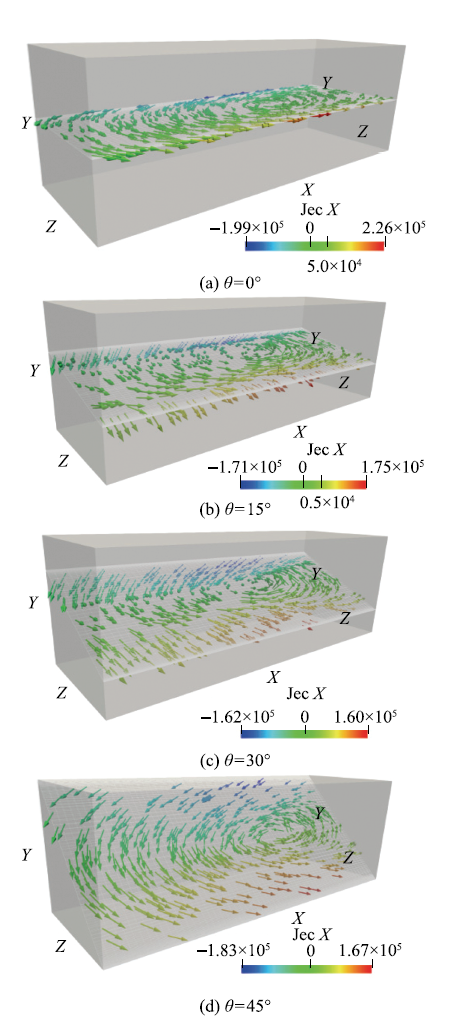
图10 不同磁场倾角下磁场递减段中三维电流分布
Fig.10 Three-dimensional electric current distribution with different angles under the decreasing magnetic field
磁场递减段的电流分布如图10所示.不同倾角下,在垂直于磁场的中心截面上均出现了沿流向的三维环形电流,且电流随磁场的倾斜而倾斜,与磁场方向始终保持垂直.
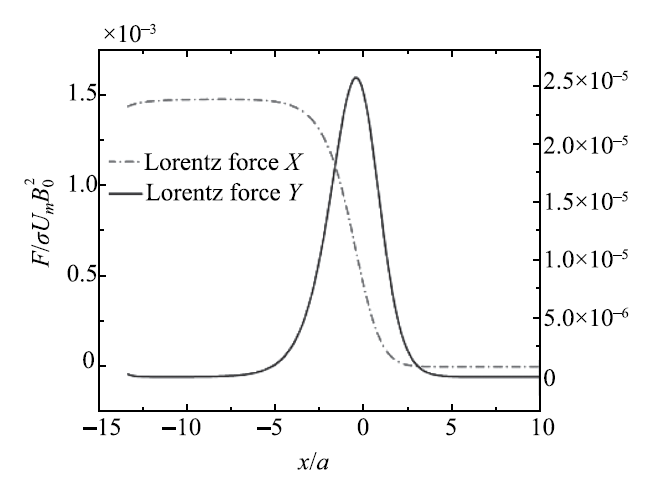
图11给出了$\theta = 0^{\circ}$时,磁场递减段垂直于磁场方向$y / a =0$截面上电流、洛伦兹力和压力分布.相比于磁场均匀段,在磁场递减段形成了逆时针方向的三维环形电流,通过对感应电流表达式取涡量来解释电流涡的成因
\begin{equation}\label{eq7} \left[ { \nabla \times J} \right]_z = - \sigma u\frac{\partial B_Z }{\partial x} - \sigma B_z \frac{\partial u}{\partial x}\tag{7}\end{equation}
由式7可知,在磁场递减段存在着较大的磁场梯度,因此等式右边第一项将对电流涡的形成起主导作用.右边第一项的符号为负,是电流涡呈逆时针方向的主要原因.图11中的三维电流涡,沿流向的电流密度在壁面处达到最大,根据右手定则判定洛伦兹力的方向,在壁面处势必会产生指向壁面的洛伦兹力,即形成将流体由中心向壁面推的趋势,因此导致壁面处的高速射流不因磁场的减弱而减小,反而再次加速.由于磁场递减段的洛伦兹力均由中心指向壁面,因此截面上的压力变为非均匀分布,中心区为低压区,侧壁面为高压区,从而产生额外的三维磁流体压降.
图11 递减磁场段电流、洛伦兹力和压力分布图 ($y/a $= 0,$\theta $ = 0$^\circ$)
Fig.11 The distribution of electric current, Lorentz force and pressure with the decreasing magnetic field on the plane $y$/$a $=0, $\theta $ = 0$^\circ$
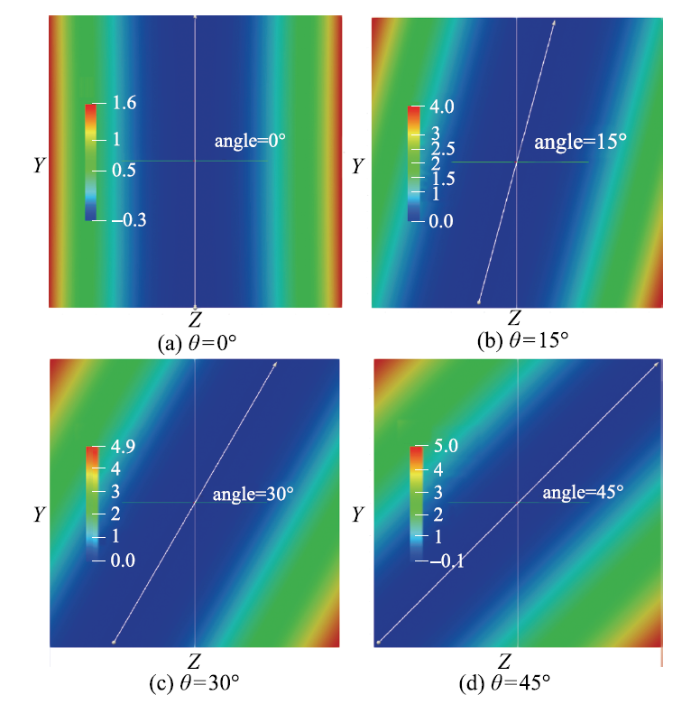
如图12所示,由于磁场沿流向递减,随磁场的倾斜,在相同截面上的压力分布随之倾斜,并呈现近似对称分布,其对称线过截面中心位置与磁场方向平行,压力梯度的方向与磁场方向垂直.即使在磁场下降段,随着磁场的倾斜,截面横向的压力梯度方向仍与磁场保持垂直.
图12 磁场递减段横截面上的压力云图$(x/a=0)$
Fig.12 The colored contours of the pressure at the cross section with decreasing magnetic field ($x$/$a = $0)
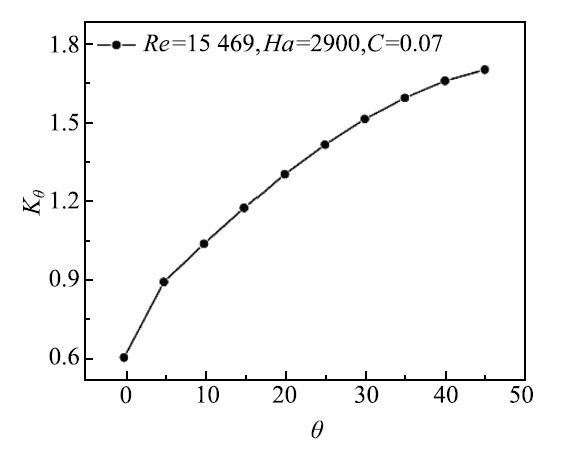
由图3可知,非均匀磁场产生的三维磁流体压降在$x/a $=0处有最大值,因此只需考虑最大压降即可. 以$x/a $=0截面上的最大压力和最小压力之差除以特征长度作为三维无量纲压力梯度gradP$^{2}$,除以相应倾角下的磁场均匀段的流向压力梯度gradP$^{1}$,即定义$R_{\theta}$=gradP$^{2}$/gradP$^{1}$,用来表示不同磁场倾角下,三维磁流体压降所占相应的磁场均匀段压力梯度的比值,以表征磁场倾斜对三维磁流体效应的影响.由图13可知,横向三维磁流体压降随磁场倾角的增加而非线性单调增大,当$\theta=0^{\circ}$时,横向三维磁流体压降是磁场均匀段压降的0.6倍,而当$\theta= 45^{\circ}$时,其值增加到1.71倍.
图13 递减磁场段无量纲三维磁流体压降
Fig.13 The dimensionless MHD pressure drop with the decreasing magnetic field
倾斜递减磁场作用下,管道夹角处射流的位置发生转移,流速的改变主要由洛伦兹力引起,图14给出了沿流向角B处洛伦兹力的分布情况.在磁场均匀段$( - 15 \le x / a \le -5)$洛伦兹力与流向方向相同,拉动流体快速流动,形成了角B处的射流;在磁场递减段($- 5 \le x / a \le5)$,与流向方向相同的洛伦兹力迅速衰减,导致角B处射流随之衰减.在三维磁流体效应的作用下,产生了指向$Y$方向的洛伦兹力,使角B处的射流逐渐转移向角A处.角D处射流的产生及转移原因与角B相同.
图14 管道90$^\circ$角B处沿流向洛伦兹力分布
Fig.14 The distribution of Lorentz force at the position B along the flow direction
4 结 论
倾斜非均匀磁场作用下导电方管中液态金属流体:
(1) 在倾斜磁场均匀段,随磁场倾斜角度增大,截面上的高低速分界面始终与磁场倾斜方向保持平行,电势梯度与磁场方向保持垂直,电流线沿磁场方向成反对称分布.压力梯度随磁场倾角的增加先增大后减小,最大压力梯度发生在倾角为15$^\circ$.
(2) 在倾斜磁场递减段,不同的磁场倾角作用下,相同截面上的压力逐渐呈不均匀分布,压力梯度的方向始终与磁场方向垂直;由于磁场的衰减,三维磁流体压降随磁场倾角的增加而增大,并使管道夹角处射流的位置发生了转移,且随着磁场的倾斜,磁流体在流出磁场后出现了层流向湍流的转捩现象,本文的计算中转捩现象首先发生在倾角为40$^\circ$时.当磁场倾斜后会引起更大的横截面磁流体压降,侧壁面的射流峰值减小,且向垂直磁场方向管道壁面相交的夹角处转移.截面上射流峰值的变化和转移是由洛伦兹力在同一位置沿流向的变化所引起的.
在液态包层的设计中需要考虑倾斜非均匀磁场磁流体效应引起的速度、压力的分布变化及复杂流动现象.
致谢
本文作者衷心感谢美国阿贡国家实验室Dr. Claude B. Reed和他的同事提供的图2和图3中未曾发表的实验数据.
The authors have declared that no competing interests exist.
参考文献
| [1] |
Present understanding of mhd and heat transfer phenomena for liquid metal blankets . |
| [2] |
MHD and heat transfer considerations for the us DCLL blanket for DEMO and ITER TBM .
|
| [3] |
MHD therm of luid issues of liquid-metal blankets: Phenomena and advances .
|
| [4] |
Turbulent-laminar coexistence in wall flows with coriolis, buoyancy or lorentz forces . |
| [5] |
沟槽方向对湍流边界层流动结构影响的实验研究 .Flow structure in the turbulent boundary layer over directional riblets surfaces . |
| [6] |
Experimental investigation and theoretical analysis of two-dimensional magnetohydrodynamic effects in a rectangular duct .
|
| [7] |
Layout of an experimental liquid-metal circuit based on MHD considerations .
|
| [8] |
FCI related MHD experimental and the oretic results from SWIP LMEL facility//9th. China-Japan Symposium on Materials for Aolvanced Energy System and Fission & |
| [9] |
等离子体激励器诱导射流的湍流特性研究 .Investigation on the turbulent characteristics of the jet induced by a plasma actuator . |
| [10] |
哈特曼边界层的初级稳定性分析 .
The primary stability analysis of Hartmann boundary layer .
|
| [11] |
Direct numerical simulations of transverse and spanwise magnetic field effects on turbulent flow in a 2:1 aspect ratio rectangular duct .
|
| [12] |
低磁雷诺数不可压缩磁流体槽道湍流电场相关特性的直接数值模拟 .
Direct numerical simulation of turbulent field correlation in a low magnetic Reynolds number incompressible magnetic fluid channel.
|
| [13] |
Liquid magnetohydrodynamics --- recent progress and future directions for fusion . |
| [14] |
Experimental facility for studying mhd effects in liquid metal cooled blankets . |
| [15] |
Experimental and analytical investigations of magnetohydrodynamic flows near the entrance to a strong magnetic field .
|
| [16] |
Liquid-metal flow in a thin conducting pipe near the end of a region of uniform magnetic field .
|
| [17] |
ALEX results: A comparison of measurements from a round and a rectangular duct with 3-D code predictions // |
| [18] |
Experimental investigation of 3-D MHD flows at high hartmann number and interaction parameter.Liquid Metal Magnetohydrodynamics .
|
| [19] |
MHD thermal hydraulic analysis of three-dimensional liquid-metal flows in fusion blanket ducts .
|
| [20] |
Sidewall flow instabilities in liquid metal MHD flow under blanket relevant conditions . |
| [21] |
Analyticmodels of heterogenous magnetic fields for liquid metal flow simulations . |
| [22] |
Effects of the consistency of the fringing magnetic field on direct numerical simulations of liquid--metal flow . |
| [23] |
Direct numerical simulation of turbulent liquid metal flow entering a magnetic field . |
| [24] |
Turbulent duct flows in a liquid metal magnetohydrodynamic power generator . |
| [25] |
Effect of fringing magnetic field on magnetohydrodynamic flow in rectangular duct . |
| [26] |
Laminar pipe flow at the entrance into transverse magnetic field . |
| [27] |
Numerical investigation of natural convection in a rectangular cavity under different directions of uniform magnetic field . |
| [28] |
Hall effects on MHD flow in a rotating channel in the presence of an inclined magnetic field . |
| [29] |
Effects of hall current and rotation on unsteady mhd couette flow in the presence of an inclined magnetic field . |
| [30] |
|
| [31] |
Magnetohydrodynamics . |
| [32] |
A current density conservative scheme for incompressible mhd flows at a low magnetic reynolds number. Part I: On a rectangular collocated grid system . |
| [33] |
基于OpenFOAM 的投影法磁流体求解器开发与验证 .Liu Ke et al. Development and validation of magnetohydrodynamic solver with projection in OpenFOAM environmentNuclear . |

/
| 〈 |
|
〉 |