引 言
地球自诞生以来就不断受到地外天体撞击,这些撞击事件对地球的环境和生命演化产生了至关重要的影响.在人类文明高度发达的今天,如何避免或减弱地球受到地外天体的灾难性撞击,尽可能减小人员和财产损失、维持人类社会的持续发展已成为国际社会的一个热点问题.
天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害.
1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝.
我国也多次发生过小行星撞击事件. 1976年3月8日,在吉林市北郊上空一个大火球从天而降,随即分裂成许多小火球.在地面收 集到3000余块总重2t的陨石,其中最大的一块陨石重达1170 kg,是世界上已知最重的石陨石[13 ] .最近的流星陨落事件发生在2017年10月4日云南香格里拉以及2018年6月1日云南西双版纳,被大量目击者观察到并用视频记录下来.
国际社会对行星防御非常重视[14 ] .2013年和2014年美国政府和军方举行联合应急演习,2016年1月NASA成立行星防御协调办公 室.美国、欧空局和日本等均成立了专门的近地天体监测预警中心,实施和部署了若干对于近地天体直接探测以及轨道偏离计划.自2009年起国际宇航科学院(IAA)已经举办5届行星防御会议. 在2012年国际空间探索协调组(International Space Exploration Coordination Group,ISECG)会议上,经12个成员国协调,将"试验减缓近地小行星撞击地球风险的方法"定为小行星探测的三项基本目的之一.2013年10月联合国大会正式批准成立"国际小行星预警网"来组织、协调、共享近地小行星监测资料以及碰撞地球的风险信息.
我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨.
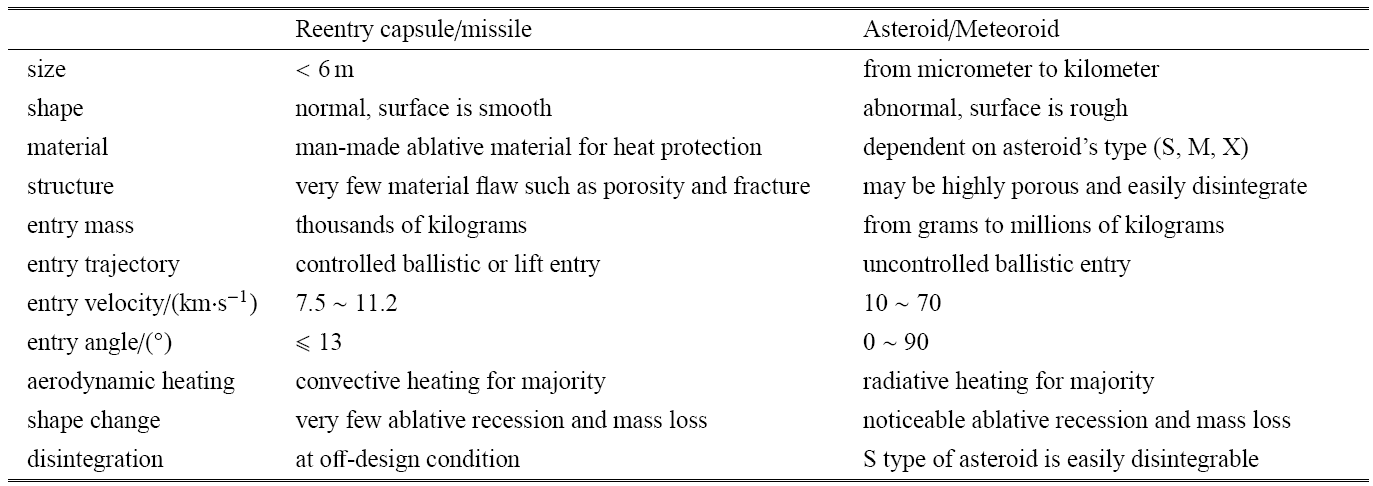
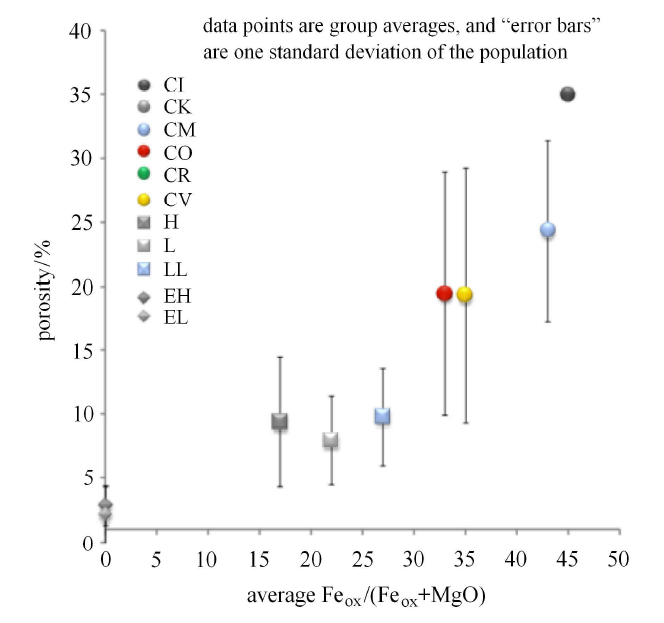
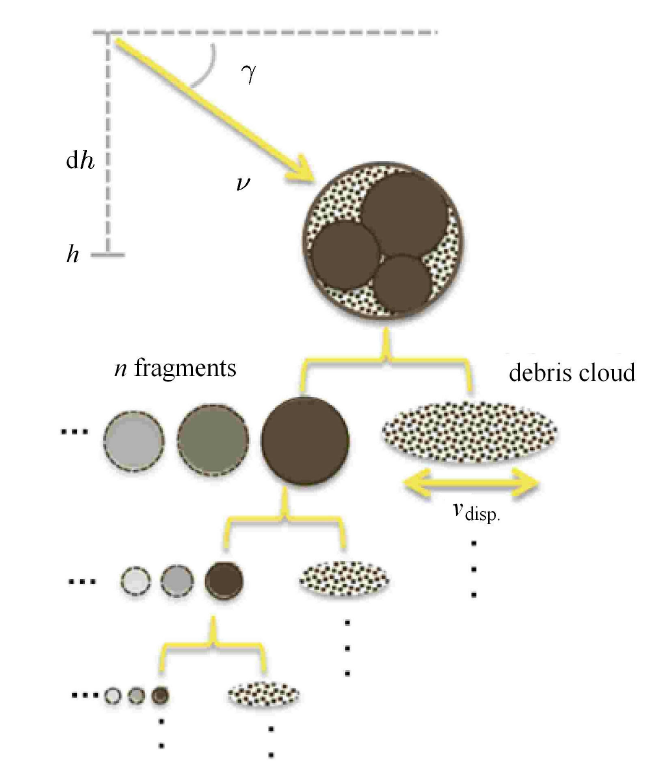
小行星进入地球大气与撞击地球表面过程中将会发生非常复杂的物理化学和力学现象[4 -5 ,28 ] (图1 ).小行星进入地球大气速度极高(典型速度12 ~ 20 km/s),远超人造航天器的再入速度(7.5 ~ 11.2 km/s).极大的进入速度产生巨大的气动加热,使得激波层温度超过20 000 K,产生远超对流热流的辐射热流;严酷的热环境引起材料大规模熔融、汽化和烧蚀,导致严重的质量损失和外形变化.与航天飞行器经过人类精心设计的材料和结构不同,小行星的材料和结构是自然形成的,不仅呈现各向异性的特征,而且充满孔隙和裂纹,在强大的气动力、热载荷的共同作用下可能多次解体,甚至产生空中爆炸形成火球.当大尺寸小行星穿透大气层撞击地球表面后,可能会产生撞击坑、反溅碎片云、地震和海啸等现象,其反溅碎片云抛向大气甚至影响气候变化.
图1 小行星撞击地球过程中的典型现象
Fig.1 Typical phenomena of asteroids impacting Earth
在上述现象背后存在着复杂的科学问题. 总的来说,对于小行星撞击地球,存在超高速空气动力学和超高速碰撞动力学两个方面的问题.本文对这些问题进行了分析、梳理和归纳,并从地面试验和数值计算两方面指出研究手段的现状和不足,提出需要开展深入研究的方向和课题.
由于小行星撞击地球可能造成的严重危害,需要建立小行星进入与撞击效应分析评估技术. 本文综合小行星进入地球大气层的弹道方程、质量损失方程、解体模型以及空爆火球在地面所导致的超压和热辐射损伤模型等,初步建立了小行星进入与撞击效应分析评估方法,并以Chelyabinsk和Tunguska两次流星事件为例进行计算分析.
1 超高速空气动力学问题
小行星撞击地球的超高速空气动力学问题主要存在于进入大气过程中,总共有五个方面的问题:极高速进入条件下的气动力与轨迹;极高速进入条件下的小行星气动加热与烧蚀机理;极高速气动加热条件下的小行星结构传热与热响应;极高速进入条件下的高温气体效应;小行星进入过程的物理特征. 下面分别进行阐述.
需要说明的是,本文中的极高速特指小行星撞击地球的典型速度:12~20 km/s.
1.1 极高速进入条件下的气动力与轨迹
小行星在大气中的运动服从牛顿运动定律,其速度变化的微分方程为
$$ \dfrac{{\rm d}V}{{\rm d}t} = - C_{\rm d} \cdot \dfrac{1}{2m}\rho _{\rm air} V^2 \cdot A - g\sin \gamma+ \\ \qquad \omega ^2r_{\rm t} \cos \phi \left( {\sin \gamma \cos \phi - \cos \gamma \sin \psi \sin \phi } \right) (1)$$
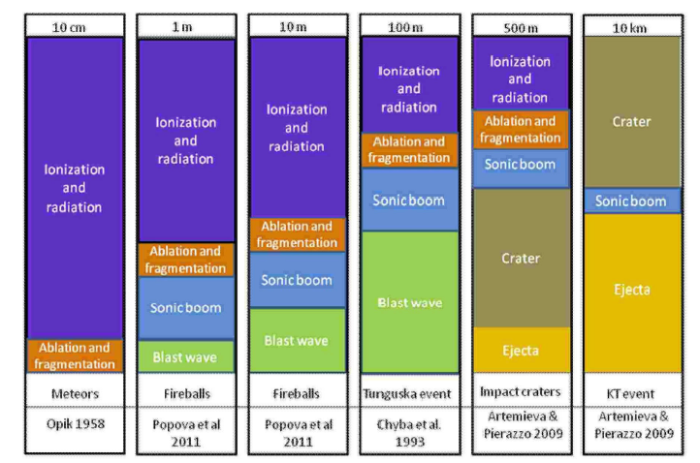
其中,$m$和$V$分别是小行星的质量和速度, $\varPhi $是纬度,$\gamma $和$\psi$分别是飞行航迹角和航向角,$\omega $是地 球自转角速度,$g$是重力加速度,$r_{t}$是小行星距地心的距离,$A$是阻力参考面积. 而$C_{ d}$是阻力系数,与小行星的流动分 区紧密相关.若定义克努森数(Knudsen number, $Kn$)为气体分子平均自由程与流动特征长度的比值,根据20世纪40年代钱学森等[29 ] 提出的准则,流动区域范围大致分为:连续流区(Kn<10- 3 )、过渡流区(10-3 <Kn<10)、自由分子流区(Kn>10);过渡区气体 流动又可细分为近连续流(10-3 <Kn<0.01)、滑移流(0.01<Kn<0.1)、稀薄过渡流(0.1<Kn<10)等. 图2 展示了以小行星半 径作为流动特征长度、基于上述克努森数划分的小行星在不同海拔高度的流动区域.若考虑小行星从高度100 km进入地球大气,对 于我们感兴趣的小行星比如Chelyabinsk流星(半径9.9 m),在100~94 km之间为滑移流,94~79 km之间为近连续流, 当飞行至79 km以下为连续流.因此小行星进入地球大气过程中气动力的模拟是典型的跨流域空气动力学问题. 几十年来,伴随着各种再入飞行器和临近空间飞行器的研制,跨流域空气动力学得到长足发展,已经建立起来基本的地面试验和数值计算手段.但是仍然存 在很多问题[30 ] ,例如对跨流域流动机理认识不清、模拟方法有待完善、计算和试验精度有待提高等.可以设想,当飞行速度从目前研究的范畴(小于第二宇宙速度)提高到小行星进入地球大气的速度时,上述问题不仅一直存在,而且在更加复杂的物理化学现象的耦合下会更加严重.
图2 基于克努森数和小行星半径的流动分区图
Fig.2 Flow regime based on Knudsen number and meteoroid radius
对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离.
小行星解体后形成碎片云的变形往往依靠下式预测[36 ]
$$V_{\rm disp} = V\sqrt {C_{\rm disp} \rho _{\rm air} / \rho } (2)$$
其中,$V_{\rm disp}$是碎片云的扩散速度,$V$是飞行速度,$\rho_{\rm air}$和 $\rho $分别是大气及小行星密度. 但是扩散系数$C_{\rm disp}$并不确定,不同研究者给出的取值往往差异较大$^{[36 -37 ] }$. 此外,目前在理论上还无法确定[8 ] 扩散后碎片云半径与解体前小行星初始半径的比值大到多少时,碎片云中小碎片(液滴、灰尘)彼此之间不存在气动干扰,以至于碎片云在气动上不能作为一个整体对待.
1.2 极高速进入条件下的小行星气动加热与烧蚀机理
在极高的进入速度下,小行星将经历严酷的气动加热,准确预测热环境是评估烧蚀和质量损失的前提. 质量损失可用下式描述[28 ,31 ,33 ]
$$\dfrac{{\rm d}m}{{\rm d}t} = - \dfrac{1}{2}\rho _{\rm air} V^3A\sigma (3) $$
$$\sigma = \dfrac{C_{\rm H}}{Q} (4) $$
其中,$\sigma $是烧蚀系数,$C_{\rm H}$是热流系数,$Q$是烧蚀热,$A$是参考面积.
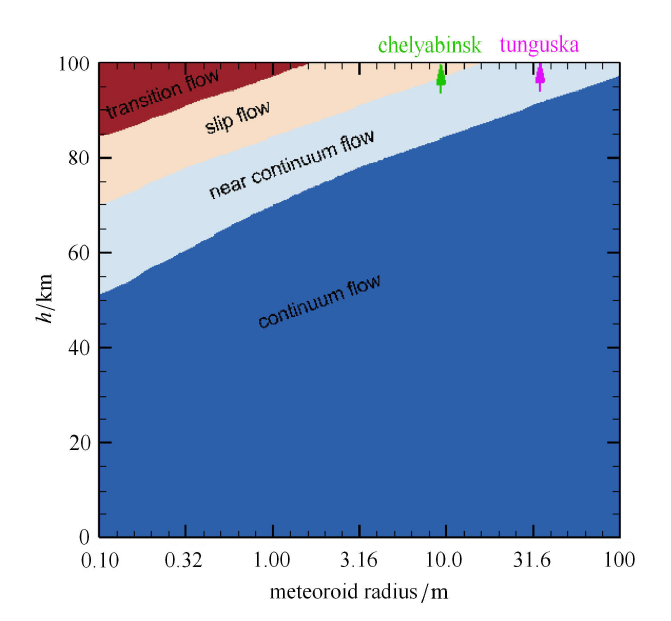
热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题.
图3 半径15 m球头的热流分布[38 ]
Fig.3 Heat flux distribution along a sphere surface with radius of 15 m[38 ]
烧蚀热$Q$由小行星材料种类和烧蚀机理决定.典型再入飞行器热防护系统的材料是经过人为设计的烧蚀防护层,以硅基和碳基烧蚀材 料为主.小行星材料是天然形成的,大致分为三类[43 ] :铁陨石、石-铁陨石、石陨石.因而在航天器再入研究中建立的烧蚀机理不再适用于小行星材料,需要针对具体的小行星材料研究烧蚀机理.具体来说需要研究的问题包括:小行星材料的气面反应机制、物面的质量和能量平衡机理、熔融层的运动对烧蚀的影响、烧蚀引起的质量引射对气动力/热的影响.
1.3 极高速气动加热条件下的小行星结构传热与热响应
小行星是天然形成的,其结构并不像人类加工材料那样多呈现各向同性,而是通常情况下呈现各向异性,因此需要研究各向异性材料和结构的传热及热响应.研究指出,由于在漫长的历史演化中与其他天体碰撞和风化作用,大多数小行星结构具有较高的孔隙率[44 ] (图4 )和裂纹[45 ] (图5 ). 孔隙和裂纹对结构响应有着重要影响.
图4 球粒状陨石孔隙率随铁元素氧化态的变化[44 ]
Fig.4 Porosity vs. oxidation state for chondrite Falls[44 ]
图5 球粒状陨石的裂纹[45 ] (伦敦自然历史博物馆)
Fig.5 Fractures in a chondrite meteorite exhibited in Natural History Museum, London[45 ]
解体爆炸是小行星进入地球大气中的常见现象.解体爆炸的机理是什么?目前国外天文界广泛应用的解体判据[4 -5 ] 认为:当驻点压力$P$超过强度$S$,小行星就会解体,即
$$P=\rho_{\rm air} V^2 >S (5)$$
由于小行星的力、热载荷分布不均匀,并且孔隙、裂纹以及材料熔融和烧蚀会减小强度,上述解体判据略显粗糙,需要研究更准确、更能代表解体机理的解体判据以应用于地面危害评估. 根据Popovao(2011)对大量观测结果的总结[46 ] ,0.1~10$^{6}$\,kg质量范围的石质小行星的解体强度为0.1~10 MPa,而材料的平均拉伸强度为30 MPa,压缩强度和屈服强度更大.解体强度$S$与小行星的实际强度存在什么关系,怎样获得初次解体时的强度,需要进行研究.解体强度也和小行星尺寸有关,Weibull通过对地球上岩石强度的观测和分析,总结出Weibull定律[47 ] ,Artemieva和Wheeler$^{[33 ,48 ] }$将其应用于解体后碎片强度的计算中,即
$$ \dfrac{S_{\rm c} }{S_{\rm p} } = \left( {\dfrac{m_{\rm p} }{m_{\rm c} }} \right)^\alpha (6) $$
其中,下标"c"表示子碎片,下标"p"表示父碎片. Popovao发现很多违反Weibull定律的事实[46 ] .例如Morávka流星[32 ] 的主解体事件发生时的动压为5 MPa,而后面的一次解体却发生在更小的动压2.3 MPa下,并且地面收集到碎片没有烧蚀痕迹,表明在2~3 km/s较低速度下(烧蚀停止)仍存在解体.因此,需要研究Weibull之外的解体强度与碎片尺寸的关系.
解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性.
1.4 极高速进入条件下的高温气体效应
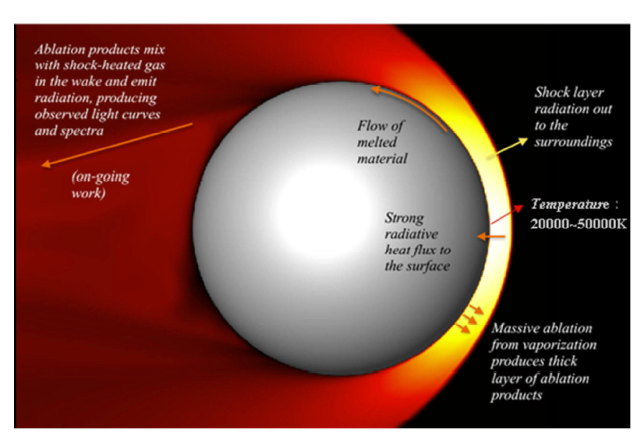
如图6 所示,在小行星进入大气层的极高速度下,小行星驻点区的空气将处于20 000~50 000K的高温,除了出现传统再入物理所关心的振动和电子能级激发、离解、电离以及能量松弛等非平衡现象,还会出现二次电离现象并产生新的组分如N$^{ + + }$, O$^{ + +}$等[51 -52 ] ;分子中的电子受到激发,在各能级之间跃迁并发射或吸收光子,产生严重的激波层辐射[51 -52 ] ;在严酷的热环境下,小行星材料受到大规模烧蚀,物面的液体熔融层在气流的作用下向后移动,烧蚀气体在物面附近产生较厚的烧蚀层[51 -52 ] ;大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射.
图6 极高速下的高温气体效应示意图[52 ]
Fig.6 Sketch of high temperature effect at ultra-high velocity[52 ]
当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题.
传统的气动热力学研究主要针对速度在第二宇宙速度之下的超高速飞行器,流场温度通常低于20 000 K,此时,高温激波层辐射对流动及相关物理化学过程的影响可以忽略.在小行星进入地球大气的极高速、极高温、强辐射和强烧蚀环境下,高温气体流场、辐射和烧蚀强烈耦合[39 -40 ,51 ] ,必须考虑三者之间的相互影响.文献[39 ,51 ] 的研究指出,在流场计算中耦合辐射减小了激波脱体距离,降低了激波层温度;在流场计算中耦合烧蚀大大降低了物面辐射热流.
1.5 小行星进入过程的物理特征
在小行星进入地球大气过程中,主要存在如下物理特征:空中解体爆炸波及其引起的地面超压和风,火球的光辐射,火球的热辐射,音爆(sonic boom)、次声(infrasonic sound). 这些物理特征是观测小行星进入过程的对象,也是重要的科学问题.
空中爆炸是小行星(尤其是石质小行星)进入过程显著的现象之一[4 -5 ] .
空中爆炸发生时,爆炸波向地面传播,在地面形成超压,且在爆炸波波前后面的低压区因周围空气的补充形成风,对地面人员和设施造成危害.在Chelyabinsk流星事件中,大量建筑物窗户的玻璃受到地面超压的破坏而震碎[9 ] .在Tunguska流星事件后,发现地面大范围的树木呈幅状倒伏且未收集到陨石,研究者认为这是地面超压造成的[6 ] .
在小行星物理中,把超高速飞行以及空中爆炸产生的高温流场称为"火球"[4 ] .火球能够产生较强的光辐射,可被肉眼或仪器 观测到,是小行星撞击地球最显著的特征.光辐射数据通常可转换为能量沉积数据[9 ] ,是小行星进入地球大气过程最重要的观测数据之一,可用于校验模拟方法或作为模拟的输入[58 ] . 图7 是Chelyabinsk流星事件的视频截图,从中可以看到火球较强的光辐射.
图7 Chelyabinsk流星事件视频截图[58 ]
Fig.7 Video capture of Chelyabinsk event[58 ]
火球不仅产生光辐射,也存在热辐射效应[4 ] . 从本质上讲,光辐射和热辐射是火球产生的电磁辐射在不同波段范围内的表现形式. 热辐射会导致地面人员的热灼伤,严重时引发火灾. 在Chelyabinsk流星事件中,很多人报告感受到火球的热辐射[9 ] . 在Tunguska流星事件中,发现地面树木有大范围燃烧的痕迹[6 ] .
在小行星进入地球大气过程中,还会有声学方面的问题. 至少存在二类声信号,分别是音爆[59 ] 和次声[60 ] . 小行星进入过程音爆的形成机理与超声速飞机类似,都是超声速飞行产生的激波向地面传播形成的. 不同的是,小行星飞行马赫数极高,马赫数极小,形成的激波形状类似圆柱形,且激波强度更大. 次声信号是空中爆炸产生的低频率声波,是空中爆炸的重要特征之一[60 ] . 研究人员可根据地震台站监测到的次声信号以及地震站位置,分析得出小行星的解体时序和进入轨迹[32 ,60 ] .
此外,当人类采用雷达设备探测并研究小行星进入过程时,还会存在小行星对雷达波的电磁散射特征. 与传统的再入物理类似,这里面包含小行星本体和高温流场的电磁散射.
2 超高速碰撞问题
小行星撞击地球表面可分为撞击陆地与海洋两种情况,陆地表面在受撞击后将出现地震效应,而海洋表面受撞击后可能会产生海啸,两种受撞击情况又都伴随着撞击成坑以及碎片反溅等现象. 下面从陆地撞击成坑与反溅碎片云、海洋撞击与海啸、撞击过程的地震效应等三个方面,对小行星撞击地球的超高速碰撞动力学问题进行分析.
2.1 陆地撞击成坑与反溅碎片云
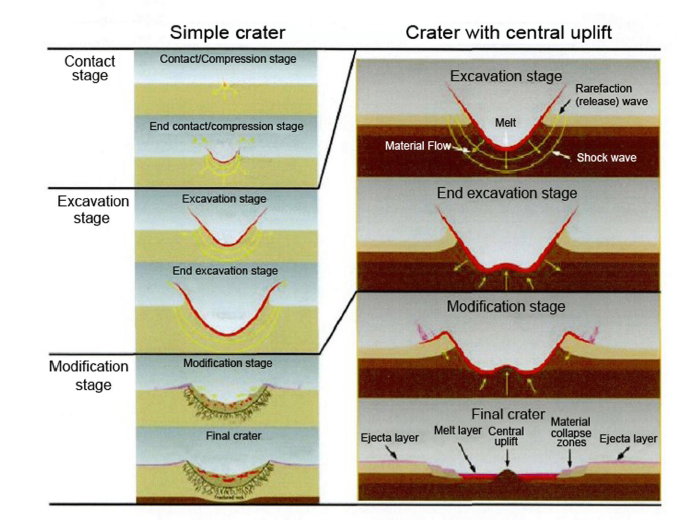
小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ]
$$ D_{{\rm crat}} = \left( {\dfrac{Y}{0.952}} \right)^{1 / 3} (7) $$
其中,$D_{\rm crat}$为撞击坑直径,$Y$是以百万吨(Mt)TNT当量为单位的小行星撞击能量.
图8 撞击坑形成过程[61 ]
Fig.8 Sketch of cratering process[61 ]
碰撞产生的强冲击波还将引起小行星和地表介质气化,甚至导致小行星完全蒸发.地表介质气化质量可达到小行星质量的数倍,并可能 抛射到较高大气层. 与此同时,小行星体积60~100倍的地表物质被掘起,以反溅碎片的形式连同挥发性物质一起被抛向天空,其高度可达100 km以上[66 ] .研究表明[67 ] ,地表介质在小行星撞击下的气化质量$M_{\rm R}$与撞击小行星的质量$m$、速度$V$以及引起介质气化所需的最小 速度$V_{\rm R}$有关,其量级可用下式计算
$$ M_{\rm R} ~ m\left( {\dfrac{V}{V_{\rm R} }} \right)^2 (8)$$
由于小行星撞击陆地是一个多尺度、多材料和多物理因素耦合的问题[68 ] ,式(7)和式(8)的普适性有待进一步研究.
影响撞击成坑与反溅碎片云两种现象的典型物理因素较为一致. 将成坑尺寸与反溅碎片云质量和速度作为撞击的典型特征,研究适用于撞击过程的缩尺律关系是小行星撞击陆地表面研究的核心内容之一,也是开展地面缩比试验研究的前提. 小行星撞击陆地表面过程中的材料属性(包括密度、强度、孔隙率等)、撞击速度以及撞击角度等都对最终撞击特征有着重要的影响[69 ] ,研究各因素与成坑尺寸、反溅碎片云质量和速度等撞击特征之间的函数关系、拟合经验公式,是研究中的典型问题. 相比于超高速动能武器研究和空间碎片防护中的超高速碰撞问题,小行星与地球陆地表面有着完全不同的材料,需要研究撞击过程中地表材料的物理和力学性质,完善超高速撞击下材料特性的模型. 此外,小行星撞击后地面坑形的形貌特征和成坑的分界条件也是需要研究的问题.
当大尺度(千米级)小行星撞击地球表面时,引起的反溅碎片云及其在大气中的传播可能会导致严重的气候变化,需要进行特别关注和研究.
2.2 海洋撞击与海啸
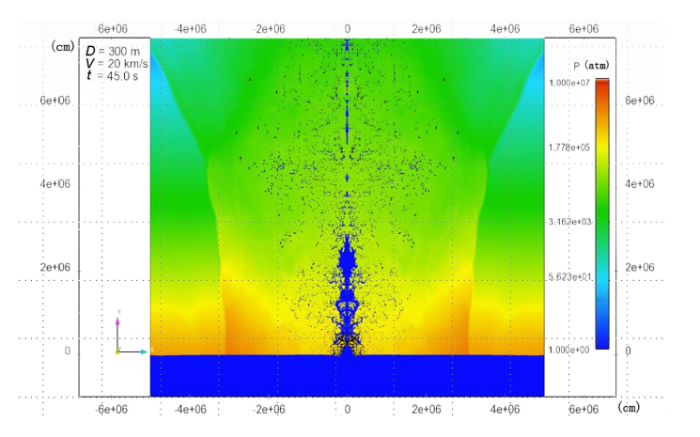
海洋面积约占地球表面总面积的70%,海洋水体是小行星撞击地球表面最主要的靶标对象. 相比于撞击陆地的情况,撞击成坑与反溅碎片云并非撞击海洋中最值得关注的典型现象. 在小行星撞击海面后的数十秒内,大量海水被排开,小行星甚至可能撞击海底并进一步接触地幔[70 ] . 小行星撞击海洋后,将会把大量的海水反溅或蒸发入大气中. 研究指出[71 ] ,当半径5 km的小行星撞击海洋时,会蒸发其质量4倍的海洋水汽. 此外,如果撞击到海底,在抛向大气的材料中,还包含地表、地幔和小行星材料[70 ] . 图9 展示为中国空气动力研究与发展中心超高速碰撞中心运用NTS软件仿真小行星撞击海面的压强云图.
图9 撞击海面反溅碎片云压强云图(二维,$D = 300$\,m,$V=20$\,km/s)
Fig.9 Pressure distribution of ejecta debris caused by asteroid impacting the ocean(2D,$D = 300$ m,$V = 20$ km/s)
海啸是小行星撞击海洋过程中最典型的自然现象. 当小行星撞击海洋时,将迅速挤压海水,产生的冲击波在水体内传播,引起海啸,产生一定高度的"海墙"在海面传播. 据研究,直径1 km的小行星撞击在1000 km以外海域仍能形成100 m高海啸[72 ] . 据报道,有颗名为Eltain直径4 km的小行星,曾撞击到南太平洋底部,在距其1 200~1 500 km远的海域引起高度达到200~300 m的海啸[73 ] . 小行星撞击海洋表面的破坏半径比撞击陆地更大,破坏半径大约与小行星撞击能量的1/2次方成正比[74 ] . 海啸形成高度可通过拟合公式来表示[36 ]
$$ h_{\rm w} = 22.7\left( {\dfrac{Y}{10}} \right)^{0.54}\dfrac{1000}{r} (9)$$
其中,$h_{\rm w}$是海啸高度,$Y$是以十亿吨(Gt) TNT当量为单位的小行星动能,$r$是以千米为单位的距撞击点距离.
撞击海洋研究需要考虑水体作为靶标材料的特殊性. 海啸的产生与传播是小行星撞击海洋研究中的核心问题. 当前描述撞击产生海啸的模型还不够精确,并且难以开展地面试验研究. 利用式(9)计算海啸高度略显粗糙,需要研究的内容包括:小行星直径、速度和撞击角度等撞击参数对海啸高度的影响;撞击前、撞击过程中和撞击后冲击波在水体中的传播机制以及对海岸线的破坏作用;海啸对沿岸威胁的危害评估模型[75 ] .
2.3 撞击过程的地震效应
小行星撞击地表后产生极强烈的冲击波,冲击波的传播可以诱发地震. 小行星撞击过程中,大部分能量用于成坑,小部分能量用于产生地震效应. 文献[36 ] 给出震源处里氏震级与撞击能量的关系式
$$ M = 3.9 + 0.7{\rm lg}\left( {\dfrac{Y}{kt}} \right) (10)$$
其中,$M$为里氏震级数,$Y$是撞击总能量,$k$是影响参数,$t$是传播时间.
针对小行星撞击过程的地震效应,考虑到地震的产生与传播主要与小行星撞击后冲击波的传播有关,需要研究冲击波在地球表面的产生、传播与衰减机制以及地震的演化规律,从而推导地震强度与小行星直径、撞击速度、传播距离和时间的关系式.
3 研究手段的现状和不足
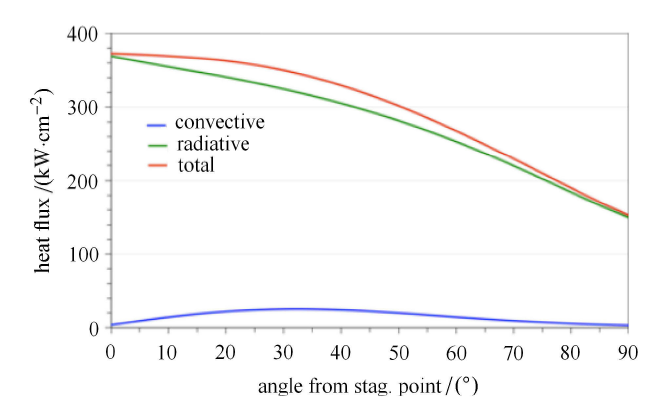
表1 从尺寸、形状、速度、材料等方面对小行星进入地球大气与返回舱、再入弹头等超高速飞行器再入地球大气进行了比较.由于问题的相似性,小行星进入与撞击问题可用目前的超高速空气动力学和超高速碰撞动力学中的研究手段进行研究,然而由于在速度、材料和结构上存在较大差异,现有的研究手段存在很多不足.
3.1 地面试验
小行星进入速度极高,典型速度为12~20 km/s,对应的风洞试验气流总焓为72~200 mJ/kg. 如果要在地面试验设备中对前述超高速空气动力学和超高速碰撞动力学问题进行研究,则气流速度、模型的飞行速度或者气流总焓必须达到小行星撞击地球时的量值. 当然,可以根据地面试验相似准则设计风洞试验,降低模拟难度,从而对某一个具体问题进行研究. 但是由于小行星撞击地球中的超高速问题异常复杂,很多问题都耦合在一起,只有地面试验条件达到小行星撞击地球时的速度或总焓,才能反映问题的本质,模拟结果才可靠有效.
目前超高速空气动力学和超高速碰撞动力学地面试验设备根据运行原理可分为五类,分别是高超声速风洞、激波管/风洞、电弧加热器/风洞、等离子体风洞和弹道靶.
高超声速风洞是常规高压下吹暂冲式风洞,一般不能正确模拟高焓流动[76 ] . 美国AEDC 9号风洞以及中国空气动力研究与发展中心的$\Phi 1$ m高超声速风洞都属于此类风洞. AEDC 9号风洞的试验能力为[76 ] :马赫数7~16.5;总压$<140$ MPa;总温$<2 000 $K.
激波管/风洞通过运动激波对气体进行加热,通过喷管使气流加速,是模拟高焓流动的主要设备之一,缺点是运行时间较短(毫秒量级)[76 ] . 美国LENS系列激波风洞代表了这一类型风洞的发展水平,其主要参数为[76 -77 ] :速度$ \leqslant $13 km/s;试验时间$ \leqslant $100 ms.
电弧加热器/风洞[76 ,78 ] 利用高电压直流产生电弧并加热驻室气体,从而形成高温热气流,并通过喷管使气流加速到一定速度,能够复现再入过程的高焓,常用于材料烧蚀试验. 缺点是产生的气流经常受到污染或者不均匀. 意大利的SCIROCCO电弧加热器在世界上这一类型设备中功率最大,其试验能力为[76 ,78 ] :总焓2.5~45.0 mJ/kg;功率$ \leqslant $70 mW.
高频等离子体风洞[79 ] 采用感应加热的方式产生等离子体,主要用于航天飞行器防热材料表面催化、氧化、辐射特性、材料光电特性、高温气体辐射特性以及等离子体与电磁波相互作用特性等方面的研究与试验. 作为这一类型风洞的典型代表,中国空气动力研究与发展中心1 mW高频等离子体风洞的运行参数为[80 ] :总焓10~60 mJ/kg,功率1 mW,驻点压力0.5~20\,kPa.
弹道靶[76 ] 一般采用二级轻气炮发射试验模型,模型可以很高的速度在靶室中自由飞行,通过在飞行段和靶标附近安装的纹影、高速相机、辐射计等测量设备,可以对超高速流场和超高速碰撞效应进行定量测量. 弹道靶设备可以真实模拟超高速空气动力学和超高速碰撞动力学的飞行条件. 但是受限于发射能力,模型质量和尺寸通常都比较小. 美国AEDC
G靶和中国空气动力研究与发展中心的200 m自由飞弹道靶代表了超高速弹道靶设备的最高水平,其主要运行参数为[76 ] :发射速度1.5~7 km/s;靶室全长200~300 m,靶室直径3 m;模拟高度:0~68 km. 针对小行星撞击地球表面的超高速碰撞问题,常规的用于开展超高速撞击试验的水平弹道靶存在较大的局限性,不能复现撞击碎片反溅、掉落堆积等现象,也无法进行变角度斜碰撞以及撞击水体的模拟. 超高速垂直弹道靶能较好地解决上述问题,NASA已经建立超高速垂直靶AVGR,而国内尚无此种设备.
从以上五类地面设备试验能力的现状可以看出,当前设备在超高速空气动力学和超高速碰撞动力学模拟方面已经具备一定的基础,但是距离模拟小行星进入与撞击地球这种极高速、高焓、极高温的问题还有较大差距.
3.2 数值计算
地面试验花费大、不能完全满足真实问题的模拟条件,经常用作观测物理现象、校验数值计算模型. 经过几十年的发展,数值计算在超高速空气动力学和超高速碰撞动力学中发挥了越来越重要的作用. 但是针对小行星进入与撞击地球的极高速、极高温以及强耦合的问题,目前的数值计算还存在着很多不足.
跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究.
如图2 所示,对于我们感兴趣的小行星尺寸(半径大于1 m),在进入地球大气绝大部分飞行范围内,流动处于连续流区,CFD是主要的研究手段. 目前CFD已经建立起考虑化学反应、内能激发、热力学非平衡以及烧蚀气体进入流场的模型,发展了多种空间和时间格式,在超高速飞行器的研制中发挥了重要作用. 但是针对小行星进入的极高速、极高温条件,大于20 000 K的热化学模型很不完备[39 ,51 ] ,目前的可压缩湍流模型还需要验证和校核. 当前CFD模拟火球时往往引入额外的能量释放以考虑空中爆炸的影响[84 ] ,并且由于不清楚小行星内部结构,计算和观测仅在定性上一致.
对于高温流场的辐射热流以及火球的光辐射和热辐射计算,当前的辐射基础数据还不完备. 在流场、辐射和烧蚀的耦合计算中,需要研究烧蚀气体与空气的化学反应动力学以及辐射对化学反应影响的光化学反应动力学模型. 当前的耦合方法主要是松耦合,需要进一步完善和改进[85 ] . 此外,耦合计算中辐射计算的逐线法计算量大,需要研究效率更高的计算方法.
结构传热和热响应的有限元方法已经发展成熟,但针对小行星材料和结构的研究工作很少.
超高速碰撞动力学主要使用Euler法、光滑粒子模拟方法以及Lagrange法等数值计算方法[86 ] ,这些方法在超高速动能毁伤和空间碎片防护研究中发挥了巨大作用. 但现有针对超高速碰撞的研究多以常见金属材料为研究目标,由于小行星材料的特殊性,地面难以获得采样样本,仿真中缺少描述超高速撞击下小行星材料特点的材料模型和高状态相变数据,这也限制了数值计算研究的准确性.
综上所述,针对小行星撞击地球的超高速问题,当前的数值计算方法已经初步具备研究能力,但在热化学模型、辐射基础数据、多物理效应的耦合以及典型材料的模型和高状态相变数据上还存在诸多不足.
4 小行星进入与撞击效应分析评估技术及我们的尝试
针对小行星对地球可能的撞击,如果主动防御手段不奏效,或者当小行星尺寸较小而不能较早提前发现时,需要基于小行星进入与撞击效应分析评估技术,通过快速的计算分析,评估小行星对地面人员和设施的危害,为地面人员疏散和防灾减灾提供支撑.
美国已经组织开发了小行星进入与撞击风险分析评估系统[87 ] ,设定小行星撞击地球的场景,可定量分析进入和撞击过程对地球人口和基础设施的危害,提出应急疏散策略和方案,并构成了美国政府、军方小行星撞击联合应急演习的主要内容.
针对Chelyabinsk和Tunguska两次流星事件,我们从小行星进入地球大气的弹道方程、质量损失方程、解体判据和解体模型等出发,初步建立了小行星进入与撞击效应分析评估模型,并评估了空爆火球在地面所导致的超压和热辐射损伤.
4.1 小行星进入与撞击效应分析评估模型
采用圆球地球模型并考虑地球自转,仅考虑飞行中的阻力,则可写出包括式(1)的单个飞行体的弹道方程组[88 ]
$$ \left.\!\! \dfrac{{\rm d}h}{{\rm d}t} = V\sin \gamma \\ \dfrac{{\rm d}\theta }{{\rm d}t} = \dfrac{V\cos \gamma \cos \psi }{r_{\rm t} \cos \phi } \\ \dfrac{{\rm d}\phi }{{\rm d}t} = \dfrac{V\cos \gamma \sin \psi }{r_{\rm t} } \\ \dfrac{{\rm d}V}{{\rm d}t} = - C_{\rm d} \cdot \dfrac{1}{2m}\rho _{{\rm air}} V^2 \cdot A - g\sin \gamma + \\ \qquad \omega ^2r_{\rm t} \cos \phi \left( {\sin \gamma \cos \phi - \cos \gamma \sin \psi \sin \phi } \right) \\ V\dfrac{{\rm d}\gamma }{{\rm d}t} = - g\cos \gamma + \dfrac{V^2}{r_{\rm t} }\cos \gamma + \\ \qquad 2\omega V\cos \psi \cos \phi + \\ \qquad \omega ^2r_{\rm t} \cos \phi \left( {\cos \gamma \cos \phi + \sin \gamma \sin \psi \sin \phi } \right) \\ V\dfrac{{\rm d}\psi }{{\rm d}t} = - \dfrac{V^2}{r_{\rm t} }\cos \gamma \cos \psi {\rm tan}\phi + \\ \qquad 2\omega V\left( {{\rm tan}\gamma \sin \psi \cos \phi - \sin \phi } \right) - \\ \qquad \dfrac{\omega ^2r_{\rm t} }{\cos \gamma }\cos \psi \sin \phi \cos \phi\!\!\right\} (11)$$
其中,$h$为飞行高度; $\theta $ 和 $\varPhi $ 分别是经度、纬度; $\gamma $ 是飞行航迹角,定义为速度矢量与当地水平面的夹角,速度矢量在当地水平面上方为正; $\psi $ 是航向角,定义为速度矢量在当地水平面的投影与当地纬线方向的夹角;$C_{\rm d}$是阻力系数,在本文的计算中取常值1.0;$A$是横截面积,在计算中假定小行星为球形,则$A= \pi r^{2}$; $r_{t}$是小行星到地心的距离;采用美国1976年标准大气模型计算大气密度$\rho _{\rm air}$.
小行星的质量损失方程采用式(3)和式(4). 当驻点压力$P$超过强度$S$,小行星解体,即解体判据采用式(5). 在解体后,需要应用解体模型确定小行星的存在形式及质量分数. 本文采用NASA最近发展的FCM解体模型. FCM模型(图10 )认为,小行星每次解体为一系列大尺度的碎片和一个由小碎片、液滴组成的碎片云. 碎片以及碎片云都是独立的飞行体,其运动服从方程组(11),其质量分布随着求解问题的不同而不同. 碎片云的变形采用Pancake模型计算,其扩散速度$V_{\rm disp}$采用式(2)计算,解体后碎片的强度采用式(6)计算.
图10 FCM模型(fragment-cloud model)示意图
Fig.10 Sketch of FCM model(fragment-cloud model)
给定小行星的初始参数:质量、密度、高度、经度、纬度、速度、进入角(航迹角)、航向角,通过数值求解弹道方程组(11)和质量损失方程(3)和(4),利用解体判据(5)判断解体,利用FCM模型确定解体后小行星的存在形式,就能得到小行星的进入轨迹、解体和能量沉积情况. 其中能量沉积定义为每单位高度上动能的变化.
根据Chyba的方法[8 ] ,把能量沉积最大值所在的飞行高度定义为空中爆炸高度,则可以利用美国核试验的数据[89 ] 评估超压和火球热辐射在地面的损伤范围.
总结起来,本文在小行星进入与撞击效应分析评估模型中采用如下假设:
(1)小行星及其碎片外形是球形;
(2)仅考虑阻力,不考虑升力,且阻力系数为常值;
(3)烧蚀系数为常值;
(4)采用解体判据$P = \rho _{{\rm air}} V^2 > S$;
(5)解体强度与尺寸的关系采用Weibull定律,且强度指数为常值;
(6)采用FCM解体模型,未考虑解体后碎片之间以及与碎片云之间的气动干扰,采用随意给定的方式确定解体后碎片和碎片云的质量分布;
(7)采用式(2)给定的碎片云扩散速度计算方法,在计算中对碎片云半径不进行限制.
(8)假定能量沉积最大值所在的高度为空中爆炸的高度,把空中爆炸当做发生在该高度处的以初始动能为爆炸能量的点爆炸,采用与核爆
炸类比的方法评估超压和火球热辐射在地面的影响范围.
4.2 Chelyabinsk流星事件计算结果
Chelyabinsk流星事件的计算条件如表2 所示,其中初始质量、初始直径、流星材料、流星密度、进入高度、进入速度和进入角取自观测结果[9 -10 ] ,解体强度和烧蚀系数取自石质小行星的典型值,强度指数和每次解体后生成的子碎片(云)数及其质量分数在计算中自行给定.
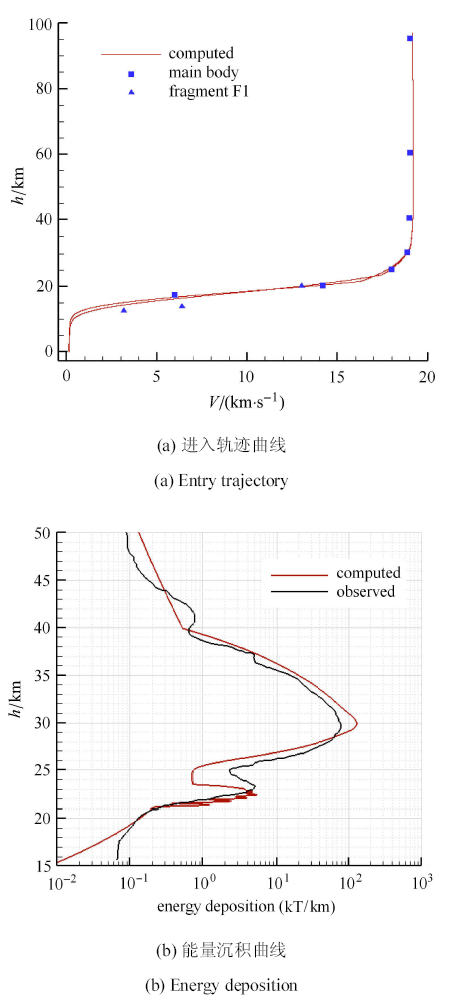
图11 是Chelyabinsk流星事件计算结果,其中图11 (a)是进入轨迹曲线,图11 (b)是能量沉积曲线.可以看到进入轨迹和能量沉积都与观测 结果符合较好,说明本文的计算方法具有一定的合理性.但是仍未能反映Chelyabinsk流星事件观测结果的某些特征,比如无法预测碎片F1对主飞行方向的偏离,预测落地的最大碎片质量(120\,kg)与地面收集到的最大陨石质量(570 kg)尚有偏差.
图11 Chelyabinsk流星事件计算结果
Fig.11 Computational results of Chelyabinsk event
4.3 Tunguska流星事件计算结果
Tunguska流星事件发生在1908年6月30日俄罗斯西伯利亚Tunguska,目击者观察到白光的直径很大,似乎发生爆炸.地面大范围的 树木倒伏且很多具有燃烧的痕迹,地面无陨石坑及碎片. 地震仪测量到竖直方向7$\times$10$^{13}$\,kg$\cdot $m/s脉冲信号.大多数研究者把该事件归因到小行星撞击地球上,但在小行星种类和初始进入参数上存在较大争议[6 -8 ] .研究者通过地震波分析和地面树木倒伏形状的试验模拟[6 -8 ] ,认为爆炸高度在8.5 km左右.
计算条件如表2 所示,其中Tunguska流星事件小行星种类和初始进入参数采用Chyba研究成果,解体强度、烧蚀系数和流明效率在石质小行星的范围内取值,强度指数、每次解体后生成的子碎片(云)数及其质量分数在计算中自行给定.
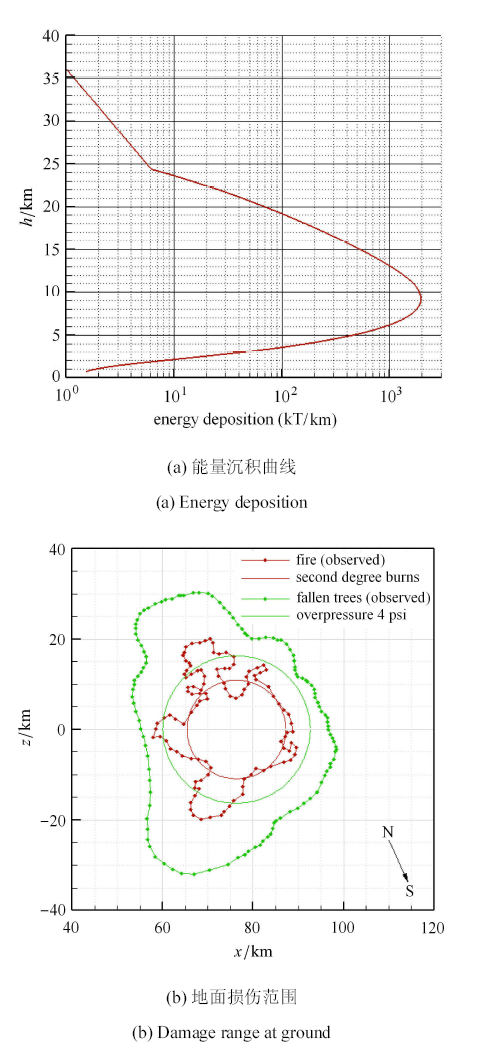
从图12 (a)的计算结果看,得到的最大能量沉积高度为9.2 km,与文献中的8.5 km比较接近.所采用的FCM解体模型充分考虑了大块碎片和由小碎片、液滴组成的碎片云两种类型解体产物的可能性,在计算中可以自由设定质量分数,能够得到与观测一致的结果(地面无碎片、无陨石坑). 图12 (b)给出超压4 psi(能够很容易吹倒建筑物)和二级烧伤(相当于点燃阔叶林)的地面损伤范围,并给出实测的树木倒伏区域和 森林着火区域.可以看出,计算能够定性反映出超压和火球热辐射的损伤效果,但在量值上与观测存在较大偏差.原因如下:一是使得Tunguska当地森林树木倒伏的超压最小值未知;二是二级烧伤相当于点燃阔叶林,而Tunguska当地主要是针叶林;三是流明效率取值范围大;四是未考虑到地形变化.
图12 Tunguska流星事件计算结果
Fig.12 \ Computational results of Tunguska event
5 结束语
小行星撞击地球是人类生存面临的潜在威胁之一.在小行星进入地球大气与撞击地球表面过程中,存在烧蚀、解体、空中爆炸、火球、撞击成坑、反溅碎片云、地震以及海啸等一系列复杂的物理化学和力学现象.本文首先对这些现象后面的超高速问题进行了分析、梳理,指出需要深入研究的方向和课题.然后从地面试验和数值计算两方面,分析现有研究手段的不足.最后,本文综合小行星进入地球大气层的弹道方程、质量损失方程、解体判据和解体模型等,初步建立了小行星进入与撞击效应分析评估模型,并以Chelyabinsk和Tunguska两次流星事件为例,分析计算了进入过程的质量损失和解体等问题,评估了空爆火球在地面所导致的超压和热辐射损伤. 通过本文的研究,可以认为:
(1)在小行星进入地球大气过程中,有5方面的超高速空气动力学问题:极高速($V=12~20$\,km/s)进入条件下的气动力与轨迹;极高速进入条件下的小行星气动加热与烧蚀机理;极高速气动加热条件下的小行星结构传热与热响应;极高速进入条件下的高温气体效应;小行星进入过程的物理特征.
(2)在小行星撞击地球表面过程中,有3方面超高速碰撞动力学问题:陆地撞击成坑与反溅碎片云;海洋撞击与海啸;撞击过程的地震效应.
(3)针对小行星撞击地球的超高速问题,当前地面试验设备已经具备一定的基础,但是距离模拟小行星进入与撞击地球这种极高速、高焓、极高温的问题还有较大差距;当前的数值计算方法已经初步具备研究能力,但在热化学模型、辐射基础数据、多物理效应的耦合以及典型材料的模型和高状态相变数据上还存在诸多不足.
(4)初步建立了小行星进入与撞击效应分析评估模型,并对Chelyabinsk和Tunguska两次流星事件进行了计算分析,得到了与部分观测数据较为一致的结果.
致谢 本文在研究中得到中国空气动力研究与发展中心超高速空气动力研究所的石卫波、李海燕和粟斯尧等同志的帮助,在此向他们表示感谢.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
赵海斌 . 近地小行星探测和危险评估. [博士论文]
. 北京: 中国科学院研究生部 , 2008
[本文引用: 3]
(Zhao Haibin Survey and risk assessment of near earth asteroids. [PhD Thesis]
. Beijing: Graduate University of Chinese Academy of Science , 2008 (in Chinese))
[本文引用: 3]
[2]
.
URL
[本文引用: 1]
[3]
Harris AW D’Abramo G The population of near-earth asteroids
. Icarus , 2015 , 257 : 302 -312
[本文引用: 1]
[4]
Collins GS Melosh HJ Marcus RA Earth impact effects program: a web-based computer program for calculating the regional environmental consequences of a meteoroid impact on earth
. Meteoritics & Planetary Science , 2005 , 40 (Nr6 ): 817 -840
[本文引用: 6]
[5]
Mathias DL Wheeler LF Dotson JL A probabilistic asteroid impact risk model: assessment of sub-300m impact
. Icarus , 2017 , 289 : 106 -119
[本文引用: 4]
[6]
Vasilyev NV The tunguska meteorite problem today
. Planetary and Space Science , 1998 , 46 (2-3 ): 129 -150
[本文引用: 6]
[7]
Zotkin IT Tsikulin MA Simulation of the explosion of the tungus meteorite
. Soviet Physics Doklady , 1966 , 11 : 183 -186
[8]
Chyba CF Thomas PJ Zahnle KJ The 1908 tunguska explosion: atmospheric disruption of a stony asteroid
. Nature , 1993 , 361 : 40 -44
[本文引用: 6]
[9]
Popova OP Jenniskens P Emel’yanenko V et al .Chelyabinsk airburst, damage assessment, meteorite recovery and characterization
. Science , 2013 , 342 (6162 ): 1069 -1073
[本文引用: 5]
[10]
Borovi$\check{c}$ka J Spurn$\acute{y}$ P Brown P et al . The trajectory, structure and origin of the chelyabinsk asteroidal impactor
. Nature , 2013 , 503 (7475 ): 235 -237
[本文引用: 4]
[11]
Schulte P Alegret L Arenillas I et al .The chicxulub asteroid impact and mass extinction at the cretaceous-paleogene boundary
. Science , 2010 , 327 : 1214 -1218
[本文引用: 1]
[12]
Gupta SC Ahrens TJ Yang WB Shock induced vaporization of anhydrite and global cooling from the KT impact
. Earth and Planetary Science Letters , 2001 , 188 (34 ): 399 -412
[本文引用: 1]
[13]
秦丽荣 . 对”天外来客”吉林陨石保护问题的初步探讨
. 博物馆研究 , 2013 , 4 : 87 -91
[本文引用: 1]
(Qin Lirong A preliminary study on the protection of Jilin meteorite
. Museum Research , 2013 , 4 : 87 -91 (in Chinese))
[本文引用: 1]
[14]
刘雪奇 , 孙海彬 , 孙胜利 . 近地小行星防御策略分析
. 深空探测学报 , 2017 , 4 (6 ): 557 -563
[本文引用: 2]
(Liu Xueqi Sun Haibin Sun Shengli Analysis of defense strategies of near-earth asteroids
. Journal of Deep Space Exploration , 2017 , 4 (6 ): 557 -563 (in Chinese))
[本文引用: 2]
[15]
Li B Zhao HB Distribution of PSF of the near earth object survey telescope
. Chinese Astronomy and Astrophysics , 2013 , 37 (1 ): 97 -106
[本文引用: 2]
[16]
王斌 , 赵海斌 , 李斌 . 基于图像位移叠加方法探测暗弱小行星
. 天文学报 , 2017 , 58 (5 ): 95 -107
[本文引用: 1]
(Wang Bin Zhao Haibin Li Bin Detection of faint asteroids based on image shifting and stacking method
. Acta Astronomica Sinica , 2017 , 58 (5 ): 95 -107 (in Chinese))
[本文引用: 1]
[17]
李俊峰 , 曾祥远 . 不规则小行星引力场内的飞行动力学
. 力学进展 , 2017 , 47 : 201712
[本文引用: 1]
(Li Junfeng Zeng Xiangyuan Flight dynamics in the gravitational fields of irregular asteroids
. Advance in Mechanics , 2017 , 47 : 201712 (in Chinese))
[本文引用: 1]
[18]
Baoyin HX Li JF A survey on orbit and navigation of asteroid missions
. Acta Mechanica Sinica , 2014 , 30 (3 ): 282 -293
[本文引用: 1]
[19]
李飞 , 孟林智 , 王彤 等 . 国外近地小行星撞击地球防御技术研究
. 航天器工程 , 2015 , 24 (2 ): 87 -95
[本文引用: 1]
(Li Fei Meng Linzhi Wang Tong et al .Summary of near Earth asteroid defense technology
. Spacecraft Engineering , 2015 , 24 (2 ): 87 -95 (in Chinese))
[本文引用: 1]
[20]
马鹏斌 , 宝音贺西 . 近地小行星威胁与防御研究现状
. 深空探测学报 , 2016 , 3 (1 ): 10 -17
[本文引用: 1]
(Ma Pengbin Baoyin Hexi Research status of the near-earth asteroids' hazard and mitigation
. Journal of Deep Space Exploration , 2016 , 3 (1 ): 10 -17 (in Chinese))
[本文引用: 1]
[21]
黄川 , 傅容珊 .小行星撞击对地球的上地幔对流的影响
.地球物理学报 , 2014 , 57 (5 ): 1534 -1542
[本文引用: 1]
(Huang Chuang Fu Rongshan Perturbations of Earth's upper mantle convection caused by asteroid impact
. Chinese Journal of Geophysics , 2014 , 57 (5 ): 1534 -1542 (in Chinese))
[本文引用: 1]
[22]
李毅 , 陈鸿 , 兰胜威 等 . 一种提升近地小行星防御中拦截效率的方法
. 航天器环境工程 , 2017 , 34 (6 ): 585 -592
[本文引用: 1]
(Li Yi Chen Hong Lan Shengwei et al .A method to improve interception efficiency in the defense against near-Earth asteroids
. Spacecraft Environment Engineering , 2017 , 34 (6 ): 585 -592 (in Chinese))
[本文引用: 1]
[23]
柳森 , 黄洁 , 李毅 等 . 小行星撞击地球的超高速气动与碰撞问题
//全国第一届行星防御研讨会,绵阳 , 2018
(Liu Sen Huang Jie Li Yi et al . Hyervelocity aerodynamics and impact dynamics issues of earth impact by asteroids
//1st National Conference on Planetary Defense, Mianyang , 2018 (in Chinese))
[24]
柳森 , 黄洁 , 李毅 等 . 行星防御中的超高速问题
//香山科学会议, 北京 , 2018
(Liu Sen Huang Jie Li Yi et al .Hyervelocity issues of planetary defense//Xiangshan Scientific Conference,
Beijing , 2018 (in Chinese))
[25]
李毅 , 柳森 , 陈鸿 等 . NTS软件在近地小行星撞击与防御中的应用
// 全国第一届行星防御研讨会,绵阳 , 2018
(Li Yi Liu Sen Chen Hong et al .Application of NTS software on planetary defense
//1st National Conference on Planetary Defense, Mianyang , 2018 (in Chinese))
[26]
石卫波 . 小行星进入三维瞬态传热有限元计算初步研究
//全国第一届行星防御研讨会, 绵阳 , 2018
(Shi Weibo 3D transient heat transfer of asteroids during entry to Earth
//1st National Conference on Planetary Defense,Mianyang , 2018 (in Chinese))
[27]
李海燕 . 流星体进入地球大气辐射加热数值分析
//全国第一届行星防御研讨会, 绵阳 , 2018
[本文引用: 1]
(Li Haiyan Numerical analysis on radiating heating of meteoroids during entry to Earth
//1st National Conference on Planetary Defense, Mianyang Sichuan , 2018 (in Chinese))
[本文引用: 1]
[28]
$\ddot{O}$pik EJ Physics of Meteor Flight in the Atmosphere.
New York: Interscience Publishers Inc. , 1958
[本文引用: 3]
[29]
Tsien HS Superaerodynamics, mechanics of rarefied gases
. J Aero Sci , 1964 , 13 (12 ): 653 -664
[本文引用: 1]
[30]
杨彦广 , 李明 , 李中华 等 .高超声速飞行器跨流域气动力/热预测技术研究
.空气动力学学报 , 2016 , 34 (1 ): 5 -13
[本文引用: 1]
(Yang Yanguang Li Ming Li Zhonghua et al .Aerodynamics force/heating measurement on hypersonic vehicle across different flow regions
. Acta Aerodynamica Sinica , 2016 , 34 (1 ): 5 -15 (in Chinese))
[本文引用: 1]
[31]
Allen GA Prabhu DK Jr Saunders DA Trajectory simulation of meteors assuming mass loss and fragmentation
//1st International Workshop on PHA Characterization, Atmospheric Entry and Risk Assessment, NASA Ames Research Center, California , 2015
[本文引用: 2]
[32]
BoroviKa1 J Kalenda P The Morávka meteorite fall : 4 meteoroid dynamics and fragmentation in the atmosphere
. Meteoritics & Planetary Science, 2003, 38, Nr 7 : 1023 -1043
[本文引用: 3]
[33]
Wheeler LF Register PJ Mathias DJ A fragment-cloud model for asteroid breakup and atmospheric energy deposition
. Icarus , 2017 , 295 : 149 -169
[本文引用: 4]
[34]
Mehta PM Minisci E Vasile M Break-up modelling and trajectory simulation under uncertainty for asteroids
//4th IAA Planetary Defense Conference, Rome, Italy , 2015
[本文引用: 1]
[35]
Revelle DO Recent advances in bolide entry modeling: A bolide potpourri.
Earth, Moon, and Planets , 2004 , 95 (1-4 ): 441 -476
[本文引用: 2]
[36]
Hills JG Goda MP The fragmentation of small asteroids in the atmosphere
. The Astronomical Journal , 1993 , 105 (3 ): 1114 -1144
[本文引用: 6]
[37]
Passey QR Melosh HJ Effects of atmospheric breakup on crater field formation
. Icarus , 1980 , 42 : 211 -233
[本文引用: 1]
[38]
Prabhu D Saunders D Agrawal P et al .Thermophysics issues relevant to highspeed earth entry of large asteroids
//AIAA SciTech 2016: Special Session: Aerothermodynamics of Meteor Entries, San Diego, USA , 2016
[本文引用: 4]
[39]
Johnston CO Stern EC Impact of coupled radiation and ablation on the aerothermodynamics of meteor entries
//47th AIAA Thermophysics Conference, Denver, USA , 2017
[本文引用: 5]
[40]
Johnston CO Gnoffo PA Sutton K The influence of ablation on radiative heating for earth entry
. Journal of Spacecraft and Rocket , 2009 , 46 (3 ): 481 -491
[本文引用: 2]
[41]
陈坚强 , 涂国华 , 张毅锋 等 .高超声速边界层转捩研究现状与发展趋势
. 空气动力学学报 , 2017 , 35 (3 ): 311 -337
[本文引用: 1]
(Chen Jianqiang Tu Guohua Zhang Yifeng et al .Hypersonic boundary layer transition: what we know, where shall we go
. Acta Aerodynamics Sinica , 2017 , 35 (3 ): 311 -337 (in Chinese))
[本文引用: 1]
[42]
Roy CJ Blottner FG Review and assessment of turbulence models for hypersonic flows: 2d/asymmetric cases
. Progress in Aerospace Sciences , 2006 , 42 (7-8 ): 469 -530
[本文引用: 1]
[43]
Mason BH Meteorites
. American Scientist , 1967 , 55 (4 ): 429 -455
[本文引用: 1]
[44]
Macke RJ Survey of meteorite physical properties: density, porosity and magnetic susceptibility.
[PhD Thesis]. Orlando, USA: University of Central Florida , 2010
[本文引用: 3]
[45]
Bryson KL Agrawal P Ostrowski DR et al .Fracture characterization of meteorites
//78th Annual Meeting of Meteoritical Socity, California, USA , 2015
[本文引用: 3]
[46]
Popova O Borovi$\check{c}$ka J, Hartmann WK, et al. Very low strengths of interplanetary meteoroids and small asteroids
. Meteoritics & Planetary Science , 2011 , 46 (Nr10 ): 1525 -1550
[本文引用: 2]
[47]
Weibull WA Sweden S A statistical distribution function of wide applicability
. Journal of Applied Mechanics , 1951 , 18 : 293 -297
[本文引用: 1]
[48]
Artemieva NA Shuvalov VV Motion of a fragmented meteoroid through the planetary atmosphere
. Journal of Geophysical Research , 2011 , 106 (E2 ): 3297 -3309
[本文引用: 1]
[49]
Park C Brown J Modeling of spreading of meteoroid fragments
//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, USA , 2012
[本文引用: 1]
[50]
Paul J Register A Donovan L et al .Asteroid fragmentation approaches for modeling atmospheric energy deposition
. Icarus , 2017 , 284 : 157 -166
[本文引用: 1]
[51]
Johnston CO Brandis AM Aerothermodynamic characteristics of 16-22 km/s earth entry
. AIAA Paper 2015-3110 , 2015
[本文引用: 8]
[52]
Stern EC Entry modeling for asteroid threat assessment
//61st Course of Hypersonic Meteoroid Entry Physics, Sicily, Italy , 2017
[本文引用: 6]
[53]
McBride BJ Zehe MJ Gordon S NASA glenn coefficients for calculating coefficients for calculating thermodynamic properties of individual species.
NASA TP 2002--211556
[本文引用: 1]
[54]
Wright MJ Bose D Palmer G Recommended collision integrals for transport property computations part 1: Air species
. AIAA Journal , 2005 , 43 (12 ): 2558 -2564
[本文引用: 1]
[55]
Wright MJ Hwang H Recommended collision integrals for transport property computations part 2: mars and venus entries
. AIAA Journal , 2007 , 45 (1 ): 281 -288
[本文引用: 1]
[56]
Gnoffo PA Gupta RN Shinn JL Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium
. NASA-TP-2867 , 1989
[本文引用: 1]
[57]
Lee JH Basic governing for the flight regimes of aeroassisted orbital transfer vehicles
. AIAA Paper 1984-1729 , 1984
[本文引用: 1]
[58]
Popova O Shuvalov V Jenniskens P Simulations of the entry and damaging effects of asteroid impacts
. NASA Ames Planetary Defense Workshop , 2015
[本文引用: 3]
[59]
Nemeca M Aftosmis MJ Brown PG Numerical prediction of meteoric infrasound signatures
. Planetary and Space Science , 2017 , 140 : 11 -20
[本文引用: 1]
[60]
Brown PG Kalendad P Revelle DO et al . The Morávka meteorite fall: 2. interpretation of infrasonic and seismic data
. Meteoritics & Planetary Science , 2003 , 38, Nr 7: 989 -1003
[本文引用: 3]
[61]
丁宁 . 撞击坑中央隆起构造研究. [博士论文]
. 武汉: 中国地质大学 , 2016
[本文引用: 3]
(Ding Ning Structure of the central uplift complex of impact craters. [PhD Thesis]
. Wuhan: China University of Geosciences , 2016 (in Chinese))
[本文引用: 3]
[62]
Hamilton CJ Terrestrial Impact Craters . 2001
[本文引用: 1]
[63]
Melosh HJ Impact Cratering: A Geologic Process . London, UK : Oxford University Press , 1989
[64]
游振东 , 刘嵘 . 陨石撞击构造作用的研究现状与前景
. 地质力学学报 , 2008 , 14 (1 ): 22 -32
[本文引用: 1]
(You Zhendong Liu Rong Research on impact tectonics and impactites: Status and prospects
. Journal of Geomechanics , 2008 , 14 (1 ): 22 -32 (in Chinese))
[本文引用: 1]
[65]
Ivanov BA Bazilevskiy AT Sazonova LV Formation of the central uplift in meteoric craters
. NASA TM-88427 , 1986
[本文引用: 1]
[66]
马配学 , 穆治国 . 陨石撞击、环境灾变与生物绝灭
. 科学中国人 , 1997 (6 ): 49 -51
[本文引用: 1]
(Ma Peixue Mu Zhiguo Meteorite impact, environmental catastrophe and biological extinction. Scientific Chinese , 1997 (6 ): 49 -51 (in Chinese))
[本文引用: 1]
[67]
张庆明 ,黄风雷 . 从慧木碰撞谈地球安全. 中国安全科学学报 , 1995 (1 ): 21 -26
[本文引用: 1]
(Zhang Qingming Huang Fenglei Effects on the earth resulted from the impact of planetoid. China Safety Science Journal , 1995 (1 ): 21 -26 (in Chinese))
[本文引用: 1]
[68]
Pierazzo E Melosh HJ Hydrocode modeling of oblique impacts: the fate of the projectile
. Meteoritics & Planetary Science , 2000 , 35 (1 ): 117 -130
[本文引用: 1]
[69]
Stewart ST Ahrens TJ Porosity effects on impact processes in solar system materials
//Conference on Shock Compression of Condensed Matter, Utah, USA , 1999
[本文引用: 1]
[70]
Saito T Kaiho K Abe A et al .Numerical simulations of hypervelocity impact of asteroid/comet on the Earth
. International Journal of Impact Engineering , 2006 , 33 (1 ): 713 -722
[本文引用: 2]
[71]
Pierazzo E Assessing atmospheric water injection from oceanic impacts
//36th Annual Lunar and Planetary Science Conference, Texas, USA , 2005
[本文引用: 1]
[72]
Dawsona AG Stewartb I Tsunami deposits in the geological record
. Sedimentary Geology , 2007 , 200 (3-4 ): 166 -183
[本文引用: 1]
[73]
Ward SN Asphaug E Impact tsunami-Eltanin
. Deep Sea Research Part II: Topical Studies in Oceanography , 2002 , 49 (6 ): 1073 -1079
[本文引用: 1]
[74]
苏旸 . 小天体撞击灾害
. 自然灾害学报 , 2001 (3 ): 119 -125
[本文引用: 1]
(Su Yang The impact hazard of small objects
. Journal of Natural Disasters , 2001 (3 ): 119 -125 (in Chinese))
[本文引用: 1]
[75]
Melosh HJ Impact-generated tsunamis: An over-rated hazard
//34th Annual Lunar and Planetary Science Conference, Texas, USA , 2003
[本文引用: 1]
[76]
Frank L Marren D Advanced hypersonic test facilities.
American Institute of Aeronautics and Astronautics, inc, USA , 2002
[本文引用: 8]
[77]
Philippe R Survey of high-enthalpy shock facilities in the perspective of radiation and chemical kinetics investigations
. Progress in Aerospace Sciences , 2016 , 85 : 1 -32
[本文引用: 1]
[78]
Caristia S De Filippis F Del Vecchio A Scirocco PWT facility for high temperature resistant material assembies test
//54th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law, Bremen, Germany , 2003
[本文引用: 2]
[79]
Smith RK Cunningham J A survey of current and future plasma arc-heated test facilities for aerospace and commercial applications
. AIAA Paper 1998-0146 , 1998
[本文引用: 1]
[80]
.
URL
[本文引用: 1]
[81]
杨超 , 孙泉华 . 高温气体热化学反应的 DSMC 微观模型分析
. 力学学报 , 2018 , 50 (4 ): 722 -733
[本文引用: 1]
(Yang Chao Sun Quanhua Analysis of DSMC reaction models for high temperature gas simulation
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (4 ): 722 -733 (in Chinese))
[本文引用: 1]
[82]
李中华 ,党雷宁 ,李志辉 .高超声速化学非平衡流动Navier-Stokes/DSMC耦合算法
. 航空学报 , 2018 , 39 (10 ): 122229
[本文引用: 1]
(Li Zhonghua Dang Leining Li Zhihui Study on Navier-Stokes/DSMC hybrid numerical method with chemical non-equilibrium for hypersonic flow
. Acta Aeronautica et Astronautica Sinica , 2018 , 39 (10 ): 122229 (in Chinese))
[本文引用: 1]
[83]
吴俊林 . 热化学非平衡Boltzmann模型方程统一算法与返回舱再入跨流域应用研究. [博士论文]
. 中国绵阳:中国空气动力研究与发展中心研究生部 , 2018
[本文引用: 1]
(Wu Junlin Study of gas-kinetic unified algorithm based on thermochemical non- equilibrium boltzmann model equation and application for re-entry flows of spacecraft capsule covering various flow regimes. [PhD Thesis]
. Mianyang: Graduate faculty of China Aerodynamics Research and Development Center , 2018 (in Chinese))
[本文引用: 1]
[84]
Artemieva1 NA Shuvalov VV From tunguska to chelyabinsk via jupiter
. Annual Review of Earth and Planetary Sciences , 2016 , 44 : 37 -56
[本文引用: 1]
[85]
Palmer G White T Barnhardt M et al . Direct coupling of the NEQAIR radiation and DPLR CFD codes
. AIAA Paper , 2010-5051, 2015
[本文引用: 1]
[86]
Schill W Wasem JV Owen JM Modelling and simulation of cratering and ejecta production during high velocity impacts
. Journal of Dynamic Behavior of Materials , 2017 , 3 (2 ): 1 -9
[本文引用: 1]
[87]
Motiwala SA Mathias DL Mattenberger CJ An integrated physics-based risk model for assessing the asteroid threat
//International Topical Meeting on Probabilistic Safety Assessment and Analysis, Idaho, USA , 2015
[本文引用: 1]
[88]
Vinh NS Flight Mechanics of High-Performance Aircraft. London : Cambridge University Press , 1999
[本文引用: 1]
[89]
Glasstone S Dolan PJ The Effects of Nnuclear Weapons, 3rd edition
. Washington DC: United States Department of Defense and Department of Energy , 1977
[本文引用: 1]
近地小行星探测和危险评估. [博士论文]
3
2008
... 天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害. ...
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
... [1 ,15 -16 ].李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
近地小行星探测和危险评估. [博士论文]
3
2008
... 天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害. ...
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
... [1 ,15 -16 ].李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
1
... 天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害. ...
The population of near-earth asteroids
1
2015
... 天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害. ...
Earth impact effects program: a web-based computer program for calculating the regional environmental consequences of a meteoroid impact on earth
6
2005
... 天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害. ...
... 小行星进入地球大气与撞击地球表面过程中将会发生非常复杂的物理化学和力学现象[4 -5 ,28 ] (图1 ).小行星进入地球大气速度极高(典型速度12 ~ 20 km/s),远超人造航天器的再入速度(7.5 ~ 11.2 km/s).极大的进入速度产生巨大的气动加热,使得激波层温度超过20 000 K,产生远超对流热流的辐射热流;严酷的热环境引起材料大规模熔融、汽化和烧蚀,导致严重的质量损失和外形变化.与航天飞行器经过人类精心设计的材料和结构不同,小行星的材料和结构是自然形成的,不仅呈现各向异性的特征,而且充满孔隙和裂纹,在强大的气动力、热载荷的共同作用下可能多次解体,甚至产生空中爆炸形成火球.当大尺寸小行星穿透大气层撞击地球表面后,可能会产生撞击坑、反溅碎片云、地震和海啸等现象,其反溅碎片云抛向大气甚至影响气候变化. ...
... 解体爆炸是小行星进入地球大气中的常见现象.解体爆炸的机理是什么?目前国外天文界广泛应用的解体判据[4 -5 ] 认为:当驻点压力$P$超过强度$S$,小行星就会解体,即 ...
... 空中爆炸是小行星(尤其是石质小行星)进入过程显著的现象之一[4 -5 ] . ...
... 在小行星物理中,把超高速飞行以及空中爆炸产生的高温流场称为"火球"[4 ] .火球能够产生较强的光辐射,可被肉眼或仪器 观测到,是小行星撞击地球最显著的特征.光辐射数据通常可转换为能量沉积数据[9 ] ,是小行星进入地球大气过程最重要的观测数据之一,可用于校验模拟方法或作为模拟的输入[58 ] . 图7 是Chelyabinsk流星事件的视频截图,从中可以看到火球较强的光辐射. ...
... 火球不仅产生光辐射,也存在热辐射效应[4 ] . 从本质上讲,光辐射和热辐射是火球产生的电磁辐射在不同波段范围内的表现形式. 热辐射会导致地面人员的热灼伤,严重时引发火灾. 在Chelyabinsk流星事件中,很多人报告感受到火球的热辐射[9 ] . 在Tunguska流星事件中,发现地面树木有大范围燃烧的痕迹[6 ] . ...
A probabilistic asteroid impact risk model: assessment of sub-300m impact
4
2017
... 天文学上把与地球轨道距离小于0.3天文单位(4500万千米)的小天体称为"近地天体"(简称NEO),把其中直径大于140m且与地球的交会距离小于0.05天文单位(750万千米,约20倍地月距离)的近地天体称为"潜在威胁天体"(简称PHA)[1 ] .截止到2018年8月,国际上已经观测发现了1928颗直径在140m以上的"潜在威胁天体",但是这个数目还不到人们估计总数[2 -3 ] 的三分之一.近地天体包括小行星和彗星,其中小行星在数量和撞击地球的频率上远大于彗星,因此本文主要关注小行星.不同尺寸的小行星碰撞地球产生的危害不同. 尺寸较小的小行星进入地球大气层一般会烧毁,不会对地面产生危害.尺寸较大的小行星撞击地球则会带来严重危害,这些危害有以下三种形式[4 -5 ] :一是在进入稠密大气层后发生爆炸通过冲击波和热辐射形式对地面人员、建筑、设施造成伤害;二是直接撞击地表,以直接碰撞、空气中的冲击波、地壳中的表面波、横波和纵波等形式对人员和建筑造成伤害,当小行星尺寸更大时还会引发地震和火山喷发,并且撞击产生的大量尘土反溅物将进入大气层,通过遮挡阳光使地面持续降温形成恶劣气候,最终使地球生态系统受到严重损害,乃至导致物种灭绝;三是直接撞击海洋或者在海面之上爆炸形成海啸,对沿海城市造成危害. ...
... 小行星进入地球大气与撞击地球表面过程中将会发生非常复杂的物理化学和力学现象[4 -5 ,28 ] (图1 ).小行星进入地球大气速度极高(典型速度12 ~ 20 km/s),远超人造航天器的再入速度(7.5 ~ 11.2 km/s).极大的进入速度产生巨大的气动加热,使得激波层温度超过20 000 K,产生远超对流热流的辐射热流;严酷的热环境引起材料大规模熔融、汽化和烧蚀,导致严重的质量损失和外形变化.与航天飞行器经过人类精心设计的材料和结构不同,小行星的材料和结构是自然形成的,不仅呈现各向异性的特征,而且充满孔隙和裂纹,在强大的气动力、热载荷的共同作用下可能多次解体,甚至产生空中爆炸形成火球.当大尺寸小行星穿透大气层撞击地球表面后,可能会产生撞击坑、反溅碎片云、地震和海啸等现象,其反溅碎片云抛向大气甚至影响气候变化. ...
... 解体爆炸是小行星进入地球大气中的常见现象.解体爆炸的机理是什么?目前国外天文界广泛应用的解体判据[4 -5 ] 认为:当驻点压力$P$超过强度$S$,小行星就会解体,即 ...
... 空中爆炸是小行星(尤其是石质小行星)进入过程显著的现象之一[4 -5 ] . ...
The tunguska meteorite problem today
6
1998
... 1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
... [6 -8 ],这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
... 空中爆炸发生时,爆炸波向地面传播,在地面形成超压,且在爆炸波波前后面的低压区因周围空气的补充形成风,对地面人员和设施造成危害.在Chelyabinsk流星事件中,大量建筑物窗户的玻璃受到地面超压的破坏而震碎[9 ] .在Tunguska流星事件后,发现地面大范围的树木呈幅状倒伏且未收集到陨石,研究者认为这是地面超压造成的[6 ] . ...
... 火球不仅产生光辐射,也存在热辐射效应[4 ] . 从本质上讲,光辐射和热辐射是火球产生的电磁辐射在不同波段范围内的表现形式. 热辐射会导致地面人员的热灼伤,严重时引发火灾. 在Chelyabinsk流星事件中,很多人报告感受到火球的热辐射[9 ] . 在Tunguska流星事件中,发现地面树木有大范围燃烧的痕迹[6 ] . ...
... Tunguska流星事件发生在1908年6月30日俄罗斯西伯利亚Tunguska,目击者观察到白光的直径很大,似乎发生爆炸.地面大范围的 树木倒伏且很多具有燃烧的痕迹,地面无陨石坑及碎片. 地震仪测量到竖直方向7$\times$10$^{13}$\,kg$\cdot $m/s脉冲信号.大多数研究者把该事件归因到小行星撞击地球上,但在小行星种类和初始进入参数上存在较大争议[6 -8 ] .研究者通过地震波分析和地面树木倒伏形状的试验模拟[6 -8 ] ,认为爆炸高度在8.5 km左右. ...
... [6 -8 ],认为爆炸高度在8.5 km左右. ...
Simulation of the explosion of the tungus meteorite
1966
The 1908 tunguska explosion: atmospheric disruption of a stony asteroid
6
1993
... 1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
... 其中,$V_{\rm disp}$是碎片云的扩散速度,$V$是飞行速度,$\rho_{\rm air}$和 $\rho $分别是大气及小行星密度. 但是扩散系数$C_{\rm disp}$并不确定,不同研究者给出的取值往往差异较大$^{[36 -37 ] }$. 此外,目前在理论上还无法确定[8 ] 扩散后碎片云半径与解体前小行星初始半径的比值大到多少时,碎片云中小碎片(液滴、灰尘)彼此之间不存在气动干扰,以至于碎片云在气动上不能作为一个整体对待. ...
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
... 根据Chyba的方法[8 ] ,把能量沉积最大值所在的飞行高度定义为空中爆炸高度,则可以利用美国核试验的数据[89 ] 评估超压和火球热辐射在地面的损伤范围. ...
... Tunguska流星事件发生在1908年6月30日俄罗斯西伯利亚Tunguska,目击者观察到白光的直径很大,似乎发生爆炸.地面大范围的 树木倒伏且很多具有燃烧的痕迹,地面无陨石坑及碎片. 地震仪测量到竖直方向7$\times$10$^{13}$\,kg$\cdot $m/s脉冲信号.大多数研究者把该事件归因到小行星撞击地球上,但在小行星种类和初始进入参数上存在较大争议[6 -8 ] .研究者通过地震波分析和地面树木倒伏形状的试验模拟[6 -8 ] ,认为爆炸高度在8.5 km左右. ...
... -8 ],认为爆炸高度在8.5 km左右. ...
Chelyabinsk airburst, damage assessment, meteorite recovery and characterization
5
2013
... 1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
... 空中爆炸发生时,爆炸波向地面传播,在地面形成超压,且在爆炸波波前后面的低压区因周围空气的补充形成风,对地面人员和设施造成危害.在Chelyabinsk流星事件中,大量建筑物窗户的玻璃受到地面超压的破坏而震碎[9 ] .在Tunguska流星事件后,发现地面大范围的树木呈幅状倒伏且未收集到陨石,研究者认为这是地面超压造成的[6 ] . ...
... 在小行星物理中,把超高速飞行以及空中爆炸产生的高温流场称为"火球"[4 ] .火球能够产生较强的光辐射,可被肉眼或仪器 观测到,是小行星撞击地球最显著的特征.光辐射数据通常可转换为能量沉积数据[9 ] ,是小行星进入地球大气过程最重要的观测数据之一,可用于校验模拟方法或作为模拟的输入[58 ] . 图7 是Chelyabinsk流星事件的视频截图,从中可以看到火球较强的光辐射. ...
... 火球不仅产生光辐射,也存在热辐射效应[4 ] . 从本质上讲,光辐射和热辐射是火球产生的电磁辐射在不同波段范围内的表现形式. 热辐射会导致地面人员的热灼伤,严重时引发火灾. 在Chelyabinsk流星事件中,很多人报告感受到火球的热辐射[9 ] . 在Tunguska流星事件中,发现地面树木有大范围燃烧的痕迹[6 ] . ...
... Chelyabinsk流星事件的计算条件如表2 所示,其中初始质量、初始直径、流星材料、流星密度、进入高度、进入速度和进入角取自观测结果[9 -10 ] ,解体强度和烧蚀系数取自石质小行星的典型值,强度指数和每次解体后生成的子碎片(云)数及其质量分数在计算中自行给定. ...
The trajectory, structure and origin of the chelyabinsk asteroidal impactor
4
2013
... 1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
... 对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... [10 ]指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... Chelyabinsk流星事件的计算条件如表2 所示,其中初始质量、初始直径、流星材料、流星密度、进入高度、进入速度和进入角取自观测结果[9 -10 ] ,解体强度和烧蚀系数取自石质小行星的典型值,强度指数和每次解体后生成的子碎片(云)数及其质量分数在计算中自行给定. ...
The chicxulub asteroid impact and mass extinction at the cretaceous-paleogene boundary
1
2010
... 1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
Shock induced vaporization of anhydrite and global cooling from the KT impact
1
2001
... 1908年6月30日,俄罗斯西伯利亚的通古斯河地区上空发生天外飞来物体大爆炸------通古斯事件(Tunguska event)[6 ] , 约1000~4 000万吨TNT当量,2 000多平方公里范围内的树木倒伏,欧亚的很多地震站都有纪录.研究指出[6 -8 ] ,这是直径40~60 m的近地天体在约5~10 km高度空中爆炸造成的.2013年2月15日,一颗小行星以20 km/s的速度进入大气层,在俄罗斯车里雅宾斯克(Chelyabinsk)地区上空约30 km高度发生猛烈爆炸[9 -10 ] ,此次事件中有1 500多人受伤,1 000多房屋受损.据评估该小行星直径约为20 m,爆炸当量约50万吨TNT当量.KT(白垩纪与第三纪)界面事件是距今最近的一次地球物种灭绝事件,期间地球上60%~80%的生物物种灭绝.现在普遍认为[11 -12 ] ,KT事件源于约6 500万年前一颗直径超过10 km的小行星撞击墨西哥尤卡坦半岛附近,产生的反溅碎片云和烟尘进入并长期滞留在地球大气层中,隔断了近90%的太阳辐射,使得全球生物食物链中断,导致大规模物种灭绝. ...
对”天外来客”吉林陨石保护问题的初步探讨
1
2013
... 我国也多次发生过小行星撞击事件. 1976年3月8日,在吉林市北郊上空一个大火球从天而降,随即分裂成许多小火球.在地面收 集到3000余块总重2t的陨石,其中最大的一块陨石重达1170 kg,是世界上已知最重的石陨石[13 ] .最近的流星陨落事件发生在2017年10月4日云南香格里拉以及2018年6月1日云南西双版纳,被大量目击者观察到并用视频记录下来. ...
对”天外来客”吉林陨石保护问题的初步探讨
1
2013
... 我国也多次发生过小行星撞击事件. 1976年3月8日,在吉林市北郊上空一个大火球从天而降,随即分裂成许多小火球.在地面收 集到3000余块总重2t的陨石,其中最大的一块陨石重达1170 kg,是世界上已知最重的石陨石[13 ] .最近的流星陨落事件发生在2017年10月4日云南香格里拉以及2018年6月1日云南西双版纳,被大量目击者观察到并用视频记录下来. ...
近地小行星防御策略分析
2
2017
... 国际社会对行星防御非常重视[14 ] .2013年和2014年美国政府和军方举行联合应急演习,2016年1月NASA成立行星防御协调办公 室.美国、欧空局和日本等均成立了专门的近地天体监测预警中心,实施和部署了若干对于近地天体直接探测以及轨道偏离计划.自2009年起国际宇航科学院(IAA)已经举办5届行星防御会议. 在2012年国际空间探索协调组(International Space Exploration Coordination Group,ISECG)会议上,经12个成员国协调,将"试验减缓近地小行星撞击地球风险的方法"定为小行星探测的三项基本目的之一.2013年10月联合国大会正式批准成立"国际小行星预警网"来组织、协调、共享近地小行星监测资料以及碰撞地球的风险信息. ...
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
近地小行星防御策略分析
2
2017
... 国际社会对行星防御非常重视[14 ] .2013年和2014年美国政府和军方举行联合应急演习,2016年1月NASA成立行星防御协调办公 室.美国、欧空局和日本等均成立了专门的近地天体监测预警中心,实施和部署了若干对于近地天体直接探测以及轨道偏离计划.自2009年起国际宇航科学院(IAA)已经举办5届行星防御会议. 在2012年国际空间探索协调组(International Space Exploration Coordination Group,ISECG)会议上,经12个成员国协调,将"试验减缓近地小行星撞击地球风险的方法"定为小行星探测的三项基本目的之一.2013年10月联合国大会正式批准成立"国际小行星预警网"来组织、协调、共享近地小行星监测资料以及碰撞地球的风险信息. ...
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
Distribution of PSF of the near earth object survey telescope
2
2013
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
... ,15 -16 ].李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
基于图像位移叠加方法探测暗弱小行星
1
2017
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
基于图像位移叠加方法探测暗弱小行星
1
2017
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
不规则小行星引力场内的飞行动力学
1
2017
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
不规则小行星引力场内的飞行动力学
1
2017
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
A survey on orbit and navigation of asteroid missions
1
2014
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
国外近地小行星撞击地球防御技术研究
1
2015
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
国外近地小行星撞击地球防御技术研究
1
2015
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
近地小行星威胁与防御研究现状
1
2016
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
近地小行星威胁与防御研究现状
1
2016
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
小行星撞击对地球的上地幔对流的影响
1
2014
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
小行星撞击对地球的上地幔对流的影响
1
2014
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
一种提升近地小行星防御中拦截效率的方法
1
2017
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
一种提升近地小行星防御中拦截效率的方法
1
2017
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
NTS软件在近地小行星撞击与防御中的应用
2018
NTS软件在近地小行星撞击与防御中的应用
2018
小行星进入三维瞬态传热有限元计算初步研究
2018
小行星进入三维瞬态传热有限元计算初步研究
2018
流星体进入地球大气辐射加热数值分析
1
2018
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
流星体进入地球大气辐射加热数值分析
1
2018
... 我国的近地天体观测设备口径小、数量少、站址单一,与美国等国家差距明显;在小行星偏离、进入与撞击风险评估等方面只进行了局部的探索性研究工作,尚未开展系统性研究.中国科学院紫金山天文台研制了近地天体望远镜[1 ,15 ] ,在小行星监测和撞击预警方面开展了卓有成效的工作[1 ,15 -16 ] .李俊峰等[17 -18 ] 研究了小行星附近的轨道动力学以及小行星探测技术,刘雪奇等[14 ,19 -20 ] 研究了小行星轨道偏离的方法,黄川等[21 ] 通过数值模拟手段研究了小行星撞击对地球的上地幔对流的影响.中国空气动力研究与发展中心超高速所对小行星进入地球大气、撞击地球表面和动能撞击小行星过程进行了初步研究[22 -27 ] , 包括高温气体辐射、烧蚀、解体以及小行星撞击地面和水体的过程.为了促进全国行星防御领域内的学术交流,我国于2018年1月在绵阳召开第一届全国行星防御研讨会,并在2018年9月于北京召开的香山科学会议上,就"小行星监测预警、安全防御和资源利用的前沿科学问题及关键技术"进行了研讨. ...
Physics of Meteor Flight in the Atmosphere.
3
1958
... 小行星进入地球大气与撞击地球表面过程中将会发生非常复杂的物理化学和力学现象[4 -5 ,28 ] (图1 ).小行星进入地球大气速度极高(典型速度12 ~ 20 km/s),远超人造航天器的再入速度(7.5 ~ 11.2 km/s).极大的进入速度产生巨大的气动加热,使得激波层温度超过20 000 K,产生远超对流热流的辐射热流;严酷的热环境引起材料大规模熔融、汽化和烧蚀,导致严重的质量损失和外形变化.与航天飞行器经过人类精心设计的材料和结构不同,小行星的材料和结构是自然形成的,不仅呈现各向异性的特征,而且充满孔隙和裂纹,在强大的气动力、热载荷的共同作用下可能多次解体,甚至产生空中爆炸形成火球.当大尺寸小行星穿透大气层撞击地球表面后,可能会产生撞击坑、反溅碎片云、地震和海啸等现象,其反溅碎片云抛向大气甚至影响气候变化. ...
... 对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... 在极高的进入速度下,小行星将经历严酷的气动加热,准确预测热环境是评估烧蚀和质量损失的前提. 质量损失可用下式描述[28 ,31 ,33 ] ...
Superaerodynamics, mechanics of rarefied gases
1
1964
... 其中,$m$和$V$分别是小行星的质量和速度, $\varPhi $是纬度,$\gamma $和$\psi$分别是飞行航迹角和航向角,$\omega $是地 球自转角速度,$g$是重力加速度,$r_{t}$是小行星距地心的距离,$A$是阻力参考面积. 而$C_{ d}$是阻力系数,与小行星的流动分 区紧密相关.若定义克努森数(Knudsen number, $Kn$)为气体分子平均自由程与流动特征长度的比值,根据20世纪40年代钱学森等[29 ] 提出的准则,流动区域范围大致分为:连续流区(Kn<10- 3 )、过渡流区(10-3 <Kn<10)、自由分子流区(Kn>10);过渡区气体 流动又可细分为近连续流(10-3 <Kn<0.01)、滑移流(0.01<Kn<0.1)、稀薄过渡流(0.1<Kn<10)等. 图2 展示了以小行星半 径作为流动特征长度、基于上述克努森数划分的小行星在不同海拔高度的流动区域.若考虑小行星从高度100 km进入地球大气,对 于我们感兴趣的小行星比如Chelyabinsk流星(半径9.9 m),在100~94 km之间为滑移流,94~79 km之间为近连续流, 当飞行至79 km以下为连续流.因此小行星进入地球大气过程中气动力的模拟是典型的跨流域空气动力学问题. 几十年来,伴随着各种再入飞行器和临近空间飞行器的研制,跨流域空气动力学得到长足发展,已经建立起来基本的地面试验和数值计算手段.但是仍然存 在很多问题[30 ] ,例如对跨流域流动机理认识不清、模拟方法有待完善、计算和试验精度有待提高等.可以设想,当飞行速度从目前研究的范畴(小于第二宇宙速度)提高到小行星进入地球大气的速度时,上述问题不仅一直存在,而且在更加复杂的物理化学现象的耦合下会更加严重. ...
高超声速飞行器跨流域气动力/热预测技术研究
1
2016
... 其中,$m$和$V$分别是小行星的质量和速度, $\varPhi $是纬度,$\gamma $和$\psi$分别是飞行航迹角和航向角,$\omega $是地 球自转角速度,$g$是重力加速度,$r_{t}$是小行星距地心的距离,$A$是阻力参考面积. 而$C_{ d}$是阻力系数,与小行星的流动分 区紧密相关.若定义克努森数(Knudsen number, $Kn$)为气体分子平均自由程与流动特征长度的比值,根据20世纪40年代钱学森等[29 ] 提出的准则,流动区域范围大致分为:连续流区(Kn<10- 3 )、过渡流区(10-3 <Kn<10)、自由分子流区(Kn>10);过渡区气体 流动又可细分为近连续流(10-3 <Kn<0.01)、滑移流(0.01<Kn<0.1)、稀薄过渡流(0.1<Kn<10)等. 图2 展示了以小行星半 径作为流动特征长度、基于上述克努森数划分的小行星在不同海拔高度的流动区域.若考虑小行星从高度100 km进入地球大气,对 于我们感兴趣的小行星比如Chelyabinsk流星(半径9.9 m),在100~94 km之间为滑移流,94~79 km之间为近连续流, 当飞行至79 km以下为连续流.因此小行星进入地球大气过程中气动力的模拟是典型的跨流域空气动力学问题. 几十年来,伴随着各种再入飞行器和临近空间飞行器的研制,跨流域空气动力学得到长足发展,已经建立起来基本的地面试验和数值计算手段.但是仍然存 在很多问题[30 ] ,例如对跨流域流动机理认识不清、模拟方法有待完善、计算和试验精度有待提高等.可以设想,当飞行速度从目前研究的范畴(小于第二宇宙速度)提高到小行星进入地球大气的速度时,上述问题不仅一直存在,而且在更加复杂的物理化学现象的耦合下会更加严重. ...
高超声速飞行器跨流域气动力/热预测技术研究
1
2016
... 其中,$m$和$V$分别是小行星的质量和速度, $\varPhi $是纬度,$\gamma $和$\psi$分别是飞行航迹角和航向角,$\omega $是地 球自转角速度,$g$是重力加速度,$r_{t}$是小行星距地心的距离,$A$是阻力参考面积. 而$C_{ d}$是阻力系数,与小行星的流动分 区紧密相关.若定义克努森数(Knudsen number, $Kn$)为气体分子平均自由程与流动特征长度的比值,根据20世纪40年代钱学森等[29 ] 提出的准则,流动区域范围大致分为:连续流区(Kn<10- 3 )、过渡流区(10-3 <Kn<10)、自由分子流区(Kn>10);过渡区气体 流动又可细分为近连续流(10-3 <Kn<0.01)、滑移流(0.01<Kn<0.1)、稀薄过渡流(0.1<Kn<10)等. 图2 展示了以小行星半 径作为流动特征长度、基于上述克努森数划分的小行星在不同海拔高度的流动区域.若考虑小行星从高度100 km进入地球大气,对 于我们感兴趣的小行星比如Chelyabinsk流星(半径9.9 m),在100~94 km之间为滑移流,94~79 km之间为近连续流, 当飞行至79 km以下为连续流.因此小行星进入地球大气过程中气动力的模拟是典型的跨流域空气动力学问题. 几十年来,伴随着各种再入飞行器和临近空间飞行器的研制,跨流域空气动力学得到长足发展,已经建立起来基本的地面试验和数值计算手段.但是仍然存 在很多问题[30 ] ,例如对跨流域流动机理认识不清、模拟方法有待完善、计算和试验精度有待提高等.可以设想,当飞行速度从目前研究的范畴(小于第二宇宙速度)提高到小行星进入地球大气的速度时,上述问题不仅一直存在,而且在更加复杂的物理化学现象的耦合下会更加严重. ...
Trajectory simulation of meteors assuming mass loss and fragmentation
2
2015
... 对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... 在极高的进入速度下,小行星将经历严酷的气动加热,准确预测热环境是评估烧蚀和质量损失的前提. 质量损失可用下式描述[28 ,31 ,33 ] ...
The Morávka meteorite fall : 4 meteoroid dynamics and fragmentation in the atmosphere
3
... 对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... 其中,下标"c"表示子碎片,下标"p"表示父碎片. Popovao发现很多违反Weibull定律的事实[46 ] .例如Morávka流星[32 ] 的主解体事件发生时的动压为5 MPa,而后面的一次解体却发生在更小的动压2.3 MPa下,并且地面收集到碎片没有烧蚀痕迹,表明在2~3 km/s较低速度下(烧蚀停止)仍存在解体.因此,需要研究Weibull之外的解体强度与碎片尺寸的关系. ...
... 在小行星进入地球大气过程中,还会有声学方面的问题. 至少存在二类声信号,分别是音爆[59 ] 和次声[60 ] . 小行星进入过程音爆的形成机理与超声速飞机类似,都是超声速飞行产生的激波向地面传播形成的. 不同的是,小行星飞行马赫数极高,马赫数极小,形成的激波形状类似圆柱形,且激波强度更大. 次声信号是空中爆炸产生的低频率声波,是空中爆炸的重要特征之一[60 ] . 研究人员可根据地震台站监测到的次声信号以及地震站位置,分析得出小行星的解体时序和进入轨迹[32 ,60 ] . ...
A fragment-cloud model for asteroid breakup and atmospheric energy deposition
4
2017
... 对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... 在极高的进入速度下,小行星将经历严酷的气动加热,准确预测热环境是评估烧蚀和质量损失的前提. 质量损失可用下式描述[28 ,31 ,33 ] ...
... 由于小行星的力、热载荷分布不均匀,并且孔隙、裂纹以及材料熔融和烧蚀会减小强度,上述解体判据略显粗糙,需要研究更准确、更能代表解体机理的解体判据以应用于地面危害评估. 根据Popovao(2011)对大量观测结果的总结[46 ] ,0.1~10$^{6}$\,kg质量范围的石质小行星的解体强度为0.1~10 MPa,而材料的平均拉伸强度为30 MPa,压缩强度和屈服强度更大.解体强度$S$与小行星的实际强度存在什么关系,怎样获得初次解体时的强度,需要进行研究.解体强度也和小行星尺寸有关,Weibull通过对地球上岩石强度的观测和分析,总结出Weibull定律[47 ] ,Artemieva和Wheeler$^{[33 ,48 ] }$将其应用于解体后碎片强度的计算中,即 ...
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
Break-up modelling and trajectory simulation under uncertainty for asteroids
1
2015
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
Recent advances in bolide entry modeling: A bolide potpourri.
2
2004
... 对于未解体的小行星或解体后单独飞行不受其他小行星碎片干扰的碎片,其运动轨迹的模拟有着成熟的模型和方法[28 ,31 ] .目 前已经建立起包括质量损失方程在内的小行星运动方程组.小行星解体爆炸后,可能会形成大块碎片以及由小碎片、液滴、灰尘组成的碎片云.大块碎片之间的气动干扰及其对运动的影响、碎片云如何变形及运动,都是值得研究的空气动力学问题.对俄罗斯Chelyabinsk流星事件[10 ] 和捷克Morávka流星事件[32 ] 的观测指出,个别碎片在解体时获得了较大的横向(垂直于弹道方向)速度. 例如Chelyabinsk流星解体后碎片F1的弹道偏离了主飞行方向约1.3$^\circ$$\pm$0.4$^\circ$,意味着在解体时获得了(400$\pm $130)m/s的横向速度.文献[10 ] 指出,这样大的横向速度用现有的空气动力学理论和地面试验无法解释.在以FCM模型为代表的目前的解体模型[33 -35 ] 中,对解体后碎片之间的气动干扰没有考虑或者建模不准确,也就无法预测类似Chelyabinsk流星解体后F1碎片对主弹道的偏离. ...
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
The fragmentation of small asteroids in the atmosphere
6
1993
... 小行星解体后形成碎片云的变形往往依靠下式预测[36 ] ...
... 其中,$V_{\rm disp}$是碎片云的扩散速度,$V$是飞行速度,$\rho_{\rm air}$和 $\rho $分别是大气及小行星密度. 但是扩散系数$C_{\rm disp}$并不确定,不同研究者给出的取值往往差异较大$^{[36 -37 ] }$. 此外,目前在理论上还无法确定[8 ] 扩散后碎片云半径与解体前小行星初始半径的比值大到多少时,碎片云中小碎片(液滴、灰尘)彼此之间不存在气动干扰,以至于碎片云在气动上不能作为一个整体对待. ...
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
... 海啸是小行星撞击海洋过程中最典型的自然现象. 当小行星撞击海洋时,将迅速挤压海水,产生的冲击波在水体内传播,引起海啸,产生一定高度的"海墙"在海面传播. 据研究,直径1 km的小行星撞击在1000 km以外海域仍能形成100 m高海啸[72 ] . 据报道,有颗名为Eltain直径4 km的小行星,曾撞击到南太平洋底部,在距其1 200~1 500 km远的海域引起高度达到200~300 m的海啸[73 ] . 小行星撞击海洋表面的破坏半径比撞击陆地更大,破坏半径大约与小行星撞击能量的1/2次方成正比[74 ] . 海啸形成高度可通过拟合公式来表示[36 ] ...
... 小行星撞击地表后产生极强烈的冲击波,冲击波的传播可以诱发地震. 小行星撞击过程中,大部分能量用于成坑,小部分能量用于产生地震效应. 文献[36 ] 给出震源处里氏震级与撞击能量的关系式 ...
Effects of atmospheric breakup on crater field formation
1
1980
... 其中,$V_{\rm disp}$是碎片云的扩散速度,$V$是飞行速度,$\rho_{\rm air}$和 $\rho $分别是大气及小行星密度. 但是扩散系数$C_{\rm disp}$并不确定,不同研究者给出的取值往往差异较大$^{[36 -37 ] }$. 此外,目前在理论上还无法确定[8 ] 扩散后碎片云半径与解体前小行星初始半径的比值大到多少时,碎片云中小碎片(液滴、灰尘)彼此之间不存在气动干扰,以至于碎片云在气动上不能作为一个整体对待. ...
Thermophysics issues relevant to highspeed earth entry of large asteroids
4
2016
... 热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
... [38 ].在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
... 半径15 m球头的热流分布[38 ] ...
... Heat flux distribution along a sphere surface with radius of 15 m[38 ] ...
Impact of coupled radiation and ablation on the aerothermodynamics of meteor entries
5
2017
... 热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
... 传统的气动热力学研究主要针对速度在第二宇宙速度之下的超高速飞行器,流场温度通常低于20 000 K,此时,高温激波层辐射对流动及相关物理化学过程的影响可以忽略.在小行星进入地球大气的极高速、极高温、强辐射和强烧蚀环境下,高温气体流场、辐射和烧蚀强烈耦合[39 -40 ,51 ] ,必须考虑三者之间的相互影响.文献[39 ,51 ] 的研究指出,在流场计算中耦合辐射减小了激波脱体距离,降低了激波层温度;在流场计算中耦合烧蚀大大降低了物面辐射热流. ...
... [39 ,51 ]的研究指出,在流场计算中耦合辐射减小了激波脱体距离,降低了激波层温度;在流场计算中耦合烧蚀大大降低了物面辐射热流. ...
... 如图2 所示,对于我们感兴趣的小行星尺寸(半径大于1 m),在进入地球大气绝大部分飞行范围内,流动处于连续流区,CFD是主要的研究手段. 目前CFD已经建立起考虑化学反应、内能激发、热力学非平衡以及烧蚀气体进入流场的模型,发展了多种空间和时间格式,在超高速飞行器的研制中发挥了重要作用. 但是针对小行星进入的极高速、极高温条件,大于20 000 K的热化学模型很不完备[39 ,51 ] ,目前的可压缩湍流模型还需要验证和校核. 当前CFD模拟火球时往往引入额外的能量释放以考虑空中爆炸的影响[84 ] ,并且由于不清楚小行星内部结构,计算和观测仅在定性上一致. ...
The influence of ablation on radiative heating for earth entry
2
2009
... 热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
... 传统的气动热力学研究主要针对速度在第二宇宙速度之下的超高速飞行器,流场温度通常低于20 000 K,此时,高温激波层辐射对流动及相关物理化学过程的影响可以忽略.在小行星进入地球大气的极高速、极高温、强辐射和强烧蚀环境下,高温气体流场、辐射和烧蚀强烈耦合[39 -40 ,51 ] ,必须考虑三者之间的相互影响.文献[39 ,51 ] 的研究指出,在流场计算中耦合辐射减小了激波脱体距离,降低了激波层温度;在流场计算中耦合烧蚀大大降低了物面辐射热流. ...
高超声速边界层转捩研究现状与发展趋势
1
2017
... 热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
高超声速边界层转捩研究现状与发展趋势
1
2017
... 热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
Review and assessment of turbulence models for hypersonic flows: 2d/asymmetric cases
1
2006
... 热流系数$C_{\rm H}$包含对流热流和辐射热流两部分的贡献.文献[38 ] 对半径15 m的球头在速度20 km/s、总压30 bar条件下的热流进行了初步计算分析,并如图3 所示,可见辐射热流比对流热流大很多,在总热流中占主导地位.在小行星进入地球大气的极高速下,高温气体流场、激波层辐射和烧蚀紧密耦合[39 -40 ] ,准确获得辐射热流需要进行流场、辐射和烧蚀的耦合计算分析.此外,由于具有较高的速度以及较大的尺寸(最大可达千米量级),在很多情况下绕小行星的流场是湍流.转捩和湍流对对流热流和辐射热流都有着较大的影响[38 ] .在当前的超高速空气力学研究中,转捩和湍流是热点研究领域,有很多基础性问题尚未解决[41 -42 ] .在小行星进入地球大气这种极高速、高温的条件下,当前研究中建立起来的模型和模拟方法是否适用以及如何模拟转捩和湍流,是一个 需要深入研究的问题. ...
Meteorites
1
1967
... 烧蚀热$Q$由小行星材料种类和烧蚀机理决定.典型再入飞行器热防护系统的材料是经过人为设计的烧蚀防护层,以硅基和碳基烧蚀材 料为主.小行星材料是天然形成的,大致分为三类[43 ] :铁陨石、石-铁陨石、石陨石.因而在航天器再入研究中建立的烧蚀机理不再适用于小行星材料,需要针对具体的小行星材料研究烧蚀机理.具体来说需要研究的问题包括:小行星材料的气面反应机制、物面的质量和能量平衡机理、熔融层的运动对烧蚀的影响、烧蚀引起的质量引射对气动力/热的影响. ...
Survey of meteorite physical properties: density, porosity and magnetic susceptibility.
3
2010
... 小行星是天然形成的,其结构并不像人类加工材料那样多呈现各向同性,而是通常情况下呈现各向异性,因此需要研究各向异性材料和结构的传热及热响应.研究指出,由于在漫长的历史演化中与其他天体碰撞和风化作用,大多数小行星结构具有较高的孔隙率[44 ] (图4 )和裂纹[45 ] (图5 ). 孔隙和裂纹对结构响应有着重要影响. ...
... 球粒状陨石孔隙率随铁元素氧化态的变化[44 ] ...
... Porosity vs. oxidation state for chondrite Falls[44 ] ...
Fracture characterization of meteorites
3
2015
... 小行星是天然形成的,其结构并不像人类加工材料那样多呈现各向同性,而是通常情况下呈现各向异性,因此需要研究各向异性材料和结构的传热及热响应.研究指出,由于在漫长的历史演化中与其他天体碰撞和风化作用,大多数小行星结构具有较高的孔隙率[44 ] (图4 )和裂纹[45 ] (图5 ). 孔隙和裂纹对结构响应有着重要影响. ...
... 球粒状陨石的裂纹[45 ] (伦敦自然历史博物馆) ...
... Fractures in a chondrite meteorite exhibited in Natural History Museum, London[45 ] ...
Borovi$\check{c}$ka J, Hartmann WK, et al. Very low strengths of interplanetary meteoroids and small asteroids
2
2011
... 由于小行星的力、热载荷分布不均匀,并且孔隙、裂纹以及材料熔融和烧蚀会减小强度,上述解体判据略显粗糙,需要研究更准确、更能代表解体机理的解体判据以应用于地面危害评估. 根据Popovao(2011)对大量观测结果的总结[46 ] ,0.1~10$^{6}$\,kg质量范围的石质小行星的解体强度为0.1~10 MPa,而材料的平均拉伸强度为30 MPa,压缩强度和屈服强度更大.解体强度$S$与小行星的实际强度存在什么关系,怎样获得初次解体时的强度,需要进行研究.解体强度也和小行星尺寸有关,Weibull通过对地球上岩石强度的观测和分析,总结出Weibull定律[47 ] ,Artemieva和Wheeler$^{[33 ,48 ] }$将其应用于解体后碎片强度的计算中,即 ...
... 其中,下标"c"表示子碎片,下标"p"表示父碎片. Popovao发现很多违反Weibull定律的事实[46 ] .例如Morávka流星[32 ] 的主解体事件发生时的动压为5 MPa,而后面的一次解体却发生在更小的动压2.3 MPa下,并且地面收集到碎片没有烧蚀痕迹,表明在2~3 km/s较低速度下(烧蚀停止)仍存在解体.因此,需要研究Weibull之外的解体强度与碎片尺寸的关系. ...
A statistical distribution function of wide applicability
1
1951
... 由于小行星的力、热载荷分布不均匀,并且孔隙、裂纹以及材料熔融和烧蚀会减小强度,上述解体判据略显粗糙,需要研究更准确、更能代表解体机理的解体判据以应用于地面危害评估. 根据Popovao(2011)对大量观测结果的总结[46 ] ,0.1~10$^{6}$\,kg质量范围的石质小行星的解体强度为0.1~10 MPa,而材料的平均拉伸强度为30 MPa,压缩强度和屈服强度更大.解体强度$S$与小行星的实际强度存在什么关系,怎样获得初次解体时的强度,需要进行研究.解体强度也和小行星尺寸有关,Weibull通过对地球上岩石强度的观测和分析,总结出Weibull定律[47 ] ,Artemieva和Wheeler$^{[33 ,48 ] }$将其应用于解体后碎片强度的计算中,即 ...
Motion of a fragmented meteoroid through the planetary atmosphere
1
2011
... 由于小行星的力、热载荷分布不均匀,并且孔隙、裂纹以及材料熔融和烧蚀会减小强度,上述解体判据略显粗糙,需要研究更准确、更能代表解体机理的解体判据以应用于地面危害评估. 根据Popovao(2011)对大量观测结果的总结[46 ] ,0.1~10$^{6}$\,kg质量范围的石质小行星的解体强度为0.1~10 MPa,而材料的平均拉伸强度为30 MPa,压缩强度和屈服强度更大.解体强度$S$与小行星的实际强度存在什么关系,怎样获得初次解体时的强度,需要进行研究.解体强度也和小行星尺寸有关,Weibull通过对地球上岩石强度的观测和分析,总结出Weibull定律[47 ] ,Artemieva和Wheeler$^{[33 ,48 ] }$将其应用于解体后碎片强度的计算中,即 ...
Modeling of spreading of meteoroid fragments
1
2012
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
Asteroid fragmentation approaches for modeling atmospheric energy deposition
1
2017
... 解体模型描述小行星解体后的存在形式,是描述以超高速飞行的小行星在气动力、热载荷的作用下解体行为的重要方面.经过几十年发展,研究者发展了一系列解体模型,包括连续的Pancake模型[8 ,36 ] 和Park模型[49 ] 、离散的"collective wake"模型[35 ] 和"independent wake"模型[34 ] ,以及把离散和连续模型综合起来的耦合模型[50 ] 及其改进后的FCM模型[33 ] .FCM模型把大块碎片和由小碎片、液滴、灰尘构成的碎片云分别处理,具有其他模型不具备的优势.但FCM以及其他解体模型在解体后碎片数量以及碎片和碎片云的质量分布上采用假定的方式,存在较大的随意性. ...
Aerothermodynamic characteristics of 16-22 km/s earth entry
8
... 如图6 所示,在小行星进入大气层的极高速度下,小行星驻点区的空气将处于20 000~50 000K的高温,除了出现传统再入物理所关心的振动和电子能级激发、离解、电离以及能量松弛等非平衡现象,还会出现二次电离现象并产生新的组分如N$^{ + + }$, O$^{ + +}$等[51 -52 ] ;分子中的电子受到激发,在各能级之间跃迁并发射或吸收光子,产生严重的激波层辐射[51 -52 ] ;在严酷的热环境下,小行星材料受到大规模烧蚀,物面的液体熔融层在气流的作用下向后移动,烧蚀气体在物面附近产生较厚的烧蚀层[51 -52 ] ;大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... [51 -52 ];在严酷的热环境下,小行星材料受到大规模烧蚀,物面的液体熔融层在气流的作用下向后移动,烧蚀气体在物面附近产生较厚的烧蚀层[51 -52 ] ;大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... [51 -52 ];大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... [51 -52 ],而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
... 传统的气动热力学研究主要针对速度在第二宇宙速度之下的超高速飞行器,流场温度通常低于20 000 K,此时,高温激波层辐射对流动及相关物理化学过程的影响可以忽略.在小行星进入地球大气的极高速、极高温、强辐射和强烧蚀环境下,高温气体流场、辐射和烧蚀强烈耦合[39 -40 ,51 ] ,必须考虑三者之间的相互影响.文献[39 ,51 ] 的研究指出,在流场计算中耦合辐射减小了激波脱体距离,降低了激波层温度;在流场计算中耦合烧蚀大大降低了物面辐射热流. ...
... ,51 ]的研究指出,在流场计算中耦合辐射减小了激波脱体距离,降低了激波层温度;在流场计算中耦合烧蚀大大降低了物面辐射热流. ...
... 如图2 所示,对于我们感兴趣的小行星尺寸(半径大于1 m),在进入地球大气绝大部分飞行范围内,流动处于连续流区,CFD是主要的研究手段. 目前CFD已经建立起考虑化学反应、内能激发、热力学非平衡以及烧蚀气体进入流场的模型,发展了多种空间和时间格式,在超高速飞行器的研制中发挥了重要作用. 但是针对小行星进入的极高速、极高温条件,大于20 000 K的热化学模型很不完备[39 ,51 ] ,目前的可压缩湍流模型还需要验证和校核. 当前CFD模拟火球时往往引入额外的能量释放以考虑空中爆炸的影响[84 ] ,并且由于不清楚小行星内部结构,计算和观测仅在定性上一致. ...
Entry modeling for asteroid threat assessment
6
2017
... 如图6 所示,在小行星进入大气层的极高速度下,小行星驻点区的空气将处于20 000~50 000K的高温,除了出现传统再入物理所关心的振动和电子能级激发、离解、电离以及能量松弛等非平衡现象,还会出现二次电离现象并产生新的组分如N$^{ + + }$, O$^{ + +}$等[51 -52 ] ;分子中的电子受到激发,在各能级之间跃迁并发射或吸收光子,产生严重的激波层辐射[51 -52 ] ;在严酷的热环境下,小行星材料受到大规模烧蚀,物面的液体熔融层在气流的作用下向后移动,烧蚀气体在物面附近产生较厚的烧蚀层[51 -52 ] ;大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... -52 ];在严酷的热环境下,小行星材料受到大规模烧蚀,物面的液体熔融层在气流的作用下向后移动,烧蚀气体在物面附近产生较厚的烧蚀层[51 -52 ] ;大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... -52 ];大量烧蚀产物进入流场,不仅对流场和辐射加热产生强烈的影响[51 -52 ] ,而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... -52 ],而且随流动进入尾迹区,产生强烈的尾迹光辐射. ...
... 极高速下的高温气体效应示意图[52 ] ...
... Sketch of high temperature effect at ultra-high velocity[52 ] ...
NASA glenn coefficients for calculating coefficients for calculating thermodynamic properties of individual species.
1
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
Recommended collision integrals for transport property computations part 1: Air species
1
2005
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
Recommended collision integrals for transport property computations part 2: mars and venus entries
1
2007
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium
1
1989
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
Basic governing for the flight regimes of aeroassisted orbital transfer vehicles
1
1984
... 当前的高温气体热化学模型是1980年代以后基于超高速飞行器的研制而建立起来的,普遍应用的模型包括:Gordon和McBride的20 000 K气体热力学特性曲线拟合数据[53 ] ,Wright[54 -55 ] 关于空气、金星和火星大气组元的20 000 K输运截面数据,Dunn等[56 ] 的5,7,11组元化学动力学模型.在小行星进入地球大气的极高温、强辐射和强烧蚀环境下,上述模型适用性降低.具体来说需要研究的问题包括[39 ,51 ] :高于20 000 K高温气体组分的热力学模型和输运特性模型,二次电离反应、光催化反应以及烧蚀气体组分和空气组分反应的反应动力学模型,二次电离组分和烧蚀气体组分的辐射基础数据.此外,当前的高温气体效应模型基于弱电离假设[57 ] .在小行星进入地球大气的极高速和高温下,弱电离假设是否成立,需要重新审视.在传统再入物理中,一般应用双温度热力学非平衡模型就可以很好地解决工程问题.在小行星进入地球大气的极高速和高温下,双温度模型是否足够准确,是否需要使用更复杂的热力学非平衡模型,是一个值得研究的问题. ...
Simulations of the entry and damaging effects of asteroid impacts
3
2015
... 在小行星物理中,把超高速飞行以及空中爆炸产生的高温流场称为"火球"[4 ] .火球能够产生较强的光辐射,可被肉眼或仪器 观测到,是小行星撞击地球最显著的特征.光辐射数据通常可转换为能量沉积数据[9 ] ,是小行星进入地球大气过程最重要的观测数据之一,可用于校验模拟方法或作为模拟的输入[58 ] . 图7 是Chelyabinsk流星事件的视频截图,从中可以看到火球较强的光辐射. ...
... Chelyabinsk流星事件视频截图[58 ] ...
... Video capture of Chelyabinsk event[58 ] ...
Numerical prediction of meteoric infrasound signatures
1
2017
... 在小行星进入地球大气过程中,还会有声学方面的问题. 至少存在二类声信号,分别是音爆[59 ] 和次声[60 ] . 小行星进入过程音爆的形成机理与超声速飞机类似,都是超声速飞行产生的激波向地面传播形成的. 不同的是,小行星飞行马赫数极高,马赫数极小,形成的激波形状类似圆柱形,且激波强度更大. 次声信号是空中爆炸产生的低频率声波,是空中爆炸的重要特征之一[60 ] . 研究人员可根据地震台站监测到的次声信号以及地震站位置,分析得出小行星的解体时序和进入轨迹[32 ,60 ] . ...
The Morávka meteorite fall: 2. interpretation of infrasonic and seismic data
3
2003
... 在小行星进入地球大气过程中,还会有声学方面的问题. 至少存在二类声信号,分别是音爆[59 ] 和次声[60 ] . 小行星进入过程音爆的形成机理与超声速飞机类似,都是超声速飞行产生的激波向地面传播形成的. 不同的是,小行星飞行马赫数极高,马赫数极小,形成的激波形状类似圆柱形,且激波强度更大. 次声信号是空中爆炸产生的低频率声波,是空中爆炸的重要特征之一[60 ] . 研究人员可根据地震台站监测到的次声信号以及地震站位置,分析得出小行星的解体时序和进入轨迹[32 ,60 ] . ...
... [60 ]. 研究人员可根据地震台站监测到的次声信号以及地震站位置,分析得出小行星的解体时序和进入轨迹[32 ,60 ] . ...
... ,60 ]. ...
撞击坑中央隆起构造研究. [博士论文]
3
2016
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
... 撞击坑形成过程[61 ] ...
... Sketch of cratering process[61 ] ...
撞击坑中央隆起构造研究. [博士论文]
3
2016
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
... 撞击坑形成过程[61 ] ...
... Sketch of cratering process[61 ] ...
1
2001
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
陨石撞击构造作用的研究现状与前景
1
2008
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
陨石撞击构造作用的研究现状与前景
1
2008
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
Formation of the central uplift in meteoric craters
1
1986
... 小行星对陆地的撞击坑根据其形状特征主要分为简单撞击坑和复杂撞击坑两种,复杂撞击坑又主要表现为中央隆起撞击坑,两种撞击坑的形成包括初期接触、碰撞挖掘、回填调整三个阶段[61 ] (图8 ).简单撞击坑一般尺寸相对较小,深度和直径比范围为1:5~1:7,坑壁光滑、陡峭、无阶梯状内壁,且撞击坑中间无中央峰的出现,典型简单撞击坑如美国Arizona州的Meteor crater[62 -64 ] .复杂撞击坑不仅在坑径尺寸上远大于简单撞击坑,其他特征也与简单撞击坑呈现出极大的不同,其深度与直径比范围为1:10~1:20,且坑壁滑塌,呈阶梯状分布,其最主要的特点是坑内有中央峰的出现[65 ] .撞击成坑的形状与尺寸是表征撞击坑特征最主要的两个指标.目前的主流观点认为,超高速撞击过程成坑直径主要与撞击物的能量有关,简要的表达式为[36 ] ...
陨石撞击、环境灾变与生物绝灭
1
1997
... 碰撞产生的强冲击波还将引起小行星和地表介质气化,甚至导致小行星完全蒸发.地表介质气化质量可达到小行星质量的数倍,并可能 抛射到较高大气层. 与此同时,小行星体积60~100倍的地表物质被掘起,以反溅碎片的形式连同挥发性物质一起被抛向天空,其高度可达100 km以上[66 ] .研究表明[67 ] ,地表介质在小行星撞击下的气化质量$M_{\rm R}$与撞击小行星的质量$m$、速度$V$以及引起介质气化所需的最小 速度$V_{\rm R}$有关,其量级可用下式计算 ...
陨石撞击、环境灾变与生物绝灭
1
1997
... 碰撞产生的强冲击波还将引起小行星和地表介质气化,甚至导致小行星完全蒸发.地表介质气化质量可达到小行星质量的数倍,并可能 抛射到较高大气层. 与此同时,小行星体积60~100倍的地表物质被掘起,以反溅碎片的形式连同挥发性物质一起被抛向天空,其高度可达100 km以上[66 ] .研究表明[67 ] ,地表介质在小行星撞击下的气化质量$M_{\rm R}$与撞击小行星的质量$m$、速度$V$以及引起介质气化所需的最小 速度$V_{\rm R}$有关,其量级可用下式计算 ...
1
... 碰撞产生的强冲击波还将引起小行星和地表介质气化,甚至导致小行星完全蒸发.地表介质气化质量可达到小行星质量的数倍,并可能 抛射到较高大气层. 与此同时,小行星体积60~100倍的地表物质被掘起,以反溅碎片的形式连同挥发性物质一起被抛向天空,其高度可达100 km以上[66 ] .研究表明[67 ] ,地表介质在小行星撞击下的气化质量$M_{\rm R}$与撞击小行星的质量$m$、速度$V$以及引起介质气化所需的最小 速度$V_{\rm R}$有关,其量级可用下式计算 ...
1
... 碰撞产生的强冲击波还将引起小行星和地表介质气化,甚至导致小行星完全蒸发.地表介质气化质量可达到小行星质量的数倍,并可能 抛射到较高大气层. 与此同时,小行星体积60~100倍的地表物质被掘起,以反溅碎片的形式连同挥发性物质一起被抛向天空,其高度可达100 km以上[66 ] .研究表明[67 ] ,地表介质在小行星撞击下的气化质量$M_{\rm R}$与撞击小行星的质量$m$、速度$V$以及引起介质气化所需的最小 速度$V_{\rm R}$有关,其量级可用下式计算 ...
Hydrocode modeling of oblique impacts: the fate of the projectile
1
2000
... 由于小行星撞击陆地是一个多尺度、多材料和多物理因素耦合的问题[68 ] ,式(7)和式(8)的普适性有待进一步研究. ...
Porosity effects on impact processes in solar system materials
1
1999
... 影响撞击成坑与反溅碎片云两种现象的典型物理因素较为一致. 将成坑尺寸与反溅碎片云质量和速度作为撞击的典型特征,研究适用于撞击过程的缩尺律关系是小行星撞击陆地表面研究的核心内容之一,也是开展地面缩比试验研究的前提. 小行星撞击陆地表面过程中的材料属性(包括密度、强度、孔隙率等)、撞击速度以及撞击角度等都对最终撞击特征有着重要的影响[69 ] ,研究各因素与成坑尺寸、反溅碎片云质量和速度等撞击特征之间的函数关系、拟合经验公式,是研究中的典型问题. 相比于超高速动能武器研究和空间碎片防护中的超高速碰撞问题,小行星与地球陆地表面有着完全不同的材料,需要研究撞击过程中地表材料的物理和力学性质,完善超高速撞击下材料特性的模型. 此外,小行星撞击后地面坑形的形貌特征和成坑的分界条件也是需要研究的问题. ...
Numerical simulations of hypervelocity impact of asteroid/comet on the Earth
2
2006
... 海洋面积约占地球表面总面积的70%,海洋水体是小行星撞击地球表面最主要的靶标对象. 相比于撞击陆地的情况,撞击成坑与反溅碎片云并非撞击海洋中最值得关注的典型现象. 在小行星撞击海面后的数十秒内,大量海水被排开,小行星甚至可能撞击海底并进一步接触地幔[70 ] . 小行星撞击海洋后,将会把大量的海水反溅或蒸发入大气中. 研究指出[71 ] ,当半径5 km的小行星撞击海洋时,会蒸发其质量4倍的海洋水汽. 此外,如果撞击到海底,在抛向大气的材料中,还包含地表、地幔和小行星材料[70 ] . 图9 展示为中国空气动力研究与发展中心超高速碰撞中心运用NTS软件仿真小行星撞击海面的压强云图. ...
... [70 ]. 图9 展示为中国空气动力研究与发展中心超高速碰撞中心运用NTS软件仿真小行星撞击海面的压强云图. ...
Assessing atmospheric water injection from oceanic impacts
1
2005
... 海洋面积约占地球表面总面积的70%,海洋水体是小行星撞击地球表面最主要的靶标对象. 相比于撞击陆地的情况,撞击成坑与反溅碎片云并非撞击海洋中最值得关注的典型现象. 在小行星撞击海面后的数十秒内,大量海水被排开,小行星甚至可能撞击海底并进一步接触地幔[70 ] . 小行星撞击海洋后,将会把大量的海水反溅或蒸发入大气中. 研究指出[71 ] ,当半径5 km的小行星撞击海洋时,会蒸发其质量4倍的海洋水汽. 此外,如果撞击到海底,在抛向大气的材料中,还包含地表、地幔和小行星材料[70 ] . 图9 展示为中国空气动力研究与发展中心超高速碰撞中心运用NTS软件仿真小行星撞击海面的压强云图. ...
Tsunami deposits in the geological record
1
2007
... 海啸是小行星撞击海洋过程中最典型的自然现象. 当小行星撞击海洋时,将迅速挤压海水,产生的冲击波在水体内传播,引起海啸,产生一定高度的"海墙"在海面传播. 据研究,直径1 km的小行星撞击在1000 km以外海域仍能形成100 m高海啸[72 ] . 据报道,有颗名为Eltain直径4 km的小行星,曾撞击到南太平洋底部,在距其1 200~1 500 km远的海域引起高度达到200~300 m的海啸[73 ] . 小行星撞击海洋表面的破坏半径比撞击陆地更大,破坏半径大约与小行星撞击能量的1/2次方成正比[74 ] . 海啸形成高度可通过拟合公式来表示[36 ] ...
Impact tsunami-Eltanin
1
2002
... 海啸是小行星撞击海洋过程中最典型的自然现象. 当小行星撞击海洋时,将迅速挤压海水,产生的冲击波在水体内传播,引起海啸,产生一定高度的"海墙"在海面传播. 据研究,直径1 km的小行星撞击在1000 km以外海域仍能形成100 m高海啸[72 ] . 据报道,有颗名为Eltain直径4 km的小行星,曾撞击到南太平洋底部,在距其1 200~1 500 km远的海域引起高度达到200~300 m的海啸[73 ] . 小行星撞击海洋表面的破坏半径比撞击陆地更大,破坏半径大约与小行星撞击能量的1/2次方成正比[74 ] . 海啸形成高度可通过拟合公式来表示[36 ] ...
小天体撞击灾害
1
2001
... 海啸是小行星撞击海洋过程中最典型的自然现象. 当小行星撞击海洋时,将迅速挤压海水,产生的冲击波在水体内传播,引起海啸,产生一定高度的"海墙"在海面传播. 据研究,直径1 km的小行星撞击在1000 km以外海域仍能形成100 m高海啸[72 ] . 据报道,有颗名为Eltain直径4 km的小行星,曾撞击到南太平洋底部,在距其1 200~1 500 km远的海域引起高度达到200~300 m的海啸[73 ] . 小行星撞击海洋表面的破坏半径比撞击陆地更大,破坏半径大约与小行星撞击能量的1/2次方成正比[74 ] . 海啸形成高度可通过拟合公式来表示[36 ] ...
小天体撞击灾害
1
2001
... 海啸是小行星撞击海洋过程中最典型的自然现象. 当小行星撞击海洋时,将迅速挤压海水,产生的冲击波在水体内传播,引起海啸,产生一定高度的"海墙"在海面传播. 据研究,直径1 km的小行星撞击在1000 km以外海域仍能形成100 m高海啸[72 ] . 据报道,有颗名为Eltain直径4 km的小行星,曾撞击到南太平洋底部,在距其1 200~1 500 km远的海域引起高度达到200~300 m的海啸[73 ] . 小行星撞击海洋表面的破坏半径比撞击陆地更大,破坏半径大约与小行星撞击能量的1/2次方成正比[74 ] . 海啸形成高度可通过拟合公式来表示[36 ] ...
Impact-generated tsunamis: An over-rated hazard
1
2003
... 撞击海洋研究需要考虑水体作为靶标材料的特殊性. 海啸的产生与传播是小行星撞击海洋研究中的核心问题. 当前描述撞击产生海啸的模型还不够精确,并且难以开展地面试验研究. 利用式(9)计算海啸高度略显粗糙,需要研究的内容包括:小行星直径、速度和撞击角度等撞击参数对海啸高度的影响;撞击前、撞击过程中和撞击后冲击波在水体中的传播机制以及对海岸线的破坏作用;海啸对沿岸威胁的危害评估模型[75 ] . ...
Advanced hypersonic test facilities.
8
2002
... 高超声速风洞是常规高压下吹暂冲式风洞,一般不能正确模拟高焓流动[76 ] . 美国AEDC 9号风洞以及中国空气动力研究与发展中心的$\Phi 1$ m高超声速风洞都属于此类风洞. AEDC 9号风洞的试验能力为[76 ] :马赫数7~16.5;总压$<140$ MPa;总温$<2 000 $K. ...
... [76 ]:马赫数7~16.5;总压$<140$ MPa;总温$<2 000 $K. ...
... 激波管/风洞通过运动激波对气体进行加热,通过喷管使气流加速,是模拟高焓流动的主要设备之一,缺点是运行时间较短(毫秒量级)[76 ] . 美国LENS系列激波风洞代表了这一类型风洞的发展水平,其主要参数为[76 -77 ] :速度$ \leqslant $13 km/s;试验时间$ \leqslant $100 ms. ...
... [76 -77 ]:速度$ \leqslant $13 km/s;试验时间$ \leqslant $100 ms. ...
... 电弧加热器/风洞[76 ,78 ] 利用高电压直流产生电弧并加热驻室气体,从而形成高温热气流,并通过喷管使气流加速到一定速度,能够复现再入过程的高焓,常用于材料烧蚀试验. 缺点是产生的气流经常受到污染或者不均匀. 意大利的SCIROCCO电弧加热器在世界上这一类型设备中功率最大,其试验能力为[76 ,78 ] :总焓2.5~45.0 mJ/kg;功率$ \leqslant $70 mW. ...
... [76 ,78 ]:总焓2.5~45.0 mJ/kg;功率$ \leqslant $70 mW. ...
... 弹道靶[76 ] 一般采用二级轻气炮发射试验模型,模型可以很高的速度在靶室中自由飞行,通过在飞行段和靶标附近安装的纹影、高速相机、辐射计等测量设备,可以对超高速流场和超高速碰撞效应进行定量测量. 弹道靶设备可以真实模拟超高速空气动力学和超高速碰撞动力学的飞行条件. 但是受限于发射能力,模型质量和尺寸通常都比较小. 美国AEDC ...
... G靶和中国空气动力研究与发展中心的200 m自由飞弹道靶代表了超高速弹道靶设备的最高水平,其主要运行参数为[76 ] :发射速度1.5~7 km/s;靶室全长200~300 m,靶室直径3 m;模拟高度:0~68 km. 针对小行星撞击地球表面的超高速碰撞问题,常规的用于开展超高速撞击试验的水平弹道靶存在较大的局限性,不能复现撞击碎片反溅、掉落堆积等现象,也无法进行变角度斜碰撞以及撞击水体的模拟. 超高速垂直弹道靶能较好地解决上述问题,NASA已经建立超高速垂直靶AVGR,而国内尚无此种设备. ...
Survey of high-enthalpy shock facilities in the perspective of radiation and chemical kinetics investigations
1
2016
... 激波管/风洞通过运动激波对气体进行加热,通过喷管使气流加速,是模拟高焓流动的主要设备之一,缺点是运行时间较短(毫秒量级)[76 ] . 美国LENS系列激波风洞代表了这一类型风洞的发展水平,其主要参数为[76 -77 ] :速度$ \leqslant $13 km/s;试验时间$ \leqslant $100 ms. ...
Scirocco PWT facility for high temperature resistant material assembies test
2
2003
... 电弧加热器/风洞[76 ,78 ] 利用高电压直流产生电弧并加热驻室气体,从而形成高温热气流,并通过喷管使气流加速到一定速度,能够复现再入过程的高焓,常用于材料烧蚀试验. 缺点是产生的气流经常受到污染或者不均匀. 意大利的SCIROCCO电弧加热器在世界上这一类型设备中功率最大,其试验能力为[76 ,78 ] :总焓2.5~45.0 mJ/kg;功率$ \leqslant $70 mW. ...
... ,78 ]:总焓2.5~45.0 mJ/kg;功率$ \leqslant $70 mW. ...
A survey of current and future plasma arc-heated test facilities for aerospace and commercial applications
1
1998
... 高频等离子体风洞[79 ] 采用感应加热的方式产生等离子体,主要用于航天飞行器防热材料表面催化、氧化、辐射特性、材料光电特性、高温气体辐射特性以及等离子体与电磁波相互作用特性等方面的研究与试验. 作为这一类型风洞的典型代表,中国空气动力研究与发展中心1 mW高频等离子体风洞的运行参数为[80 ] :总焓10~60 mJ/kg,功率1 mW,驻点压力0.5~20\,kPa. ...
1
... 高频等离子体风洞[79 ] 采用感应加热的方式产生等离子体,主要用于航天飞行器防热材料表面催化、氧化、辐射特性、材料光电特性、高温气体辐射特性以及等离子体与电磁波相互作用特性等方面的研究与试验. 作为这一类型风洞的典型代表,中国空气动力研究与发展中心1 mW高频等离子体风洞的运行参数为[80 ] :总焓10~60 mJ/kg,功率1 mW,驻点压力0.5~20\,kPa. ...
高温气体热化学反应的 DSMC 微观模型分析
1
2018
... 跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究. ...
高温气体热化学反应的 DSMC 微观模型分析
1
2018
... 跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究. ...
高超声速化学非平衡流动Navier-Stokes/DSMC耦合算法
1
2018
... 跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究. ...
高超声速化学非平衡流动Navier-Stokes/DSMC耦合算法
1
2018
... 跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究. ...
热化学非平衡Boltzmann模型方程统一算法与返回舱再入跨流域应用研究. [博士论文]
1
2018
... 跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究. ...
热化学非平衡Boltzmann模型方程统一算法与返回舱再入跨流域应用研究. [博士论文]
1
2018
... 跨流域流动的有效模拟主要是基于仿真粒子运动概率统计的DSMC方法、NS/DSMC耦合算法和基于Boltzmann模型方程的数值求解和各类耦合. DSMC可以模拟热化学非平衡流动[81 ] ,但对于小行星的进入条件缺乏大于20 000 K的热化学模型. NS/DSMC耦合算法除了缺乏大于20 000 K的热化学模型之外,在数值求解NS方程和DSMC两种算法的耦合技术方面还需要进一步研究[82 ] . 尽管Boltzmann模型方程统一算法(GKUA)已经初步具备混合气体和化学反应的模拟能力[83 ] ,但对于包含所有真实气体效应的热化学非平衡流动的数值模拟还远未达到DSMC和CFD那样的水平. 此外,在这些跨流域空气动力学的数值计算方法中,都未开展与辐射和烧蚀的耦合计算研究. ...
From tunguska to chelyabinsk via jupiter
1
2016
... 如图2 所示,对于我们感兴趣的小行星尺寸(半径大于1 m),在进入地球大气绝大部分飞行范围内,流动处于连续流区,CFD是主要的研究手段. 目前CFD已经建立起考虑化学反应、内能激发、热力学非平衡以及烧蚀气体进入流场的模型,发展了多种空间和时间格式,在超高速飞行器的研制中发挥了重要作用. 但是针对小行星进入的极高速、极高温条件,大于20 000 K的热化学模型很不完备[39 ,51 ] ,目前的可压缩湍流模型还需要验证和校核. 当前CFD模拟火球时往往引入额外的能量释放以考虑空中爆炸的影响[84 ] ,并且由于不清楚小行星内部结构,计算和观测仅在定性上一致. ...
Direct coupling of the NEQAIR radiation and DPLR CFD codes
1
2015
... 对于高温流场的辐射热流以及火球的光辐射和热辐射计算,当前的辐射基础数据还不完备. 在流场、辐射和烧蚀的耦合计算中,需要研究烧蚀气体与空气的化学反应动力学以及辐射对化学反应影响的光化学反应动力学模型. 当前的耦合方法主要是松耦合,需要进一步完善和改进[85 ] . 此外,耦合计算中辐射计算的逐线法计算量大,需要研究效率更高的计算方法. ...
Modelling and simulation of cratering and ejecta production during high velocity impacts
1
2017
... 超高速碰撞动力学主要使用Euler法、光滑粒子模拟方法以及Lagrange法等数值计算方法[86 ] ,这些方法在超高速动能毁伤和空间碎片防护研究中发挥了巨大作用. 但现有针对超高速碰撞的研究多以常见金属材料为研究目标,由于小行星材料的特殊性,地面难以获得采样样本,仿真中缺少描述超高速撞击下小行星材料特点的材料模型和高状态相变数据,这也限制了数值计算研究的准确性. ...
An integrated physics-based risk model for assessing the asteroid threat
1
2015
... 美国已经组织开发了小行星进入与撞击风险分析评估系统[87 ] ,设定小行星撞击地球的场景,可定量分析进入和撞击过程对地球人口和基础设施的危害,提出应急疏散策略和方案,并构成了美国政府、军方小行星撞击联合应急演习的主要内容. ...
1
1999
... 采用圆球地球模型并考虑地球自转,仅考虑飞行中的阻力,则可写出包括式(1)的单个飞行体的弹道方程组[88 ] ...
The Effects of Nnuclear Weapons, 3rd edition
1
1977
... 根据Chyba的方法[8 ] ,把能量沉积最大值所在的飞行高度定义为空中爆炸高度,则可以利用美国核试验的数据[89 ] 评估超压和火球热辐射在地面的损伤范围. ...