高超声速飞行复现风洞理论与方法1)
SHOCK TUNNEL THEORY AND METHODS FOR DUPLICATING HYPERSONIC FLIGHT CONDITIONS1)
中图分类号: V211.7
文献标识码: A
通讯作者:
收稿日期: 2018-07-19
接受日期: 2018-07-19
网络出版日期: 2018-11-18
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
作者简介:
2) 姜宗林,教授,主要研究方向:高温气体动力学. E-mail:zljiang@imech.ac.cn
展开
摘要
针对高超声速飞行伴随的热化学反应流动,本文回顾了郭永怀先生的科研理念和学科布局,综述了他亲手成立的高温气动团队在高超声速飞行风洞实验模拟理论与方法方面的研究进展.高温气体的迅速产生与迅速应用是一种理想的风洞运行方法,而激波管就是这样一种实验装备.论文首先介绍了激波管技术的基本理论与方程,指出将其用于高超声速流动实验模拟时所具有的独特优势.然后讨论了应用激波风洞复现需要的高超声速飞行状态的可行性、基本方程和需要解决的关键问题.针对这些关键问题,进一步介绍了如何应用爆轰现象研发激波风洞驱动技术的理论,并给出了基于爆轰驱动方法的技术发展和工程应用验证.最后,论文介绍了爆轰驱动激波风洞的界面匹配条件,该条件奠定了长实验时间激波风洞运行基础,是其他驱动方法尝试解决而没能完全解决的难题.高温气动团队关于高超声速飞行复现风洞的理论与技术研究,实现了郭永怀先生的战略规划,成就了国际领先的高超声速热化学反应流动研究平台.
关键词:
Abstract
This paper reviews the scientific research philosophy and discipline layout of Prof. Yung-huai Kuo in the field of thermo-chemically reacting flows occurring in hypersonic flights, and summarizes the research progress in shock tunnel theories and methods for duplicating hypersonic flight conditions. The work has been achieved from 50 years effort dedicated by the High Temperature Gas Dynamics Research Team founded by Prof. Kuo. Rapid generation and rapid application of high temperature gas are an ideal method for wind tunnel operation, and a shock tunnel is such an experimental facility. The fundamental theory and governing equations for shock tunnel are presented first, and these demonstrate the unique advantages of shock tunnel technology for the ground-based testing of hypersonic vehicles. Then the feasibility, basic equations and key problems in the shock tunnel technology for duplicating required hypersonic flight conditions are discussed. Aiming at solving the key problems, a theory is proposed for the detonation-driven shock tunnel from the technical development of detonation driver and its engineering application/verification. Finally, the tailored condition for the detonation-driven shock tunnel is introduced, and lays the foundation for the operation of shock tunnels with long test time. This condition is one of the most difficult problems encountered in developing high-enthalpy shock tunnels. The problem has been investigated for decades, but not solved perfectly. With the proposed theory and methods, several high-enthalpy tunnels are developed for covering the full flight envelope of hypersonic vehicles and its applications show that the theory proposed here is successful and important for aerodynamic and kinetic study in the hypersonic research field.The Team's research work on the hypersonic ground testing facilities has realized the strategic goal of Prof. Kuo's discipline planning, and a world leading research platform was established for exploring hypersonic thermo-chemically reacting flows.
Keywords:
引 言
从1903年莱特兄弟尝试有动力飞行一百年来,人们在航空领域实现了超声速飞行;在航天领域,实现了月球登陆,建立了空间站.现在航空航天科技领域,已经进入一个探索高超声速飞行技术的时代.如果乘坐未来的高超声速飞机,人们可以在2 h内到达地球的任何地方.如果水平起飞、天地往返、可重复使用的多级入轨系统研发成功,人们往返太空的成本可以削减90%以上. 所以,在可预见的将来,高超声速飞行技术给人类文明带来的影响是颠覆性的. 经过60多年的不断探索,世界上几个宇航大国都实现了不同测试目标的短暂高超声速飞行试验,取得了里程碑式的重大成就. 但也遇到许多气动问题,困扰着先进空天飞行器设计、关键技术研发和飞行试验规划[1-2].
空天飞行器,诸如大气再入的宇宙飞船、航天飞机、在大气层里飞行的高超声速飞行器,在高超声速飞行时,强烈的头部激波和黏性摩擦阻力,使得飞行器周围的空气被加热到数千度、甚至上万度的高温.高温导致了空气分子的振动激发、解离、甚至电离,使得普通空气变成一种随着气体温度变化而不断进行着热化学反应的复杂介质[2-3].高超声速流动也就成为一种伴随能量转移和热能传递的非平衡过程.郭永怀先生在讨论现代空气动力学的问题时指出[4]:"因为有分离和电离的发生,在空气动力学里就产生以下的一些问题: (1)空气的组成:从实验上知道,不仅有氮和氧的原子出现, 还有一氧化氮存在.(2)弛豫时间:在解离、电离等现象发生以后,实际问题里所要知道的,便是决定从这个现象的开始到达热力学平衡状态的过渡时间.知道了这个时间,我们方能决定,在一个问题里,哪里的气体已达到平衡,哪里的气体是在非平衡状态.此外我们还要知道:(1)空气的热力学函数;(2) 传导系数(即热传导,扩散,黏性等系数) ; (3) 碰撞截面; (4) 化学反应速率等等.这一系列问题的研究是要从理论和实验双方进行的. 它们的解决,对于将来航空工业新技术的发展,是有莫大的贡献的".关于热化学反应对流动的影响,郭永怀先生进一步指出:"在马赫数12,实际上能达到的温度几乎是理想气体中温度的一半.对于驻点温度的影响是这样大,对于流场其他的变量也是一样.这类现象对于未来航空工业的重要是不难想象的".
时至今日,高超声速的相关研究有60多年的历史了.验证关键技术的飞行试验数据与地面实验结果和计算模拟相比依然存在很大差异,并在不同程度上,影响着飞行器的设计与控制.美国空军研究院的专家Bertin[2],在回顾高超声速研究的关键问题时把气动热力学作为首要研究问题提出.并在讨论气动热力学实验研究时指出,目前依旧缺乏能够复现高超声速飞行器热环境的地面实验装置.他特别强调:气动热力学实验结果受限与地面试验装置产生的流动状态,计算结果受限于采用的计算方法和气动物理模型,这与计算机硬件如何强大无关.实验和计算都涉及到高温反应气体流动的模化问题.地面试验装置的流动模化依赖于风洞技术,而计算流体力学的气动物理模型也依赖于人们对于气动热物理现象的实验观测和认知,最基本的问题还是依赖于可靠的地面实验数据[1-2].对于高超声速研究,飞行试验数据是宝贵的、昂贵的、也是有限的.所以发展先进的高超声速风洞实验技术一直是国际航空航天领域高度关注的重要领域[5].
关于高超声速气动热力学研究,郭永怀先生认为,当气体进入高温高速极端条件时,气体内部的动理学问题是不能回避的,也不能用经验去替代,必须求诸于"物理力学"的研究,才能实现动力学与动理学相结合的发展[6-7].当年中国科学院力学研究所把物理力学组和激波管组重组融合,其目标就是通过激波管试验研究来揭示高温反应气体的本质,并结合气体的微观动理学理论,以喷气推进与高超声速气流中的高温现象和气体性质为对象进行实验研究[8].这是物理力学的核心研究理念.对于发展高温反应气体流动的地面实验技术,郭先生进一步指出:"大型高超声速风洞将来是不可缺少的.我国经济和技术基础还很差,难以仿效发达国家依靠大型常规高超声速风洞试验的研究途径,何况常规高超声速风洞加热达到的高温受限,难以模拟超高速飞行器周围的高温绕流[9]""激波管能产生高温和高压气体,已产生的试验气流速度高达15km/s,这一方面的技术目前正在发展, 前途是无限的"[10].
依据郭永怀先生阐述的关于高超声速热反应气体流动研究的学科方向、科研理念与研究规划,中科院力学研究所的高温气动团队经过50多年的努力,提出了系统的爆轰驱动激波风洞理论,建立了完整的高超声速飞行复现风洞技术体系,研制成功世界首座复现高超声速飞行条件的超大型激波风洞,并在国家重大项目实施和高温气体动力学前沿学科问题探索方面发挥了不可替代的作用[11-12].
本文将系统介绍爆轰驱动复现高超声速飞行条件激波风洞和超高速风洞的理论基础,并结合国家重大科研装备研究项目进展讨论相关的关键技术突破和性能评估.
1 激波管基本理论与方程
对于高超声速风洞,要求实验气体的总焓很高,即总温很高.如何实现高焓风洞的正常运行,避免高热负荷对风洞装备造成损害是风洞技术发展时必须考虑的首要问题[5].直接加热空气方法是目前比较广泛应用的高焓风洞技术,能够模拟的流动马赫数上限为7(总温为2300 K左右).限制直接加热风洞技术发展的因素不仅是热源的加热能力,还有风洞设备材料的承热能力.所以,高温气体的迅速产生与迅速应用是一种理想的风洞运行方法,而激波管就是这样一种实验装备.郭先生在介绍激波时这样说:"从激波的特性看来,正激波是一个很有效的压缩和产生温度的工具. 譬如说,激波的马赫数等于4或5,激波后面的压强就有20到30个大气压,而绝对温度就能达到1800K. 在实验室里产生这样强度的激波是很容易的. 有了这样的工具,我们便能利用它来研究化学反应的问题"[10].
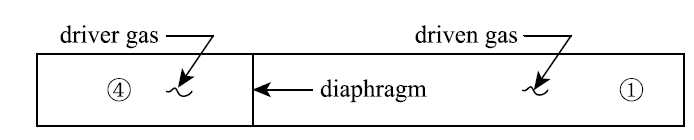
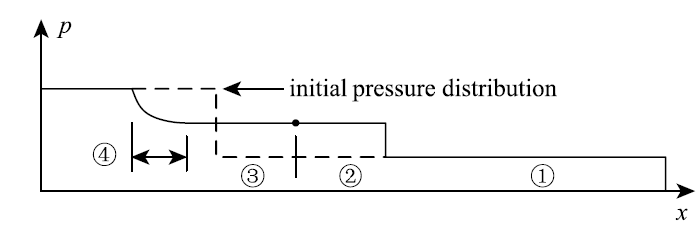
激波管的基本概念如图1所示. 激波管由主膜片分为两个区:④区为高压驱动气体,①区为低压被驱动气体.按照激波管功能区分,分别称为驱动段和被驱动段.膜片打开之后,即形成图2 所示,由压力分布表示的激波管波系运动状态.图2最右边的压力起跳是入射激波,其传播速度由激波马赫数$M_s$表示.激波后形成具有高压、高温特点的②区气动状态,是应用于激波管实验的气体状态.入射激波后还存在一个接触间断,分开了驱动气体和被驱动气体,形成了③区气体. ③区和②区气体的压力相同,但是温度和密度一般不同. 由④区到③区存在一个膨胀波系,在气体动力学教科书上可以找到相应的解析解.
图2 破膜后激波管内压力分布
Fig.2 Pressure distribution along shock tube after diaphragm rupture
如何产生需要强度的入射激波,首要影响参数是④区与①区的压比.选定驱动和被驱动气体及其初始的热力学状态,压比和入射激波马赫数的关系由下式确定
$$\dfrac{p_4 }{p_1 } = \left[ {1 + \dfrac{2\gamma _1}{\gamma _1 + 1}\left( {M_s^2 - 1} \right)} \right]\cdot$$$$\left[ {1 - \dfrac{\gamma _4 - 1}{\gamma_1 + 1}\dfrac{a_1 }{a_4 }\left( {M_s - \dfrac{1}{M_s }} \right)}\right]^{\frac{ - 2\gamma _4 }{\gamma _4 - 1}} (1)$$
上式为激波管流动的基本公式,其中$p_{4}$是驱动压力,$\gamma_{4}$和$\gamma _{1}$分别表示④区与①区的气体比热,$a_{4}$ 和$a_{1}$分别表示相应的声速. 理论上讲,如果能够建立足够高的压比,在驱动气体声速也足以支撑的条件下,就能获得需要的入射激波马赫数.这里涉及了两个关键参数:气动参数(压比)和介质特性(声速).
在理想气体假设的条件下,下面的公式给出了②区的热力学参数与入射激波马赫数的关系
$$ \frac{p_2 }{p_1 } = 1 + \frac{2\gamma }{\gamma + 1}(M_s^2 - 1)(2)$$ $$\frac{T_2 }{T_1 } = \frac{\left[ {2\gamma _1 M_s^2 -\left( {\gamma _1 - 1} \right)} \right]\left[ {\left( {\gamma _1 -1} \right)M_s^2 } \right] + 2}{\left( {\gamma _1 - 1} \right)}(3)$$$$\frac{\rho _2 }{\rho _1 } = \frac{\left( {\gamma _1 +1} \right)M_s^2 }{\left( {\gamma _1 - 1} \right)M_s^2 + 2} (4)$$
一般来讲,$T_{1}$是由实验室环境温度确定的.依据对于$T_{2}$温度的需求,由式(3)能够确定需要的入射激波马赫数$M_{S}$.对于给定的$M_{S}$,在保持压比不变的条件下,通过改变$p_{1}$可以获得需要的$p_{2}$.②区压力和温度不直接相关,能够单独选择,体现了激波管性能的优点和激波管实验技术的灵活性.$T_{2}$和$P_{2}$的实验气体状态是激波管实验的常用主要参数.
2 激波风洞与飞行条件
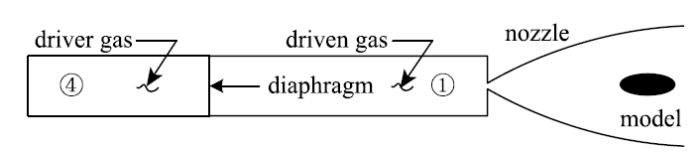
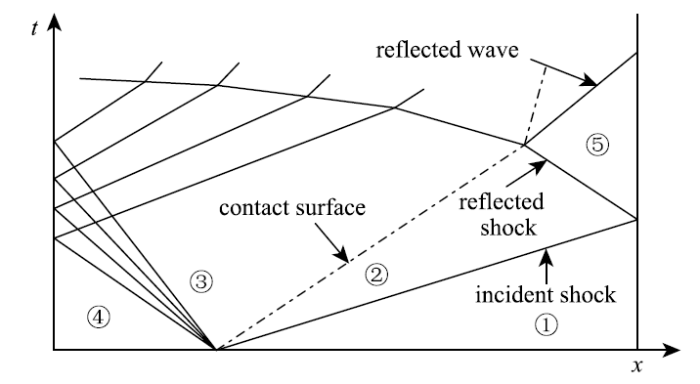
激波风洞是激波管技术的扩展,其基本原理如图3所示.激波风洞的基本配置是在激波管被驱动段的末端连接一个喷管,并采用膜片分开喷管与被驱动段.当激波风洞运行时,入射激波在被驱动段末端实现全反射,形成流动静止的⑤区状态,即传统风洞的高压气源.入射激波反射导致实验气体压力的第二次升高,达到设计的实验状态.这时膜片在高压气体的作用下实现破膜,起动了高压、高温气体在喷管内的膨胀加速过程.图4是激波风洞运行时,风洞内部的基本波系运动状态的$x$-$t$图.反射激波后气体速度为零,入射激波马赫数与反射波后气体热力学参数的关系可由下面的公式表述
$$\frac{p_5 }{p_1 } =\frac{\left[ {2\gamma _1 M_s^2 \!-\! \left( {\gamma _1\!-\! 1} \right)} \right]\left[ {\left( {3\gamma _1 \!-\! 1}\right)M_s^2 \!-\! 2\left( {\gamma _1 \!-\! 1} \right)}\right]}{\left( {\gamma _1 \!+\! 1} \right)\left[ {\left( {\gamma_1 \!-\! 1} \right)M_s^2 + 2} \right]}(5)$$$$\frac{T_5 }{T_1 } =\frac{\left[ {2\left( {\gamma _1 \!-\! 1} \right)M_s^2\!-\! \left( {\gamma _1 \!-\! 3} \right)} \right]\left[ {\left({3\gamma _1 \!-\! 1} \right)M_s^2 - 2\left( {\gamma _1 \!-\! 1}\right)}\right]}{\left( {\gamma _1 \!+\! 1} \right)^2M_s^2 }(6)$$$$\frac{\rho _5 }{\rho _1 }=\qquad \frac{\left( {\gamma _1 + 1}\right)M_s^2 \left[ {2\gamma _1 M_s^2 + 1 - \gamma _1 }\right]}{\left[ {2\left( {\gamma _1 - 1} \right)M_s^2 - \left({\gamma _1 - 3} \right)} \right]\left[ {\left( {\gamma _1 - 1}\right)M_s^2 + 2} \right]}(7)$$对于复现飞行条件风洞来讲,如果假设喷管膨胀过程是可逆的,$p_{5}$、$T_{5}$就是需要获得的飞行条件下的滞止状态.通过适当的喷管设计,就可以在喷管出口获得匹配实际飞行条件的流动状态,即飞行速度和飞行高度对应的静温和静压.
在风洞运行状态的设计过程中,首先依据飞行速度和高度,获得飞行条件下的滞止温度和总压($T_{5}$和$p_{5})$.然后根据实验室温度$T_{1}$,由式(6)获得需要的入射激波马赫数.进一步应用$M_{S}$和$p_{5}$,由式(5)可以计算获得被驱动气体的压力$p_{1}$.这样就定义了风洞运行的基本状态.当飞行高度变化时,入射激波马赫数不变,$p_{5}$的需求变化能够通过调整$p_{1}$实现.但是,由式(1)可见,如果入射激波马赫数不变,$p_{1}$的提高势必带来$p_{4}$的增加.由上述激波风洞理论分析可知:飞行条件是可以复现的,关键点在于激波管的驱动段必须能够提供足够高的驱动压力.对于高超声速飞行,这是复现风洞理论和技术发展必须解决的关键问题,也是最有挑战性的核心技术.
3 爆轰驱动理论与方法
激波风洞理论分析表明:复现飞行条件的空气动力学参数和热力学是可行的,但是高超声速飞行地面复现实验还有更重要的问题需要考虑.在讨论宇宙飞船大气再入问题时,郭永怀先生说:"举氮气分离来说.如果分离是由于两个原子的自由振动被激过猛而破裂,那么所算出的弛豫时间,在2000$^\circ$C左右,大约是千分之一秒.如果温度高,分子相碰的动能强,分离的产生就可以不必等待自由振动的激发.这样的话,弛豫时间便是1.0$\times$10$^{ - 7}$ s.假设气流速度是每秒6000 m,平衡长度,根据头一个弛豫时间,就要6 m;根据第二个便是0.06 cm. 这就是说,弛豫时间如果是千分之一秒,6 m长的机身,在飞速是每秒6000m的时候,机身外的气流便都不在平衡状态."对于飞行速度6km/s的飞行器,由于头部激波是弓形的,高温和低温是并存的.因此复现飞行器周边的化学反应进程,产生足够大的流场,保障能够应用足够大的飞行器模型对于复现风洞是必要的[6].
关于复现风洞实验流场的大小,如果考虑目前国际上已经开展飞行试验的飞行器的尺度,那么配备2.5$\sim$3.0m直径的喷管是必须的,这样可以基本保证飞行器全部处于风洞流场的菱形区.由于高超声速流动的核心物理过程是高温热化学反应,而且化学反应尺度不随模型小而变化,那么传统风洞实验的模型缩比准则就不再成立.对于可靠的高超声速地面实验模拟,高超声速风洞实验技术需要解决对4个难题:(1)化学反应机制模拟,替代气体不能用,需要采用纯净空气作为实验气体;(2)化学反应进程模拟:不存在相似参数,必须达到实际的总温和总压,保证真实的化学反应速率.(3)化学反应尺度模拟:模型尺度应该远大于反应尺度,使得在飞行器的对应部位能够以正确的速率,发生正确的化学反应;(4)对于气动力和超声速燃烧研究,还要有足够的实验时间,以建立稳定流场.这个要求对于获得稳定燃烧和需要的测力周期是非常重要的.上述四个问题实际上就意味着要在风洞实验中复现飞行条件,这对空气动力学实验技术是挑战性的,对于传统空气动力学实验方法也是颠覆性的.发展高超声速风洞技术的首要困难是风洞的驱动功率问题. 如果要复现30km高空、马赫数为8的飞行状态,此时试验气流的总温将近3000 K.假如有效流场直径为3m,那么复现风洞的输出功率约为90万千瓦,输入功率就更大,对比葛洲坝水电站总装机容量272万千瓦,可知如此高的总温和功率需求使得长试验时间、连续式、大型高超声速风洞几乎不可能实现.这个功率需求也远远超过了国际常用的自由活塞驱动和加热高压轻气体驱动技术目前的能力极限.
爆轰是激波在可燃气体中传播诱导的强烈燃烧反应阵面.考虑一个大气压下的氢氧混合气,单位面积爆轰波阵面的能量释放率高达20GW,如此巨大的能量释放率,带来的破坏能力也是非常惊人的.所以爆轰现象危害千年,很少有被成功利用的先例.
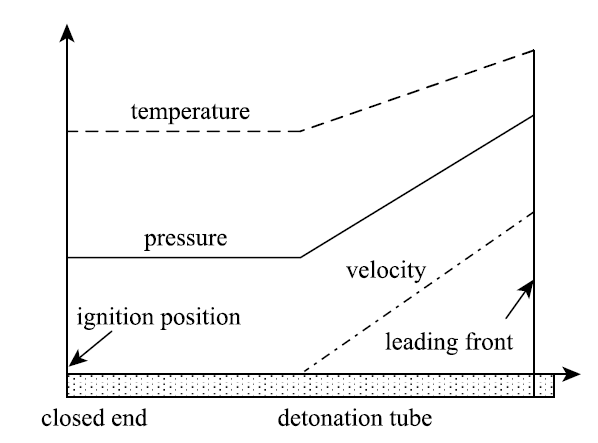
如何认识爆轰现象,这里给出一个经典范例.取一个圆形截面的钢管,一端封闭,一端敞开,作为爆轰管.爆轰管内充满可燃气体.在爆轰管的封闭端起爆,形成的爆轰波向另一端传播.如果可燃气是当量比的氢氧混合气,爆轰波的传播速度可以高达2.8 km/s. 根据泰勒膨胀波理论,爆轰管内部的压力和速度分布如图5所示.由此图可见:可燃混合气在前导激波的压缩下,达到了自燃极限,爆轰瞬时释放出大量化学能,使燃气的压力、温度和速度升高至C-J值.同时由于封闭端边界条件的限制,爆轰波后形成稀疏波系,燃气流动速度逐渐减小,最终达到静止状态.处于静止状态下的气柱长度大约是爆轰波传播距离的一半,依然具有很高的温度与压力.
图5 基于Taylor膨胀波理论描述的轰波传播特性示意图
Fig.5 Schematic diagram of the distribution of detonation wave properties along the length of a detonation tube based Taylor expansion wave theory
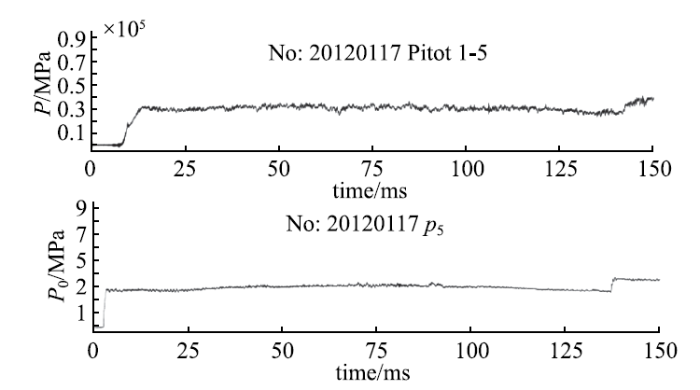
在激波风洞驱动器研发领域,如何利用爆轰波超强的驱动能力,自从Bird[13]首次尝试,一直是一个难题.实际上,爆轰驱动器的发展也就是如何解决爆轰波的生成、控制、应用和风洞安全问题.俞鸿儒经过多年的探索,提出了一个巧妙的创新方法.即把激波风洞的被驱动段配置在爆轰管的封闭端;采用一个足够强度的膜片,模拟固壁边界条件;再配置一个卸爆段在爆轰管另一端,用于收容正向爆轰携带的巨大动能,以保障风洞的运行安全.这样一个反向爆轰加卸爆段的概念首先应用于德国亚圳工业大学的TH2-D爆轰驱动激波风洞.获得成功之后,俞鸿儒等[14]在国际激波期刊上给出了系统总结.反向爆轰驱动模式的成功应用还取决于另外两项技术,它们在JF12复现风洞的研制过程中得到圆满解决[12].其中一项技术是能量多级放大直接起爆技术,能保障反向爆轰驱动可利用部分的完整性和平稳性.另一项是双临界预压成型膜片技术,降低了驱动气体破膜时的能量损失,避免膜片破碎.图6给出了JF12复现风洞的$p_5$曲线和皮托压力分布.陡立的激波起跳和压力分布的平稳性表明了JF12反向爆轰驱动器的优异性能,也验证了上述两项关键技术的设计理论与工程性能.
图6 JF12复现风洞的驻室$p_{5}$曲线和皮托压力曲线
Fig.6 Reservoir pressure $p_{5}$ and Pitot pressure histories for shock tunnel JF12
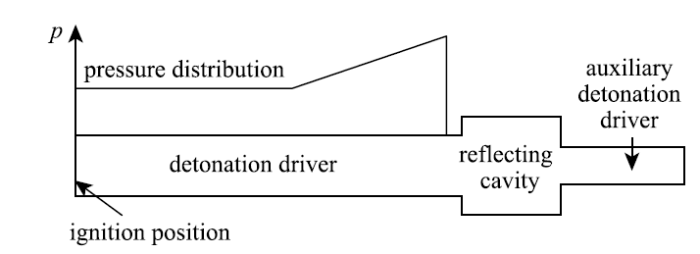
基于充气技术和风洞安全性,反向爆轰驱动能够模拟的总温一般不大于4000K,受限于$p_{4}$的极限.由图5可知道,正向爆轰波阵面具有远高于波尾的能量,因为波头部分的气体不仅压力高,而且动量大.理论估计利用正向爆轰做驱动源能够获得5倍于反向爆轰驱动器的驱动能力.但是泰勒膨胀波的存在导致前导激波的不断衰减,使得正向爆轰气体很难直接用作激波风洞气源.为了解决这个问题,Jiang等[15]提出一个基于激波反射概念的空腔型正向爆轰驱动器,其结构示意图如图7所示.
图7 激波反射型正向轰波驱动器示意图
Fig.7 Schematic diagram of forward detonation driver with a shock reflecting cavity
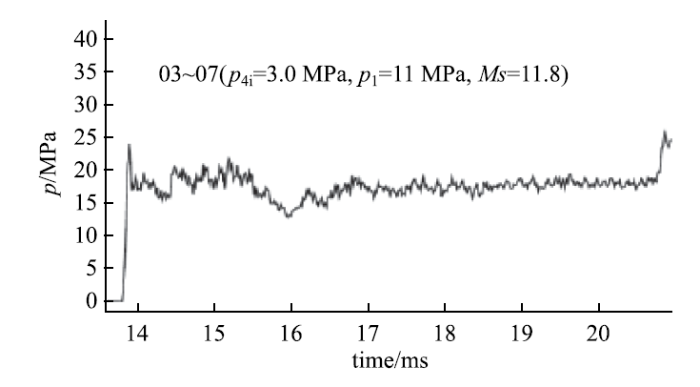
激波反射型正向轰波驱动器由3部分组成:爆轰驱动段、激波反射腔和辅爆轰段.当具有如图7中所示压力分布的爆轰波进入反射腔时,中间部分的爆轰波直接进入辅爆轰段,周边的环状爆轰波被剪裁,产生壁面反射,形成上行激波.上游来流通过这个上行激波,压力和温度都得到不同程度的提高.爆轰驱动段的截面直径大于辅爆轰段,这种"大"驱"小"的模式对于提高流经反射腔的气体压力具有重要贡献.在激波反射型正向轰波驱动器的内部激波结构中,产生的上行激波越强,下行激波越弱对于改善驱动气流的性能越有利,也是激波反射型正向轰波驱动器优化设计的原则.激波反射型正向轰波驱动器被成功地应用于JF10爆轰驱动高焓激波风洞,能够产生总温高达7000K的高焓气流.图8给出了JF10高焓激波风洞的$p_{5}$曲线,压力随时间分布的平稳性表明激波反射型正向轰波驱动器成功地消除了泰勒膨胀波的影响,获得了6 ms的实验时间,给出了优异的驱动性能.
图8 JF10爆轰驱动高焓激波风洞驻室压力曲线
Fig.8 Reservoir pressure $p_{5}$ history for detonation shock tunnel JF10
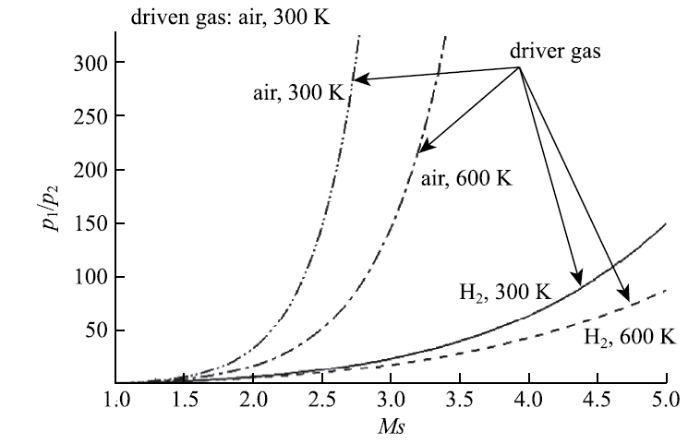
驱动压力强弱是评价激波风洞驱动器的重要指标之一.另外一个关键参数是驱动气体的声速. 由式(1)可知:①区的气体和热力学状态是确定的,那么改变入射激波马赫数的方法就是改变驱动气体介质特性和温度.图9给出了驱动气体特性和驱动压比与入射激波马赫数的关系.由此图可见,如果采用常用室温空气作为驱动气体,当入射激波马赫数大于2时,需要的驱动压力将急剧增加.采用加热空气技术能够通过提高声速来提高驱动能力,但是当入射激波马赫数大于3时,驱动压力需求也将急剧增加.采用轻气体作为驱动气体,并应用加热技术,也能够大大提高入射激波.例如,采用氢气作为驱动气体,能够获得马赫5的入射激波.再采用加热技术,能够获得更高一些的入射激波马赫数.但是大量氢气的加热和排放给风洞安全运行带来严重问题,限制了加热轻气体技术的应用,特别是在更高入射激波马赫数方面的需求.
图9 驱动气体特性和驱动压比与入射激波马赫数的关系
Fig.9 Mach number of incident shock versus properties of driver gas and pressures ratio of driver and driven gases
氢氧爆轰后的混合气体具有3000K左右的温度,这是目前的加热轻气体技术难以达到的.加入氮气之类的惰性气体,还能够调节爆轰温度和驱动气体的物性参数.所以爆轰具有更优异的驱动能力,超越了目前能够应用的激波风洞驱动方法.
4 爆轰驱动激波风洞界面匹配条件
激波风洞的实验时间是一个关键性能参数,一般都是以毫秒为单位计算.世界上最大的自由活塞驱动高焓激波风洞HEIST的实验时间也只有2$\sim$5ms.Holden指出,传统激波风洞仅适用于冷壁热流测量,延长时间可以做吸气动力、火箭/羽流相互作用、气动力、甚至动力学等试验.长时间超高速爆轰驱动激波风洞(LHDst, JF12)已经达到100 ms[16].激波风洞的实验时间与其中波的传播过程密切相关,其中最重要的一个波过程是入射激波在被驱动段端面和实验与驱动气体界面之间的往复反射.这种波反射影响了风洞驻室压力的平稳性,缩短了有效实验时间.
对于激波风洞来讲,不产生往复反射波是获得最长试验时间的基本条件,这种界面状态称为风洞运行界面匹配条件,也称为缝合运行状态.界面匹配运行状态能消除了接触面处反射波对驻室气体热力学状态的干扰,可将试验时间提高数倍以上.在界面匹配条件下,反射激波直接穿过界面,而不会产生反射波.因此$p_{5}=p_{7}$,$u_{5}=u_{7} \approx 0$.由于界面两边压力相同,可得$p_{2}=p_{3},u_{2}=u_{3}$.反射激波为在{\kaishu ②}区气体中传播的左行波
$$\dfrac{{u}_2 }{{a}_2 } =\dfrac{\dfrac{{p}_5 }{{p}_2 } - 1}{\sqrt {\dfrac{{\gamma}_2 \left( {{\gamma }_2 - 1} \right)}{2}\left[ {\dfrac{\left({{\gamma }_2 + 1} \right){p}_5 }{\left( {{\gamma }_2 - 1}\right){p}_2 } + 1} \right]} }(8)$$
透射激波同样是在{\kaishu ③}区气流中传播的左行波,因此
$$\dfrac{u_3 }{a_3 } = \dfrac{\dfrac{p_7 }{p_3 } - 1}{\sqrt{\dfrac{\gamma _3 \left( {\gamma _3 - 1} \right)}{2}\left[{\dfrac{\left( {\gamma _3 + 1}\right)p_7 }{\left( {\gamma _3 - 1} \right)p_3 } + 1} \right]} } =\dfrac{\dfrac{p_5 }{p_2 } - 1}{\sqrt {\dfrac{\gamma _3\left( {\gamma _3 - 1} \right)}{2}\left[ {\dfrac{\left( {\gamma _3+ 1} \right)p_5 }{\left( {\gamma _3 - 1} \right)p_2 } + 1}\right]} } (9)$$式(8)除以式(9),加上$\gamma _{2}=\gamma _{1}$,$\gamma _{3}=\gamma_{4}$得出
\begin{equation}\label{eq10} \dfrac{a_2 }{a_3 } = \dfrac{\gamma _1 }{\gamma _4 }{\dfrac{1 + \dfrac{\left( {\gamma _1 + 1} \right)}{2\gamma _1}\left( {\dfrac{p_5 }{p_2 } - 1} \right)}{1 + \dfrac{\left({\gamma _4 + 1} \right)}{2\gamma _4 }\left( {\dfrac{p_5 }{p_2 } -1} \right)}} {10}\end{equation}
这就是驱动气体和被驱动气体的界面匹配条件.适当的简化、整理可得下式
$$\dfrac{a_4 }{a_1 } = \dfrac{2}{\gamma _1 + 1}\left( {M_s - \dfrac{1}{M_s }}\right)\left\{ {\dfrac{\left( {\gamma _4 - 1} \right)M_s^2 +2}{2\gamma _1 \left( {M_s^2 - 1} \right)}}\cdot \right.\left.\left[ {\gamma _4^2 + \dfrac{\gamma _1 \gamma _4\left( {\gamma _4 + 1} \right)\left( {M_s^2 - 1} \right)}{\left({\gamma _1 - 1} \right)M_s^2 + 2}} \right]^{0.5} + \dfrac{\gamma_4 - 1}{2} \right\} \quad(11)$$
从上式可以看出,界面匹配马赫数$M_{S}$是驱动与被驱动气体声速比$a_{4}/ a_{1}$ 与比热比$\gamma _{1}$和$\gamma _{4}$的函数.只要知道驱动与被驱动气体的组分和初始温度,就可决定声速比$a_{4} /a_{1}$,即可确定缝合马赫数.
激波风洞产生的试验气流总焓取决于入射激波的强度.通常被驱动段内的实验气体为室温空气,因此,若驱动气体的状态参数给定,界面匹配激波马赫数也随之确定,即实验气体的总焓确定.对于常规高压气体驱动,为了获得总焓不同的试验气流,并保持风洞运行于缝合状态,需调整驱动气体的组分和热力学状态参数.一种方法是采用声速高的轻气体,如氢气、或者氦气作为驱动气体.另外一种方法是加热驱动气体以提高其声速,进而提高界面匹配激波马赫数.反之,为了降低实验气体的总焓,可采用声速较低的驱动气体,如氮气和氩气等.
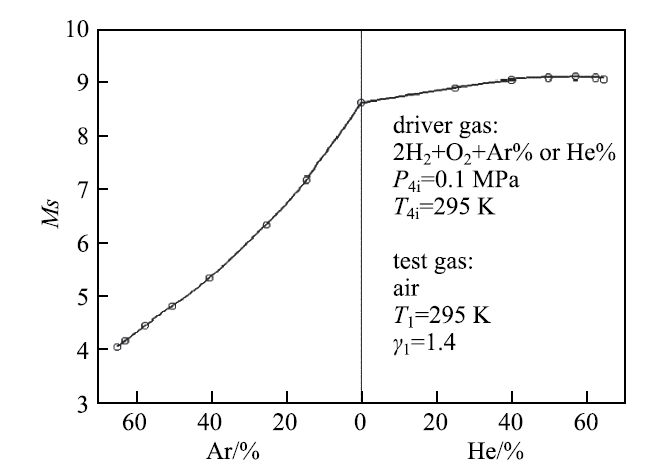
爆轰驱动方法和常规高压气体驱动一样,可以通过调整驱动气体的初始组分获得不同强度的缝合激波马赫数,从而获得总焓不同的试验气体.基于理论分析的计算结果由图10给出[12].爆轰驱动界面匹配激波马赫数随着初始驱动气体氦气含量的增大而增大,随氩气含量增大而减小.在驱动气体中增加氢气和氮气也可起到类似的作用.图10的结果还表明:在降低氩气组分的同时,不仅通过改变气体物性提高了驱动气体声速,而且还提高了单位可燃气体的放热量,即在提高驱动气体声速的同时,还提高了驱动压力.爆轰驱动方法的这种双参数效应,非常有利于缝合激波马赫数匹配和驱动能力的提升.对于当量比的氢氧混合气,通过加入氦气提高声速,进而提高缝合激波马赫数也是有效的,但也是有限的.因为,氦气组分的增加,降低了爆轰温度和压力.对于氢氧爆轰来讲,激波马赫数9是一个极限点,虽然远远高于目前应用的加热轻气体驱动技术,能够模拟总温高达7000K的高焓气流.但是,探索新的可燃混合气组合,提高缝合激波马赫数依然是非常有意义的研究方向.
图10 爆轰驱动界面匹配激波马赫数与驱动气体初始组分的关系
Fig.10 Incident shock Mach number versus concentration of helium or argon dilution for stoichiometric oxyhydrogen for tailored conditions in a detonation-driven shock tube
5 结 论
本文构建了高超声速飞行条件复现风洞实验模拟的理论体系.它基于激波管技术能够选择性模拟温度与压力和高温气源即生即用的优势,应用爆轰驱动方法满足了激波风洞对于驱动高压和界面匹配的关键需求.建立的复现风洞理论还包括反向爆轰驱动方法、激波反射型正向轰波驱动方法及其反向和正向爆轰生成、控制和应用的关键技术.高温气体动力学国家重点实验室系列高焓风洞的研制应用表明这里提出的理论体系是成功的,解决了高超声速飞行器全空域、全速域飞行走廊的覆盖模拟问题.复现风洞的研究进展完成了郭永怀先生的战略规划和学科托付,对于在高超声速领域实现把动力学与动理学相结合,开展基于物理力学方法论的热化学反应流动研究具有重要意义.
致谢:本文工作得益于高温气动激波风洞团队全体成员的辛勤努力,同时感谢国家自然科学基金委的支持(11532014,11727901).
The authors have declared that no competing interests exist.
参考文献
| [1] |
Fifty years of hypersonics: Where we've been, where we're going . |
| [2] |
Critical hypersonic aerothermodynamic phenomena . |
| [3] |
Theories and technologies for duplicating hypersonic flight conditions for ground testing . |
| [4] |
现代空气动力学的问题 .Modern Aerodynamic Problems // |
| [5] |
Advanced Hypersonic Test Facilities . |
| [6] |
宇宙飞船的回地问题 .The Problems of Space Craft Back to Earth . |
| [7] |
Dissociation effects in hypersonic viscous flows . |
| [8] |
郭永怀与高温气体物理力学研究 //李家春主编,Yung-huai Kuo and High Temperature Gas Physical Mechanics Research //Li Jiachun ed. |
| [9] |
郭永怀先生引导我做实验 .Yung-huai Kuo led me to experiments . |
| [10] |
激波的介绍 //Introduction to Shock Waves . |
| [11] |
Experiments and development of long-test-duration hypervelocity detonation-driven shock tunnels (LHDst) . |
| [12] |
长试验时间爆轰驱动激波风洞技术研究, Investigating into techniques for extending the test-duration of detonation-driven shock tunnels . |
| [13] |
A note on combustion driven tubes . |
| [14] |
Gaseous detonation driver for a shock tunnel . |
| [15] |
Forward-running detonation drivers for high-enthalpy shock tunnels . |
| [16] |
Extension of LENS shock tunnel test time and lower Mach number caaibility . |
| [17] |
爆轰驱动激波管缝合激波马赫数计算 .
Numerical computation on the tailored shock Mach numbers for a hydro-gen/oxygen detonation shock tube .
|

/
| 〈 |
|
〉 |