空化可压缩流动空穴溃灭激波特性研究1)
北京理工大学机械与车辆学院,北京 100081
NUMERICAL SIMULATION OF SHOCK WAVE DYNAMICS IN TRANSIENT TURBULENT CAVITATING FLOWS1)
中图分类号: O352
文献标识码: A
通讯作者:
收稿日期: 2018-07-2
网络出版日期: 2018-09-18
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
展开
摘要
为深入研究空化可压缩流动中空泡/空泡团溃灭过程中激波产生、传播及其与空穴相互作用规律,本文采用数值模拟方法对空化可压缩流动空穴溃灭激波特性展开了研究.数值计算基于OpenFOAM开源程序,综合考虑蒸汽相和液相的压缩性,通过在原无相变两相可压缩求解器的控制方程中耦合模拟空化汽液相间质量交换的源项,实现了对空化流动的非定常可压缩计算.利用上述考虑汽/液相可压缩性的空化流动求解器,对周期性云状空化流动进行了数值模拟,并重点研究了空穴溃灭激波特性.结果表明:上述数值计算方法可以准确捕捉到空穴非定常演化过程及大尺度脱落空泡云团溃灭激波现象,大尺度脱落空泡云团溃灭过程分为3个阶段:(1) U型空泡团形成; (2) U型空泡团头部溃灭; (3) U型空泡团腿部溃灭.在U 型空泡团腿部溃灭瞬间,观察到激波产生,并向上游和下游传播,向上游传播的激波与空穴相互作用,导致水翼吸力面新生的附着型片状空穴回缩,直至完全溃灭.并且空穴溃灭激波存在回弹现象, 抑制了下一周期的空化发展.
关键词:
Abstract
To investigate the cloud cavity collapse induced shock wave dynamics in unsteady cavitating flows,especially the shock wave formation,propagation,and the interaction between shock wave and cavity,numerical simulation is conducted to study the shock wave dynamics dominated unsteady cloud cavitating flows.The numerical method is achieved by implementing phase change model into the native pressure-based compressible two-phase flow solver,based on the open source software OpenFOAM,considering the compressibility of both liquid and vapor.The numerical results are presented for the typical shock wave dominated unsteady partial cavitating flow,characterized by low Strouhal number around a NACA66 hydrofoil at $\alpha=6$°and $\sigma=1.25$.The results show that the predicted unsteady cavity behaviors agree well with the experiments,especially the large scale cloud cavity collapse induced shock wave phenomena.The large scale cloud cavity collapse process can be depicted into three stages:(1) the formation of U-shape cloud cavity; (2) the collapse of U-shape cloud cavity head; (3) the collapse of U-shape cloud cavity legs.The shock wave is generated and emitted during the third stage and will propagate both upstream and downstream.When the shock wave propagates to the new attached cavity sheet,it will cause the attached cavity sheet collapse,and with the shock wave propagation within the cavity sheet,the attached cavity sheet is shorten until totally collapsed.Following,the shock wave rebound phenomena occurs.The shock wave propagation and rebound are responsible for the increase in cavity evolution cycle and thus the low cavitation Strouhal number.The shock wave dynamics analysis shows that the flow parameters across the shock wave front during the interaction between shock wave and cavity satisfies the 1-D shock wave relationship.
Keywords:
引 言
空化发生于高速水流中的低压区域,不同于蒸发、沸腾等由热力学因素驱动的近似定压相变过程,空化是由水动力学因素驱动的近似恒温相变过程,从力学角度来看,空化是应力作用下的一种液体介质连续性的断裂,是液体的一种力学破坏形式[1].空化流动是包含相变、多相湍流、非定常性和可压缩性等几乎所有复杂物理现象的多相复杂流动[2-4].近年来,实验表明,附着型空穴断裂及空泡脱落存在回射流机制和激波机制,其中激波机制与空穴溃灭激波密切相关,激波的产生及传播是空化不稳定性和材料破坏的重要来源[5-10], 空穴溃灭过程与空化流动中汽相、液相及其混相介质压缩性密切相关[11-12].附着型空穴断裂及空泡脱落过程,尤其是大尺度脱落空泡云团溃灭,会造成剧烈的压力脉动、强烈的振动、激烈的噪声和严重的材料空蚀破坏,涉及到水力机械、水中兵器、水下发射、航空航天等多个工程领域中面临的核心关键技术问题的解决[13-16].
空化可压缩性的早期研究集中在水体中空泡溃灭行为的理论计算,研究发现,在空泡溃灭阶段($R<(0.02\sim0.04)R_{\rm{max}}$) ,空泡壁的运动速度会超过水体音速,甚至达到2.2个马赫数,水体的压缩性对空泡溃灭末期具有重要影响[17-18].另一方面,多相介质中声速的理论研究发现,气液混合物中声速会显著降低,远低于单一纯气体/纯液体的声速[19-20],甚至低至几米每秒.Shamsborhan等[21]采用压力传感器和光学探针对空化流动中声速进行了实验测量,实验结果表明,空化流动中声速可低至10 m/s以下,测量到的马赫数可达到1.2,证实了空化是具有高度压缩性的音速/超音速流动.Leroux等[6]采用压力传感器对绕水翼空化流动不稳定性进行了实验研究,研究发现,当空穴长度大于一半水翼弦长时,压力脉动增加,空化不稳定性加剧, 并且斯特劳哈尔数显著降低,进一步的研究发现,大尺度空泡云团溃灭激波现象是空化不稳定性的重要来源. 尽管理论和试验从不同侧面揭示了空化流动可压缩特性及其与空化不稳定的关系[22-23],然而由于空化流动是非均匀非稳态的复杂多相流动,剧烈瞬态相变与高度压缩性的耦合使得空化流动的物理机理更为复杂,为了更加深刻全面地认识可压缩空化流动特性,尤其是空泡/空泡团溃灭激波特性,开展可压缩空化流动的数值模拟研究具有重要科学意义.
目前,空化流动的数值计算研究多基于不可压缩两相Navier-Stokes (N-S) 方程组的求解,在计算中将汽相和液相密度视为定值,不可压缩的计算方法可以对如附着型空穴断裂、脱落,空穴尾部回射流产生及其推进等非定常过程进行很好的捕捉,被广泛应用于绕水翼、回转体、文丘里管内空化流动研究[24-26].然而,空化激波动力学特性研究,如空穴溃灭激波产生及其传播特性以及导致材料空蚀破坏的高幅值压力的捕捉,必须采用综合考虑汽相和液相可压缩性的计算方法.Kunz 等[27]采用预处理策略,基于人工压缩性方法,对绕回转体片状和云状空化流动进行了计算,数值结果与实验吻合良好,并且发现,考虑可压缩性有助于对空化动力特性的更好捕捉,然而由于其算法没有考虑介质物理压缩性,无法对激波动力学进行研究.Saito 等[28]基于有限体积法求解可压缩两相N-S 方程对绕NACA0015 水翼空化流动进行了数值研究,其中液相采用Tamman状态方程、汽相采用理想气体状态方程进行热力学闭合, 捕捉到了云状空化U型脱落空泡云团.Schnerr等[29]采用修正的黎曼方法求解了介质状态方程闭合的可压缩空化流动控制方程,采用纳秒尺度的时间步长,捕捉到绕扭曲NACA0009水翼空化流动中高达230 bar (23 MPa)的空穴溃灭高压.在可压缩空化流动算法上,Gnanaskandan和Mahesh[30]发展了预测—修正的方法求解两相可压缩N-S 方程, 在预测步采用无耗散对称算法,在修正步采用基于特征截断的二阶TVD 算法, 采用动态大涡模拟方法对收缩扩张流道内片状/云状空化转捩进行了可压缩计算,捕捉到空穴溃灭产生的周期性压力波现象.为提高计算效率,Egerer等[31]发展了基于4个网格单元的离散方式、耦合显式大涡模拟的可压缩空化流动计算方法,对空泡及空泡团溃灭现象和空化湍流混合层进行了计算,表现出较高的准确性.OpenFOAM作为大型开源软件,具有良好的扩展性,并且自身含有空化流动不可压缩求解器,逐渐被应用于空化流动的数值模拟研究中[32,33]. Wang等[11]基于OpenFOAM开源软件平台, 通过在空化流动求解中求解能量方程, 并引入水相和汽相的状态方程, 对绕NACA66水翼云状空化流动进行了数值模拟研究, 准确捕捉到了空穴溃灭诱导激波现象, 并进一步发现, 相对于回射流过程, 激波产生、传播过程会诱导高幅值压力脉冲, 剧烈的空穴体积脉动, 是空化不稳定性的重要来源, 然而, 关于空穴溃灭激波动力学特性尚需进一步的深入研究.
本文以OpenFOAM软件中两相可压缩求解器为基础,通过在该求解器的控制方程中(相方程和压力方程) 耦合模拟汽液相间质量交换过程的空化源项[11],实现了对空化可压缩非定常流动的数值计算.在此基础上,利用该可压缩空化流动求解器,对周期性云状空化流动进行了数值计算,并重点分析了溃灭激波特性.本文的研究目的在于:(1) 发展了基于OpenFOAM软件的可压缩空化流动数值计算方法; (2) 基于可压缩空化流动数值计算方法对周期性云状空化流动进行了数值模拟, 并重点分析了空穴溃灭激波产生、传播特性及其与空穴相互作用规律.
1 计算模型
1.1 控制方程
在空化流动数值模拟中,汽/液混合物被认为是均相流体介质,计算中采用均质平衡流假设,可压缩质量守恒方程、动量方程、能量方程以及含汽率输运方程分别为
\begin{align*}&\dfrac{\partial\rho_{\rm m}}{\partial t}+\nabla\cdot(\rho_{\rm{m}} U)=0 \tag*{(1)}\\&\dfrac{\partial(\rho_{\rm m} U)}{\partial t}+\nabla\cdot(\rho_{\rm{m}}{U}\otimes{U})=-\nabla p+\nabla\cdot\bigg\{\mu_{\rm m}\Big[\nabla U+\\&\quad\quad\quad (\nabla U)^{\rm T}-\dfrac{2}{3}(\nabla\cdot U){\rm I}\Big]\bigg\}-\sigma\nabla\cdot(\nabla\alpha_{\rm l}/|\alpha_{\rm l}|)\nabla\alpha_{\rm l} \tag*{(2)}\end{align*}\begin{align*}&\dfrac{\partial\rho_{\rm m}e}{\partial t}+\nabla\cdot(\rho_{\rm m} Ue)+\dfrac{\partial\rho_{\rm m}K}{\partial t}+\nabla\cdot(\rho_{\rm m} UK)-\nabla\cdot\\&\quad\quad\quad (\alpha_{\rm{eff}}\nabla e)=-\nabla\cdot(P U) \tag*{(3)}\\&\dfrac{\partial\rho_{\rm m}\alpha_{\rm v}}{\partial t}+\nabla\cdot(\rho_{\rm m}\alpha_{\rm v} U)+\nabla\cdot\big[ U_{\rm r}\alpha_{\rm v}(1-\alpha_{\rm v})\big]=m^+-m^- \tag*{(4)}\\&\rho_{\rm m}=\alpha_{\rm v}\rho_{\rm v}+\alpha_{\rm l}\rho_{\rm l} \tag*{(5)}\\&\mu_{\rm m}=\alpha_{\rm v}\mu_{\rm v}+\alpha_{\rm l}\mu_{\rm l} \tag*{(6)}\\&\kappa_{\rm m}=\alpha_{\rm v}\kappa_{\rm v}+\alpha_{\rm l}\kappa_{\rm l} \tag*{(7)}\end{align*}
其中,$\rho$,$ U$,$e$,$K$和$\alpha$分别代表密度、速度、内能、动能和含汽率,$\nabla U$,$\nabla\cdot U$,$\nabla\otimes U$分别代表梯度、散度和旋度; $\mu$,$\kappa$,$C_p$分别为介质黏性、热导率和定压比热容,$I$为单位张量; $\sigma=0.072$~8为表面张力,$ U_{\rm r}$ 为相间速度,$\dot{m}^+$和$\dot{m}^-$ 分别为蒸汽蒸发速率和凝结速率,由空化模型给出; 由均相流假设$T=T_{\rm m}=T_{\rm v}=T_{\rm l}$,$u=u_{\rm m}=u_{\rm v}=u_{\rm l}$,$p=p_{\rm m}=p_{\rm v}=p_{\rm l}$,下标m,l,v表示汽/液混相介质、液相和汽相,$i$,$j$,$k$ 表示坐标轴方向.
1.2 蒸汽和水的热力学状态方程
控制方程组采用介质热力学状态方程闭合,水蒸汽采用理想气体状态方程
\begin{equation*}p_{\rm v}=\rho_{\rm v}R_{\rm v}T_{\rm v}\tag*{(8)}\end{equation*}
其中,$R_{\rm v}$为蒸汽的气体常数,取$R_{\rm v}=461.6$ J/(kg$\cdot$K).
水采用Tait形式的状态方程[34]
\begin{equation*}\dfrac{p_{\rm l}+B}{p_{\rm{l,sat}}+B}=\left\lgroup\dfrac{\rho_{\rm l}}{\rho_{\rm{l,sat}}}\right\rgroup^N\tag*{(9)}\end{equation*}
其中,$B=3.06\times 10^8$,$N=7.1$,根据美国国家标准和技术机构(NIST) 数据,水的饱和蒸汽压力和饱和密度取20°C参数,$p_{\rm{l,sat}}=2338$,$\rho_{\rm{l,sat}}=998.16 ~\rm{kg/m}^3$.
1.3 空化模型和湍流模型
Saito空化模型[28]是基于平板蒸发/凝结理论[35]发展而来的输运方程形式的空化模型,蒸汽生成速率和凝结速率表示为
\begin{align*}&\dot{m}^+=C_{\rm e}\alpha_{\rm v}~^2(1-\alpha_{\rm v})^2\dfrac{\rho_{\rm l}}{\rho_{\rm v}}\dfrac{{\rm{max}}\big((p_{\rm v}-p),0\big)}{\sqrt{2\textrm{π} R_{\rm v}T}},p<p_{\rm v}\tag*{(10)}\\&\dot{m}^-=C_{\rm c}\alpha_{\rm v}~^2(1-\alpha_{\rm v})^2\dfrac{{\rm{max}}\big((p-p_{\rm v}),0\big)}{\sqrt{2\textrm{π} R_{\rm v}T}},p>p_{\rm v}\tag*{(11)}\end{align*}
其中,$\alpha_{\rm v}$为蒸汽相体积分数,$\rho_{\rm l}$为液相密度,$\rho_{\rm v}$为蒸汽相密度,$R_{\rm v}$为蒸汽气体常数,$T$为温度,$p_{\rm v}$是饱和蒸汽压力,$p$为当地静压,$C_{\rm c}$是当地静压大于饱和蒸汽压力时蒸汽凝结速率,$C_{\rm e}$为当地压力低于饱和蒸汽压力时蒸汽生成速率,在本文工作中,采用$C_{\rm c}=C_{\rm e}=0.1$[28]. 饱和蒸汽压力采用温度函数,由经验公式[36]给出
\begin{equation*}\begin{split}p_{\rm v}=&p_{\rm c}{\rm{exp}}\Bigg[\dfrac{T_{\rm c}}{T}(-7.85823\theta+1.83991\theta^{1.5}-11.7811\theta^3+\\&22.6705\theta^{3.5}-15.9393\theta^4+1.77516\theta^{7.5})\Bigg]\end{split}\tag*{(12)}\end{equation*}
其中,$\theta=1-T/T_{\rm c}$,下标“c”表示临界状态参数,对于水,$p_{\rm c}=22.064$ MPa,$\rho_{\rm c}=322~{\rm{kg/m}}^3$,$T_{\rm c}=647.14~{\rm K}$.
湍流模型采用耦合RANS/LES混合模型SST-SAS湍流模型[37],该模型采用基于当地流场速度的von Karman长度尺度作为湍流模型的耦合尺度,而不是使用LES的基于网格的滤波尺度,该尺度在流动稳定时远大于流动不稳定时,具有根据当地流场结构调节当地耗散的能力,并且该长度引入了速度导数,可以反映一定的湍流输运效应,因此可以改善湍流模型的预测精度.
$k$和$\omega$的输运方程如下所示
\begin{align*}&\dfrac{{\rm D}\rho k}{{\rm D}t}=P_{\rm k}-\rho c_{µ}k\omega+\dfrac{\partial}{\partial x_j}\left[\left\lgroup\mu+\dfrac{\mu_{\rm T}}{\sigma_{\rm k}}\right\rgroup\dfrac{\partial k}{\partial x_j}\right]\tag*{(13)}\\&\dfrac{{\rm D}\rho\omega}{{\rm D}t}=\dfrac{\partial}{\partial X_j}\left[\left\lgroup\mu+\dfrac{\mu_{\rm T}}{\sigma_{\omega}}\right\rgroup\dfrac{\partial\omega}{\partial X_j}\right]+\alpha\dfrac{\omega}{k}P_{\rm k}-\rho\beta\omega^2+\\&\quad\quad\quad(1-F_1)\dfrac{2\rho}{\sigma_{\omega2}}\dfrac{1}{\omega}CD_{k\omega}+\small\begin{matrix}\underbrace{Q_{\rm{SAS}}}\\{\rm{addition~term}}\end{matrix}\tag*{(14)}\end{align*}
其中$P_{\rm k}=-\tau_{ij}\partial U_i/\partial x_j$是湍动能生成项,$CD_{\rm{k\omega}}=\partial k/$$\partial x_j\cdot\partial\omega/\partial x_j$是湍动能交叉耗散项,$\mu_{\rm T}=\alpha_1k/{\rm{max}}$ $(\alpha_1\omega,$SF$_2)$,$S=\sqrt{S_{ij}S_{ij}}$,$F_1$和$F_2$是混合函数,$Q_{\rm{SAS}}$项为
\begin{equation*}\begin{split}&Q_{\rm{SAS}}={\rm{max}}\Bigg[\rho\zeta_2\kappa S^2\left\lgroup\dfrac{L}{L_{\rm{v_K}}}\right\rgroup^2-C_{\rm{SAS}}\dfrac{2\rho k}{\sigma_\Phi}{\rm{max}}\\&\quad\quad\quad\left\lgroup\dfrac{1}{k^2}\dfrac{\partial k}{\partial x_j}\dfrac{\partial k}{\partial x_j},\dfrac{1}{\omega ^2}\dfrac{\partial\omega}{\partial x_j}\dfrac{\partial\omega}{\partial x_j}\right\rgroup,0\Bigg]\end{split}\tag*{(15)}\end{equation*}其中,$L_{\rm{vk}}=\kappa\Bigg|\dfrac{\partial U/\partial y}{\partial ^2 U/\partial y^2}\Bigg|$,$\zeta_2=3.51$,$\sigma_Φ =2/3$, ~$C_{\rm{SAS}}=2.0$,$L=\sqrt{k}/(c^{1/4}_{µ}\cdot\omega)$是模化湍流长度.
1.4 计算方法及无量纲数定义
本文数值模拟采用基于有限体积法的OpenFOAM[38]开源软件,采用VOF 方法捕捉汽液相界面,本文发展的可压缩空化流动数值计算方法是在OpenFOAM$-$4.0 下的两相可压缩流动求解器基础上,通过在可压缩相输运方程和可压缩压力方程中耦合模拟空化流动的相间质量交换源项发展而来,本文对可压缩空化流动相输运方程及可压缩空化流动压力方程进行了详细推导见附录.关于OpenFOAM基于压力的多相数值方法的详细数值算法参考文献[39],其中求解的可压缩空化流动相输运方程如下
\begin{equation*}\begin{split}\dfrac{\partial\alpha_{\rm l}}{\partial t}&+\nabla(\alpha_1 U)+\nabla\cdot( U_{\rm r}\alpha_1\alpha_2)=\alpha_1\alpha_2\Bigg\lgroup\dfrac{1}{\rho_2}\dfrac{{\rm D}\rho_2}{{\rm D}t}-\dfrac{1}{\rho_1}\\&\dfrac{{\rm D}\rho_1}{{\rm D}t}\Bigg\rgroup+\dot{m}\Bigg[\dfrac{1}{\rho_1}-\alpha_{\rm l}\Bigg\lgroup\dfrac{1}{\rho_1}-\dfrac{1}{\rho_2}\Bigg\rgroup\Bigg]+\alpha_1\nabla\cdot U\end{split}\tag*{(16)}\end{equation*}
该方程左边第三项为采用Weller提出人工对流压缩项,以避免数值耗散带来的相界面模糊性,$ U_{\rm r}$为模化的相间相对速度,在OpenFOAM开源软件中,为了降低相界面附近的相分数的数值耗散,该方程采用MULES求解器求解.
可压缩空化流动压力方程如下
\begin{equation*}\begin{split}&\Bigg\lgroup\dfrac{\alpha_1}{\rho_1}\psi_1+\dfrac{\alpha_2}{\rho_2}\psi_2\Bigg\rgroup\Bigg\lgroup\dfrac{\partial p}{\partial t}+ U\nabla\cdot p\Bigg\rgroup+\nabla\cdot U= \\&\quad\quad\quad\Bigg\lgroup\dfrac{\alpha_1}{\rho_1}-\dfrac{\alpha_2}{\rho_2}\Bigg\rgroup\dot{m}\end{split}\tag*{(17)}\end{equation*}
其中,$\psi_{\rm l}=\dfrac{{\rm d}\rho_{\rm l}}{{\rm d}p}=\dfrac{\rho_1}{(\rho_{\rm l}/\rho_{\rm{l,sat}})^NN(p_{\rm{l,sat}}+B)}$,$\psi_{\rm g}=\dfrac{{\rm d}\rho_{\rm g}}{{\rm d}p}=\dfrac{1}{R_{\rm g}T}$为液相和汽相可压缩性.
本文采用的无量纲参数定义如下
空化数:$\sigma=(p-p_{\rm v})/(0.5\rho_{\rm l}U^2)$
雷诺数:$Re=Uc/$
斯特劳哈尔数:$St=fc/U$
其中,$U$为来流速度,$\rho_{\rm l}$为液体密度,$p_{\rm v}$为饱和蒸汽压力,$p$ 为环境压力,$c$为水翼弦长,ν为运动黏度系数,$f$为空穴脱落周期.
1.5 计算网格及边界条件设置
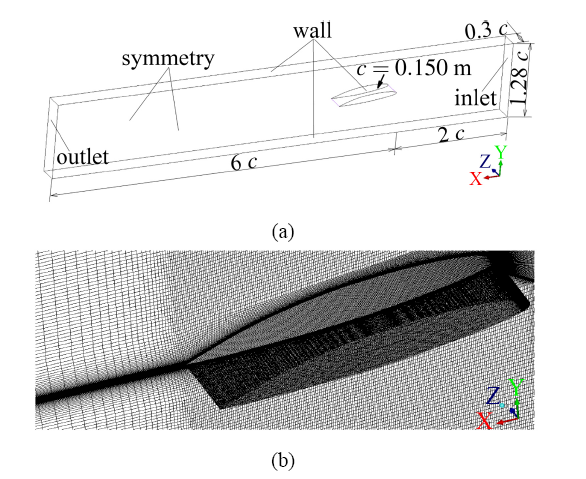
本文对绕NACA66水翼的非定常云状空化流动进行了计算,Leroux等[6]对该水翼进行了系列的实验研究,发现在6°攻角下,绕NACA66水翼云状空化流动呈现以空穴溃灭激波占主导的非定常流动特点,本文对该工况进行了数值模拟研究.三维几何模型如图1(a)所示,水翼攻角为6°,几何模型、计算域的尺寸与实验[6]保持一致,弦长$c=0.150~{\rm m}$.计算区域的入口距翼型前缘约为$2~c$,出口距翼型尾缘为$5~c$,上下壁面距离为$1.14~c$,为节省计算资源,本文采用$0.3~c$作为展向长度,该处理方式由Sagaut[40] 提出,已在空化流动中得到应用[41].三维结构化网格如图1(b)所示,对近壁面网格进行加密,保证$y^+\leqslant 1$,展向布置80个网格节点,网格总数为250万.
流动介质参数与20°水和水蒸汽保持一致,边界条件与实验保持一致,如图1(a)所示,入口速度大小为$U=5.33$ m/s,$Re=0.8\times 10^6$.出口采用压力边界条件,为避免压力在进出口反射,进出口均采用无反射边界条件.同时根据调节不同出口压力来控制流场空化数$\sigma=1.25$,需要注意的是,在实验中,空化数的计算依据进口压力,在本文数值模拟中,通过调节出口压力使进口压力保持稳定在实验水平.在可压缩空化流动计算中,时间步长的选择非常重要,依据OpenFOAM软件多相流算法对库朗数的要求,本文时间步长的选择满足${\rm{max}}Co\leqslant 0.4$,以保证数值计算的稳定性.
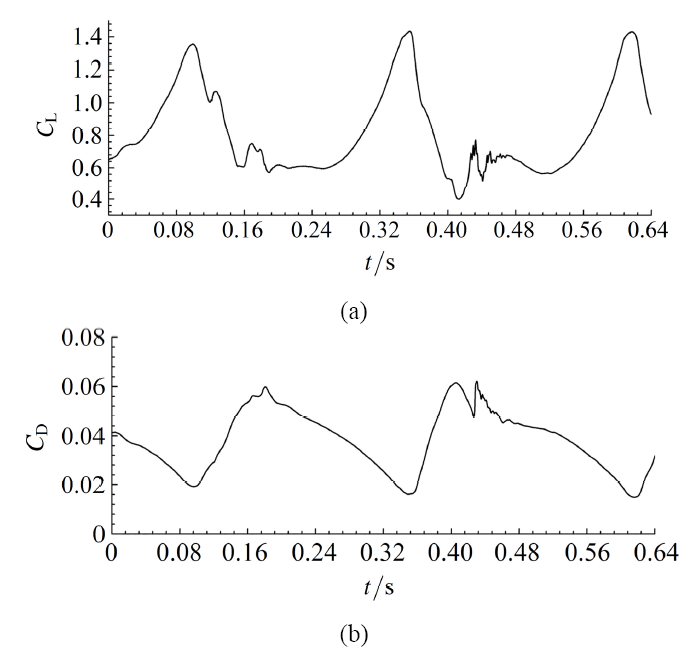
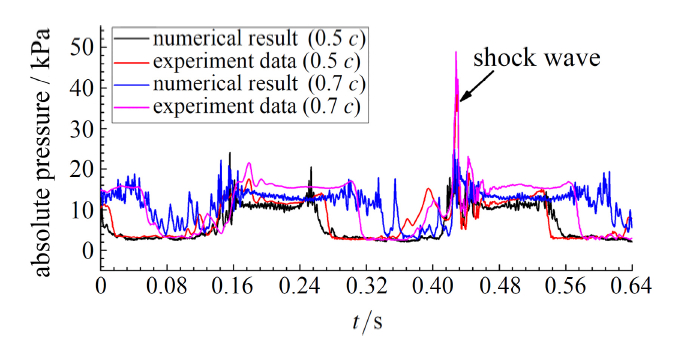
图2给出了计算所得的水翼升阻力系数演化,可以看出,升阻力呈现周期性的脉动变化,周期为$T_{\rm{ref}}=284.1$ ms,频率为$f=3.52$ Hz,则基于水翼弦长的斯特劳哈尔数为$St=fc/U=0.099$,已知实验所得该工况下斯特劳哈尔数为$St=0.102$,本文计算误差为$2.9\%$,与实验结果吻合良好,很好地捕捉到了云状空化流动的周期性.图3 给出了水翼吸力面尾部0.5 $c$和0.7 $c$位置处计算所得压力波动与实验测量数据的对比,可以看出,计算结果很好地模拟了空穴演化诱导压力周期性波动特点,并且捕捉到了空穴溃灭激波产生的压力峰值,同时,数值计算压力值与实验存在差异,这是由于翼型吸力面上压力分布受空泡覆盖影响严重,在空泡覆盖区呈现低压力值,由于空泡的非定常效应和三维效应,而导致与实验测量结果的偏差.
图3 水翼吸力面0.5 $c$和0.7 $c$处计算所得压力波动与文献[
Fig.3 Comparisons of absolute pressure evolution on foil suction side at $x/c=0.5$ and 0.7,respectively,between the present numerical results and experiment data [
2 结果分析
2.1 非定常空穴结构演化过程分析
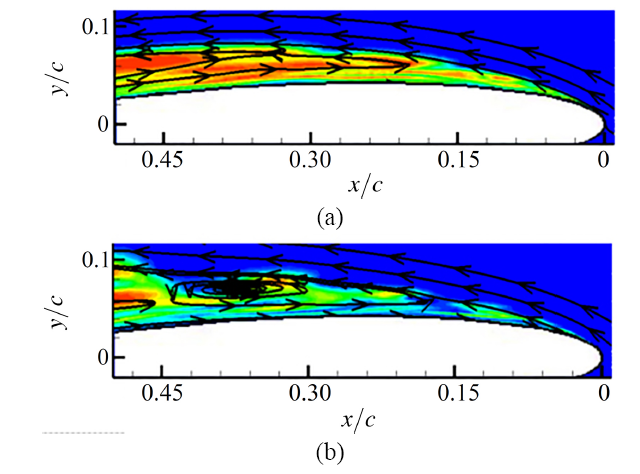
空化流动具有高度的非定常特性,空穴结构的演化呈现出准周期性的特点.从Leroux 等[6]的实验结果已知,不同于回射流主导的云状空化非定常流动,绕6°攻角NACA66水翼云状空化流动呈现出脱落空泡云团溃灭后、新生附着型空穴回缩再生长的非定常流动特征.图4给出了数值计算所得的绕NACA66水翼在约一个空化周期内空穴结构演化过程与Leroux等[6]的实验结果的对比.从图中可以看出,本文采用的可压缩数值模拟方法很好地捕捉到了空穴的非定常演化过程,尤其是伴随着大尺度空泡云团脱落、溃灭过程,新生附着型空穴的生长、回缩过程.图中,流动方向为从右向左,如时刻(a)中箭头所示,相邻时刻间隔为0.14 $T_{\rm{ref}}$,时刻(e)和(f)中为回射流推进过程,图5给出了翼型中截面位置水翼前缘含汽率和流线分布,时刻(g), (h)和(i)中黄色虚线表示附着型空穴尾缘位置, 带箭头红色直线表示附着型空穴长度.下面将针对该工况下云状空化流动典型非定常空穴结构演化进行详细分析.
图4 绕NACA66水翼非定常云状空穴结构演化过程(实验:文献[
Fig.4 Comparisons of the numerically predicted vapor fraction ($\alpha_{\rm v}=0.15$) and experimentally observed cavitation pattern [
图5 回射流推进过程水翼中截面位置含汽率和流线分布(图(a)和图(b)分别对应
Fig.5 Vapor fraction contour along with streamlines on foil mid-plane during the re-entrant flow development process.(a) is for the instance of
绕6°攻角NACA66水翼云状空化流动典型非定常演化过程可以分为4个阶段:(1)附着型空穴生长阶段(a)$\sim$(d),(i); (2)回射流推进及附着型空穴断裂阶段(e),(f); (3)大尺度空泡云团脱落及新生附着型空穴生长阶段(g); (4)大尺度空泡云团溃灭及新生附着型空穴回缩阶段(h).在附着型空穴生长阶段(a)$\sim$(d),(i),附着型空穴产生于水翼前缘(a),紧贴翼型吸力面,向下游生长(b)$\sim$(d),(i),可以观察到,附着型空穴尾部呈现剧烈波动的特点,非定常效应较为明显.在空穴发展第二阶段(e),(f),随着附着型空穴的发展,当空穴生长到一定长度时, 在空穴底部会产生向上游运动的流动,即回射流,该回射流主要由液体组成,在运动过程中会夹带当地蒸汽.当该反向流动运动到空穴前缘与空穴界面相互作用,会导致附着型空穴的断裂,断裂的空穴被抬升在主流的
作用下,卷起形成脱落空泡云团向下游运动.在空穴发展第三阶段(g),伴随着大尺度空泡云团向下游输运,处于低压区的水翼前缘生长出新的附着型空穴.在空穴发展第四阶段(h),大尺度脱落空泡云团被输运到下游高压区,在内外压差的作用下溃灭,同时,观察到新生附着型空穴出现回缩现象(h).由上述观察可以看出,大尺度脱落空泡云团溃灭后,新生附着型空穴回缩过程抑制了下一周期空穴的发展,延长了空穴发展周期.
2.2 大尺度脱落空泡云团溃灭激波动力学分析
2.2.1 大尺度脱落空泡云团溃灭过程
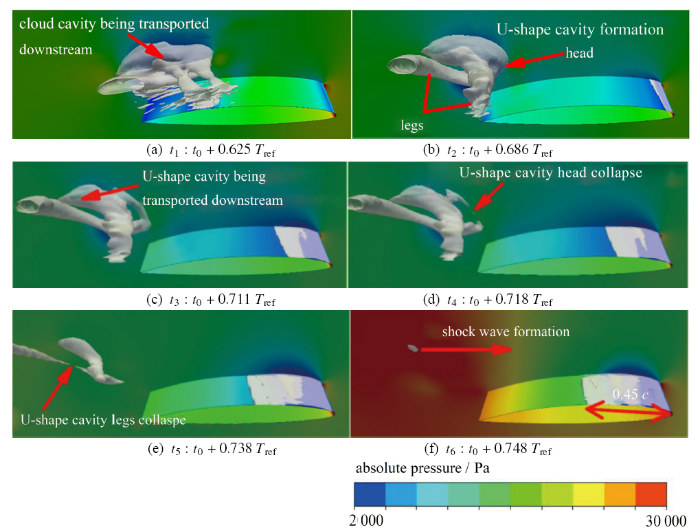
在非定常云状空化流动中,大尺度脱落空泡云团具有强大的能量,是空化不稳定性的主要来源, 为深入分析脱落空泡云团行为,图6给出了大尺度空泡云团脱落及溃灭过程中空穴结构和翼型表面及侧面的压力分布演化.从图中可以看出,大尺度空泡云团脱落、溃灭过程分为三个典型阶段:(1) 大尺度空泡云团向下游输运并形成U型空穴结构($0.625~T_{\rm{ref}}\sim0.686~T_{\rm{ref}}$),(2) U型空穴结构向下游输运,U型空穴结构头部溃灭($0.711~T_{\rm{ref}}\sim0.718 T_{\rm{ref}}$),(3) U型空穴结构腿部溃灭($0.738~T_{\rm{ref}}\sim0.748~T_{\rm{ref}}$),在空穴完全溃灭的瞬间,观察到以溃灭点为中心的高压区域,即激产生.同时,伴随着大尺度空泡云团的脱落过程,翼型前缘的新生附着型空穴逐渐生长,至空穴溃灭时刻($0.748~T_{\rm{ref}}$),新生附着型空穴长度达到$0.45~c$.
图6 大尺度空泡云团脱落溃灭过程空穴结构(含汽率等值面:$\alpha_{\rm v}=0.15$)及压力分布
Fig.6 Bird view of predicted isosurface of vapor fraction $\alpha_{\rm v}=0.15$ and absolute pressure contour on the foil surface and side plane in the process of large scale cloud cavity collapse
2.2.2 空穴溃灭激波传播过程及其动力学分析
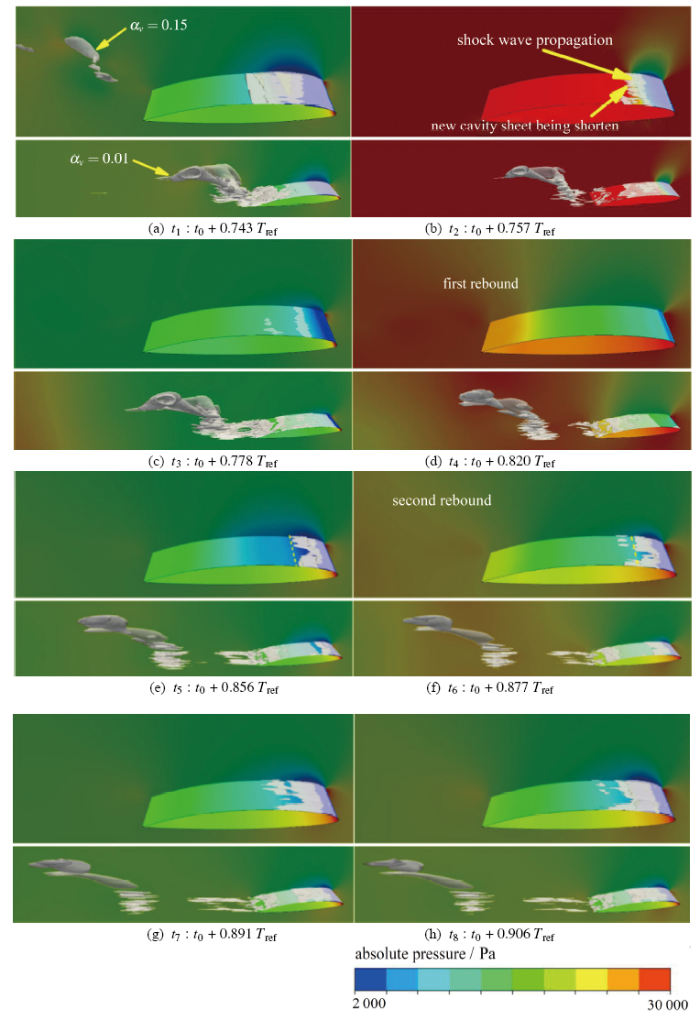
为分析空穴溃灭激波传播规律,图7给出了空泡云团溃灭激波产生、传播及其回弹过程空穴结构($\alpha_{\rm v}=0.15$)和压力演化,并给出了极低含气率结构($\alpha_{\rm v}=0.01$). 从压力云图中可以看出,激波传播过程分为第一次溃灭激波传播和两次回弹,并且激波能量逐次衰减.在第一次激波传播过程中,随着激波前缘的推进,高压区逐渐覆盖翼型吸力面,当激波前缘接触新生附着型空穴,将导致空穴溃灭,伴随着激波前缘的推进,新生附着型空穴呈现回缩现象(0.757 $T_{\rm{ref}}$),直至高压区完全覆盖翼型,当激波传播过后,在来流的作用下,翼型表面出现低压区,并且低压区逐渐扩大,翼型吸力面出现零星随机蒸汽空穴(0.778 $T_{\rm{ref}}$).结合极低含汽率分布,可以看出,在激波产生传播过程中,极低含汽率受激波作用产生溃灭,但是激波并未造成蒸汽完全溃灭(0.757 $T_{\rm{ref}}$),空化区域存在极低含汽率,并向下游输运.激波过后,极低含气率体积增大(0.778 $T_{\rm{ref}}$).当极低含汽率输运到下游高压区,出现再次溃灭行为(0.877 $T_{\rm{ref}}$),在空穴溃灭激波传播过后的第一次回弹过程,高压区逐渐覆盖翼型吸力面,低压区消失(0.820 $T_{\rm{ref}}$),翼型吸力面蒸汽空穴再次溃灭(0.820 $T_{\rm{ref}}$),同时可以看出相比第一次激波传播时强度,回弹激波强度已大大衰减.在第一次回弹过后,低压区再次从翼型吸力面前缘开始向下游扩展,同时伴随着低压区的扩大,附着型空穴开始生长(0.856 $T_{\rm{ref}}$).第一次回弹过后,极低含汽率结构体积增大(0.856 $T_{\rm{ref}}$),当其运动到下游,紧接着存在第二次溃灭行为即第二次回弹,在激波传播过后的第二次回弹过程,此时回弹激波能量已非常小,回弹激波的传播仅带来翼型吸力面压力的小幅度增(0.877 $T_{\rm{ref}}$),加,并且不能使翼型前缘附着型空穴溃灭,但是可以观察到,激波回弹过程与极低含气率结构密切相关,同时, 回弹激波抑制了附着型空穴生长速度(0.877 $T_{\rm{ref}}$), 二次回弹激波过后,附着型空穴开始生长(0.891 $T_{\rm{ref}}$,0.898 $T_{\rm{ref}}$),开始新的空化周期.
图7 大尺度空泡云团溃灭激波传播及其回弹过程空穴结构(含汽率等值面,上:$\alpha_{\rm v}=0.15$,下:$\alpha_{\rm v}=0.01$)和压力分布演化
Fig.7 Bird view of predicted isosurface of vapor fraction (up:$\alpha_{\rm v}=0.15$,down:$\alpha_{\rm v}=0.01$) and absolute pressure contour on the foil surface and side plane in the process of cloud cavity collapse induced shock wave generation and rebound
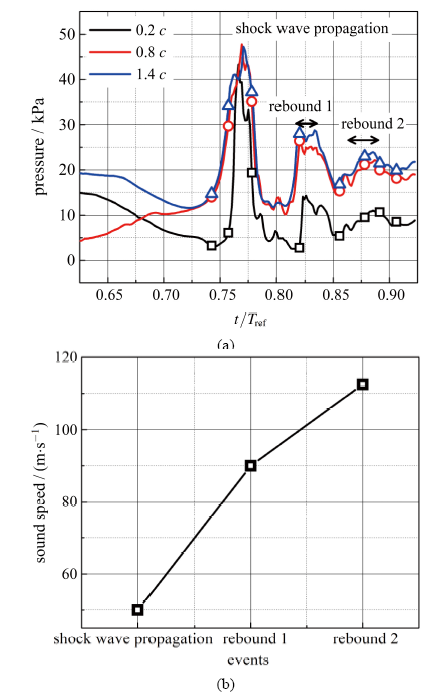
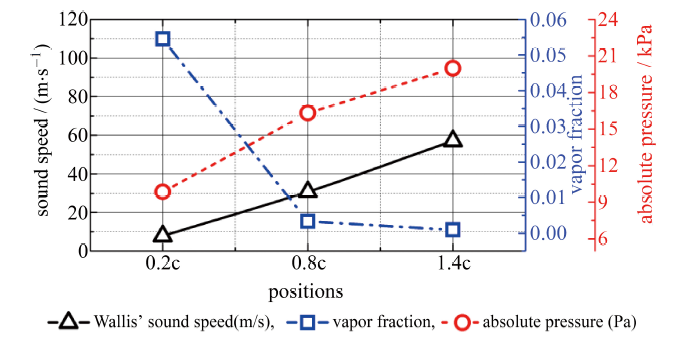
为定量分析空穴溃灭激波传播及其回弹过程压力波动特性,图8给出了大尺度空泡云团溃灭激波传播及回弹过程中压力波动及激波传播速度.其中图8(a)中标号分别对应图7中时刻.其中压力波动监测点分别位于水翼吸力面0.2 $c$,0.8 $c$和水翼尾部下游1.4 $c$ 位置处,激波传播速度由压力峰值时刻差得到.从图8(a)中可以看出,激波由水翼尾部下游空穴溃灭位置向水翼前缘传播,在激波从下游向水翼前缘传播过程中,激波能量不断衰减,且\mbox{1.4 $c$} 至0.8 $c$ 路径之间激波衰减幅度小于0.8 $c$至0.2 $c$,结合图7新生附着型空穴主要分布在0.2 $c$至0.8 $c$,可以推断空穴会增加激波衰减幅度.同时,随着激波回弹,回弹激波能量也在不断减弱,激波前缘宽度增加同时当地压力爬升速度减缓.激波传播、一次回弹和二次回弹过程中激波传播速度逐渐增加,考虑到激波传播速度与当地含汽率密切相关[2],随着激波的传播及多次回弹,流场中含汽率不断减小,当地声速增加,进而导致激波传播速度的增加.为定量分析流场中含汽率、压力及理论声速分布规律,图9给出了激波传播和回弹过程不同位置处平均含汽率、Wallis声速$\Bigg(\dfrac{1}{\rho c^2}=\dfrac{\alpha_{\rm v}}{\rho_{\rm v}c_{\rm v}^2}+\dfrac{1-\alpha_{\rm v}}{\rho_{\rm l}c_{\rm l}^2}\Bigg)$和平均压力分布,从图中可以看出,水翼下游距空穴溃灭中心最近处(1.4 $c$)平均压力最大, 距空穴溃灭中心最远处水翼前缘(0.2 $c$)平均压力最小,且1.4 $c$ 至0.8 $c$路径中平均压力降幅小于0.8 $c$至0.2 $c$路径,证明了激波传播过程中能量衰减特性及空穴对激波衰减的增强作用.同时,根据平均含汽率预测了Wallis 声速,该声速值与图8(b)由压力峰值计算得到的激波传播速度处于同一量级,说明了可压缩空化流动中激波传播速度与当地含汽率密切相关.
图8 (a)大尺度空泡云团溃灭激波传播及其回弹过程压力波动,(b) 大尺度空泡云团溃灭激波传播及其两次回弹过程中激波传播速度(水翼表面0.2 $c$、0.8 $c$ 和水翼尾部下游1.4 $c$).标号对应
Fig.8 (a) Absolute pressure evolution on foil suction side at $x/c=0.2$,0.8 and 1.4,and (b) the shock wave speed during the large scale cloud cavity collapse induced shock wave generation and rebound. The symbols indicate the instances in
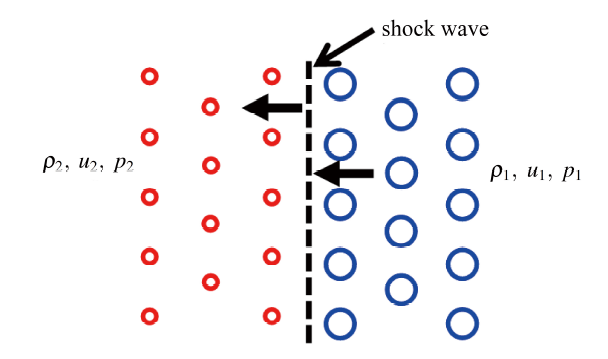
为进一步分析激波与空穴相互作用规律,本文基于连续性方程和动量方程对激波前后流动参数进行了分析,如图10所示.由连续性方程和动量方程
\begin{align*}&\rho_1u_1=\rho_2u_2\tag*{(18)}\\&p_1=\rho_1u_1^2=p_2+\rho_2u_2^2\tag*{(19)}\end{align*}
其中,$\rho$为密度,$u$为速度,$p$为压力,下标1代表激波前参数,下标2代表激波后参数,如图9所示,得到激波推进速度
\begin{equation*}u_1^2=\dfrac{p_2-p_2}{\rho_1}\dfrac{\rho_2}{\rho_2-\rho_1}\tag*{(20)}\end{equation*}
又由$\rho_i\approx\rho_L(1-\alpha_i)$得
\begin{equation*}u_1^2=\dfrac{p_2-p_1}{\rho_L}\dfrac{1-\alpha_1}{(1-\alpha_2)(\alpha_1-\alpha_2)}\tag*{(21)}\end{equation*}
式(21)给出了激波推进速度与波前、波后流动参数之间的关系.
图9 空穴溃灭激波传播及回弹过程中水翼吸力面及尾部下游不同位置处平均含汽率、Wallis声速和平均压力分布
Fig.9 Average vapor fraction distribution,Wallis sound speed and average absolute pressure during the cloud cavity collapse induced shock wave propagation and rebound process
图10 两相流动激波前后参数示意
Fig.10 Schematic of parameters across the shock wave front in two-phase flows
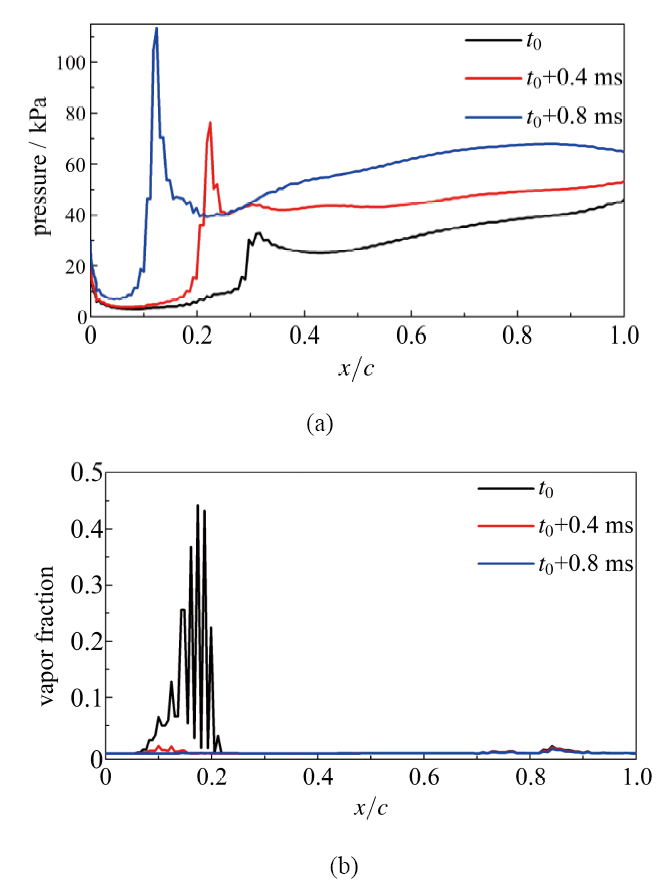
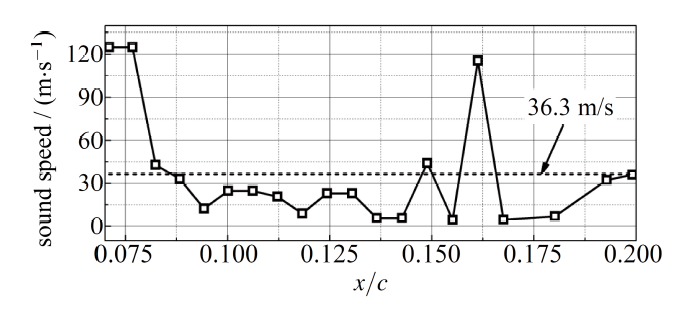
图11给出了激波与空穴相互作用过程中空穴形态与翼型表面和侧面压力分布,翼型中截面含汽率云图和压力云图,可以观察到随着激波前缘的推进,新生附着型空穴出现回缩现象,激波过后,压力增加,含汽率减小.图12定量给出了水翼表面压力和含汽率分布,通过压力波动峰值计算得到激波在空穴内部传播速度分别为34.9 m/s 和37.7 m/s.通过提取水翼表面0.07 $c$ 至0.2 $c$之间激波过后压力及含汽率变化数据,将激波前后压力及含汽率数据代入式(21),得到根据激波动力学预测的激波在附着型空穴内的推进速度,如图13所示,并且附着型空穴内部激波平均传播速度为36.3 m/s, 与由压力峰值得到的速度基本一致.激波前后流动参数的跳跃关系进一步说明了空穴溃灭诱导的激波特性.
图11 激波与空穴相互作用过程中空穴结构(左列,含汽率等值面:$\alpha_{\rm v}=0.15$),水翼中截面含汽率(中间)和压力(右列)分布
Fig.11 Isosurface of vapor fraction (left,$\alpha_{\rm v}=0.15$),vapor fraction contour and absolute pressure contour on mid-plane during the shock wave and cavity structure interaction process
图12 激波与空穴相互作用过程中水翼吸力面中截线位置处压力波动和含汽率分布
Fig.12 The absolute pressure and vapor fraction distribution on foil mid-span line during the shock wave and cavity structure interaction process
图13 激波与空穴相互作用过程中水翼吸力面不同位置处激波动力学预测激波推进速度
Fig.13 The shock wave propagation speed predicted by the jump relationship across the shock wave front on the foil suction side
3 结论
采用可压缩空化流动数值计算方法对绕6°攻角NACA66水翼云状空化流动的非定常演化和空穴溃灭激波特性进行了研究,分析了空穴溃灭激波产生及传播规律,以及激波与空穴相互作用机理,主要结论如下:
(1)绕6°攻角NACA66水翼的云状空化流动呈现激波与回射流交互作用的特点,激波主导非定常空化流动不稳定性,空穴的非定常演化过程分为4个阶段:(a)附着型空穴生长阶段; (b)回射流推进及附着型空穴断裂; (c)脱落空泡云团向下游输运,和(d)脱落空泡云团溃灭激波产生及传播.
(2)大尺度脱落空泡云团溃灭过程分为3个阶段:(a)U型空泡团形成; (b)U型空泡团头部溃灭; (c)U型空泡团双腿溃灭.在空穴溃灭的第三阶段激波产生,向上游传播的激波与空穴相互作用导致水翼吸力面新生的附着型片状空穴回缩,直至完全溃灭,抑制下一周期空化发展,造成空化演化周期增大.
(3)空穴溃灭激波传播过程具有回弹的特点,回弹过程与极低含气率分布密切相关,激波从下游向上游传播过程中,激波能量不断衰减,并且在空化区域激波衰减幅度增加,随着激波的回弹,激波能量逐渐减小,激波传播及其回弹过程抑制了空化的发展.
附录:
附A含相变可压缩相分数输运方程推导
可压缩相连续性方程
\begin{equation*}\dfrac{\partial\alpha_1\rho_1}{\partial t}+\nabla\cdot(\rho_1\alpha_1 U)=\dot{m}\tag*{(A1)}\end{equation*}\begin{equation*}\dfrac{\partial\alpha_2\rho_2}{\partial t}+\nabla\cdot(\rho_2\alpha_2 U)=-\dot{m}\tag*{(A2)}\end{equation*}
对式(A1)展开
\begin{equation*}\alpha_1\dfrac{\partial\rho_1}{\partial t}+\rho_1\dfrac{\partial\alpha_1}{\partial t}+\rho_1\nabla\cdot(\alpha_1 U)+\alpha_1 U\nabla\rho_1=\dot{m}\tag*{(A3)}\end{equation*}
对式(A3)进行整理
\begin{equation*}\dfrac{\partial\alpha_1}{\partial t}+\nabla\cdot(\alpha_1 U)=-\dfrac{\alpha_1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}+\dfrac{\dot{m}}{\rho_1}\tag*{(A4)}\end{equation*}
同理式(A2)有
\begin{equation*}\dfrac{\partial\alpha_2}{\partial t}+\nabla\cdot(\alpha_2 U)=-\dfrac{\alpha_2}{\rho_2}\dfrac{{\rm D}\rho_2}{{\rm D}t}-\dfrac{\dot{m}}{\rho_2}\tag*{(A5)}\end{equation*}
两式相加,则得含相变可压缩空化流动连续性方程
$$\nabla\cdot U=-(\frac{\alpha_2}{\rho_2}\frac{{\rm D}\rho_2}{{\rm D}t}+\frac{\alpha_1}{\rho_1}\frac{{\rm D}\rho_1}{{\rm D}t})+\dot{m}(\frac{1}{\rho_1}-\frac{1}{\rho_2})(A6)$$
进一步对式(A4)展开
\begin{equation*}\dfrac{\partial\alpha_1}{\partial t}+\alpha_1\nabla\cdot U+ U\nabla\alpha_1=-\dfrac{\alpha_1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}+\dfrac{\dot{m}}{\rho_1}\tag*{(A7)}\end{equation*}
将连续性方程(A6)代入式(A7)
\begin{equation*}\begin{split}\dfrac{\partial\alpha_1}{\partial t}&+\alpha_1\left[-\left\lgroup\dfrac{\alpha_1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}+\dfrac{\alpha_2}{\rho_2}\dfrac{{\rm D}\rho_2}{{\rm D}t}\right\rgroup+\dot{m}\left\lgroup\dfrac{1}{\rho_1}-\dfrac{1}{\rho_2}\right\rgroup\right]+ \\& U\cdot\nabla\alpha_1=-\dfrac{\alpha_1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}+\dfrac{\dot{m}}{\rho_1}\end{split}\tag*{(A8)}\end{equation*}
得到
\begin{equation*}\begin{split}\dfrac{\partial\alpha_1}{\partial t}&+ U\cdot\nabla\alpha_1=\alpha_1\alpha_2\left\lgroup\dfrac{1}{\rho_2}\dfrac{{\rm D}\rho_2}{{\rm D}t}-\dfrac{1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}\right\rgroup+ \\&\dot{m}\left[\dfrac{1}{\rho_1}-\alpha_l\left\lgroup\dfrac{1}{\rho_1}-\dfrac{1}{\rho_2}\right\rgroup\right]\end{split}\tag*{(A9)}\end{equation*}
进一步
\begin{equation*}\begin{split}\dfrac{\partial\alpha_1}{\partial t}&+\nabla(\alpha_1 U)=\alpha_1\alpha_2\left\lgroup\dfrac{1}{\rho_2}\dfrac{{\rm D}\rho_2}{{\rm D}t}-\dfrac{1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}\right\rgroup+ \\&\dot{m}\left[\dfrac{1}{\rho_1}-\alpha_{\rm l}\left\lgroup\dfrac{1}{\rho_1}-\dfrac{1}{\rho_2}\right\rgroup\right]+\alpha_1\nabla\cdot U\end{split}\tag*{(A10)}\end{equation*}
该方程采用MULES(multidimensional universal limiter with explicit solution)求解,在OpenFOAM开源软件中,为了降低相界面附近的相分数的数值耗散,采用Weller提出的添加一种人工的对流压缩项以避免数值耗散带来的相界面模糊性.
\begin{equation*}\begin{split}\dfrac{\partial\alpha_1}{\partial t}&+\nabla(\alpha_1 U)+\nabla\cdot( U_{\rm r}\alpha_1\alpha_2)=\alpha_1\alpha_2 \\&\Bigg\lgroup\dfrac{1}{\rho_2}\dfrac{{\rm D}\rho_2}{{\rm D}t}-\dfrac{1}{\rho_1}\dfrac{{\rm D}\rho_1}{{\rm D}t}\Bigg\rgroup+\dot{m}\Bigg[\dfrac{1}{\rho_1}- \\&\alpha_{\rm l}\Bigg\lgroup\dfrac{1}{\rho_1}-\dfrac{1}{\rho_2}\Bigg\rgroup\Bigg]+\alpha_1\nabla\cdot U\end{split}\tag*{(A11)}\end{equation*}
$ U_{\rm r}$为模化的相间相对速度,定义为
\begin{equation*} U_{\rm r}=c_\alpha|U|\tag*{(A12)}\end{equation*}
其中,$c_\alpha$为相界面压缩因子.即为最终求解的含相变可压缩相分数输运方程.
附B 含相变可压缩压力方程推导
在OpenFOAM中,通过求解动量预测方程可得到预测速度$ U_{\rm p}^{\rm r}$, 此时的预测速度并不满足连续性方程,需要通过压力方程进行压力的求解和速度、通量的更新.
可压缩连续性方程
\begin{equation*}\dfrac{\partial\rho_1}{\partial t}+\nabla\cdot(\rho_1 U)=\dot{m}\tag*{(A13)}\end{equation*}\begin{equation*}\dfrac{\partial\rho_1}{\partial t}+\nabla\cdot(\rho_2 U)=-\dot{m}\tag*{(A14)}\end{equation*}
物质的热力学状态方程
\begin{equation*}\rho=\psi p\tag*{(A15)}\end{equation*}
将式(A15)代入式(A13)展开
\begin{equation*}\begin{split}\dfrac{\partial(\psi_1p)}{\partial t}&+\nabla,\big(\psi_1p U\big)=\psi_1\dfrac{\partial p}{\partial t}+p\dfrac{\partial\psi_1}{\partial t}+ \\&\psi_1p\nabla U+ U\nabla\big(\psi_1p\big)=\dot{m}\end{split}\tag*{(A16)}\end{equation*}
其中$\psi$为物质压缩性参数,与时间无关,进一步,式(A16)展开为
\begin{equation*}\psi_1\dfrac{\partial p}{\partial t}+\psi_1 U\nabla(p)+\rho_1\nabla U=\psi_1\dfrac{{\rm D}p}{{\rm D}t}+\rho_1\nabla U=\dot{m}\tag*{(A17)}\end{equation*}
同理,式(A14)整理为
\begin{equation*}\psi_2\dfrac{{\rm D}p}{{\rm D}t}+\rho_2\nabla U=-\dot{m}\tag*{(A18)}\end{equation*}
则得含相变可压缩压力方程为
\begin{equation*}\begin{split}\Bigg\lgroup\dfrac{\alpha_1}{\rho_1}&\psi_1+\dfrac{\alpha_2}{\rho_2}\psi_2\Bigg\rgroup\left\lgroup\dfrac{\partial p}{\partial t}+ U\nabla\cdot p\right\rgroup+ \\&\nabla\cdot U=\left\lgroup\dfrac{\alpha_1}{\rho_1}-\dfrac{\alpha_2}{\rho_2}\right\rgroup\dot{m}\end{split}\tag*{(A19)}\end{equation*}
The authors have declared that no competing interests exist.
参考文献
| [1] |
Cavitation in a flowing liquid . |
| [2] |
|
| [3] |
Dynamics of attached turbulent cavitating flows .
|
| [4] |
Numerical simulation of ultra-high speed supercavitating flows considering the effects of the water compressibility, |
| [5] |
Observations of shock waves in cloud cavitation . |
| [6] |
An experimental study of unsteady partial cavitation . |
| [7] |
Numerical simulation and analysis of condensation shocks in cavitating flow .
|
| [8] |
Unsteady pressure fluctuation characteristics in the process of breakup and shedding of sheet/cloud cavitation .
|
| [9] |
附着型空穴断裂及脱落机制的实验研究 .
Experimental investigation on the breakup and shedding mechanisms of unsteady attached cavitating flows .
|
| [10] |
Compressible effect on the cavitating flow:A numeric study . |
| [11] |
Numerical simulation of transient turbulent cavitating flows with special emphasis on shock wave dynamics considering the water/vapor compressibility . |
| [12] |
Numerical simulation of cavitation vortex dynamics in unsteady cavitating flow with shock wave propagation . |
| [13] |
绕水翼空化流动及振动特性的实验研究 .Experimental investigation of the vibration characteristics of hydrofoil in cavitating flow . |
| [14] |
轴对称体空泡流的噪声特性与空泡界面瞬态特征 .
Noise feature of cavitation flows on axisymmetric bodies and transient characteristics of cavity interface .
|
| [15] |
航行体水下垂直发射空泡脱落条件研究 .
Investigation of cavities shedding condition on underwater vehicles in the vertical launch process .
|
| [16] |
航行体水下发射流固耦合效应分析 .Study of coupling effects of underwater launched vehicle . |
| [17] |
The equation of bubble dynamics in a compressible liquid . |
| [18] |
单液滴内空化气泡的生长及溃灭研究 .Study of the growth and collapse of cavitation bubble within a droplet . |
| [19] |
The speed of sound in a gas-vapour bubbly liquid . |
| [20] |
飞机尾涡演变及快速预测的大涡模拟研究 .Large eddy simulation on the evolution and the fast-time prediction of aircraft wake vortices . |
| [21] |
Experimental determination of the speed of sound in cavitating flows, |
| [22] |
Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities . |
| [23] |
Bubbly shock propagation as s mechanism of shedding in separated cavitating flows.Journal of Hydrodynamics Ser . |
| [24] |
Large eddy simulation and Euler-Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil . |
| [25] |
Large eddy simulation of turbulent attached cavitating flow with special emphasis on large scale structures of the hydrofoil wake and turbulence-cavitation interactions .
|
| [26] |
Verification and validation of URANS simulations of the turbulent cavitating flow around the hydrofoil . |
| [27] |
A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction . |
| [28] |
Numerical analysis of unsteady behavior of cloud cavitation around a NACA0015 foil . |
| [29] |
Numerical investigation of three-dimensional cloud cavitation with special emphasis on collapse induced shock wave dynamics . |
| [30] |
Large eddy simulation of the transition from sheet to cloud cavitation over a wedge . |
| [31] |
Efficient implicit LES method for the simulation of turbulent cavitating flows . |
| [32] |
Implicit large eddy simulation of unsteady cloud cavitation around a plane-convex hydrofoil . |
| [33] |
Large eddy simulation of unsteady cavitating flow around a highly skewed propeller in nonuniform wake . |
| [34] |
Underwater Explosion . |
| [35] |
Adiabatic Waves in Liquid-Vapor Systems . |
| [36] |
Properties of Water and Stream in SI-Units.Oldenbourg, |
| [37] |
Development and application of SST-SAS Turbulence model in the DESIBER Project.Second Symposium on Hybrid RANS-LES Methods,Corfu, |
| [38] |
Error analysis and estimation for the finite volume method with applications to fluid flows .[Ph~D~Thesis]. |
| [39] |
A pressure-based,compressible,two-phase flow finite volume method for underwater explosions . |
| [40] |
Large Eddy Simulation for Incompressible Flows . |
| [41] |
Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil . |

/
| 〈 |
|
〉 |