弹簧-金属丝网橡胶组合减振器迟滞力学模型及实验研究1)
HYSTERESIS MECHANICAL MODEL AND EXPERIMENTAL STUDY OF SPRING METAL-NET RUBBER COMBINATION DAMPER1)
中图分类号: V252.1
文献标识码: A
通讯作者:
收稿日期: 2018-05-21
网络出版日期: 2018-09-18
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
展开
摘要
金属丝网橡胶材料是一种完全由金属丝编织成的多孔复合材料,与传统螺旋卷制金属橡胶材料相比,其改进了成型工艺,剔除了制备过程中大量的手工工艺干扰,提高机械化程度,重合度更高,拥有更稳定的力学性能.由于金属丝网橡胶材料具有承载能力高、阻尼大、耐高温、耐低温、耐老化、抗油抗腐蚀等优良特性,在很多方面强于传统橡胶,多用于航空航天、船舶、军事武器等军工工业.弹簧$\!$-$\!$-$\!$金属丝网橡胶组合减振器具有可设计刚度和较高承载能力,但因其具有复杂的非线性迟滞特性,目前相关材料的本构模型还难以准确描述其力学特性.本文在弹簧$\!$-$\!$-$\!$金属丝网橡胶组合减振器静态迟滞力学性能实验的基础上,结合其干摩擦阻尼迟滞特性,提出了一种迟滞力学性能理论模型.根据减振器迟滞实验恢复力$\!$-$\!$-$\!$位移曲线特点,利用参数分离的方法将迟滞曲线分解为弹性恢复力和干摩擦阻尼力,分别建模求解等效刚度和干摩擦阻尼系数,以此建立了组合减振器理论模型,并与实验结果进行对比及进行误差分析,验证了理论模型的准确性.
关键词:
Abstract
Metal-net rubber is a porous material composed entirely of metal wire woven. Compared with the traditional spiral coiled metal rubber material, the molding technology of metal-net rubber material is improved, which eliminates a large number of manual process interferences in preparation process. The metal-net rubber material has higher mechanization degree, better coincidence and more stable mechanical properties. With the excellent characteristics of bearing capacity, large damping, high temperature resistance, low temperature resistance, aging resistance, oil and corrosion resistance, metal-net rubber material is better than traditional rubber in many ways, which is widely used in aerospace, shipbuilding, military weapons and other military industries. Spring metal-net rubber combination damper has designable stiffness and high bearing capacity. Because of its complex nonlinear hysteresis characteristics, the constitutive model of related materials is difficult to describe its mechanical properties accurately. Based on the static hysteresis mechanical performance experiment of spring metal-net rubber combination damper, combined with the hysteresis characteristics of dry friction damping, a theoretical modeling model of hysteresis mechanical properties is proposed. According to the characteristics of restoring force-displacement curve of damper hysteresis experiment, the hysteresis curve is decomposed into elastic recovery force and dry friction damping force by parameter separation method. The equivalent stiffness and dry friction damping coefficient are solved respectively by modeling to establish the theoretical model of the combination damper. By comparing with the experimental results, the error analysis is carried out to verify the accuracy of the theoretical model.
Keywords:
引 言
减振隔振材料一直是力学领域的前沿问题,各类减振材料在航空航天、船舶、交通和建筑等领域都有愈来愈广泛的应用.许多学者对其相关的隔振系统、非线性隔振、阻尼器、迟滞系统、振动控制等方面做了大量研究[1-5]. 金属丝网橡胶是一种新型的干摩擦阻尼材料,由金属丝网编织挤压成型,内部金属丝间相互勾连,在受到振动、冲击等载荷时,相互接触的金属丝相对滑移产生摩擦,消耗能量,从而起到减振耗能作用. 由于具有更强的承载能力、更强的环境适应性以及更长的使用寿命,金属丝网橡胶逐渐在航空航天、军事武器等领域替代传统橡胶成为用来减振隔振的重要新型材料.
国内外学者已经对金属橡胶材料进行了半个世纪的研究,发展至今已改善了其制备方法、成型工艺,目前,国内对金属丝网橡胶的研究主要集中在本构模型的建立、静态力学性能和各种振动、冲击、吸声特性等方面的实验测试及理论研究$^{[6\hbox{-}19]}$.在众多实验研究的基础上,理论研究相比较少,且并不统一. 在理论研究方面,其中较具代表性的研究有北京航空航天大学陈艳秋等[20]提出的以小曲梁模型建立的金属橡胶静力学非线性 本构关系;石家庄军械工程学院李宇明等[21]提出的金属橡胶的动态力学模型;白鸿柏等$^{[22\hbox{-}23]}$提出的双折线模型等金属橡胶材料的力学分析模型;姜洪源等$^{[24\hbox{-}27]}$对于动力学理论参数识别进行了研究;路纯红等$^{[28\hbox{-}29]}$建立了滞回曲线分解参数识别方法;由于国内大多数对金属橡胶的研究局限于传统制备工艺,基于此工艺彭威等[30-32]根据螺旋卷制法的金属橡胶材料提出了微弹簧和变长度曲梁力学模型;而金属丝网橡胶是利用金属丝编织成网后冷冲压成型,根据其独特的成型特点,文献[33,34,35]建立了圆环嵌套模型,详细介绍了金属丝网橡胶材料的建模思想,并对其静动力学性能进行了实验及理论研究.
由于制备工艺的显著差异,提出更为贴切金属丝网橡胶力学特性的力学模型显得尤为重要.本文在静态实验研究的基础上,结合金属丝网橡胶材料的成型参数与力学特性,提出一种新的刚度阻尼参数分离的迟滞模型描述金属丝网橡胶材料的力学特性,并进行组合金属丝网橡胶减振器静态迟滞实验研究,利用控制变量法研究了相对密度、预紧量、变形幅值、弹簧刚度对组合金属丝网橡胶减振器静态迟滞力学性能的影响,讨论所提出刚度迟滞理论模型的适用性,将其静态实验数据拟合曲线,计算迟滞模型参数,并将实验结果与理论值进行对比分析,验证模型的可靠性.
1 刚度干摩擦阻尼理论模型
1.1 金属橡胶减振器设计
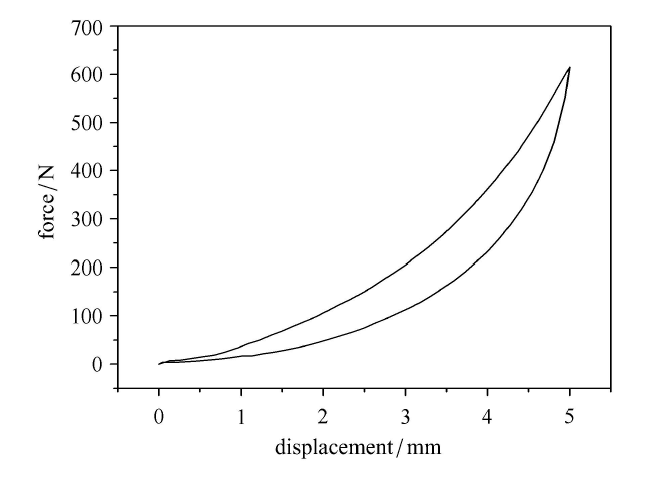
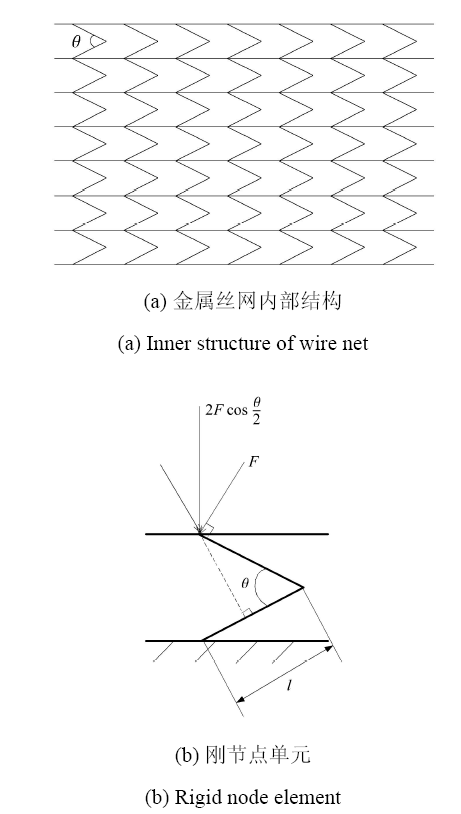
金属丝网橡胶呈多孔隙结构,多用于压缩环境,不能用于承载拉伸载荷,在受到压缩载荷后孔隙变小,试件更加致密,承载能力增强,同时经过大量实验测试可知:金属丝网橡胶材料的静压曲线呈现一定的超弹性,并且由于其干摩擦阻尼特性,静态曲线仍体现迟滞特性,其静态压缩实验曲线如 图1所示.
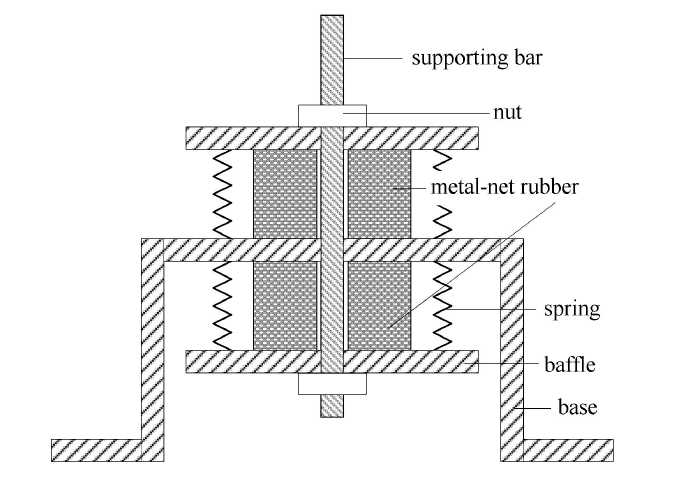
在工程实际应用中,金属丝网橡胶材料多用于在特殊环境下的大型机械、仪器仪表、管路等设备的被动减振用途,常常工作在周期性载荷作用下,设计一种新型金属丝网橡胶减振器结构,如图2所示,使其可以承受一个自由度两个方向的应力,在施加一定预紧力及一定范围的振幅前提下,能够保证减振器中金属丝网橡胶试件均在压缩载荷状态下,而减振器整体结构可承受周期性的拉压载荷,并根据其对称性可知,该减振结构在一个周期下的恢复力$\!$-$\!$-$\!$位移曲线呈中心对称,因此可采取参数分离的方法对其进行理论建模.
1.2 迟滞曲线参数分离模型
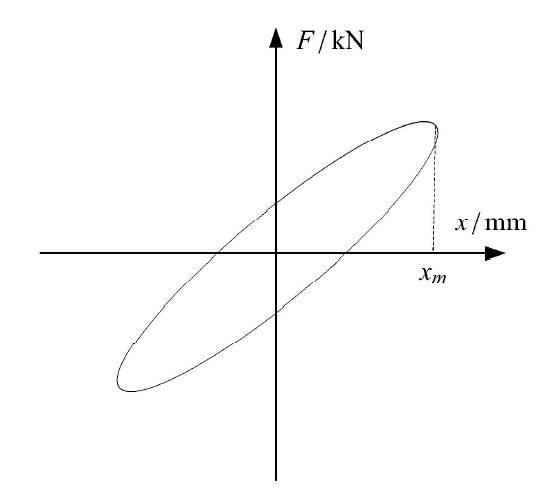
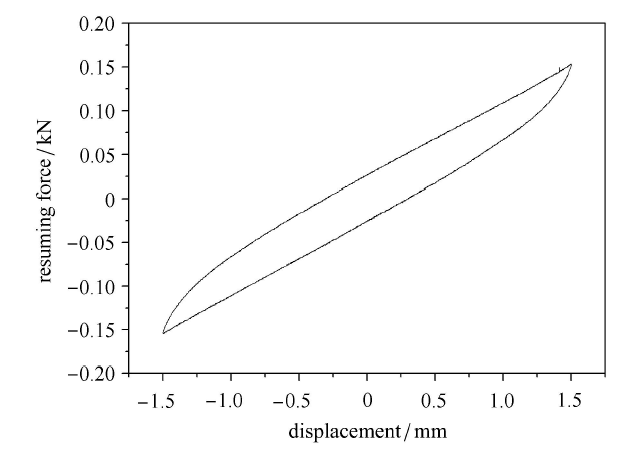
金属丝网橡胶材料干摩擦迟滞特性不同于传统橡胶的黏性阻尼,其通过受载变形后内部金属丝之间滑移储存弹性变形能并产生干摩擦做功消耗部分能量,因此在准静态迟滞实验中,金属丝网橡胶材料的加载曲线与卸载曲线不重合,表现出明显的迟滞特性,两条曲线首尾相连围成的迟滞环的面积即为过程中消耗的能量.减振结构(图2)在周期载荷作用下迟滞曲线示意图如图3所示.
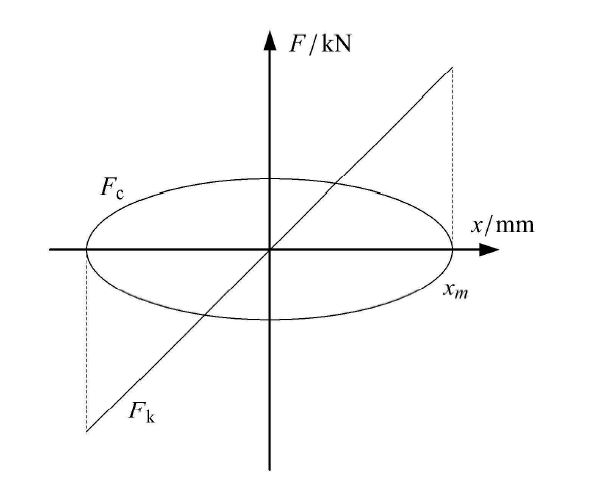
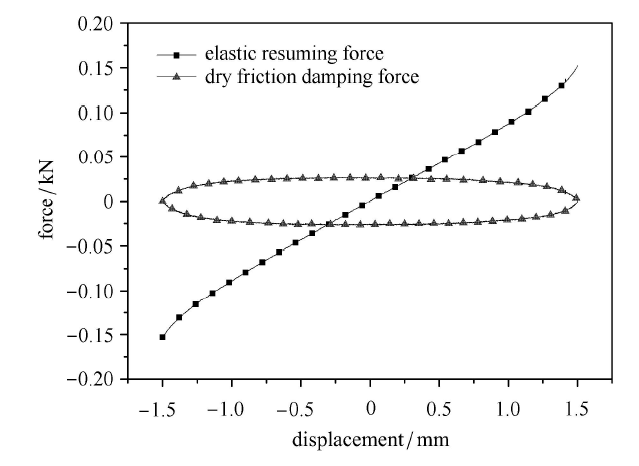
利用参数分离的思想可将图3中的曲线分解为一条斜直线和一条椭圆曲线,分解结果如图4所示.
金属丝网橡胶材料的干摩擦阻尼机理不同于传统橡胶黏弹性特性,阻尼力为变形速度无关量,因此可以得到刚度迟滞参数分离力学模型为
$$F(x) = F_{\rm k} (x) + F_{\rm c} (x) (1)$$
其中,$F_{\rm k}$代表减振结构的线性弹性恢复力,$F_{\rm c}$代表减振结构的阻尼力,表示其干摩擦阻尼迟滞特性.
$F_{\rm k}$表达式为
$$F_{\rm k} (x) = k_{\rm e} x (2)$$
其中$k_{\rm e}$为等效刚度. 设阻尼力迟滞椭圆曲线方程为式(3),可得阻尼力为
$$\dfrac{x^2}{{ a}^2} + \dfrac{F_{\rm c}^2 }{{ b}^2} = 1 (3)$$
$$F_{\rm c} = \pm { b}\sqrt {1 - \dfrac{x^2}{{ a}^2}} (4)$$
式中,$a$,$b$分别为分解出的阻尼迟滞椭圆曲线半长轴及半短轴,且$a=x_{m}$,因此将式(2)、式(4)代入式(1)可得式(5),即刚度迟滞参数分离力学模型数学表达式
$$F(x) = k_{\rm e} x\pm { b}\sqrt {1 - \dfrac{x^2}{{ a}^2}} =k_{\rm e} x\pm \dfrac{b}{x_m }\sqrt {x_m - x^2} (5)$$
2 金属橡胶减振器刚度参数识别
2.1 金属橡胶试样等效刚度
采用金属丝网橡胶材料作为减振器减振耗能材料,其制备工艺不同于传统的螺旋卷金属橡胶.
金属丝网橡胶内部金属丝排列可大致分为两类:一类为压制成型后形成的横向梁单元,在金属丝网橡胶受压缩载荷发生变形时,横向梁单元不发生变形,仅不同层横向梁单元相对距离缩小;另一类为纵向刚节点单元,这类单元是由金属丝网成型过程中金属丝接触点相互作用产生的,在金属丝网橡胶受压缩载荷后,由于金属丝内轴力很小,可以忽略,纵向刚节点单元发生弯曲变形为主要变形,因此可将金属丝网橡胶内部模型简化为如图5(a)所示结构,其中图5(b)为纵向刚节点单元示意图.由于单位网格各层之间纵向刚节点单元等效的刚度为串联关系,单位网格刚度$k_{l}$等同于单个纵向刚节点单元刚度,因此可知单位网 格刚度为
$$k_l = \dfrac{P}{\Delta x} (6)$$
图5 金属丝网橡胶内部结构简化图
Fig. 5 Simplified diagram of the internal structure of metal-net rubber
其中,$P$为单元受到的纵向压力,$\Delta x$为单元纵向变形. 利用积分法可求得其纵向位移为
$$\Delta x = 2\dfrac{Fl^3}{3EI}\cos \dfrac{\theta }{2} + 2\dfrac{F\sin ( {\pi }/{2} - \theta )l^3}{3EI}\cos\dfrac{\theta }{2} (7)$$
式中,$F$为图5(b)中所示力,$l$为单位网格金属丝长度的一半,$I$为金属丝截惯性矩,其表达式为式(8),$E$为金属丝弹性模量. 因此将式(7)、式(8)代入式(6)即可得到单位网格刚度为
$I = \frac{\pi d_{\rm s}^4 }{64} (8)$
$ k_l = {2F\cos \dfrac{\theta }{2}}\Bigg / \,\Bigg [ 2\dfrac{Fl^3}{3EI}\cos \dfrac{\theta }{2}+ 2\dfrac{F\sin (\dfrac{{ \pi }}{2} - \theta )l^3}{3EI}\cos \dfrac{\theta }{2} \Bigg] =$
$ \frac{3E\pi d_{\rm s}^4 }{64l^3(1 + \cos \theta ) } (9)$
式中,$d_{\rm s}$为金属丝直径.同时测量金属丝网长度$L$且其与金属橡胶初始相对密度成正比关系,设比例系数$A$,单位网宽$z$,因此可知金属丝网橡胶试件的刚度$k$为
$$k = \dfrac{3E\pi d_{\rm s}^4 L}{32l^3(1 + \cos \theta )z}= \dfrac{3E\pi d_{\rm s}^4 A \bar {\rho }}{32l^4(1 + \cos \theta )\cos\dfrac{\theta }{2}} (10)$$
2.2 金属橡胶试样刚度非线性
金属丝网橡胶材料的刚度存在较为明显的非线性特性,这是由于金属丝网各单位网格之间并不是简单的并联关系,由于其模具冷冲压成型方式,在其成型后各单位网格金属丝结构相互挤压、叠加造成其刚度随相对密度的变化呈非线性. 而相对密度的变化又分为两类:一类为初始相对密度的不同,因为减振结构的需求不同,常常会采用不同相对密度的金属丝网橡胶试件,因此在体积参数相同的前提下相对密度的不同导致了试件内部孔隙大小不同,即相对密度越大,试件内部孔隙越小,金属丝之间相互挤压、叠加增加致使金属丝网橡胶材料刚度呈非线性变化;另一类则是在初始相对密度固定的前提下,金属丝网橡胶试件随压缩载荷加载发生变形后,体积不断变小,试件内部孔隙变小,金属丝之间挤压、叠加程度增大,致使试件相对密度变大,造成其刚度非线性变化,且根据李宇燕等的研究可知其呈五次非线性变化关系. 不过由于所采用减振器的对称式结构,体积变化对减振器的非线性影响较小,在本文中忽略体积非线性影响.
不考虑金属丝网橡胶材料内部金属丝挤压、叠加时,由式(10)可知等效刚度与相对密度呈正比关系,不过由于初始相对密度也会改变金属丝挤压、叠加相互支撑效应造成刚度的非线性,因此采用叠加高次项的方式拟合金属丝挤压、叠加产生的刚度非线性效应,且设相对密度为0时刚度为0,故拟合的刚度多项式无常数项为
$$k = \dfrac{3E\pi d_{\rm s}^4 A}{32l^4(1 + \cos \theta )\cos \dfrac{\theta}{2}}(\bar {\rho } + A_1 \bar {\rho }^2 + A_2 \bar {\rho }^3) (11)$$
2.3 金属橡胶减振器等效刚度
由于减振器的对称式设计结构,两试件在弹性恢复力上体现出并联模式,因此在仅考虑初始相对密度影响的前提下,设金属丝网橡胶件外部的弹簧刚度为$k_{s}$,可得到金属丝网橡胶减振器等效刚度$K$如式(12)所示
$ K = 2k + k_{\rm s} = \frac{3E\pi d_{\rm s}^4 A}{16l^4(1 + \cos \theta )\cos {\theta }/{2}} \cdot (\bar {\rho } + A_1 \bar {\rho }^2 + A_2 \bar {\rho }^3) +k_{\rm s} (12)$
3 干摩擦阻尼参数识别
干摩擦迟滞阻尼是金属丝网橡胶材料的重要力学特性,是决定减振器减振耗能效果的参数. 金属丝网橡胶受载荷作用后内部金属丝摩擦消耗的能量即为恢复力$\!$-$\!$-$\!$位移迟滞曲线围成的面积,也就是分解曲线中椭圆曲线的面积,因此有
$$\Delta W = S_{\rm TY} (13)$$
式中,$\Delta W$为干摩擦耗散能量,$S_{\rm TY}$为分解曲线中椭圆曲线的面积,设曲线与$x$轴交点为$a$,与$y$轴交点为$b$. 因此其可分别表示为
$\Delta W = S_{ w} \Delta w (14)$
$S_{ TY} = \pi ab = \pi x_m b (15)$
其中,$S_{\rm w}$为金属丝网层间接触面积,$\Delta w$为单位长度金属丝网干摩擦消耗能量.由金属丝网成型工艺可知,层间接触面积为2倍金属丝网面积. 相对密度$\bar {\rho }$可表示为
$S_{ w}= 4Lh (16)$
$\bar {\rho } = \frac{\rho _{\rm MR} }{\rho _{ s} } = \frac{m}{V_0 \rho _{ s} }= \frac{\Delta m \cdot lh}{V_0 \rho _{ s} } (17)$
式中,$L$表示金属丝网长度,$h$表示金属丝网宽度, $\rho_{\rm MR}$为金属丝网橡胶试件密度,$V_{0}$为金属丝网橡胶试件初始体积, $\rho_{\rm s}$为金属丝密度,$\Delta$为单位面积金属丝网质量, $\rho_{\rm s}$, $\Delta$是丝材和丝径的相关量. 结合式(16)、式(17)可得层间接触面积为式(18),因此层间接触面积与金属丝网橡胶相对密度呈正比关系,有
$$S_{\rm w} = \dfrac{4V_0 \rho _{\rm s} }{\Delta m} \cdot \bar {\rho } (18)$$
单位长度金属丝网干摩擦消耗能量$\Delta$表达式如式(19),结合上式可得参数$b$表达式
$\Delta w = \int_0^{x_m } {\mu F_{\rm N} d x} (19)$
$b = \frac{4V_0 \rho _{ s} \mu }{\pi \Delta m} \cdot F_ {N} \bar {\rho } (20)$
其中, $\mu $ 为金属丝之间摩擦系数,$F_{N}$为单位面积金属丝网层间正应力,由于试件高度不变,其值与初始相对密度呈正比关系,故有$F_{\rm N}=B\bar {\rho}_0 $,定义干摩擦阻尼系数$c$为
$$c = \dfrac{4V_0 \rho _{\rm s} \mu B\bar {\rho }_0 }{\pi \Delta m} (21)$$
4 静态迟滞实验及理论系数识别
4.1 参数识别
组合金属丝网橡胶减振器分离参数刚度迟滞理论模型中涉及到很多金属丝网橡胶成型参数,具体包括试件初始高度$h_{0}$,内径$D$,外径$d$,金属丝弹性模量$E$,金属丝直径$d_{s}$,金属丝网长度与相对密度换算比例系数$A$,单位网宽常数$l$,金属丝密度 $\rho _{s}$,单位面积金属丝网质量$\Delta m$,金属丝网模型纵向刚节点单元夹角$\theta $,本文设$\theta =90^{\circ}$.因此各项参数数值见表1.本文只讨论初始相对密度改变造成的刚度非线性影响,在组合金属丝网橡胶减振器中忽略体积改变对刚度非线性产生的影响.对刚度公式进行计算,并进行系数拟合可得多项式系数$A_{1} \approx 0$,$A_{2} =86.77$,可得到组合金属丝网橡胶减振器等效刚度为
$$K = 0.1572(\bar {\rho } + 86.77\bar {\rho }^3) + k_{\rm s} (22)$$
同理对干摩擦阻尼系数进行计算公式为
$$c = 1.022\,2\bar {\rho }_0 (23)$$
表1 金属丝网橡胶主要成型参数
Table 1 Main forming parameters of metal-net rubber
| h0 mm | D/ mm | d/ mm | E /MPa | ds / mm | A | l Ps / mm (kg m-3 | Am/ )(kg m-2) |
|---|---|---|---|---|---|---|---|
| 20 | 40 | 11.8 | 1.93x10s | 0.23 | 0.037 | 3.5 7 930 | 571.43 |
4.2 静态实验及结果分析
通过控制变量法分别对不同相对密度试件、预紧量、加载幅值及弹簧刚度的组合金属丝网橡胶减振器进行静态迟滞力学性能实验,不同实验组别的编号及组合减振器参数如表2所示.
表2 不同实验组编号及减振器参数
Table 2 Number of different experiment groups and damper parameters
| A1 | 0.16 | 4 | 1.5 | 0 |
|---|---|---|---|---|
| A2 | 0.18 | 4 | 1.5 | 0 |
| A3 | 0.20 | 4 | 1.5 | 0 |
| A4 | 0.22 | 4 | 1.5 | 0 |
| B1 | 0.18 | 4 | 1.0 | 0 |
| B2 | 0.18 | 4 | 2.0 | 0 |
| C1 | 0.18 | 5 | 1.5 | 44.25 |
| C2 | 0.18 | 5 | 1.5 | 103.55 |
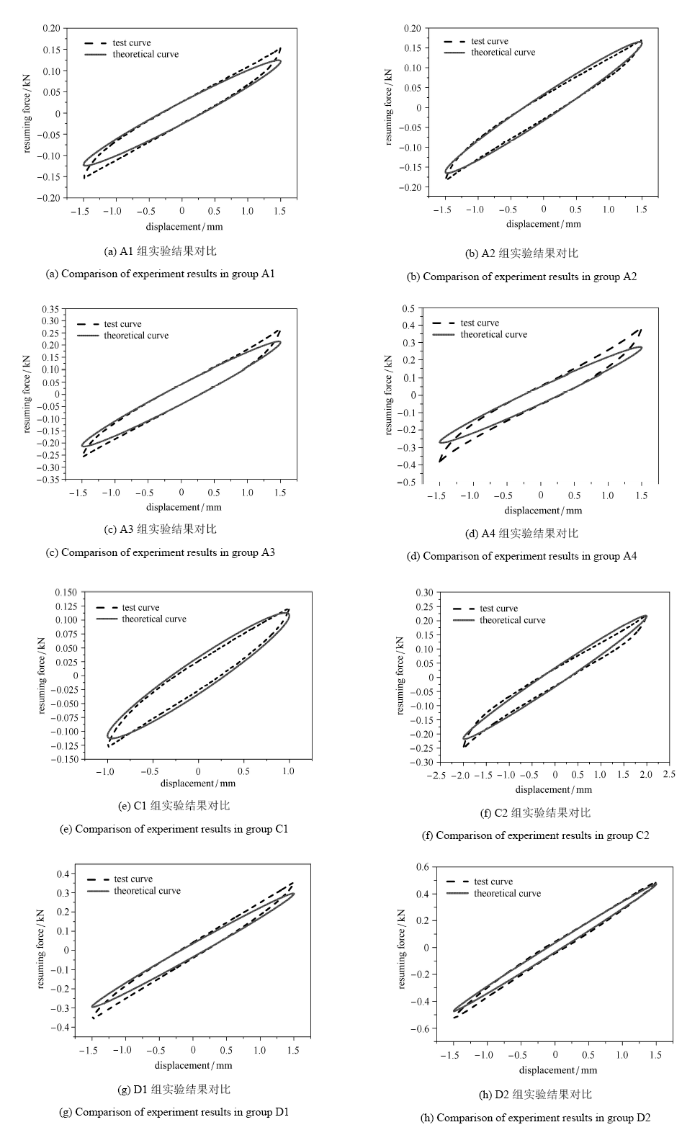
静态迟滞实验采用万能材料实验机进行加载,使用特定设计的加载转接头及固支,使其可进行拉压加载并记录数据,实验装置见图6. 加载速度为0.5\,mm/min,令减振器支撑轴轴向为加载方向.在实验开始记录数据前按照实验载荷对组合金属丝网橡胶减振器进行3次以上的反复加卸载直至恢复力$\!$-$\!$-$\!$位移曲线重合,减小实验误差. 实验得到恢复 力$\!$-$\!$-$\!$位移曲线如图7所示,图8为实验迟滞曲线分解图. 因此可计算各实验组等效刚度及干摩擦阻尼系数理论值并与实验测得参数数值进行对比如表3及表4所示.由表中数据绘制理论与实验组合金属丝网橡胶减振器静态迟滞恢复力$\!$-$\!$-$\!$位移曲线对比图像如 图9.
表3 等效刚度理论值与实验值对比结果
Table 3 Contrast results between theoretical and experimental values of equivalent stiffness
| Test group | Equivalent stiffness theoretical value/ (kNmm-1) | Equivalent stiffness test value/ (kNmm-1) | Error/ % |
|---|---|---|---|
| A1 | 0.0810 | 0.085 9 | 5.72 |
| A2 | 0.1078 | 0.0995 | 8.30 |
| A3 | 0.140 6 | 0.1441 | 2.41 |
| A4 | 0.179 8 | 0.1908 | 6.11 |
| B1 | 0.1078 | 0.1056 | 2.10 |
| B2 | 0.1078 | 0.0945 | 14.0 |
| C1 | 0.1963 | 0.2106 | 6.79 |
| C2 | 0.3149 | 0.306 7 | 2.68 |
表4 干摩擦阻尼系数理论值与实验值对比结果
Table 4 Contrast results between theoretical and experimental values of dry friction damping coefficient
| Test group | Theoretical value of dry friction damping coefficient | Test value of dry friction damping coefficient | Error/ % |
|---|---|---|---|
| A1 | 0.163 6 | 0.1638 | 0.12 |
| A2 | 0.1840 | 0.163 7 | 12.4 |
| A3 | 0.2044 | 0.2050 | 0.29 |
| A4 | 0.224 9 | 0.241 5 | 6.87 |
| B1 | 0.1840 | 0.1652 | 11.4 |
| B2 | 0.1840 | 0.1678 | 9.65 |
| C1 | 0.1958 | 0.2068 | 5.31 |
| C2 | 0.195 8 | 0.2226 | 12.0 |
图6 减振器静态迟滞特性实验装置图
Fig. 6 Experiment device for static hysteresis characteristic of shock absorber
图9 组合金属丝网橡胶减振器静态迟滞恢复力$\!$-$\!$-$\!$位移曲线理论与实验对比
Fig.9 Theoretical and experimental comparison of resuming force-displacement curves for combined metal-net rubber shock absorbers with static hysteresis
从图9中可以看出,理论求解的组合减振器静态迟滞恢复力$\!$-$\!$-$\!$位移曲线与实验测得曲线重合较好,因建立的理论模型中不讨论金属丝网橡胶试件由体积带来的刚度非线性的影响,导致在各实验组中靠近加载幅值时理论曲线存在一定误差,不过通过多组实验对比,此误差在分析组合减振器静态迟滞特性时影响小于15%,因此可利用该理论模型对弹簧$\!$-$\!$-$\!$金属丝网橡胶组合减振器进行迟滞性能预测及定量分析.
5 结 论
本文利用参数分离的思想提出了弹簧$\!$-$\!$-$\!$金属丝网橡胶组合减振器理论模型,将恢复力$\!$-$\!$-$\!$位移曲线分解为弹性恢 复力和干摩擦阻尼力的叠加.建立了金属丝网橡胶材料刚度模型,将复杂的金属丝网简化为横向梁单元与纵向刚节点单元的规律性排列,推导出金属丝网橡胶试件的等效刚度与成型参数关系公式,识别出经验参数,同时对初始相对密度、体积改变造成的金属丝网橡胶刚度非线性影响进行分析.从干摩擦耗能的角度对弹簧$\!$-$\!$-$\!$金属丝网橡胶组合减振器迟滞特性进行了理论推导,定义了其干摩擦阻尼系数,定量描述了弹簧$\!$-$\!$-$\!$金属丝网橡胶组合减振器迟滞耗能特性.
对不同相对密度试件、不同预紧量、不同加载幅值及不同组合减振器进行了静态迟滞实验,分别计算各实验组减振器减振耗能评价参数,并对比理论计算值,可得出以下结论:
(1)试件相对密度越大,组合减振器等效刚度越大,干摩擦阻尼越大,且均呈非线性变化,这是由于在其他成型参数及减振器条件相同的前提下,相对密度越大,金属丝网橡胶材料内部孔隙越小,试件更密实,导致减振器等效刚度增大. 能量耗散系数变化较小,且与相对密度无明显关系.
(2)减振器预紧量越大,其等效刚度越大,干摩擦阻尼越大,且均呈线性变化,能量耗散系数变大. 这是由于在其他成型参数及减振器条件相同的前提下,预紧量越大,金属丝网橡胶材料内部孔隙越小,试件更密实,导致减振器等效刚度增大,金属丝网层间正应力增加,使其干摩擦力变大.
(3)减振器所受加载幅值越大,其等效刚度及干摩擦阻尼基本不变,但由于幅值的不同,单位体积耗散能量及能量耗散系数均呈线性增大趋势. 可以证明在其他成型参数及减振器条件相同的前提下,加载幅值对组合金属丝网橡胶减振器的静态迟滞特性无影响,仅改变其做功多少且呈线性趋势,对其等效刚度以及干摩擦阻尼数值无明显作用.
(4)组合减振器弹簧刚度增大,其等效刚度等同于减振器等效刚度与弹簧刚度的叠加,同时其干摩擦阻尼基本不变,验证了所提出的刚度与阻尼参数分离的可靠性.
(5)通过理论计算组合减振器参数,将其值与实验测得数据进行误差计算,误差均小于15%,其中等效刚度仅有一组误差在14.03%,其余均小于10%. 干摩擦阻尼系数有三组在10%$\sim$13%之间,其余均在10%以下,建立其理论恢复力$\!$-$\!$-$\!$位移迟滞模型,与实验曲线进行对比,其重合度较好.
The authors have declared that no competing interests exist.
参考文献
| [1] |
一类分段光滑隔振系统的非线性动力学设计方法 .Nonlinear dynamics design for piecewise smooth vibration isolation system . |
| [2] |
非线性被动隔振的若干进展 .
Some recent progresses in nonlinear passive isolations of vibrations .
|
| [3] |
微振激励下黏弹性阻尼器微观链结构力学模型 .
Microscopic molecular chain structure model of viscoelastic damper under micro-vibration excitations .
|
| [4] |
随机激励下滞迟系统的稳态响应闭合解 .
The closed-form solution of steady state response of hysteretic system under stochastic excitation .
|
| [5] |
梯度波阻板的地基振动控制研究 .Analysis of ground vibration control by graded wave impeding block . |
| [6] |
基于湍流类比的金属橡胶吸声特性定量分析 .
Thrbulent like quantitative analysis on the sound absorbing characteristics of metal rubber .
|
| [7] |
金属橡胶非线性减振系统混沌特性研究 .
Chaotic characteristic of nonlinear metal rubber vibration isolation system .
|
| [8] |
金属橡胶隔振器的非线性响应特性 .
The nonlinear response characteristics of the metal rubber absorber .
|
| [9] |
金属橡胶静刚度特性及其力学模型研究 .
Research on stiffness characteristics and mechanics model of metal rubber .
|
| [10] |
金属橡胶消极减振系统复杂响应特性研究 .
Complex response characteristics of a passive metal-rubber vibration isolation system .
|
| [11] |
金属橡胶压缩性能影响因素及细观模型研究 .
Influencing factors of compression properties and mesoscopic model of metal rubber .
|
| [12] |
静载荷作用下金属橡胶失效判据及耐久性试验 .
Failure criterion and durability characteristics of metal rubber under static compression load .
|
| [13] |
压缩比对金属橡胶结构和压缩力学性能影响 .
Influence of compression ratio on microstructure and mechanical behavior of metal rubber .
|
| [14] |
常用金属橡胶静刚度理论模型比较研究 .
The comparison of common static stiffness theory model of metal rubber .
|
| [15] |
Compression mechanics of nickel-based superalloy metal rubber .
|
| [16] |
The mechanics of shape memory alloy metal rubber .
|
| [17] |
System identification methods dor metal rubber devices .
|
| [18] |
Theoretical and experimental steadystate rotordynamics of an adaptive air film damper with metal rubber .
|
| [19] |
金属橡胶材料的动态力学建模及参数辨识 .
Dynamic mechanical modeling and parameter identification of metal-rubber materials .
|
| [20] |
金属橡胶减震垫刚度特性及本构关系研究 .The investigation of the stiffness characteristics and the stress-strain relation of metal rubber . |
| [21] |
金属橡胶材料的动态力学模型 .Dynamic mechanics model of metal-rubber materials . |
| [22] |
2自由度迟滞振动系统简谐激励响应的等效线性化计算方法研究 .
et al Equivalent linearization approximate method of response computation of a two degree of freedom hysteretic vibration system under sinusoidal excitation .
|
| [23] |
干摩擦振动系统响应计算方法研究 .
Study on response computation of dry friction damped vibration system .
|
| [24] |
金属橡胶隔振器的非线性动力学 .
Nonlinear dynamics of metal rubber damper .
|
| [25] |
金属橡胶隔振器动力学模型与分析 .
Modeling and analysis of dynamic characteristics of metal rubber isolator.
|
| [26] |
Damping characteristics analysis of squeeze film damperwith metal rubber .
|
| [27] |
Turning the vibration of a rotor with shape memory alloy metal rubber supports .
|
| [28] |
金属橡胶/橡胶复合叠层耗能器试验建模与参数辨识 .
Dynamic modeling and parameter identification of metal rubber/rubber composite laminated energy dissipater .
|
| [29] |
金属橡胶/橡胶复合叠层耗能器动力学模型 .
Dynamic modeling and of metal rubber/rubber composite laminated damper .
|
| [30] |
金属橡胶恢复力的迟滞模型研究 .Research on hysteresis model of restoring force of metal rubber . |
| [31] |
金属橡胶的刚度特性和阻尼试验研究 .
An experimental study on stiffness characteristics and damping of metal rubber .
|
| [32] |
金属橡胶材料基于微弹簧组合变形的细观本构模型 .A micromechanics constitutive model of the metal rubber materials based on the radial and axial combined deformation of the microsprings . |
| [33] |
金属丝网橡胶的本构关系 .Constitutive relation of metal-net rubber . |
| [34] |
丝网编织金属橡胶的静态力学性能研究 .Research on static mechanical properties of metal rubber made of wire mesh . |
| [35] |
预紧量与振动量级对金属橡胶减振器振动特性影响研究 .Effects of preloading and vibration level on the vibration characteristics of metal rubber damper . |

/
| 〈 |
|
〉 |