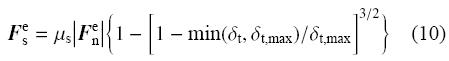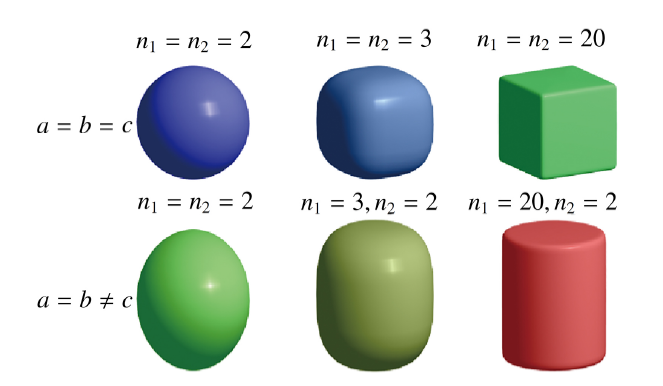引言
离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] .
颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用.
在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型.
本文通过建立超二次曲面单元描述非球形颗粒形态, 并通过非线性牛顿迭代方法精确计算单元间的接触碰撞作用. 针对非球形颗粒接触模式的复杂性, 提出考虑不同模式下基于局部接触点处等效半径函数的非线性黏弹性接触模型. 为检验超二次曲面算法及接触模型的有效性, 对球形颗粒间的法向碰撞、椭球体颗粒间斜冲击的回弹特性、圆柱体的静态堆积和椭球体的卸料过程进行离散元模拟, 并与有限元的数值结果及试验结果进行对比验证. 在此基础之上, 进一步分析了颗粒长宽比和表面尖锐度对卸料过程中颗粒流动特性的影响规律.
1 基于超二次曲面单元的离散单元方法
1.1 超二次曲面单元的构造方法
在数学意义上, 描述非球形颗粒的普遍方法是超二次曲面方程. 它允许描述凸面体和凹面体形状, 其函数形式可归纳成以下两种[35 -36 ]
式中, $a$, $b$和$c$分别表示颗粒沿三个主轴方向的半轴长, 形状参数$n_1$控制$x$$-$$z$和$y$$-$$z$ 平面的尖锐度, 而参数$n_2$则控制$x$$-$$y$平面的尖锐度. 以上两式除在表述形式上不同外并无本质差别, 当$n_1=n_2$可化简得到[37 ]
\begin{equation*}\Bigg|\dfrac{x}{a}\Bigg|^{n_2}+\Bigg|\dfrac{y}{b}\Bigg|^{n_2}+\Bigg|\dfrac{z}{c}\Bigg|^{n_2}-1=0\tag*{(3)}\end{equation*}
上式方程难以准确地描述类似柱状的颗粒形态, 因此本文以式(1)为超二次曲面标准方程. 当$n_1=n_2=2$时, 可得到球体或椭球体的颗粒单元; 当$n_1\gg 2$且$n_2=2$时, 可得到类似柱体的颗粒单元; 当$n_1=n_2\gg 2$时, 可得到类似块体的颗粒单元. 图1 为在超二次曲面方程中改变不同的半轴长及形状参数得到的不同形态颗粒单元.
图1 不同颗粒形态的超二次曲面单元
Fig.1 Super-quadric elements with various shapes
1.2 超二次曲面单元间的接触判断
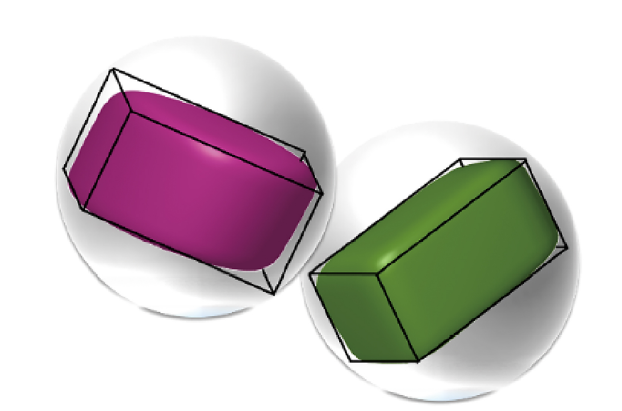
非球形颗粒间的接触搜索是影响离散元方法计算效率的关键. 在传统空间网格的基础上, 考虑颗粒长宽比及不同接触模式下的颗粒取向, 发展相应的球形包围盒和方向包围盒(oriented bounding box, OBB), 如图2 所示. 这两种方法可以有效地减少潜在接触对的数量, 提高程序的运行效率.
图2 包围球体和方向包围盒
Fig.2 Bounding spheres and oriented bounding boxes
球形包围盒作为单元间第一次接触判断, 其接触理论基于球体单元接触碰撞的处理方法. 该方法具有计算简单、运行高效等特点. 如果两球体间球心的距离小于其半径和, 则接触, 否则不接触, 其可表述为
\begin{equation*}\delta_{12}=| {X}_1-{X}_2|-r_1-r_2\begin{cases}\leqslant 0, \text{contact}\\>0, \text{separate}\end{cases}\tag*{(4)}\end{equation*}
式中, $ {X}_1$和$ {X}_2$为两个超二次曲面单元的三维形心坐标点; $r_1$和$r_2$为两个超二次曲面单元的包围球体半径, 可表示为$r_1=\sqrt{a_1^2+b_1^2+c_1^2}$和$r_1=\sqrt{a_2^2+b_2^2+c_2^2}$.
OBB作为单元间第二次接触判断, 其最大的特点是方向的任意性, 可以根据非球形颗粒的形状特点及方向选择最小尺寸的六面体[38 ] . 该方法通常基于分离轴定理, 并通过寻找潜在的分离轴来判断OBB的相交状态,进而快速剔除不可能发生碰撞的潜在接触对. 如果两个包围盒在空间向量上的投影相交, 则接触, 否则不接触.
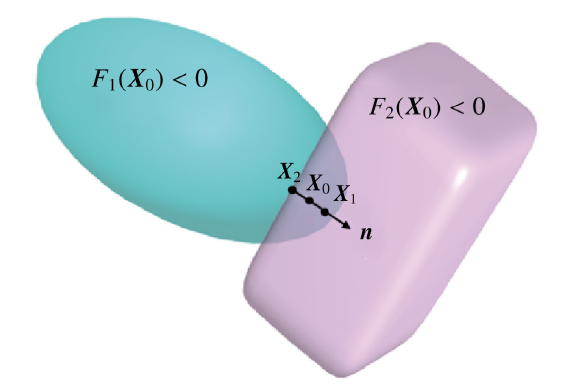
单元间精确的接触判断是接触力计算的理论基础. 这里采用非线性牛顿迭代方法, 同时将求解单元间最短距离的优化问题转化为四元非线性方程组进行数值求解, 如图3 所示.
图3 超二次曲面单元间的接触判断
Fig.3 Contact detection between super-quadric elements
考虑超二次曲面单元接触时表面法向平行且反向, 同时考虑中间点到两个单元表面的几何势能相等建立四元非线性方程组[38 -39 ]
\begin{equation*}\left.\begin{split}&\nabla F_1( X)+\mu^2\nabla F_2( X)=0\\&F_1( X)-F_2( X)=0\end{split}\right\}\tag*{(5)}\end{equation*}
式中, $F_1( X)$和$F_2( X)$分别表示单元1和2的函数方程, $\nabla F_1( X)$和$\nabla F_2( X)$ 为两个单元的导函数方程, $\mu^2$表示单元间的外法向平行且方向相反. 因此, 相应的牛顿迭代公式可表述为
\begin{equation*}\begin{split}&\begin{bmatrix}\nabla^2F_1( X)+\lambda^2\nabla^2F_2( X) & 2\mu\nabla F_2( X) \\\nabla F_1( X)-\nabla F_2( X) & 0\end{bmatrix}\begin{pmatrix}\delta X\\\delta \mu\end{pmatrix}=\\&\quad\quad\quad-\begin{bmatrix}\nabla F_1( X)+\mu^2\nabla F_2( X) F_1( X)-F_2( X)\end{bmatrix}\end{split}\tag*{(6)}\end{equation*}
式中, $\nabla^2F_1( X)$和$\nabla^2F_2( X)$分别为单元1和2的二阶导函数. 同时, ${X}^{(i+1)}={X}^{(i)}+\delta {X}$, $\mu^{(i+1)}=\mu^{(i)}+\delta\mu$. 如果计算结果${X}_0$ 同时满足$F_1( X_0)<0$和$F_2( X_0)<0$, 则表明两个单元发生接触, 接触法向定义为$ n=\nabla F_1( X_0)/\big|\big|\nabla F_1( X_0)\big|\big|$或
$ n=-\nabla F_2( X_0)/\big|\big|\nabla F_2( X_0)\big|\big|$. 在此基础之上, 单元表面点$ X_1$和$ X_2$可表示为未知参数$\alpha$和$\beta$的函数, 即: $ X_1= X_0+\alpha n$ 和$ X_2= X_0+\beta n$. 引入一元非线性牛顿迭代公式对参数$\alpha$和$\beta$进行数值求解, 即$\alpha^{(i+1)}=\alpha^{(i)}-f( X_0+\alpha^{(i)} n)/\left[\nabla f( X_0+\alpha^{(i)} n)\cdot n\right]$
$\beta^{(i+1)}=\beta^{(i)}-f( X_0+\beta^{(i)} n)/\left[\nabla f( X_0+\beta^{(i)} n)\cdot n\right]$
由此, 单元间的法向重叠量可表述为: $\delta_\text{n}= X_1- X_2$.
1.3 考虑等效曲率影响的非线性接触模型
考虑超二次曲面单元在不同接触模式下的颗粒形状及表面曲率, 可建立合理的非线性接触模型. 因此, 单元间接触力$ F$主要由法向力$ F_\text n$和切向力$ F_\text s$组成, 同时考虑法向力和切向力不通过单元形心引起的力矩$ M_\text{n}$和$ M_\text{s}$以及单元间发生相对转动时引起的附加力矩$ M_\text r$.
颗粒单元间法向接触力$ F_\text n$主要由弹性力${ F^\text{e}_\text n}$和黏滞力${ F^\text{d}_\text{n}}$组成, 可分别表述为
\begin{align*}&{ F^\text e_\text n}=4/3E^*(R^*)^{1/2}\delta_\text n^{3/2}\cdot n\tag*{(7)}\\&{ F^\text d_\text n}=C_\text n(8m^*E^*\sqrt{R^*\delta_\text n})^{1/2}\cdot v_\text n\tag*{(8)}\end{align*}
式中, $E^*=\dfrac{E}{2(1-v^2)}$, $R^*=\dfrac{R_1\cdot R_2}{R_1+R_2}$, $m^*=\dfrac{m_1\cdot m_2}{m_1+m_2}$. $E$, $v$和$C_\text n$分别为颗粒材料的弹性模型、泊松比和法向阻尼系数; $ v_\text n$为单元间法向相对速度; $R$为单元间局部接触点处的曲率半径, 可表述为: $R=1/K_\text{mean}$, 如图4 所示. 其中, $K_\text{mean}$为接触点处的平均曲率, 可表述为[40 ]
\begin{equation*}\begin{split}&K_{\rm mean}=\Bigg[\nabla F^\text T\cdot\nabla^2F\cdot\nabla F-\\&\quad\quad\big|\nabla F\big|^2\left\lgroup\dfrac{\partial^2F}{\partial x^2}+\dfrac{\partial^2F}{\partial y^2}+\dfrac{\partial^2F}{\partial z^2}\right\rgroup\Bigg]\Bigg/2\big|\nabla F\big|^3\end{split}\tag*{(9)}\end{equation*}
图4 超二次曲面单元间的非线性接触模型
Fig.4 The non-linear force model between the super-quadric elements
单元间的切向接触力$ F_\text s$借鉴球形切向接触模型的处理方法[41 ] , 主要由弹性力${ F^\text e_\text s}$和黏滞力${ F^\text d_\text s}$ 组成, 并考虑Mohr-Coulomb摩擦定律. 则切向弹性力${ F^\text e_\text s}$ 可表述为
式中, $\mu_\text s$为颗粒间的滑动摩擦系数, $\delta_\text t$为切向重叠量, $\delta_\text{t,max}=\mu_\text s(2-\upsilon)/2(1-\upsilon)\cdot\delta_\text n$.
切向黏滞力${ F^\text d_\text s}$可表述为
式中, $C_\text t$为切向黏滞系数, $ v_\text t$为单元间的切向相对速度.
对于颗粒间存在的最大重叠量, 球形颗粒的理论计算较为完备, 且与材料的屈服强度及加载和卸载过程密切相关[42 -45 ] . 对于非球形颗粒系统, 该临界值通常取决于法向接触刚度[36 ,46 ] , 并假定三维空间下接触刚度为$10^6:10^8~\text{N/m}$ 时, 其临界值为单元直径的$0.1\%:0.5\%$. 本文基于上述非球形颗粒的接触假定, 且颗粒间的平均重叠量与超二次曲面单元三个方向最小轴长的比率小于$0.5\%$.
2 超二次曲面单元接触模型和宏观特性的离散元分析及试验验证
2.1 超二次曲面单元接触模型的试验及有限元验证
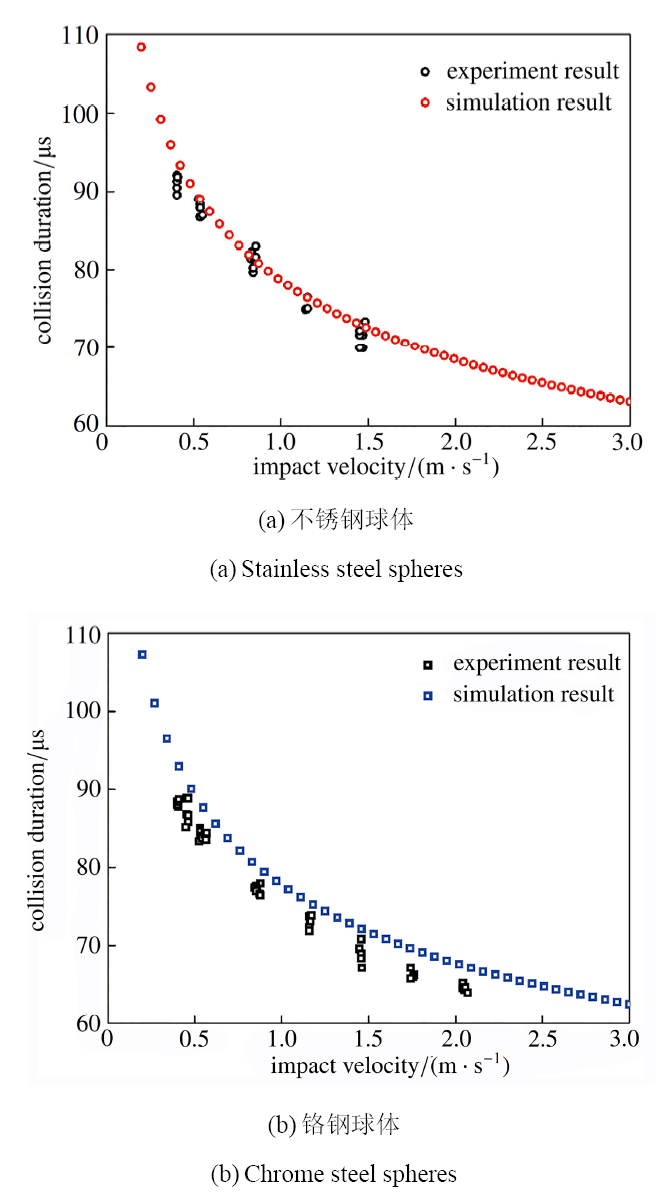
采用超二次曲面构造两个球形颗粒, 考虑不同冲击速度下颗粒间的法向碰撞[42 -43 ] , 并与文献[47 ] 中的试验结果进行对比. 超二次曲面方程中函数参数满足: $a=b=c=0.012~7~\text m$, $n_1=n_2=2$. 不锈钢球的杨氏模量为$1.93\times10^{11}~\text{Pa}$, 泊松比为0.35, 密度为$8030~\text{kg}/\text m^3$; 铬钢球的杨氏模量为$2.03\times10^{11}~\text{Pa}$, 泊松比为0.28, 密度为$7830~\text{kg}/\text m^3$. 离散元模拟中法向阻尼系数为零, 时间步长为$3\times10^{-8}~\text s$. 图5 所示为不同颗粒材料的接触时间随冲击速度的变化关系. 从图5 可以发现, 接触时间随着冲击速度的增大而延长. 此外, 对于两种材料, 模拟结果均大于实验结果. 这主要是由于在碰撞过程中未考虑颗粒间的非弹性碰撞和塑性变形, 从而导致接触时间的延长.
图5 不同法向冲击速度下接触时间变化过程的离散元模拟与实验结果[47 ] 对比
Fig.5 Comparison of contact time between DEM simulation results and experiment results[47 ] under different impact velocities
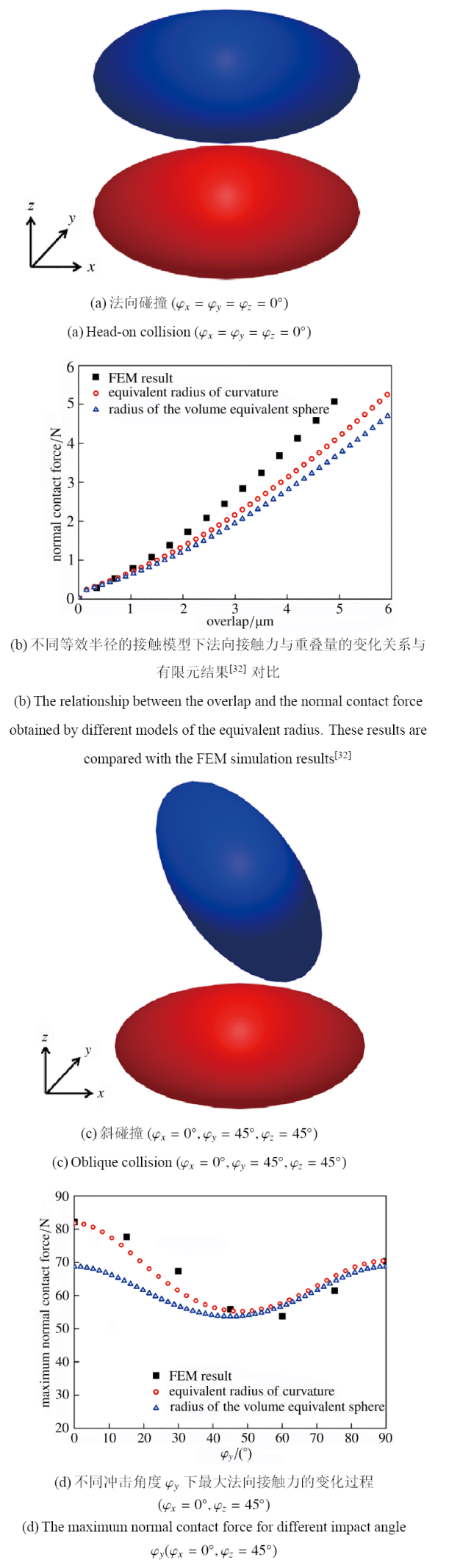
在此基础之上, 采用超二次曲面构造两个椭球体颗粒, 模拟不同冲击角度下法向接触力的变化关系, 并与文献[32 ] 中的有限元结果进行对比. 超二次曲面方程中函数参数满足: $a=0.005~\text m$, $b=c=0.002~5~\text m$, $n_1=n_2=2$. 其中, 杨氏模量为$10~\text{GPa}$, 泊松比为0.3, 密度为$2~500~\text {kg}/\text m^3$, 时间步长为$5\times 10^{-8}~\text s$. 颗粒在三个方向的转角分别为$\varphi_x$, $\varphi_y$和 $\varphi_z$, 且满足$\varphi_x=\varphi_y=\varphi_z=0^\circ$时, 颗粒实现法向碰撞, 如图6 (a) 所示. 在此过程中, 法向阻尼系数为0.02且分别采用等效曲率的非线性模型和等体积球体为等效半径的非线性模型模拟法向接触力随重叠量的变化关系, 并与有限元的计算结果[32 ] 进行对比, 如图6 (b)所示. 可以发现, 法向接触力随重叠量的增加呈现非线性增大, 同时与等体积球体为等效半径的非线性模型相比, 考虑等效曲率的接触模型与有限元结果更接近.
图6 两个椭球体碰撞的离散元分析
Fig.6 DEM analysis of two ellipsoidal collisions
此外, 通过变化$\varphi_y$进而实现不同冲击角度的碰撞过程, 如图6 (c)所示. 在此过程中, 法向阻尼系数为0.11且将不同冲击角度下最大法向接触力进行统计, 如图6 (d)所示. 可以发现, 接触模型中引入等效曲率的计算结果与有限元结果更好的吻合. 这主要是由于冲击角度变化时, 接触点位置和方向发生改变, 进而影响颗粒间的法向接触力和冲击回弹过程. 然而, 传统等体积球体为等效半径的非线性模型中未考虑接触点变化引起接触刚度的改变, 因此通过引入局部接触点处的等效曲率半径可以更加合理地反映非球形颗粒系统的运动规律.
2.2 圆柱颗粒静态堆积的离散元模拟及试验验证
采用超二次曲面单元构造250个圆柱形颗粒, 在圆柱体容器中以任意位置和角度随机产生并在重力作用下实现堆积, 同时与文献[48 ] 的试验结果进行对比. 超二次曲面方程中函数参数满足: $a=b=4~\text{mm}$, $c=2.65~\text{mm}$, $n_1=8$, $n_2=2$, 主要的离散元计算参数列于表1 中. 离散元的计算结果与试验结果[48 ] 如图7 所示. 离散元模拟的堆积高度为$(53.8\pm2.0)~\text{mm}$, 体积分数为$0.59\pm0.02$; 而试验结果的堆积高度为$(53.3\pm2.0)~\text{mm}$, 体积分数为$0.61\pm0.02$. 尽管离散元计算的数值结果与试验结果存在一定的偏差, 但在一定程度上可以很好地反映非球形颗粒材料的宏观堆积特性, 同时表明超二次曲面算法和接触模型的有效性.
图7 圆柱体静态堆积
Fig.7 Static packing of cylinders
2.3 椭球颗粒卸料过程的离散元模拟及试验验证
采用超二次曲面单元构造10 500个椭球体颗粒, 在长方体容器中考虑单元的随机位置和角度并在重力作用下实现堆积. 超二次曲面方程中函数参数满足: $2a=13.56~\text{mm}$, $2b=2c=7.19~\text{mm}$, $n_1=n_2=2$, 主要的离散元计算参数列于表2 中. 容器的长为290 mm, 宽为55 mm, 并在底部设置孔径分别为$D_0=54$和63 mm的卸料口. 当容器内颗粒无相对运动时, 卸料口打开并将离散元模拟的数值结果和文献[49 ] 中的试验结果进行对比.
图8 给出了$t=0$, 0.9, 1.8, 2.7, 3.6, 4.5, 6.6 s 时超二次曲面颗粒的流动过程和试验结果[49 ] 的对比. 颗粒在重力作用下呈现V形流动图案. 随着颗粒数量的减小, V 形图案逐渐消失并最终在容器两侧产生堆积. 图9 给出了孔径分别为54 mm和63 mm时容器内剩余颗粒百分比随时间的变化曲线. 当孔径$D_0=54~\text{mm}$时, 离散元的数值结果与试验结果基本吻合; 当$D_0=63~\text{mm}$时, 数值结果略小于试验结果. 这主要是由于当孔径变大且颗粒间的相对流速变快时, 摩擦系数和阻尼系数对颗粒流动产生显著影响.
图8 不同时刻下颗粒流动过程的试验结果[49 ] (上) 和离散元数值结果(下) 的对比
Fig.8 Snapshots of the flow pattern between experiment[49 ] (top) and DEM simulation (bottom) at different moments
图9 对于孔径$D_0=54$ 和63 mm, 漏斗内颗粒百分比随时间的变化关系
Fig.9 Percentage of particles remaining in the hopper as a function of time: $D_0=54$ and 63 mm
3 超二次曲面单元形状对卸料过程的影响
3.1 不同形态颗粒卸料过程的离散元模拟
为分析单元形态对颗粒材料流动特性的影响, 这里采用式(1)的超二次曲面方程进一步构造不同形态的颗粒单元以模拟颗粒材料的卸料过程, 同时考虑颗粒长宽比和表面尖锐度对流动速率的影响. 超二次曲面方程中函数参数满足: $D=2b=2c=4~\text{mm}$, 长宽比满足: $\sigma=2a/D$ 且$\sigma\in[0.5,1.5]$. 通过改变$\sigma$值以调整颗粒形态. 长方形卸料容器长为$11D$, 宽为$4D$, 并在宽度方向施加周期性边界条件. 同时, 底部卸料口长为$3.6D$, 宽为$4D$, 该卸料模型与文献[50 ,51 ,52 ] 类似. 颗粒密度、摩擦系数和DEM 时间步长分别为$2500~\text{kg}/\text m^{3}$, 0.1 和$1\times 10^{-6}$, 其余离散元主要计算参数列于表2 中. 采用超二次曲面单元数值模拟的不同时刻不同形状的颗粒材料卸料过程如图10 所示. 由此可发现, 不同形态的颗粒材料具有不同的流动特性, 其在最后时刻的颗粒存量具有较大差异. 下面将进一步通过改变颗粒形态来定量分析颗粒流动性能的差异.
图10 不同形态超二次曲面单元的三维卸料过程$t=0~\text s$~(左); $t=1~\text s$~(中); $t=3~\text s$~(右)
Fig.10 Simulated 3D discharging of different shaped particles $t=0~\text s$~(left); $t=1~\text s$~(middle); $t=3~\text s$~(right)
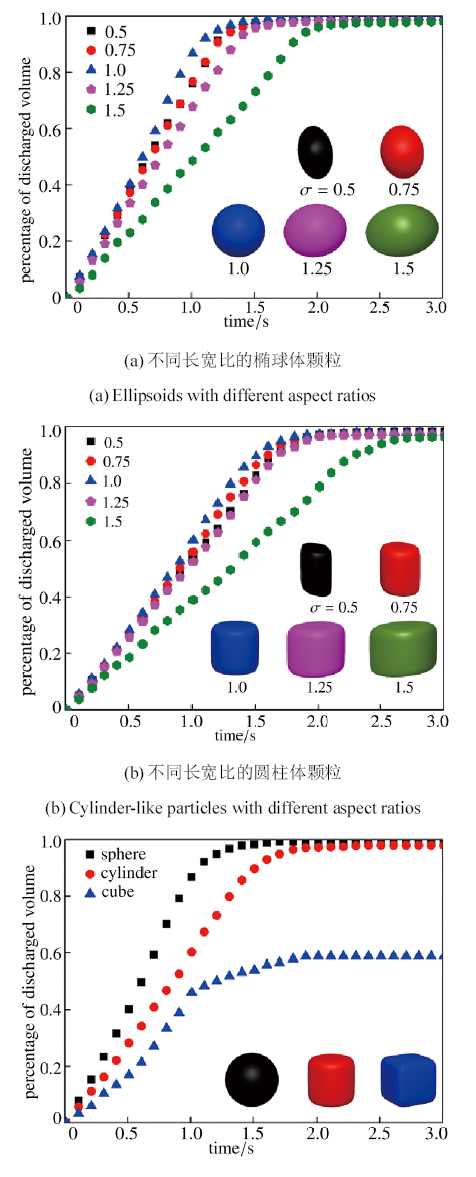
3.2 颗粒单元长宽比对流动性能的影响
为对比分析颗粒单元长宽比对卸料过程的影响, 这里分别取长宽比$\sigma=0.5$, 0.75, 1, 1.25 和1.5, 对椭球体和圆柱体颗粒的流动过程进行离散元分析, 其从漏斗中流出体积百分比随时间的变化过程如图11 所示. 此外, 图中标出了不同形态的颗粒单元及其所对应的长宽比 . 图11 (a) 和图11 (b)结果表明, 椭球体和圆柱体颗粒在长宽比$\sigma=1$时流动速率最快, 长宽比增大或减小都会使流动速率减慢. 这主要是由于长宽比增加了颗粒流动过程中的碰撞次数, 同时产生的咬合互锁效应显著影响颗粒的流动性能. 将长宽比为1的球体、圆柱体和正方体颗粒的流出体积百分比随时间的变化关系进行对比, 如图11 (c)所示. 可以发现, 球形颗粒具有最快的流动速率, 而块体颗粒的流动速率是最慢的. 对于块体颗粒, 颗粒单元间的面接触会导致颗粒在容器两侧形成堆积, 同时约有59\%的颗粒流出. 该数值小于文献[52 ] 中65\% 块体颗粒流出的试验结果. 这主要是文献[52 ] 中采用的是固定边界, 而本文采用的周期性边界条件消除了固定边界对颗粒堆积的影响, 从而使得颗粒在容器两侧更容易形成堆积以及产生更低的流出量.
图11 不同长宽比及颗粒形态影响下流出体积百分比随时间的变化关系
Fig.11 Percentage of discharged volume as a function of time for different aspect ratios and particle shapes
3.3 颗粒单元尖锐度对流动特性的影响
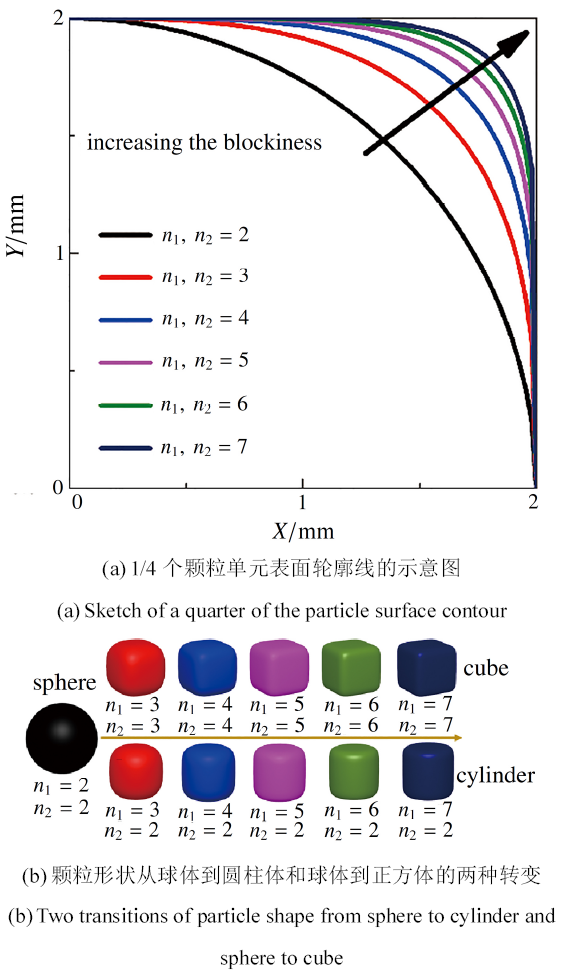
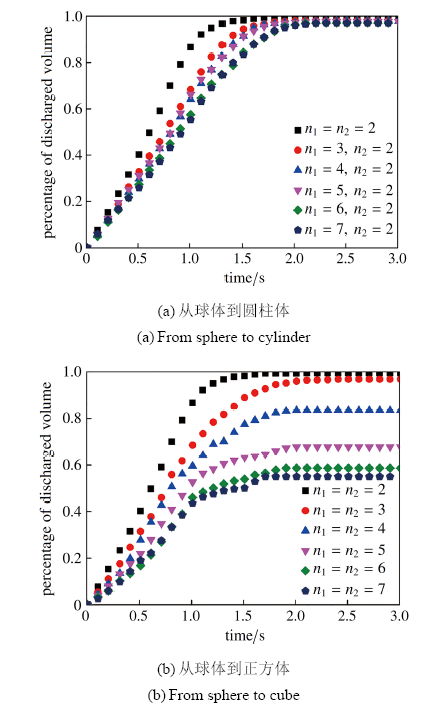
为研究颗粒表面尖锐度对颗粒材料流动特性的影响, 这里通过调整超二次曲面方程中单元的形状参数来控制颗粒的表面形态. 为显示形状参数对颗粒表面几何形态的影响, 图12 (a)给出了1/4个颗粒单元表面轮廓随形状参数$n_1$和$n_2$从2到7变化过程. 同时, 通过函数形状参数的连续变化可实现颗粒形状从球体到圆柱体、球体到正方体的两种形态转变, 如图12 (b)所示.
图12 函数形状参数对颗粒形状的影响
Fig.12 The influence of blockiness parameters on the particle shapes
按如图12 所示颗粒形态的构造方法, 对不同形态颗粒材料从漏斗中流出的卸料过程进行离散元分析. 当颗粒单元形态分别从球体到圆柱体、球体到正方体的变化过程中, 即单元表面尖锐度增加过程中, 颗粒材料从漏斗中流出体积百分比变化过程如图13 所示. 从中可以发现, 随着颗粒尖锐度的增加, 颗粒的流动速率均呈减小趋势. 然而, 不同的是从球体到圆柱体变化过程中没有出现容器两侧的堆积, 即颗粒材料均能从漏斗中全部流出; 然而, 颗粒形状从球体到正方体变化过程中, 随着尖锐度的增加, 容器两侧颗粒的堆积数量显著增加. 这主要是由于球体和圆柱体颗粒具有更加光滑的几何表面, 而正方形颗粒随着尖锐度的增加, 颗粒间的面接触可增加系统的稳定性从而降低了颗粒的流动性能.
图13 单元形态变化过程中颗粒材料从漏斗中流出体积百分数随时间的变化过程
Fig.13 The time series of percentage of discharged granular materials from hopper with the changing of particle shapes
4 结论
本文在基于连续函数包络的超二次曲面方程构造非球形颗粒形态中, 考虑了单元形状及表面曲率对接触模式的影响, 并在传统非线性接触模型的基础上引入局部接触点处的曲率半径, 发展了相应的非线性黏弹性接触模型. 为验证超二次曲面单元的数值算法和力学模型的有效性, 对圆柱体的静态堆积和椭球体的动态卸料过程进行了离散元分析, 计算值与试验结果对比良好. 由此表明基于接触点处等效曲率的超二次曲面模型能合理地描述非球形颗粒形态及运动规律. 在此基础之上, 进一步采用超二次曲面单元数值分析了颗粒长宽比和表面尖锐度对卸料过程中颗粒流动特性的影响. 计算结果表明: 球形颗粒具有最快的流动速率, 而块体颗粒的流动速率最慢. 同时, 增加或减小椭球体和圆柱体颗粒的长宽比都会增加颗粒间的碰撞次数和咬合互锁效应, 从而产生更低的流动速率. 此外, 表面尖锐度会增加颗粒间的面接触, 不利于颗粒间的相对滑动和转动, 进而增强颗粒系统的稳定性并降低颗粒的流动速率.
针对非球形颗粒间复杂的接触模式, 还需要进一步考虑恢复系数与单元间相对速度的变化关系. 同时, 在后续工作中需考虑能量准则的加载和卸载过程并建立基于超二次曲面单元的最大重叠量与塑性变形相关的理论模型.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Cundall PA Strack ODL A discrete numerical model for granular assemblies
. Géotechnique , 1979 , 29 (1 ): 47 -65
[本文引用: 1]
[2]
Zhu HP Zhou ZY Yang RY et al .Discrete particle simulation of particulate systems: A review of major applications and findings
. Chemical Engineering Science , 2008 , 63 (23 ): 5728 -5770
[本文引用: 1]
[3]
孙其诚 , 王光谦 . 颗粒流动力学及其离散模型评述
. 力学进展 , 2008 , 38 (1 ): 87 -100
(Sun Qicheng Wang Guangqian Review on granular flow dynamics and its discrete element method
. Advances in Mechanics , 2008 , 38 (1 ): 87 -100 (in Chinese))
[4]
孙其诚 , 刘晓星 , 张国华 等 . 密集颗粒物质的介观结构
. 力学进展 , 2017 , 47 (1 ): 263 -308
(Sun Qicheng Liu Xiaoxing Zhang Guohua et al .The mesoscopic structures of dense granular materials
. Advances in Mechanics , 2017 , 47 (1 ): 263 -308 (in Chinese))
[5]
季顺迎 , 孙珊珊 , 陈晓东 . 颗粒材料剪切流动状态转变的环剪试验研究
. 力学学报 , 2016 , 48 (5 ): 1061 -1072
(Ji Shunying Sun Shanshan Chen Xiaodong Shear cell test on transition of shear flow states of granular materials
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (5 ): 1061 -1072 (in Chinese))
[6]
赵子渊 , 李昱君 , 王富帅 等 . 玻璃-橡胶混合颗粒体系的弹性行为研究
. 物理学报 , 2018 , 67 (10 ): 104502
[本文引用: 1]
(Zhao Ziyuan Li Yujun Wang Fushuai et al .Elastic behavior of glass-rubber mixed particles system
. Acta Physica Sinica , 2018 , 67 (10 ): 104502 (in Chinese))
[本文引用: 1]
[7]
常晓林 , 马刚 , 周伟 等 . 颗粒形状及粒间摩擦角对堆石体宏观力学行为的影响
. 岩土工程学报 , 2012 , 34 (4 ): 646 -653
[本文引用: 1]
(Chang Xiaolin Ma Gang Zhou Wei et al .Influences of particle shape and inter-particle friction angle on macroscopic response of rockfill
. Chinese Journal of Geotechnical Engineering , 2012 , 34 (4 ): 646 -653 (in Chinese))
[本文引用: 1]
[8]
严颖 , 赵金凤 , 季顺迎 . 块石含量和空间分布对土石混合体抗剪强度影响的离散元分析
. 工程力学 , 2017 , 34 (6 ): 146 -156
(Yan Ying Zhao Jinfeng Ji Shunying Discrete element analysis of the influence of rock content and rock spatial distribution on shear strength of rock-soil mixtures
. Engineering Mechanics , 2017 , 34 (6 ): 146 -156 (in Chinese))
[9]
蒋明镜 , 张安 , 付昌 等 . 各向异性砂土宏微观特性三维离散元分析
. 岩土工程学报 , 2017 , 39 (12 ): 2165 -2172
[本文引用: 1]
(Jiang Mingjing Zhang An Fu Chang et al .Macro and micro-behaviors of anisotropy granular soils using 3D DEM simulation
. Chinese Journal of Geotechnical Engineering , 2017 , 39 (12 ): 2165 -2172 (in Chinese))
[本文引用: 1]
[10]
Lu G Third JR Müller CR Discrete element models for non-spherical particle systems: From theoretical developments to applications
. Chemical Engineering Science , 2015 , 127 : 425 -465
[本文引用: 1]
[11]
Zhong W Yu A Liu X et al .Dem/cfd-dem modelling of non-spherical particulate systems: Theoretical developments and applications
. Powder Technology , 2016 , 302 : 108 -152
[本文引用: 1]
[12]
Zhao S Zhang N Zhou X et al .Particle shape effects on fabric of granular random packing
. Powder Technology , 2017 , 310 : 175 -186
[本文引用: 1]
[13]
Gui N Yang X Tu J et al .Effect of roundness on the discharge flow of granular particles
. Powder Technology , 2017 , 314 : 140 -147
[14]
Govender N Wilke DN Pizette P et al .A study of shape non-uniformity and poly-dispersity in hopper discharge of spherical and polyhedral particle systems using the blaze-dem gpu code
. Applied Mathematics and Computation , 2017 , 319 : 318 -336
[本文引用: 1]
[15]
赵金凤 , 严颖 , 季顺迎 . 基于离散元模型的土石混合体直剪试验分析
. 固体力学学报 , 2014 , 35 (2 ): 124 -134
[本文引用: 1]
(Zhang Jinfeng Yan Ying Ji Shunying Analysis of direct shear test of soil-rock mixture based on discrete element model
. Chinese Journal of Soid Mechanics , 2014 , 35 (2 ): 124 -134 (in Chinese))
[本文引用: 1]
[16]
刘扬 , 韩燕龙 , 贾富国 等 . 椭球颗粒搅拌运动及混合特性的数值模拟研究
. 物理学报 , 2015 , 64 (11 ): 264 -271
[本文引用: 1]
(Liu Yang Han Yanlong Jia Fuguo et al .Numerical simulation on stirring motion and mixing characteristics of ellipsoid particles
. Acta Physica Sinica , 2015 , 64 (11 ): 264 -271 (in Chinese))
[本文引用: 1]
[17]
刘璐 , 龙雪 , 季顺迎 . 基于扩展多面体的离散单元法及其作用于圆桩的冰载荷计算
. 力学学报 , 2015 , 47 (6 ): 1046 -1057
[本文引用: 1]
(Liu Lu Long Xue Ji Shunying Dilated polyhedra based discrete element method and its application of ice load on cylindrical pile
. Chinese Journal of Theoretical and Applied Mechanics , 2015 , 47 (6 ): 1046 -1057 (in Chinese))
[本文引用: 1]
[18]
孙珊珊 , 严颖 , 赵春发 等 . 往复荷载下铁路道砟沉降特性的扩展多面体离散元分析
. 铁道学报 , 2015 , 37 (11 ): 89 -95
[本文引用: 1]
(Sun Shanshan Yan Ying Zhao Chunfa et al .Dilated polyhedral discrete element analysis of settlement characteristics of railway ballast under cyclic loading
. Journal of The China Railway Society , 2015 , 37 (11 ): 89 -95 (in Chinese))
[本文引用: 1]
[19]
崔泽群 , 陈友川 , 赵永志 等 . 基于超二次曲面的非球形离散单元模型研究
. 计算力学学报 , 2013 , 30 (6 ): 854 -859
[本文引用: 1]
(Cui Zequn Chen Youchuan Zhao Yongzhi et al .Study of discrete element model for non-sphere particles base on super-quadric
. Chinese Journal of Computational Mechanics , 2013 , 30 (6 ): 854 -859 (in Chinese))
[本文引用: 1]
[20]
Cleary PW Hilton JE Sinnott MD Modelling of industrial particle and multiphase flows
. Powder Technology , 2016 , 314 : 232 -252
[本文引用: 1]
[21]
Sinnott MD Cleary PW The effect of particle shape on mixing in a high shear mixer
. Computational Particle Mechanics , 2015 , 3 (4 ): 477 -504
[本文引用: 1]
[22]
Cleary PW Sinnott MD Morrison RD et al .Analysis of cone crusher performance with changes in material properties and operating conditions using dem
. Minerals Engineering , 2017 , 100 : 49 -70
[23]
王嗣强 , 季顺迎 . 基于超二次曲面的颗粒材料缓冲性能离散元分析
. 物理学报 , 2018 , 67 (9 ): 094501
[本文引用: 1]
(Wang Siqiang Ji Shunying Discrete element analysis of buffering capacity of non-spherical granular materials based on super-quadric method
. Acta Physica Sinica , 2018 , 67 (9 ): 094501 (in Chinese))
[本文引用: 1]
[24]
Lu G Third JR Müller CR Critical assessment of two approaches for evaluating contacts between super-quadric shaped particles in dem simulations
. Chemical Engineering Science , 2012 , 78 (34 ): 226 -235
[本文引用: 1]
[25]
冯春 , 李世海 , 刘晓宇 . 基于颗粒离散元法的连接键应变软化模型及其应用
. 力学学报 , 2016 , 48 (1 ): 76 -85
[本文引用: 1]
(Feng Chun Li Shihai Liu Xiaoyu Particle-dem based linked bar strain softening model and its application
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (1 ): 76 -85 (in Chinese))
[本文引用: 1]
[26]
修晨曦 , 楚锡华 . 基于微形态模型的颗粒材料中波的频散现象研究
. 力学学报 , 2018 , 50 (2 ): 315 -328
(Xiu Chenxi Chu Xihua Study on dispersion behavior and band gap in granular materials based on a micromorphic model
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (2 ): 315 -328 (in Chinese))
[27]
王增会 , 李锡夔 . 基于介观力学信息的颗粒材料损伤-愈合与塑性宏观表征
. 力学学报 , 2018 , 50 (2 ): 284 -296
[本文引用: 1]
(Wang Zenghui Li Xikui Meso-mechanically informed macroscopic characterization of damage- healing-plasticity for granular materials
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (2 ): 284 -296 (in Chinese))
[本文引用: 1]
[28]
Zhu HP Zhou ZY Yang RY et al .Discrete particle simulation of particulate systems: Theoretical developments
. Chemical Engineering Science , 2007 , 62 (13 ): 3378 -3396
[本文引用: 1]
[29]
Feng Yuntian Zhao Tingting Kato Jun et al .Stochastic discrete element modelling of rough particles-a random normal interaction law
. Chinese Journal of Computational Mechanics , 2016 , 33 (4 ): 629 -636
[30]
叶晓燕 , 王等明 , 郑晓静 . 基于应力波动的修正非局部流变模型
. 力学学报 , 2016 , 48 (1 ): 40 -47
[本文引用: 1]
(Ye Xiaoyan Wang Dengming Zheng Xiaojing A modified nonlocal rheology model for dense granular flow
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (1 ): 40 -47 (in Chinese))
[本文引用: 1]
[31]
Feng YT Han K Owen DRJ Energy-conserving contact interaction models for arbitrarily shaped discrete elements
. Computer Methods in Applied Mechanics and Engineering , 2012 , 205 (1 ): 169 -177
[本文引用: 1]
[32]
Zheng QJ Zhou ZY Yu AB Contact forces between viscoelastic ellipsoidal particles
. Powder Technology , 2013 , 248 : 25 -33
[本文引用: 3]
[33]
Lu G Third JR Müller CR Effect of wall rougheners on cross-sectional flow characteristics for non-spherical particles in a horizontal rotating cylinder
. Particuology , 2014 , 12 (1 ): 44 -53
[本文引用: 1]
[34]
Delaney GW Morrison RD Sinnott MD et al .Dem modelling of non-spherical particle breakage and flow in an industrial scale cone crusher
. Minerals Engineering , 2015 , 74 : 112 -122
[本文引用: 1]
[35]
AH B Superquadrics and angle-preserving transformations
. IEEE Comput Graph Appl , 1981 , 1 (1 ): 11 -23
[本文引用: 1]
[36]
Cleary PW Sawley ML Dem modelling of industrial granular flows: 3d case studies and the effect of particle shape on hopper discharge
. Applied Mathematical Modelling , 2002 , 26 (2 ): 89 -111
[本文引用: 2]
[37]
Cleary PW Large scale industrial DEM modeling
. Engineering Computations , 2004 , 21 (2-3-4 ): 169 -204
[本文引用: 1]
[38]
Portal R Dias J De Sousa L Contact detection between convex superquadric surfaces
. Archive of Mechanical Engineering , 2010 , 57 (2 ): 165 -186
[本文引用: 2]
[39]
Podlozhnyuk A Pirker S Kloss C Efficient implementation of superquadric particles in discrete element method within an open-source framework
. Computational Particle Mechanics , 2016 , 4 (1 ): 101 -118
[本文引用: 1]
[40]
Goldman R Curvature formulas for implicit curves and surfaces
. Computer Aided Geometric Design , 2005 , 22 (7 ): 632 -658
[本文引用: 1]
[41]
Di Renzo A Di Maio FP Comparison of contact-force models for the simulation of collisions in dem-based granular flow codes
. Chemical Engineering Science , 2004 , 59 (3 ): 525 -541
[本文引用: 1]
[42]
Zhou Y A theoretical model of collision between soft-spheres with Hertz elastic loading and nonlinear plastic unloading
. Theoretical & Applied Mechanics Letters , 2011 , 1 (4 ): 34 -39
[本文引用: 2]
[43]
Zhou Y Modeling of softsphere normal collisions with characteristic of coefficient of restitution dependent on impact velocity
. Theoretical & Applied Mechanics Letters , 2013 , 3 (2 ): 16 -20
[本文引用: 1]
[44]
Wojtkowski M Pecen J Horabik J et al .Rapeseed impact against a flat surface: Physical testing and DEM simulation with two contact models
. Powder Technology , 2010 , 198 (1 ): 61 -68 .
[45]
Dubey A Sarkar A Ierapetritou M et al .Computational Approaches for Studying the Granular Dynamics of Continuous Blending Processes, 1 - DEM Based Methods
. Macromolecular Materials & Engineering , 2011 , 296 (3-4 ): 290 -307
[本文引用: 1]
[46]
Sinnott MD Cleary PW Vibration-induced arching in a deep granular bed
. Granular Matter , 2009 , 11 (5 ): 345 -364
[本文引用: 1]
[47]
Stevens AB Hrenya CM Comparison of soft-sphere models to measurements of collision properties during normal impacts
. Powder Technology , 2005 , 154 (2 ): 99 -109
[本文引用: 3]
[48]
Kodam M Bharadwaj R Curtis J et al .Cylindrical object contact detection for use in discrete element method simulations, part ii—experimental validation
. Chemical Engineering Science , 2010 , 65 (22 ): 5863 -5871
[本文引用: 2]
[49]
Liu SD Zhou ZY Zou RP et al .Flow characteristics and discharge rate of ellipsoidal particles in a flat bottom hopper
. Powder Technology , 2014 , 253 : 70 -79
[本文引用: 4]
[50]
Langston PA Al-Awamleh MA Fraige FY et al .Distinct element modelling of non-spherical frictionless particle flow
. Chemical Engineering Science , 2004 , 59 (2 ): 425 -435
[本文引用: 1]
[51]
Dong K Wang C Yu A A novel method based on orientation discretization for discrete element modeling of non-spherical particles
. Chemical Engineering Science , 2015 , 126 : 500 -516
[本文引用: 1]
[52]
Fraige FY Langston PA Chen GZ Distinct element modelling of cubic particle packing and flow
. Powder Technology , 2008 , 186 (3 ): 224 -240
[本文引用: 3]
A discrete numerical model for granular assemblies
1
1979
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
Discrete particle simulation of particulate systems: A review of major applications and findings
1
2008
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
玻璃-橡胶混合颗粒体系的弹性行为研究
1
2018
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
玻璃-橡胶混合颗粒体系的弹性行为研究
1
2018
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
颗粒形状及粒间摩擦角对堆石体宏观力学行为的影响
1
2012
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
颗粒形状及粒间摩擦角对堆石体宏观力学行为的影响
1
2012
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
块石含量和空间分布对土石混合体抗剪强度影响的离散元分析
2017
块石含量和空间分布对土石混合体抗剪强度影响的离散元分析
2017
各向异性砂土宏微观特性三维离散元分析
1
2017
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
各向异性砂土宏微观特性三维离散元分析
1
2017
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
Discrete element models for non-spherical particle systems: From theoretical developments to applications
1
2015
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
Dem/cfd-dem modelling of non-spherical particulate systems: Theoretical developments and applications
1
2016
... 离散单元法(discrete element method, DEM)由Cundall和Strack提出后经近四十年的发展已成为一种模拟颗粒材料力学特性并解决相关工程问题的重要工具[1 ] . 该方法最早采用二维圆盘或三维球体的规则单元, 其具有计算简单和运行高效等特点[2 -6 ] . 然而, 自然界或工业中普遍是以非球形颗粒组成的复杂体系. 球形与非球形颗粒在单元排列、动力过程和运动形态等方面均有很大差异, 同时非球形颗粒间的多碰撞、低流动性和咬合互锁效应显著影响颗粒介质的宏观力学性质[7 -9 ] . 因此, 从球形颗粒系统得到的颗粒宏细观力学性质不能简单地推广到非球形颗粒系统[10 -11 ] . ...
Particle shape effects on fabric of granular random packing
1
2017
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
Effect of roundness on the discharge flow of granular particles
2017
A study of shape non-uniformity and poly-dispersity in hopper discharge of spherical and polyhedral particle systems using the blaze-dem gpu code
1
2017
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于离散元模型的土石混合体直剪试验分析
1
2014
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于离散元模型的土石混合体直剪试验分析
1
2014
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
椭球颗粒搅拌运动及混合特性的数值模拟研究
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
椭球颗粒搅拌运动及混合特性的数值模拟研究
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于扩展多面体的离散单元法及其作用于圆桩的冰载荷计算
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于扩展多面体的离散单元法及其作用于圆桩的冰载荷计算
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
往复荷载下铁路道砟沉降特性的扩展多面体离散元分析
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
往复荷载下铁路道砟沉降特性的扩展多面体离散元分析
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于超二次曲面的非球形离散单元模型研究
1
2013
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于超二次曲面的非球形离散单元模型研究
1
2013
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
Modelling of industrial particle and multiphase flows
1
2016
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
The effect of particle shape on mixing in a high shear mixer
1
2015
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
Analysis of cone crusher performance with changes in material properties and operating conditions using dem
2017
基于超二次曲面的颗粒材料缓冲性能离散元分析
1
2018
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于超二次曲面的颗粒材料缓冲性能离散元分析
1
2018
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
Critical assessment of two approaches for evaluating contacts between super-quadric shaped particles in dem simulations
1
2012
... 颗粒形状对微观-介观-宏观三个空间结构尺度下颗粒材料动力学行为的影响引起广泛关注[12 -14 ] . 为合理地描述具有非规则形态的颗粒材料, 基于规则颗粒的粘结和镶嵌单元[15 -16 ] 、基于Minknowski Sum方法的扩展多面体单元[17 -18 ] 、基于连续函数包络的超二次曲面单元[19 -20 ] 等不同的非球形单元构造方法不断发展和完善. 其中, 超二次曲面单元能更加真实地描述自然界中约80% 的颗粒几何形状, 同时可以容易地改变函数中三个主轴方向的半轴长及两个形状参数, 进而控制颗粒的长宽比和表面尖锐度[21 -23 ] . 近年来, 基于离散函数包络的超二次曲面方法得到快速发展, 但在保证足够精度下非球形颗粒表面离散点的自适应分布及如何快速搜索接触点等问题尚需进一步研究[24 ] . 为此, 本文将在连续函数包络基础上建立超二次曲面单元, 将单元间的接触判断问题转化为求解单元间距离最小值的优化问题, 并通过非线性牛顿迭代方法计算单元间的接触碰撞作用. ...
基于颗粒离散元法的连接键应变软化模型及其应用
1
2016
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
基于颗粒离散元法的连接键应变软化模型及其应用
1
2016
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
基于微形态模型的颗粒材料中波的频散现象研究
2018
基于微形态模型的颗粒材料中波的频散现象研究
2018
基于介观力学信息的颗粒材料损伤-愈合与塑性宏观表征
1
2018
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
基于介观力学信息的颗粒材料损伤-愈合与塑性宏观表征
1
2018
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
Discrete particle simulation of particulate systems: Theoretical developments
1
2007
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
Stochastic discrete element modelling of rough particles-a random normal interaction law
2016
基于应力波动的修正非局部流变模型
1
2016
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
基于应力波动的修正非局部流变模型
1
2016
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
Energy-conserving contact interaction models for arbitrarily shaped discrete elements
1
2012
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
Contact forces between viscoelastic ellipsoidal particles
3
2013
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
... 在此基础之上, 采用超二次曲面构造两个椭球体颗粒, 模拟不同冲击角度下法向接触力的变化关系, 并与文献[32 ] 中的有限元结果进行对比. 超二次曲面方程中函数参数满足: $a=0.005~\text m$, $b=c=0.002~5~\text m$, $n_1=n_2=2$. 其中, 杨氏模量为$10~\text{GPa}$, 泊松比为0.3, 密度为$2~500~\text {kg}/\text m^3$, 时间步长为$5\times 10^{-8}~\text s$. 颗粒在三个方向的转角分别为$\varphi_x$, $\varphi_y$和 $\varphi_z$, 且满足$\varphi_x=\varphi_y=\varphi_z=0^\circ$时, 颗粒实现法向碰撞, 如图6 (a) 所示. 在此过程中, 法向阻尼系数为0.02且分别采用等效曲率的非线性模型和等体积球体为等效半径的非线性模型模拟法向接触力随重叠量的变化关系, 并与有限元的计算结果[32 ] 进行对比, 如图6 (b)所示. 可以发现, 法向接触力随重叠量的增加呈现非线性增大, 同时与等体积球体为等效半径的非线性模型相比, 考虑等效曲率的接触模型与有限元结果更接近. ...
... [32 ]进行对比, 如图6 (b)所示. 可以发现, 法向接触力随重叠量的增加呈现非线性增大, 同时与等体积球体为等效半径的非线性模型相比, 考虑等效曲率的接触模型与有限元结果更接近. ...
Effect of wall rougheners on cross-sectional flow characteristics for non-spherical particles in a horizontal rotating cylinder
1
2014
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
Dem modelling of non-spherical particle breakage and flow in an industrial scale cone crusher
1
2015
... 在离散元方法中, 二维圆盘或三维球形单元间接触力模型得到不断完善[25 -27 ] , 包括线弹簧模型和Hertz-Mindlin非线性模型等[28 -30 ] . 然而, 这些接触力模型并不适用于非球形颗粒形态. 近年来, 对于任意形状的能量保守理论开展了相关的研究, 但重叠体积的精确计算导致计算效率降低, 不易于大规模并行[31 ] . 此外, 针对椭球体颗粒的构造特点, 在球体非线性接触理论基础上考虑表面曲率进行修正, 并与有限元的数值结果较好地吻合[32 ] . 然而, 将该方法扩展到超二次曲面单元则变得十分复杂, 无法精确计算不同形状及尖锐度下的修正参数. 目前针对超二次曲面单元间接触力的计算基本采用线性近似接触模型, 接触刚度通常采用经验值, 难以准确反映非球形颗粒不同接触模式下单元形状和局部曲率, 并在很大程度上影响了计算精度[33 -34 ] . 为此, 本文将在球体的赫兹接触模型和椭球体表面曲率的接触模型之上, 考虑超二次曲面单元在不同接触模式下局部接触点处的等效曲率半径进而建立相对合理的非线性接触模型. ...
Superquadrics and angle-preserving transformations
1
1981
... 在数学意义上, 描述非球形颗粒的普遍方法是超二次曲面方程. 它允许描述凸面体和凹面体形状, 其函数形式可归纳成以下两种[35 -36 ] ...
Dem modelling of industrial granular flows: 3d case studies and the effect of particle shape on hopper discharge
2
2002
... 在数学意义上, 描述非球形颗粒的普遍方法是超二次曲面方程. 它允许描述凸面体和凹面体形状, 其函数形式可归纳成以下两种[35 -36 ] ...
... 对于颗粒间存在的最大重叠量, 球形颗粒的理论计算较为完备, 且与材料的屈服强度及加载和卸载过程密切相关[42 -45 ] . 对于非球形颗粒系统, 该临界值通常取决于法向接触刚度[36 ,46 ] , 并假定三维空间下接触刚度为$10^6:10^8~\text{N/m}$ 时, 其临界值为单元直径的$0.1\%:0.5\%$. 本文基于上述非球形颗粒的接触假定, 且颗粒间的平均重叠量与超二次曲面单元三个方向最小轴长的比率小于$0.5\%$. ...
Large scale industrial DEM modeling
1
2004
... 式中, $a$, $b$和$c$分别表示颗粒沿三个主轴方向的半轴长, 形状参数$n_1$控制$x$$-$$z$和$y$$-$$z$ 平面的尖锐度, 而参数$n_2$则控制$x$$-$$y$平面的尖锐度. 以上两式除在表述形式上不同外并无本质差别, 当$n_1=n_2$可化简得到[37 ] ...
Contact detection between convex superquadric surfaces
2
2010
... OBB作为单元间第二次接触判断, 其最大的特点是方向的任意性, 可以根据非球形颗粒的形状特点及方向选择最小尺寸的六面体[38 ] . 该方法通常基于分离轴定理, 并通过寻找潜在的分离轴来判断OBB的相交状态,进而快速剔除不可能发生碰撞的潜在接触对. 如果两个包围盒在空间向量上的投影相交, 则接触, 否则不接触. ...
... 考虑超二次曲面单元接触时表面法向平行且反向, 同时考虑中间点到两个单元表面的几何势能相等建立四元非线性方程组[38 -39 ] ...
Efficient implementation of superquadric particles in discrete element method within an open-source framework
1
2016
... 考虑超二次曲面单元接触时表面法向平行且反向, 同时考虑中间点到两个单元表面的几何势能相等建立四元非线性方程组[38 -39 ] ...
Curvature formulas for implicit curves and surfaces
1
2005
... 式中, $E^*=\dfrac{E}{2(1-v^2)}$, $R^*=\dfrac{R_1\cdot R_2}{R_1+R_2}$, $m^*=\dfrac{m_1\cdot m_2}{m_1+m_2}$. $E$, $v$和$C_\text n$分别为颗粒材料的弹性模型、泊松比和法向阻尼系数; $ v_\text n$为单元间法向相对速度; $R$为单元间局部接触点处的曲率半径, 可表述为: $R=1/K_\text{mean}$, 如图4 所示. 其中, $K_\text{mean}$为接触点处的平均曲率, 可表述为[40 ] ...
Comparison of contact-force models for the simulation of collisions in dem-based granular flow codes
1
2004
... 单元间的切向接触力$ F_\text s$借鉴球形切向接触模型的处理方法[41 ] , 主要由弹性力${ F^\text e_\text s}$和黏滞力${ F^\text d_\text s}$ 组成, 并考虑Mohr-Coulomb摩擦定律. 则切向弹性力${ F^\text e_\text s}$ 可表述为 ...
A theoretical model of collision between soft-spheres with Hertz elastic loading and nonlinear plastic unloading
2
2011
... 对于颗粒间存在的最大重叠量, 球形颗粒的理论计算较为完备, 且与材料的屈服强度及加载和卸载过程密切相关[42 -45 ] . 对于非球形颗粒系统, 该临界值通常取决于法向接触刚度[36 ,46 ] , 并假定三维空间下接触刚度为$10^6:10^8~\text{N/m}$ 时, 其临界值为单元直径的$0.1\%:0.5\%$. 本文基于上述非球形颗粒的接触假定, 且颗粒间的平均重叠量与超二次曲面单元三个方向最小轴长的比率小于$0.5\%$. ...
... 采用超二次曲面构造两个球形颗粒, 考虑不同冲击速度下颗粒间的法向碰撞[42 -43 ] , 并与文献[47 ] 中的试验结果进行对比. 超二次曲面方程中函数参数满足: $a=b=c=0.012~7~\text m$, $n_1=n_2=2$. 不锈钢球的杨氏模量为$1.93\times10^{11}~\text{Pa}$, 泊松比为0.35, 密度为$8030~\text{kg}/\text m^3$; 铬钢球的杨氏模量为$2.03\times10^{11}~\text{Pa}$, 泊松比为0.28, 密度为$7830~\text{kg}/\text m^3$. 离散元模拟中法向阻尼系数为零, 时间步长为$3\times10^{-8}~\text s$. 图5 所示为不同颗粒材料的接触时间随冲击速度的变化关系. 从图5 可以发现, 接触时间随着冲击速度的增大而延长. 此外, 对于两种材料, 模拟结果均大于实验结果. 这主要是由于在碰撞过程中未考虑颗粒间的非弹性碰撞和塑性变形, 从而导致接触时间的延长. ...
Modeling of softsphere normal collisions with characteristic of coefficient of restitution dependent on impact velocity
1
2013
... 采用超二次曲面构造两个球形颗粒, 考虑不同冲击速度下颗粒间的法向碰撞[42 -43 ] , 并与文献[47 ] 中的试验结果进行对比. 超二次曲面方程中函数参数满足: $a=b=c=0.012~7~\text m$, $n_1=n_2=2$. 不锈钢球的杨氏模量为$1.93\times10^{11}~\text{Pa}$, 泊松比为0.35, 密度为$8030~\text{kg}/\text m^3$; 铬钢球的杨氏模量为$2.03\times10^{11}~\text{Pa}$, 泊松比为0.28, 密度为$7830~\text{kg}/\text m^3$. 离散元模拟中法向阻尼系数为零, 时间步长为$3\times10^{-8}~\text s$. 图5 所示为不同颗粒材料的接触时间随冲击速度的变化关系. 从图5 可以发现, 接触时间随着冲击速度的增大而延长. 此外, 对于两种材料, 模拟结果均大于实验结果. 这主要是由于在碰撞过程中未考虑颗粒间的非弹性碰撞和塑性变形, 从而导致接触时间的延长. ...
Rapeseed impact against a flat surface: Physical testing and DEM simulation with two contact models
2010
Computational Approaches for Studying the Granular Dynamics of Continuous Blending Processes, 1 - DEM Based Methods
1
2011
... 对于颗粒间存在的最大重叠量, 球形颗粒的理论计算较为完备, 且与材料的屈服强度及加载和卸载过程密切相关[42 -45 ] . 对于非球形颗粒系统, 该临界值通常取决于法向接触刚度[36 ,46 ] , 并假定三维空间下接触刚度为$10^6:10^8~\text{N/m}$ 时, 其临界值为单元直径的$0.1\%:0.5\%$. 本文基于上述非球形颗粒的接触假定, 且颗粒间的平均重叠量与超二次曲面单元三个方向最小轴长的比率小于$0.5\%$. ...
Vibration-induced arching in a deep granular bed
1
2009
... 对于颗粒间存在的最大重叠量, 球形颗粒的理论计算较为完备, 且与材料的屈服强度及加载和卸载过程密切相关[42 -45 ] . 对于非球形颗粒系统, 该临界值通常取决于法向接触刚度[36 ,46 ] , 并假定三维空间下接触刚度为$10^6:10^8~\text{N/m}$ 时, 其临界值为单元直径的$0.1\%:0.5\%$. 本文基于上述非球形颗粒的接触假定, 且颗粒间的平均重叠量与超二次曲面单元三个方向最小轴长的比率小于$0.5\%$. ...
Comparison of soft-sphere models to measurements of collision properties during normal impacts
3
2005
... 采用超二次曲面构造两个球形颗粒, 考虑不同冲击速度下颗粒间的法向碰撞[42 -43 ] , 并与文献[47 ] 中的试验结果进行对比. 超二次曲面方程中函数参数满足: $a=b=c=0.012~7~\text m$, $n_1=n_2=2$. 不锈钢球的杨氏模量为$1.93\times10^{11}~\text{Pa}$, 泊松比为0.35, 密度为$8030~\text{kg}/\text m^3$; 铬钢球的杨氏模量为$2.03\times10^{11}~\text{Pa}$, 泊松比为0.28, 密度为$7830~\text{kg}/\text m^3$. 离散元模拟中法向阻尼系数为零, 时间步长为$3\times10^{-8}~\text s$. 图5 所示为不同颗粒材料的接触时间随冲击速度的变化关系. 从图5 可以发现, 接触时间随着冲击速度的增大而延长. 此外, 对于两种材料, 模拟结果均大于实验结果. 这主要是由于在碰撞过程中未考虑颗粒间的非弹性碰撞和塑性变形, 从而导致接触时间的延长. ...
... 不同法向冲击速度下接触时间变化过程的离散元模拟与实验结果[47 ] 对比 ...
... Comparison of contact time between DEM simulation results and experiment results[47 ] under different impact velocities ...
Cylindrical object contact detection for use in discrete element method simulations, part ii—experimental validation
2
2010
... 采用超二次曲面单元构造250个圆柱形颗粒, 在圆柱体容器中以任意位置和角度随机产生并在重力作用下实现堆积, 同时与文献[48 ] 的试验结果进行对比. 超二次曲面方程中函数参数满足: $a=b=4~\text{mm}$, $c=2.65~\text{mm}$, $n_1=8$, $n_2=2$, 主要的离散元计算参数列于表1 中. 离散元的计算结果与试验结果[48 ] 如图7 所示. 离散元模拟的堆积高度为$(53.8\pm2.0)~\text{mm}$, 体积分数为$0.59\pm0.02$; 而试验结果的堆积高度为$(53.3\pm2.0)~\text{mm}$, 体积分数为$0.61\pm0.02$. 尽管离散元计算的数值结果与试验结果存在一定的偏差, 但在一定程度上可以很好地反映非球形颗粒材料的宏观堆积特性, 同时表明超二次曲面算法和接触模型的有效性. ...
... [48 ] 如图7 所示. 离散元模拟的堆积高度为$(53.8\pm2.0)~\text{mm}$, 体积分数为$0.59\pm0.02$; 而试验结果的堆积高度为$(53.3\pm2.0)~\text{mm}$, 体积分数为$0.61\pm0.02$. 尽管离散元计算的数值结果与试验结果存在一定的偏差, 但在一定程度上可以很好地反映非球形颗粒材料的宏观堆积特性, 同时表明超二次曲面算法和接触模型的有效性. ...
Flow characteristics and discharge rate of ellipsoidal particles in a flat bottom hopper
4
2014
... 采用超二次曲面单元构造10 500个椭球体颗粒, 在长方体容器中考虑单元的随机位置和角度并在重力作用下实现堆积. 超二次曲面方程中函数参数满足: $2a=13.56~\text{mm}$, $2b=2c=7.19~\text{mm}$, $n_1=n_2=2$, 主要的离散元计算参数列于表2 中. 容器的长为290 mm, 宽为55 mm, 并在底部设置孔径分别为$D_0=54$和63 mm的卸料口. 当容器内颗粒无相对运动时, 卸料口打开并将离散元模拟的数值结果和文献[49 ] 中的试验结果进行对比. ...
... 图8 给出了$t=0$, 0.9, 1.8, 2.7, 3.6, 4.5, 6.6 s 时超二次曲面颗粒的流动过程和试验结果[49 ] 的对比. 颗粒在重力作用下呈现V形流动图案. 随着颗粒数量的减小, V 形图案逐渐消失并最终在容器两侧产生堆积. 图9 给出了孔径分别为54 mm和63 mm时容器内剩余颗粒百分比随时间的变化曲线. 当孔径$D_0=54~\text{mm}$时, 离散元的数值结果与试验结果基本吻合; 当$D_0=63~\text{mm}$时, 数值结果略小于试验结果. 这主要是由于当孔径变大且颗粒间的相对流速变快时, 摩擦系数和阻尼系数对颗粒流动产生显著影响. ...
... 不同时刻下颗粒流动过程的试验结果[49 ] (上) 和离散元数值结果(下) 的对比 ...
... Snapshots of the flow pattern between experiment[49 ] (top) and DEM simulation (bottom) at different moments ...
Distinct element modelling of non-spherical frictionless particle flow
1
2004
... 为分析单元形态对颗粒材料流动特性的影响, 这里采用式(1)的超二次曲面方程进一步构造不同形态的颗粒单元以模拟颗粒材料的卸料过程, 同时考虑颗粒长宽比和表面尖锐度对流动速率的影响. 超二次曲面方程中函数参数满足: $D=2b=2c=4~\text{mm}$, 长宽比满足: $\sigma=2a/D$ 且$\sigma\in[0.5,1.5]$. 通过改变$\sigma$值以调整颗粒形态. 长方形卸料容器长为$11D$, 宽为$4D$, 并在宽度方向施加周期性边界条件. 同时, 底部卸料口长为$3.6D$, 宽为$4D$, 该卸料模型与文献[50 ,51 ,52 ] 类似. 颗粒密度、摩擦系数和DEM 时间步长分别为$2500~\text{kg}/\text m^{3}$, 0.1 和$1\times 10^{-6}$, 其余离散元主要计算参数列于表2 中. 采用超二次曲面单元数值模拟的不同时刻不同形状的颗粒材料卸料过程如图10 所示. 由此可发现, 不同形态的颗粒材料具有不同的流动特性, 其在最后时刻的颗粒存量具有较大差异. 下面将进一步通过改变颗粒形态来定量分析颗粒流动性能的差异. ...
A novel method based on orientation discretization for discrete element modeling of non-spherical particles
1
2015
... 为分析单元形态对颗粒材料流动特性的影响, 这里采用式(1)的超二次曲面方程进一步构造不同形态的颗粒单元以模拟颗粒材料的卸料过程, 同时考虑颗粒长宽比和表面尖锐度对流动速率的影响. 超二次曲面方程中函数参数满足: $D=2b=2c=4~\text{mm}$, 长宽比满足: $\sigma=2a/D$ 且$\sigma\in[0.5,1.5]$. 通过改变$\sigma$值以调整颗粒形态. 长方形卸料容器长为$11D$, 宽为$4D$, 并在宽度方向施加周期性边界条件. 同时, 底部卸料口长为$3.6D$, 宽为$4D$, 该卸料模型与文献[50 ,51 ,52 ] 类似. 颗粒密度、摩擦系数和DEM 时间步长分别为$2500~\text{kg}/\text m^{3}$, 0.1 和$1\times 10^{-6}$, 其余离散元主要计算参数列于表2 中. 采用超二次曲面单元数值模拟的不同时刻不同形状的颗粒材料卸料过程如图10 所示. 由此可发现, 不同形态的颗粒材料具有不同的流动特性, 其在最后时刻的颗粒存量具有较大差异. 下面将进一步通过改变颗粒形态来定量分析颗粒流动性能的差异. ...
Distinct element modelling of cubic particle packing and flow
3
2008
... 为分析单元形态对颗粒材料流动特性的影响, 这里采用式(1)的超二次曲面方程进一步构造不同形态的颗粒单元以模拟颗粒材料的卸料过程, 同时考虑颗粒长宽比和表面尖锐度对流动速率的影响. 超二次曲面方程中函数参数满足: $D=2b=2c=4~\text{mm}$, 长宽比满足: $\sigma=2a/D$ 且$\sigma\in[0.5,1.5]$. 通过改变$\sigma$值以调整颗粒形态. 长方形卸料容器长为$11D$, 宽为$4D$, 并在宽度方向施加周期性边界条件. 同时, 底部卸料口长为$3.6D$, 宽为$4D$, 该卸料模型与文献[50 ,51 ,52 ] 类似. 颗粒密度、摩擦系数和DEM 时间步长分别为$2500~\text{kg}/\text m^{3}$, 0.1 和$1\times 10^{-6}$, 其余离散元主要计算参数列于表2 中. 采用超二次曲面单元数值模拟的不同时刻不同形状的颗粒材料卸料过程如图10 所示. 由此可发现, 不同形态的颗粒材料具有不同的流动特性, 其在最后时刻的颗粒存量具有较大差异. 下面将进一步通过改变颗粒形态来定量分析颗粒流动性能的差异. ...
... 为对比分析颗粒单元长宽比对卸料过程的影响, 这里分别取长宽比$\sigma=0.5$, 0.75, 1, 1.25 和1.5, 对椭球体和圆柱体颗粒的流动过程进行离散元分析, 其从漏斗中流出体积百分比随时间的变化过程如图11 所示. 此外, 图中标出了不同形态的颗粒单元及其所对应的长宽比 . 图11 (a) 和图11 (b)结果表明, 椭球体和圆柱体颗粒在长宽比$\sigma=1$时流动速率最快, 长宽比增大或减小都会使流动速率减慢. 这主要是由于长宽比增加了颗粒流动过程中的碰撞次数, 同时产生的咬合互锁效应显著影响颗粒的流动性能. 将长宽比为1的球体、圆柱体和正方体颗粒的流出体积百分比随时间的变化关系进行对比, 如图11 (c)所示. 可以发现, 球形颗粒具有最快的流动速率, 而块体颗粒的流动速率是最慢的. 对于块体颗粒, 颗粒单元间的面接触会导致颗粒在容器两侧形成堆积, 同时约有59\%的颗粒流出. 该数值小于文献[52 ] 中65\% 块体颗粒流出的试验结果. 这主要是文献[52 ] 中采用的是固定边界, 而本文采用的周期性边界条件消除了固定边界对颗粒堆积的影响, 从而使得颗粒在容器两侧更容易形成堆积以及产生更低的流出量. ...
... [52 ]中采用的是固定边界, 而本文采用的周期性边界条件消除了固定边界对颗粒堆积的影响, 从而使得颗粒在容器两侧更容易形成堆积以及产生更低的流出量. ...