引言
液滴撞击固体壁面的现象不仅存在于自然界,在3D打印、高效传热、农药喷洒、微透镜的制造和喷涂印染等工农业领域[1 -11 ] 也有着广泛的应用.液滴撞击固体壁面后的结果有沉积、部分溅射、冠状溅射、回缩破碎、部分回弹及完全回弹等几种形式[12 ] ,液滴动态行为的不同与液滴的物性、撞击条件以及碰撞表面的理化特性等因素密切相关.
研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道.
本文将3种不同微观结构的纳米颗粒(颗粒状的纳米石墨粉、片状的石墨烯以及圆柱状的多壁碳纳米管)分散到环氧树脂中,制备出不同质量分数的均匀稳定纳米流体,使用旋转流变仪对配制纳米流体的流变特性进行了测量.基于高速摄像技术,对3种不同的纳米流体液滴撞击固壁过程的进行可视化研究.通过研究不同纳米流体液滴的动力学参数如铺展因子﹑动态接触角﹑无量纲高度随时间的变化规律,探索了剪切变稀特性﹑壁面浸润特性及惯性力对液滴铺展行为的影响.本工作通过对纳米流体液滴撞击固体壁面的动力学行为的深入研究,为基于液滴沉积的增益冷却技术以及微型高导热材料的制造提供理论依据和技术指导.
1 实验装置与方法
1.1 液滴撞击实验台的建立
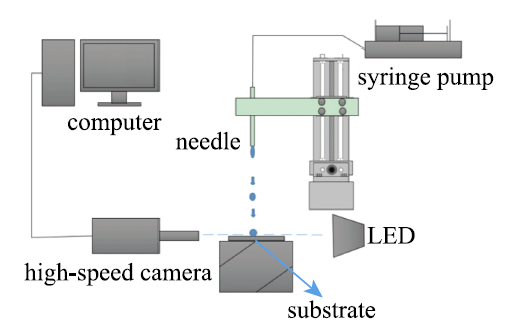
图1 为液滴撞击固体壁面可视化实验装置示意图.本实验通过微流量注射泵(SDK-0609, 嘉善瑞创)和毛细管(G21,内径0.5mm)精确控制液滴产生的频率和尺寸. 使用高速数码相机(Phantom V1611,Dantec Dynamics),配合显微镜头对液滴撞击固体壁面的过程进行微距拍摄,拍摄速度设置为10000帧/秒,图像分辨率为$1280\times 720$.采用背光法拍摄液滴撞击过程,背景光源为LED冷光源.显微镜头、撞击底板(亲水性的玻璃板,疏水性的Teflon基板)与光源中心设置在同一条直线上.
图 1 实验装置示意图
Fig.1 Experimental setup
通过改变液滴与撞击底板之间的距离获得不同的撞击速度,撞击速度是根据液滴撞击基板的临界图像与其上一帧图像的垂直距离与两张图像时间间隔的比值得到.液滴在下落过程中并不是一个规则的球体,而是一个垂直方向长度大于水平方向长度的椭球体,所以依据式(1)
\begin{equation}\label{eq1} d = \sqrt[3]{d_{\rm v} d_{\rm h} ^2}\tag{1}\end{equation}
对液滴的半径进行修正. 其中$d$代表撞击液滴直径,$d_{\rm h}$和$d_{\rm v}$分别代表下落液滴的水平长度和竖直长度,计算结果表明液滴的直径差别较小,约为2.5$\pm$0.05 mm. 实验采用雷诺数$Re = \rho Vd / \mu $和韦伯数$ {We = }\rho V^2d / \sigma$对液滴撞击过程进行描述,其中雷诺数和韦伯数分别针对牛顿流体和非牛顿流体,$\rho$代表流体密度,$V$代表撞击速度,$\mu $代表液体黏度,$\sigma$代表表面张力.实验温度为$25$℃,液滴在基板上的相变过程可以忽略.液滴撞击固体壁面后,其自由表面(固液气接触面)的位置随时间不断变化,本文引入液滴撞击后的铺展因子$D^\ast$、无量纲高度$H^\ast $和动态接触角DCA(dynamic contact angle)对液滴的运动行为进行分析.在本文中定义无量纲参数铺展因子$D^\ast (D^\ast = d_t / d_0),$式中$d_t $为撞击后的瞬时直径,$d_0 $为液滴的水平初始直径.定义无量纲参数无量纲高度$H^\ast (H^\ast = h_v /h),$公式中$h$代表液滴的垂直初始直径,$h_v$代表液滴撞击过程中其最高点距壁面的距离,具体示意图见图2 .液滴撞击过程中的动态接触角是指在空气、液滴、底板(气液固)三相交点处所作的气液界面的切线穿过液滴与固液交界线之间的夹角$\theta $. 本研究实验数据的误差范围为4%.
图 2 液滴无量纲高度、铺展因子定义图
Fig. 2 The definition diagram of droplet dimensionless height,spreading facto
1.2 纳米流体的制备
本研究选择3种不同微观结构的纳米颗粒,从而探索纳米分散相的微观结构对纳米流体的流变特性及液滴铺展动力学特性的影响.3种纳米颗粒分别为颗粒状的纳米石墨粉(直径40 nm,纯度99%,中国科学院成都有机化学研究所),片状的石墨烯 (厚度3.4$\sim$7nm,片层直径10$\sim$50 $\mu$m,层数5$\sim$10,纯度为95%,苏州碳丰石墨烯科技有限公司)以及经酸化处理后的圆柱状的多壁碳纳米管(直径小于8nm, 长度0.5$\sim $2$\mu$m,羧基含量为3.86%,纯度为98%,中国科学院成都有机化学研究所).基液为W52型环氧树脂(环氧值0.44$\sim$0.48,密度为$1100$ kg/m$^3$黏度为$1.57$ Pa$\cdot$s).
由于纳米颗粒之间存在着较强的范德华力,常使纳米颗粒以团聚的状态出现在基液中[32 ] .添加分散剂来提高纳米流体的分散稳定性是制备纳米流体时一种常用的方法,但分散剂同时会对纳米流体的其他特性(如表面张力、黏度等)产生影响.为了能够准确分析纳米颗粒对液滴铺展过程的影响,本研究在不引入分散剂的情况下,选用高黏度的基液来克服纳米颗粒间的范德华力.使用超声波细胞破碎仪(150W,TL96-{Ⅱ},江苏天翎),利用超声空化作用在流体内部形成的剪切流打破纳米颗粒间的团聚状态,细化流体内部的纳米颗粒,将其均匀稳定的分散到环氧树脂中,配制出质量分数为0.05%,0.1%和0.2%的纳米流体.
配制的纳米流体在静止24h后,使用倒置显微镜对纳米颗粒的分散状态进行观察分析.图3 为不同质量分数碳纳米管纳米流体的显微图像.从图3 (a)$\sim$图3 (c)可以发现,经过超声处理后的纳米流体没有出现大范围的纳米颗粒团聚,对比图3 (d)中Ma等[32 ] 拍摄的0.33%碳纳米管/环氧树脂分散良好的显微图像,可以判定本研究所配制的纳米流体分散良好,均匀稳定.
图 3 不同质量分数的碳纳米管/环氧树脂的显微图像
Fig. 3 Micro magnification image of MWNTs with different mass fraction
1.3 纳米流体物性测量
使用表面张力测量仪(CAM101,KSV),应用悬滴法对液滴的表面张力进行测量,纳米流体的密度通过量筒和电子天平(BT125D,赛多利斯)所测量.使用旋转式流变仪(Discovery DHR-Ⅱ,TA)对纳米流体进行流变测试,实验温度$25$℃.
如图4 所示,环氧树脂黏度为$1.57$ Pa$\cdot$s, 表现出牛顿流体特性.纳米颗粒的加入增大了环氧树脂的剪切黏度,且不同分散相的纳米流体表现出的剪切黏度不同.从剪切黏度曲线同样可知,实验配制的纳米流体具有剪切变稀的非牛顿流体特性,这是因为随着剪切速率的增大,悬浮在基液中的颗粒会沿着剪切力方向解缠绕和取向,导致流体黏度迅速下降.本文采用非牛顿幂律模型来拟合纳米流体的剪切变稀特性,式 (2)
中系数$K$为稠度系数, $n$为幂律指数,$\dot {\gamma}$为剪切速率,$\eta $为剪切黏度
\begin{equation}\label{eq2} \eta = K\dot {\gamma }^{n - 1}\tag{2}\end{equation}
基于Levenberg-Marquardt算法[33 ] 拟合的参数见表1 .分析拟合参数可以发现,随着纳米颗粒质量分数的增大,纳米流体的稠度系数$K$增大,幂律指数$n$减小.这说明更大的质量分数可以给纳米流体带来更大的剪切黏度及剪切变稀程度.比较3种分散有不同颗粒的纳米流体可以发现,分散有碳纳米管的纳米流体拥有较大的剪切黏度而分散有纳米石墨粉的纳米流体表现出较强的剪切变稀特性.
图 4 纳米流体剪切黏度曲线
Fig. 4 The shear viscosity of test nanofluids
2 可视化实验结果与分析
用来刻画液滴撞击壁面动力学行为的无量纲参数包括$We$、$Re$、$Oh$和$Ca$.然而,除 $We$之外的无量纲参数中均包含黏性力项,而本研究的纳米流体是剪切黏度是随着剪切速率动态变化的非牛顿流体,因此只采用$We$来表征撞击时的条件,图5 表示3种不同液滴撞击亲水壁面的动态过程.在不发生溅射的情况下,液滴撞击固体壁面后的变形过程可分为4个过程[12 ] :下落、铺展、回缩以及平衡.从图中可以看出, 液滴在撞击20ms后达到平衡状态,在液滴撞击过程,纳米颗粒的加入改变了环氧树脂液滴的动力学行为,在质量分数为0.1%时,石墨粉/环氧树脂液滴的铺展和回缩程度大于多壁碳纳米管/环氧树脂液滴.下文将会详细讨论影响纳米流体液滴撞击壁面动态铺展特性的关键因素.
图 5 液滴以3.43m/s撞击亲水壁面过程($We$$\approx$800),(a)环氧树脂、(b) 0.1%纳米石墨粉、(c) 0.1%多壁碳纳米管液滴. 撞击速度为3.43 m/s
Fig. 5 Impact sequence of droplet impact on hydrophilic surface at a velocity of 3.43 m/s ($We$$ \approx $800), (a) pure resin,(b)0.1%Nano powder, (c) 0.1%MWNTs
2.1 液滴剪切特性对撞击过程的影响
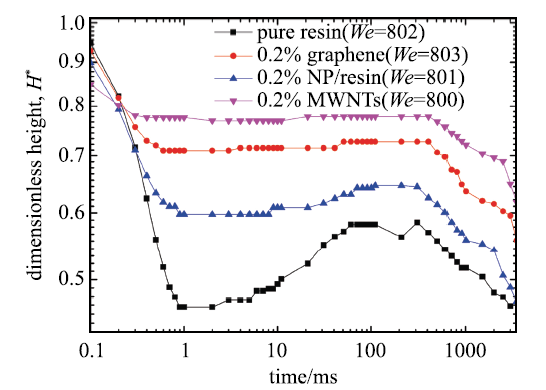
图6 和图7 分别为不同种类的纳米流体液滴铺展因子和无量纲高度随时间的变化曲线图.
图 6 纳米流体铺展因子($We$$ \approx $800)
Fig. 6 The spreading factor of nanofluids($We$$ \approx $800)
图 7 纳米流体无量纲高度($We$$ \approx $800)
Fig. 7 The dimensionless height of nanofluids ($We$$ \approx $800)
从图6 中能够发现,纳米颗粒的加入抑制了液滴的铺展过程,同时拥有最小稠度系数的纳米流体(纳米石墨粉/环氧树脂),相比其他纳米流体液滴其液滴铺展因子变化范围最大.从图7 中可以看出纯的环氧树脂液滴在1$\sim$100ms时间段内经历了明显的回缩过程,但随着纳米颗粒的加入,环氧树脂液滴的回缩被抑制,其中纳米石墨粉对环氧树脂液滴回缩的抑制程度最小.基于B-Spline Snake模型[34 ] ,获得了铺展过程中液滴的动态接触角(DCA),从图8 可以发现,稠度系数更大的液滴在铺展中的动态接触角相对更大.从图6 $\sim$图8 能够发现在铺展阶段纳米流体的黏度对撞击后液滴铺展影响较小,但对于纳米流体液滴的回缩阶段影响较大,主要因为液滴撞击后其内部的剪切流场在较低剪切速率时,纳米分散相对剪切黏度的影响更为显著.拥有较小稠度系数的液滴其铺展和回缩的范围更大,其变化形态更加接近纯的环氧树脂.
图 8 纳米流体动态接触角($We$$ \approx $200)
Fig. 8 The DCA of nanofluids ($We$$ \approx $200)
2.2 撞击表面润湿性对撞击过程的影响
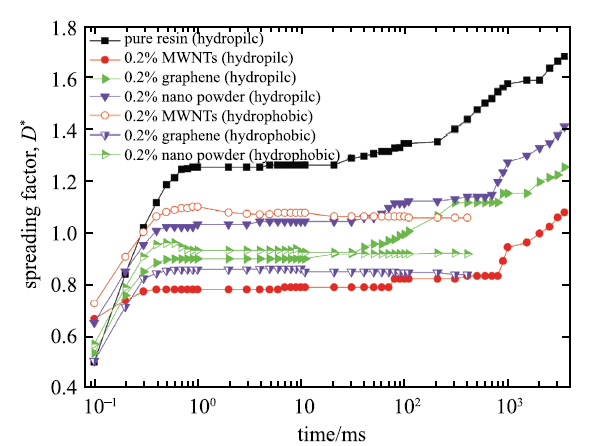
图9 表示撞击速度为3.43 m/s($We$$ \approx$800)的情况下,不同纳米流体液滴撞击亲水表面(玻璃板)和疏水表面(Teflon基板)时,铺展因子随时间的变化曲线.从图中能够发现,在1$\sim$100ms的时间段内,相同的纳米流体液滴在撞击到玻璃板表面时其铺展因子变化缓慢,在100ms后,其铺展因子显著上升. 液滴撞击疏水表面时,当时间大于100ms时液滴的铺展因子保持不变.撞击疏水表面时纳米流体液滴的铺展过程被抑制的更明显,这使得纳米流体液滴达到最终平衡状态的速度更快.
图 9 不同纳米流体撞击不同润湿性表面时铺展因子变化曲线
Fig. 9 The spreading factor of droplets impact on hydrophilic(glass) and hydrophobic (Teflon) surface
2.3 液滴惯性力的影响
图10 为不同撞击速度下纳米流体液滴的无量纲高度随时间的变化曲线.当液滴以1.71 m/s 的速度撞击固体壁面时,不同液滴的无量纲高度在前1ms的变化趋势并无明显差异,而在1$\sim$100ms范围内,不同液滴的无量纲高度变化显著,纯环氧树脂液滴的相对高度在此范围内存在明显的先下降后上升的趋势,纳米流体液滴的相对高度并无明显变化.当液滴以3.43 m/s 的速度撞击固体壁面时,不同液滴的无量纲高度在前0.3ms的变化趋势并无明显差异,在0.3$\sim$100ms范围内,纯环氧树脂液滴内表现出明显的先下降后上升的趋势,而纳米流体液滴的相对高度变化幅度较小.通过图10 能够发现,在较高的撞击速度下,纳米流体液滴初始铺展时的无量纲高度变化范围更大,这说明液滴的惯性力在其初始的铺展阶段起着主导作用.
图 10 纳米流体无量纲高度($We$$ \approx $200, $We$$ \approx $800)
Fig. 10 The dimensionless height of nanofluids ($We$$ \approx$200,$We$$ \approx $800)
3 结 论
本文采用两步法和超声波分散技术配制出均匀稳定不同分散相的纳米流体,基于高速摄像及图像后处理技术,对不同种类的纳米流体液滴撞击固体壁面行为进行可视化研究,得出如下结论.
(1)流变学分析表明纳米颗粒的加入使得环氧树脂基液表现出剪切变稀行为,且添加了不同纳米分散相的基液表现出的剪切变稀程度不同.
(2)纳米分散相的加入有效的抑制了液滴撞击固体壁面时的铺展和回缩行为,在相同的碰撞$We$及纳米颗粒质量分数的情况下,稠度系数$K$较大的纳米流体如碳纳米管/环氧树脂纳米流体,其铺展因子和无量纲高度的变化范围最小,即其液滴在壁面上的铺展行为被抑制的最为显著.
(3)比较液滴撞击不同润湿性表面的过程,撞击疏水表面时纳米流体液滴的铺展过程被抑制的更明显,这使得纳米流体液滴能更快达到最终平衡状态.液滴的惯性力主导者液滴的初始铺展阶段,不同液滴在在惯性力相同时其初始铺展阶段($We$$\approx $200时为前1 ms, $We$$ \approx $800时为前0.3ms)的变化趋势并无明显差异.随着液滴撞击惯性力的增大,液滴的铺展及回缩的速度更快,变化幅度也更大.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Wang CH Tsai HL Wu YC et al .Investigation of molten metal droplet deposition and solidification for 3D printing techniques
. Journal of Micromechanics & Microengineering , 2016 , 26 (9 ): 095012
[本文引用: 1]
[2]
Moita AS Herrmann D Moreira ALN Fluid dynamic and heat transfer processes between solid surfaces and non-Newtonian liquid droplets
. Applied Thermal Engineering , 2015 , 88 : 33 -46
[3]
Wirth W Storp S Jacobsen W Mechanisms controlling leaf retention of agricultural spray solutions
. Pest Management Science , 1991 , 33 (4 ): 411 -420
[4]
Bertola V An impact regime map for water drops impacting on heated surfaces
. International Journal of Heat & Mass Transfer , 2015 , 85 : 430 -437
[5]
Andrade R Skurtys O Osorio F Drop impact behavior on food using spray coating: Fundamentals and applications
. Food Research International , 2013 , 54 (1 ): 397 -405 .
[6]
Jiao Z Li F Xie L et al .Experimental research of drop-on-demand droplet jetting 3D printing with molten polymer
.Journal of Applied Polymer Science , 2018 , 135 (9 ): 45933
[7]
Mogalicherla AK Lee S Pfeifer P et al .Drop-on-demand inkjet printing of alumina nanoparticles in rectangular microchannels
. Microfluidics & Nanofluidics , 2014 ,16 (4 ): 655 -666
[8]
Srikar R Gambaryan-Roisman T Steffes C et al .Nanofiber coating of surfaces for intensification of drop or spray impact cooling
. International Journal of Heat & Mass Transfer , 2009 , 52 (25 ): 5814 -5826
[9]
李春曦 , 杨保才 , 叶学民 . 分离压对波状基底上活性剂液滴铺展过程的影响
. 力学学报 , 2015 , 47 (1 ):71 -81
(Li Chunxi Yang Baocai Ye Xuemin Effect of disjoining pressure on spreading of liquid droplet containing surfactant over corrugated topography surface
. Chinese Journal of Theoretical and Applied Mechanics , 2015 , 47 (1 ): 71 -81 (in Chinese))
[10]
焦云龙 , 刘小君 , 刘焜 . 离散型织构表面液滴的铺展及其接触线的力学特性分析
. 力学学报 , 2016 , 48 (2 ): 353 -360
(Jiao Yunlong Liu Xiaojun Liu Kun Mechanical analysis of a droplet spreading on the discrete textured surfaces
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (2 ): 353 -360 (in Chinese))
[11]
王昭 , 严红 . 基于气液相界面捕捉的统一气体动理学格式
. 力学学报 , 2018 , 50 (4 ): 711 -721
[本文引用: 1]
(Wang Zhao Yan Hong Unified gas-kinetic scheme for two phase interface capturing
. Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (4 ): 711 -721 (in Chinese))
[本文引用: 1]
[12]
Rioboo R Marengo M Tropea C Outcomes from a Drop Impact on Solid Surfaces
. Atomization & Sprays , 2001 , 11 (2 ): 155 -166
[本文引用: 2]
[13]
Josserand C Thoroddsen ST Drop impact on a solid surface
. Annual Review of Fluid Mechanics , 2017 , 48 (48 ): 365 -391
[本文引用: 1]
[14]
郭亚丽 , 陈桂影 , 沈胜强 等 . 盐水液滴撞击固体壁面接触特性实验研究
. 工程热物理学报 , 2015 , 36 (7 ): 1547 -1552
(Guo Yali Chen Guiying Shen Shengqiang et al .Experimental study of spread characteristics of brine droplets impact on solid surface
. Journal of Engineering Thermophysics , 2015 , 36 (7 ): 1547 -1552 (in Chinese))
[15]
宋云超 , 宁智 , 孙春华 等 . 液滴撞击湿润壁面的运动形态及飞溅运机制
. 力学学报 , 2013 , 45 (6 ): 833 -842
(Song Yunchao Ning Zhi Sun Chunhua et al .Movement and splashing of droplet impact on a wet surface,
Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (6 ): 833 -842 (in Chinese))
[16]
刘冬薇 , 宁智 , 吕明 等 . 液滴撞击超疏水壁面反弹及破碎行为研究
. 计算力学学报 , 2016 , 33 (1 ): 106 -112
(Liu Dongwei Ning Zhi Lü Ming et al .Study on the rebound and breakup of the droplet after impacting on the super-hydrophic wall
. Chinese Journal of Computational Mechanics , 2016 , 33 (1 ): 106 -112 (in Chinese))
[17]
Castrejón-Pita JR Betton ES Kubiak KJ et al .The dynamics of the impact and coalescence of droplets on a solid surface
. Biomicrofluidics , 2011 , 5 (1 ): 14112
[本文引用: 1]
[18]
Bergeron V Bonn D Martin JY et al .Controlling droplet deposition with polymer additives
. Nature , 2000 , 405 (6788 ): 772
[本文引用: 1]
[19]
Bergeron V Designing intelligent fluids for controlling spray applications
. Comptes Rendus Physique , 2003 , 4 (2 ): 211 -219
[本文引用: 1]
[20]
Huh HK Jung S Seo KW et al .Role of polymer concentration and molecular weight on the rebounding behaviors of polymer solution droplet impacting on hydrophobic surfaces
. Microfluidics & Nanofluidics , 2015 , 18 (5-6 ): 1221 -1232
[本文引用: 1]
[21]
An S M Sang Y L Maximum spreading of a shear-thinning liquid drop impacting on dry solid surfaces
. Experimental Thermal & Fluid Science , 2012 , 38 (1 ): 140 -148
[本文引用: 1]
[22]
吴延鹏 , 王晓东 , 张欣欣 . 非牛顿幂律流体液滴铺展特性
. 沈阳建筑大学学报(自然科学版) , 2008 , 24 (6 ): 1060 -1065
[本文引用: 1]
(Wu Yanpeng Wang Xiaodong Zhang Xinxin Non-newtonian power law fluid droplet spreading characteristics
. Journal of Shenyang Architecture University , 2008 , 24 (6 ): 1060 -1065 (in Chinese))
[本文引用: 1]
[23]
闵琪 , 段远源 , 王晓东 等 . 非牛顿流体液滴铺展过程的格子Boltzmann模拟
. 热科学与技术 , 2013 , 12 (4 ): 335 -341
[本文引用: 1]
(Min Qi Duan Yuanyuan Wang Xiaodong et al .Lattice boltzmann simulation of droplet spreading of non-newtonian fluid
. Journal of Thermal Science and Technology , 2013 ,12 (4 ): 335 -341 (in Chinese))
[本文引用: 1]
[24]
郭健 , 唐正宁 . 流体黏弹性对喷墨印刷液滴参数影响
. 包装工程 , 2014 (15 ): 118 -123
[本文引用: 1]
(Guo Jian Tang Zhengning Effect of fluid viscoelasticity on droplet parameters of inkjet printing
. Packaging Engineering , 2014 (15 ): 118 -123 (in Chinese))
[本文引用: 1]
[25]
Bartolo D Boudaoud A Narcy G et al .Dynamics of non-Newtonian droplets
. Physical Review Letters , 2007 , 99 (17 ): 174502
[本文引用: 1]
[26]
Biance AL Clanet C Quéré D First steps in the spreading of a liquid droplet
. Physical Review E Statistical Nonlinear & Soft Matter Physics , 2004 , 69 (1 Pt 2 ): 016301
[27]
Rozhkov A Prunet-Foch B Vignes-Adler M Impact of drops of polymer solutions on small targets
. Physics of Fluids , 2003 , 15 (7 ): 2006 -2019
[本文引用: 1]
[28]
Zang D Wang X Geng X et al .Impact dynamics of droplets with silica nanoparticles and polymer additives
. Soft Matter , 2012 , 9 (2 ): 394 -400
[本文引用: 1]
[29]
Hao C Zhou Y Zhou X et al .Dynamic control of droplet jumping by tailoring nanoparticle concentrations
. Applied Physics Letters , 2016 , 109 (2 ): 61
[本文引用: 1]
[30]
Lee J B Lee S H Dynamic wetting and spreading characteristics of a liquid droplet impinging on hydrophobic textured surfaces
. Langmuir the Acs Journal of Surfaces & Colloids , 2011 , 27 (11 ): 65 -73
[本文引用: 1]
[31]
陈石 , 陶英 , 沈胜强 等 . 平壁液滴静态铺展影响因素的研究
. 力学学报 , 2014 , 46 (3 ): 329 -335
[本文引用: 1]
(Chen Shi Tao Ying Shen Shengqiang et al .Static spreading of droplet impact on solid surface: Influence factor
. Chinese Journal of Theoretical and Applied Mechanics , 2014 , 46 (3 ): 329 -335 (in Chinese))
[本文引用: 1]
[32]
Ma AWK Chinesta F Mackley MR The rheology and modeling of chemically treated carbon nanotubes suspensions
. Journal of Rheology , 2009 , 53 (3 ): 547 -57
[本文引用: 2]
[33]
Wilamowski BM Yu H Improved computation for Levenberg--Marquardt training
. IEEE Transactions on Neural Networks , 2010 , 21 (6 ): 930 -937
[本文引用: 1]
[34]
Stalder AF Kulik G Sage D et al .A snake-based approach to accurate determination of both contact points and contact angles
. Colloids and Surfaces A: Physicochemical and Engineering Aspects , 2006 , 286 (1-3 ): 92 -103
[本文引用: 1]
Investigation of molten metal droplet deposition and solidification for 3D printing techniques
1
2016
... 液滴撞击固体壁面的现象不仅存在于自然界,在3D打印、高效传热、农药喷洒、微透镜的制造和喷涂印染等工农业领域[1 -11 ] 也有着广泛的应用.液滴撞击固体壁面后的结果有沉积、部分溅射、冠状溅射、回缩破碎、部分回弹及完全回弹等几种形式[12 ] ,液滴动态行为的不同与液滴的物性、撞击条件以及碰撞表面的理化特性等因素密切相关. ...
Fluid dynamic and heat transfer processes between solid surfaces and non-Newtonian liquid droplets
2015
Mechanisms controlling leaf retention of agricultural spray solutions
1991
An impact regime map for water drops impacting on heated surfaces
2015
Drop impact behavior on food using spray coating: Fundamentals and applications
2013
Experimental research of drop-on-demand droplet jetting 3D printing with molten polymer
2018
Drop-on-demand inkjet printing of alumina nanoparticles in rectangular microchannels
2014
Nanofiber coating of surfaces for intensification of drop or spray impact cooling
2009
分离压对波状基底上活性剂液滴铺展过程的影响
2015
分离压对波状基底上活性剂液滴铺展过程的影响
2015
离散型织构表面液滴的铺展及其接触线的力学特性分析
2016
离散型织构表面液滴的铺展及其接触线的力学特性分析
2016
基于气液相界面捕捉的统一气体动理学格式
1
2018
... 液滴撞击固体壁面的现象不仅存在于自然界,在3D打印、高效传热、农药喷洒、微透镜的制造和喷涂印染等工农业领域[1 -11 ] 也有着广泛的应用.液滴撞击固体壁面后的结果有沉积、部分溅射、冠状溅射、回缩破碎、部分回弹及完全回弹等几种形式[12 ] ,液滴动态行为的不同与液滴的物性、撞击条件以及碰撞表面的理化特性等因素密切相关. ...
基于气液相界面捕捉的统一气体动理学格式
1
2018
... 液滴撞击固体壁面的现象不仅存在于自然界,在3D打印、高效传热、农药喷洒、微透镜的制造和喷涂印染等工农业领域[1 -11 ] 也有着广泛的应用.液滴撞击固体壁面后的结果有沉积、部分溅射、冠状溅射、回缩破碎、部分回弹及完全回弹等几种形式[12 ] ,液滴动态行为的不同与液滴的物性、撞击条件以及碰撞表面的理化特性等因素密切相关. ...
Outcomes from a Drop Impact on Solid Surfaces
2
2001
... 液滴撞击固体壁面的现象不仅存在于自然界,在3D打印、高效传热、农药喷洒、微透镜的制造和喷涂印染等工农业领域[1 -11 ] 也有着广泛的应用.液滴撞击固体壁面后的结果有沉积、部分溅射、冠状溅射、回缩破碎、部分回弹及完全回弹等几种形式[12 ] ,液滴动态行为的不同与液滴的物性、撞击条件以及碰撞表面的理化特性等因素密切相关. ...
... 用来刻画液滴撞击壁面动力学行为的无量纲参数包括$We$、$Re$、$Oh$和$Ca$.然而,除 $We$之外的无量纲参数中均包含黏性力项,而本研究的纳米流体是剪切黏度是随着剪切速率动态变化的非牛顿流体,因此只采用$We$来表征撞击时的条件,图5 表示3种不同液滴撞击亲水壁面的动态过程.在不发生溅射的情况下,液滴撞击固体壁面后的变形过程可分为4个过程[12 ] :下落、铺展、回缩以及平衡.从图中可以看出, 液滴在撞击20ms后达到平衡状态,在液滴撞击过程,纳米颗粒的加入改变了环氧树脂液滴的动力学行为,在质量分数为0.1%时,石墨粉/环氧树脂液滴的铺展和回缩程度大于多壁碳纳米管/环氧树脂液滴.下文将会详细讨论影响纳米流体液滴撞击壁面动态铺展特性的关键因素. ...
Drop impact on a solid surface
1
2017
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
The dynamics of the impact and coalescence of droplets on a solid surface
1
2011
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Controlling droplet deposition with polymer additives
1
2000
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Designing intelligent fluids for controlling spray applications
1
2003
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Role of polymer concentration and molecular weight on the rebounding behaviors of polymer solution droplet impacting on hydrophobic surfaces
1
2015
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Maximum spreading of a shear-thinning liquid drop impacting on dry solid surfaces
1
2012
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
非牛顿幂律流体液滴铺展特性
1
2008
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
非牛顿幂律流体液滴铺展特性
1
2008
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
非牛顿流体液滴铺展过程的格子Boltzmann模拟
1
2013
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
非牛顿流体液滴铺展过程的格子Boltzmann模拟
1
2013
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
流体黏弹性对喷墨印刷液滴参数影响
1
2014
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
流体黏弹性对喷墨印刷液滴参数影响
1
2014
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Dynamics of non-Newtonian droplets
1
2007
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
First steps in the spreading of a liquid droplet
2004
Impact of drops of polymer solutions on small targets
1
2003
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Impact dynamics of droplets with silica nanoparticles and polymer additives
1
2012
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Dynamic control of droplet jumping by tailoring nanoparticle concentrations
1
2016
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
Dynamic wetting and spreading characteristics of a liquid droplet impinging on hydrophobic textured surfaces
1
2011
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
平壁液滴静态铺展影响因素的研究
1
2014
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
平壁液滴静态铺展影响因素的研究
1
2014
... 研究液滴撞击壁面的瞬态过程,是认识液滴铺展动力学特性的重要依据.国内外学者们对于水和乙醇等牛顿流体液滴撞击固壁的行为进行了大量研究[13 - 17 ] ,但关于非牛顿流体液滴撞击固壁的动力学特性研究尚少.《自然》杂志最先报道了Bergeron等[18 ] 有关非牛顿流体液滴撞击固体壁面的研究结果,他们发现添加微量的高分子材料在牛顿流体基液中,基液的拉伸黏度增大,液滴的回缩和反弹被强烈的抑制.同时Bergeron[19 ] 指出从改变液滴性质出发抑制液滴撞击壁面后回弹的方式主要有两种:一种是增大液滴的黏性力,另一种是减小液滴的表面张力.Huh等[20 ] 发现液滴撞击固壁时的回缩趋势随着基液中所添加高分子材料的浓度和分子量的增大而减小.An等[21 ] 研究了剪切变稀流体液滴撞击不同疏水性表面的过程后指出在撞击过程中动态变化的剪切黏度影响着液滴的铺展.吴延鹏等[22 ] 提出了剪切变稀和剪切增稠流体液滴撞击壁面时铺展半径与时间的非单一幂指函数关系.闵琪等[23 ] 通过建立两项流动格子Boltzmann模型,模拟了幂指流体液滴的铺展过程.郭建等[24 ] 研究了流体黏弹性对喷墨印刷液滴的影响后发现,对于非牛顿黏弹性流体,虽然高分子聚合物在整个流体中所占比例很小,但是它的存在对流体黏弹性变化影响十分显著.大量有关在基液中添加高分子材料的研究发现,液滴撞壁后的回缩速度随着高分子材料质量分数的增大显著减小[25 -27 ] . 其原因是液滴的黏度随着高分子材料质量分数的增大而增大,这抑制了液滴在撞击过程中的变形与二次飞溅液滴的产生.然而对具有非牛顿流体特性的纳米流体液滴撞击固体壁面的行为的相关研究尚少.Zang等[28 ] 指出纳米颗粒的加入同样可抑制液滴在基板上的铺展及回弹行为,Hao等[29 ] 指出随着硅纳米颗粒的加入会显著的增加流体的黏性耗散,从而抑制液滴在撞击在固体表面后的弹起现象.Lee等[30 ] 研究了液滴撞击固体壁面后的润湿和铺展行为后,指出在液滴的初始铺展阶段起主要作用的是液滴撞击壁面时的惯性力大小.陈石等[31 ] 研究了影响液滴静态铺展半径的因素后指出液滴的静态铺展半径随着液滴密度及体积的增大而增大,随着表面张力系数及接触角的增大而减小.综上所述,目前关于非牛顿流体液滴撞击固体壁面的动力学行为的研究,主要集中于传统的高分子添加物阶段,但关于添加了纳米颗粒的纳米流体液滴撞击壁面的铺展动力学研究鲜有报道. ...
The rheology and modeling of chemically treated carbon nanotubes suspensions
2
2009
... 由于纳米颗粒之间存在着较强的范德华力,常使纳米颗粒以团聚的状态出现在基液中[32 ] .添加分散剂来提高纳米流体的分散稳定性是制备纳米流体时一种常用的方法,但分散剂同时会对纳米流体的其他特性(如表面张力、黏度等)产生影响.为了能够准确分析纳米颗粒对液滴铺展过程的影响,本研究在不引入分散剂的情况下,选用高黏度的基液来克服纳米颗粒间的范德华力.使用超声波细胞破碎仪(150W,TL96-{Ⅱ},江苏天翎),利用超声空化作用在流体内部形成的剪切流打破纳米颗粒间的团聚状态,细化流体内部的纳米颗粒,将其均匀稳定的分散到环氧树脂中,配制出质量分数为0.05%,0.1%和0.2%的纳米流体. ...
... 配制的纳米流体在静止24h后,使用倒置显微镜对纳米颗粒的分散状态进行观察分析.图3 为不同质量分数碳纳米管纳米流体的显微图像.从图3 (a)$\sim$图3 (c)可以发现,经过超声处理后的纳米流体没有出现大范围的纳米颗粒团聚,对比图3 (d)中Ma等[32 ] 拍摄的0.33%碳纳米管/环氧树脂分散良好的显微图像,可以判定本研究所配制的纳米流体分散良好,均匀稳定. ...
Improved computation for Levenberg--Marquardt training
1
2010
... 基于Levenberg-Marquardt算法[33 ] 拟合的参数见表1 .分析拟合参数可以发现,随着纳米颗粒质量分数的增大,纳米流体的稠度系数$K$增大,幂律指数$n$减小.这说明更大的质量分数可以给纳米流体带来更大的剪切黏度及剪切变稀程度.比较3种分散有不同颗粒的纳米流体可以发现,分散有碳纳米管的纳米流体拥有较大的剪切黏度而分散有纳米石墨粉的纳米流体表现出较强的剪切变稀特性. ...
A snake-based approach to accurate determination of both contact points and contact angles
1
2006
... 从图6 中能够发现,纳米颗粒的加入抑制了液滴的铺展过程,同时拥有最小稠度系数的纳米流体(纳米石墨粉/环氧树脂),相比其他纳米流体液滴其液滴铺展因子变化范围最大.从图7 中可以看出纯的环氧树脂液滴在1$\sim$100ms时间段内经历了明显的回缩过程,但随着纳米颗粒的加入,环氧树脂液滴的回缩被抑制,其中纳米石墨粉对环氧树脂液滴回缩的抑制程度最小.基于B-Spline Snake模型[34 ] ,获得了铺展过程中液滴的动态接触角(DCA),从图8 可以发现,稠度系数更大的液滴在铺展中的动态接触角相对更大.从图6 $\sim$图8 能够发现在铺展阶段纳米流体的黏度对撞击后液滴铺展影响较小,但对于纳米流体液滴的回缩阶段影响较大,主要因为液滴撞击后其内部的剪切流场在较低剪切速率时,纳米分散相对剪切黏度的影响更为显著.拥有较小稠度系数的液滴其铺展和回缩的范围更大,其变化形态更加接近纯的环氧树脂. ...