一种模拟大规模高频声场的双层奇异边界法
河海大学 工程与科学数值模拟软件中心 水文水资源与水利工程国家重点实验室 力学与材料学院, 南京 211100
A DUAL-LEVEL SINGULAR BOUNDARY METHOD FOR LARGE-SCALE HIGH FREQUENCY SOUND FIELD ANALYSIS
中图分类号: O302
文献标识码: A
通讯作者:
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
展开
摘要
大规模高频声场的数值模拟是一项非常有计算挑战性的课题. 为了解决传统边界型离散方法由于全局支撑的满阵限制, 不易应用于大规模高频声场模拟的计算瓶颈, 本文提出了一种用于模拟大规模高频声场的双层奇异边界法. 在该方法中, 通过引入双层结构, 细网格上的全局支撑的满阵被转化为局部支撑的大规模稀疏矩阵, 传统奇异边界法模拟大规模问题时所面临的高计算量以及过度存储需求遂得以解决. 其次, 双层奇异边界法仅通过粗网格评估远场作用, 且独立于特定的插值核函数. 相较于快速多级方法, 该方法具有更强的适应性和灵活性, 且多层结构使该方法具有一定的预调节作用, 非常适合求解具有大规模、高秩、高条件数特点的高频波矩阵. 在其后的散射球模型算例中, 双层奇异边界法配置10万个节点, 成功模拟了无量纲波数高达160的声散射问题. 在对于人头模型的声散射特性分析中, 双层奇异边界法比COMSOL软件计算速度快了约78.13
关键词:
Abstract
Numerical simulation of the large-scale high frequency sound field is a computational challenging task. To solve the difficulty that the traditional boundary collocation methods are not easy to be applied to large-scale problems thanks to the resulting large-scale fully-populated matrix, a dual-level singular boundary method is proposed in this study. By introducing a dual level structure, the fully-populated matrix is transformed to a large-scale locally supported sparse matrix on fine mesh. The bottleneck of excessive storage requirements and a large number of operations encountered by the traditional singular boundary method is hereby avoided. Secondly, the method uses only coarse mesh nodes to evaluate far-field contributions, and it is a kernel-independent algorithm. In comparison with the fast multipole method, the dual-level singular boundary method performs higher adaptability and flexibility. In addition, the dual level structure plays a role of preconditioner, which makes the method is very efficient for solving matrix with large scale, high rank and high condition number. In scattering sphere example, the dual-level singular boundary method simulates well the acoustic scattering problem with up to dimensionless wavenumber of 160 when the number of degrees of freedom is taken as 100 000. In the benchmark human head sound scattering, the dual-level singular boundary method using 80 000 degrees of freedom performs 78.13% faster than the COMSOL, and it is noted that the computational frequency is up to 25 kHz, which is far beyond the limit of hearing of human ear.
Keywords:
大规模声场分析在实际工程和科学计算中占有重要的地位, 如结构振动分析[1]、潜艇水下声呐探测[2]、主动噪声控制[3]等. 在实际工程计算中, 由于需要处理大规模高频声场所导致的大规模、高条件数(L2-norm)、高秩矩阵, 该类问题的数值模拟一直是一个极其困难且具有挑战性的课题.
传统的有限元方法[4]因其全局剖分的性质, 在模拟声场问题时, 自由度数量一般需要随声波频率呈立方式增长. 考虑到污染效应, 在实际计算中, 其自由度数量的增长速度往往更快. 且在频域条件下, 声场问题一般需要在无限域内模拟Helmholtz方程, 有限元法还需要人工截断边界以满足无限远处的辐射边界条件. 这导致在模拟大规模高频声场问题时, 有限元法往往伴随着巨大的计算成本.
边界元方法[5-7]和边界配点型无网格方法[8-9], 如奇异边界法[10-11], 无网格局部强弱法[12]等, 以Helmholtz方程的基本解作为插值基函数, 在无限远处自动满足辐射条件, 在模拟声场问题时, 仅需要边界离散, 可将问题复杂程度降低一维, 故其自由度数量随计算频率呈平方式增长. 但该类方法属于全局支撑方法, 最后需要求解一个全局支撑的大型满阵. 这在进行大规模高频声场分析时, 其所带来的存储量和计算量往往是单台计算机难以承受的. 为了解决这一问题, 近年来, 一系列快速方法应运而生, 如快速多级方法[13]、快速傅里叶变换法[14]、 多层快速多级方法[15]等. 然而, 快速多级方法依赖于特定核函数的多级和局部扩展, 因此, 该方法是核依赖的, 且对于远场贡献的处理效率不高; 快速傅里叶变换法需要边界的均匀离散, 难以适应具有复杂边界的声场模拟; 多层快速多级方法推导复杂, 编程复杂, 限制了该方法的实际工程应用. 此外, 为了求解最后所得到的大规模高度病态的线性方程组, 该类方法还需要结合相应的预调节方法, 这进一步增加了该类方法的计算和编程复杂度. 此外需要注意的是, 目前的这些快速算法对于具有高秩特点的高频波矩阵, 其加速和求解效率往往不高.
为了克服上述不足, 本文提出一种改进双层算法, 以解决传统边界型离散方法难以应用于大规模问题的困难. 考虑到奇异边界法是一种无积分、无网格、编程容易、稳定性高的新型径向基函数方法, 本研究将所给出的改进双层算法[16]和奇异边界法[17-18]相结合, 提出一种用于大规模高频声场分析的双层奇异边界法. 需要强调的是, 改进双层算法并不局限于和奇异边界法结合, 所有以具有原点奇异性的基本解作为基函数的边界型离散方法, 原则上均可以与改进双层算法结合, 以用于大规模问题的模拟. 在双层奇异边界法中,通过忽略远场贡献的残差, 全局支撑的大型满矩阵被转化为细网格上的局部支撑的大型稀疏矩阵. 其后通过在粗网格上以全场贡献对细网格所得结果进行校正, 并进一步将所得结果映射到细网格上进行递归计算, 最终由大型满阵所导致的过度存储需求和计算量瓶颈得以解决, 且双层奇异边界法最终需要求解的是一个细网格上的大规模稀疏矩阵, 相较于传统的快速多级方法, 这种双层结构也提供了前者所不具备的矩阵预调节功能, 这一特性在处理具有高秩、高条件数、大规模特点的高频波矩阵时, 往往具有非常明显的比较优势.
文献[16]中首次尝试将改进双层算法应用于位势理论, 并简要地测试了该方法在求解Helmholtz方程时的数值特性和求解效率. 在本文中, 我们进一步将双层奇异边界法理论拓展至声学领域, 并应用该方法模拟了大规模高频声散射问题. 需要特别注意的是, 本项研究所模拟的小尺寸, 大规模, 高频率声场问题, 是目前其他类似的数值算法在单台计算机上所无法成功模拟的. 在其后的数值实验部分, 我们应用双层奇异边界法分析了经典的散射球模型, 并进行了人头声散射特性实验. 其后, 与成熟的商业软件COMSOL Multiphysics进行了比较, 系统分析了所提出方法的计算效率、计算精度和工程应用潜力. 受于篇幅限制, 本文仅讨论了对于Dirichlet 和Neumann边界条件下的声场问题. 但需要强调的是, 双层奇异边界法是核独立算法, 其求解效率、算法结构不受特定的偏微分方程和边界条件影响. 本质上, 双层奇异边界法是奇异边界法和改进双层算法的有机结合. 作为基本算法, 奇异边界法决定了双层奇异边界法的数值精度、数值效率和数值特性; 改进双层算法的主要作用在于克服奇异边界法所导致的稠密矩阵所造成的高度病态性和过度的存储需求以及过高的计算量的问题, 理论上对偏微分方程类型和边界条件类型不敏感. 对于应用奇异边界法模拟更复杂的声学问题, 读者可以参阅文献[3,17-18].
本文其余部分安排如下: 第1节介绍了双层奇异边界法的基本逻辑结构; 第2节对所提出方法进行相关数值实验论证; 第3节对目前研究做了一个总结和展望.
1 双层奇异边界法技术路线
1.1 奇异边界法基本公式回顾
本节回顾奇异边界法的基本插值公式. 声场问题在频域上可简化为三维Helmholtz方程
其中,
在奇异边界法中, 我们以Helmholtz方程的基本解函数作为插值基函数
$\begin{equation*}\left.\begin{split}&G(x,y)=\dfrac{{\rm e}^{{\rm i}kr}}{4{π}r}\\&Q(x,y)=\dfrac{\partial G(x,y)}{\partial n(x)}=\\&\quad\quad\quad\dfrac{{\rm e}^{{\rm i}kr}}{4{π}r^3}({\rm i}kr-1)\big\langle(x,y)\cdot n(x)\big\rangle\end{split}\right\}\tag*{(4)}\end{equation*}$
其中, $i=\sqrt{-1}$,
考虑到, 当配点和源点重合时, 基本解会出现奇异性问题, 在奇异边界法中, 我们用源点强度因子代替式(5)和式(6)中的奇异项. 源点强度因子的公式推导在附录1中给出. 故其插值矩阵可表示为
或者
将方程中的已知项移至方程右端, 未知项移至方程左端, 式(7)或式(8)可写为
其中
1.2 双层奇异边界法基本思想
类似于快速远场近似[19], 双层奇异边界法将全场对于目标点的相互作用划分为远场相互作用与近场相互作用. 奇异边界法属于全局支撑算法, 虽然远场相互作用无法忽略. 但远场作用残差却是可以忽略的, 这就类似于在计算电荷电势时, 对于超过一定距离之外的电荷, 我们可将之看作点电荷, 而忽略电荷几何形状所造成的电势残差. 在奇异边界法中, 这种远场作用残差来源于将无限自由度的自然系统离散为有限自由度的离散系统过程中所产生的离散误差.
双层奇异边界法的核心思想就是通过在细网格上忽略远场贡献残差, 将全局支撑的大规模满阵转化为一个局部支撑的大规模稀疏矩阵. 通过求解这样一个稀疏矩阵, 将所得到的结果映射到粗网格上, 再由粗网格通过全场贡献校正所得到的细网格结果, 其后再将所得结果映射到细网格上, 进行进一步的递归计算, 如此通过粗细网格间的若干次循环, 最终得到所需要的数值结果.
通过采用双层结构, 双层奇异边界法主要具有以下特点:
(1)细网格上的满阵被转化为稀疏矩阵, 克服了边界型离散方法的过度存储需求和过高计算负荷;
(2)最终需要求解的矩阵是一个细网格上的稀疏矩阵, 双层结构起到了预调节的作用;
(3)双层奇异边界法仅通过粗网格计算远场相互作用, 提高了奇异边界法的计算效率.
1.3 双层奇异边界法逻辑步骤
为使推导步骤简洁明了, 本节推导过程中所用到的相关变量命名如表1所示.
表1 双层奇异边界法变量命名表
Table 1 Nomenclature in the dual-level singular boundary method
| sparse matrix on the fine mesh | |
|---|---|
| coarse mesh subscript | |
| fine mesh subscript | |
| positive projection operator | |
| negative projection operator | |
| preset convergence criterion | |
| * | characteristic radius of range of influence of near |
| field region |
在本节中, 我们演示双层奇异边界法求解线性方程组(9)的逻辑步骤, 具体包括:
步骤1: 计算
子步骤1: 在粗网格上求解下列线性方程组
子步骤2: 将
步骤2: 计算
子步骤1: 计算
子步骤2: 计算
其中, 矩阵
步骤3: 评估
$\begin{equation*}Rerr^0_{\varOmega_2}=\sqrt{\sum^{N_{\varOmega_2}}_{i=1}\Bigg|b^i_{\varOmega_2}-\sum^{N_{\varOmega_2}}_{j=1}A^{ij}_{{\varOmega_2}}\bigg(\gamma^0_{\varOmega_2}\bigg)_j\Bigg|^2\Bigg/\sum^{N_{\varOmega_2}}_{i=1}\Big|b^i_{\varOmega_2}\Big|^2}\tag*{(15)}\end{equation*}$
循环条件满足: 若
经
步骤4: 计算
子步骤1: 计算
子步骤2: 通过逆投影算子
步骤5: 计算
步骤6: 计算
子步骤1: 计算
子步骤2: 计算
子步骤3: 计算
子步骤4: 计算
步骤7: 评估
程序结束条件满足: 若
2 数值实验
为了评估双层奇异边界法的计算效率, 计算精度和计算稳定性, 本文给出平均相对误差(
其中,
本文所给出实验均在配置为Intel Core i7-4710MQ 2.50 GHz处理器和16GB RAM的笔记本电脑上计算获得.
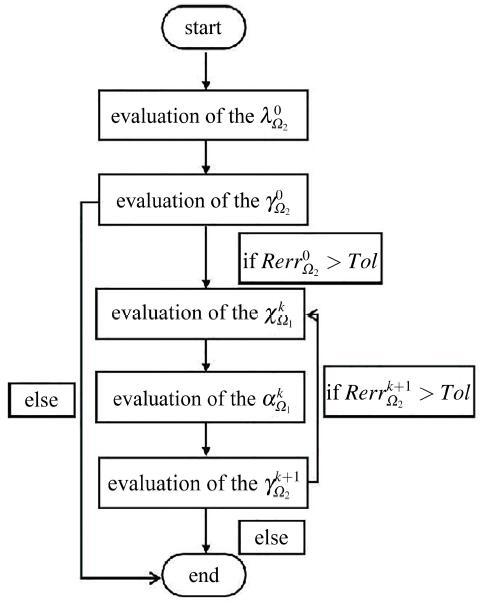
图 1 双层奇异边界法程序框图.
Fig.1 The block diagram of the dual-level singular boundary method
算例1 考虑一个经典散射球模型, 球半径
其中,
工况1: 对于软边界条件, 边界上的总声压为0, 即
故, 系数
其中,
首先, 我们来考察双层奇异边界法的数值收敛性, 取粗网格配点数402, 预设收敛标准
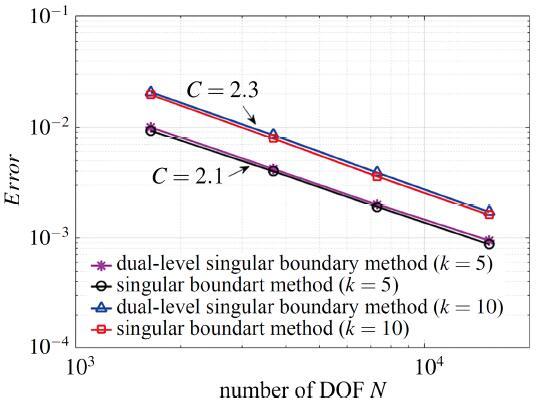
图 2 双层奇异边界法与奇异边界法收敛图.
Fig.2 Convergence of the dual-level singular boundary method and the singular boundary method
表2 双层奇异边界法CPU时间 (单位: s)
Table 2 CPU time of the dual-level singular boundary method (unit: s)
| Nodes | 1646 | 3686 | 7291 | 15 284 |
|---|---|---|---|---|
| CPU( | 2.9 | 5.9 | 18.3 | 109.5 |
| CPU( | 5.6 | 10.5 | 29.3 | 146.3 |
表3 奇异边界法CPU时间 (单位: s)
Table 3 CPU time of the singular boundary method (unit: s)
| Nodes | 1646 | 3686 | 7291 | 15 284 |
|---|---|---|---|---|
| CPU( | 0.4 | 1.7 | 6.1 | 28.1 |
| CPU( | 0.4 | 2.4 | 15.1 | 34.8 |
由图2可以发现, 双层奇异边界法的收敛阶与数值精度和奇异边界法几乎一样. 双层奇异边界法在奇异边界法基础上所添加的双层结构并没有对奇异边界法的数值精度和收敛速度造成任何影响. 对于不同的计算波数, 可以看到两种方法均以二阶收敛. 需要指出的是, 为了直观地比较奇异边界法和双层奇异边界法的数值特性, 本算例所计算的自由度数目较小. 由表2和表3可以观察到, 当自由度数目相同时, 双层奇异边界法的计算CPU时间要略高于奇异边界法. 这主要是由于粗网格和细网格之间的递归计算使得当双层奇异边界处理规模较小的问题时, 其操作量反而会大于奇异边界法. 这一现象同样出现在快速多级算法和其他类似的快速算法当中. 由于普通的奇异边界法所导致的插值矩阵是一个稠密矩阵, 其存储量和计算量会随着自由度数目增加而呈现平方式指数增长, 从而使得奇异边界法无法处理大规模问题. 需要指出的是, 奇异边界法无法在单台笔记本电脑上模拟自由度数目超过2万的问题. 双层奇异边界法的提出即是为了解决奇异边界法的这一计算瓶颈, 随着计算自由度的增加, 双层奇异边界法的计算优势将逐渐显现.
其次, 我们测试双层奇异边界法对于高频问题的计算情况, 取粗网格配点数20 512, 细网格配点数101 875, 预设收敛标准
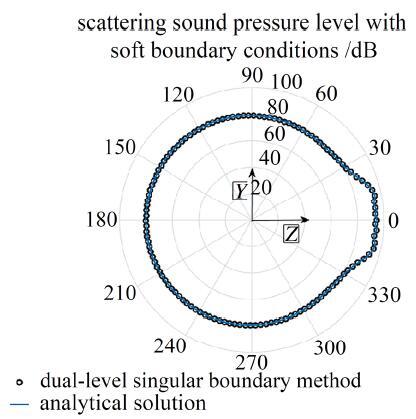
图 3 散射球声散射特性极坐标图.
Fig.3 Polar diagram of the acoustic scattering characteristics of scattering sphere
数值报告显示, 双侧奇异边界法所得数值结果的平均相对误差
工况2: 对于硬边界条件, 边界上的总声压的法向导数为0, 即
故, 系数
为考察双层奇异边界法在实际工程问题中的应用潜力, 在本工况中, 我们将双层奇异边界法与成熟的商业计算软件COMSOL进行比较.
首先, 取粗网格配点数10 330, 细网格配点数101 875, 预设收敛标准
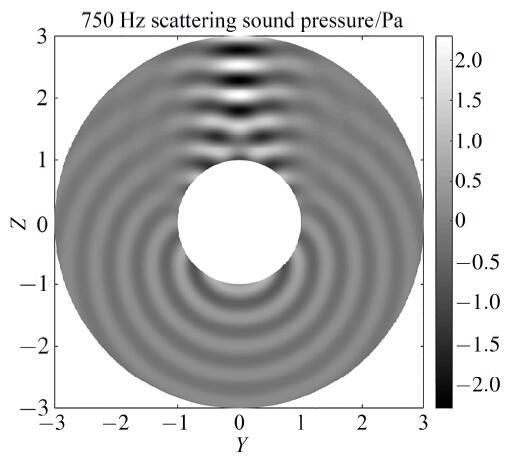
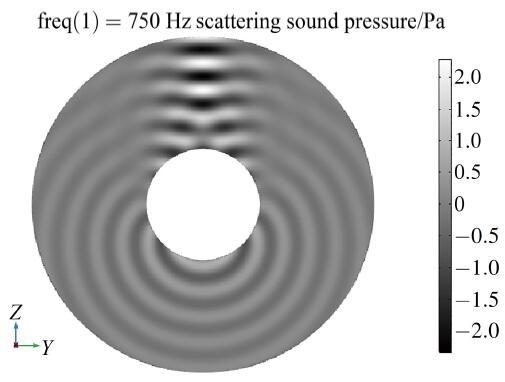
图 4 双层奇异边界法散射压力场.
Fig.4 Scattered sound pressure evaluated by the dual-level singular boundary method
计算报告显示, 双层奇异边界法耗费CPU计算时间
其后, 我们设置COMSOL每个方向一个波长的采样频率为6, 计算频率750 Hz, 计算域取为半径为3 m的球, 取自由度数目7 498 550. 数值报告显示COMSOL耗费11 133 s得到和双层奇异边界法类似的结果, 所得到的散射压力场如图5所示. 如果同样在图5中随机取50个计算点, 发现COMSOL 计算结果的平均相对误差为1.14%.
通过比较可以发现, 双层奇异边界法仅需要有限元方法自由度数目的1.36%和CPU计算时间的61.53%就可以得到相似的数值结果. 且需要强调的是, 作为一种新颖的数值方法, 目前双层奇异边界法的计算程序仍有很大的优化和提升空间, 而作为一款成熟的商业软件, COMSOL中内嵌的有限元代码已经得到了充分的优化, 未来的提升和改进空间有限.
算例2 考虑一个真实人头模型, 模型尺寸为: 0.152 m×0.213 m×0.168 m. 声速
其中,
首先, 我们将人头看作硬边界条件. 在双层奇异边界法中, 取粗网格配点数1631, 细网格配点数22 286, 预设收敛标准
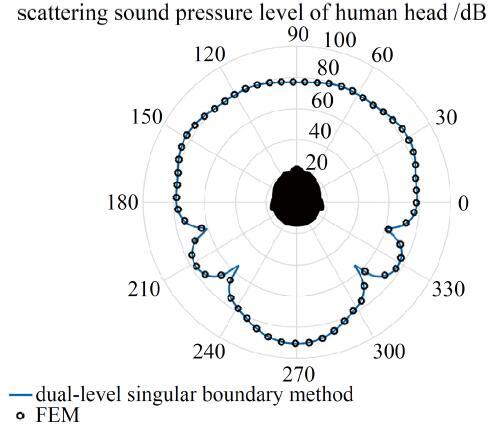
图 6 人头模型声散射特性极坐标图.
Fig.6 Polar diagram of the acoustic scattering characteristics of human head model
计算报告显示, 双层奇异边界法耗费CPU计算时间373.72 s,
可以发现, 在本算例中, 双层奇异边界法的自由度数目和计算CPU时间分别只相当于有限元方法的0.47%和26.87%.
其后, 我们将人头视为软边界条件, 考察双层奇异边界法在高频计算条件下的数值特性. 取粗网格配点数15 198, 细网格配点数80 704, 预设收敛标准
3 结 论
本文提出了一种用于模拟大规模高频声场的双层奇异边界法. 与传统的奇异边界法相比, 双层奇异边界法保持了无网格, 无积分, 易于使用的特点, 通过将传统奇异边界法的单层配点结构修改为双层配点结构, 传统奇异边界法无法适用于大规模问题的计算瓶颈被克服.
相较于快速多极算法, 本文所提出的双层奇异边界法不依赖于特定核函数的多级扩展和局部扩展, 因此是一种核独立算法. 且在评估远场相互作用方面, 双层奇异边界法仅通过粗网格评估远场相互作用, 效率更高; 相较于快速傅里叶变换方法, 双层奇异边界法无必须均匀布点的剖分要求, 因此适应性更强. 此外, 双层奇异边界法所应用的双层结构具有预调节作用, 通过将大型满阵转化为细网格上的大规模稀疏矩阵, 该方法最终需要求解的是一个局部支撑的稀疏矩阵, 非常适合求解大规模高频声场问题所导致的大规模、高条件数、高秩矩阵.
其后的数值实验可以发现, 双层奇异边界法可以有效地模拟大规模高频声场问题. 在散射球的高频模拟实验中, 当配置10万个配点, 双层奇异边界法已可成功模拟无量纲波数高达160的计算工况. 其后的人头声散射实验, 双层奇异边界法的计算速度比COMSOL快了约78.13%, 当配置8万个配点时, 该算法成功模拟了计算频率高达25 kHz时的人头声散射问题, 这一计算频率已远远超过了人耳的听力极限, 达到了超声的范畴.
考虑到双层奇异边界法无网格、无积分、程序编写相对简单, 且独立于特定的核函数, 经过进一步的理论和数值探究之后, 该方法具有和目前主流的快速多级算法和快速傅里叶变换方法相竞争的潜力.
附录 1
本附录仅简要列出源点强度因子的表达式以供读者参考. 如需了解源点强度因子的详细推导过程和物理意义及数学证明, 参见文献[11,16-18,21-23].
拉普拉斯方程的零场积分方程可以表示为[24]
其中
对于光滑边界, 假设源点
由此可得到[2222]
式(A4)即为拉普拉斯方程Neumann条件下的源点强度因子公式.
对于Dirichlet边界条件, 考虑拉普拉斯方程的如下特解[16,21,23]
注意到, 当
式(A8)即为拉普拉斯方程Dirichlet条件下的源点强度因子公式.
考虑到拉普拉斯方程和赫姆霍兹方程的基本解在原点具有奇异相似性[18,25]
我们有
类似地
式(A9)与式(A10)即为赫姆霍兹方程源点强度因子公式. 本附录所推导源点强度因子公式程序均可在奇异工具箱V2.0中找到, 下载网址:
https://doi.org/10.13140/RG.2.2.13247.00162.
The authors have declared that no competing interests exist.
参考文献
| [1] |
曲线加筋Kirchhoff-Mindlin板自由振动分析 .Free vibration analysis of curvilinearly stiffened Kirchhoff-Mindlin plates . |
| [2] |
Underwater sonar image detection: A combination of non-local spatial information and quantum-inspired shuffled frog leaping algorithm . |
| [3] |
Singular boundary method based on time-dependent fundamental solutions for active noise control . |
| [4] |
近场动力学与有限元方法耦合求解热传导问题 .Study of thermal conduction problem Using coupled peridynamics and finite element method . |
| [5] |
A double-layer interpolation method for implementation of BEM analysis of problems in potential theory . |
| [6] |
Improved complex variable moving least squares approximation for three-dimensional problems using boundary integral equations .
|
| [7] |
集成单元边界元法及其在主动冷却热防护系统分析中的应用 .
Integrated unit bem and its application in analysis of actively cooling tps .
|
| [8] |
Element differential method and its application in thermal-mechanical problems . |
| [9] |
Analysis of the complex moving least squares approximation and the associated element-free Galerkin method .
|
| [10] |
A modified singular boundary method for three-dimensional high frequency acoustic wave problems . |
| [11] |
Error bounds of singular boundary method for potential problems . |
| [12] |
无网格局部强弱法求解不规则域问题 .Meshless local strong-weak (MLSW) method for irregular domain problems . |
| [13] |
An adaptive fast multipole boundary element method for three-dimensional acoustic wave problems based on the Burton-Miller formulation . |
| [14] |
Precorrected-FFT accelerated singular boundary method for large-scale three-dimensional potential problems . |
| [15] |
Efficient MLFMA, RPFMA, and FAFFA algorithms for EM scattering by very large structures . |
| [16] |
A modified dual-level algorithm for large-scale three-dimensional Laplace and Helmholtz equation . |
| [17] |
基于时间依赖基本解的奇异边界法模拟二维狄利克雷边界标量波方程 .Fu ZhuoJia. Singular boundary method based on time-dependent fundamental solution for 2D scalar wave equation . |
| [18] |
Burton-Miller-type singular boundary method for acoustic radiation and scattering . |
| [19] |
Efficient 3-D moment-method analysis for reflector antennas using a far-field approximation technique . |
| [20] |
Analysis of mutiple-shepers radiation and scattering problems by using a null-field integral equation approach . |
| [21] |
Single layer regularized meshless method for three dimensional exterior acoustic problem . |
| [22] |
改进的奇异边界法模拟三维位势问题 .Improved singular boundary method for three dimensional potential problems . |
| [23] |
Single layer regularized meshless method for three dimensional Laplace problem . |
| [24] |
大规模边界元模态分析的高效数值方法 .An efficient numerical method for large-scale modal analysis using boundary element method . |
| [25] |
Numerical investigation on the obliquely incident water wave passing through the submerged breakwater by singular boundary method . |

/
| 〈 |
|
〉 |