灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率.
半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂.
本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试.
1 传统灵敏度分析与刚体位移误差消除方法
1.1 传统灵敏度分析方法
传统半解析灵敏度分析方法从单元入手将载荷、刚度矩阵等对设计变量的导数表示为差分近似. 静力问题位移灵敏度分析基本方程
∂ u ∂ d = K - 1 Q = K - 1 ∂ F ∂ d - ∂ K ∂ d u
其中, u 为结构整体位移向量, d 为设计变量, F 为施加在结构上的外载荷, K 为结构总体刚度阵, Q 为拟载荷向量. 对于载荷与设计变量无关的情况静力问题半解析方法的拟载荷公式表达如下, 其中 K e u e
Q = - ∑ e K e ( d + Δ d ) - K e ( d ) Δ d u e
对于静力问题, 传统方法的程序实现需要提取摄动前后两组单元刚度矩阵. 再者对于自振、屈曲特征值问题, 还需提取摄动前后的两组质量阵或应力刚度阵, 较低的单元刚度读入读出效率将使灵敏度总体计算效率下降.
1.2 传统ESA误差消除方法
程耿东等[16 ] 研究表明, 半解析灵敏度分析方法应用于某些结构的形状优化问题会出现较大误差, 其原因为
$\begin{align*}&\textbf{{K}}\textbf{{Φ}}_r=0\tag*{(4)}\\&\dfrac{\partial\textbf{{K}}}{\partial d}\textbf{{Φ}}_r=-\textbf{{K}}\dfrac{\partial\textbf{{Φ}}_r}{\partial d}\tag*{(5)}\\
&F_{rr}=\textbf{{Φ}}_r^{\rm T}\textbf{{Q}}_r=-\textbf{{Φ}}_r^{\rm T}\dfrac{\partial\textbf{{K}}}{\partial d}\textbf{{Φ}}_r=\textbf{{Φ}}_r^{\rm T}\textbf{{K}}\dfrac{\partial\textbf{{Φ}}_r}{\partial d}=0\tag*{(6)}\end{align*}$
F rr ∂ K ∂ d F rr ≠ 0 [2 ] 中所阐述的ESA基于单元级别进行误差修正, 其形式如下
$\begin{equation*}\textbf{{Φ}}_r^{k\rm T}\left\lgroup\dfrac{\Delta\textbf{{K}}_e}{\Delta d}+\textbf{{E}}_e\right\rgroup\textbf{{Φ}}_r^l=0~~~(i,j,k,l\in\{1,2,\dots,n_r\})\tag*{(7)}\end{equation*}$
误差修正项 E e
$\begin{equation*}\textbf{{E}}_e=a_{ij}\textbf{{Φ}}_r^i\textbf{{Φ}}_r^{j\rm T}\tag*{(8)}\end{equation*}$
对于经过正交单位化处理得到的刚体位移来说, 其系数 a ij
$\begin{equation*}a_{ij}=-\textbf{{Φ}}_r^i\dfrac{\Delta\textbf{{K}}_e}{\Delta d}\textbf{{Φ}}_r^j\tag*{(9)}\end{equation*}$
式中$\textbf{\textit{Φ}}_r^j~{\rm (}j=1,2,\dots, n_r{\rm )}$
为单元的刚体转动位移向量(已经过正交单位化处理), n r n r 2 a ij n r 2
2 改进半解析灵敏度分析方法
2.1 改进半解析敏度分析方法公式推导
对于带有修正项的半解析敏度分析方法, 考虑将基于单元的公式转换到结构层次, 将矩阵形式表达的修正项转换为向量或数值形式. 首先对于静力问题, 从单元角度考虑的带有矩阵修正项的基本公式为
Q = - ∑ e Δ K e Δ d + E e u e
其中 E e u e F
Q = - ∑ e K e ( d + Δ d ) u e - F Δ d + e
对于静力问题其误差修正项表达形式为
由式(11), 对于公式中摄动前部分, 无须计算初始刚度阵与位移的乘积, 直接提取施加在结构上的外荷载 F . 对于修正项, 根据式(12), 其计算流程如下: (1)计算系数 a ij c j u e 怺 c j . (3)计算系数 β i . (4)得到修正项单元上的 u e . 由于修正项形式为向量, 因此, 可方便累加于总体得到 e
下面讨论非重特征值问题, 从自振与屈曲两种分析类型进行公式推导. 对于自振分析, 从单元角度考虑的带有矩阵修正项的非重特征值灵敏度基本公式为
$\begin{equation*}
\dfrac{\partial\lambda}{\partial d}=\sum_e\textbf{{φ}}_e^{\rm T}
\left\lgroup\dfrac{\Delta\textbf{{K}}_e}{\Delta d}+\textbf{{E}}_e\right\rgroup\textbf{{φ}}_e-\lambda\sum_e\textbf{{φ}}_e^{\rm T}\left\lgroup\dfrac{\Delta\textbf{{M}}_e}{\Delta d}\right\rgroup\textbf{{φ}}_e\tag*{(13)}\end{equation*}$
将自振分析特征向量$\textbf{\textit{φ}}_e$乘入括号后, 每项分别累加于总体得
$\begin{align*}&\dfrac{\partial\lambda}{\partial d}=\dfrac{\eta{\rm '}-\eta}{\Delta d}-\lambda\dfrac{\xi{\rm '}-\xi}{\Delta d}+\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{E}}_e\textbf{{φ}}_e\tag*{(14)}\\&\dfrac{\partial\lambda}{\partial d}=\dfrac{\eta{\rm '}-\eta}{\Delta d}-\lambda\dfrac{\xi{\rm '}-\xi}{\Delta d}+\sum_{e=1}^Na_{ij}\textbf{{φ}}_e^{\rm T}\textbf{{Φ}}_r^i\textbf{{Φ}}_r^{j\rm T}\textbf{{φ}}_e\tag*{(15)}\end{align*}$
其中
$\begin{equation*}\eta'=\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{K}}_e(d+\Delta d)\textbf{{φ}}_e,\eta=\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{K}}_e(d)\textbf{{φ}}_e\tag*{(16)}\end{equation*}$
$\begin{equation*}\xi'=\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{M}}_e(d+\Delta d)\textbf{{φ}}_e,\xi=\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{M}}_e(d)\textbf{{φ}}_e\tag*{(17)}\end{equation*}$
由自振分析的特性[30 ]
$\begin{equation*}\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{K}}_e(d)\textbf{{φ}}_e=\lambda\tag*{(18)}\end{equation*}$
$\begin{equation*}\lambda\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{M}}_e(d)\textbf{{φ}}_e=\lambda\tag*{(19)}\end{equation*}$
则有
$\begin{equation*}\begin{split}\dfrac{\partial\lambda}{\partial d}=&\left[\sum_e\textbf{{φ}}_e^{\rm T}\textbf{{K}}_e(d+\Delta d)\textbf{{φ}}_e-\lambda\sum_e\textbf{{φ}}_e^{rm T}\textbf{{M}}_e(d+\Delta d)\textbf{{φ}}_e\right]\bigg/\\&\Delta d+e\end{split}\tag*{(20)}\end{equation*}$
对于屈曲非重特征值灵敏度问题[31 ] , 从单元角度考虑的带有矩阵修正项的特征值灵敏度公式为
$\begin{equation*}\dfrac{\partial\lambda}{\partial d}=\sum_e\textbf{{φ}}_e^{\rm T}\left\lgroup\dfrac{\Delta\textbf{{K}}_{Ee}}{\Delta d}+E\right\rgroup\textbf{{φ}}_e+\lambda\sum_e\textbf{{φ}}_e^{\rm T}\left\lgroup\dfrac{\Delta\textbf{{K}}_{\sigma e}}{\Delta d}\right\rgroup\textbf{{φ}}_e\tag*{(21)}\end{equation*}$
同理可得屈曲问题改进方法列式
$\begin{equation*}\begin{split}\dfrac{\partial\lambda}{\partial d}=&\left[\sum_e\textbf{\textit{φ}}_e^{\rm T}\textbf{\textit{K}}_{Ee}(d+\Delta d)\textbf{\textit{φ}}_e+\lambda\sum_e\textbf{\textit{φ}}_e^{\rm T}\textbf{\textit{K}}_{\sigma e}(d+\Delta d)\textbf{\textit{φ}}_e\right]\bigg/\\&\Delta d+e\end{split}\tag*{(22)}\end{equation*}$
特征值问题中, 误差修正项表达形式为
$\begin{equation*}\left.\begin{split}e&=\sum_e\mu_e=\sum_{e=1}^Na_{ij}\textbf{{φ}}_e^{\rm T}\textbf{{Φ}}_r^i\textbf{{Φ}}_r^{j\rm T}\textbf{{φ}}_e\\\mu_e&=a_{ij}c^ic^j\\c^i&=\textbf{{φ}}_e^{\rm T}\textbf{{Φ}}_r^i\quad \quad(i,j=1,2,\dots n_r)\end{split}\right\}\tag*{(23)}\end{equation*}$
由式(20)和式(22), 对于式中摄动前的部分, 直接提取屈曲/自振分析特征向量所对应的特征值, 无须初始刚度阵、质量阵、几何刚度阵的提取. 对于修正项, 根据式(23)其计算流程如下: (1)计算系数 a ij c i c i n r μ e
2.2 单元刚体位移推导
误差修正项的构造基于单元刚体位移向量, 本文针对梁与壳两种单元, 探讨其刚体位移推导方法.
2.2.1梁单元刚体位移推导
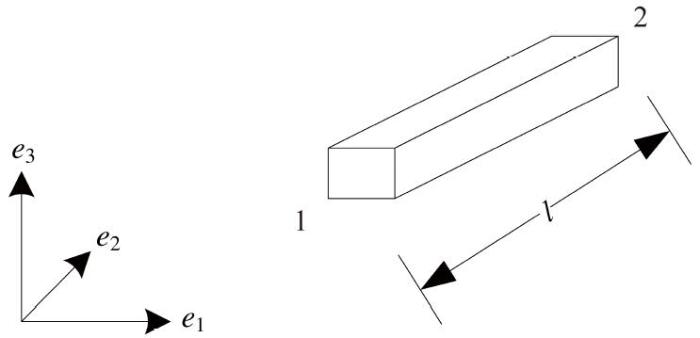
两节点欧拉伯努力空间梁单元如图1 所示, 每一节点包含6个自由度. 其单元位移可表示为
u e = u e 1 u e 2 T u e i = u i v i w i θ 1 i θ 2 i θ 3 i T ̃ ( i = 1,2 )
式中, u e i i u i v i w i i e 1 e 2 e 3 θ pi ( p = 1,2 , 3 ) i e p
Φ ̅ t 1 = 100000100000 T Φ ̅ t 2 = 010000010000 T Φ ̅ t 3 = 001000001000 T
式中, Φ ̅ t 1 , Φ ̅ t 2 , Φ ̅ t 3 e 1 e 2 e 3
图1 梁单元.对于刚体转动位移, 考虑$\textbf{\textit{KΦ}}_r=0$, 刚体位移为刚度矩阵的0特征值所对应的特征向量, 因此可通过解析求解单元刚度阵的0特征向量来获得单元刚体转动位移, 其求解结果如式(26), 结果表明, 梁单元的刚体转动位移只与单元长度有关
Fig. 1 Beam element model
Φ ̅ r 1 = 000100000100 T Φ ̅ r 2 = 00 l 010000010 T Φ ̅ r 3 = 0 - l 0001000001 T
Φ ̅ r 1 , Φ ̅ r 2 , Φ ̅ r 3 e 1 e 2 e 3
$\begin{equation*}\textbf{{Φ}}^{n\text{*}}=\bar{{\varPhi}}_t^n~~~~(n=1,2,3)\tag*{(27)}\end{equation*}$
对于刚体转动位移, 采用施密特正交化进行处理
$\begin{equation*}\begin{split}\textbf{{Φ}}^{n\text{*}}=&\bar{{\varPhi}}_r^{n-3}-a_1\textbf{{Φ}}^{1\text{*}}-a_2\textbf{{Φ}}^{2\text{*}}-\cdots-a_{n-1}\textbf{{Φ}}^{n-1\text{*}}\\&(n=4,5,6)\end{split}\tag*{(28)}\end{equation*}$
其中
$\begin{equation*}a_k=\dfrac{\left\langle\bar{{\varPhi}}_r^{n-3},\textbf{{Φ}}^k\ast\right\rangle}{\left\langle\textbf{{Φ}}^k\ast,\textbf{{Φ}}^k\ast\right\rangle}~~~~(k=1,2,\dots,n-1)\tag*{(29)}\end{equation*}$
由于梁的刚体位移形式简单, 只与梁长有关, 因此很方便地得到正交化后的刚体转动位移, 表达如下
$\begin{equation*}\left.\begin{split}\textbf{{Φ}}^{4\text{*}}&=\left[0~~~0~~~0~~~1~~~0~~~0~~~0~~~0~~~0~~~1~~~0~~~0\right]^{\rm T}\\\textbf{{Φ}}^{5\text{*}}&=\left[0~~~0~~\dfrac{l}{2}~~0~~~1~~~0~~~0~-\dfrac{l}{2}~0~~~0~~1~~~0\right]^{\rm T}\\\textbf{{Φ}}^{6\text{*}}&=\left[0~-\dfrac{l}{2}~~0~~0~~0~~~1~~~0~~\dfrac{l}{2}~~0~~~0~~~0~~~1\right]^{\rm T}\end{split}\right\}\tag*{(30)}\end{equation*}$
再将 怺 怺
2.2.2壳单元刚体位移推导
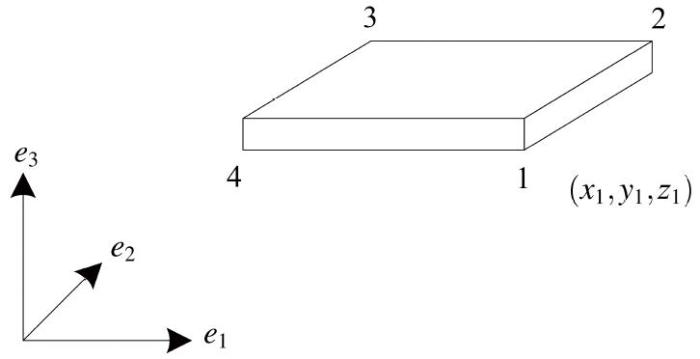
四节点考虑面内转角的克西霍夫壳单元如图2 所示, 每一节点包含6个自由度, 其单元位移可以表示为
u e = u e 1 u e 2 u e 3 u e 4 T u e i = u i v i w i θ 1 i θ 2 i θ 3 i T ( i = 1,2 , 3,4 )
图 2 壳单元.对于空间壳单元其刚体平动位移是容易获得的, 如式(32)和式(33).
Fig. 2 Shell element model
Φ ̅ t p = Φ ̅ t 1 p Φ ̅ t 2 p Φ ̅ t 3 p Φ ̅ t 4 p T ( p = 1,2 , 3 )
其中
Φ ̅ ti 1 = 100000 T Φ ̅ ti 2 = 010000 T Φ ̅ ti 3 = 001000 T ( i = 1,2 , 3,4 )
其刚体转动位移可通过运动学方法获得. 设单元某个节点的坐标向量为 x i T = x i , y i , z i ( i = 1,2 , 3,4 ) e p ( p = 1,2 , 3 ) e p × x i p u i v i w i
e 1 = 100 T , e 2 = 010 T , e 3 = 001 T
四节点壳单元刚体转动位移的表示形式为
Φ ̅ r p = Φ ̅ r 1 p Φ ̅ r 2 p Φ ̅ r 3 p Φ ̅ r 4 p Φ ̅ r p = e p × x 1 r p e p × x 2 r p e p × x 3 r p e p × x 4 r p T ( p = 1,2 , 3 )
其中
Φ ̅ ri 1 = e 1 × x i ⋮ r 1 = 0 - z i y i ⋮ 100 T Φ ̅ ri 2 = e 2 × x i ⋮ r 2 = - z i 0 - x i ⋮ 010 T Φ ̅ ri 3 = e 3 × x i ⋮ r 3 = - y i x i 0 ⋮ 001 T ( i = 1,2 , 3,4 )
Φ ̅ ri P i p Φ ̅ ri P i p Φ ̅ t 1 , Φ ̅ t 2 , Φ ̅ t 3 ; Φ ̅ r 1 , Φ ̅ r 2 , Φ ̅ r 3 ~ 怺 . 将 怺
3 算例测试
3.1 测试算例1
3.1.1测试模型
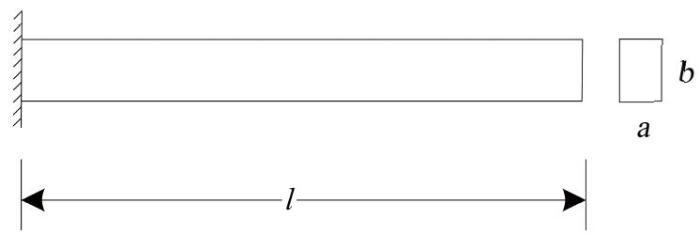
如图3 所示悬臂梁, l = 40 a = 1 b = 2 E = 2 × 1 0 5 N / m m 2 7.8 × 1 0 - 9 t / m m 3 . 下文分别采用梁单元与壳单元模拟该悬臂结构. 将该悬臂结构长度 l
图 3 悬臂梁模型.
Fig. 3 Cantilever beam model
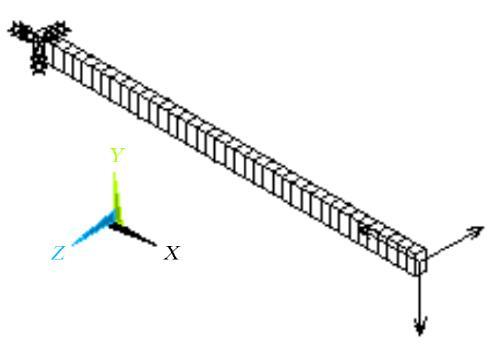
欧拉空间梁单元建模, 如图4 . 测试1: 划分单元数为40个. 测试2: 划分单元数为20到100个. 静力分析时, 力方向如图, 大小为1 N. 屈曲分析时, 在梁末端施加F x = - 3 .
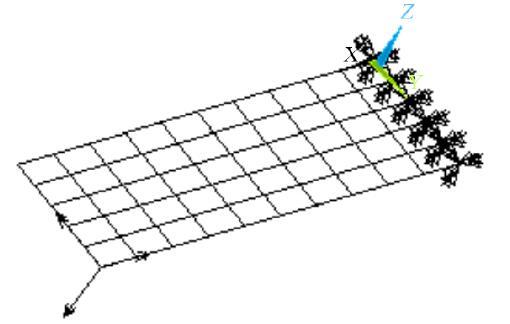
柯西霍夫四边形空间壳单元建模, 如图5 . 测试1: 沿梁高方向划分单元份数为2. 沿梁长方向划分单元份数为20. 测试2: 沿梁高方向单元份数为2不变, 沿梁长方向单元份数由10到100发生变化. 静力分析时, 力方向如图, 大小为1 N. 屈曲分析时, 在末端3个节点均施加 F x = - 1 .
图 4 梁单元构造有限元模型
Fig. 4 Cantilever beam modeled by beam elements
图5 壳单元构造有限元模型.
Fig. 5 Cantilever beam modeled by shell elements
3.1.2测试结果
测试针对静力分析位移灵敏度、自振、屈曲稳定性分析特征值灵敏度, 其中: GFD为全局差分法, SA 为无误差修正的半解析方法, ESA为带有经典误差修正项的半解析方法, MESA为带有改进误差修正项的改进半解析方法.
由于ESA与MESA方法经算例测试, 其数值、走势近乎重合, 因此ESA方法未列于图中. 设灵敏度精确值为 Δ F 0
Δ F S cal S A = Δ F S A Δ F 0 , Δ F S cal M ESA = Δ F M ESA Δ F 0 , Δ F S cal G FD = Δ F G FD Δ F 0
取 z Δ F 0 = - 1.20 × 1 0 - 2 ) , 自振基频灵敏度( Δ F 0 = - 1.03 × 1 0 6 ) , 屈曲一阶特征值灵敏度( Δ F 0 = - 8.60 × 1 0 - 4 ). 图6 ~ 图8 为相对灵敏度随摄动步长的变化规律, 其中 δ = - l g Δ L L 图6 (a) ~ 图8 (a), 用 Δ F s cal b 图6 (b) ~ 图8 (b), 用 Δ F s cal s
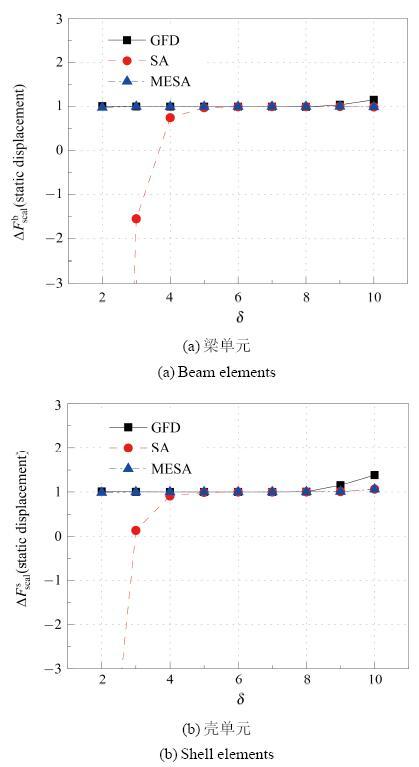
图 6 静力位移相对灵敏度随摄动步长变化.
Fig. 6 Relationship between scaled sensitivity of displacement and perturbation step length in static analysis
图 7 自振一阶特征值相对灵敏度随摄动步长变化.
Fig. 7 Relationship between scaled sensitivity of 1s t
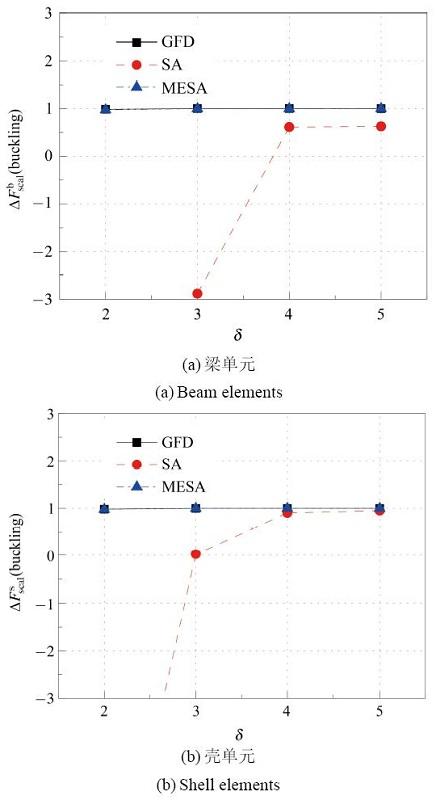
图 8 屈曲一阶特征值相对灵敏度随摄动步长变化.
Fig. 8 Relationship between scaled sensitivity of 1s t
SA方法, 在摄动步长较大时存在较大误差, 其符号有时也与稳定值相反, 随步长减小趋于稳定, 而GFD 与之相反, 在大步长时, 较为稳定, 小步长时存在较大误差, 对于MESA, 其在步长较大与较小时都能得到较好的结果.
对于静力位移与自振特征值灵敏度, 3种方法稳定值均能重合. 而对屈曲问题, SA方法, 对于梁单元模型, 稳定值在 δ = 4 δ = 4
综上所述, 相对灵敏度随摄动步长变化, 用壳单元建模模拟梁结构产生的误差小于梁单元. 另外同SA 与GFD方法相比MESA方法可以得到较好结果, 有效的延长了半解析方法摄动步长的可用范围, 在一定程度上提高了其计算精度, 尤其对屈曲问题的改善较大.
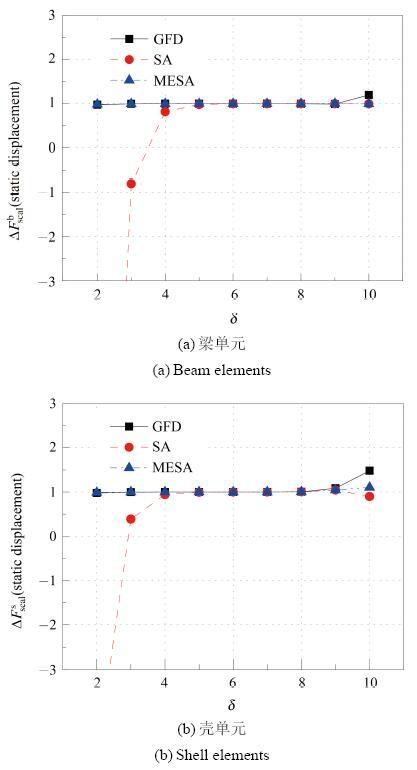
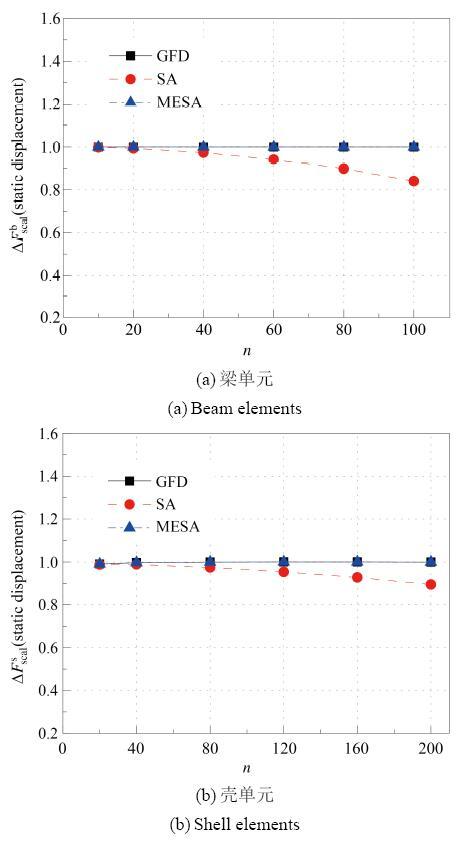
图9~图11 为相对灵敏度随单元数目的变化规律, 取δ = 5 . 梁单元结果绘于图9 (a) ~ 图11 (a). 壳单元结果绘于图9 (b) ~ 图11 (b).
图 9 静力位移相对灵敏度随单元数变化.
Fig. 9 Relationship between scaled sensitivity of displacement and element number in static analysis
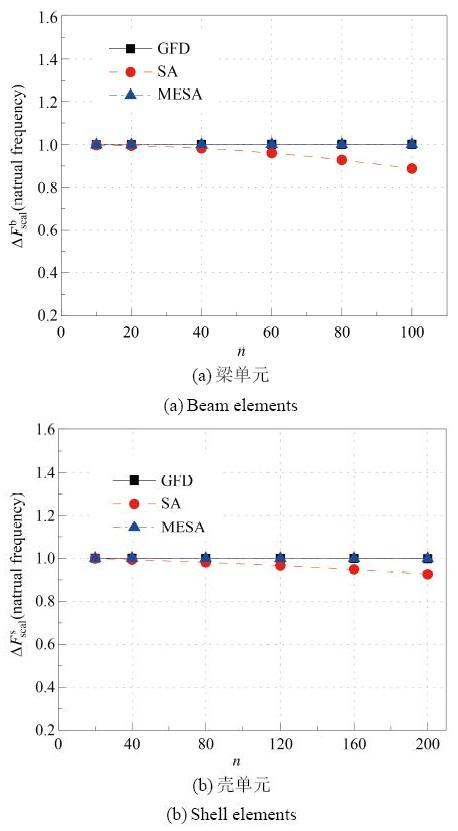
图 10 自振特征值相对灵敏度随单元数变化.
Fig. 10 Relationship between scaled sensitivity of 1s t
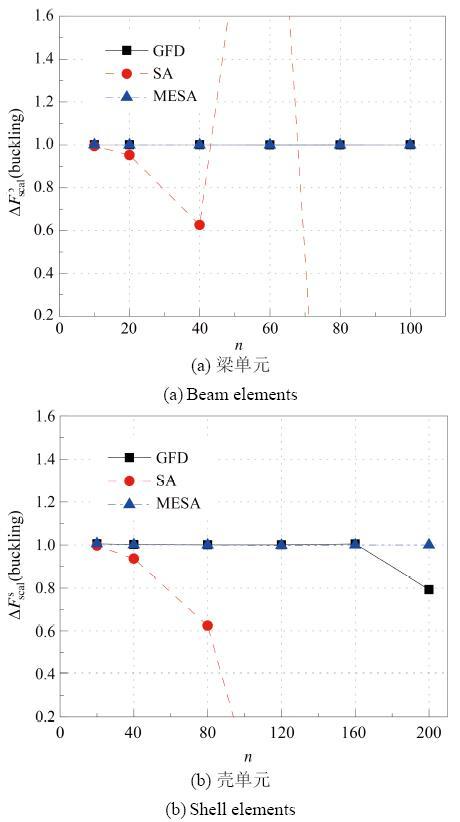
图 11 屈曲特征值相对灵敏度随单元数变化.
Fig. 11 Relationship between scaled sensitivity of 1s t
SA方法, 在单元数目较少时, 求得的灵敏度值可以保持在误差较小的范围内, 随单元个数增多, 逐渐偏离稳定值. 当SA方法引入误差修正, 即可消除单元数目对精确度造成的影响, 有时, 其结果好于全局差分法.
对于静力位移灵敏度, SA方法见图9 中, 当梁单元个数大于20, 壳单元个数大于40时, 其值较为明显地偏离稳定值, 且随单元数目增加, 误差不断增大. 对于自振特征值灵敏度, SA方法见图10 中, 当梁单元个数大于40, 壳单元个数大于80时, 其值较为明显地偏离稳定值, 可见在静力与自振分析中, 随单元数不断增大壳单元半解析方法误差增加较梁单元缓慢. 而对于GFD与MESA方法无论在自振还是静力分析中, 走势重合, 都表现出较好的数值稳定性. 对于屈曲问题, 由图 11 无论梁单元还是壳单元, SA方法误差增加较为迅速, 整体来看, 未出现稳定段. 对于GFD方法在单元数大于160时, 也失去数值稳定性. 而MESA较好地保持了算法精度. 综上所述, 相对灵敏度随单元数目变化, 壳单元误差增加较梁单元缓慢. 与SA和GFD方法相比, MESA方法可以得到较好的结果, 尤其在屈曲稳定性问题上得到了较大的改善.
3.2 测试算例2
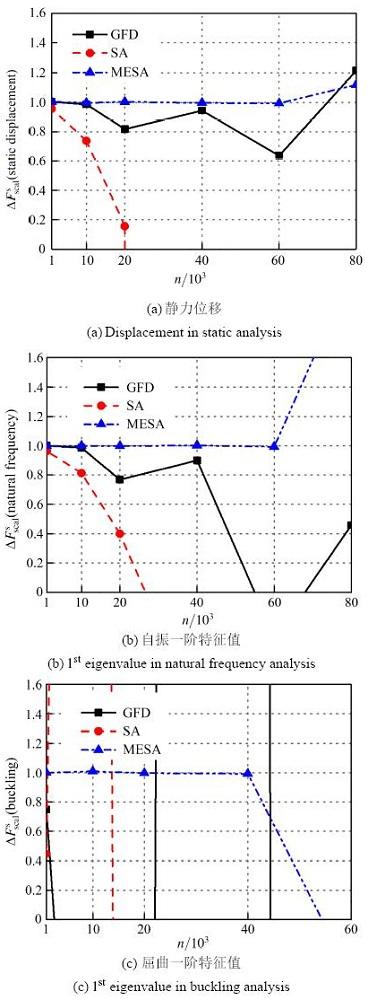
为测试GFD, SA, MESA算法在更大规模问题中的应用, 构建图12 所示800 mm × 200 mm × 1 mm悬臂板模型以便划分更多单元(1万到8万个单元). 静力分析: 自由端一点施加方向如图, 大小为1 N 的集中力, 屈曲分析: 自由端左右两点施加 F x = - 0.01 N . 以板长为设计变量, 分别计算施加载荷点 z Δ F 0 = - 0.333 ) , 自振一阶特征值灵敏度( Δ F 0 = - 0.190 ) 以及屈曲一阶特征值灵敏度( Δ F 0 = - 1.65 ). 由图13 可见, 对于静力位移与自振特征值问题, SA方法在单元数为 1 0 3 1 0 3
图 12 悬壁板有限元模型.
Fig. 12 Cantilever plane modeled by shell elements
图 13 悬臂板模型相对灵敏度测试结果.
Fig. 13 Scaled sensitivity results of cantilever plane
3.3 效率测试
形状优化中, 常使用非结构化网格建模, 结构上各单元形状均不同, 即需求解所有单元的误差修正项. 因此, 为更符合实际需求, 便于控制单元划分数目, 继续采用图12 模型, 假定所有单元误差修正项均不相同. 为使无关时间项的影响降到最低, 省略3种方法共同需要计算部分的时间记录. 对于静力问题T G FD T E SA T M ESA T G FD T E SA T M ESA Δ T E SA = | T E SA - T G FD | , Δ T M ESA = | T M ESA - T G FD | . 表1 为静力分析位移灵敏度的效率测试结果, 当单元数为1万时, 3种方法所消耗的时间近乎相同. 随单元数不断增大, Δ T E SA 表2 为自振分析特征值灵敏度的效率测试结果, 在单元数较少时, ESA与MESA方法都显示出了效率上的优势, 随单元数目增加优势越发明显. 因对于自振分析, 需要迭代求解过程, 而半解析方法无相关过程, 这使得使用半解析方法在计算效率上有更大的优势. MESA 的误差修正项构造无需矩阵生成, 基于常数累加, 因此效率高于传统ESA方法更具优势.
4 结论
(1)对于灵敏度分析部分, 改进方法区别于传统方法需提取摄动前后两组刚度矩阵, 几何刚度矩阵等, 只需提取摄动后结构的一组有限元矩阵. 节省了矩阵提取时间.
(2)对于误差修正部分, 将矩阵形式的误差修正项进行转化. 静力分析问题转化为向量累加, 特征值问题转化为数值累加. 通过程序实践表明, 改进方法在效率上较原方法有一定的提高.
(3)构造灵敏度分析与误差修正可分离等式, 可直接修正灵敏度分析结果, 使得已有灵敏度分析程序可以充分利用. 该方法对于多种设计变量具有通用性, 例如适用于在同一优化过程中既具有形状变量又具有尺寸变量的问题, 在形状变量时直接在灵敏度结果处进行修正, 在尺寸变量时, 不调用修正项计算. 无需针对两种设计变量分别编写两组灵敏度实现程序.
(4)以欧拉梁单元与克西霍夫壳单元建立悬臂梁模型, 将半解析灵敏度分析误差消除方法在静力、自振、屈曲稳定性多种分析类型上的适用性进行验证. 结果表明, 半解析方法使用梁单元建模误差开展程度大于壳单元. 误差消修正方法不仅适用于静力问题, 在特征值问题敏度分析上也达到了较好的效果, 其中对于屈曲特征值灵敏度的精度改善较大.
致谢
在此特别感谢程耿东院士对本文工作的指导与帮助.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
程耿东 , 汪榴 . 旋转体形状优化及敏度分析的拟解析法
. 大连工学院学报 ,1986 , 25 (3 ): 19 -25
[本文引用: 1]
(Cheng Gengdong Wang Liu Shape optimization of axisymmetric body and sensitivity analysis by quasi-analytical method
.Journal of Dalian Institute of Technology 1986 , 25 (3 ): 19 -25 (in Chinese))
[本文引用: 1]
[2]
Bletzinger KU Firl M Daoud F Approximation of derivatives in semi-analytical structural optimization
.Computers & Structures , 2008 , 86 (13 ): 1404 -1416
[本文引用: 3]
[3]
Van Keulen F Haftka RT Kim NH Review of options for structural design sensitivity analysis
.Computer Methods in Applied Mechanics and Engineering , 2005 , 194 (30 ): 3213 -3243
[本文引用: 1]
[4]
Takezawa A Kitamura M Sensitivity analysis and optimization of vibration modes in continuum systems
.Journal of Sound and Vibration , 2013 , 332 (6 ): 1553 -1566
[本文引用: 1]
[5]
Liu ST Cheng GD Gu Y et al .Mapping method for sensitivity analysis of composite material property
.Structural and Multidisciplinary Optimization , 2002 , 24 (3 ): 212 -217
[本文引用: 1]
[6]
张升刚 , 王彦伟 , 黄正东 . 等几何壳体分析与形状优化
. 计算力学学报 , 2014 , 31 (1 ): 115 -119
[本文引用: 1]
(Zhang Shenggang Wang Yanwei Huang Zhengdong Isogeometric shell analysis and shape optimization
.Chinese Journal of Computational Mechanics 2014 , 31 (1 ): 115 -119 (in Chinese))
[本文引用: 1]
[7]
Cheng GD Liu YW A new computation scheme for sensitivity analysis
.Engineering Optimization , 1987 , 12 (3 ): 219 -234
[本文引用: 1]
[8]
顾元宪 , 程耿东 . 结构形状优化设计数值方法的研究和应用
. 计算结构力学及其应用 ,1993 , 10 (3 ): 321 -335
[本文引用: 1]
(Gu Yuanxian Cheng Gengdong Research and applications of numerical methods of structural shape optimization
.Computational Structural Mechanics and Applications 1993 , 10 (3 ): 321 -335 (in Chinese))
[本文引用: 1]
[9]
易龙 , 彭云 , 孙秦 . 基于改进的灵敏度分析的有限元优化技术研究
. 机械强度 ,2008 , 30 (3 ): 483 -487
[本文引用: 1]
(Yi Long Peng Yun Sun Qin Research of the optimal design based on the fem and improved sensitivity analysis
.Journal of Mechanical Strength 2008 , 30 (3 ): 483 -487 (in Chinese))
[本文引用: 1]
[10]
Haftka RT Semi-analytical static nonlinear structural sensitivity analysis
.AIAA Journal , 1993 , 31 (4 ): 1307 -1312
[本文引用: 1]
[11]
Fenyes P Lust RV Error analysis of semianalytic displacement derivatives for shape and sizing variables,
AIAA Journal , 1991 , 29 (2 ): 271 -279
[本文引用: 1]
[12]
Olho N Rasmussen J Study of inaccuracy in semi-analytical sensitivity analysis—a model problem,
Structural Optimization , 1991 , 3 (4 ): 203 -213
[本文引用: 1]
[13]
Barthelemy B Chon CT Haftka RT Accuracy problems associted with semi-analytical derivatives of static response
.Finite Elements in Analysis and Design , 1988 , 4 (3 ): 249 -265
[本文引用: 1]
[14]
Pauli P Cheng GD Rasmussen. On accuracy problems for semi-analytical sensitivity analyses
.Journal of Structural Mechanics , 1989 , 17 (3 ): 373 -384
[本文引用: 1]
[15]
程耿东 , 刘英卫 . 梁的半解析法计算灵敏度的误差分析
. 大连理工大学学报 , 1989 , 29 (4 ): 415 -422
[本文引用: 1]
(Cheng Gengdong Liu Yingwei Study of error of semi-analytic sensitivity analysis in beam problems
.Journal of Dalian University of Technology 1989 , 29 (4 ): 415 -422 (in Chinese))
[本文引用: 1]
[16]
Barthelemy B Haftka RT Accuracy analysis of the semi-analytical method for shape sensitivity calculation
.Mechanics of Structures and Machines , 1990 , 18 (3 ): 407 -432
[本文引用: 2]
[17]
Cheng GD Olhoff N Rigid body motion test against error in semi-analytical sensitivity analysis
.Computers & Structures , 1993 , 46 (3 ): 515 -527
[本文引用: 1]
[18]
Van Keulen F De Boer H Rigorous improvement of semi-analytical design sensitivities by exact differentiation of rigid body motions
.International Journal for Numerical Methods in Engineering , 1998 , 42 (1 ): 71 -91
[本文引用: 1]
[19]
De Boer H Van Keulen F Vervenne K Refined second order semi-analytical design sensitivities
.International Journal for Numerical Methods in Engineering , 2002 , 55 (9 ): 1033 -1051
[本文引用: 1]
[20]
Olhoff N Rasmussen J Lund E A method of “exact” numerical differentiation for error elimination in finite-element-based semi-analytical shape sensitivity analyses
.Journal of Structural Mechanics , 1993 , 21 (1 ): 1 -66
[本文引用: 1]
[21]
Lund E Olhoff N Shape design sensitivity analysis of eigenvalues using ‘exact’ numerical differentiation of finite element matrices,
Structural Optimization , 1994 , 8 (1 ): 52 -59
[22]
Wang WJ Clausen PM Bletzinger KU Improved semi-analytical sensitivity analysis using a secant stiffness matrix for geometric nonlinear shape optimization
.Computers & Structures , 2015 , 146 : 143 -151 .
[本文引用: 1]
[23]
亢战 , 罗阳军 . 基于凸模型的结构非概率可靠性优化
. 力学学报 , 2006 , 38 (6 ): 807 -815
[本文引用: 1]
(Kang Zhan Luo Yangjun On structural optimization for non-probabilistic reliability based on convex models,
Chinese Journal of Theoretical and Applied Mechanics 2006 , 38 (6 ): 807 -815 (in Chinese))
[本文引用: 1]
[24]
亢战 , 程耿东 . 非确定性结构静动态特性稳健优化设计
. 力学学报 , 2006 , 38 (1 ): 57 -65
[本文引用: 1]
(Kang Zhan Cheng Gengdong Structural robust design concerning static and dynamic performance based on perturbation stochastic finite element method
.Chinese Journal of Theoretical and Applied Mechanics 2006 , 38 (1 ): 57 -65 (in Chinese))
[本文引用: 1]
[25]
夏人伟 , 刘鹏 . 一种有效的结构优化设计方法
. 力学学报 , 1987 , 19 (3 ): 52 -63
[本文引用: 1]
(Xia Renwei Liu Peng An efficient method for structural optimization
.Acta Mechanica Sinica 1987 , 19 (3 ): 52 -63 (in Chinese))
[本文引用: 1]
[26]
吴曼乔 , 朱继宏 , 杨开科 等 . 面向压电智能结构精确变形的协同优化设计方法
. 力学学报 , 2017 , 49 (2 ): 380 -389
[本文引用: 1]
(Wu Manqiao Zhu Jihong Yang Kaike et al .Integrated layout and topology optimization design of piezoelectric smart structure in accurate shape control
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (2 ): 380 -389 (in Chinese))
[本文引用: 1]
[27]
龙凯 , 王选 , 韩丹 . 基于多相材料的稳态热传导结构轻量化设计
. 力学学报 , 2017 , 49 (2 ): 359 -366
[本文引用: 1]
(Long Kai Wang Xuan Han Dan Structural light design for steady heat conduction using multi-material
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (2 ): 359 -366 (in Chinese))
[本文引用: 1]
[28]
王选 , 胡平 , 祝雪峰 等 . 考虑结构自重的基于NURBS插值的3D拓扑描述函数法
. 力学学报 , 2016 , 48 (6 ): 1437 -1445
[本文引用: 1]
(Wang Xuan Hu Ping Zhu Xuefeng et al .Topology description function approach using NURBS interpolation for 3D structures with self-weight loads
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (6 ): 1437 -1445 (in Chinese))
[本文引用: 1]
[29]
郭旭 , 顾元宪 , 赵康 . 广义变分原理的结构形状优化伴随法灵敏度分析
. 力学学报 , 2004 , 36 (3 ): 288 -295
[本文引用: 1]
(Guo Xu Gu Yuanxian Zhao Kang Adjoint shape sensitivity analysis based on generalized variational principle
.Chinese Journal of Theoretical and Applied Mechanics 2013 , 45 (2 ): 214 -222 (in Chinese))
[本文引用: 1]
[30]
Haftka R T Adelman H M Recent developments in structural sensitivity analysis
.Structural Optimization , 1989 , 1 (3 ): 137 -151
[本文引用: 1]
[31]
Gu YX Zhao GZ Zhang HW et al .Buckling design optimization of complex built-up structures with shape and size variables
.Structural and Multidisciplinary Optimization , 2000 , 19 (3 ): 183 -191
[本文引用: 1]
旋转体形状优化及敏度分析的拟解析法
1
1986
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
旋转体形状优化及敏度分析的拟解析法
1
1986
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
Approximation of derivatives in semi-analytical structural optimization
3
2008
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
... F rr ∂ K ∂ d F rr ≠ 0 [2 ] 中所阐述的ESA基于单元级别进行误差修正, 其形式如下 ...
Review of options for structural design sensitivity analysis
1
2005
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
Sensitivity analysis and optimization of vibration modes in continuum systems
1
2013
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
Mapping method for sensitivity analysis of composite material property
1
2002
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
等几何壳体分析与形状优化
1
2014
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
等几何壳体分析与形状优化
1
2014
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
A new computation scheme for sensitivity analysis
1
1987
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
结构形状优化设计数值方法的研究和应用
1
1993
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
结构形状优化设计数值方法的研究和应用
1
1993
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
基于改进的灵敏度分析的有限元优化技术研究
1
2008
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
基于改进的灵敏度分析的有限元优化技术研究
1
2008
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
Semi-analytical static nonlinear structural sensitivity analysis
1
1993
... 灵敏度分析方法是结构优化实现的基础, 采用简洁高效的灵敏度分析方法更是提高优化效率的关键[1 ] . 已有的灵敏度求解方法包括: 全局差分法, 解析法与半解析法. 全局差分法[2 ,3 ] , 不牵涉设计的有限元模型和性能的计算方法和程序细节, 但每做一次敏度分析, 针对 n n + 1 [4 ,5 ] , 虽效率较高, 但推导过程较为繁琐, 尤其对于形状优化问题, 形状设计变量与有限元单元列式关系不仅复杂而且依赖于单元类型, 推导和编程均不具有通用性[6 ] . 为此, 程耿东等[7 ] 提出了半解析灵敏度分析方法, 为将有限元和结构优化高效结合起来提供了途径. 该方法将现有的有限元程序视为“黑箱”, 具有较强通用性, 求解多个设计变量的敏度只需一次完整有限元分析,具有较高的效率, 因此广泛地应用于结构优化问题中[8 ,9 ,10 ] . 但在传统半解析敏度分析的程序实现过程中, 通常从单元级别公式考虑, 需读入摄动前后两组单元刚度阵、质量阵、应力刚度阵等, 影响灵敏度求解总效率. ...
Error analysis of semianalytic displacement derivatives for shape and sizing variables,
1
1991
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Study of inaccuracy in semi-analytical sensitivity analysis—a model problem,
1
1991
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Accuracy problems associted with semi-analytical derivatives of static response
1
1988
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Rasmussen. On accuracy problems for semi-analytical sensitivity analyses
1
1989
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
梁的半解析法计算灵敏度的误差分析
1
1989
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
梁的半解析法计算灵敏度的误差分析
1
1989
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Accuracy analysis of the semi-analytical method for shape sensitivity calculation
2
1990
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
... 程耿东等[16 ] 研究表明, 半解析灵敏度分析方法应用于某些结构的形状优化问题会出现较大误差, 其原因为 ...
Rigid body motion test against error in semi-analytical sensitivity analysis
1
1993
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Rigorous improvement of semi-analytical design sensitivities by exact differentiation of rigid body motions
1
1998
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Refined second order semi-analytical design sensitivities
1
2002
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
A method of “exact” numerical differentiation for error elimination in finite-element-based semi-analytical shape sensitivity analyses
1
1993
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
Shape design sensitivity analysis of eigenvalues using ‘exact’ numerical differentiation of finite element matrices,
1994
Improved semi-analytical sensitivity analysis using a secant stiffness matrix for geometric nonlinear shape optimization
1
2015
... 半解析方法求解灵敏度, 使用差分近似替代刚度阵等对于设计变量求导, 虽简便计算, 但应用于某些结构的形状优化时有误差产生[11 ,12 ] . Barthelemy等[13 ] 发现, 使用半解析方法求解形状设计变量灵敏度时,误差随单元数目增加以平方形式增长. Pauli等[14 ] 对长度为设计变量的悬臂梁算例进行研究, 证明了此种模型的误差与梁长及单元划分数目有关. 其后, 程耿东等[15 ] 对梁单元, 长度为优化设计变量, 使用半解析法计算灵敏度的误差进行推导分析, 并提出采用中心差分可以提高精度. 随后Barthelemy 等[16 ] 的研究表明, 对于形状设计变量, 不仅梁单元, 其他单元建模的类梁结构使用半解析法进行灵敏度求解都会产生误差. 1993年程耿东等[17 ] 找到了误差产生的真正原因: 有限单元的刚体转动, 并给出相应误差判据. 在此之后, 刚体位移误差消除工作逐步开展. 目前最常用的方法有两种, 一种为RSA方法(refined semi-analytical technique)[18 ,19 ] , 致力于将位移分解为纯变形位移与刚体位移, 从提高导数的精度入手精化半解析灵敏度值. 另一种为ESA方法(exact semi-analytical technique)[2 ,20 -22 ] , 形式较为简单, 只在差分的刚度阵处加一修正项, 便可消除刚体位移误差的影响. 但在其修正项的构造过程中, 包含多个矩阵生成与运算, 修正项形式亦为矩阵, 尤其对于非结构化网格建模的复杂结构, 因每个单元的误差修正项均不相同, 矩阵形式修正项的多次构造使效率受到一定的影响. 此外, 无论是已有的RSA或ESA方法, 均在单元级别进行修正, 需要修改灵敏度分析代码内部结构, 不便于与已有的灵敏度分析代码进行结合. 另外, 半解析灵敏度分析只针对形状设计变量, 且单元具有较大刚体转动位移时出现误差. 大多数情况, 如尺寸设计变量, 无需修正. 因此, 对于同时具有形状设计变量与尺寸设计变量的混合优化问题, 需要两组灵敏度分析代码分别针对两种设计变量进行求解, 使得实现过程较为复杂. ...
基于凸模型的结构非概率可靠性优化
1
2006
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
基于凸模型的结构非概率可靠性优化
1
2006
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
非确定性结构静动态特性稳健优化设计
1
2006
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
非确定性结构静动态特性稳健优化设计
1
2006
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
一种有效的结构优化设计方法
1
1987
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
一种有效的结构优化设计方法
1
1987
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
面向压电智能结构精确变形的协同优化设计方法
1
2017
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
面向压电智能结构精确变形的协同优化设计方法
1
2017
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
基于多相材料的稳态热传导结构轻量化设计
1
2017
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
基于多相材料的稳态热传导结构轻量化设计
1
2017
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
考虑结构自重的基于NURBS插值的3D拓扑描述函数法
1
2016
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
考虑结构自重的基于NURBS插值的3D拓扑描述函数法
1
2016
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
广义变分原理的结构形状优化伴随法灵敏度分析
1
2013
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
广义变分原理的结构形状优化伴随法灵敏度分析
1
2013
... 本文在已有的研究工作基础上考虑以下改进(基于直接法[23 ,24 ,25 ] 灵敏度分析列式进行讨论, 该思想亦可应用于伴随方法[26 ,27 ,28 ,29 ] ): (1)从总体角度入手考虑半解析灵敏度分析公式, 公式摄动前部分对于静力分析即为外载荷, 自振与屈曲稳定性分析即为特征值, 避免初始刚度阵等矩阵的提取. (2)针对ESA 方法进行探究, 将修正项形式进行转化, 对于静力问题转化为一简单向量, 对于特征值问题转化为常数, 使得修正项求解过程无需矩阵的生成与操作. 构造可分离形式修正项, 在总体级别消除误差并能直接附加于灵敏度结果之后, 无需改变原灵敏度分析程序内部结构, 使已有程序充分利用. (3)针对梁与壳两类单元进行详细的刚体位移推导, 并说明其误差修正项构造方式. (4)现有的工作多基于静力问题, 本文以梁单元与壳单元为例, 进行静力、自振以及屈曲稳定性的灵敏度分析算例测试. ...
Recent developments in structural sensitivity analysis
1
1989
Buckling design optimization of complex built-up structures with shape and size variables
1
2000
... 对于屈曲非重特征值灵敏度问题[31 ] , 从单元角度考虑的带有矩阵修正项的特征值灵敏度公式为 ...