引言
试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响.
国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果.
上述模型能够在某 些加载条件下对砂土的应力应变响应进行模拟,如单调加载条件或者循环加载条件,但很少见到能在静力加载以及循环加 载等复杂加载条件下同时适用的模型.
通过引入状态参量 ψ p -- q
1 e p
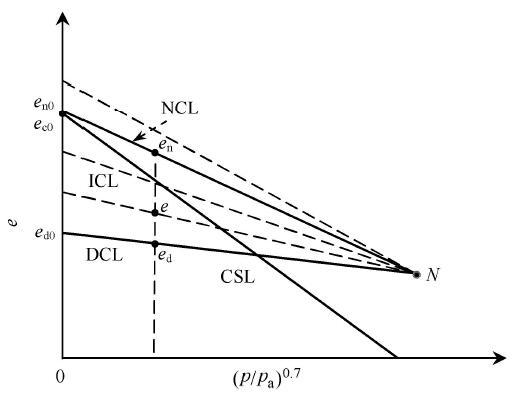
不同于黏土在 e -- ln p e -- ( p / p a ) ζ 图1 所示的曲线.
图1 在e ( p / p a ) ζ
Fig. 1 Series of compression lines and critical state line in e ( p / p a ) ζ
由图1 可见,假设e -- ( p / p a ) ζ e d 0 N .
对于正常压缩线,可将其表达为 e n = e n 0 - c t ( p p a ) ζ ( 1 )
回弹线,可表示为 e s = e 0 - c e ( p p a ) ζ ( 2 )
临界状态线表示为 e c = e c 0 - c c ( p p a ) ζ ( 3 )
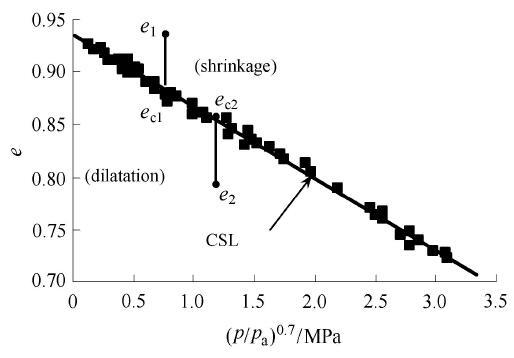
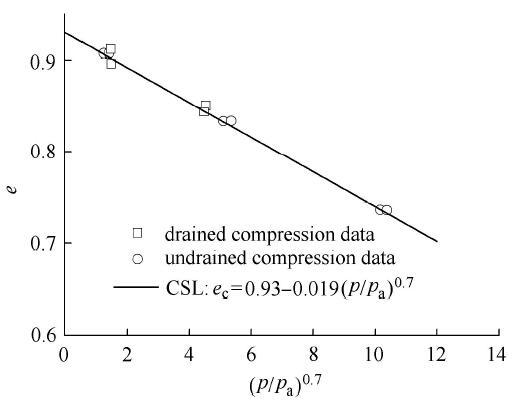
由图2 所示,图中黑色方框点表示Verdugo 和 Ishihara[22 ] 于1996年对Toyoura 砂土的试验数据,由图可见,在幂函数坐标系中,临界状态线可以用直线来表达. 由于临界状态线的唯一性,因而可以借鉴Been等的建议, 采用当前孔隙比与对应相同球应力下CSL线上的孔隙比之差 ψ
图2 在e ( p / p a ) ζ
Fig. 2 Critical state line of Toyoura sand in e p / p a ) ζ
2 本构模型
2.1 p q
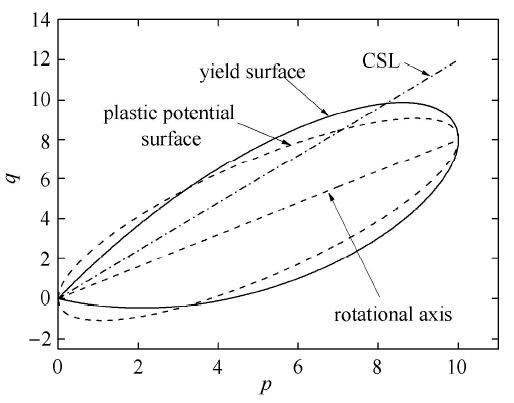
如图3 所示,在p -- q
图3 在p q
Fig. 3 Yielding surface and Plastic potential surface in p q
屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
由试验结果可知,针对密砂随初始密度的不同而出现不同程度的剪胀,其所对应剪胀发生时刻的应力比也会发生变化,与此同理,不同密度密砂的峰值应力比也会出现差异,通常按照试验规律可知,当初始孔隙比越小,则对应剪胀发生时刻的变相应力比越小,对应的峰值应力比越大,而相对的临界状态应力比不随密度发生变化. 由此,可建立变相应力比与峰值应力比与临界状态应力比的函数关系,将上述两个变量应力比表示为状态参量 R
M c = M a exp ( - mR ) , m onotonic M a , c yclic ( 10 )
M f = M exp ( nR ) , - 1.5 cm m onotonic 6 M 2 12 3 - M R 1 + M 2 12 3 - M R - M 2 12 3 - M R , - 1.5 cm c yclic ( 11 )
M p = M exp ( - mR ) , m onotonicM , c yclic ( 12 )
在单调加载条件下,则状态变量 R = e c - e e c p e -( p / p a ) ζ e
对于非单调加载路径下的情况,由于会涉及到卸载再加载等应力路径的影响,因而可利用应力比参量来替代孔隙比之差作为状态参量. 且应力比参量可参照动力UH模型的 R R R = p p a e N 0 - e - c e p / p a ζ c t - c e - 1 ζ α ( 13 ) α α α ~ 1 之间. 对于黏土,取为1,对于饱和砂土,通常可取为0.1. 对于对于过度应力比 M n
M n = M exp ( n R 1 ) , m onotonicM , c yclic ( 14 )
R 1 = e c - e n ( 15 )
其中, e n e -( p / p a ) ζ p
对于屈服面转轴的变化规律,可采用增量公式表达 d β ij = 1.5 M c p m b - β d ε d p η ̂ ij η * ( 16 ) d ε d p d ε d p = λ ∂ g ∂ s ij ∂ g ∂ s ij λ A
A = 1.5 η η * ζ P m b - β p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - 1 ⋅
3 η ̂ ij β ij - 2 M a 2 M a 2 - χ η * 2 2 ( 17 )
2.2 状态参量 χ
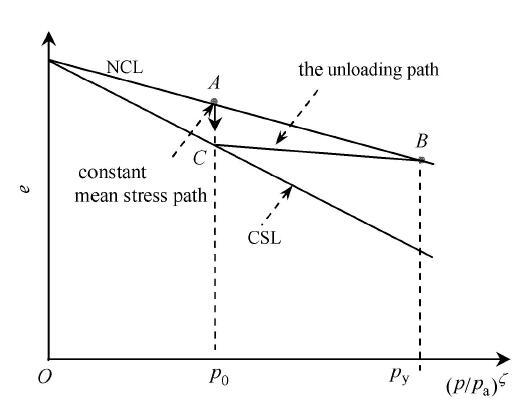
参照图4 可得到确定状态参量 χ p AB AC χ .
图4 在e ( p / p a ) ζ
Fig. 4 Isotropic loading and unloading curves of sand in e ( p / p a ) ζ
若不考虑旋转硬化的屈服面方程可退化为 f = η 2 M 2 - χ η 2 + 1 - p y p = 0 ( 18 ) η = q / p M p y 图4 所示, χ
对式(1)全微分有 d e n = - c t ζ p y p a ζ - 1 d p y p a ( 19 ) d e n p = - c t - c e ζ p y p a ζ - 1 d p y p a ( 20 )
塑性体应变增量 d ε v p d e n p d ε v p = - d e n p 1 + e ( 21 ) ∫ 1 + e c t - c e d ε v p = ∫ ζ p y p a ζ - 1 d p y p a = p y p a ζ - p 0 p a ζ ( 22 ) d H = 1 + e c t - c e d ε v p ( 23 ) ∫ d H = H = ∫ 1 + e c t - c e d ε v p = p y p a ζ - p 0 p a ζ ( 24 ) p 0 p y = p a ζ H + P 0 ζ 1 ζ ( 25 ) f = η 2 M 2 - χ η 2 + 1 - 1 p p a ζ H + p 0 ζ 1 ζ = 0 ( 26 )
对砂土沿着等 p p = p 0 η = M ) AC 11 - χ + 1 - p a p 0 ζ Δ e n p c t - c e + 1 1 ζ = 0 ( 27 )
在等 p p = p 0 Δ e p = c c - c t p 0 p a ζ ( 28 ) χ = 1 - c c - c e c t - c e 1 ζ - 1 - 1 ( 29 )
2.3 硬化参数确定
2.3.1 等向硬化参数分析
构成硬化参数的表达式主要由两部分组成,第1部分为考虑体积压缩硬化部分,第2部分为考虑应力诱导各向异性的剪切屈服硬化部分. H 1 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p ( 30 )
采用所提的模型对饱和砂土在常规三轴压缩不排水条件下进行模拟,考虑不同初始密度对于应力路径以及应力应变关系的影响, 图5 ~ 图9 分别为对应3种密度砂土的计算结果. 文中所用到的应力量若无特意说明,一律认为是有效应力.
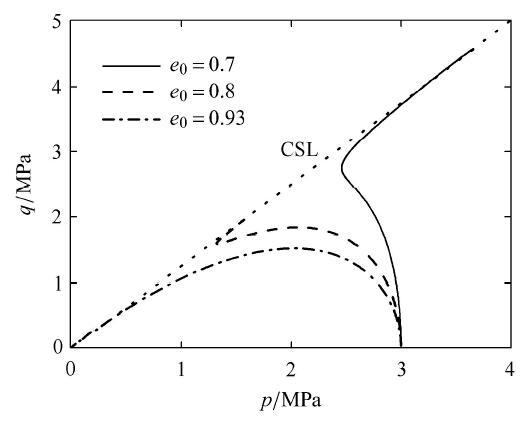
图5 在p q
Fig. 5 Three typical stress paths of sand under undrained condition in p q
图6 不同初始密度砂土的3条超净孔隙水压力曲线.
Fig. 6 Three typical pore pressure curves with different initial density
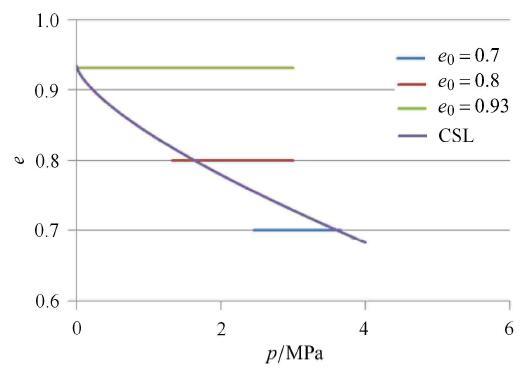
图7 在e p
Fig. 7 Three typical stress paths of sand under undrained condition in e p
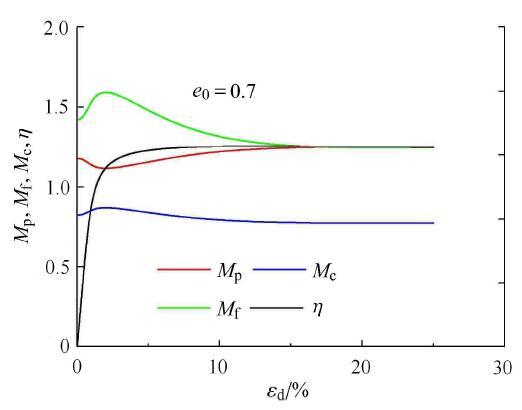
图8 孔隙比为0.7下4种应力比的变化过程.
Fig. 8 Changing process of four kinds of stress ratios with void ratio equals 0.7
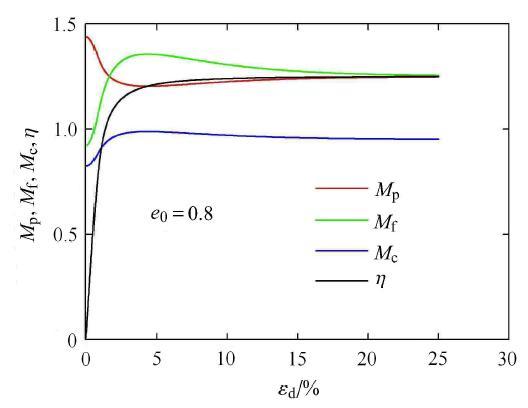
图9 孔隙比为0.8下4种应力比的变化过程.
Fig. 9 Changing process of four kinds of stress ratios with void ratio equals 0.8
图5 所示为3种典型的不排水应力路径,其中,初始压力为各向等压状态,p 0 = 3 图6 所示为对应的孔压与轴应变的关系曲线. 其中,临界状态线在p = 0 p 0 = 3 图6 中孔压也达到了3 MPa,表明土单元应力完全由孔隙水压力承担. 对应于孔隙比为0.7, 0.8时,则由图5 可见,随着加载的进行,出现剪胀现象,且随着孔隙比的增大,剪胀现象逐渐减弱,图6 中孔压也随着出现先增大后减小 的现象,且随着孔隙比的增大,孔压减小量递减. 当沿着初始密度为0.8的中密砂的路径行进时,则首先一直水平向左进行,在越过CSL线后过了最左侧点后,由于剪胀的作用,超静孔隙水 压力变为负孔压,此时,有效应力增大,再返回直到达到CSL线上. 对于密砂的应力路径,从p 0 = 3
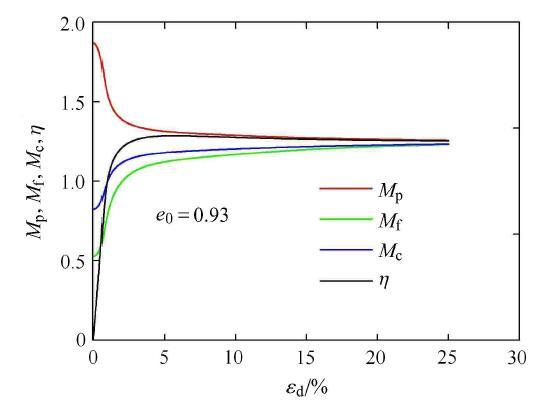
图8~图10 分别为当初始孔隙比为0.7, 0.8, 0.93时所对应的4种应力比指标的加载全过程曲线. 横坐标为广义剪应变,由对比 可见,当密度足够大时,则变相应力比M p M f M p H 1 M f
图10 孔隙比为0.93下4种应力比的变化过程 .
Fig. 10 Changing process of four kinds of stress ratios with void ratio equals 0.93
考察硬化参数第一项增量部分 d H 1 = M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p ( 31 )
(1)当砂土 属于密砂时,则当应力比η < M p < M f d ε v p > 0 d H 1 > 0 M p < η < M f d ε v p < 0 d H 1 > 0 M p = η = M f = M d ε v p = 0
(2)当砂土 属于松砂时,则当应力比 η < M f < M p d ε v p > 0 d H 1 > 0 M f < η < M p d ε v p > 0 d H 1 < 0 M p = η = M f = M d ε v p = 0 η < M p d σ ij = 0
(3)考察当进行等方向压缩应力路径时,则由于 η = 0 d H 1 = M f 4 M n 4 d ε v p M n M n = M f d H 1 = d ε v p M f < M n M f > M n
2.3.2 旋转硬化参数分析
构成硬化参数的第2部分为考虑应力诱导各向异性的剪切屈服硬化部分,考虑旋转硬化参数可表达为 H 2 = ∫ A d ε d p ( 32 ) d H 2 = A d ε d p = η M ∂ f ∂ β ij d β ij ( 33 ) d f = ∂ f ∂ σ ij d σ ij + ∂ f ∂ β ij d β i j - M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p - η M ∂ f ∂ β ij d β ij = 0 ( 34 )
显然当达到临界状态时,则式(34)可以变换为如下形式 d f = 1 - η M ∂ f ∂ β ij d β ij = 0 ( 35 )
当应力比达到 M ∂ f ∂ β ij d β ij
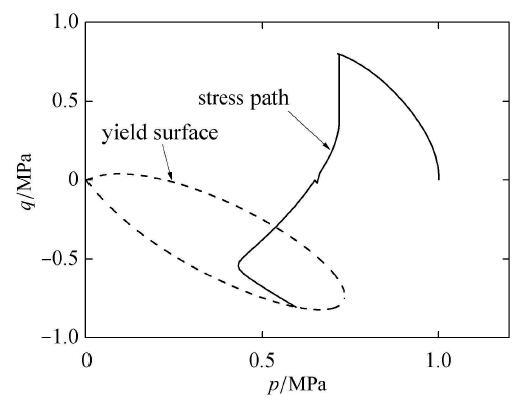
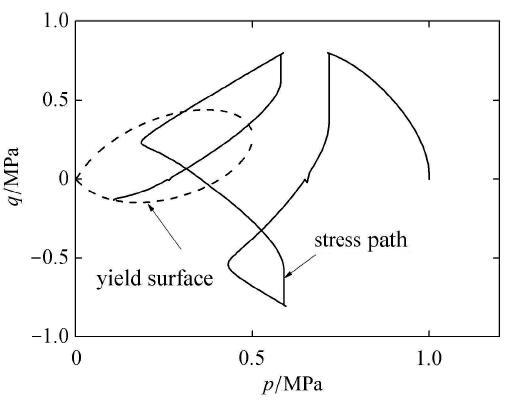
仍然采用所提的模型对往返活动性过程进行模拟分析,图11 ~ 图20 为对应的往返活动性现象的有效应力路径以及孔压的各阶 段 分解图. 其中 图11 ~ 图15 分别为往返活动性现象下的典型应力路径分解图. 记三轴压缩加卸载及三轴伸长加卸载为一个循环,则图示为在初始球应力为1 MPa下作用 7 / 4 图11 所示为当广义剪应力作用在三轴伸长路径下达到预定幅值时的状态,此时,屈服面由于在相对应力比分量的指引下,其转轴向下顺时针旋转到达最下端,且屈服面形状变为接近楔形的水滴形. 图12 为在三轴压缩作用下有效应力减小到最小时的状态,此时,屈服面由于在三轴伸长卸载过程中,应力比变化较小,此时,相对应力比的增量也很小,因此,转轴沿逆时针旋转也很缓慢,随着转轴逆时针转动,转轴绝对值 β 图13 为完成 5 / 4 图14 为1.5个循环完成后, 在反向卸载过程中,由于屈服面在坐标系中位置为类似于 K 0 p 图15 为三轴伸长加载到预定幅值时的状态,此时,转轴依然随应力比快速到达最下端.
图11 往返活动性应力路径过程图1 .
Fig. 11 Figure 1 of process of stress path for cyclic mobility
图12 往返活动性应力路径过程图2 .
Fig. 12 Figure 2 of process of stress path for cyclic mobility
图13 往返活动性应力路径过程图3 .
Fig. 13 Figure 3 of process of stress path for cyclic mobility
图14 往返活动性应力路径过程图4 .
Fig. 14 Figure 4 of process of stress path for cyclic mobility
图15 往返活动性应力路径过程图5 .
Fig. 15 Figure 5 of process of stress path for cyclic mobility
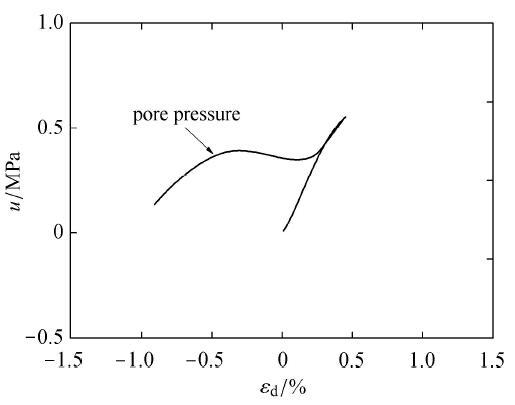
图16 往返活动性孔压发展过程图1
Fig. 16 Figure 1 of process of pore water pressure for cyclic mobility
图17 往返活动性孔压发展过程图2 .
Fig. 17 Figure 2 of process of pore water pressure for cyclic mobility
图18 往返活动性孔压发展过程图3 .
Fig. 18 Figure 3 of process of pore water pressure for cyclic mobility
图19 往返活动性孔压发展过程图4 .
Fig. 19 Figure 4 of process of pore water pressure for cyclic mobility
图20 往返活动性孔压发展过程图5 .
Fig. 20 Figure 5 of process of pore water pressure for cyclic mobility
图16~图20 分别为对应的超静孔隙水压力随轴应变的发展过程图. 图16 为对应三轴压缩然后卸载且反向加载后的孔压状态图, 孔压经历了先增大然后逐步减小的过程. 图17 中当三轴伸长卸载且继续三轴压缩加载时孔压继续快速增大. 图18 为对应的应力比趋近于临界状态应力比时,此时,由于应力比越过变相应力比,此时出现剪胀,孔压持续缓慢减小. 图19 为对应三轴压缩后卸载的过程阶段,此时孔压先是短暂剧烈减小,然后缓慢增大. 图20 中对应的阶段为当继续三轴伸长加载时,此时孔压逐渐减小的过程.
Seed[29 ] 曾把在循环加载后第一次发生液化时候的状态称之为“初始液化”,循环加载后也会产生往返活动性现象. 由于状态 参量 χ
当初始孔隙比较大时,即对应的密度状态量 χ 图21 ~ 图23 为所提模型对于准静态液化的模拟结果. 由图可见,当图21 中有效应力路径达到原点,此时图23 中孔压也达到了初始围压值,产生了液化现象. 对于较为密实的砂土,则会导致往返活动性现象,图24 ,图25 所示为当 χ = 0.13
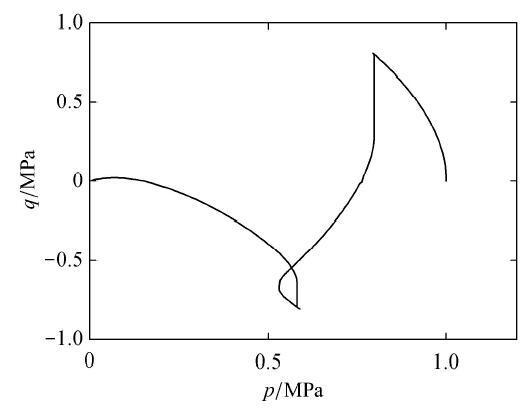
图21 循环加载下液化应力路径.
Fig. 21 Stress path of liquefaction under undrained cyclic loading condition
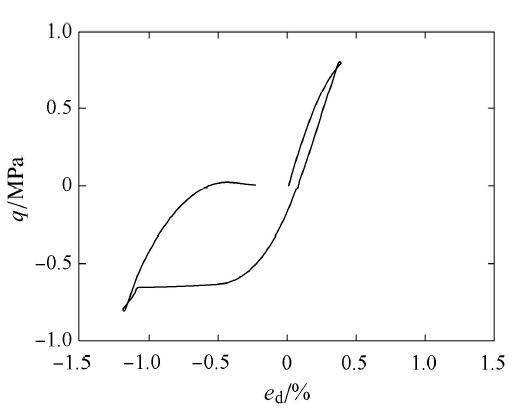
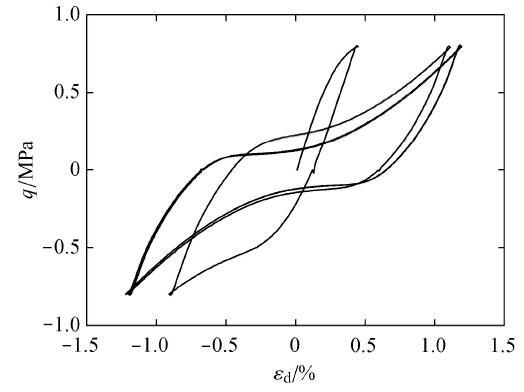
图22 循环加载下液化应力应变关系.
Fig. 22 Stress strain relationship of liquefaction under undrained cyclic loading condition
图23 往返活动性孔压发展过程图.
Fig. 23 Figure of process of pore water pressure for cyclic mobility
图24 往返活动性现象典型的应力路径.
Fig. 24 Typical stress path of cyclic mobility phenomena
图25 往返活动性现象典型的应力应变关系.
Fig. 25 Typical stress strain relationship of cyclic mobility phenomena
图22 为对应的液化应力应变曲线模拟结果,当经过1个循环周期后,再加载后应力路径直接趋向原点,广义偏应力为零,此时液化 现象触发. 此处,表明所提模型功能能够用于反映液化现象.
3 本构方程
3.1 弹塑性本构方程
根据对式(4)进行全微分,可得 ∂ f ∂ σ ij d σ ij + ∂ f ∂ β ij d β ij - Ω d ε v p 䆃 Ω A
Ω = M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 ( 37 )
A = 1.5 η η * ζ P m b - β p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - 1 ⋅
3 η ̂ ij β ij - 2 M a 2 M a 2 - χ η * 2 2 ( 38 )
由应力增量关系可知 d σ ij = D ijkl e d ε kl e = D ijkl e d ε kl - d ε kl p ( 39 )
弹性模量可表示为 E = 3 1 - 2 ν p a ζ ζ c e p ζ - 1 ( 40 )
弹性剪切模量 G = E 2 1 + ν = 3 1 - 2 ν p a ζ 2 1 + ν ζ c e p ζ - 1 ( 41 )
拉梅系数 L = E 3 1 - 2 ν - 23 G ( 42 )
将式(39)代入 式(36),可得到
∂ f ∂ σ ij D ijkl e d ε kl - λ ∂ f ∂ σ ij D ijkl e ∂ g ∂ σ kl + ∂ f ∂ β ij d β ij - M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p 䆃
∂ f ∂ σ ij = ζ c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - 1 ⋅ 13 1 + η * 2 M a 2 - χ η * 2 δ ij + M a 2 3 η ̂ ij - η kl η ̂ kl δ ij M a 2 - χ η * 2 2
(44)
∂ g ∂ σ ij = ζ c p p a ζ p 1 + η * 2 M c 2 ζ - 1 ⋅ 13 1 + η * 2 M c 2 δ ij + 3 η ̂ ij - η kl η ̂ kl δ ij M c 2 ( 45 )
∂ f ∂ β ij d β ij = 3 λ m b - β η * 2 ζ 2 pM c p M c 2 p a 2 ζ M a 2 - χ η * 2 2 ⋅ p 1 + η * 2 M a 2 - χ η * 2 ζ - 1 p 1 + η * 2 M c 2 ζ - 1 ⋅ 3 η ̂ kl β kl - 2 M a 2 ( 46 )
d σ ij = D ijkl d ε kl ( 47 )
D ijkl = D ijkl e - D ijmn e ∂ g ∂ σ mn ∂ f ∂ σ s t D stkl e / X ( 48 )
D ijkl = L δ ij δ kl + G δ ik δ jl + δ il δ jk -
L ∂ g ∂ σ mm δ ij + 2 G ∂ g ∂ σ ij L ∂ f ∂ σ nn δ kl + 2 G ∂ f ∂ σ kl / X
(49)
X = L ∂ f ∂ σ ii ∂ g ∂ σ ̃ kk + 2 G ∂ f ∂ σ ij ∂ g ∂ σ ij + T 1 + T 2 ( 50 )
T 1 = M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 ∂ g ∂ σ ij δ ij ( 51 )
T 2 = η M - 1 ∂ f ∂ β ij d β ij ( 52 )
3.2 加卸载准则
所提模型在复杂应力路径下的加卸载准则可根据如下公式进行判断 ∂ f ∂ σ ij D ijkl e ⋅ d ε kl > 0 , l oading ∂ f ∂ σ ij D ijkl e ⋅ d ε kl = 0 , n eutral ∂ f ∂ σ ij D ijkl e ⋅ d ε kl < 0 , u nloading ( 53 )
4 模型预测
4.1 单调加载下模型预测
利用所提模型对单调加载条件下的砂土应力应变关系进行预测. 所提模型共需要9个参数,其中根据等向压缩可得到参数回弹 系数 e n 0 c t c e c c ζ m n M m b . 泊松比 ν α .
压缩与回弹参数 c t c e e -- p λ κ
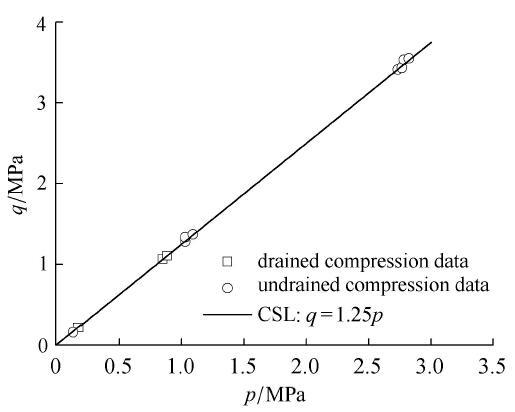
图26 和图27 分别为在应力空间与孔隙比空间确定临界状态线的方法,分别做常规三轴压缩排水与不排水试验,得到对应的最终临 界状态的 应力比强度值,排水条件下量测此时的体变,并计算得到此时的孔隙比,不排水条件下则量测此时的有效应力,并整理得到 有效球应力 p . 经整理后,可利用直线拟合数据,分别得到所需要的参数 M e n 0 c c ζ .
图26 p q M
Fig. 26 Calibration of M for slope of CSL in p q
图27 e p
Fig. 27 Calibration of CSL in e p
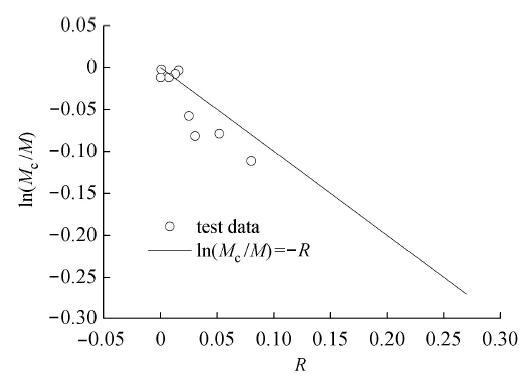
图28 为对应的确定变相应力比参数 m ln ( M c / M ) R m
图28 变相应力比参数m
Fig. 28 Calibration of phase transformation stress ratio parameter m
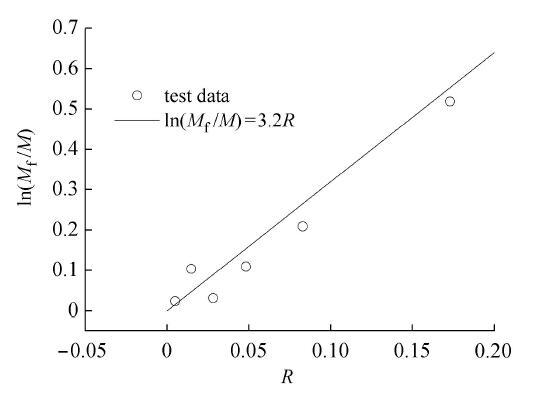
图29 为对应的确定峰值应力比参数 n ln ( M f / M ) R n
图29 峰值应力比参数n
Fig. 29 Calibration of peak stress ratio parameter n
m b ~ M α ~ 1 之间.
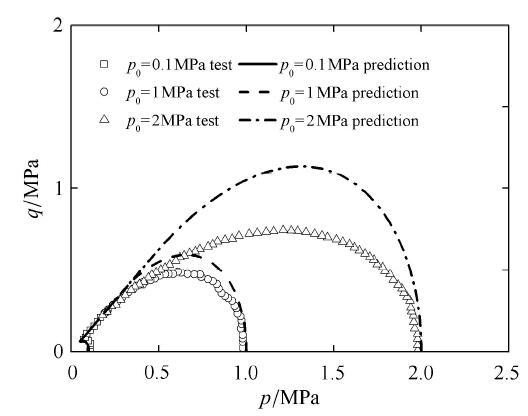
Verdugo和Ishihara曾针对Toyoura饱和砂土进行了一系列三轴剪切加载测试. 加载方式包括不排水常规三轴剪切以及排水常规三轴剪切. 图30 为初始孔隙比为0.735时的不排水应力路径测试以及预测对比图. 在较大初始密度下,分别对应有4种初始球应力作为初始压密状态,分别为0.1, 1.0, 2.0, 3.0 MPa. 在同样密度下,随着围压的增大,砂土由剪缩到剪胀的过渡应力比即变相应力比逐渐增大,高围压下密砂表现出类似于松砂在低围压下的路径特点.
图30 孔隙比0.735不排水应力路径三轴压缩预测与试验对比.
Fig. 30 Comparison between prediction and test results for stress paths under undrained triaxial compression condition with void ratio equals 0.735
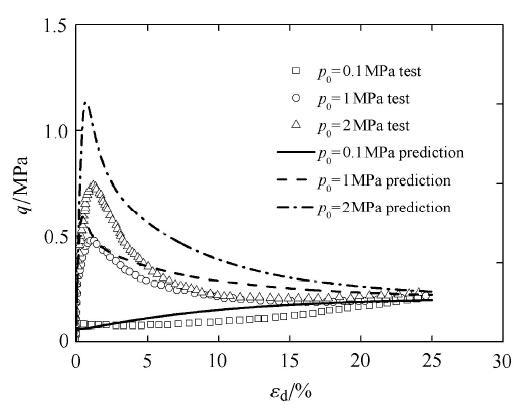
图31 为对应图30 应力路径的广义偏应力与偏应变的测试与预测对比. 由图可见,预测结果与测试结果能较好的吻合.
图31 孔隙比0.735不排水应力应变关系三轴压缩预测与试验对比.
Fig. 31 Comparison between prediction and test results for stress-strain relationship under undrained triaxial compression condition with void ratio equals 0.735
图32 和图33 分别为对应初始孔隙比为0.833时的应力路径以及应力应变关系对比图. 由图可见,在围压较小时,砂土应力路径以及应力应变关系表现出了典型的密砂特点.
图32 孔隙比0.833不排水应力路径三轴压缩预测与试验对比.
Fig. 32 Comparison between prediction and test results for stress paths under undrained triaxial compression condition with void ratio equals 0.833
图33 孔隙比0.833不排水应力应变关系三轴压缩预测与试验对比.
Fig. 33 Comparison between prediction and test results for stress-strain relationship under undrained triaxial compression condition with void ratio equals 0.833
图34 和图35 为对应初始孔隙比为0.907时的应力路径以及应力应变关系对比图. 由图可见,在较大围压下,砂土表现出 了强烈的松砂变形特性以及典型的应力路径. 预测结果在围压为2 MPa时过高的估计了其峰值偏应力强度. 表明所提模型在对松砂的压缩体变预估显得不足.
图34 孔隙比0.907不排水应力路径三轴压缩预测与试验对比.
Fig. 34 Comparison between prediction and test results for stress paths under undrained triaxial compression condition with void ratio equals 0.907
图35 孔隙比0.907不排水应力应变关系三轴压缩预测与试验对比.
Fig. 35 Comparison between prediction and test results for stress-strain relationship under undrained triaxial compression condition with void ratio equals 0.907
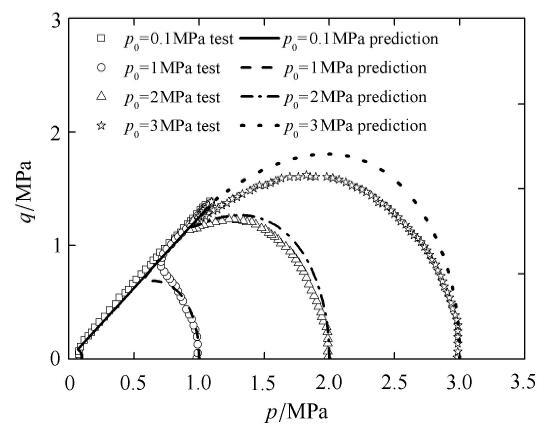
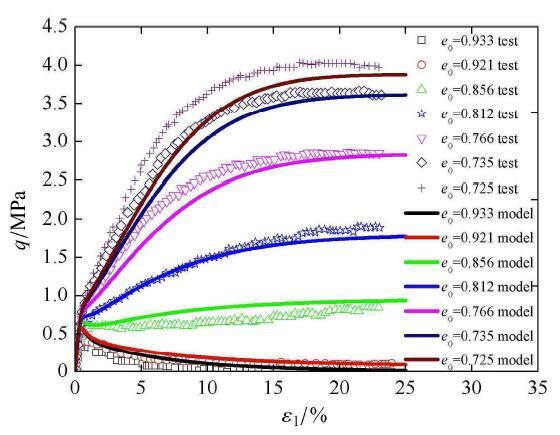
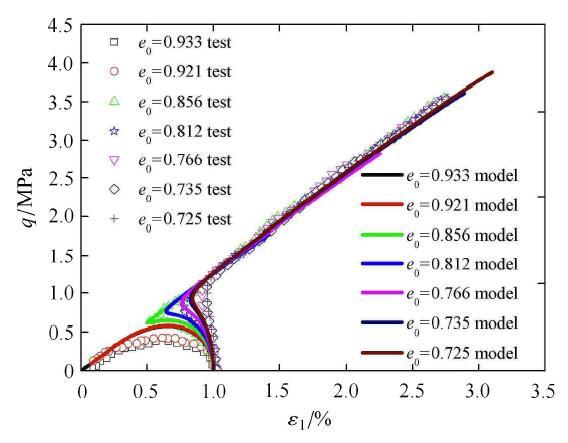
图36 表示在相同的初始球应力 p 图37 为对应的有效应力路径. 对于密砂,在孔隙比为0.725下广义偏应力强度预测值稍偏小,在松砂状态,当初始孔隙比为0.921及0.933时,预测值的峰值广义偏应力稍偏大. 由应力路径可见,在0.933时,模拟能够达到静态液化结果. 在松砂到密砂的中间密度状态,所提模型能够很好的对广义偏应力以及对应的应力路径较好的描述. 密砂的应变硬化以及松砂的应变软化特点,所提模型都能完全描述.
图36 不同初始孔隙比常规三轴不排水应力应变关系预测与试验对比.
Fig. 36 Comparison between prediction and test results for stress-strain relationship under undrained triaxial compression condition with various initial value of void ratio
图37 不同初始孔隙比常规三轴不排水应力路径关系预测与试验对比.
Fig. 37 Comparison between prediction and test results for stress paths under undrained triaxial compression condition with various initial value of void ratio
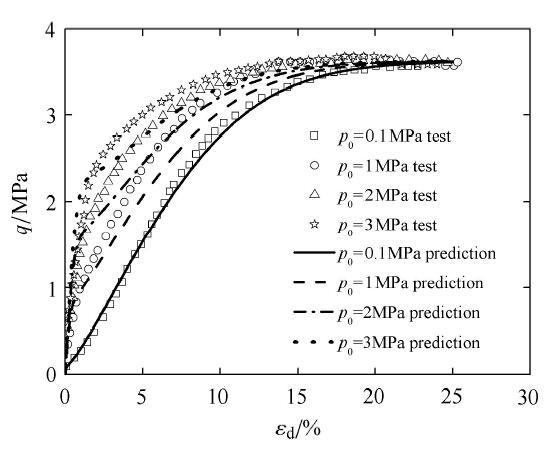
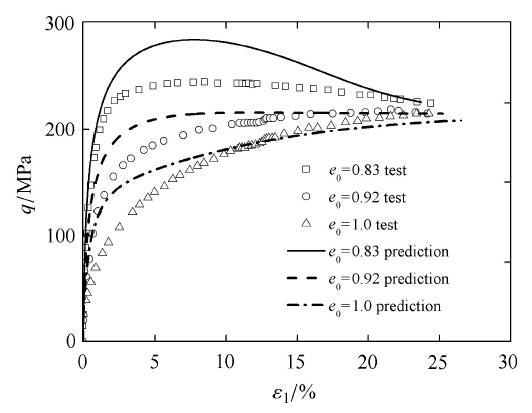
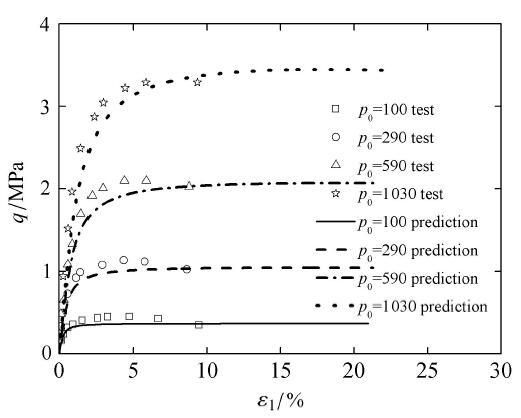
图38 和图39 为对于3种初始密度分别为0.83, 0.92, 1.0下,初始围压为0.1 MPa时的常规三轴压缩预测对比结果,对于中密砂0.83的峰值广义偏应力预测偏大.
图38 p 0 = 0.1
Fig. 38 Comparison between prediction and test results for generalized deviatoric stress versus void ratio under drained triaxial compression condition with initial value of p 0
图39 p 0 = 0.1
Fig. 39 Comparison between prediction and test results for generalized deviatoric stress versus the principal strain under drained triaxial compression condition with initial value of p 0
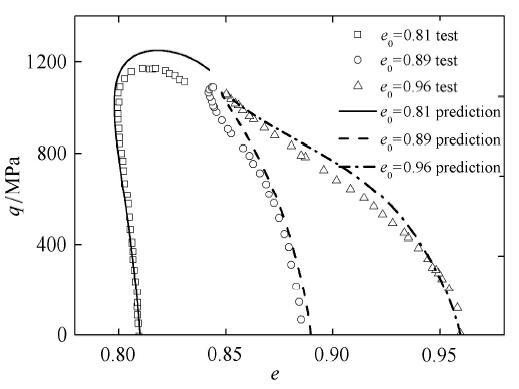
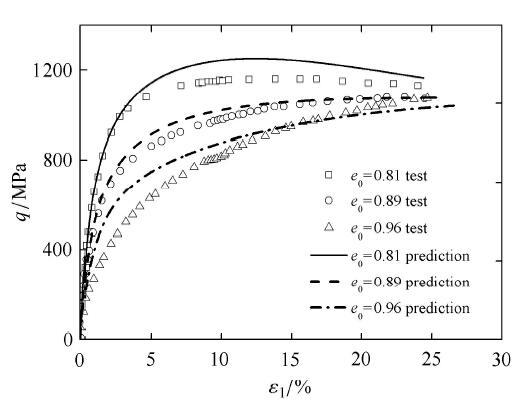
图40 和图41 为对于3种初始密度分别为0.81, 0.89, 0.96下,初始围压为0.5 MPa时的常规三轴压缩预测对比结果,由图可见,预测与测试结果吻合较好.
图40 p 0 = 0.5
Fig. 40 Comparison between prediction and test results for generalized deviatoric stress versus void ratio under drained triaxial compression condition with initial value of p 0
图41 p 0 = 0.5
Fig. 41 Comparison between prediction and test results for generalized deviatoric stress versus the principal strain under drained triaxial compression condition with initial value of p 0
为对比松砂以及密砂在不同初始围压下的体变关系,Lee和Seed[30 ] 对Sacramento河砂土进行了一系列排水常规三轴压 缩试验. 其中,图42 和图43 为对应松砂的应力应变关系对比图,图44 和图45 为对应密砂的预测对比图.
图42 Sacramento河松砂排水常规三轴压缩下的广义偏应力与大主应变关系测试与预测对比.
Fig. 42 Comparison between prediction and test results for generalized deviatoric stress versus the principal strain under drained triaxial compression condition of Sacramento river loose sand
图43 Sacramento河松砂排水常规三轴压缩下的体应变与大主应变关系测试与预测对比.
Fig. 43 Comparison between prediction and test results for volumetric strain versus the principal strain under drained triaxial compression condition of Sacramento river loose sand
图44 Sacramento河密砂排水常规三轴压缩下的广义偏应力与大主应变关系测试与预测对比.
Fig. 44 Comparison between prediction and test results for generalized deviatoric stress versus the principal strain under drained triaxial compression condition of Sacramento river dense sand
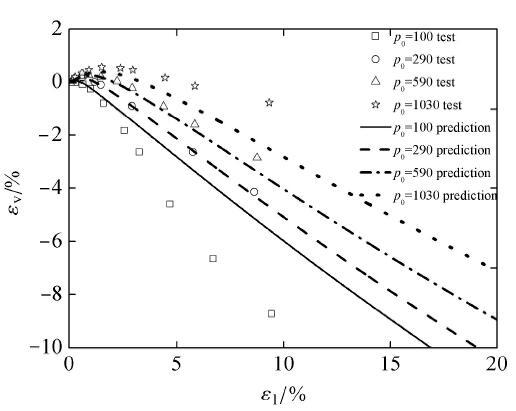
图45 Sacramento河密砂排水常规三轴压缩下的体应变与大主应变关系测试与预测对比.
Fig. 45 Comparison between prediction and test results for volumetric strain versus the principal strain under drained triaxial compression condition of Sacramento river dense sand
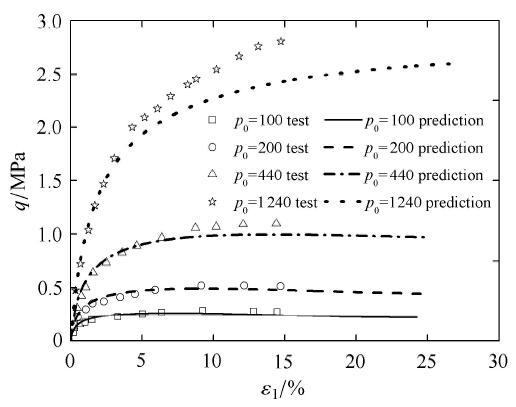
图42 为对应初始孔隙比为0.87时的广义偏应力与大主应变关系对比结果,在高围压下1 240 kPa下,对峰值偏应力预 测稍小,图43 为对应的体应变与大主应变关系对比,由图可见,体变预测吻合 较好.
图44 为对应初始孔隙比为0.61时的广义偏应力与大主应变关系对比结果,在4种不同围压下,广义偏应力与大主应变预测较好, 图45 中对于小围压的剪胀体变幅值预测偏小,在高围压下的剪胀体变幅值偏大. 在初始球应力为290 kPa, 590 kPa下所对应的体应变预测较好.
4.2 循环加载下模型预测
为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
图46 为对应松砂和密砂两种密度的Sacramento河砂土在等方向压缩加载路径下的预测对比图. 图中小方格表示为对应初始孔隙比 为0.87下的循环压缩测试结果,小圆圈表示初始孔隙比为0.61下的结果. 由对比可见,预测与试验结果吻合较好.
图46 Sacramento河砂等方向压缩下的孔隙比与球应力关系测试与预测对比.
Fig. 46 Comparison between prediction and test results for void ratio versus the mean stress under isotropic compression condition of Sacramento river sand
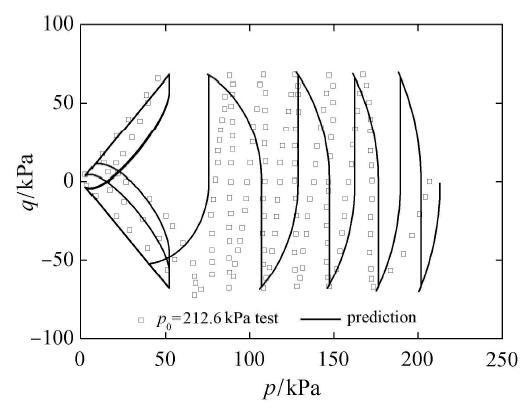
图47 和图48 为Ishihara等[44 ] 对Niigata砂土进行的双路不排水三轴循环加载测试结果,在初始球应力为212.6 kPa,初始孔 隙比为0.737下的对比结果,测试结果应力路径表明,在5个循环周期后,在第6个循环加载过程中,产生了往返活动性现象. 预测结果为在第5个循环加载过程中,产生了往返活动性应力路径. 图48 在出现往返活动性路径时,同时伴随着大主应变的剧烈增大,对比结果可较好地吻合这一规律. 由于在三轴伸长路径,未进行三轴伸长路径应力比强度的修正,造成了预测幅值偏大,这可通过将所提模型三维化来解决.
图47 Niigata砂双路不排水循环加载下的应力路径测试与预测对比.
Fig. 47 Comparison between prediction and test results for stress path under two way undrained cyclic loading condition of Niigata sand
图48 Niigata砂双路不排水循环加载下的应力应变关系测试与预测对比.
Fig. 48 Comparison between prediction and test results for stress strain relationship under two way undrained cyclic loading condition of Niigata sand
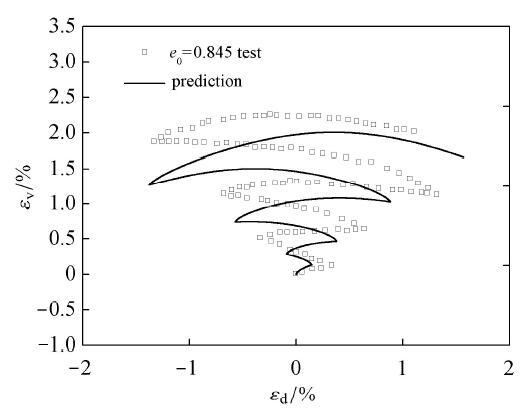
图49 和图50 为Pradhan等[45 ] 对Toyoura松砂进行的等 p
图49 Toyoura松砂在p = 98.1 p
Fig. 49 Comparison between prediction and test results for stress strain relationship under drained compression with constant p
图50 Toyoura松砂在p = 98.1 p
Fig. 50 Comparison between prediction and test results for volumetric strain versus generalized deviatoric strain under drained compression with constant p = 98.1
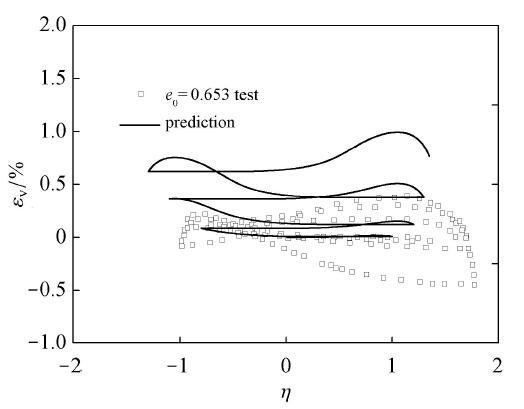
图51 和图52 为Pradhan等对Toyoura密砂进行的等 p
图51 Toyoura密砂在p p
Fig. 51 Comparison between prediction and test results for stress strain relationship under drained compression with constant p
图52 Toyoura密砂在p = 98.1 p
Fig. 52 Comparison between prediction and test results for volumetric strain versus generalized deviatoric strain under drained compression with constant p = 98.1
5 结 论
在临界状态土力学框架体系下提出了一个能考虑初始密度与围压且能反映循环加载等复杂应力路径的饱和砂土弹塑性本构模型. 该模型具备以下一些基本特点:
(1) 模型通过引入状态参量R
(2) 引入修正屈服面形状的状态参量 χ
(3) 在硬化参数中引入了考虑应力诱导各向异性的旋转硬化参量部分,与各向同性硬化部分共同作用. 由于屈服面与塑性势面均引入了能反映循环加载作用特性的转轴,塑性偏应变也对屈服面的硬化过程贡献作用. 在不排水往复循环作用下,能反映塑性体应变的循环累积作用,能反映塑性偏应变的往复滞回特点,如往返活动性现象. 同时对于松砂以及密砂的循环加载作用响应结果能较好的描述.
模型表明,仅用一套参数,可以对不同初始密度、围压以及三轴不排水、三轴排水等多种状态和路径下的应力应变关系给出较好的预测结果,表明所提模型对于砂土这种密度与压力依存性材料具有较好的描述能力.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Hashiguchi K Chen ZP Elastoplastic constitutive equation of soils with the subloading surface and the rotational hardening
.International Journal for Numerical and Analytical Methods in Geomechanics , 2015 , 22 (3 ): 197 -227
[本文引用: 1]
[2]
Roscoe KH Schofield AN Thurairajah A Yielding of clays in state wetter than critical
.Geotechnique , 1963 , 13 (3 ): 211 -240
[本文引用: 1]
[3]
Been K Jefferies MG A state parameter for sands
.Geotechnique , 1985 ,35 (2 ): 99 -112
[本文引用: 1]
[4]
Cai ZY Li XS Deformation characteristics and critical state of sand
.Chinese Journal of Geotechnical Engineering , 2004 , 26 (5 ): 697 -701
[本文引用: 1]
[5]
Zhang JM Wang G A constitutive model for evaluating small to large cyclic strains of saturated sand during liquefaction process
.Chinese Journal of Geotechnical Engineering , 2004 , 26 (4 ): 546 -552
[本文引用: 1]
[6]
Taiebat M Dafalias YF Sanisand: Simple anisotropic and plasticity model
.International Journal for Numerical and Analytical Methods in Geomechanics , 2008 , 32 (8 ): 915 -948
[本文引用: 1]
[7]
Gao ZW Zhao JD Constitutive modeling of anisotropic sand behavior in monotonic and cyclic loading
.Journal of Engineering Mechanics 2015 (8 ): 04105017
[本文引用: 1]
[8]
Li XS Dafalias YF A constitutive framework for anisotropic sand including nonproportional loading
.Geotechnique , 2004 , 54 (1 ): 41 -55
[本文引用: 1]
[9]
栾茂田 ,许成顺 ,何杨 等 . 主应力方向对饱和松砂不排水单调剪切特性影响的试验研究
. 岩土工程学报 , 2006 , 28 (9 ): 1085 -1089
[本文引用: 1]
(Luan Maotian Xu Chengshun He Yang et al .Experimental study on effect of orientation of the principal stress on undrained behavior of saturated loose sand under monotonic shearing
.Chinese Journal of Geotechnical Engineering 2006 , 28 (9 ): 1085 -1089 (in Chinese))
[本文引用: 1]
[10]
刘汉龙 , 周云东 , 高玉峰 . 砂土地震液化后大变形特性试验研究
. 岩土工程学报 , 2002 , 24 (2 ): 142 -146
[本文引用: 1]
(Liu Hanlong Zhou Yundong Gao Yufeng Study on the behavior of large ground displacement of sand due to seismic liquefaction
.Chinese Journal of Geotechnical Engineering 2002 , 24 (2 ): 142 -146 (in Chinese))
[本文引用: 1]
[11]
黄茂松 , 李学丰 , 贾苍琴 . 基于材料状态相关临界状态理论的砂土双屈服面模型
. 岩土工程学报 , 2010 , 32 (11 ): 1764 -1771
[本文引用: 1]
(Huang Maosong Li Xuefeng Jia Cangqin A double yield surface constitutive model for sand based on state-dependent critical state theory
.Chinese Journal of Geotechnical Engineering 2010 , 32 (11 ): 1764 -1771 (in Chinese))
[本文引用: 1]
[12]
董晓丽 , 赵成刚 , 张卫华 . 考虑相变状态的较密实饱和砂土弹塑性模型
. 工程力学 , 2017 , 34 (1 ): 51 -57
[本文引用: 1]
(Dong Xiaoli Zhao Chenggang Zhang Weihua The saturated dense sand elastic-plastic model considering phase transition state
.Engineering Mechanics 2017 , 34 (1 ): 51 -57 (in Chinese))
[本文引用: 1]
[13]
董全杨 , 蔡袁强 , 王军 等 . 松散砂土不稳定性试验研究
. 岩石力学与工程学报 , 2014 , 33 (3 ): 623 -630
[本文引用: 1]
(Dong Quanyang Cai Yuanqiang Wang Jun et al .Experimental study of instability of loose sand
.Chinese Journal of Rock Mechanics and Engineering 2014 , 33 (3 ): 623 -630 (in Chinese))
[本文引用: 1]
[14]
许成顺 , 高英 , 杜修力 等 . 双向耦合剪切条件下饱和砂土动强度特性试验研究
. 岩土工程学报 , 2014 , 36 (12 ): 2335 -2340
[本文引用: 1]
(Xu Chengshun Gao Ying Du Xiuli et al .Dynamic strength of saturated sand under bi-directional cyclic loading
.Chinese Journal of Geotechnical Engineering 2014 , 36 (12 ): 2335 -2340 (in Chinese))
[本文引用: 1]
[15]
陈国兴 , 庄海洋 . 基于Davidenkov骨架曲线的土体动力本构关系及其参数研究
. 岩土工程学报 , 2005 , 27 (8 ): 860 -864
[本文引用: 1]
(Chen Guoxing Zhuang Haiyang Developed nonlinear dynamic constitutive relations of soils based on Davidenkov skeleton curve
.Chinese Journal of Geotechnical Engineering 2005 , 27 (8 ): 860 -864 (in Chinese))
[本文引用: 1]
[16]
耿大将 , Peijun Guo 周顺华. 结构性软土弹塑性模型的隐式算法实现
. 力学学报 , 2018 , 50 (1 ): 78 -86
[本文引用: 1]
(Gen Dajiang Peijun Guo Zhou Shunhua Implicit numerical integration of an elasto-plastic constitutive model for structured clays
.Chinese Journal of Theoretical and Applied Mechanics 2018 , 50 (1 ): 78 -86 (in Chinese))
[本文引用: 1]
[17]
林皋 . 地下结构地震响应的计算模型
. 力学学报 , 2017 , 49 (3 ): 528 -542
[本文引用: 1]
(Lin Gao A computational model for seismic response analysis of underground structures
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (3 ): 528 -542 (in Chinese))
[本文引用: 1]
[18]
周健 , 史旦达 , 吴峰 等 . 基于数字图像技术的砂土液化可视化动三轴试验研究
. 岩土工程学报 , 2011 , 33 (1 ): 81 -87
[本文引用: 1]
(Zhou Jian Shi Danda Wu Feng et al .Visualized cyclic triaxial tests on sand liquefaction using digital imaging technique
.Chinese Journal of Geotechnical Engineering 2011 , 33 (1 ): 81 -87 (in Chinese))
[本文引用: 1]
[19]
陈育民 , 刘汉龙 , 邵国建 等 . 砂土液化及液化后流动特性试验研究
. 岩土工程学报 , 2009 , 31 (9 ): 1408 -1413
[本文引用: 1]
(Chen Yumin Liu Hanlong Shao Guojian et al .Laboratory tests on flow characteristics of liquefied and post-liquefied sand
.Chinese Journal of Geotechnical Engineering 2009 , 31 (9 ): 1408 -1413 (in Chinese))
[本文引用: 1]
[20]
王星华 , 周海林 . 砂土液化动稳态强度分析
. 岩石力学与工程学报 , 2003 , 22 (1 ): 96 -102
[本文引用: 1]
(Wang Xinghua Zhou Hailin Study on dynamic steady state strength of sand soil liquefaction
.Chinese Journal of Rock Mechanics and Engineering 2003 , 22 (1 ): 96 -102 (in Chinese))
[本文引用: 1]
[21]
迟明杰 , 赵成刚 , 李小军 . 砂土剪胀机理的研究
. 土木工程学报 , 2009 , 42 (3 ): 99 -104
[本文引用: 1]
(Chi Mingjie Zhao Chenggang Li Xiaojun Stress-dilation mechanism of sands
.China Civil Engineering Journal 2009 , 42 (3 ): 99 -104 (in Chinese))
[本文引用: 1]
[22]
Verdugo R Ishihara K The steady state of sandy soils
.Soils and Foundations , 1996 , 36 (2 ): 81 -91
[本文引用: 1]
[23]
Yao YP Sun DA Matsuoka H A unified constitutive model for both clay and sand with hardening parameter independent on stress path
.Computers and Geotechnics , 2008 , 35 : 210 -222
[本文引用: 1]
[24]
Yao YP Sun DA Luo T A critical state model for sands dependent on stress and density
.International Journal for Numerical and Analytical Methods in Geomechanics , 2004 , 28 : 323 -337
[本文引用: 1]
[25]
Yao YP Hou W Zhou AN UH model: Three-dimensional unified hardening model for overconsolidated clays
.Geotechnique , 2009 , 59 (5 ): 451 -469
[本文引用: 1]
[26]
Yao YP Matsuoka H Sun DA. A unified elastoplastic model for clay and sand with the SMP criterion//Proc. , 8th Australia New Zealand Conf. on Geomechanics , Hobart , 1999 ,Vol
.Ⅱ: 997 -1003
[本文引用: 1]
[27]
姚仰平 , 侯伟 , 周安楠 . 基于Hvorslev面的超固结土本构模型
. 中国科学:技术科学 , 2007 , 37 (11 ): 1417 -1429
[本文引用: 1]
(Yao Yangping Hou Wei Zhou Annan Constitutive model for overconsolidated clays
.Science China-Technological Sciences 2007 , 37 (11 ): 1417 -1429 (in Chinese))
[本文引用: 1]
[28]
姚仰平 , 余亚妮 . 基于统一硬化参数的砂土临界状态本构模型
. 岩土工程学报 , 2011 , 33 (12 ): 1827 -1832
[本文引用: 1]
(Yao Yangping Yu Yani Extended critical state constitutive model for sand based on unified hardening parameter
.Chinese Journal of Geotechnical Engineering 2011 , 33 (12 ): 1827 -1832 (in Chinese))
[本文引用: 1]
[29]
Seed HB Martin PP Lysmer J Pore pressure changes during soil liquefaction
.Journal of Geotechnical Engineering Division, ASCE , 1976 , 102 (4 ): 323 -346
[本文引用: 1]
[30]
Lee KL Seed HB Drained strength characteristics of sands
.Journal of the Soil Mechanics and Foundations Division. Proceedings of the American Society of Civil Engineers , 1967 , 93 (SM6 ): 117 -141
[本文引用: 1]
[31]
Yao YP Lu DC Zhou AN et al .Generalized non-linear strength theory and transformed stress space
.Science in China Ser. E , 2004 , 47 (6 ): 691 -709
[本文引用: 1]
[32]
Gao ZW Zhao JD Yao YP A generalized anisotropic failure criterion for geomaterials
.International Journal of Solids and Structures , 2010 , 47 (22-23 ): 3166 -3185
[本文引用: 1]
[33]
Matsuoka H Yao YP Sun DA The Cam-clay models revised by the SMP criterion
.Soils and Foundations , 1999 , 39 (1 ): 81 -95
[本文引用: 1]
[34]
Yao YP Wang ND Transformed stress method for generalizing soil constitutive models
.Journal of Engineering Mechanics , 2014 , 140 (3 ): 614 -629
[本文引用: 1]
[35]
Nakai T Matsuoka H Shear behaviors of sand and clay under three-dimensional stress condition
.Soils and Foundations , 1983 , 23 (2 ): 26 -42
[本文引用: 1]
[36]
Matsuoka H Nakai T Stress-deformation and strength characteristics of soil under three difference principal stresses
.Proceedings fo the Japan Society of Civil Engineers , 1974 , 232 : 59 -70
[本文引用: 1]
[37]
Yao YP Sun DA Application of Lade’s criterion to Cam-Clay model
.Journal of Engineering Mechanics ASCE , 2000 , 126 (1 ): 112 -119
[本文引用: 1]
[38]
Yao YP Zhou AN Lu DC Extended transformed stress space for geomaterials and its application
.Journal of Engineering Mechanics ASCE , 2007 , 133 (10 ): 1115 -1123
[本文引用: 1]
[39]
Yao YP Hou W Zhou AN UH model: Three-dimensional unified hardening model for overconsolidated clays
.Geotechnique , 2009 , 59 (5 ): 451 -469
[本文引用: 1]
[40]
Yao YP Niu L Cui WJ Unified hardening (UH) model for overconsolidated unsaturated soils
.Canadian Geotechnical Journal , 2014 , 51 (7 ): 810 -821
[本文引用: 1]
[41]
Yao YP Cui WJ Wang ND Three-dimensional dissipative stress space considering yield behavior in deviatoric plane
.Science China-Technological Sciences , 2013 , 56 (8 ): 1999 -2009
[本文引用: 1]
[42]
万征 , 姚仰平 , 孟达 . 复杂加载下混凝土的弹塑性本构模型
. 力学学报 , 2016 , 48 (5 ): 1159 -1171
[本文引用: 1]
(Wan Zheng Yao Yangping Meng Da An elastoplastic constitutive model of concrete under complicated load
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (5 ): 1159 -1171 (in Chinese))
[本文引用: 1]
[43]
万征 , 秋仁东 , 郭金雪 . 岩土的一种强度准则及其变换应立法
. 力学学报 , 2017 , 49 (3 ): 726 -740
[本文引用: 1]
(Wan Zheng Qiu Rendong Guo Jinxue A kind of strength and yield criterion for geomaterials and its transformation stress method
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (3 ): 726 -740 (in Chinese))
[本文引用: 1]
[44]
Ishihara K Tatsuoka F Yasuda S Undrained deformation and liquefaction of sand under cyclic stresses
.Soils and Foundations , 1975 , 15 (1 ): 29 -44
[本文引用: 1]
[45]
Pradhan TBS Tatsouka F Sato Y Experimental stress-dilatancy relations of sand subjected to cyclic loading
.Soils and Foundations , 1989 , 29 (1 ): 45 -64
[本文引用: 1]
Elastoplastic constitutive equation of soils with the subloading surface and the rotational hardening
1
2015
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
Yielding of clays in state wetter than critical
1
1963
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
A state parameter for sands
1
1985
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
Deformation characteristics and critical state of sand
1
2004
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
A constitutive model for evaluating small to large cyclic strains of saturated sand during liquefaction process
1
2004
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
Sanisand: Simple anisotropic and plasticity model
1
2008
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
Constitutive modeling of anisotropic sand behavior in monotonic and cyclic loading
1
2015
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
A constitutive framework for anisotropic sand including nonproportional loading
1
2004
... 试验及现场实测表明,饱和砂土是一种状态相关材料. 密度可直接影响其应力应变关系,如松砂在排水剪切载荷下体积剪缩,而密砂在同种 加载条件下则会产生体积剪胀现象,此外,围压也会对其产生影响,如松砂在较低围压下也会产生类似密砂的变形特点,而 密砂在高围压下 也会产生类似松砂的变形规律,显然密度与围压存在交叉耦合影响. 早期学者,如Hashiguchi等[1 ] 曾经将相对密度作为物性参数来使用,将其引入到模型中,来描述不同初始密度饱和砂土的 应力应变关系, 这种做法虽然并未明确提出状态参数的概念,但本质上却已经暗含了将其作为一种状态参量来使用的途径. 作为状态参量,显然需要一个不受初始条件如密度、围压等因素影响的稳定状态作为参照才可方便将状态量定量化,显然,临界 状态就是 一种稳定状态,临界状态首先是针对饱和黏土而提出的,Roscoe等[2 ] 发现 e p [3 ] 将在 e -- p ψ [4 ] 利用上述状态参量构造剪胀方程,并在 p -- q g ( θ ) [5 ] 着眼于砂土液化后循环加载的变形特性,将剪切加载所引起的体变分解为可逆体变与不可逆体变,在边界面 框架内定义映 射法则以及加载转折机制,从而能够描述液化后不排水循环加载下的往返活动性现象. Taiebat等[6 ] 在 p -- q ψ [7 ] 从原生各向异性的角度来阐释各向异性对于体变的影响,采用由一个反映砂土微观组构张量的参量来修正硬化参数和状态 参量,进而修正剪胀方程,最终能够用于描述主应力加载方向与沉积面成不同夹角时的不同应力应变关系,并能用于模拟砂土静态液化现象. Li等[8 ] 采用能反映原生各向异性的应力联合不变量和加载方向向量来构建一个反映各向异性的状态变量,利用上述各向异性状态量 可以反映组构各向异性以及非比例加载下的应力历史对应力应变关系的影响. ...
主应力方向对饱和松砂不排水单调剪切特性影响的试验研究
1
2006
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
主应力方向对饱和松砂不排水单调剪切特性影响的试验研究
1
2006
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土地震液化后大变形特性试验研究
1
2002
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土地震液化后大变形特性试验研究
1
2002
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
基于材料状态相关临界状态理论的砂土双屈服面模型
1
2010
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
基于材料状态相关临界状态理论的砂土双屈服面模型
1
2010
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
考虑相变状态的较密实饱和砂土弹塑性模型
1
2017
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
考虑相变状态的较密实饱和砂土弹塑性模型
1
2017
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
松散砂土不稳定性试验研究
1
2014
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
松散砂土不稳定性试验研究
1
2014
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
双向耦合剪切条件下饱和砂土动强度特性试验研究
1
2014
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
双向耦合剪切条件下饱和砂土动强度特性试验研究
1
2014
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
基于Davidenkov骨架曲线的土体动力本构关系及其参数研究
1
2005
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
基于Davidenkov骨架曲线的土体动力本构关系及其参数研究
1
2005
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
周顺华. 结构性软土弹塑性模型的隐式算法实现
1
2018
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
周顺华. 结构性软土弹塑性模型的隐式算法实现
1
2018
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
地下结构地震响应的计算模型
1
2017
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
地下结构地震响应的计算模型
1
2017
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
基于数字图像技术的砂土液化可视化动三轴试验研究
1
2011
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
基于数字图像技术的砂土液化可视化动三轴试验研究
1
2011
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土液化及液化后流动特性试验研究
1
2009
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土液化及液化后流动特性试验研究
1
2009
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土液化动稳态强度分析
1
2003
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土液化动稳态强度分析
1
2003
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土剪胀机理的研究
1
2009
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
砂土剪胀机理的研究
1
2009
... 国内学者针对饱和砂土的变形及强度特性也开展了大量深入的研究工作,也取得了一定的成果. 栾茂田等[9 ] 采用自主开发的土工静动 三轴扭转多功能剪切仪,对饱和砂土在主应力方向影响下的强度及变形特性进行了试验研究,结果表明,大主应力与竖向之间夹角越大,则砂土内摩擦角越低,初始相对密度越低,砂土越容易发生软化现象. 刘汉龙等[10 ] 采用多功能三轴仪开展了砂土液化后大变形试验,并基于试验结果提出了一个能描述液化后砂土应力应变关系的双曲线模型. 黄茂松等[11 ] 在分析饱和砂土剪切变形以及压缩变形机理上提出了一个双屈服面模型,可以较好地反映静力加载条件下密度与围压依存性对应力应变关系的影响. 董晓丽等[12 ] 改进了CASM模型,通过引入剪胀应力比以及采用一种与应力路径无关硬化参数的方式得到了修正CASM模型,可用于反映中密砂土的应力应变关系. 董全杨等[13 ] 对于松砂的不稳定性进行了试验研究,结果表明,松砂无论排水与否都是在同一应力比下达到不稳定状态. 许成顺等[14 ] 用双向耦合多功能剪切仪对饱和砂土开展了循环耦合剪切试验,砂土液化动强度与相位差及幅值比值密切相关. 陈国兴等[15 ] 对描述一维动应力--应变关系的Davidenkov骨架曲线,利用曼辛法则修正了加载再加载的动应力应变关系曲线,得到了一个动剪切模量比与阻尼比符合试验结果的动本构模型. 在将模型的有限元应用研究中,耿大将等[16 ] 对考虑结构性的SANICLAY模型进行了隐式算法实现. 林皋[17 ] 提出了一种新的关于岩土介质在结构物上的动力加载方法,具有简单高效的特点. 此外,周健等[18 ] ,陈育民等[19 ] ,王星华等[20 ] ,迟明杰等[21 ] 针对砂土液化以及剪胀特性方面取得了有特色的成果. ...
The steady state of sandy soils
1
1996
... 由图2 所示,图中黑色方框点表示Verdugo 和 Ishihara[22 ] 于1996年对Toyoura 砂土的试验数据,由图可见,在幂函数坐标系中,临界状态线可以用直线来表达. 由于临界状态线的唯一性,因而可以借鉴Been等的建议, 采用当前孔隙比与对应相同球应力下CSL线上的孔隙比之差 ψ
A unified constitutive model for both clay and sand with hardening parameter independent on stress path
1
2008
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
A critical state model for sands dependent on stress and density
1
2004
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
UH model: Three-dimensional unified hardening model for overconsolidated clays
1
2009
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
Vol
1
1999
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
基于Hvorslev面的超固结土本构模型
1
2007
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
基于Hvorslev面的超固结土本构模型
1
2007
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
基于统一硬化参数的砂土临界状态本构模型
1
2011
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
基于统一硬化参数的砂土临界状态本构模型
1
2011
... 屈服面表达式为 f = c p p a ζ p 1 + η * 2 M a 2 - χ η * 2 ζ - p 0 ζ - H = 0 ( 4 ) g = c p p a ζ p 1 + η * 2 M c 2 ζ - p 0 ζ - H = 0 ( 5 ) c p = c t - c e 1 + e 0 c t e -( p / p a ) ζ c e e 0 p 0 p a M a = M 2 - β 2 M β β = 1.5 β ij β ij β ij β ij = s β ij p β = σ β ij - p β δ ij p β σ β ij p β p β = σ β ij δ ij / 3 . η * η * = 1.5 η ̂ ij η ̂ ij = 1.5 η ij - β ij η ij - β ij ( 6 ) χ η ̂ ij = η ij - β ij ( 7 ) η ij = s ij p = σ ij - p δ ij p ( 8 ) [23 ,24 ,25 ,26 ,27 ,28 ] 建议的统一硬化参数,可经过修正表达为 H = H 1 + H 2 = ∫ M p 4 M n 4 M f 4 - η 4 M p 4 - η 4 d ε v p + ∫ A d ε d p ( 9 ) M c M f M n M p M c M p
Pore pressure changes during soil liquefaction
1
1976
... Seed[29 ] 曾把在循环加载后第一次发生液化时候的状态称之为“初始液化”,循环加载后也会产生往返活动性现象. 由于状态 参量 χ
Drained strength characteristics of sands
1
1967
... 为对比松砂以及密砂在不同初始围压下的体变关系,Lee和Seed[30 ] 对Sacramento河砂土进行了一系列排水常规三轴压 缩试验. 其中,图42 和图43 为对应松砂的应力应变关系对比图,图44 和图45 为对应密砂的预测对比图. ...
Generalized non-linear strength theory and transformed stress space
1
2004
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
A generalized anisotropic failure criterion for geomaterials
1
2010
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
The Cam-clay models revised by the SMP criterion
1
1999
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Transformed stress method for generalizing soil constitutive models
1
2014
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Shear behaviors of sand and clay under three-dimensional stress condition
1
1983
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Stress-deformation and strength characteristics of soil under three difference principal stresses
1
1974
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Application of Lade’s criterion to Cam-Clay model
1
2000
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Extended transformed stress space for geomaterials and its application
1
2007
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
UH model: Three-dimensional unified hardening model for overconsolidated clays
1
2009
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Unified hardening (UH) model for overconsolidated unsaturated soils
1
2014
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Three-dimensional dissipative stress space considering yield behavior in deviatoric plane
1
2013
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
复杂加载下混凝土的弹塑性本构模型
1
2016
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
复杂加载下混凝土的弹塑性本构模型
1
2016
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
岩土的一种强度准则及其变换应立法
1
2017
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
岩土的一种强度准则及其变换应立法
1
2017
... 为便于将所提模型应用到循环加载等复杂加载路径中,采用变换应力方法[31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ] 将模型拓展为三维弹塑性本构模型. 为验证所提模型在循环加载下的应力应变关系的适用性,采用等方向循环压缩加载路径、双路不排水循环加载以及等 p
Undrained deformation and liquefaction of sand under cyclic stresses
1
1975
... 图47 和图48 为Ishihara等[44 ] 对Niigata砂土进行的双路不排水三轴循环加载测试结果,在初始球应力为212.6 kPa,初始孔 隙比为0.737下的对比结果,测试结果应力路径表明,在5个循环周期后,在第6个循环加载过程中,产生了往返活动性现象. 预测结果为在第5个循环加载过程中,产生了往返活动性应力路径. 图48 在出现往返活动性路径时,同时伴随着大主应变的剧烈增大,对比结果可较好地吻合这一规律. 由于在三轴伸长路径,未进行三轴伸长路径应力比强度的修正,造成了预测幅值偏大,这可通过将所提模型三维化来解决. ...
Experimental stress-dilatancy relations of sand subjected to cyclic loading
1
1989
... 图49 和图50 为Pradhan等[45 ] 对Toyoura松砂进行的等 p