液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道.
1 双矩形腔静压推力轴承动态特性
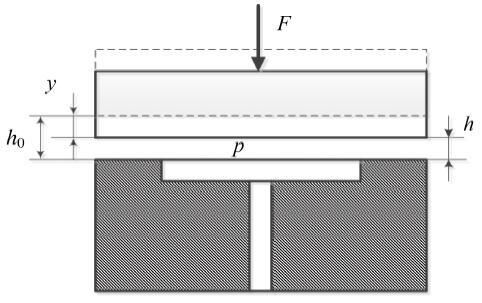
液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ]
图1 双矩形腔静压推力轴承工作原图
Fig.1 Working principle of hydrostatic thrust bearing with double rectangular cavities
1.1 油膜变化过程
初始工作状态, 只承受轴系重力及惯性力, 轴承油膜间隙为$h_0$, 若突然施加阶跃载荷, 油膜厚度由$h_0$ 变为$h$, 在此瞬间旋转工作台获得向下运动速度为$\dot{h}$, 向下运动加速度为$\ddot{h}$.
1.2 承受载荷特性
静压推力轴承在工作过程中, 主要承受轴向载荷和切削力, 由于切削力突然施加到轴承系统上, 因此, 将突加切削力作为阶跃载荷, 其函数形式为
\begin{equation*}\begin{split}f(t)=\begin{cases}F,\quad &t\geqslant0\\0,&t<0\end{cases}\end{split}\tag*{(1)}\end{equation*}
其拉氏变换形式为
\begin{equation*}f(s)=\dfrac{F}{s}\tag*{(2)}\end{equation*}
1.3阶跃载荷作用下静压推力轴承系统特性
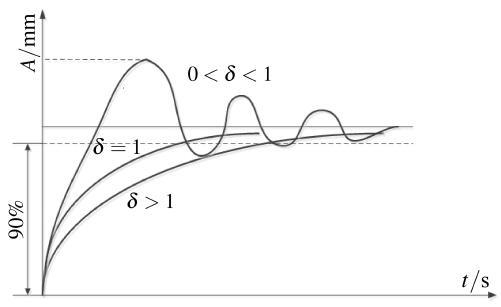
静压推力轴承在受到外界突加载荷作用, 从初始稳定状态恢复到新的平衡状态, 需要一个过渡过程, 各种过渡过程表现形式如图2 所示.
图2 过渡过程表现形式\
Fig.2 Transition process forms
当阻尼率$\delta\geqslant 1$时, 过渡过程呈现单调增长趋势, 即位移量为非周期性的单调上升, 经过一段响应时间后, 位移重新稳定在平衡位置.
当$0<\delta<1$时, 呈现出衰减振荡过渡, 即位移量围绕着新的平衡位置衰减振荡, 最终逐渐稳定于新的平衡位置.
当$\delta=0$时, 呈现无衰减等幅振荡变化, 此时静压推力轴承系统处于临界稳定状态, 但这种状态在实际工作中并不会出现.
2动态特性分析数学模型
2.1 油膜刚度方程
当静压支承负载发生变化时, 将产生沿负载方向位移, 流体膜厚也将发生相应变化. 刚度就是表示单位流体膜厚变化所须负载变化量, 平均刚度表示为
\begin{equation*}k=\dfrac{{d}W}{{d}h}\tag*{(3)}\end{equation*}
式中, $W$为载荷, $h$为油膜厚度.
当$h$油膜变化量趋近于零时, 即为静刚度.
油腔压力
\begin{equation*}P=\dfrac{6\mu Qb_1l_1}{h^3\Big[b_1(B-b_1)+l_1(L-l_1)\Big]}\tag*{(4)}\end{equation*}
式中, $\mu$为黏度, $Q$为流量, $B, L, b_1, l_1$分别为双矩形油垫的宽度、长度、封油边的宽度和封油边长度.
承载力方程
\begin{equation*}W=PA_e=\dfrac{6\mu Qb_1l_1(B-b_1)(L-l_1)}{h^3\Big[b_1(B-b_1)+l_1(L-l_1)\Big]}\tag*{(5)}\end{equation*}
油膜刚度
\begin{equation*}k=\dfrac{18\mu Qb_1l_1(B-b_1)(L-l_1)}{h^4\Big[b_1(B-b_1)+l_1(L-l_1)\Big]}\tag*{(6)}\end{equation*}
2.2 油膜阻尼系数方程
阶跃载荷作用瞬间, 轴承间隙流出的润滑油流量等于油腔压力作用下挤出润滑油流量, 由液体连续性方程可知, 被挤出油流量为
\begin{equation*}Q_2=LB\dot{h}\tag*{(7)}\end{equation*}
则从窄缝流出的总流量为
\begin{equation*}Q_1=Q+Q_2\tag*{(8)}\end{equation*}
式中, $Q=Q_X+Q_Y$, $Q_X$为沿$X$轴方向的流量, $Q_Y$为沿$Y$轴方向的流量.
由平板流量方程
\begin{equation*}\dfrac{{d}P}{{d}X}=\dfrac{12\mu}{h^3(B-b_1)}(Q_1-Q_Y-Q_2),\quad X\in(L-l_1,L)\tag*{(9)}\end{equation*}
对$X$取积分, 得到油腔沿$X$正方向压力差, 此压差为油腔与外界压力差, 故
\begin{equation*}P=\dfrac{12l_1\mu}{h^3(B-b_1)}(Q_1-Q_y-Q_2) \tag*{(10)}\end{equation*}
同理
\begin{equation*}\dfrac{{d}P}{{d}Y}=\dfrac{12\mu}{h^3(L-l_1)}(Q_1-Q_X-Q_2),\quad Y\in(B-b_1,B)\tag*{(11)}\end{equation*}
对$Y$取积分, 得到油腔沿$Y$正方向压力差, 此压差为油腔与外界压力差, 故
\begin{equation*}P=\dfrac{12b_1\mu}{h^3(L-l_1)}(Q_1-Q_X-Q_2)\tag*{(12)}\end{equation*}
施加载荷前油腔压力为
\begin{equation*}\begin{split}P=\dfrac{6b_1\mu}{h^3(L-l_1)}(Q_1-Q_X-Q_2)+\\\dfrac{6l_1\mu}{h^3(B-b_1)}(Q_1-Q_Y-Q_2)\end{split}\tag*{(13)}\end{equation*}
经整理可得加载后腔内静压力为
\begin{equation*}P_1=\dfrac{6b_1\mu}{h^3(L-l_1)}(Q_1-Q_X)+\dfrac{6l_1\mu}{h^3(B-b_1)}(Q_1-Q_Y)\tag*{(14)}\end{equation*}
旋转工作台运动时被挤出缝隙所增加的油腔压力为
\begin{equation*}P_2=-\Bigg(\dfrac{6b_1\mu}{h^3(L-l_1)}+\dfrac{6l_1\mu}{h^3(B-b_1)}\Bigg)LB\dot{h}\tag*{(15)}\end{equation*}
当油膜厚度变薄时, $\dot{h}$为负值, 故$P_2$为正, 它与油膜移动速度成正比, 与间隙的立方成正比. 挤压油膜作用的阻尼力
\begin{equation*}f=-\Bigg(\dfrac{12b_1\mu}{h^3(L-l_1)}+\dfrac{12l_1\mu}{h^3(B-b_1)}\Bigg)LB(b_1L+l_1B)\dot{h}\tag*{(16)}\end{equation*}
油腔阻尼系数为
\begin{equation*}N=\Bigg(\dfrac{24b_1\mu}{h^3(L-l_1)}+\dfrac{24l_1\mu}{h^3(B-b_1)}\Bigg)LB(b_1L+l_1B)\tag*{(17)}\end{equation*}
2.3 静压推力轴承系统等效
旋转工作台质量为$M$, 阻尼力作用方向与运动速度方向相反, 矩形油腔有效承载面积为$A_{e}$, 在随时间变化载荷$F$ 作用下的动力学方程为
\begin{equation*}M\ddot{y}+N\dot{y}+P_1A_{e}=F\tag*{(18)}\end{equation*}
油腔推力$P_1A_{e}$是非线性量, 建立油腔静压力$P_1$与油膜厚度变化量$y$ 之间的线性方程非常困难, 为保证分析的精确性, 假设扰动力与原有载荷相比较小, 则其引起的各种变化量也很小, 此时油腔压力增量和位移增量呈现线性变化规律, 则式(18) 可以写成
\begin{equation*}M\ddot{y}+N\dot{y}+ky=F\tag*{(19)}\end{equation*}
式中, $F$为作用载荷, $y$为位移增量, $k$为油膜静刚度, $N$为油膜阻尼系数.
静压推力轴承动力学系统可简化为质量弹簧阻尼系统, 如图3 所示.
图3 静压推力轴承动力学系统
Fig.3 Dynamics system of hydrostatic thrust bearing
2.4 静压推力轴承系统传递函数
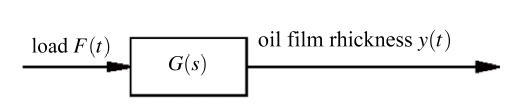
在静压推力轴承系统中, 输入量(激励)为外加载荷$F(t)$, 输出量(响应)为油膜厚度$y(t)$, 为了研究输入输出之间的关系, 在这里引入传递函数$G(s)$, 其关系式如图4 所示.
图4 静压推力轴承系统传递函数
Fig.4 Transfer function of hydrostatic thrust bearing system
已知静压推力轴承系统的二阶微分方程, 在零初始条件下对其进行拉氏变换, 整理后可得系统的传递函数为
\begin{equation*}\begin{split}G(s)=&\dfrac{Y(s)}{F(s)}=\dfrac{1}{Ms^2+Ns+k}=\\&\dfrac{1}{k}\cdot\dfrac{k}{M}\Bigg/\Bigg(s^2+\dfrac{N}{M}s+\dfrac{k}{M}\Bigg)\end{split}\tag*{(20)}\end{equation*}
将上式与二阶系统传递函数的标准形式进行比较, 可以得到
\begin{equation*}\begin{split}G(s)=&\dfrac{Y(s)}{F(s)}=\dfrac{1}{Ms^2+Ns+k}=\\&\dfrac{1}{k}\dfrac{\omega^2_n}{s^2+2\delta\omega_ns+\omega^2_n}\end{split}\tag*{(21)}\end{equation*}
式中, $\omega_n$为系统固有角频率, $\delta$为系统阻尼率.
双矩形腔静压推力轴承为二阶质量弹簧阻尼系统, 过阻尼状态$\delta>1$时, 将上述传递函数标准式进行拉氏反变换, 阶跃载荷作用下油膜位移量时域函数为
\begin{equation*}\begin{split}y(t)=&\dfrac{1}{k}\Bigg[1-\dfrac{1}{2(1+\delta\sqrt{\delta^2-1}-\delta^2)} {e}^{-(\delta-\sqrt{\delta^2-1})\omega_nt}-\\&\dfrac{1}{2(1-\delta\sqrt{\delta^2-1}-\delta^2)} {e}^{-(\delta+\sqrt{\delta^2-1})\omega_nt}\Bigg]\end{split}\tag*{(22)}\end{equation*}
将上式两边同时对时间$t$求导, 得阶跃响应的速率$V(t)$
\begin{equation*}\begin{split}V(t)=&\dfrac{{d}y(t)}{{d}t}=\dfrac{1}{k}\Bigg[\dfrac{(\delta-\sqrt{\delta^2-1})\omega_n }{2(1+\delta\sqrt{\delta^2-1}-\delta^2)}{e}^{-(\delta-\sqrt{\delta^2-1})\omega_nt}+\\&\dfrac{(\delta+\sqrt{\delta^2-1})\omega_n}{2(1-\delta\sqrt{\delta^2-1}-\delta^2)} {e}^{-(\delta+\sqrt{\delta^2-1})\omega_nt}\Bigg]\end{split}\tag*{(23)}\end{equation*}
将$V(t)$对$t$求导得单位阶跃响应的加速度$\alpha(t)$
\begin{equation*}\begin{split}\alpha(t)=&\dfrac{{d}V(t)}{{d}t}=\dfrac{1}{k}\Bigg[-\\&\dfrac{(\delta-\sqrt{\delta^2-1})^2\omega^2_ n}{2(1+\delta\sqrt{\delta^2-1}-\delta^2)}{e}^{-(\delta-\sqrt{\delta^2-1})\omega_nt}-\\&\dfrac{(\delta+\sqrt{\delta^2-1})^2\omega^2 _n}{2(1-\delta\sqrt{\delta^2-1}-\delta^2)}{e}^{-(\delta+\sqrt{\delta^2-1})\omega_nt}\Bigg]\end{split}\tag*{(24)}\end{equation*}
3阶跃载荷作用下油膜动特性
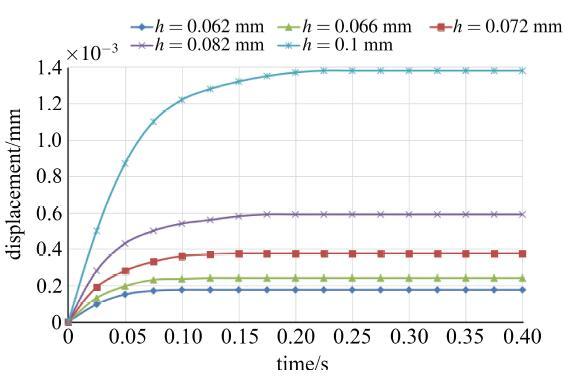
利用Matlab软件对阶跃载荷作用下不同油膜厚度、不同润滑油黏度、不同油腔面积时油膜稳定位移量进行分析, 得到了位移量与油膜厚度、润滑油黏度及油腔面积之间的关系, 如图5 $\sim$图7 所示.
图5 不同油膜厚度位移响应
Fig.5 The displacement response under different oil film thickness
图6 不同黏度位移响应
Fig.6 The displacement response under different oil viscosity
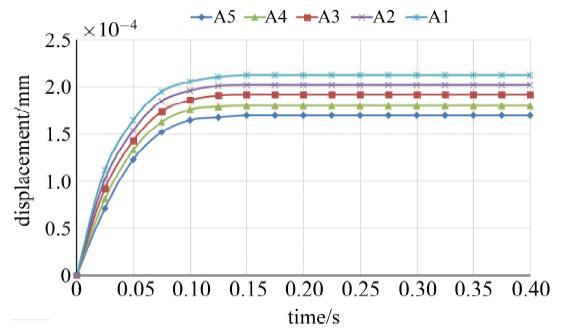
图7 不同油腔面积位移响应
Fig.7 The displacement response under different oil cavity area
由仿真结果分析可知: 双矩形腔静压推力轴承系统的阻尼比$\delta>1$, 突加载荷作用下, 油膜位移量呈现单调上升趋势, 最终稳定在新的平衡位置, 因而双矩形腔静压推力轴承稳定. 润滑油黏度与突加载荷一定时, 随着油膜厚度的减小, 系统响应时间变短, 这是由于系统供油量不变时, 油膜厚度减小, 油腔压力增大, 继而油膜刚性增大, 油膜抵抗变形能力增强, 恢复稳态所用时间也变短, 故在相同载荷作用下, 油膜越薄, 油膜刚度越大, 油膜变形量越小. 当油膜厚度一定时, 润滑油在不同黏度条件下, 随着黏度降低, 系统响应时间随之增长, 油膜位移量也随之增大. 这是因为油膜刚度与润滑油黏度成正比, 当润滑油黏度降低, 油膜刚度特性也随之将低, 油膜抵御外界冲击载荷能力下降, 故而响应时间延长, 稳定位移量增大. 当油腔面积增大, 系统响应时间减小, 稳定位移量减小, 这是由于油腔面积增大进而有效承载面积增大, 润滑油膜承载能力提高, 油膜刚性增大.
4 正弦载荷作用下轴承稳定性
在润滑油膜黏性阻尼作用下系统的固有频率为$\omega_n=\sqrt{\dfrac{k}{M}}$, 阻尼率为$\delta=\dfrac{N}{2\sqrt{Mk}}$, 油膜动刚度公式
\begin{equation*}k_a=k\sqrt{\Bigg[1-\Bigg(\dfrac{\omega_p}{\omega_0}\Bigg)^2\Bigg]^2+\Bigg(2\sigma\dfrac{\omega_p}{\omega_0}\Bigg)^2}\tag*{(25)}\end{equation*}
动态位移增量为$y_a=\dfrac{P_a}{k_a}$, 其中$\omega_p=0$时, 油膜动刚度等于静刚度. 当静载荷增量绝对值等于$P_a$时, 所产生的静态位移增量为$y=\dfrac{P}{k}$. 则静刚度与动刚度的比值公式为
\begin{equation*}\dfrac{k}{k_a}=\dfrac{y_a}{y}=\dfrac{1}{\sqrt{\Bigg[1-\Bigg(\dfrac{\omega_p}{\omega_0}\Bigg)^2\Bigg]^2+\Bigg(2\sigma \dfrac{\omega_p}{\omega_0}\Bigg)^2}}\tag*{(26)}\end{equation*}
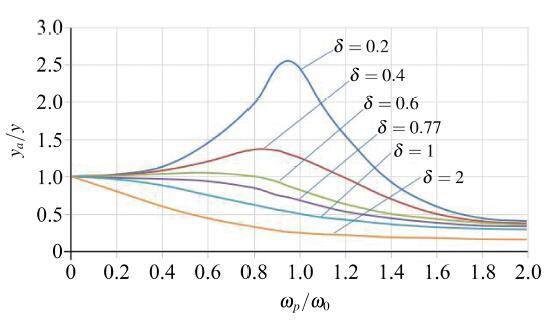
可见静动刚度比值随着阻尼率$\delta$和频率$\omega_p$的变化而变化, 其关系曲线如图7 所示.
图8 幅频特性曲线
Fig.8 Amplitude frequency characteristic curve.
由曲线可知, 当阻尼比$\delta>0.707$时, 发现无论频率如何变化, 静刚度与动刚度比值永远小于1, 由前可知双矩形腔静压推力轴承阻尼系数$\delta>1$, 因而, 任何工况时双矩形腔静压推力轴承油膜动刚度永远大于静刚度. 又得当正弦加载频率在高频段, ${\omega_p}/{\omega_n}$的值很大, 则${y_a}/{y}$的值很小, 即$y_a$很小, 油膜动态位移增量很小, 油膜不会发生大幅度振动, 故高频加载并不影响系统稳定性. 计算发现当正弦加载频率达到固有频率, 其动刚度依然很大, 振幅较小, 系统不会发生共振破坏, 故双矩形腔静压轴承系统稳定.
5实验验证
5.1实验装置与传感器
因刚度和阻尼等动态特性无法直接测量, 所以通过运行时间和间隙油膜厚度的关系间接验证动态稳定性. 空载油膜测厚试验在3.5 m立车上进行, 该机床最大可加工半径3.5 mm的工件, 工作台实际半径3.15 mm, 共12个油腔, 传感器与机床轴线夹角约30°, 最大承载能力32 t, 最高转速200 r/min.
图9 实验装置
Fig.9 Experimental setup
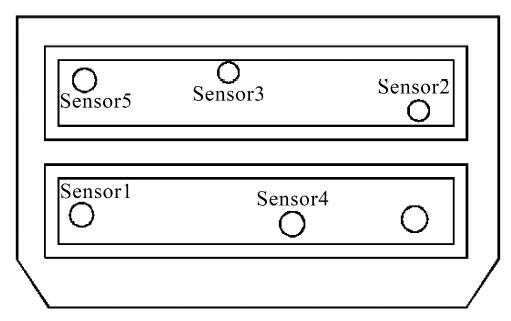
图10 油腔分布
Fig.10 Oil cavities distribution
测试过程共用10支位移传感器, 其型号为BI1.5-EG08-LU, 其工作原理为电磁感应式, 工作电压为24VDC, 测量范围0.25$\sim$1.25 mm, 灵敏度高可达$0.1 \mu{m}$.
图11 位移传感器安装
Fig.11 Displacement sensors installation
5.2 实验数据与数据分析
实验在空载和承载12 t载荷两种工况下进行, 通过油膜厚度变化验证双矩形腔静压推力轴承运行的动态稳定性. 空载和承载12 t时油膜稳定性测量结果如图12 和图13 所示.
图12 数据采集与显示装置
Fig.12 Data acquisition and display device
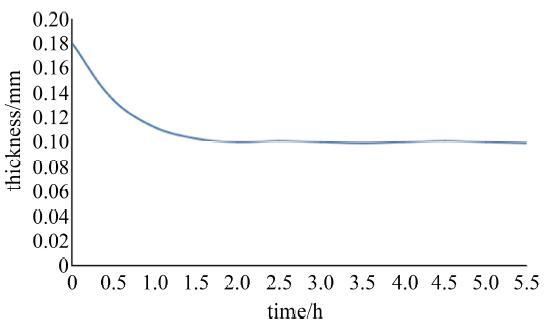
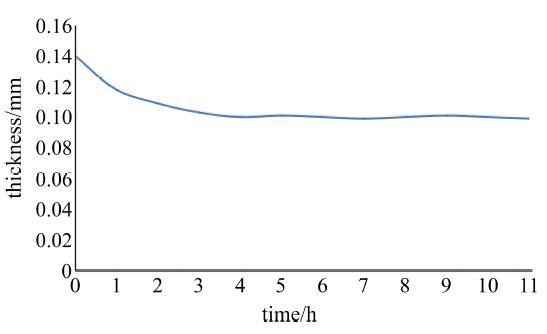
图13 空载工况油膜厚度随运行时间变化曲线
Fig.13 Change of oil film thickness with running time in no-load condition
图14 承载12 t时油膜厚度随运行时间变化曲线
Fig.14 Change of oil film thickness with running time in 12 t condition
由图12 可以看出, 工作台运转3 h达到热平衡, 油膜厚度由0.18 mm降至0.109 mm, 系统达到动态稳定. 从图13 试验结果发现, 旋转工作台运转3 h达到热平衡, 油膜厚度由0.14 mm降至\mbox{0.12 mm}, 变化量为0.02 mm. 因为承载后油膜刚度提高, 动态稳定性更好.
6 结论
采用理论分析方法研究了阶跃载荷作用下润滑油黏度、油膜厚度和油腔面积对轴承动态特性的影响, 揭示了油膜动态响应规律, 探究了正弦载荷作用双矩形腔静压推力轴承油膜稳定性, 并进行了动态稳定性的实验验证.
当润滑油黏度与油腔面积一定时, 随着油膜厚度的降低, 系统响应时间变短, 油膜越薄, 油膜刚度越大, 油膜变形量越小. 当油膜厚度与油腔面积一定时, 随着润滑油黏度降低, 系统响应时间随之增长, 油膜位移量也随之增大. 当油膜厚度与润滑油黏度一定时, 油腔面积增大, 润滑油膜承载能力提高, 油膜刚性增加, 在承受阶跃载荷作用下, 旋转台能在较短时间到达新的平衡位置. 正弦载荷作用双矩形腔静压推力轴承具有超强稳定性能, 较大阻尼系数, 较大阻尼率, 保证油膜较大动刚度, 其承受不同频率正弦载荷都保持较小振幅, 轴承稳定运行.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Osman T A Dorid M Safar ZS et al .Experimental assessment of hydrostatic thrust bearing performance
. Tribology International , 1996 , 29 (3 ): 233 -239
[本文引用: 1]
[2]
Du YK Mao KM Zhu YM et al .Dynamic modeling of hydrostatic guideway considering compressibility and inertia effect
. Frontiers of Mechanical Engineering , 2015 , 10 (1 ): 78 -88
[本文引用: 1]
[3]
庞志成 , 陈世家 , 王瑜 等 . 精密测试转台空气静压轴承动态特征
. 中国惯性技术学报 , 1997 , 3 : 50 -53
[本文引用: 1]
(Pang Zhicheng Chen Shijia Wang Yu et al . Dynamic testing of aerostatic bearing precision test turntable
. Chinese Journal of Inertial Technology , 1997 , 3 : 50 -53 (in Chinese))
[本文引用: 1]
[4]
孟心斋 , 孟昭焱 . 液体静压支承动态性能新表达式探索与实验验证
. 中国工程科学 , >2003 (3 ): 62 -66
[本文引用: 1]
(Meng Xinzhai Meng Zhao yan . Exploration and experimental verification of a new expression for dynamic performance of hydrostatic supports.Chinese Journal of Engineering Science , 2003 (3 ): 62 -66 (in Chinese))
[本文引用: 1]
[5]
王宝沛 , 翟鹏 , 秦磊 . 液体静压轴承动态特性的探讨
. 液压与气动 , >2007 (8 ): 58 -62
[本文引用: 1]
(Wang Baopei Zhai Peng Qin Lei Discussion on dynamic characteristics of hydrostatic bearing
. Hydraulic and Pneumatic , 2007 (8 ): 58 -62 (in Chinese))
[本文引用: 1]
[6]
江桂云 , 王勇勤 , 严兴春 等 . 基于小孔节流的静压油膜轴承动态特性分析
. 机械设计 , 2014 , 31 (7 ): 64 -69
[本文引用: 1]
(Jiang Guiyun Wang Yongqin Yan Xingchun et al .Dynamic analysis of hydrostatic bearing based on pinhole throttling
. Mechanical Design , 2014 , 31 (7 ): 64 -69 (in Chinese))
[本文引用: 1]
[7]
时鑫 . 立式车床液体静压导轨的性能分析与研究[硕士论文] . 沈阳 :东北大学 , 2010
[本文引用: 1]
(Jiang Guiyun Wang Yongqin Shi Xin .Performance analysis and research of hydraulic lathe for vertical lathe. [Master Thesis]. . Shenyang :Northeastern University , 2010 , (in Chinese))
[本文引用: 1]
[8]
胡琪 , 曾良才 , 蒋林 . 基于动网格的旋转液压伺服关节动态特性研究
. 液压与气动 , 2014 , 2 : 39 -43
[本文引用: 1]
(Hu Qi Zeng Liangcai Jiang Lin Stud
. on dynamic characteristics of rotating hydraulic servo joints based on moving grids. Hydraulic and Pneumatic , 2014 , 2 : 39 -43 (in Chinese))
[本文引用: 1]
[9]
Yoshimoto S Anno Y Stati
. characteristics of a rectangular hydrostatic thrust bearing with a self-controlled restrictor employing a floating disk. Journal of Tribology , 1993 , 15 (2 ): 307 -311
[本文引用: 1]
[10]
Chen XD Zhu JC Chen H Dynami.characteristics of ultra-precision aerostatic bearings
. Advances in Manufacturing , 2013 , 1 (1 ): 82 -86
[本文引用: 1]
[11]
Yadav SK Sharma SC Finit element analysis of tilted thrust pad bearings of various recesses shapes considering thrust pad flexibi-lity
. Journal of Engineering Tribology , 2016 , 230 : 872 -893
[本文引用: 1]
[12]
卢黎明 . 机床静压推力滑动轴承的动态特性分析
. 机床与液压 , 2008 , 36 (4 ): 247 -248
[本文引用: 1]
(Lu Liming Analysi of dynamic characte-ristics of static pressurized thrust bearings in machine tool
. Machine Tool and Hydraulics , 2008 , 36 (4 ): 247 -248 (in Chinese))
[本文引用: 1]
[13]
权好 . 液体静压支承系统的动态性能研究. [硕士论文]
. 北京:北京工业大学 , 2012
[本文引用: 1]
(Quan Hao Study on dynamic performance of hydrostatic bearing system. [Master Thesis]
. Beijing: Beijing University of Technology , 2012 (in Chinese))
[本文引用: 1]
[14]
李晓阳 , 权好 . 波动载荷下频率对液体静压支承系统的影响
. 北京工业大学学报 , 2013 , 39 (5 ): 671 -677
[本文引用: 1]
(Li Xiaoyang Quan Hao Effect
. of frequency under hydrodynamic pressure on hydrostatic bearing system. Journal of Beijing University of Technology , 2013 , 39 (5 ): 671 -677 (in Chinese))
[本文引用: 1]
[15]
孟晶 . 液体动静压轴承承载特性的分析与实验研究. [硕士论文]
.上海: 东华大学 , 2012
[本文引用: 1]
(Meng Jing Analysis and experimental research on bearing characteristics of hydrostatic bearing. [Master Thesis]
. Shanghai: Donghua University , 2012 (in Chinese))
[本文引用: 1]
[16]
董胜先 , 马求山 . 动静压轴承支撑高速主轴系统基本性能分析
. 制造技术与机床 , >2011 (9 ): 136 -139
[本文引用: 1]
(Dong Shengxian Ma Qiushan Basic performance analysis of high speed spindle system supported by dynamic and static pressures
. Manufacturing Technology & Machine Tool , 2011 (9 ): 136 -139 (in Chinese))
[本文引用: 1]
[17]
王勇勤 ,刘志芳 ,严兴春 等 .毛细管节流静压油膜轴承动态特性分析
.重庆大学学报 , 2011 , 34 (3 ): 25 -31
[本文引用: 1]
(Wang Yongqin Liu Zhifang Yan Xingchun et al .Analysis of dynamic characteristics of capillary throttling and static pressure oil film bearing
. Journal of Chongqing University , 2011 , 34 (3 ): 25 -31 (in Chinese))
[本文引用: 1]
[18]
荣涵锐 , 付国宏 . 倾斜腔液体动静压混合轴承的动态特性分析计算
. 哈尔滨工业大学学报 , >1994 (2 ): 77 -83
[本文引用: 1]
(Rong Hanrui Fu Guohong Dynamic analysis of dynamic characteristics of inclined cavity fluid dynamic hybrid bearing
. Journal of Harbin Institute of Technology , 1994 (2 ): 77 -83 (in Chinese))
[本文引用: 1]
[19]
王锋 . 径向滑动轴承的动态特性及其稳定性研究. [硕士论文]
.武汉:武汉科技大学 , 2016
[本文引用: 1]
(Wang Feng Study on dynamic characteristics and stability of radial plain bearings. [Master Thesis]
. Wuhan: Wuhan University of Science and Technology , 2016 (in Chinese))
[本文引用: 1]
[20]
孟磊 . 多孔质静压气体轴承承载性能的理论与实验研究. [硕士论文]
. 哈尔滨: 哈尔滨工业大学 , 2017 (Meng Lei. Physical and experimental study on bearing performance of porous hydrostatic pneumatic bearings. [Master Thesis]. Harbin: Harbin Institute of Technology, 2017 (in Chinese))
[本文引用: 1]
[21]
彭万欢 . 静压气体径向轴承的静动特性研究. [硕士论文]
. 北京:中国工程物理研院 , 2006
[本文引用: 1]
(Peng Wanhuan Study on the static and dynamic characteristics of radial bearing with static pressure. [Master Thesis]
. Beijing: China Academy of Engineering Physics , 2006 (in Chinese))
[本文引用: 1]
[22]
赵玉洁 . 高速角接触球轴承结构参数与不同加载对其动态特性影响的研究. [硕士论文]
. 长春: 吉林大学 , 2017
[本文引用: 1]
(Zhao Yujie Research on the structure parameters of high speed angular contact ball bearings and influence of different loading on their dynamic characteristics. [Master Thesis]
. Changchun: Jilin University , 2017 (in Chinese))
[本文引用: 1]
[23]
李德水 , 陈国定 , 余永健 . 基于拟动力学高速角接触球轴承动态特性分析
. 航空动力学报 , 2017 , 32 (3 ): 730 -739
[本文引用: 1]
(Li Deshui Chen Guoding Yu Yongjian Analysi
. of dynamic characteristics of high speed angular contact ball bearings based on quasi-kinetics. Journal of Aerospace Power , 2017 , 32 (3 ): 730 -739 (in Chinese))
[本文引用: 1]
[24]
贾晨辉 , 庞焕杰 , 邱明 . 球面螺旋槽动静压气体轴承的动态特性分析及稳定性预测
.航空动力学报 , 2017 , 32 (6 ): 1400 -1411
[本文引用: 1]
(Jia Chenhui Pang Huanjie Qiu Ming Analysi and stability prediction of spherical helical groove dynamic and static gas bearings
. Journal of Aerospace Power , 2017 , 32 (6 ): 1400 -1411 (in Chinese))
[本文引用: 1]
[25]
刘强 , 刘周 , 白鹏 等 . 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
. 力学学报 , 2016 , 48 (2 ): 269 -277
[本文引用: 1]
(Liu Qiang Liu Zhou Bai Peng et al .Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at low reynolds mumber
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (2 ): 269 -277 (in Chinese))
[本文引用: 1]
[26]
赵宇 ,王国玉 ,黄彪 等 .非定常空化流动涡旋运动及其流体动力特性
.力学学报 , 2014 , 46 (2 ): 191 -200
[本文引用: 1]
(Zhao Yu Wang Guoyu Huang Biao et al .Study of turbulent vortex and hydraulic dynamics in transient sheet/cloud cavitating flows
. Chinese Journal of Theoretical and Applied Mechanics , 2014 , 46 (2 ): 191 -200 (in Chinese))
[本文引用: 1]
[27]
崔海龙 , 岳晓斌 , 张连新 等 . 基于数值模拟的小孔节流空气静压轴承静动态特性研究
.机械工程学报 , 2016 , 52 (9 ): 116 -121
[本文引用: 1]
(Cui Hailong Yue Xiaobin Zhang Lianxin et al .Static and dynamic characteristics of a small-diameter throttle-air hydrostatic bearing based on numerical simulation
. Journal of Mechanical Engineering , 2016 , 52 (9 ): 116 -121 (in Chinese))
[本文引用: 1]
[28]
刘利琴 , 郭颖 , 赵海祥 等 . 浮式垂直轴风机的动力学建模、仿真与实验研究
. 力学学报 , 2017 , 49 (2 ): 299 -307
[本文引用: 1]
(Liu Liqing Guo Ying Zhao Haiyang et al .Dynamic modeling simulation and model tests research on the floating vawt
. Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (2 ): 299 -307 (in Chinese))
[本文引用: 1]
[29]
斯坦斯菲尔德 FM . 静压支承在机床上的应用. 北京 : 机械工业出版社 , 2003
[本文引用: 1]
(Stansfield FM. Application of Hydrostatic Bearings on Machine Tools. Beijing : Mechanical Industry Press , 2003 (in Chinese))
[本文引用: 1]
[30]
陈燕生 . 液体静压支承原理和设计.北京 : 国防工业出版社 , 1980
[本文引用: 1]
(Chen Yansheng. Hydrostatic pressure bearing principle and design. Beijing : National Defense Industry Press , 1980 (in Chinese))
[本文引用: 1]
[31]
丁振乾 . 液体静压支承设计 . 上海 : 上海科学技术出版社 ,1986
[本文引用: 1]
(Ding Zhenqian . Hydrostatic Support Design. Shanghai : Shanghai Science and Technology Press , 1986 (in Chinese))
[本文引用: 1]
[32]
章本照 . 流体力学数值方法 . 北京 : 机械工业出版社 , 2003
[本文引用: 1]
(Zhang Benzhao. Principles of Numerical Methods of Hydrodynamics. Beijing : Machinery Industry Press , 2003 (in Chinese))
[本文引用: 1]
[33]
王福军 . 计算流体动力学分析—FLUENT软件原理与应用 . 北京 : 清华大学出版社 , 2004
[本文引用: 1]
(Wang Fujun. Computational Fluid Dynamics Analysis—FLUENT Software Principles and Applications. Beijing : Tsinghua University Press , 2004 (in Chinese))
[本文引用: 1]
[34]
韩占忠 , 王敬 , 兰小平 . FLUENT流体工程仿真计算实例与应用 .北京 : 北京理工大学出版社 , 2004
[本文引用: 1]
(Han Zhanzhong Wang Jing Lan Xiaoping. FLUENT Fluid Engineering Simulation Calculation and Application. Beijing : Beijing Institute of Technology Press , 2004 (in Chinese))
[本文引用: 1]
Experimental assessment of hydrostatic thrust bearing performance
1
1996
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
Dynamic modeling of hydrostatic guideway considering compressibility and inertia effect
1
2015
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
精密测试转台空气静压轴承动态特征
1
1997
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
精密测试转台空气静压轴承动态特征
1
1997
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体静压支承动态性能新表达式探索与实验验证
1
>2003
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体静压支承动态性能新表达式探索与实验验证
1
>2003
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体静压轴承动态特性的探讨
1
2007
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体静压轴承动态特性的探讨
1
2007
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于小孔节流的静压油膜轴承动态特性分析
1
2014
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于小孔节流的静压油膜轴承动态特性分析
1
2014
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
1
2010
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
1
2010
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于动网格的旋转液压伺服关节动态特性研究
1
2014
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于动网格的旋转液压伺服关节动态特性研究
1
2014
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
Stati
1
1993
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
Dynami.characteristics of ultra-precision aerostatic bearings
1
2013
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
Finit element analysis of tilted thrust pad bearings of various recesses shapes considering thrust pad flexibi-lity
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
机床静压推力滑动轴承的动态特性分析
1
2008
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
机床静压推力滑动轴承的动态特性分析
1
2008
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体静压支承系统的动态性能研究. [硕士论文]
1
2012
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体静压支承系统的动态性能研究. [硕士论文]
1
2012
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
波动载荷下频率对液体静压支承系统的影响
1
2013
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
波动载荷下频率对液体静压支承系统的影响
1
2013
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体动静压轴承承载特性的分析与实验研究. [硕士论文]
1
2012
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
液体动静压轴承承载特性的分析与实验研究. [硕士论文]
1
2012
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
动静压轴承支撑高速主轴系统基本性能分析
1
2011
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
动静压轴承支撑高速主轴系统基本性能分析
1
2011
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
毛细管节流静压油膜轴承动态特性分析
1
2011
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
毛细管节流静压油膜轴承动态特性分析
1
2011
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
倾斜腔液体动静压混合轴承的动态特性分析计算
1
1994
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
倾斜腔液体动静压混合轴承的动态特性分析计算
1
1994
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
径向滑动轴承的动态特性及其稳定性研究. [硕士论文]
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
径向滑动轴承的动态特性及其稳定性研究. [硕士论文]
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
多孔质静压气体轴承承载性能的理论与实验研究. [硕士论文]
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
静压气体径向轴承的静动特性研究. [硕士论文]
1
2006
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
静压气体径向轴承的静动特性研究. [硕士论文]
1
2006
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
高速角接触球轴承结构参数与不同加载对其动态特性影响的研究. [硕士论文]
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
高速角接触球轴承结构参数与不同加载对其动态特性影响的研究. [硕士论文]
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于拟动力学高速角接触球轴承动态特性分析
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于拟动力学高速角接触球轴承动态特性分析
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
球面螺旋槽动静压气体轴承的动态特性分析及稳定性预测
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
球面螺旋槽动静压气体轴承的动态特性分析及稳定性预测
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
非定常空化流动涡旋运动及其流体动力特性
1
2014
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
非定常空化流动涡旋运动及其流体动力特性
1
2014
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于数值模拟的小孔节流空气静压轴承静动态特性研究
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
基于数值模拟的小孔节流空气静压轴承静动态特性研究
1
2016
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
浮式垂直轴风机的动力学建模、仿真与实验研究
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
浮式垂直轴风机的动力学建模、仿真与实验研究
1
2017
... 液体静压支承具有高运动速度, 低摩擦功耗, 大承载能力, 长使用寿命等诸多优异性能, 所以得到广泛应用. 然而在静压推力轴承研究中, 学者过多关注油膜对轴承润滑及摩擦性能影响, 而忽略了载荷作用下油膜变动规律及油膜波动对轴承系统稳定性的影响研究. Osman等[1 ] 基于流体动力学分析方法, 研究了动载荷作用下静压支承油腔形状结构尺寸变化对润滑油膜阻尼效应、承载能力、供油流量的影响. Du等[2 ] 在考虑转台运动惯性及油膜压缩性影响条件下对建立的静压导轨模型进行了动态数值模拟分析, 发现将静压支承等效为具有质量的弹簧阻尼系统是研究支承动态性能的最理想途径. 庞志成等[3 ] 对空气静压轴承进行研究并发现, 由于空气可压缩性, 工作过程中气膜发生振荡因而会对主轴刚度以及主轴运动精度有较大影响, 进行了阶跃载荷及正弦载荷作用下气膜过渡特性及动刚度分析, 为空气轴承动态性能分析提供了理论基础. 孟心斋等[4 ] 根据力平衡方程与流量连续性方程建立了静压支承系统传递函数, 进一步推导出系统动态性能表达式, 即轴承系统稳定性判别公式、固有频率与抗突加载干扰作用下油膜最大波动幅度及油膜动刚度. 王宝沛等[5 ] 从轴承动态特性角度优化了高速精密静压轴承设计目标函数, 简化了高精密轴承的设计制造过程, 节约了大量成本. 江桂云等[6 ] 对小孔节流静压支承动态性能进行了深入研究, 建立了该型支承系统流量连续性方程, 运用动力学方程搭建轴承传递函数, 分析了该种节流形式静压轴承系统的动态性能, 对比不同工况下突加作用力影响下轴承维持稳定响应时间变化情况. 时鑫[7 ] 提出了薄膜反馈式节流供油系统替代工业生产中常用的定量供油系统, 对系统静态特性承载能力和油膜刚度特性进行了分析, 通过动态特性分析对比了新型供油系统与原有系统之间优劣关系, 从而为新系统良好性能提供了论证依据. 胡琪等[8 ] 基于流体仿真软件FLUENT, 运用动网格及UDF技术对旋转液压伺服关节运动形态进行了动态仿真分析, 发现系统供油压力、阀芯转速、 外负载力矩等相关参数对关节动态性能的影响规律. Yoshimoto等[9 ] 以矩形油腔自反馈式节流静压推力轴承为研究对象, 通过对间隙油膜承载能力进行分析发现, 油腔面积大小决定承载力大小, 供油压力及润滑油黏度并不是影响承载力的关键. Chen等[10 ] 对高速精密空气静压支承动态刚度和阻尼系数进行研究, 发现非线性频率的干扰对轴承动态性能影响显著. Yadav等[11 ] 分析了流体润滑毛细供油管可倾式油垫静压轴承性能特点, 运用有限元法求解雷诺方程以及油垫变形的三维平衡方程, 得到了矩形、圆形、正方形油腔压力分布规律, 揭示了油垫倾斜角度和油垫变形量对轴承润滑性能的影响, 研究发现油垫变形会直接影响油膜的刚度系数以及油膜的阻尼系数. 卢黎明等[12 ] 通过分析液体静压滑动轴承在阶跃载荷作用下动态性能, 得到润滑油黏度参数、油膜间隙等对轴承特性的影响. 权好等[13 ] 通过数值模拟方法对液体静压支承润滑油膜流场进行了模拟, 利用流固耦合分析方法对正弦载荷作用下的油膜波动进行了研究. 李晓阳等[14 ] 针对静压推力轴承研究了正弦载荷作用下, 加载频率对油膜厚度、承载能力以及油膜动刚度的影响. 孟晶等[15 ] 从模态分析角度研究了静压推力轴承的油膜厚度、油腔尺寸以及油腔数量等主要参数对轴承系统固有频率及振型的影响. 董胜先等[16 ] 分析了高速水润滑动静压滑动轴承主轴转速、系统供水压力、承载力等相关参数对该轴承系统性能的影响, 并识别了该轴承系的动态特性系数. 王勇勤等[17 ] 在对流经轴承各油腔流量模型进行线性化处理的基础上, 建立了毛细管节流静压轴承流量连续性方程及轴承主轴系统动力学方程, 推导出毛细管节流径向和推力静压油膜轴承的传递函数, 同时探讨了供油压力、油膜厚度对毛细管节流径向静压轴承动态特性的影响规律. 荣涵锐等[18 ] 在小扰动假设前提下, 采用迭加和差分概念相结合的算法, 求得可变节流动静压混合轴承的8个动特性系数, 并分析计算了固定节流轴承的动特性. 根据相关文献[19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ] 可发现对滚动轴承动态特性研究相对较多, 而对推力轴承动态性能及影响因素研究较少, 对双矩形腔静压推力轴承动态性能的研究目前为止尚未见报道. ...
1
2003
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2003
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
1980
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
1980
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
1986
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
1986
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2003
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2003
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2004
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2004
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2004
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...
1
2004
... 液体静压轴承节流形式多样, 小孔节流、薄膜节流、窄缝节流等双矩形腔静压推力轴承采用窄缝节流形式,其模型如图1 所示[29 ,30 ,31 ,32 ,33 ,34 ] ...