含时滞反馈与涨落质量的记忆阻尼系统的随机共振
STOCHASTIC RESONANCE OF A MEMORIAL-DAMPED SYSTEM WITH TIME DELAY FEEDBACK AND FLUCTUATING MASS
中图分类号: O324
文献标识码: A
通讯作者:
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
展开
摘要
针对具有记忆效应的欠阻尼系统, 存在时滞反馈与涨落质量, 本文主要研究了其输出稳态响应振幅的随机共振效应. 首先通过引入新变量和运用小时滞近似展开理论, 将具有非马尔科夫特性的原系统转化为等价的两维马尔科夫线性系统, 再利用Shapiro-Loginov公式和Laplace变换获得了系统响应的一阶稳态矩和稳态响应振幅的解析表达式. 结果表明: 当系统参数满足Routh-Hurwitz稳定条件时, 稳态响应振幅随质量涨落噪声强度、周期驱动信号频率以及时滞的变化均存在随机共振现象, 其中随机多共振现象也被观察到. 在适当范围内, 通过控制时滞反馈, 系统的随机共振效应随着时滞的增大而增强, 而较长的记忆时间及增大阻尼参数均对共振行为呈现抑制作用.有效调控时滞反馈与记忆效应的变化关系将有助于增强系统对周期驱动信号的响应强度. 最后, 通过数值模拟计算验证了理论结果的有效性.
关键词:
Abstract
The stochastic resonance (SR) in the memorial under-damped system with time delay feedback and fluctuating mass is investigated in this paper. The non-Markovian original system is reformulated into two-dimensional Markovian linear system through introducing variable transformations and using the small time delay approximation. Further, the analytic expressions for the first moment of the response and the steady response amplitude are derived by using the Shapiro-Loginov formula and the Laplace transformation technique. All the research results show that when the Routh-Hurwitz stability is satisfied, the phenomenon of SR is shown with the variations of mass fluctuation noise intensity, driving frequency and time delay, respectively. The stochastic multi-resonance phenomenon is also observed. Moreover, the SR is enhanced with an increase in time delay by introducing the time delay feedback and instead, the SR is suppressed for large memory time and damping parameter. By adjusting the time delay feedback and the memory effects, the response of the system to a harmonic signal can be further improved. Finally, the theoretical results are well verified through numerical simulations
Keywords:
随机共振是Benzi等[1]在1981年研究古气象冰川问题时首次提出的, 描述了强噪声背景中的弱输入信号在最优噪声强度处被放大. 目前, 关于随机共振的发展和应用已经延伸到了广泛的科学领域内[2-10]. 比如化学[2]、生物[5]、能量收集[8]、机械故障诊断[10] 等. 但上述研究对象通常被刻画为具有马尔科夫特性的系统模型, 而当粒子在例如湍流、黏性材料或渗透媒介等非均匀介质中运动时, 其运动速度产生记忆效应, 系统呈现非马尔科夫性. 该系统通常被描述为一类具有记忆核的广义Langevin方程(GLE)[11-19], 其在非平衡统计物理中已被广泛研究. 例如: 具有不同记忆核函数的GLE 在反常扩散现象和随机共振中得到研究. 包景东等[14-16]基于指数型记忆核函数细致研究了弹道扩散现象. 文献[17]在耦合的GLEs中发现了双指数耗散记忆核诱导的一类非马尔科夫扩散. 在双稳态系统模型中, Srokowski[18]和Neiman等[19]分别在携有幂函数型记忆核和指数型记忆核的GLE中探讨了随机共振现象. 在适当范围内, 记忆时间则分别增强和减弱随机共振.
时滞普遍存在于自然界, 其产生的根源在于系统中的物质、能量或信息存在传递时间, 转换速度, 或者源于系统本身固有的记忆效应. 因此, 在复杂无序的非均匀环境中, 时滞是研究相关动力学问题不可忽视的一个重要因素, 甚至微弱的时滞也能够定性地改变系统的动力学特征. 近年来, 研究时滞对系统动力学行为的影响已经吸引了大量学者的关注[20-28]. 其中, 靳艳飞[26]研究了受互关联噪声激励的时滞系统的相干共振和随机共振现象. 钟苏川等[27]在具有时滞的分数阶线性系统中讨论了稳态响应振幅随时滞变化的一类广义随机共振, 且较小的噪声相关率能够导致随机多共振现象. 此外, 文献[28]在小世界神经网络元模型中也展示了时滞诱导的随机多共振现象.
另一方面, 在具有记忆效应的系统中, 由涨落耗散理论可知, 记忆核函数依赖于系统内部噪声. 而外部噪声对系统的干扰不仅反映在系统的阻尼涨落[29]和固有频率涨落[30]上,而且能够在振子质量中被体现到[4]. 实际上, 在复杂多变的环境中, 媒介分子对系统粒子通常具有吸附能力而使得系统存在质量涨落, 其中常见的质量涨落模型有: 可变质量振荡器[31], 离子间的化学反应系统[32], 粒状材料的聚合过程[33]等. 但在该类质量涨落系统中, 未同时考虑复杂非均匀环境下记忆阻尼与时滞对系统共振行为的影响. 鉴于此, 针对具有时滞反馈和指数型记忆核的质量涨落系统, 本文首先获得系统稳态响应振幅的解析表达式, 然后详细讨论时滞反馈、记忆阻尼及质量涨落对共振行为的影响, 最后由数值模拟验证理论结果的有效性.
1 系统模型
考虑由广义Langevin方程描述的受时滞反馈与质量涨落噪声作用的记忆阻尼系统如下
其中, m表示系统粒子的质量,
其中,
其中,
本文考虑系统粒子质量受随机扰动而引入的乘性外噪声
其中,
基于方程(2)和(3), 内噪声
其中
针对系统(1)引入新变量
依据式(4)
其中
在式(7)中, 对时滞项
2 系统稳态响应振幅
为获得系统的稳态响应振幅, 下文基于矩方程将在推导过程中利用对称二值噪声所满足的Shapiro-Loginov公式[35]
在方程(9)和式(8)两边分别进行统计平均, 并利用式(10)得到系统响应一阶矩的微分方程
由于式(12)中出现了新的耦合项
对于在式(14)中又出现的新耦合项
最后, 方程(12)
其中,
通过式(16)可获得
其中
对式(17)两边做逆Laplace变换, 得到系统响应一阶矩
其中,
当粒子运动时间足够长时, 初始条件对系统响应一阶矩的影响消失, 故式(18)在充分长时间后演化为一阶稳态矩
即式(19)可视作周期驱动信号
根据式(17)和式(19), 获得系统稳态响应振幅
其中系数
3 随机共振行为的讨论和数值验证
3.1 稳态响应振幅的共振行为
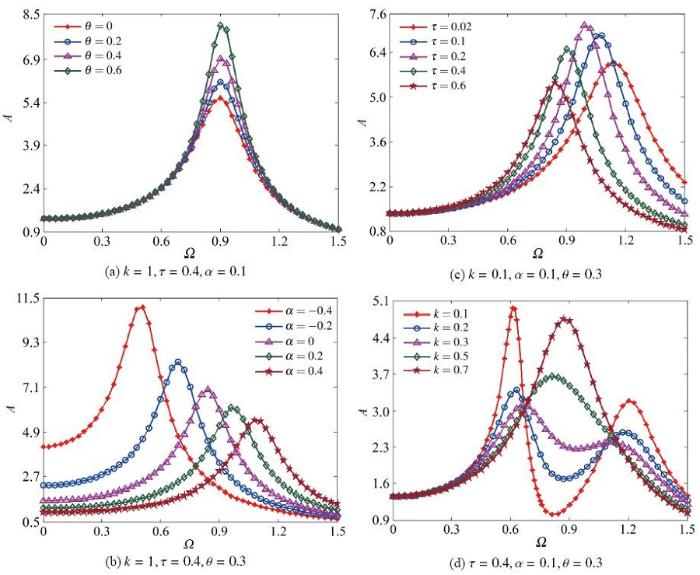
这一节我们将讨论式(20)中稳态响应振幅
当质量涨落噪声强度
且当
图2描述了稳态响应振幅
稳态响应振幅
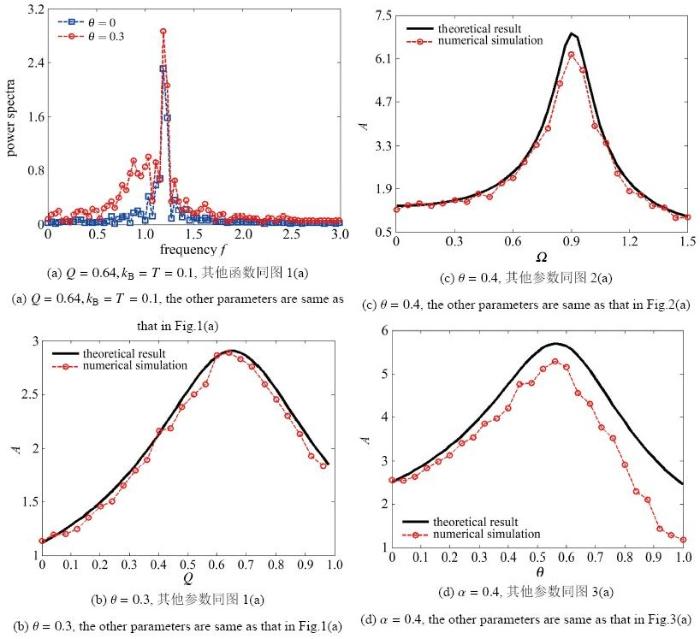
3.2 数值验证
为检验上述理论结果的有效性, 有必要进行数值模拟验证. 采用四阶Runge-Kutta算法对方程(1)进行数值离散化, 为最大化减小误差, 选择时间步长为
图4 系统(1)的响应功率谱, 稳态响应振幅的理论结果与数值模拟对比.
Fig.4 The power spectra of the system (1), the contrast between theoretical and numerical simulation
4 结论
本文研究了由时滞反馈、质量涨落噪声及周期驱动信号共同作用的具有记忆效应的欠阻尼系统的随机共振. 通过引入新变量, 并利用小时滞展开理论, 将广义Langevin方程描述的非马尔科夫系统嵌入为等价的马尔科夫线性系统. 进一步, 获得系统稳态响应振幅的解析表达式, 并分析了时滞反馈、质量涨落噪声及记忆核对其影响. 研究结果表明: 稳态响应振幅随质量涨落噪声强度的变化出现随机共振现象, 且共振行为随着时滞的增大而增强, 随着记忆时间的增大而减弱; 随着周期驱动信号频率的变化出现真实共振行为, 其中存在最优记忆时间使得共振峰值达到最优, 且较小的质量涨落噪声相关率使得系统出现随机多共振现象. 此外, 在适当参数范围内, 稳态响应振幅随着时滞的变化也出现共振现象. 相反于时滞对系统响应的增强作用, 较长的记忆时间仍对系统共振行为起到抑制作用, 合理控制时滞与记忆时间的变化关系将有助于增强系统对周期驱动信号的响应强度. 最后, 通过数值计算的输出响应振幅验证了理论结果的有效性.
该记忆阻尼模型在实际的物理及生物系统中被广泛应用, 特别地被应用于研究反常扩散现象, 比如研究黑体辐射中带电粒子的弹道扩散现象[14]. 上述结论分析了此非马尔科夫系统的共振行为, 在复杂环境中, 为深入研究介质分子的吸附能力及时滞反馈对系统共振行为的影响提供了理论依据.
附录 A
系数
附录 B
系数
{Invalid MML}
The authors have declared that no competing interests exist.
参考文献
| [1] |
The mechanism of stochastic resonance .
|
| [2] |
Stochastic Resonance .
|
| [3] |
Coherence and stochastic resonance in a periodic potential driven by multiplicative dichotomous and additive white noise .
|
| [4] |
Stochastic resonance in a harmonic oscillator with random mass subject to asymmetric dichotomous noise .
|
| [5] |
Information-based measures for logical stochastic resonance in a synthetic gene network under Lévy flight superdiffusion .
|
| [6] |
Stochastic resonance across bifurcation cascades .
|
| [7] |
Stochastic resonance in coupled weakly-damped bistable oscillators subjected to additive and multiplicative noises .
|
| [8] |
An application of stochastic resonance for energy harvesting in a bistable vibrating system .
|
| [9] |
Stochastic resonance in linear systems subject to multiplicative and additive noise .
|
| [10] |
Multi-stable stochastic resonance and its application research on mechanical fault diagnosis .
|
| [11] |
Origin of hyperdiffusion in generalized Brownian motion .
|
| [12] |
Nonequilibrium statistical description of anomalous diffusion .
|
| [13] |
Nonergodic solutions of the generalized Langevin equation .
|
| [14] |
Ballistic diffusion of a charged particle in a blackbody radiation field .
|
| [15] |
Numerical integration of a non-markovian langevin equation with a thermal band-passing noise .
|
| [16] |
Ballistic diffusion induced by a thermal broadband noise .
|
| [17] |
随机双指数记忆耗散系统的非马尔可夫扩散 .Non-markovian diffusion of the stochastic system with a biexponentical dissipative memory kernel . |
| [18] |
Bistable generalised langevin dynamics driven by correlated noise possessing a long jump distribution: Barrier crossing and stochastic resonance .
|
| [19] |
Memory effects on stochastic resonance .
|
| [20] |
Stochastic resonance in coupled oscillator systems with time delay .
|
| [21] |
飞机结构气动弹性分析与控制研究 .
Studies on aeroelastic analysis and control of aircraft structures .
|
| [22] |
Coherence and stochastic resonance in threshold crossing detectors with delayed feedback .
|
| [23] |
一类含时滞的半主动悬架系统的动力学分析 .
Dynamical analysis on a kind of semi-active suspension with time delay .
|
| [24] |
Modulating resonance behaviors by noise recycling in bistable systems with time delay .
|
| [25] |
时滞耦合系统非线性动力学的研究进展 .
Review on nonlinear dynamics in systems with coulpling delays .
|
| [26] |
Noise-induced dynamics in a delayed bistable system with correlated noises .
|
| [27] |
Nonlinear effect of time delay on the generalized stochastic resonance in a fractional oscillator with multiplicative polynomial noise .
|
| [28] |
Effects of time delay on the stochastic resonance in small-world neuronal networks . |
| [29] |
Harmonic oscillator with fluctuating damping parameter .
|
| [30] |
具有固有频率涨落的记忆阻尼线性系统的随机共振 .
Stochastic resonance of a memorial-damped linear system with natural frequency fluctuation .
|
| [31] |
Oscillator with random trichotomous mass .
|
| [32] |
Nonequilibrium thermodynamics versus model grain growth: derivation and some physical implications .
|
| [33] |
Modeling the electrophoretic deposition of colloidal particles .
|
| [34] |
L’Heureux I, Longtin A. Small delay approximation of stochastic delay differential equations .
|
| [35] |
“Formulae of differentiation” and their use for solving stochastic equations .
|
| [36] |
|
| [37] |
Stochastic resonance as a bona fide resonance .
|

/
| 〈 |
|
〉 |