引言
固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解.
然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础.
陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA).
从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性.
1 S-R和分解定理
S-R和分解定理[13 ] 证明: “给定一个物理可能的位移函数, 此函数在形变体点集域内是单值连续的, 处处具有一阶导数, 则此运动变换总可以分解为正交与对称两个子变换的直和. 正交变化体现点集的转动, 而对称变换体现点集的形变.”
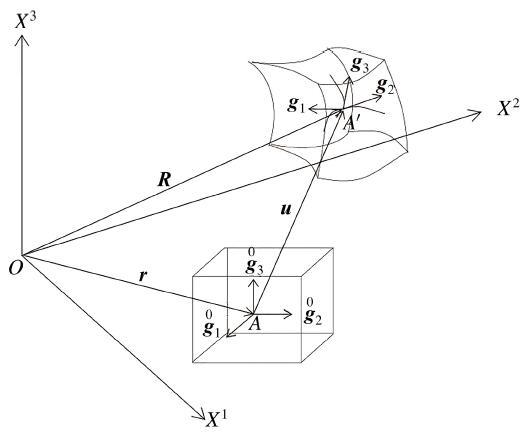
为了描述欧式空间 E 3 图1 所示. (1) 全局固定参考系 X i ( i = 1,2 , 3 ) x i ( i = 1,2 , 3 ) . 其坐标线会随着物体形变而变形.
图1 三维欧式空间中变形体示意图.
Fig.1 A deformable body in three-dimension Euclidean space
图1 中, r R u g 0 i g i ( i = 1,2 , 3 ) r R ) 和位移矢量(u ) 满足如下关系
R = r + u ( 1 )
变形前后拖带坐标系中的基矢量分别定义如下
g 0 i = ∂ r ∂ x i , i = 1,2 , 3 ( 2 )
g i = ∂ R ∂ x i , i = 1,2 , 3 ( 3 )
将式(2)和式(3)代入式(1)得到
∂ R ∂ x i = ∂ r ∂ x i + ∂ u ∂ x i ( 4 )
在曲线坐标系下
∂ u ∂ x i = ∂ ∂ x i u j g 0 j = u j | i g 0 j ( 5 )
其中
u j | i = ∂ u j ∂ x i + Γ ik j 0 u k ( 6 )
Γ ik j 0 = 1 2 g jl 0 ∂ g 0 li ∂ x k + ∂ g 0 lk ∂ x i - ∂ g 0 ik ∂ x l ( 7 )
其中, u j | i u j x i Γ ik j 0
g i = F i j g 0 j ( 8 )
F i j = δ i j + u j | i ( 9 )
其中, F δ i j
换句话说, S-R和分解定理可以表述为: 任何一个可逆的线性微分变换函数 F
F = S + R ( 10 )
其中, S R [13 ] 证明了和分解定理的存在性和唯一性, 这里只是给出其中相关的数学结果.
应变张量和转动张量分别为
S j i = 1 2 u i | j + u i | j T - L k i L j k ( 1 - c os θ ) ( 11 )
R j i = δ j i + L j i s in θ + L k i L j k ( 1 - c os θ ) ( 12 )
其中, L j i
L j i = 1 2 s in θ u i | j - u i | j T ( 13 )
其中, θ
2 基于更新拖带坐标法的增量变分方程
2.1 增量变分方程
假设从0到 t t + Δ t t + Δ t [25 ]
δ t + Δ t J = ∫ Ω ( t + Δ t ) t + Δ t σ j i δ t + Δ t V j | | i d Ω - t + Δ t R = 0 ( 15 )
式中,δ为变分符号;J为泛函;σi j 为应力张量;t + Δ t t + Δ t V i t + Δ t t + Δ t g i t + Δ t R
Ȃ t + Δ t R = ∫ S p ( t + Δ t ) t + Δ t P i δ t + Δ t V i d S + ∫ Ω ( t + Δ t ) t + Δ t ρ f i δ t + Δ t V i d Ω ( 16 )
其中, P f
假设所考虑的问题为准静力学问题, 根据速度梯度和应力的线性近似逼近有
t + Δ t V k | | i = δ l k - Δ u k | | j V j | | i ( 17 )
t + Δ t σ j i = t σ j i + Δ t σ ̇ j i ( 18 )
其中, Δ u k | | j Δ u k t g i σ ̇ j i t t g i Δ u j | | k = Δ t V j | | k
Δ t ∫ σ ̇ j i δ V j | | i d Ω - Δ t ∫ σ j i V j | | k δ V k | | i d Ω = t + Δ t R - ∫ σ j i δ V j | | i d Ω ( 19 )
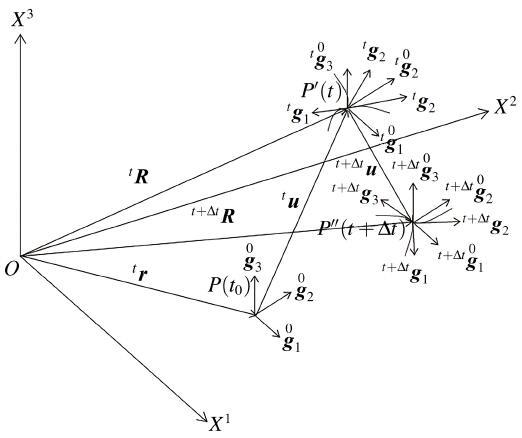
2.2 更新拖带坐标法
在更新拖带坐标法[25 ] 中, 是以 t t g 0 i t V 0 i 图2 所示, 设质点在初始时刻 t 0 P P g 0 i . 在 t P ' P ' t g 0 i t g i . 在由 t t + Δ t t t g 0 i ( 一般取为标准直角坐标系)作为参考基准. 这样, t t g i t V i | | j
t V i | | j = t V k 0 | l ∂ x i ∂ t x k ∂ t x l ∂ x j ( 20 )
对 t V k 0 | l
t V k 0 | l = S ̅ ̇ l k + R ̅ ̇ l k ( 21 )
式中
S ̅ ̇ l k = 1 2 i V k 0 | l + i V k 0 | l T ( 22 )
R ̅ ̇ l k = L t k θ ̅ ̇ = 1 2 i V k 0 | l + i V k 0 | l T ( 23 )
图2 更新拖带坐标系.
Fig.2 Update of the three-dimension co-moving coordinate
其中, t t g 0 i
将式(20)运用到式(19)中
Δ t ∫ σ ̅ ̇ j i δ t V j 0 | i d Ω - Δ t ∫ σ ̅ j i t V j 0 | k δ t V k 0 | i d Ω = t + Δ t R - ∫ σ ̅ j i δ t V j 0 | i d Ω ( 24 )
上式中
σ ̅ j i = σ l k ∂ x l ∂ t x j ∂ t x i ∂ x k ( 25 )
σ ̅ ̇ j i = σ ̇ l k ∂ x l ∂ t x j ∂ t x i ∂ x k ( 26 )
以 t g 0 i
σ ̅ ̇ j i = C ̅ jl ik S ̅ ̇ k l ( 27 )
其中
C ̅ jl ik = C nt ms ∂ x n ∂ t x j ∂ t x i ∂ x m ∂ x t ∂ t x l ∂ t x k ∂ x s ( 28 )
对于各向同性体有 C ̅ jl ik = C jl ik .
将式(27)代入式(24)中
Δ t ∫ C ̅ jl ik S ̅ ̇ k l δ S ̅ ̇ i j d Ω - Δ t ∫ σ ̅ j i S ̅ ̇ k j δ S ̅ ̇ i k d Ω - Δ t ∫ σ ̅ j i R ̅ ̇ k j δ R ̅ ̇ i k d Ω - Δ t ∫ σ ̅ j i S ̅ ̇ k j δ R ̅ ̇ i k + σ ̅ j i R ̅ ̇ k j δ S ̅ ̇ i k d Ω + Δ t ∫ σ ̅ ̇ j i δ R ̅ ̇ i j d Ω = t + Δ t R - ∫ σ ̅ j i δ S ̅ ̇ i j d Ω ( 29 )
如果不考虑体力矩的影响, 假设初始系为正交系, 文献[25 ] 利用如下结果
σ ̅ ̇ j i = σ ̅ k i S ̅ ̇ j k - S ̅ ̇ k i σ ̅ j k ( 30 )
对式(29)进行简化
Δ t ∫ C ̅ jl ik S ̅ ̇ k l δ S ̅ ̇ i j d Ω - Δ t ∫ σ ̅ j i S ̅ ̇ k j δ S ̅ ̇ i k d Ω - Δ t ∫ σ ̅ j i R ̅ ̇ k j δ R ̅ ̇ i k d Ω - Δ t ∫ σ ̅ j i R ̅ ̇ k j δ S ̅ ̇ i k + σ ̅ k j S ̅ ̇ j i δ R ̅ ̇ i k d Ω = t + Δ t R - ∫ σ ̅ j i δ S ̅ ̇ i j d Ω ( 31 )
此式可作为全局弱形式无网格法的增量变分方程.
更新拖带坐标法最大的特点是, 在每一次迭代步结束后, 重新选择初始拖带系, 不仅保证了应力速率的客观性, 自动消除了转动的影响, 使应力分量不随时间改变, 而且大大简化了增量变分方程求解中的系数矩阵, 降低了增量变分方程的求解难度,利于算法实现和推广应用[34 ] .
3 基于无网格Galerkin法的系统离散方程
在无网格方法中, 问题域被离散成一组节点 x k ( k = 1,2 , ⋯ , n ) t t Δ u t V
t Δ u = ∑ k = 1 n t ϕ k ( x ) t Δ u k ( 32 )
t V = ∑ k = 1 n t ϕ k ( x ) t V ( 33 )
其中, t ϕ k t k t Δ u k t V t k
类似于式(6), 对于 V j | | i
V j | | i = ∂ V j ∂ x i + Γ il j V l ( 34 )
将式(32)和式(33)分别代入式(6)和式(34)中
t Δ u j | i = ∑ k = 1 n ∂ t ϕ k ∂ x i t Δ u k j + Γ il j ∑ k = 1 n t ϕ k t Δ u k l ( 35 )
t V j | i = ∑ k = 1 n ∂ t ϕ k ∂ x i t V k j + Γ il j ∑ k = 1 n t ϕ k t V k l ( 36 )
另外
Δ S ̅ = Δ t S ̅ ̇ , Δ R ̅ = Δ t R ̅ ̇ ( 37 )
从而可以将式(22), (23)和式(37)改写成矩阵形式
Δ S ̅ = B s t Δ u , Δ R ̅ = B r t Δ u ( 38 )
S ̅ ̇ = B s t V , R ̅ ̇ = B r t V ( 39 )
以上两式中
t Δ u = t Δ u 1 1 , t Δ u 1 2 , t Δ u 1 3 , ⋯ , t Δ u n 1 , t Δ u n 2 , t Δ u n 3 ( 3 n × 1 ) T ( 40 )
t V = t V 1 1 , t V 1 2 , t V 1 3 , ⋯ , t V n 1 , t V n 2 , t V n 3 ( 3 n × 1 ) T ( 41 )
B s = B 1 s , B 2 s , ⋯ , B n s ( 6 × 3 n ) ( 42 )
B r = B 1 r , B 2 r , ⋯ , B n r ( 6 × 3 n ) ( 43 )
Δ S ̅ = Δ S ̅ 1 1 , Δ S ̅ 2 2 , Δ S ̅ 3 3 , 2 Δ S ̅ 2 1 , 2 Δ S ̅ 3 2 , 2 Δ S ̅ 3 1 6 × 1 T ( 44 )
Δ R ̅ = 2 Δ R ̅ 2 1 , 2 Δ R ̅ 3 2 , 2 Δ R ̅ 3 1 3 × 1 T ( 45 )
S ̅ ̇ = S ̅ ̇ 1 1 , S ̅ ̇ 2 2 , S ̅ ̇ 3 3 , 2 S ̅ ̇ 2 1 , 2 S ̅ ̇ 3 2 , 2 S ̅ ̇ 3 1 6 × 1 T ( 46 )
R ̅ ̇ = 2 R ̅ ̇ 2 1 , 2 R ̅ ̇ 3 2 , 2 R ̅ ̇ 3 1 3 × 1 T ( 47 )
而
B i s = ∂ N k ∂ x 1 + Γ 11 1 N k Γ 12 1 N k Γ 13 1 N k Γ 21 2 N k ∂ N k ∂ x 2 + Γ 22 2 N k Γ 23 2 N k Γ 13 3 N k Γ 32 3 N k ∂ N k ∂ x 3 + Γ 33 3 N k ∂ N k ∂ x 2 + ( Γ 21 1 + Γ 11 2 ) N k ∂ N k ∂ x 1 + ( Γ 22 1 + Γ 12 2 ) N k ( Γ 23 1 + Γ 13 2 ) N k ( Γ 31 2 + Γ 21 3 ) N k ∂ N k ∂ x 3 + ( Γ 32 2 + Γ 22 3 ) N k ∂ N k ∂ x 2 + ( Γ 33 2 + Γ 23 3 ) N k ∂ N k ∂ x 3 + ( Γ 31 1 + Γ 11 3 ) N k ( Γ 32 1 + Γ 12 3 ) N k ∂ N k ∂ x 1 + ( Γ 33 1 + Γ 13 3 ) N k ( 48 )
B i r = ∂ N k ∂ x 2 + ( Γ 21 1 + Γ 11 2 ) N k - ∂ N k ∂ x 1 + ( Γ 22 1 - Γ 12 2 ) N k ( Γ 23 1 - Γ 13 2 ) N k ( Γ 31 2 - Γ 21 3 ) N k ∂ N k ∂ x 3 + ( Γ 32 2 + Γ 22 3 ) N k - ∂ N k ∂ x 2 + ( Γ 33 2 - Γ 23 3 ) ) N k ∂ N k ∂ x 3 + ( Γ 31 1 - Γ 11 3 ) N k ( Γ 32 1 + Γ 12 3 ) N k - ∂ N k ∂ x 1 + ( Γ 33 1 + Γ 13 3 ) N k ( 49 )
在更新拖带坐标法中, 如果初始拖带系和直线直角系胚
Γ jk i = Γ jk i 0 = 0 ( 50 )
将式(38)和式(39)代入式(31)中, 并根据 δ t V T
t K L - t K N ⋅ t Δ u = t + Δ t R - t F ( 51 )
其中
t K L = ∫ Ω ( t ) B s T D B s d Ω ( 52 )
t K N = ∫ Ω ( t ) B s T σ 1 B s d Ω - ∫ Ω ( t ) B r T σ 2 B r d Ω - ∫ Ω ( t ) B s T σ 3 B r d Ω - ∫ Ω ( t ) B r T σ 3 T B s d Ω ( 53 )
t + Δ t R = ∫ sp ( t ) ϕ T P d S + ∫ Ω ( t ) ϕ T ρ f d S ( 54 )
t F = ∫ Ω ( t ) B s T σ d Ω ( 55 )
上式中, D
σ = { σ 1 1 , σ 2 2 , σ 3 3 , σ 2 1 , σ 3 2 , σ 3 1 } T ( 56 )
σ 1 = σ 1 1 0 0 σ 2 1 2 0 σ 3 1 2 0 σ 2 2 0 σ 1 2 2 - 1 mm σ 3 2 2 0 0 0 σ 3 3 0 σ 2 3 2 σ 1 3 2 σ 1 2 2 σ 2 1 2 0 σ 1 1 + σ 2 2 4 σ 3 1 4 σ 3 2 4 0 σ 2 3 2 σ 3 2 2 σ 1 3 4 σ 2 2 + σ 3 3 4 σ 1 2 4 σ 1 3 2 0 σ 3 1 2 σ 2 3 4 σ 2 1 4 σ 1 1 + σ 3 3 4 ( 57 )
σ 2 = - 1 4 σ 1 1 + σ 2 2 - σ 3 1 σ 3 2 - σ 1 3 σ 2 2 + σ 3 3 σ 1 2 σ 2 3 σ 2 1 σ 1 1 + σ 3 3 ( 58 )
σ 3 = - 1 2 σ 2 1 0 - 1 2 σ 3 1 1 2 σ 1 2 - 1 2 σ 3 2 0 0 1 2 σ 2 3 1 2 σ 1 3 1 4 ( σ 1 1 - σ 2 2 ) - 1 4 σ 3 1 - 1 4 σ 3 2 - 1 4 σ 1 3 1 4 ( σ 2 2 - σ 3 3 ) 1 4 σ 1 2 - 1 4 σ 2 3 1 4 σ 2 1 1 4 ( σ 1 1 - σ 3 3 ) ( 59 )
在本文中, 采用直接法来施加本质边界条件, 即通过直接修改系统增量方程(51)中的刚度矩阵和总体力向量. 在本文的无网格法数值计算过程中, 其它一些必要的参数设置见表1 .
4 数值算例
4.1 悬臂梁结构的非线性弯曲计算
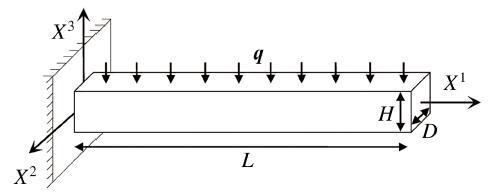
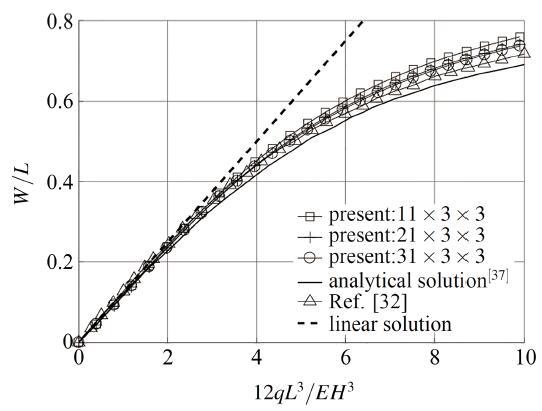
图3 所示为一上表面受均布载荷 q L = 254 D = H = 25.4 E = 82.74 쀻 . 图4 给出了该算例中梁右端中点的无量纲挠度值与无量纲均布载荷值之间的关系, 其中包括本文数值方法收敛性的验证, 以及本文结果与罗丹[32 ] 和Holden[37 ] 的结果、小变形线性理论的结果之间的比较. 由不同节点数之间的对比可以反映出本文三维S-R无网格法在该算例中的收敛性特点, 可以发现当采用 21 × 3 × 3 [32 ] 的结果进行比较, 可以发现本文的结果与罗丹[32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性.
图3 受均布载荷的空间悬臂梁.
Fig.3 3D cantilever beam subjected to a uniform load
图4 梁右端中点挠度与载荷的关系
Fig.4 The right end central deflection of beam versus load
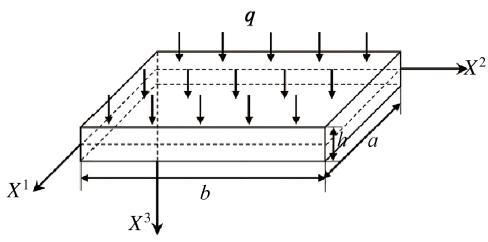
4.2 矩形板结构的非线性弯曲计算
图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的.
图5 受均布载荷的矩形板结构示意图.
Fig.5 3D rectangle plate subjected to a uniform load
图6 平板中面中点挠度与载荷关系(各向同性板).
Fig.6 The central deflection of rectangle plate’s mid-plane versus load (isotropic plate)
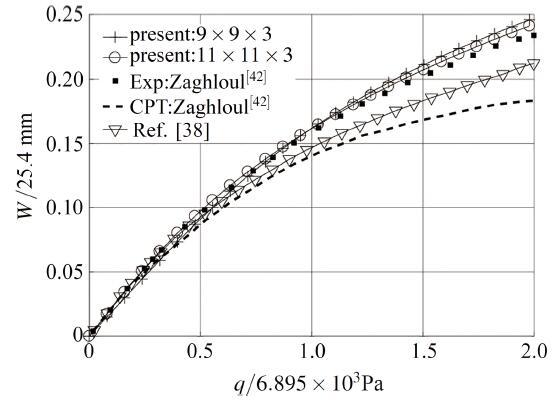
同样以图5 为例, 若板为正交各向异性材料, 杨氏模量有 E 1 = 2.069 × 1 0 4 E 2 = 8.826 × 1 0 3 G 12 = G 13 = G 23 = 2.551 × 1 0 3 µ = 0.32 a = b = 304.8 h = 3.5 图7 给出该算例的平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系. 同样可以发现当节点数为 11 × 11 × 3 [38 ] 给出的结果, 这是与前文的各向同性板算例不一样的. 相对于Zaghoul 等[42 ] 给出的经典解(CPT) 和Shen[38 ] 的结果, 本文的三维S-R 无网格法计算结果与Zaghoul[42 ] 给出的实验值最接近. 因此充分说明了本文三维S-R无网格法的准确性, 也说明了S-R 和分解理论相对于其它有限变形理论的优越性.
图7 平板中点挠度与载荷的关系(正交各向异性板).
Fig.7 The central deflection of rectangle plate’s mid-plane versus load (orthotropic plate)
5 结 论
本文将基于S-R和分解定理的二维无网格数值方法扩展到三维情况, 给出了3D-SR-EFG数值计算方法, 并通过对梁、板结构的非线性弯曲问题典型算例进行了对比分析, 验证了该方法在求解三维几何非线性问题时的合理性、有效性和准确性. 另外, 对于本文提出的方法在与其他方法进行对比时所表现出来的一些差异性, 也给出了合理的解释. 在受均布载荷的四边简支正交各向异性方形板的算例中, 本文提出的数值计算方法是在所有对比方法中最接近实验结果的一种方法, 说明了3D-SR-EFG方法可以作为一种更加可靠的几何非线性数值计算方法.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
谢和平 . 非线性力学理论与实践 . 徐州 : 中国矿业大学出版社 , 1997
[本文引用: 1]
(Xie Heping Theory of Nonlinear Mechanics and Its Application . Xuzhou : China University of Mining and Technology Press , 1997 (in Chinese))
[本文引用: 1]
[2]
Fan H Zheng H He S S-R decomposition based numerical manifold method
.Computer Methods in Applied Mechanics and Engineering , 2016 , 304 : 452 -478
[本文引用: 2]
[3]
Liu GR Gu YT An Introduction to Meshfree Methods and Their Programming . Netherlands : Springer , 2005
[本文引用: 1]
[4]
Li G Belytschko T Element-free Galerkin method for contact problems in metal forming analysis
.Engineering Computations , 2001 , 18 : 62 -78
[本文引用: 1]
[5]
Belytschko T Lu YY Gu L Element-free Galerkin methods
.International Journal for Numerical Methods in Engineering , 1994 , 37 (2 ): 229 -256
[本文引用: 1]
[6]
邵玉龙 , 段庆林 , 高欣 等 . 自适应一致性高阶无单元伽辽金法
. 力学学报 , 2017 , 49 (1 ): 105 -116
[本文引用: 1]
(Shao Yulong Duan Qinglin Gao Xin et al .Adaptive consistent high order element-free Galerkin method
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (1 ): 105 -116 (in Chinese))
[本文引用: 1]
[7]
杨建军 , 郑健龙 . 无网格局部强弱法求解不规则域问题
. 力学学报 , 2017 , 49 (3 ): 659 -666
[本文引用: 1]
(Yang Jianjun Zheng Jianlong Meshless local strong-weak (MLSW) method for irregular domain problems
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (3 ): 659 -666 (in Chinese))
[本文引用: 1]
[8]
Chen JS Pan C Wu CT et al .Reproducing Kernel particle methods for large deformation analysis of non-linear structures
.Computer Methods in Applied Mechanics & Engineering , 1996 , 139 (1-4 ): 195 -227
[本文引用: 1]
[9]
Li S Hao W Liu WK Numerical simulations of large deformation of thin shell structures using meshfree methods
.Computational Mechanics , 2000 , 25 (2-3 ): 102 -116
[本文引用: 1]
[10]
Liew KM Ng TY Wu YC Meshfree method for large deformation analysis-a reproducing kernel particle approach
.Engineering Structures , 2002 , 24 (5 ): 543 -551
[本文引用: 1]
[11]
Zhang LW Song ZG Liew KM Nonlinear bending analysis of FG-CNT reinforced composite thick plates resting on Pasternak foundations using the element-free IMLS-Ritz method
.Composite Structures , 2015 , 128 : 165 -175
[本文引用: 1]
[12]
Do VNV Lee CH Bending analyses of FG-CNTRC plates using the modified mesh-free radial point interpolation method based on the higher-order shear deformation theory
.Composite Structures , 2017 , 168 : 485 -497
[本文引用: 1]
[13]
陈至达 . 有理力学:非线性连续体力学 . 徐州 : 中国矿业大学出版社 , 1988
[本文引用: 5]
(Chen Zhida Rational Mechanics .Xuzhou : China University of Mining and Technology Press , 1988 (in Chinese))
[本文引用: 5]
[14]
陈至达 . 杆、板、壳大变形理论 . 北京 : 科学出版社 , 1994
[本文引用: 2]
(Chen Zhida Finite Deformation Theory of Link, Plate and Shell . Beijing : Science Press , 1994 (in Chinese))
[本文引用: 2]
[15]
陈至达 . 连续介质有限变形力学几何场论
. 力学学报 , 1979 , 15 (2 ): 107 -117
[本文引用: 1]
(Chen Zhida Geometric field theory of finite deformation mechanics for continuum
.Chinese Journal of Theoretical and Applied Mechanics 1979 , 15 (2 ): 107 -117 (in Chinese))
[本文引用: 1]
[16]
陈至达 . 连续介质有限变形力学几何场论(续)(弹性有限变形能量原理)
. 清华大学学报(自然科学版) , 1979 , 19 : 45 -57
[本文引用: 1]
(Chen Zhida Geometric field theory of finite deformation mechanics for continuum (continued)(elastic finite deformation energy principle)
.Journal of Tsinghua University (Science and Technology )1979 , 19 : 45 -57 (in Chinese))
[本文引用: 1]
[17]
Chen M Liang J Chen X et al .On uniqueness, existence and objectivity of S-R decomposition theorem
.Applied Mathematics and Mechanics (English Edition )1997 , 18 (9 ): 817 -823
[本文引用: 1]
[18]
陈至达 . 连续体力学中有限变形与转动的计算增量法
. 应用数学和力学 , 1985 , 6 (9 ): 769 -774
[本文引用: 1]
(Chen Zhida Increment method of Finite deformation and rotational computing in continuum mechanics
.Applied Mathematics and Mechanics 1997 , 18 (9 ): 817 -823 (in Chinese))
[本文引用: 1]
[19]
秦忠 . 基于新的大变形理论的非线性有限元及其应用. [博士论文] . 北京 : 中国矿业大学(北京) , 1986
[本文引用: 1]
(Qin Zhong Nonlinear finite element and its applications based on new large deformation thoery. [PhD Thesis] . Beijing : China University of Mining and Technology (Beijing) , 1986 (in Chinese))
[本文引用: 1]
[20]
尚勇 . 带有接触摩擦边界弹塑性大变形问题的理论和有限元分析. [博士论文] . 北京 : 中国矿业大学(北京) , 1987
[本文引用: 1]
(Shang Yong The theory and finite element analysis of the elastoplasticity large deformation problem with contact friction boundary. [PhD Thesis] . Beijing : China University of Mining and Technology (Beijing) , 1987 (in Chinese))
[本文引用: 1]
[21]
尚勇 , 陈至达 . 橡胶环直径方向受压大变形问题
. 计算结构力学及其应用 , 1989 , 6 (4 ): 13 -20
[本文引用: 1]
(Shang Yong Chen Zhida Large deformation problem of rubber ring compressed in diameter direction
.Journal of Computational Structural Mechanics and Applications 1989 , 6 (4 ): 13 -20 (in Chinese))
[本文引用: 1]
[22]
尚勇 , 陈至达 . 带有摩擦的单边接触大变形问题的研究(I)——增量变分方程
. 应用数学和力学 , 1989 , 10 (12 ): 1049 -1058
[本文引用: 1]
(Shang Yong Chen Zhida On large deformation unilateral contact problem with friction(I)-Incremental variational equation
.Applied Mathematics and Mechanics 1989 , 10 (12 ): 1049 -1058 (in Chinese))
[本文引用: 1]
[23]
尚勇 , 陈至达 . 带有摩擦的单边接触大变形问题的研究(II)——非线性有限元解及应用
. 应用数学和力学 , 1990 , 11 (1 ): 1 -11
[本文引用: 1]
(Shang Yong Chen Zhida On large deformation unilateral contact problem with friction(II)-nonlinear finite element technique and its application
.Applied Mathematics and Mechanics 1990 , 11 (1 ): 1 -11 (in Chinese))
[本文引用: 1]
[24]
李平 . 非线性大变形有限元分析的更新拖带坐标法及其应用. [博士论文] . 北京 : 中国矿业大学(北京) , 1991
[本文引用: 1]
(Li Ping The updated co-moving coordinate formulation for the nonlinear lager deformation finite element analysis and application. [PhD Thesis] . Beijing : China University of Mining and Technology (Beijing) , 1991 (in Chinese))
[本文引用: 1]
[25]
Li P Chen ZD The updated co-moving coordinate formulation of continuum mechanics based on the SR decomposition theorem
.Computer Methods in Applied Mechanics and Engineering , 1994 , 114 (1-2 ): 21 -34
[本文引用: 4]
[26]
高立堂 , 李晓东 , 陈礼刚 等 . 火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(II: 算例分析)
. 固体力学学报 , 2006 , 27 : 138 -142
[本文引用: 1]
(Gao Litang Li Xiaodong Chen Ligang et al .Thermal-elastic-plastic finite element analysis of reinforced slabs under fire-based on S-R decomposition theorem(II: Analysis of examples)
.Acta Mechanica Solida Sinica 2006 , 27 : 138 -142 (in Chinese))
[本文引用: 1]
[27]
高立堂 , 宋玉普 , 董毓利 . 火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(I: 理论)
. 计算力学学报 , 2007 , 24 (1 ): 86 -90
[本文引用: 1]
(Gao Litang Song Yupu Dong Yuli Thermal-elastic-plastic finite element analysis of reinforced slabs under fire-based on S-R decomposition theorem(I: Theories)
.Chinese Journal of Computational Mechanics 2007 , 24 (1 ): 86 -90 (in Chinese))
[本文引用: 1]
[28]
何满潮 , 郭宏云 , 陈新 等 . 基于和分解有限变形力学理论的深部软岩巷道开挖大变形数值模拟分析
. 岩石力学与工程学报 , 2010 , 29 (s2 ): 4050 -4055
[本文引用: 1]
(He Manchao Guo Hongyun Chen Xin et al .Numerical simulation analysis of large deformation of deep soft rock engineering based on solar decomposition theorem
.Chinese Journal of Rock Mechanics and Engineering 2010 , 29 (s2 ): 4050 -4055 (in Chinese))
[本文引用: 1]
[29]
谢和平 , 陈至达 . 非线性大变形边界元法探讨
. 中国矿业大学学报 , 1986 (4 ): 101 -109
[本文引用: 1]
(Xie Heping Chen Zhida The boundary element method of nolinear large deformation
.Journal of China University of Mining & Technology 1986 (4 ): 101 -109 (in Chinese))
[本文引用: 1]
[30]
谢和平 . 非线性大变形问题的边界元分析法
. 应用数学和力学 , 1988 , 9 (12 ): 1087 -1096
[本文引用: 1]
(Xie Heping Analysis of nonlinear large deformation problems by boundary element method
.Applied Mathematics and Mechanics 1988 , 9 (12 ): 1087 -1096 (in Chinese))
[本文引用: 1]
[31]
Gao Y Feng G Yeung MCR Modification of discontinuous deformation analysis method based on finite deformation theory
.Chinese Journal of Rock Mechanics and Engineering , 2011 , 30 (11 ): 2360 -2365
[本文引用: 1]
[32]
罗丹 . 基于S-R和分解定理的几何非线性问题的无网格Galerkin法分析. [硕士论文] . 长沙 : 湖南大学 , 2011
[本文引用: 5]
(Luo Dan Based on S-R decomposition theorem analysis of element free Galerkin method on geometric nonlinear problems. [Master Thesis] . Changsha : Hunan University , 2011 (in Chinese))
[本文引用: 5]
[33]
陈芳祖 , 罗丹 . 基于S-R和分解定理的无网格Galerkin法求解几何非线性问题
. 湖南大学学报(自科版) , 2012 , 39 (1 ): 42 -46
[本文引用: 2]
(Chen Fangzu Luo Dan Element free Galerkin method for geometrically nonlinear problems based on the S-R decomposition theorem
.Journal of Hunan Unviersity (Natural Sciences )2012 , 39 (1 ): 42 -46 (in Chinese))
[本文引用: 2]
[34]
宋彦琦 , 郝亮钧 , 李向上 . 基于S-R和分解定理的几何非线性问题的数值计算分析
. 应用数学和力学 , 2017 , 38 (9 ):1029 -1040
[本文引用: 3]
(Song Yanqi Hao Liangjun Li Xiangshang Numerical analysis geometrically nonlinear problems based on The S-R decompostion theorem
.Applied Mathematics and Mechanics 2017 , 38 (9 ): 1029 -1040 (in Chinese))
[本文引用: 3]
[35]
Fan H Zheng H Zhao J Discontinuous deformation analysis based on strain-rotation decomposition
.International Journal of Rock Mechanics & Mining Sciences , 2017 , 92 : 19 -29
[本文引用: 2]
[36]
Fan H Zheng H Zhao J Three-dimensional discontinuous deformation analysis based on strain-rotation decomposition
.Computers & Geotechnics , 2018 , 95 : 191 -210
[本文引用: 3]
[37]
Bathe KJ Ramm E Wilson EL Finite element formulations for large deformation dynamic analysis
.International Journal for Numerical Methods in Engineering , 2010 , 9 (2 ): 353 -386
[本文引用: 2]
[38]
Shen HS Large deflection of composite laminated plates under transverse and in-plane loads and resting on elastic foundations
.Composite Structures , 1999 , 45 (2 ): 115 -123
[本文引用: 8]
[39]
Levy S Bending of rectangular plates with large deflections. NACA Tech, Note No. 846 , 1942
[本文引用: 6]
[40]
Gorji M On large deflection of symmetric composite plates under static loading
.Journal of Mechanical Engineering Science , 1986 , 200 (1 ): 13 -19
[本文引用: 6]
[41]
刘人怀 , 薛江红 . 复合材料层合板壳非线性力学的研究进展
. 力学学报 , 2017 , 49 (3 ): 487 -506
[本文引用: 1]
(Liu Renhuai Xue Jianghong Development of nonlinear mechanics for laminated composite
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (3 ): 487 -506 (in Chinese))
[本文引用: 1]
[42]
Zaghloul SA Kennedy JB Nonlinear behavior of symmetrically laminated plates
.Journal of Applied Mechanics , 1975 , 42 (1 ): 234 -236
[本文引用: 2]
1
1997
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
1
1997
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
S-R decomposition based numerical manifold method
2
2016
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
2005
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
Element-free Galerkin method for contact problems in metal forming analysis
1
2001
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
Element-free Galerkin methods
1
1994
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
自适应一致性高阶无单元伽辽金法
1
2017
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
自适应一致性高阶无单元伽辽金法
1
2017
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
无网格局部强弱法求解不规则域问题
1
2017
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
无网格局部强弱法求解不规则域问题
1
2017
... 固体几何非线性和物理非线性问题的建模和求解方法等一直都是非线性力学的重点课题之一[1 ] . 由于非线性问题在数学求解上的复杂性, 很难找到问题的解析解, 因此更多时候是从数值模拟方面寻找解答. 在传统固体几何非线性问题的数值模拟方法中, 一般都采用全拉格朗日格式(total Lagrange formulation, 简称 T.L. 格式)和更新拉格朗日格式(updated Lagrange formulation, 简称 U.L. 格式)的有限元方法(FEM)来进行求解[2 ] . 但由于FEM对单元具有依赖性, 对于大变形问题, 单元的畸变会严重影响FEM的求解精度[3 ] . 为了避免对单元网格的依赖, 无网格法(element-free methods)是一个很好的选择, 例如, Li和Belytschko[4 ] 利用无网格Galerkin 法(EFG)[5 ] 对金属成形过程中的接触冲击大变形问题进行了分析. 邵玉龙等[6 ] 在一致性无单元Galerkin法(consistent EFG, CEFG)的基础之上, 发展了自适应分析方法, 进一步提高它求解局部高梯度问题的计算效率. 杨建军和郑健龙[7 ] 基于无网格局部强弱法(meshless local strong-weak, 简称MLSW), 对不规则域问题进行了求解. ...
Reproducing Kernel particle methods for large deformation analysis of non-linear structures
1
1996
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
Numerical simulations of large deformation of thin shell structures using meshfree methods
1
2000
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
Meshfree method for large deformation analysis-a reproducing kernel particle approach
1
2002
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
Nonlinear bending analysis of FG-CNT reinforced composite thick plates resting on Pasternak foundations using the element-free IMLS-Ritz method
1
2015
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
Bending analyses of FG-CNTRC plates using the modified mesh-free radial point interpolation method based on the higher-order shear deformation theory
1
2017
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
5
1988
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
... [13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
... S-R和分解定理[13 ] 证明: “给定一个物理可能的位移函数, 此函数在形变体点集域内是单值连续的, 处处具有一阶导数, 则此运动变换总可以分解为正交与对称两个子变换的直和. 正交变化体现点集的转动, 而对称变换体现点集的形变.” ...
... 其中, S R [13 ] 证明了和分解定理的存在性和唯一性, 这里只是给出其中相关的数学结果. ...
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
5
1988
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
... [13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
... S-R和分解定理[13 ] 证明: “给定一个物理可能的位移函数, 此函数在形变体点集域内是单值连续的, 处处具有一阶导数, 则此运动变换总可以分解为正交与对称两个子变换的直和. 正交变化体现点集的转动, 而对称变换体现点集的形变.” ...
... 其中, S R [13 ] 证明了和分解定理的存在性和唯一性, 这里只是给出其中相关的数学结果. ...
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
2
1994
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
2
1994
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
连续介质有限变形力学几何场论
1
1979
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
连续介质有限变形力学几何场论
1
1979
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
连续介质有限变形力学几何场论(续)(弹性有限变形能量原理)
1
1979
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
连续介质有限变形力学几何场论(续)(弹性有限变形能量原理)
1
1979
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
On uniqueness, existence and objectivity of S-R decomposition theorem
1
1997
... 然而在传统几何非线性无网格数值方法中, 绝大多数都是采用Green应变张量作为有限变形理论的基础. 例如Chen 等[8 ] 、Li 等[9 ] 、Liew等[10 ] , 采用了无网格RKPM (reproducing kernel particle method)法对一些结构的大变形问题进行了数值计算. 又例如最近几年, Zhang 等[11 ] 、Do等[12 ] 分别利用无网格IMLS-Ritz法(improved moving least-square ritz method)和无网格RPIM 法(radial point interpolation method)对功能梯度碳纳米管增强复合材料板的大变形弯曲问题进行了数值讨论. 虽然Green应变张量克服了Cauchy应变张量在变形体作纯转动时产生虚假应变这一缺点, 但是由于没有导出相应的转动张量和应变张量相匹配, 因此会限制其在大位移和大转动问题中的应用[13 ,14 ] . 陈至达等[13 ,15 -16 ] 提出的S-R(strain-rotation)和分解定理, 克服了Green应变张量的缺点, 应变和局部转动是同时发生的, 并且应变是唯一确定的[17 ] . 因此S-R和分解定理可以为几何非线性数值方法提供精确完备的数学力学基础. ...
连续体力学中有限变形与转动的计算增量法
1
1997
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
连续体力学中有限变形与转动的计算增量法
1
1997
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
1986
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
1986
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
1987
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
1987
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
橡胶环直径方向受压大变形问题
1
1989
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
橡胶环直径方向受压大变形问题
1
1989
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
带有摩擦的单边接触大变形问题的研究(I)——增量变分方程
1
1989
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
带有摩擦的单边接触大变形问题的研究(I)——增量变分方程
1
1989
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
带有摩擦的单边接触大变形问题的研究(II)——非线性有限元解及应用
1
1990
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
带有摩擦的单边接触大变形问题的研究(II)——非线性有限元解及应用
1
1990
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
1991
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
1
1991
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
The updated co-moving coordinate formulation of continuum mechanics based on the SR decomposition theorem
4
1994
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 假设从0到 t t + Δ t t + Δ t [25 ] ...
... 在更新拖带坐标法[25 ] 中, 是以 t t g 0 i t V 0 i 图2 所示, 设质点在初始时刻 t 0 P P g 0 i . 在 t P ' P ' t g 0 i t g i . 在由 t t + Δ t t t g 0 i ( 一般取为标准直角坐标系)作为参考基准. 这样, t t g i t V i | | j
... 如果不考虑体力矩的影响, 假设初始系为正交系, 文献[25 ] 利用如下结果 ...
火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(II: 算例分析)
1
2006
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(II: 算例分析)
1
2006
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(I: 理论)
1
2007
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理(I: 理论)
1
2007
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
基于和分解有限变形力学理论的深部软岩巷道开挖大变形数值模拟分析
1
2010
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
基于和分解有限变形力学理论的深部软岩巷道开挖大变形数值模拟分析
1
2010
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
非线性大变形边界元法探讨
1
1986
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
非线性大变形边界元法探讨
1
1986
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
非线性大变形问题的边界元分析法
1
1988
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
非线性大变形问题的边界元分析法
1
1988
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
Modification of discontinuous deformation analysis method based on finite deformation theory
1
2011
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
5
2011
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性. ...
... 图3 所示为一上表面受均布载荷 q L = 254 D = H = 25.4 E = 82.74 쀻 . 图4 给出了该算例中梁右端中点的无量纲挠度值与无量纲均布载荷值之间的关系, 其中包括本文数值方法收敛性的验证, 以及本文结果与罗丹[32 ] 和Holden[37 ] 的结果、小变形线性理论的结果之间的比较. 由不同节点数之间的对比可以反映出本文三维S-R无网格法在该算例中的收敛性特点, 可以发现当采用 21 × 3 × 3 [32 ] 的结果进行比较, 可以发现本文的结果与罗丹[32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
... [32 ]的结果进行比较, 可以发现本文的结果与罗丹[32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
... [32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
5
2011
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性. ...
... 图3 所示为一上表面受均布载荷 q L = 254 D = H = 25.4 E = 82.74 쀻 . 图4 给出了该算例中梁右端中点的无量纲挠度值与无量纲均布载荷值之间的关系, 其中包括本文数值方法收敛性的验证, 以及本文结果与罗丹[32 ] 和Holden[37 ] 的结果、小变形线性理论的结果之间的比较. 由不同节点数之间的对比可以反映出本文三维S-R无网格法在该算例中的收敛性特点, 可以发现当采用 21 × 3 × 3 [32 ] 的结果进行比较, 可以发现本文的结果与罗丹[32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
... [32 ]的结果进行比较, 可以发现本文的结果与罗丹[32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
... [32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
基于S-R和分解定理的无网格Galerkin法求解几何非线性问题
2
2012
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性. ...
基于S-R和分解定理的无网格Galerkin法求解几何非线性问题
2
2012
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性. ...
基于S-R和分解定理的几何非线性问题的数值计算分析
3
2017
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性. ...
... 更新拖带坐标法最大的特点是, 在每一次迭代步结束后, 重新选择初始拖带系, 不仅保证了应力速率的客观性, 自动消除了转动的影响, 使应力分量不随时间改变, 而且大大简化了增量变分方程求解中的系数矩阵, 降低了增量变分方程的求解难度,利于算法实现和推广应用[34 ] . ...
基于S-R和分解定理的几何非线性问题的数值计算分析
3
2017
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... 从前面的文献综述可以看出, 基于S-R定理的无网格法的研究依然较少, 由于在大变形问题分析中, 无网格法相对于FEM更有优势, 因此目前结合S-R定理和无网格数值方法的研究依然值得关注. 另外文献[32 ,33 ,34 ] 只是对二维问题进行了讨论, 并未给出基于S-R和分解定理的三维无网格法离散格式. 基于以上认识, 本文将S-R无网格法进一步延伸到三维情况: 采用由更新拖带坐标法和势能率原理推导出来的增量变分方程, 利用基于全局弱势的无网格Galerkin法得到了用于求解三维空间问题的离散格式, 其本质边界条件的施加是通过直接修改系统离散方程中的刚度矩阵和总体力向量来实现的. 利用MATLAB编制三维S-R 无网格法程序, 对受均布载荷的三维悬臂梁和四边简支矩形板结构的非线性弯曲问题进行了计算. 最后将所得的数值模拟结果与现有文献进行比较, 验证了本文的三维S-R无网格数值模拟算法的合理性和准确性. ...
... 更新拖带坐标法最大的特点是, 在每一次迭代步结束后, 重新选择初始拖带系, 不仅保证了应力速率的客观性, 自动消除了转动的影响, 使应力分量不随时间改变, 而且大大简化了增量变分方程求解中的系数矩阵, 降低了增量变分方程的求解难度,利于算法实现和推广应用[34 ] . ...
Discontinuous deformation analysis based on strain-rotation decomposition
2
2017
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... [35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
Three-dimensional discontinuous deformation analysis based on strain-rotation decomposition
3
2018
... 陈至达等[18 ] 基于S-R和分解定理, 采用拖带坐标描述法和势能率变分原理, 给出了用以数值求解的位移增量方程, 为S-R 和分解定理在数值方法中的应用奠定了基础. 到目前为止, 基于S-R和分解定理的数值模拟方法的研究大多数以FEM为主: 秦忠[19 ] 提出了基于S-R定理的节理单元和曲壳单元, 编制了非线性有限元计算程序SNAP, 对岩体蠕变和壳体大变形问题进行了求解; 尚勇等[20 ,21 ,22 ,23 ] 进一步拓展了S-R定理和拖带坐标描述法在有限元中的应用, 建立了连续体大变形变边界变分公式和大变形接触问题的计算模型; 李平等[24 ,25 ] 提出了更新拖带坐标法(updated co-moving system, 简称U.C. 法)的大变形有限元计算方法, 编制了程序NASRAC, 并与采用U.L. 格式的程序ADINA 进行了比较; 高立堂等[26 ,27 ] 采用李平的更新拖带坐标有限元法对火灾作用下的钢筋混凝土板进行了数值计算; 何满潮等[28 ] 开发了有限元程序“深部软岩工程大变形力学设计分析系统”, 对巷道的不同埋深下进行开挖的巷道围岩大变形进行数值模拟. 除了FEM之外, 一些学者将S-R定理也应用到了其他一些数值方法中. 谢和平[29 ,30 ] 导出了基于S-R定理的非线性边界元计算格式, 编写了NBEM程序; 高亚楠等[31 ] 采用S-R 和分解理论对原有非连续变形分析(DDA)程序进行了修正; 罗丹[32 ] 、 陈芳祖和罗丹[33 ] 、宋彦琦等[34 ] 都采用了更新拖带坐标描述法, 导出了基于S-R 定理的二维无网格Galerkin法离散方程, 对二维平面大变形梁结构算例进行了求解; 最近, Fan等[2 ] 同样基于S-R 定理和更新拖带坐标描述法, 利用动量守恒定律给出了动态增量变分方程, 并结合数值流形法(numerical manifold method, NMM), 建立了二维情况下的S-R 动态数值流形法(S-R-D-based NMM); 随后Fan等[35 ,36 ] 又根据自己推导的动态增量变分方程, 给出了三维情况下的离散格式[36 ] , 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... [36 ], 并结合DDA, 分别建立了基于S-R 定理的二维DDA方法(SR-2D-DDA)[35 ] 和三维[36 ] DDA方法(SR-3D-DDA). ...
... [36 ]DDA方法(SR-3D-DDA). ...
Finite element formulations for large deformation dynamic analysis
2
2010
... 图3 所示为一上表面受均布载荷 q L = 254 D = H = 25.4 E = 82.74 쀻 . 图4 给出了该算例中梁右端中点的无量纲挠度值与无量纲均布载荷值之间的关系, 其中包括本文数值方法收敛性的验证, 以及本文结果与罗丹[32 ] 和Holden[37 ] 的结果、小变形线性理论的结果之间的比较. 由不同节点数之间的对比可以反映出本文三维S-R无网格法在该算例中的收敛性特点, 可以发现当采用 21 × 3 × 3 [32 ] 的结果进行比较, 可以发现本文的结果与罗丹[32 ] 的结果之间存在微小的差异. 在罗丹的所有算例中, 结构都是有厚度的, 因此实际上都应该是三维空间结构. 当他们使用自己的二维S-R无网格法来求解这些三维问题时, 必定需要满足如下假设(以这里的悬臂梁为例): 所有物理量与厚度方向的坐标( X 2 ) 是没有关系的, 即所有物理量只是另外两个方向坐标( X 1 , X 3 ) 的函数; 沿厚度方向的物理分量( σ i 3 , ε i 3 , u 3 , i = 1,2 , 3 ) 都为零. 本文的三维S-R 无网格数值法未对该算例中的问题作以上的假设近似简化处理, 因此本文方法对于该算例的求解应该具有更高的精度. 而由于Holden[37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
... [37 ] 采用不同的有限变形理论, 因此与之比较起来差异性会更加明显一点. 通过该算例的求解, 可以验证本文三维S-R 无网格法的收敛性和合理性. ...
Large deflection of composite laminated plates under transverse and in-plane loads and resting on elastic foundations
8
1999
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [38 ]、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [38 ]是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [38 ]、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... 同样以图5 为例, 若板为正交各向异性材料, 杨氏模量有 E 1 = 2.069 × 1 0 4 E 2 = 8.826 × 1 0 3 G 12 = G 13 = G 23 = 2.551 × 1 0 3 µ = 0.32 a = b = 304.8 h = 3.5 图7 给出该算例的平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系. 同样可以发现当节点数为 11 × 11 × 3 [38 ] 给出的结果, 这是与前文的各向同性板算例不一样的. 相对于Zaghoul 等[42 ] 给出的经典解(CPT) 和Shen[38 ] 的结果, 本文的三维S-R 无网格法计算结果与Zaghoul[42 ] 给出的实验值最接近. 因此充分说明了本文三维S-R无网格法的准确性, 也说明了S-R 和分解理论相对于其它有限变形理论的优越性. ...
... [38 ] 的结果, 本文的三维S-R 无网格法计算结果与Zaghoul[42 ] 给出的实验值最接近. 因此充分说明了本文三维S-R无网格法的准确性, 也说明了S-R 和分解理论相对于其它有限变形理论的优越性. ...
6
1942
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [39 ]、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [39 ]、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [39 ]采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
On large deflection of symmetric composite plates under static loading
6
1986
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [40 ]给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [40 ]都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [40 ]则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [40 ]三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
... [40 ] 之间的差异性也是可以解释的. ...
复合材料层合板壳非线性力学的研究进展
1
2017
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
复合材料层合板壳非线性力学的研究进展
1
2017
... 图5 所示为一上表面受均布载荷q b a h . 在该算例中, 假定板为各向同性材料(µ = 0.316 ) , 并且a = b 图6 , 给出了平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系曲线, 与之作为对比的结果是来自于Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] . 首先可以看到在该算例中采用节点数11 × 11 × 3 [38 ] 、Levy[39 ] 、Gorgi[40 ] 给出的结果. Shen[38 ] 、Levy[39 ] 、Gorgi[40 ] 都是在位移几何关系中加入冯·卡门(Von Kármán)应变项来实现非线性的考虑, 只是三者采用了不同板壳理论和不同的偏微分方程求解方法. Levy[39 ] 采用的是经典板壳理论(classic plate theory, CPT), 通过三角级数展开法对方程进行了求解. Gorgi[40 ] 则利用一阶剪切变形理论(first order shear deformation theory, FSDT), 通过有限差分法和有限单元法进行的求解. Shen[38 ] 是基于Reddy的高阶剪切变形理论(higher order shear deformation plate theory, HSDT), 最后通过摄动法对非线性方程进行求解. 但是经典板壳理论和绝大多数剪切变形板壳理论包括一阶剪切变形理论和Reddy的高阶剪切变形理论, 会采用一些假设, 如假设沿厚度方向的正应变ε z = 0 . 而本文方法所采用的理论基础未做任何近似假设, 因此同本文的三维方法相比较而言, Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 三者的准确性应该相对较低. 在传统板壳几何非线性分析中, 都是采用Von Kármán应变项来实现非线性的考虑[41 ] . 而作者认为Von Kármán应变在本质上为Green 应变张量, 而Green 应变张量理论最致命的缺点是没有导出相应的转动张量和应变张量相匹配[13 ,14 ] . 总结以上的讨论, 该算例同样验证了本文三维S-R 无网格法的收敛性, 并且同Shen[38 ] 、Levy[39 ] 和Gorgi[40 ] 之间的差异性也是可以解释的. ...
Nonlinear behavior of symmetrically laminated plates
2
1975
... 同样以图5 为例, 若板为正交各向异性材料, 杨氏模量有 E 1 = 2.069 × 1 0 4 E 2 = 8.826 × 1 0 3 G 12 = G 13 = G 23 = 2.551 × 1 0 3 µ = 0.32 a = b = 304.8 h = 3.5 图7 给出该算例的平板中面中点的无量纲挠度与无量纲均布载荷强度之间的关系. 同样可以发现当节点数为 11 × 11 × 3 [38 ] 给出的结果, 这是与前文的各向同性板算例不一样的. 相对于Zaghoul 等[42 ] 给出的经典解(CPT) 和Shen[38 ] 的结果, 本文的三维S-R 无网格法计算结果与Zaghoul[42 ] 给出的实验值最接近. 因此充分说明了本文三维S-R无网格法的准确性, 也说明了S-R 和分解理论相对于其它有限变形理论的优越性. ...
... [42 ] 给出的实验值最接近. 因此充分说明了本文三维S-R无网格法的准确性, 也说明了S-R 和分解理论相对于其它有限变形理论的优越性. ...
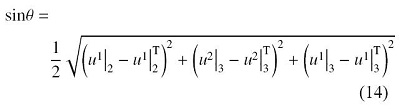
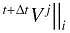 表示在
表示在 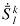 和
和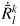 分别表示应变速率和转动速率; 顶标“‒”表示相应物理量是在
分别表示应变速率和转动速率; 顶标“‒”表示相应物理量是在