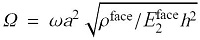引言
多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] .
针对已有的大多数三维求解方法仅能求解少数形状规则,边界条件简单且铺层方式正交铺设的多层复合结构的限制,本文以独立铺层为建模对象,结合广义谱方法与微分求积技术建立了一种适用一般边界条件和铺层方式的多层复合壳体三维分析半解析方法——谱--微分求积混合法,以期为多层复合壳体振动计算分析提供高效可靠的参考方法.
1 多层复合壳体三维振动力学模型
1.1 分析模型
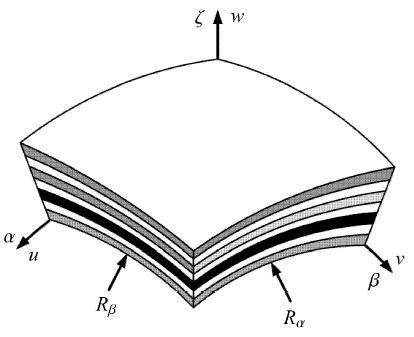
考虑如图1 所示的多层复合壳体. 假设参考坐标系为正交曲线坐标系 αβζ . 其中, α β ζ u v w α β ζ R α R β α β
图1 多层复合壳体模型及参考坐标系.
Fig. 1 Schematic illustration of a multilayered shell and the curvilinear coordinate system
1.2 几何方程及物理方程
当壳体因振动产生微小位移时,壳体上任意点的6个应变分量为
其中, ε α ε β ε ζ γ αβ γ αζ γ βζ A α A β [15 ] .
1.3 计算面选取及应变应变分量计算
本文方法先从独立子层入手,沿子层厚度方向配置若干计算面并引入微分求积技术将结构的三维偏微分问题转化为二维偏微分问题进行求解.
假设第 k ζ k + 1 ζ k . 为了提高方法收敛性和计算速度,本文所选取的各计算面满足切比雪夫零点分布形式,各计算面横向坐标为
ζ k 1 = ζ k ζ k J k = ζ k + 1 ζ k j = ζ k 1 + ζ k J k 2 - h k 2 cos 2 j π - 3 π 2 J k - 4 , j = 2,3 , ⋯ ( 2 )
式中, J k h k k
将第 k j
u ( ζ k j ) = u k j , A α ( ζ k j ) = A α k j v ( ζ k j ) = v k j , A β ( ζ k j ) = A β k j w ( ζ k j ) = w k j , A ζ ( ζ k j ) = A ζ k j ( 3 )
ε α ( ζ k j ) = ε α k j , γ βζ ( ζ k j ) = γ βζ k j ε β ( ζ k j ) = ε β k j , γ αζ ( ζ k j ) = γ αζ k j ε ζ ( ζ k j ) = ε ζ k j , γ αβ ( ζ k j ) = γ αβ k j ( 4 )
因此,将式 (3)和式(4)代入式(1)并进行微分求积可得 ε α k j = 1 A α k j ∂ u k j ∂ α + v k j A α k j A β k j ∂ A α k j ∂ β + w k j A α k j ∑ r a kjr A α k r ε β k j = u k j A α k j A β k j ∂ A β k j ∂ α + 1 A β k j ∂ v k j ∂ β + w k j A β k j ∑ r a kjr A β k r ε ζ k j = ∑ r a kjr w k r γ βζ k j = 1 A β k j ∂ w k j ∂ β + A β k j ∑ r a kjr v k r A k β r * γ αζ k j = 1 A α k j ∂ w k j ∂ α + A α k j ∑ r a kjr u k r A k α r * γ αβ k j = A β k j A α k j ∂ ∂ α v k j A β k j + A α k j A β k j ∂ ∂ β u k j A α k j ( 5 )
式中,权重系数 a kjr
a kjr = 1 ζ k r - ζ k j ∏ s ≠ r , j J k ζ k j - ζ k s ζ k r - ζ k s , r ≠ j - ∑ r ≠ j a kjr , r = j ( 6 )
根据拉格朗日插值定理,结构第 k
u , v , w = L k j ( ζ ) ∑ j u k j , v k j , w k j { A α , A β , A ζ } = L k j ( ζ ) ∑ j A α k j , A β k j , A ζ k j ε α , ε β , ε ζ = L k j ( ζ ) ∑ j ε α k j , ε β k j , ε ζ k j γ βζ , γ αζ , γ αβ = L k j ( ζ ) ∑ j γ βζ k j , γ αζ k j , γ αβ k j ( 7 )
其中 L k j ( ζ )
L k j ( ζ ) = ∏ r ≠ j J k ζ - ζ k r ζ k j - ζ k r , ζ k 1 # x 2264 ; ζ # x 2264 ; ζ k J k ( 8 )
根据胡克定律,第 k σ k = T k C k T k T ε k σ k = [ σ α , σ β , σ ζ , τ βζ , τ αζ , τ αβ ] T ε k = [ ε α , ε β , ε ζ , γ βζ , γ αζ , γ αβ ] T ( 9 )
式中, σ α σ β σ ζ α β ζ τ αβ τ αζ τ βζ C k T k [20 ] .
第 k
U sk = 1 2 ∫ α ∫ β ∫ ζ k ζ k + 1 ε k T T k C k T k T v k A α A β A ζ d ζ d β d α T k = 1 2 ∫ α ∫ β ∫ ζ k ζ k + 1 ρ k ( u ̇ 2 + v ̇ 2 + w ̇ 2 ) A α A β A ζ d ζ d β d α ( 10 )
借助哈密尔顿变分原理,式(10)可推导得到到结构的振动控制微分方程,具体形式参考文献[17 ].
1.4 子层特征矩阵及整体方程求取
多层复合壳体的边界条件可以分为3大类:几何边界条件、自然边界条件和混合边界条件. 在实际求解中,只有几何形状规则、至少一对边简支、铺层对称的极少数多层复合结构才能找到既满足控制微分方程又满足边界约束条件的解析解. 对于其他情况,可将结构的边界条件方程和控制微分方程转化成能量泛函,然后通过求解泛函的极值问题进行求解. 本文考虑几何边界条件下层合壳体的振动问题,为了适用一般边界条件,通过引入罚函数,将边界约束条件改写为如下泛函
Π pk = 1 2 ∫ ∫ ζ k ζ k + 1 ∑ l = 0 1 k ku α l u 2 + k kv α l v 2 + k kw α l w 2 | α = α l A β A ζ d ζ d β + 1 2 ∫ ∫ ζ k ζ k + 1 ∑ l = 0 1 k ku β l u 2 + k kv β l v 2 + k kw β l w 2 | β = β l A α A ζ d ζ d α ( 11 )
式中 k ku α l , k kv α l , k kw α l , k ku β l , k kv β l , k kv β l 表1 给出了不同边界条件下罚参数的取值情况.
考虑到Chebyshev多项式良好的稳定性和收敛性,本文借助其来表述计算面上的场变量,从而将获取的二维偏微分方程转化为以场变量展开系数为未知量的线性代数方程组,避免了对超越方程的求解. 第 k j
u k j ( α , β , t ) = ∑ n = 1 N ∑ m = 1 M u k jmn ( t ) T m ( α ) T n ( β ) v k j ( α , β , t ) = ∑ n = 1 N ∑ m = 1 M v k jmn ( t ) T m ( α ) T n ( β ) w k j ( α , β , t ) = ∑ n = 1 N ∑ m = 1 M w k jmn ( t ) T m ( α ) T n ( β ) ( 12 )
其中, u k jmn v k jmn w k jmn T n T m n m M N α β [ - 1 , + 1 ]
由式(10)和式(11)可知,子层 k
Π k t otal = T k - U sk - Π pk ( 13 )
将计算面位移表达式(12)代入式 (13),经变分得到第 k
K k - ω 2 M k G k = 0 ( 14 )
式中, K k M k G k
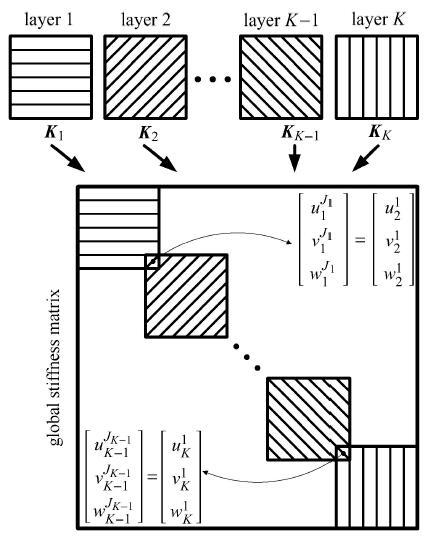
层合结构层间界面需要满足位移连续和横向应力连续两个条件. 本文解法属于基于能量变分原理的位移解法,当所求得的解满足层间位移连续条件,层间横向应力连续条件将自动满足[17 ] . 为了便于后续层与层之间特征矩阵的装配,在式(2)中,每一子层的上下表面分别选为该层的第一和最后一个计算面. 因此,式(14)中刚度/质量矩阵的第一行和最后一行分别为计算面位移场 u k 1 v k 1 w k 1 u k J k v k J k w k J k k k - 1 k k + 1 图2 所示(质量矩阵和系数向量同理可得). 通过对整体矩阵方程进行特征值分解即可得到壳体振动特性信息.
图2 整体刚度矩阵组装方式
Fig. 2 Assemblage of the global stiffness matrix
2 多层复合壳体振动算例与讨论
在前面推导的基础上,文中通过多层复合板和圆柱壳算例来验证方法的可靠性. 下文采用字母F,S,C来表示自由、简支和固支边界条件.
2.1 多层复合板算例分析
表2 给出了 [ 0 ∘ / 9 0 ∘ ] 2 [ 0 ∘ / 9 0 ∘ ] 4 Ω = ω h ρ / E 2 18 ,19 ]的对比情况. 文献[18 ]采用的是状态空间与微分求积混合架构的半解析解法,其边界条件采用混合变量的方式直接描述,而文献[19 ]采用的是基于广义变分的位移解法. 复合板的材料和几何参数分别为: E 1 = 40 E 2 G 12 = G 13 = 0.6 E 2 G 23 = 0.5 E 2 ν 12 = ν 13 = 0.25 ν 23 = 0.49 a = b = 1 h / a = 0.1 . 计算面数 J k = 5 M = N = 15 . 可以看出,各种边界条件下,本文方法得到的解与文献[18 ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性.
表3 给出了[0/90/0]复合板前四阶无量纲频率表2 所用一致,面内截断量取 M = N = 15 . 可以看出,四边自由和四边简支边界条件下,计算面数取 J k = 4 J k = 6
表4 给出的是四边简支软芯夹层方板( h / a = 0.1 ) 的无量纲频率参数 20 ]的对比情况,其中, m λ n λ E 1 E 2 E 3 ν 12 ν 13 ν 23 G 12 G 13 G 23 ρ J k = 5 M = N = 15 . 对比结果一方面说明了等效单层理论计算误差较大.
2.2 多层复合圆柱壳算例分析
表5 给出了不同边界条件和周向波数下一软芯夹层圆柱壳结构的第一阶固有频率与文献[21 ]的对比情况. 其中, n 表3 所用的芯体材料相同. 计算面数取 J k = 5 M = 15 . 可以看出,本文方法具有良好的计算精度.
3 结 论
本文以独立铺层为建模对象,结合广义谱方法与微分求积技术建立了一种多层复合壳体三维分析新方法——谱--微分求积混合法. 该方法的特点为:(1)应用三维弹性理论对独立铺层进行精确建模;(2)引入微分求积技术对铺层进行数值离散,从而将三维偏微分问题转化为二维偏微分问题;(3)应用广义谱方法近似地表述离散计算面上的场变量,从而将获取的二维偏微分方程转化为以场变量谱展开系数为未知量的线性代数方程组. 与传统三维求解方法相比,谱--微分求积混合法在处理不同边界条件、铺层方式时具有很好的普适性和灵活性. 针对给定的不同边界条件和铺层方式,仅需要通过改变相关参数设置来完成边界约束的施加和铺层方式的配置而不需要逐一重新编程处理. 数值验证结果表明该方法收敛性好,计算精度高.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
陈建霖 , 励争 , 储鹏程 . 大开口复合材料层合板强度破坏研究
. 力学学报 , 2016 , 48 (7 ):1326 -1333
[本文引用: 1]
(Chen Jianlin Li Zheng Chu Pengcheng Strength analysis of fiber reinforced composite laminates with big cutouts
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (7 ): 1326 -1333 (in Chinese))
[本文引用: 1]
[2]
马强 , 周凤玺 , 刘杰 . 梯度波阻板的地基振动控制研究
. 力学学报 ,2017 ,49 (7 ):1360 -1369
[本文引用: 1]
(Ma Qiang Zhou Fengxi Liu Jie Analysis of ground vibration control by graded wave impeding block
. Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (7 ): 1360 -1369 (in Chinese))
[本文引用: 1]
[3]
郭洪宝 , 王波 , 贾普荣 等 . 平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
. 力学学报 , 2016 , 48 (3 ): 361 -368
[本文引用: 1]
(Guo Hongbao Wang Bo Jia Purong et al .Mesoscopic damage behaviors of plain woven ceramic composite under in-plane shear loading
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (3 ): 361 -368 (in Chinese))
[本文引用: 1]
[4]
Reddy JN Mechanics of Laminated Composite Plates and Shells: Theory and Analysis . Florida : CRC Press , 2003
[本文引用: 1]
[5]
Jin G Ye T Wang X et al .A unified solution for the vibration analysis of FGM doubly-curved shells of revolution with arbitrary boundary conditions
. Composites Part B Engineering , 2016 , 89 : 230 -252
[本文引用: 1]
[6]
Ye T Jin G Elasticity solution for vibration of generally laminated beams by a modified Fourier expansion-based sampling surface method
. Computers & Structures , 2016 , 167 : 115 -130
[本文引用: 1]
[7]
瞿叶高 , 华宏星 , 谌勇 等 . 复合材料旋转壳自由振动分析的新方法
. 力学学报 , 2013 , 45 (1 ): 139 -143
[本文引用: 1]
(Qu Yegao Hua Hongxing Chen Yong et al .Vibroacoustic performance of simply supported honeycomb sandwich panels
. Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (1 ): 139 -143 (in Chinese))
[本文引用: 1]
[8]
Carrera E Historical review of zig-zag theories for multilayered plates and shells
. Applied Mechanics Reviews , 2003 , 56 (3 ): 287 -308
[本文引用: 1]
[9]
任树伟 , 辛锋先 , 卢天健 . 蜂窝层芯夹层板结构振动与传声特性研究
. 力学学报 , 2013 , 45 (3 ): 349 -358
[本文引用: 1]
(Ren Shuwei Xin Fengxian Lu Tianjian Vibroacoustic performance of simply supported honeycomb sandwich panels
. Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (3 ): 349 -358 (in Chinese))
[本文引用: 1]
[10]
刘人怀 , 薛江红 . 复合材料层合板壳非线性力学的研究进展
. 力学学报 , 2017 , 49 (3 ): 487 -506
[本文引用: 1]
(Liu Renhuai Xue Jianghong Development of non-linear theories for laminated composite plates and shells
. Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (1 ): 139 -143 (in Chinese))
[本文引用: 1]
[11]
Liu B Xing Y Exact solutions for free vibrations of orthotropic rectangular Mindlin plates
. Composite Structures , 2011 , 93 : 1664 -1672
[本文引用: 1]
[12]
吴振 . 高性能整体--局部高阶理论及高阶层合板单元. [博士论文] . 大连 :大连理工大学 , 2007
[本文引用: 2]
(Wu Zhen Higher-performance global-local higher-order theory and higher-order laminated plate elements. [PhD Thesis] . Dalian : Dalian University of Technology , 2001 (in Chinese))
[本文引用: 2]
[13]
Lo SH Zhen W Cheung YK et al .Hygrothermal effects on multilayered composite plates using a refined higher order theory
. Composite Structures , 2010 , 92 (3 ): 633 -646
[本文引用: 1]
[14]
吕朝锋 . 基于状态空间架构的微分求积法及其应用. [博士论文] . 杭州 :浙江大学 , 2006
[本文引用: 1]
(Lü Chaofeng State-space-based differential quadrature method and its applications. [PhD Thesis] . Hangzhou : Zhejiang University , 2006 (in Chinese))
[本文引用: 1]
[15]
Saada AS Elasticity: Theory and Applications, second ed . Florida : Ross Publishing Inc , 2009
[本文引用: 1]
[16]
Ye T Jin G Su Z Three-dimensional vibration analysis of sandwich and multilayered plates with general ply stacking sequences by a spectral-sampling surface method
. Composite Structures , 2017 , 176 : 1124 -1142
[17]
Reddy JN Energy Principles and Variational Methods in Applied Mechanic . New York : John Wiley & Sons , 1984
[本文引用: 2]
[18]
Chen WQ Lü CF 3D free vibration analysis of cross-ply laminated plates with one pair of opposite edges simply supported
. Composite Structures , 2005 , 69 (1 ): 77 -87
[本文引用: 3]
[19]
Qu Y Wu S Li H et al .Three-dimensional free and transient vibration analysis of composite laminated and sandwich rectangular parallelepipeds: Beams, plates and solids
. Composites Part B: Engineering , 2015 , 73 : 96 -110
[本文引用: 3]
[20]
Rao MK Desai YM Analytical solutions for vibrations of laminated and sandwich plates using mixed theory
. Composite Structures , 2004 , 63 (3 ): 361 -373
[本文引用: 2]
[21]
Qu Y Meng G Dynamic analysis of composite laminated and sandwich hollow bodies of revolution based on three-dimensional elasticity theory
. Composite Structures , 2014 , 112 : 378 -396
[本文引用: 4]
大开口复合材料层合板强度破坏研究
1
2016
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
大开口复合材料层合板强度破坏研究
1
2016
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
梯度波阻板的地基振动控制研究
1
2017
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
梯度波阻板的地基振动控制研究
1
2017
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
1
2016
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
1
2016
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
1
2003
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
A unified solution for the vibration analysis of FGM doubly-curved shells of revolution with arbitrary boundary conditions
1
2016
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
Elasticity solution for vibration of generally laminated beams by a modified Fourier expansion-based sampling surface method
1
2016
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
复合材料旋转壳自由振动分析的新方法
1
2013
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
复合材料旋转壳自由振动分析的新方法
1
2013
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
Historical review of zig-zag theories for multilayered plates and shells
1
2003
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
蜂窝层芯夹层板结构振动与传声特性研究
1
2013
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
蜂窝层芯夹层板结构振动与传声特性研究
1
2013
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
复合材料层合板壳非线性力学的研究进展
1
2013
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
复合材料层合板壳非线性力学的研究进展
1
2013
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
Exact solutions for free vibrations of orthotropic rectangular Mindlin plates
1
2011
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
2
2001
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
... [12 ]. 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
2
2001
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
... [12 ]. 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
Hygrothermal effects on multilayered composite plates using a refined higher order theory
1
2010
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
1
2006
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
1
2006
... 多层复合结构广泛应用于航空航天、高速列车、防卫装备等高科技行业,其振动特性分析一直是相关领域的研究焦点之一[1 ,2 ,3 ] . 常用的多层复合结构振动建模理论主要有:经典等效单层理论、剪切变形理论、锯齿理论和三维层合理论四大类[4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ] . 经典等效单层理论和剪切变形理论都是传统的板壳理论对多层复合结构的直接推广应用. 这两种理论先在厚度方向上把多层复合结构等效成各向异性的单一薄层,然后用结构中面的位移或者应力分量描述结构的整体振动行为. 由于组成材料的各向异性 及呈层性等特点,多层复合结构受载后的应力状态和振动行为十分复杂,其振动位移沿厚度方向呈锯齿形分布且层间剪切和拉、压应力呈三维耦合状态. 因此,当结构厚度比 较大或者各层材料差异较为明显时,位移连续但层间应力不连续的等效单层理论的建模误差急剧增大. 锯齿理论是以上述两类理论为基础,结合层间应力连续条件而得到的理论. 这类理论一般通过在结构的面内位移分量添加锯齿函数从而使横向剪切应力满足层间连续条件. 但该理论一般不满足上下表面自由边界条件也无法得到准确的层间应力[12 ] . 直接应用三维层合理论可以满足位移和横向应力层间连续条件,这一理论和等效单层理论及锯齿理论最大的区别在于结构的每一个子层都看作是用独立的函数来描述的三维实体. 众所周知,只有边界条件和铺层方式简单的少数规则结构才能得到解析解,对其他较为复杂的边界条件、铺层方式以及结构形式,只能借助数值方法或者其他近似解法来求解[14 ] . ...
1
2009
... 其中, ε α ε β ε ζ γ αβ γ αζ γ βζ A α A β [15 ] . ...
Three-dimensional vibration analysis of sandwich and multilayered plates with general ply stacking sequences by a spectral-sampling surface method
2017
2
1984
... 借助哈密尔顿变分原理,式(10)可推导得到到结构的振动控制微分方程,具体形式参考文献[17 ]. ...
... 层合结构层间界面需要满足位移连续和横向应力连续两个条件. 本文解法属于基于能量变分原理的位移解法,当所求得的解满足层间位移连续条件,层间横向应力连续条件将自动满足[17 ] . 为了便于后续层与层之间特征矩阵的装配,在式(2)中,每一子层的上下表面分别选为该层的第一和最后一个计算面. 因此,式(14)中刚度/质量矩阵的第一行和最后一行分别为计算面位移场 u k 1 v k 1 w k 1 u k J k v k J k w k J k k k - 1 k k + 1 图2 所示(质量矩阵和系数向量同理可得). 通过对整体矩阵方程进行特征值分解即可得到壳体振动特性信息. ...
3D free vibration analysis of cross-ply laminated plates with one pair of opposite edges simply supported
3
2005
... 表2 给出了 [ 0 ∘ / 9 0 ∘ ] 2 [ 0 ∘ / 9 0 ∘ ] 4 Ω = ω h ρ / E 2 18 ,19 ]的对比情况. 文献[18 ]采用的是状态空间与微分求积混合架构的半解析解法,其边界条件采用混合变量的方式直接描述,而文献[19 ]采用的是基于广义变分的位移解法. 复合板的材料和几何参数分别为: E 1 = 40 E 2 G 12 = G 13 = 0.6 E 2 G 23 = 0.5 E 2 ν 12 = ν 13 = 0.25 ν 23 = 0.49 a = b = 1 h / a = 0.1 . 计算面数 J k = 5 M = N = 15 . 可以看出,各种边界条件下,本文方法得到的解与文献[18 ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性. ...
... ]的对比情况. 文献[18 ]采用的是状态空间与微分求积混合架构的半解析解法,其边界条件采用混合变量的方式直接描述,而文献[19 ]采用的是基于广义变分的位移解法. 复合板的材料和几何参数分别为: E 1 = 40 E 2 G 12 = G 13 = 0.6 E 2 G 23 = 0.5 E 2 ν 12 = ν 13 = 0.25 ν 23 = 0.49 a = b = 1 h / a = 0.1 . 计算面数 J k = 5 M = N = 15 . 可以看出,各种边界条件下,本文方法得到的解与文献[18 ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性. ...
... . 可以看出,各种边界条件下,本文方法得到的解与文献[18 ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性. ...
Three-dimensional free and transient vibration analysis of composite laminated and sandwich rectangular parallelepipeds: Beams, plates and solids
3
2015
... 表2 给出了 [ 0 ∘ / 9 0 ∘ ] 2 [ 0 ∘ / 9 0 ∘ ] 4 Ω = ω h ρ / E 2 18 ,19 ]的对比情况. 文献[18 ]采用的是状态空间与微分求积混合架构的半解析解法,其边界条件采用混合变量的方式直接描述,而文献[19 ]采用的是基于广义变分的位移解法. 复合板的材料和几何参数分别为: E 1 = 40 E 2 G 12 = G 13 = 0.6 E 2 G 23 = 0.5 E 2 ν 12 = ν 13 = 0.25 ν 23 = 0.49 a = b = 1 h / a = 0.1 . 计算面数 J k = 5 M = N = 15 . 可以看出,各种边界条件下,本文方法得到的解与文献[18 ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性. ...
... ]采用的是状态空间与微分求积混合架构的半解析解法,其边界条件采用混合变量的方式直接描述,而文献[19 ]采用的是基于广义变分的位移解法. 复合板的材料和几何参数分别为: E 1 = 40 E 2 G 12 = G 13 = 0.6 E 2 G 23 = 0.5 E 2 ν 12 = ν 13 = 0.25 ν 23 = 0.49 a = b = 1 h / a = 0.1 . 计算面数 J k = 5 M = N = 15 . 可以看出,各种边界条件下,本文方法得到的解与文献[18 ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性. ...
... ,19 ]的数据对比吻合良好,最大偏差分别小于0.26%和0.25%, 从而说明了本文方法的正确性. ...
Analytical solutions for vibrations of laminated and sandwich plates using mixed theory
2
2004
... 式中, σ α σ β σ ζ α β ζ τ αβ τ αζ τ βζ C k T k [20 ] . ...
...
表4 给出的是四边简支软芯夹层方板(
h / a = 0.1 ) 的无量纲频率参数
与文献[
20 ]的对比情况,其中,
m λ 和
n λ 分别表示长度和宽度方向的振动波数. LW和ESL分别代表文献中基于分层理论(LW)和单层等效理论(ESL)给出的解. 该夹层板由复合表层与软芯中间层复合而成, 即[0°/90°/core/0°/90°],各层厚度比为1:1:20:1:1. 各层材料参数[
E 1 ,
E 2 ,
E 3 ,
ν 12 ,
ν 13 ,
ν 23 ,
G 12 ,
G 13 ,
G 23 ,
ρ ]为:表层-[131 GPa, 10.34 GPa, 10.34 GPa, 0.22, 0.22, 0.49, 6.895 GPa, 6.205 GPa, 6.895 GPa, 1 627 kg/m3], 芯-[6.89 GPa, 6.89 GPa, 6.89 GPa, 0, 0, 0, 3.45 GPa, 3.45 GPa, 3.45 GPa, 97 kg/m3]. 计算面数取
J k = 5 ,面内截断量取
M = N = 15 . 对比结果一方面说明了等效单层理论计算误差较大. ...
Dynamic analysis of composite laminated and sandwich hollow bodies of revolution based on three-dimensional elasticity theory
4
2014
... 表5 给出了不同边界条件和周向波数下一软芯夹层圆柱壳结构的第一阶固有频率与文献[21 ]的对比情况. 其中, n 表3 所用的芯体材料相同. 计算面数取 J k = 5 M = 15 . 可以看出,本文方法具有良好的计算精度. ...
... The first frequencies of sandwich circular cylindrical shell for different boundary conditions
n F-F S-S C-C Pre. 3D[21 ] Pre. 3D[21 ] Pre. 3D[21 ] 296.1 295.9 445.2 444.8 455.5 455.0 16.87 16.89 251.7 251.5 293.4 292.6 35.90 35.88 152.6 152.5 204.8 203.8 57.57 57.54 112.3 112.2 157.9 156.9 82.88 82.85 108.7 108.6 140.2 139.3 112.4 112.3 126.5 126.4 145.2 144.6 146.3 146.3 156.0 155.9 166.6 166.2 184.8 184.8 192.7 192.7 199.0 198.7
3 结 论 本文以独立铺层为建模对象,结合广义谱方法与微分求积技术建立了一种多层复合壳体三维分析新方法——谱--微分求积混合法. 该方法的特点为:(1)应用三维弹性理论对独立铺层进行精确建模;(2)引入微分求积技术对铺层进行数值离散,从而将三维偏微分问题转化为二维偏微分问题;(3)应用广义谱方法近似地表述离散计算面上的场变量,从而将获取的二维偏微分方程转化为以场变量谱展开系数为未知量的线性代数方程组. 与传统三维求解方法相比,谱--微分求积混合法在处理不同边界条件、铺层方式时具有很好的普适性和灵活性. 针对给定的不同边界条件和铺层方式,仅需要通过改变相关参数设置来完成边界约束的施加和铺层方式的配置而不需要逐一重新编程处理. 数值验证结果表明该方法收敛性好,计算精度高. ...
... [
21 ]
Pre. 3D[21 ] 296.1 295.9 445.2 444.8 455.5 455.0 16.87 16.89 251.7 251.5 293.4 292.6 35.90 35.88 152.6 152.5 204.8 203.8 57.57 57.54 112.3 112.2 157.9 156.9 82.88 82.85 108.7 108.6 140.2 139.3 112.4 112.3 126.5 126.4 145.2 144.6 146.3 146.3 156.0 155.9 166.6 166.2 184.8 184.8 192.7 192.7 199.0 198.7 3 结 论 本文以独立铺层为建模对象,结合广义谱方法与微分求积技术建立了一种多层复合壳体三维分析新方法——谱--微分求积混合法. 该方法的特点为:(1)应用三维弹性理论对独立铺层进行精确建模;(2)引入微分求积技术对铺层进行数值离散,从而将三维偏微分问题转化为二维偏微分问题;(3)应用广义谱方法近似地表述离散计算面上的场变量,从而将获取的二维偏微分方程转化为以场变量谱展开系数为未知量的线性代数方程组. 与传统三维求解方法相比,谱--微分求积混合法在处理不同边界条件、铺层方式时具有很好的普适性和灵活性. 针对给定的不同边界条件和铺层方式,仅需要通过改变相关参数设置来完成边界约束的施加和铺层方式的配置而不需要逐一重新编程处理. 数值验证结果表明该方法收敛性好,计算精度高. ...
... [
21 ]
296.1 295.9 445.2 444.8 455.5 455.0 16.87 16.89 251.7 251.5 293.4 292.6 35.90 35.88 152.6 152.5 204.8 203.8 57.57 57.54 112.3 112.2 157.9 156.9 82.88 82.85 108.7 108.6 140.2 139.3 112.4 112.3 126.5 126.4 145.2 144.6 146.3 146.3 156.0 155.9 166.6 166.2 184.8 184.8 192.7 192.7 199.0 198.7 3 结 论 本文以独立铺层为建模对象,结合广义谱方法与微分求积技术建立了一种多层复合壳体三维分析新方法——谱--微分求积混合法. 该方法的特点为:(1)应用三维弹性理论对独立铺层进行精确建模;(2)引入微分求积技术对铺层进行数值离散,从而将三维偏微分问题转化为二维偏微分问题;(3)应用广义谱方法近似地表述离散计算面上的场变量,从而将获取的二维偏微分方程转化为以场变量谱展开系数为未知量的线性代数方程组. 与传统三维求解方法相比,谱--微分求积混合法在处理不同边界条件、铺层方式时具有很好的普适性和灵活性. 针对给定的不同边界条件和铺层方式,仅需要通过改变相关参数设置来完成边界约束的施加和铺层方式的配置而不需要逐一重新编程处理. 数值验证结果表明该方法收敛性好,计算精度高. ...
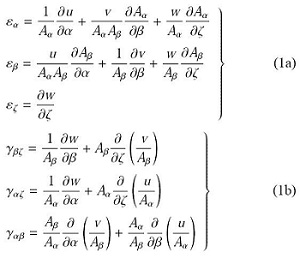
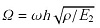
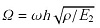 的收敛情况. 复合板的 材料和几何参数与表2所用一致,面内截断量取
的收敛情况. 复合板的 材料和几何参数与表2所用一致,面内截断量取 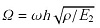 收敛情况
收敛情况
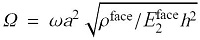 与文献[20]的对比情况,其中,
与文献[20]的对比情况,其中,