复合材料的宏观性质主要取决于由多相材料构成的微观结构. 通过适当的微观结构设计, 复合材料的性能甚至可以超过组分中任何的单相材料bib1. 因此, 分析微观结构的影响是评估复合材料整体宏观性能的关键. 对于微观结构简单和非均质性程度较低的复合材料, 可以通过解析的方法求得其宏观性能参数.
研究者[2 -3 ]对微观结构较为简单的夹杂材料展开了大量的研究. 基于统计均匀性条件和MMM (micro-mini-macro)原理, Hashin和Shtrikman研究了有效张量的理论界限bib4. 研究人员在许多方面对H-S模型进行了补充和改进, 如泊松比界限bib5和多相材料bib6. Mori-Tanaka方法认为在复合材料的代表性体积元中, 单夹杂问题中的远场作用应变为基体的平均应变. 对于没有基体的多晶体材料, Budiansky 等bib7提出了自洽方法, 该方法认为另外的物质点对特定的一个物质点的作用能够用平均场等效, 忽略了不同物质点的相互作用. 张庆华等bib8 用自洽方法得到了混凝土弹性模量的均质化计算公式, 该方法可以同时满足平衡条件和连续性条件. 朱合华等bib3提出了一种新的参考介质下两相夹杂材料的有效模量表达式, 较传统有效介质方法的计算精度有所提升.
虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ].
为了拓展非线性均质化方法的应用, 本文将基于非线性弹性问题对周期性复合材料展开研究. 从基本理论出发, 推导出非线性弹性均质化公式, 并利用程序语言进行实现. 为了验证方法的可靠性, 将对二维平面问题进行研究, 并针对三维空间问题探讨多尺度下均质化方法的应用.
1 非线性弹性均质化
1.1 非线性弹性均质化理论
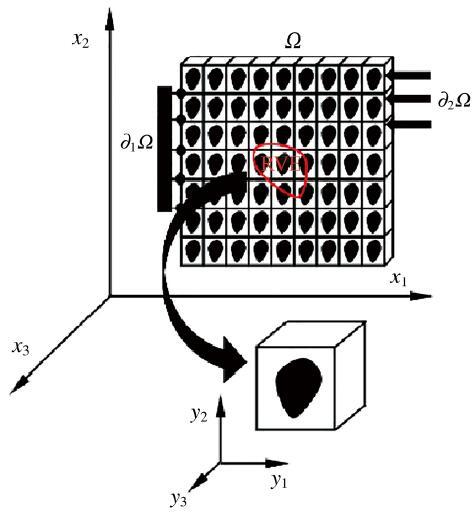
基于均匀化的理论, 周期性复合材料的边值问题可以分解为局部(微观)问题和全局(宏观)问题. 周期性复合结构及代表性体积元结构如图1 所示, x i y i Ω Y ∂ 1 Ω ∂ 2 Ω
图1 周期性复合材料及代表性体积元.
Fig.1 Periodic composite materials and RVE
当单位体积元相对于整个目标区域足够小时, 可以引入一个小参数ε ( ε ≪ 1 ) y = x / ε x i y i 1 ]. 每一个跟坐标相关的量都可以用宏观坐标x i y i
∂ ∂ x ε = ∂ ∂ x + 1 ε ∂ ∂ y
按照渐进展开的方法, 可以将位移基于 ε ε 12 ,16 -17 ]
u i ( x , y ) = u i ( 0 ) ( x , y ) + ε u i ( 1 ) ( x , y ) + ε 2 u i ( 2 ) ( x , y )
将位移的展开式(2)代入几何方程, 结合式(1), 可得到宏观和微观坐标系下的应变表达[12 ,17 ]
ε ij = ε - 1 ε ij ( 0 ) + ε 0 ε ij ( 1 ) + ε ε ij ( 2 ) + O ( ε 2 )
其中
ε ij ( 0 ) = 1 2 ( ∂ u i ( 0 ) ∂ y j + ∂ u j ( 0 ) ∂ y i ) ε ij ( 1 ) = 1 2 ( ∂ u i ( 0 ) ∂ x j + ∂ u j ( 0 ) ∂ x i + ∂ u i ( 1 ) ∂ y j + ∂ u j ( 1 ) ∂ y i ) ε ij ( 2 ) = 1 2 ( ∂ u i ( 1 ) ∂ x j + ∂ u j ( 1 ) ∂ x i + ∂ u i ( 2 ) ∂ y j + ∂ u j ( 2 ) ∂ y i )
再将式(3)代入物理方程中, 可以得到
σ ij = ε - 1 σ ij ( 0 ) + ε 0 σ ij ( 1 ) + ε σ ij ( 2 ) + O ( ε 2 )
其中, 对于非线性弹性问题, 由于弹性矩阵 D σ ij ( n ) = D ijkl ( ε ) ε kl ( n ) n = 0,1 , 2 .
将式(5)代入平衡方程中, 可得
ε ( - 2 ) ∂ σ ij ( 0 ) ∂ y j + ε ( - 1 ) ( ∂ σ ij ( 0 ) ∂ x j + ∂ σ ij ( 1 ) ∂ y j ) + ε ( 0 ) ( ∂ σ ij ( 1 ) ∂ x j + ∂ σ ij ( 2 ) ∂ y j + f i ) + L = 0
对于不同具体问题, 宏观坐标 x i y i ε
ε ( - 2 ) : ∂ σ ij ( 0 ) ∂ y j = 0
ε ( - 1 ) : ∂ σ ij ( 0 ) ∂ x j + ∂ σ ij ( 1 ) ∂ y j = 0
ε ( 0 ) : ∂ σ ij ( 1 ) ∂ x j + ∂ σ ij ( 2 ) ∂ y j + f i = 0
式(6)中对微观坐标积分为0, 即 σ ij ( 0 ) y j x i
σ ij ( 0 ) = σ ij ( 0 ) ( x )
根据式(4)和式(5), 以二维为例, 将张量展开, 利用了弹性张量的对称性, 得
σ ij ( 0 ) ( x ) = 1 2 D ijkl ( ε ) ( ∂ u k ( 0 ) ∂ y l + ∂ u l ( 0 ) ∂ y k ) = 1 2 [ D ij 11 ( ε ) ( 2 ∂ u 1 ( 0 ) ∂ y 1 ) + D ij 12 ( ε ) ( ∂ u 1 ( 0 ) ∂ y 2 + ∂ u 2 ( 0 ) ∂ y 1 ) + D ij 21 ( ε ) ( ∂ u 2 ( 0 ) ∂ y 1 + ∂ u 1 ( 0 ) ∂ y 2 ) + D ij 22 ( ε ) ( 2 ∂ u 2 ( 0 ) ∂ y 2 ) ] = D ij 11 ( ε ) ∂ u 1 ( 0 ) ∂ y 1 + D ij 12 ( ε ) ∂ u 1 ( 0 ) ∂ y 2 + D ij 21 ( ε ) ∂ u 2 ( 0 ) ∂ y 1 + D ij 22 ( ε ) ∂ u 2 ( 0 ) ∂ y 2 = D ijkl ( ε ) ∂ u k ( 0 ) ∂ y l
依据上式及材料周期性关系, 可以进一步得到
σ ij ( 0 ) ( x ) = 0 , ∂ u i ( 0 ) ∂ y j = 0
将式(11)代入式(7), 可得
∂ σ ij ( 1 ) ∂ y j = ∂ ∂ y j [ D ijkl ( ε ) ( ∂ u k ( 0 ) ∂ x l + ∂ u k ( 1 ) ∂ y l ) ] = 0
引入一个特征位移 χ i kl u i ( 1 ) u k ( 0 ) 12 ,17 ]
u i ( 1 ) = - χ i kl ∂ u k ( 0 ) ∂ x l
然后, 将式(13)代入式(12), 可得
∂ ∂ y i [ D ijkl ( ε ) ( I kl mn - ∂ χ k mn ∂ y l ) ] = 0
对式(14)进行整个体积元上的积分, 可以得到宏观等效参数
D ijmn H ( ε ) = 1 | Y | ∫ Y D ijkl ( ε ) ( I kl mn - ∂ χ k mn ∂ y l ) d Y
1.2 非线性弹性均质化实现
线弹性问题可以由式(15)退化得到, 其等效弹性参数可以表示为bib14
D ijmn H = 1 | Y | ∫ Y D ijkl ( I kl mn - ∂ χ k mn ∂ y l ) d Y
其中, D ijkl χ k mn
∫ Y D ijkl ∂ χ k mn ∂ y l ∂ v i ∂ y j d Y = ∫ Y D ijmn ∂ v i ∂ y j d Y , ∀ v i ∈ V ̃ Y
其中 v i V ̃ Y χ k mn
对于式(16)和式(17)可以利用有限元方法进行求解. 依照有限单元法的思想, 特征位移可以用节点的位移 u I N I
χ = N I u I
结合有限元方法的格式, 式(16)可以写成矩阵形式bib1
D H = 1 | Y | ∫ Y ( I - B I u I ) T D ( I - B I u I ) d Y
为避免重复计算刚度矩阵, 将式(19)中的 D B I B I D K
D H = 1 | Y | ( B I - 1 I - u I ) T K ( B I - 1 I - u I )
要得到产生特征位移 χ u I u I . 对于二维问题来说, 施加的应变情况有3种bib16
ε 0 ( 11 ) = 100 , ε 0 ( 22 ) = 010 , ε 0 ( 12 ) = 001
对于非线性弹性问题, 等效弹性参数依照式(19)写成矩阵形式
D H = 1 | Y | ∫ Y ( I - B I u I ) T D ( ε ) ( I - B I u I ) d Y
对于非线性弹性问题, 由于弹性矩阵 D
(1) 给定一个初始应变 ε ( 0 ) D ( 0 ) , n = 0
(2) 计算等效弹性矩阵 D ( n ) H
D ( n ) H = 1 | Y | ∫ Y ( I - B I u I ) T D ( n ) ( I - B I u I ) d Y
(3) 计算第 n ε ( n + 1 )
ε ( n + 1 ) = ε ̅
(4) 判断收敛条件, 如果收敛, 停止迭代, 输出结果; 否则, 转到步骤(2), 继续进行迭代.
2 二维非线性弹性问题
为了验证方法的精度, 本文采用3种典型的非线性本构关系, 以细致模型的计算结果为基准, 从应变能、泊松比和最大位移等方面对多孔材料的均质模型进行了评估.
2.1 材料本构关系
在本章中, 选取了双线性函数, 指数函数和幂函数作为典型的非线性弹性本构方程, 见表1 . 假设研究对象是应变率不敏感材料, 应力‒应变关系可以通过显式的方法给出.
2.2 均质化模型
本文采用如图2 所示的多孔材料周期性结构bib1作为研究对象. 模型的整体尺寸是 10 × 10 1 × 1 d . 以 d d x 表1 中的三种典型本构关系.
图2 多孔材料结构示意图.
Fig.2 Porous material structure
对于这样一个二维结构可以作为平面应变问题处理. 根据平面应变的定义, 结构的泊松比为[17 -18 ]
v ' = - ε y ε x
2.3 均质化结果
针对3种本构关系下的平面结构, 计算了它们 x 图2 所示的平面多孔材料周期性结构的整体结构模型, 包含所有的体积元体. 图 3 ~图5 的图例中, 后缀“homo”表示均质模型结果, 后缀“re_T” 和“re_Q”分别表示三角形网格和四边形网格细致模型结果. 根据对材料体积元圆孔所设置的一系列直径参数 d ( d = 0.2,0.3,0.4,0.5,0.6,0.7,0.8 )
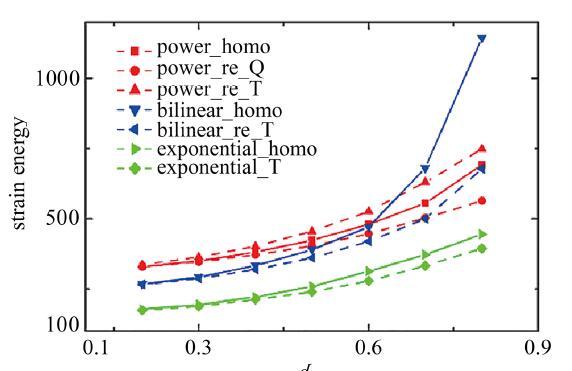
图3 多孔材料应变能.
Fig.3 The strain energy of porous material structure
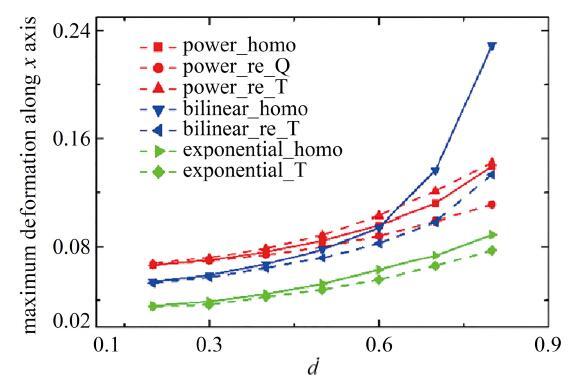
图4 多孔材料x
Fig.4 The maximum deformation along x
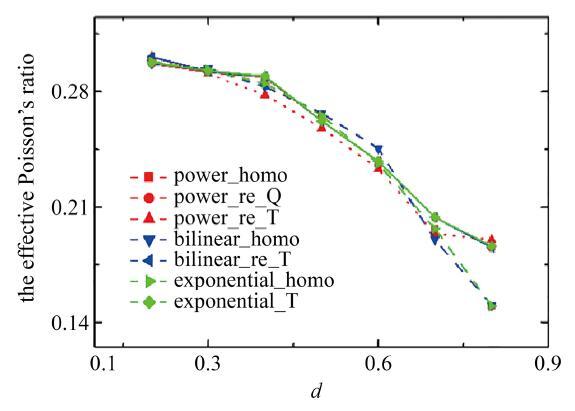
图5 多孔材料等效泊松比.
Fig.5 The equivalent Poisson’s ratio of porous material structure
细致模型和等效的均质模型的应变能如图3 所示. 随着直径d d d < 0.5 d = 0.8
结构沿 x 图4 所示. 最大变形的趋势与应变能类似, 直径越大, 最大变形越大. 这是由于直径 d d > 0.5
利用式(22), 得到各模型的泊松比. 与应变能和 x d 图5 , 通过观察幂函数模型的泊松比, 可以发现均质模型和细致模型之间没有明显的上限或下限关系. 3 种本构关系对应的结构泊松比都十分接近. 这是因为材料的泊松比设定为一个常数, 与应力‒应变关系和几何因素无关. 虽然指数模型具有最大误差, 但它的误差最大值也只有10%( d = 0.8 d
3 多尺度均匀化
3.1 玻璃纤维芯铅丝(网)增强橡胶复合材料
帘线增强橡胶基复合材料是一种广泛运用于轮胎、传送带等工程领域的柔性纤维增强复合材料bib19. 基于铅柔软、延展性强、阻尼较高的材料特性, 吕丽等[20 -21 ] 提出了一种新型玻璃纤维芯铅丝(网)增强橡胶复合材料(GF/Pb/R). 针对铅力学性能较差的缺点, 研究者通过用铅丝包裹玻璃纤维芯的方式来提高其成形性, 然后编织成网作为增强材料, 如图6 所示. 最后将玻璃纤维芯铅丝(网)与丁腈橡胶混炼和硫化得到如图所示的玻璃纤维芯铅丝(网)增强橡胶复合材料, 如图7 所示.
图6 玻璃纤维芯铅丝网bib21.
Fig.6 GF/Pb wirebib21
图7 GF/Pb 网与橡胶交替铺层复合结构图[21]
Fig.7 Ply scheme of GF/Pb wire mesh and rubberbib21
3.2 芯丝尺度
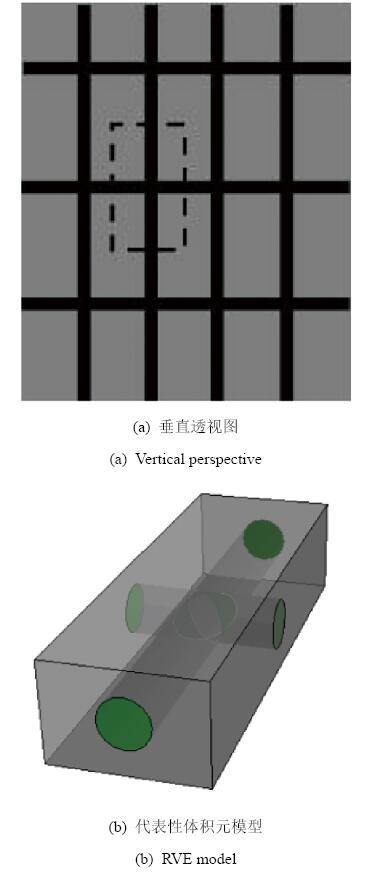
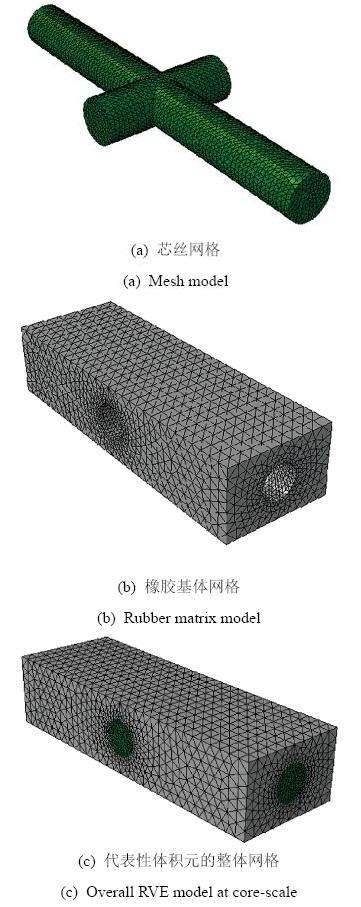
在此维度上, 玻璃纤维被铅丝包裹, 通过编织形成正交的网, 网通过与橡胶基体的结合形成厚度为2 mm 的芯丝薄层. 图8 (a)为GF/Pb薄层沿垂直于铺层方向的透视图, 选取虚线部分为代表性体积元, 其三维结构如图8 (b)所示. 有限元模型如图9 所示. 整个单元体的几何尺寸为9 mm× 3 mm× 2 mm, 其中GF/Pb 丝的直径为0.5 mm, GF/Pb 丝占代表性体积元体积比为4.36% . 单元体各组分弹性参数参照文献[21 ]中的组分性能参数.
图8 GF/Pb网几何模型
Fig.8 GF/Pb wire geometric model at core-scale
图9 体积元有限元模型
Fig.9 RVE model at core-scale
3.3 层间尺度
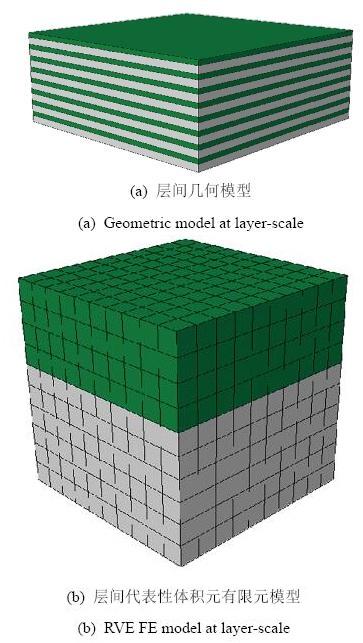
层间整体结构实际模型尺寸为100 mm × × 图10 所示, 图10 (a) 为8层橡胶增强材料的几何模型, 其中绿色部分为薄层, 灰色部分为橡胶层: 图10 (b)是层间尺度下代表性体积元的有限元模型. GF/Pb 网增强橡胶薄层与橡胶层之间使用绑定连接, 即认为薄层之间的连接为完美连接. 橡胶的弹性参数采用文献[22 ]中橡胶拉伸实验数据.
图10 层间模型.
Fig.10 Layer-scale model
3.4 多尺度均匀化方法
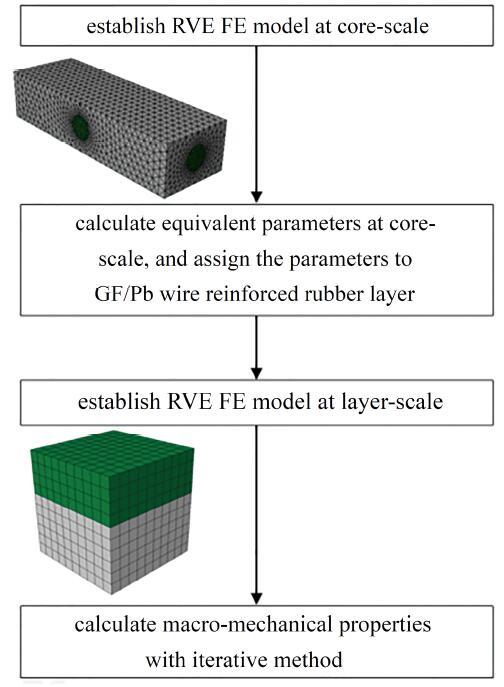
本章在充分考虑了两个尺度下代表性体积元的微观结构的基础上, 利用多尺度均质化预测整体 结构力学性能. 为了更好地表达此方法, 在图11 中对整个的等效过程进行了阐述.
图11 多尺度均质化流程图.
Fig.11 Flow chart of multi-scale homogenization
(a) 在芯丝尺度下, 通过计算代表性体积元在单位应变下的位移, 得到其等效的弹性系数D ijkl . 所得到的弹性参数, 作为GF/Pb网增强橡胶薄层的力学性能参数赋给层间尺度, 将GF/Pb网增强橡胶薄层视为一种均匀分布的横观各向同性材料.
(b) 在层间尺度下, 将芯丝尺度的等效参数作为GF/Pb网增强橡胶薄层材料参数. 层间尺度涉及非线性弹性, 只能针对特定的载荷条件给出特定的宏观特性结果, 如最大位移、泊松比、应变能等. 经过迭代收敛得到的弹性模量, 可以作为该种载荷下材料整体性能的参考. 3.5多尺度均匀化结果
为了和实验结果对比, 需要进一步将均质化等效模量转化为工程弹性参数的形式, 转化的结果如表2 所示, 弹性模量的单位均为MPa.
在获得芯丝尺度的等效弹性系数之后, 在层间尺度中将它作为GF/Pb薄层的材料参数, 取如图10 (b)所示的单元体模型. 取丁腈橡胶的拉伸试验数据bib22, 通过最小二乘法对其进行拟合, 将其作为橡胶的本构关系赋给橡胶基体. 在层间尺度利用非线性弹性均质化方法对结构进行压缩实验, 图12 为压缩实验有限元模型. 对层间结构的底部施加固定约束, 在顶部施加压力.
图12 层间模型.
Fig.12 Layer-scale model
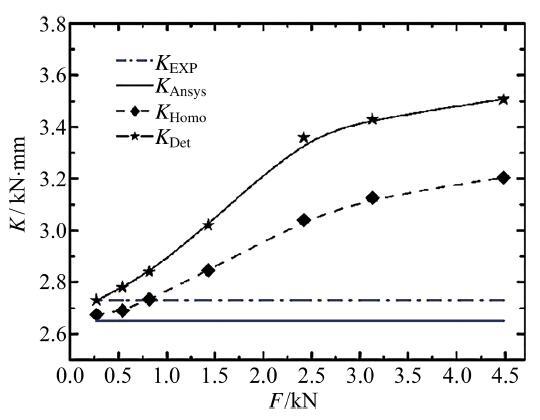
对迭代收敛的结果进行后处理, 计算给定载荷下的模型的刚度K = F / U F U 图13 是层间尺度细致模型、等效模型和文献数据刚度的对比. 实验值K Exp K Ansys K Ansys 图13 可以看到, 当压力小于1 kN时, 均质化刚度K Homo K Det % . 但是随着压力的增大, K Homo K Det K Exp K Ansys K Homo K Exp % K Det K Exp % . 均质化刚度K Homo K Det % % . 误差主要来自于非线性等效中没有考虑大变形因素, 所以随着变形的增大, 与细致模型的误差也就增大.
图13 不同层间模型刚度值比较.
Fig.13 The comparisons among the stiffness obtained by different layer-scale models
4 结论
本文从线弹性问题的均质化理论出发, 推导了非线性弹性问题的均质化方程, 通过对平面问题和多尺度问题的计算, 验证了计算方法的精度和收敛性. 得出以下结论:
(1) 非线性弹性均质化方法对于平面二维问题而言, 具有很好的精度. 均质化结构的应变能、最大位移和等效泊松比同细致模型的结果误差基本上保持在10%
(2) 在变形较小时, 非线性弹性均质化方法在多尺度下依然可以较为准确的预测材料的宏观力学性能. 尽管由于缺少实验数据, 无法说明较大变形的精度, 但是从变化趋势上来说与理论上是吻合.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Eric L Zhongpu Z Chang CC et al .Numerical homogenization for incompressible materials using selective smoothed finite element method
.Composite Structures , 2015 , 123 : 216 -232
[本文引用: 1]
[2]
朱合华 , 陈庆 . 多相材料有效性能预测的高精度方法
. 力学学报 , 2017 , 49 (1 ): 41 -47
[本文引用: 1]
(Zhu Hehua Chen Qing An approach for predicting the effective properties of multiphase composite with high accuracy
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (1 ): 41 -47 (in Chinese))
[本文引用: 1]
[3]
付云伟 , 倪新华 , 刘协权 等 . 颗粒缺陷相互作用下复合材料的细观损伤模型
. 力学学报 , 2016 , 48 (6 ): 1334 -1342
[本文引用: 1]
(Fu Yunwei Ni Xinhua Liu Xiequan et al .Micro-damage model of composite materials with particle and defect interaction
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (6 ): 1334 -1342 (in Chinese))
[本文引用: 1]
[4]
Hashin Z Analysis of composite materials
.Journal of Applied Mechanics , 1983 , 50 (2 ): 481 -505
[本文引用: 1]
[5]
Capdeboscq Y Kang H Improved Hashin-Shtrikman bounds for elastic moment tensors and an application
.Applied Mathematics & Optimization , 2008 , 57 (2 ): 263 -288
[6]
Zimmerman R W Hashin-Shtrikman bounds on the Poisson ratio of a composite material
.Mechanics Research Communications , 1992 , 19 (6 ): 563 -569
[7]
Mura T Micromechanics of Defects in Solids
. Germany: Springer Science & Business Media , 2013 : 10 -53
[8]
张庆华 , 刘西拉 , 朱振宇 . 用自洽方法计算混凝土的弹性模量
.上海交通大学学报 , 2001 (10 ): 1503 -1506
(Zhang Qinghua Liu Xila Zhu Zhengyu Applying self-consistent method to calculate concrete modulus
.Journal of Shanghai Jiaotong University 2001 (10 ): 1503 -1506 (in Chinese))
[9]
Nasution MRE Watanabe N Kondo A et al . A novel asymptotic expansion homogenization analysis for 3-D composite with relieved periodicity in the thickness direction
.Composites Science and Technology , 2014 , 97 (16 ): 63 -73
[本文引用: 1]
[10]
魏志刚 , 汤文成 . 复合材料网格结构模态分析的均匀化等效建模
. 复合材料学报 , 2008 (2 ): 188 -193
[本文引用: 1]
(Wei Zhigang Tang Wencheng Homogenization modeling of composite lattice structure for mode analysis
.Acta Materiae Compositae Sinica 2008 (2 ): 188 -193 (in Chinese))
[本文引用: 1]
[11]
王飞 , 庄守兵 , 虞吉林 . 用均匀化理论分析蜂窝结构的等效弹性参数
.力学学报 , 2002 , 36 (6 ): 914 -923
[本文引用: 1]
(Wang Fei, Zhuang Shoubing,Yu Jilin . Application of homogenization FEM to the equivalent elastic constants of honeycomb structures
.Acta Mechanica Sinica , 2002 , 36 (6 ): 914 -923 (in Chinese))
[本文引用: 1]
[12]
Pinho J Oliveira JA Teixeira-Dias F Asymptotic homogenization in linear elasticity. Part I: Mathematical formulation and finite element modeling
.Computational Materials Science , 2009 , 45 (4 ): 1073 -1080
[本文引用: 5]
[13]
Doghri I Ouaar A Homogenization of two-phase elasto-plastic composite materials and structures:<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml138-0459-1879-50-4-837"><mml:mi mathvariant="normal"> </mml:mi></mml:math></inline-formula>study of tangent operators, cyclic plasticity and numerical algorithms
.International Journal of Solids and Structures , 2003 , 40 (7 ): 1681 -1712
[本文引用: 1]
[14]
Andrianov IV Danishevs Kyy VV Ryzhkov OI et al .Dynamic homogenization and wave propagation in a nonlinear 1D composite material
.Wave Motion , 2013 , 50 (2 ): 271 -281
[本文引用: 1]
[15]
Hoang TH Guerich M Yvonnet J Determining the size of RVE for nonlinear random composites in an incremental computational homogenization framework
.Journal of Engineering Mechanics , 2016 , 142 (5 ): 1 -21
[本文引用: 1]
[16]
Cheng G Cai Y Xu L Novel implementation of homogenization method to predicteffective properties of periodic materials
.Acta Mechanica Sinica , 2013 , 29 (4 ): 550 -556
[本文引用: 1]
[17]
沈观林 , 胡更开 , 刘彬 . 复合材料力学. 第2版 . 北京 : 清华大学出版社 , 2013 : 48 -52
[本文引用: 4]
(Shen Guanlin Hu Gengkai Liu Bin Mechanics of Composite Materials. Second Edition. Beijing : Tinghua University Press , 2013 : 48 -52 (in Chinese))
[本文引用: 4]
[18]
龙述尧. 计算力学 . 第1版. 长沙 : 湖南大学出版社 , 2007 : 92 -186
[本文引用: 1]
(Long Shurao. Computational Mechanics. The first edition. Changsha : Hunan University Press , 2007 : 92 -186 (in Chinese))
[本文引用: 1]
[19]
黄小双 , 彭雄奇 , 张必超 . 帘线/橡胶复合材料各向异性黏-超弹性本构模型
. 力学学报 , 2016 , 48 (1 ): 140 -145
(Huang Xiaoshuang Peng Xiongqi Zhang Bichao An anisotropic visco-hyperelastic constitutive model for cord-rubber composites
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (1 ): 140 -145 (in Chinese))
[20]
吕丽 , 白书欣 , 张虹 等 . 玻璃纤维芯铅丝增强橡胶复合材料阻尼性能研究
.材料科学与工程学报 , 2006 (6 ): 843 -846
[本文引用: 1]
(Lü Li Bai Shuxin Zhang Hong et al .Damping property of glass-fiber-cored lead-wire reinforced rubber composite
.Journal of Materials Science and Engineering 2006 (6 ): 843 -846 (in Chinese))
[本文引用: 1]
[21]
吕丽 . 玻璃纤维芯铅网(丝)增强橡胶阻尼复合材料性能研究: [博士论文]
. 长沙: 国防科学技术大学 , 2006 :70 -151
[本文引用: 2]
(Lü Li The mechanical and damping properties of glass-fiber-net and glass-fiber-wire reinforced rubber composites. [PhD Thesis]
. Changsha: National University of Defense Technology , 2006 : 70 -151 (in Chinese))
[本文引用: 2]
[22]
程哲 , 张正艺 , 宋杨 等 . 橡胶材料超弹性本构模型的简化标定方法
. 固体力学学报 , 2010 (s1 ): 50 -53
[本文引用: 1]
(Cheng Zhe, Zhang Zheng yi, Song Yang , et al . A simplified calibration method for the elastic constitutive model of rubber material
. Acta Mechanica Solida Sinica #2010 (s1 ): 50 -53 (in Chinese))
[本文引用: 1]
Numerical homogenization for incompressible materials using selective smoothed finite element method
1
2015
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
多相材料有效性能预测的高精度方法
1
2017
... 研究者[2 -3 ]对微观结构较为简单的夹杂材料展开了大量的研究. 基于统计均匀性条件和MMM (micro-mini-macro)原理, Hashin和Shtrikman研究了有效张量的理论界限bib4. 研究人员在许多方面对H-S模型进行了补充和改进, 如泊松比界限bib5和多相材料bib6. Mori-Tanaka方法认为在复合材料的代表性体积元中, 单夹杂问题中的远场作用应变为基体的平均应变. 对于没有基体的多晶体材料, Budiansky 等bib7提出了自洽方法, 该方法认为另外的物质点对特定的一个物质点的作用能够用平均场等效, 忽略了不同物质点的相互作用. 张庆华等bib8 用自洽方法得到了混凝土弹性模量的均质化计算公式, 该方法可以同时满足平衡条件和连续性条件. 朱合华等bib3提出了一种新的参考介质下两相夹杂材料的有效模量表达式, 较传统有效介质方法的计算精度有所提升. ...
多相材料有效性能预测的高精度方法
1
2017
... 研究者[2 -3 ]对微观结构较为简单的夹杂材料展开了大量的研究. 基于统计均匀性条件和MMM (micro-mini-macro)原理, Hashin和Shtrikman研究了有效张量的理论界限bib4. 研究人员在许多方面对H-S模型进行了补充和改进, 如泊松比界限bib5和多相材料bib6. Mori-Tanaka方法认为在复合材料的代表性体积元中, 单夹杂问题中的远场作用应变为基体的平均应变. 对于没有基体的多晶体材料, Budiansky 等bib7提出了自洽方法, 该方法认为另外的物质点对特定的一个物质点的作用能够用平均场等效, 忽略了不同物质点的相互作用. 张庆华等bib8 用自洽方法得到了混凝土弹性模量的均质化计算公式, 该方法可以同时满足平衡条件和连续性条件. 朱合华等bib3提出了一种新的参考介质下两相夹杂材料的有效模量表达式, 较传统有效介质方法的计算精度有所提升. ...
颗粒缺陷相互作用下复合材料的细观损伤模型
1
2016
... 研究者[2 -3 ]对微观结构较为简单的夹杂材料展开了大量的研究. 基于统计均匀性条件和MMM (micro-mini-macro)原理, Hashin和Shtrikman研究了有效张量的理论界限bib4. 研究人员在许多方面对H-S模型进行了补充和改进, 如泊松比界限bib5和多相材料bib6. Mori-Tanaka方法认为在复合材料的代表性体积元中, 单夹杂问题中的远场作用应变为基体的平均应变. 对于没有基体的多晶体材料, Budiansky 等bib7提出了自洽方法, 该方法认为另外的物质点对特定的一个物质点的作用能够用平均场等效, 忽略了不同物质点的相互作用. 张庆华等bib8 用自洽方法得到了混凝土弹性模量的均质化计算公式, 该方法可以同时满足平衡条件和连续性条件. 朱合华等bib3提出了一种新的参考介质下两相夹杂材料的有效模量表达式, 较传统有效介质方法的计算精度有所提升. ...
颗粒缺陷相互作用下复合材料的细观损伤模型
1
2016
... 研究者[2 -3 ]对微观结构较为简单的夹杂材料展开了大量的研究. 基于统计均匀性条件和MMM (micro-mini-macro)原理, Hashin和Shtrikman研究了有效张量的理论界限bib4. 研究人员在许多方面对H-S模型进行了补充和改进, 如泊松比界限bib5和多相材料bib6. Mori-Tanaka方法认为在复合材料的代表性体积元中, 单夹杂问题中的远场作用应变为基体的平均应变. 对于没有基体的多晶体材料, Budiansky 等bib7提出了自洽方法, 该方法认为另外的物质点对特定的一个物质点的作用能够用平均场等效, 忽略了不同物质点的相互作用. 张庆华等bib8 用自洽方法得到了混凝土弹性模量的均质化计算公式, 该方法可以同时满足平衡条件和连续性条件. 朱合华等bib3提出了一种新的参考介质下两相夹杂材料的有效模量表达式, 较传统有效介质方法的计算精度有所提升. ...
Analysis of composite materials
1
1983
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
Improved Hashin-Shtrikman bounds for elastic moment tensors and an application
2008
Hashin-Shtrikman bounds on the Poisson ratio of a composite material
1992
Micromechanics of Defects in Solids
2013
A novel asymptotic expansion homogenization analysis for 3-D composite with relieved periodicity in the thickness direction
1
2014
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
复合材料网格结构模态分析的均匀化等效建模
1
2008
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
复合材料网格结构模态分析的均匀化等效建模
1
2008
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
用均匀化理论分析蜂窝结构的等效弹性参数
1
2002
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
用均匀化理论分析蜂窝结构的等效弹性参数
1
2002
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
Asymptotic homogenization in linear elasticity. Part I: Mathematical formulation and finite element modeling
5
2009
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
... 当单位体积元相对于整个目标区域足够小时, 可以引入一个小参数ε ( ε ≪ 1 ) y = x / ε x i y i 1 ]. 每一个跟坐标相关的量都可以用宏观坐标x i y i
... 按照渐进展开的方法, 可以将位移基于 ε ε 12 ,16 -17 ] ...
... 将位移的展开式(2)代入几何方程, 结合式(1), 可得到宏观和微观坐标系下的应变表达[12 ,17 ] ...
... 引入一个特征位移 χ i kl u i ( 1 ) u k ( 0 ) 12 ,17 ] ...
Homogenization of two-phase elasto-plastic composite materials and structures:<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml138-0459-1879-50-4-837"><mml:mi mathvariant="normal"> </mml:mi></mml:math></inline-formula>study of tangent operators, cyclic plasticity and numerical algorithms
1
2003
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
Dynamic homogenization and wave propagation in a nonlinear 1D composite material
1
2013
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
Determining the size of RVE for nonlinear random composites in an incremental computational homogenization framework
1
2016
... 虽然基于夹杂物的均质化方法已经考虑了微结构, 但仅适合微观结构简单的复合材料. 对于具有复杂周期性结构的材料, 代表性体积元法与渐进展开方法能够给出很好的宏观性能预测结果. 但体积元法并不具有严格的理论推导, 理论上不够严谨. 相比之下, 基于摄动理论的双渐近展开方法具有严格的数学推导, 在数学上是完备的[1 ,9 ]. 从最小势能原理和有限元法的基本思想出发, 对胞元拉伸和剪切载荷下的细观力学分析;通过引进新的特征函数, 将计算特征函数的非齐次方程转化为齐次, 得到具有精确周期性边界条件的双渐进展开均质化方法. 魏志刚等[10 ]通过模拟颗粒随机分布的复合材料, 应用渐进展开方法预测出材料的宏观等效弹性参数, 研究颗粒的统计特性, 探讨了颗粒尺寸、分布状态和几何形态差异对宏观复合材料特性的影响. 王飞等[11 ]应用双渐进展开均质化方法研究了不同相对密度下规则蜂窝结构的等效弹性模量和泊松比. 与线性问题相比, 均质化的非线性问题要困难得多[12 ]. Hill[4 ] 提出了用增量迭代的方式解决黏弹性问题, 为解决非线性均质化问题提供了解决方案. Doghri等[13 ]开发了两相弹塑性复合材料的均质方法和数值算法, 并应用Hill 型增量公式模拟了卸载和周期载荷的过程. Andrianov 等[14 ]使用一维模型研究了非线性弹性材料中的波动传播. 该模型虽然简单, 但仍显示出主波特性的非线性效应. 对于非线性随机复合材料, 代表性体积元的尺寸可以通过使用增量均匀化方法来确定[15 ]. ...
Novel implementation of homogenization method to predicteffective properties of periodic materials
1
2013
... 按照渐进展开的方法, 可以将位移基于 ε ε 12 ,16 -17 ] ...
4
2013
... 按照渐进展开的方法, 可以将位移基于 ε ε 12 ,16 -17 ] ...
... 将位移的展开式(2)代入几何方程, 结合式(1), 可得到宏观和微观坐标系下的应变表达[12 ,17 ] ...
... 引入一个特征位移 χ i kl u i ( 1 ) u k ( 0 ) 12 ,17 ] ...
... 对于这样一个二维结构可以作为平面应变问题处理. 根据平面应变的定义, 结构的泊松比为[17 -18 ] ...
4
2013
... 按照渐进展开的方法, 可以将位移基于 ε ε 12 ,16 -17 ] ...
... 将位移的展开式(2)代入几何方程, 结合式(1), 可得到宏观和微观坐标系下的应变表达[12 ,17 ] ...
... 引入一个特征位移 χ i kl u i ( 1 ) u k ( 0 ) 12 ,17 ] ...
... 对于这样一个二维结构可以作为平面应变问题处理. 根据平面应变的定义, 结构的泊松比为[17 -18 ] ...
1
2007
... 对于这样一个二维结构可以作为平面应变问题处理. 根据平面应变的定义, 结构的泊松比为[17 -18 ] ...
1
2007
... 对于这样一个二维结构可以作为平面应变问题处理. 根据平面应变的定义, 结构的泊松比为[17 -18 ] ...
帘线/橡胶复合材料各向异性黏-超弹性本构模型
2016
帘线/橡胶复合材料各向异性黏-超弹性本构模型
2016
玻璃纤维芯铅丝增强橡胶复合材料阻尼性能研究
1
2006
... 帘线增强橡胶基复合材料是一种广泛运用于轮胎、传送带等工程领域的柔性纤维增强复合材料bib19. 基于铅柔软、延展性强、阻尼较高的材料特性, 吕丽等[20 -21 ] 提出了一种新型玻璃纤维芯铅丝(网)增强橡胶复合材料(GF/Pb/R). 针对铅力学性能较差的缺点, 研究者通过用铅丝包裹玻璃纤维芯的方式来提高其成形性, 然后编织成网作为增强材料, 如图6 所示. 最后将玻璃纤维芯铅丝(网)与丁腈橡胶混炼和硫化得到如图所示的玻璃纤维芯铅丝(网)增强橡胶复合材料, 如图7 所示. ...
玻璃纤维芯铅丝增强橡胶复合材料阻尼性能研究
1
2006
... 帘线增强橡胶基复合材料是一种广泛运用于轮胎、传送带等工程领域的柔性纤维增强复合材料bib19. 基于铅柔软、延展性强、阻尼较高的材料特性, 吕丽等[20 -21 ] 提出了一种新型玻璃纤维芯铅丝(网)增强橡胶复合材料(GF/Pb/R). 针对铅力学性能较差的缺点, 研究者通过用铅丝包裹玻璃纤维芯的方式来提高其成形性, 然后编织成网作为增强材料, 如图6 所示. 最后将玻璃纤维芯铅丝(网)与丁腈橡胶混炼和硫化得到如图所示的玻璃纤维芯铅丝(网)增强橡胶复合材料, 如图7 所示. ...
玻璃纤维芯铅网(丝)增强橡胶阻尼复合材料性能研究: [博士论文]
2
2006
... 帘线增强橡胶基复合材料是一种广泛运用于轮胎、传送带等工程领域的柔性纤维增强复合材料bib19. 基于铅柔软、延展性强、阻尼较高的材料特性, 吕丽等[20 -21 ] 提出了一种新型玻璃纤维芯铅丝(网)增强橡胶复合材料(GF/Pb/R). 针对铅力学性能较差的缺点, 研究者通过用铅丝包裹玻璃纤维芯的方式来提高其成形性, 然后编织成网作为增强材料, 如图6 所示. 最后将玻璃纤维芯铅丝(网)与丁腈橡胶混炼和硫化得到如图所示的玻璃纤维芯铅丝(网)增强橡胶复合材料, 如图7 所示. ...
... 在此维度上, 玻璃纤维被铅丝包裹, 通过编织形成正交的网, 网通过与橡胶基体的结合形成厚度为2 mm 的芯丝薄层. 图8 (a)为GF/Pb薄层沿垂直于铺层方向的透视图, 选取虚线部分为代表性体积元, 其三维结构如图8 (b)所示. 有限元模型如图9 所示. 整个单元体的几何尺寸为9 mm× 3 mm× 2 mm, 其中GF/Pb 丝的直径为0.5 mm, GF/Pb 丝占代表性体积元体积比为4.36% . 单元体各组分弹性参数参照文献[21 ]中的组分性能参数. ...
玻璃纤维芯铅网(丝)增强橡胶阻尼复合材料性能研究: [博士论文]
2
2006
... 帘线增强橡胶基复合材料是一种广泛运用于轮胎、传送带等工程领域的柔性纤维增强复合材料bib19. 基于铅柔软、延展性强、阻尼较高的材料特性, 吕丽等[20 -21 ] 提出了一种新型玻璃纤维芯铅丝(网)增强橡胶复合材料(GF/Pb/R). 针对铅力学性能较差的缺点, 研究者通过用铅丝包裹玻璃纤维芯的方式来提高其成形性, 然后编织成网作为增强材料, 如图6 所示. 最后将玻璃纤维芯铅丝(网)与丁腈橡胶混炼和硫化得到如图所示的玻璃纤维芯铅丝(网)增强橡胶复合材料, 如图7 所示. ...
... 在此维度上, 玻璃纤维被铅丝包裹, 通过编织形成正交的网, 网通过与橡胶基体的结合形成厚度为2 mm 的芯丝薄层. 图8 (a)为GF/Pb薄层沿垂直于铺层方向的透视图, 选取虚线部分为代表性体积元, 其三维结构如图8 (b)所示. 有限元模型如图9 所示. 整个单元体的几何尺寸为9 mm× 3 mm× 2 mm, 其中GF/Pb 丝的直径为0.5 mm, GF/Pb 丝占代表性体积元体积比为4.36% . 单元体各组分弹性参数参照文献[21 ]中的组分性能参数. ...
橡胶材料超弹性本构模型的简化标定方法
1
2010
... 层间整体结构实际模型尺寸为100 mm × × 图10 所示, 图10 (a) 为8层橡胶增强材料的几何模型, 其中绿色部分为薄层, 灰色部分为橡胶层: 图10 (b)是层间尺度下代表性体积元的有限元模型. GF/Pb 网增强橡胶薄层与橡胶层之间使用绑定连接, 即认为薄层之间的连接为完美连接. 橡胶的弹性参数采用文献[22 ]中橡胶拉伸实验数据. ...
橡胶材料超弹性本构模型的简化标定方法
1
2010
... 层间整体结构实际模型尺寸为100 mm × × 图10 所示, 图10 (a) 为8层橡胶增强材料的几何模型, 其中绿色部分为薄层, 灰色部分为橡胶层: 图10 (b)是层间尺度下代表性体积元的有限元模型. GF/Pb 网增强橡胶薄层与橡胶层之间使用绑定连接, 即认为薄层之间的连接为完美连接. 橡胶的弹性参数采用文献[22 ]中橡胶拉伸实验数据. ...