力学学报 2018 , 50 (4): 810-819 https://doi.org/10.6052/0459-1879-18-113

Orginal Article

非常规态型近场动力学热黏塑性模型及其应用

王涵, 黄丹^*^,, 徐业鹏, 刘一鸣

河海大学力学与材料学院, 南京 211100

NON-ORDINARY STATE-BASED PERIDYNAMIC THERMAL-VISCOPLASTIC MODEL AND ITS APPLICATION

Wang Han, Huang Dan^*^,, Xu Yepeng, Liu Yiming

College of Mechanics and Materials , Hohai University , Nanjing 211100, China

中图分类号: O130.10

文献标识码: A

通讯作者: ^*黄丹, 教授, 主要研究方向: 计算固体力学. E-mail: danhuang@hhu.edu.cn^*黄丹, 教授, 主要研究方向: 计算固体力学. E-mail: danhuang@hhu.edu.cn

基金资助: 国家自然科学基金(51679077, 11132003), 中央高校基本科研业务费(2015B18314, 2017B13014)和NSFC-广东联合基金(第二期)超级计算科学应用研究专项(U1501501)资助项目.

展开

摘要

在非常规态型近场动力学(non-ordinary state-based peridynamics, NOSB-PD) 理论框架下构建了考虑应变率效应、塑性硬化、热软化效应和材料断裂特征的非局部三维热黏塑性固体本构模型以及相应的非局部空间积分型数值算法, 并应用于金属类材料和构件在冲击载荷作用等工况下的高应变率热黏塑性变形与破坏分析. 通过对经典含初始裂纹Kalthoff-Winkler板冲击试验进行三维近场动力学模拟, 可得到裂纹的起裂角度、扩展路径、扩展速度以及裂纹扩展过程中靶板等效应力和温度分布, 所得结果与已有试验结果和其他数值方法结果吻合较好. 在此基础上, 应用该模型分析了不同冲击速度作用下金属靶板的变形与裂纹扩展过程, 结果表明: 该模型能较好地模拟不同冲击速度(应变率)情况下靶板的变形与破坏全过程. 随着冲击速度变化, 初始裂纹的起裂时间、扩展方向和扩展速度呈一定规律变化. 冲击速度越低, 起裂时间越晚(直至冲击速度低于某值时初始裂纹不扩展), 裂纹扩展速度峰值越低, 冲击过程中靶板温度峰值越低, 完全扩展所需时间越长.

关键词： 冲击破坏 ; 热黏塑性 ; 非常规态型近场动力学 ; 裂纹扩展 ; 非局部模型 ; Kalthoff-Winkler试验

Abstract

A three-dimensional non-local thermo-visco-plastic solid model considering the strain rate effect, plastic hardening, thermal softening and fracture characteristics of materials, together with corresponding non-local spatial integral-type numerical method, have been proposed under the configuration of the recently developed non-ordinary state-based peridynamic (NOSB-PD) theory, and the model and numerical method have been employed to analyze the high-rate thermal-viscoplastic deformation and failure behavior of metallic materials and components under impact loads. The validity of the proposed model and algorithms was established through simulating the three-dimensional classical Kalthoff-Winkler impact experiment and comparing the numerical results including the cracking initiation time and orientation, crack propagation path and propagation speed, and the distribution of temperature and equivalent stresses in the target with experimental observations and available numerical results in literature. The proposed model and method were further applied to simulate the deformation and failure mechanism of double-notched metallic plates subjected to impact loads with different impacting velocities. Numerical results show that the present model inherits the advantages of both peridynamics and classical thermo-visco-plastic models, and is able to describe the whole elastic and plastic deformation and crack propagation processes qualitatively as well as quantitatively. Moreover, the effect of impact velocity on crack initiation time, crack propagation path and crack propagation speed were investigated. When subjected to impact load with lower impacting velocity, the crack initiation time of the target plate will be later (until no crack propagation appears when impacting velocity is lower than some value), and both the crack propagation speed and the peak temperature in the target plate will decrease.

Keywords： impact failure ; thermo-visco-plasticity ; non-ordinary stated-based peridynamics ; crack propagation ; non-local model ; Kalthoff-Winkler experiment

PDF (5878KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

王涵, 黄丹, 徐业鹏, 刘一鸣. 非常规态型近场动力学热黏塑性模型及其应用[J]. 力学学报, 2018, 50(4): 810-819 https://doi.org/10.6052/0459-1879-18-113

Wang Han, Huang Dan, Xu Yepeng, Liu Yiming. NON-ORDINARY STATE-BASED PERIDYNAMIC THERMAL-VISCOPLASTIC MODEL AND ITS APPLICATION[J]. Acta Mechanica Sinica, 2018, 50(4): 810-819 https://doi.org/10.6052/0459-1879-18-113

材料与结构在冲击载荷作用下的变形与破坏机制与准静态载荷作用下有明显区别. 构建能准确描述材料在冲击载荷作用下变形特性和力学行为的本构模型以及能模拟材料和结构的冲击变形与损伤破坏全过程的数值方法, 有利于深入揭示冲击响应的内在机制. 在连续介质力学理论框架下考虑率效应开展动力本构建模与数值模拟是研究冲击响应问题的重要途径. 典型如李杰等[1]曾提出混凝土材料的黏塑性动力损伤模型, 在静力弹塑性损伤本构模型基础上考虑塑性应变及损伤演化的率敏感性, 并应用于混凝土结构在强动力载荷作用下的数值模拟. Li等[2-3]应用无网格伽辽金法结合经典热黏塑性模型, 成功模拟了金属材料和结构在冲击载荷作用下的剪切带萌生与扩展过程. Rabczuk等[4] 结合无网格法和板壳动力学理论来模拟薄壳的塑性大变形和非线性动态断裂问题. 然而, 基于经典连续介质力学理论框架的数值方法在描述裂纹破坏等强不连续问题时, 往往在裂纹区域需要特殊的数学处理, 如章鹏[5]等引入比例有限元求解裂纹面的接触问题, 童第华[6]等采用权函数分析半无限板边缘裂纹问题. 采用传统理论在模拟三维动态断裂问题时尤其复杂, 计算精度和效率等问题仍有待进一步深入研究. 为了从根本上避免基于连续性假设的传统模型和数值方法在分析固体破坏等不连续现象时的困难, 2000 年Silling[7]首次正式提出了基于非局部作用思想、通过求解空间积分方程(而非偏微分方程)描述固体力学行为的近场动力学(peridynamics, PD)理论框架, 并在不同尺度的各种大变形和静、动态破坏问题分析中表现出明显的优势[8-9]. 与传统方法相比, PD方法的优势主要体现在对不连续力学问题的描述和求解上, 由于采用了基于空间积分方程的求解模式, 因此对各种不连续力学问题尤其是冲击破坏等复杂的强不连续力学问题, 可以高效率进行求解, 而不需要引入传统的裂尖增强或奇异性处理等技术. 早期提出的键型近场动力学(bond-based peridynamics)模型[8] 曾被大量应用于准脆性材料的变形、损伤[10-12]和冲击破坏模拟[13-16], 然而键型近场动力学本构模型中将物质点间的相互作用简化为“中心弹簧”, 故而在应用范围和计算精度等方面均受到限制, 难以描述金属材料在高速冲击载荷下的黏塑性等力学行为. 为弥补键型近场动力学理论的不足, Silling 等[17-18]提出了新的态型近场动力学(state-based peridynamics) 理论和本构建模思路, 引入“状态”概念对物质点间的“中心弹簧”作用进行修正, 并与传统连续介质力学本构模型中的物理量联系起来, 进而描述材料的各种非线性力学行为. 近年的相关理论建模工作在此方面展开较多, 如Mitchell[19]和Warren等[20]先后分别在常规态型(ordinary state-based, OSB) 和非常规态型(non-ordinary state-based, NOSB) 近场动力学理论框架下构建了考虑硬化效应的弹塑性本构模型; Weckner等[21]和Nikabdullah等[22]构建了态型近场动力学黏弹性模型, Oterkus等[23-24]实现了态型近场动力学理论中的热力耦合模型; Foster等[25] 和Tupek等[26]分别基于非常规态型近场动力学理论建立了不考虑温度效应的黏塑性模型, 实现了不含温度软化的黏塑性模型; Amani 等 [27]将传统的Johnson-Cook模型在非常规态型近场动力学理论中进行非局部重构, 可同时描述材料的塑性硬化、热软化以及断裂行为. 由于常规态型PD本构模型与传统力学模型之间的联系尚不明确, 因而传统理论中的本构模型以及断裂准则难以直接应用在常规态型PD模拟中; 非常规态型PD理论与传统理论结合更加紧密, 该理论中包含对传统应力应变等物理量的定义, 因此可以更好地在该理论框架下开展传统本构模型的重构.

针对金属材料在冲击载荷作用下的热黏塑性变形与损伤破坏特征和已有研究现状, 本文在非常规态型近场动力学(NOSB-PD)理论框架下, 构建了可同时描述材料率效应、塑性硬化、热软化效应和断裂特征的三维热黏塑性固体非局部本构模型以及相应的空间积分型数值算法, 并基于C++平台编程实现. 通过对经典Kalthoff-Winkler冲击试验数值模拟验证了提出的模型和算法, 并进一步分析了热黏塑性冲击破坏问题中冲击速度的影响.

1 非常规态型近场动力学热黏塑性模型

1.1 近场动力学基本方程

在近场动力学理论中, 将固体物质离散为一系列包含本构信息的物质点. 每个物质点与其邻域内一定范围内的其他物质点间存在相互作用, 如图1所示. $x, x'$ 为有相互作用的两物质点在参考构形中的位置; $y = x + u$ , $y' = x' + u'$ 分别为 $t$ 时刻两物质点在现时构形中的位置; $u, u'$ 为 $t$ 时刻两物质点的位移; $\textbf{\textit{ξ}}=\bm{x'}\textbf{\textit{~‒~x}}$为参考构形中两物质点间的相对位置; $\textbf{\textit{η}}=\bm{u'}\textbf{\textit{~‒~u}}$为两物质点间的相对位移量.

为弥补键型近场动力学理论[7-8]的不足, 借鉴分子动力学方法中的描述原子间相互作用的镶嵌原子势理论以及传统连续介质力学理论中的应力、应变张量的球量、偏量分解方法, Silling 等[17-18] 提出了态型近场动力学理论和本构建模思路, 引入物质点的“ 状态”概念. “ 状态”描述物质点的物理行为, 可以是非线性不连续的, 分为标量状态(scalar state)、矢量状态(vector state) 和双状态(double state). 在图1中, 引入形变矢量状态 $\bar{Y} 〈 ξ 〉$ 来描述由两个有相互作用的物质点 $x, x'$ 构成的物质点对的变形(注: 本文中所有状态量均以带下划线的变量表示, 与态型近场动力学理论基础文献[17,18]及目前相关文献中通常采用的表述方法一致), 该状态量可以与传统理论中的形变梯度张量联系起来, 在现时构形中可表示为

$\bar{Y} 〈 ξ 〉 = y' - y = ξ + η$

引入状态量 $\bar{T} [x, t] 〈 x' ₈$ 描述 $t$ 时刻由两个有相互作用的物质点 $x, x'$ 构成的物质点对之间的相互作用导致的在物质点 $x$ 处的力矢量状态, 考虑到物质点 $x$ 与其邻域内一定范围(即近场范围, peridynamic horizon)内其他物质点的相互作用, 其运动方程可记为

$\begin{array}{l} ρ (x) & \ddot{u} (x, t) = b (x, t) + \\ \int_{H_{x}} ‍ (\bar{T} [x, t] 〈 x' ₈ \end{array}$

式中, $ρ$ 为物质密度, $\ddot{u}$ 为加速度, $b$ 为外力密度, $H_{x}$ 表示物质点 $x$ 的近场范围内物质点的集合.

显示原图| 下载原图ZIP| 生成PPT

图1 物质点的相互作用。

Fig.1 Interaction between material points

对于一般的固体材料, 描述力矢量状态和形变矢量状态之间的关系, 即可构成态型近场动力学理论框架下的非局部本构模型[17-18]. 对于有相互作用的两个物质点而言, 如果描述物质点间作用力的力矢量 $\bar{T}$ 与描述物质点对变形的形变矢量 $\bar{Y} 〈 $ 共线, 则通常称之为常规态型近场动力学模型, 否则称为非常规态型近场动力学模型. 前者只是一种简化处理, 而构建能描述材料各种非线性和复杂力学行为的非常规态型近场动力学模型, 是近几年相关领域研究的重点.

1.2 NOSB-PD热黏塑性本构模型

在态型近场动力学基本理论框架下[17-18], 首先基于参考构形中物质点相对位置矢量的并矢乘积定义一个二阶正定可逆的对称非局部形状张量

$K [x, t] = \int_{H_{x}} ‍ ω (| ξ |) (ξ \otimes ξ) d V_{x'}$

式中, $ω (| ξ |)$ 为影响函数, 与物质点间距有关. 早期的研究中常简化为 $ω (| ξ |) = 1$ . 考虑到近场范围内物质点间相互作用影响强度的尺寸效应, 一般可采用Gauss函数形式[18]来表示.

通过物质点从初始构形到形变后现时构形的运动定义形变梯度张量 $F$

$F = \frac{\partial y (x, t)}{\partial x}$

参考经典连续介质力学分析, 非局部形变梯度可由形状张量近似表示为

$F [x, t] = \int_{H_{x}} ‍ ω (| ξ |) (\bar{Y} 〈 ξ 〉 \otimes ξ) d V_{x'} K^{- 1}$

形变梯度率可记为

$\dot{F} = \int_{H_{x}} ‍ ω (| ξ |) (\bar{v} \otimes ξ) d V_{x'} K^{- 1}$

式中 $\bar{v}$ 为物质点的速度矢量状态.

速度梯度张量可由形变梯度表示为

$L = \frac{\partial v}{\partial x} = \dot{F} F^{- 1}$

相应地, 形变率张量 $D$ 以及旋转张量 $W$ 可通过速度梯度张量表示为

$D = \frac{1}{2} (L + L^{T}), W = \frac{1}{2} (L - L^{T})$

考虑热黏塑性变形过程, 假设形变率由弹性形变率、黏塑性形变率及热形变率三部分组成, 即

$D = D^{e} + D^{v p} + D^{T}$

其中弹性形变率

$D^{e} = B : \overset{\nabla}{τ}$

式中 $B$ 为四阶柔度张量, $\overset{\nabla}{τ}$ 为Kirchhoff应力的Jaumann应力率.

黏塑性形变率可描述为[28-29]

$D^{v p} = \frac{3 \dot{\overset{̅}{ε}}}{2 \overset{̅}{σ}} \overset{̅}{S}$

式中 $\overset{̅}{S}$ 定义如下

$\overset{̅}{S} = S - α$

$S$ 为偏应力张量

$S = τ - \frac{1}{3} τ : I$

其中, $τ$ 为Kirchhoff应力, $α$ 为背应力(back stress), 在本文模型中, 取等向强化情况, $α_{ij} = 0$ , 即 $\overset{̅}{S} = S$ . $\dot{\overset{̅}{ε}}$ 为等效塑性应变率, 用幂函数描述为[30]

$\dot{\overset{̅}{ε}} = {\dot{\overset{̅}{ε}}}_{0} {(\frac{\overset{̅}{σ}}{g (\overset{̅}{ε}, T)})}^{m}$

其中, ${\dot{ε}}_{0}$ 为参考应变率, $\overset{̅}{σ}$ 为Von Mises等效应力, $m$ 为应变率强化系数(率敏感参数), $g (\overset{̅}{ε}, T)$ 表征准静态应变 $\overset{̅}{ε}$ 和给定温度 $T$ 条件下的应力‒应变关系

$g (\overset{̅}{ε}, T) = σ_{0} {(1 + \frac{\overset{̅}{ε}}{ε_{0}})}^{n} [1 - δ_{0} (e^{\frac{T - T_{0}}{κ}} - 1)]$

式中, $n$ 为应变强化指数, $δ_{0}$ , $κ$ 为热软化系数, $T_{0}$ 为参考温度, $σ_{0}$ 为屈服应力, $ε_{0} = σ_{0} / E$ , $E$ 为弹性模量.

热形变率可表示为

$D^{T} = α \dot{T} I$

式中 $α$ 为热膨胀系数. 为方便计算, 考虑物质点的绝热升温, 则有

$\dot{T} = \frac{χ \dot{\overset{̅}{ε}} \overset{̅}{σ}}{ρ C_{p}}$

式中 $ρ$ 为材料密度, $C_{p}$ 为定压比热器, $χ$ 为材料的Taylor-Quinney系数.

对于受冲击变形的等向硬化热黏塑性材料, Von Mises等效应力可记为

$\overset{̅}{σ} = (\frac{3}{2} S : S)^{\frac{1}{2}}$

等效塑性应变可通过黏塑性形变率张量表示为

$\overset{̅}{ε} = \int_{0}^{t} ‍ (\frac{2}{3} D^{v p} : D^{v p})^{\frac{1}{2}} d t$

基于上述热黏塑性模型, 可求解第一Piola-Kirchhoff应力

$P = τ F^{- T}$

进而求解得到非常规态型近场动力学模型中的力矢量状态

$\bar{T} 〈 ξ 〉 = ω 〈 ξ 〉 P K^{- 1} ξ$

由此可将力矢量状态与形变矢量状态联系起来, 在非局部思想框架下构建考虑热效应、塑性硬化和率效应的非常规态型近场动力学(NOSB-PD)热黏塑性模型.

1.3 非常规态型近场动力学破坏模型

在键型近场动力学理论以及常规态型近场动力学理论中, 通常简单地采用物质点对的临界伸长率来表征物质点对的断裂[8,17]. 该准则虽然也可应用于非常规态型近场动力学模型中, 但其数值稳定性较差, 在模拟材料破坏过程时通常要面对奇异矩阵求逆的问题. 在本文中, 通过Kirchhoff 应力计算Cauchy应力

$σ = J^{- 1} τ$

再通过Cauchy应力可求得最大主应力. 当物质点间的相互作用导致局部最大主应力 $σ_{r}$ 大于材料的断裂强度 $[σ]$ 时, 物质点对无法继续承载, 发生破坏. 通过引入布尔函数描述这一过程

$μ (t) = (\begin{array}{l} 1, σ_{r} < [σ] \\ 0, o thers \end{array}$

将布尔函数与影响函数结合, 即可描述近场动力学模型中物质点对的破坏

$ω (| ξ |) = ω_{0} (| ξ |) μ$

式中 $ω_{0} (| ξ |)$ 为Gauss影响函数.

算例表明, 在非常规态型近场动力学模型由此定义物质点对的断裂, 能较准确和高效率地模拟裂纹扩展过程, 且避免了以往近场动力学模拟中用临界伸长率定义物质点对断裂时的计算精度以及收敛性差等缺点.

1.4 数值离散与求解

对式(2)进行离散

$\begin{array}{l} ρ (x_{i}) & \ddot{u} (x_{i}, t) = b (x_{i}, t) + \sum_{j}^{=} ‍ (\bar{T} [x_{i}, t] 〈 x_{j} - x_{i} 〉 - \\ \bar{T} [x_{j}, t] 〈 x_{i} - x_{j} 〉) Δ V_{x_{j}}, i = 1,2, \dots, N \end{array}$

式中, $i$ 为物质点编号, $N$ 为物质点总数, $j$ 为近场域内物质点编号, $m$ 为近场域内物质点总数. 通过离散的运动方程, 即可描述物质点的运动信息.

本构模型中物理信息的更新采用显式迭代求解. 为保证数值计算精度与稳定性, 对Kirchhoff应力的更新采用如下方式

$τ_{n + 1} = τ_{n} + {\dot{τ}}_{n + 1} Δ t$

式中, $\dot{τ}$ 可通过Jaumann应力率 $\overset{\nabla}{τ}$ 来计算

${\dot{τ}}_{n + 1} = {\overset{\nabla}{τ}}_{n + 1} + W_{n + 1} \cdot τ_{n} + τ_{n} W_{n + 1}^{T}$

由式(9) $~$ 式(11)、式(16), Jaumann应力率可写为

$\begin{array}{l} \overset{\nabla}{τ} = C : (D - D^{v p} - D^{T}) = C : (D - \frac{3 \dot{\overset{̅}{ε}}}{2 \overset{̅}{σ}} S - α \dot{T} I) \end{array}$

式中, $C$ 为弹性张量.

参考Needleman[28-29]提出的切线模量法, 对等效塑性应变进行泰勒展开

$\begin{array}{l} Δ {\overset{̅}{ε}}_{n + 1} & = O (Δ t^{3}) + {\dot{\overset{̅}{ε}}}_{n} Δ t + \\ Δ t^{2} {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial \overset{̅}{ε}})}_{n} {\dot{\overset{̅}{ε}}}_{n + 1} + {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial \overset{̅}{σ}})}_{n} {\dot{\overset{̅}{σ}}}_{n + 1} + {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial T})}_{n} {\dot{T}}_{n + 1} \end{array}$

$\begin{array}{l} {\dot{\overset{̅}{ε}}}_{n + 1} & = O (Δ t^{2}) + {\dot{\overset{̅}{ε}}}_{n} + \\ Δ t {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial \overset{̅}{ε}})}_{n} {\dot{\overset{̅}{ε}}}_{n + 1} + {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial \overset{̅}{σ}})}_{n} {\dot{\overset{̅}{σ}}}_{n + 1} + {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial T})}_{n} {\dot{T}}_{n + 1} \end{array}$

考虑材料的有限变形, 等效应力率满足

$\dot{\overset{̅}{σ}} = \frac{3}{2 \overset{̅}{σ}} S : \overset{\nabla}{τ}$

定义

$P_{n + 1} = C : p_{n}, p_{n} = \frac{3}{2} \frac{S_{n}}{{\overset{̅}{σ}}_{n}}$

可得

${\dot{\overset{̅}{ε}}}_{n + 1} = \frac{{\dot{\overset{̅}{ε}}}_{n}}{1 + ξ_{n + 1}} + \frac{ξ_{n + 1}}{(1 + ξ_{n + 1}) H_{n + 1}} P_{n + 1} : D_{n + 1}$

式中, $H_{n + 1}$ 和 $ξ_{n + 1}$ 分别为

$\begin{array}{l} H_{n + 1} = 3 μ - {(\frac{\partial \dot{\overset{̅}{ε}} / \partial \overset{̅}{ε}}{\partial \dot{\overset{̅}{ε}} / \partial \overset{̅}{σ}})}_{n} - {(\frac{\partial \dot{\overset{̅}{ε}} / \partial T}{\partial \dot{\overset{̅}{ε}} / \partial \overset{̅}{σ}})}_{n} α \frac{χ {\overset{̅}{σ}}_{n}}{ρ C_{p}} \\ ξ_{n + 1} = Δ t {(\frac{\partial \dot{\overset{̅}{ε}}}{\partial \overset{̅}{σ}})}_{n} H_{n + 1} \end{array}\}$

综上, Jaumann应力率可表示为

$\begin{array}{l} {\overset{\nabla}{τ}}_{n + 1} = & C_{n + 1}^{t an} : D_{n + 1} - \\ \frac{{\dot{\overset{̅}{ε}}}_{n}}{1 + ξ_{n + 1}} (P_{n + 1} + 3 λα \frac{χ {\overset{̅}{σ}}_{n + 1}}{ρ C_{p}} I) \end{array}$

式中

$\begin{array}{l} C_{n + 1}^{t an} = & C - \frac{ξ_{n + 1}}{H_{n + 1} (1 + ξ_{n + 1})} \cdot \\ P_{n + 1} \otimes P_{n + 1} + (3 λ + 2 μ) α \frac{χ {\overset{̅}{σ}}_{n + 1}}{ρ C_{p}} I \otimes P_{n + 1} \end{array}$

其中 $λ$ 和 $μ$ 为拉梅系数.

由上述推导过程即可实现物质点运动方程的迭代求解.

2 模型验证

Kalthoff-Winkler冲击试验[31-32]是经典的金属动态断裂问题, 在该试验中用刚性弹丸冲击带有对称预置裂纹的金属靶板, 观测裂纹的扩展过程, 包括起裂时间、扩展方向和路径等. 在高速冲击试验过程中, 可观测到刚性弹丸撞击靶板后产生的应力波经板底反射后与裂尖相互作用; 裂纹扩展路径与冲击速度有关, 且裂纹扩展区温度效应明显. 作为一种复杂的冲击作用下热黏塑性变形与破坏过程, Kalthoff-Winkler 试验的仿真已成为检验本构模型和数值方法的经典考题. Li等[2-3,33]、Belytschko等[34]和Song等[35] 均采用不同的数值方法对该试验进行了数值建模与过程仿真.

经典Kalthoff-Winkler试验模型几何尺寸如图2所示. 靶板材料为C300钢, 参数为: ${\dot{ε}}_{0}$ 和 $ε_{0}$ 分别为0.001和0.01, $m$ 和 $n$ 分别为70和0.01, $σ_{0}$ 和 $E$ 分别为2 和200 GPa, $T_{0}$ 和 $κ$ 分别为293和500 K, $δ_{0}$ 和 $χ$ 分别为0.8和0.9, $C_{P}$ 为448 J $\cdot$ (kg $\cdot$ K) $^{- 1}$ , $α$ 为11.2 K $^{- 1}$ , $ρ$ 为7830 kg/m $^{3}$ , $v$ 为0.3.

显示原图| 下载原图ZIP| 生成PPT

图2 Kalthoff-Winkler试验的几何模型.

Fig.2 Model for Kalthoff-Winkler test

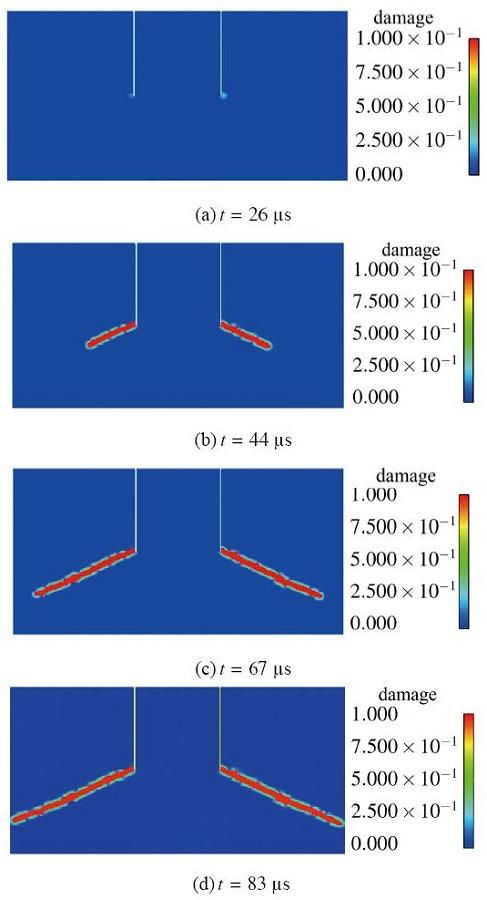
为验证本文提出的模型与数值算法, 对试验中弹丸冲击速度为 $32 m / s$ 的情况进行三维近场动力学模拟. 在近场动力学模型中, 物质点间距 $Δ x = 0.75 m m$ , 近场范围 $δ = 3 m m$ , 时间步长 $Δ t = 6 \times 1 0^{- 8} s$ .

该工况下采用本文模型和算法得到的裂纹扩展过程如图3所示. 在该冲击荷载作用下, 起裂时间为26 $µ s$ , 裂纹扩展方向与竖直方向夹角为67.997°, 分别略低于试验结果的29 $µ s$ 和70°. 至83 $µ s$ 时, 裂纹对称扩展至靶板两侧边缘, 裂纹扩展过程结束, 此结果与Belytschko采用其他数值方法[34]得到的结果(82 $µ s$ )也吻合较好.

显示原图| 下载原图ZIP| 生成PPT

图3 Kalthoff-Winkler试验的裂纹扩展路径.

Fig.3 Crack propagation of the Kalthoff-Winkler test

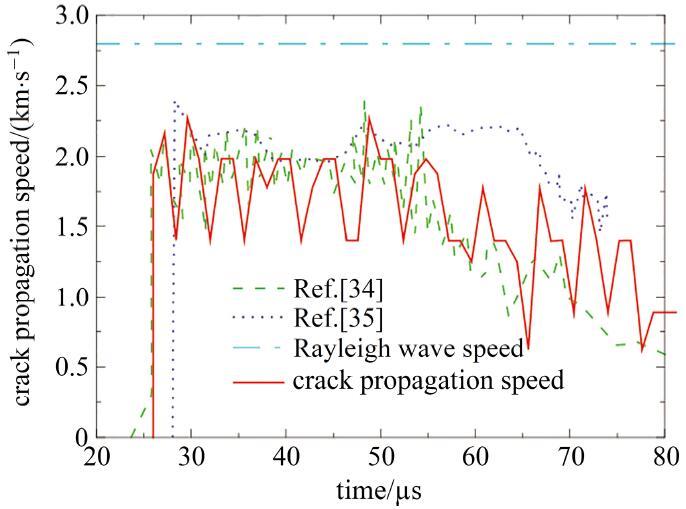
为进一步验证本文模型, 本文分析了靶板中的裂尖扩展速度. 计算第 $i$ 个时间段内的裂尖平均扩展速度

$v_{i} = \frac{y_{i} - y_{i - l}}{t_{i} - t_{i - l}} = \frac{y_{i} - y_{i - l}}{Δ t}$

式中 $v_{i}$ 表示第 $i$ 时刻裂尖的扩展速度, $y_{i}$ 以及 $y_{i - l}$ 表示裂尖在第 $i$ 和第 $i - l$ 时刻的裂纹位置.

模拟所得裂纹扩展速度与Belytschko等[34]以及Song等[35] 所得结果的对比如图4. 该实验问题的瑞利波速(Rayleigh wave speed)为2799.2 m/s. 裂纹萌生时间为26 $µ s$ , 这一时间与Belytschko结果一致; 起裂速度约为1875 m/s, 略低于Belytschko 所得的2049 m/s. 在 $26 ~ 65 µ s$ 中, 本文所得裂纹扩展速度及其变化趋势与Belytschko等[34]所得结果吻合更好, 低于Song等[35] 的结果. 在 $29.6 µ s$ 时, 本文所得裂纹扩展速度达到峰值2 266.9 m/s, 约为81%的瑞利波速. 在 $65 ~ 83 µ s$ 中, 本文所得裂纹扩展速度变化趋势与Belytschko等[34]所得结果吻合较好, 但此时本文所得裂纹扩展速度整体高于Belytschko等[34]所得结果, 低于Song等[35] 所得结果.

显示原图| 下载原图ZIP| 生成PPT

图4 裂纹扩展速度.

Fig.4 Crack propagation speed

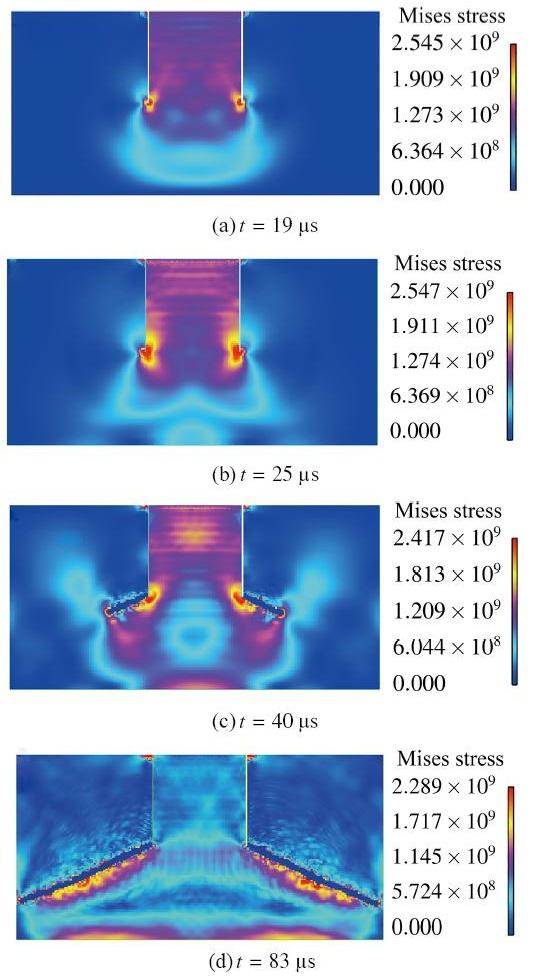
图5所示为模拟过程中的Mises应力云图, 图5(a)为冲击初始阶段, 此时弹丸冲击靶板形成应力波; 图5(b)为应力波传递至靶板底而被其反射; 图5(c)为应力波与裂尖相互作用而引起靶板的拉剪破坏; 图5(d)为裂纹扩展过程结束.采用本文模型能准确地再现实验过程[30-31]中观测到的裂纹扩展过程, 并反映其扩展机制.

显示原图| 下载原图ZIP| 生成PPT

图5 Mises应力云图.

Fig.5 Mises stress contours

3 热黏塑性近场动力学模型的应用

在验证模型的有效性后, 本文对不同冲击速度工况进行了数值模拟, 得到了不同冲击速度下靶板的裂纹起裂与贯通时间、裂纹扩展角度、裂尖扩展速度以及冲击过程中靶板的最高温度.

3.1 裂纹起裂、贯通时间以及裂纹扩展角度

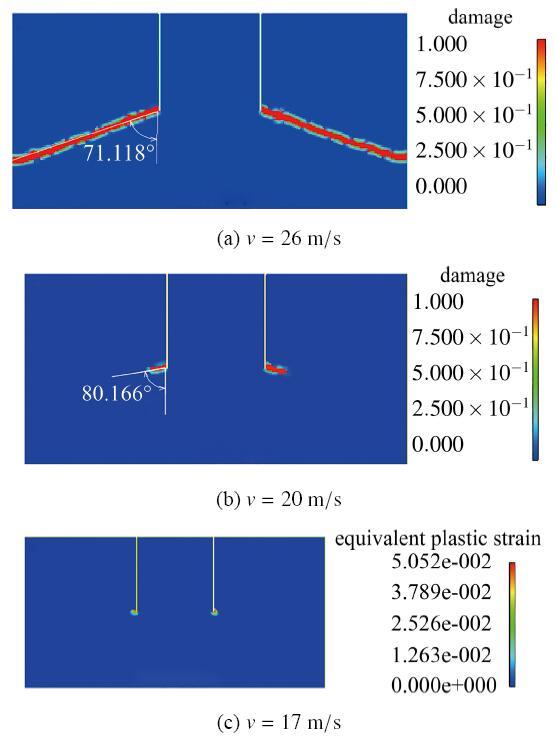
表1所示为不同冲击速度下靶板的起裂与贯通时间以及裂纹扩展的角度. 结合表1、图5和图6可知, 随着冲击速度降低, 裂纹起裂越晚, 贯通所需时间越长; 裂纹扩展角度将逐渐增大, 裂纹扩展趋势越趋向水平. 冲击速度为20 m/s 时, 靶板将在 $45.6 µ s$ 时停止裂纹扩展, 并形成图6(b)所示的裂纹扩展结果. 当冲击速度为17 m/s时, 靶板由于冲击作用将产生图6(c)所示的塑性变形, 但由于冲击能量过低而不能引起裂纹扩展. 这一模拟结果与Kalthoff实验[31-32]中所观测到的实验结果相同.

表1 裂纹扩展角度

Table 1 Crack propagation angle

Impacting	Crack initiation	Cutting-through	Angle/
velocity/(m $\cdot$ s $^{- 1}$ )	time/μs	time/μs	(°)
	26	83	67.997
	28	86	69.693
	29	92	71.118
	30	93	75.362
	36	‒	80.166

新窗口打开

显示原图| 下载原图ZIP| 生成PPT

图6 裂纹的起裂和扩展。

Fig.6 Crack initiation and propagation

3.2 裂纹扩展速度

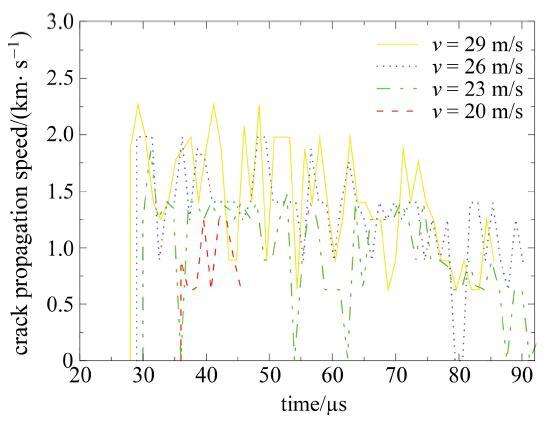
图7所示为不同冲击速度下裂纹的扩展速度. 随着冲击速度降低, 裂纹扩展速度所能达到的峰值也会有所减少, 冲击速度分别为29 m/s, 26 m/s, 23 m/s, 20 m/s时, 其对应的裂纹扩展速度峰值分别为2267 m/s, 1982 m/s, 1875 m/s, 1250 m/s.

显示原图| 下载原图ZIP| 生成PPT

图7 不同工况裂纹扩展速度。

Fig.7 Crack propagation speed in different cases

当冲击速度低于23 m/s时, 裂纹在扩展过程中会出现略微的停滞; 由于冲击能量降低, 初始裂纹出现时间相对滞后, 裂纹完全扩展所需时间越长. 同时模拟结果表明, 当冲击速度处于20 m/s时, 裂纹开展一段时间后即停止扩展, 不能完成贯通. 当冲击速度低于17 m/s时, 靶板将仅产生塑性变形, 而不会出现裂纹扩展.

3.3 靶板的最高温度

图8所示为靶板在冲击过程中的破坏区域(试验观测到的剪切带)最高温度变化过程, 表2为冲击过程中靶板的最高温度峰值. 由图表可知, 在冲击初始阶段, 温度变化趋势基本相同, 此时为预置裂纹尖端仅产生变形的阶段.

显示原图| 下载原图ZIP| 生成PPT

图8 冲击过程中靶板的最高温度变化。

Fig.8 The peak temperature in the target plate during the impact

表2 靶板的最高温度

Table 2 The peak temperature of the target plate

Impacting velocity/(m $\cdot$ s $^{- 1}$ )	Maximum temperature/K
	422.5
	369.5
	348.4
	310.1
	308.4
	308.6
	298.1
	294.7
	293.0

新窗口打开

在裂纹开始扩展阶段, 随着冲击速度的降低, 靶板所能到达的温度峰值总体成下降趋势. 在冲击速度高于23 m/s 的各个工况中, 一方面如前文所述, 裂纹会沿不同角度扩展直至板边缘; 另一方面在裂纹扩展区域, 温度上升的幅度随着冲击速度的增大显著增加, 增幅明显. 另外值得一提的是, 冲击速度17 m/s时靶板中上升达到的温度峰值高于速度为20 m/s的温度峰值. 这是由于速度20 m/s时, 冲击产生断裂消耗了一部分能量; 而速度为17 m/s 时, 靶板仅发生塑性变形而不出现裂纹扩展.

当冲击速度为8 m/s时, 由于此时冲击能量过低, 温度的峰值为293.0 K, 即冲击过程中靶板没有发生温度变化. 结合式(15)可知, 此时靶板中不产生塑性应变, 仅发生弹性变形.

4 结论

本文在非常规态型近场动力学理论框架下构建非局部热黏塑性固体模型并应用于经典金属板冲击问题模拟, 得到以下结论:

(1)本文构建的非常规态型近场动力学热黏塑性本构模型以及相应的非局部数值计算体系, 能以较高精度和计算效率模拟金属材料和结构在冲击载荷作用下的变形和破坏过程, 得到裂纹起裂时间、扩展方向, 定量描述整个裂纹扩展过程以及冲击过程中的剪切温升, 反映率效应.

(2)通过对冲击速度32 m/s工况下的Kalthoff-Winkler试验进行数值模拟, 得到了初始裂纹的扩展角度、扩展速度与裂纹开裂过程中等效应力的分布. 模拟结果所得裂纹扩展角度与实验结果高度吻合, 所得裂纹扩展速度的大小与变化趋势与文献结果一致. 模拟中可再现破坏的物理机制: 应力波经靶板反射后与裂尖相互作用, 最终形成破坏.

(3)应用本文模型分析不同冲击速度下经典Kalthoff-Winkler冲击试验中裂纹的扩展角度、扩展速度, 以及冲击过程中靶板剪切带的温度变化. 随着冲击速度下降, 裂纹的扩展角度(与竖直方向的夹角)将不断增大, 起裂越晚, 裂纹扩展速度峰值越低, 冲击过程中靶板破坏区域(剪切带)的温度峰值越低, 裂纹完全扩展至边缘所需时间越长. 冲击速度低于17 m/s时, 靶板将仅产生塑性变形而不会产生裂纹扩展, 此时所能达到的温度峰值高于冲击速度为20 m/s的温度峰值. 当冲击速度为低于8 m/s 时, 靶板中不产生温度变化, 仅发生弹性变形.

(4)上述结果验证了本文构建的非常规态型近场动力学热黏塑性固体模型在分析金属类材料冲击响应方面的可行性与有效性. 在此基础上, 可望在后续工作中针对复杂条件下金属类材料和结构的三维冲击损伤破坏问题开展定量规律研究和全过程数值模拟, 并为类似问题的深入研究提供参考.

The authors have declared that no competing interests exist.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	李杰, 任晓丹, 黄桥平. 混凝土黏塑性动力损伤本构关系 . 力学学报, 2011, 43(1): 193-201 (Li Jie, Ren Xiaodan, Huang Qiaoping. A viscoplastic damage constitutive model for concrete .Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 193-201 (in Chinese))
[2]	Li S, Liu WK, Qian D, et al. Dynamic shear band propagation and micro-structure of adiabatic shear band .Computer Methods in Applied Mechanics and Engineering, 2001, 191(1): 73-92
[3]	Li S, Liu WK, Rosakis AJ, et al. Mesh-free galerkin simulations of dynamic shear band propagation and failure mode transition .International Journal of Solids and Structures, 2002, 39(5): 1213-1240
[4]	Rabczuk T, Areias P, Belytschko T. A meshfree thin shell method for non-linear dynamic fracture .International Journal for Numerical Methods in Engineering, 2007, 72(5): 524-548
[5]	章鹏, 杜成斌, 江守燕. 比例边界有限元法求解裂纹面接触问题 . 力学学报, 2017, 49(6): 1335-1347 (Zhang Peng, Du Chengbin, Jiang Shouyan. Crack face contact problem analysis using the scaled boundary finite element method .Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(6): 1335-1347 (in Chinese))
[6]	童第华, 吴学仁, 胡本润. 半无限板边缘裂纹的权函数解法与评价 . 力学学报, 2017, 49(4): 848-857 (Tong Dihua, Wu Xueren, Hu Benrun. Weight function methods and assessment for an edge crack in a semi-infinite plate .Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(4): 848-857 (in Chinese))
[7]	Silling SA. Reformulation of elasticity theory for discontinuities and long-range forces .Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209
[8]	Madenci E, Oterkus E. Peridynamic Theory and Its Applications . Springer, 2014
[9]	黄丹, 章青, 乔丕忠等. 近场动力学方法及其应用 . 力学进展, 2010, 40(4): 448-459 (Huang Dan, Zhang Qing, Qiao Pizhong, et al. A review on peridynamics method and its application .Advance in Mechanics, 2010, 40(4): 448-459 (in Chinese))
[10]	Huang D, Lu GD, Qiao PZ. An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis .International Journal of Mechanical Sciences, 2015, 94(95): 111-122
[11]	Silling SA, Demmie P, Warren TL. Peridynamic simulation of high-rate material failure// Proceedings of 2007 Applied Mechanics and Materials Conference, Austin,TX, 2007
[12]	胡祎乐, 余音, 汪海. 基于近场动力学理论的层压板损伤分析方法 . 力学学报, 2013, 45(4): 624-628 (Hu Yile, Yu Yin, Wang Hai. Damage analysis method for laminates based on peridynamic theory .Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 624-628 (in Chinese))
[13]	郁杨天, 章青, 顾鑫. 含单边缺口混凝土梁冲击破坏的近场动力学模拟 . 工程力学, 2016(12): 80-85 (Yu Yangtian, Zhang Qing, Gu Xin. Impact failure simulation of a single-edged notched concrete beam based on peridynamics .Engineering Mechanics, 2016(12): 80-85 (in Chinese))
[14]	Huang D, Zhang Q, Qiao PZ. Damage and progressive failure of concrete structures using non-local peridynamic modeling .Science China Technological Science, 2011, 54(3): 591-596
[15]	Hu W, Wang Y, Yu J, et al. Impact damage on a thin glass plate with a thin polycarbonate backing .International Journal of Impact Engineering, 2013, 62(24): 152-165
[16]	章青, 顾鑫, 郁杨天. 冲击载荷作用下颗粒材料动态力学响应的近场动力学模拟 . 力学学报, 2016, 48(1): 56-63 (Zhang Qing, Gu Xin, Yu Yangtian. Peridynamics simulation for dynamic response of granular materials under impact loading .Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 56-63 (in Chinese))
[17]	Silling SA, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling .Journal of Elasticity, 2007, 88(2): 151-184 [本文引用: 1]
[18]	Silling SA. Linearized theory of peridynamic states .Journal of Elasticity, 2010, 99(1): 85-111 [本文引用: 1]
[19]	Mitchell JA. A nonlocal, ordinary, state-based plasticity model for peridynamics. Report of Sandia National Laboritories, Albuquerque, New Mexico, 2011
[20]	Warren TL, Silling SA, Askari A, et al. A non-ordinary state-based peridynamic method to model solid material deformation and fracture .International Journal of Solids and Structures, 2009, 46(5): 1186-1195
[21]	Weckner O, Abdullah N, Mohamed N. Viscoelastic material models in peridynamics .Applied Mathematics and Computation, 2013, 219: 6039-6043
[22]	Nikabdullah N, Azizi MA, Alebrahim R, et al. The application of peridynamic method on prediction of viscoelastic materials .AIP Conference Proceedings, 2014, 357: 1602-1609
[23]	Oterkus S, Madenci E, Agwai A. Peridynamic thermal diffusion .Journal of Computational Physics, 2014, 265(1): 71-96
[24]	Oterkus S, Madenci E, Agwai A. Fully coupled peridynamic thermomechanics .Journal of the Mechanics and Physics of Solids, 2014, 64(1): 1-23
[25]	Foster J, Silling SA, Chen W. Viscoplasticity using peridynamics .International Journal for Numerical Methods in Engineering, 2010, 81(10): 1242-1258
[26]	Tupek M, Rimoli J, Radovitzky R. An approach for incorporating classical continuum damage models in state-based peridynamics .Computer Methods in Applied Mechanics and Engineering, 2013, 263(1): 20-26
[27]	Amani J, Oterkus E, Areias P, et al. A non-ordinary state-based peridynamics formulation for thermoplastic fracture .International Journal of Impact Engineering, 2016, 87(1): 83-94
[28]	Needleman A. Material rate dependent and mesh sensitivity in localization problems .Computer Methods in Applied Mechanics and Engineering, 1988, 67(1): 68-85
[29]	Needleman A. Dynamic shear band development in plane strain .Journal of Applied Mechanics, 1989, 56(1): 1-9
[30]	Zhou M, Ravichandran G, Rosakis AJ. Dynamically propagating shear bands in impact-loaded prenotched plates--II. Numerical simulations .Journal of the Mechanics of Physics and Solids, 1996, 44(2): 1007-1032
[31]	Kalthoff JF. Modes of dynamic shear failure in solids .International Journal of Fracture, 2000, 101(1-2): 1-31
[32]	Kalthoff JF, Burgel A. Influence of loading rate on shear fracture toughness for failure mode transition .International Journal of Impact Engineering, 2004, 30(8-9): 957-971
[33]	Simkins DC, Li S. Meshfree simulations of thermo-mechanical ductile fracture .Computational Mechanics, 2006, 38(3): 235-249
[34]	Belytschko T, Chen J, Xu J, et al. Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment .International Journal for Numerical Methods in Engineering, 2003, 58(12): 1873-1905
[35]	Song JH, Areias P, Belytschko T. A method for dynamic crack and shear band propagation with phantom nodes .International Journal for Numerical Methods in Engineering, 2006, 67(6): 868-893

混凝土黏塑性动力损伤本构关系

2011

混凝土黏塑性动力损伤本构关系

2011

Dynamic shear band propagation and micro-structure of adiabatic shear band

2001

Mesh-free galerkin simulations of dynamic shear band propagation and failure mode transition

2002

A meshfree thin shell method for non-linear dynamic fracture

2007

比例边界有限元法求解裂纹面接触问题

2017

比例边界有限元法求解裂纹面接触问题

2017

半无限板边缘裂纹的权函数解法与评价

2017

半无限板边缘裂纹的权函数解法与评价

2017

Reformulation of elasticity theory for discontinuities and long-range forces

2000

Peridynamic Theory and Its Applications

2014

近场动力学方法及其应用

2010

近场动力学方法及其应用

2010

An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis

2015

Peridynamic simulation of high-rate material failure//

2007

基于近场动力学理论的层压板损伤分析方法

2013

基于近场动力学理论的层压板损伤分析方法

2013

含单边缺口混凝土梁冲击破坏的近场动力学模拟

2016

含单边缺口混凝土梁冲击破坏的近场动力学模拟

2016

Damage and progressive failure of concrete structures using non-local peridynamic modeling

2011

Impact damage on a thin glass plate with a thin polycarbonate backing

2013

冲击载荷作用下颗粒材料动态力学响应的近场动力学模拟

2016

冲击载荷作用下颗粒材料动态力学响应的近场动力学模拟

2016

Peridynamic states and constitutive modeling

2007

... 为弥补键型近场动力学理论[7-8]的不足, 借鉴分子动力学方法中的描述原子间相互作用的镶嵌原子势理论以及传统连续介质力学理论中的应力、应变张量的球量、偏量分解方法, Silling 等[17-18] 提出了态型近场动力学理论和本构建模思路, 引入物质点的“ 状态”概念. “ 状态”描述物质点的物理行为, 可以是非线性不连续的, 分为标量状态(scalar state)、矢量状态(vector state) 和双状态(double state). 在图1中, 引入形变矢量状态

\bar{Y} 〈 ξ 〉

来描述由两个有相互作用的物质点

x, x'

构成的物质点对的变形(注: 本文中所有状态量均以带下划线的变量表示, 与态型近场动力学理论基础文献[17,18]及目前相关文献中通常采用的表述方法一致), 该状态量可以与传统理论中的形变梯度张量联系起来, 在现时构形中可表示为 ...

Linearized theory of peridynamic states

2010

\bar{Y} 〈 ξ 〉

来描述由两个有相互作用的物质点

x, x'

A nonlocal, ordinary, state-based plasticity model for peridynamics. Report of Sandia National Laboritories, Albuquerque,

2011

A non-ordinary state-based peridynamic method to model solid material deformation and fracture

2009

Viscoelastic material models in peridynamics

2013

The application of peridynamic method on prediction of viscoelastic materials

2014

Peridynamic thermal diffusion

2014

Fully coupled peridynamic thermomechanics

2014

Viscoplasticity using peridynamics

2010

An approach for incorporating classical continuum damage models in state-based peridynamics

2013

A non-ordinary state-based peridynamics formulation for thermoplastic fracture

2016

Material rate dependent and mesh sensitivity in localization problems

1988

Dynamic shear band development in plane strain

1989

Dynamically propagating shear bands in impact-loaded prenotched plates--II. Numerical simulations

1996

Modes of dynamic shear failure in solids

2000

Influence of loading rate on shear fracture toughness for failure mode transition

2004

Meshfree simulations of thermo-mechanical ductile fracture

2006

Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment

2003

A method for dynamic crack and shear band propagation with phantom nodes

2006

〈

〉

非常规态型近场动力学热黏塑性模型及其应用

NON-ORDINARY STATE-BASED PERIDYNAMIC THERMAL-VISCOPLASTIC MODEL AND ITS APPLICATION

1 非常规态型近场动力学热黏塑性模型

1.1 近场动力学基本方程

1.2 NOSB-PD热黏塑性本构模型

1.3 非常规态型近场动力学破坏模型

1.4 数值离散与求解

2 模型验证

3 热黏塑性近场动力学模型的应用

3.1 裂纹起裂、贯通时间以及裂纹扩展角度

3.2 裂纹扩展速度

3.3 靶板的最高温度

4 结 论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

4 结论

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子