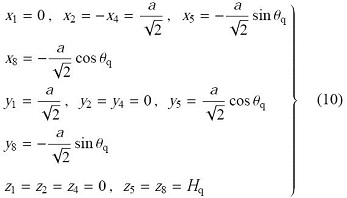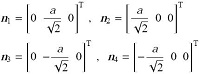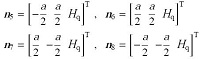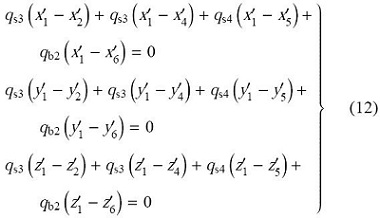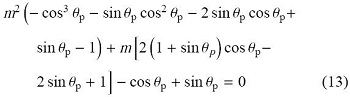张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] .
起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应.
近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析.
综上可知,目前对于张拉整体结构的外形设计主要集中在张拉整体的单体结构以及将柱状或球状张拉整体结构作为胞元按照不同的方法进行大规模组合的拓展结构,而关于球柱组合式张拉整体结构的研究相对缺乏. 本文以课题组前期工作[23 ,37 ] 为基础,拟选取四棱柱状张拉整体结构和截角正八面体球状张拉整体结构为基本胞元,采用节点连接节点的方式搭建球柱组合式数字状张拉整体结构,并对其进行力学性能分析. 此外,还将搭建实物模型验证设计方法的可行性. 研究结果将丰富大型张拉整体结构的外形种类,为结构在土木建筑、结构材料等领域的实际应用提供备选方案.
1 理论基础
1.1 自平衡条件
自平衡状态是指结构在无外载、无外部约束的条件下,单元内力在所有节点处的合力为零的状态.此时对任意节点i ,记与其相连的节点编号为j ,则存在如下平衡方程
$\sum_j \dfrac{{ p}_i - { p}_j }{l_{ij} }{ t}_{ij} = {\bf 0} (1)$
式中,${ p}_i $为节点$i$的坐标矢量${ p}_i = [x_i ,y_i ,z_i]^{\rm T}$,$x_{i}$, $y_{i}$,$z_{i}$为坐标分量,$l_{ij}$为连接节点$i$和节点$j$的单元的长度$l_{ij} = \left\| {{ p}_i - { p}_j } \right\|$,$t_{ij}$为单元$ij$的内力.
将平衡方程用矩阵的形式表示,可写成
$A\cdot t = 0 (2)$
式中,${ A}$为平衡矩阵,由全部单元的方向矢量组成,即${A}_{ij} = \left( {{ p}_i - { p}_j } \right) / l_{ij}$,${ t}$为单元内力矢量,即${ t} = [ \cdots \ \ t_{ij} \ \\cdots ]^{\rm T}$.
定义$q_{ij} = t_{ij} / l_{ij} $为单元$ij$的力密度,则式(1)也可表示为
$\sum_j {q_{ij} \left( {{ p}_i - { p}_j } \right)} = 0(3)$
通过节点坐标矢量${p} = [ \cdots , {p}_i^{T}, \cdots ]^{T}$,将式(3)写成基于应力矩阵的表达形式
$S\cdot p = 0(4)$
式中,${ S}$为应力矩阵,计算表达式为
$S = D \otimes I (5)$
式中,${ I} ={\rm dig}\left( { 1,1,1 } \right)$为三阶单位矩阵,$ \otimes$
为张量积符号[23 ,39 ],${ D}$为减缩的应力矩阵,其表达式为
$D =C^{T} \cdot Q \cdot C (6)$
式中,${ Q} = {\rm dig}\left( { \cdots ,q_{e(ij)} , \cdots }\right)$为单位力密度组成的对角矩阵,${ C}$为连通矩阵,其表达式为
$\begin{equation}{ C}_{ik} = \left\{ \begin{array}{ll} 1\,, &{\rm if} \ i \ {\rm is \ the \ first \ node \ of \ element}\ k\\-1\,, & {\rm if} \ i \ {\rm is \ the \ second \ node \ of \ element} \ k \\ 0\,, & {\rm otherwise} \end{array} \right. \end{equation}(7)$
自平衡条件是判定结构构型在预应力作用下能否存在的依据,是胞元设计和结构组装的基础.
1.2 稳定性判据
结构在受外界微小扰动作用后,能恢复到原来的自平衡状态,则其处于稳定状态. 结构的稳定性可通过刚度矩阵K 的正定性进行判定[13 ,19 ] . 刚度矩阵的表达式为[20 ,23 ]
${ K} = { S} + { A} \cdot { G} \cdot { A }^{\rm T} - { A} \cdot { Q} \cdot { A }^{\rm T} (8)$
式中,G 为单元轴向刚度组成的对角矩阵.
刚度矩阵给出了位移增量与载荷增量之间的关系,即${ K} \cdot d { p} = d { f}$.刚度矩阵可分解为两部分:材料刚度矩阵${ K}_{\rm M} = { A} \cdot \left( {{ G} - { Q}} \right) \cdot { A}^{\rm T}$和几何刚度矩阵${ K}_{\rm G} = {S }$,即${ K} = { K}_{\rm G} + { K}_{\rm M}$. ${ K}_{\rm M}$与单元材料的弹性模量相关,由常规正刚度材料组成的结构,其材料刚度矩阵均为半正定,即对任意位移矢量${ u}$,均有${ u}^{\rm T} \cdot { K}_{\rm M} \cdot { u} \geqslant 0$.${ K}_{\rm T}$为几何刚度矩阵,仅与单元的预应力大小相关.
除常规的稳定性定义外,针对张拉整体结构还存在一个特定的稳定性概念------预应力稳定性. 张拉整体结构的平衡矩阵及其转置均为非满秩矩阵,可存在一个或多个位移${ u}'$使得${ A}^{\rm T} \cdot { u}' ={\bf 0}$,此类位移称为无穷小机构位移模式. 当结构发生位移${ u}'$时,材料刚度项将退化,${ u}'^{\rm T} \cdot {K}_{\rm M} \cdot { u}' = 0$,仅有几何刚度项发挥作用,即${u}'^{\rm T} \cdot { K} \cdot { u}' = { u}'^{\rm T} \cdot { K}_{\rm G} \cdot { u}'$. 如果对于任意的无穷小机构位移,几何刚度项的产出功均为正值${u}'^{\rm T} \cdot { K}_{\rm G} \cdot { u}' \geqslant0$,则定义结构具有预应力稳定性. 对于预应力稳定的结构,均可通过选择刚度合适的材料而使其处于稳定状态[14 ,40 ] .
1.3 力学响应的数值模拟
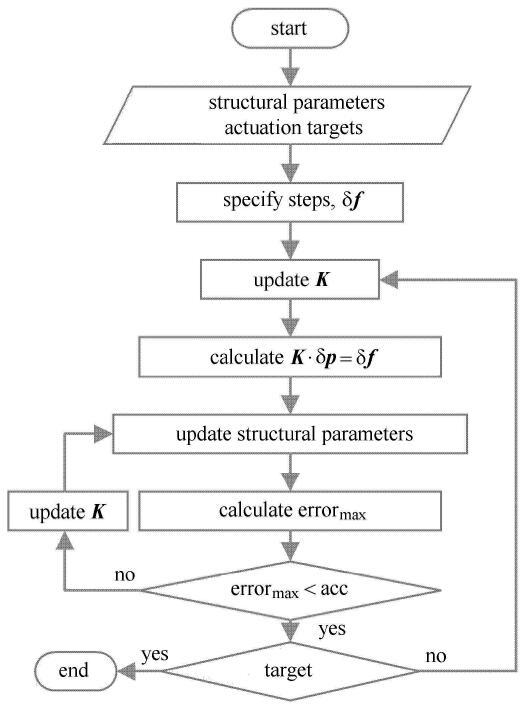
张拉整体结构的力学响应分析主要是评估结构在载荷作用下的变形行为,本文采用基于结构刚度矩阵的数值方法模拟张拉整体结构的力学响应. 数值方法的核心思路是采用增量--迭代联合算法,选用牛顿--拉普森迭代法进行增量步内的非线性求解[23 ] ,计算流程如图1 所示. 接下来对流程图进行如下补充说明:
图1 基于结构刚度的数值方法流程图(1) 输入自平衡结构参数:索单元数、杆单元数、单元总数、节点总数、连通矩阵、节点初始坐标、单元弹性模量、单元截面积、单元初始预应力、约束条件和目标载荷,并指定载荷增量.
Fig. 1 Flow chart of the structural stiness matrix based numerical method established
(2) 迭代计算:更新结构刚度,计算位移增量,并更新结构参数,计算新构型的节点力误差(外部节点力增量累加值与单元内力在各个节点处合力的最大值) error$_{\max}$并将其与迭代精度acc进行比较.当误差满足迭代精度时,进入第3计算步;当不满足精度时,则重复当前计算步.
(3) 增量计算:将外部节点力增量累积值与目标载荷进行比较. 当累计值达到目标值时,终止程序,输出计算结果:节点坐标、索单元状态、计算过程数据、相关力学响应数据等;当未达到目标值时,则返回第2 计算步,继续进行载荷增量的累加.
2 结构胞元
2.1 四棱柱状胞元
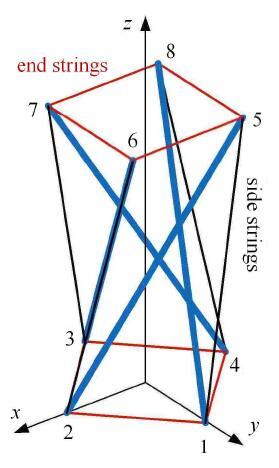
棱柱状结构是一类典型的张拉整体结构,因拓扑关系是按照棱柱多面体的外形进行构造而得名.棱柱状胞元的索单元可分为两类:围成上下端面的端面索和立于结构侧面的侧面索. 图2 所示为四棱柱状张拉整体结构,端面索连接节点对1-2, 2-3, 3-4,1-4, 5-6, 6-7, 7-8 和5-8,侧面索连接节点对1-5, 2-6,3-7 和4-8,杆连接节点对1-8, 2-5, 3-6 和4-7. 构建四棱柱状张拉整体结构胞元的局部直角坐标系,以下端面中心点为原点,x 轴和y 轴分别通过节点2, 1,定义胞元高度为$H_{q}$,端面索长度为$a$,上端面与下端面之间的相对扭转角为$\theta_{q}$.
记端面索、侧面索和杆的力密度分别为$q_{\rm s1}$, $q_{\rm s2}$ 和$q_{\rm b1}$,则节点1处的平衡关系式可写为
$\begin{equation}\left.\!\! \begin{array}{l} q_{\rm s1} \left( {x_1 - x_2 } \right) + q_{\rm s1} \left( {x_1 - x_4} \right) + q_{\rm s2} \left( {x_1 - x_5 } \right) +\\ \qquad q_{\rm b1} \left( {x_1 - x_8 } \right) =0 \\ q_{\rm s1} \left( {y_1 - y_2 } \right) + q_{\rm s1} \left( {y_1 - y_4} \right) + q_{\rm s2} \left( {y_1 - y_5 } \right) + \\ \qquad q_{\rm b1} \left( {y_1 - y_8 } \right) =0 \\ q_{\rm s1} \left( {z_1 - z_2 } \right) + q_{\rm s1} \left( {z_1 - z_4} \right) + q_{\rm s2}\left( {z_1 - z_5 } \right) + \\ \qquad q_{\rm b1} \left( {z_1 - z_8 } \right) =0 \end{array}\!\!\right\}\end{equation}(9)$
图2 四棱柱状张拉整体结构
Fig. 2 Quadruplex prismatic tensegrity structure
为了对式(9)进行求解,需要使用结构高度$H_{q}$,端面索长度$a$和相对扭转角 $\theta _{q}$建立节点1, 2, 4, 5和8的坐标表达式
将式(10) 代入式(9),求得结构的找形结果[19 ]
$\theta _{\rm q} = \dfrac{\pi}{4}\,, \ \ q_{\rm s1} = - \dfrac{\sqrt 2}{2}q_{\rm b1}\,, \ \ q_{\rm s2} = - q_{\rm b1} (11)$
式(11) 确定了四棱柱状结构自平衡构型中结构的几何和力密度参数应满足的关系.
接下来,按照如下过程生成四棱柱状胞元的自平衡构型. 首先,由几何关系得到下端面4 个节点的坐标
然后,将下端面4个节点逆时针旋转角度$\theta _{q}$,并向上平移高度$H_{q}$,得到上端面4个节点的坐标
确定全部节点坐标后,按照图2 所示连接关系,依次添加端面索、侧面索和杆,于是生成了四棱柱状胞元结构.
2.2 截角正八面体球状胞元
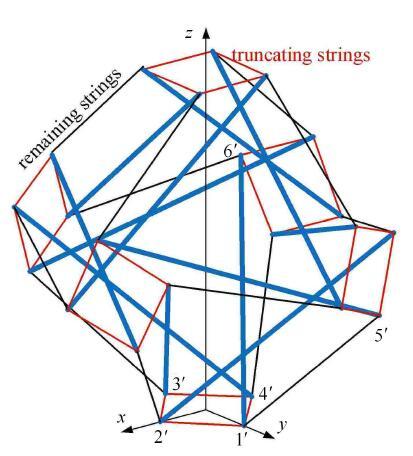
球状胞元结构是另一类典型的张拉整体结构,因拓扑关系来源于截角正多面体,外观似球而得名.顶点被截断后,生成的平面称为截角面;原边被截断后,剩余部分称为残边. 球状胞元的索单元也可以分成两类:连接截角面的截角边索,和连接残边的残边索. 图3 所示为截角正八面体球状胞元结构,截角边索、残边索和杆分别连接了节点对$1'$-$2'$,$1'$-$5'$和$1'$-$6'$. 构建截角正八面体球状胞元的过程中,以其体心为坐标系原点,如图3 所示方向建立局部直角坐标系,取正八面体原边长为$b$,截断长度为$c$,则截断比$m=c/b$,定义结构高度为$H_{p}$, 结构截角面相对于正多面体截角面的扭转角为$\theta_{\rm p}$. 根据几何关系,可使用边长计算 结构高度$H_{p} = \sqrt 2 (b - c) = \sqrt 2 b(1 - m)$.
图3 截角正八面体球状张拉整体结构
Fig. 3 Truncated regular octahedral tensegrity structure
记截角边索、残边索和杆的力密度分别为$q_{\rm s3}$, $q_{\rm s4}$和$q_{b2}$,则节点1'处的平衡关系式可写为
为了对式(12)进行求解,需要使用结构高度$H_{\rm p}$,截断长度$c$和相对扭转角 $\theta _{\rm p}$建立节 点$1', 2',4', 5'$和$6'$的坐标表达式,在此略去其具体结果,详细可参见文献[7 ] .将上述节点坐标代入式(12),便可求得结构的找形结果[7 ]
$\begin{equation}\left.\begin{array}{l} q_{\rm s3} = - \dfrac{1 + m\left( { - 1 + 2\cos \theta _{\rm p} + \sin\theta _{\rm p} } \right)}{2m\cos \theta _{\rm p} }q_{\rm b2} \\ q_{\rm s4} = - \dfrac{1 + m\left( { - 1 + \sin \theta _{\rm p} }\right)}{1 - m\left( {1 + \cos \theta _{\rm p} } \right)}q_{\rm b2} \end{array} \right \} \end{equation} (14)$
式(13) 和式(14) 分别确定了截角正八面体球状结构自平衡构型中结构的几何和力密度参数应满足的关系.
接下来,采用坐标变换的方法,按照如下过程生成截角正八面体球状胞元的自平衡构型. 首先,由几何关系得到节点1’的坐标为
${ n}'_1 = \left[ { - \dfrac{c}{\sqrt 2 }\sin \theta _{\rm p} } \ \ {\dfrac{c}{\sqrt 2}\cos \theta _{\rm p} } \ \ { - \dfrac{H_{\rm p} }{2}} \right]^{\rm T}$
接着以底面形心$\left( 0 \ \ 0 \ \ - H_{\rm p} / 2 \right)$为旋转中心,$c /{\sqrt2}$为半径,旋转出底面的其余3个节点,即${ n}'_2 = { R} \cdot { n}'_1 $,${ n}'_3 = { R}^2\cdot { n}'_1 $,${ n}'_4 = { R}^3 \cdot { n}'_1 $,式中${ R} = {\rm Rot}Z({\pi }/2)$为绕$z$轴旋转$ {\pi } / 2$弧度的旋转矩阵. 将节点$1', 2', 3'$和$4'$的坐标组成底面节点坐标阵${ B}$.类似引入绕$x$轴旋转$\pi $弧度的旋转矩阵${\rm Rot}X( {\pi })$和绕$y$轴旋转${\pi } /2$弧度的旋转矩阵${\rm Rot}Y( \pi /2)$,定义${ F} = {\rm Rot}X( \pi ) \cdot {\rm Rot}Y(\pi /2)$.将${ B}$按照${ R}$, ${ F}$矩阵进行旋转操作,生成顶部(${ T}$)和前后左右(${ E}$, ${W}$, ${ S}$, ${ N}$)共计5个方向的截角面节点坐标阵,即${ N} = { F} \cdot { B} $,${E} = { R} \cdot { N} $,${ S} = { R} \cdot { E} $,${ W} = { R} \cdot {S}$,${ t} = { F} \cdot { S }$.确定全部节点坐标后,按照图3 所示连接关系,依次添加截角边索、残边索和杆,便生成了截角正八面体球状胞元结构.
3 组合设计
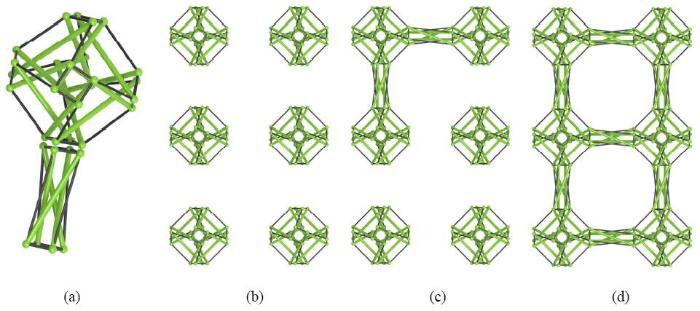
使用上节得到的四棱柱状胞元和截角正八面体球状胞元进行组合,本节将设计构造数字状张拉整体结构. 由于截角正八面体球状胞元具有三组相互垂直的截角面,故将其作为数字拼接过程中的“直角拐点”,将四棱柱状胞元作为拼接过程中的“连接线”. 由于四棱柱状胞元的上下端面与截角正八面体球状胞元的截角面均为正四边形,故当两胞元中的四边形尺寸相同时,即$a =c$,便可采用节点连接节点的方法,将两者进行拼接(如图4 (a)所示)
图4 数字8 状张拉整体结构的组装过程
Fig. 4 Assembly process of number eight-shaped tensegrity
四棱柱状胞元上下端面间相对扭转角为$\theta _{\rm q} = {\pi}/4$,若想按照节点连接节点的方式将截角正八面体 球状胞元与其进行连接,则球状胞元的相对扭转角应取值为$\theta_{\rm p} = {\pi}/8$,由式(13)求解相对应的截断比取值为$m = 0.248$.
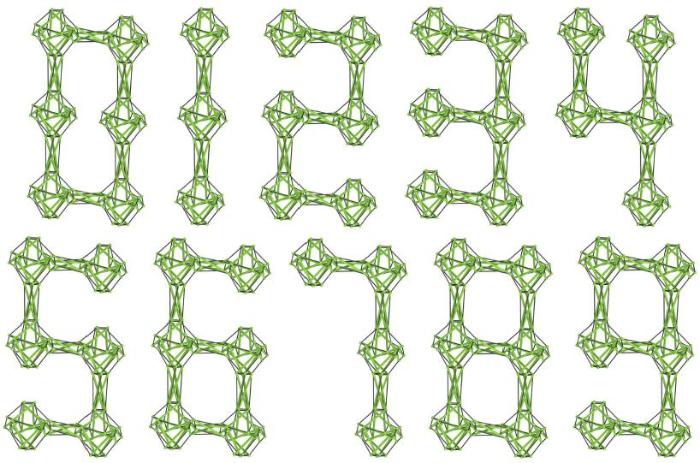
下面以形如8的数字状张拉整体结构为例,说明此类组合式结构的组装过程. 如图4 (b) ~图4 (d)所示,按照液晶数字的外形放置6个截角正八面体球状胞元,然后使用7个四棱柱状胞元将其依次连接便得到了所设计的组合结构. 按照此连接方法可以对应连接出形如数字0~9的所有数字状张拉整体结构(如图5 所示).
图5 数字状张拉整体结构
Fig. 5 Number-shaped tensegrity structures
拓展后得到的数字模型中,每一个胞元仍然保持结构的完整性,各胞元的力密度水平仍为独立状态,只需在连接处的索单元力密度做加和处理即可,连接过程中为截角正八面体球状胞元的截角边索与四棱柱状胞元的端面索相连接,故连接处的力密度$q_{\rmss}$可表示为
$\begin{equation}q_{{\rm ss}} = q_{{\rm s1}} + q_{{\rm s3}} =\\ \qquad - \dfrac{\sqrt 2 }{2}q_{{\rm b1}} - \dfrac{1 + m\left( { - 1 + 2\cos\theta _{\rm p} + \sin \theta _{\rm p} } \right)}{2m\cos \theta _{\rm p} }q_{{\rm b2}} \end{equation}(15)$
对数字状张拉整体结构的各节点列平衡方程,通过分析与整理可知:当四棱柱状胞元和截角正八面体球状胞元的节点坐标和单元力密度满足各自的自平衡条件即式(11)、式(13) 和式(14) 时,便可保证数字状张拉整体结构亦处于自平衡状态,其理论证明详见文献[37 ] .
4 力学响应
本节以数字8 状张拉整体结构(如图4 (d) 所示)为例,使用基于结构刚度矩阵的张拉整体结构大变形数值求解方法[23],对数字状张拉整体结构的力学响应进行模拟研究. 模型中:杆的直径为0.6 cm,长度为10 cm,选取3 种材料,分别为铝合金、Q235钢、黄铜;索的直径为0.1 cm,无应力状态下,截角边索长度为1 cm、残边索长度为2.5 cm、端面索长度为1 cm 和侧边索长度为8.79 cm,选取3 种材料,分别为弹簧、尼龙、Q235 钢. 上述材料的属性参数列于表1 . 索的质量远低于杆的质量,故后续分析过程中仅考虑杆的质量. 组合结构的自平衡构型中,设定两种胞元中杆的力密度相等,模拟分析中取3种初始预应力水平,分别为$q_{\rm b} = - 50$\,N/cm, $ - 100$\,N/cm 和$ -200$\,N/cm,其余索的预应力值可基于杆的预应力由式(11)和式(14)进行求解.数字8 状张拉整体结构包含144 个节点,故具有大小为432$\times $432 的结构刚度矩阵,可求解出432 个特征值. 针对以上不同材料和初始预应力水平组合而成的27 种工况进行刚度矩阵的特征值求解. 结果表明,对于上述任意工况,在结构未添加任何约束、未施加任何载荷时,除由本身具有刚体位移而存在6 个零特征值,其余所有特征值均大于零,表明刚度矩阵是正定的,数字8 状张拉整体结构自平衡构型满足稳定性要求.
利用MATLAB 软件编写力学响应分析程序,对数字8 状张拉整体结构在自重载荷作用下的变形行为进行求解. 设定重力沿竖直方向,将结构分别沿x 轴、y 轴、z 轴方向竖直放置,如图6 所示. 自重载荷施加过程中约束底部节点. 本文以将结构沿x 轴放置为例进行细节的说明,对不同组件材料和初始预应力水平的结构在自重载荷作用下的变形进行数值求解和分析.
图6 数字8 状张拉整体结构的不同姿态
Fig. 6 Di_erent attitudes of number eight-shaped tensegrity structure
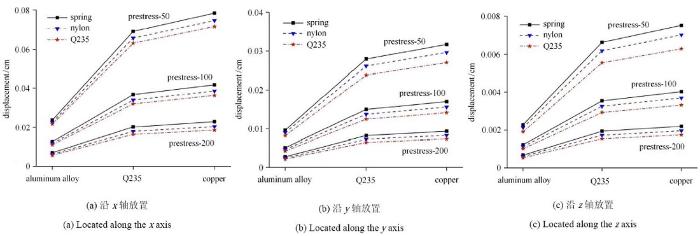
如图6 (a) 所示,结构在未施加任何形式的外载荷时,约束${yz}$ 平面内的节点N93-N96, N117-N120,第4 期朱世新等:数字状张拉整体结构的构型设计与力学性能模拟805此状态下结构高度约为53.88 cm,记录顶部节点N1-N4, N25-N28 位移变化量的平均值如图7 (a) 所示.由计算结果可知,27 种工况下结构变形量最大值为0.078 cm、最小值为0.006 cm,应变量最大值为0.14%.单元初始预应力水平是影响结构变形的主要因素,随着初始预应力水平的提高,结构变形量明显减少. 在初始预应力水平一定的情况下,结构变形量随着杆密度的增加而增加,但随着索弹性模量的增加而减小. 值得指出的是,杆弹性模量几乎不影响结构的变形量,这是由于本文所选择的杆具有显著强于索的轴向刚度(弹性模量与截面积的乘积),结构的弹性势能主要储存于索内.
图7 数字8 状张拉整体结构仅受重力时位移变化量
Fig. 7 Displacement of eight-shaped tensegrity structure under self-weight loading
类似地,对结构沿y 轴、z 轴放置时不同材料和初始预应力水平的结构在自重载荷作用下的变形量进行求解,分别如图7 (b)、图7 (c) 所示. 对比3 种放置条件下结构的变形行为可知,结构沿$x$ 轴放置时结构的变形量最大,沿$y$轴放置时的变形量次之,沿$z$轴放置时的
变形量最小,这意味 3种放置方式下结构对重力载荷的承载刚度大小排序为$z$轴$>y$轴$>x$轴.
通过分析上述数据,本文选用密度最小的铝合金杆和弹性模量居中便于搭接的尼龙绳,根据第2节中结构胞元的几何和拓扑关系,搭建了7 个柱状胞元和6 个球状胞元,接着根据第3 节提出的组合方法,将上述胞元进行搭接,得到数字8 状张拉整体结构的实物模型,如图8 所示.
图8 数字8 状张拉整体结构实物模型
Fig. 8 Physical sculpture of number eight-shaped tensegrity structure
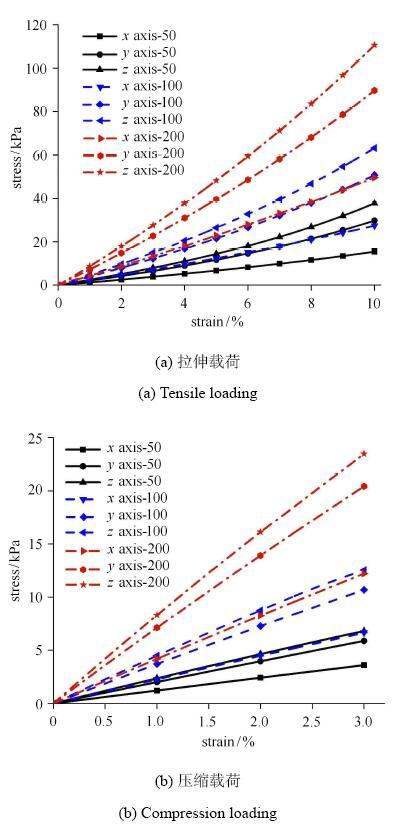
对不同初始预应力水平下的数字8状张拉整体结构在单轴拉伸及压缩载荷作用下的变形行为进行分析,如图6 所示,结构分别沿$x$轴、$y$轴、$z$轴方向放置.载荷施加过程中约束底部节点,分别对顶部节点施加沿$x$轴、$y$轴、$z$轴方向的拉伸位移载荷,结构应变达到10%时停止加载;压缩位移载荷,结构应变达到3%时停止加载. 将结构等效为53.88cm$\times $32.81cm$\times$11.73cm长方体,以作用于各节点的合力于结构等效横截面积的比值作为等效应力,图9 即为结构沿3个不同方向放置时的等效应力应变曲线. 由图9 可知,随着结构应变量的增大,结构力学响应的非线性越加明显.由图9 (a)可知,施加拉伸位移载荷过程中,顶部节点合力逐步增大,结构刚度也随之逐渐增大.由图9 (b)可知,施加压缩位移载荷过程中,顶部节点合力逐步增大,结构刚度随之逐渐减小.
图9 形如数字8 的张拉整体结构承受单轴载荷时的等效应力--应变曲线
Fig. 9 Mechanical responses of number eight-shaped tensegrity structure under uniaxial loading
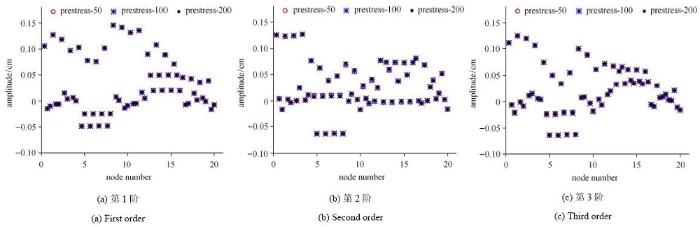
最后,对不同初始预应力水平下的数字8状张拉整体结构进行动力学模态分析. 矩阵${ M}^{ - 1}{K}$的特征值即 为结构固有频率的平方,特征值对应的特征向量即为结构的模态振型,${M}$为结构的质量矩阵$^{[6,41]}$.求解得到的结构前六阶固有频率列于表2 ,可以看出,固有频率随着初始预应力水平的增加而增加.图10 给出了节点编号1$\sim$20的节点的前3阶模态振型,结果表明,结构在不同初始预应力水平下的振型基本保持不变;其余节点振型的分布规律与前20个节点相同,模态振型与初始预应力水平无关.
图10 不同初始预应力下前三阶固有频率的模态振型。
Fig. 10 Modal shape of third lowest natural frequencies for various prestress levels
5 结论
针对大型张拉整体结构的设计问题,本文选取了四棱柱状张拉整体结构和截角正八面体球状张拉整体结构作为基本胞元,采用节点连接节点的方式搭建了球柱组合式数字状张拉整体结构,并对其力学性能进行了分析,可以得出以下几点结论:
(1) 将四棱柱状胞元与截角正八面体球状胞元进行组合拼接,可以得到外形与液晶数字类似、处于自平衡和稳定状态的数字状张拉整体大型结构;(2) 数字状张拉整体结构可在适当的材料属性和内力分布条件下发生微小变形以满足实际应用中的刚度需求,其中初始预应力水平是影响其刚度的最主要因素;
(3) 数字状张拉整体结构在单轴拉压作用下,载荷--位移曲线呈现非线性,拉伸刚度随变形量的增加而增加,压缩刚度随变形量的增加而减小;
(4) 数字状张拉整体结构的固有频率随着初始预应力水平的增加而增加,其模态振型基本不变.本文重点开展的是数字状张拉整体结构的自平衡性质及其在多种载荷作用下的静态和动态力学响应的仿真研究,其中未考虑节点处的摩擦阻尼、单元材料阻尼和构型误差等干扰因素. 然而,上述因素客观存在于实物模型中,并影响着结构的变形行为.对数字状张拉整体结构的基本力学性质进行实验测试,是值得进一步开展的研究工作.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
刘锡良 . 现代空间结构 . 天津 : 天津大学出版社 , 2003
[本文引用: 1]
(Liu Xiliang . Modern Space Structure .Tianjin : Tianjin University Press , 2003 (in Chinese))
[本文引用: 1]
[2]
Motro R Tensegrity: Structural Systems for the Future. London:
Butterworth-Heinemann , 2003
[本文引用: 1]
[3]
Zhang JY Ohsaki M Tensegrity Structures: Form, Stability, and Symmetry
. Tokyo: Springer , 2015
[本文引用: 1]
[4]
王博 , 周演 , 周昳鸣 . 面向连续体拓扑优化的多样性设计求解方法
. 力学学报 , 2016 , 48 (4 ): 984 -993
[本文引用: 1]
(Wang Bo Zhou Yan Zhou Yiming Multiple designs approach for continuum topology optimization
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (4 ): 984 -993 (in Chinese))
[本文引用: 1]
[5]
刘人怀 , 薛江红 . 复合材料层合板壳非线性力学的研究进展
. 力学学报 , 2017 , 49 (3 ): 487 -506
[本文引用: 1]
(Liu Renhuai Xue Jianghong Development of nonlinear mechanics for laminated composite plates and shells
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (3 ): 487 -506 (in Chinese))
[本文引用: 1]
[6]
Murakami H Nishimura Y Static and dynamic characterization of regular truncated icosahedral and dodecahedral tensegrity modules
.International Journal of Solids and Structures , 2001 , 38 (50-51 ): 9359 -9381
[本文引用: 1]
[7]
Murakami H Nishimura Y Infinitesimal mechanism modes of tensegrity modules
.Solid Mechanics and Its Applications , 2003 , 106 : 273 -284
[本文引用: 3]
[8]
姜涛 . 球状张拉整体单元的找形问题研究. [硕士论文]
. 杭州: 浙江大学 , 2005
[本文引用: 1]
(Jiang Tao Form-finding of spherical tensegrity structures. [Master Thesis]
. Hangzhou: Zhejiang University , 2005 (in Chinese))
[本文引用: 1]
[9]
Lee S Lee J A novel method for topology design of tensegrity structures
.Composite Structures , 2016 , 152 : 11 -19
[本文引用: 1]
[10]
Koohestani K On the analytical form-finding of tensegrities
.Composite Structures , 2017 , 166 : 114 -119
[本文引用: 1]
[11]
Feng XD The optimal initial self-stress design for tensegrity grid structures
.Computers & Structures 2017 , 193 : 21 -30
[本文引用: 1]
[12]
Cai JG Wang XY Deng XW et al .Form-finding method for multi-mode tensegrity structures using extended force density method by grouping elements
.Composite Structures , 2018 , 187 : 1 -9
[本文引用: 1]
[13]
张沛 , 冯健 . 张拉整体结构的稳定性判定及刚度分析
. 土木工程学报 , 2013 (10 ): 48 -57
[本文引用: 2]
(Zhang Pei Feng Jian Stability criterion and stiffness analysis of tensegrity structures
.China Civil Engineering Journal 2013 (10 ): 48 -57 (in Chinese))
[本文引用: 2]
[14]
Zhang LY Li Y Cao YP et al .Self-equilibrium and super-stability of truncated regular polyhedral tensegrity structures: A unified analytical solution
.Proceedings of the Royal Society A , 2012 , 468 : 3323 -3347
[本文引用: 2]
[15]
Zhang LY Li Y Cao YP et al .A unified solution for self-equilibrium and super-stability of rhombic truncated regular polyhedral tensegrities
.International Journal of Solids and Structures , 2013 , 50 : 234 -245
[本文引用: 1]
[16]
罗阿妮 , 王龙昆 , 刘贺平 等 . 张拉整体三棱柱构型和结构稳定性分析
. 哈尔滨工业大学学报 , 2016 , 48 (7 ): 82 -87
[本文引用: 1]
(Luo Ani Wang Longkun Liu Heping et al .Analysis of configuration and structural stability of 3-bar tensegrity prism
.Journal of Harbin Institute of Technology 2016 , 48 (7 ): 82 -87 (in Chinese))
[本文引用: 1]
[17]
Liu HP Zhang JY Ohsaki M New 3-bar prismatic tensegrity units
.Composite Structures , 2018 , 84 : 306 -313
[本文引用: 1]
[18]
Li Y Feng XQ Cao YP et al .A Monte Carlo form-finding method for large scale regular and irregular tensegrity structures
.International Journal of Solids and Structures , 2016 , 47 (14 ): 1888 -1898
[19]
Zhang LY Li Y Cao YP et al .Stiffness matrix-based form-finding method of tensegrity structures
.Engineering Structures , 2014 , 58 (7 ): 36 -48
[本文引用: 3]
[20]
Zhang LY Zhu SX Li SX et al .Analytical form-finding of tensegrities using determinant of force-density matrix
.Composite Structures , 2018 , 189 : 87 -98
[本文引用: 2]
[21]
Kebiche K Kazi-Aoual MN Motro R Geomerical non-linear analysis of tensegrity systems
.Engineering Structures , 1999 , 21 : 864 -876
[本文引用: 1]
[22]
Tran HC Lee J Geometric and material nonlinear analysis of tensegrity structures
.Acta Mechanica Sinica , 2011 , 27 (6 ): 938 -949
[本文引用: 1]
[23]
Zhang LY Li Y Cao YP et al .A numerical method for simulating nonlinear mechanical responses of tensegrity structures under large deformations
.Journal of Applied Mechanics , 2013 , 80 (6 ): 061018
[本文引用: 5]
[24]
Zhang LY Xu GK Negative stiffness behaviors emerging in elastic instabilities of prismatic tensegrities under torsional loading
.International Journal of Mechanical Sciences , 2015 , 103 : 189 -198
[本文引用: 1]
[25]
Zhang LY Zhao ZL Zhang QD et al .Chirality induced by structural transformation in a tensegrity: Theory and experiment
.Journal of Applied Mechanics , 2016 , 83 (4 ): 041003
[本文引用: 1]
[26]
Zhang L Cao Q Zhang HW An efficient algorithm for mechanical analysis of bimodular truss and tensegrity structures
.International Journal of Mechanical Sciences , 2013 , 70 (5 ): 57 -68
[本文引用: 1]
[27]
Zhang L Lu MK Zhang HW et al .Geometrically nonlinear elasto-plastic analysis of clustered tensegrity based on the co-rotational approach
.International Journal of Mechanical Sciences , 2015 , 93 : 154 -165
[本文引用: 1]
[28]
Zhang L Cao Q Liu Y et al .An efficient finite element formulation for nonlinear analysis of clustered tensegrity
.Engineering Computations , 2016 , 33 (1 ): 252 -273
[本文引用: 1]
[29]
Luo H Bewley TR Accurate simulation of near-wall turbulence over a compliant tensegrity fabric
.Proceedings of SPIE , 2005 , 5757 : 184 -197
[本文引用: 1]
[30]
Li Y Feng XQ Cao YP et al .Constructing tensegrity structures from one-bar elementary cells
.Proceedings Mathematical Physical and Engineering Sciences , 2010 , 466 : 45 -61
[本文引用: 1]
[31]
Feng XQ Li Y Cao YP et al .Design methods of rhombic tensegrity structures
. Acta Mechanica Sinica , 2010 , 466 (2113 ): 559 -565
[本文引用: 1]
[32]
张幸锵 , 袁行飞 . 新型三棱柱张拉整体平板结构研究
. 建筑结构 , 2011 (3 ): 24 -27
[本文引用: 1]
(Zhang Xinqiang Yuan Xingfei Research of a new triangular prism tensegrity plate structure
.Building Structure 2011 (3 ): 24 -27 (in Chinese))
[本文引用: 1]
[33]
Liu HP Geng JS Luo AN Tensegrity configuration method for connecting tensegrity units along their axes
.Composite Structures .2017 , 162 : 341 -350
[本文引用: 1]
[34]
Zhang LY Zhao HP Feng XQ Constructing large-scale tensegrity structures with bar-bar connecting using prismatic elementary cells
.Archive of Applied Mechanics , 2015 , 85 (3 ): 383 -394
[本文引用: 1]
[35]
Fraddosio A Marzano S Pavone G et al .Morphology and self-stress design of V-expander tensegrity cells
.Composites Part B Engineering , 2017 , 115 : 102 -116
[本文引用: 1]
[36]
Rimoli JJ Pal RK Mechanical response of 3-dimensional tensegrity lattices
.Composites Part B , 2017 , 115 : 30 -42
[本文引用: 1]
[37]
Zhang LY Li SX Zhu SX et al .Automatically assembled large-scale tensegrities by truncated regular polyhedral and prismatic elementary cells
.Composite Structures , 2018 , 184 : 30 -40
[本文引用: 3]
[38]
章孝顺 , 章定国 , 洪嘉振 . 考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
. 力学学报 , 2016 , 48 (3 ): 692 -701
[本文引用: 1]
(Zhang Xiaoshun Zhang Dingguo Hong Jiazhen Rigid-flexible coupling dynamic modeling and simulation with the longitudinal deformation induced curvature effect for a rotating flexible beam under large deformation
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (3 ): 692 -701 (in Chinese))
[本文引用: 1]
[39]
Masic M Skelton RE Gill PE Algebraic tensegrity form-finding
.International Journal of Solids and Structures , 2005 , 42 (16 ): 4833 -4858
[本文引用: 1]
[40]
Zhang JY Structural morphology and stability of tensegrity structures
. Kyoto: Kyoto University , 2007
[本文引用: 1]
[41]
Ali NBH Smith IFC Dynamic behavior and vibration control of a tensegrity structure
.International Journal of Solids and Structures , 2010 , 47 (9 ):1285 -1296
1
2003
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
1
2003
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
Tensegrity: Structural Systems for the Future. London:
1
2003
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
Tensegrity Structures: Form, Stability, and Symmetry
1
2015
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
面向连续体拓扑优化的多样性设计求解方法
1
2016
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
面向连续体拓扑优化的多样性设计求解方法
1
2016
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
复合材料层合板壳非线性力学的研究进展
1
2017
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
复合材料层合板壳非线性力学的研究进展
1
2017
... 张拉整体结构作为现代空间结构体系的典型代表,被誉为``未来的结构体系[1 ,2 ] . 随着其在结构领域的大规模发展,已经受到了越来越多国内外学者的青睐. 这种由压杆和拉索组成的大规模网格状自平衡结构,不仅造型美观,而且具有良好的力学性能. 近年来国内外力学、数学和土木工程等多个领域的研究学者对张拉整体结构的拓扑设计、找形分析和力学响应求解都进行了广泛的研究,取得了丰硕的研究成果[3 ,4 ,5 ] . ...
Static and dynamic characterization of regular truncated icosahedral and dodecahedral tensegrity modules
1
2001
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
Infinitesimal mechanism modes of tensegrity modules
3
2003
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 为了对式(12)进行求解,需要使用结构高度$H_{\rm p}$,截断长度$c$和相对扭转角 $\theta _{\rm p}$建立节 点$1', 2',4', 5'$和$6'$的坐标表达式,在此略去其具体结果,详细可参见文献[7 ] .将上述节点坐标代入式(12),便可求得结构的找形结果[7 ] ...
... [7 ] ...
球状张拉整体单元的找形问题研究. [硕士论文]
1
2005
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
球状张拉整体单元的找形问题研究. [硕士论文]
1
2005
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
A novel method for topology design of tensegrity structures
1
2016
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
On the analytical form-finding of tensegrities
1
2017
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
The optimal initial self-stress design for tensegrity grid structures
1
2017
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
Form-finding method for multi-mode tensegrity structures using extended force density method by grouping elements
1
2018
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
张拉整体结构的稳定性判定及刚度分析
2
2013
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 结构在受外界微小扰动作用后,能恢复到原来的自平衡状态,则其处于稳定状态. 结构的稳定性可通过刚度矩阵K 的正定性进行判定[13 ,19 ] . 刚度矩阵的表达式为[20 ,23 ] ...
张拉整体结构的稳定性判定及刚度分析
2
2013
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 结构在受外界微小扰动作用后,能恢复到原来的自平衡状态,则其处于稳定状态. 结构的稳定性可通过刚度矩阵K 的正定性进行判定[13 ,19 ] . 刚度矩阵的表达式为[20 ,23 ] ...
Self-equilibrium and super-stability of truncated regular polyhedral tensegrity structures: A unified analytical solution
2
2012
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 除常规的稳定性定义外,针对张拉整体结构还存在一个特定的稳定性概念------预应力稳定性. 张拉整体结构的平衡矩阵及其转置均为非满秩矩阵,可存在一个或多个位移${ u}'$使得${ A}^{\rm T} \cdot { u}' ={\bf 0}$,此类位移称为无穷小机构位移模式. 当结构发生位移${ u}'$时,材料刚度项将退化,${ u}'^{\rm T} \cdot {K}_{\rm M} \cdot { u}' = 0$,仅有几何刚度项发挥作用,即${u}'^{\rm T} \cdot { K} \cdot { u}' = { u}'^{\rm T} \cdot { K}_{\rm G} \cdot { u}'$. 如果对于任意的无穷小机构位移,几何刚度项的产出功均为正值${u}'^{\rm T} \cdot { K}_{\rm G} \cdot { u}' \geqslant0$,则定义结构具有预应力稳定性. 对于预应力稳定的结构,均可通过选择刚度合适的材料而使其处于稳定状态[14 ,40 ] . ...
A unified solution for self-equilibrium and super-stability of rhombic truncated regular polyhedral tensegrities
1
2013
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
张拉整体三棱柱构型和结构稳定性分析
1
2016
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
张拉整体三棱柱构型和结构稳定性分析
1
2016
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
New 3-bar prismatic tensegrity units
1
2018
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
A Monte Carlo form-finding method for large scale regular and irregular tensegrity structures
2016
Stiffness matrix-based form-finding method of tensegrity structures
3
2014
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 结构在受外界微小扰动作用后,能恢复到原来的自平衡状态,则其处于稳定状态. 结构的稳定性可通过刚度矩阵K 的正定性进行判定[13 ,19 ] . 刚度矩阵的表达式为[20 ,23 ] ...
... 将式(10) 代入式(9),求得结构的找形结果[19 ] ...
Analytical form-finding of tensegrities using determinant of force-density matrix
2
2018
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 结构在受外界微小扰动作用后,能恢复到原来的自平衡状态,则其处于稳定状态. 结构的稳定性可通过刚度矩阵K 的正定性进行判定[13 ,19 ] . 刚度矩阵的表达式为[20 ,23 ] ...
Geomerical non-linear analysis of tensegrity systems
1
1999
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
Geometric and material nonlinear analysis of tensegrity structures
1
2011
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
A numerical method for simulating nonlinear mechanical responses of tensegrity structures under large deformations
5
2013
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
... 综上可知,目前对于张拉整体结构的外形设计主要集中在张拉整体的单体结构以及将柱状或球状张拉整体结构作为胞元按照不同的方法进行大规模组合的拓展结构,而关于球柱组合式张拉整体结构的研究相对缺乏. 本文以课题组前期工作[23 ,37 ] 为基础,拟选取四棱柱状张拉整体结构和截角正八面体球状张拉整体结构为基本胞元,采用节点连接节点的方式搭建球柱组合式数字状张拉整体结构,并对其进行力学性能分析. 此外,还将搭建实物模型验证设计方法的可行性. 研究结果将丰富大型张拉整体结构的外形种类,为结构在土木建筑、结构材料等领域的实际应用提供备选方案. ...
... 为张量积符号[23 ,39 ],${ D}$为减缩的应力矩阵,其表达式为 ...
... 结构在受外界微小扰动作用后,能恢复到原来的自平衡状态,则其处于稳定状态. 结构的稳定性可通过刚度矩阵K 的正定性进行判定[13 ,19 ] . 刚度矩阵的表达式为[20 ,23 ] ...
... 张拉整体结构的力学响应分析主要是评估结构在载荷作用下的变形行为,本文采用基于结构刚度矩阵的数值方法模拟张拉整体结构的力学响应. 数值方法的核心思路是采用增量--迭代联合算法,选用牛顿--拉普森迭代法进行增量步内的非线性求解[23 ] ,计算流程如图1 所示. 接下来对流程图进行如下补充说明: ...
Negative stiffness behaviors emerging in elastic instabilities of prismatic tensegrities under torsional loading
1
2015
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
Chirality induced by structural transformation in a tensegrity: Theory and experiment
1
2016
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
An efficient algorithm for mechanical analysis of bimodular truss and tensegrity structures
1
2013
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
Geometrically nonlinear elasto-plastic analysis of clustered tensegrity based on the co-rotational approach
1
2015
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
An efficient finite element formulation for nonlinear analysis of clustered tensegrity
1
2016
... 起初,学者们多致力于张拉整体单体结构的找形分析和力学响应研究.找形分析方面,Murakami和Nishimura[6 ,7 ] 使用基于平衡矩阵的分析方法求解了基于截角正多面体的球状张拉整体结构的找形结果.姜涛[8 ] 也对球状张拉整体单元的找形问题进行了深入研究.Seunghye [9 ] 将遗传算法和力密度矩阵算法相结合,提出了一种用于特定形态张拉整体结构找形的新方法.Koohestani$[10 ] 基于Faddeevl-Leverrier算法开发了用于张拉整体结构找形分析的计算平台.Feng[11 ] 将张拉整体结构找形问题转化非线性规划问题,利用最小值优化算法求解.Cai等[12 ] 基于扩展的力密度法,提出了针对多稳态结构的找形方法.张沛和冯健[13 ] 以切线刚度矩阵的正定性为判据,建立了张拉整体结构找形结果的稳定性条件. Zhang等[14 ,15 ] 建立了球状张拉整体结构自平衡与超稳定构型的统一形式解.罗阿妮等[16 ] 以三杆柱状张拉整体结构为对象,研究了添加附加索对结构稳定性构型存在区间的影响.Liu等[17 ] 设计了一种新型的三棱柱张拉整体结构.Li等$^{[18]}$基于蒙特卡洛算法提出只需要给出节点连接关系的找形方法. Zhang等[19 ,20 ] 分别基于切线刚度矩阵和力密度矩阵,提出了可用于张拉整体结构找形分析的通用数值方法和解析方法.力学响应研究方面,Kebiche等[21 ] 使用非线性有限元的方法,分析了四棱柱状结构在拉压弯扭等多种载荷形式下的力学响应.Tran和Lee[22 ] 建立了同时考虑几何非线性和材料非线性的有限元求解方程,比较了全拉格朗日格式与更新的拉格朗日格式在模拟张拉整体结构力学行为时的差异.Zhang等[23 ] 建立了基于结构刚度矩阵的张拉整体结构大变形求解方法.Zhang等[24 ,25 ] 还对张拉整体结构特异的力学响应进行了研究,发现了棱柱状张拉整体结构在扭矩作用下的负刚度行为,并对平面X状张拉整体结构在拉伸载荷作用下的手性失稳行为进行了理论分析和实验验证.Zhang等[26 ,27 ,28 ] 基于参数变分原理和共旋坐标方法,将结构单元的变形量分解为刚体转动和轴向伸长两种模式分别加以计算,模拟研究了传统铰接式张拉整体结构和集群式张拉整体结构的非线性力学响应. ...
Accurate simulation of near-wall turbulence over a compliant tensegrity fabric
1
2005
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Constructing tensegrity structures from one-bar elementary cells
1
2010
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Design methods of rhombic tensegrity structures
1
2010
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
新型三棱柱张拉整体平板结构研究
1
2011
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
新型三棱柱张拉整体平板结构研究
1
2011
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Tensegrity configuration method for connecting tensegrity units along their axes
1
2017
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Constructing large-scale tensegrity structures with bar-bar connecting using prismatic elementary cells
1
2015
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Morphology and self-stress design of V-expander tensegrity cells
1
2017
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Mechanical response of 3-dimensional tensegrity lattices
1
2017
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Automatically assembled large-scale tensegrities by truncated regular polyhedral and prismatic elementary cells
3
2018
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
... 综上可知,目前对于张拉整体结构的外形设计主要集中在张拉整体的单体结构以及将柱状或球状张拉整体结构作为胞元按照不同的方法进行大规模组合的拓展结构,而关于球柱组合式张拉整体结构的研究相对缺乏. 本文以课题组前期工作[23 ,37 ] 为基础,拟选取四棱柱状张拉整体结构和截角正八面体球状张拉整体结构为基本胞元,采用节点连接节点的方式搭建球柱组合式数字状张拉整体结构,并对其进行力学性能分析. 此外,还将搭建实物模型验证设计方法的可行性. 研究结果将丰富大型张拉整体结构的外形种类,为结构在土木建筑、结构材料等领域的实际应用提供备选方案. ...
... 对数字状张拉整体结构的各节点列平衡方程,通过分析与整理可知:当四棱柱状胞元和截角正八面体球状胞元的节点坐标和单元力密度满足各自的自平衡条件即式(11)、式(13) 和式(14) 时,便可保证数字状张拉整体结构亦处于自平衡状态,其理论证明详见文献[37 ] . ...
考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
1
2016
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
1
2016
... 近年,许多学者将研究兴趣扩展至张拉整体结构的组合构型设计. Luo 和Bewley[29 ] 将简单棱柱状张拉整体结构组合成了大尺寸的布状材料,并分析了该材料在近壁湍流作用下的性能. Li 等[30 ] 和Feng等[31 ] 提出了一种基于单杆胞元的组合设计方法,设计出了几乎所有传统类型的张拉整体结构,还可以得到一些新颖的结构形式,如凸面心形结构、碳纳米管结构等. 张幸锵和袁行飞[32 ] 利用柱状张拉整体结构左、右旋的特点,采用节点连接节点的方式构造出了一种张拉整体平板结构,将其与普通四角锥网架对比,表明张拉整体平板结构具有更好的整体刚度,在实际工程应用中具有可行性. Liu 等[33 ] 提出了一种将张拉整体胞元沿轴向拓展构建结构的方法. Zhang 等[34 ] 提出了一种棱柱状胞元通过错切仿射的方式进行组合搭接的方法,构造出了多种旋转梁式、曲板式、三维块式的张拉整体结构. Aguinaldo等[35 ] 基于V 型拓展准则,设计了5 种可用于大规模张拉整体结构的拓展的张拉整体结构胞元. Julian和Raj[36 ] 利用截角正八面体胞元拓展了平板式、块式大型张拉整体结构. Zhang 等[37 ] 提出利用截角正多面体球状张拉整体结构与棱柱状张拉整体结构作为胞元组合大型三维张拉整体结构,并对特殊结构的力学响应行为进行了分析. 章孝顺等[38 ] 对大变形柔性结构刚柔耦合动力学问题进行了建模和仿真分析. ...
Algebraic tensegrity form-finding
1
2005
... 为张量积符号[23 ,39 ],${ D}$为减缩的应力矩阵,其表达式为 ...
Structural morphology and stability of tensegrity structures
1
2007
... 除常规的稳定性定义外,针对张拉整体结构还存在一个特定的稳定性概念------预应力稳定性. 张拉整体结构的平衡矩阵及其转置均为非满秩矩阵,可存在一个或多个位移${ u}'$使得${ A}^{\rm T} \cdot { u}' ={\bf 0}$,此类位移称为无穷小机构位移模式. 当结构发生位移${ u}'$时,材料刚度项将退化,${ u}'^{\rm T} \cdot {K}_{\rm M} \cdot { u}' = 0$,仅有几何刚度项发挥作用,即${u}'^{\rm T} \cdot { K} \cdot { u}' = { u}'^{\rm T} \cdot { K}_{\rm G} \cdot { u}'$. 如果对于任意的无穷小机构位移,几何刚度项的产出功均为正值${u}'^{\rm T} \cdot { K}_{\rm G} \cdot { u}' \geqslant0$,则定义结构具有预应力稳定性. 对于预应力稳定的结构,均可通过选择刚度合适的材料而使其处于稳定状态[14 ,40 ] . ...
Dynamic behavior and vibration control of a tensegrity structure
2010