力学学报 2018 , 50 (4): 776-786 https://doi.org/10.6052/0459-1879-17-392

Orginal Article

等离子体激励器诱导射流的湍流特性研究

张鑫¹^,^*^,, 黄勇², 阳鹏宇², 唐坤², 李华星¹

1西北工业大学航空学院, 西安 710072
2中国空气动力研究与发展中心, 四川绵阳 621000);

INVESTIGATION ON THE TURBULENT CHARACTERISTICS OF THE JET INDUCED BY A PLASMA ACTUATOR

Zhang Xin¹^,^*^,, Huang Yong², Yang Pengyu², Tang Kun², Li Huaxing¹

1School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China);
2China Aerodynamics Research and Development Center, Mianyang 621000, Sichuan, China);

中图分类号: V211

文献标识码: A

通讯作者: ^*张鑫, 助理研究员, 主要研究方向: 等离子体流动控制技术研究. E-mail:lookzx@mail.edu.cn^*张鑫, 助理研究员, 主要研究方向: 等离子体流动控制技术研究. E-mail:lookzx@mail.edu.cn

基金资助: 装备预先研究项目资助(51313010204).

展开

摘要

为了进一步掌握等离子体流动控制机理, 完善等离子体激励器数学模型, 提升等离子体激励器扰动能力, 采用粒子图像测速技术, 在静止空气下开展了介质阻挡放电等离子体激励器诱导射流特性研究. 实验时, 将非对称布局激励器布置在平板模型上, 随后将带有激励器的模型放置在有机玻璃箱内, 从而避免环境气流对测试结果的影响. 基于激励器诱导流场, 分析了激励电压对诱导射流特性的影响, 揭示了较高电压下诱导射流近壁区的拟序结构, 获得了卷起涡、二次涡等拟序结构的演化发展过程, 计算了卷起涡脱落频率, 阐述了卷起涡与启动涡的区别, 初步探索了卷起涡的耗散机制. 结果表明: (1)层流射流不能完全概括等离子体诱导射流特性, 激励电压是影响射流特性的重要参数. 当电压较低时, 诱导射流为层流射流; 当电压较高时, 诱导射流的雷诺数提高, 射流剪切层不稳定, 层流射流逐渐发展为湍流射流. (2)等离子体诱导湍流射流包含着卷起涡、二次涡等拟序结构; 在固定电压下, 这些涡结构存在恒定的卷起频率. (3)当激励电压较高时, 流动不稳定使得卷起涡发生了拉伸、变形, 引起了流场湍动能增大, 从而加速了卷起涡的耗散. 研究结果为全面认识激励器射流特性, 进一步挖掘激励器卷吸掺混能力, 提升激励器控制能力积累基础.

关键词： 湍流特性 ; 射流 ; 等离子体 ; 介质阻挡放电 ; 拟序结构

Abstract

In order to understand the controlling mechanism of plasma actuator and develop the mathematical model of plasma actuator, the turbulent characteristics of the jet induced by a dielectric barrier discharge (DBD) plasma actuator in quiescent air was studied in a closed chamber using particle image velocimetry (PIV). Here, an asymmetrical DBD plasma actuator was mounted on the plate model. First, measured time-averaged velocity field induced by the DBD plasma actuator indicated that voltage amplitude is an important parameter and could affect the flow characteristics of the induced jet. When the plasma actuator was driven at low voltage, the induced jet was a laminar wall jet. On the other hand, the Reynolds number of induced jet was improved and the shear layer was instability when the plasma actuator was actuated at high voltage. Then the induced jet became a turbulent wall jet. Secondly, the results of transient flow field structure suggested that the induced turbulent wall jet had some coherent structures, such as rolling up vortex and secondary vortex in the near-wall region. And these structures were linked to a dominant frequency of $f 0 = 109$ Hz. The rolling up vortices had the process of formation, movement, merging and breakdown. Thirdly, the rolling vortex was stretched and collapsed due to the instability of flow field when the plasma actuator was actuated at high voltage. Then turbulence kinetic energy of induced flow filed was increased and the breakdown of rolling vortex was accelerated. The turbulent characteristics of the induced jet could enhance the entrainment effect of plasma actuator between the outside airflow and boundary layer flow, which is very important for flow control applications.

Keywords： turbulent characteristics ; jet ; plasma ; dielectric barrier discharge ; coherent structure

PDF (27250KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

张鑫, 黄勇, 阳鹏宇, 唐坤, 李华星. 等离子体激励器诱导射流的湍流特性研究[J]. 力学学报, 2018, 50(4): 776-786 https://doi.org/10.6052/0459-1879-17-392

Zhang Xin, Huang Yong, Yang Pengyu, Tang Kun, Li Huaxing. INVESTIGATION ON THE TURBULENT CHARACTERISTICS OF THE JET INDUCED BY A PLASMA ACTUATOR[J]. Acta Mechanica Sinica, 2018, 50(4): 776-786 https://doi.org/10.6052/0459-1879-17-392

等离子体流动控制技术是典型的主动流动控制技术之一. 该技术因具有结构简单、工作稳定、响应迅速等优点, 近十五年以来是流动控制研究领域的热点, 数十个国家的研究人员开展过该项研究[1-23].

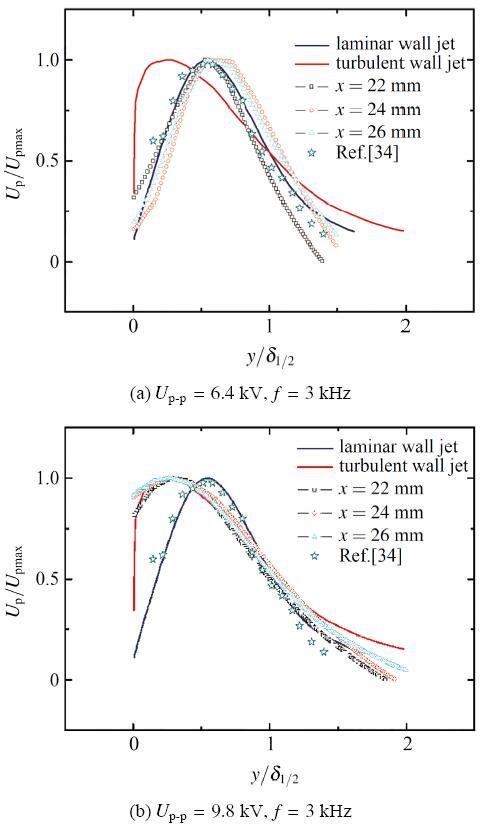
在研究中,介质阻挡放电(dielectric barrier discharge, DBD)等离子体激励器(以下简称激励器)作为该项技术的核心, 其诱导流场特性研究成为该项研究的重点之一. 对于正弦交流电源激励的激励器来说, 一般认为通过激励器诱导射流产生的动量效应是主要的控制机理[24-26]. 自1998年, 美国田纳西州立大学Roth等[27]发现激励器诱导射流效应以来, 已有来自几十个科研院所的研究人员开展过此项研究. 更高的诱导射流速度、更广的诱导流场范围、更强的激励器控制能力, 是研究人员追求的目标. 但研究结果发现[28], 单个激励器的最大诱导射流速度不超过10 m/s. 而常规飞行器的起降、巡航速度多在70 m/s以上. 与来流相比, 由激励器诱导射流提供的动量较小. 然而近年来部分研究结果表明: 采用正弦交流激励的等离子体激励器已在 $Ma = 0.4$ 及 $Re = 2 \times 1 0^{6}$ 的实验条件下实现了对翼型失速分离的控制[29-30]; 并且在低雷诺数下, 激励器能起到促进转捩的作用, 实现转捩带的功能[31]. 等离子体流动控制效果较大程度上取决于等离子体气动激励对流动不稳定性的控制[32-33]. 激励器诱导射流速度的高低并不能完全决定激励器控制效果的好坏. 因此, 深刻认识激励器诱导射流特性, 是提升激励器控制能力, 掌握控制机理的关键之一.

2007年, 英国诺丁汉大学Jukes等[34]首次对诱导射流特性给予了描述. 他通过将诱导射流速度剖面与典型的层流射流速度剖面进行对比, 指出激励器诱导射流为层流射流. 但该实验的激励电压较低. 因此, 实验结果能否全面描述诱导射流特性还需进一步验证. 本文采用高频粒子图像测速(particle image velocimetry, PIV)技术, 在不同激励电压下, 开展激励器诱导射流特性研究, 分析射流特性与激励电压之间的关系, 研究较高电压下诱导射流近壁区的拟序结构, 为深刻理解等离子体流动控制机理, 全面认识激励器激励特性, 进一步提升激励器控制能力, 提供科学支撑.

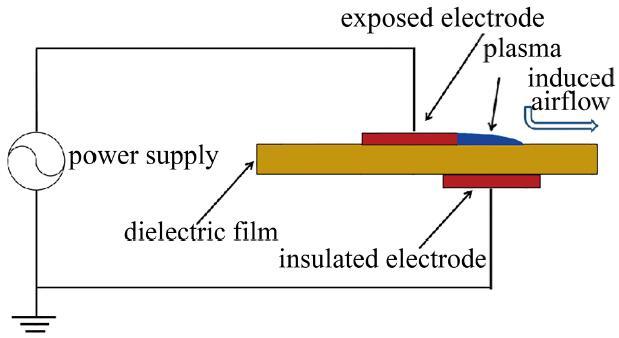
1 DBD等离子体基本原理

图1给出了典型的激励器布局示意图. 激励器由上、下两层电极、绝缘介质以及激励电源等组成. 两层电极由绝缘介质隔开, 并与激励电源相连. 当交流电压超过一定阈值时, 电极周围的空气发生电离. 由电离产生的带电粒子在电场作用下, 发生定向运动. 在运动过程中, 带电粒子与空气分子发生碰撞, 从而产生射流[35-36].

显示原图| 下载原图ZIP| 生成PPT

图1 典型的激励器布局示意图.

Fig.1 The typical layout of DBD plasma actuator

2 实验系统

实验在静止空气下进行. 采用由德国LaVision公司研制的高速PIV系统开展激励器诱导流场研究. 图2给出了实验设备布局图. 如图2所示, 为了减少环境气流对测量结果的影响, 将激励器及平板模型放置在密封箱体内. 箱体由有机玻璃制成, 其长宽高分别为800 mm $\times$ 600 mm $\times$ 600 mm. CCD相机布置在箱体侧面. 相机分辨率为1024 $\times$ 1024像素, 拍摄视场面积为32 mm $\times$ 32 mm. LDY-300(Nd:YLF) 激光器布置在箱体顶端, 激光片光与相机轴线垂直, 相交于测量平面. 激光器的重复频率为20 kHz, 单脉冲能量为30 mJ. 实验时, CCD相机的采集频率为3 kHz, 采集时间为6 s.

显示原图| 下载原图ZIP| 生成PPT

图2 实验设备布局图.

Fig.2 Schematic of the experimental set-up

采用由德国生产的Laskin粒子发生器播撒示踪粒子. 示踪粒子为DEHS(Di-ethyl-hexyl-sebacate), 粒径为1 μm. 实验前, 通过烟雾进气口将示踪粒子注入到腔体内. 随后, 通过盖板将烟雾进气口封上. 待粒子分布均匀后, 再开展实验. 数据处理时, 运算窗口大小为16像素 $\times$ 16像素, 重叠量为50%, 速度误差小于3%.

平板模型由有机玻璃制成, 其长宽高分别为240 mm $\times$ 150 mm $\times$ 10 mm. 采用支撑座对平板模型进行支撑.

激励器采用传统非对称布局布置, 并粘贴在平板模型上. 采用宽度5 mm、厚度0.05 mm的铜箔电极作为激励器上、下两层电极. 两层电极的搭接长度为0. 采用4层聚酰亚胺绝缘胶带将两层电极隔开. 该绝缘胶带的单层厚度为0.1 mm. 坐标原点定义在两层电极的搭接处. 实验时, 通过走线孔, 将高压电源的输出端引至激励器, 并分别与上、下两层电极相连.

采用西安浩宁电子科技有限公司生产的多相位交流电源作为激励电源. 该电源的电压峰值范围为0 $~$ 10 kV, 频率范围为0.1 $~$ 6 kHz. 实验时, 激励器的工作状态为定常激励, 即占空比为100%.

3 实验结果及分析

3.1 时均流场

图3给出了两种电压下激励器诱导的平均速度场. 其中 $U_{p - p}$ 代表峰峰值电压, $f$ 表示激励频率; $U_{} p$ 代表诱导流场沿 $x$ 方向的速度, $V_{} p$ 表示诱导流场沿 $y$ 方向的速度. 由图可知, (1)两种激励电压下, 激励器诱导流场的形态近似相同. 诱导射流以上、下两层电极的搭接处为“源头”, 向远离上层电极的方向发展. (2)随着激励电压的升高, 诱导射流速度增大, 激励强度提高[28].

显示原图| 下载原图ZIP| 生成PPT

图3 静止空气下激励器诱导平均速度场.

Fig.3 Time-averaged velocity field induced by the DBD plasma actuator in quiescent air

图4给出了两种激励电压下, 不同弦向位置的诱导射流无量纲速度剖面. 其中 $U_{} pmax$ 表示每一处 $x$ 位置的诱导射流最大切向速度, 即每一处 $x$ 位置存在一个最大速度; $δ_{1 / 2}$ 表示当地射流速度到达最大值的一半时所对应的 $y$ 向位置. 从图上看出, (1)在低电压下, 如图4(a)所示, 诱导射流速度剖面与层流射流剖面相似, 诱导射流近似为层流射流, 该结果与文献[34]吻合; (2)在较高电压下, 如图4(b)所示, 诱导射流速度剖面与湍流射流剖面相似, 诱导射流近似为湍流射流, 因此, 层流射流并不能完全概括等离子体诱导射流特性, 激励电压的高低决定了射流特性.

显示原图| 下载原图ZIP| 生成PPT

图4 静止空气下激励器诱导射流无量纲速度剖面.

Fig.4 Non-dimensional velocity profiles of the DBD plasma actuator in quiescent air

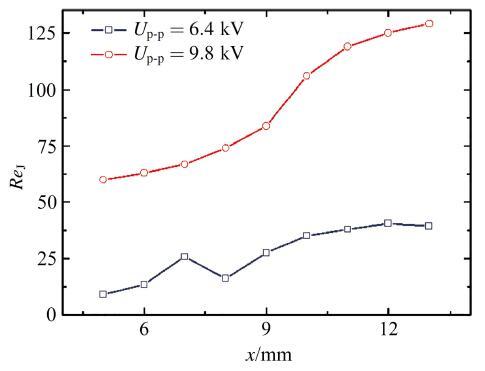
图5给出了两种电压下, 诱导射流雷诺数随 $x$ 方向距离的变化. 其中 $R e_{} J$ 代表射流雷诺数 $(R e_{} J = U_{} \max δ_{1 / 2} / ν)$ [37]. 从图上可以看出, 在低电压下, 诱导射流雷诺数较低, 一般不超过40; 较高电压下, 诱导射流雷诺数沿 $x$ 方向不断增大, 并且射流雷诺数远大于低电压时的射流雷诺数. 由文献[37]可知, 典型的层流射流临界雷诺数为57. 当射流雷诺数大于临界雷诺数时, 射流开始发生转捩. 在较高电压下, 射流雷诺数已超过临界雷诺数. 因此, 激励器诱导射流特性发生改变. 层流射流逐渐变成湍流射流. 射流雷诺数成为判断激励器诱导射流特性的判据之一. 该结果与图4的速度剖面结果吻合.

显示原图| 下载原图ZIP| 生成PPT

图5 静止空气下激励器诱导射流雷诺数随 $x$ 方向距离变化.

Fig.5 Reynolds number of plasma jet over the surface in quiescent air

3.2 瞬时流场

图6给出了相同时刻 $(t = 0.85 s)$ , 两种工况下的PIV原始图. 由图6可知, (1)在低电压下, 激励器诱导产生启动涡; 诱导射流沿壁面流动, 但在近壁区并未发现任何拟序结构(如图6(a)所示). 该结果与文献[34]的结果一致性较好. (2)在高电压下, 激励器除了诱导启动涡外, 还在壁面附近发现一些拟序结构. 由图6(b)可知, 拟序结构主要包括两种涡结构, 一是卷起涡(rolling-up vortex), 二是二次涡(secondary vortex). 当诱导射流雷诺数超过临界值时, 射流剪切层开始不稳定; 随着时间的推移, 诱导射流在剪切层内开始形成卷起涡. 卷起涡不断演化发展, 向激励器下游运动, 从而形成一系列的涡结构. 卷起涡在运动过程中, 由于无滑移壁面条件, 在卷起涡下方形成了二次涡. (3)卷起涡与文献[38]中提到的启动涡不同: 一是形成机理不同, 激励器在刚启动的瞬间, 在壁面附近会产生一股气流, 造成壁面附近的压力降低. 在压力差的作用下, 电极上方的空气会被“ 拉拽”到电极附近, 从而产生启动涡; 而卷起涡是由于射流雷诺数增大, 剪切层不稳定而卷起产生的; 二是尺度不同, 启动涡的尺度远大于卷起涡的尺度; 三是运动轨迹不同, 随着时间的增长, 启动涡的尺度逐渐增大, 并不断向远离壁面的方向运动, 而卷起涡的运动范围相对狭窄, 主要集中在壁面附近; 四是涡的个数不同, 启动涡是单独的大尺度涡结构, 而卷起涡与二次涡是一系列涡结构. 3.3拟序结构从上述研究结果来看, 激励器诱导射流特性与激励电压有关; 当电压较高时, 诱导射流为湍流射流, 并包含着卷起涡、二次涡等一系列拟序结构, 为实现掺混、抑制流动分离提供了重要支撑. 下面将针对拟序结构, 开展进一步分析.

显示原图| 下载原图ZIP| 生成PPT

图6 静止空气下激励器诱导流场的PIV原始图.

Fig.6 Original PIV images of the flow field induced by plasma actuator in quiescent air

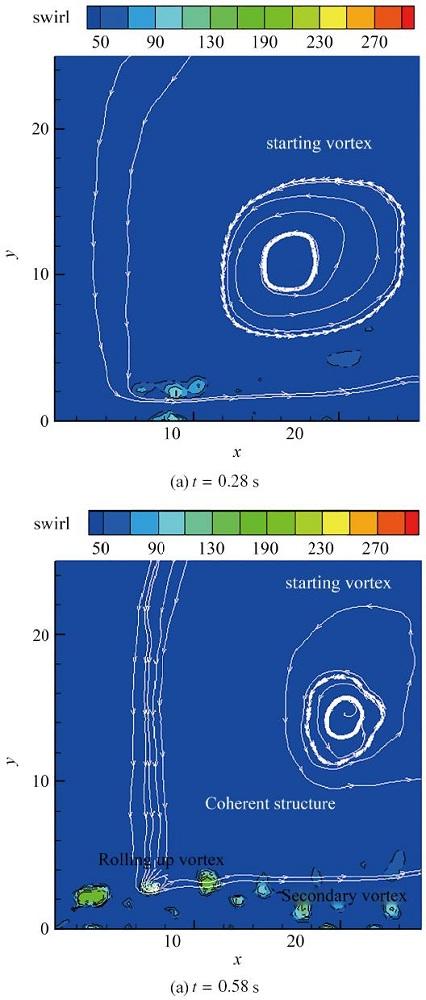
由瞬态流场结果可知(如图6(b)所示), 卷起涡及二次涡随时间不断向激励器下游发展. 因此, 通过频域分析, 可以获得卷起涡及二次涡的特征频率. 根据射流理论[39], 在起始 $(x$ 在 $0 ~ 8 mm$ 之间 $)$ 、发展 $(x$ 在 $8 ~ 20 mm$ 之间 $)$ 及主流 $(x > 20 mm)$ 三个阶段, 选取计算点进行分析. 其中起始阶段是指卷起涡、二次涡等拟序结构产生前的区域; 发展阶段主要包括了卷起涡的产生、演化及耗散过程; 主流阶段是指射流充分发展区. 具体计算位置如图7所示. 为了精确获得频谱, 在不同 $x$ 位置取切向速度 $U_{} p$ 均方根最大值所在位置为计算点坐标.

显示原图| 下载原图ZIP| 生成PPT

图7 射流计算点的位置.

Fig.7 The locations of the calculation point A to C |||| $(x A = 7.6 mm$ ; $x B = 13.2 mm$ ; $x C = 28.3 mm$ )

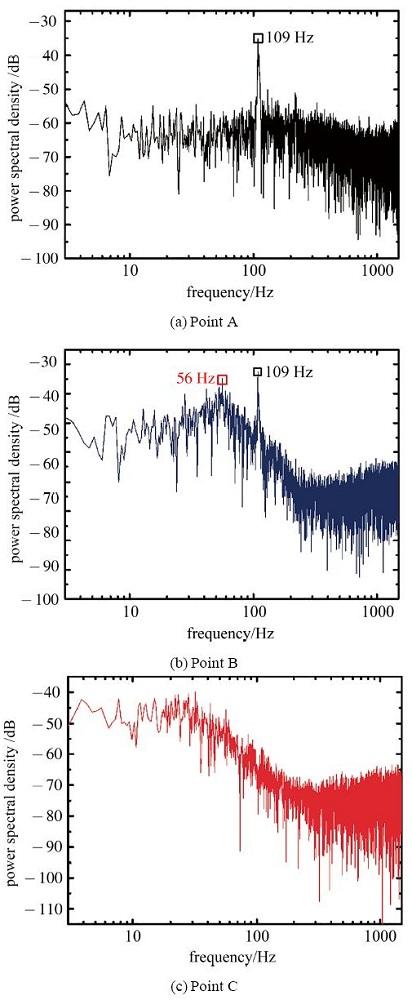
将每一个点的法向脉动速度 $V_{} p^{'}$ 进行傅里叶变换, 获得频谱图像(如图8所示). 从图上可以看出: (1)在起始阶段, 卷起涡的主频, 即卷起频率(rolling-up frequency) $f_{0}$ 为109 Hz; (2) 在射流发展阶段, 由于出现了涡的融合, 因此, 除了主频外, 还存在半频 $f_{1}$ ( $f_{1} = 56$ Hz, 它表示主频的一半); 但在此工况下, 半频的峰值略低于主频峰值, 表明涡的融合过程在卷起涡发展过程中不占主导; (3)在射流主流阶段, 诱导射流发展为湍流射流, 因此, 频谱内没有特征频率出现.

显示原图| 下载原图ZIP| 生成PPT

图8 不同位置的法向脉动速度功率谱.

Fig.8 Power spectra of the vertical fluctuating velocity at different locations

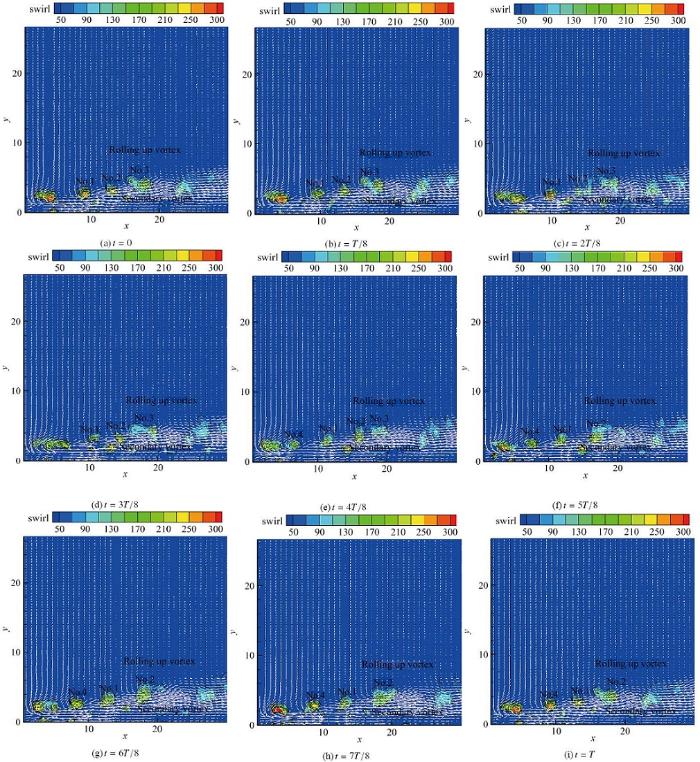
依据主频, 获得了卷起涡的运动周期. 图9给出了一个周期内, 旋涡强度分布随时间变化情况. 其中swirl 是速度梯度张量特征值的虚部, 代表旋涡强度. 不少研究人员常采用旋涡强度去探测及分析旋涡, 具体的计算方法请参照文献[40]. 由图9可知, 诱导流场在壁面附近出现了几个旋涡强度较高的离散区域; 其中紧贴壁面的区域代表二次涡, 而二次涡上方的集中区域代表了卷起涡.

显示原图| 下载原图ZIP| 生成PPT

图9 一个周期内旋涡强度的演化过程( $T$ 表示一个周期).

Fig.9 Evolution of swirling strength in one cycle |||||( $T$ stands for cycle time)

为了便于分析, 在图中对每一个卷起涡进行标注. 如图9(a)所示, 刚开始时, 流场中出现1号、2号、3号卷起涡. 随着时间的推移, 3个卷起涡同时向激励器下游运动(如图9(b) $~$ 图9(d)所示); 在运动的过程中, 3号卷起涡不断伸展, 变大(如图9(b) $~$ 图9(d)所示); 当 $t = 4 T / 8$ 时, 4号卷起涡产生(如图9(e)所示); 当 $t = 5 T / 8$ 时, 3号卷起涡耗散消失(如图9(f)所示); 随后, 1, 2, 4号卷起涡一同向激励器下游运动(如图9(g) $~$ 图9(h)所示); 如图9(i)所示, 当4号涡运动到图9(a)中1号涡的位置时, 卷起涡完成一个周期的运动.

值得注意的是, 一是相邻卷起涡之间的间距近似相等, 表明卷起涡是以固定的频率(109 Hz)向激励器下游发展[41], 这与图8(a)、图8(b)的结果一致; 二是在整个周期内, 涡的融合过程不是特别显著. 这与B点频谱(如图8(b)所示)结果相吻合. 在图8(b)中, 半频的尖峰低于主频峰值.

4 转捩分析

为了进一步理解等离子体激励器诱导湍流射流的产生机制, 对诱导射流的转捩过程进行初步分析. 图10给出了较高电压激励下, 旋涡强度分布随时间变化情况. 从图10可以看出: (1) 当 $t = 0.38$ s时, 旋涡强度主要集中在上层电极边缘, 近壁区鲜有旋涡强度较高的离散区域; (2)当 $t = 0.58$ s时, 激励器在壁面附近诱导产生了卷起涡、二次涡等拟序结构.

显示原图| 下载原图ZIP| 生成PPT

图10 不同时刻下诱导射流旋涡强度分布 $(U AC (p - p) = 9.8 kV, f AC = 3 kHz)$

Fig.10 The swirling strength distribution at different times $U AC (p - p) = 9.8 kV, f AC = 3 kHz)$

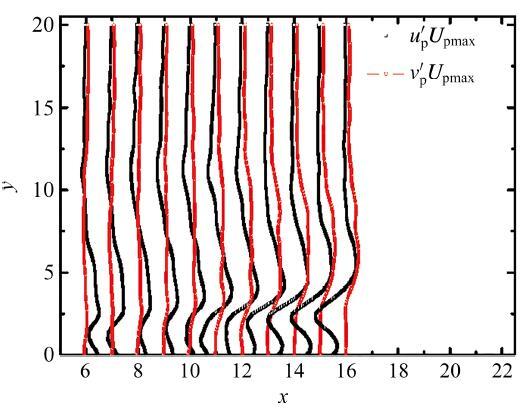
由图10可知, 拟序结构是在一定时刻才出现的, 表明诱导射流经历了从层流到湍流的转捩过程. 图11给出了不同切向位置的均方根脉动速度剖面. $u^{'} p$ 代表诱导流场沿 $x$ 方向的脉动速度, $v^{'} p$ 表示诱导流场沿 $y$ 方向的脉动速度. 由图可知, 刚开始时, $u^{'} p$ 的增长速度较快 $(x$ 在 $6 ~ 10 mm)$ 之间, 并且 $u^{'} p$ 的峰值大于 $v^{'} p$ 的峰值, 表明T-S波(Tollmien-Schlichting)在壁面发展[42-43]. 随着 $x$ 方向距离的增大, $v^{'} p$ 增长速度较快, 并且峰值与 $u^{'} p$ 的峰值接近, 表明在这些区域出现了K-H (Kelvin-Helmholtz)不稳定[42-43].

显示原图| 下载原图ZIP| 生成PPT

图11 均方根脉动速度剖面沿 $x$ 方向变化情况 $(U p - p = 9.8 kV, f AC = 3 kHz)$

Fig.11 Root-mean-squared (r.m.s.) velocity profiles over the surface of flat plate $(U p - p = 9.8 kV, f AC = 3 kHz)$

显示原图| 下载原图ZIP| 生成PPT

图12 最大切向速度、最大法向脉动及最大雷诺应力沿 $x$ 方向变化情况 $(U p - p = 9.8 kV, f AC = 3 kHz)$ |||| (a) 最大切向脉动速度; (b) 最大法向脉动速度; (c) 最大雷诺应力.

Fig.12 Distributions of the maximum streamwise r.m.s. velocity, the maximum vertical r.m.s. velocity, and the maximum Reynolds shear stress over the surface of flat plate $(U p - p = 9.8 kV, f AC = 3 kHz)$ |||| (a) The maximum streamwise r.m.s. velocity ; (b) The maximum vertical r.m.s. velocity; (c) The maximum Reynolds shear stress

此外, 最大雷诺应力值沿 $x$ 方向的指数发展过程也可用于转捩过程分析[44]. 图12给出了最大切向与最大法向脉动速度、最大雷诺应力沿 $x$ 方向的指数变化情况. 其中纵坐标为对数坐标. 由图可知, 最大雷诺应力沿 $x$ 方向的变化规律与最大法向脉动速度沿 $x$ 方向的变化规律类似. 这表明K-H不稳定是引起射流剪切层发生转捩的主要原因[45].

5 卷起涡的耗散机制

下面将对卷起涡耗散机制进行初步分析. 由图9可知, 当 $t = 4 T / 8$ 时, 3号卷起涡发生了显著地拉伸; 当 $t = 5 T / 8$ 时, 3号卷起涡耗散. 图13给出了 $t = 4 T / 8$ 时刻, 湍动能的分布情况. 从图可以看出, 与1, 2号卷起涡附近流场相比, 3号卷起涡附近出现了湍动能较高的离散区域. 结合流动不稳定性可知(如图11和图12所示), 在射流发展区, 流动不稳定使得卷起涡发生了扭曲、变形, 从而引起了流场湍动能增大, 加速了卷起涡的耗散[46].

显示原图| 下载原图ZIP| 生成PPT

图13 湍动能分布 $(t = 4 T / 8, U AC (p - p) = 9.8 kV, f AC = 3 kHz)$ .

Fig.13 The distributions of turbulence kinetic energy $(t = 4 T / 8, U AC (p - p) = 9.8 kV, f AC = 3 kHz)$

6 结论

本文采用PIV技术, 以非对称布局等离子体激励器为研究对象, 开展了激励器诱导射流特性研究, 分析了激励电压对诱导射流特性的影响, 揭示了诱导湍流射流近壁区拟序结构, 得到以下结论:

(1)等离子体诱导射流有层流、湍流两种类型, 激励电压的高低决定了诱导射流特性. 激励电压较低时, 诱导射流为层流射流, 激励电压较高时诱导射流为湍流射流. 射流雷诺数可以作为判别射流特性的标准之一.

(2)诱导湍流射流包含着卷起涡、二次涡等拟序结构; 首先, 这些涡结构与启动涡不同; 一是产生机理不同; 当激励器刚触发时, 激励器在壁面会产生一股气流, 使得壁面附近压力减小, 在压力差作用下, 激励器上方的空气被吸引到壁面, 从而产生启动涡; 而卷起涡是由于射流剪切层不稳定而卷起形成的; 二是尺度大小不同; 启动涡的尺度远大于卷起涡、二次涡的尺度; 三是运动轨迹不同; 启动涡的运动范围较大, 而卷起涡与二次涡的活动范围相对狭窄, 主要集中在壁面附近; 四是涡的个数不同; 启动涡是单独的大尺度涡结构, 而卷起涡、二次涡是一系列涡结构. 其次, 卷起涡与二次涡都经历了产生、发展及耗散等过程; 在射流起始与发展阶段, 这些涡结构存在固定的频率.

(3)结合切向、法向脉动速度、雷诺应力沿 $x$ 方向变化情况与诱导流场湍动能分布, 初步认为, 流动不稳定使得卷起涡发生了拉伸、变形, 引起了流场湍动能增大, 加速了卷起涡的耗散.

在近壁区, 拟序结构含有较高的能量. 因此, 控制拟序结构就能控制、提升这些结构蕴含的能量. 下一步将深入研究拟序结构与激励参数之间的关系, 摸清影响卷起涡特征频率的因素, 为提高激励器扰动能力提供科学支撑.

The authors have declared that no competing interests exist.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	Corke TC, Enloe CL, Wilkinson SP. Dielectric barrier discharge plasma actuators for flow control .Annual Review of Fluid Mechanics, 2010, 42(1): 505-529
[2]	Li YH, Wu Y, Li J. Review of the investigation on plasma flow control in China .International Journal of Flow Control, 2013, 4(1): 1-18
[3]	吴云, 李应红. 等离子体流动控制研究进展与展望 . 航空学报, 2015, 36(2): 381-405 (Wu Yun, Li Yinghong. Progress and outlook of plasma flow control .Acta Aeronoutica et Astronautica Sinica, 2015, 36(2): 381-405 (in Chinese))
[4]	Wang JJ, Choi KS, Feng LH, et al. Recent developments in DBD plasma flow control .Progress in Aerospace Sciences, 2013, 62: 52-78
[5]	Zhang PF, Liu AB, Wang JJ. Aerodynamic modification of a NACA 0012 aerofoil by trailing-edge plasma Gurney flap .AIAA Journal, 2009, 47(10): 2467-2474
[6]	冯立好, 王晋军, Choi KS. 等离子体环量控制翼型增升的实验研究 . 力学学报, 2013, 45(6): 815-821 ( Feng Lihao, Wang Jinjun, Choi Ks. Experimental investigation on lift increment of a plasma circulation control airfoil .Acta Mechanica Sinica, 2013, 45(6): 815-821 (in Chinese))
[7]	杜海, 史志伟, 程克明. 纳秒脉冲等离子体分离流控制频率优化及涡运动过程分析 . 航空学报, 2016, 37(7): 2102-2111 (Du Hai, Shi Zhiwei, Cheng Keming. Frequency optimization and vortex dynamic process analysis of separated flow control by nanosecond pulsed plasma dischage .Acta Aeronoutica et Astronautica Sinica, 2016, 37(7): 2102-2111 (in Chinese))
[8]	车学科, 聂万胜, 侯志勇等. 地面实验模拟高空等离子体流动控制效果 . 航空学报, 2015, 36(2): 441-448 (Che Xueke, Nie Wansheng, Hou Zhiyong, et al. High altitude plasma flow control simulation through ground experiment .Acta Aeronoutica et Astronautica Sinica, 2015, 36(2): 441-448 (in Chinese))
[9]	Che XK, Shao T, Nie WS, et al. Numerical simulation on a nanosecond-pulse surface dielectric barrier discharge actuator in near space .Journal of Physics D: Applied Physics, 2012, 45: 145201
[10]	孟宣市, 杨泽人, 陈琦等. 低雷诺数下层流分离的等离子体控制 . 航空学报, 2016, 37(7): 2112-2122 (Meng Xuanshi, Yang Zeren, Chen Qi, et al. Laminar separation control at low Reynolds numbers using plasma actuator .Acta Aeronoutica et Astronautica Sinica, 2016, 37(7): 2112-2122 (in Chinese))
[11]	赵光银, 李应红, 梁华等. 纳秒脉冲表面介质阻挡等离子体激励唯象学仿真 . 物理学报, 2015, 64(1): 015101-015112 (Zhao Guangyin, Li Yinghong, Liang Hua, et al. Phenomenological modeling of nanosecond pulsed surface dielectric barrier discharge plasma actuation for flow control .Acta Physica Sinica, 2015, 64(1): 015101-015112 (in Chinese))
[12]	林麒, 黄印阳, 潘波等. 新型等离子体主动流动控制器及其诱导流场研究 . 空气动力学学报, 2012, 30(3): 146-150 (Lin Qi, Huang Yinyang, Pan Bo, et al. Investigation on new-style plasma active flow controllers and its induced flow field .Acta Aerodynamica Sinica, 2011, 32(1): 312-317 (in Chinese))
[13]	史志伟, 杜海, 李铮等. 等离子体流动控制技术原理及典型应用 . 高压电器, 2017, 53(4): 72-78 (Shi Zhiwei, Du Hai, Li Zheng, et al. Mechanism and applications of plasma flow control technology .High Voltage Apparatus, 2017, 53(4): 72-78 (in Chinese))
[14]	Feng LH, Shi TY, Liu YG. Lift enhancement of an airfoil and an unmanned aerial vehicle by plasma Gurney flaps .AIAA Journal, 2017, 55(5): 1622-1632
[15]	Xu SY, Cai JS, Li J. Modeling and simulation of plasma gas flow driven by a single nanosecond-pulsed dielectric barrier discharge .Physics of Plasma, 2016, 23(10): 505-529
[16]	Wu Z, Wong CW, Wang L, et al. A rapidly settled closed-loop control for airfoil aerodynamics based on plasma actuation .Experiments in Fluids, 2015, 56: 1-15
[17]	吴云, 张海灯, 于贤君等. 轴流压气机等离子体流动控制 . 工程热物理学报, 2017, 38(7): 1396-1414 (Wu Yun, Zhang Haideng, Yu Xianjun, et al. Plasma flow control of axial compressor .Journal of Engineering Thermophysics, 2017, 38(7): 1396-1414 (in Chinese))
[18]	李应红, 吴云, 张海灯等. 等离子体激励式压气机 . 推进技术, 2017, 38(10): 2164-2171 (Li Yinghong, Wu Yun, Zhang Haideng, et al. Plasma actuated compressor .Journal of Propulsion Technology, 2017, 38(10): 2164-2171 (in Chinese))
[19]	魏彪, 梁华, 牛中国等. 三角翼微秒脉冲等离子体流动控制的试验研究 . 高电压技术, 2016, 42(3): 782-789 (Wei Biao, Liang Hua, Niu Zhongguo, et al. Experimental investigation of delta-wing flow control by microsecond pulse plasma actuator .High Voltage Engineering, 2016, 42(3): 782-789 (in Chinese))
[20]	吴阳阳, 贾敏, 王蔚龙等. 新型介质阻挡放电等离子体激励器的放电与诱导流动特性实验 . 电工技术学报, 2016, 31(24): 45-53 (Wu Yangyang, Jia Min, Wang Weilong, et al. Experimental research on the discharge and induced flow characteristics of a new dielectric barrier discharge plasma actuator .Transaction of China Electrotechnical Society, 2016, 31(24): 45-53 (in Chinese))
[21]	陈庆亚, 田希晖, 车学科. 平流层表面介质阻挡放电等离子体流动控制相似准则验证 . 高电压技术, 2016, 42(3): 821-827 (Chen Qingya, Tian Xihui, Che Xueke. Verification on similarity of SDBD plasma actuator induced jet for stratospheric flow control .High Voltage Engineering, 2016, 42(3): 821-827 (in Chinese))
[22]	Yan HJ, Yang L, Qi XH, et al. Improving thrust by pulse induced breakdown enhancement in AC surface dielectric barrier discharge actuators for airflow control .Journal of Physics D: Applied Physics, 2016, 42(1): 505-529
[23]	于金革, 牛中国, 梁华等. 等离子体用于三角翼模型流动控制试验研究 . 空气动力学学报, 2017, 35(2): 305-309 (Yu Jinge, Niu Zhongguo, Liang Hua, et al. Experimental investigation on delta wing flow control by plasma .Acta Aerodynamica Sinica, 2017, 35(2): 305-309 (in Chinese))
[24]	杜海, 史志伟, 耿玺. 等离子体激励器对微型飞行器横航向气动力矩控制的实验研究 . 航空学报, 2012, 33(10): 1781-1790 (Du Hai, Shi Zhiwei, Geng Xi. Experimental study of directional-lateral aerodynamic moment control of micro air vehicle by plasma actuator .Acta Aeronoutica et Astronautica Sinica, 2012, 33(10): 1781-1790 (in Chinese))
[25]	车学科, 聂万胜, 周朋辉等. 亚微秒脉冲表面介质阻挡放电等离子体诱导连续漩涡的研究 . 物理学报, 2013, 62(22): 279-288 (Che Xueke, Nie Wansheng, Zhou Penghui, et al. Study on continuous vortices induced by sub-microsecond pulsed surface dielectric barrier discharge plasma .Acta Physica Sinica, 2013, 62(22): 279-288 (in Chinese))
[26]	Wu Y, Li YH, Jia M, et al. Experimental investigation into characteristics of plasma aerodynamic actuation generated by dielectric barrier discharge .Chinese Journal of Aeronautics, 2010, 23(1): 39-45
[27]	Roth JR, Sherman DM, Wilkinson SP. Boundary layer flow control with a one atmosphere uniform glow discharge plasma//36th Aerospace Sciences Meeting and Exhibit, Reno, 1998: 1-28
[28]	Forte M, Jolibois J, Pons J, et al. Optimization of a dielectric barrier discharge actuator by stationary and non-stationary measurements of the induced flow velocity: application to airflow control .Experiments in Fluids, 2007, 43(6): 917-928
[29]	Kelley CL, Bowles PO, Cooney J. Leading edge separation control using alternating-current and nanosecond pulse plasma actuator .AIAA Journal, 2014, 52(9): 1871-1884
[30]	Zhang X, Huang Y, Wang XN. Turbulent boundary layer separation control using plasma actuator at Reynolds number 2 000 000 .Chinese Journal of Aeronautics, 2016, 29(5): 1237-1246
[31]	Sekimoto S, Nonomura T, Fujii K. Burst-mode frequency effects of dielectric barrier discharge plasma actuator for separation control .AIAA Journal, 2017, 55(4): 1385-1392
[32]	Zhang X, Li HX, Huang Y. Wing flow separation control using asymmetrical and symmetrical plasma actuator .Journal of Aircraft, 2017, 54(1): 301-309
[33]	Zhang X, Huang Y, Wang WB. Unmanned air vehicle flow separation control using dielectric barrier discharge plasma at high wind speed .Science China: Physics, Mechanics & Astronomy, 2014, 57(6): 1160-1168
[34]	Jukes TN, Choi K-S, Johnson GA, et al. Turbulent boundary-layer control for drag reduction using surface plasma//2nd AIAA Flow Control Conference, Portland, 2004: 1-11 [本文引用: 2]
[35]	梁华, 李应红, 宋慧敏等. 等离子体气动激励诱导空气流动的PIV研究 . 实验流体力学, 2011, 25(4): 22-25 (Liang Hua, Li Yinghong, Song Huimin, et al. PIV investigation on flow induced by plasma aerodynamic actuation .Journal of Experimental in Fluids Mechanics, 2011, 25(4): 22-25 (in Chinese))
[36]	梁华, 吴云, 李军等. 等离子体气动激励改善增升装置气动性能的试验 . 航空学报, 2016, 37(8): 2603-2613 (Liang Hua, Wu Yun, Li Jun, et al. Test of high lift system flow control by plasma aerodynamic actuation .Acta Aeronoutica et Astronautica Sinica, 2016, 37(8): 2603-2613 (in Chinese))
[37]	Chun DH, Schwarz WH. Stability of the plane incompressible viscous wall jet subjected to small disturbances .Physics of Fluids, 1967, 10: 911-915 [本文引用: 1]
[38]	Whalley RD, Choi KS. The starting vortex in quiescent air induced by dielectric-barrier-discharge plasma .Journal of Fluid Mechanics, 2013, 703: 192-203 [本文引用: 1]
[39]	刘沛清. 自由紊动射流理论. 北京: 北京航空航天大学出版社, 2008 (Liu Peiqing.The Theory of Free Turbulent Jet. Beijing: Beihang University Press, 2008 (in Chinese))
[40]	Zhou J, Adrian RJ, Balachandar S. Mechanisms for generating coherent packets of hairpin vortices in channel flow .Journal of Fluid Mechanics, 1999, 387: 353-396 [本文引用: 1]
[41]	Yarusevych S, Sullivan P, Kawall JG. On vortex shedding from an airfoil in low Reynolds number flow .Journal of Fluid Mechanics, 2009, 632: 245-271
[42]	Feng LH, Choi KS, Wang JJ. Flow control over an airfoil using virtual Gurney flaps .Journal of Fluid Mechanics, 2015, 767: 595-626.
[43]	Boutilier MSH, Yarusevych S. Separated shear layer transition over an airfoil at a low Reynolds number .Physics of Fluids, 2012, 24: 084105
[44]	Burgmann S, Schroder W. Investigation of the vortex induced unsteadiness of a separation bubble via time-resolved and scanning PIV measurements .Experiments in Fluids, 2008, 45(4): 675-691
[45]	Hatman A, Wang T. A prediction model for separated flow transition .Journal of Turbomachinery, 1998, 121(3): 594-602
[46]	Spalart P R. Airplane trailing vortices .Annual Review of Fluid Mechanics, 1998, 30: 107-138

Dielectric barrier discharge plasma actuators for flow control

2010

Review of the investigation on plasma flow control in China

2013

等离子体流动控制研究进展与展望

2015

等离子体流动控制研究进展与展望

2015

Recent developments in DBD plasma flow control

2013

Aerodynamic modification of a NACA 0012 aerofoil by trailing-edge plasma Gurney flap

2009

等离子体环量控制翼型增升的实验研究

2013

等离子体环量控制翼型增升的实验研究

2013

纳秒脉冲等离子体分离流控制频率优化及涡运动过程分析

2016

纳秒脉冲等离子体分离流控制频率优化及涡运动过程分析

2016

地面实验模拟高空等离子体流动控制效果

2015

地面实验模拟高空等离子体流动控制效果

2015

Numerical simulation on a nanosecond-pulse surface dielectric barrier discharge actuator in near space

2012

低雷诺数下层流分离的等离子体控制

2016

低雷诺数下层流分离的等离子体控制

2016

纳秒脉冲表面介质阻挡等离子体激励唯象学仿真

2015

纳秒脉冲表面介质阻挡等离子体激励唯象学仿真

2015

新型等离子体主动流动控制器及其诱导流场研究

2011

新型等离子体主动流动控制器及其诱导流场研究

2011

等离子体流动控制技术原理及典型应用

2017

等离子体流动控制技术原理及典型应用

2017

Lift enhancement of an airfoil and an unmanned aerial vehicle by plasma Gurney flaps

2017

Modeling and simulation of plasma gas flow driven by a single nanosecond-pulsed dielectric barrier discharge

2016

A rapidly settled closed-loop control for airfoil aerodynamics based on plasma actuation

2015

轴流压气机等离子体流动控制

2017

轴流压气机等离子体流动控制

2017

等离子体激励式压气机

2017

等离子体激励式压气机

2017

三角翼微秒脉冲等离子体流动控制的试验研究

2016

三角翼微秒脉冲等离子体流动控制的试验研究

2016

新型介质阻挡放电等离子体激励器的放电与诱导流动特性实验

2016

新型介质阻挡放电等离子体激励器的放电与诱导流动特性实验

2016

平流层表面介质阻挡放电等离子体流动控制相似准则验证

2016

平流层表面介质阻挡放电等离子体流动控制相似准则验证

2016

Improving thrust by pulse induced breakdown enhancement in AC surface dielectric barrier discharge actuators for airflow control

2016

等离子体用于三角翼模型流动控制试验研究

2017

等离子体用于三角翼模型流动控制试验研究

2017

等离子体激励器对微型飞行器横航向气动力矩控制的实验研究

2012

等离子体激励器对微型飞行器横航向气动力矩控制的实验研究

2012

亚微秒脉冲表面介质阻挡放电等离子体诱导连续漩涡的研究

2013

亚微秒脉冲表面介质阻挡放电等离子体诱导连续漩涡的研究

2013

Experimental investigation into characteristics of plasma aerodynamic actuation generated by dielectric barrier discharge

2010

Boundary layer flow control with a one atmosphere uniform glow discharge plasma//36th Aerospace Sciences Meeting and Exhibit,

1998

Optimization of a dielectric barrier discharge actuator by stationary and non-stationary measurements of the induced flow velocity: application to airflow control

2007

Leading edge separation control using alternating-current and nanosecond pulse plasma actuator

2014

Turbulent boundary layer separation control using plasma actuator at Reynolds number 2 000 000

2016

Burst-mode frequency effects of dielectric barrier discharge plasma actuator for separation control

2017

Wing flow separation control using asymmetrical and symmetrical plasma actuator

2017

Unmanned air vehicle flow separation control using dielectric barrier discharge plasma at high wind speed

2014

Turbulent boundary-layer control for drag reduction using surface plasma//2nd AIAA Flow Control Conference,

2004

... 图4给出了两种激励电压下, 不同弦向位置的诱导射流无量纲速度剖面. 其中

U_{} pmax

表示每一处

x

位置的诱导射流最大切向速度, 即每一处

x

位置存在一个最大速度;

δ_{1 / 2}

表示当地射流速度到达最大值的一半时所对应的

y

向位置. 从图上看出, (1)在低电压下, 如图4(a)所示, 诱导射流速度剖面与层流射流剖面相似, 诱导射流近似为层流射流, 该结果与文献[34]吻合; (2)在较高电压下, 如图4(b)所示, 诱导射流速度剖面与湍流射流剖面相似, 诱导射流近似为湍流射流, 因此, 层流射流并不能完全概括等离子体诱导射流特性, 激励电压的高低决定了射流特性. ...

... 图6给出了相同时刻

(t = 0.85 s)

, 两种工况下的PIV原始图. 由图6可知, (1)在低电压下, 激励器诱导产生启动涡; 诱导射流沿壁面流动, 但在近壁区并未发现任何拟序结构(如图6(a)所示). 该结果与文献[34]的结果一致性较好. (2)在高电压下, 激励器除了诱导启动涡外, 还在壁面附近发现一些拟序结构. 由图6(b)可知, 拟序结构主要包括两种涡结构, 一是卷起涡(rolling-up vortex), 二是二次涡(secondary vortex). 当诱导射流雷诺数超过临界值时, 射流剪切层开始不稳定; 随着时间的推移, 诱导射流在剪切层内开始形成卷起涡. 卷起涡不断演化发展, 向激励器下游运动, 从而形成一系列的涡结构. 卷起涡在运动过程中, 由于无滑移壁面条件, 在卷起涡下方形成了二次涡. (3)卷起涡与文献[38]中提到的启动涡不同: 一是形成机理不同, 激励器在刚启动的瞬间, 在壁面附近会产生一股气流, 造成壁面附近的压力降低. 在压力差的作用下, 电极上方的空气会被“ 拉拽”到电极附近, 从而产生启动涡; 而卷起涡是由于射流雷诺数增大, 剪切层不稳定而卷起产生的; 二是尺度不同, 启动涡的尺度远大于卷起涡的尺度; 三是运动轨迹不同, 随着时间的增长, 启动涡的尺度逐渐增大, 并不断向远离壁面的方向运动, 而卷起涡的运动范围相对狭窄, 主要集中在壁面附近; 四是涡的个数不同, 启动涡是单独的大尺度涡结构, 而卷起涡与二次涡是一系列涡结构. 3.3拟序结构从上述研究结果来看, 激励器诱导射流特性与激励电压有关; 当电压较高时, 诱导射流为湍流射流, 并包含着卷起涡、二次涡等一系列拟序结构, 为实现掺混、抑制流动分离提供了重要支撑. 下面将针对拟序结构, 开展进一步分析. ...

等离子体气动激励诱导空气流动的PIV研究

2011

等离子体气动激励诱导空气流动的PIV研究

2011

等离子体气动激励改善增升装置气动性能的试验

2016

等离子体气动激励改善增升装置气动性能的试验

2016

Stability of the plane incompressible viscous wall jet subjected to small disturbances

1967

... 图5给出了两种电压下, 诱导射流雷诺数随

x

方向距离的变化. 其中

R e_{} J

代表射流雷诺数

(R e_{} J = U_{} \max δ_{1 / 2} / ν)

[37]. 从图上可以看出, 在低电压下, 诱导射流雷诺数较低, 一般不超过40; 较高电压下, 诱导射流雷诺数沿

x

方向不断增大, 并且射流雷诺数远大于低电压时的射流雷诺数. 由文献[37]可知, 典型的层流射流临界雷诺数为57. 当射流雷诺数大于临界雷诺数时, 射流开始发生转捩. 在较高电压下, 射流雷诺数已超过临界雷诺数. 因此, 激励器诱导射流特性发生改变. 层流射流逐渐变成湍流射流. 射流雷诺数成为判断激励器诱导射流特性的判据之一. 该结果与图4的速度剖面结果吻合. ...

The starting vortex in quiescent air induced by dielectric-barrier-discharge plasma

2013

... 图6给出了相同时刻

(t = 0.85 s)

2008

Mechanisms for generating coherent packets of hairpin vortices in channel flow

1999

... 依据主频, 获得了卷起涡的运动周期. 图9给出了一个周期内, 旋涡强度分布随时间变化情况. 其中swirl 是速度梯度张量特征值的虚部, 代表旋涡强度. 不少研究人员常采用旋涡强度去探测及分析旋涡, 具体的计算方法请参照文献[40]. 由图9可知, 诱导流场在壁面附近出现了几个旋涡强度较高的离散区域; 其中紧贴壁面的区域代表二次涡, 而二次涡上方的集中区域代表了卷起涡. ...

On vortex shedding from an airfoil in low Reynolds number flow

2009

Flow control over an airfoil using virtual Gurney flaps

2015

Separated shear layer transition over an airfoil at a low Reynolds number

2012

Investigation of the vortex induced unsteadiness of a separation bubble via time-resolved and scanning PIV measurements

2008

A prediction model for separated flow transition

1998

Airplane trailing vortices

1998

〈

〉

等离子体激励器诱导射流的湍流特性研究

INVESTIGATION ON THE TURBULENT CHARACTERISTICS OF THE JET INDUCED BY A PLASMA ACTUATOR

1 DBD等离子体基本原理

2 实验系统

3 实验结果及分析

3.1 时均流场

3.2 瞬时流场

4 转捩分析

5 卷起涡的耗散机制

6 结 论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

6 结论

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子