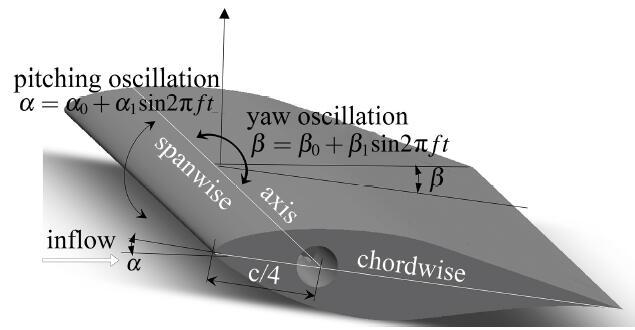
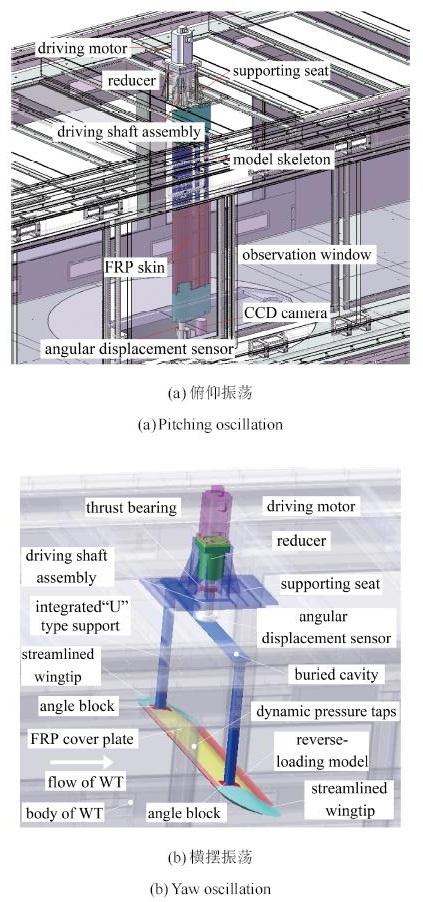
风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度.
图 1 翼型振荡形式示意图.
Fig.1 Schematic of airfoil oscillation types
翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少.
目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用.
1 试验设备与模型
1.1 风洞
试验在中国空气动力研究与发展中心FL-11风洞中完成, 该风洞是一座低速回流式风洞, 其试验段入口尺寸为1.8 m (宽) × 1.4 m (高) ,出口尺寸为1.84 m (宽) × 1.4 m (高), 长度为5.8 m, 模型中心距试验段入口下游2.6 m. 风速低于70 m/s 时湍流度达到0.000 8, 轴向静压梯度优于规范指标0.005, 试验稳定风速范围 10 ~ 105
1.2 驱动装置
驱动装置由工控机、运动控制柜、电机、减速机、电机支座和传动轴组件构成. 工控机运行人机界面软件, 实现系统参数设置、控制指令输入和运行状态监视等功能, 通过以太网与伺服运动控制器通讯, 运动控制器是该控制系统的核心, 实现系统组态、位置闭环控制、凸轮轨迹规划等功能, 如图2 (a)所示. 控制系统采用位置伺服控制技术, 主要由全数字运动控制器(位控板)、全数字交流伺服系统、驱动模块和角位移传感器等组成, 如图2 (b)所示; 在位控板的控制下, 驱动模块使伺服电机按给定的变速运动规律转动. 驱动装置的核心就是用 “电子凸轮”取代机械凸轮, 不但简化了机械装置结构, 还实现了振荡频率和振荡角度的无级变化.
图 2 驱动装置控制.
Fig.2 Control of driving device
1.3 试验模型
本文以翼型试验模型来近似模拟风力机叶片的一个片段, 进而研究正弦振荡对翼型气动特性的影响规律. 如图3 所示, 模型为S809翼型, 其弦长为 300 mm, 展长为 1 400 mm, 展弦比为4.67, 俯仰振荡传动轴位于1/4弦长处, 横摆振荡传动轴位于1/2 展长处. 模型为由中间段和两端翼尖组成的三段式结构. 模型俯仰振荡时, 采用图3 (a)中的等直翼尖结构; 横摆振荡时, 端部采用整流翼尖结构, 如图3 (b) 所示. 模型试验阻塞度范围为 3.5 % (0°迎角)至 8.3 % (30°迎角). 采用玻璃钢蒙皮和铝合金骨架结构, 中间加铺PMI 泡沫芯材, 模型重量为 35 kg, 惯量为0.2 kg ⋅ 2 . 模型中间剖面为动态压力测量剖面, 共布置 27 个内径 1.6 mm 的测压孔; 距离中间剖面 300 mm的截面共布置 51个内径 0.6 mm的静压测压孔. 动态压力将传输到模型内部布置的差压式动态压力传感器, 模型内铺设参考压软管和108 根电缆, 并从模型一端引出, 51根静压管路则从另一端引出. 模型表面测压点处开孔通过预埋测压铜管实现. 压力传感器的参考压由共用的参考压软管输入, 压力信号传输电缆采用AF200—0.25, 预先铺设在模型内部, 单个传感器与引入电缆焊接4个接头. 模型开设可拆卸式盖板, 方便连接传感器和测压管.
图 3 S809翼型模型.
Fig.3 S809 airfoil model
1.4 测试设备
1.4.1 角位移传感器
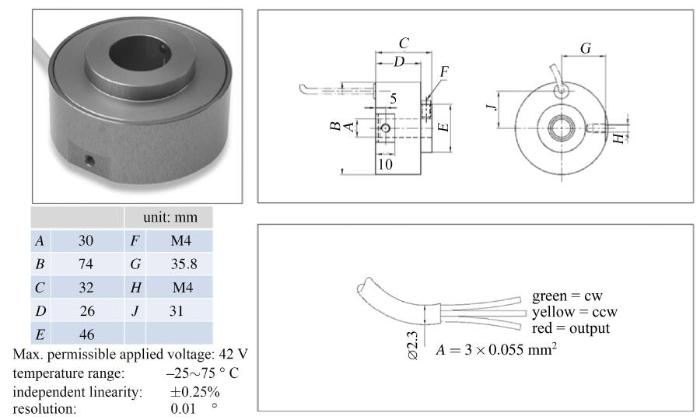
安装于试验模型端的电位计式角位移传感器的输出信号与交流伺服电机端的光电编码器输出信号同时作用于运动控制器, 构成位置反馈双闭环伺服控制系统, 实现振荡运动规律的精确控制; 角位移传感器输出的绝对值模拟信号与动态压力传感器信号一起接入动态数据采集系统, 实现角位移信号与对应动态压力信号的同步采集. 角位移传感器采用CONTELEC GL300 型电位计, 性能指标如图4 所示.
图 4 电位计外形及性能.
Fig.4 The shape and performance of potentiometer
1.4.2动态压力传感器
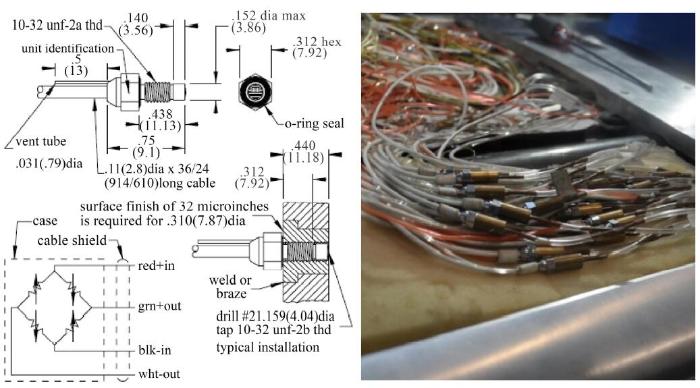
测压元件采用ENDVECO 8510B系列差压式动态压力传感器, 单个传感器连接四根电缆, 并引入参考压及测量端压力两根测压软管. 传感器的尺寸及外形如图5 所示, 其中括号内数字的单位为毫米.
图 5 动态压力传感器 (8510B型)尺寸及外形.
Fig.5 Size and shape of dynamic pressure sensor (8510B type)
1.4.3速压采集系统
参考速压用T4-800型风速管测得, 风速管的静压管和总压管接入压力采集系统进行实时采集. 风速管安装在靠翼型下翼面一侧试验段上游位置, 既保证对翼型周围流场的干扰较小, 又能实时准确测量出来流的速压, 在风洞中安装如图6 所示.
图 6 实时速压测量风速管.
Fig.6 Pitot-static tube for measuring wind speed
1.4.4流态测量系统
试验采用LaVision公司的TR-PIV (time-resolved particle image velocimetry)系统, 采用单CCD 相机的二维PIV测量方案. TR-PIV系统主要由HS5.1高速相机系统、LDY304 Nd:YLF激光器系统、控制器、高性能计算机及采集处理软件组成, 如图7 (a) 所示. 试验用DEHS (癸二酸二辛脂)示踪粒子采用加热型的DF-1500粒子播放器播撒. 相机布置在翼型下方并与传动轴固连随动, 如图7 (b)所示, 可拍摄翼型吸力面上方300 m m × 300 m m
图 7 翼型俯仰振荡试验PIV系统及外触发装置.
Fig.7 PIV system and external triggering device for airfoil pitching oscillation test
本试验所用PIV系统的相机采用外触发方式触发, 外触发信号为TTL电频格式的方波信号, 在上升沿5 V 触发, 触发后PIV系统可按照内部时钟采集. 试验设计的电子外触发装置, 如图7 (c)所示, 将电位计采集信号传给触发装置进行标定, 当翼型振荡到达设定好的采集角后, 由触发装置触发相机进行采集记录. 外触发系统由电位计传感器、电压信号采集卡、实时控制器和数字信号输出卡等组成. 其中, 电位计传感器直接安装于翼型转轴, 减少了中间传动环节, 提高了翼型角度测量精度; 实时控制器具有实时操作系统, 不仅可进行物理逻辑编程, 还可进行时序逻辑开发. 利用电位计传感器信号, 可判断翼型振荡运动方向, 实时解算获得角度值, 分辨率高达0.01º, 从而保证触发信号具有较小的位移偏差; 利用实时控制器, 可实现微秒量级的逻辑运算和输入/输出控制, 从而保证触发信号具有较小的时间偏移.
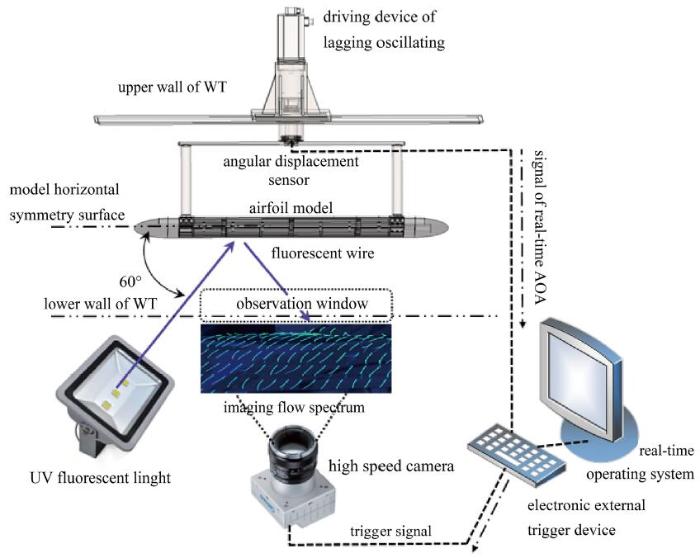
采用夜光鱼线制作技术和外触发荧光摄影技术, 建立了低速风洞荧光丝线流动显示方法, 如图8 所示. 发明的荧光丝线包括纸带、胶带和若干荧光丝线; 荧光丝线采用直径为0.1 mm的特制纤维线, 荧光丝线之间的间隔为25 mm, 荧光丝线的长度为25 mm, 试验时将纸带揭开贴在模型表面即可, 提高了丝线粘贴质量. 采用主波长为395 nm、功率为60 W的紫外线光源以和来流方向成60°的入射角照射, 诱导荧光丝线发光, 然后用相机对处于试验状态中的丝线进行拍摄. 利用荧光视觉反差得到较好的流谱显示效果, 丝线的流动跟随性好, 丝线的运动 (转动、抖动或倒转)可以清晰判别气流方向、分离区位置和空间涡位置转向等. 采用上文所述电子外触发方式触发相机实时地捕捉复杂的动态流动现象.
图 8 翼型横摆振荡荧光丝线流动测量方法.
Fig.8 Fluorescent-wire method for measuring the flow of yaw oscillating airfoil
1.4.5 PXI数采系统
PXI总线数据采集系统由前置放大器、数据采集器、通讯卡、控制计算机和数据处理计算机等部分组成, 并配套编写相应的数据采集和处理程序.
2 试验技术与方法
静态压力测量方面, 静压管连接至PSI DTC Initium电子扫描压力测量系统进行采集, 作为动态压力试验研究的静态参考基准. 当雷诺数(以翼型弦长为参考长度)为 6.2 × 1 0 5 - 10 ~ 20 ° 范围内间隔2°采集翼型静态压力(静态失速迎角8°附近为间隔1°).
动态压力测量方面, 主要开展翼型俯仰振荡和横摆振荡两部分试验, 翼型俯仰振荡迎角变化规律
α = α 0 + α 1 s in 2 <
试验在不同的平衡迎角 α 0 α 1 f V
翼型横摆振荡横摆角变化规律
β = β 0 + β 1 s in 2 <
试验在不同的初始横摆角 β 0 β 1 f V α 0
具体试验方法如下: 由安装在洞顶上的电机提供驱动力, 采用“电子凸轮”技术代替机械凸轮, 实现模型的俯仰振荡和横摆振荡. 驱动电机、减速机及传动轴组件安装在洞体上方的电机支座上, 俯仰振荡时, 模型“顶天立地”安放在风洞正中央, 电机连接减速机输出扭矩, 由俯仰振荡传动轴组件通过法兰盘与翼型连接, 驱动模型做正弦振荡, 传动轴穿过翼型的下端, 并通过一对7010AC型角接触球轴承和下支撑座连接, 保证整个驱动中轴的同心度和定位精度. 该装置同时兼顾了研究横摆振荡动态“掠效应”问题, 采用“模型对称中截面为动态测压剖面, 支杆连接模型两端”的构型, 其设计依据是: (1) 支杆放置两端、测压孔居中可以最大程度地减小支杆和模型端部三维效应对动态压力测量的气动干扰; (2) 模型横摆运动时, 正中的测压截面在旋转方向的线速度分量最小甚至可以忽略, 便于只针对横摆角周期性正弦变化, 即“掠效应”问题直接开展研究. 横摆振荡运动具体实现方法是: 驱动装置的位置和连接方式不变, 模型被水平横跨在风洞中央, 通过横摆振荡传动轴组件连接模型“U”形支杆来驱动翼型做正弦振荡; 横摆振荡在不同的固定迎角( α 0 = - 4 ~ 20 ° , 间隔3°)下开展, 迎角的变化通过更换支杆和模型之间的角度块来实现. 俯仰振荡和横摆振荡模型安装方式如图9 所示. 从模型中引出的动态压力测量电缆和静压管跟随模型一起随体运动, 并且保证翼型上下两端的密封性. PIV试验时, 相机随转轴一起作俯仰振荡, 以保证始终在一个视角观察拍摄翼型周围流场. 为保证翼型模型风洞试验的流动二元性, 俯仰振荡时, 在模型上下端分别连接端板, 端板跟随翼型一起转动; 横摆振荡时模型采用整流翼尖替换等直翼尖以降低端部三维效应. 动态压力信号采集传输方法是, 从模型内部通过一侧端板引出线缆及参考压软管, 软管置于洞外稳流球中以提供参考大气压, 传感器信号线缆通过J30J-37型转接头与8根双绞双屏蔽软电缆8- 2 × 0.15
图 9 装置驱动模型作正弦振荡示意图.
Fig.9 Schematic diagram for the sinusoidal oscillation of model driven by the driving device
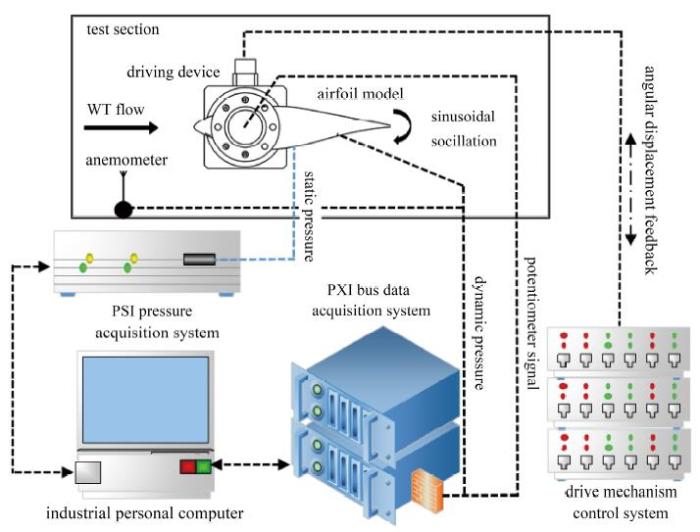
采用PXI总线数据采集系统保证多通道同步采集能力, 同步采集参数主要包括风洞来流总/静压、模型实时角位移、模型压力数据等, 如图10 所示. 将翼型角位移作为一个参数实时采集, 确保与27个压力数据采集同步. 试验时压力采样采用电位计任意位置信号触发, 不同模型振荡频率, 每周期采样数量皆为256个点, 采样周期固定为16个. 对采集后的压力传感器数据进行六阶傅立叶滤波和低通滤波处理, 再平均成1个周期数据, 将1周期数据进行六阶最小二乘多项式拟合, 按等相位角间隔输出固定数量角位移(256个点)和对应的压力数据.
图 10 翼型动态测压试验同步测量采集示意图.
Fig.10 Scheme of synchronous measurement and acquisition for airfoil dynamic pressure test
3 数据处理与分析
3.1 数据处理方法
模型气动系数按照风轴系给出. 风轴系定义为: 原点为翼型模型对称剖面弦线1/4位置, x y z
数据处理按照以下步骤进行:
第一步: 数据采集. 针对27个动态压力传感器, 同步采集各自16个周期原始电压数据, 再按每个传感器标定系数计算到压力差值, 输出初读数和吹风数压力值(存储文件名为: 初读数*.ini, 吹风数*.tst).
第二步: 周期平均. 扣除初读数, 将16周期数据平均成1个周期数据, 形成每个传感器的单周期压力数据(存储文件名: *_PA.txt).
第三步: 系数计算. 按式(3)计算成压力系数(存储文件名: *_CP.txt);此步完成后, 可从“*_CP.txt”文件中将27个传感器相同当地角位移的压力数据取出, 绘制当地角位移的压力分布曲线.
第四步: 压力积分. 按下文数据处理公式进行压力积分, 获取升力系数和俯仰力矩系数(存储文件名: *_CP_rst.txt).
压力系数按如下公式计算
C Pi = P i - P ∞ ρ V 2 / 2 = P i - P ∞ q ∞ = P i - P ∞ P 0 - P ∞
其中, C Pi P i P ∞ P 0 q ∞
以上完成后进行压力积分, 计算法向力系数、轴向力系数.
作用在翼型上的法向力系数 C N C A
C N = ∫ 0 1 C p l d x ̅ - ∫ 0 1 C p u d x ̅
C A = ∫ y ̅ l max y ̅ u max C p b e d y ̅ - ∫ y ̅ l max y ̅ u max C p a f d y ̅
式中, C p u C p l C p b e C p a f x ̅ = x / c x c y ̅ = y / c y c y ̅ u max y ̅ l max c
根据升力系数定义, 可以求出翼型升力系数 C L
C L = C N c os α - C A s in α
翼型绕1/4弦点的俯仰力矩系数 C m
C m = ∫ 0 1 ( C p l - C p u ) ( 0.25 - x ̅ ) d x ̅ + ∫ y ̅ l max y ̅ u max C p b e y ̅ d y ̅ - ∫ y ̅ l max y ̅ u max C p a f y ̅ d y ̅
最终得到的试验结果主要是 C L - α , C m - α C L - β C m - β
数据处理程序具备复算功能, 能根据原始数据复算出各个 α β C p l - x ̅ , C p u - x ̅ , C p be - y ̅ , C p af - y ̅ α β C L C m C L C m
3.2 数据分析
3.2.1数据考核验证
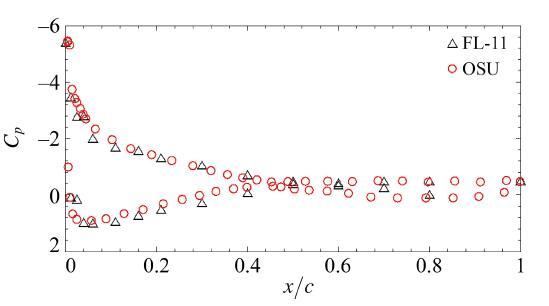
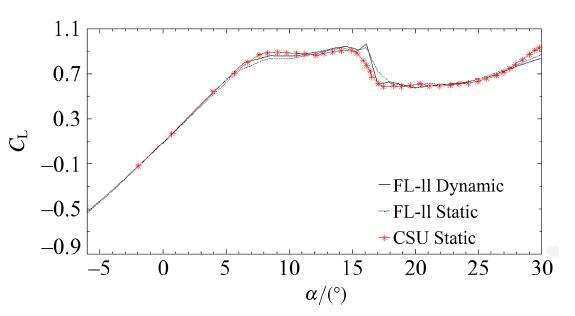
雷诺数为 6.2 × 1 0 5 [11 ] 、CSU (科罗拉多州立大学)[31 ] 的风洞数据分别进行对比验证. 比较动态压力传感器测得的翼型表面压力分布(图 11 )和升力系数曲线(图 12 )可知, FL-11风洞试验结果和这两家机构的结果吻合良好, 且FL-11风洞动态压力孔测量获得的 C L - α
图 11 迎角16.1°下, 翼型表面压力分布与OSU风洞数据对比.
Fig.11 Comparison of surface pressure distribution of airfoil with OSU wind tunnel data at 16.1 °AOA
图 12 动态压力传感器测得翼型C L - α
Fig.12 C L - α
图13 给出了Re = 6.2 × 1 0 5 α = 5 ∘ ± 1 0 ∘ s in < α ̇ > 0 ) - 5 ∘ ~ 6 ∘ α ̇ < 0 ) 时翼型分离涡重建的延迟引起的.
图 13 Re = 6.2 × 1 0 5
Fig.13 Comparison of dynamic and static results with Re = 6.2 × 1 0 5
在满足折算频率和雷诺数相似前提下, 对翼型俯仰振荡α 0 = 8 ∘ , α 1 = 1 0 ∘ , f = 1.38 H z , V = 37.3 m / s 图 14 所示. 由于模型尺度和风洞指标的差别, 不同风洞动态试验结果之间存在一定差异. FL-11 试验的失速迎角在OSU的失速迎角之前, 但在西工大的NF-3风洞试验的失速迎角之后, 在5 ∘ ~ 1 5 ∘ [32 ] 认为动态试验的随机误差和洞壁干扰等因素使得不同风洞得到的动态试验结果很难接近.
Fig.14 Comparison of dynamic test results of different wind tunnels under the similarity of Re k
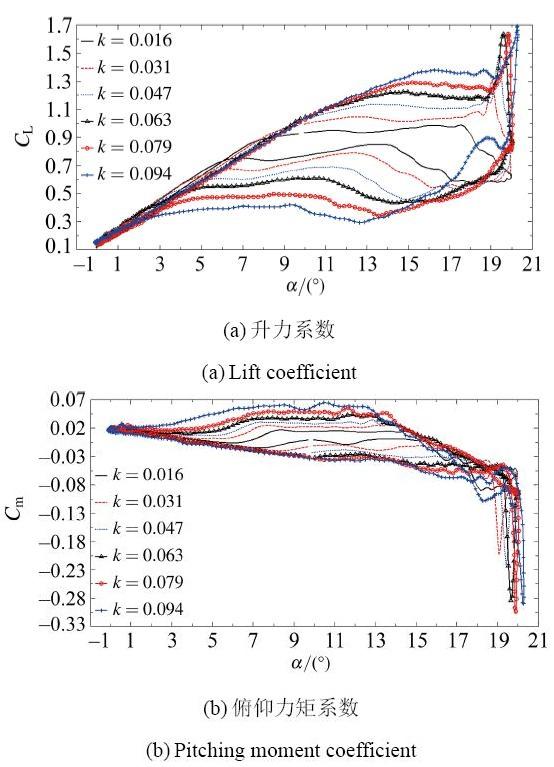
图 15 为α = 1 0 ∘ ± 1 0 ∘ s in 2 < Re = 6.2 × 1 0 5 0.5 ~ 3 H z k 0.016 ~ 0.094 ) , C L , C m k
图 15 不同折算频率下翼型动态气动特性曲线.
Fig.15 Dynamic aerodynamic characteristics of airfoil under different conversion frequencies
3.2.3横摆振荡频率影响
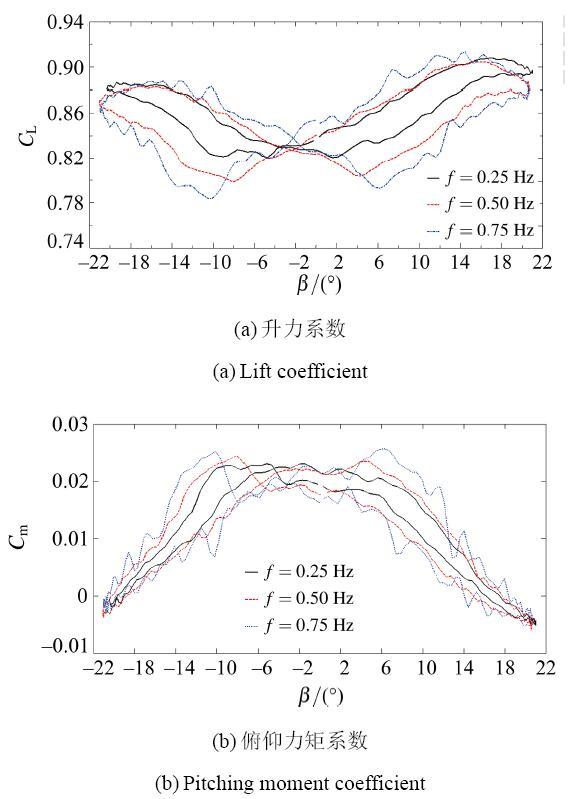
在Re = 6.2 × 1 0 5 图 16 表明, 随着翼型振荡频率的升高, 横摆振荡翼型的升力系数、俯仰力矩系数的迟滞环面积也在增大, C L C m
图 16 α 0 = 1 4 ∘ , β 1 = 2 0 ∘
Fig.16 α 0 = 1 4 ∘ , β 1 = 2 0 ∘
3.2.4流态分析
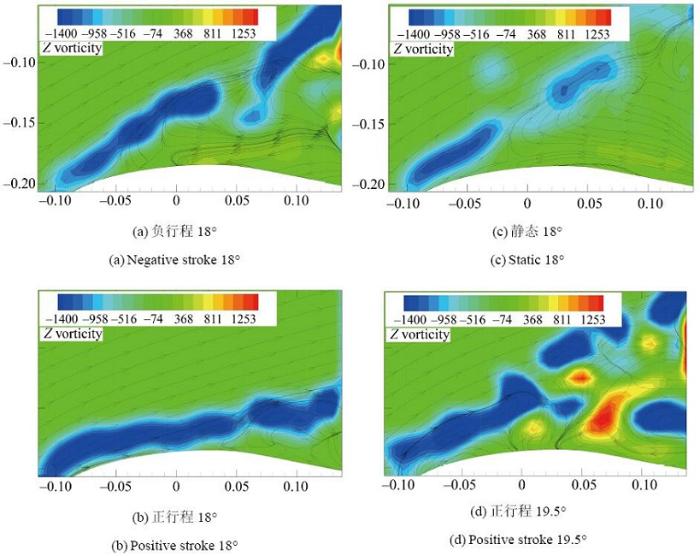
如图17 所示, 速压540 Pa, α 0 = 1 0 ∘ α 1 = 1 5 ∘ f = 0.5 H z [33 ] .
图 17 速压540 Pa, α 0 = 1 0 ∘ , α 1 = 1 5 ∘ , f = 0.5 H z
Fig.17 q ∞ = 540 P a , α 0 = 1 0 ∘ , α 1 = 1 5 ∘ , f = 0.5 H z
横摆振荡模型反装时, 如图18 所示, 在视场范围内, 可以观察出带整流翼尖端部的翼型流动和等直翼尖端部的翼型流动差异明显, 整流翼尖端部使得翼型的有效二维流动沿展向延长; 等直翼尖端部的翼型展向三维流动明显, 等直翼尖后缘附近的流线明显向翼型中部偏折, 这是翼尖涡的卷绕造成的; 同时可以观察出, 图18 (a)和图18 (b)所示的翼型后缘气流倒流和失速分离区域差异明显. 为了研究翼型三维效应中的横摆振荡动态掠效应, 应将翼尖端部三维效应弱化, 以减小其对掠效应研究的干扰. 因此, 上文中的所有横摆振荡影响规律的研究均在整流翼尖端部下开展.
图 18 反装状态模型横摆振荡上翼面流态.
Fig.18 The flow regime on the top surface of yaw oscillation reverse-loading airfoil
4 洞壁干扰分析
目前普遍采用的基于壁压信息法和面元法的洞壁干扰修正方法[34 ] 皆为线性理论的修正方法, 当气动力和力矩系数与迎角呈线性关系时, 修正效果较好, 但是在翼型静态大迎角分离[35 ] 和动态失速分离以后, 非线性特征突出, 以上修正方法很难适用. 直接采用面元法修正动态数据会导致修正后的数据振幅不对称和迟滞环变形, 且翼型的大幅高频振荡, 会引起风洞实时速压和壁压的波动和相位延迟, 这些都给动态数据修正带来极大的困难. 目前, 翼型动态试验洞壁干扰修正方面的数值研究很少, 主要集中在研究上下洞壁二维的气动干扰[36 ,37 ] , 且没有形成可靠的方法和可信的理论. 因此, 研究动态试验洞壁干扰产生机理和影响规律, 建立低速风洞动态试验数据修正方法, 对实现翼型动态气动数据精准测试意义重大.
本文基于计算流体力学和风洞试验数据, 开展非线性动态试验洞壁干扰修正研究, 探索洞壁干扰对翼型动态气动特性的影响规律. 用实测的试验段入口、出口及洞壁附近的非定常压力、温度、粗糙度等物理量建立经验公式, 来模拟翼型动态试验风洞流场的边界条件, 计算出翼型在风洞试验中的压力分布及气动力; 再以无洞壁的自由来流远场边界条件代替风洞洞壁的边界条件, 计算出该翼型在自由绕流环境下的压力分布及气动力; 两者之差即为洞壁干扰的修正量.
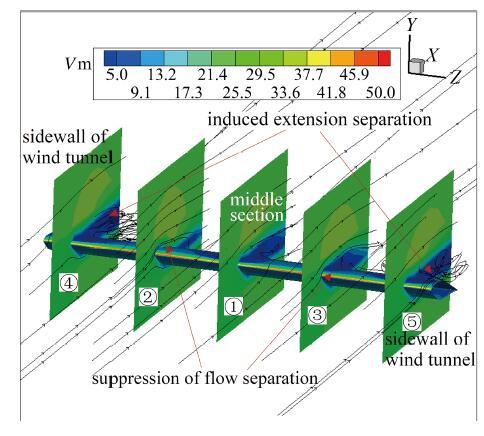
由图19 速度云和流线图可看出, 在负行程15.52°时, 相对模型中间截面1, 因为侧壁的存在, 其两侧的2, 3两个截面的流向分离得到明显抑制, 且侧壁面明显诱导了其附近的4, 5两个截面的展向分离流.
图 19 速压540 Pa, α 0 = 1 0 ∘ , α 1 = 1 0 ∘ , f = 0.5 H z
Fig.19 q ∞ = 540 P a , α 0 = 1 0 ∘ , α 1 = 1 0 ∘ , f = 0.5 H z
图20 为风洞洞壁影响下翼型动态失速涡发展过程, cross flow为展向和法向速度的均方根, 表征翼型表面涡的三维流动. 图 20 (a)显示, 前缘靠近1/4弦长附近区域出现动态失速涡, 模型两端出现翼尖涡; 中间涡和翼尖涡较其他位置涡强度更大, 并且发展很快, 中间部位的涡会从翼型表面分离, 并呈Ω型. 进一步抽象为翼型三维动态失速的流动发展拓扑, 即存在动态失速涡、翼尖涡和剪切层涡三种涡, 它们之间相互作用相互影响的过程非常复杂, 剪切层涡对动态失速涡开始和发展的影响相对于翼尖涡来说要小得多[38 ] . 在图20 (a)中, 中间截面附近的涡强度比靠外侧截面的涡强度大, 并开始迅速地向尾缘移动. 值得注意的是, 中间部位的涡和翼尖涡移动得比其他位置涡要快, 随着翼型迎角的增大, 如图20 (b)所示, 就存在一个被中间部位的涡和叶尖涡一起强行“拉”向下游而加速的过程, 并且在这个过程中, 中间部位的涡会从翼型表面分离, 从而形成所谓的Ω型的涡结构.
图 20 洞壁干扰下翼型三维动态失速涡Q等值面发展图, α 0 = 1 0 ∘ , α 1 = 1 0 ∘ , f = 3 H z
Fig.20 The 3-D airfoil dynamic stall vortex under wall interference, Q isosurface development
图 21 为速压540 Pa, α 0 = 1 0 ∘ α 1 = 1 0 ∘ f = 3 H z
图 21 速压540 Pa, α 0 = 1 0 ∘ , α 1 = 1 0 ∘ , f = 3 H z
Fig.21 q ∞ = 540 P a , α 0 = 1 0 ∘ , α 1 = 1 0 ∘ , f = 3 H z
5 结 论
本文建立了风力机翼型俯仰振荡和横摆振荡动态气动特性风洞试验研究手段, 首次开展了翼型横摆振荡动态试验, 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 探索了翼型动态试验洞壁干扰影响机制. 开展了翼型静态测压、动态测压、PIV和荧光丝线等试验研究, 试验结果准度较高、规律合理、可靠性较好, 研究结果表明:
(1) 翼型横摆振荡试验方法减小了支杆对翼型中部动态压力测量截面的气动干扰, 规避了中间截面动态压力测量受横摆运动引起的弦长方向线速度变化的影响;
(2) 横摆振荡时翼型气动参数随横摆角变化的曲线也存在明显的迟滞效应;
(3) 随着振荡频率的升高, 翼型俯仰振荡和横摆振荡下的气动迟滞效应均增强;
(4) 为了研究翼型横摆振荡动态气动特性, 应将端部三维效应弱化,以减小其对掠效应影响规律的干扰;
(5) PIV 结果显示, 翼型俯仰振荡正行程相比于静态同样迎角下的动态失速涡破裂有所延迟;
(6) 所建立的翼型横摆振荡动态试验技术可为风力机翼型的动态掠效应的研究提供技术支撑;
(7) 洞壁与模模型端部交界处的强三维效应不可忽略, 引起的洞壁干扰对翼型压力分布影响较大.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
黎作武 , 贺德馨 . 风能工程中流体力学问题的研究现状与进展
. 力学进展 , 2013 , 43 (5 ): 472 -525
[本文引用: 1]
(Li Zuowu He Dexin Reviews of fluid dynamics researches in wind energy engineering
.Advances in Mechanics 2013 , 43 (5 ): 472 -525 (in Chinese))
[本文引用: 1]
[2]
胡海岩 , 赵永辉 , 黄锐 . 飞机结构气动弹性分析与控制研究
. 力学学报 , 2016 , 48 (1 ): 1 -27
[本文引用: 1]
(Hu Haiyan Zhao Yonghui Huang Rui Studies on aeroelastic analysis and control of aircraft structures
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (1 ): 1 -27 (in Chinese))
[本文引用: 1]
[3]
王珑 , 王同光 . 风力机设计及其空气动力学问题
. 中国科学 , 2013 , 43 (12 ): 1579 -1588
[本文引用: 2]
(Wang Long Wang Tongguang Wind turbine design and its aerodynamic issues
.Scientia Sinica 2013 , 43 (12 ): 1579 -1588 (in Chinese))
[本文引用: 2]
[4]
刘雄 , 梁湿 . 风力机翼型在复合运动下的动态失速数值分析
. 工程力学 , 2016 , 33 (12 ): 248 -256
[本文引用: 2]
(Liu Xiong Liang Shi Numerical investigation on dynamic stall of wind turbine airfoil undergoing complex motion
.Engineering Mechanics 2016 , 33 (12 ): 248 -256 (in Chinese))
[本文引用: 2]
[5]
Hansen AC Butterfield CP Aerodynamics of horizontal axis wind turbines
.Annu. Rev. Fluid Mech , 1993 , 25 : 115 -149
[本文引用: 1]
[6]
Paker AG Bicknell J Some measurements on dynamic stall
.J Aircraft , 1974 , 11 (2 ): 371 -374
[本文引用: 1]
[7]
Bjorck A Dynamic stall and three-dimensional effects: Final report for the EC DGXII Joule II Project JOU2-CT93-0345?
. Bromma: Flygteksnika örsöks-anstalten , 1995
[本文引用: 1]
[8]
Walker JM Helin HE Strickland JH An experimental investigation of an airfoil undergoing large-amplitude pitching motions
.AIAA Journal , 1985 , 23 (8 ): 1141 -1142
[本文引用: 1]
[9]
Favier D Belledue J Maresca C Influence of coupling incidence and velocity variations on the airfoil dynamic stall//
Presented at the AHS 48th Annual Forum, Washington D C,June 1992
[本文引用: 1]
[10]
Babbitt AL Strike JA Mertes CE et al . Dynamic characterization of a wind turbine blade section
. AIAA Paper 2011-350 , 2011
[本文引用: 1]
[11]
Ramsay R Hoffman M Effects of grit roughness and pitch oscillations on the S809 airfoil. NREL/TP-442-7817 , 1995 .12
[本文引用: 2]
[12]
汤瑞源 , 赵明亮 , 吴永健 等 . 测力法在翼型动态失速试验研究中的应用
. 气动实验与测量控制 , 1995 , 9 (2 ): 16 -20
[本文引用: 2]
(Tang Ruiyuan Zhao Mingliang Wu Yongjian , et at . The application of the force measurement method on experimental study of airfoil dynamic stall
.Aerodynamic Experiment and Measurement & Control 1995 , 9 (2 ): 16 -20 (in Chinese))
[本文引用: 2]
[13]
Ma J Xu J Guo R et al . PIV experimental study of a 2-D wind turbine airfoil
. AIAA 2010-6513 2010
[本文引用: 1]
[14]
周瑞兴 , 上官云信 , 解亚军 等 . 两种厚度翼型动态失速特性的研究
. 西北工业大学学报 , 1999 , 17 (3 ): 475 -479
[本文引用: 1]
(Zhou Ruixing Shangguan Yunxin Xie Yajun et al. Dynamic stall characteristics of two different rotor-blade airfoils
.Journal of Northwestern Poly Technical University 1999 , 17 (3 ): 475 -479 (in Chinese))
[本文引用: 1]
[15]
惠增宏 , 王龙 , 徐倩 . 风力机翼型动态测压试验技术研究
. 实验流体力学 , 2012 , 26 (4 ): 6 -10
[本文引用: 2]
(Hui Zenghong Wang Long Xu Qian, et at. Dynamic pressure measurement techniques on wind turbine airfoil
.Journal of Experiments in Fluid Mechanics 2012 , 26 (4 ): 6 -10 (in Chinese))
[本文引用: 2]
[16]
林永峰 , 黄建萍 , 黄水林 等 . 直升机旋翼翼型动态失速特性试验研究
. 航空科学技术 , 2012 , 4 : 25 -28
[本文引用: 1]
(Lin Yongfeng Huang Jianping Huang Shuilin et al .Experimental investigation of rotor airfoil dynamic stall characteristics
.Aeronautical Science & Technology 2012 , 4 : 25 -28 (in Chinese))
[本文引用: 1]
[17]
王清 , 招启军 , 赵国庆 . 旋翼翼型动态失速流场特性PIV试验研究及L-B模型修正
. 力学学报 , 2014 , 46 (4 ): 631 -634
[本文引用: 1]
(Wang Qing Zhao Qijun Zhao Guoqing PIV experiments on flowfield characteristics of rotor airfoil dynamic stall and modifications of L-B model
.Chinese Journal of Theoretical and Applied Mechanics 2014 , 46 (4 ): 631 -634 (in Chinese))
[本文引用: 1]
[18]
史志伟 , 耿存杰 . 旋翼翼型俯仰沉浮运动非定常气动特性实验研究
. 实验流体力学 , 2007 , 21 (3 ): 19 -23
[本文引用: 1]
(Shi Zhiwei Geng Cunjie Experimental investigation on unsteady aerodynamics of rotor-blade airfoil
.Journal of Experiments in Fluid Mechanics 2007 , 21 (3 ): 19 -23 (in Chinese))
[本文引用: 1]
[19]
王清 , 招启军 , 赵国庆 . 变来流速度下旋翼翼型非定常气动特性分析
. 航空动力学报 , 2017 , 32 (2 ): 364 -372
[本文引用: 1]
(Wang Qing Zhao Qijun Zhao Guoqing Unsteady aerodynamic characteristic analysis of rotor airfoil under variational free stream velocity condition
.Journal of Aerospace Power 2017 , 32 (2 ): 364 -372 (in Chinese))
[本文引用: 1]
[20]
史志伟 , 明晓 , 王同光 . 非定常自由来流对二维翼型气动特性的影响研究
. 空气动力学报 , 2008 , 26 (4 ): 493 -497
[本文引用: 1]
(Shi Zhiwei Ming Xiao Wang Tongguang The effects of unsteady free stream on the static and pitching airfoils
.Acta Aerodynamica Sinica 2008 , 26 (4 ): 493 -497 (in Chinese))
[本文引用: 1]
[21]
Leishman JG Modeling sweep of leading edge thrust phenomena
,Journal of Aircraft , 1980 , 17 (12 ): 890 -897 .
[本文引用: 1]
[22]
LEISS . Unsteady sweep-A key to simulation of three dimensional rotor blade airloads//11th European Rotorcraft Forum
, London , 1985
[本文引用: 1]
[23]
刘峥 . 动态失速对直升机空中共振的影响分析. [硕士论文]
. 南京: 南京航空航天大学 , 2013
[本文引用: 1]
(Liu Zheng Investigation of the influence of dynamic stall on helicopter air resonance stability. [Master Thesis]
. Nanjing: Nanjing University of Aeronautics and Astronautics , 2013 (in Chinese))
[本文引用: 1]
[24]
宋辰瑶 , 徐国华 . 旋翼翼型非定常动态失速响应的计算
. 空气动力学学报 , 2007 , 25 (4 ): 461 -467
[本文引用: 1]
(Song Chenyao Xu Guohua Computations of unsteady dynamic stall responses on rotor airfoils
.Acta Aerodynamica Sinica 2007 , 25 (4 ): 461 -467 (in Chinese))
[本文引用: 1]
[25]
崔伟伟 , 项效镕 , 杜建一 等 . 掠效应对高负荷跨音转子性能的影响
. 工程热物理学报 , 2012 , 33 (5 ): 753 -756
[本文引用: 1]
(Cui Weiwei Xiang Xiaorong Du Jianyi et al .Effects of sweep on the performance of highly loaded transonic rotors
.Journal of Engineering Thermophysics 2012 , 33 (5 ): 753 -756 (in Chinese))
[本文引用: 1]
[26]
Yang J Ganesh B Komerath N Radial flow measurements downstream of forced dynamic separation on a rotor blade//36th AIAA Fluid Dynamics Conference and Exhibit,
California , 2006
[本文引用: 1]
[27]
Henkner J Ranke H Unsteady boundary layer separation on swept and unswept wings in sinusoidal dynamic stall motion//
New Results in Numerical and Experimental Fluid Mechanics, Vieweg+ Teubner Verlag , 1997
[本文引用: 1]
[28]
Salari K Roache P The influence of sweep on dynamic stall produced by a rapidly pitching wing//
Aerospace Sciences Meeting , 2013
[本文引用: 1]
[29]
Lorber PF Dynamic stall of sinusoidally oscillating three-dimen-sional swept and unswept wings in compressible flow//Annual Forum Proceedings-American Helicopter Society,
Washington , 1992
[本文引用: 1]
[30]
陆夕云 , 庄礼贤 , 尹协远 等 . 大迎角水平振动翼型绕流的数值模拟
. 航空学报 , 1993 , 14 (11 ): 632 -635
[本文引用: 1]
(Lu Xiyun Zhuang Lixian Yin Xieyuan et al .Numerical simulation of flows past a longitudinally oscillating airfoil at high incidences
.Acta Aeronautica et Astronautica Sinica 1993 , 14 (11 ): 632 -635 (in Chinese))
[本文引用: 1]
[31]
Butterfield CP Musial WP Simms DA Combined experiment phase I final report.
NREL/TP-257-4655, Golden,Colorado: NREL , 1992
[本文引用: 1]
[32]
夏玉顺 , 郗忠祥 , 周瑞兴 等 . NACA0012翼型动态失速特性和测压方法的研究
. 航空学报 , 1996 , 17 (7 ): 26 -31
[本文引用: 1]
(Xia Yushun Xi Zhongxiang Zhou Ruixing et al .Dynamic stall characters of NACA0012 airfoil and investigations of dynamic pressure measure methods
.Acta Aeronautica et Astronautica Sinica 1996 , 17 (7 ): 26 -31 (in Chinese))
[本文引用: 1]
[33]
刘强 , 刘周 , 白鹏 等 . 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
. 力学学报 , 2016 , 48 (2 ): 269 -277
[本文引用: 1]
(Liu Qiang Liu Zhou Bai Peng et al .Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at low Reynolds number
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (2 ): 269 -277 (in Chinese))
[本文引用: 1]
[34]
张卫国 , 武杰 , 兰波 等 . 旋翼翼型低速风洞静、动态试验技术研究//中国力学大会-2015论文摘要集,
上海 , 2015
[本文引用: 1]
(Zhang Weiguo Wu Jie Lan Bo et al .Static and dynamic test technology for rotor airfoil low speed wind tunnel//Summary of the 2015 China mechanics Conference,
Shanghai , 2015 (in Chinese))
[本文引用: 1]
[35]
白井艳 , 张磊 , 李星星 等 . 风洞洞壁对风力机翼型气动特性测量的影响分析
. 中国科学: 物理学力学天文学 , 2015 , 46 (12 ): 124707
[本文引用: 1]
[36]
Cheng J Wang XM Lowenberg M et al .Wind tunnel wall interference effects on an oscillating aerofoil in the stall regime
. AIAA 2015-2717 , 2015
[本文引用: 1]
[37]
Duraisamy K McCroskey WJ, Baeder JD . Analysis of wind tunnel wall interference effects on subsonic unsteady airfoil flows
.Journal of Aircraft , 2007 , 44 (5 ): 1683 -1690
[本文引用: 1]
[38]
吕超 , 王同光 . 三维动态失速模型研究
. 应用数学和力学 , 2011 , 32 (4 ): 375 -382
[本文引用: 1]
风能工程中流体力学问题的研究现状与进展
1
2013
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
风能工程中流体力学问题的研究现状与进展
1
2013
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
飞机结构气动弹性分析与控制研究
1
2016
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
飞机结构气动弹性分析与控制研究
1
2016
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
风力机设计及其空气动力学问题
2
2013
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
风力机设计及其空气动力学问题
2
2013
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
风力机翼型在复合运动下的动态失速数值分析
2
2016
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
风力机翼型在复合运动下的动态失速数值分析
2
2016
... 风电行业近年来主力机型从兆瓦发展到多兆瓦级, 超大型化叶片的重量随着叶轮直径增大而成立方关系地急剧上升[1 ] . 大型风力机的实际运动过程很复杂, 叶片或翼型常常工作在动态失速状态下, 动态失速是一个严重的非线性、非定常气动现象[2 ] . 目前还缺乏对非定常失速气动特性的深刻理解, 无法全面准确描述动态失速现象和规律[3 ] . 动态振荡过程往往伴随着俯仰(迎角α 周期性变化)和横摆(后掠角β 周期性变化)同时进行[4 ] , 如图1 所示, 俯仰振荡会造成风力机实际极限载荷高于设计和计算值, 而横摆运动多数时候可能会减小极限载荷. 以前对许多动态问题不清楚的阶段, 工程上不惜以增加叶片结构重量为代价而采用偏安全的设计, 所以通常忽略横摆振荡的影响, 国内外关于翼型动态特性的研究主要集中在俯仰振荡方面. 为了提高叶片性能、降低叶片重量, 气动载荷评估应该更加精确, 以减少设计裕度. ...
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
Aerodynamics of horizontal axis wind turbines
1
1993
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
Some measurements on dynamic stall
1
1974
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
Dynamic stall and three-dimensional effects: Final report for the EC DGXII Joule II Project JOU2-CT93-0345?
1
1995
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
An experimental investigation of an airfoil undergoing large-amplitude pitching motions
1
1985
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
Influence of coupling incidence and velocity variations on the airfoil dynamic stall//
1
1992
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
Dynamic characterization of a wind turbine blade section
1
2011
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
2
1995
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
... 雷诺数为 6.2 × 1 0 5 [11 ] 、CSU (科罗拉多州立大学)[31 ] 的风洞数据分别进行对比验证. 比较动态压力传感器测得的翼型表面压力分布(图 11 )和升力系数曲线(图 12 )可知, FL-11风洞试验结果和这两家机构的结果吻合良好, 且FL-11风洞动态压力孔测量获得的 C L - α
测力法在翼型动态失速试验研究中的应用
2
1995
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
... [12 ]、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
测力法在翼型动态失速试验研究中的应用
2
1995
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
... [12 ]、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
PIV experimental study of a 2-D wind turbine airfoil
1
2010
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
两种厚度翼型动态失速特性的研究
1
1999
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
两种厚度翼型动态失速特性的研究
1
1999
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
风力机翼型动态测压试验技术研究
2
2012
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
... [15 ]和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
风力机翼型动态测压试验技术研究
2
2012
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
... [15 ]和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
直升机旋翼翼型动态失速特性试验研究
1
2012
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
直升机旋翼翼型动态失速特性试验研究
1
2012
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
旋翼翼型动态失速流场特性PIV试验研究及L-B模型修正
1
2014
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
旋翼翼型动态失速流场特性PIV试验研究及L-B模型修正
1
2014
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
旋翼翼型俯仰沉浮运动非定常气动特性实验研究
1
2007
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
旋翼翼型俯仰沉浮运动非定常气动特性实验研究
1
2007
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
变来流速度下旋翼翼型非定常气动特性分析
1
2017
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
变来流速度下旋翼翼型非定常气动特性分析
1
2017
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
非定常自由来流对二维翼型气动特性的影响研究
1
2008
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
非定常自由来流对二维翼型气动特性的影响研究
1
2008
... 翼型动态试验最早是从直升机旋翼开始的, 美国NASA、德国荷兰DNW、法国ONERA和俄罗斯TsAGI等机构在风洞中纷纷建立了旋翼翼型俯仰振荡动态试验装置和技术. 后来, 各国研究机构针对风力机也开展了类似的研究试验.在国外, 水平轴风力机叶片俯仰振荡动态特性试验研究始于20世纪80年代末期, 在此之前, 对水平轴风力机的性能和载荷分析中并不包含动态失速和非稳态空气动力影响, Hansen等[5 ] 通过测量一个直径为10 m的水平轴风力机的压力分布, 对动态失速的存在进行了量化研究. 针对二维翼型动态失速的研究相对要早一些, 文献[6 ,7 ,8 ,9 ,10 ] 采用多种手段对俯仰振荡翼型动态失速特性进行大量的风洞试验研究: 当迎角大于静态失速迎角时, 动态失速涡的存在对翼型上表面速度和压力分布存在重大影响; 随着折算频率、平衡迎角及振荡幅值的增大, 翼型动态失速效应增强. 针对风力机专用翼型动态气动特性开展相对较多研究的是俄亥俄州立大学(OSU) [11 ] , 20世纪90 年代, 其在AARL 3×5 亚音速风洞中开展了粗糙度和俯仰振荡运动参数影响研究, 但是受到测量设备和手段的限制, 得到的动态数据并不完整. 为此, 国际能源署(IEA) 呼吁世界各地研究机构开展翼型动态试验研究, 以获取“更精准、更全面”的气动数据[3 ] , 这将对大直径风力机的设计以及建造兆瓦级风力发电机组具有重要意义. 国内方面, 南京航空航天大学[12 ,13 ] 、西北工业大学[14 ,15 ] 、 中航工业直升机所[16 ] 建立和发展了翼型的动态试验设备和技术, 拓展了翼型动态试验测力[12 ] 、测压[15 ] 和粒子图像测速[17 ] 等多种手段,由俯仰振荡单自由度向俯仰沉浮两自由度振荡[18 ] 发展, 由定常来流向非定常来流[19 ,20 ] 发展. 然而, 由于我国在翼型动态风洞试验技术研究上起步晚, 技术水平明显低于欧美等国家, 差距集中表现为: 测试试验技术不能满足数据高精准度要求, 动态结果受到装置运动、洞壁干扰、同步采集等多个环节影响, 国内对以上这些方面开展的研究较少. ...
Modeling sweep of leading edge thrust phenomena
1
1980
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
Unsteady sweep-A key to simulation of three dimensional rotor blade airloads//11th European Rotorcraft Forum
1
1985
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
动态失速对直升机空中共振的影响分析. [硕士论文]
1
2013
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
动态失速对直升机空中共振的影响分析. [硕士论文]
1
2013
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
旋翼翼型非定常动态失速响应的计算
1
2007
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
旋翼翼型非定常动态失速响应的计算
1
2007
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
掠效应对高负荷跨音转子性能的影响
1
2012
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
掠效应对高负荷跨音转子性能的影响
1
2012
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
Radial flow measurements downstream of forced dynamic separation on a rotor blade//36th AIAA Fluid Dynamics Conference and Exhibit,
1
2006
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
Unsteady boundary layer separation on swept and unswept wings in sinusoidal dynamic stall motion//
1
1997
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
The influence of sweep on dynamic stall produced by a rapidly pitching wing//
1
2013
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
Dynamic stall of sinusoidally oscillating three-dimen-sional swept and unswept wings in compressible flow//Annual Forum Proceedings-American Helicopter Society,
1
1992
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
大迎角水平振动翼型绕流的数值模拟
1
1993
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
大迎角水平振动翼型绕流的数值模拟
1
1993
... 目前, 有少量关于旋翼翼型带固定后掠角下的俯仰振荡[21 ,22 ] 或翼型径向流动 [23 ,24 ,25 ,26 ] 的研究, 可认为是关于后掠角不变的静态“掠效应(sweep effect)”的研究: 后掠翼型的三维非定常边界层分离相比二维流动情况下的分离呈现出明显不同的特点[27 ,28 ,29 ] . 然而, 风力机摆振过程是伴随着后掠角不断变化和水平振动[30 ] 的动态“掠效应”, 摆振和其他非定常运动耦合会导致失速更加复杂[4 ] . 本文首次开展的翼型横摆振荡试验就是要模拟风力机叶片摆振过程中后掠角周期性变化的物理现象, 即三维的动态“掠效应”, 迄今为止, 公开文献中尚无直接开展翼型横摆振荡的技术和研究, 为了获得风力机更加全面、准确的载荷值, 获得多目标优化的设计方案, 需要研究横摆振荡对翼型动态载荷特性的影响规律. 风洞试验是认识翼型动态失速特性和流动机理的主要手段, 鉴于此, 本文建立了翼型俯仰振荡和横摆振荡动态风洞试验手段, 开展了风力机翼型动态失速特性试验研究. 基于设计的电子外触发装置拓展了流态同步测量手段, 并实现了风洞来流、模型角位移和动态压力数据的实时同步采集, 可为风力机翼型动态“掠效应”的研究提供重要技术支撑, 将会对提升我国大型风力机自主设计研发能力发挥至关重要的支撑作用. ...
Combined experiment phase I final report.
1
1992
... 雷诺数为 6.2 × 1 0 5 [11 ] 、CSU (科罗拉多州立大学)[31 ] 的风洞数据分别进行对比验证. 比较动态压力传感器测得的翼型表面压力分布(图 11 )和升力系数曲线(图 12 )可知, FL-11风洞试验结果和这两家机构的结果吻合良好, 且FL-11风洞动态压力孔测量获得的 C L - α
NACA0012翼型动态失速特性和测压方法的研究
1
1996
... 在满足折算频率和雷诺数相似前提下, 对翼型俯仰振荡α 0 = 8 ∘ , α 1 = 1 0 ∘ , f = 1.38 H z , V = 37.3 m / s 图 14 所示. 由于模型尺度和风洞指标的差别, 不同风洞动态试验结果之间存在一定差异. FL-11 试验的失速迎角在OSU的失速迎角之前, 但在西工大的NF-3风洞试验的失速迎角之后, 在5 ∘ ~ 1 5 ∘ [32 ] 认为动态试验的随机误差和洞壁干扰等因素使得不同风洞得到的动态试验结果很难接近. ...
NACA0012翼型动态失速特性和测压方法的研究
1
1996
... 在满足折算频率和雷诺数相似前提下, 对翼型俯仰振荡α 0 = 8 ∘ , α 1 = 1 0 ∘ , f = 1.38 H z , V = 37.3 m / s 图 14 所示. 由于模型尺度和风洞指标的差别, 不同风洞动态试验结果之间存在一定差异. FL-11 试验的失速迎角在OSU的失速迎角之前, 但在西工大的NF-3风洞试验的失速迎角之后, 在5 ∘ ~ 1 5 ∘ [32 ] 认为动态试验的随机误差和洞壁干扰等因素使得不同风洞得到的动态试验结果很难接近. ...
低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
1
2016
... 如图17 所示, 速压540 Pa, α 0 = 1 0 ∘ α 1 = 1 5 ∘ f = 0.5 H z [33 ] . ...
低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
1
2016
... 如图17 所示, 速压540 Pa, α 0 = 1 0 ∘ α 1 = 1 5 ∘ f = 0.5 H z [33 ] . ...
旋翼翼型低速风洞静、动态试验技术研究//中国力学大会-2015论文摘要集,
1
2015
... 目前普遍采用的基于壁压信息法和面元法的洞壁干扰修正方法[34 ] 皆为线性理论的修正方法, 当气动力和力矩系数与迎角呈线性关系时, 修正效果较好, 但是在翼型静态大迎角分离[35 ] 和动态失速分离以后, 非线性特征突出, 以上修正方法很难适用. 直接采用面元法修正动态数据会导致修正后的数据振幅不对称和迟滞环变形, 且翼型的大幅高频振荡, 会引起风洞实时速压和壁压的波动和相位延迟, 这些都给动态数据修正带来极大的困难. 目前, 翼型动态试验洞壁干扰修正方面的数值研究很少, 主要集中在研究上下洞壁二维的气动干扰[36 ,37 ] , 且没有形成可靠的方法和可信的理论. 因此, 研究动态试验洞壁干扰产生机理和影响规律, 建立低速风洞动态试验数据修正方法, 对实现翼型动态气动数据精准测试意义重大. ...
旋翼翼型低速风洞静、动态试验技术研究//中国力学大会-2015论文摘要集,
1
2015
... 目前普遍采用的基于壁压信息法和面元法的洞壁干扰修正方法[34 ] 皆为线性理论的修正方法, 当气动力和力矩系数与迎角呈线性关系时, 修正效果较好, 但是在翼型静态大迎角分离[35 ] 和动态失速分离以后, 非线性特征突出, 以上修正方法很难适用. 直接采用面元法修正动态数据会导致修正后的数据振幅不对称和迟滞环变形, 且翼型的大幅高频振荡, 会引起风洞实时速压和壁压的波动和相位延迟, 这些都给动态数据修正带来极大的困难. 目前, 翼型动态试验洞壁干扰修正方面的数值研究很少, 主要集中在研究上下洞壁二维的气动干扰[36 ,37 ] , 且没有形成可靠的方法和可信的理论. 因此, 研究动态试验洞壁干扰产生机理和影响规律, 建立低速风洞动态试验数据修正方法, 对实现翼型动态气动数据精准测试意义重大. ...
风洞洞壁对风力机翼型气动特性测量的影响分析
1
2015
... 目前普遍采用的基于壁压信息法和面元法的洞壁干扰修正方法[34 ] 皆为线性理论的修正方法, 当气动力和力矩系数与迎角呈线性关系时, 修正效果较好, 但是在翼型静态大迎角分离[35 ] 和动态失速分离以后, 非线性特征突出, 以上修正方法很难适用. 直接采用面元法修正动态数据会导致修正后的数据振幅不对称和迟滞环变形, 且翼型的大幅高频振荡, 会引起风洞实时速压和壁压的波动和相位延迟, 这些都给动态数据修正带来极大的困难. 目前, 翼型动态试验洞壁干扰修正方面的数值研究很少, 主要集中在研究上下洞壁二维的气动干扰[36 ,37 ] , 且没有形成可靠的方法和可信的理论. 因此, 研究动态试验洞壁干扰产生机理和影响规律, 建立低速风洞动态试验数据修正方法, 对实现翼型动态气动数据精准测试意义重大. ...
Wind tunnel wall interference effects on an oscillating aerofoil in the stall regime
1
2015
... 目前普遍采用的基于壁压信息法和面元法的洞壁干扰修正方法[34 ] 皆为线性理论的修正方法, 当气动力和力矩系数与迎角呈线性关系时, 修正效果较好, 但是在翼型静态大迎角分离[35 ] 和动态失速分离以后, 非线性特征突出, 以上修正方法很难适用. 直接采用面元法修正动态数据会导致修正后的数据振幅不对称和迟滞环变形, 且翼型的大幅高频振荡, 会引起风洞实时速压和壁压的波动和相位延迟, 这些都给动态数据修正带来极大的困难. 目前, 翼型动态试验洞壁干扰修正方面的数值研究很少, 主要集中在研究上下洞壁二维的气动干扰[36 ,37 ] , 且没有形成可靠的方法和可信的理论. 因此, 研究动态试验洞壁干扰产生机理和影响规律, 建立低速风洞动态试验数据修正方法, 对实现翼型动态气动数据精准测试意义重大. ...
Analysis of wind tunnel wall interference effects on subsonic unsteady airfoil flows
1
2007
... 目前普遍采用的基于壁压信息法和面元法的洞壁干扰修正方法[34 ] 皆为线性理论的修正方法, 当气动力和力矩系数与迎角呈线性关系时, 修正效果较好, 但是在翼型静态大迎角分离[35 ] 和动态失速分离以后, 非线性特征突出, 以上修正方法很难适用. 直接采用面元法修正动态数据会导致修正后的数据振幅不对称和迟滞环变形, 且翼型的大幅高频振荡, 会引起风洞实时速压和壁压的波动和相位延迟, 这些都给动态数据修正带来极大的困难. 目前, 翼型动态试验洞壁干扰修正方面的数值研究很少, 主要集中在研究上下洞壁二维的气动干扰[36 ,37 ] , 且没有形成可靠的方法和可信的理论. 因此, 研究动态试验洞壁干扰产生机理和影响规律, 建立低速风洞动态试验数据修正方法, 对实现翼型动态气动数据精准测试意义重大. ...
三维动态失速模型研究
1
2011
... 图20 为风洞洞壁影响下翼型动态失速涡发展过程, cross flow为展向和法向速度的均方根, 表征翼型表面涡的三维流动. 图 20 (a)显示, 前缘靠近1/4弦长附近区域出现动态失速涡, 模型两端出现翼尖涡; 中间涡和翼尖涡较其他位置涡强度更大, 并且发展很快, 中间部位的涡会从翼型表面分离, 并呈Ω型. 进一步抽象为翼型三维动态失速的流动发展拓扑, 即存在动态失速涡、翼尖涡和剪切层涡三种涡, 它们之间相互作用相互影响的过程非常复杂, 剪切层涡对动态失速涡开始和发展的影响相对于翼尖涡来说要小得多[38 ] . 在图20 (a)中, 中间截面附近的涡强度比靠外侧截面的涡强度大, 并开始迅速地向尾缘移动. 值得注意的是, 中间部位的涡和翼尖涡移动得比其他位置涡要快, 随着翼型迎角的增大, 如图20 (b)所示, 就存在一个被中间部位的涡和叶尖涡一起强行“拉”向下游而加速的过程, 并且在这个过程中, 中间部位的涡会从翼型表面分离, 从而形成所谓的Ω型的涡结构. ...