单窄条控制件对横向振荡柱体尾流 2P模式 旋涡脱落的改变
中国计量大学流体检测与仿真研究所,杭州 310018
THE SINGLE STRIP-INDUCED CHANGE OF 2P-MODE VORTEX SHEDDING IN THE WAKE OF A TRANSVERSELY OSCILLATING CYLINDER
中图分类号: O35
文献标识码: A
通讯作者:
收稿日期: 2018-01-1
接受日期: 2018-01-1
网络出版日期: 2018-07-18
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
展开
摘要
横向强迫振荡柱体尾流控制是柱体涡激振动控制的基础,在海洋、土木等工程中具有重要意义. 横向强迫振荡柱体尾流中存在一种锁频旋涡脱落模式,即在一个振荡周期内柱体上、下侧各脱落旋转方向相反的一对涡,称为2P模式. 本文将相对宽度b/D=0.32的窄条控制件置于横向强迫振荡柱体下游,对振幅比A/D=1.25, 无量纲振频f_e D/V_∞=0.22,雷诺数Re=1 200的2P模式旋涡脱落进行干扰,并通过改变控制件位置,研究旋涡的变化规律. 采用二维大涡模拟和实验验证方法进行研究,在控制件位置范围0.8≤X/D≤3.2, 0.4≤Y/D≤3.2内,得到了2P, 2S, P+S和另外6种新发现的旋涡脱落模式,并对各模式旋涡的形成过程作了详细描述. 在控制件位置平面上给出了各旋涡模式的存在区域,画出了旋涡脱落强度的等值线图,并发现在一个相当大的区域内,旋涡脱落强 度可减小一半以上,尾流变窄. 发现柱体大幅振荡引起的横向剪切流在旋涡生成中起关键作用. 探讨了控制件对横向剪切流的影响,分析了控制件在每种旋涡模式形成中的作用机制.
关键词:
Abstract
The control of vortex shedding from a forced oscillating cylinder is the basis of control of vortex-induced cylinder vibration, and of significance in civil and ocean engineering. A lock-on mode of vortex shedding called 2P mode exists in the wake of an oscillating cylinder, i.e., in a period of oscillation, a pair of vortices shed from each side. A strip element of width b/D=0.32 is used and set in the wake to influence the 2P mode vortex shedding at oscillating amplitude A/D=1.25, frequency f_e D/V_∞=0.22, and Reynolds number Re=V_∞ D/ν=1 200. Using the method of 2D large eddy simulation with experimental confirmation, we find that with the change of strip position in the area 0.8≤X/D≤3.2, 0.4≤Y/≤3.2, vortex shedding is changed between 2P, 2S, P+S and other 6 new modes. The detailed generation process of every mode of vortex shedding is described in the paper. The zones of the modes and the contours of vortex strength are figured out on the plane of strip position. It is shown that vortex strength can be reduced by 50% or more and the wake is narrowed if the strip is set at places in a considerably large region. The transverse shear flow induced by large amplitude cylinder oscillation plays a key role in the generation of vortex shedding. The influence of the strip on the transverse shear flow is discussed and the mechanism of the strip function to the formation of every mode of vortex shedding is analyzed.
Keywords:
一定速度的均匀定常流绕过固定柱体时,会在柱体两侧交替产生旋涡脱落,并在柱体下游形成规则排列的卡门涡街. 旋涡脱落可激发柱体结构的振动[1]、增加流体阻力[2],并产生噪声[3,4]. 涡激振动问题在很多工程领域中出现,造成很多破坏性结果,对它的控制具有广泛的实际意义和重要的理论意义.
工程中的柱体结构涡激振动(vortex-induced vibration)除了与流动条件如雷诺数等因素有关外,还与几何条件如柱体长径比,端部约束条件(悬臂、简支、弹性支撑等),以及材质条件如刚度、阻尼比,及流固质量比[5,6,7,8,9,10]等条件有关,涉及的参数众多,非常复杂,对其进行系统研究极其困难,因此需要进行简化处理.
常见的柱体结构涡激振动,很多是单模态激发,即柱体以同一个振频振动,且振幅沿长度方向变化较缓慢. 因此在理论上可以把某个截面的振动单独提取出来研究[11], 将所提取的截面振动的振幅、振频,以及该截面上游的来流速度,分别作为二维刚性柱体的振幅、振频及来流速度,所形成的振动柱体流动,就成为强迫振荡柱体绕流问题.
强迫振荡柱体绕流与涡激自由振动柱体绕流之间有一定差别. 对于涡激自由振动,能量主要由流体输入给固体,而对于强迫振荡,根据振幅的不同,能量可能由固体输入给流体,也可能由流体输入给固体[11,12,13,14]. 在相同来流条件下,如果涡激振动的柱体运动(位移随时间的变化)与强迫振荡柱体的运动完全相同,那么两者的尾流流动也是相同的[11]. 这样,用强迫振荡柱体绕流模拟涡激振动问题,就将流固耦合问题转为纯粹的流体力学问题, 使之得到简化.
影响强迫振荡柱体绕流的参数有雷诺数Re=V_∞ D/v、无量纲振幅A/D和无量纲振频f_e D/V_∞,其中D为柱体直径,f_e为柱体振荡频率. 工程中常用折算速度(reduced velocity)V_∞/f_e D来表示振频的影响,但当柱体振频很小,即f_e接近0时,折算速度为无穷大,应用不便,因此这里采用无量纲振频f_e D/V_∞代替.
强迫振荡柱体绕流可以分为: (1)横向振荡柱体绕流和(2)流向振荡柱体绕流. 根据 Ongoren & Rockwell[15,16]的研究,一般斜向振荡柱体尾流的各种旋涡脱落模式都在横向和流向振荡柱体尾流中出现,因此研究好 上述两种振荡柱体绕流最为重要. 在一般的柱体涡激振动中,横向振动起主要作用,其振幅远大于流向振幅[17]. Williamson和Roshko[18]对横向振荡柱体尾流基本流动做了系统研究,发现了2S(柱体两侧交替脱落单涡),2P(柱体两侧交替脱落对 涡(双涡),P+S(单涡和对涡交替脱落)等几种不同的锁频旋涡脱落模式,并在以无量纲振动波长(折减速度)为横坐标,以相对振幅为纵 坐标的图中划分出了各旋涡模式所存在的区域. Khalak和Williamson[12],及Williamson和 Govardhan[1]发现,弹簧支撑的刚性柱体涡激振动尾流中也存在2P模式旋涡脱落,而且其在振频--振幅平面中的存在区域很大. 大长径比弹性柱体,如海底输油管线和深海钻井平台导管,长径比达102甚至103量级,在海流作用下其中部核心区涡激振动 的振幅可达1倍至数倍直径[19,20],出现2P模式旋涡脱落的机会很大.
人们对静止柱体尾流做了大量控制研究,提出了很多抑制旋涡脱落的方法[21,22,23,24,25,26]. 国内外许多研究者直接将抑制静止钝体尾流的方法用于抑制钝体涡激振动[27,28,29,30], 取得较多成果. 但是,由于涡激振动的复杂性,这些研究都局限于特定参数条件,缺少普遍性. 对于强迫振荡柱体尾流的控制,目前研究很少.
在以往的研究中发现,在静止柱体的近尾流中放置一个静止的窄条控制件,可以在高雷诺数下有效抑制尾流的旋涡脱落[31,32]. 此后发现这种方法对流向振荡柱体绕流旋涡脱落同样具有较好的抑制效果[33].
与流向振荡柱体锁频旋涡脱落模式一般出现在较小振幅下的情况不同,横向强迫振荡柱体在较大振幅情况下才出现2P旋涡模式,此时旋涡强度更大,尾流更宽,两侧旋涡之间的距离较大. 静止窄条控制件对大幅横向振荡柱体尾流旋涡脱落有什么影响,有无抑制效果,目前还不清楚. 本文将采用数值模拟和实验验证方法,就窄条对2P模式锁频旋涡脱落的作用开展研究.
1 求数值模拟方法
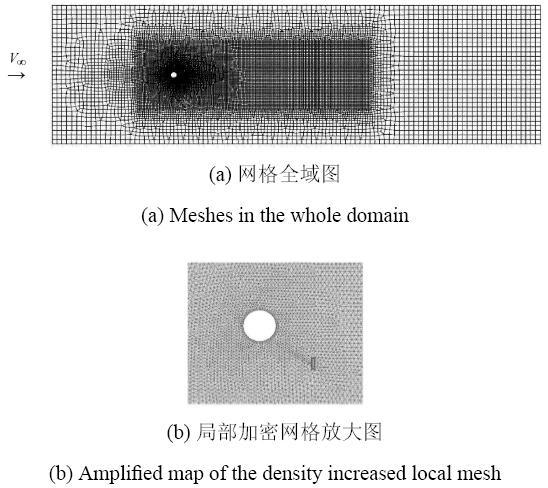
计算区域为:上、下侧边界距离柱体振荡中心 均为12D,上游和下游边界距离柱体振荡中心分别为20D和60D. 在圆柱振荡中心附近设置加密的动网格,动网格区域: 从振荡中心上游6D到下游16D上下两侧各宽6D,但不包括控制件及其周围的一个小区域.
控制件周围的小区域及动网格区外的其他区域采用固定网格. 动网格与固定网格之间,通过滑移面(interface)分隔. 圆柱受 迫在y轴上振荡运动的形式由UDF定义实现. 设圆柱以振幅A和频率f_e作间谐振荡,则在UDF中定义速度随时间t的变化 U(t)=2πf_e Acos2πf_e t 图1(a)是整个计算区域的网格划分,图1(b)为圆柱附近和控制件附近加密动网格的局部放大.
本文用大涡模拟(LES)方法进行数值计算. 采用Smagorinsky-Lilly亚格子模型(Smagorinsky常数C_s取为0.1), 压力--速度耦合方法,及Simple格式求解N-S方程. 时间导数项离散采用二阶隐格式(second order implicit). 空间离散:扩散项 (梯度项,gradient)用基于单元体的最小二乘方法(least-square method)差值;对流项(动量项,momentum)采用有界中心差分 (bounded central differencing)格式; 压力项采用二阶精度离散.
边界条件:上游入口采用速度入口边界条件,入口速度同实验条件一致,为V_∞=0.7 m/s. 下游出口边界条件为Outflow自由出流. 计算域上、下边界采用剪切力为0的条件. 振荡柱体表面采用壁面黏附条件,流体速度与柱体表面运动速度相同. 窄条控制件表面采用壁面黏附条件,流速为零.
模拟所用流体为空气,在实验室温度15 。C下,流体密度ρ=1.225 kg/m3,运动黏性系数 ν=14.4×10^(-6) m2/s.
为了测试网格依赖性,对雷诺数Re=855的均匀流绕静止圆柱的流动,选择5种不同密度的网格,进行数值计算和比较. 各网格对应的时均阻力系数C_D和Strouhal数St 计算结果如表1所示.
表 1 网格密度对
Table 1 Influence of mesh density on the numerical results of flow across a stationary cylinder at
| Mesh | Grid number | ||
|---|---|---|---|
| Mesh1 | 16 881 | 0.212 5 | 1.280 7 |
| Mesh2 | 25 891 | 0.218 0 | 1.302 3 |
| Mesh3 | 36 401 | 0.221 0 | 1.321 5 |
| Mesh4 | 72 207 | 0.220 8 | 1.322 8 |
随着网格数的增大,St数和C_D增大,到Mesh3 时S_t达到0.221 0, C_D达到1.321 5. 此后再增加网格数St和C_D变化很慢. Mesh4网格数比Mesh3增加约一倍,但两者St数相对误差仅为0.02%,C_D相对误差仅为0.13%.
表2是用Mesh3网格计算的静止圆柱结果与其他研究者的结果的比较. 可以看出,本文计算的St数比其他两个数值研究结果更接近于实验值;C_D值介于其他两个数值结果之间而比实验结果高.
表 2
Table 2 Comparisons with other authors’ results of flow across a stationary cylinder at
| Refs. | Ref.[34] | Ref.[35] | Ref.[36] | Ref.[37] | Present |
|---|---|---|---|---|---|
| (Num.) | (Num.) | (Num.) | (Exp.) | (Num.) | |
| 0.236 | 0.238 | 0.210 | 0.210 | 0.221 | |
| 1.440 | 1.200 | 1.330 | 1.100 | 1.321 |
2 实验方法
实验在中国计量大学回流式风洞中进行. 风洞实验段长2.0 m,横截面积0.6 m×0.6 m,可提供速度为0.6 ~ 30 m/s,湍流度小于0.5% 的均匀来流.
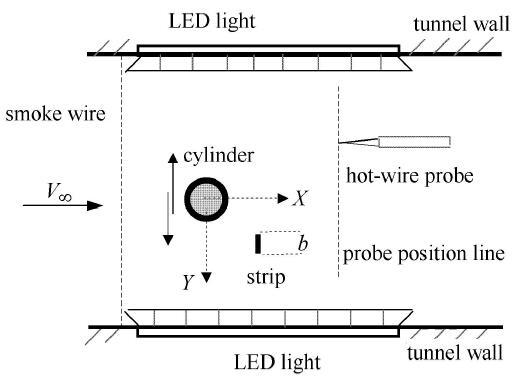
在实验段的侧壁上开一个长100 mm,宽30 mm的竖直槽,用于柱体的横向振荡运动. 在风洞外设一振动平台, 该平台由调频电机通过 转轮和连杆机构驱动. 在转轮上沿一条径线设置一个小槽, 用螺栓穿过小槽和连杆上的开孔, 将连杆和转轮固结在一起. 连杆另一端用螺栓与平台固接. 一个长1 m,外径D=25 mm,厚度8 mm的铝合金管作为振荡柱体. 铝合金管的一端用卡条和螺栓固结在平台上,另一端用带螺扣的圆柱形塞封闭,并通过实验段侧壁的竖槽深入风洞内部,使柱体保持水平, 轴线与来流垂直,且柱体在风洞内的长度略小于0.6 m. 实验设备与模型布置示意图见图2.
图2 实验设备与模型布置示意图.
Fig. 2 Sketch of experimental aparatus and model arrangement .
通过改变螺栓在转轮小槽的位置,可调节平台及柱体的振幅. 通过改变电机转速来调节柱体振频. 受电机功率、振动平台机械承载能 力、柱体变形,及噪音等条件限制,当振幅较大时,振频不能太高. 在模型尺度较小,振频不高的情况下,要达到2P模式存在的f_e D/V_∞值,唯有降低来流速度来实现. 本文选择来流速度V_∞=0.7 m/s,对应的雷诺数Re=1 200.
如图1所示,在柱体下游放置一个宽为b=8 mm, 厚为1 mm,长度为0.6 m的不锈钢窄条,作为控制件. 实验中控制件两端紧顶在风洞前后壁面上固定,轴线与柱体轴线 平行. 在实验段内壁上贴有坐标纸,用于窄条定位. 由于风速很低,实验中窄条不会出现振动或被吹斜的现象.
未施加控制件与施加控制件后的尾流由烟线方法进行流动显示. 在柱体上游一定距离处,竖直放置一根直径为40 m的钼丝, 钼丝两端分别连接到电容器的正负极上. 电容器的充电与放电由控制电路控制. 实验前在钼丝上涂抹甘油,待风速稳定后,按下控制键使电容放电,加热钼丝燃烧甘油发烟,形成片烟流(smoke sheet). 在实验段顶壁和底壁分别开一长条形缝隙,并在缝隙上放置条形LED灯管作为片光源. 灯管照射烟流,从而显示出烟流的旋涡结构. 实验段前壁为透明玻璃,在玻璃壁外设置全帧拍摄速度为1000帧/每秒的高速相机Photron FASTCAM Mini UX50,以拍摄烟流旋涡结构的变化.
未施加控制件与施加控制件后的尾流速度脉动情况由DANTEC热线风速仪的一维单丝探头进行测量. 在x/D=4的竖直线上布置8个测点,分别为:Y/D = ±1.6,±2.4,±3.2,±4.0. 在每个流动状态下,对各个测点分别进行热线测量采样,采样频率为256 Hz. 用Matlab程序对每个采样数据进行快速傅里叶变换,得到各点脉动速度的频谱图,以及8点平均的频谱图.
3 结果与分析
大幅横向振荡柱体流动显示与热线测量工作量巨大. 与实验相比,数值模拟进度快、 更经济.
本文以实验得到的典型结果为标准,通过不同网格划分、不同计算格式和参数的设置,进行计算调试,使模拟结果最大程度地与实验结果接近. 选定计算格式和网格划分方法后,对各种窄条位置下的横向振荡柱体绕流进行数值模拟,以研究窄条对旋涡脱落模式的改变.
3.1 数值模拟与实验结果的比较
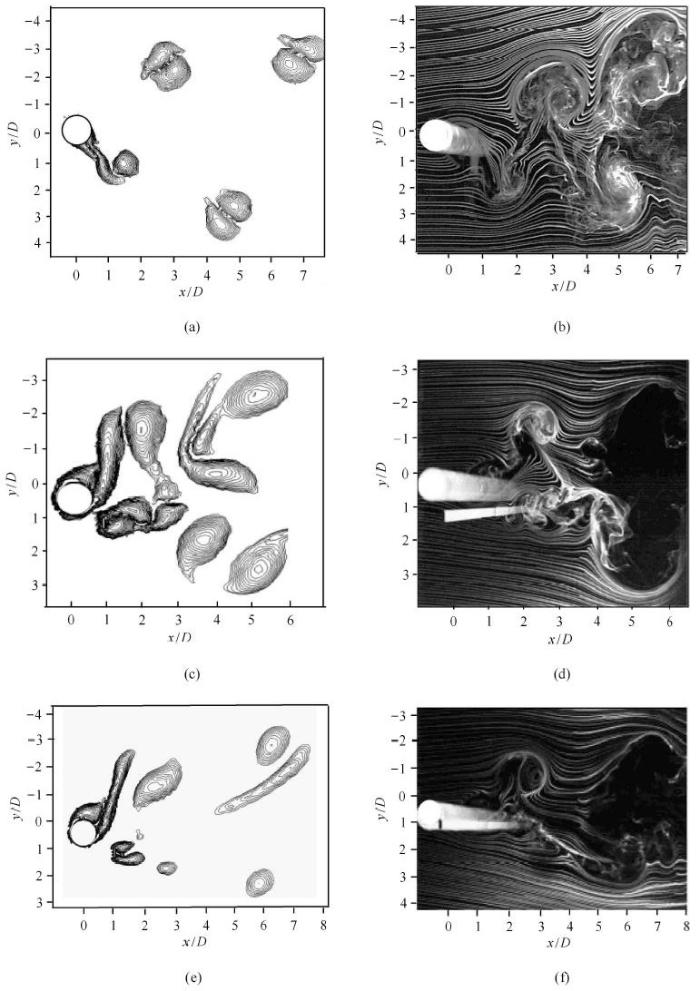
图3(a)和图3(b)分别为未加控制件时的数值模拟涡量场和烟线流动显示流场. 可以看到每个振荡周期内尾流上、下侧各有一对旋转方 向相反的旋涡. 起初,下侧的对涡中,逆时针涡在前(下游),顺时针 紧跟在后;上侧的对涡中,顺时针涡在前,逆时针涡紧跟在后. 但向下游运动过程中,每侧的对涡逐渐由前后排列变为上下排列,这是典型的2P模式. 2P模式旋涡强度大,两侧对涡之间距离大,尾迹很宽. 可知对于未加控制件的尾流,数值模拟与实验在旋涡形态方面符合良好.
图3 无控制件和有控制件时的数值模拟与实验结果对比, Re=1 200, A/D=1.25, f_e D/V_∞=0.22 |||| (a) 数值模拟涡量场,无控制件;(b) 烟线流场,无控制件; (c) 数值模拟涡量场,控制件位于X/D=0.8, Y/D=1.2;(d) 烟线流场,控制件位于 X/D=0.8, Y/D=1.2; (e) 数值模拟涡量场,控制件位于X/D=1.0, Y/D=1.2; (f) 烟线流场,控制件位于X/D=1.0, Y/D=1.2
Fig. 3 Comparisons between numerical and experimental results of the wakes without and with a strip, Re=1 200, A/D=1.25, f_e D/V_∞=0.22 ||||(a) numerical vorticity field, without element;(b) experimental flow field, without element; (c) numerical vorticity field, the strip at X/D=0.8,Y/D=1.2; (d) experimental flow field, the strip at X/D=0.8,Y/D=1.2; (e) numerical vorticity field, the strip at X/D=1.0,Y/D=1.2; (f) experimental flow field, the strip at X/D=1.0,Y/D=1.2
在X/D=0.8, Y/D=1.2 施加宽度b/D=0.32 的单控制件后的数值模拟和实验结果分别如图3(c)和图3(d)所示. 在上侧,由于离控制件较远,从柱体上侧脱落的一对涡,向下游 运动而不受干扰;在下侧,当柱体向下运动到下端时脱落一个逆时针涡, 柱体从下端开始向上运动时脱落一个瞬时针涡, 这两个涡组成一对,先向斜下方运动,从控制件下侧流向下游. 尽管控制件上也有旋涡脱落,但由于控制件位置离尾流中心线较近,而柱体脱落旋涡的位置离尾流中心线较远,控制件尾流未对柱 体的旋涡脱落造成大的影响,因而柱体仍保持2P模式涡脱落. 可以看到,数值模拟与实验结果符合良好.
当控制件流向位置稍向下游变动,到X/D=1.0,横向位置保持Y/D=1.2时,如图3(e),在上侧,从柱体上仍脱落一对涡,未受控制件干扰;在下侧,柱体旋涡脱落受到干扰,旋涡的尺度和强度均减小. 这种单侧抑制的状态,也出现于静止柱体施加窄条于特殊位置时的流动中[28]. 一侧有较强的对涡存在,另一侧仅有较弱旋涡的情况,说明两侧对涡之间的相互作用和相互依存度较弱. 对比图3(e)和图3(f),可知数值模拟结果与实验结果总体上相似度较高,仅在一些细节上有差别.
为了定量研究旋涡抑制效果,在实验和数值模拟中都沿横线x/D=4布置相同的8个监测点,监测每点的脉动速度,并对各点脉动速度进行谱分析,然后得到8点谱的平均谱. 用平均谱最高峰值作为旋涡特征强度.
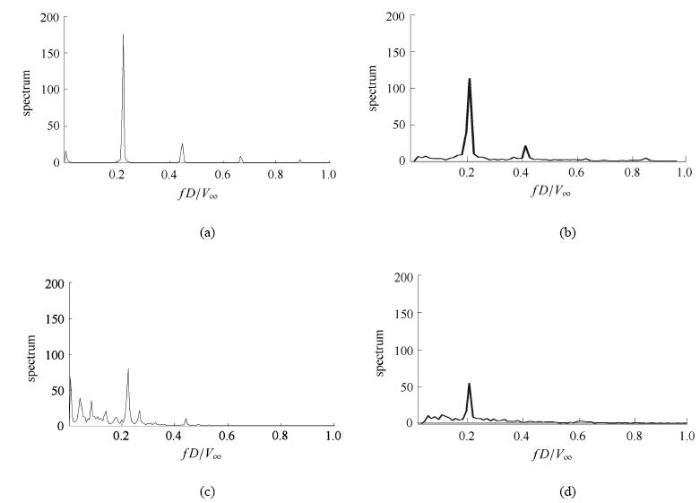
图4(a)和图4(b)分别为无控制件时数值模拟和实验得到的脉动速度功率谱. 每个谱上都存在几个尖峰,其中与振荡频率相同点的尖峰最高, 称为第一尖峰; 其他几处的尖峰频率都是振频的倍数, 峰值依 次减小. 实验谱除尖峰外,其他频率也具有一定谱值,这是来流湍流度及尾流无规则脉动的结果. 模拟谱能量集中在尖峰频率处,其他频率含能近于0,未体现出尾流的无规则脉动.
图4 无控制件和有控制件时数值模拟与实验脉动速度功率谱的对比,Re=1 200, A/D=1.25, f_e D/V_∞=0.22 |||| (a) 数值模拟谱,无控制件;(b) 实验谱,无控制件; (c) 数值模拟谱,控制件位于X/D=0.8,Y/D=1.2; (d) 实验谱,控制杆位于X/D=0.8,Y/D=1.2
Fig.4 Comparisons between experimental and numerical spectra of fluctuating velocities in the wakes without and with a strip element.||||Re=1 200, A/D=1.25, f_e D/V_∞=0.22(a) Numerical spectrum, no strip; (b) Experimental spectrum, no strip; (c)Experimental spectrum, the strip at X/D=0.8,Y/D=1.2; (d) Numerical spectrum, the strip at X/D=0.8,Y/D=1.2
在X/D=0.8,Y/D=1.2布置单控制件后,数值模拟和实验测量的脉动速度功率谱分别如图4(c)和图4(d)所示. 第一尖峰均比无控制件时有明显减小,其他尖峰也接近消失. 但数值模拟 中,出现了几个低频小峰. 实验谱和模拟谱的谱值分布均较广,都体现了尾流的湍流性质.
对比可知模拟谱与实验谱吻合良好.
3.2 窄条控制件对2P模式旋涡脱落的影响
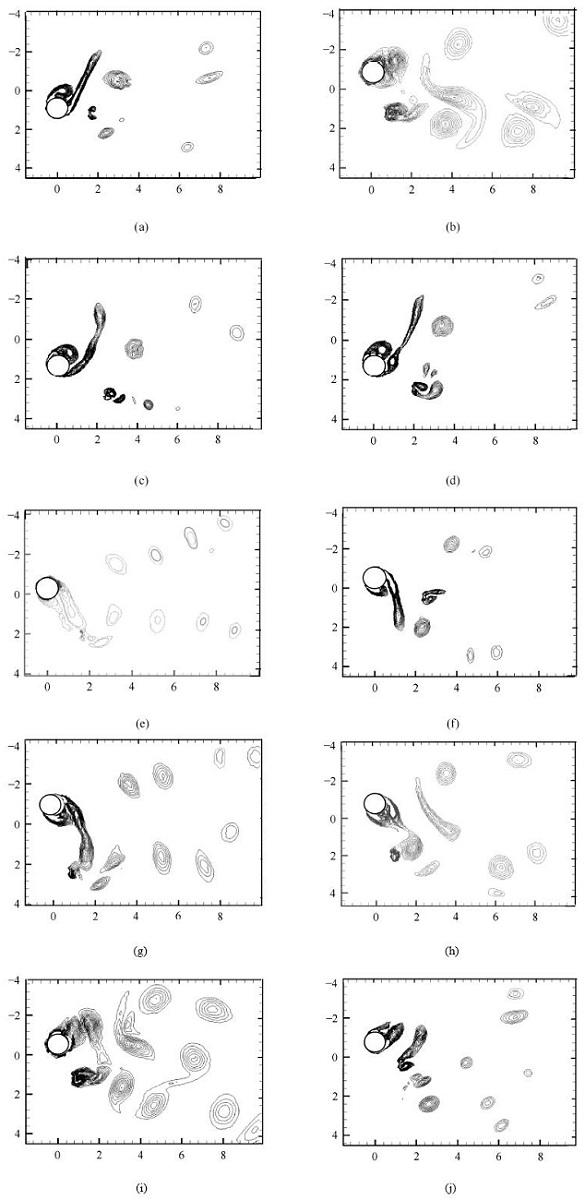
施加控制件后,对尾流旋涡脱落模式的影响,是本文关心的重点. 如图5所示,当b/D=0.32的控制件放于柱体尾流中心线下侧时, 根据控制件位置的不同,存在如下9种不同的旋涡脱落模式.
图5 控制件位于尾流中心线下侧时各种旋涡脱落模式,Re=1 200, A/D=1.25, f_e D/V_∞=0.22, b/D=0.32 |||| (a) P+S模式,上侧对涡、下侧单涡;(b) P+S模式,上侧单涡、下侧对涡;(c) 2S模式;(d) P模式;(e) 2S+2S模式;(f) 2P模式; (g) P+T模式;(h) S+T模式; (i) S+S+P模式;(j) P+S+P模式
Fig. 5 Various modes of vortex shedding in the wake with an element on the lower side of the wake centerline, Re=1 200, A/D=1.25, f_e D/V_∞=0.22, b/D=0.32 ||||(a) P+S mode, upper side vortex-pair and lower side anti-clockwise single vortex, (b) P+S mode, upper side clockwise single vortex and lower side vortex-pair, (c) 2S mode, (d) P mode, (e) 2S+2S mode, (f) 2P mode, (g) P+T mode, (h) S+T mode, (i) 3S mode, (j) P+S+P mode
(1)P+S模式, 见图5(a). 当控制件位于下侧的 X/D=1.6, Y/D=1.2位置时,原为2P模式旋涡脱落变为上侧对涡,下侧逆时针单涡的P+S模式, 即在一个柱体振荡周期内,有控制件的一 侧有一个单涡,另一侧有一对旋转方向相反的对涡交替地从柱体上脱落下来. 对涡中的逆时针涡靠外侧,顺时针涡靠内侧. 这种模式还有另一种形式,即控制件所在的一侧脱落一对涡,无控制件的一侧脱落单涡. 如图5(b),控制件位于下侧的X/D=0.8, Y/D=1.2时,在一个柱体振荡周期内,上侧一个顺时针单涡,下侧一对转向相反的对涡交替脱落下来. 涡对中的逆时针涡靠外,顺时针涡靠内. 本文中,将这两种形式归为一类,统称为P+S模式.
(2) 2S模式,见图5(c). 当控制件位于下侧X/D=2.4, Y/D=2.6时,一个柱体振荡周期内,上侧有一个逆时针单涡,下侧有一个顺时针单 涡交替脱落下来,在下游形成两个交错排列的涡列. 但与卡门涡街中涡的内旋侧顺时针、下侧逆时针)不同,这里的涡为外旋,组成“反”卡门涡街. 另外,也有小涡从控制件上交替地脱落下来,但在下游不远处耗散消失. 此种模式不稳定,经过一段时间会转化为P+S模式.
(3) P模式, 见图5(d). 当控制件位于下侧的X/D=2.0, Y/D=2.6时,在一个振荡周期内,有转向相反的一对涡先后从上侧脱落 下来,组成一对涡,而下侧没有可见大涡在下游存在,形成上、下侧不对称的涡结构. 对涡中顺时针涡靠近尾流中心线,逆时针涡靠外侧.
(4) 2S+2S模式,见图5(e). 当控制件位于下侧的X/D=1.6, Y/D=2.0,上下两侧各有一列涡存在,每一列中相邻两涡旋转方向 相反. 即在一个振荡周期内,上侧先后有两个不同转向的涡脱落下来,并且呈前后排列;接着下侧也先后有两个转向不同的涡脱落下来, 并且也呈前后排列.
(5) 2P模式,见图5(f). 当控制件位于下侧靠近尾流中心的X/D=2.4, Y/D=0.4点时,柱体两侧脱落的对涡都不受控制件阻碍, 从控制件旁边绕过后向下游运动,保持未加控制件时的基本模式,即一个振荡周期内上下两侧各有一对涡交替脱落,上、下两侧的对 涡都是逆时针涡靠外,顺时针涡靠内.
(6) P+T模式,见图5(g). 控制件位于下侧离柱体较远的X/D=0.8, Y/D=2.4点. 柱体向上运动到上端时,脱落一个顺时针涡,柱体 从上端开始向下运动不久又脱落一个逆时针涡. 柱体向下运动,带动周围流体将逆时针涡撕裂成两部分,一部分单独成涡并与瞬时针涡形成对涡(称为P)留在上侧,另一部分被带过尾 流中心线到下侧,从控制件上侧绕过,与控制件脱落涡混合,形成新的逆时针单涡流向下游. 当柱体到达下端前和从下端开始向上运动时先后脱落一个逆时针涡和一个顺时针涡,其中顺时针涡从控制件下侧,逆时针涡从控制件上 侧绕过,在下游形成对涡并紧跟在逆时针单涡后面,形成三涡结构,与Williamson 和 Jauvtis [38] 发现的三涡结构相似,称为T涡结构.
这种模式还有另一种形式,即在一个振荡周期内,上侧形成一个单涡,接着又形成一对涡,下侧形成一对涡. 本文中将这两种情况归为一类.
(7) S+T模式,见图5(h). 当控制件位于下侧离柱体较远的X/D=0.8, Y/D=2.0点时,上侧脱落的对涡不受控制件影响,而下侧脱落 的对涡被控制件分开,顺时针涡从控制件的内侧(靠近尾流中心线一侧)绕过,并穿过尾流中心线到上侧,而逆时针涡从控制件下侧绕过. 这样在一个振荡周期内上侧有一个三涡结构(T)出现,下侧一个逆时针单涡(用S表示)出现. 此外,还存在另一种S+T模式,即在一个振荡周期内,控制件所在的一侧形成一个单涡,又跟着形成一对涡,另一侧形成一个单涡. 本文将这两种情况归为一类. 需要指出的是,在柱体开始启动作振荡的初期,旋涡脱落模式为P+S,经过一段时间后,才转变为S+T模式并稳定下来.
(8) S+S+P模式,见图5(i). 当控制件位于X/D=0.8, Y/D=1.2点时,控制件到尾流中心线的距离与柱体振幅接近. 此时下游出 现三列涡结构,上列为顺时针涡列,中间为逆时针涡列,下侧为一对对旋转方向相反的涡组成的涡列. 其形成过程为:当柱体向上运动到上端时,脱落一个顺时针涡;柱体从上端向下运动到尾流中心线附近时,脱落一个逆时针涡;当柱 体从尾流中心线附近向下运动直到到达下端时,脱落一个逆时针涡,此涡从控制件上侧脱落;柱体由下端开始向上运动时,脱落一个顺 时针涡,此涡也从控 制件上侧脱落,与前一个从控制件脱落的涡组成对涡. 这样,在一个振荡周期内,上侧和中间各形成一个涡,下侧形成一对涡. 与S+T模式情况一样,在柱体启动开始振荡的初期,旋涡脱落模式为P+S,经过一段时间后,才变为稳定的S+S+P模式.
(9) P+S+P模式,见图5(j). 当控制件靠近尾流中心线的X/D=1.2,Y/D=0.4时,出现此种模式. 当柱体向上运动到上端前,脱落 一个瞬时针涡,从上端开始下降时,脱落一个逆时针涡,这两个涡在尾流中心线上侧组成对涡,并向斜上方运动. 当柱体向下运动并从控制件旁边经过时,从控制件下侧脱落一个逆时针涡,该涡向尾流中心线方向运动. 当柱体接近下端时,从柱体脱落一个逆时针涡,该涡向斜下方运动;柱体从下端开始向上运动时,又从柱体脱落一个顺时针涡; 下侧的这两个涡形成旋转方向相反的一对涡.
3.3 窄条作用下旋涡模式的区域分布
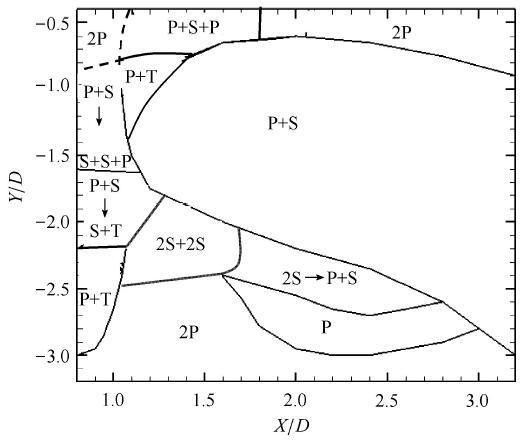
图6为根据数值模拟结果得到的各种旋涡脱落模式在控制件位置平面中的区域划分. 可知控制件离柱体振荡中心很近(X/D,Y/D都很小), 或位于柱体下游1.8倍直径以外的尾流中心线附近,或X/D=1.3附近且Y/D>2的区域,以及X/D,Y/D均较小时,柱体的旋涡脱落为2P模式,说明单控制件在这些区域对流动的影响较小. 柱体斜下方有一个很大的区域,旋涡脱落变为P+S模式. 控制件与柱体的流向距离X/D较小时,随着Y/D由小变大,旋涡模式变化频繁,出现了S+S+P,S+T,P+T等模式,并在局部区域出现两种模式之间的转换现象,说明施加单侧控制件于这些区域对柱体旋涡脱落的影响很大,流动的非对称性加强. 当控制件位于柱 体尾流剪切层附近时,出现2S+2S,及单侧的2P和2S等模式,说明控制件位于该长条形区域时其影响也较复杂. 控制件的某些局部区域,计算收敛性差,旋涡模式的边界不精确,用虚线表示. 与2P模式相比,其他模式旋涡脱落的尾流都有不同程度的变窄,尤 其是2S和P模式,尾流宽度仅为2P模式时的一半 (见图5).
图6 单控制件的影响:各旋涡脱落模式在控制件位置平面中的区域 分布,Re=1 200, A/D=1.25, f_e D/V_∞=0.22, 控制件宽度b/D=0.32
Fig. 6 The influence of single element:zones of vortex shedding modes on the plane of element position, Re=1 200, A/D=1.25, f_e D/V_∞=0.22, element width b/D=0.32
3.4 窄条控制件的抑制效果
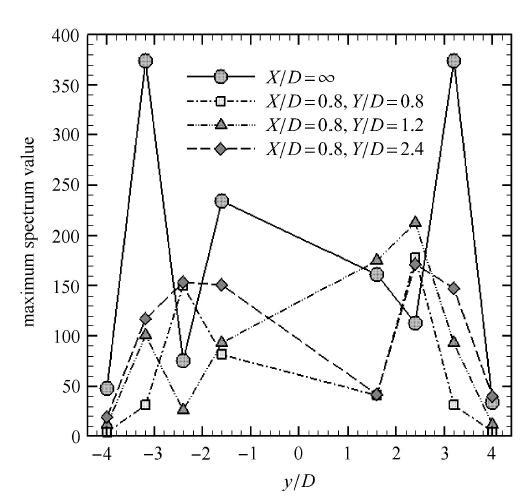
8点平均的脉动速度功率谱仅反应尾流截面的 整体脉动含能情况,不能反映各空间点脉动强度的 分布. 对于某空间点来说,其脉动速度谱上的第一峰值(最高尖峰之值)的大小,基本上代表该点的主频脉动强度. 图7为无控制件和有控 制件时谱上 第一峰值在横截面不同测点的分布,图中∞点代表 无控制件情况. 可知无控制件时,监测点y/D=±2.4处的峰值最大,说明该点附近是速度脉动最剧烈之处. 再往外侧迅速减小,说明已经到达尾流外缘. 在一些位置上施加宽度b/D=0.32的控制件后,各点监测的脉动速度谱最大值相比无控制件时第一峰值都有明显减小,说明施加控制件后对旋涡脱落引起的规则速度脉 动具有一定抑制作用.
图7 脉动速度功率谱最大峰值随采样点y/D (沿x/D=4.0) 的变化, Re=1 200, A/D=1.25, f_e D/V_∞=0.22,b/D=0.32
Fig. 7 Maximum spectrum value of fluctuating velocity v.s sampling position y/D on line x/D=4.0, Re=1 200, A/D=1.25, f_e D/V_∞=0.22,b/D=0.32
施加控制件后尾流脉动速度谱最高峰值P与未加控制件尾流脉动速度谱最高峰值P_0之比P/P_0,代表控制件对旋涡脱落的抑制 程度,它与控制件位置有关. P/P_0越小,说明控制件位于该位置对振荡柱体尾流旋涡脱落的抑制效果越好.
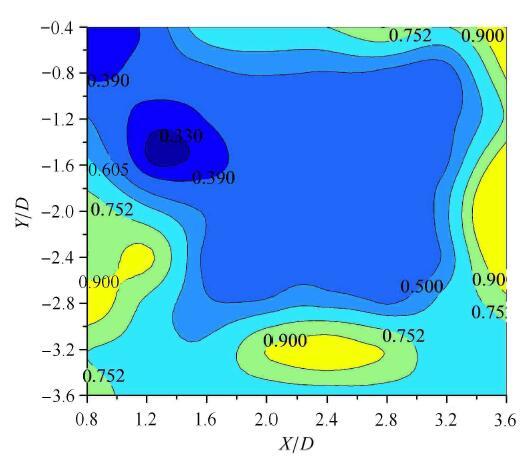
图8为P/P_0在控制件位置平面中的等值线图. 可知P/P_0<0.39的区域分为两小块,一小块区域接近柱体振荡中心,另一小块位 于柱体振荡中心侧后方45。角斜线附近. 当比值P/P_0放宽到小于0.5时,区域面积增大数倍. 说明在较大的位置区域内单控制件对2P旋涡脱落有一定抑制效果,但都不足以完全抑制旋涡脱落.
图8 谱峰比P/P_0 在控制件位置(X/D,Y/D)平面中的等值线图,其中P和P_0分别为有单控制件和无控制件尾流脉动速度功率谱 (8点平均谱)最高峰值, Re=1 200, A/D=1.25, f_e D/V_∞=0.22,b/D=0.32
Fig. 8 Contours of peak spectrum ratio P/P_0 on the plane of element position (X/D,Y/D), where P and P_0 are respectively the maximum values in 8-points averaged power spectrum of fluctuating velocity in the wakes with and without an element, Re=1 200, A/D=1.25, f_e D/V_∞=0.22,b/D=0.32
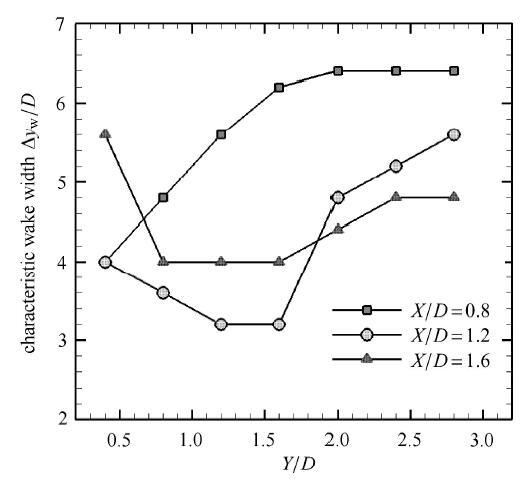
脉动速度谱峰值随采样点y/D而变化(x/D固定). 尾流上侧谱峰值最高的点y_2/D 与下侧谱峰值最高的点y_1/D之间的距离Δy_w/D=(y_2-y_1)/D, 其在某种程度上代表剖面x/D处的尾流宽度. 未加控制时尾流宽度Δy_w/D=6.4 (见图7). 施加尺度b/D=0.32的单控制件,并且控制件流向位置X/D不变,横向位置Y/D变化时,尾流宽度Δy_w/D 的变化情况如图9所示. 当控制件流向位置在靠近柱体的X/D=0.8时,仅当控制件横向位置Y/D<1.6的范围内尾流宽度有所减小. 当控制件向下游移动到X/D=1.2时,控制件各横向位置Y/D的尾流都比未加控制件时窄,尤其是控制件距离尾流中心Y/D在1.7~2.1之间的情况,尾流宽度减小了一半. 继续增大流向间距 X/D=1.6,则呈现两种趋势:当控制件距离尾流中心较近(Y/D<1.8)时, 尾流变宽;而距离尾流中心较远(Y/D>1.8)时,尾流变窄. 对比图8和图9可发现一个大致趋势:抑制效果较好、旋涡强度较小的 区域,尾流也较窄,而抑制效果较差、旋涡强度较大的区域,尾流也较宽.
图9 柱体尾流特征宽度随控制件横向位置Y/D的变化 Re=1 200, A/D=1.25, f_e D/V_∞=0.22,b/D=0.32
Fig. 9 Changes of the characteristic wake width with element position Y/D,Re=1 200, A/D=1.25, f_e D/V_∞=0.22,b/D=0.32
尾流宽度与流体阻力之间存在正相关性 [39],窄条控制件使振荡柱体尾流变窄,说明其具有一定减阻效果.
4 关于旋涡脱落模式生成机制的讨论
对静止柱体绕流旋涡脱落机理进行了长期研究,提出了一些观点和理论模型,但直到目前,这个问题仍在探索之中. 早期的物理模型和 近期的数学模型如下.
(1) 背压吸力引起剪切层弯曲[40],形成旋涡. 这个观点可以解释旋涡的形成原因,但无法解释旋涡的周期性交替脱落.
(2) 两侧剪切层相互作用,形成旋涡脱落. 按照Gerrard[41] 的说法,正在生成的旋涡在生长过程中相对于柱体静止,这个旋涡的诱导作用使另一侧的剪切层向内弯曲并通过尾流中心线,最后 切断了正在生成旋涡的涡量供应,并决定旋涡脱落频率. 这个模型没有说明正在生成的旋涡是如何开始生成,而是说明了下一个旋涡在对面产生的原因:剪切层被诱导发生弯曲,并越过尾流 中心线,这就是旋涡产生的最初动因. Gerrard 认为柱体背压吸力对旋涡脱落产生没有贡献. 为了证明这个观点,他比较了在柱体后驻点连接一个长隔离板与没有隔离板的情况,两者的背压是一样的,但有隔离板时没有旋涡脱落. Gerrard 解释说,隔离板的存在,使生成旋涡不能诱导对面一侧的剪切层发生弯曲,更不能被拖过尾流中心线,即隔绝了两侧的相互作用,因而不 能生成旋涡脱落. 也就是说,Gerrard 模型中,两侧旋涡是共生关系.
Gerrard的模型直至今天仍得到工程界广泛认可. 但是,我们在静止柱体后面放置小窄条,使一侧的旋涡脱落得到抑制后,另一侧的旋涡 脱落仍存在,且其尺度和脱落频率没有变化[31,32]. 说明这种 “单侧旋涡脱落”,在下游形成的确实是单侧Karmann涡街,而不是剪切层KH不稳定性波所形成的高频小涡. 一侧旋涡消失,没有生成涡的诱导作用,另一侧剪切层是怎样弯曲并通过尾流中心线的,用Gerrard模型无法解释.
(3) 尾流整体不稳定性理论. 1980年代末期至1990年代初,人们引入尾流的整体不稳定性概念,认为旋涡脱落是尾流内在不稳定 的必然结果[42]. 线性整体稳定性分析得到的最不稳定模态频率与旋涡脱落频率近乎一致,说明这个理论的合理性. 但是,整体稳定性理论缺少因果关系,不能令人满意.
(4) 绝对不稳定性理论. 在1990年代初,人们引入局部绝对不稳定性和对流不稳定性概念,对静止柱体尾流速度剖面进行分析,得到近尾流 中存在一个绝对不稳定性区,其下游为对流不稳定性区[43]. 绝对不稳定性区中的任意瞬时小扰动,都会在当地发展放大,最终以优势频率形成稳定的扰动源,并且扰动信号从扰动源向下游传播, 最终形成旋涡脱落. Monkewitz等[44]用弱非线性稳定性理论建立了绝对不稳定性与整体不稳定性之间的联系,即当绝对不稳定性区足够大时,才能引 起整体不稳定性.
(5) 信号传播放大理论. 钝体尾流的小扰动稳定性理论中,除了绝对不稳定性机制以外,还存在一种信号传播机制,也能引起旋涡脱落:即 在上游施加连续的周期性扰动,则扰动会向下游传播,并在传播过程中不断放大,最终形成旋涡脱落和卡门涡街[45].
对于小幅振荡的柱体尾流来说,绝对不稳定性机制和信号机制存在竞争关系. 当振幅很小时,信号强度较弱,被不断放大的绝对不 稳定性信号掩盖. 此时,旋涡脱落频率与静止柱体的自然涡脱落频率相同,而与柱体振荡频率无关.
当振幅增大到一定值后,形势发生逆转,柱体振荡引起的扰动信号完全掩盖了绝对不稳定性扰动. 柱体振荡信号向下游传播过程中继续 放大,形成旋涡脱落. 此时,旋涡脱落频率完全由柱体振荡频率决定.
在以往的研究中,我们用尾流速度剖面的线性稳定性分析方法,解释了小振幅流向振荡柱体尾流的旋涡脱落形成以及抑制机制[33]. 我们发现,在流向振荡柱体尾流中施加窄条控制件以后,尾流速度剖面发生变化,信号放大系数大幅减小,是旋涡脱落得到抑制的原因.
当柱体振幅增大到与柱体尺度相同量级以后,小扰动稳定性理论不再适用. 特别是大幅横向振荡柱体,近尾流的横向速度与流向速度为相 同量级,仅用流向速度剖面已经无法准确描述其流动特性. 另外旋涡在柱后(X/D很小处)迅速形成,而不是像信号问题一样在下游移动一段距离以后逐渐形成,也与局部小扰动理论的要求不符.
注意到横向剪切流在大幅横向振荡柱体尾流旋涡脱落的形成过程中起到重要作用,这与静止、流向振荡甚至小幅横向振荡柱体尾流的旋 涡脱落机制明显不同. 本文中,柱体横向运动最大速度为:U_e=2πAf_e=2π(A/D)(f_e D/V_∞)V_∞≈1.73V_∞. 柱体的横向运动使其周围流体也随之以同样量级的速度形成横向流动.
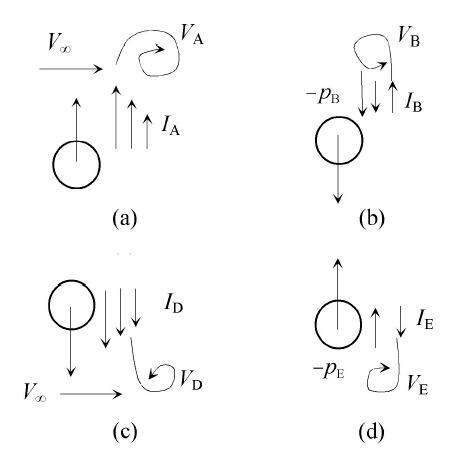
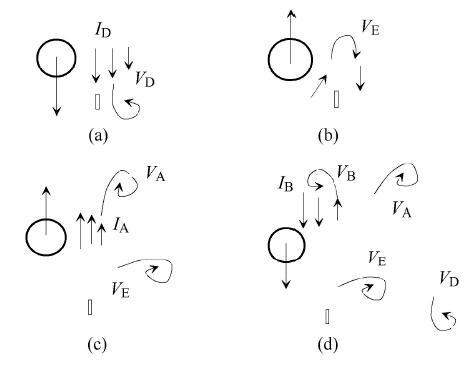
未施加控制件情况下,如图10(a)所示, 当柱体由尾流中心线附近向上运动时,柱体背面(面向下游的一侧)附近的流体也随之向上运动,且越靠近柱体,向上速度越高,越离开柱体,向上速度越低,这样就形成一个向上的横向剪切流I_A. 由于柱体的阻挡,柱体背风面的流向速度很小. 当柱体到达上端,停止运动时,由于惯性,横向剪切流继续向上运动后遇到来流,横向剪切流在来流作用下向下游弯曲,形成瞬时针旋涡 V_A.
图10 无控制件时的2P模式旋涡脱落示意图 ||||(a)上侧顺时针涡V_A,(b)上侧逆时针涡V_B,(c)下侧逆时针涡V_D,(d)下侧顺时针涡V_E
Fig. 10 Sketch of 2P mode vortex shedding generation in the wake without strip element ||||(a) Clock-wise vortex V_A on the upper side, (b) Anti-clock-wise vortex V_B on the upper side, (c) Anti-clock-wise vortex V_D on the lower side, (d) Clock-wise vortex V_E on the lower side
如图10(b)所示,当柱体由上端开始向下运动时,柱后流体随柱体一起向下运动,但此时柱体下游的流体仍以惯性向上运动,这样就形成一个局部很强的逆向剪切流I_B,在柱体移动形成的较强背压吸引下,该逆向剪切流I_B向左弯曲,在尾流上侧形成逆时针涡V_B. 逆时针涡与早前形成的顺时针涡形成一对涡.
如图10(c)所示,当柱体继续向下移动过程中形成向下的剪切流I_D. 当柱体到达下端停止运动时,剪切流I_D及在惯性作用下继续向下运动,遇到下侧来流,并在来流作用下向下游弯曲形成逆时针旋涡V_D.
如图10(d)所示,柱体从下端开始向上运动时,柱后流体随之向上流动,但下游按惯性向下的剪切流并未完全消失,这样两股相反的流动形成剪切流I_E. I_E在柱后低压吸引下形成瞬时针旋涡V_E. V_D和V_E组成一对旋转方向相反的旋涡. 这就是2P旋涡模式形成机制的一个物理解释.
由此可知,横向振荡柱体尾流中旋涡形成的重要因素是横向剪切流和流向作用力,即:横向剪切流I+流向作用力F→弯曲 →旋涡V. 横向速度的梯度决定剪切流强度,而剪切流宽度决定了所形成旋涡的尺度.
在没有控制件的情况下,对剪切流或旋涡的主动作用力除来流冲力和柱体背部负压吸力外,还有其他已形成旋涡的诱导力. 被动力主要是湍流涡黏性力. 主动力的横向分量决定旋涡的走向、旋涡排列方式,甚至旋涡脱落模式. 被动力可减弱旋涡强度及旋涡运动速度.
控制件的存在,对横向振荡柱体旋涡脱落的作用包括:
(a)控制件对剪切流的阻挡和分流,改变剪切流I的宽度及其流动方向,对旋涡形成有重要影响;
(b)控制件表面摩擦力对剪切流I的影响,可改变I的强度;
(c)控制件背压吸力,对柱体脱落涡走向有影响;
(d)控制件旋涡脱落对柱体脱落涡的作用,同向涡合并增强,异向涡抵消减弱. 当柱体旋涡与控制件旋涡具有某种同步性时,这种作用较大;
(e)控制件尾流对柱体脱落涡的湍流耗散.
控制件位于不同区域,上述各因素作用的大小不同,从而产生不同的效果. 下面分别讨论决定每种旋涡模式的主要因素及其作用.
4.1 P+S+P模式
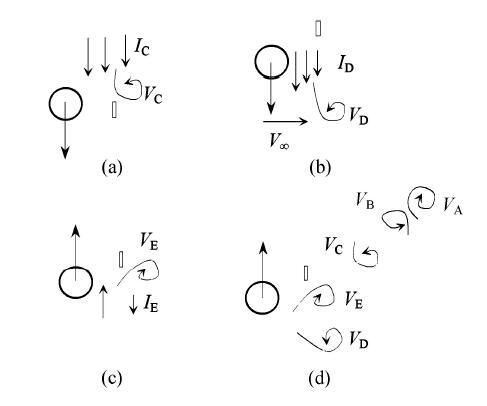
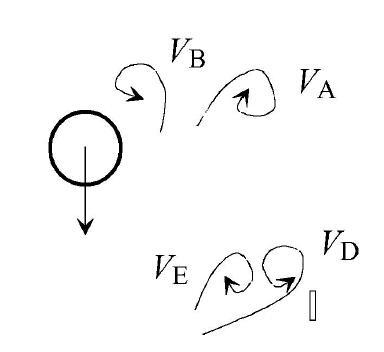
当控制件位于下侧,与尾流中心线的距离较小, 与柱体在流向有一定距离时,它对上侧一对涡的形成没有影响,如图10(a)和图10(b)所示,柱体到达上端及离开上端过程中, 形成剪切流I_A,I_B及旋涡V_A, V_B. 但是当上侧的对涡形成以后,柱体继续向下越过尾流中心线并到达控制件附近时,如图11(a)所示, 跟随柱体向下的剪切流I_C受控制件阻挡而分成两部分,一部分向下游方向弯曲,形成逆时针涡V_C,V_C经控制件上侧向下游移动;另一部分继续随柱体向下运动,掠过控制件前侧表面时,受控制件表面摩擦力影响迅速形成新的剪切流I_D,在柱体到达下端以后I_D按惯性继续向下并在来流作用下弯曲形成逆时针涡V_D (图11(b)). 柱体从下端开始向上运动,柱后流体随之向上,与按惯性向下的流动形成剪切流I_E. 受控制件阻挡,I_E的一部分在到达控制件时下游弯曲形成瞬时针涡V_E (图11(c)),另一部分形成剪切流I_A继续向上. 综合整个过程,如图11(d)所示,就形 成P+S+P模式旋涡脱落.
图11 有控制件时P+S+P模式旋涡脱落生成示意图 |||| (a)中间单涡V_C,(b)下侧逆时针涡V_D,(c)下侧顺时针涡V_E, (d)一个周期内各旋涡的形成
Fig. 11 Sketch of P+S+P mode vortex shedding generation in the strip disturbed wake ||||(a) The single vortex S=V_C in the middle, (b) Anti-clockwise vortex V_D on the lower side, (c) Clockwise vortex V_E on the lower side, (d) Generation of the vortices in a cycle
4.2 S+T模式
控制件位置X/D坐标保持较小,Y/D坐标继续增大到略超过柱体的行程范围的1.5 ~ 2.0时,控制件后形成较稳定的旋涡脱落. 控制件旋涡脱落频率f_1与柱体振荡频率f_e之间的关系为 f_1 f_e=f_1 b/V_∞ f_e D/V_∞ 1b/D=0.210.2210.32≈3 即柱体在下侧的半个周期内,从控制件脱落3个涡,但从柱体脱落两个涡.
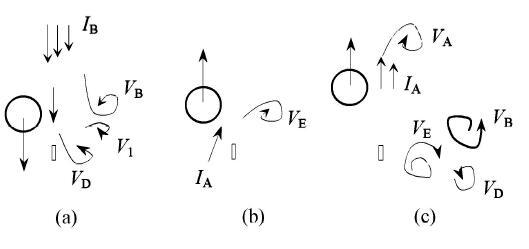
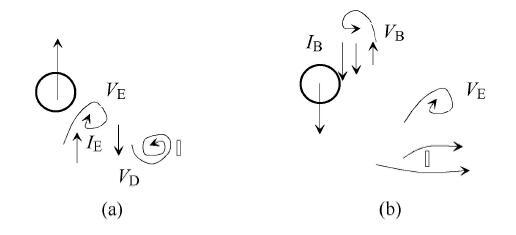
如图12(a)所示, 当柱体从上端向下运动时形成向下的剪切流I_B. 柱体到尾流中心线下侧时,I_B被从控制件上侧脱落的顺时针涡V_1切断,I_B的上半部分形成逆时针涡V_B,V_B吞没了从控制件上侧脱落的顺时针涡V_1后,在向下的惯性和来流作用下向斜下方移动. I_B的下半部分由于惯性继续向下运动,在控 制件分流作用下,形成新的逆时针涡V_D,V_D从控制件上侧脱落,合并了从控制件下侧脱落的逆时针涡后,向下游移动. 如图12(b)所示,当柱体从下端开始向上运动时,形成向上的剪切流I_A. 在柱体向上运动的初期,I_A协助从控制件上侧脱落的顺时针涡增长,形成旋涡V_E. 下侧形成的三个涡V_B,V_D和V_E组成三涡结构(T涡结构). 柱体继续向上运动,剪切流I_A随之向上运动. 由于在下侧协助V_E,I_A消耗了部分能量,因而不能在下侧形成新的旋涡. 如图12(c)所示,直到柱体到达上端,I_A由惯性继续向上运动,在来流作用下向下游弯曲,形成旋涡V_A.
图12 控制件作用下S+T模式旋涡脱落的生成 ||||(a)下侧逆时针涡V_B和V_D, (b) 下侧瞬时针涡V_E, (c) 上侧顺时针涡V_A 及下侧已生成的涡
Fig. 12 Sketch of S+T mode vortex generation in the strip disturbed wake ||||(a) The anti-clock-wise vortex V_B and V_D on the lower side, (b) The clock-wise vortex V_E on the lower side, (c) The clock-wise vortex V_A on the upper side and the earlier formed vortices on the lower side
当柱体从上端开始向下运动时,柱后流体跟随向下运动,与由惯性向上运动的流动形成剪切流I_B. 由于剪切流I_A在下 侧的消耗,当柱体到达上端时由惯性继续向上的流动持续时间缩短,影响了剪切流I_B的剪切强度,使之不能在柱体向下运动的初期形成旋涡.
4.3 P+T模式
当控制件位置X/D坐标保持较小,Y/D坐标进一步增大到大于2.2时,下侧仍形成三涡结构. 此时控制件到柱体行程上端的距离足够 大,控制件对上侧的影响减弱. 与未加控制件情况一样,上侧能够形成V_A和V_B两个涡,组成P+T模式.
4.4 S+S+P模式
当控制件位置X/D坐标保持较小,Y/D坐标与柱体振幅接近时,柱体尾流对控制件旋涡脱落的影响不大,在半个振荡柱体振荡周期 内,控制件旋涡脱落个数仍能维持为3个. 与S+T模式的形成过程(图12)类似,只是柱体由上端到控制件影响区的距离缩短,生成的旋涡V_B从柱体获得向下的惯性减小,使V_B停留在尾流中心线附近,从而在上侧形成V_A,中间存在V_B,下侧V_D和V_E形成旋转方向相反的对涡.
4.5 2S+2S模式
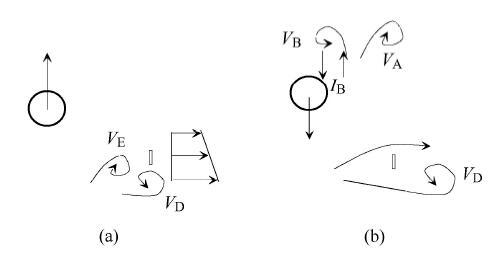
控制件在X/D=1.2左右,Y/D=2.0附近时出现. 柱体向下运动到达下端时,如图13(a)所示,控制件位于柱体的斜下方,剪切流按 惯性向下运动时被控制件分流,大部分在到达控制件后向下游弯曲形成旋涡V_D,少部分通过柱体与控制件之间的通道后,被来流冲击也向下游弯曲,与控制件尾流的小旋涡混合后被旋涡V_D吸收. 如图13(b)所示,当柱体由下端向上运动时,随柱体向上的剪切流经过柱体与控制件之间的通道时,方向变为斜上方,流体通过通道 以后发生扩张,在控制件后负压吸引下,迅速形成旋涡V_E. 如图13(c)所示,柱体继续向上运动,形成新的剪切流I_A. 柱体到达上端前时,I_A在旋涡V_E诱导作用下,向下游弯曲,形成旋涡V_A. 在来流作用下,V_A得到加强. 旋涡V_A在来流作用和V_E诱导下,向下游移动的速度较快. 如图13(d)所示,柱体从上端下降时形成旋涡V_B. V_B形成时,V_A已经向下游移动一定距离,两涡不是相互靠近的一对涡,而是一前一后在上侧形成2S模式.
图13 控制件作用下2S+2S模式各旋涡的生成 |||| (a)下侧逆时针涡,(b)下侧顺时针涡,(c)上侧顺时针涡, (d) 上侧逆时针涡
Fig. 13 Generation of the vortices of mode 2S+2S in the strip disturbed wake ||||(a) Lower side clockwise vortex, (b) Lower side anti-clockwise vortex, (c) Upper side clockwise vortex, (d) Upper side anti-clockwise vortex
在下侧,旋涡V_E在初时受旋涡V_A的诱导作用,向下游移动速度较慢,与旋涡V_D拉开一定距离. 此后 由于V_E和V_A的距离拉大,相互作用减弱,V_E速度加快,与前面的旋涡V_D保持一定距离,在下侧形成一前一后的2S模式. 这样在整个柱体下游得到2S+2S模式.
4.6 P模式
控制件位置再向斜下方移动一定距离后,出现此种模式. 如图14所示,当柱体向下运动到下端时形成旋涡V_D,V_D向 下游移动时碰到控制件上缘而速度减缓. 柱体由下端向上运动不久形成旋涡V_E,V_E向下游移动并靠近受阻的V_D. 两旋转方向相反的涡靠近后相互抵消,加上控制件尾流的耗散作用(控制件处于柱体尾流剪切层之中,剪切层剪切参数K=Gb/V_∞~b/δ 为1的量级,抑制了控制件的旋涡脱落,增大了控制件尾流的湍流耗散),V_D和V_E在控制件附近很快消失. 柱体继续向上运动到达上端时形成旋涡V_A. 柱体从上端向下运动不久形成旋涡V_B. 由于控制件离柱体行程的上端较远不能产生影响,V_A和V_B 像未加控制件时一样组成一对涡.
图14 上侧P模式旋涡脱落的形成
Fig. 14 The formation of P-mode vortex shedding on the upper side
4.7 2S模式
如图15(a)所示,当控制件位置再稍向内变动(更靠近尾流中心线)时,柱体向下到达下端时形成的逆时针涡V_D,在向下游移动 到控制件正前方时停止移动. 柱体由下端开始向上运动时形成剪切流I_E. 由于涡V_D的诱导力部分抵消了柱体背压吸力,推迟了I_E的弯曲和顺时针涡V_E的生成. 涡V_E生成后在 下侧来流、柱体背部负压和涡V_D的诱导作用下向 斜上方移动,越过尾流中心线后向下游移动. 此后柱体的向上运动直至到达上端,仅为顺时针涡V_E提供涡量,不再生成新的涡.
如图15(b)所示, 柱体由上端开始向下运动不久 生成逆时针涡V_B. 下侧位于控制件前的旋涡V_D被控制件表面摩擦力消耗而逐渐消 失. 这样在一个振荡周期内,在尾流中心线下侧没有旋涡向下游传播,在上侧形成两个涡,其中顺时针涡V_E在内(靠近尾流中心线),逆时针涡V_B在外(远离尾流中心线),形成上下交错的2S旋涡模式. 与卡门涡街相反,此2S涡结构是顺时针涡在下排,逆时针涡在上排.
图15 控制件作用下的2S模式旋涡脱落 |||| (a) 控制件对下侧逆时针涡VD的阻挡及涡VD的诱导作用推迟 顺时针涡VE的生成; (b)上侧2S模式旋涡脱落的生成及 下侧涡VD的消失
Fig.15 The effect of the strip on 2S mode vortex generation ||||(a) The strip blocks the downstream movement of anti-clock-wise vortex VD, and the induction of VD delays the formation of vortex VE, (b) The formation of 2S mode vortex shedding on the upper side, and the vanishing of vortex VD on the lower side
当控制件距柱体的流向距离超出一定范围时,下侧的旋涡V_D到达控制件之前尺度变大,控制件对它的阻碍作用变弱,就 不再能形成2P或2S模式.
4.8 P+S模式
控制件位置继续向尾流中心线方向移动一定距离后出现该种模式. 如图16(a)所示,柱体向下运动到下端和从下端向上运动时分别 形成逆时针涡V_D和瞬时针涡V_E, V_D在前V_E在后,向下游移动. 到达控制件时V_D由控制件下侧绕过,而V_E可能有三种情况:一是由控制件下侧绕过,二是由控制件上侧绕过,三是停留在控制件前. 如图16(a)所示,柱体在下侧运动时对来流具有阻挡作用,使下侧局部区域流体的纵向速度减小. 纵向速度减小作用传播到控制件需要一定时间. 在这段时间内,柱体已经到达上侧;而纵向速度经过这段时间延时后,在控制件后面形成流向剪切层. 逆时针涡V_D 经过控制件下侧时,流向剪切层提供逆时针涡量使V_D得到加强;顺时针涡V_E 到达控制件时,无论是从控制件上侧,还是下侧绕过,都被流向剪切层削弱,直至消失; V_E 停留在控制件前时,也被控制件表面摩擦力消耗并最后消失.
图16 控制件作用下的P+S模式旋涡脱落 |||| (a)纵向剪切流使下侧 的逆时针涡变强,顺时针涡减弱; (b) 上侧对涡的生成和 下侧单涡的生成
Fig. 16 The strip effect on P+S mode vortex generation ||||(a) Stream-wise shear flow enhances the anti-clock-wise vortex and weakens the clock-wise vortex on the lower side, (b) The formation of the vortex-pair on the upper side and the formation of single vortex on the lower side
如图16(b)所示,柱体向上运动到上端时,形成 旋涡V_A. 柱体由上端向下运动不久,形成旋涡V_B. 从而在一个振 荡周期内,上侧形成旋转方向相反的一对涡V_A和V_B,下侧一个逆时针单涡V_D.
4.9 2P模式
当控制件位置离尾流中心线足够远(Y/D足够大)时,控制件的影响消失,柱体后恢复2P旋涡模式. 当控制件靠近尾流中 心线(Y/D较小),但与柱体的流向距离X/D较大时,控制件对柱后两侧对涡的形成没有影响,两侧对涡在向下游移动过程中离尾流中心 线的距离也在增加,两侧对涡离控制件及其尾流较远,受影响很小,从而保持2P旋涡模式. 当控制件离柱体振荡中心很近(X/D和Y/D都小)时,柱体到达控制件附近时运动速度达到最高,振荡形成的横向剪切流的大部分都从 控制件后面经过,且由于惯性大,横向剪切流弯曲小,柱后能够维持2P模式旋涡脱落.
5 结 论
在一定雷诺数和振频、振幅参数下,在横向振荡柱体尾流中找到了2P模式旋涡脱落. 用宽度比b/D=0.32的窄条控制件放于振荡柱体尾 流中,对这种模式的旋涡脱落进行干扰和抑制. 采用2维大涡模拟方法进行数值计算. 通过对未加窄条的2P模式旋涡脱落尾流和典型窄条位置条件下尾流的数值模拟结果与实验结果对比,发现两者吻合良好.
在柱体下游X/D=0.8~3.6, Y/D=0.4~3.6的区域内,以ΔX/D=ΔY/D=0.2为间距,布置控 制件位置点,并对每个位置下的流动进行计算.
在不同的控制件位置上,发现了2P,2S,P+S等3种已知旋涡模式,以及S+T,P+T,S+S+P,P,2S+2S,P+S+P等6种新的旋涡模式. 找出了各旋涡脱落模式在控制件位置平面上的存在区域.
以柱体下游x/D=4横截面上8点平均的脉动速度功率谱最大峰值为旋涡脱落特征强度,画出了旋涡相对强度在控制件位置平面上的 等值线图,发现在一个较大的控制件位置区域内,旋涡强度可减少一半以上.
控制件对尾流宽度具有重要影响,其影响趋势为:旋涡脱落强度较低的控制件区域,尾流特征宽度较小,旋涡脱落强度较高的控 制件区域,尾流特征宽度较大.
发现柱体大幅振荡引起的横向剪切流对柱后旋涡脱落的形成起关键作用. 探讨了控制件对横向剪切流的改变,分析了控制件位置的 影响. 对每种旋涡脱落模式的形成机制做了细致研究,发现横向剪切流受来流纵向冲击、控制件阻挡和分流、柱后背压吸力,已生成旋涡 的诱导,及控制件尾流旋涡脱落等因素作用,各因素的不同组合作用形成了柱体尾流中不同的旋涡脱落模式.
The authors have declared that no competing interests exist.
参考文献
| [1] |
A brief review of recent results in vortex-induced vibrations . |
| [2] |
Perspectives on bluff body aerodynamics . |
| [3] |
The effect of sound on vortex shedding from cylinders . |
| [4] |
Control of flow induced noise behind a circular cylinder using splitter plates . |
| [5] |
Vortex-induced oscillations . |
| [6] |
A critical review of the intrinsic nature of vortex-induced vibrations . |
| [7] |
Pressure-fluctuation measurements on an oscillating circular cylinder . |
| [8] |
Vortex shedding from oscillating bluff bodies . |
| [9] |
二维圆柱涡激振动的数值模拟 .Numerical simulation of vortex-induced vibration on 2D cylinders . |
| [10] |
海洋立管涡激振动的研究现状、热点与展望 .An overview on the study of vortex-induced vibration of marine risers . |
| [11] |
Controlled oscillations of a cylinder: Forces and wake modes . |
| [12] |
Motions, forces, and mode transitions in vortex-induced vibrations at low mass damping . |
| [13] |
|
| [14] |
Forces on oscillating uniform and tapered cylinders in cross flow . |
| [15] |
Flow structure from an oscillating cylinder. Part 1 Mechanisms of phase shift and recovery in the near wake . |
| [16] |
Flow structure from an oscillating cylinder. Part 2 Mode competition in the near wake . |
| [17] |
海洋立管横流向与双流向涡激振动研究 .Study on the 1-DOF and 2-DOF VIV of marine riser . |
| [18] |
Vortex formation in the wake of an oscillating cylinder . |
| [19] |
Towing tank experiements on the vortex-induced vibrations of low mass ratio long flexible cylinders . |
| [20] |
王国平等. 复合材料立管涡激振动数值模拟 .Numerical calculations of vortex-induced vibration of composite riser . |
| [21] |
Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding . |
| [22] |
Hydrodynamics around Cylindrical Structures . |
| [23] |
|
| [24] |
Modification of a circular cylinder wake with synthetic jet: Vortex shedding modes and mechanism. |
| [25] |
Circular cylinder vortex-synchronization control with a synthetic jet positioned at the real stagnation point . |
| [26] |
On the wake with and without vortex shedding suppression behind a two-dimensional square cylinder in proximity to a plane wall . |
| [27] |
深海立管涡激振动被动抑制措施的研究 .Study on suppression measures for vortex-induced vibration of deep water risers . |
| [28] |
三根附属控制杆对海洋立管涡激振动抑制作用实验研究 .Experimental investigation of suppression of vortex-induced vibration of marine risers by three control rods . |
| [29] |
大跨度桥梁涡激振动及其气动减振措施研究. [硕士论文] .Study on vortex-induced vibration of large span bridge and its aerodynamic reduction measures. [Master Thesis] . |
| [30] |
桥梁结构涡激振动及其控制措施. [硕士论文] .Vortex-induced vibration of bridge structures and its control. [Master Thesis]. Xi’an: |
| [31] |
Control of vortex shedding from a square cylinder . |
| [32] |
钝体尾流控制机理及方法研究进展 .Advances in the study of methods and mechanism of bluff body wake control . |
| [33] |
流向振荡柱体尾流控制研究进展 .Advances in the control of wakes behind an in-line oscillating cylinder . |
| [34] |
Flow structure in the wake of an oscillating cylinder. Transactions of ASME,
|
| [35] |
Interaction of a steady approach flow and a circular cylinder undergoing forced oscillation. Transactions of ASME,
|
| [36] |
Regimes of vortex shedding from an in-line oscillating circular cylinder in the uniform flow .
|
| [37] |
Flow structure from an oscillating cylinder, Part 2. Mode competition in the near wake .
|
| [38] |
A high-amplitude 2T mode of vortex-induced vibration for a light body in XY motion. European Journal of Mechanics B/ |
| [39] |
On the wake and drag of bluff bodies . |
| [40] |
Generation of oscillatory flows//Naudascher E ed. Flow Induced Structural Vibration, |
| [41] |
The mechanics of the formation region of vortices behind bluff bodies . |
| [42] |
Global dynamics of symmetric and asymmetric wakes . |
| [43] |
Absolute instability in the near-wake of two-dimensional bluff bodies . |
| [44] |
Global linear stability analysis of weakly non-parallel shear flows . |
| [45] |
Local and global instabilities in spatially developing flows . |

/
| 〈 |
|
〉 |