气液相界面运动的研究无论是在科学还是工程领域都是非常重要的[1-2 ]. 为了精确捕捉气液相界面, 一般有两种思路: (1)界面追踪, 该方法需要求解界面对流输运方程, 最具代表性的有流体体积法(VOF)[3-4 ]和水平集方法[5 ]. 以上两种方法均是以求解 Navier-Stokes (N-S)方程为基础;(2)自动捕捉, 亦即通过求解气液相变引起的分离, 来捕捉气液相界面. 该方法相对于界面追踪更有优势. 首先不需要求解界面的对流输运方程, 加之它是以波尔兹曼方程为基础, 对物理现象的描述更接近本质, 所以计算结果更加精确.
由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献.
如前所述, 格子波尔兹曼方程适用于低速不可压连续流体的模拟, 虽然通过高阶矩的方法试图将格子波尔兹曼方法推广至稀薄流动 [26-29 ], 但是限于弱非平衡态. 近年来, 基于气体动理学BGK 方程, 离散速度空间的方法发展起来了一套适用于全流域的统一气体动理学格式(unified gas-kinetic scheme, UGKS) [30-32]. 该格式的精要在于将自由输运和粒子碰撞耦合起来更新宏观物理量和微观气体分布函数. 不同于其他诸多方法的关键是, 在计算网格界面通量时采用动理学方程的积分解. 该积分解描述的是两尺度的物理过程, 其一为粒子碰撞所带来的平衡态的积分所体现的流体力学尺度, 其二则是粒子自由输运所体现的动理学尺度. 二者之间的权重取决于网格分辨率和时间步长. 因此, 该格式适用于全流域的计算.
本文通过将范德瓦尔斯状态方程引入到统一气体动理学格式之中, 建立了基于气液相界面捕捉的UGKS. 利用该方法, 得到麦克斯韦等面积律(Maxwell construction)的数值解, 观察其与理论解的符合程度. 而后, 通过对范德瓦尔斯状态方程所描述的液滴表面张力进行数值计算, 验证拉普拉斯定理, 此外, 通过模拟两个液滴的碰撞过程, 进一步证明该格式的有效性.
1 问题描述
对于实际气体而言, 由于考虑了分子间的相互作用力, 故而其状态方程与理想气体状态方程是有本质区别的, 其中, 最早提出关于实际气体状态方程的便是著名的范德瓦尔斯状态方程. 由于在临界温度下, 该方程其所描述的压力‒密度曲线是非单调的, 故而可以实现气液两相共存.
通过临界参数加以无量纲化的范德瓦尔斯方程为
p = 8 ρ T 3 - ρ - 3 ρ 2
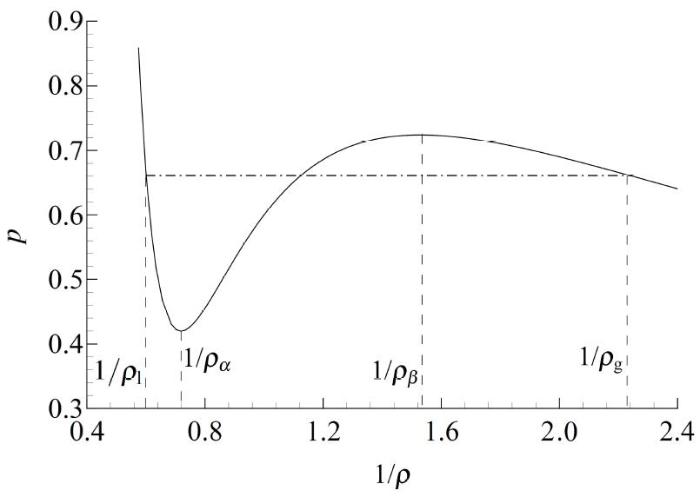
此时, 恒温下, 范德瓦尔斯状态方程所描述的曲线如图1 所示. 通过麦克斯韦等面积律则可求得两相共存的相参数, 亦即 ρ l ρ g p . 此外, ρ α ρ β
图1 范德瓦尔斯状态方程的曲线示意图.
Fig.1 The schematic diagram for van der Waals equation of state.
流体密度可按照如下分类[33]: (1) 1 ρ < 1 ρ l 1 ρ l < 1 ρ < 1 ρ α 1 ρ α < 1 ρ < 1 ρ β 1 ρ β < 1 ρ < 1 ρ g 1 ρ g < 1 ρ
当流体密度处于椭圆域时, 由于 ∂ p / ∂ ρ
综上所述, 将范德瓦尔斯状态方程所表达的非理想气体效应引入统一气体动理学格式之中, 便可以得到尖锐的相界面以及正确的物理解.
2 基于气液相界面捕捉的统一气体动理学格式
2.1 动理学模型
对于单组分二维气液两相流而言, 其流场控制方程为
f t + u f x + v f y = g - f τ
这里, 平衡态 g = ρ λ < . 其中, τ ρ ( U , V ) K ξ 2 = ξ 1 2 + ξ 2 2 + ⋯ + ξ K 2 . 其中, ξ 1 , ξ 2 , ⋯ , ξ K λ 33 ]. 其形式如下
λ = ρ 2 p = 3 - ρ 6 ρ 2 - 18 ρ + 16 T = Λ ( ρ )
2.2 简化动理学模型
对于二维模型而言, 定义如下的简化气体分布函数
H = ∫ fd ξ
宏观量可如下表示
W = ρ ρ U ρ V = ∫ H uH vH dudv
此时的动理学方程变为
H t + u H x + v H y = H eq - H τ
其中, H eq = ρ λ < .
2.3 基于气液相界面捕捉的统一气体动理学格式
统一气体动理学格式是一种有限体积方法, 二维情况下的物理域可划分为控制体 Ω i , j . 时空离散的分布函数为
H i , j n = H i , j , α , β n = H ( t n , x i , y j , u α , v β )
此时, 宏观量的表达为
W i , j n = ∑ κ α , β H i , j n κ α , β H i , j n u α κ α , β H i , j n v β
其中, κ α , β ( u α , v β )
通过守恒性原理, 易得分布函数随时间的演化为
H i , j , α , β n + 1 = H i , j , α , β n + 1 Δ x ∫ t n t n + 1 f i - 1 / 2 , α , β H - f i + 1 / 2 , α , β H dt + 1 Δ y ∫ t n t n + 1 g j - 1 / 2 , α , β H - g j + 1 / 2 , α , β H dt + Δ t 2 ⋅ H eq , i , j , α , β n + 1 - H i , j , α , β n + 1 τ n + 1 + H eq , i , j , α , β n - H i , j , α , β n τ n
宏观量随时间的演化为
W i , j n + 1 = W i , j n + 1 Δ x F i - 1 / 2 , j - F i + 1 / 2 , j + 1 Δ y G i , j - 1 / 2 - G i , j + 1 / 2
其中
F i - 1 / 2 , j = ∫ t n t n + 1 ∫ u ψ H i - 1 / 2 , j dudvdt G i , j - 1 / 2 = ∫ t n t n + 1 ∫ v ψ H i , j - 1 / 2 dudvdt ψ = ( 1 , u , v ) T f i - 1 / 2 , α , β H = ∫ u H i - 1 / 2 , j dudv , g j - 1 / 2 , α , β H = ∫ v H i , j - 1 / 2 dudv n +1步的宏观量, 从而得到对应的平衡态, 以此来更新式(7), 得到n +1 步的分布函数. 故而, 发展UGKS 的核心便在于如何构造界面的气体分布函数.
下面对构造界面气体分布函数加以详细说明. 为了简单起见, 本文采用方向分裂技术来构造格式, 即对于二维流动而言, 认为在y 方向上分布函数分布是均匀的, 亦即 H y = 0 . 于是, 在x 方向上, 动理学方程变为
H t + u H x = H eq - H τ
上式存在局部解析解, 以时间步 t n = 0 x i + 1 / 2 = 0
H ( 0 , t , u ) = 1 τ ∫ 0 t H eq ( x ' , t ' , u ' ) e - ( t - t ' ) / τ dt ' + e - t / τ H 0 ( x n , 0 , u n )
其中, x ' = - u ( t - t ' ) .
初始时刻界面附近的分布函数 H 0
H 0 ( x , 0 , u α ) = H i + 1 / 2 , α L + σ i , α H x , x 0 H i + 1 / 2 , α R + σ i + 1 , α H x , x > 0
亦即
H i + 1 / 2 , α L = H i , α + ( x i + 1 / 2 - x i ) σ i , α H
其中
H i + 1 / 2 , α R = H i + 1 , α - ( x i + 1 - x i + 1 / 2 ) σ i + 1 , α H
H eq ( x , t , u α ) = H eq 0 [ 1 + ( 1 - H [ x ] ) a H L x + H [ x ] a H R x + A H t ]
而界面附近的平衡态分布函数近似由泰勒展开为
H eq 0
其中, x = 0 t = 0 H ( 0 , t , u α ) = M t 1 H eq 0 + M t 2 ( α H L H [ u α ] + α H R ( 1 - H [ u α ] ) ) ⋅ u α H eq 0 + M t 3 A H H eq 0 + e - t / τ [ ( H i + 1 / 2 , α L + ( - u α t ) σ i , α H ) H [ u α ] + ( H i + 1 / 2 , α R + ( - u α t ) σ i + 1 , α H ) ( 1 - H [ u α ] ) ]
M t 1 = 1 - e - t / τ
其中, M t 2 = τ ( - 1 + e - t / τ ) + t e - t / τ M t 3 = τ ( t / τ - 1 + e - t / τ ) α H L , α H R , A H .
上式中各系数 σ i H , σ i + 1 , α Δ t 34 ].
综上所述, 对基于气液相界面捕捉的统一气体动理学格式的构造方法作如下总结:
(1) 将原始的动理学方程(2)变为简化分布函数所对应的方程(9).
(2) 网格界面的简化气体分布函数通过动理学方程的积分解(10)而得到.
(3) 通过式(7)和式(8)分别更新分布函数和宏观量.
(4) 对以上三步进行循环, 便可求得流场的时间演化解.
3 算例验证
本节通过求出麦克斯韦等面积律数值解, 并与其对应的理论解相比较, 从而验证格式的有效性. 而后, 通过对范德瓦尔斯状态方程所描述的液滴表面张力的求取, 验证拉普拉斯定理. 最后模拟两个液滴的碰撞过程. 其中, 插值所使用的限制器为van Leer限制器. 时间步长 τ τ = χ 1 Δ t + χ 2 | p l - p r | p l + p r
p l = Λ ( ρ l ) , p r = Λ ( ρ r )
其中, χ 1 = 0.05 , χ 2 = 200 T = 0.9 .
3.1 麦克斯韦等面积律
气液两相均有稳态、亚稳态与完全非稳态三种状态. 下面采用本文提出的方法首先计算 ( X , Y ) ∈ [ 0,0.05 ] × [ 0,1 ] × ρ ( y ) = ρ ini , g + ρ ini , l - ρ ini , g 2 [ tanh 2 ( y - 15 L ) Υ - tanh 2 ( y - 45 L ) Υ ] 60 个均匀网格. X 与Y 方向均采用周期性边界条件. 初始速度为零, 密度分布为[36 ]
ρ ini , g , ρ ini , l
其中, 初始的气液密度分布 L Υ Y 方向网格边长, Υ = 2 L ( ρ ini , g = 0.4257 , ρ ini , l = 1.6573 ) . 为了避免表面张力对密度分布的影响, 初始的相界面是水平的.
例1. 初始值为麦克斯韦等面积律的理论解所对应的气液相密度, 即 ρ g = 0.4194 .
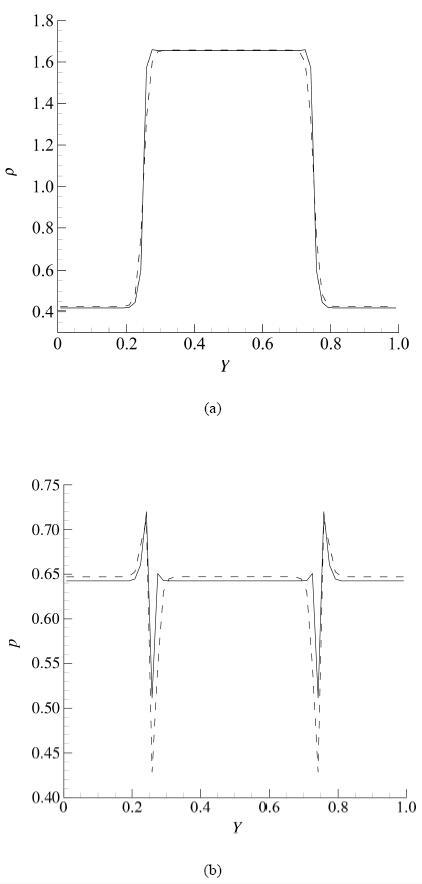
如图2 所示, 虚线为初始密度和压力分布, 实线便是数值计算所得到的结果, 其具体数值为 ρ l = 1.6550 ( ρ ini , g = 0.3 , ρ ini , l = 1.85 ) 12 ]的结果是一致的. 这是由于气相密度较小, 故而液相发生很小的数值振荡便会引起气相的较大偏差. 此外, 在相界面附近, 压力发生了急剧变化, 这与物理实际是不相符的, 究其原因, 这是由于范德瓦尔斯方程并非真实的状态方程所导致的. 范德瓦尔斯方程在两相共存区与实际情况偏差较大, 其所描述的相变线并非实际的相变过程线. 相界面处的密度分布在两相之间, 由图1 可知, 其对应的压力分布或大于气液两相的共存压力, 或小于气液两相的共存压力, 故而会在相界面处出现急剧变化, 这与文献[36 ]中图1 (b) 所示结果是一致的.
图2 例1: 虚线为初始分布, 实线为麦克斯韦等面积律的数值解.
Fig.2 Case1: The dotted line is the initial distribution. The solid line is the numerical result of Maxwell Construction.
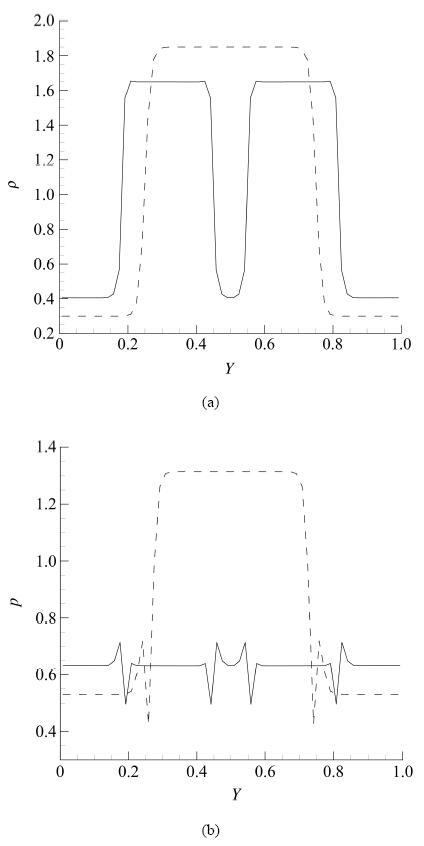
例2. 气液相初始密度均处于稳态, 具体值为 1 ρ α < 1 ρ ini , g < 1 ρ β . 其数值结果如图3 所示. 不同于例1的是Y = 0.5处由液相蒸发为气相, 这应该是由于初始液相的压力远大于平衡压力, 如图3 (b) 所示, 因此随着时间的演化, 液相通过相界面将压力扰动传到气相, 故而远离相界面的液相(Y = 0.5)压力便会急剧下降, 从而变为气相. 其压力与两侧的液体平衡, 如图3 (b)中实线所示. 如果降低初始液相的压力, 该现象便会消失. 总之, 无论最终存在几个相界面, 气液两相的压力是相等的, 且收敛在理论解附近.
图3 例2: 虚线为初始分布, 实线为麦克斯韦等面积律的数值解.
Fig.3 Case2: The dotted line is the initial distribution. The solid line is the numerical result of Maxwell Construction.
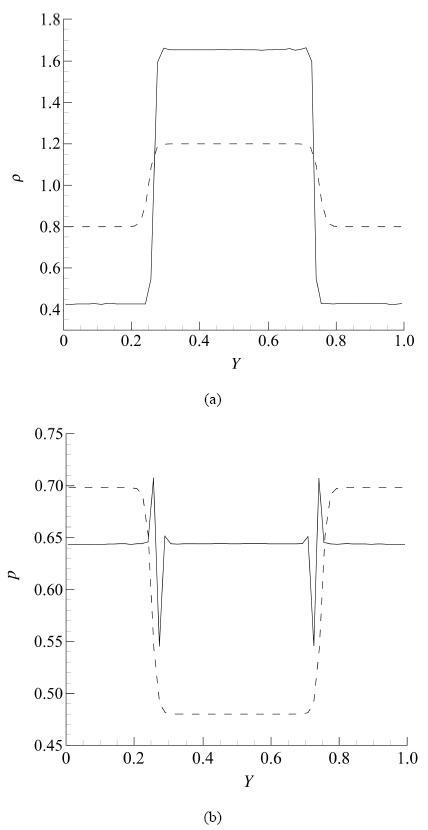
例3. 气液相初始密度均处于完全不稳定椭圆域, 即 1 ρ α < 1 ρ ini , l < 1 ρ β ( ρ ini , g = 0.8 , ρ ini , l = 1.2 ) . 具体值为 ∂ p / ∂ ρ .
其数值结果如图4 所示. 可以看到, 当气液两相初始密度均处于完全不稳定椭圆域时, 会通过蒸发和液化实现相分离, 并最终稳定在理论解附近.
图4 例3: 虚线为初始分布, 实线为麦克斯韦等面积律的数值解.
Fig.4 Case3: The dotted line is the initial distribution. The solid line is the numerical result of Maxwell Construction.
以上3种初值所对应的数值解对比如表1 所示, 结果表明, 数值解最终都可以回到适定的气液相密度, 即使麦克斯韦等面积律没有在格式中显式体现. 数值与理论的相对误差小于5%, 且网格界面可以用2到3个网格来捕捉, 从而证明该格式是稳定且有效的. 这也是由于范德瓦尔斯状态方程的物理特性所导致的. 对例2而言, 气液相初始密度均处于稳态. 由于两相压力不等, 液相压力大于理论解, 而气相压力小于理论解. 为了达到平衡, 如图1 所示, 液相参数便沿着范德瓦尔斯曲线向下游变化, 与此同时, 气相参数沿着曲线向上游运动, 于是在理论解附近达到平衡. 再如例3所示, 当流体密度处于椭圆域时, 由于 p / ρ < 0
为了进一步确认该格式有效性, 计算不同温度下, 以理论解为初值的数值解, 绘制出气液两相的共存曲线, 并与理论解相比较.
例4. 如上所述, 分别计算T = 0.847 5, 0.86, 0.88, 0.90, 0.92, 0.94, 0.96, 0.98八个温度下的数值解, 并与理论解对比, 其结果如图5 所示. 温度1为临界情况, 对应的便是图5 中的顶点, 此时流体由单一的气相变为气液共存相. 温度越低, 共存气液两相的密度比越大, 故而共存曲线为抛物线型. 显然, 数值解与理论解相符良好.
图5 范德瓦尔斯状态方程所描述的共存曲线.
Fig.5 Coexistence curve of vdW equation of state.
需要强调的是, 由于范德瓦尔斯方程的刚性, 由式(1)可知, 当T < 0.844时, 图1 所示的范德瓦尔斯曲线上, 相界面处的压力会出现负值, 从而导致$p/\rho < 0$, 亦即 λ < 0 λ λ > 0 . 因此利用该方程所构造的格式仅适用于T > 0.844的气液两相流计算. 通过理论解可知, T = 0.844 时的气液共存密度比为5. 随着温度的降低, 共存密度比会越大. 故而, 利用范德瓦尔斯方程构造的格式所适用的密度比小于5.
3.2 液滴表面张力
例5. 利用该格式计算范德瓦尔斯状态方程所描述的液滴表面张力, 验证其是否满足拉普拉斯定理. 对于UGKS而言, 计算域为1 × 1 , 温度T = 0.9, 速度为零. 初始的密度分布为[35 ] ρ ( x , y ) = ρ ini , l + ρ ini , g 2 - ρ ini , l + ρ ini , g 2 . tanh 2 ( x - x 1 ) 2 + ( y - y 1 ) 2 - R 0 Υ
其中, ρ ini , l = 1.6573 ρ ini , g = 0.4257 ( x 1 , y 1 ) R 0
根据拉普拉斯定理, 液滴内外的压力差与液滴半径成反比, 亦即 Δ P = P in - P out = σ / R
其中, σ R ρ = ( ρ in + ρ out ) / 2 Δ P R 0 = 0.1,0.15,0.2,0.25,0.3
通过对 × 1.75 × 1 0 - 3 , 1.2 × 1 0 - 3 , 8.5 × 1 0 - 4 , 6.7 × 1 0 - 4 , 6 × 1 0 - 4 180 时进行数值模拟可知, 液滴的内外压差分别为 σ = 1.75 × 1 0 - 4 . 以上结果与文献[36 ] 中图3 所示的结果在量级上是一致的. 易得其值与半径成反比, 如图6 所示, 计算可得表面张力 ×
图6 液滴内外压差与半径之间的关系.
Fig.6 The relationship between the pressure difference and the radius of droplet .
从物理上来讲, 由于范德瓦尔斯状态方程所描述的分子之间存在范德瓦尔斯力, 亦即相互作用势, 导致在相界面处势函数的法向二阶导数不等于切向二阶导数, 从而根据表面张力的定义[37-38 ], 可知由于范德瓦尔斯力的存在, 在物理上液滴表面会出现相应的表面张力, 进一步证明了上述数值结果的可靠性. 事实上, 之前已有诸多文献采用范德瓦尔斯模型中的内聚力来处理表面张力[39-41 ]. 因为从微观角度看, 表面张力就是由于液体表面的分子所受上层空间气相分子引力小于内部液相分子对它的吸引力造成, 合力方向指向液体内部.
3.3 液滴碰撞
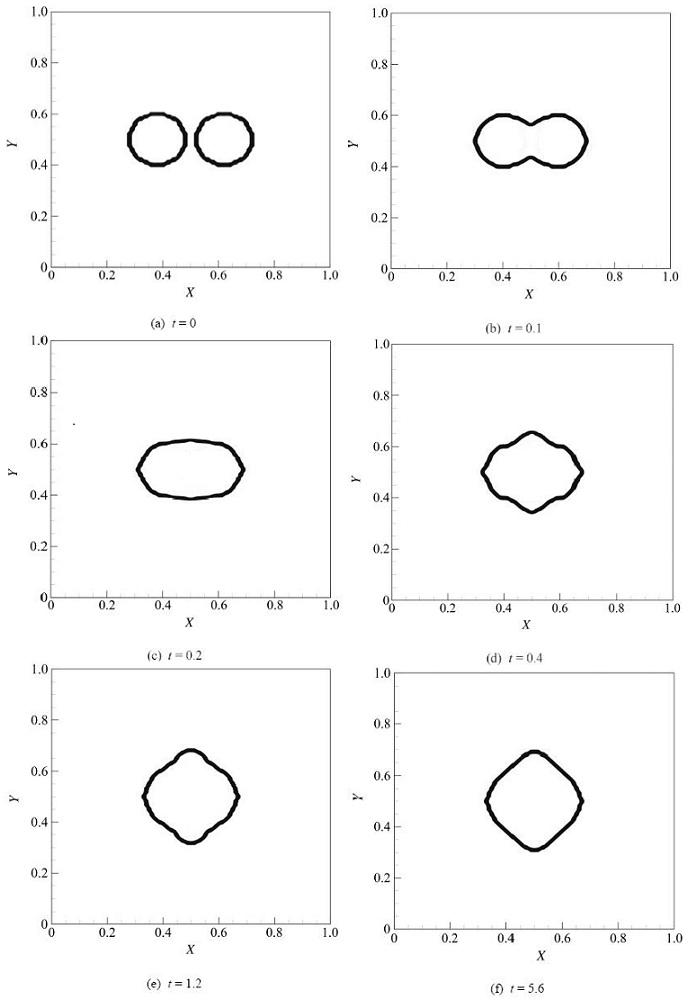
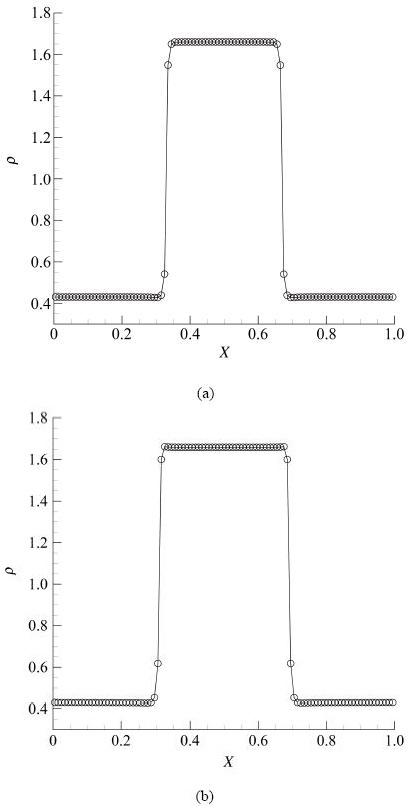
例6. 利用该格式计算两个液滴的碰撞, 计算域为1 ( ρ ini , g = 0.4257 , ρ ini , l = 1.6573 ) 1 , 温度T = 0.9. 初始的气液密度分布为置为麦克斯韦等面积律所对应的理论解, 亦即 × . 计算域划分为 100{Invalid MML}100. 两个液滴的中心坐标分别为(0.38,0.5)和(0.62,0.5), 其半径均为0.1, 如图7 (a) 所示. 两个液滴各自以U = 0.3 的初始速度对碰. 图7 为液滴形状随时间之演化, 可以看到液滴的碰撞和融合, 其过程与文献[33 ]相类似. 当两个液滴相向运动靠近时, 介于二者之间的气体就会被压缩形成一层气膜, 同时压强升高, 液滴发生微小变形. 因为液滴运动缓慢, 气膜内的气体在液滴接触之前有足够的时间流出, 所以液滴间就会发生微小变形后聚合 [42 ]. 由于耗散的作用, 液滴最终形态与标准的圆形还有些差异 [39 ]. 此外, 如图8 所示, 时间t = 1.6时所得X 和Y 方向的中心线的密度分布中, 两个网格点便可以捕捉一个尖锐的相界面.
图7 两个液滴碰撞的演化过程.
Fig.7 Time evolution of the collision of two droplets.
图8 密度分布: (a)图7 (f)中沿X 方向中心线, (b)图7 (f)中沿Y 方向中心线.
Fig.8 The density distribution (a) along the central line of Fig.7 (f) in the X direction and (b) along the central line of Fig.7 (f) in the Y direction.
需要强调的是, 该格式没有计算能量的演化, 亦即仅关注了相变所带来的传质问题, 而没有考虑相应的传热问题, 这也是下一步需要努力的方向.
4 结论
本文将范德瓦尔斯状态方程所表达的非理想气体效应引入统一气体动理学格式之中来捕捉气液相界面. 利用该方法得到麦克斯韦等面积律的数值解, 并与其对应的理论解相比较, 二者符合较好. 而后, 通过对范德瓦尔斯状态方程所描述的液滴表面张力进行数值计算, 验证了拉普拉斯定理. 此外, 通过模拟两个液滴的碰撞过程, 进一步证明了该格式的有效性. 但是, 由于范德瓦尔斯状态方程的特性, 其所构造的格式仅适用于液/气两相密度比小于5的情况. 下一步将致力于构造能够适用于大密度比(> 1000 )计算的数值格式.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
刘文超 , 刘曰武 . 低渗透煤层气藏中气‒水两相不稳定渗流动态分析
. 力学学报 , 2017 , 49 (4 ): 828 -835
[本文引用: 1]
(Liu Wenchao Liu Yuewu Dynamic analysis on gas-water two-phase unsteady seepage flow in low-permeable coalbed gas reservoirs
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (4 ): 828 -835 (in Chinese))
[本文引用: 1]
[2]
李康 , 刘娜 , 何志伟 等 . 一种基于双界面函数的界面捕捉方法
. 力学学报 , 2017 , 49 (6 ): 1290 -1300
(Li Kang Liu Na He Zhiwei et al .A new interface capturing method based on double interface functions
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (6 ): 1290 -1300 (in Chinese))
[3]
Hirt CW Nichols BD Volume of fluid (VOF) method for the dynamics of free boundaries
.J Comput Phys , 1981 , 39 (1 ): 201 -225
[本文引用: 1]
[4]
张洋 , 陈科 , 尤云祥 等 . 壁面约束对裙带气泡动力学的影响
. 力学学报 , 2017 , 49 (5 ): 1050 -1058
(Zhang Yang Chen Ke You Yunxiang et al .Confinement effect on the rising dynamics of a skirted bubble
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (5 ): 1050 -1058 (in Chinese))
[5]
Sussman M Smereka P Osher S A level set approach for computing solutions to incompressible two-phase flow
.J Comput Phys , 1994 , 114 (1 ): 146 -159
[本文引用: 1]
[6]
郭照立 , 郑楚光 . 格子Boltzmann 方法的原理及应用. 北京 : 科学出版社 , 2009
[本文引用: 1]
(Guo Zhaoli Zheng Chuguang. Principle and Application of Lattice Boltzmann Method. Beijing : Science Press , 2009 (in Chinese))
[本文引用: 1]
[7]
Shan X Chen H Lattice Boltzmann model for simulating flows with multiple phases and components
.Phys Rev E , 1993 , 47 (3 ): 1815 -1819
[本文引用: 2]
[8]
Shan X Chen H Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation
.Phys Rev E , 1994 , 49 (4 ): 2941 -2948
[9]
Gunstensen AK Rothman DH, aleski SZ, et al. Lattice Boltzmann model of immiscible fluids
.Phys Rev A , 1991 , 43 (8 ): 4320 -4327
[10]
Swift MR Osborn WR Yeomans JM Lattice Boltzmann simulation of nonideal fluids
.Phys Rev Lett , 1995 , 75 (5 ): 830 -833
[11]
Zhang R Chen H Lattice Boltzmann method for simulations of liquid-vapor thermal flows
.Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics , 2003 , 67 (6 ): 66711
[本文引用: 1]
[12]
Yuan, P , Schaefer L . Equations of state in a lattice Boltzmann model
.Phys Fluids , 2006 , 18 (4 ): 42101
[本文引用: 2]
[13]
Kupershtokh AL Karpov DI Medvedev DA et al .Stochastic models of partial discharge activity in solid and liquid dielectrics
.IET Science, Measurement & Technology , 2007 , 1 (6 ): 303 -311
[本文引用: 2]
[14]
胡安杰 . 多相流动格子Boltzmann 方法研究. [博士论文]
. 重庆: 重庆大学 , 2015
[本文引用: 1]
(Hu Anjie Study on lattice Boltzmann method for multiphase flow. [PhD Thesis]
. Chongqing: Chongqing University , 2015 (in Chinese))
[本文引用: 1]
[15]
Li Q Luo KH Kang QJ et al .Lattice Boltzmann methods for multiphase flow and phase-change heat transfer
.Progress in Energy and Combustion Science , 2016 , 52 : 62 -105
[16]
Chikatamarla SS Karlin IV Entropic lattice Boltzmann method for multiphase flows
.Physical Review Letters , 2015 , 114 (17 ): 174502
[17]
Wang Y Shu C Huang HB et al .Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio
.Journal of Computational Physics , 2015 , 280 : 404 -423
[18]
Liu H Kang Q Leonardi CR et al .Multiphase lattice Boltzmann simulations for porous media applications
.Computational Geosciences , 2016 , 20 (4 ): 777 -805
[19]
Lycett-Brown D Luo KH Improved forcing scheme in pseudopotential lattice Boltzmann methods for multiphase flow at arbitrarily high density ratios
.Physical Review E , 2015 , 91 (2 ): 023305
[20]
Shao JY Shu C A hybrid phase field multiple relaxation time lattice Boltzmann method for the incompressible multiphase flow with large density contrast
.International Journal for Numerical Methods in Fluids , 2015 , 77 (9 ): 526 -543
[21]
郭宇隆. 基于格子 Boltzmann 方法的气液混合流体模拟. [硕士论文]
. 广州: 华南理工大学 , 2015
(Guo Yulong Study on gas-liquid mixed fluid simulation based on lattice Boltzmann method [Master Thesis]
. Guangzhou: South China University of Technology , 2015 (in Chinese))
[22]
史冬岩 , 王志凯 , 张阿漫 . 一种模拟气液两相流的格子波尔兹曼改进模型
. 力学学报 , 2013 , 46 (2 ): 224 -233
(Shi Dongyan Wang Zhikai Zhang Aman Improved model of simulating gas-liquid two-phase flow by lattice Boltzmann
.Chinese Journal of Theoretical and Applied Mechanics 2013 , 46 (2 ): 224 -233 (in Chinese))
[23]
曾建邦 , 李隆键 , 廖全 等 . 格子 Boltzmann 方法在相变过程中的应用
. 物理学报 , 2010 , 59 (1 ): 178 -185
(Zeng Jianbang Li Longjian Liao Quan et al .Application of lattice Boltzmann method in phase transition process
.Acta Physica Sinica 2010 , 59 (1 ): 178 -185 (in Chinese))
[24]
Gong S Cheng P A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer
.International Journal of Heat and Mass Transfer , 2012 , 55 (17-18 ): 4923 -4927
[本文引用: 1]
[25]
Dong L Gong S Cheng P Direct numerical simulations of film boiling heat transfer by a phase-change lattice Boltzmann method
.International Communications in Heat and Mass Transfer , 2018 , 91 : 109 -116
[本文引用: 2]
[26]
Guo Z Zhao T S Shi Y Physical symmetry, spatial accuracy, and relaxation time of the lattice Boltzmann equation for micro gas flows
.Journal of Applied Physics , 2006 , 99 (7 ): 074903
[本文引用: 1]
[27]
Zhang Y Qin R Emerson DR Lattice Boltzmann simulation of rarefied gas flows in microchannels
.Physical Review E , 2005 , 71 (4 ): 047702
[28]
Guo Z Zheng C Shi B Lattice Boltzmann equation with multiple effective relaxation times for gaseous microscale flow
.Physical Review E , 2008 , 77 (3 ): 036707
[29]
Shan X Yuan XF Chen H Kinetic theory representation of hydrodynamics: a way beyond the Navier-Stokes equation
.Journal of Fluid Mechanics , 2006 , 550 (1 ): 413 -441
[30]
Xu K Huang JC A unified gas-kinetic scheme for continuum and rarefied flows
.Journal of Computational Physics , 2010 , 229 (20 ): 7747 -7764
[31]
毛枚良 , 江定武 , 李锦 等 . 气体动理学统一算法的隐式方法研究
. 力学学报 , 2015 , 47 (5 ): 822 -829
(Mao Meiliang Jiang Dingwu Li Jin et al .Study on implicit implementation of the unified gas kinetic scheme
.Chinese Journal of Theoretical and Applied Mechanics 2015 , 47 (5 ): 822 -829 (in Chinese))
[32]
江定武 , 毛枚良 , 李锦 等 . 气体动理学统一算法中相容性条件不满足引起的数值误差及其影响研究
. 力学学报 , 2015 , 47 (1 ):163 -168
(Jiang Dingwu Mao Meiliang Li Jin et al .Study on the numerical error introduced by dissatisfying the conservation constraint in UGKS and its effects
.Chinese Journal of Theoretical and Applied Mechanics 2015 , 47 (1 ): 163 -168 (in Chinese))
[33]
Xu K A kinetic method for hyperbolic-elliptic equations and its application in two-phase flow
.Journal of Computational Physics , 2001 , 166 (2 ): 383 -399
[本文引用: 2]
[34]
Wang Z Yan H Li Q et al .Unified gas-kinetic scheme for diatomic molecular flow with translational, rotational, and vibrational modes
.Journal of Computational Physics , 2017 , 350 : 237 -259
[本文引用: 1]
[35]
Huang H Sukop M Lu X Multiphase Lattice Boltzmann Methods: Theory and Application
. Beijing: John Wiley & Sons , 2015
[本文引用: 1]
[36]
Hu A Li L Chen S et al .On equations of state in pseudo-potential multiphase lattice Boltzmann model with large density ratio
.International Journal of Heat and Mass Transfer , 2013 , 67 : 159 -163
[本文引用: 3]
[37]
Hu A Li L Uddin R Force method in a pseudo-potential lattice Boltzmann model
.Journal of Computational Physics , 2015 , 294 : 78 -89
[本文引用: 1]
[38]
Shan X Pressure tensor calculation in a class of nonideal gas lattice Boltzmann models
.Physical Review E , 2008 , 77 (6 ): 066702
[39]
强洪夫 , 陈福振 , 高巍然 . 基于 SPH 方法的低韦伯数下三维液滴碰撞聚合与反弹数值模拟研究
. 工程力学 , 2012 , 29 (2 ): 21 -28
[本文引用: 1]
(Qiang Hongfu Chen Fuzhen Gao Weiran Simulation of coalescence and bouncing of three-dimensional droplet collisions with low weber numbers based on SPH method
.Journal of Engineering Mechanics 2012 , 29 (2 ): 21 -28 (in Chinese))
[本文引用: 1]
[40]
Nugent S Posch HA Liquid drops and surface tension with smoothed particle applied mechanics
.Physical Review E , 2000 , 62 : 4968 -4975
[41]
Meleán Y Sigalotti LDG Coalescence of colliding van der Waals liquid drops
.International Journal of Heat and Mass Transfer , 2005 , 48 : 4041 -4061
[42]
夏盛勇 . 三氧化二铝液滴碰撞机理及模型研究. [博士论文]
. 西安: 西北工业大学 , 2015
[本文引用: 1]
(Xia Shengyong Physics and model of alumina droplet collisions. [PhD Thesis]
. Xi’an: Northwestern Polytechnical University , 2015 (in Chinese))
[本文引用: 1]
低渗透煤层气藏中气?水两相不稳定渗流动态分析
1
2017
... 气液相界面运动的研究无论是在科学还是工程领域都是非常重要的[1-2 ]. 为了精确捕捉气液相界面, 一般有两种思路: (1)界面追踪, 该方法需要求解界面对流输运方程, 最具代表性的有流体体积法(VOF)[3-4 ]和水平集方法[5 ]. 以上两种方法均是以求解 Navier-Stokes (N-S)方程为基础;(2)自动捕捉, 亦即通过求解气液相变引起的分离, 来捕捉气液相界面. 该方法相对于界面追踪更有优势. 首先不需要求解界面的对流输运方程, 加之它是以波尔兹曼方程为基础, 对物理现象的描述更接近本质, 所以计算结果更加精确. ...
低渗透煤层气藏中气?水两相不稳定渗流动态分析
1
2017
... 气液相界面运动的研究无论是在科学还是工程领域都是非常重要的[1-2 ]. 为了精确捕捉气液相界面, 一般有两种思路: (1)界面追踪, 该方法需要求解界面对流输运方程, 最具代表性的有流体体积法(VOF)[3-4 ]和水平集方法[5 ]. 以上两种方法均是以求解 Navier-Stokes (N-S)方程为基础;(2)自动捕捉, 亦即通过求解气液相变引起的分离, 来捕捉气液相界面. 该方法相对于界面追踪更有优势. 首先不需要求解界面的对流输运方程, 加之它是以波尔兹曼方程为基础, 对物理现象的描述更接近本质, 所以计算结果更加精确. ...
Volume of fluid (VOF) method for the dynamics of free boundaries
1
1981
... 气液相界面运动的研究无论是在科学还是工程领域都是非常重要的[1-2 ]. 为了精确捕捉气液相界面, 一般有两种思路: (1)界面追踪, 该方法需要求解界面对流输运方程, 最具代表性的有流体体积法(VOF)[3-4 ]和水平集方法[5 ]. 以上两种方法均是以求解 Navier-Stokes (N-S)方程为基础;(2)自动捕捉, 亦即通过求解气液相变引起的分离, 来捕捉气液相界面. 该方法相对于界面追踪更有优势. 首先不需要求解界面的对流输运方程, 加之它是以波尔兹曼方程为基础, 对物理现象的描述更接近本质, 所以计算结果更加精确. ...
A level set approach for computing solutions to incompressible two-phase flow
1
1994
... 气液相界面运动的研究无论是在科学还是工程领域都是非常重要的[1-2 ]. 为了精确捕捉气液相界面, 一般有两种思路: (1)界面追踪, 该方法需要求解界面对流输运方程, 最具代表性的有流体体积法(VOF)[3-4 ]和水平集方法[5 ]. 以上两种方法均是以求解 Navier-Stokes (N-S)方程为基础;(2)自动捕捉, 亦即通过求解气液相变引起的分离, 来捕捉气液相界面. 该方法相对于界面追踪更有优势. 首先不需要求解界面的对流输运方程, 加之它是以波尔兹曼方程为基础, 对物理现象的描述更接近本质, 所以计算结果更加精确. ...
1
2009
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
1
2009
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
Lattice Boltzmann model for simulating flows with multiple phases and components
2
1993
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
... ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation
1994
Rothman DH, aleski SZ, et al. Lattice Boltzmann model of immiscible fluids
1991
Lattice Boltzmann simulation of nonideal fluids
1995
Lattice Boltzmann method for simulations of liquid-vapor thermal flows
1
2003
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
Equations of state in a lattice Boltzmann model
2
2006
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
... 如图2 所示, 虚线为初始密度和压力分布, 实线便是数值计算所得到的结果, 其具体数值为 ρ l = 1.6550 ( ρ ini , g = 0.3 , ρ ini , l = 1.85 ) 12 ]的结果是一致的. 这是由于气相密度较小, 故而液相发生很小的数值振荡便会引起气相的较大偏差. 此外, 在相界面附近, 压力发生了急剧变化, 这与物理实际是不相符的, 究其原因, 这是由于范德瓦尔斯方程并非真实的状态方程所导致的. 范德瓦尔斯方程在两相共存区与实际情况偏差较大, 其所描述的相变线并非实际的相变过程线. 相界面处的密度分布在两相之间, 由图1 可知, 其对应的压力分布或大于气液两相的共存压力, 或小于气液两相的共存压力, 故而会在相界面处出现急剧变化, 这与文献[36 ]中图1 (b) 所示结果是一致的. ...
Stochastic models of partial discharge activity in solid and liquid dielectrics
2
2007
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
... ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
多相流动格子Boltzmann 方法研究. [博士论文]
1
2015
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
多相流动格子Boltzmann 方法研究. [博士论文]
1
2015
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
Lattice Boltzmann methods for multiphase flow and phase-change heat transfer
2016
Entropic lattice Boltzmann method for multiphase flows
2015
Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio
2015
Multiphase lattice Boltzmann simulations for porous media applications
2016
Improved forcing scheme in pseudopotential lattice Boltzmann methods for multiphase flow at arbitrarily high density ratios
2015
A hybrid phase field multiple relaxation time lattice Boltzmann method for the incompressible multiphase flow with large density contrast
2015
Boltzmann 方法的气液混合流体模拟. [硕士论文]
2015
Boltzmann 方法的气液混合流体模拟. [硕士论文]
2015
一种模拟气液两相流的格子波尔兹曼改进模型
2013
一种模拟气液两相流的格子波尔兹曼改进模型
2013
Boltzmann 方法在相变过程中的应用
2010
Boltzmann 方法在相变过程中的应用
2010
A lattice Boltzmann method for simulation of liquid-vapor phase-change heat transfer
1
2012
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
Direct numerical simulations of film boiling heat transfer by a phase-change lattice Boltzmann method
2
2018
... 由波尔兹曼方程离散所得的格子波尔兹曼方程, 在特定条件下(低马赫数), 通过 Chapman-Enskog 展开可以推导出不可压 N-S 方程[6 ]. 以此为基础的格子波尔兹曼方法由于不再受理想气体的限制, 在近几十年里得到充分的发展和广泛的应用[7-23 ]. 为了能够自动捕捉相界面, 需要对非理想状态下, 分子之间的作用力加以建模. 基于此, 学者们已经建立了多种模型 [7-10 ]. 其中, 单组分伪势模型由于形式简洁受到广泛应用. Zhang 和Chen [11 ]在 2003 年对单组分伪势模型引入范德瓦尔斯(van der Waals, vdW)状态方程, 并提出直接采用势函数的方式计算粒子间相互作用力来提高伪势模型的稳定性. 为提高模型模拟的密度比, 2006 年, Yuan等 [12 ] 引入不同非理想气体状态方程, 发现模型可以在很高密度下(>1000)仍然保持稳定. 2007 年, Kupeshtokh 等 [13 ]发现, 当采用修正平衡态分布函数作用力方法时, 模拟所得的结果受松弛时间的影响, 这与物理实际不吻合. 为解决这个问题, 他们提出了一种新的作用力模型 [13 ], 即有限差分模型(EDM). 此模型基本解决了单组份伪势模型在大密度比条件下不稳定的问题, 但是其采用对比态方程中涉及物理单位与实际单位的转换关系不满足格子波尔兹曼模拟的相似性原理, 会使其在应用中出现很多问题. 另外, 模型的提出大多源于经验, 缺乏理论基础. 因此, 针对以上问题, 胡安杰 [14 ]对这个模型进行理论分析, 并且基于其模型做出了改进. 此外, 2012 年Gong 和Cheng [24 ]通过将密度和温度分布函数引入格子波尔兹曼方法, 并嵌入了Peng-Robinson 状态方程, 研究了气泡的生长和脱离水平壁面问题. 最近, 该团队又通过修正伪势模型研究了水平面的薄膜沸腾传热问题 [25 ], 为格子波尔兹曼方法在传热方面的应用做出很大贡献. ...
... 例6. 利用该格式计算两个液滴的碰撞, 计算域为1 ( ρ ini , g = 0.4257 , ρ ini , l = 1.6573 ) 1 , 温度T = 0.9. 初始的气液密度分布为置为麦克斯韦等面积律所对应的理论解, 亦即 × . 计算域划分为 100{Invalid MML}100. 两个液滴的中心坐标分别为(0.38,0.5)和(0.62,0.5), 其半径均为0.1, 如图7 (a) 所示. 两个液滴各自以U = 0.3 的初始速度对碰. 图7 为液滴形状随时间之演化, 可以看到液滴的碰撞和融合, 其过程与文献[33 ]相类似. 当两个液滴相向运动靠近时, 介于二者之间的气体就会被压缩形成一层气膜, 同时压强升高, 液滴发生微小变形. 因为液滴运动缓慢, 气膜内的气体在液滴接触之前有足够的时间流出, 所以液滴间就会发生微小变形后聚合 [42 ]. 由于耗散的作用, 液滴最终形态与标准的圆形还有些差异 [39 ]. 此外, 如图8 所示, 时间t = 1.6时所得X 和Y 方向的中心线的密度分布中, 两个网格点便可以捕捉一个尖锐的相界面. ...
Physical symmetry, spatial accuracy, and relaxation time of the lattice Boltzmann equation for micro gas flows
1
2006
... 如前所述, 格子波尔兹曼方程适用于低速不可压连续流体的模拟, 虽然通过高阶矩的方法试图将格子波尔兹曼方法推广至稀薄流动 [26-29 ], 但是限于弱非平衡态. 近年来, 基于气体动理学BGK 方程, 离散速度空间的方法发展起来了一套适用于全流域的统一气体动理学格式(unified gas-kinetic scheme, UGKS) [30-32]. 该格式的精要在于将自由输运和粒子碰撞耦合起来更新宏观物理量和微观气体分布函数. 不同于其他诸多方法的关键是, 在计算网格界面通量时采用动理学方程的积分解. 该积分解描述的是两尺度的物理过程, 其一为粒子碰撞所带来的平衡态的积分所体现的流体力学尺度, 其二则是粒子自由输运所体现的动理学尺度. 二者之间的权重取决于网格分辨率和时间步长. 因此, 该格式适用于全流域的计算. ...
Lattice Boltzmann simulation of rarefied gas flows in microchannels
2005
Lattice Boltzmann equation with multiple effective relaxation times for gaseous microscale flow
2008
Kinetic theory representation of hydrodynamics: a way beyond the Navier-Stokes equation
2006
A unified gas-kinetic scheme for continuum and rarefied flows
2010
气体动理学统一算法中相容性条件不满足引起的数值误差及其影响研究
2015
气体动理学统一算法中相容性条件不满足引起的数值误差及其影响研究
2015
A kinetic method for hyperbolic-elliptic equations and its application in two-phase flow
2
2001
... 这里, 平衡态 g = ρ λ < . 其中, τ ρ ( U , V ) K ξ 2 = ξ 1 2 + ξ 2 2 + ⋯ + ξ K 2 . 其中, ξ 1 , ξ 2 , ⋯ , ξ K λ 33 ]. 其形式如下 ...
... 例6. 利用该格式计算两个液滴的碰撞, 计算域为1 ( ρ ini , g = 0.4257 , ρ ini , l = 1.6573 ) 1 , 温度T = 0.9. 初始的气液密度分布为置为麦克斯韦等面积律所对应的理论解, 亦即 × . 计算域划分为 100{Invalid MML}100. 两个液滴的中心坐标分别为(0.38,0.5)和(0.62,0.5), 其半径均为0.1, 如图7 (a) 所示. 两个液滴各自以U = 0.3 的初始速度对碰. 图7 为液滴形状随时间之演化, 可以看到液滴的碰撞和融合, 其过程与文献[33 ]相类似. 当两个液滴相向运动靠近时, 介于二者之间的气体就会被压缩形成一层气膜, 同时压强升高, 液滴发生微小变形. 因为液滴运动缓慢, 气膜内的气体在液滴接触之前有足够的时间流出, 所以液滴间就会发生微小变形后聚合 [42 ]. 由于耗散的作用, 液滴最终形态与标准的圆形还有些差异 [39 ]. 此外, 如图8 所示, 时间t = 1.6时所得X 和Y 方向的中心线的密度分布中, 两个网格点便可以捕捉一个尖锐的相界面. ...
Unified gas-kinetic scheme for diatomic molecular flow with translational, rotational, and vibrational modes
1
2017
... 上式中各系数 σ i H , σ i + 1 , α Δ t 34 ]. ...
Multiphase Lattice Boltzmann Methods: Theory and Application
1
2015
... 例5. 利用该格式计算范德瓦尔斯状态方程所描述的液滴表面张力, 验证其是否满足拉普拉斯定理. 对于UGKS而言, 计算域为1 × 1 , 温度T = 0.9, 速度为零. 初始的密度分布为[35 ] ρ ( x , y ) = ρ ini , l + ρ ini , g 2 - ρ ini , l + ρ ini , g 2 . tanh 2 ( x - x 1 ) 2 + ( y - y 1 ) 2 - R 0 Υ
On equations of state in pseudo-potential multiphase lattice Boltzmann model with large density ratio
3
2013
... 气液两相均有稳态、亚稳态与完全非稳态三种状态. 下面采用本文提出的方法首先计算 ( X , Y ) ∈ [ 0,0.05 ] × [ 0,1 ] × ρ ( y ) = ρ ini , g + ρ ini , l - ρ ini , g 2 [ tanh 2 ( y - 15 L ) Υ - tanh 2 ( y - 45 L ) Υ ] 60 个均匀网格. X 与Y 方向均采用周期性边界条件. 初始速度为零, 密度分布为[36 ] ...
... 如图2 所示, 虚线为初始密度和压力分布, 实线便是数值计算所得到的结果, 其具体数值为 ρ l = 1.6550 ( ρ ini , g = 0.3 , ρ ini , l = 1.85 ) 12 ]的结果是一致的. 这是由于气相密度较小, 故而液相发生很小的数值振荡便会引起气相的较大偏差. 此外, 在相界面附近, 压力发生了急剧变化, 这与物理实际是不相符的, 究其原因, 这是由于范德瓦尔斯方程并非真实的状态方程所导致的. 范德瓦尔斯方程在两相共存区与实际情况偏差较大, 其所描述的相变线并非实际的相变过程线. 相界面处的密度分布在两相之间, 由图1 可知, 其对应的压力分布或大于气液两相的共存压力, 或小于气液两相的共存压力, 故而会在相界面处出现急剧变化, 这与文献[36 ]中图1 (b) 所示结果是一致的. ...
... 通过对 × 1.75 × 1 0 - 3 , 1.2 × 1 0 - 3 , 8.5 × 1 0 - 4 , 6.7 × 1 0 - 4 , 6 × 1 0 - 4 180 时进行数值模拟可知, 液滴的内外压差分别为 σ = 1.75 × 1 0 - 4 . 以上结果与文献[36 ] 中图3 所示的结果在量级上是一致的. 易得其值与半径成反比, 如图6 所示, 计算可得表面张力 ×
Force method in a pseudo-potential lattice Boltzmann model
1
2015
... 从物理上来讲, 由于范德瓦尔斯状态方程所描述的分子之间存在范德瓦尔斯力, 亦即相互作用势, 导致在相界面处势函数的法向二阶导数不等于切向二阶导数, 从而根据表面张力的定义[37-38 ], 可知由于范德瓦尔斯力的存在, 在物理上液滴表面会出现相应的表面张力, 进一步证明了上述数值结果的可靠性. 事实上, 之前已有诸多文献采用范德瓦尔斯模型中的内聚力来处理表面张力[39-41 ]. 因为从微观角度看, 表面张力就是由于液体表面的分子所受上层空间气相分子引力小于内部液相分子对它的吸引力造成, 合力方向指向液体内部. ...
Pressure tensor calculation in a class of nonideal gas lattice Boltzmann models
2008
SPH 方法的低韦伯数下三维液滴碰撞聚合与反弹数值模拟研究
1
2012
... 从物理上来讲, 由于范德瓦尔斯状态方程所描述的分子之间存在范德瓦尔斯力, 亦即相互作用势, 导致在相界面处势函数的法向二阶导数不等于切向二阶导数, 从而根据表面张力的定义[37-38 ], 可知由于范德瓦尔斯力的存在, 在物理上液滴表面会出现相应的表面张力, 进一步证明了上述数值结果的可靠性. 事实上, 之前已有诸多文献采用范德瓦尔斯模型中的内聚力来处理表面张力[39-41 ]. 因为从微观角度看, 表面张力就是由于液体表面的分子所受上层空间气相分子引力小于内部液相分子对它的吸引力造成, 合力方向指向液体内部. ...
SPH 方法的低韦伯数下三维液滴碰撞聚合与反弹数值模拟研究
1
2012
... 从物理上来讲, 由于范德瓦尔斯状态方程所描述的分子之间存在范德瓦尔斯力, 亦即相互作用势, 导致在相界面处势函数的法向二阶导数不等于切向二阶导数, 从而根据表面张力的定义[37-38 ], 可知由于范德瓦尔斯力的存在, 在物理上液滴表面会出现相应的表面张力, 进一步证明了上述数值结果的可靠性. 事实上, 之前已有诸多文献采用范德瓦尔斯模型中的内聚力来处理表面张力[39-41 ]. 因为从微观角度看, 表面张力就是由于液体表面的分子所受上层空间气相分子引力小于内部液相分子对它的吸引力造成, 合力方向指向液体内部. ...
Liquid drops and surface tension with smoothed particle applied mechanics
2000
Coalescence of colliding van der Waals liquid drops
2005
三氧化二铝液滴碰撞机理及模型研究. [博士论文]
1
2015
... 例6. 利用该格式计算两个液滴的碰撞, 计算域为1 ( ρ ini , g = 0.4257 , ρ ini , l = 1.6573 ) 1 , 温度T = 0.9. 初始的气液密度分布为置为麦克斯韦等面积律所对应的理论解, 亦即 × . 计算域划分为 100{Invalid MML}100. 两个液滴的中心坐标分别为(0.38,0.5)和(0.62,0.5), 其半径均为0.1, 如图7 (a) 所示. 两个液滴各自以U = 0.3 的初始速度对碰. 图7 为液滴形状随时间之演化, 可以看到液滴的碰撞和融合, 其过程与文献[33 ]相类似. 当两个液滴相向运动靠近时, 介于二者之间的气体就会被压缩形成一层气膜, 同时压强升高, 液滴发生微小变形. 因为液滴运动缓慢, 气膜内的气体在液滴接触之前有足够的时间流出, 所以液滴间就会发生微小变形后聚合 [42 ]. 由于耗散的作用, 液滴最终形态与标准的圆形还有些差异 [39 ]. 此外, 如图8 所示, 时间t = 1.6时所得X 和Y 方向的中心线的密度分布中, 两个网格点便可以捕捉一个尖锐的相界面. ...
三氧化二铝液滴碰撞机理及模型研究. [博士论文]
1
2015
... 例6. 利用该格式计算两个液滴的碰撞, 计算域为1 ( ρ ini , g = 0.4257 , ρ ini , l = 1.6573 ) 1 , 温度T = 0.9. 初始的气液密度分布为置为麦克斯韦等面积律所对应的理论解, 亦即 × . 计算域划分为 100{Invalid MML}100. 两个液滴的中心坐标分别为(0.38,0.5)和(0.62,0.5), 其半径均为0.1, 如图7 (a) 所示. 两个液滴各自以U = 0.3 的初始速度对碰. 图7 为液滴形状随时间之演化, 可以看到液滴的碰撞和融合, 其过程与文献[33 ]相类似. 当两个液滴相向运动靠近时, 介于二者之间的气体就会被压缩形成一层气膜, 同时压强升高, 液滴发生微小变形. 因为液滴运动缓慢, 气膜内的气体在液滴接触之前有足够的时间流出, 所以液滴间就会发生微小变形后聚合 [42 ]. 由于耗散的作用, 液滴最终形态与标准的圆形还有些差异 [39 ]. 此外, 如图8 所示, 时间t = 1.6时所得X 和Y 方向的中心线的密度分布中, 两个网格点便可以捕捉一个尖锐的相界面. ...