引言
移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象.
上述研究都是针对压力脉动提出了各种缓解压力振荡的方法, 然而对引起压力振荡的原因并没有进行详尽地研究.本文将对MPS方法中压力脉动的机理展开研究.首先通过对粒子模型的一维简化, 阐述了MPS方法中压力波动与由于粒子之间相互位置关系所引起的粒子数密度偏差波动之间的相互关系.并且通过在MPS方法中加入碰撞模型的方法, 控制在模拟过程中粒子之间的相互位置, 从而研究数密度偏差波动和压力波动之间的关系.并且对比了采用两种不同核函数时压力振荡的波动情况, 通过从核函数与粒子数密度偏差之间的相互关系出发, 探讨核函数与压力脉动之间的联系.
1 数值计算方法
1.1 控制方程
对于不可压缩流体, 其连续性方程和Navier-Stokes方程可写成如下形式
d ρ dt = 0 (1)
ρ du dt = - ∇ P + μ ∇ 2 u + G (2)
其中, u 表示流体的速度, P 表示流体的压力, ρ μ G 表示重力加速度, t 表示时间.
1.2 MPS方法的数值模型
1.2.1 核函数
在MPS方法中, 粒子间相互作用模型是用来离散微分算子的.其中最基本的一个函数就是核函数, 粒子间的相互作用的关系在MPS法中最基本的体现就是通过核函数来实现的, 核函数也是MPS 法中其他所有模型的基础.N-S方程中的微分算子是通过核函数来转化为粒子之间的相互作用.在MPS 方法中, 核函数的公式如下
$\begin{equation}W(r)=\begin{cases} \dfrac{r_e}{r}-1,& 0<r<r_e\\ 0,& r\geqslant r_e \end{cases}\end{equation}$ (3)
其中, ${r=|r_i-r_j}$|是两个粒子之间的距离, ${r_i}$是{i}粒子的位置, ${r}_j$ 是{i}粒子支持域内的{j} 粒子的位置, ${r}_e$ 是粒子作用域的半径, 一般${r}_e=2.1 l_{0}$, ${l}_0$是初始粒子间距. 核函数${w(r)}$实质上是一种权函数, 也可认为是粒子同周围邻居的作用力函数, 其值由粒子间的距离所决定. 粒子之间距离相近, 核函数${w(r)}$ 的值就大;粒子之间距离较远, 核函数${w(r)}$ 的值就小. 并且, 研究的粒子不依赖于粒子作用域的半径${r_e}$以外的粒子. 以外的粒子.
1.2.2 粒子数密度
MPS法通过引入粒子数密度来替代密度的概念, 粒子数密度反映的是流场中粒子分布.粒子数密度的公式如下
$\begin{equation}n_i=\sum_{j\neq i}w\begin{pmatrix}\begin{vmatrix}r_j-r_i\end{vmatrix}\end{pmatrix}\end{equation}$(4)
其中, 粒子${j}$是在粒子${i}$支持域内的粒子. 粒子数密度正比于流体密度, 对于不可压缩流体, 粒子数密度为常数, 并且${n_i=n^0}$, 其中${n^0}$ 是初始的粒子数密度.
1.2.3 梯度模型
梯度模型是根据其数学概念离散表示粒子之间的相互作用. 假定$\phi$ 为任意标量, 那么表示粒子之间相互作用的梯度模型可写为
$\begin{equation}\big\langle\nabla{\phi}\big\rangle_i=\dfrac{d}{n^0}\sum_{j\neq i}\begin{bmatrix}\dfrac{{\phi}_j-{\phi}_i}{|r_j-r_i|^2}(r_j-r_i)w_{ij}\end{bmatrix}\end{equation}$ (5)
上式中, ${d}$是空间维度, ${n^0}$是初始粒子数密度值, ${w_{ij}}$表示${w(|r_j-r_i|)}$. 在MPS 法的模拟中, 只有作为标量的压力值{P}参与上式的计算. 为了增加计算的稳定性, 本文采用的梯度模型如下
$\begin{equation}\big\langle\nabla P\big\rangle=\dfrac{d}{n^0}\sum_{j\neq i}\begin{bmatrix}\dfrac{P_j-P_{i\rm min}}{|r_j-r_i|^2}(r_j-r_i)w_{ij}\end{bmatrix}\end{equation}$(6)
式中, ${P_j}$是{i}粒子的支持域内粒子的压力, ${P_{i\rm min}}$ 是{i}粒子支持域内所有粒子中压力最小的粒子.
1.2.4 拉普拉斯模型
拉普拉斯微分算子是用来度量物理量的空间扩散.假定Φ 为任意标量, 那么表示粒子之间相互作用的拉普拉斯模型可写为
$\begin{equation}\big\langle\nabla^2{\phi}\big\rangle_i=\dfrac{2d}{\lambda n^0}\sum_{j\neq i}\begin{bmatrix}({\phi}_j-{\phi}_i)w_{ij}\end{bmatrix}\end{equation}$ (7)
其中,d是空间维度, λ
$\begin{equation}\lambda=\sum_{j\neq i}\begin{vmatrix}r_j-r_i\end{vmatrix}^2w_{ij}/\sum_{j\neq i}w_{ij}\end{equation}$(8)
λ
1.2.5 压力泊松方程
在传统的MPS方法中, 压力的求解是通过求解压力泊松方程得到的, 其中, 系数矩阵项的离散通过拉普拉斯模型进行离散, 源项采用的是粒子数密度的偏差, 其公式如下
$\begin{equation}\dfrac{2d}{\lambda n^0}\sum_{j\neq i}\begin{bmatrix}\begin{pmatrix}P_j-P_i\end{pmatrix}w_{ij}\end{bmatrix}=-\dfrac{\rho}{\Delta t^2}\dfrac{\langle n^*\rangle_i-n^0}{n^0}\end{equation}$(9)
1.3 碰撞模型
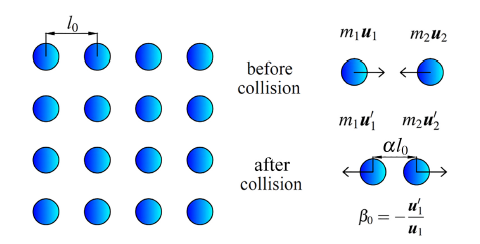
对于流体内部粒子, 当粒子相互靠近时, 粒子之间的排斥力会增加, 特别在流体剧烈运动时, 流体内部会出现两个粒子之间距离非常接近的情况, 此时粒子之间的压力将会非常大, 从而流体内部会出现压力振荡.对于自由表面粒子, 由于自由表面粒子的压力在计算过程中被设置为0, 当飞溅的自由表面粒子突然碰撞自由表面并进入流体内部时, 此时该粒子的压力会突然增加, 这也是造成压力计算不稳定性的一个重要原因.针对上述情况, 在计算过程中加入了一个碰撞模型, 这个碰撞模型采用Lee[17 ] 在其研究中提出的碰撞模型.图1 是碰撞模型的示意图.在初始时刻, 粒子均匀分布, 粒子之间的距离为${l_0}$, 两个相互碰撞的粒子在碰撞前的质量和速度分别为当粒子之间的间距小于${al_0}$ 时, 粒子发生碰撞, 碰撞后的速度分别为${\textbf{u}^\prime_1}$和~${\textbf{u}^\prime_2}$. 其中$\alpha$ 是碰撞模型发生作用的系数, 一般取0.5~0.9之间, ${\beta_0}$ 是粒子碰撞后的反弹速度系数, 一般取0.2.
图1 碰撞模型示意图
Fig.1 Schematic diagram of collision model
2 压力振荡机理分析
在传统MPS方法中, 压力的求解是通过求解压力泊松方程得到的. 观察压力泊松方程, 即式(9)可以发现, 压力的求解与核函数和粒子数密度密切相关. 首先, 选择式(3)中的核函数作为研究对象. 式(3)中的核函数是MPS 方法中应用最为广泛的核函数, 在本研究中称之为MPS核函数. 为了更为清楚地分析MPS 方法中压力脉动的机理, 将问题简化为一维粒子模型, 图2 是在MPS核函数下粒子运动的一维化简图, 其中红色粒子为中心粒子, 蓝色粒子为其支持域内的周围粒子. 在求解压力泊松方程的中间步有一个临时可压缩阶段, 以下分析该过程的物理机理. 图2 中的蓝色虚线粒子表示的是蓝色粒子1 在临时可压缩过程中向右运动X倍${l_0}$的距离. 纵坐标是MPS核函数的粒子数密度偏差${(n_i-n^0)/n^0}$.当X>0 时, 粒子1 远离红色中心粒子, 流体处于拉伸状态, 粒子数密度偏差${(n_i-n^0)/n^0}$<0, 中心粒子与粒子1 之间的压力变小. 当X<0 时, 粒子1靠近红色中心粒子, 此时流体处于压缩状态, 粒子数密度偏差${(n_i-n^0)/n^0}$>0, 中心粒子与粒子1 之间的压力变大.
图2 MPS核函数下粒子的一维化简
Fig.2 Simplified one-dimensional particle model of MPS kernel function
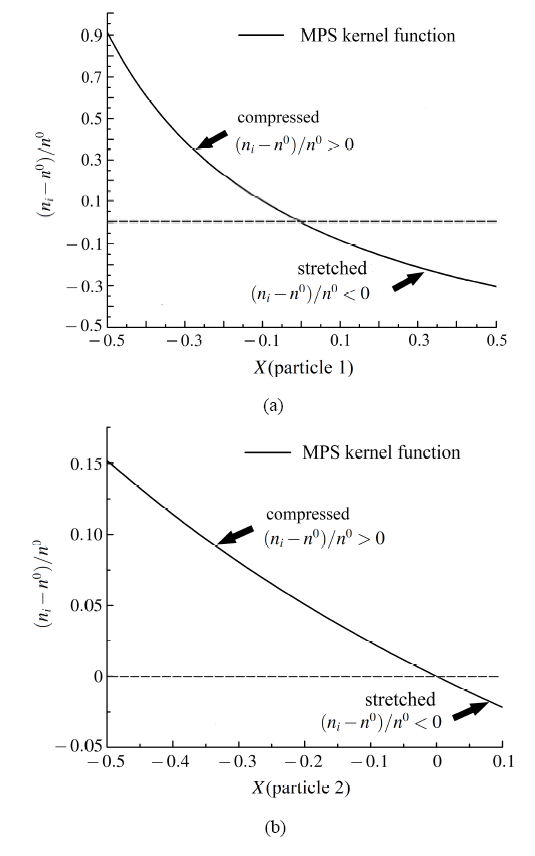
同理, 图3(b)横坐标是粒子2向右移动X倍${l_0}$ 距离, 纵坐标是MPS 核函数的粒子数密度偏差${(n_i-n^0)/n^0}$. 同样, 当${X}>0$时, 粒子2远离红色中心粒子, 流体处于拉伸状态, 粒子数密度偏差${(n_i-n^0)/n^0}<0$, 中心粒子与粒子2 之间的压力变小. 当${X}<0$时, 粒子2 靠近红色中心粒子, 此时流体处于压缩状态, 粒子数密度偏差${(n_i-n^0)/n^0>0}$, 中心粒子与粒子2 之间的压力变大. 对比粒子1 和粒子2, 移动相同距离后, 粒子1 造成的粒子数密度偏差比粒子2 大, 所以距离红色中心粒子较近的粒子1 对红色中心粒子的压力波动影响较大. 上述就是一维情况下的压力振荡机理, 当处理二维和三维问题时, 其基本的原理和一维情况是类似的, 但是粒子之间的相互位置关系会随着维度的增加而变得复杂.
图3 粒子1, 2向右移动距离和粒子数密度偏差$(n_i-n^0)/n^0$之间的关系
Fig.3 The deviation in particle number density of different particle displacement
3 数值计算
3.1 溃坝模型
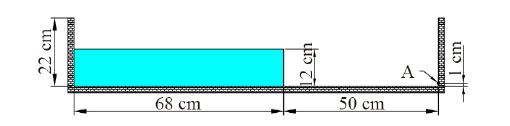
溃坝模型是一个经典的自由表面大变形问题, 在溃坝过程中, 流体的流动具有强烈的非线性特征. 很多学者[25 -30 ] 采用粒子法对溃坝问题进行模拟, 并且取得了很好的效果. 在本研究中, 选用溃坝模型作为算例来研究MPS方法中压力振荡现象. Hu等[31 ] 在其自由表面流动问题中, 采用实验的方法对溃坝问题进行了研究, 并且测量了在溃坝过程中的压力-时间曲线. 本研究采用的溃坝模型尺寸和文献[31 ] 的溃坝模型相同. 图4 是溃坝模型的具体尺寸, 溃坝高22 cm, 溃坝长118 cm, 流体高12 cm, 流体长68 m. 流体为水, 密度为1000kg/m3 , 水的动力黏度为1.000 6×10-6 m2 /s, 溃坝竖直壁面上的A 点是压力监测点. 重力加速度为9.8m/s2 , 初始粒子间距等于0.005 m, 粒子数量等于4592 个, 时间步长为0.001s.
图4 溃坝模型示意图
Fig.4 Schematic diagram of dam break model
3.2 数值计算方案
在压力振荡的机理分析中, 粒子数密度偏差${(n_i-n^0)/n^0}$的波动将会造成局部流体处于拉伸或者压缩状态, 从而造成局部流体粒子间的压力波动. 为了控制粒子之间相互位置在模拟过程中的波动程度, 采用碰撞模型来控制模拟过程中粒子之间的相互位置关系. ${\alpha}$ 是判断两个粒子是否相互碰撞的参数, 当粒子之间的间距小于${\alpha}l_0$ 时, 碰撞模型将发生作用, 两个相互靠近的粒子将由于碰撞模型的作用而发生相互分离. 那么当${\alpha}$ 取不同的数值, 粒子之间的距离将会控制在不同的范围内. 图5 的横坐标是图2 一维模型中粒子1 向右移动{X}倍${l_0}$ 的距离, 纵坐标是粒子数密度偏差${(n_i-n^0)/n^0}$.
从图5 中可以看到, 当 X = - 0.1 ( n i - n 0 ) / n 0 = 0.101 X = 0.1 ( n i - n 0 ) / n 0 = - 0.083 α l 0 ( n i - n 0 ) / n 0 表1 是采用MPS 核函数时, 在不同碰撞系数下的粒子数密度偏差的最大波动值.从表1 中可以看到, 随着α ( n i - n 0 ) / n 0 α
图5 $\alpha=0.9$时粒子数密度偏差的波动范围示意图
Fig.5 The fluctuation of the deviation in particle number density when $\alpha=0.9$
3.3 MPS核函数计算结果
图6 是采用MPS核函数时, 压力‒时间、粒子数密度偏差‒时间变化示意图.从图中可以看出, 在碰撞系数a不同的取值下, 压力振荡的幅度是不相同的.从图6 (a)中可以看到, 碰撞系数 α = 0.5 t = 0.95 α = 0.7 图6 (b) 中可以看到, 当碰撞系数α = 0.9 图6 (c)中可以看到, 当碰撞系数α = 0.95 α > 0.9
图7 是采用MPS核函数时, 溃坝问题在不同碰撞系数下不同时刻的压力场对比图, 从图中可以看到, 在不同的碰撞系数下, 压力场都存在较为明显的 局部压力过大和局部压力骤小的情况.对于${\alpha}=0.5$时可以看到在{t} = 0.625${ s}$ 时, 整个流场已经初步出现了粒子发散和不稳定的现象.对于${\alpha}$ = 0.7时, 流场计算能够稳定的进行下去, 但是压力场中压力局部变大的情况仍较为明显. 对于${\alpha}$ = 0.9时, 压力场中局部压力过大的现象有所缓减. 对于${\alpha}$ = 0.95时, 压力场的分布仍然出现非物理的局部压力过大的现象.上述结果也说明了在传统MPS 方法中确实存在着较为严重的压力振荡现象.
图6 MPS核函数下压力、粒子数密度差‒时间变化示意图
Fig.6 Time histories of pressure and deviation in particle number density at point A by MPS kernel function
图7 MPS核函数在不同时刻时溃坝压力分布对比图
Fig.7 Comparison of dam break pressure field at different instants by MPS kernel function
3.4 高斯核函数
为了进一步的研究MPS方法中的压力振荡问题, 此次选择高斯核函数进行计算, 高斯核函数的公式如下
$\begin{equation}w(r)=\begin{cases} {e}^{-3(r/r_e)^2},& 0<r<r_e\\ 0,& r\geqslant r_e \end{cases}\end{equation} $ (10)
其中, ${r=|r_i-r_j|}$是两个粒子之间的距离, ${r_i}$是i粒子的位置, ${r_j}$是i粒子支持域内的j粒子的位置, ${r_e}$是粒子作用域的半径.
表2 是采用高斯核函数时, 在不同碰撞系数下的粒子数密度偏差的最大波动值.从表2 中可以看到, 随着α ( n i - n 0 ) / n 0 α
3.5 高斯核函数计算结果
图8 是采用高斯核函数时, 压力‒时间、粒子数从图8 (a) 中可以看出, 当碰撞系数α 图8 (a)~ 图8 (c) 随着碰撞系数 α α α
图8 高斯核函数下压力和粒子数密度差‒时间变化示意图
Fig.8 Time histories of pressure and deviation in particle number density at point A by Gauss kernel function
图8 高斯核函数下压力和粒子数密度差—时间变化示意图(续)
Fig.8 Time histories of pressure and deviation in particle number density at point A by Gauss kernel function(continued)
3.6 MPS核函数和高斯核函数的对比分析
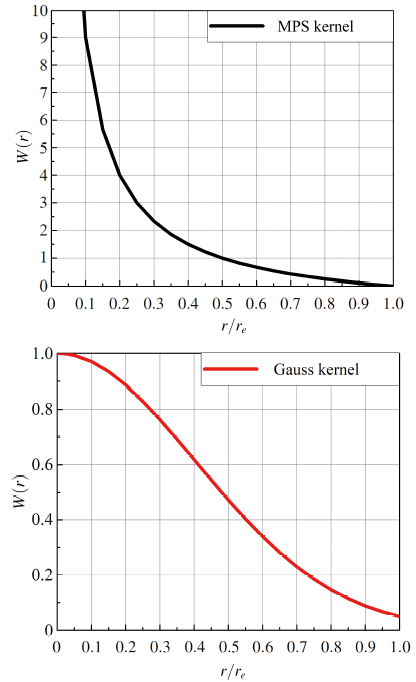
内不同区域的权重有关, 而具体的核函数的数值小大无关.图9 是两个核函数曲线, 对比两个图形可以看到, MPS 核函数在靠近0 时, 核函数的数值急剧增大, 这意味着两个粒子之间的相互影响也急剧增大, 而高斯核函数在靠近0时, 核函数数值也在增大, 但变化的幅度相对于MPS核函数要小很多.
图9 两种核函数曲线
Fig.9 Curves of two kernel functions
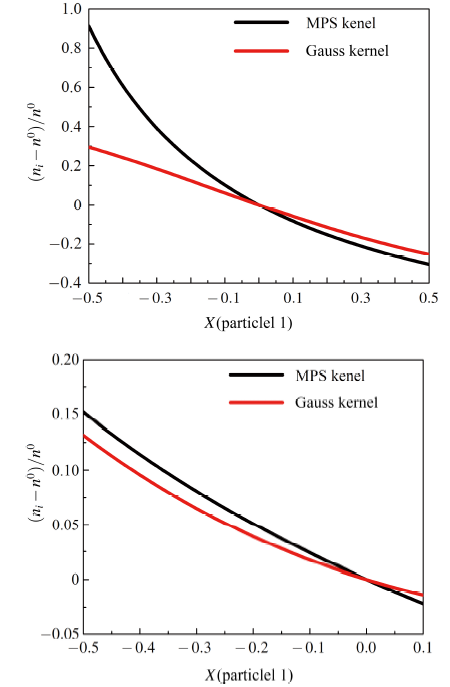
图10 是MPS核函数和高斯核函数下粒子1, 2移动距离和粒子数密度偏差 ( n i - n 0 ) / n 0 图10 (a)可以看到, 在粒子1移动相同距离的情况下, 采用不同的核函数造成的粒子数密度偏差的变化是不同的, 采用MPS 核函数时的粒子数密度偏差大于采用高斯核函数时的粒子数密度偏差.同样的, 在图10 (b)可以看到, 对于粒子2 的情况是相同的, 粒子2 移动相同距离时, 采用MPS核函数时产生的粒子数密度偏差大于采用高斯核函数产生的粒子数密度偏差. 这是由于两种不同核函数在支持域内不同分布形式所决定的, MPS核函数在支持域内的变化更为剧烈, 因此移动相同距离时, 其产生的粒子数密度偏差更大.这意味着产生更大的压力振荡幅度.
图10 两种核函数的粒子1, 2移动距离和粒子数密度偏差$(n_i-n_0)/n_0$之间的关系
Fig.10 The deviation in particle number density of different particle displacement by two kernel functions
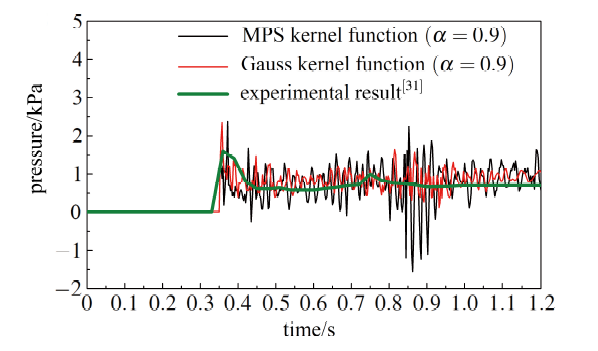
图11 是MPS核函数、高斯核函数的压力‒时间曲线与文献[31 ]的实验结果对比图, 从图中可以看到.高斯核函数的压力振荡幅度是小于MPS核函数的压力振荡幅度.这是因为在粒子运动相同距离时, 高斯核函数引起的粒子数密度偏差是小于MPS核函数因为的粒子数密度偏差的, 从而其压力振荡的幅度也相对较小.并且从图中可以看出, MPS核函数的容易出现负压力的情况, 这是因为流体处于拉伸状态时, MPS核函数的粒子数密度偏差波动是大于高斯核函数的粒子数密度偏差的波动.而采用高斯核函数时, 能够较好地缓减出现负压力的情况.虽然采用以上两种核函数并不能完全地消除计算过程中的压力振荡现象, 但是两种核函数的压力值与文献[31 ]的实验值在均值上非常接近的.
图11 MPS核函数和高斯核函数下 压力‒时间变化示意图
Fig.11 Comparison of time histories of pressure at point A by two kernel functions and Hu’s experimental result
图12 是MPS核函数和高斯核函数在不同时刻时溃坝压力分布对比图, 对比不同时刻的压力场图可以看到, 高斯核函数的压力分布相对比MPS核函数更为光滑, 采用高斯核函数进行计算时, 流体最底部的压力最大, 而自由表面处压力最小, 这与物理实际相一致.这是因为高斯核函数造成的粒子数密度波动小于MPS 核函数造成的粒子数密度波动, 所以压力振荡相对比与MPS核函数也更小.
图12 MPS核函数和高斯核函数在不同时刻时溃坝压力分布对比图
Fig.12 Comparison of dam break pressure field at different instants by two kernel functions
4 结论
本文针对在MPS方法中的压力振荡现象进行了研究.首先通过对粒子模型的一维简化, 阐述了粒子运动过程中, 粒子之间的相互位置关系对粒子数密度偏差造成的影响.并且采用了经典的溃坝模型作为本研究的算例, 通过在MPS方法中加入了碰撞模型来控制计算过程中粒子之间的相互位置关系, 从而控制溃坝流体在计算过程的压力振荡.结果表面, 随着碰撞系数 α > 0.9
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Koshizuka S A particle method for incompressible viscous flow with fluid fragmentation
. Comput Fluid Dynamics J , 1995 , 4 : 29 -46
[本文引用: 1]
[2]
Koshizuka S Moving-particle semi-implicit method for fragmentation of incompressible fluid
. Nuclear Science & Engineering the Journal of the American Nuclear Society , 1996 , 123 (3 ): 421 -434
[本文引用: 1]
[3]
Koshizuka S Ikeda H Oka Y Numerical analysis of fragmentation mechanisms in vapor explosions
. Nuclear Engineering and Design , 1998 , 189 (1-3 ): 423 -433
[本文引用: 1]
[4]
Koshizuka S Oka Y Application of moving particle semi-implicit method to nuclear reactor safety
. Computational Fluid Dynamics , 2001 , 9 : 366 -375
[本文引用: 1]
[5]
Xie H Koshizuka S Oka Y Simulation of drop deposition process in annular mist flow using three-dimensional particle method
. Nuclear Engineering and Design , 2005 , 16 (235 ): 1687 -1697
[本文引用: 1]
[6]
Tian W Ishiwatari Y Ikejiri S et al .Numerical computation of thermally controlled steam bubble condensation using moving particle semi-implicit (MPS) method
. Annals of Nuclear Energy , 2010 , 1 (37 ): 5 -15
[本文引用: 1]
[7]
Yoon HY Koshizuka S Oka Y A mesh-free numerical method for direct simulation of gas-liquid phase interface
. Nuclear Science and Engineering , 1999 , 133 : 1 -9
[本文引用: 1]
[8]
Yoon HY Koshizuka S Oka Y Direct calculation of bubble growth, departure and rise in nucleate pool boiling
. International Journal of Multiphase Flow , 2011 , 27 (2 ): 277 -298
[本文引用: 1]
[9]
Chen R Chen L Guo K et al .Numerical analysis of the melt behavior in a fuel support piece of the BWR by MPS
. Annals of Nuclear Energy , 2017 , 102 : 422 -439
[本文引用: 1]
[10]
Li Y Chen R Guo K et al .Numerical analysis of the dissolution of uranium dioxide by molten zircaloy using MPS method
. Progress in Nuclear Energy , 2017 , 100 : 1 -10
[本文引用: 1]
[11]
Jena D Biswal KC A numerical study of violent sloshing problems with modified MPS method
. Journal of Hydrodynamics, Ser.B , 2017 , 29 (4 ): 659 -667
[本文引用: 1]
[12]
Shibata K Koshizuka S Numerical analysis of shipping water impact on a deck using a particle method
. Ocean Engineering , 2007 , 34 (3-4 ): 585 -593
[本文引用: 1]
[13]
Sueyoshi M Kashiwagi M Naito S Numerical simulation of wave-induced nonlinear motions of a two-dimensional floating body by the moving particle semi-implicit method
. Journal of Marine Science and Technology , 2008 , 13 (2 ): 85 -94
[本文引用: 1]
[14]
Shibata K Koshizuka S Tanizawa K Three-dimensional numerical analysis of shipping water onto a moving ship using a particle method
. Journal of Marine Science and Technology , 2009 , 14 (2 ): 214 -227
[本文引用: 2]
[15]
Guo K Chen R Li Y et al .Numerical investigation of the fluid-solid mixture flow using the focus code
. Progress in Nuclear Energy , 2017 , 97 : 197 -213
[本文引用: 1]
[16]
Khayyer A Gotoh H Modified Moving Particle Semi-implicit methods for the prediction of 2D wave impact pressure
. Coastal Engineering , 2009 , 56 (4 ): 419 -440
[本文引用: 2]
[17]
Lee B Park J Kim M et al .Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads
. Computer Methods in Applied Mechanics and Engineering , 2011 , 200 (9-12 ): 1113 -1125
[本文引用: 3]
[18]
Sueyoshi M Naito S A study of nonlinear fluid phenomena with particle method (Part 2)
. Journal of Kansai Society Naval Architects , 2002 , 2002 (237 ): 181 -186
[本文引用: 1]
[19]
Khayyer A Gotoh H A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method
. Applied Ocean Research , 2010 , 32 (1 ): 124 -131
[本文引用: 1]
[20]
Kondo M Koshizuka S Improvement of stability in moving particle semi-implicit method
. International Journal for Numerjcal Methpds in Fluids , 2011 , 65 (6 ): 638 -654
[本文引用: 1]
[21]
Tanaka M Masunaga T Stabilization and smoothing of pressure in MPS method by quasi-compressibility
. Journal of Computational Physics , 2010 , 229 (11 ): 4279 -4290
[本文引用: 1]
[22]
Shibata K Masaie I Kondo M et al .Improved pressure calculation for the moving particle semi-implicit method
. Computational Particle Mechanics , 2015 , 2 (1 ): 91 -108
[本文引用: 1]
[23]
潘徐杰 , 张怀新 .移动粒子半隐式法晃荡模拟中的压力震荡现象研究
.水动力学研究与进展 , 2008 , 23 (4 ): 453 -463
[本文引用: 1]
(Pan Xujie Zhang Huaixin A study on the oscillations appearing in pressure calculation for sloshing simulation by using moving-particle semi-implicit method
. Chinese Journal of Hydrodynamics , 2008 , 23 (4 ): 453 -463 (in Chinese))
[本文引用: 1]
[24]
Duan G Chen B Koshizuka S et al .Stable multiphase moving particle semi-implicit method for incompressible interfacial flow
. Computer Methods in Applied Mechanics and Engineering , 2017 , 318 : 636 -666
[本文引用: 1]
[25]
郑仙佩 , 顾声龙 , 任立群 .基于SWE-SPH的下游为湿河床的溃坝水流模拟
.青海大学学报 , 2016 , 34 (5 ): 40 -44
[本文引用: 1]
(Zheng Xianpei Gu Shenglong Ren Liqun Simulation of dam-break flow with wet bed at downstream based on SWE-SPH
. Journal of Qinghai University , 2016 , 34 (5 ): 40 -44 (in Chinese))
[本文引用: 1]
[26]
李婧文 , 陈昌平 , 孙家文 等 .基于溃坝模型的SPH方法光滑函数模拟
.中国海洋平台 , 2017 , 32 (2 ): 34 -40
(Li Jingwen Chen Changping Sun Jiawen et al .Smoothing fution simulation of SPH method based on dam-break model
. China Offshore Platform , 2017 , 32 (2 ): 34 -40 (in Chinese))
[27]
刘汉涛 , 干湧 , 常建忠 等 .溃坝问题的粒子方法模拟
.应用力学学报 , 2016 , 33 (4 ): 547 -552
(Liu Hantao Gan Yong Chang Jianzhong et al .Dam break simulation employing particle methods
. Chinese Journal of Applied Mechanics , 2016 , 33 (4 ): 547 -552 (in Chinese))
[28]
陈健云 , 李静 , 徐强 等 .溃坝涌浪及其对重力坝影响的数值模拟
.浙江大学学报(工学版) , 2016 , 50 (11 ): 2164 -2169
(Chen Jianyun Li Jing Xu Qiang et al .Numerical simulation of Landslide surge and its effects on gracity dam
. Journal of Zhejiang University (Engineering Science )2016 , 50 (11 ): 2164 -2169 (in Chinese))
[29]
许晓阳 , 任胜章 , 邓方安 .三维溃坝流的光滑粒子动力学方法模拟
.计算力学学报 , 2016 , 33 (5 ): 676 -682
(Xu Xiaoyang Ren Shengzhang Deng Fang’an Numerical simulation of 3D dam-break flow using smoothed particle hydrodynamics
. Chinese Journal of Computational Mechanics , 2016 , 33 (5 ): 676 -682 (in Chinese))
[30]
Daneshvar FA Rakhshandehroo GR Talebbeydokhti N New modified gradient models for MPS method applied to free-surface flow simulations
. Applied Ocean Research , 2017 , 66 : 95 -116
[本文引用: 1]
[31]
Hu C Kashiwagi M A CIP-based method for numerical simulations of violent free-surface flows
. Journal of Marine Science and Technology , 2004 , 9 : 143 -157
[本文引用: 4]
A particle method for incompressible viscous flow with fluid fragmentation
1
1995
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Moving-particle semi-implicit method for fragmentation of incompressible fluid
1
1996
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical analysis of fragmentation mechanisms in vapor explosions
1
1998
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Application of moving particle semi-implicit method to nuclear reactor safety
1
2001
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Simulation of drop deposition process in annular mist flow using three-dimensional particle method
1
2005
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical computation of thermally controlled steam bubble condensation using moving particle semi-implicit (MPS) method
1
2010
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
A mesh-free numerical method for direct simulation of gas-liquid phase interface
1
1999
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Direct calculation of bubble growth, departure and rise in nucleate pool boiling
1
2011
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical analysis of the melt behavior in a fuel support piece of the BWR by MPS
1
2017
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical analysis of the dissolution of uranium dioxide by molten zircaloy using MPS method
1
2017
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
A numerical study of violent sloshing problems with modified MPS method
1
2017
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical analysis of shipping water impact on a deck using a particle method
1
2007
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical simulation of wave-induced nonlinear motions of a two-dimensional floating body by the moving particle semi-implicit method
1
2008
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Three-dimensional numerical analysis of shipping water onto a moving ship using a particle method
2
2009
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
... [14 ]应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Numerical investigation of the fluid-solid mixture flow using the focus code
1
2017
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Modified Moving Particle Semi-implicit methods for the prediction of 2D wave impact pressure
2
2009
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
... [16 ,19 ]通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads
3
2011
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
... [17 ]认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
... 对于流体内部粒子, 当粒子相互靠近时, 粒子之间的排斥力会增加, 特别在流体剧烈运动时, 流体内部会出现两个粒子之间距离非常接近的情况, 此时粒子之间的压力将会非常大, 从而流体内部会出现压力振荡.对于自由表面粒子, 由于自由表面粒子的压力在计算过程中被设置为0, 当飞溅的自由表面粒子突然碰撞自由表面并进入流体内部时, 此时该粒子的压力会突然增加, 这也是造成压力计算不稳定性的一个重要原因.针对上述情况, 在计算过程中加入了一个碰撞模型, 这个碰撞模型采用Lee[17 ] 在其研究中提出的碰撞模型.图1 是碰撞模型的示意图.在初始时刻, 粒子均匀分布, 粒子之间的距离为${l_0}$, 两个相互碰撞的粒子在碰撞前的质量和速度分别为当粒子之间的间距小于${al_0}$ 时, 粒子发生碰撞, 碰撞后的速度分别为${\textbf{u}^\prime_1}$和~${\textbf{u}^\prime_2}$. 其中$\alpha$ 是碰撞模型发生作用的系数, 一般取0.5~0.9之间, ${\beta_0}$ 是粒子碰撞后的反弹速度系数, 一般取0.2. ...
A study of nonlinear fluid phenomena with particle method (Part 2)
1
2002
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method
1
2010
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Improvement of stability in moving particle semi-implicit method
1
2011
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Stabilization and smoothing of pressure in MPS method by quasi-compressibility
1
2010
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Improved pressure calculation for the moving particle semi-implicit method
1
2015
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
移动粒子半隐式法晃荡模拟中的压力震荡现象研究
1
2008
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
移动粒子半隐式法晃荡模拟中的压力震荡现象研究
1
2008
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
Stable multiphase moving particle semi-implicit method for incompressible interfacial flow
1
2017
... 移动粒子半隐式法(moving particle semi-implicit method. MPS)是一种基于拉格朗日框架的无网格方法, 它首先是由东京大学的Koshizuka[1 ,2 ] 提出的, 并且被广泛地应用于核工业领域[3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ] 和海洋工程领域[11 ,12 ,13 ,14 ,15 ] .MPS 方法提出至今, 一直存在着严重的压力振荡问题. Khayyer等[16 ] 在其研究中对于静水压力的模拟, Shibata等[14 ] 应用MPS 方法对甲板上浪产生的拍击压力的模拟, Lee等[17 ] 应用MPS 方法对溃坝问题进行的模拟, 都发现了较大的压力振荡现象.很多学者对此也进行了相关的研究, Sueyoshi等[18 ] 在研究压力振荡问题时, 通过对压力进行后处理光滑平均处理得到光滑的压力曲线, 这种方式确实能够得到适用于工程实际的压力数据, 但是并未从本质上解决压力振荡问题.Khayyer 和Gotoh[16 ,19 ] 通过采用一种高精度的压力梯度模型和全新的压力泊松方程源项, 并且对压力泊松方程的系数矩阵项引入弱可压缩条件, 将MPS方法中压力振荡进行抑制.Kondo和Koshizuka[20 ] 提出了一种新型的压力泊松方程源项, 该源项包含三个部分: 一个主要项和两个误差补偿项, 并且通过对静水问题、溃坝问题的研究说明提出的新型源项能够成功地减轻模拟过程中存在的压力振荡.Lee等[17 ] 认为影响压力振荡的因素包括压力泊松方程的源项、梯度模型、粒子碰撞模型和自由表面的识别等, 并且对上述因素进行改进, 减轻了压力振荡现象.Tanaka和Masunaga[21 ] 通过对自由表面处的粒子数密度和初始粒子数密度进行重构的方式, 为压力泊松方程提供了更为精确的压力边界条件, 从而在一定程度上缓解了MPS 方法中的压力振荡问题.Shibata 等[22 ] 针对MPS 方法中的压力振荡问题也进行了深入的研究, 提出了一种新型的自由表面识别方案, 为压力泊松方程的计算提供了准确的边界条件.同时通过加入虚拟粒子的概念, 提出了一种新型的压力梯度模型和拉普拉斯算子模型, 并应用到模拟溃坝问题、静水问题等, 结果表明压力振荡能够得到很好的抑制.潘徐杰和张怀新[23 ] 通过对比不同核函数下压力振荡的表现, 判断了核函数的适用性, 但是并没有解释核函数通过何种方式影响MPS 方法中的压力振荡问题.Duan等[24 ] 通过对MPS方法中加入平均密度和连续加速度的方法, 稳定了MPS 方法中的压力波动现象. ...
基于SWE-SPH的下游为湿河床的溃坝水流模拟
1
2016
... 溃坝模型是一个经典的自由表面大变形问题, 在溃坝过程中, 流体的流动具有强烈的非线性特征. 很多学者[25 -30 ] 采用粒子法对溃坝问题进行模拟, 并且取得了很好的效果. 在本研究中, 选用溃坝模型作为算例来研究MPS方法中压力振荡现象. Hu等[31 ] 在其自由表面流动问题中, 采用实验的方法对溃坝问题进行了研究, 并且测量了在溃坝过程中的压力-时间曲线. 本研究采用的溃坝模型尺寸和文献[31 ] 的溃坝模型相同. 图4 是溃坝模型的具体尺寸, 溃坝高22 cm, 溃坝长118 cm, 流体高12 cm, 流体长68 m. 流体为水, 密度为1000kg/m3 , 水的动力黏度为1.000 6×10-6 m2 /s, 溃坝竖直壁面上的A 点是压力监测点. 重力加速度为9.8m/s2 , 初始粒子间距等于0.005 m, 粒子数量等于4592 个, 时间步长为0.001s. ...
基于SWE-SPH的下游为湿河床的溃坝水流模拟
1
2016
... 溃坝模型是一个经典的自由表面大变形问题, 在溃坝过程中, 流体的流动具有强烈的非线性特征. 很多学者[25 -30 ] 采用粒子法对溃坝问题进行模拟, 并且取得了很好的效果. 在本研究中, 选用溃坝模型作为算例来研究MPS方法中压力振荡现象. Hu等[31 ] 在其自由表面流动问题中, 采用实验的方法对溃坝问题进行了研究, 并且测量了在溃坝过程中的压力-时间曲线. 本研究采用的溃坝模型尺寸和文献[31 ] 的溃坝模型相同. 图4 是溃坝模型的具体尺寸, 溃坝高22 cm, 溃坝长118 cm, 流体高12 cm, 流体长68 m. 流体为水, 密度为1000kg/m3 , 水的动力黏度为1.000 6×10-6 m2 /s, 溃坝竖直壁面上的A 点是压力监测点. 重力加速度为9.8m/s2 , 初始粒子间距等于0.005 m, 粒子数量等于4592 个, 时间步长为0.001s. ...
New modified gradient models for MPS method applied to free-surface flow simulations
1
2017
... 溃坝模型是一个经典的自由表面大变形问题, 在溃坝过程中, 流体的流动具有强烈的非线性特征. 很多学者[25 -30 ] 采用粒子法对溃坝问题进行模拟, 并且取得了很好的效果. 在本研究中, 选用溃坝模型作为算例来研究MPS方法中压力振荡现象. Hu等[31 ] 在其自由表面流动问题中, 采用实验的方法对溃坝问题进行了研究, 并且测量了在溃坝过程中的压力-时间曲线. 本研究采用的溃坝模型尺寸和文献[31 ] 的溃坝模型相同. 图4 是溃坝模型的具体尺寸, 溃坝高22 cm, 溃坝长118 cm, 流体高12 cm, 流体长68 m. 流体为水, 密度为1000kg/m3 , 水的动力黏度为1.000 6×10-6 m2 /s, 溃坝竖直壁面上的A 点是压力监测点. 重力加速度为9.8m/s2 , 初始粒子间距等于0.005 m, 粒子数量等于4592 个, 时间步长为0.001s. ...
A CIP-based method for numerical simulations of violent free-surface flows
4
2004
... 溃坝模型是一个经典的自由表面大变形问题, 在溃坝过程中, 流体的流动具有强烈的非线性特征. 很多学者[25 -30 ] 采用粒子法对溃坝问题进行模拟, 并且取得了很好的效果. 在本研究中, 选用溃坝模型作为算例来研究MPS方法中压力振荡现象. Hu等[31 ] 在其自由表面流动问题中, 采用实验的方法对溃坝问题进行了研究, 并且测量了在溃坝过程中的压力-时间曲线. 本研究采用的溃坝模型尺寸和文献[31 ] 的溃坝模型相同. 图4 是溃坝模型的具体尺寸, 溃坝高22 cm, 溃坝长118 cm, 流体高12 cm, 流体长68 m. 流体为水, 密度为1000kg/m3 , 水的动力黏度为1.000 6×10-6 m2 /s, 溃坝竖直壁面上的A 点是压力监测点. 重力加速度为9.8m/s2 , 初始粒子间距等于0.005 m, 粒子数量等于4592 个, 时间步长为0.001s. ...
... [31 ]的溃坝模型相同. 图4 是溃坝模型的具体尺寸, 溃坝高22 cm, 溃坝长118 cm, 流体高12 cm, 流体长68 m. 流体为水, 密度为1000kg/m3 , 水的动力黏度为1.000 6×10-6 m2 /s, 溃坝竖直壁面上的A 点是压力监测点. 重力加速度为9.8m/s2 , 初始粒子间距等于0.005 m, 粒子数量等于4592 个, 时间步长为0.001s. ...
... 图11 是MPS核函数、高斯核函数的压力‒时间曲线与文献[31 ]的实验结果对比图, 从图中可以看到.高斯核函数的压力振荡幅度是小于MPS核函数的压力振荡幅度.这是因为在粒子运动相同距离时, 高斯核函数引起的粒子数密度偏差是小于MPS核函数因为的粒子数密度偏差的, 从而其压力振荡的幅度也相对较小.并且从图中可以看出, MPS核函数的容易出现负压力的情况, 这是因为流体处于拉伸状态时, MPS核函数的粒子数密度偏差波动是大于高斯核函数的粒子数密度偏差的波动.而采用高斯核函数时, 能够较好地缓减出现负压力的情况.虽然采用以上两种核函数并不能完全地消除计算过程中的压力振荡现象, 但是两种核函数的压力值与文献[31 ]的实验值在均值上非常接近的. ...
... ]的实验结果对比图, 从图中可以看到.高斯核函数的压力振荡幅度是小于MPS核函数的压力振荡幅度.这是因为在粒子运动相同距离时, 高斯核函数引起的粒子数密度偏差是小于MPS核函数因为的粒子数密度偏差的, 从而其压力振荡的幅度也相对较小.并且从图中可以看出, MPS核函数的容易出现负压力的情况, 这是因为流体处于拉伸状态时, MPS核函数的粒子数密度偏差波动是大于高斯核函数的粒子数密度偏差的波动.而采用高斯核函数时, 能够较好地缓减出现负压力的情况.虽然采用以上两种核函数并不能完全地消除计算过程中的压力振荡现象, 但是两种核函数的压力值与文献[31 ]的实验值在均值上非常接近的. ...