引言
高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] .
列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响.
涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出.
目前的研究工作利用改进型延迟分离涡模拟方法 的简化缩尺模型的绕流流场进行数值计算. 通过 Q λ 2 Ω Ω
1 数值模拟方法
1.1 高速列车简化模型及计算域
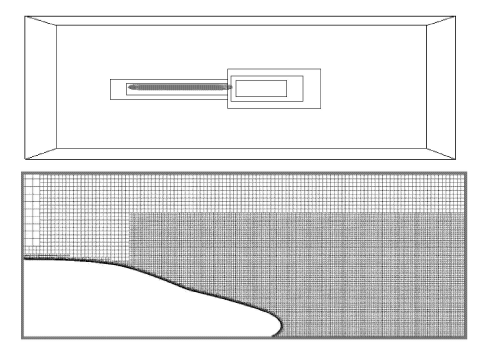
用于模拟的是缩尺比例为1:30的CRH380A高速动车组模型,由头车和尾车组成,长度约为 15 H ( H [16 ] (用形状简单的外罩包裹转向架的复杂结构),这里将转向架删除,并用与边缘重合的盖板密封原来转向架所在位置的空腔,如图1 所示. 通过对模型底部结构的简化,一定程度上降低了局部流动可能导致的计算上的不稳定性. 列车模型在整体上保留了对列车车体表面边界层以及近尾流区流动拟序结构的生成和发展起重要作用的基本几何特征,即较大的长细比、小高宽比以及头车和尾车的流线型头部.
图1 基于CRH380A高速列车的简化模型
Fig. 1 Simplified model based on the CRH380A HST
1.2 计算域及其边界条件
计算域的几何尺寸及边界条件如图2 所示. 基于模型高度 H U ∞ Re ≈ 3 × 1 0 5 ( Re = U ∞ ⋅ H / υ K υ K × 10 -5 m2 /s),马赫数 Ma ≈ 0.12 ( Ma = U ∞ / c c U ∞
图2 计算域几何尺寸及边界条件
Fig. 2 Dimensions and boundary conditions of the computational domain
1.3 数值求解方案
模拟采用IDDES方法,Huang等[31 ] 利用该方法对平均流动雷诺数同样为3 × 10 <sup>5</sup>的高速列车绕流流场进行数值研究,气动特性相关的计算结果是令人满意的. 在基于SST k - ω l h yb
l h yb = f d ̃ ( 1 + f e ) l t + ( 1 - f d ̃ ) C D ES Δ I DDES (1)
式中, l t Δ I DDES f d ̃ f e C D ES
在数值计算中,应用有限体积法(finite volume method)将控制方程转换为能够进行数值求解的离散形式. 二阶迎风格式(second-order upwind scheme)和边界中心差分格式(bounded central-differencing scheme)分别用于RANS模式和LES模式,离散求解对流和扩散通量的面值;湍流模型中使用二阶迎风格式对湍流量进行求解;时间项离散采用隐式二阶格式. 通过隐式耦合求解器对非稳态流动进行数值求解,将CFL(Courant-Friedrichs-Lewy)数设为0.5. 根据之前的研究工作[32 ,34 ] ,时间步长 Δ t 0.02 H / U ∞ 200 H / U ∞
1.4 网格
计算网格主要由近壁面区域的棱柱层(prism layer)以及远离壁面区域的六面体结构网格(hexahedral mesh)构成,两者通过切割体网格(trimmed mesh)过渡连接. 车体表面设置12层边界层网格(即棱柱层),其中第一层边界层网格单元的无量纲厚度 ξ + H ξ [17 ] 相似的方法,对车身周围以及尾流区进行网格加密;共细化了5个区域的网格,为了能够获取影响 尾车气动特性的大尺度涡旋结构,其中有3个网格细化区设置在近尾流区域,如图3 所示.
在此基础上进行网格无关性验证. 验证所用模型的长度约为22 H 6 , 10.5×106 和6.3×106 .
图3 网格加密区示意图及局部放大
Fig. 3 Schematic view and close-up of the zones with grids refined
图4 给出了利用3种网格得到的近尾流区中流 向速度 U TKE = 12 u ' i u ' i ¯ i
如图4 所示,MM曲线与FM曲线在速度和湍动能分布上总是能够保持一致的趋势,并彼此吻合得较好. 而图4 (b)中的CM速度曲线有些偏 离其他两条曲线,并且CM湍动能曲线沿车长方向的变化趋势表现出明显的不同.
根据验证结果划分计算网格,用于研究讨论尾流区涡旋结构. 其中,加密区网格单元尺寸控制在0.02H~0.08 H 6 .
图4 利用3种网格计算得到的近尾流区流向速度和湍动能沿车长方向的时均分布
Fig. 4 Time-averaged profiles of streamwise velocity and TKE
1.5 数值结果的验证
列车风是高速列车尾流区域中典型的流动现象,其发展与涡旋结构有紧密的联系. 这里,鉴于模拟中高速列车模型是静止的,将列车风 速度 u S x - y
$u_{\rm S} = \sqrt {(U_\infty - u_x )^2 + u_y ^2} (2)$
式中, u x u y x ) 和展向( y ) 方向上的瞬时流动速度.
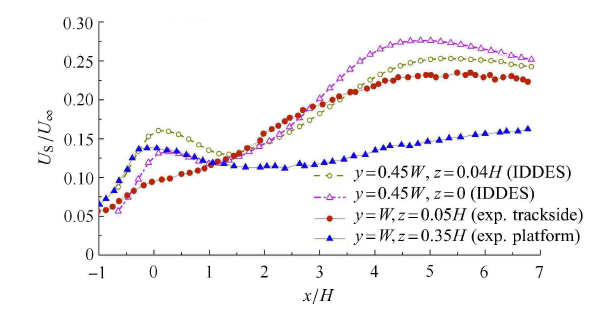
图5 给出了数值模拟与试验得到的列车风速度曲线图. 图中 W W / H ≈ 0.91 x = 0 y = 0 z = 0 [12 ] 的风洞试验中,封闭测试段安装有分流平台,以削弱地面边界层效应;相似地,目前模拟中计算域地面采用无滑移运动边界条件,同样可以显著减小该效应.
图5 尾流区中列车风速度沿流向的变化曲线
Fig. 5 Time-averaged slipstream as a function of the streamwise distance from the tail
显然,数值曲线显示出近尾流区列车风分布的一般特征,即尾端( x = 0 ) 附近的局部峰值以及下游流向位置处速度最大值. 通过对比可以看到,数值曲线均与轨旁试验曲线表现出很好的一致性,而由于站台结构对流动的限制,使得相应试验曲线趋势较为平缓且最大值出现明显滞后. 总的来说,目前的数值模拟所得到的近尾流区流动信息是合理可信的.
2 涡旋识别方法
Hunt等[26 ] 以压力最低为附加条件,用速度梯度 ∇ u Q Q
$Q = \dfrac{1}{2}\left( {u_{i,i}^2 - u_{i,j} u_{j,i} } \right) =\dfrac{1}{2}\left( {\vert \vert {\pmb\varpi} \vert \vert ^2 - \vert \vert {\pmb s} \vert \vert ^2} \right) (3) $
式中, s ϖ ∇ u | | ϖ | | = [ t r ( ϖϖ T ) ] 1 / 2 | | s | | = [ t r ( ss T ) ] 1 / 2 . 该式表明, Q Q > 0
Jeong 和 Hussain[28 ] 从Navier-Stokes方程出发,得到压力的二阶梯度张量表达式
$ - \dfrac{1}{\rho }p_{,ij} = \dfrac{{\rm D}s_{ij} }{{\rm D}t} - \upsilon s_{ij,kk} + \varpi _{ik} \varpi _{kj} + s_{ik} s_{kj} (4)$
式(4)等号右边前两项分别代表非定常应变效应和黏性效应. 他们提出仅考虑( ϖ ik ϖ kj + s ik s kj ) λ 2 ) 中位于涡核的两个特征值为负,也就是说,涡核所在区域中第二特征值 ∇ × u = R + ( ∇ × u - R )
Liu等[25 ] 认为速度梯度的非对称部分可能并不与涡旋运动直接相关,即涡量由于包含了与变形相关的涡量成分,不能直 接表征涡旋的存在. 根据Helmholtz分解,提出将涡量分成涡旋结构部分和非涡旋结构部分,即
$\nabla \times {\pmb u} = {\pmb R} + (\nabla \times {\pmb u} -{\pmb R}) $(5)
其中, ∇ × u R Ω
$\varOmega = \dfrac{(\nabla \times {\pmb u} \cdot {\pmb R})^2}{\left\| {\nabla \times {\pmb u}} \right\|_2^2 \cdot \left\| {\pmb R} \right\|_2^2 } (6) $
根据式(6), Ω s
$\varOmega = \dfrac{\left\| {\pmb \varpi} \right\|_{\rm F}^2 }{\left\| {\pmb s } \right\|_{\rm F}^2 + \left\| {\pmb \varpi} \right\|_{\rm F}^2 + \varepsilon } (7)$
式中,${\pmb s}$和 ${\pmb \varpi }$分别为速度梯度$\nabla {\pmb u}$的对称和反对称部分; $\varepsilon $是正的小量, 用以避免分母为零的情况.
3 数值结果及讨论
图6(a) $\sim $图6 (c)分别显示的是利用$Q$准则、 $\lambda_{2}$准则以及$\varOmega$准则得到的尾流涡旋结构,其中$Q$和$\lambda_{2}$的取值用($U_{\infty }/H)^{2}$无量纲化, $\varOmega =0.52$为Liu等[25 ] 的建议值.
由图6可以看出,3种方法识别出的尾流涡旋基本相同.靠近尾车处,涡旋具有明显较大的强度(涡量高),并成对从鼻部不断脱落,随着向下游传播,形成类似于卡门涡街的流向涡列,其中远离尾车的涡旋逐渐增大,但涡旋强度明显减弱.另一方面,图6(c)与图6(a)$\sim $图6(b)之间较为明显的不同在于流线型尾部的表面上覆盖的与剪切应变相关联的高涡量区. 对此,利用$Q$准则和 $\varOmega $方法作进一步讨论.
图6 利用不同方法识别出的尾流涡旋
Fig. 6 Wake vortices identified by different methods
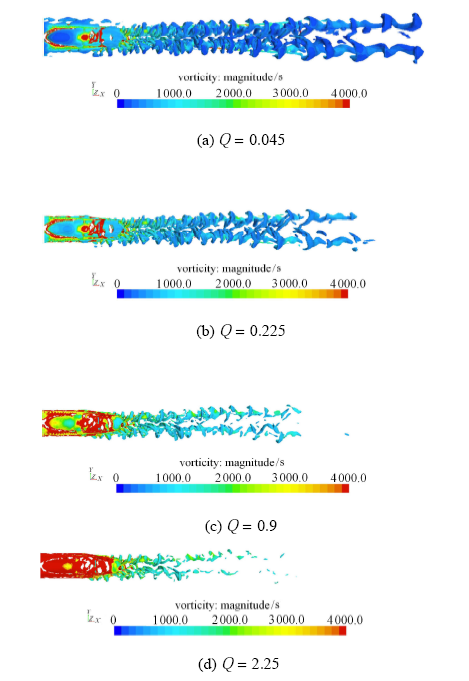
图7显示的是$Q$准则根据不同取值识别出的尾涡结构.当$Q$值增大时,覆盖于尾部表面的高涡量层更清晰地显现出来,并且尾流中尤其是靠近尾端的位置,由于分离的剪切层含有很高的涡量,强度大的涡旋仍然能够被$Q$准则很好的捕捉到,但是,尾车下游较弱的涡旋(涡量较低)逐渐消失.
图7 对应于不同Q值的尾涡结构
Fig. 7 Wake vortex structures with Q values varied
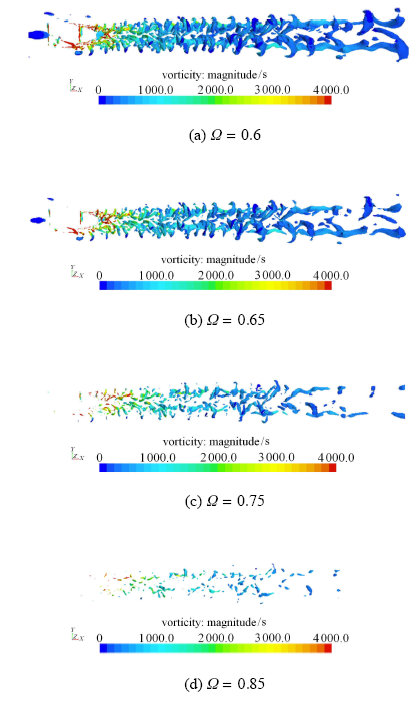
另一方面,如图8 所示,近尾流区涡旋结构随着 Ω Ω
图8 对应于不同 Ω
Fig. 8 Wake vortex structures with Ω = 0.52
涡量和变形对定义流动中的涡旋都是很重要的. 流体微团受到强剪切的作用时,变形是显著的,但因此产生的涡量可能并不与涡旋运动直接相关,涡旋涡量会下降. 正如Liu等[25 ] 所指出的,当旋转很强时,涡量可能会很小;而旋转很弱甚至没有时,涡量却可能很大.
基于此,可以预料,头部表面的高涡量层与局部流体微团的剪切变形有密切关系,某种程度上暗示出流线型几何外形延迟了由车体表面发展出的边界层的流动分离,而这也将影响到流向尾涡的形成和脱落.随着剪切分离的发生,局部的低压区驱使周围空气流入近尾流区,加之与底部区域流动的相互作用,从而形成螺旋流动[12 ,30 ] .在这个过程中,流体微团因剪切作用而发生的变形是显著的,同时边界层流动的分离也使得较高的涡量在尾端附近进行扩散,这些为较强涡旋的形成和脱落提供了重要条件,正如图9所示,流向涡旋的形成是局部流动中重要的物理过程,以至于涡边界($\varOmega= 0.52$)未出现,即变形与涡量是相当的.不过,较大的剪切应变往往因为黏性效应而具有高耗散性,相应的涡量会有较为明显的衰减,并且在下游位置,对已形成的涡旋而言,图8中更大$\varOmega $ 值表明,较弱的涡旋是尾涡结构的主要部分,它们的涡量超过流体微团的变形,并且如图9(b)~图9(c)所示,涡旋涡量的占比增大,意味着剪切的影响作用在下降,虽然涡核的强度明显减小,但此时的耗散较低且旋转运动具有主导影响,这对尾涡结构能够处于相对稳定的状态是很重要的.
图9 不同流向位置处(x = 0.5 H, 2H, 4 H)的流向涡核(时均$Q$和 $\varOmega $等值线分别对应$0.5 Q_{max}$和0.52)
Fig. 9 Streamwise vortex cores at the varied streamwise positions x = 0.5 H, $2 H, 4 H (Time-averaged $Q$ and $\varOmega $ contour lines represent $0.5 Q_{max}$ and 0.52, respectively)
Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制.
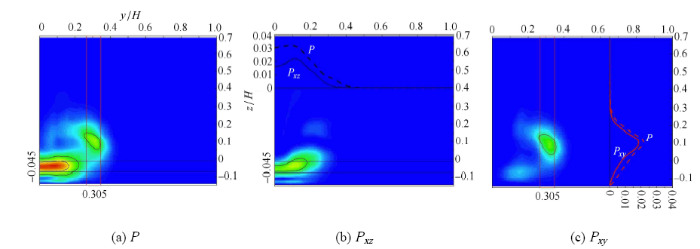
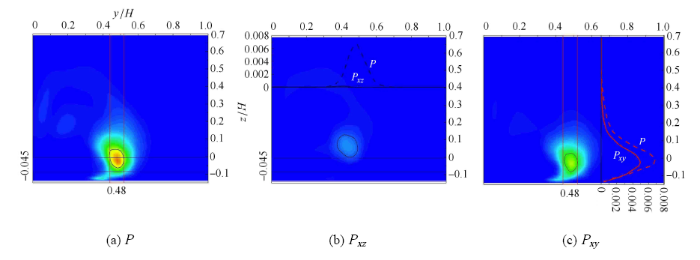
图10~图12分别给出了不同流向位置处湍流产生的$y$-$z$平面时均分布(其中,$P_{xy}$和$P_{xz}$分别表征涡旋在$x$-$y$平面和$x$-$z$平面平均剪切($S_{xy}$和$S_{xz}$)的作用下对湍流产生的贡献,$P$代表局部总的湍流产生).如图10所示,在靠近尾车的位置($x = 0.5H$),$P_{xy}$和$P_{xz}$分别对局部的湍流产生过程有较大的贡献,而相应的分离剪切层应该与模型底部和侧表面上发展起来的边界层流动有很大的关联性.而通过图11~图12可观察到,随着流向涡的移动,湍流产生较为显著的位置展向外移,同时,$P$曲线的峰值明显下移,并且局部的涡旋主要依赖于$x$-$y$平面剪切在产生湍流能量方面作出突出的贡献.基于此,我们认为,通过流向涡与地面之间的相互作用,局部速度场以及应力场受到扰动,虽然涡旋强度会不可避免地逐渐衰减,但重要的是,剪切能够得以维系,使局部的涡旋继续从平均流动中获取能量,这样有助于实现涡旋的自维持,从而尾涡结构能够处于相对稳定的状态.
图10 在流向位置$x = 0.5 H$,$P$, $P_{xz}$和$P_{xy}$的y-z平面时均分布
Fig. 10 Time-averaged $y$-$z$ plane profiles of the $P$, $P_{xz}$, and $P_{xy}$ at $x = 0.5 H$
图11 在流向位置$x = 2 H$,$P$, $P_{xz}$和$P_{xy}$的$y$-$z$平面时均分布
Fig. 11 Time-averaged $y$-$z$ plane profiles of the $P$, $P_{xz}$, and $P_{xy}$ at $x = 2 H$
图12 在流向位置$x = 4 H$,$P$, $P_{xz}$和$P_{xy}$的$y$-$z$平面时均分布
Fig. 12 Time-averaged $y$-$z$ plane profiles of the $P$, $P_{xz}$, and $P_{xy}$ at $x = 4 H$
4 结 论
本文通过IDDES对基于高速列车气动外形的简化缩尺模型的绕流流场进行模拟,以获取尾流流动的数值结果,进而利用涡旋识别方法,对高速列车尾涡结构进行研究.
可以观察到,在靠近尾车的局部流动中分布有高涡量的尾流涡旋,而随着尾涡结构向下游发展,其中更多的是低涡量涡旋,它们分布在较大的近尾流区域中,反映出尾涡结构处于相对稳定状态. 结合无量纲参数 $\varOmega $ 的物理意义,我们认为:边界层分离是尾端附近复杂流动的关键机制,即一方面,与之相关的剪切变形以及高涡量的扩散对具有较大强度的尾涡的形成起到了重要作用,也正因如此,局部尾流具有很显著的湍流特性;不过,对于低涡量涡旋而言,由于强剪切的高耗散,总涡量中的涡旋涡量是主要部分,相对于变形,流体微团的旋转运动是主导的,此时,耗散较为缓慢,并且重要的是,在流向涡核接近地面的情况下,涡旋与地面间的相互作用成为涡旋自维持的重要机制,使尾涡结构能够在向下游发展的过程中处于相对稳定的状态.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
姚拴宝 , 郭迪龙 , 杨国伟 等 . 高速列车气动阻力分布特性研究
. 铁道学报 , 2012 , 34 (7 ): 18 -23
[本文引用: 1]
(Yao Shuanbao Guo Didong Yang Guowei et al . Distribution of high-speed train aerodynamic drag
.Journal of the China Railway Society , 2012 , 34 (7 ): 18 -23 (in Chinese))
[本文引用: 1]
[2]
姚拴宝 , 郭迪龙 , 杨国伟 . 基于径向基函数网格变形的高速列车头型优化
. 力学学报 , 2013 , 45 (6 ): 982 -986
[本文引用: 1]
(Yao Shuanbao Guo Didong Yang Guowei Aerodynamic optimization of high speed train based on RBF mesh deformation
.Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (6 ): 982 -986 (in Chinese))
[本文引用: 1]
[3]
安翼 , 莫晃锐 , 刘青泉 . 高速列车头型长细比对气动噪声的影响
. 力学学报 , 2017 , 49 (5 ): 985 -996
[本文引用: 2]
(An Yi Mo Huangrui Liu Qingquan Study on the influence of the nose slenderness ratio of high-speed train on the aerodynamic noise
.Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (5 ): 985 -996 (in Chinese))
[本文引用: 2]
[4]
Yu Huahua Li Jiachun Zhang Huiqin On aerodynamic noises radiated by the pantograph system of high-speed trains
.Acta Mechanica Sinica , 2013 , 29 (3 ): 399 -410
[本文引用: 1]
[5]
于梦阁 , 张继业 , 张卫华 . 随机风速下高速列车的运行安全可靠性
. 力学学报 , 2013 , 45 (4 ): 483 -492
[本文引用: 1]
(Yu Mengge Zhang Jiye Zhang Weihua Operational safety reliability of high-speed trains under stochastic winds
.Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (4 ): 483 -492 (in Chinese))
[本文引用: 1]
[6]
杨国伟 , 魏宇杰 , 赵桂林 等 . 高速列车的关键力学问题
. 力学进展 , 2015 , 45 : 217 -460
[本文引用: 2]
(Yang Guowei Wei Yujie Zhao Guilin et al . Current research progress in the mechanics of high speed rails
.Advances in Mechanics , 2015 , 45 : 217 -460 (in Chinese))
[本文引用: 2]
[7]
Baker CJ Dalley SJ Johnson T et al . The slipstream and wake of a high-speed train
. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit 2001 , 215 (2 ): 83 -99 .
[本文引用: 1]
[8]
Baker CJ The flow around high speed trains
.Journal of Wind Engineering & Industrial Aerodynamics , 2010 , 98 (6-7 ): 277 -298
[本文引用: 3]
[9]
Baker CJ Quinn A Sima M et al . Full-scale measurement and analysis of train slipstreams and wakes. Part 1: Ensemble averages
.Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit 2014 , 228 (5 ): 451 -467
[本文引用: 1]
[10]
Schulte-Werning B Heine B Matschke C Slipstream development and wake flow characteristics of modern high-speed trains
.Journal of Applied Mathematics & Mechanics 2001 , 81 (S3 ): 789 -790
[本文引用: 1]
[11]
Schulte-Werning B Heine B Matschke C Unsteady wake flow characteristics of high-speed trains
.Proceedings in Applied Mathematics and Mechanics , 2003 , 2 (1 ): 332 -333
[本文引用: 1]
[12]
Bell JR Burton D Thompson M et al . Wind tunnel analysis of the slipstream and wake of a high-speed train
.Journal of Wind Engineering & Industrial Aerodynamics 2014 , 134 : 122 -138
[本文引用: 4]
[13]
Bell JR Burton D Thompson MC et al . Moving model analysis of the slipstream and wake of a high-speed train
.Journal of Wind Engineering & Industrial Aerodynamics 2015 , 136 : 127 -137
[本文引用: 2]
[14]
Bell JR Burton D Thompson MC et al . Flow topology and unsteady features of the wake of a generic high-speed train
.Journal of Fluids & Structures 2016 , 61 : 168 -183
[本文引用: 2]
[15]
Bell JR Burton D Thompson MC et al . Dynamics of trailing vortices in the wake of a generic high-speed train
.Journal of Fluids & Structures 2016 , 65 : 238 -256
[本文引用: 2]
[16]
Muld TW Analysis of Flow Structures in Wake Flows for Train Aerodynamics. Stockholm,
Sweden: Royal Institute of Technology , 2010
[本文引用: 3]
[17]
Muld TW Efraimsson G Dan SH Flow structures around a high-speed train extracted using proper orthogonal decomposition and dynamic mode decomposition
.Computers & Fluids 2012 , 57 (4 ): 87 -97
[本文引用: 3]
[18]
Muld TW Efraimsson G Henningson DS Wake characteristics of high-speed trains with different lengths
.Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit 2014 , 228 (4 ): 333 -342
[本文引用: 3]
[19]
Xia C Wang H Shan X et al . Effects of ground configurations on the slipstream and near wake of a high-speed train
.Journal of Wind Engineering & Industrial Aerodynamics 2017 , 168 :177 -189
[本文引用: 1]
[20]
田红旗 . 中国高速轨道交通空气动力学研究进展及发展思考
. 中国工程科学 , 2015 (4 ): 30 -41
[本文引用: 1]
(Tian Hongqi Development of research on aerodynamics of high-speed rails in China
. Engineering Sciences 2015 (4 ): 30 -41 (in Chinese))
[本文引用: 1]
[21]
Morel T Effect of base slant on flow in the near wake of an axisymmetric cylinder
.Aeronautical Quarterly , 1980 , 31 : 132 -147
[本文引用: 1]
[22]
Pauley WR Eaton JK Experimental study of the development of longitudinal vortex pairs embedded in a turbulent boundary layer
.AIAA Journal , 1988 , 26 (7 ): 816 -823
[本文引用: 1]
[23]
Rowe A Fry ALA Motallebi F Influence of boundary-layer thickness on base pressure and vortex shedding frequency
.AIAA Journal , 2001 , 39 (4 ): 754 -756
[本文引用: 1]
[24]
Küchemann D Report on the I.U.T.A.M. symposium on concentrated vortex motions in fluids
.Journal of Fluid Mechanics , 1965 , 21 (1 ): 1 -20
[本文引用: 1]
[25]
Liu CQ Wang YQ Yang Y et al . New omega vortex identification method
.Science China Physics, Mechanics & Astronomy 2016 , 59 (8 ): 684711
[本文引用: 5]
[26]
Hunt JCR Wray AA Moin P Eddies, streams, and convergence zones in turbulent flows//
Center for Turbulence Research Proceedings of the Summer Program , 1988 : 193 -208
[本文引用: 2]
[27]
Chong MS Perry AE Cantwell BJ A general classification of three-dimensional flow fields
.Physics of Fluids A , 1990 , 2 (5 ): 765 -777
[本文引用: 1]
[28]
Jeong J Hussain F On the identification of a vortex
.Journal of Fluid Mechanics , 1995 , 285 (4 ): 69 -94
[本文引用: 2]
[29]
Yao SB Sun ZX Guo DL et al . Numerical study on wake characteristics of high-speed trains
.Acta Mechanica Sinica , 2013 , 29 (6 ): 811 -822
[本文引用: 1]
[30]
Hemida H Baker C Gao G The calculation of train slipstreams using large-eddy simulation
.Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit 2014 , 228 (1 ): 25 -36
[本文引用: 1]
[31]
Huang S Hemida H Yang M Numerical calculation of the slipstream generated by a CRH2 high-speed train
. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit 2016 , 230 (1 ): 103 -116
[本文引用: 1]
[32]
潘永琛 , 姚建伟 , 李昌烽 . 高速列车近尾流区湍流涡旋的数值计算及动力学讨论. 力学季刊 , 2017 (2 ): 351 -358
[本文引用: 4]
(Pan Yongchen Yao Jianwei Li Changfeng Numerical simulation and dynamics discussion of turbulent eddies in the near wake of a high speed train
. Chinese Quarterly of Mechanics 2017 (2 ): 351 -358 (in Chinese))
[本文引用: 4]
[33]
Robinson SK Coherent motions in the turbulent boundary layer
. Annual Review of Fluid Mechanics , 1991 , 23 : 601 -639
[本文引用: 1]
[34]
潘永琛 , 姚建伟 , 梁策 等 . 高速列车近尾流区涡旋结构的湍流特性分析
. 中国铁道科学 , 2017 , 38 (2 ): 83 -88
[本文引用: 3]
(Pan Yongchen Yao Jianwei Liang Ce et al . Analysis on turbulence characteristics of vortex structures in the near wake of a high-speed train
.China Railway Science , 2017 , 38 (2 ): 83 -88 (in Chinese))
[本文引用: 3]
[35]
Tennekes H Lumley J. A First Course in Turbulence. Cambridge : MIT Press , 1972
[本文引用: 1]
[36]
Corjon A Poinsot T Behavior of wake vortices near ground
.AIAA Journal , 1997 , 35 (5 ): 849 -855
[本文引用: 1]
[37]
Perkins HJ The formation of streamwise vorticity in turbulent flow
.Journal of Fluid Mechanics , 1970 , 44 (4 ): 721 -740
[本文引用: 1]
高速列车气动阻力分布特性研究
1
2012
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
高速列车气动阻力分布特性研究
1
2012
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
基于径向基函数网格变形的高速列车头型优化
1
2013
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
基于径向基函数网格变形的高速列车头型优化
1
2013
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
高速列车头型长细比对气动噪声的影响
2
2017
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
高速列车头型长细比对气动噪声的影响
2
2017
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
On aerodynamic noises radiated by the pantograph system of high-speed trains
1
2013
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
随机风速下高速列车的运行安全可靠性
1
2013
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
随机风速下高速列车的运行安全可靠性
1
2013
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
高速列车的关键力学问题
2
2015
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
高速列车的关键力学问题
2
2015
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
The slipstream and wake of a high-speed train
1
2001
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
The flow around high speed trains
3
2010
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
... [8 ]认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Full-scale measurement and analysis of train slipstreams and wakes. Part 1: Ensemble averages
1
2014
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
Slipstream development and wake flow characteristics of modern high-speed trains
1
2001
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
Unsteady wake flow characteristics of high-speed trains
1
2003
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
Wind tunnel analysis of the slipstream and wake of a high-speed train
4
2014
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
... 图5 给出了数值模拟与试验得到的列车风速度曲线图. 图中 W W / H ≈ 0.91 x = 0 y = 0 z = 0 [12 ] 的风洞试验中,封闭测试段安装有分流平台,以削弱地面边界层效应;相似地,目前模拟中计算域地面采用无滑移运动边界条件,同样可以显著减小该效应. ...
... 基于此,可以预料,头部表面的高涡量层与局部流体微团的剪切变形有密切关系,某种程度上暗示出流线型几何外形延迟了由车体表面发展出的边界层的流动分离,而这也将影响到流向尾涡的形成和脱落.随着剪切分离的发生,局部的低压区驱使周围空气流入近尾流区,加之与底部区域流动的相互作用,从而形成螺旋流动[12 ,30 ] .在这个过程中,流体微团因剪切作用而发生的变形是显著的,同时边界层流动的分离也使得较高的涡量在尾端附近进行扩散,这些为较强涡旋的形成和脱落提供了重要条件,正如图9所示,流向涡旋的形成是局部流动中重要的物理过程,以至于涡边界($\varOmega= 0.52$)未出现,即变形与涡量是相当的.不过,较大的剪切应变往往因为黏性效应而具有高耗散性,相应的涡量会有较为明显的衰减,并且在下游位置,对已形成的涡旋而言,图8中更大$\varOmega $ 值表明,较弱的涡旋是尾涡结构的主要部分,它们的涡量超过流体微团的变形,并且如图9(b)~图9(c)所示,涡旋涡量的占比增大,意味着剪切的影响作用在下降,虽然涡核的强度明显减小,但此时的耗散较低且旋转运动具有主导影响,这对尾涡结构能够处于相对稳定的状态是很重要的. ...
Moving model analysis of the slipstream and wake of a high-speed train
2
2015
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Flow topology and unsteady features of the wake of a generic high-speed train
2
2016
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Dynamics of trailing vortices in the wake of a generic high-speed train
2
2016
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Analysis of Flow Structures in Wake Flows for Train Aerodynamics. Stockholm,
3
2010
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
... 用于模拟的是缩尺比例为1:30的CRH380A高速动车组模型,由头车和尾车组成,长度约为 15 H ( H [16 ] (用形状简单的外罩包裹转向架的复杂结构),这里将转向架删除,并用与边缘重合的盖板密封原来转向架所在位置的空腔,如图1 所示. 通过对模型底部结构的简化,一定程度上降低了局部流动可能导致的计算上的不稳定性. 列车模型在整体上保留了对列车车体表面边界层以及近尾流区流动拟序结构的生成和发展起重要作用的基本几何特征,即较大的长细比、小高宽比以及头车和尾车的流线型头部. ...
Flow structures around a high-speed train extracted using proper orthogonal decomposition and dynamic mode decomposition
3
2012
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
... 计算网格主要由近壁面区域的棱柱层(prism layer)以及远离壁面区域的六面体结构网格(hexahedral mesh)构成,两者通过切割体网格(trimmed mesh)过渡连接. 车体表面设置12层边界层网格(即棱柱层),其中第一层边界层网格单元的无量纲厚度 ξ + H ξ [17 ] 相似的方法,对车身周围以及尾流区进行网格加密;共细化了5个区域的网格,为了能够获取影响 尾车气动特性的大尺度涡旋结构,其中有3个网格细化区设置在近尾流区域,如图3 所示. ...
Wake characteristics of high-speed trains with different lengths
3
2014
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
... [18 ]认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Effects of ground configurations on the slipstream and near wake of a high-speed train
1
2017
... 高速列车的尾流是非常复杂的湍流流动,具有很高的湍流强度. 尤其在近尾流区域内,存在重要的湍流涡旋结构,对气动问题发挥着重要的影响作用. 比如,姚拴宝等[1 ,2 ] 指出尾车部位由于存在涡旋的生成和脱落等,对压差阻力的贡献明显,而针对头型的优化设计具有较好减阻效果;安翼等[3 ] 认为,车尾部是重要的噪声区,这与受电弓气动噪声[4 ] 相似,局部流动的涡旋结构发挥着重要的作用. 此外,高速列车运行的稳定性往往与气动特性关系密切,其中与尾涡相关的气动力是不容忽视的[5 ,6 ] . 因此,很多学者对高速列车的尾流流动及其涡旋结构进行了深入研究[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ] . ...
中国高速轨道交通空气动力学研究进展及发展思考
1
2015
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
中国高速轨道交通空气动力学研究进展及发展思考
1
2015
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Effect of base slant on flow in the near wake of an axisymmetric cylinder
1
1980
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Experimental study of the development of longitudinal vortex pairs embedded in a turbulent boundary layer
1
1988
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Influence of boundary-layer thickness on base pressure and vortex shedding frequency
1
2001
... 列车车体的显著特点是大长细比(长细比,即列车长度与高度的比值),因此,车身表面的边界层要厚得多,从而分离剪切层也会很厚[8 ,20 ] ;高速列车尾车头部形状类似于Morel[21 ] 试验研究中的几何模型,由于头型截面的变化,导致车身表面湍流边界层的流动分离以及流向的螺旋流动,Baker[8 ] 认为这些现象是尾涡结构产生机理的构成要素. 尾涡结构的最主要特征是成对且反向旋转的流向涡旋. 研究发现,流向涡对当向下游传播时,由于彼此之间的诱导以及与地面之间的相互作用,会向下(垂向)以及向外侧(展向)进行移动,该现象与“Common-Flow-Down”型涡对[22 ] 相似;并且,尾涡结构表现出展向振荡,类似于卡门涡街的周期性脱落,而与此相关的气动力振荡频率如果十分接近列车本身横向振动频率,会加剧列车横向振动[6 ] . Bell等[12 ,13 ,14 ,15 ] 分别对ICE2和ICE3的缩尺模型进行风洞试验研究,讨论了尾流涡旋的拓扑结构以及该尾涡结构空间移动和展向振荡现象,深入分析了列车风与尾涡结构之间的联系. 在Muld等[16 ,17 ,18 ] 利用本征正交分解方法 对高速列车尾流涡旋的讨论中,数值结果显示,由2, 3和4节车厢组成的列车模型,其涡旋脱落主频值分别为0.13, 0.095和0.085;根据Rowe等[23 ] 针对平板钝形尾端处涡旋脱落与边界层厚度之间的关系的研究,所谓的“有效扩散长度”(effective diffusion length)依赖于边界层厚度以及平板两侧边界层间的有效分离距离(effective separation distance),对环量在尾流中的输运以及涡旋形成的所需时间发挥着显著的作用,因此Muld等[18 ] 认为,高速列车边界层厚度随车体长度不同而变化,从而对尾涡脱落的特征时间尺度产生影响. ...
Report on the I.U.T.A.M. symposium on concentrated vortex motions in fluids
1
1965
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
New omega vortex identification method
5
2016
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
... [25 ]引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
... Liu等[25 ] 认为速度梯度的非对称部分可能并不与涡旋运动直接相关,即涡量由于包含了与变形相关的涡量成分,不能直 接表征涡旋的存在. 根据Helmholtz分解,提出将涡量分成涡旋结构部分和非涡旋结构部分,即 ...
... 图6(a) $\sim $图6 (c)分别显示的是利用$Q$准则、 $\lambda_{2}$准则以及$\varOmega$准则得到的尾流涡旋结构,其中$Q$和$\lambda_{2}$的取值用($U_{\infty }/H)^{2}$无量纲化, $\varOmega =0.52$为Liu等[25 ] 的建议值. ...
... 涡量和变形对定义流动中的涡旋都是很重要的. 流体微团受到强剪切的作用时,变形是显著的,但因此产生的涡量可能并不与涡旋运动直接相关,涡旋涡量会下降. 正如Liu等[25 ] 所指出的,当旋转很强时,涡量可能会很小;而旋转很弱甚至没有时,涡量却可能很大. ...
Eddies, streams, and convergence zones in turbulent flows//
2
1988
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
... Hunt等[26 ] 以压力最低为附加条件,用速度梯度 ∇ u Q Q
A general classification of three-dimensional flow fields
1
1990
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
On the identification of a vortex
2
1995
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
... Jeong 和 Hussain[28 ] 从Navier-Stokes方程出发,得到压力的二阶梯度张量表达式 ...
Numerical study on wake characteristics of high-speed trains
1
2013
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
The calculation of train slipstreams using large-eddy simulation
1
2014
... 基于此,可以预料,头部表面的高涡量层与局部流体微团的剪切变形有密切关系,某种程度上暗示出流线型几何外形延迟了由车体表面发展出的边界层的流动分离,而这也将影响到流向尾涡的形成和脱落.随着剪切分离的发生,局部的低压区驱使周围空气流入近尾流区,加之与底部区域流动的相互作用,从而形成螺旋流动[12 ,30 ] .在这个过程中,流体微团因剪切作用而发生的变形是显著的,同时边界层流动的分离也使得较高的涡量在尾端附近进行扩散,这些为较强涡旋的形成和脱落提供了重要条件,正如图9所示,流向涡旋的形成是局部流动中重要的物理过程,以至于涡边界($\varOmega= 0.52$)未出现,即变形与涡量是相当的.不过,较大的剪切应变往往因为黏性效应而具有高耗散性,相应的涡量会有较为明显的衰减,并且在下游位置,对已形成的涡旋而言,图8中更大$\varOmega $ 值表明,较弱的涡旋是尾涡结构的主要部分,它们的涡量超过流体微团的变形,并且如图9(b)~图9(c)所示,涡旋涡量的占比增大,意味着剪切的影响作用在下降,虽然涡核的强度明显减小,但此时的耗散较低且旋转运动具有主导影响,这对尾涡结构能够处于相对稳定的状态是很重要的. ...
Numerical calculation of the slipstream generated by a CRH2 high-speed train
1
2016
... 模拟采用IDDES方法,Huang等[31 ] 利用该方法对平均流动雷诺数同样为3 × 10 <sup>5</sup>的高速列车绕流流场进行数值研究,气动特性相关的计算结果是令人满意的. 在基于SST k - ω l h yb
Numerical simulation and dynamics discussion of turbulent eddies in the near wake of a high speed train
4
2017
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
... 在数值计算中,应用有限体积法(finite volume method)将控制方程转换为能够进行数值求解的离散形式. 二阶迎风格式(second-order upwind scheme)和边界中心差分格式(bounded central-differencing scheme)分别用于RANS模式和LES模式,离散求解对流和扩散通量的面值;湍流模型中使用二阶迎风格式对湍流量进行求解;时间项离散采用隐式二阶格式. 通过隐式耦合求解器对非稳态流动进行数值求解,将CFL(Courant-Friedrichs-Lewy)数设为0.5. 根据之前的研究工作[32 ,34 ] ,时间步长 Δ t 0.02 H / U ∞ 200 H / U ∞
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
... [32 ,34 ],也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
Numerical simulation and dynamics discussion of turbulent eddies in the near wake of a high speed train
4
2017
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
... 在数值计算中,应用有限体积法(finite volume method)将控制方程转换为能够进行数值求解的离散形式. 二阶迎风格式(second-order upwind scheme)和边界中心差分格式(bounded central-differencing scheme)分别用于RANS模式和LES模式,离散求解对流和扩散通量的面值;湍流模型中使用二阶迎风格式对湍流量进行求解;时间项离散采用隐式二阶格式. 通过隐式耦合求解器对非稳态流动进行数值求解,将CFL(Courant-Friedrichs-Lewy)数设为0.5. 根据之前的研究工作[32 ,34 ] ,时间步长 Δ t 0.02 H / U ∞ 200 H / U ∞
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
... [32 ,34 ],也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
Coherent motions in the turbulent boundary layer
1
1991
... 涡旋如同流体运动的肌腱[24 ] 是非常重要的,对于高速列车尾流同样如此. 作为流体力学重要的研究内容之一,涡旋的科学定义和识别方法长期以来一直是热门问题. 在早期研究中,一般会利用涡量诱导出湍流流动中的拟序结构以及识别涡核,但涡量作为局部变量并不能总是表征流体整体上的旋转运动,比如层流流动[25 ] . 因此,涡旋不仅 要有涡量的集中区,而且其涡核应满足广义的Galilean不变性. 这样,基于Galilean不变性的涡旋定义[26 ,27 ,28 ] 被相继提出,包括较为经典的 Q λ 2 [3 ,29 -32 ] . 最近,Liu等[25 ] 引入无量纲参数 Ω [33 ] 进行识别. 进一步的介绍会在后文中给出. ...
高速列车近尾流区涡旋结构的湍流特性分析
3
2017
... 在数值计算中,应用有限体积法(finite volume method)将控制方程转换为能够进行数值求解的离散形式. 二阶迎风格式(second-order upwind scheme)和边界中心差分格式(bounded central-differencing scheme)分别用于RANS模式和LES模式,离散求解对流和扩散通量的面值;湍流模型中使用二阶迎风格式对湍流量进行求解;时间项离散采用隐式二阶格式. 通过隐式耦合求解器对非稳态流动进行数值求解,将CFL(Courant-Friedrichs-Lewy)数设为0.5. 根据之前的研究工作[32 ,34 ] ,时间步长 Δ t 0.02 H / U ∞ 200 H / U ∞
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
... ,34 ],也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
高速列车近尾流区涡旋结构的湍流特性分析
3
2017
... 在数值计算中,应用有限体积法(finite volume method)将控制方程转换为能够进行数值求解的离散形式. 二阶迎风格式(second-order upwind scheme)和边界中心差分格式(bounded central-differencing scheme)分别用于RANS模式和LES模式,离散求解对流和扩散通量的面值;湍流模型中使用二阶迎风格式对湍流量进行求解;时间项离散采用隐式二阶格式. 通过隐式耦合求解器对非稳态流动进行数值求解,将CFL(Courant-Friedrichs-Lewy)数设为0.5. 根据之前的研究工作[32 ,34 ] ,时间步长 Δ t 0.02 H / U ∞ 200 H / U ∞
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
... ,34 ],也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
1
1972
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
Behavior of wake vortices near ground
1
1997
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...
The formation of streamwise vorticity in turbulent flow
1
1970
... Tennekes 和Lumley[35 ] 认为,涡旋须要通过剪切的旋转和拉伸来维持自身的能量,研究表明[32 ,34 ] ,靠近尾车处的雷诺应力和湍流能量产生速率最为突出,但同时下降得也十分迅速,这一定程度上反映出局部剪切层的强度和耗散性均是很显著的.然而,在离开尾车的下游,依然会有较低水平的雷诺应力以及湍流产生过程[32 ,34 ] ,也就是说,还有弱剪切对涡旋获取平均流能量发挥着作用,鉴于此,当低涡量涡核较靠近地面,并且旋转运动发挥主导作用时,涡旋与地面间的相互作用[36 -37 ] 被认为是维持局部流动剪切的重要机制. ...