引 言

机械结构中存在着大量的结合面,一般情况下,机床中的结合面的接触刚度约占机床总刚度的60%-80% ^[1],而阻尼占到了90% ^{[2, 3]}以上,和机器零件本身的阻尼相比,结合面阻尼占有绝对优势,因此人们对结合面接触刚度和接触阻尼做了许多理论与实验研究工作 ^{[4,5,6,7,8,9,10,11]}。结合面阻尼是由结合面法向阻尼和切向阻尼所组成。Mindlin^[12]最早从理论上分析了弹性体接触时的切向微观滑移行为,推导出单位周期内能量耗散的变化规律;王东、徐超^[13]在假定微凸体的接触行为满足Mindlin解的基础上,建立了一种考虑粗糙接触的结合面黏滑摩擦模型;张学良等^[14]基于分形接触理论及其修正模型以及结合面阻尼损耗机理,建立了计及微接触面积分布的域扩展因子影响的结合面切向接触阻尼能量耗散的弹塑性分形模型;姜来等^[15]基于三维接触分形理论和固定结合面切向接触阻尼耗能机理,建立了考虑弹塑性接触变形机制的固定结合面切向接触阻尼分形模型;李小彭等^[16]提出结合面“固-隙-固”接触模型,并建立了考虑摩擦因素影响的结合面切向接触阻尼分形预估模型;Zhang等^[17]基于MB接触分形理论及其修正模型和结合面切向阻尼耗能机理,建立了结合面切向接触阻尼能量耗散模型;Fujimoto等^[18]通过理论和实验研究了完全塑性接触条件下切向载荷和相对位移之间的关系,认为切向载荷和相对位移之间为双线性关系。

上述的相关研究表明结合面切向阻尼及其能量耗散在结构动态特性中的重要作用,但是均未考虑在法向载荷和切向载荷的同时作用下,结合面黏滑摩擦行为对结合面切向接触阻尼的影响。为此本文在考虑法向载荷下微凸体的弹性、弹塑性和塑性变形机制基础上,结合Mindlin和Fujimoto理论,建立一种考虑结合面黏滑摩擦行为的结合面切向接触阻尼模型,通过数值仿真揭示结合面法向载荷、切向激振频率和动态位移幅值对结合面切向接触阻尼系数的影响规律,并且与实验结果对比分析。

1 结合面切向接触阻尼模型假设

研究表明,两个粗糙表面间的接触可以等效为一个刚性光滑平面与一个粗糙表面之间的接触问题,本文模型假设与Greenwood和Williamson所提出的模型^[19]（即GW模型）所作的假设类似,即所有微凸体具有相同的曲率半径,峰高分布服从高斯分布,并且假设粗糙表面各微凸体独立且互不干涉。

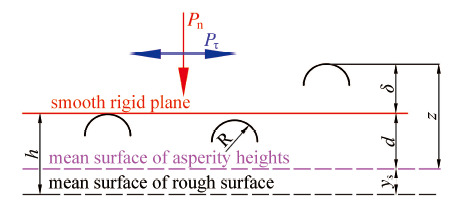
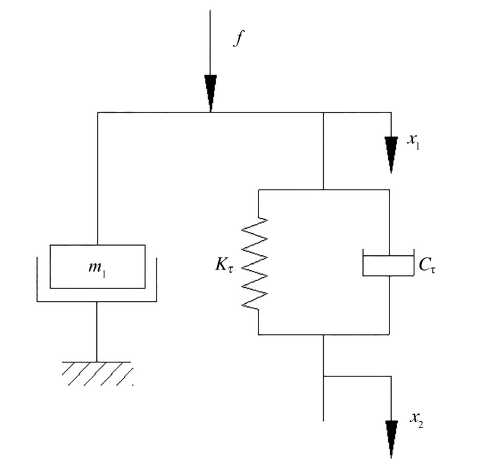
如图1所示,z是从凸峰顶部到微凸体平均高度值,d是刚性平面到微凸体平均高度的距离,h是理想刚性平面与表面平均高度平面间的距离,${y}_{\rm s}$为表面平均高度平面和微凸体平均高度平面之间的距离,R为微凸体的曲率半径,$P_n$和$P_\tau$分别为微凸体所承受的法向静态载荷和切向振动周期载荷.当在刚性平面施加法向载荷时,微凸体将发生变形, 法向变形量为

$\delta=z-d$ (1)

图1中两表面平均距离d可表示为

$d=h-\rm {{y}}_{\rm s}$ (2)

${{y}}_{\rm s}=\dfrac{4\sigma}{({\rm \pi}\zeta)^{1/2}}$ (3)

$\zeta=\dfrac{0.896~8}{1-(\sigma_s/\sigma)^2}$ (4)

$\dfrac{\sigma_{\rm s}}{\sigma}={\left[1-\dfrac{3.717\times10^{-4}}{(\sigma R \eta)^{2}}\right]^{1/2}}$ (5)

式中,$\sigma$ 为等效粗糙表面微凸体高度的均方差,$\sigma_{{\rm s}}$ 为微凸体顶端标准高度偏差,$\zeta$ 为表征粗糙表面形貌特性的中间参数,$\eta$ 为微凸体的面积密度,$R$ 为等效粗糙表面微凸体的曲率半径,定义$\beta=\sigma R \eta$ 为粗糙表面形貌参数.

如果两个粗糙表面微凸体的曲率半径和均方差分别为 $R_{1},R_{2};\sigma_{1},\sigma_{2}$;两接触材料的弹性模量、剪切模量和泊松比分别为 $E_{1},E_{2};G_{1} ,G_{2};v_{1},v_{2}$;可以将两粗糙表面的平均微凸体半径$R_{1}$和$R_{2}$等效为

$\dfrac{1}{R}=\dfrac{1}{R_{1}}=\dfrac{1}{R_{2}}$ (6)

等效粗糙表面微凸体的均方差为

$\sigma=\sqrt{\sigma_{1}{^{2}}+\sigma_{2}{^{2}}}$ (7)

等效粗糙表面的微凸体的弹性模量为

$\dfrac{1}{E}=\dfrac{1-v_{1}{^{2}}}{E_{1}}+\dfrac{1-v_{2}{^{2}}}{E_{2}} $ (8)

等效粗糙表面的微凸体剪切模量为

$\dfrac{1}{G}=\dfrac{2-v_{1}}{G_{1}}+\dfrac{2-v_{2}}{G_{2}}$ (9)

等效泊松比为

$v=\dfrac{E}{2G}-1$ (10)

假设表面粗糙峰高度分布服从正态分布,可用高斯概率分布密度函数来表示表面轮廓的微凸体高度分布

$z(x)=\frac{1}{\sqrt{2{\rm \pi}}\sigma}{\rm exp}\left(-\frac{z^{2}}{2\sigma^{2}}\right)$ (11)

当法向载荷较小时,微凸体之间主要发生弹性变形;随着微凸体变形量$\delta$增大,将进入弹‒塑性变形阶段;随着其进一步增大,微凸体的应力超过屈服应力,发生塑性变形.因此,表面微凸体的变形随着法向载荷的增大,将经历由弹性、弹塑性和塑性的变形过程.在法向载荷的作用下,微凸体受到切向振动周期载荷的作用后,产生相应的动态切向相对位移为 $\xi$,当切向作用力小于摩擦力时,微凸体将处于黏滑状态;但大于摩擦力时,微凸体将处于微观滑动状态.本文将在考虑微凸体法向三种变形过程和切向两种变化状态的基础上,推导结合面切向接触阻尼计算模型.

2 结合面切向接触阻尼统计模型

2.1 微凸体弹性变形阶段

当微凸体发生法向弹性变形时,根据赫兹接触理论^[20],单个微凸体的法向接触载荷为

$p_{\rm ne}=\dfrac{4}{3}ER^{1/2}\delta^{3/2}$ (12)

发生弹性变形的微凸体在受到切向载荷$P_{\textrm{τ}\rm e}$ 的作用后,将产生切向相对位移$\xi$. 经典Mindlin理论给出了切向载荷与相对位移之间的关系

${{p}_{\tau e}}=\left\{ \begin{matrix} \mu {{p}_{ne}}\left[ 1-{{\left( 1-\frac{\xi }{{{\xi }_{e}}} \right)}^{{3}/{2}\;}} \right] & \xi \le {{\xi }_{e}} \\ \mu {{p}_{ne}} & \xi >{{\xi }_{e}} \\ \end{matrix} \right.$ (13)

式中,$\xi_{\rm e}=\dfrac{\mu E \delta_{\rm ee}(2-v)}{4G}$,$\delta_{\rm ee}=\left\lgroup\dfrac{3p_{\tau 0}}{4E\mu\sqrt{R}}\right\rgroup^{2/3}$,$\mu$ 为摩擦系数, ${{p}_{\tau 0}}$ 为切向振动载荷的最大值.

式(13)中第1式表示微凸体处于黏滑状态的接触,第2式表示微凸体发生宏观滑动的切向力— 位移关系.根据文献^[21] 所给出的迟滞曲线,即加卸载过程中载荷与变形的关系,可以得到弹性阶段黏滑状态和滑动状态的阻尼能量耗散,分别如下.

1 弹性阶段黏滑状态：

迟滞曲线

${{p}_{\tau e1}}=\left\{ \begin{align} & \frac{4}{3}E{{R}^{\frac{1}{2}}}\mu {{\delta }^{\frac{3}{2}}}\left( 1-{{\left( 1-\frac{\xi }{{{\xi }_{e}}} \right)}^{\frac{3}{2}}} \right)\ \ \text{Loading}\left( {{p}_{\tau e1l}} \right) \\ & {{p}_{\tau max}}-2{{p}_{\tau e}}\left( \frac{{{\xi }_{max}}-\xi }{2} \right)\ \ \ \ \ \ \ \text{Unloading}\left( {{p}_{\tau e1d}} \right) \\ \end{align} \right.$ (14)

式中,$p_{\tau {\rm max}}$ 为迟滞曲线中的最大作用力,$\xi_{{\rm max}}$ 为迟滞曲线中的最大相对位移.

阻尼能量耗散

${{d}_{e1}}=\int_{-{{\xi }_{max}}}^{{{\xi }_{max}}}{\left( {{p}_{\tau e1l}}-{{p}_{\tau e1d}} \right)d\xi }$ (15)

② 弹性阶段滑动状态：

迟滞曲线：

${{p}_{\tau e2}}=\left\{ \begin{align} & \frac{4}{3}E{{R}^{{}^{1}/{}_{2}}}\mu {{\delta }^{{}^{3}/{}_{2}}}\ \ \ \ \ \text{Loading}\left( {{p}_{\tau e2l}} \right) \\ & -\frac{4}{3}E{{R}^{{}^{1}/{}_{2}}}\mu {{\delta }^{{}^{3}/{}_{2}}}\ \ \text{Unloading}\left( {{p}_{\tau e2d}} \right) \\ \end{align} \right.$ (16)

阻尼能量耗散：

${{d}_{e2}}=\int_{-{{\xi }_{e}}}^{{{\xi }_{e}}}{\left( {{p}_{\tau e1l}}-{{p}_{\tau e1d}} \right)d\xi }+\int_{-\left( {{\xi }_{max}}-{{\xi }_{e}} \right)}^{\left( {{\xi }_{max}}-{{\xi }_{e}} \right)}{\left( {{p}_{\tau e2l}}-{{p}_{\tau e2d}} \right)d\xi }$ (17)

2.2 微凸体塑性变形阶段

当微凸体法向变形量$\delta$ 进入完全塑性变形范围,即 $\delta\geqslant 110\delta_{\rm e}$ 时,微凸体将处于完全塑性变形阶段,$\delta_{\rm e}$ 为微凸体从弹性变形过渡为弹塑性变形的临界值^[22],可由下式获得

${{\delta }_{e}}={{\left( \frac{\pi kH}{2E} \right)}^{2}}R$ (18)

式中,$k$ 为硬度系数$k=0.454+0.41v$,$H$ 为较软材料的硬度.

根据Abbott模型^[23],可得处于完全塑性变形阶段的微凸体的接触载荷为

$ p_{\rm np}=2{\rm \pi} RH\delta $ (19)

与弹性变形阶段相似,发生塑性变形的微凸体在受到切向载荷${{p}_{\tau p}}$ 的作用后,将产生切向相对位移$\xi$,Fujimoto 等^[18]通过理论和实验研究了完全塑性条件下切向载荷与相对位移的关系,认为发生塑性变形的微凸体切向载荷与切向位移之间为双线性关系,即

${{p}_{\tau p}}=\left\{ \begin{align} & {\mu {{p}_{np}}\xi }/{{{\xi }_{p}}}\;\ \ \ \xi \le {{\xi }_{p}} \\ & \mu {{p}_{np}}\ \ \ \ \ \ \ \ \ \xi >{{\xi }_{p}} \\ \end{align} \right.$ (20)

式中：$\xi_{\rm p}=\dfrac{\mu H(2R\delta_{\rm pp})^{1/2}}{2G}$,$\delta_{\rm pp}=\dfrac{P_{\tau\rm 0}}{2{\rm \pi} RH \mu}$.

根据文献^[21]所给出的迟滞曲线,可以得到塑性阶段黏滑状态和滑动状态的阻尼能量耗散,分别如下：

1 塑性阶段黏滑状态：

迟滞曲线

${{p}_{\tau p1}}=\left\{ \begin{align} & {2\pi \mu RH\delta \xi }/{{{\xi }_{p}}}\;\ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Loading}\left( {{p}_{\tau p1l}} \right) \\ & {{p}_{\tau max}}-2{{p}_{\tau p}}\left( \frac{{{\xi }_{max}}-\xi }{2} \right)\ \ \text{Unloading}\left( {{p}_{\tau p1d}} \right) \\ \end{align} \right.$ (21)

阻尼能量耗散：

${{d}_{p1}}=\int_{-{{\xi }_{max}}}^{{{\xi }_{max}}}{\left( {{p}_{\tau p1l}}-{{p}_{\tau p1d}} \right)d\xi }$ (22)

② 塑性阶段滑动状态：

迟滞曲线：

${{p}_{\tau p2}}=\left\{ \begin{align} & 2\pi \mu RH\delta \ \ \ \text{Loading}\left( {{p}_{\tau p2l}} \right) \\ & -2\pi \mu RH\delta \ \text{Unloading}\left( {{p}_{\tau p2d}} \right) \\ \end{align} \right.$ (23)

阻尼能量耗散：

${{d}_{p2}}=\int_{-{{\xi }_{max}}}^{{{\xi }_{max}}}{\left( {{p}_{\tau p2l}}-{{p}_{\tau p2d}} \right)d\xi }$ (24)

2.3 微凸体弹塑性变形阶段

根据Kogut \asbibref{bib22}有限元分析结果,当法向变形量位于$\delta_{\rm e} \leqslant \delta \leqslant 110\delta_{\rm e} $ 范围时,微凸体处于弹塑性变形阶段,此阶段又可以分为弹塑性${\rm I}$ 区($\delta_{\rm e} \leqslant \delta \leqslant 6\delta_{\rm e}$) 和${\rm II} $区(6$\delta_{\rm e} \leqslant \delta \leqslant 110\delta_{\rm e} $),接触载荷分别表示为:

弹塑性Ⅰ区：

${{p}_{nep1}}=\frac{2.06}{3}kH\pi R{{\delta }_{e}}{{\left( \frac{\delta }{{{\delta }_{e}}} \right)}^{\frac{36}{25}}}$ (25)

弹塑性Ⅱ区：

${{p}_{nep2}}=\frac{2.8}{3}kH\pi R{{\delta }_{e}}{{\left( \frac{\delta }{{{\delta }_{e}}} \right)}^{\frac{63}{50}}}$ (26)

在弹塑性阶段,以Fujimoto模型为基础,结合Cattaneo和Mindlin理论,推导出切向载荷作用下处于弹塑性接触状态的微凸体微观位移特性.

$p_{{\tau}\rm ep}=\left\{\begin{split}&\mu p_{1} \left [ 1-\left\lgroup1-\frac{\xi}{\xi_{\rm eep}}\right\rgroup^{\frac{3}{2}}\right]+\frac{\mu p_{2}\xi}{\xi_{\rm pep}},\\&\quad\quad\xi \leqslant \xi_{\rm ep}\\&\mu p_{\rm nep},\\&\quad\quad\xi > \xi_{\rm ep}\end{split}\right.$ (27)

式中, p1=2π∫rpr‍p(a)ada, ξeep=16Gr3(2-v)μp1, r为接触面半径, rp为塑性区半径, a为接触面内任一半径, p(a)=3pnep2πr21-ar20.5,p2=πrp2py,ξpep=3μ2GHπ0.5P20.5, py为材料屈服强度, ξep为弹塑性阶段微凸体由黏滑状态向滑动状态转变的临界切向相对位移,可由式(27) 推导而得.

结合Kogut有限元分析结果和弹塑性条件下切向载荷与相对位移的关系bib24,根据法向变形量 δ的值^[25,26],可将处于弹塑性接触状态的微凸体在受到切向载荷时的变化过程分为4个区域

$\begin{equation}\left.\begin{split}&\delta_{\rm e} \leqslant \delta \leqslant \delta_{\rm ep1},\quad\quad~~{\rm elastic-plastic~I~slip~state}\\&\delta_{\rm ep1} \leqslant \delta \leqslant 6\delta_{\rm e},\quad\quad{\rm elastic-plastic~I~slip~state}\\&6\delta_{\rm e} \leqslant \delta \leqslant \delta_{\rm ep2},\quad\quad{\rm elastic-plastic~II~slip~state}\\&\delta_{\rm ep2} \leqslant \delta \leqslant 110\delta_{\rm e},\quad{\rm elastic-plastic~II~slip~state}\end{split}\right\}\end{equation}$

其中

δep1=δe3pτ02.06kHπRδeμ2536

δep2=δe3pτ02.8kHπRδeμ5063

根据文献^[21]中的迟滞曲线,可以分别得到微凸体在4个区域中的阻尼能量耗散.

1 弹塑性 I区黏滑状态:

迟滞曲线

pτep11=μp11-1-ξξeep32+μp2ξξpep,loading(pτep11l)pτmax-2pτepξmax-ξ2,unloading(pτep11d)(28)

阻尼能量耗散

dep11=∫-ξmaxξmax‍(Pτep11l-Pτep11d)dξ(29)

2 弹塑性 I区滑动状态:

迟滞曲线

pτep12=2.063kHRμπδeδδe3625,loading(pτep12l)-2.063kHRμπδeδδe3625,unloading(pτep12d)(30)

阻尼能量耗散

dep12=∫-ξepξep‍(pτep11l-pτep11d)dξ+∫-(ξmax-ξep)(ξmax-ξep)‍(pτep12l-pτep12d)dξ(31)

3 弹塑性 II区黏滑状态:

迟滞曲线

pτep21=μp11-1-ξξeep32+μp2ξξpep,loading(pτep21l)pτmax-2pτepξmax-ξ2,unloading(pτep21d)(32)

阻尼能量耗散

dep21=∫-ξmaxξmax‍(pτep21l-pτep21d)dξ(33)

4 弹塑性 II区滑动状态:

迟滞曲线

pτep22=2.83kHRμπδeδδe6350,loading(pτep22l)-2.83kHRμπδeδδe6350,unloading(pτep22d)(34)

阻尼能量耗散

dep22=∫-ξepξep‍(pτep21l-pτep21d)dξ+∫-(ξmax-ξep)(ξmax-ξep)‍(pτep22l-pτep22d)dξ(35)

2.4 结合面切向接触阻尼模型

采用概率统计分析的方法分别建立整个粗糙接触表面法向载荷与法向接触变形、切向载荷与切向相对位移之间的关系,其无量纲表达式如下

pn*=43βσR12A1+2πHβEA2+2.06kHπδe*3A3+2.8kHπδe*3A4(36)

其中

$\begin{equation}\begin{split}A_{1}&=\int^{h^{\ast}-y_{\rm s}^{\ast}+\delta_{\rm e}^{\ast}}_{h^{\ast}-y_{\rm s}^{\ast}}\delta{^{\ast}}{^{\frac{3}{2}}}\varphi^{\ast}(z^{\ast}){\rm d}z^{\ast}\\A_{2}&=\int^{+\infty}_{h^{\ast}-y_{\rm s}^{\ast}+110\delta_{\rm e}^{\ast}}\delta^{\ast}\varphi^{\ast}(z^{\ast}){\rm d}z^{\ast}\\A_{3}&=\frac{\beta}{E}\int^{h^{\ast}-y_{\rm s}^{\ast}+6\delta_{\rm e}^{\ast}}_{h^{\ast}-y_{\rm s}^{\ast}+\delta_{\rm e}^{\ast}}\left \lgroup \frac{\delta^{\ast}}{\delta^{\ast}_{\rm e}}\right\rgroup^{\frac{36}{25}}\varphi^{\ast}(z^{\ast}){\rm d}z^{\ast}\\A_{4}&=\frac{\beta}{E}\int^{h^{\ast}-y_{\rm s}^{\ast}+110\delta_{\rm e}^{\ast}}_{h^{\ast}-y_{\rm s}^{\ast}+6\delta_{\rm e}^{\ast}}\left \lgroup \frac{\delta^{\ast}}{\delta^{\ast}_{\rm e}}\right\rgroup^{\frac{63}{50}}\varphi^{\ast}(z^{\ast}){\rm d}z^{\ast}\end{split}\end{equation}$

$\begin{split}P_{\textrm{\tau}}{^{*}}(\xi^{*})=&\frac{4\beta \mu}{3\sigma \sqrt{R}}B_{1}+\frac{4\beta \mu}{3\sigma \sqrt{R}}B_{2}+ \frac{2 {\rm \pi} \beta \mu H}{\sigma E}B_{3}+ \\ &\frac{2^{\frac{3}{2}} {\rm \pi} G \beta}{\sigma \sqrt{R} E}B_{4}+ \frac{2.06 \beta k H {\rm \pi} \mu}{3\sigma E}B_{5}+ \\ &\frac{\beta}{\sigma R E}B_{6}+ \frac{2.8 \beta k H {\rm \pi} \mu}{3\sigma E}B_{7}+ \frac{\beta}{\sigma R E}B_{8} \end{split}$ (37)

其中

$\begin{equation}B_{1}=\int^{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm ee}{^{*}}}_{h^{*}-y_{\rm s}{^{*}}}\delta^{*\frac{3}{2}}\varphi^{*}(z^{*}){\rm d}z^{*}\end{equation}$

$\begin{equation}\begin{split}B_{2}&=\int^{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm e}{^{*}}}_{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm ee}{^{*}}}\delta^{*{\frac{3}{2}}}\left[1-\left\lgroup 1-\frac{\xi^{*}}{\xi_{\rm e}{^{*}}}\right\rgroup^{\frac{3}{2}}\right] \varphi^{*}(z^{*}){\rm d}z^{*}\\ B_{3}&=\int^{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm pp} {^{*}}}_{h^{*}-y_{\rm s}{^{*}}+110\delta_{\rm e}{^{*}}}\delta^{*}\varphi^{*}(z^{*}){\rm d}z^{*} \\ B_{4}&=\int^{+\infty}_{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm pp}{^{*}}}\xi^{*}\delta^{*\frac{1}{2}}\varphi^{*}(z^{*}){\rm d}z^{*} \\ B_{5}&=\int^{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm ep1}{^{*}}}_{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm e}{^{*}}} \delta_{\rm e}{^{*}}\left\lgroup\frac{\delta^{*}}{\delta_{\rm e}{^{*}}}\right\rgroup^{\frac{36}{25}}\varphi^{*}(z^{*}){\rm d}z^{*} \\ B_{6}&=\int^{h^{*}-y_{\rm s}{^{*}}+6\delta_{\rm e}{^{*}}}_{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm ep1}{^{*}}} \Bigg\{ \mu p_{1}{^{*}}\left[1-\left\lgroup 1-\frac{{\xi^{*}}}{\xi_{\rm eep}{^{*}}}\right\rgroup^{\frac{3}{2}}\right] + \\ &\quad\frac{\mu p_{2}{^{*}}\xi^{*}}{\xi_{\rm pep}{^{*}}} \Bigg\} \varphi^{*}(z^{*}){\rm d}z^{*} \\ B_{7}&=\int^{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm ep2}{^{*}}}_{h^{*}-y_{\rm s}{^{*}}+6\delta_{\rm e}{^{*}}} \delta_{\rm e}{^{*}}\left \lgroup \frac{\delta^{*}}{\delta_{\rm e}{^{*}}}\right \rgroup^{\frac{63}{50}}\varphi^{*}(z^{*}){\rm d}z^{*} \\ B_{8}&=\int^{h^{*}-y_{\rm s}{^{*}}+110\delta_{\rm e}{^{*}}}_{h^{*}-y_{\rm s}{^{*}}+\delta_{\rm ep2}{^{*}}} \Bigg\{\mu p_{1}{^{*}}\left[1-\left \lgroup 1-\frac{\xi^{*}}{\xi_{\rm eep}{^{*}}}\right \rgroup^{\frac{3}{2}}\right] + \\ &\quad\frac{\mu p_{2}{^{*}}\xi^{*}}{\xi_{\rm pep}{^{*}}}\Bigg\}\varphi^{*}(z^{*}){\rm d}z^{*} \end{split} \end{equation}$

同理可以得到结合面在一个振动周期内的切向阻尼能量耗散

D*=βERAσ(C1+C2+C3+C4+C5+C6+C7+C8)(38)

其中

$\begin{equation}\begin{split} C_1&=\int_{h^*-y_{\rm s}{^*}}^{h^*-y_{\rm s}{^*}+\delta_{\rm ee}{^*}}d_{\rm e2}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_2&=\int_{h^*-y_{\rm s}{^*}+\delta_{\rm ee}{^{*}}}^{h^*-y_{\rm s}{^*}+\delta_{\rm e}{^*}} d_{\rm e1}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_3&=\int_{h^*-y_{\rm s}{^*}+\delta_{\rm e}{^{*}}}^{h^*-y_{\rm s}{^*}+\delta_{\rm ep1}{^*}} d_{\rm ep12}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_4&=\int_{h^*-y_{\rm s}{^*}+\delta_{\rm ep1}{^{*}}}^{h^*-y_{\rm s}{^*}+6\delta_{\rm e}{^*}} d_{\rm ep11}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_5&=\int_{h^*-y_{\rm s}{^*}+6\delta_{\rm e}{^{*}}}^{h^*-y_{\rm s}{^*}+\delta_{\rm ep2}{^*}} d_{\rm ep22}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_6&=\int_{h^*-y_{\rm s}{^*}+\delta_{\rm ep2}{^{*}}}^{h^*-y_{\rm s}{^*}+110\delta_{\rm e}{^*}} d_{\rm ep21}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_7&=\int_{h^*-y_{\rm s}{^*}+110\delta_{\rm e}{^{*}}}^{h^*-y_{\rm s}{^*}+\delta_{\rm pp}{^*}} d_{\rm p2}{^*}\varphi ^*(z^*){\rm d}z^*\\ C_8&=\int_{h^*-y_{\rm s}{^*}+\delta_{\rm pp}{^{*}}}^{+\infty} d_{\rm p1}{^*}\varphi ^*(z^*){\rm d}z^* \end{split} \end{equation}$

式中, A为粗糙表面名义接触面积, ϕ*(z*)为微凸体高度分布的概率密度函数

ϕ*(z*)=1/2π(σ/R)exp[-0.5(σ/σs)2z*2]

根据粘性阻尼等效原理可知bib27,无量纲的等效黏性阻尼系数 C*为

C*=D*πω*X*2(39)

式中, ω*为无量纲激振频率,是激振频率与采样频率bib20 之比,其值影响迟滞曲线中的最大相对位移 ξmax,ω*越小,则 ξmax越大. X*为无量纲动态相对位移幅值,是振动幅值与静态变形量之比,其值由施加在结合面上的切向振动载荷的最大值 pτ0所决定.

3 不同因素对结合面切向接触阻尼的影响规律分析

本节根据所建立的结合面切向接触阻尼模型,考察法向接触载荷、激振频率和动态相对位移幅值对切向接触阻尼的影响规律.假设两个接触表面的材料性能参数为: E1=150GPa,E2=150GPa,较软材料的硬度 H=2.07GPa,泊松比 v1=v2=0.25,摩擦系数 μ=0.15,材料屈服强度 py=18GPa,微凸体的曲率半径 R=6.89×10-4mm,名义接触面积 A=7.07×10-4m2, 粗糙表面形貌参数 β=0.14,粗糙表面高度分布的标准偏差 σ=1.89×10-6.采样频率为 1000Hz.

3.1 法向接触载荷对切向接触阻尼的影响

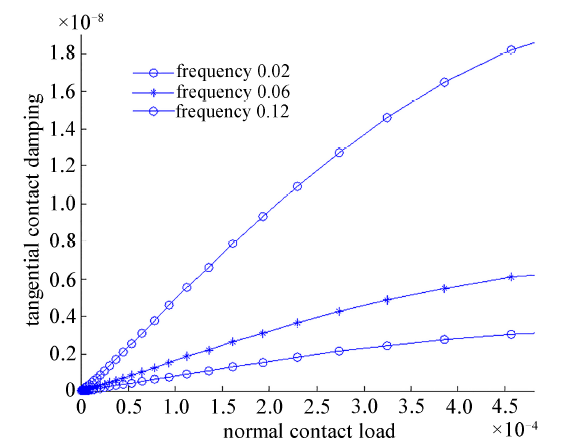
图2给出了在动态相对位移幅值为0.015,不同激振频率下的切向接触阻尼与法向接触载荷之间的关系.由图可以看出,在3组不同的激振频率下,结合面切向阻尼随着法向接触载荷的增大而呈非线性增大.这是因为在结合面切向振动载荷作用下,随着结合面法向接触载荷的增大,结合面发生实际接触的微凸体数目增多,这所产生的微凸体形变能耗也就增大.从而其切向接触阻尼也就增大.

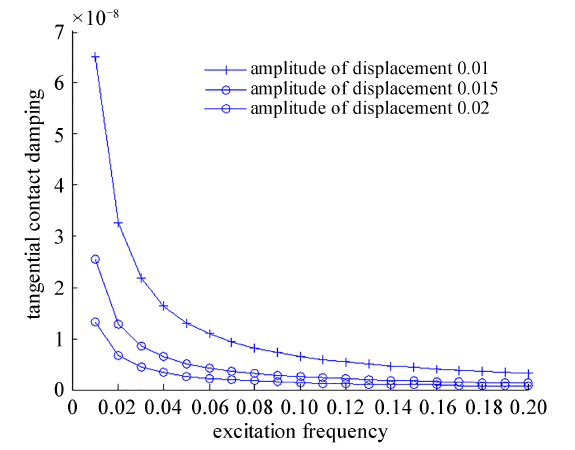
3.2 激振频率对切向接触阻尼的影响

图3给出了在法向接触载荷为 2.664×10-4,不同动态相对位移幅值下的切向接触阻尼与激振频率之间的关系.由图可以看出,在3组不同的动态相对位移幅值条件下,当激振频率较低时,结合面切向接触阻尼随着激振频率的增大而迅速减小,当频率较大时,结合面切向接触阻尼随着激振频率的变化幅度变小.这是因为随着激振频率的增大,迟滞曲线所包围的面积减小,从而使单位周期内的切向阻尼能量耗散减小,这样就造成结合面间的切向接触阻尼也随之减小.

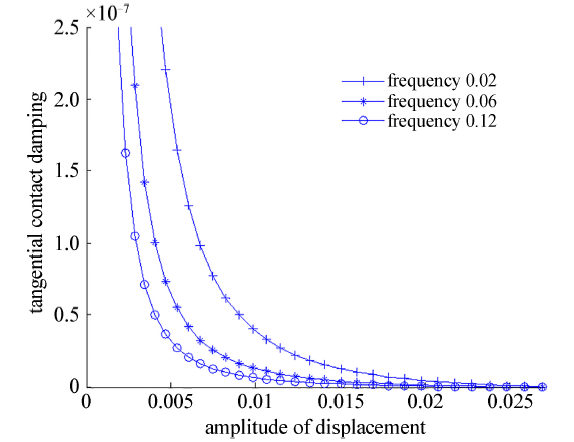
3.3 动态相对位移幅值对切向接触阻尼的影响

图4给出了在法向接触载荷为 2.664×10-4,不同激振频率下的切向接触阻尼与动态相对位移幅值之间的关系.由图可以看出,在动态相对位移幅值较小的范围内,结合面切向接触阻尼随着动态相对位移幅值的增大而迅速减小,到一定的幅值后,结合面切向接触阻尼几乎不随动态相对位移幅值的变化而变化.实际上,仿真分析可以得到,阻尼能量耗散是随动态相对位移幅值增大而呈指数规律增大的,但增长指数没有达到2次方,由于式(39) 分母中幅值 X*的抵消作用,故切向接触阻尼系数随动态相对位移幅值增大而减小.

4 结合面切向阻尼模型的实验验证

4.1 实验装置

图5给出了结合面切向实验装置和传感器布置图,其中图5(a)为实验箱体全景图,图5(b)为左(右)试件和中间试件以及相关传感器安装布置图.

中间试件与左(右)试件之间接触表面构成实验结合面.切向静态力传感器和动态力传感器布置在中间试件上,分别用于测量中间试件上受到的加力螺杆施加的切向静态载荷和激振杆施加的切向简谐动态载荷.法向静态力传感器布置在左试件上,用于测量施加在左(右)试件上的法向静态载荷. width=6.5cm5a.jpg (a) 实验装置全景两个涡流位移传感器和两个加速度计对称布置在中间试件上,分别用于测量中间试件与左(右)试件之间的相对动态位移以及中间试件的加速度响应.所有传感器采集的原始信号通过m+p动态分析系统进行分析,再经过计算机的进一步数据处理,可以获得单位面积结合面切向接触阻尼.

4.2 实验原理

图6表示由中间试件与左(右)试件构成的结合面等效动力学模型.图中: f为作用在中间试件上的简谐激振力: m1为中间试件的质量; Kτ和 Cτ分别为结合面动态接触刚度和阻尼; x1和 x2分别为中间试件、左(右)试件位移.

取中间试件为分离体,根据结合面动力学模型建立如下方程

m1ẍ1+fτ=f(40)

fτ=Kτxτ+Cτẋτ(41)

xτ=x1-x2(42)

式中, ẍ1为中间试件的加速度,由加速度计获得; xτ为结合面间相对动态位移,由涡流位移传感器获得; fτ为作用在结合面上的切向动态力,由加速度计测得的 ẍ1和动态力传感器测得的 f,根据式(40)获得.

当对中间试件施加简谐激励时,不计高次谐波成分的影响,可令

fτ=Fτcosωt(43)

xτ=Xτcos(ωt-φτ)(44)

其中, φτ为 xτ与 fτ之间的相位差.

将式(43)和式(44)代入式(41),并引入结合面名义面积A,可推得结合面切向单位面积接触阻尼为:

cτ=FτsinφτωXτA(45)

式中, Fτ, Xτ和 φτ可以通过 m+ p动态分析系统进行传递函数分析获得.

4.3 理论与实验对比分析

实验采用的中间试件和左(右)试件实验材料为铸铁HT300,加工方式为磨削淬火,其接触面积 A=7.07×10-4m2,实验材料属性参数为弹性模量 E1=E2=150GPa,泊松比 v1=v2=0.25,硬度 H=2.07GPa.

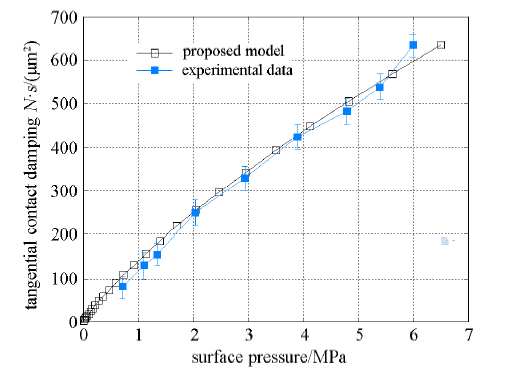
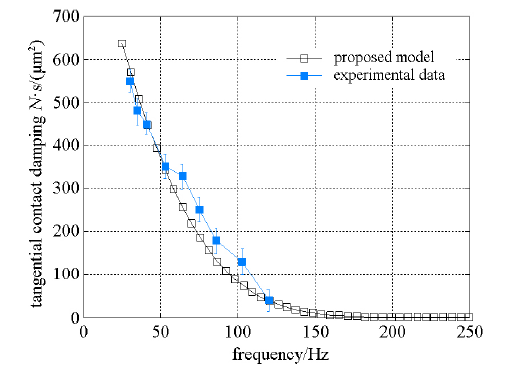
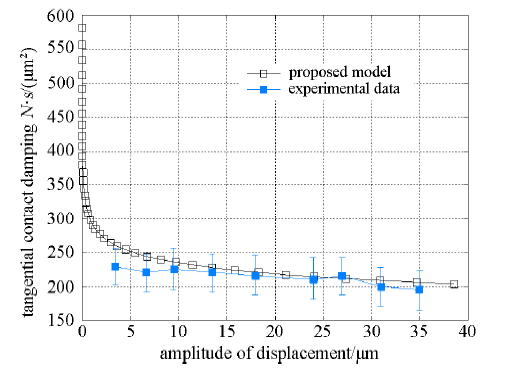
图7表示动态位移幅值为15μm、频率为20 Hz时,理论和实验获得的结合面切向接触阻尼与法向面压的关系.图8表示法向面压为6.5 MPa、动态位移幅值为15μm 时, 理论和实验获得的结合面切向接触阻尼与切向激振频率的关系.图9表示法向面压为6.5 MPa、频率为20 Hz时,理论和实验获得的结合面切向接触阻尼与切向动态位移幅值的关系.图7和图8 显示,理论与实验结果的变化规律基本一致,但实验值稍大于理论值.图9显示,在动态相对位移幅值较大的范围内,理论阻尼与实验阻尼的变化规律基本一致,但实验值稍大于理论值;而在动态相对位移幅值较小的范围内,理论值大于实验值.

在给定实验条件下,上述理论模型与实验结果之间对比存在的相对误差范围在0.34%~5.56%.分析误差原因主要来自3个方面: 一是本文以GW模型假设为基础,将2 个粗糙表面接触简化为刚性平面与等效粗糙表面的接触,忽略了微凸体相互作用和侧接触的影响;二是理论模型中的表面形貌与实际加工表面形貌以及参数之间存在一定偏差;三是对于图9而言,虽然式(39) 表示的理论阻尼与式(45)表示的实验阻尼本质上都是描述结合面宏观等效黏性阻尼,但就式中能量耗散D与动态相对位移幅值X之间的变化规律而言,理论模型规律为 D∝X1.628,而实验规律为 D=FτXτsinφτ∝X1.973因而造成按式(39) 计算的理论阻尼和按式(45) 计算的实验阻尼仍然与分母中动态相对幅值位移有关,即都随着振动幅值的增大而减小,而减小的幅度有差异.导致这种能量耗散变化规律的理论与实验之间差别的原因仍然与前面两个误差原因有关.

5 结论

(1)本文在Mindlin和Fujimoto理论的基础上,建立了一种考虑结合面黏滑摩擦行为的结合面切向接触阻尼统计模型,数值仿真了法向接触载荷、激振频率和动态相对位移幅值对结合面切向接触阻尼系数的影响,并对理论模型进行了实验验证.虽然理论阻尼值与实验阻尼值存在一定误差,但理论模型变化规律与实验结果趋势和数量级基本保持一致,证明了本文模型的正确性和有效性.

(2)结合面切向接触阻尼系数与法向接触载荷、 激振频率和动态相对位移幅值之间存在显著的非线性关系,阻尼系数随着法向接触载荷的增大而呈非线性增大,随着激振频率和切向动态相对位移幅值的增大而呈非线性减小;在切向动态相对位移幅值较大的范围内,激振频率和位移幅值对切向阻尼系数影响很小.

(3)为了进一步分析考察微凸体相互作用和侧接触的影响,后期将研究考虑微凸体侧接触以及相互作用的结合面切向接触阻尼计算模型.

The authors have declared that no competing interests exist.

---

参考文献

文献选项

• 原文顺序
• 文献年度倒序
• 文中引用次数倒序
• 被引期刊影响因子

[1]	Ren Y. Identification of ‘effective’ lnear joints using coupling and joint identification techniques . Journal of Vibration & Acoustics, 1998, 120(2): 331-338 [本文引用: 1]
[2]	Ibrahim RA, Pettit CL. Uncertainties and dynamic problems of bolted joints and other fasteners . Journal of Sound & Vibration, 2005, 279(3): 857-936 [本文引用: 1]
[3]	Burdekin M, Back N, Cowley A. Analysis of the local deformations in machine joints . Journal of Mechanical Engineering Science, 1979, 21(1): 25-32 [本文引用: 1]
[4]	Chandrasekar S, Eriten M, Polycarpou AA. An improved model of asperity interaction in normal contact of rough surfaces . Journal of Applied Mechanics, 2013, 80(1): 1025-1036 [本文引用: 1]
[5]	Gao Z, Fu W, Wang W, et al. Normal damping model of mechanical joints interfaces considering asperities in lateral contact . Journal of Tribology, 2017, 140(2): 021404-021412 [本文引用: 1]
[6]	Jha KK, Suksawang N, Lahiri D, et al. Evaluating initial unloading stiffness from elastic work-of-indentation measured in a nanoindentation experiment . Journal of Materials Research, 2013, 28(6): 789-797 [本文引用: 1]
[7]	Kucharski S, Starzynski G. Study of contact of rough surfaces: Modeling and experiment . Wear, 2014, 311(1-2): 167-179 [本文引用: 1]
[8]	Li L, Etsion I, Talke FE. Contact area and static friction of rough surfaces with high plasticity index . Journal of Tribology, 2010, 132(3): 031401-031410 [本文引用: 1]
[9]	Zhao B, Zhang S, Qiu Z. Analytical asperity interaction model and numerical model of multi-asperity contact for power hardening materials . Tribology International, 2015, 92(1), 57-66 [本文引用: 1]
[10]	傅卫平, 娄雷亭, 高志强等. 机械结合面法向接触刚度和阻尼的理论模型 . 机械工程学报, 2017, 53(9), 73-82 [本文引用: 1]      (Fu Weiping, Lou Leiting, Gao zhiqiang, et al. Theoretical model for the contact stiffness and damping of mechanical joint surface . Journal of Mechanical Engineering, 2017, 53(9): 73-82 (in Chinese)) [本文引用: 1]
[11]	王雯, 吴洁蓓, 傅卫平等. 机械结合面法向动态接触刚度理论模型与试验研究 . 机械工程学报, 2016, 52(13): 123-130 [本文引用: 1]      (Wang Wen, Wu jiebei, Fu Weiping, et al. Theoretical and experimental research on normal dynamic contact stiffness of machined joint surfaces . Journal of Mechanical Engineering, 2016, 52(13): 123-130 (in Chinese)) [本文引用: 1]
[12]	Mindlin RD, Deresiewicz H. Elastic spheres in contact under varying oblique forces . Journal of Applied Mechined, 1953, 20(3): 327-344 [本文引用: 1]
[13]	王东, 徐超. 一种考虑粗糙结合面切向黏滑摩擦模型 . 机械工程学报, 2014, 50(13): 129-134 [本文引用: 1]      (Wang Dong, Xu Chao. A tangential stick-slip friction model for rough interface . Journal of Mechanical Engineering, 2014, 50(13): 129-134 (in Chinese)) [本文引用: 1]
[14]	张学良, 王南山, 温淑花等. 机械结合面切向接触阻尼能量耗散弹塑性分形模型 . 机械工程学报, 2013, 49(12): 43-49 [本文引用: 1]      (Zhang Xueliang, Wang Nanshan, Wen Suhua, et al. Elastoplastic fractal model for tangential contact damping energy dissipation of machine joint interfaces . Journal of Mechanical Engineering, 2013, 49(12): 43-49 (in Chinese)) [本文引用: 1]
[15]	姜来, 张学良, 陈永会等. 固定结合面切向接触阻尼分形模型 . 太原科技大学学报, 2014, 35(5): 380-385 [本文引用: 1]      (Jiang Lai, Zhang Xueliang, Chen Yonghui, et al. A fractal model of the tangential contact damping on fixed joint surfaces . Journal of Taiyuan University of Science and Technology, 2014, 35(5): 380-385 (in Chinese)) [本文引用: 1]
[16]	李小彭, 王伟, 赵米鹊等. 考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真 . 机械工程学报, 2012, 48(23): 46-50 [本文引用: 1]      (Li Xiaopeng, Wang Wei, Zhao Mique, et al. Fractal prediction model for tangential contact damping of joint surface considering friction factors and its imulation, Journal of Mechanical Engineering 2012, 48(23): 46-50 (in Chinese)) [本文引用: 1]
[17]	Zhang X, Wang N, Lan G, et al. Tangential damping and its dissipation factor models of joint interfaces based on fractal theory with simulations . Journal of Tribology, 2014, 136(1): 011704-011716 [本文引用: 1]
[18]	Fujimoto T, Kagami J, Kawaguchi T, et al. Micro-displacement characteristics under tangential force . Wear, 2000, 241(2): 136-142 [本文引用: 2]
[19]	Greenwood JA, Williamson JBP. Contact of nominally flat surfaces . Proceedings of the Royal Society of London, 1966, 295(1442): 300-319 [本文引用: 1]
[20]	赵永武, 吕彦明, 蒋建忠. 新的粗糙表面弹塑性接触模型 . 机械工程学报, 2007, 43(3): 95-101 [本文引用: 1]      (Zhao Yongwu, Lü Yanming, Jiang JianZhong. New elastic-plastic model for the contact of rough surfaces . Journal of Mechanical Engineering, 2007, 43(3): 95-101 (in Chinese)) [本文引用: 1]
[21]	Gorbatikh L, Popova M. Modeling of a locking mechanism between two rough surfaces under cyclic loading . International Journal of Mechanical Sciences, 2006, 48(9): 1014-1020 [本文引用: 3]
[22]	Kogut L, Etsion I. A finite element based elastic-plastic model for the contact of rough surfaces . Modelling and Simulation in Engineering, 2011, 2011(3): 383-390 [本文引用: 1]
[23]	Abbott EJ, Firestone FA. Specifying surface quality-A method on accurate measurement and comparison . Mechanical Engineering ASME, 1933, 55(7): 569-572 [本文引用: 1]
[24]	温淑花, 张学良, 陈永会等. 结合面切向接触等效黏性阻尼分形模型 . 西安交通大学学报, 2017, 51(1): 1-8 (Wen Suhua, Zhang Xueliang, Chen Yonghui, et al. Fractal model of equivalent viscous damping for tangential contact in joint interfaces . Journal of Xi’an Jiaotong University, 2017, 51(1): 1-8 (in Chinese))
[25]	蔡力钢, 杨成, 赵永胜等. 基于接触表面非均匀压强分布的栓接结合部动力学模型 . 北京工业大学学报, 2016, 42(11): 1609-1616 [本文引用: 1]      (Cai Ligang,Yang Cheng, Zhao Yongsheng, et al. Dynamics model of bolted joint based on uneven pressure distribution of the surface . Journal of Beijing University of Technology, 2016, 42(11): 1609-1616 (in Chinese)) [本文引用: 1]
[26]	吴波, 王增全, 王旭兰等. 机械结合面动态特性测试与仿真 . 机械科学与技术, 2016(2): 320-324 [本文引用: 1]      (Wu Bo, Wang Zengquan, Wang Xulan, et al. Test and simulation of dynamic characteristics of joint interface in machine . Mechanical Science and Technology for Aerospace Engineering, 2016(2): 320-324 (in Chinese)) [本文引用: 1]
[27]	戴德沛. 阻尼减振降噪技术. 西安: 西安交通大学出版社, 1986. (Dai Depei.Damping and Noise Reduction Technology. Xi’an: Xi’an Jiaotong University Press, 1986 (in Chinese))