引言
破损-安全的设计原则对安全保障要求高的工程结构非常重要,如航天器、飞机、船舶和其他工程结构等[1 ,2 ] . “911”事件中两架民航客机撞毁美国纽约世贸大厦,使建筑结构师也意识到破损-安全设计 的必要性[3 ] ,破损-安全设计成为研究热点. Melosh等[4 ] 于1968年提出破损-安全设计概念,按破损-安全设计的结构受到了局部破坏, 整体结构仍能满足性能需求. Niu[1 ,2 ] 给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏.
随着计算机性能提升及计算力学的发展,基于结构优化设计的方法进行结构设计得到广泛应用,结构拓扑优化技术因能 取得更大的经济效果及 具有结构拓扑创新的能力,往往能突破结构设计师的经验想象,受到工程界的热烈追捧[5 ,6 ] . 然而,通过不考虑破损-安全的结构优化方法设计的结构通常“物尽其用”,如结构拓扑优化通常得到静定结 构形式,由于结构过于“高效”, 缺少冗余,结构的每个杆件均成为关键部件,故而对局部破坏非常敏感. 因而,在安全性要求高的工程领域,常被认为经济但缺乏安全保障,故此,在结构优化中考虑“破损-安全”具有 重要的工程应 用价值.
Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响.
考虑破损-安全的结构拓扑优化设计与截面优化设计相比具有双重困难,除了考虑结构的局部破坏的研究难点外,还 有结构 拓扑优化建模与求解的难点. 另外,如果桁架结构拓扑优化设计可以从桁架基结构中将指定的单个杆件作为破损模式,那么连续体结构拓扑优化设计的破损模 式以及如 何运作就成了解决困难问题的瓶颈,而Jansen等[17 ] 首先克服了这一困难,他们通过指定一定大小的方块面积(二维)或体 积(三维)的局部破损,将其中心布置于其结构的单元中心上,从而建立起体积约束下极小化结构柔顺度的破损-安全 拓扑优化模型, 应用K-S函数方法凝聚众多函数进行求解. 然而,由于文献[17 ] 采取了每个单元的中心布置一个结构局部破损模式,局部破损区域数量与其结构的单元数量几乎相同,因此所 有含局部破损区域的基机构对应的柔顺度数量也与之相同,导致工作量极大,即使采用并行算法,此方法的计算速度都难以接受.
Zhou等[18 ] 为了克服上述困难,选取适当大小的局部破损区域,与邻近的局部破损区域中心距离拉开,使得含局部破损区域的 基机构数目骤然下降,其对应的柔顺度数量也极大减小,令相应的建模与求解的计算能够被接受,可贵的是,文献[18 ]对采取的做 法进行了理论论证. 这是Zhou等做出的重大贡献.
本文在梳理了该方向学者们以往相关研究的基础上,做出了如下工作:
(1)系统阐述了破损-安全拓扑优化的基本概念,如结构局部破损模式(structural local failure mode)、结构局部破损区域(structural local failure region)、结构破损状况(structural failure case)、结构破损状况的预估分布(pre-estimation distribution of structural failure cases)等.
(2)代替目前破损-安全拓扑优化研究中以结构柔顺度为目标函数,转换为含结构局部破损区域的全部基结构的最大体积的极小化为目标,避免结构柔顺度为优化目标建模时需要先验地确定结构体积的不合理性.
(3)基于Minimax的概念,将全部结构破损状况的最大体积的极小化的问题转化为单个的目标,避免结构柔顺度的优化目标模型需要利用应用K-S函数方法凝聚目标进行求解的繁重计算量.
(4)基于上述策略,依托结构拓扑优化ICM方法,建立了结构力学性能约束下体积极小化的破损-安全拓扑优化模型, 不仅避免了以往研究先验地指定体积比约束的不合理性,而且对多载荷工况、多性能约束问题,都能够有效地建模.
(5)采用对偶序列二次规划法求解优化模型.
1 连续体结构破损-安全拓扑优化建模前处理
的基本概念和策略
回顾该方向学者们以往相关研究,无论Jansen等[17 ] 的开创性策略还是Zhou等[18 ] 的重大进展,从本质上看,可以 理解为模拟载荷 工况,类比出结构破损状况. 为了推广成果,本研究系统阐述了破损-安全拓扑优化的基本概念,引申出建模前处理策略.
对连续体结构进行考虑破损-安全的拓扑优化设计,其核心的困难在于如何考虑结构的局部破损. 因为在指定的设计域内,结构拓扑是未知的,结构的破损状况也是未知的.
导致结构破损的原因很多,如爆炸、撞击、火灾、疲劳损伤等,其共同的特点是结构破损范围具有局部性及随机性. 而破损-安全的设计原则是要求在结构局部破损的情况下,仍能满足工程结构一定的使用性能要求.
结构破损具有局部性特征. 本文以如下方式考虑结构破损“局部性”. 通过在基结构(对应于设计域)内指定一定形状的破损区域模拟结构的局部破损,如图1 所示,灰色为基结构 Ω D s . 在进行拓扑优化设计时,拓扑设计仍在整个设计域内进行,但出现在破损区域内的结构构件将破损,即不考虑此部分结构. 在基于基结构的拓扑设计方法中,可以将破损区域内的材料设定为空单元(拓扑变量 t = 0 ρ = 0
图1 结构局部破损区域及结构破损状况
Fig. 1 Structural local failure region and structural failure case
本文认为,考虑破损-安全的连续体结构拓扑优化建模前处理策略可以细化为如下4个概念.
1.1 结构局部破损模式
由于导致结构破损的因素很多,其结构局部破损区域的范围大小及形状各不相同,在建立破损-安全的拓扑优化模型中,可以依据工程问题,设定一定大小的规则破损区域,如方形、圆形、长条形等. 在此将一定形状及大小的破损区域称为结构局部破损模式. 结构局部破损模式只表征结构局部破损区域的形状和大小两个要素,而与几何位置无关.
1.2 结构局部破损区域
加进了其在结构中的几何位置的结构局部破损模式称为结构局部破损区域. 结构局部破损区域是有具体坐标的结构局部破损模式,而结构局部破损模式是抽象的、没有具体坐标的结构局部破损区域.
1.3 结构破损状况
当基结构中含有不同的结构局部破损区域时,原本单一的基机构,就派生出多个基结构了. 称含有一个结构局部破损区域的基结构为一个 结构破损状况,如图1 所示.
1.4 结构破损状况的预估分布
如果同一破损模式可以出现在设计域内的任何地方,则可完全满足结构破损的“随机性”特征,但这将导致无穷多个破损区域,也即无穷多个结构破损状况. 为使问题可求解,需要将无穷分布的破损区域变成有限分布,或者说,“随机性”模型化为“确定性”. 这就是Jansen等[17 ] 首先完成的工作.
于是,就可以建立预估有限分布破损区域下的优化模型了. 在此,将特定结构局部破损区域布置于基结构内的排布方式称为 结构局部破损区域的预估分布,又可称为结构破损状况的预估分布,这是因为一个结构局部破损区域放置于基结构中就是一个结构破损状况的缘故.
前述Zhou等[18 ] 将邻近的局部破损区域中心距离实施拉开的方案有两种:第一种是将结构局部破损模式无缝相连地铺满在整个基结构上,他们称之为层级一模型;第二种是将第一种方案邻近的局部破损区域中心的中点也增加为新的局部破损区域中心,放置相应的破损区域,于是局部破损区域相互就有了重叠,Zhou等[18 ] 称之为层级二模型.
在目前常用的计算资源下,两种方案使连续体结构破损-安全拓扑优化的计算量降低到运行时间可接受的范围内[18 ] .
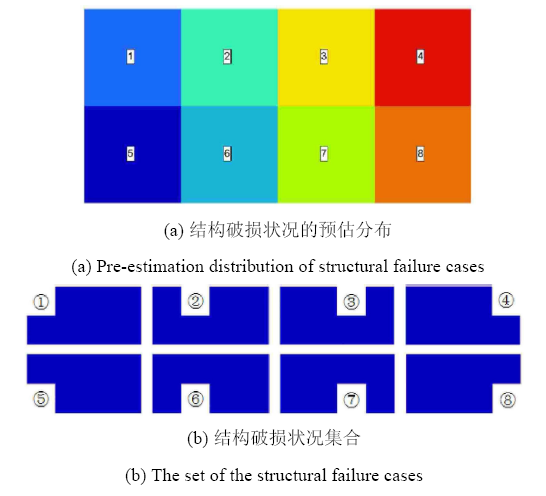
以Zhou等[17 ] 正方形结构局部破损模式为例予以说明,此示例对应于下文算例1中所采用的结构破损状况的预估分布. 定义的结构破损状况预估分布为无缝平铺,如图2 (a)所示,8个正方形的破损区域无缝平铺在整个基结构上. 图2 (b)为对应于正方形破损区域布置于基结构上的8个结构破损状况,这8个结构破损状况组成结构破损状况集合 Φ
Φ = Ω s | Ω s = Ω - D s ( s = 1,2 , ⋯ , S ) ( 1 )
其中, D s ( s = 1,2 , ⋯ , S ) s S Ω Ω s s s
图2 结构局部破损模式取正方形时某破损-安全设计示例[18 ]
Fig. 2 An example of fail-safe design while structural local failure mode taking square[18 ]
2 连续体结构破损-安全拓扑优化模型
2.1 一般表达和基于结构破损状况的模型
基于基结构表示的破损-安全结构拓扑优化问题可写为如下一般的形式
$\left.\begin{array}{ll} {\rm Find } \ & {\pmb x} \in E^N \\ {\rm Make } \ & f ( x,\varPhi ) \to {\rm min} \\ {\rm s.t.} \ \ & g_j (x,\varPhi ) \leqslant \overline g_j , j = 1,2, \cdots ,J \\ & 0 \leqslant x_i \leqslant 1 , \ \ i = 1,2, \cdots ,N \end{array} \right\} (2)$
其中, x f g f g Φ
2.2 目标函数为结构柔顺度的模型
Jansen等[17 ] 及Zhou等[18 ] 之所以能对式(2)进行求解,是因为其对结构破损状况进行了预估分布,他们研究的均是体积约束下柔顺度极小的拓扑优化问题,其拓扑模型为
$\left.\begin{array}{ll} {\rm Find } \ & {\pmb x} \in E^N \\ {\rm Make } \ & \mathop {\max}\limits_{s = 1,2,\cdots,S} C_s (x) \to \min \\ {\rm s.t.} \ & V (x) \leqslant \overline V \\ & 0 \leqslant x_i \leqslant 1 ; \ i = 1,2, \cdots ,N \end{array} \right \} (3) $
其中 x C s ( x ) s Ω s V V ¯
式(3)的目标函数为结构破损状况集合 Φ Ω s [17 ] 采用K-S函数进行凝聚转化为单目标优化问题求解,Zhou等[18 ] 采取将原目标函数转化为柔顺度的上限约束然后使上限极小化予以求解[19 ] .
2.3 基于ICM方法目标函数为结构体积的模型
本文基于ICM方法,建立性能约束下体积(或重量)极小化的优化模型. 解析[20 ] 及数值[21 ] 算例均表明:当性能为位移约束时,在集中力作用时,可以与体积约束下柔顺度极小问题建立对应模型. 以位移约束体积极化小的破损-安全拓扑优化为例,应用ICM方法,建立的结构拓扑优化模型为
$\left.\begin{array}{ll} {\rm Find } & {\pmb t} \in E^N \\ {\rm Make } & V(\pmb t,\varPhi) = \mathop {\max}\limits_{s = 1,2,\cdots,S} V_s ( t) \to \min \\ {\rm s.t.} & u_{jls} ({\pmb t}) \leqslant \overline {u_j } \\ & (j = 1,2,\cdots,J ; \ l = 1,2,\cdots,L ; & \ s = 1,2,\cdots,S) \\ & \underline{t_i } \leqslant t_i \leqslant 1 \ (i = 1,2, \cdots ,N) \end{array}\!\! \right \} (4) $
其中, t V ( t , Φ ) Φ u jls ( t ) Φ s Ω s l j u j ¯ j J L t i ¯ t i ¯ = 0.01 .
因基结构总体积为 V ( t ) s Ω s V s ( t ) v s ( t )
$V_s ({\pmb t}) = V({\pmb t}) - v_s ({\pmb t}) (5{\rm a})$
因为 Ω s ( s = 1,2 , ⋯ , S )
$V_s ({\pmb t}) \leqslant V({\pmb t}) (5{\rm b})$
自然有
$\mathop {\max}\limits_{s = 1,2,\cdots,S} V_s ({\pmb t}) \leqslant V({\pmb t}) (6) $
根据式(6),式(4)的Minimax问题就可以被如下单目标函数的极小化问题替代
$\left.\begin{array}{ll} {\rm Find } & {\pmb t} \in E^N \\ {\rm Make } & V({\pmb t}) = \sum_{i = 1}^N f_v (t_i )v_i^0 \to \min \\ {\rm s.t.} & u_{jls} ({\pmb t}) \leqslant \overline {u_j } \\ & ( j = 1,2,\cdots,J ; \ l = 1,2,\cdots,L ; \ s = 1,2, \cdots,S) \\ & \underline{t_i } \leqslant t_i \leqslant 1 \ (i = 1,2,\cdots ,N) \end{array} \right \} (7)$
其中,目标函数的显式化是根据ICM方法处理[22 ,23 ] .
由于式(6)的存在,式(7)的解不小于式(4)的解,因而保证是安全的邻近解,符合破损-安全的本意. 模型(7)相比于模型(4)的好处在于避免了处理Minimax问题用K-S函数的巨大计算量.
式(7)比式(3)优越之处,首先在于不需要先验地指定一个人为的体积约束,其次对多载荷工况问题也不存在柔顺度目标的指定加权系数的先验性,另外,结构的所有力学性能(如本文以位移约束为例)都可以根据需要作为约束建立在优化模型中,且可以在迭代寻优中自动得到满足.
2.4 基于ICM方法的约束显式化及模型的求解
2.3节以某个预估排列方式布置结构局部破损区域,得到所有结构破损状况对应的基结构 f k ( t i )
进一步对位移约束进行显式化,为此首先引入如下变换
$x_i = \dfrac{1}{f_k (t_i )} = \dfrac{1}{t_i^\alpha } (8)$
其中 k i = f k ( t i ) K i 0 α α = 3 u m ( t ) ( m = 1,2 , ⋯ , M ) .
在将位移约束函数显式化之前,考虑到为使优化算法推导简洁,宜将式(7)亦即式(4)中的位移约束函数的三维矩阵或三维数组表示为向量或一维数组 M = J × L × S x i ( k ) .
根据单位虚载荷法或Mohr定理,位移约束函数可以表达为
$u_m = \sum_{i = 1}^N \dfrac{x_i }{x_i^{(k)} } ({\pmb\delta}_{im}^{V})^{\rm T} {\pmb F}_{im}^{R} (9)$
其中 k i δ im V F im R i i
$ A_{im} = ({\pmb\delta}_{im}^{\rm V} )^{\rm T}{\pmb F}_{im}^{\rm R} (10)$
为单元 j x i ¯ = 1 t i α ¯
$ c_{im} = A_{im} / x_i^{( k)} (11)$
为位移约束方程系数. 则位移约束近似显式为
$u_m = \sum_{i = 1}^N \dfrac{x_i }{x_i^{(k)} } ({\pmb\delta}_{im}^{\rm V} )^{\rm T}{\pmb F}_{im}^{\rm R} =\sum_{i = 1}^N c_{im} x_i (12)$
优化模型(7)转化为
$\left.\begin{array}{ll} {\rm Find } & {\pmb x} \in E^N \\ {\rm Make } & V({\pmb x}) = \sum_{i = 1}^N v_i^0 / x_i^\alpha \to \min \\ {\rm s.t.} & u_m ({\pmb x}) = \sum_{i = 1}^N c_{im} x_i \leqslant \overline {u_m } \\ & m = 1,2, \cdots ,M \\ & 1 \leqslant x_i \leqslant \overline {x_i } ; \ i = 1,2, \cdots ,N \end{array}\!\! \right \} (13)$
其中$\overline {x_i } = \dfrac{1}{\underline{t_i^\alpha }}$.
模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] .
从方便比较出发,本文采用与文献[25 ] 相同的收敛准则[25 ]
$\varDelta = \mathop {\max}\limits_{i = 1,2,\cdots,N} ( \vert t_i^{(k + 1)} - t_i^{(k)} \vert ) \leqslant \varepsilon (14)$
其中收敛精度$\varepsilon $取0.01.
3 数值算例及讨论
3.1 算例1
如图3 所示,基结构尺寸为100 ×50,厚度为1,左边25 E = 2.1 × 1 0 5 25 灰色正方形为破损模式,结构局部破损区域无缝平铺的预估分布如图2 所示,材料弹性模量 F × [18 ] . 采用100 × 50 的单元边长为1的正方形有限元网格进行计算.
图3 算例1拓扑设计问题定义
Fig. 3 Definition of the topology design problem for example 1
在20%体积比约束下,不考虑破损-安全的最小化柔顺度拓扑优化,Zhou等[18 ] 得到的最优拓 扑如图4 (a)所示,最优点柔顺度58.72. 应用88行代码得到的最优拓扑如图4 (b)所示,得到的拓扑图形与 Zhou等[18 ] 的相同,最优拓扑结构的柔顺度为57.39,对应集中力作用方向的位移值为0.057 39. 参考文献[21 ] 的做法,以0.057 39为位移约束值,不考虑破损-安全的体积极小化拓扑优化得到的最优拓扑如图4 (c)所示,拓扑图形与前两者相同,最优点体积比20.1%,由此验证了单个集中力作用时,体积约束下极小柔顺度问题与位移约束下极小体积问题存在模型的对应转换关系.
图4 不考虑破损-安全的拓扑优化得到最优拓扑
Fig. 4 Optimal topologies obtained by topology optimization without fail-safe
Zhou等[18 ] 得到的考虑破损-安全的最优拓扑如图5 (a)所示,其体积约束仍为20%,在相同体积约束下,与不考虑破损-安全的拓扑优化相比,结构更为复杂.
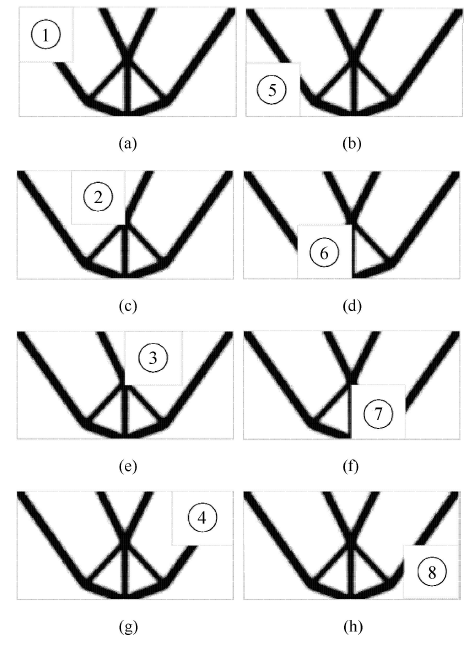
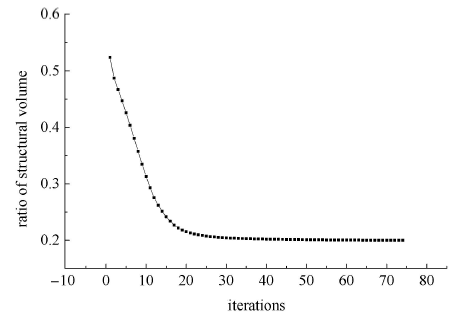
位移约束下体积极小化模型得到的破损-安全最优拓扑如图5 (b)所示,此时结构体积比为20%,位移约 束0.188 5. 可以看到本文的拓扑图形与文献[18 ]是相同的. 以位移约束0.188 5进行不考虑破 损-安全的拓扑优化,得到的最优拓扑如图6 所示,结构体积比为7.22%. 可以看到,在同样位移约束下,破损-安全拓扑优化得到的体积增大许多,并且图形更复杂,即结构具有更多的冗余, 可以更好 满足破损-安全的设计原则. 含各破损区域的最优拓扑图形如图7 所示,目标函数及位移约束迭代曲线分别如图8 和图9 所示,迭代次数74次. 当破损区域位置为2,3,6和7(如图7 (c)、图7 (d)、图7 (e)及图7 (f))时为有效约束,最优点时位移值为0.188 5,破损区域 位置1,4,5和8(如图7 (a)、图7 (b)、图7 (g)及图7 (h))时不是有效约束,位移值为0.172 1. 可见,结构局部破损出现在不同位置时,对结构的影响也是不同的,有些位置的局部破损对结构影响大,致使其对应的结构破 损状况下的位移约束为有效约束,而另一些位置的局部破损对结构的影响可能很小,甚至在没有杆件通过的情况下没有任何 影响,因而其对应的结构破损状况下的位移约束为非有效约束.
图5 破损-安全拓扑优化得到最优拓扑
Fig. 5 Optimal topologies obtained by the topology optimization with fail-safe
图6 与图5 (b)相同位移约束不考虑破损-安全的拓扑优化得到的最优拓扑
Fig. 6 Optimal topology obtained by the topology optimization without fail-safe with the same displacement constraint of Fig.5 (b)
图 7 不同破损区域位置及其拓扑
Fig. 7 Topologies with different positions of fail regions
图8 目标函数迭代曲线
Fig. 8 Iteration curve of the objective
图9 位移约束迭代曲线
Fig. 9 Iteration curves of the displacement constraints
3.2 算例2
此算例参考文献[18 ] ,如图10 所示,基结构尺寸为180 ×60,厚度为1,采用22 E = 1.0 22 的正方形作为结构局部破损模式,如图10 中灰色正方形所示,采用Zhou等[18 ] 研究中的结构破损状况预估分布如 图11 所示. 材料弹性模量 P = 1.0 × . 采用180 × 60 网格进行计算. 位移约束集中力作用方向的位移小于570. 过滤半径采用1.5,收敛精度采用0.01.
图10 算例2拓扑设计问题定义
Fig. 10 Definition of the topology design problem for example 2
图11 文献[11 ]及本文所采用的破损区域排列形式
Fig. 11 Arrangement pattern of fail regions adopted in Ref.[11] and this paper
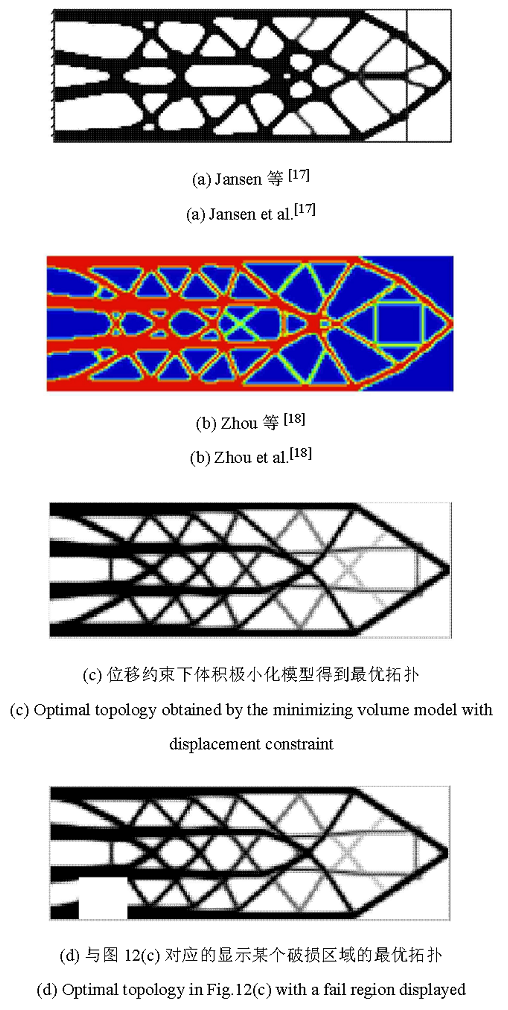
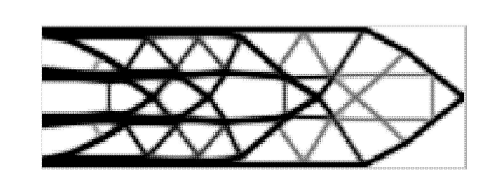
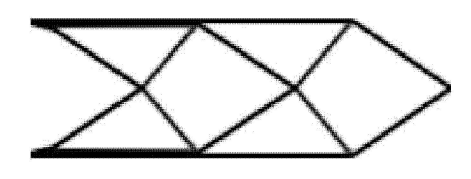
本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布.
图12 考虑破损-安全得到的最优拓扑
Fig. 12 Optimal topologies obtained by the topology optimization with fail-safe
文献[17 ] 与文献[18 ] 及本文所采用的结构破损状况预估分布是不同的,文献[17 ] 以每个单元为中心布置破损模式,而本文 采用的是文献[18 ] 的无缝平铺的排列方式(如图11 ).
收敛准则及收敛精度对结果也有影响,本文结果与文献[18 ] 的结果虽更为相似但也有所不同,主要是采用了不同的收敛准则 及收敛精度.
图13 是本文方法求解过程中的一个中间结果,可以看到其尖端的构件与图12 (b)一样为曲线形式,更为相似,但随着优化的进行, 演变成了图12 (c)所示的直线形式.
图13 位移约束下体积极小化模型得到某个中间结果
Fig. 13 A transitional topology obtained by the minimizing volume model with displacement constraint
顺便指出,采用不考虑-破损-安全的拓扑优化得到的最优拓扑如图14 所示,最优体积比为16.86%. 这一点印证了破损-安全考虑的必要性.
图14 不考虑破损-安全的拓扑优化得到最优拓扑
Fig. 14 Optimal topologies obtained by the topology optimization without fail-safe
3.3 算例3
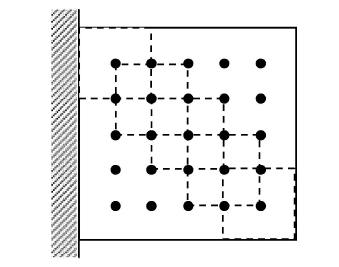
依照文献[25 ] 的做法,采用无量纲化的数据,这也是文献[17 ] 和文献[18 ] 中算例的做法. 基结构尺寸为150 × 150 ,厚度为1,如图15 所示. 其中左边50 d 50 灰色正方形为结构局部破损模式,采用间距 F 1 = 1 图16 所示,一个黑色圆点为一个正方形破损区域的形心位置,对应于25个结构破损状况. 由于破损区域重叠,若把所有破损区域均绘制出来,线条重叠会相互干扰以至看不清楚,因此只把对角线位置上的5个破损区域表示出来,其他破损区域就不显示了. 受两种载荷工况作用,工况1为一集中载荷 F 2 = 1 E d = 25
图15 150 ×150网格正方形平板拓扑优化问题定义
Fig. 15 Definition of the topology optimization problem of a square plate with 150 ×150 mesh
图16 基结构中破损区域间距d = 25
Fig. 16 Arrangement of failure regions with the space of e ̆
鉴于例1和例2的结构破损状况预估分布采用了层级一模型,本例则采用了层级二模型,旨在考核其可行性. 计算结果表明本文提出的方法,对于两种方案都是支持的.
考虑破损-安全拓扑优化得到的最优拓扑如图17 (a)所示,最优体积比为40.31%.
图17 最优拓扑
Fig. 17 Optimal topologies
采用不考虑破损-安全的拓扑优化得到的最优拓扑如图17 (b)所示,最优体积比为19.34%.
从优化结果可以看到:对多工况多位移约束问题,考虑破损-安全的拓扑优化设计结构比不考虑破损-安全的拓扑优化结果更复杂.
4 结 论
基于ICM方法,对连续体结构进行破损-安全拓扑优化的建模及求解,得到如下结论.
(1) 通过指定一个特定局部破损区域的方式模拟结构局部破损,使之破损模式确定,从而降低了连续体结构破损-安全拓扑优化问题最不利结构破损状况“双盲”困难的难度,有利于建立破损-安全拓扑优化的模型,原因在于此做法与许多工程实践相符合,如爆炸、失火、碰撞等事故通常也是发生在结构的一处局部位置.
(2)基于ICM方法建立的性能(如位移)约束下体积极小化的优化模型,不需要先验指定体积约束值,对多工况问题,也不需要人为指定工况间的加权系数组合成单目标. 取不含破损区域的基结构对应的体积为目标函数,将极小化极大值问题转化为了单目标问题. 类比于载荷工况,将在不同位置包含结构局部破损模式的基结构定义为结构破损状况,在优化模型中以约束的形式考虑,使所有结构破损状况的性能得到满足.
(3)考虑破损-安全的拓扑优化得到的最优结构,最终的结构拓扑构形更复杂,使结构具有更多的冗余,最优结构的体积也更大,亦即使用的材料更多,从而满足破损-安全设计原则的要求,以适度增加的材料用量换来结构的冗余度的增加,抵抗因偶然因素造成的结构局部破坏可能造成的灾难性后果,因此可以在预估的所有结构破损状况下满足结构的性能要求.
(4)破损模式无缝平铺于基结构或破损模式重叠排列于基结构的两种方案均可采用,不同结构破损状况的预估分布,对最优结构拓扑有显著影响,需根据结构工程应用实际情况,恰当定义结构破损状况及其预估分布. 而其对最优结构拓扑的影响是一个值得深入研究的内容.
(5)由于ICM方法与SIMP方法很多共性,我们相信在SIMP方法的框架下,建立体积极小化目标受位移约束的模型,同样可以建立类似的合理模型.
作为破损-安全的连续体结构拓扑优化研究的一个新方向,尚存在许多问题,可以进一步地进行探索.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Niu MCY . Airframe Structural Design. Hongkong : Conmilit Press Ltd ., 1988
[本文引用: 2]
[2]
Niu MCY. Airframe Stress Analysis and Sizing. Hongkong : Conmilit Press Ltd ., 1997
[本文引用: 2]
[3]
Zdeněk P Bažant Yong Z . Why does the world trade center collapse? — Simple analysis
.International Journal of Structural Stability and Dynamics , 2012 , 1 (4 ): 603 -615
[本文引用: 1]
[4]
Melosh RJ Johnson JR Luik R Structural survivability analysis
//Second Conference on Matrix Methods in Structural-Mechanics, WPAFB, Ohio , 1968
[本文引用: 1]
[5]
Bendsøe MP Sigmund O . Topology Optimization - Theory, Methods and Applications
. Berlin: Springer , 2004
[本文引用: 1]
[6]
Deaton J Grandhi RV A survey of structural and multidisciplinary continuum topology optimization: Post 2000
.Struct Multidiscip Optim , 2014 , 49 (1 ): 1 -38
[本文引用: 1]
[7]
Sun PF Arora JS Haug EJ Fail-safe optimal design of structure
.Engineering Optimization , 1976 , 2 (1 ): 43 -53
[本文引用: 2]
[8]
Arora J Govil A Haskell D Optimal design of large structures for damage tolerance
.AIAA Journal , 1980 , 18 (5 ): 563 -570
[本文引用: 2]
[9]
Nguyen DT Arora JS Fail-safe optimal design of complex structures with substructures
.Journal of Mechanical Design , 1982 , 104 (4 ): 861 -868
[本文引用: 2]
[10]
Feng Y The theory of structural redundancy and its effect on structural design
.Computers & Structures 1988 , 28 (1 ): 15 -24
[本文引用: 1]
[11]
Feng Y Moses F Optimum design, redundancy and reliability of structural systems
.Computers & Structures 1986 , 24 (2 ): 239 -251
[本文引用: 2]
[12]
Marhadi K Venkataraman S Wong S Load redistribution mechanism in damage tolerant and redundant truss structure
.Structural and Multidisciplinary Optimization , 2011 , 44 (2 ): 213 -233
[本文引用: 1]
[13]
Marhadi K Venkataraman S Surrogate measures to optimize structures for robust and predictable progressive failure
.Structural and Multidisciplinary Optimization , 2009 , 39 (3 ): 245 -261
[本文引用: 1]
[14]
杜剑明 ,郭旭 . 基于鲁棒性优化的桁架结构失效-安全设计
. 力学学报 , 2011 , 43 (4 ): 725 -730
[本文引用: 1]
(Du Jianming Guo Xu Fail-safe optimal design of truss structures based on robust optimization
.Chinese Journal of Theoretical and Applied Mechanics , 2011 , 43 (4 ): 725 -730 (in Chinese))
[本文引用: 1]
[15]
Bendsøe M D'${\imath}$az A . A method for treating damage related criteria in optimal topology design of continuum structures
.Structural and Multidisciplinary Optimization , 1998 , 16 (2-3 ): 108 -115
[本文引用: 1]
[16]
Achtziger W Bendsøe M Optimal topology design of discrete structures resisting degradation effects
.Structural and Multidisciplinary Optimization , 1999 , 17 (1 ): 74 -78
[本文引用: 1]
[17]
Jansen M Lombaert G Schevenels M et al .Topology optimization of fail-safe structures using a simplified local damage model
.Structural and Multidisciplinary Optimization , 2013 , 49 (4 ): 657 -666
[本文引用: 11]
[18]
Zhou M Fleury R Fail-safe topology optimization
.Structural and Multidisciplinary Optimization , 2016 , 54 (7 ): 1225 -1243
[本文引用: 22]
[19]
Olhoff N Multicriterion structural optimization via bound formulation and mathematical programming
.Struct Optim , 1989 , 1 : 11 -17
[本文引用: 1]
[20]
彭细荣 . 结构刚度优化问题模型比较研究
. 湖南城市学院学报(自然科学版) , 2016 , 25 (1 ): 1 -4
[本文引用: 2]
(Peng Xirong A comparative study on models of structural stiffness optimization problems
.Journal of Hunan City University (Natural Science )2016 , 25 (1 ): 1 -4 (in Chinese))
[本文引用: 2]
[21]
彭细荣 , 隋允康 . 对连续体结构拓扑优化合理模型的再探
. 固体力学学报 , 2016 , 37 (2 ): 181 -191
[本文引用: 3]
(Peng Xirong Sui Yunkang Further discussion on rational topology optimization model of continuum structures
.Chinese Journal of Solid Mechanics , 2016 , 37 (2 ): 181 -191 (in Chinese))
[本文引用: 3]
[22]
隋允康 , 彭细荣 . 结构拓扑优化ICM方法的改善
. 力学学报 , 2005 , 37 (2 ): 190 -198
[本文引用: 2]
(Sui Yunkang Peng Xirong . The improvement for the ICM method of structural topology optimization
. Acta Mechanica Sinica 2005 , 37 (2 ): 190 -198 (in Chinese))
[本文引用: 2]
[23]
隋允康 , 叶红玲 . 连续体结构拓扑优化的ICM方法 . 北京 : 科学出版社 , 2013
[本文引用: 2]
(Sui Yunkang Ye Hongling. Continuum Topology Optimization Methods ICM. Beijing : Science Press , 2013 (in Chinese))
[本文引用: 2]
[24]
隋允康 , 彭细荣 .求解一类可分离凸规划的对偶显式模型DP-EM方法
. 力学学报 ,2017 , 49 (5 ): 1135 -1143
[本文引用: 1]
(Sui Yunkang Peng Xirong A dual explicit model based DP-EM method for solving a class separable convex programming
.Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (5 ): 1135 -1143 (in Chinese))
[本文引用: 1]
[25]
Andreassen E Clausen A Lazarov BS et al .Efficient topology optimization in MATLAB using 88 lines of code
.Structural Multidisciplinary Optimization , 2011 , 43 (1 ): 1 -16
[本文引用: 3]
2
1988
... 破损-安全的设计原则对安全保障要求高的工程结构非常重要,如航天器、飞机、船舶和其他工程结构等[1 ,2 ] . “911”事件中两架民航客机撞毁美国纽约世贸大厦,使建筑结构师也意识到破损-安全设计 的必要性[3 ] ,破损-安全设计成为研究热点. Melosh等[4 ] 于1968年提出破损-安全设计概念,按破损-安全设计的结构受到了局部破坏, 整体结构仍能满足性能需求. Niu[1 ,2 ] 给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏. ...
... [1 ,2 ]给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏. ...
2
1997
... 破损-安全的设计原则对安全保障要求高的工程结构非常重要,如航天器、飞机、船舶和其他工程结构等[1 ,2 ] . “911”事件中两架民航客机撞毁美国纽约世贸大厦,使建筑结构师也意识到破损-安全设计 的必要性[3 ] ,破损-安全设计成为研究热点. Melosh等[4 ] 于1968年提出破损-安全设计概念,按破损-安全设计的结构受到了局部破坏, 整体结构仍能满足性能需求. Niu[1 ,2 ] 给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏. ...
... ,2 ]给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏. ...
Why does the world trade center collapse? — Simple analysis
1
2012
... 破损-安全的设计原则对安全保障要求高的工程结构非常重要,如航天器、飞机、船舶和其他工程结构等[1 ,2 ] . “911”事件中两架民航客机撞毁美国纽约世贸大厦,使建筑结构师也意识到破损-安全设计 的必要性[3 ] ,破损-安全设计成为研究热点. Melosh等[4 ] 于1968年提出破损-安全设计概念,按破损-安全设计的结构受到了局部破坏, 整体结构仍能满足性能需求. Niu[1 ,2 ] 给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏. ...
Structural survivability analysis
1
1968
... 破损-安全的设计原则对安全保障要求高的工程结构非常重要,如航天器、飞机、船舶和其他工程结构等[1 ,2 ] . “911”事件中两架民航客机撞毁美国纽约世贸大厦,使建筑结构师也意识到破损-安全设计 的必要性[3 ] ,破损-安全设计成为研究热点. Melosh等[4 ] 于1968年提出破损-安全设计概念,按破损-安全设计的结构受到了局部破坏, 整体结构仍能满足性能需求. Niu[1 ,2 ] 给出的破损-安全设计定义为破损-安全结构需支撑80%~100%的使用极限载荷而不发生灾难性的破坏. ...
Topology Optimization - Theory, Methods and Applications
1
2004
... 随着计算机性能提升及计算力学的发展,基于结构优化设计的方法进行结构设计得到广泛应用,结构拓扑优化技术因能 取得更大的经济效果及 具有结构拓扑创新的能力,往往能突破结构设计师的经验想象,受到工程界的热烈追捧[5 ,6 ] . 然而,通过不考虑破损-安全的结构优化方法设计的结构通常“物尽其用”,如结构拓扑优化通常得到静定结 构形式,由于结构过于“高效”, 缺少冗余,结构的每个杆件均成为关键部件,故而对局部破坏非常敏感. 因而,在安全性要求高的工程领域,常被认为经济但缺乏安全保障,故此,在结构优化中考虑“破损-安全”具有 重要的工程应 用价值. ...
A survey of structural and multidisciplinary continuum topology optimization: Post 2000
1
2014
... 随着计算机性能提升及计算力学的发展,基于结构优化设计的方法进行结构设计得到广泛应用,结构拓扑优化技术因能 取得更大的经济效果及 具有结构拓扑创新的能力,往往能突破结构设计师的经验想象,受到工程界的热烈追捧[5 ,6 ] . 然而,通过不考虑破损-安全的结构优化方法设计的结构通常“物尽其用”,如结构拓扑优化通常得到静定结 构形式,由于结构过于“高效”, 缺少冗余,结构的每个杆件均成为关键部件,故而对局部破坏非常敏感. 因而,在安全性要求高的工程领域,常被认为经济但缺乏安全保障,故此,在结构优化中考虑“破损-安全”具有 重要的工程应 用价值. ...
Fail-safe optimal design of structure
2
1976
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
... [7 ,8 ,9 ]的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
Optimal design of large structures for damage tolerance
2
1980
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
... ,8 ,9 ]的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
Fail-safe optimal design of complex structures with substructures
2
1982
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
... ,9 ]的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
The theory of structural redundancy and its effect on structural design
1
1988
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
Optimum design, redundancy and reliability of structural systems
2
1986
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
... 文献[11 ]及本文所采用的破损区域排列形式 ...
Load redistribution mechanism in damage tolerant and redundant truss structure
1
2011
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
Surrogate measures to optimize structures for robust and predictable progressive failure
1
2009
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
基于鲁棒性优化的桁架结构失效-安全设计
1
2011
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
基于鲁棒性优化的桁架结构失效-安全设计
1
2011
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
A method for treating damage related criteria in optimal topology design of continuum structures
1
1998
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
Optimal topology design of discrete structures resisting degradation effects
1
1999
... Sun和Arora[7 ,8 ] 于1976年提出破损-安全结构优化设计,在桁架结构杆件截面优化设计中考虑结构局 部破坏的影响. Nguyen和Arora[9 ] 对复合结构进行破损-安全结构优化设计. 由于局部破坏的位置与形式的不确定性,如何考虑结构的局部破坏成为破损-安全结构优化的研究难点. 在Arora等[7 ,8 ,9 ] 的工作中,通过预先指定结构破损模式,将结构破损-安全优化问题归结为考虑各种 结构破损状况下 性能约 束的传统结构优化问题. Feng等[10 ,11 ] 针对截面优化问题探讨了结构构型与冗余间关系. Marhadi等 [12 ,13 ] 考虑非线性分析,研究了局部破损对桁架结构最优设计结果的影响. 杜剑明等[14 ] 提出桁架结构破损-安全优化的双层规划法,上层规划寻求杆件的最优尺寸,下层优化确定结构 最不利 破损状况,避免了人为设定破损状况的不足. Bendsøe等[15 ,16 ] 研究了材料性能退化对桁架及连续体结构拓扑优化的影响. ...
Topology optimization of fail-safe structures using a simplified local damage model
11
2013
... 考虑破损-安全的结构拓扑优化设计与截面优化设计相比具有双重困难,除了考虑结构的局部破坏的研究难点外,还 有结构 拓扑优化建模与求解的难点. 另外,如果桁架结构拓扑优化设计可以从桁架基结构中将指定的单个杆件作为破损模式,那么连续体结构拓扑优化设计的破损模 式以及如 何运作就成了解决困难问题的瓶颈,而Jansen等[17 ] 首先克服了这一困难,他们通过指定一定大小的方块面积(二维)或体 积(三维)的局部破损,将其中心布置于其结构的单元中心上,从而建立起体积约束下极小化结构柔顺度的破损-安全 拓扑优化模型, 应用K-S函数方法凝聚众多函数进行求解. 然而,由于文献[17 ] 采取了每个单元的中心布置一个结构局部破损模式,局部破损区域数量与其结构的单元数量几乎相同,因此所 有含局部破损区域的基机构对应的柔顺度数量也与之相同,导致工作量极大,即使采用并行算法,此方法的计算速度都难以接受. ...
... [17 ]采取了每个单元的中心布置一个结构局部破损模式,局部破损区域数量与其结构的单元数量几乎相同,因此所 有含局部破损区域的基机构对应的柔顺度数量也与之相同,导致工作量极大,即使采用并行算法,此方法的计算速度都难以接受. ...
... 回顾该方向学者们以往相关研究,无论Jansen等[17 ] 的开创性策略还是Zhou等[18 ] 的重大进展,从本质上看,可以 理解为模拟载荷 工况,类比出结构破损状况. 为了推广成果,本研究系统阐述了破损-安全拓扑优化的基本概念,引申出建模前处理策略. ...
... 如果同一破损模式可以出现在设计域内的任何地方,则可完全满足结构破损的“随机性”特征,但这将导致无穷多个破损区域,也即无穷多个结构破损状况. 为使问题可求解,需要将无穷分布的破损区域变成有限分布,或者说,“随机性”模型化为“确定性”. 这就是Jansen等[17 ] 首先完成的工作. ...
... 以Zhou等[17 ] 正方形结构局部破损模式为例予以说明,此示例对应于下文算例1中所采用的结构破损状况的预估分布. 定义的结构破损状况预估分布为无缝平铺,如图2 (a)所示,8个正方形的破损区域无缝平铺在整个基结构上. 图2 (b)为对应于正方形破损区域布置于基结构上的8个结构破损状况,这8个结构破损状况组成结构破损状况集合 Φ
... Jansen等[17 ] 及Zhou等[18 ] 之所以能对式(2)进行求解,是因为其对结构破损状况进行了预估分布,他们研究的均是体积约束下柔顺度极小的拓扑优化问题,其拓扑模型为 ...
... 式(3)的目标函数为结构破损状况集合 Φ Ω s [17 ] 采用K-S函数进行凝聚转化为单目标优化问题求解,Zhou等[18 ] 采取将原目标函数转化为柔顺度的上限约束然后使上限极小化予以求解[19 ] . ...
... 本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布. ...
... 文献[17 ] 与文献[18 ] 及本文所采用的结构破损状况预估分布是不同的,文献[17 ] 以每个单元为中心布置破损模式,而本文 采用的是文献[18 ] 的无缝平铺的排列方式(如图11 ). ...
... [17 ]以每个单元为中心布置破损模式,而本文 采用的是文献[18 ] 的无缝平铺的排列方式(如图11 ). ...
... 依照文献[25 ] 的做法,采用无量纲化的数据,这也是文献[17 ] 和文献[18 ] 中算例的做法. 基结构尺寸为150 × 150 ,厚度为1,如图15 所示. 其中左边50 d 50 灰色正方形为结构局部破损模式,采用间距 F 1 = 1 图16 所示,一个黑色圆点为一个正方形破损区域的形心位置,对应于25个结构破损状况. 由于破损区域重叠,若把所有破损区域均绘制出来,线条重叠会相互干扰以至看不清楚,因此只把对角线位置上的5个破损区域表示出来,其他破损区域就不显示了. 受两种载荷工况作用,工况1为一集中载荷 F 2 = 1 E d = 25
Fail-safe topology optimization
22
2016
... Zhou等[18 ] 为了克服上述困难,选取适当大小的局部破损区域,与邻近的局部破损区域中心距离拉开,使得含局部破损区域的 基机构数目骤然下降,其对应的柔顺度数量也极大减小,令相应的建模与求解的计算能够被接受,可贵的是,文献[18 ]对采取的做 法进行了理论论证. 这是Zhou等做出的重大贡献. ...
... 为了克服上述困难,选取适当大小的局部破损区域,与邻近的局部破损区域中心距离拉开,使得含局部破损区域的 基机构数目骤然下降,其对应的柔顺度数量也极大减小,令相应的建模与求解的计算能够被接受,可贵的是,文献[18 ]对采取的做 法进行了理论论证. 这是Zhou等做出的重大贡献. ...
... 回顾该方向学者们以往相关研究,无论Jansen等[17 ] 的开创性策略还是Zhou等[18 ] 的重大进展,从本质上看,可以 理解为模拟载荷 工况,类比出结构破损状况. 为了推广成果,本研究系统阐述了破损-安全拓扑优化的基本概念,引申出建模前处理策略. ...
... 前述Zhou等[18 ] 将邻近的局部破损区域中心距离实施拉开的方案有两种:第一种是将结构局部破损模式无缝相连地铺满在整个基结构上,他们称之为层级一模型;第二种是将第一种方案邻近的局部破损区域中心的中点也增加为新的局部破损区域中心,放置相应的破损区域,于是局部破损区域相互就有了重叠,Zhou等[18 ] 称之为层级二模型. ...
... [18 ]称之为层级二模型. ...
... 在目前常用的计算资源下,两种方案使连续体结构破损-安全拓扑优化的计算量降低到运行时间可接受的范围内[18 ] . ...
... 结构局部破损模式取正方形时某破损-安全设计示例[18 ] ...
... An example of fail-safe design while structural local failure mode taking square[18 ] ...
... Jansen等[17 ] 及Zhou等[18 ] 之所以能对式(2)进行求解,是因为其对结构破损状况进行了预估分布,他们研究的均是体积约束下柔顺度极小的拓扑优化问题,其拓扑模型为 ...
... 式(3)的目标函数为结构破损状况集合 Φ Ω s [17 ] 采用K-S函数进行凝聚转化为单目标优化问题求解,Zhou等[18 ] 采取将原目标函数转化为柔顺度的上限约束然后使上限极小化予以求解[19 ] . ...
... 如图3 所示,基结构尺寸为100 ×50,厚度为1,左边25 E = 2.1 × 1 0 5 25 灰色正方形为破损模式,结构局部破损区域无缝平铺的预估分布如图2 所示,材料弹性模量 F × [18 ] . 采用100 × 50 的单元边长为1的正方形有限元网格进行计算. ...
... 在20%体积比约束下,不考虑破损-安全的最小化柔顺度拓扑优化,Zhou等[18 ] 得到的最优拓 扑如图4 (a)所示,最优点柔顺度58.72. 应用88行代码得到的最优拓扑如图4 (b)所示,得到的拓扑图形与 Zhou等[18 ] 的相同,最优拓扑结构的柔顺度为57.39,对应集中力作用方向的位移值为0.057 39. 参考文献[21 ] 的做法,以0.057 39为位移约束值,不考虑破损-安全的体积极小化拓扑优化得到的最优拓扑如图4 (c)所示,拓扑图形与前两者相同,最优点体积比20.1%,由此验证了单个集中力作用时,体积约束下极小柔顺度问题与位移约束下极小体积问题存在模型的对应转换关系. ...
... [18 ]的相同,最优拓扑结构的柔顺度为57.39,对应集中力作用方向的位移值为0.057 39. 参考文献[21 ] 的做法,以0.057 39为位移约束值,不考虑破损-安全的体积极小化拓扑优化得到的最优拓扑如图4 (c)所示,拓扑图形与前两者相同,最优点体积比20.1%,由此验证了单个集中力作用时,体积约束下极小柔顺度问题与位移约束下极小体积问题存在模型的对应转换关系. ...
... Zhou等[18 ] 得到的考虑破损-安全的最优拓扑如图5 (a)所示,其体积约束仍为20%,在相同体积约束下,与不考虑破损-安全的拓扑优化相比,结构更为复杂. ...
... 位移约束下体积极小化模型得到的破损-安全最优拓扑如图5 (b)所示,此时结构体积比为20%,位移约 束0.188 5. 可以看到本文的拓扑图形与文献[18 ]是相同的. 以位移约束0.188 5进行不考虑破 损-安全的拓扑优化,得到的最优拓扑如图6 所示,结构体积比为7.22%. 可以看到,在同样位移约束下,破损-安全拓扑优化得到的体积增大许多,并且图形更复杂,即结构具有更多的冗余, 可以更好 满足破损-安全的设计原则. 含各破损区域的最优拓扑图形如图7 所示,目标函数及位移约束迭代曲线分别如图8 和图9 所示,迭代次数74次. 当破损区域位置为2,3,6和7(如图7 (c)、图7 (d)、图7 (e)及图7 (f))时为有效约束,最优点时位移值为0.188 5,破损区域 位置1,4,5和8(如图7 (a)、图7 (b)、图7 (g)及图7 (h))时不是有效约束,位移值为0.172 1. 可见,结构局部破损出现在不同位置时,对结构的影响也是不同的,有些位置的局部破损对结构影响大,致使其对应的结构破 损状况下的位移约束为有效约束,而另一些位置的局部破损对结构的影响可能很小,甚至在没有杆件通过的情况下没有任何 影响,因而其对应的结构破损状况下的位移约束为非有效约束. ...
... 此算例参考文献[18 ] ,如图10 所示,基结构尺寸为180 ×60,厚度为1,采用22 E = 1.0 22 的正方形作为结构局部破损模式,如图10 中灰色正方形所示,采用Zhou等[18 ] 研究中的结构破损状况预估分布如 图11 所示. 材料弹性模量 P = 1.0 × . 采用180 × 60 网格进行计算. 位移约束集中力作用方向的位移小于570. 过滤半径采用1.5,收敛精度采用0.01. ...
... [18 ]研究中的结构破损状况预估分布如 图11 所示. 材料弹性模量 P = 1.0 × . 采用180 × 60 网格进行计算. 位移约束集中力作用方向的位移小于570. 过滤半径采用1.5,收敛精度采用0.01. ...
... 本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布. ...
... 文献[17 ] 与文献[18 ] 及本文所采用的结构破损状况预估分布是不同的,文献[17 ] 以每个单元为中心布置破损模式,而本文 采用的是文献[18 ] 的无缝平铺的排列方式(如图11 ). ...
... [18 ]的无缝平铺的排列方式(如图11 ). ...
... 收敛准则及收敛精度对结果也有影响,本文结果与文献[18 ] 的结果虽更为相似但也有所不同,主要是采用了不同的收敛准则 及收敛精度. ...
... 依照文献[25 ] 的做法,采用无量纲化的数据,这也是文献[17 ] 和文献[18 ] 中算例的做法. 基结构尺寸为150 × 150 ,厚度为1,如图15 所示. 其中左边50 d 50 灰色正方形为结构局部破损模式,采用间距 F 1 = 1 图16 所示,一个黑色圆点为一个正方形破损区域的形心位置,对应于25个结构破损状况. 由于破损区域重叠,若把所有破损区域均绘制出来,线条重叠会相互干扰以至看不清楚,因此只把对角线位置上的5个破损区域表示出来,其他破损区域就不显示了. 受两种载荷工况作用,工况1为一集中载荷 F 2 = 1 E d = 25
Multicriterion structural optimization via bound formulation and mathematical programming
1
1989
... 式(3)的目标函数为结构破损状况集合 Φ Ω s [17 ] 采用K-S函数进行凝聚转化为单目标优化问题求解,Zhou等[18 ] 采取将原目标函数转化为柔顺度的上限约束然后使上限极小化予以求解[19 ] . ...
结构刚度优化问题模型比较研究
2
2016
... 本文基于ICM方法,建立性能约束下体积(或重量)极小化的优化模型. 解析[20 ] 及数值[21 ] 算例均表明:当性能为位移约束时,在集中力作用时,可以与体积约束下柔顺度极小问题建立对应模型. 以位移约束体积极化小的破损-安全拓扑优化为例,应用ICM方法,建立的结构拓扑优化模型为 ...
... 本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布. ...
结构刚度优化问题模型比较研究
2
2016
... 本文基于ICM方法,建立性能约束下体积(或重量)极小化的优化模型. 解析[20 ] 及数值[21 ] 算例均表明:当性能为位移约束时,在集中力作用时,可以与体积约束下柔顺度极小问题建立对应模型. 以位移约束体积极化小的破损-安全拓扑优化为例,应用ICM方法,建立的结构拓扑优化模型为 ...
... 本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布. ...
对连续体结构拓扑优化合理模型的再探
3
2016
... 本文基于ICM方法,建立性能约束下体积(或重量)极小化的优化模型. 解析[20 ] 及数值[21 ] 算例均表明:当性能为位移约束时,在集中力作用时,可以与体积约束下柔顺度极小问题建立对应模型. 以位移约束体积极化小的破损-安全拓扑优化为例,应用ICM方法,建立的结构拓扑优化模型为 ...
... 在20%体积比约束下,不考虑破损-安全的最小化柔顺度拓扑优化,Zhou等[18 ] 得到的最优拓 扑如图4 (a)所示,最优点柔顺度58.72. 应用88行代码得到的最优拓扑如图4 (b)所示,得到的拓扑图形与 Zhou等[18 ] 的相同,最优拓扑结构的柔顺度为57.39,对应集中力作用方向的位移值为0.057 39. 参考文献[21 ] 的做法,以0.057 39为位移约束值,不考虑破损-安全的体积极小化拓扑优化得到的最优拓扑如图4 (c)所示,拓扑图形与前两者相同,最优点体积比20.1%,由此验证了单个集中力作用时,体积约束下极小柔顺度问题与位移约束下极小体积问题存在模型的对应转换关系. ...
... 本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布. ...
对连续体结构拓扑优化合理模型的再探
3
2016
... 本文基于ICM方法,建立性能约束下体积(或重量)极小化的优化模型. 解析[20 ] 及数值[21 ] 算例均表明:当性能为位移约束时,在集中力作用时,可以与体积约束下柔顺度极小问题建立对应模型. 以位移约束体积极化小的破损-安全拓扑优化为例,应用ICM方法,建立的结构拓扑优化模型为 ...
... 在20%体积比约束下,不考虑破损-安全的最小化柔顺度拓扑优化,Zhou等[18 ] 得到的最优拓 扑如图4 (a)所示,最优点柔顺度58.72. 应用88行代码得到的最优拓扑如图4 (b)所示,得到的拓扑图形与 Zhou等[18 ] 的相同,最优拓扑结构的柔顺度为57.39,对应集中力作用方向的位移值为0.057 39. 参考文献[21 ] 的做法,以0.057 39为位移约束值,不考虑破损-安全的体积极小化拓扑优化得到的最优拓扑如图4 (c)所示,拓扑图形与前两者相同,最优点体积比20.1%,由此验证了单个集中力作用时,体积约束下极小柔顺度问题与位移约束下极小体积问题存在模型的对应转换关系. ...
... 本文考虑破损-安全拓扑优化得到的结果如图12 (c)所示,某破损区域对应的破损-安全最优结构 形式如图12 (d)所示,最优体积 比为39.46%. 文献[17 ] 及文献[18 ] 在体积比为40%约束下,得到考虑破损-安全的拓扑优化结果分别如图12 (a)和图12 (b)所示. 可以看到在几乎相同的体积比下,最优拓扑形式是类似的,但不完全相同. 在不考虑破损-安全对单个集中力作用的拓扑优化设计中,体积约束下最小化柔顺度问题与位移约束下最小化体积问题 可以 建立等价互换优化模型[20 ,21 ] ,在考虑破损-安全的拓扑优化中,同样不会由于这个原因而导致拓 扑优化结果的不同. 在算例1中已经验证了这点(见图5 ). 对最优拓扑造成影响的因素主要是结构破损状况预估分布. ...
结构拓扑优化ICM方法的改善
2
2005
... 其中,目标函数的显式化是根据ICM方法处理[22 ,23 ] . ...
... 模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] . ...
结构拓扑优化ICM方法的改善
2
2005
... 其中,目标函数的显式化是根据ICM方法处理[22 ,23 ] . ...
... 模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] . ...
2
2013
... 其中,目标函数的显式化是根据ICM方法处理[22 ,23 ] . ...
... 模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] . ...
2
2013
... 其中,目标函数的显式化是根据ICM方法处理[22 ,23 ] . ...
... 模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] . ...
求解一类可分离凸规划的对偶显式模型DP-EM方法
1
2017
... 模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] . ...
求解一类可分离凸规划的对偶显式模型DP-EM方法
1
2017
... 模型(13)可以采用对偶序列二次规划法求解,也可采用文献[24 ] 中更高效的算法求解;为了消除棋盘格及网格依赖问题,可以对位移的 贡献系数采用进行基于数字图像处理中过滤技术的方法[22 ,23 ] . ...
Efficient topology optimization in MATLAB using 88 lines of code
3
2011
... 从方便比较出发,本文采用与文献[25 ] 相同的收敛准则[25 ] ...
... [25 ] ...
... 依照文献[25 ] 的做法,采用无量纲化的数据,这也是文献[17 ] 和文献[18 ] 中算例的做法. 基结构尺寸为150 × 150 ,厚度为1,如图15 所示. 其中左边50 d 50 灰色正方形为结构局部破损模式,采用间距 F 1 = 1 图16 所示,一个黑色圆点为一个正方形破损区域的形心位置,对应于25个结构破损状况. 由于破损区域重叠,若把所有破损区域均绘制出来,线条重叠会相互干扰以至看不清楚,因此只把对角线位置上的5个破损区域表示出来,其他破损区域就不显示了. 受两种载荷工况作用,工况1为一集中载荷 F 2 = 1 E d = 25