引言
重大装备关键零部件冲击断[1 ] 裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2 ] 、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3 ] . 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值.
目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等.
传统FEM[4 ] 模拟裂纹扩展时, 裂纹必须与网格对齐, 裂纹扩展步长依赖于网格尺寸, 为捕捉裂尖应力奇异性需要布置稠密网格, 裂纹扩展过程中需要不断重新划分网格等. 频繁的网格重分重映不仅使得计算实施繁琐, 同时引入大量映射误差, 导致算法在计算动力学问题时能量守恒性差. 因此, 裂纹扩展模拟成为传统有限元经典难题之一.
XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] .
为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决.
目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响.
有鉴于此, 本文基于改进型XFEM, 采用Newmark隐式算法进行时间积分, 重点研究动力学扩展裂纹应力强度因子的求解方法, 特别地, 考虑裂纹扩展速度项与惯性项的影响. 通过数值算例研究网格单元尺寸、质量矩阵、时间步长、裂尖加强区域、惯性项、速度项及相互作用积分区域J-domain的网格与单元尺寸对DSIF求解精度的影响, 验证改进型XFEM计算动态裂纹的应力强度因子的精度问题, 并与常规XFEM计算结果进行对比.
1 动力学问题的改进型扩展有限元方法
1.1 动力学控制方程
对于计算域内每一点, 应满足应力平衡方程
$\begin{equation}\nabla\cdot{\sigma}+{b}= \rho\dfrac{\partial^2{u}}{\partial t^2}, {in} \varOmega \end{equation}$ (1)
式中, ${\sigma}$为柯西应力张量, ${b}$为单位体积的体力, $\rho$为密度, ${u}$ 为位移, $t$ 为时间.
对于线弹性体, 应力‒应变关系为
$\begin{equation} {\sigma}={D}:{\varepsilon} \end{equation}$ (2)
式中,D为弹性矩阵.
几何关系为
$\begin{equation} {\varepsilon}=\nabla_s{u} \end{equation}$ (3)
边界条件为
$\begin{equation}\left. \begin{split} {u}=\bar{{u}}({x},t), {on} {\Gamma}_{{u}} \\ {\sigma}\cdot{n}=\bar{ t}({x},t), {on} {\Gamma}_{{t}} \\ {\sigma}\cdot{n}= 0, {on} {\Gamma}_{{c}} \end{split}\right\} \end{equation}$ (4)
式中, ${n}$为单位外法向量, ${\bar{u}}$和${{\bar t}}$分别表示位移边界$ {\Gamma}_{u}$上的约束和应力边界$ {\Gamma}_{t}$ 上的约束, $ {\Gamma}_{c}$ 为裂纹面.
初始条件为
$\begin{equation}\left. \begin{split} {u}({x},t=0)=\bar{{u}}(0) \\ {\dot u}({x},t=0)={\dot{\bar{u}}}(0) \end{split}\right\} \end{equation}$ (5)
式中, ${\bar{u}}$(0) 和${\dot{\bar{u}}}$(0) 分别表示初始位移和速度.
1.2 改进型扩展有限元法
1.2.1 常规扩展有限元法
常规XFEM的位移逼近为
$\begin{equation} \begin{split} u^h({x})=\sum_{i\in N}N_iu_i+\sum_{i\in K}N_i(H({x})-H({x}_i))d_i+ \\ \sum_{i\in T}N_i\sum_k\big(\varphi_k({x})-\varphi_k({x}_i)\big)\alpha_{ki} \end{split} \end{equation}$ (6)
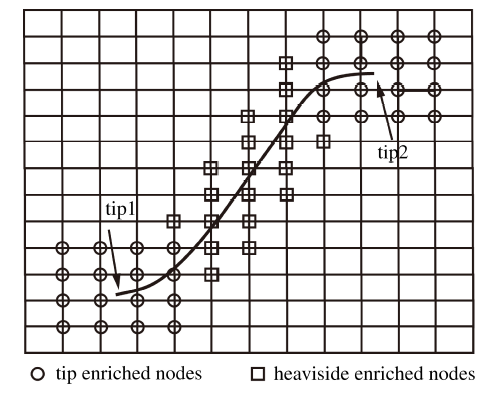
其中, $N$为所有节点集, $K$为阶跃函数加强节点集, $T$为裂尖加强节点集, 节点加强方式如图1 所示. ${d_i}$ 为阶跃加强自由度, ${a_{ki}}$为裂尖加强自由度, $H({{x}})$为Heaviside 函数, $\varphi ({{x}})$为裂尖奇异性加强函数, 其表达式为
$\begin{equation}H({x})=\begin{cases} 1, & f({x},t)\geqslant0 \\ -1, & f({x},t)<0 \end{cases}\end{equation}$ (7)
$\varphi({x})=\phi(r,\theta)=\Big\{\sqrt r {sin}(\theta/2),\sqrt r {cos}(\theta/2),\\ \sqrt r {sin}(\theta/2){sin}(\theta),\sqrt r {cos}(\theta/2){sin}(\theta) \Big\}$ (8)
$f({x},t)$为t时刻的裂纹面水平集.
图1 任意裂纹问题
Fig.1 Arbitrary crack problem
1.2.2 改进型扩展有限元法
改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式
$\begin{equation} \begin{split} u^h( x)=\sum_{i\in I}N_iu_i+\sum_{i\in K}N_i\big(H( x)-H( x_i)\big)d_i+ \\ \sum_{i\in T}\left[N_i( x)\left \lgroup\sum_{k\in I_{i}}\phi^i_k( x)u_k\right\rgroup\right] \end{split} \end{equation}$ (9)
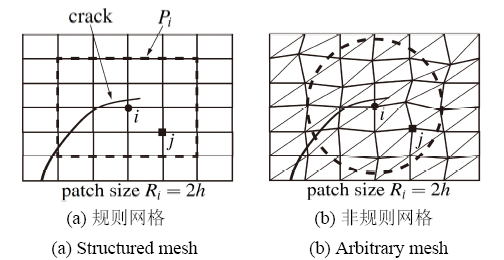
其中, $I$为非裂尖加强节点集, 即标准有限元节点和阶跃加强节点的合集; $T$为裂尖加强节点合集; ${u_i}$与${u_k}$为常规有限元自由度, ${d_i}$为阶跃加强自由度; $\phi_k^i({{x}})$为定义在节点$i$的``节点局部影响域''$P_{i}$上的局部逼近函数, $P_{i}$为距离节点$i$ 一定范围内所有单元组成的单元集, 如图2 所示. ${I_i} = \{ k \in I:{x_k}\in {P}_i^{}\}$为节点$i$ 的节点局部影响域$P_{i}$ 上节点编号集合,${J_i} = \{ k \in I:{x_i} \in {P}_k^{}\} $为包含节点$i$ 的节点局部影响域编号集合. 显然, ${I_i}$ 和${J_i}$ 两个集合完全相同,分开定义是只是为了明确逻辑关系.
图2 单元片的定义
Fig.2 Definition of nodal patch
在 P i
$\phi^i_k( x)= p^{T}( x)\Bigg[ A^{-1} p_k-\dfrac{( A^{-1} p_i)( p^{T}_i A^{-1})}{ p^{T}_i A^{-1} p_{i}} p_k+ \dfrac{ A^{-1}{ p}_{i}}{ p^{T}_i{ A}^{-1} p_i}\delta_{ik}\Bigg]$ (10)
${A}=\sum _{k\in I_i} {{p}}_k{{p}}_k^{T}$ (11)
${p}({x})=\left[1,\dfrac {x-x_i}{R_i},\dfrac {y-y_i}{R_i},\dfrac{\varphi({x})-\varphi({x}_i)}{\sqrt{R_i}}\right]^{T}$ (12)
其中, $\delta $为Kronecker delta函数, ${{p}_{k}} ={p}({x}_{k})$ , $R_{i}$代表节点局部影响域$P_{i}$ 的尺寸, $\varphi({{x}})$为裂尖奇异性加强函数, 见式(8). 由于, ${{p}_{i}} = \left[ {1,{\rm{ }}0,{\rm{}}0,{\rm{ }}\cdots,{\rm{ }}0} \right]$, 故式(10)可写为如下形式
$\begin{equation} \phi^i_k({x})={p}^{T}({x})\left\lgroup {A}^{-1}{p}_k-\dfrac{1}{{A}^{-1}_{11}}{A}^{-1}_{(1)}{A}^{-T}_{(1)}{p}_k+\dfrac{1}{{A}^{-1}_{11}}{A}^{-1}_{(1)}\delta_{ik}\right\rgroup \end{equation}$ (13)
其中, ${{A}}_{(1)}^{ - 1}$为${{A}}_{}^{ - 1}$的第1列, ${{A}}_{11}^{-1}$ 为${{A}}_{(1)}^{-1}$的第1个元素.
通过与常规扩展有限元法(式(6))对比可知, 改进型XFEM在裂尖加强区域通过周围有限元节点构造奇异性高阶逼近(对应式(9)中最后一项),消除了常规XFEM的裂尖额外自由度${a_{ki}}$.
由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29 ,30 ,31 ] .
1.3 基于改进型XFEM的控制方程离散
由含裂纹结构体动力学控制方程及改进型扩展有限元位移逼近, 运用虚功原理, 可得如下控制方程离散形式
$\begin{equation} \begin{bmatrix} {M}^{uu} {M}^{ud}\\{M}^{du} {M}^{dd} \end{bmatrix} \begin{pmatrix} {\ddot{u}}\\ {\ddot{d}} \end{pmatrix}+ \begin{bmatrix} {K}^{uu} {K}^{ud}\\{K}^{du} {K}^{dd} \end{bmatrix} \begin{pmatrix} {u}\\ {d} \end{pmatrix}= \begin{pmatrix} {F}^u\\ {F}^d \end{pmatrix} \end{equation}$ (14)
其中
${K}^{rs}_{ij}=\int_ {\Omega}\left({B}^r_i\right)^{T}{D}({B}^s_j)d {\Omega}$ (15)
${M}^{rs}_{ij}=\int_ {\Omega}\rho({N}^r_i)^{T}{N}^s_jd {\Omega}$ (16)
${F}^u_i=\int_{ {\Gamma}^t_0}{\tilde{N}}_i^{T}{\bar{t}}_{i0}{d} {\Gamma}+\int_ {\Omega}{\tilde{N}}^{T}_i{b}_i{d} {\Omega}$ (17)
${F}^d_i=\int_{ {\Gamma}^t_0}\tilde{H}{\tilde{N}}^{T}_i{\bar{t}}_{i0}{d} {\Gamma}+\int_ {\Omega}\tilde{H}{\tilde{N}}^{T}_i{b}_i{d} {\Omega}, i\in K$ (18)
其中, ${B}$为应变矩阵, 对于常规自由度为${B_{i}^{u}}$, 对于阶跃加强自由度为${B_{i}^{d}}$, 具体形式如下所示
${B}^u_i=\begin{bmatrix}{\Phi}_{i,x} & 0\\0 & {\Phi}_{i,y}\\ {\Phi}_{i,y} & {\Phi}_{i,x} \end{bmatrix}, {\Phi}= \begin{cases} \tilde{N}, i\in I \\ \sum_{k\in J_i}~\tilde{N}_k\phi^k_i, i\in T \end{cases}$ (19)
${B}^d_i= \begin{bmatrix} \left(\tilde{N}_i\tilde{H}\right)_{i,x} & 0\\ 0 & \left(\tilde{N}_i\tilde{H}\right)_{i,y}\\ \left(\tilde{N}_i\tilde{H}\right)_{i,y} & \left(\tilde{N}_i\tilde{H}\right)_{i,x} \end{bmatrix}$ (20)
其中, ${{D}}$为弹性矩阵, $\tilde H = H({{x}}) - H({{{x}}_i})$ , ${\tilde N_i}$为经过混合单元修正后的有限元形函数, 限于篇幅, 详细内容可参见文献[31 ] .
1.4 Newmark时间积分
选取Newmark法作为改进型XFEM的隐式时间积分算法. 在第n +1时间步, 空间和时间离散方程如下
${\dot{U}}_{n+1}={\dot{U}}_n+\Delta t(1-\beta){\ddot{U}}_n+\Delta t\beta{\ddot{U}}_{n+1}$ (21)
${U}_{n+1}={U}_n+\Delta t{\dot{U}}_n+\Delta t^2\left(\dfrac{1}{2}-\alpha\right){\ddot{U}}_n+\Delta t^2\alpha{\ddot{U}}_{n+1}$ (22)
${\tilde{K}U}_{n+1}=\Delta{\tilde{P}}$ (23)
${\tilde{K}}={K}+\dfrac{1}{\alpha\Delta t^2}{M}$ (24)
$\Delta{\tilde{P}}=\Delta {P}+\bigg[\bigg\lgroup\dfrac{1}{2\alpha}-1\bigg\rgroup{\ddot{U}}_n+\dfrac{1}{\alpha\Delta t}{\dot{U}}_n\bigg]{M}$ (25)
其中, ${U}$, ${{\dot U}}$, 和${{\ddot U}}$分别表示节点位移、速度和加速度, $\Delta t$ 为当前时刻的时间步长. $\alpha$ 和 $\beta$为Newmark参数, 当 $\alpha\geqslant 0.5$, $\beta \geqslant 0.25{\left( {\alpha+0.5}\right)^2}$ 时, Newmark法计算是稳定的. 本文取$\alpha=1/4$, $\beta=1/2$.
2 动态扩展裂纹的应力强度因子计算
动态应力强度因子作为表征动载作用下裂纹尖端应力‒应变场奇异程度的重要参量, 是裂纹扩展趋势或裂纹扩展驱动力的度量, 是判断裂纹起始与裂纹扩展速度的重要依据.
2.1 动力学问题相互作用积分
相互作用积分方法具有精度高、适应范围广(弹性、塑性、温度、接触等问题)的特点, 在应力强度因子求解中被广泛使用. 目前国内文献对相互作用积分的应用还多集中于静力学裂纹和动态稳定裂纹, 关于动态扩展裂纹的相互作用积分与其辅助场函数构造的文献较少.
对于线弹性各向同性材料, 动态相互作用积分可表述为[25 ]
$\begin{equation}\begin{split}I^{{int}}=\int_A\begin{bmatrix}\begin{pmatrix}\sigma ^{{aux}}_{ij}u^{{real}}_{i,k}+\sigma^{{real}}_{ij}u^{{aux}}_{i,k} \end{pmatrix}-W^{({real,aux})}\delta_{kj}\end{bmatrix}q_{k,j}{d}S+ \\ \int_A\rho\ddot{u}^{{real}}_iu^{{aux}}_{i,k}q_{k}{d}S+\int_A\rho\dot{u}^{{real}}_l\dot{u}^{{aux}}_l\delta_{kj}q_{k,j}{d}S+ \\ \int_A\begin{bmatrix}\sigma^{{aux}}_{ij,j}u_{i,k}+\rho\begin{pmatrix}\dot{u}^{{aux}}_i\dot{u}^{{real}}_{i,k}+\dot{u}^{{real}}_i\dot{u}^{aux}_{i,k}\end{pmatrix}\end{bmatrix}q_k{d}S\end{split}\end{equation}$ (26)
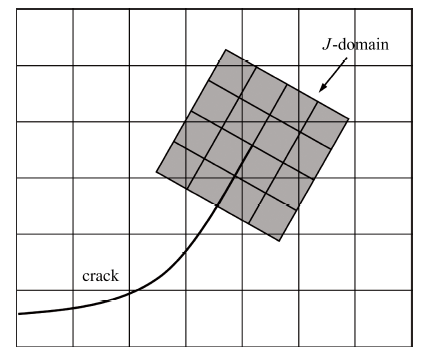
其中, $\left( {\sigma _{ij}^{{\rm{real}}},\varepsilon _{ij}^{{\rm{real}}},u_i^{{\rm{real}}}} \right)$为真实场, $\left( {\sigma _{ij}^{{\rm{aux}}},\varepsilon _{ij}^{{\rm{aux}}},u_i^{{\rm{aux}}}} \right)$为动力学裂纹辅助场; $W_{}^{({\rm{real, aux}})} = \sigma _{ij}^{{\rm{real}}}\varepsilon _{ij}^{{\rm{aux}}} = \sigma _{ij}^{{\rm{aux}}}\varepsilon _{ij}^{{\rm{real}}}$为相互作用积分应变能密度; $A$是相互作用积分区域, 为了精确计算应力强度因子, 相互作用积分区域采用图3 所示的环绕裂纹尖端的$4\times4$个额外单元, 又称为[25 -26 , 38 -42 ] . 这些单元仅用于计算动态相互作用积分, 独立于原计算网格, 且跟随裂纹尖端移动; $q$ 为虚拟裂纹扩展场, 其方向平行于裂纹表面
$\begin{equation}q=\begin{cases}0,&{outside A}\\ 1,&{at crack tip}\\ {linear,}&{inside A} \end{cases} \end{equation}$ (27)
(27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项.
图3 相互作用积分
Fig.3 Interaction integral
对于二维平面应变问题, 该能量释放率与动态应力强度因子关系为
$\begin{equation} I^{{int}}=\dfrac{2(1-v^2)}{E}(f_1(\dot{a})K^{{dyn}}_{I}K^{{aux}}_{I}+f_2(\dot{a})K^{{dyn}}_{{II}}K^{{aux}}_{{II}}) \end{equation}$ (28)
其中, K I aux K II aux f 1 ( a ̇ ) f 2 ( a ̇ ) a
$\begin{equation}\left.\begin{split} &f_i(\dot{a})=\dfrac{4\alpha_i(1-\alpha^2_j)}{(\kappa+1)D} \\ &\alpha_{d}=\sqrt{1-\bigg(\dfrac{\dot{a}}{c_{d}}\bigg)^2},~ \alpha_{s}=\sqrt{1-\bigg(\dfrac{\dot{a}}{c_{s}}\bigg)^2} \\ &D=4\alpha_{d}\alpha_{s}-(1+\alpha^2_{s})^2 \end{split}\right\} \end{equation}$ (29)
其中, c d c s
$\begin{equation} c_{d}=\sqrt{\dfrac{\lambda+2\mu}{\rho}},~c_{s}=\sqrt{\dfrac{\mu}{\rho}} \end{equation}$ (30)
$D$ 是关于裂纹扩展速度$\dot{a}$ 的函数, $\lambda$和$\mu$为拉梅常数. 当裂纹扩展速度等于瑞雷波速${c_{r}}$ 时, $D(\dot{a})=0$.
通过选择合适的裂纹辅助场, 可以得到不同的应力强度因子. 当$K_{\rm{I}}^{{\rm{aux}}} = 1$, $K_{{\rm{II}}}^{{\rm{aux}}} =0$ , 可以直接求得真实裂纹尖端场的I型分量 $K_{\rm{I}}^{{\rm{dyn}}}$. 同理, 当$K_{\rm{I}}^{{\rm{aux}}} =0$, $K_{{\rm{II}}}^{{\rm{aux}}} = 1$, 可以直接求得$K_{{\rm{II}}}^{{\rm{dyn}}}$ .
2.2 动力学问题裂纹辅助场
本节将给出计算动态应力强度因子用到的所有辅助场信息, 对Freund[37 ] 和Réthoré等[25 ] 的相关工作进行推导和总结. 限于篇幅, 本文仅以I型裂纹为例.
以裂纹尖端为原点建立坐标系, 裂纹扩展方向为$x$轴正向, 假设扩展速度为 $\dot a$, 则坐标系内任一点 $P(x,y)$的坐标可表示为
$\begin{equation} \bar{x}=x-\dot{a}t, \bar{y}=y \end{equation}$ (31)
定义
$\begin{equation} \left. \begin{split} r_{d}=\sqrt{\bar{x}^2+\alpha^2_{d}\bar{y}^2}, \theta_{d}={tan}^{-1}\left(\alpha_{d}\bar{y}/\bar{x}\right) \\ r_{s}=\sqrt{\bar{x}^2+\alpha^2_{s}\bar{y}^2}, \theta_{s}={tan}^{-1}\left(\alpha_{s}\bar{y}/\bar{x}\right) \end{split} \right\} \end{equation}$ (32)
则可以得到裂纹尖端位移场与应力场为
$\begin{equation}\left. \begin{split} u_1=&2C_{I}\left[\left(\alpha^2_{s}+1\right)\sqrt{r_{d}}~{cos}\left(\theta_{d}/2\right)-\right.\\ &\left.2\alpha_{d}\alpha_{s}\sqrt{r_{s}}~{cos}\left(\theta_{s}/2\right)\right] \\ u_2=&2C_{I}\left[-\alpha_{d}\left(\alpha^2_{s}+1\right)\sqrt{r_{d}}~{sin}\left(\theta_{d}/2\right)+\right.\\ &\left.2\alpha_{d}\sqrt{r_{s}}~{sin}\left(\theta_{s}/2\right)\right] \\ C_{I}=&K^{dyn}_{I}\bigg/\left(\mu D\sqrt{2\pi}\right) \end{split} \right\} \end{equation}$ (33)
$\begin{equation} \left. \begin{split} \sigma_{11}=&\mu C_{I}\left[\left(\alpha^2_{s}+1\right)\right.\left(2\alpha^2_{d}-\alpha^2_{s}+1\right)~{cos}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}- \\ &\left.4\alpha_{d}\alpha_{s}~{cos}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \\ \sigma_{22}=&\mu C_{I}\left[-\left(\alpha^2_{s}+1\right)^2~{cos}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}+\right. \\ &\left.4\alpha_{d}\alpha_{s}~{cos}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \\ \sigma_{12}=&\mu C_{I}\left[2\alpha_{d}\left(\alpha^2_{s}+1\right){sin}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}-\right. \\ &\left.2\alpha_{d}\left(\alpha ^2_{s}+1 \right){sin}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \end{split} \right\} \end{equation}$ (34)
由式(31)和式(32)可得
$\begin{equation} \left. \begin{split} &\partial r_i/\partial x={cos}\theta_i, \partial\theta_i/\partial x=-{sin}\theta_i/r_i \\ &\partial r_i/\partial y=\alpha_i~{cos}\theta_i, \partial\theta_i/\partial y=\alpha_i~{cos}\theta_i/r_i \\ &\partial x/\partial t=-\dot{a}, \partial y/\partial t=0, \end{split} \right\} \end{equation}$ (35)
则裂纹尖端速度场
$\begin{equation} \left. \begin{split} \dot{u}_1=&-\dot{a}C_{I}\left[\left(\alpha^2_{s}+1\right){cos}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}-\right. \\ &\left.2\alpha_{d}\alpha_{s}{cos}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \\ \dot{u}_2=&-\dot{a}C_{I}\left[\alpha_{d}\left(\alpha^2_{s}+1\right){sin}\left(\theta_{d}/2\right)\big/\sqrt{r_{d}}-\right. \\ &\left.2\alpha_{d}~{sin}\left(\theta_{s}/2\right)\big/\sqrt{r_{s}}\right] \end{split} \right\} \end{equation}$ (36)
同理, 由式(33)~式(35)可得位移和应力偏导场$u_{i,k}$ 与 $\sigma _{ij,k}$.
2.3 动力学问题裂纹扩展准则
在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ]
$\begin{equation} K_{\theta\theta}={cos}^3\left\lgroup\dfrac{\theta_{c}}{2}\right\rgroup K^{\rm{dyn}}_{I}-\dfrac{3}{2}{cos}\left\lgroup\dfrac{\theta_{c}}{2}\right\rgroup{sin}(\theta_{c})K^{\rm{dyn}}_{{II}} \end{equation}$ (37)
Freund[37 ,45 ] 给出了如下等效动态应力强度因子与裂纹扩展速度的关系式
$\begin{equation} \dot{a}= \begin{cases} 0, & K_{\theta\theta}<K_{\rm{IC}} \\ c_{r}\left\lgroup1-\left\lgroup\dfrac{K_{\rm{IC}}}{K_{\theta\theta}} \right\rgroup^2\right\rgroup, & {otherwise} \end{cases} \end{equation}$ (38)
其中, $c_{r}$为瑞雷波速, ${K_{IC}}$ 为材料断裂韧度. Freund与合作者 [45 ,46 ,47 ] 通过实验验证了该公式的正确性. 假设每个时间步中裂纹扩展速度不变, 则裂纹扩展步长可近似表述为$\Delta a = \dot a\Delta t$ , 其中$\Delta t$ 是每一步的时间步长. 裂纹的扩展方向可以根据最大周向应力准则得到
$\begin{equation} \theta_{c}=2~{arctan}\left\{\dfrac{1}{4}\left[\dfrac{K^{\rm{dyn}}_{I}}{K^{\rm{dyn}}_{{II}}}-{sign}\left(K^{\rm{dyn}}_{{II}}\right)\sqrt{8+\left\lgroup\dfrac{K^{\rm{dyn}}_{I}}{K^{\rm{dyn}}_{{II}}}\right\rgroup^2 } \right]\right\} \end{equation}$ (39)
3 算例
3.1 受拉半无限大板
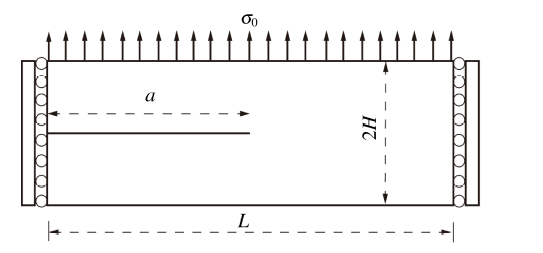
含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ]
$\begin{equation} K^{\rm{dyn}}_{I}(t)= \begin{cases} 0, & t<t_{c} \\ \dfrac{1-\dot{a}/c_{r}}{1-\dot{a}/2c_{r}}\dfrac{2\sigma_0}{1-\mu}\sqrt{\dfrac{c_{d}(t-t_{c})(1-2\mu)}{{\pi}}}, & t\geqslant t_{c} \end{cases} \end{equation}$ (40)
其中, $\dot a$ 是裂纹的瞬时扩展速度, ${t_{c}} = H/{c_{d}}$ 为应力波从梁上缘到达裂尖的时间. 若无特别说明在本论文中裂尖强化区域半径 ${R^{tip}} = 1.0h$, J-domain 区域网格为4×4, J-domain单元尺寸$h_J=1.0h$, h为网格单元尺寸, 总模拟时间t = 1.0 ms.
图4 含I型裂纹的受拉半无限大板
Fig.4 Geometry and loading for mode I semi-infinite crack problem
3.1.1 裂纹保持稳定
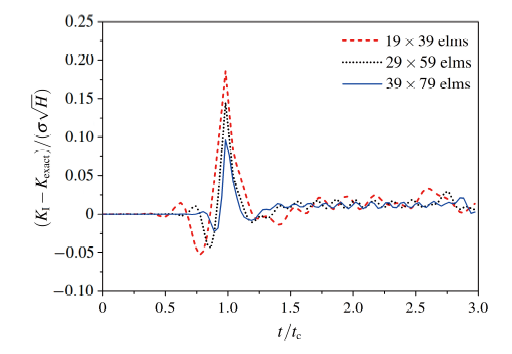
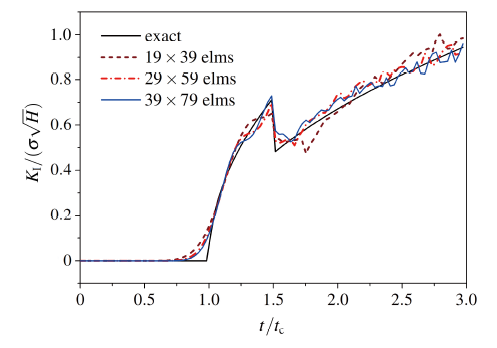
(1) 网格尺寸对DSIF的影响
采用如下3种的网格, 分别为19×39, 29×59和39×79, 计算时间步长取为$\Delta t$ = 10µs, 一致质量矩阵. 图5 给出了3种网格下应力强度因子随时间变化曲线. 由图可知: (1) 在网格较稀疏的情况下, 改进型XFEM可以获得较高的计算精度; (2) 随着网格的加密, 动态应力强度因子值越来越逼近解析解, 有着良好的收敛性.
图5 稳定裂纹动态应力强度因子随单元尺寸变化
Fig.5 DSIF vs. element size
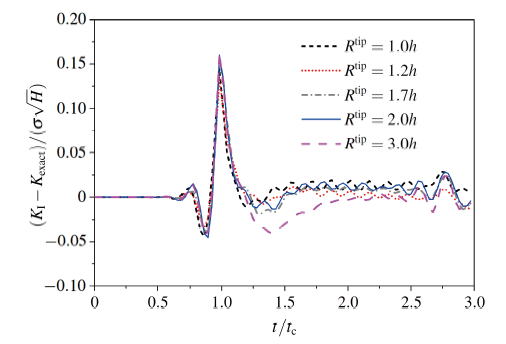
(2) 裂尖强化区域对DSIF的影响
如图6 所示, 考虑5种不同的裂尖强化区域半径, $R^{tip}$取值范围为1.0h~3.0h(小于1.0h 不能满足最小二乘插值节点个数, 大于3.0h结果偏差较大), 离散网格取$29\times 59$, 计算时间步长取$\Delta t=10 {µ}s$ , 一致质量矩阵. 图6 给出了不同裂尖加强区域下动态应力强度因子的变化情况. 由图6 可知: (1) 当裂尖强化区域半径小于2.0h 时, DSIF 对解析解逼近得越好; 当$R^{tip}<1.7h$ 时, 随强化区域增大, 精度提高; (2) 当强化区域半径大于$2.0h$ 时, 裂尖强化区域增大, DSIF 精度变差. 这是因为裂尖强化区域面积太大, 而真实裂尖场影响域相对裂纹长度是很小的. 根据笔者分析, $R^{tip}$ 的取值为$1.0h \sim 2.0h$ 时可以获得较好的结果.
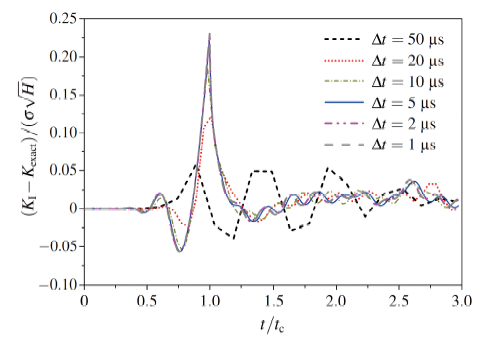
(3) 时间步长对DSIF的影响
离散网格取为19×39, 时间步长分别取为1 µs, 2µs, 5µs, 10µs, 20µs, 50µs, 一致质量矩阵. 不同时间步长对应DSIF 的误差变化曲线见图7 . 从图7 可以看出, 随着时间步长的减小, 数值解越来越逼近解析解. 但是当时间步长小于一定数值时(在网格19×39 下约为10µs, 时间步长的变化对精度影响很小. 同时较小的时间步长会导致更长的计算时间. 因此在实际应用中要同时兼顾计算效率与计算精度.
图6 稳定裂纹动态应力强度因子随裂尖加强区域变化
Fig.6 DSIF vs. tip enriched area
图7 稳定裂纹动态应力强度因子随时间步长变化
Fig.7 DSIF vs. critical time step size
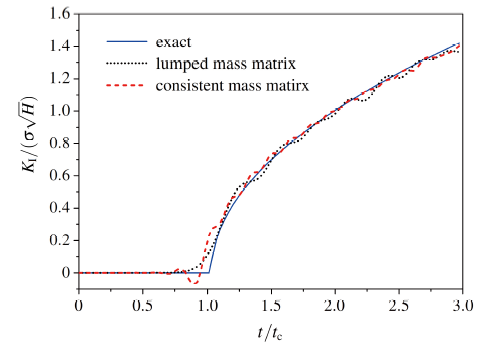
(4) 集中质量与一致质量对DSIF的影响
离散网格取为29×59, 时间步长取为$\Delta t$=10 µs, 考虑一致质量矩阵与集中质量矩阵对DSIF的影响, 结果如图8 所示. 集中质量矩阵的计算效率要高于一致质量矩阵, 两者的DSIF平均误差相差不大, 当选用集中质量矩阵时, 在t=tc 时刻作用, 误差小于一致质量矩阵, 之后随时间延长, 数值震荡要稍大于一致质量结果.
图8 质量矩阵对DSIF的影响
Fig.8 The effect of mass matrix on the DSIF
3.1.2 裂纹先稳定后扩展
对于图4 所示问题, 裂纹在t=1.5tc 之前保持稳定, 之后以1500 m/s的速度匀速扩展.
(1) 网格尺寸对DSIF的影响
采用3种不同密度的网格, 分别为19×39, 29×59和39×79, 计算时间步长取为 Δ t = 10 µs 图9 . 由图可知: (1) 裂纹扩展前后, 改进型XFEM均可以获得较高的计算精度; (2) 随着网格的加密, 动态应力强度因子值越来越逼近解析解, 有着良好的收敛性.
图9 先稳定后扩展裂纹动态应力强度因子随单元尺寸变化
Fig.9 DSIF vs. element size
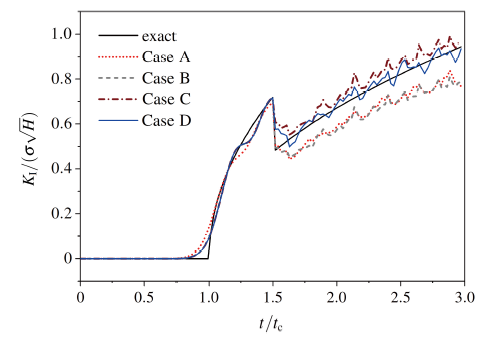
(2) 惯性项与扩展速度项对DSIF的影响
惯性项与扩展速度项是动力学裂纹应力强度因子求解与静力学的主要区别. 图10 给出了对应不考虑和考虑惯性项、扩展速度项时DSIF 的误差随时间的变化曲线, 其中Case A为不考虑惯性项与扩展速度项, 对应式(18) 第1 项; Case B 为仅考虑惯性项影响, 对应式(18) 中第1和第2项; Case C为仅考虑惯性项影响, 即式(18)中第1和第2项, 同时动态相互作用积分与动态应力强度因子的关系式(式(28))改为采用如下稳定裂纹关系式
$\begin{equation}I^{\rm{int}}=\dfrac{2(1-v^2)}{E}\left(K^{\rm{dyn}}_{I}K^{\rm{aux}}_{I}+K^{\rm{dyn}}_{\rm{II}}K^{\rm{aux}}_{\rm{II}}\right)\end{equation}$ (41)
CaseD为考虑惯性项与扩展速度项, 对应式(18)所有项.
离散网格取为39×79, 时间步长取为 Δ t = 7.5 µs 图10 可知: (1) 裂纹扩展前, 这4种方法精度相近. (2) 裂纹发生扩展后, Case C的精度要优于Case A与Case B, 这说明当不考虑裂纹扩展速度项贡献时, 裂纹扩展过程中仍然采用稳定裂纹的相互作用积分与DSIF关系式可以得到更好的结果. (3) 当裂纹发生扩展后, 考虑裂纹尖端速度项 的影响(Case D) 得到的结果精度明显高于其他几种情况, 由此说明, 在计算扩展裂纹应力强度因子时, 裂纹扩展速度项的贡献不能忽略.
图10 惯性项与扩展速度项对动态应力强度因子变化
Fig.10 The effect of inertia term and crack velocity term on the DSIF
(3) J -domain单元网格对DSIF的影响
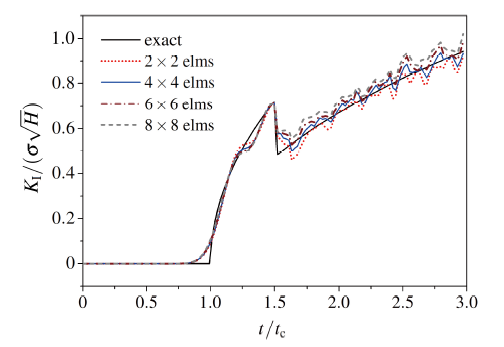
理论上相互作用积分应该是与路径无关的, 但是由于数值积分的误差造成了路径相关性, 因此, 相互作用积分区域J -domain 大小选择是否合理将直接影响DSIF的求解精度. 而J -domain的大小由其网格单元数目与单元尺寸决定.
首先考虑J -domain单元网格对DSIF的影响, 考虑如下4种J -domain网格, 分别为2×2, 4×4, 6×6 和8×8, J -domain 单元尺寸hJ =1.0h . 计算网格取为39×79, 时间步长 Δ t = 7.5 µs 图11 所示, 随着网格数的增加, 裂纹扩展后应力强度因子的数值也逐渐增大, 其中4×4与6×6 的网格精度最好. 考虑到计算效率, 推荐采用4×4的J -domain网格.
图11 J -domain单元网格对动态应力强度因子变化
Fig.11 The effect of J -domain mesh on the DSIF
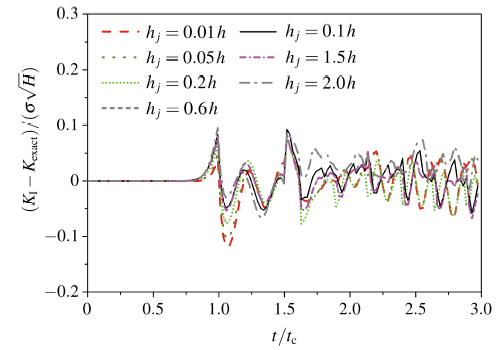
(4) J -domain单元尺寸对DSIF的影响
计算网格与时间步长如上. J -domain单元网格为4×4, J -domain单元尺寸在0.01h 到2.0h 之间取值.
图12 给出了不同J -domain单元尺寸对DSIF的影响结果. 由图可知, 结果精度对J -domain区域单元尺寸变化不敏感, 震荡幅度变化不大, 甚至当 J -domain 单元尺寸取为计算网格单元尺寸的0.01倍时, 仍可以具有较高的计算精度. 考虑到计算效率与计算稳定性, 推荐的J -domain单元尺寸取值范围为0.5h~1.5h.
图12 J -domain单元尺寸动态应力强度因子变化
Fig.12 The effect of element size of J -domain on the DSIF
(5) 与文献结果对比
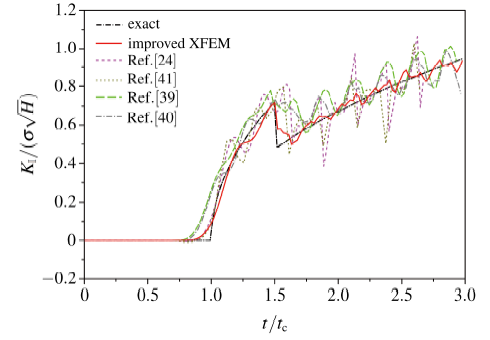
这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23 -24 ,38 -43 ] , 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39 ] .
对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答.
图13 改进型XFEM与XFEM动态应力强度因子对比
Fig.13 The comparison of improved XFEM and XFEMs on accuracy assessment of dynamic SIF for moving crack
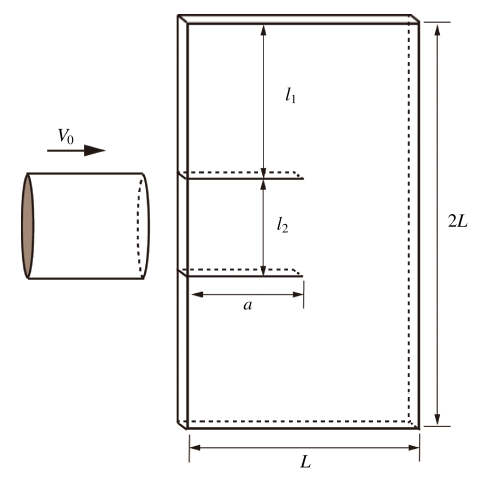
3.2 Kalthoff实验‒动态裂纹扩展测试
Kalthoff实验常常作为检验动态裂纹扩展模拟准确性的标准算例[24 ,38 -42 ] . 在实验中, 一个初速度V 0 的弹体去冲击一含两个对称边裂纹的平板, 如图14 所示, 两裂纹间距与弹体直径相对应. 其中L=100mm , H =200mm , a =50mm, 材料密度$\rho = 8000 {kg/m}^{3}$, $E=190 {GPa}$, $v=0.3$. 断裂韧度$K_{IC}=68~{MPa}\cdot \sqrt{m}$. 弹体冲击速度为: $V_{0}=20 {m/s}$. 考虑4 种计算网格, 分别为19×19, 39×39, 79×79 和199×199, 时间步长分别取为2 μs, 1 μs, 1 μs和0.5 μs, 集中质量矩阵, 模拟时间为$1.0\times10^{-4}~{s}$. 在低速冲击下, 该实验裂纹最终扩展路径与水平方向夹角在70° 左右. 裂纹扩展速度 a ̇
图14 Kalthoff实验
Fig.14 Geometry of Kalthoff’s experiment
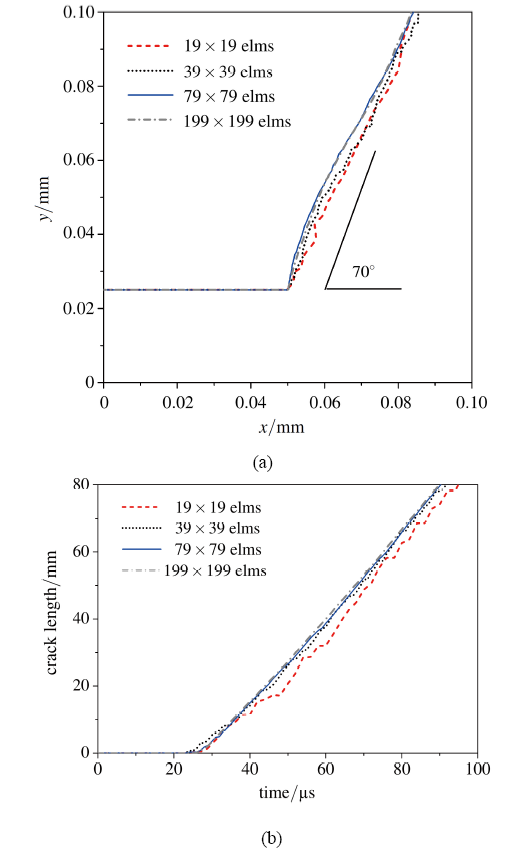
图15 给出了不同网格裂纹扩展路径与裂纹长度随时间变化曲线的结果对比. 显然, 裂纹最终路径和裂纹扩展速度随着网格加密最终收敛. 裂纹扩展方向与水平方向夹角在67°左右. 初始扩展方向约70°, 最终沿大约67°方向贯穿整个靶板. 结果与文献[38 -42 , 44 ] 结果一致.
图15 模拟结果 (a) 裂纹路径; (b) 裂纹长度随时间变化
Fig.15 Comparison of the results obtained by implicit and explicit time integrators. (a) final crack path; (b) crack length vs time
4 结论
改进型XFEM具有裂尖强化不引入额外自由度、条件性态良好、全局插值、和动力学计算实施容易等特点. 本文考虑了该方法在动力学裂纹扩展问题中的应用, 通过典型算例分析了动力学裂纹应力强度因子求解中网格、时间步长、加强区域、质量矩阵及J -domian等因素的影响, 结论如下:
(1) 改进型XFEM有着良好的收敛性. 在网格较稀疏的情况下, 可获得较高的计算精度; 随着网格加密, 数值解逼近解析解.
(2) 裂尖加强区域取值为1.0h ~ 2.0h 时, 计算结果最理想.
(3) 对于给定网格, 随着时间步长减小, 数值解越来越逼近解析解.
(4) 在动态裂纹扩展中, 惯性项与速度贡献项的影响不可忽略.
(5) 对于问题3.1, 相互作用积分区域J -domian的网格取4×4或6×6时结果最理想, 此外J -domian 网格单元尺寸的选取对DSIF影响不大, 但考虑网格质量与计算误差等因素的影响, 推荐采用0.5h~ 1.5h .
(6) 对于问题3.1, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答.
未来工作围绕复杂裂纹扩展和裂纹群相互作用展开.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
邹广平 , 谌赫 , 唱忠良 . 一种基于SHTB 的II 型动态断裂实验技术
. 力学学报 , 2017 , 49 (1 ): 117 -125
[本文引用: 1]
(Zou Guangping Chen He Chang Zhongliang A modified mode II dynamic fracture test technique based on SHTB
. Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (1 ): 117 -125 (in Chinese))
[本文引用: 1]
[2]
马天宝 , 任会兰 , 李健 等 . 爆炸与冲击问题的大规模高精度计算
. 力学学报 , 2016 , 48 (3 ): 599 -608
[本文引用: 1]
(Ma Tianbao Ren Huilan Li Jian et al . Large scale high precision computation for explosion and impact problems
. Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (3 ): 599 -608 (in Chinese))
[本文引用: 1]
[3]
Song Y Hu H Rudnicki JW Dynamic stress intensity factor (Mode I) of a permeable penny-shaped crack in a fluid-saturated poroelastic solid
. International Journal of Solids and Structures , 2017 , 110 : 127 -136
[本文引用: 1]
[4]
彭凡 , 马庆镇 , 戴宏亮 . 黏弹性功能梯度材料裂纹问题的有限元方法
. 力学学报 , 2013 , 45 (3 ): 359 -366
[本文引用: 2]
(Peng Fan Ma Qingzhen Dai Hongliang Finite element method for crack problems in viscoelastic functionally graded materials
. Chinese Journal of Theoretical and Applied Mechanics , 2013 , 45 (3 ): 359 -366 (in Chinese))
[本文引用: 2]
[5]
卢梦凯 , 张洪武 , 郑勇刚 . 应变局部化分析的嵌入强间断多尺度有限元法
. 力学学报 , 2017 , 49 (3 ): 649 -658
[本文引用: 1]
(Lu Mengkai Zhang Hongwu Zheng Yonggang Embedded strong discontinuity model based multiscale finite element method for strain localization analysis
. Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (3 ): 649 -658 (in Chinese))
[本文引用: 1]
[6]
Lei J Yun L Bui T Q et al . Numerical simulation of crack growth in piezoelectric structures by BEM
. Engineering Analysis with Boundary Elements , 2017 , 85 : 30 -42
[本文引用: 1]
[7]
Sonobe Y Koyama A Saimoto A Basic research on simulation for 3D crack growth by mesh free BFM
. Key Engineering Materials , 2016 , 713 : 5 -9
[本文引用: 1]
[8]
Kumar S Singh IV Mishra BK et al . New enrichments in XFEM to model dynamic crack response of 2-D elastic solids
. International Journal of Impact Engineering , 2016 , 87 : 198 -211
[本文引用: 2]
[9]
王振 , 余天堂 . 模拟三维裂纹问题的自适应多尺度扩展有限元法
. 工程力学 , 2016 , 33 (1 ): 32 -38
[本文引用: 1]
(Wang Zhen Yu Tiantang Adaptive multiscale extended finite element method for Modeling three-dimensional crack problems
. Engineering Mechanics , 2016 , 33 (1 ): 32 -38 (in Chinese))
[本文引用: 1]
[10]
龚迪光 , 曲占庆 , 李建雄 等 . 基于ABAQUS平台的水力裂缝扩展有限元模拟研究
. 岩土力学 , 2016 , 37 (5 ): 1512 -1520
[本文引用: 1]
(Gong Diguang Qu Zhanqing Li Jianxiong et al . Extended finite element simulation of hydraulic fracture based on ABAQUS platform
. Rock and Soil Mechanics , 2016 , 37 (5 ): 1512 -1520 (in Chinese))
[本文引用: 1]
[11]
江守燕 , 杜成斌 . 动载下缝端应力强度因子计算的扩展有限元法
. 应用数学和力学 , 2013 , 34 (6 ): 586 -597
[本文引用: 6]
(Jiang Shouyan Du Chenbin Evaluation on stress intensity factors at the crack tip under dynamic loads using extended finite element methods
. Applied Mathematics and Mechanics , 2013 , 34 (6 ): 586 -597 (in Chinese))
[本文引用: 6]
[12]
杨永涛 , 徐栋栋 , 郑宏 . 动载下裂纹应力强度因子计算的数值流形元法
. 力学学报 , 2014 , 46 (5 ): 730 -738
[本文引用: 4]
(Yang Yongtao Xu Dongdong Zheng Hong Evaluation on stress intensity factor at the crack under dynamic load using numerical manifold method
. Chinese Journal of Theoretical and Applied Mechanics , 2014 , 46 (5 ): 730 -738 (in Chinese))
[本文引用: 4]
[13]
Li W Zheng H Sun G The moving least squares based numerical manifold method for vibration and impact analysis of cracked bodies
. Engineering Fracture Mechanics , 2018 , 190 : 410 -434
[本文引用: 1]
[14]
章鹏 , 杜成斌 , 江守燕 . 比例边界有限元法求解裂纹面接触问题
. 力学学报 , 2017 , 49 (6 ): 1335 -1347
[本文引用: 1]
(Zhang Peng Du Chengbin Jiang Shouyan Crack face contact problem analysis using the scaled boundary finite element method
. Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (6 ): 1335 -1347 (in Chinese))
[本文引用: 1]
[15]
Bleyer J Roux-Langlois C Molinari J F Dynamic crack propagation with a variational phase-field model: Limiting speed, crack branching and velocity-toughening mechanisms
. International Journal of Fracture , 2017 , 204 (1 ): 79 -100 .
[本文引用: 1]
[16]
王理想 , 唐德泓 , 李世海 等 . 基于混合方法的二维水力压裂数值模拟
. 力学学报 , 2015 , 47 (6 ): 973 -983
[本文引用: 1]
(Wang Lixiang Tang Dehong Li Shihai et al . Numerical simulation of hydraulic fracturing by a mixed method in two dimensions
. Chinese Journal of Theoretical and Applied Mechanics , 2015 , 47 (6 ): 973 -983 (in Chinese))
[本文引用: 1]
[17]
Babuška I Melenk JM Partition of unity method
. International Journal for Numerical Methods in Engineering , 1997 , 40 : 727 -758
[18]
Tian R Yagawa G Terasaka H Linear dependence problems of partition of unity based generalized FEMs
. Computer Methods in Applied Mechanics and Engineering .2006 , 195 : 4768 -4782
[本文引用: 1]
[19]
Gupta V Duarte C A Babuška I et al . Stable GFEM (SGFEM): Improved conditioning and accuracy of GFEM/XFEM for three-dimensional fracture mechanics
. Computer Methods in Applied Mechanics and Engineering , 2015 , 289 : 355 -386
[20]
Babuška I Banerjee U Kergrene K Strongly stable generalized finite element method: Application to interface problems
. Computer Methods in Applied Mechanics and Engineering , 2017 , 327 : 58 -92
[21]
Agathos K Chatzi E Bordas S et al . A well-conditioned and optimally convergent XFEM for 3D linear elastic fracture
. International Journal for Numerical Methods in Engineering , 2016 , 105 (9 ): 643 -677
[22]
Agathos K Ventura G Chatzi E et al . Stable 3D XFEM/vector level sets for non-planar 3D crack propagation and comparison of enrichment schemes
. International Journal for Numerical Methods in Engineering , 2018 , 113 : 252 -276
[23]
Belytschko T Chen H Xu J et al . Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment
. International Journal for Numerical Methods in Engineering , 2003 , 58 : 1873 -1905
[本文引用: 6]
[24]
Elguedj T Gravouil A Maigre H An explicit dynamics extended finite element method. Part 1: Mass lumping for arbitrary enrichment functions
. Computer Methods in Applied Mechanics and Engineering , 2009 , 198 (30-32 ): 2297 -2317
[本文引用: 6]
[25]
Réthoré J Gravouil A Combescure A An energy-conserving scheme for dynamic crack growth using the extended finite element method
. International Journal for Numerical Methods in Engineering , 2005 , 63 : 631 -659
[本文引用: 6]
[26]
Comnescure A Gravouil A Gregoire D et al . XFEM a good candidate for energy conservation in simulation of brittle dynamic crack propagation
. Computer Methods in Applied Mechanics and Engineering , 2008 , 197 (5 ): 309 -318
[本文引用: 3]
[27]
Tian R Extra-dof-free and linearly independent enrichments in GFEM
. Computer Methods in Applied Mechanics and Engineering , 2013 , 266 : 1 -22
[本文引用: 2]
[28]
Tian R Wen L Improved XFEM-An extra-DOF free, well- conditioning, and interpolating XFEM
. Computer Methods in Applied Mechanics and Engineering , 2015 , 285 : 639 -658
[本文引用: 2]
[29]
Wen L Tian R Improved XFEM: Accurate and robust dynamic crack growth simulation
. Computer Methods in Applied Mechanics and Engineering , 2016 , 308 : 256 -285
[本文引用: 5]
[30]
田荣 , 文龙飞 . 改进型XFEM综述
. 计算力学学报 , 2016 , 33 (4 ): 469 -477
[本文引用: 3]
(Tian Rong Wen Longfei Recent progresses on improved XFEM
. Chinese Journal of Computational Mechanics , 2016 , 33 (4 ): 469 -477 (in Chinese))
[本文引用: 3]
[31]
文龙飞 . 改进型扩展有限元法及其并行程序实现. [博士论文]
. 北京: 中国科学院大学 , 2017
[本文引用: 4]
(Wen Longfei Improved extended finite element method and its parallel programming. [PhD Thesis]
. Beijing: University of Chinese Academy of Sciences , 2017 (in Chinese))
[本文引用: 4]
[32]
王理想 , 文龙飞 , 王景焘 等 . 基于改进型XFEM的裂纹分析并行软件实现
. 中国科学: 技术科学 , 已录用
[本文引用: 2]
(Wang Lixiang Wen Longfei Wang Jingtao et al . Implementations of parallel software for crack analyses based on the improved XFEM
. Scientia Sinica Technologica Accepted (in Chinese))
[本文引用: 2]
[33]
刘鹏 , 余天堂 . 压电材料二维动应力强度因子的扩展有限元计算
. 振动与冲击 , 2013 , 32 (13 ): 76 -80
[本文引用: 2]
(Liu Peng Yu Tiantang Dynamic intensity factor computation for two-dimensional piezoelectric media using an extended finit element method
. Journal of Vibration and Shock , 2013 , 32 (13 ): 76 -80 (in Chinese))
[本文引用: 2]
[34]
刘学聪 , 章青 , 夏晓舟 . 一种新型裂尖加强函数的显式动态扩展有限元法
. 工程力学 , 2017 , 34 (10 ): 10 -18
[本文引用: 2]
(Liu Xuecong Zhang Qing Xia Xiaozhou A new enrichment function of crack tip in XFEM dynamics by explicit time algrorithm
. Engineering Mechanics , 2017 , 34 (10 ): 10 -18 (in Chinese))
[本文引用: 2]
[35]
庄茁 , 柳占立 , 成斌斌 等 . 扩展有限元法 . 北京 : 清华大学出版社 , 2012
[本文引用: 2]
(Zhuang Zuo Liu Zhanli Cheng Binbin et al. The Extended Finite Element Method. Beijing : Tsinghua University Press , 2012 (in Chinese))
[本文引用: 2]
[36]
余天堂 . 扩展有限单元法‒理论、应用及程序 . 北京 : 科学出版社 , 2014
[本文引用: 2]
(Yu Tiantang. The Extended Finite Element Method-Theory, Application and Program. Beijing : Science Press , 2014 (in Chinese))
[本文引用: 2]
[37]
Freund LB . Dynamic Fracture Mechanics.
Cambridge University Press , 1990
[本文引用: 4]
[38]
Menouillard T Réthoré J Combescure A et al . Efficient explicit time stepping for the extended finite element method
. International Journal for Numerical Methods in Engineering , 2006 , 68 : 911 -938
[本文引用: 6]
[39]
Menouillard T Song JH Duan QL et al . Time dependent crack tip enrichment for dynamic crack propagation
. International Journal of Fracture , 2010 , 162 (1-2 ): 33 -49
[本文引用: 2]
[40]
Menouillard T Belytschko T Smoothed nodal forces for improved crack propagation modeling in XFEM
. International Journal for Numerical Methods in Engineering , 2010 , 84 : 47 -72
[本文引用: 1]
[41]
Gravouil A Elguedj T Maigre H An explicit dynamics extended finite element method. Part 2: Element-by-element stable-explicit/explicit dynamic scheme
. Computer Methods in Applied Mechanics and Engineering , 2009 , 198 (30-32 ): 2318 -2328
[本文引用: 2]
[42]
Liu Z L Menouillard T Belytschko T An XFEM/Spectral element method for dynamic crack propagation
. International Journal of Fracture , 2011 , 169 (2 ): 183 -198
[本文引用: 4]
[43]
Menouillard T Belytschko T Dynamic fracture with meshfree enriched XFEM
. Acta Mechanica , 2010 , 213 (1-2 ): 53 -69
[本文引用: 2]
[44]
Kalthoff J F Modes of dynamic shear failure in solids
. International Journal of Fracture , 2000 , 101 (1-2 ): 1 -31
[本文引用: 1]
[45]
Freund LB Crack propagation in an elastic solid subjected to general loading. Pt. 1. Constant rate of extension
. Journal of the Mechanics and Physics of Solids , 1972 , 20 (3 ): 129 -140
[本文引用: 2]
[46]
Freund LB Douglas AS Influence of inertia on elastic-plastic antiplane-shear crack growth
. Journal of the Mechanics and Physics of Solids , 1982 , 30 (1 ): 59 -74
[本文引用: 1]
[47]
Rosakis AJ Freund LB Optical measurement of the plastic strain concentration at a crack tip in a ductile steel plate
. Journal of Engineering Materials and Technology , 1982 , 104 (2 ): 115 -120
[本文引用: 1]
[48]
Réthoré J Gravouil A Combescure A A combined space-time extended finite element method
. International Journal for Numerical Methods in Engineering , 2005 , 64 (2 ): 260 -284
[本文引用: 1]
一种基于SHTB 的II 型动态断裂实验技术
1
2017
... 重大装备关键零部件冲击断[1 ] 裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2 ] 、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3 ] . 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值. ...
一种基于SHTB 的II 型动态断裂实验技术
1
2017
... 重大装备关键零部件冲击断[1 ] 裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2 ] 、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3 ] . 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值. ...
爆炸与冲击问题的大规模高精度计算
1
2016
... 重大装备关键零部件冲击断[1 ] 裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2 ] 、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3 ] . 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值. ...
爆炸与冲击问题的大规模高精度计算
1
2016
... 重大装备关键零部件冲击断[1 ] 裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2 ] 、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3 ] . 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值. ...
Dynamic stress intensity factor (Mode I) of a permeable penny-shaped crack in a fluid-saturated poroelastic solid
1
2017
... 重大装备关键零部件冲击断[1 ] 裂、强冲击下建筑物毁伤评估、作战设备冲击防护、高速冲击下材料层/断裂[2 ] 、以及武器跌落与炸药低冲击起爆等应用问题中均涉及动力学裂纹扩展问题. 准确描述裂纹尖端附近应力奇异场, 对于裂纹起始时间与扩展速度评估尤为重要[3 ] . 其中, 动态应力强度因子(dynamic stress intensity factor, DSIF)作为线弹性断裂力学中裂纹尖端应力场与位移场的主要描述参数, 研究其计算方法, 分析其影响参数, 提高其计算精度有着重要的科学意义与工程价值. ...
黏弹性功能梯度材料裂纹问题的有限元方法
2
2013
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... 传统FEM[4 ] 模拟裂纹扩展时, 裂纹必须与网格对齐, 裂纹扩展步长依赖于网格尺寸, 为捕捉裂尖应力奇异性需要布置稠密网格, 裂纹扩展过程中需要不断重新划分网格等. 频繁的网格重分重映不仅使得计算实施繁琐, 同时引入大量映射误差, 导致算法在计算动力学问题时能量守恒性差. 因此, 裂纹扩展模拟成为传统有限元经典难题之一. ...
黏弹性功能梯度材料裂纹问题的有限元方法
2
2013
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... 传统FEM[4 ] 模拟裂纹扩展时, 裂纹必须与网格对齐, 裂纹扩展步长依赖于网格尺寸, 为捕捉裂尖应力奇异性需要布置稠密网格, 裂纹扩展过程中需要不断重新划分网格等. 频繁的网格重分重映不仅使得计算实施繁琐, 同时引入大量映射误差, 导致算法在计算动力学问题时能量守恒性差. 因此, 裂纹扩展模拟成为传统有限元经典难题之一. ...
应变局部化分析的嵌入强间断多尺度有限元法
1
2017
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
应变局部化分析的嵌入强间断多尺度有限元法
1
2017
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
Numerical simulation of crack growth in piezoelectric structures by BEM
1
2017
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
Basic research on simulation for 3D crack growth by mesh free BFM
1
2016
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
New enrichments in XFEM to model dynamic crack response of 2-D elastic solids
2
2016
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
模拟三维裂纹问题的自适应多尺度扩展有限元法
1
2016
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
模拟三维裂纹问题的自适应多尺度扩展有限元法
1
2016
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
基于ABAQUS平台的水力裂缝扩展有限元模拟研究
1
2016
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
基于ABAQUS平台的水力裂缝扩展有限元模拟研究
1
2016
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
动载下缝端应力强度因子计算的扩展有限元法
6
2013
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... [11 -18 ], 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... (27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项. ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
动载下缝端应力强度因子计算的扩展有限元法
6
2013
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... [11 -18 ], 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... (27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项. ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
动载下裂纹应力强度因子计算的数值流形元法
4
2014
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... (27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项. ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
动载下裂纹应力强度因子计算的数值流形元法
4
2014
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... (27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项. ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
The moving least squares based numerical manifold method for vibration and impact analysis of cracked bodies
1
2018
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
比例边界有限元法求解裂纹面接触问题
1
2017
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
比例边界有限元法求解裂纹面接触问题
1
2017
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
Dynamic crack propagation with a variational phase-field model: Limiting speed, crack branching and velocity-toughening mechanisms
1
2017
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
基于混合方法的二维水力压裂数值模拟
1
2015
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
基于混合方法的二维水力压裂数值模拟
1
2015
... 目前裂纹分析方法有很多, 比如传统有限元法(FEM) [4 ] 、多尺度有限元法[5 ] 、边界元法(BEM) [6 ] 、无网格法(MLM) [7 ] 、扩展有限元法(XFEM) [8 ,9 ,10 ,11 ] 、数值流形法(NMM) [12 ,13 ] 、比例边界有限元法(SBFEM) [14 ] 、相场模型(phase-field model) [15 ] 、混合方法[16 ] 等, 其中被工业界广泛接受的方法主要为传统有限元法和扩展有限元法; 相关商业断裂软件包括FRANC3D, ZENCRACK, Abaqus及ANSYS等. ...
Partition of unity method
1997
Linear dependence problems of partition of unity based generalized FEMs
1
2006
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
Stable GFEM (SGFEM): Improved conditioning and accuracy of GFEM/XFEM for three-dimensional fracture mechanics
2015
Strongly stable generalized finite element method: Application to interface problems
2017
A well-conditioned and optimally convergent XFEM for 3D linear elastic fracture
2016
Stable 3D XFEM/vector level sets for non-planar 3D crack propagation and comparison of enrichment schemes
2018
Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment
6
2003
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... [23 -24 ]; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... [23 ,25 -26 ]. 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... [23 ]. ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
... 这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23 -24 ,38 -43 ] , 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39 ] . ...
An explicit dynamics extended finite element method. Part 1: Mass lumping for arbitrary enrichment functions
6
2009
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... [24 ]提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... 这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23 -24 ,38 -43 ] , 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39 ] . ...
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
... [24 ,39 -41 ]对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
... Kalthoff实验常常作为检验动态裂纹扩展模拟准确性的标准算例[24 ,38 -42 ] . 在实验中, 一个初速度V 0 的弹体去冲击一含两个对称边裂纹的平板, 如图14 所示, 两裂纹间距与弹体直径相对应. 其中L=100mm , H =200mm , a =50mm, 材料密度$\rho = 8000 {kg/m}^{3}$, $E=190 {GPa}$, $v=0.3$. 断裂韧度$K_{IC}=68~{MPa}\cdot \sqrt{m}$. 弹体冲击速度为: $V_{0}=20 {m/s}$. 考虑4 种计算网格, 分别为19×19, 39×39, 79×79 和199×199, 时间步长分别取为2 μs, 1 μs, 1 μs和0.5 μs, 集中质量矩阵, 模拟时间为$1.0\times10^{-4}~{s}$. 在低速冲击下, 该实验裂纹最终扩展路径与水平方向夹角在70° 左右. 裂纹扩展速度 a ̇
An energy-conserving scheme for dynamic crack growth using the extended finite element method
6
2005
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... 对于线弹性各向同性材料, 动态相互作用积分可表述为[25 ] ...
... 其中, $\left( {\sigma _{ij}^{{\rm{real}}},\varepsilon _{ij}^{{\rm{real}}},u_i^{{\rm{real}}}} \right)$为真实场, $\left( {\sigma _{ij}^{{\rm{aux}}},\varepsilon _{ij}^{{\rm{aux}}},u_i^{{\rm{aux}}}} \right)$为动力学裂纹辅助场; $W_{}^{({\rm{real, aux}})} = \sigma _{ij}^{{\rm{real}}}\varepsilon _{ij}^{{\rm{aux}}} = \sigma _{ij}^{{\rm{aux}}}\varepsilon _{ij}^{{\rm{real}}}$为相互作用积分应变能密度; $A$是相互作用积分区域, 为了精确计算应力强度因子, 相互作用积分区域采用图3 所示的环绕裂纹尖端的$4\times4$个额外单元, 又称为[25 -26 , 38 -42 ] . 这些单元仅用于计算动态相互作用积分, 独立于原计算网格, 且跟随裂纹尖端移动; $q$ 为虚拟裂纹扩展场, 其方向平行于裂纹表面 ...
... 本节将给出计算动态应力强度因子用到的所有辅助场信息, 对Freund[37 ] 和Réthoré等[25 ] 的相关工作进行推导和总结. 限于篇幅, 本文仅以I型裂纹为例. ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
XFEM a good candidate for energy conservation in simulation of brittle dynamic crack propagation
3
2008
... XFEM[8 -11 ] 因克服上述传统FEM困难而获得极大成功,目前已成为裂纹扩展模拟的主要方法之一. 然而, 在实际工程应用中, 该方法一直存在两大困扰: 一是源于单位分解插值的线性相关性[11 -18 ] , 当在局部或全求解域上进行插值强化时, 总体刚度矩阵高度病态[19-22]; 二是裂尖强化插值无法直接推广应用于动力学计算[23 -26 ] . 其中第2个问题具体又体现在: (1) 裂尖额外自由度引起"零时间步长"问题——当裂纹位置逐渐靠近强化节点时, 单元的临界时间步长会趋于零[23 -24 ] ; (2) 裂尖额外自由度引起能量正确传递问题. "零时间步长"问题直到2009 年Elguedj等[24 ] 提出裂尖质量集中技术才得以解决. 能量正确传递问题在于: 额外自由度对应的质量、速度和加速度项均与裂尖位置历史相关; 当裂尖离开单元时, 如果简单地舍弃原有裂尖强化自由度, 两个时间步之间的能量无法正确传递, 会破坏能量守恒原则[23 ,25 -26 ] . 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... -26 ]. 这一问题长期困扰XFEM在动力学问题中的应用[23 ] . ...
... 其中, $\left( {\sigma _{ij}^{{\rm{real}}},\varepsilon _{ij}^{{\rm{real}}},u_i^{{\rm{real}}}} \right)$为真实场, $\left( {\sigma _{ij}^{{\rm{aux}}},\varepsilon _{ij}^{{\rm{aux}}},u_i^{{\rm{aux}}}} \right)$为动力学裂纹辅助场; $W_{}^{({\rm{real, aux}})} = \sigma _{ij}^{{\rm{real}}}\varepsilon _{ij}^{{\rm{aux}}} = \sigma _{ij}^{{\rm{aux}}}\varepsilon _{ij}^{{\rm{real}}}$为相互作用积分应变能密度; $A$是相互作用积分区域, 为了精确计算应力强度因子, 相互作用积分区域采用图3 所示的环绕裂纹尖端的$4\times4$个额外单元, 又称为[25 -26 , 38 -42 ] . 这些单元仅用于计算动态相互作用积分, 独立于原计算网格, 且跟随裂纹尖端移动; $q$ 为虚拟裂纹扩展场, 其方向平行于裂纹表面 ...
Extra-dof-free and linearly independent enrichments in GFEM
2
2013
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
Improved XFEM-An extra-DOF free, well- conditioning, and interpolating XFEM
2
2015
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
Improved XFEM: Accurate and robust dynamic crack growth simulation
5
2016
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
... 由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29 ,30 ,31 ] . ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
改进型XFEM综述
3
2016
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
... 由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29 ,30 ,31 ] . ...
改进型XFEM综述
3
2016
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
... 由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29 ,30 ,31 ] . ...
改进型扩展有限元法及其并行程序实现. [博士论文]
4
2017
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
... 由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29 ,30 ,31 ] . ...
... 其中, ${{D}}$为弹性矩阵, $\tilde H = H({{x}}) - H({{{x}}_i})$ , ${\tilde N_i}$为经过混合单元修正后的有限元形函数, 限于篇幅, 详细内容可参见文献[31 ] . ...
改进型扩展有限元法及其并行程序实现. [博士论文]
4
2017
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
... 由于无裂尖加强自由度, 改进型XFEM在动力学计算中, 裂尖加强单元可以直接采用标准有限元的集中质量矩阵; 同样, 由于无裂尖相关额外自由度,故无需常规XFEM为保证裂尖额外自由度上能量正确传递的特殊处理(动态裂纹扩展中)[29 ,30 ,31 ] . ...
... 其中, ${{D}}$为弹性矩阵, $\tilde H = H({{x}}) - H({{{x}}_i})$ , ${\tilde N_i}$为经过混合单元修正后的有限元形函数, 限于篇幅, 详细内容可参见文献[31 ] . ...
基于改进型XFEM的裂纹分析并行软件实现
2
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
基于改进型XFEM的裂纹分析并行软件实现
2
... 为克服XFEM上述两大困难, 笔者提出一种无裂尖额外自由度、条件性态良好的改进型扩展有限元法[27 ,28 ,29 ,30 ,31 ,32 ] , 并将其用于静、动力学裂纹扩展分析. 该方法消除了裂尖额外自由度, 解决了现有XFEM线性依赖性和总体方程病态问题, 总体刚度矩阵条件数恢复了h-2 (XFEM为h-6 ) 变化的性质. 同时, 由于没有裂尖额外自由度, 裂尖单元的质量集中、零时间步长及能量正确传递问题均得到解决. ...
... 改进型XFEM基于无额外自由度单位分解法[27 ] , 消除了裂尖额外自由度, 可以达到最优收敛且整体方程条件属性良好[28 ,29 ,30 ,31 ,32 ] , 其位移逼近可表示为如下形式 ...
压电材料二维动应力强度因子的扩展有限元计算
2
2013
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... (27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项. ...
压电材料二维动应力强度因子的扩展有限元计算
2
2013
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... (27) 式(26)中第1项为静力学裂纹的相互作用积分公式, 第2项为动力学稳定裂纹分析所考虑的惯性项贡献[11 -12 ,33 ] , 后两项这里称为扩展速度贡献项. ...
一种新型裂尖加强函数的显式动态扩展有限元法
2
2017
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
一种新型裂尖加强函数的显式动态扩展有限元法
2
2017
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
2
2012
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
2
2012
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
2
2014
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
2
2014
... 目前国内关于动力学裂纹扩展的研究尚少. 江守燕等[11 ] 使用XFEM对稳定裂纹的DSIF进行分析; 杨永涛等[12 ] 基于NMM分析了稳定裂纹的DSIF; 刘鹏等[33 ] 研究压电材料中裂纹的DSIF计算方法; 刘学聪等[34 ] 给出一种新型裂尖加强函数用于显式动态裂纹分析, 将节点的奇异附加自由度由8 个减少为2个. 更多内容, 可参考庄茁等[35 ] 与余天堂[36 ] 的XFEM专著. 目前中文文献中对DSIF 的分析还多集中于稳定裂纹, 很少见之于扩展裂纹. 即便考虑裂纹扩展, 也未考虑裂纹扩展速度的影响. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
Dynamic Fracture Mechanics.
4
1990
... 本节将给出计算动态应力强度因子用到的所有辅助场信息, 对Freund[37 ] 和Réthoré等[25 ] 的相关工作进行推导和总结. 限于篇幅, 本文仅以I型裂纹为例. ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
... Freund[37 ,45 ] 给出了如下等效动态应力强度因子与裂纹扩展速度的关系式 ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
Efficient explicit time stepping for the extended finite element method
6
2006
... 其中, $\left( {\sigma _{ij}^{{\rm{real}}},\varepsilon _{ij}^{{\rm{real}}},u_i^{{\rm{real}}}} \right)$为真实场, $\left( {\sigma _{ij}^{{\rm{aux}}},\varepsilon _{ij}^{{\rm{aux}}},u_i^{{\rm{aux}}}} \right)$为动力学裂纹辅助场; $W_{}^{({\rm{real, aux}})} = \sigma _{ij}^{{\rm{real}}}\varepsilon _{ij}^{{\rm{aux}}} = \sigma _{ij}^{{\rm{aux}}}\varepsilon _{ij}^{{\rm{real}}}$为相互作用积分应变能密度; $A$是相互作用积分区域, 为了精确计算应力强度因子, 相互作用积分区域采用图3 所示的环绕裂纹尖端的$4\times4$个额外单元, 又称为[25 -26 , 38 -42 ] . 这些单元仅用于计算动态相互作用积分, 独立于原计算网格, 且跟随裂纹尖端移动; $q$ 为虚拟裂纹扩展场, 其方向平行于裂纹表面 ...
... 在动力学分析中等效动态应力强度因子可表述为[34 ,35 ,36 ,37 ,38 ] ...
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
... 这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23 -24 ,38 -43 ] , 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39 ] . ...
... Kalthoff实验常常作为检验动态裂纹扩展模拟准确性的标准算例[24 ,38 -42 ] . 在实验中, 一个初速度V 0 的弹体去冲击一含两个对称边裂纹的平板, 如图14 所示, 两裂纹间距与弹体直径相对应. 其中L=100mm , H =200mm , a =50mm, 材料密度$\rho = 8000 {kg/m}^{3}$, $E=190 {GPa}$, $v=0.3$. 断裂韧度$K_{IC}=68~{MPa}\cdot \sqrt{m}$. 弹体冲击速度为: $V_{0}=20 {m/s}$. 考虑4 种计算网格, 分别为19×19, 39×39, 79×79 和199×199, 时间步长分别取为2 μs, 1 μs, 1 μs和0.5 μs, 集中质量矩阵, 模拟时间为$1.0\times10^{-4}~{s}$. 在低速冲击下, 该实验裂纹最终扩展路径与水平方向夹角在70° 左右. 裂纹扩展速度 a ̇
... 图15 给出了不同网格裂纹扩展路径与裂纹长度随时间变化曲线的结果对比. 显然, 裂纹最终路径和裂纹扩展速度随着网格加密最终收敛. 裂纹扩展方向与水平方向夹角在67°左右. 初始扩展方向约70°, 最终沿大约67°方向贯穿整个靶板. 结果与文献[38 -42 , 44 ] 结果一致. ...
Time dependent crack tip enrichment for dynamic crack propagation
2
2010
... 这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23 -24 ,38 -43 ] , 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39 ] . ...
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
Smoothed nodal forces for improved crack propagation modeling in XFEM
1
2010
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
An explicit dynamics extended finite element method. Part 2: Element-by-element stable-explicit/explicit dynamic scheme
2
2009
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
... -41 ]对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
An XFEM/Spectral element method for dynamic crack propagation
4
2011
... 其中, $\left( {\sigma _{ij}^{{\rm{real}}},\varepsilon _{ij}^{{\rm{real}}},u_i^{{\rm{real}}}} \right)$为真实场, $\left( {\sigma _{ij}^{{\rm{aux}}},\varepsilon _{ij}^{{\rm{aux}}},u_i^{{\rm{aux}}}} \right)$为动力学裂纹辅助场; $W_{}^{({\rm{real, aux}})} = \sigma _{ij}^{{\rm{real}}}\varepsilon _{ij}^{{\rm{aux}}} = \sigma _{ij}^{{\rm{aux}}}\varepsilon _{ij}^{{\rm{real}}}$为相互作用积分应变能密度; $A$是相互作用积分区域, 为了精确计算应力强度因子, 相互作用积分区域采用图3 所示的环绕裂纹尖端的$4\times4$个额外单元, 又称为[25 -26 , 38 -42 ] . 这些单元仅用于计算动态相互作用积分, 独立于原计算网格, 且跟随裂纹尖端移动; $q$ 为虚拟裂纹扩展场, 其方向平行于裂纹表面 ...
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...
... Kalthoff实验常常作为检验动态裂纹扩展模拟准确性的标准算例[24 ,38 -42 ] . 在实验中, 一个初速度V 0 的弹体去冲击一含两个对称边裂纹的平板, 如图14 所示, 两裂纹间距与弹体直径相对应. 其中L=100mm , H =200mm , a =50mm, 材料密度$\rho = 8000 {kg/m}^{3}$, $E=190 {GPa}$, $v=0.3$. 断裂韧度$K_{IC}=68~{MPa}\cdot \sqrt{m}$. 弹体冲击速度为: $V_{0}=20 {m/s}$. 考虑4 种计算网格, 分别为19×19, 39×39, 79×79 和199×199, 时间步长分别取为2 μs, 1 μs, 1 μs和0.5 μs, 集中质量矩阵, 模拟时间为$1.0\times10^{-4}~{s}$. 在低速冲击下, 该实验裂纹最终扩展路径与水平方向夹角在70° 左右. 裂纹扩展速度 a ̇
... 图15 给出了不同网格裂纹扩展路径与裂纹长度随时间变化曲线的结果对比. 显然, 裂纹最终路径和裂纹扩展速度随着网格加密最终收敛. 裂纹扩展方向与水平方向夹角在67°左右. 初始扩展方向约70°, 最终沿大约67°方向贯穿整个靶板. 结果与文献[38 -42 , 44 ] 结果一致. ...
Dynamic fracture with meshfree enriched XFEM
2
2010
... 含I型裂纹的受拉的半无限大板问题是动态强度因子精度分析的经典算例 [11 -12 , 23 -25 , 29 , 38 -43 ] . 问题模型如图4 所示, 板长$L=10 {m}$, 高H = 2 m, 裂纹长度$a=5 {m}$, 材料密度$\rho = 8000 {kg/m}^{3}$, E = 210 GPa, v = 0.3. 平面应变假设. 在t = 0 时刻, 板上缘受到突然施加大小为$\sigma_{0} = 500 {kPa}$ 均布拉应力作用. 该问题的动态应力强度因子解析解为[37 ] ...
... 这是一个富有挑战性的算例, XFEM的很多文献对这个问题进行了模拟分析[23 -24 ,38 -43 ] , 但是得到的动态应力强度因子结果总是存在工程不可接受的数值震荡[39 ] . ...
Modes of dynamic shear failure in solids
1
2000
... 图15 给出了不同网格裂纹扩展路径与裂纹长度随时间变化曲线的结果对比. 显然, 裂纹最终路径和裂纹扩展速度随着网格加密最终收敛. 裂纹扩展方向与水平方向夹角在67°左右. 初始扩展方向约70°, 最终沿大约67°方向贯穿整个靶板. 结果与文献[38 -42 , 44 ] 结果一致. ...
Crack propagation in an elastic solid subjected to general loading. Pt. 1. Constant rate of extension
2
1972
... Freund[37 ,45 ] 给出了如下等效动态应力强度因子与裂纹扩展速度的关系式 ...
... 其中, $c_{r}$为瑞雷波速, ${K_{IC}}$ 为材料断裂韧度. Freund与合作者 [45 ,46 ,47 ] 通过实验验证了该公式的正确性. 假设每个时间步中裂纹扩展速度不变, 则裂纹扩展步长可近似表述为$\Delta a = \dot a\Delta t$ , 其中$\Delta t$ 是每一步的时间步长. 裂纹的扩展方向可以根据最大周向应力准则得到 ...
Influence of inertia on elastic-plastic antiplane-shear crack growth
1
1982
... 其中, $c_{r}$为瑞雷波速, ${K_{IC}}$ 为材料断裂韧度. Freund与合作者 [45 ,46 ,47 ] 通过实验验证了该公式的正确性. 假设每个时间步中裂纹扩展速度不变, 则裂纹扩展步长可近似表述为$\Delta a = \dot a\Delta t$ , 其中$\Delta t$ 是每一步的时间步长. 裂纹的扩展方向可以根据最大周向应力准则得到 ...
Optical measurement of the plastic strain concentration at a crack tip in a ductile steel plate
1
1982
... 其中, $c_{r}$为瑞雷波速, ${K_{IC}}$ 为材料断裂韧度. Freund与合作者 [45 ,46 ,47 ] 通过实验验证了该公式的正确性. 假设每个时间步中裂纹扩展速度不变, 则裂纹扩展步长可近似表述为$\Delta a = \dot a\Delta t$ , 其中$\Delta t$ 是每一步的时间步长. 裂纹的扩展方向可以根据最大周向应力准则得到 ...
A combined space-time extended finite element method
1
2005
... 对于震荡的原因, 目前还没有统一的认识, 主要包含如下几个方面: 裂纹跨越单元时,单元逼近函数的跳变[29 ,40 ] ; 裂纹扩展过程中能量一致性问题[24 -25 ,41 ] ; 时间离散精度不够[48 ] ; 低阶有限元引起的应力波频散[42 ] 等. 图13 将本文计算结果与其中经典文献[24 ,39 -41 ] 对于该问题的的计算结果进行了比较. 比较表明, 改进型XFEM给出该问题目前为止震荡最小、精度最好的数值解答. ...