引言

随着科技的发展,新材料的广泛使用,各种工程建筑和结构^[1,2]不断涌现,研究其力学行为以保障安全就显得尤为重要. 弹塑性断裂力学已经在工程结构设计中得到切实应用,航空部门提出了损伤容限设计思想,在选材方面有了专门的指导手册,美国电力研究院发展了以J积分为基础的弹塑性缺陷评估方法,称为EPRI方法^[3,4,5].J积分是一个定义明确,理论严密的应力、应变场参量,与线弹性断裂力学中的应力强度因子一样,J积分既能表征裂纹尖端区域应力、应变场的程度,又因与加载过程中的能量相关而容易通过实验来测定,是弹塑性断裂力学的基础参量^[6].

对于平面应变条件下断裂韧性 Jc测试,现已发展的较为成熟,Zhu等^[7]从线弹性断裂力学和弹塑性断裂力学的角度对金属材料的断裂韧性测试、评定和标准化进行了较为详细的技术综述,嵇醒^[8]对断裂力学中的判据作了扼要的综述,归纳出断裂力学判据中目前还没有较好解决的几个问题. 在现有断裂韧性评定方法中,最常见的是采用裂纹尖端具有高约束度的标准紧凑拉伸(compact tension,CT)试样或单边裂纹弯曲(single edged notched bending,SEB)试样进行断裂力学试验以获取J,这些试样已在若干测试标准^[9,10,11]中得到推荐,其中CT试样使用最广,已经涉及到蠕变分析^[12]、残余应力分析^[13]、复合材料^[14]断裂韧性测试等方面. 由Feddern和Macherauch^[15]提出的圆形紧凑拉伸试样(round compact tensile,RCT)是一种对圆棒材料裂韧性测试非常方便的试样,目前已运用到各种合金的疲劳裂纹扩展研究^[16,17]. 单边裂纹拉伸(single edged notched tension,SENT)试样因其约束特性与含裂纹管道材料约束性相近而在管道材料的断裂韧度评定中得到重视^[18,19],该试样对焊接材料的力学性能测试^[20]同样方便. 小尺寸构件不仅取样方便且能有效降低试验成本,因而研究非标准小试样具有重要理论意义和工程应用价值. Bao等^[21]开发了一种实际尺寸仅有一元硬币大小的含内侧边裂纹C形拉伸 (C-shaped inside edge-notched tension,CIET)小试样,实现了金属材料的疲劳裂纹扩展和断裂行为测试. 但晨等^[22]基于量纲一载荷分离理论建立了可用于测 定CIET试样延性断裂行为的规则化法,并完成了J阻力曲线测试. 双边裂纹板拉伸(double edge crack tension,DECT)试样也是一种在研究中使用较多的裂纹构元^[23].

现有的方法中,对于J积分的计算可以分为两大类：一类是按照简化模型或者工程估算方法进行计算,如EPRI法,另一类是通过有限元分析(finite element analysis,FEA)或者实验方法获取J积分值,如柔度法. EPRI手册J积分估算法的关键是将弹塑性J积分分解为弹性 Je和塑性 Jp两部分^[24,25,26],即

$J = J_{\rm e} + J_{\rm p} $(1)

其中弹性部分为

$J_{\rm e} = f_1 (a_{\rm e} )\dfrac{P^2}{{E}'} $(2)

式中, E'=E/(1-ν2)对应平面应变问题, E'=E对应平面应力问题; E为弹性模量; ν为泊松比. f1为与试件裂纹 大小、位置等因素有关的形状函数, ae为修正的有效裂纹长度. 塑性部分^[27]表示为

$J_{\rm p}= \alpha \sigma _0 \varepsilon _0 ch_1 \left( {\dfrac{P}{P_0 }}\right)^{n + 1} $(3)

式中, α为材料硬化系数, σ0和 ε0为屈服应力和屈服应变, n为硬化指数, c为试样剩余韧带宽度, P0为试样的参考屈服载荷; h1为 J积分全塑性解的函数,它与材料、结构、载荷以及裂纹尺寸有关. 通过有限元计算,可以得到 h1的值,EPRI手册针对多种试样提供了 h1随 n、试样几何尺寸变化的系列离散数据表格.

在断裂韧性试验时, 若采用ASTM E1820-15^[28],J积分的弹性分量 Je表示为

$J_{\rm e} = \dfrac{K^2}{{E}'} (4)$

式中, K为应力强度因子,塑性分量为

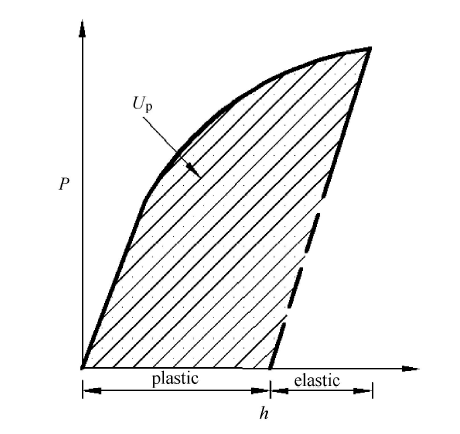
$J_{\rm p} = \eta \dfrac{U_{\rm p} }{B_{\rm N} b} $(5)

式中, b表示剩余韧带厚度, BN表示试样净厚度, Up表示塑性功如图1所示,可由载荷( P)和加载线位移( h)的试验曲线获得, η为无量纲塑性因子^[29,30]. η因子多由有限元法分析确定^[31],其步骤为建立有限元网格模型,设置材料属性,施加约束及载荷,提交运算,进而提取 J积分值,减去由 K因子得到的弹性部分,而根据 式(5)逆向求解. 在平面应变下, η近似与几何尺寸相关,在一般三维约束条件下, η不仅与几何尺寸相关,也与 n相关,但要获得 η的关于几何尺寸、硬化指数的统一表达式十分困难.

显示原图| 下载原图ZIP| 生成PPT

图1   塑性功示意图

Fig. 1   The schematic diagram of plastic work

考虑Rice在1968年针对I型裂纹构元提出的定义式^[32]

$J = - \Big(\dfrac{\partial U}{B\partial a} \Big) $(6)

式中, B表示试样厚度, a为裂纹长度. 本文基于Chen-Cai能量等效假设,采用 J积分能量定义式(6),针对不同几何的I型裂纹,提出了 J积分的工程半解析表征方法,得到 J积分和载荷-位移的半解析统一公式.

1 单向加载下构元弹塑性问题的半解析方法

Chen和Cai^{[33,34,35,36]}通过建立变形域的应变能与积分中值点位置的材料RVE(representative volume element)的应变能密度与变形域有效体积等效,以及考虑Mises等效使得复杂应力状态下RVE能量密度与单轴应力状态下RVE能量密 度等效,进而建立反映连续固体的能量、载荷、位移和材料本构关系参数关系的通用模型.

对于幂硬化材料,考虑Ramberg-Osgood应力应变关系,即

$\varepsilon = \dfrac{\sigma }{E} + \Big (\dfrac{\sigma }{C_K } \Big)^N $(7)

式中, ε表示应变, σ表示应力, CK表示应力强度系数, N表示应力硬化指数,对于纯塑性材料,有

$\varepsilon _{\rm p} =\Big (\dfrac{\sigma }{C_K } \Big)^N $(8)

由Chen-Cai能量等效假设,可得塑性应变能 Up为

$U_{\rm p } = \dfrac{NC_K }{N + 1}V_{\rm P} \varepsilon _{\rm p}^{1 / N + 1} = \dfrac{NC_K V^\ast }{N + 1}\dfrac{V_{\rm P} }{V^\ast }\varepsilon _{\rm p p}^{1 / N + 1} $(9)

式中, V表示变形域有效体积, V*表示特征体积,且 V*=A*h*, A*为特征面积, h*表示特征位移. 特征体积、特征面积、特征位移旨在用于实现不同 a/W条件下载荷、位移、应变、能量的无量纲化. 对材料的塑性有效体积和塑性等效应变做如下幂律假定

$\left. \begin{array}{l} \dfrac{V_{\rm p} }{V^\ast } = k_1 (\dfrac{h_{\rm p} }{h^\ast })^{k_2 } \\ \varepsilon _{\rm p} = k_3 (\dfrac{h_{\rm p} }{h^\ast })^{k_4 } \end{array}\!\! \right\} $(10)

其中, k1和 k2分别为有效体积系数和指数, k3和 k4分别为有效应变系数和指数, hp表示加载点在加载方向移塑性位移, h*表示特征位移,将式(10)代入式(9)可得

$U_{\rm p} = \dfrac{NC_K V^\ast }{N + 1}k_1 k_3^{1 + 1 / N} \Big(\dfrac{h_{\rm p} }{h^\ast } \Big )^{k_4 / N + k_4 + k_2 } $(11)

求导可得载荷 P的半解析公式

$ P = \dfrac{\partial U_{\rm p} }{\partial h_{\rm p} } = \dfrac{NC_K V^\ast}{(N + 1)h^\ast }k_1 k_3^{1 + 1 / N} \cdot \\ \Big (\dfrac{k_4 }{N} + k_4 + k_2\Big ) \Big (\dfrac{h_{\rm p} }{h^\ast }\Big)^{k_4 / N + k_4 + k_2 - 1} $(12)

整理可得,在塑性状态下材料的应变能与载荷、位移之间的关系为

$\left.\begin{array}{ll} \dfrac{U_{\rm p} }{U_{\rm p}^\ast } =\left\{\begin{array} \Big (\dfrac{h_{\rm p} }{h^\ast } \Big )^{m_{\rm p} + 1} \\ \Big (\dfrac{P}{P_{\rm p}^{\ast } } \Big)^{1 / m_{\rm p} + 1} \end{array}\right. \\ \dfrac{P}{P_{\rm p}^{\ast } } = \Big (\dfrac{h_{\rm p} }{h^\ast } \Big )^{m_{\rm p} } \end{array} \right\} $(13)

其中

$\left.\begin{array}{l} U_{\rm p} ^{\ast } = \dfrac{NC_K V^\ast }{N + 1}k_1 k_3^{1 + 1 / N} \\ m_{\rm p} = \dfrac{k_4 }{N} + k_4 + k_2 - 1 \\ P_{\rm p}^{\ast } = \dfrac{(1 + m_{\rm p} )NC_K V^\ast }{(N + 1) h^\ast }k_1 k_3^{1 + 1 / N} \end{array}\!\! \right\} $(14)

类似地,在线弹性范围内可以得到材料的弹性能与载荷、位移之间的关系为

$\left.\begin{array}{ll} \dfrac{U_{\rm e} }{U_{\rm e}^\ast }=\left\{\begin{array} \Big (\dfrac{h_{\rm e} }{h^\ast }\Big)^2 \\ \Big (\dfrac{P }{P_{\rm e}^\ast }\Big)^2 \end{array}\right. \\ \dfrac{P }{P_{\rm e}^\ast } = \dfrac{h_{\rm e} }{h^\ast } \end{array} \right\} $(15)

式中

$ \left. \begin{array}{l} U_{\rm e} ^{\ast} = \dfrac{k_0 EV^\ast }{2} \\ P_{\rm e}^{\ast} = k_0 EA^\ast \end{array} \right\} $(16)

2 I型裂纹构元的半解析统一公式

对于弹塑性变形,在单向加载下裂纹构元的总能量可以通过弹性能和塑性能进行工程叠加获得,即

U(P,h)=Ue(P,he)+Up(P,hp)(17)

加载线位移

h(P)=he(P)+hp(P)(18)

将式(13)和式(15)代入式(18)即可得裂纹构元的载荷-位移统一公式

$\Big(\dfrac{PA_1 }{A^\ast }\Big)^{\tfrac{1}{m_{\rm p} }} + \dfrac{PA_2 }{A^\ast }= \dfrac{h}{h^\ast } $(19)

式中

$ \left. \begin{array}{l} A_1 = \dfrac{(1 + N)}{(1 + m_{\rm p} )NC_K k_1 k_3^{1 + 1 / N} } \\ A_2 = \dfrac{1}{k_0 E} \end{array} \right\} $(20)

且

$ \left.\begin{array}{l} A\ast = WB \Big(1 - \dfrac{a}{W} \Big)^m \\ h\ast = W \\ V\ast = W^2B\Big(1 - \dfrac{a}{W} \Big)^m \end{array} \right\} $(21)

式(21)中 W表示试样宽度, m表示与裂纹长度 a相关的特征体积折减系数,对于特定的裂纹构元,其值可固定为一个适当的常数. 联立式(13)、式(15)和式(17)得到弹塑性条件下应变能为

$ U = W^2B \Big(1 - \dfrac{a}{W}\Big)^m\left[ \dfrac{NC_K }{N + 1}k_1 k_3^{1 + 1 / N} \Big(\dfrac{P}{P_{\rm p}^{\ast}} \Big)^{1 / m_{\rm p} + 1} +\right. \\ \left. \dfrac{k_0 E}{2} \Big(\dfrac{P }{P_{\rm e}^\ast }\Big)^2 \right] $(22)

联立式(22)和式(6),可得裂纹构元的 J积分-载荷统一公式为

$ J = \Big (1 - \dfrac{a}{W}\Big)^{m - 1}\Big [a_1 \Big (\dfrac{P}{P_{\rm p}^\ast}\Big)^{a_2 } + a_3 \Big (\dfrac{P}{P_{\rm e}^\ast }\Big)^2\Big] $(23)

式中

$\left.\begin{array}{ll} a_1 = Wm\dfrac{NC_K }{N + 1}k_1 k_3^{1 + 1 / N} \\ a_2 = 1 + \dfrac{1}{m_{\rm p} } \\ a_3 = Wm\dfrac{k_0 E}{2} \end{array}\right\} $(24)

如式(23)所示的 J积分-载荷统一公式, k0~k4皆为式(14)和式(16)中的未知参数,可通过载荷位移曲线获取. 同时, J积分统一公式又可以表示成如下无量纲化形式

$ \dfrac{J}{J^\ast } = a_4 \Big (\dfrac{P}{P^\ast }\Big)^{a_2 } + a_5 \Big (\dfrac{P}{P^\ast }\Big)^2 $(25)

式中

$\left.\begin{array}{ll} P^\ast = (P_{\rm p}^\ast P_{\rm e}^\ast )^{0.5} \\ J^\ast = Wm \Big(1 - \dfrac{a}{W} \Big)^{m - 1}C_K \end{array} \right\} $(26)

$ \left. \begin{array}{l} A = \dfrac{P_{\rm e}^\ast }{P_{\rm p}^\ast } = \dfrac{(N + 1)Ek_0}{(1 + m_{\rm p} )NC_K k_1 k_3^{1 + 1 / N} } \\ a_4 = \dfrac{NA^{\tfrac{1}{2}(1 + \tfrac{1}{m_{\rm p} })}}{N + 1}k_1 k_3^{1 +1 / N} \\ a_5 = \dfrac{(1 + m_{\rm p} )N}{2 (N + 1)} k_1 k_3^{1 + 1 / N} \end{array} \right\} $(27)

对于 h不是加载线位移的I型裂纹构元情形,上述公式的形式依然可假定成立.

3 J积分公式参数的确定方法

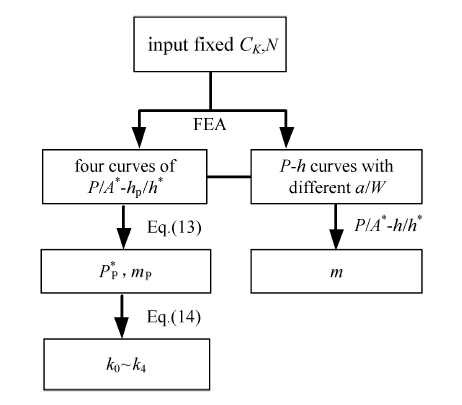
采用有限元分析通过少量计算即可获得 J积分统一公式参数,其计算过程如图2所示. 采用有限元软件ANSYS14.5计算6种I型 裂纹构元的 J积分统一公式的参数,全部采用平面应变条件,模型单元采用plane183单元,泊松比 υ=0.3,应力强度系数 CK=1000MPa,线弹性计算时取弹性模量 E=210GPa. 表1给出了各裂纹构元的尺寸,现以CT试样为例说明参数求解过程.

显示原图| 下载原图ZIP| 生成PPT

图2   参数获取流程框图

Fig. 2   Flow chart of parameters acquisition

Table 1

表 1

表 1   各类裂纹构元的尺寸

Table 1   The size of various cracked components

新窗口打开

有限元分析中,单元网格的划分对计算结果可能存在影响,本文对不同的裂尖网格密度条件下的载荷位移曲线进行了比较. 定义裂尖2 mm×1 mm范围网格数量为104时为一倍网格密度,在此基础上对裂尖区域网格加密,其余部分网格密度不变. 图3给出了网格密度对载荷位移曲线的影响,结果表明采用一倍网格时已经满足计算要求.

显示原图| 下载原图ZIP| 生成PPT

图3   裂尖网格对载荷位移曲线的影响

Fig. 3   Effect of crack tip grid on load-displacement curves

如图2的流程图所示,在有限元软件前处理时输入相应参数,计算得到不同 a/W条件下的载荷位移曲线,进行几何无关 处理( P/A*-h/h*)后可得参数 m,同时求得 a/W的适用范围,结果如图4所示. 对模型进行全塑性计算(文中模型均取 a/W=0.5),根据 式(13),可得 Pp*和 mp,并将其代入 式(14)即可得到 k1~k4,对模型进行线弹性计算,根据 式(15)可求得 k0.

计算出CT试样 J积分统一公式中各参数数值分别为 m=2.282, k0=0.1429, k1=2.2456, k2=0.0038, k3=0.3170, k4=1.0033,公式对 a/W的适用范围为0.45 ~0.75. 图5给出了全塑性条件 J积分公式预测载荷位移曲线与有限元结果的对比,弹塑性条件下公式预测的载荷位移曲线与有限元的比 较由图6(a)给出. 图7(a)和图7(b)给出了弹塑性条件下公式预测的 J积分与有限元结果的对比.

显示原图| 下载原图ZIP| 生成PPT

图4   CT试样几何无关载荷位移曲线

Fig. 4   Geometry-independent load-displacement curves of CT specimen

显示原图| 下载原图ZIP| 生成PPT

图5   预测与计算的CT全塑性载荷-位移曲线比较

Fig. 5   Comparison of fully plastic load-displacement curves predicted by formula and those from FEA for CT specimen

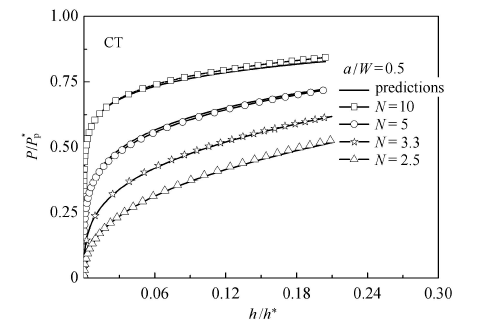
同理,本文还得到了SEB和SENT等其他5种试样 J积分统一公式的未知参数,表2给出了其参数数值,图6给出了SEB、SENT等试样 载荷位移曲线公式预测与有限元结果对比,图7给出了各试样构元在 CK=100MPa ~2 000 MPa, N=2.5~10时统一公式对J积分的预测结果与有限元对比.

Table 2

表 2

表 2   各类裂纹构元的J积分统一公式参数

Table 2   Unified formula parameters of J-integral for various cracked components

新窗口打开

显示原图| 下载原图ZIP| 生成PPT

图6   式(19)预测的弹塑性条件下载荷位移曲线与有限元比较

Fig.6   Comparison of elastoplastic load-displacement curves predicted by Eq.(19) with those from FEA

显示原图| 下载原图ZIP| 生成PPT

图7   式(23)预测的J积分与有限元结果比较

Fig. 7   Comparison of J-integral predicted by Eq.(23) with those from FEA

3 结 论

(1) 基于Chen-Cai能量等效假设,结合 J积分能量定义式,提出了一种解析求解I型裂纹构元 J积分的方法, 这种新方法 旨在针对一系列I型裂纹标准试样和非标准试样可以较易实现获得 J积分半解析的表达式,以便用于测试和断裂问题的理性分析.

(2)对于6种I型裂纹构元,通过有限元的计算给出了 J积分-载荷和载荷-位移统一公式的参数;依靠 J积分统一公式预测的 J积分结果相较有限元结果都吻合较好.

The authors have declared that no competing interests exist.

参考文献

文献选项

• 原文顺序
• 文献年度倒序
• 文中引用次数倒序
• 被引期刊影响因子